Driving Strategies for Omnidirectional Mobile Robots with Offset Differential Wheels

In this work we present some driving strategies for a type of omnidirectional mobile robot, the offset-differential robot. This system presents omnidirectionality while using any type of standard wheels, allowing for applications in all terrain. The work is based on the full kinematic and dynamic analysis of the robot, including the passive elements, to explain some unexpected behaviors that appear during its motion. The stable and unstable behaviors are characterized and some driving strategies are stated in order to achieve the desired performance regarding precise positioning and speed.

Keywords:

Subject: Engineering - Other

1. Introduction

Omnidirectional mobile robots are a desirable option in several robotics applications, especially when maneuvering in tight spaces or when extra dexterity is required.

Many of the current omnidirectional mobile robots are based on swedish, or omni wheels, see the recent reviews of [1] and [2]. These wheels, however, are not as robust as standard wheels for their application on rough terrains and outdoor applications; see for instance [3], where swedish wheels are modified to overcome some of their limitations. Active caster wheels are an attractive option because of their holonomy; the design of an actuated caster wheel can be found in [4], with a mobile platform with two independent steerable caster wheels. In a similar development, [5] designs a dual, steerable caster wheel with a differential gear mechanism. Other solutions accomplish the omnidirectionality by adding redundant degrees of freedom, see for instance [6], which in turn increases the cost and complexity in path planning and control.

One solution for omindirectionality while using standard wheels is the offset-differential robot. This type of robot has been called OmniKitty by [7], and Otbot by [8] and [9]. Our implementation is the MOBY platform, which was developed and patented at the Polythechnic University of Catalonia (UPC) [10], and is currently being used for logistics and other industrial applications. This kind of omnidirectional robots uses two standard wheels, offset from the center, and a third rotational degree of freedom about a vertical, centered axis. For practical considerations, the robot usually has a third omnidirectional point of support, usually a passive caster wheel, which is often overlooked in the analysis.

Because of its application in real tasks, MOBY presents a unique opportunity to study its behavior. The kinematics and dynamics of the robot were studied in [7] and [9]. The stability of these robots has many points in common with that of the differential robots for which the center of the robot, or the point to track, is not at the midpoint of the wheels, for instance when a look-ahead control is used. This was studied by Yun and Yamamoto in [11], where Lyapunov analysis is undertaken in order to find the stable and unstable configurations for a look-ahead control strategy. Pulling the robot, which they call driving backwards, becomes an unstable configuration. Also [12] proposes a tracking controller with an adaptive feedback linearization control, based on the same look-ahead strategy, which they extend to an inverse dynamics control with an adaptive PID in [13].

In this work, we expand the kinematic and dynamic analysis presented in [9] by including the effect of the auxiliary caster wheel, and we apply it to the MOBY design, to study the characteristics of the kinematic and dynamic behavior of this robot which appear when navigating in real terrains, and which are not intuitive. Unlike most of the publications for these robots, which aim to characterize and control only the stable internal -pushing- dynamics identified in [11], we optimize the behavior of this type of robots by developing also pull driving strategies, quantifying their differences. We compare the theoretical to the experimental results and propose techniques for its smooth and precise navigation.

2. Description of the Robot

The MOBY robot has three actuated degrees of freedom, with the aim of obtaining an omnidirectional mobile robot. The general structure of the robot is shown in the sketch at Figure 1. Unlike the differential wheeled robot, in which the two actuated wheels can spin independently in both directions and the difference between the speeds of the wheels steers the machine, MOBY has an extra actuated rotation about an axis perpendicular to the plane of motion and offset from the wheels. It is, basicallly, and offset differential robot plus a vertical rotation about a centered axis.

For the differential robot motion, the instant center of rotation is always found on the line of the axes of the wheels. The third vertical axis of MOBY allows to orient this line arbitrarily while keeping an independent orientation on the body of the robot. A caster wheel is also mounted on the base of the robot for stability.

This simple kinematic structure has been implemented in the MOBY robot that can be seen in Figure 2. It is important to notice that it is very simple to modify the type of wheels and platform to adapt this robot to indoors or outdoors applications, as seen in the figure.

3. Kinematic Analysis

The kinematic analysis of this type of robot can also be found in [7] and [9]. Here we take a very similar approach, adapting it to the particular geometry of the MOBY platform and adding the caster wheel and fork.

Let us consider the active wheels of the robot as subjected to the no-slip condition to simplify the initial analysis. We define the chassis as the differential wheels with their common axis and the structure which connects it to the platform.

The following generalized velocities describe the controlled velocities of MOBY:

The angular velocity of the right wheel, ${\dot{α}}_{R}$ (denote the angular position of the right wheel as $α_{R}$ ).
The angular velocity of the left wheel ${\dot{α}}_{L}$ , denoting $α_{L}$ as its angular position from a reference.
The angular velocity of the platform about the vertical axis $\dot{φ}$ with respect to the chassis, with angular position of the platform with respect to the chassis $φ$ .

Additionally, the following parameters, generalized coordinates and velocities will be used to describe its kinematics:

The position vector of the center of the robot with respect to a fixed frame, p = ${x, y}$ and its derivative $\dot{p} = {\dot{x}, \dot{y}}$ .
The angular position of the platform with respect to the fixed frame, $θ_{p}$ and its corresponding angular velocity ${\dot{θ}}_{p}$ .
The angular position of the chassis with respect to the fixed frame, $θ_{c}$ and its derivative ${\dot{θ}}_{c}$ .
The radius of the actuated wheels, R
The distance between the rotation axis of the actuated wheels and the vertical rotation axis, $d_{1}$ .
The distance between the actuated wheels, $d_{2}$ .

Notice that with the definitions of these variables, the actuated rotation

φ

can be expressed as a function of

θ_{c}

and

θ_{p}

as shown in Figure 3,

φ = θ_{p} - θ_{c} .

(1)

The wheels of the MOBY platform are standard fixed wheels, which impose the following constraints on the motion of the robot:

\dot{x} - (\frac{R cos (θ_{c})}{2} + \frac{R d_{1} sin (θ_{c})}{d_{2}}) {\dot{α}}_{L} - (\frac{R cos (θ_{c})}{2} - \frac{R d_{1} sin (θ_{c})}{d_{2}}) {\dot{α}}_{R} = 0,

(2)

\dot{y} - (\frac{R sin (θ_{c})}{2} - \frac{R d_{1} cos (θ_{c})}{d_{2}}) {\dot{α}}_{L} - (\frac{R sin (θ_{c})}{2} + \frac{R d_{1} sin (θ_{c})}{d_{2}}) {\dot{α}}_{R} = 0 .

(3)

A third constraint transmits the angular velocity of the platform motor from the chassis to the platform,

{\dot{θ}}_{c} + \dot{φ} - {\dot{θ}}_{p} = 0,

(4)

enforcing Equation (1). Applying the relation in Equation (10) to Equation (4), the constraint can be rewritten as

\frac{R}{d_{2}} {\dot{α}}_{R} - \frac{R}{d_{2}} {\dot{α}}_{L} + \dot{φ} - {\dot{θ}}_{p} = 0,

(5)

to explicitly show the relation between

{\dot{θ}}_{p}

and the actuated variables of the system.

To take the dynamic effects of the caster wheel assembly into account, additional variables have to be detailed:

The distance from the center of the platform to the joint of the caster fork, $d_{4}$ .
The length of the caster fork from its joint to the axis of the caster wheel, $d_{3}$ .
The radius of the caster wheel, $R_{c}$ .
The angle of the caster fork with respect to the chassis, $β$ .
The rotational velocity of the caster wheel, ${\dot{α}}_{c}$ .

These variables also allow for the non-holonomic constraints of the caster wheel assembly to be applied as described in Siegwart & Nourbakhsh [14]. The fourth constraint dictates the velocity of the caster fork as a function of the velocity and configuration of the robot. The fifth and final constraint imposes the no-slip condition on the caster wheel,

\begin{matrix} cos (β + θ_{c}) \dot{x} + sin (β + θ_{c}) \dot{y} - \frac{R}{d_{2}} (d_{3} + d_{4} sin β) {\dot{α}}_{L} + \\ \frac{R}{d_{2}} (d_{3} + d_{4} sin β) {\dot{α}}_{R} - d_{3} \dot{β} = 0, \end{matrix}

(6)

and

sin (β + θ_{c}) \dot{x} - cos (β + θ_{c}) \dot{y} + \frac{d_{4} R cos β}{d_{2}} {\dot{α}}_{L} - \frac{d_{4} R cos β}{d_{2}} {\dot{α}}_{R} - {\dot{α}}_{c} R_{c} = 0 .

(7)

3.1. Forward kinematics

The Jacobian matrix is used to model the relation between the three motors of the robot and its twist relative to the fixed frame of reference. Consider

W = {\dot{x}, \dot{y}, \dot{θ_{p}}}

the twist of the platform with respect to the fixed frame. Then, the Jacobian matrix

[J]

satisfies the equation

[\begin{matrix} \dot{x} \\ \dot{y} \\ {\dot{θ}}_{p} \end{matrix}] = [\begin{matrix} J \end{matrix}] [\begin{matrix} {\dot{α}}_{L} \\ {\dot{α}}_{R} \\ \dot{φ} \end{matrix}] .

(8)

The wheel constraints in Equation (2) and Equation (3), together with the relation between the orientation of the chassis, platform and vertical degree of freedom in Equation (5), form the Jacobian matrix.

[J] = [\begin{matrix} \frac{R cos θ_{c}}{2} + \frac{R d_{1} sin θ_{c}}{d_{2}} & \frac{R cos θ_{c}}{2} - \frac{R d_{1} sin θ_{c}}{d_{2}} & 0 \\ \frac{R sin θ_{c}}{2} - \frac{R d_{1} cos θ_{c}}{d_{2}} & \frac{R sin θ_{c}}{2} + \frac{R d_{1} cos θ_{c}}{d_{2}} & 0 \\ - \frac{R}{d_{2}} & \frac{R}{d_{2}} & 1 \end{matrix}] .

(9)

Applying the no-slip condition it is observed that the orientation of the chassis is a function of the position of the wheels,

θ_{c} = {θ_{c}}_{0} + \frac{R (α_{R} - α_{L})}{d_{2}},

(10)

where

{θ_{c}}_{0}

is the starting orientation of the chassis, and the initial values of

α_{R}

and

α_{L}

should be zero.

3.2. Inverse kinematics

For the inverse kinematics, the desired relation is

[\begin{matrix} {\dot{α}}_{L} \\ {\dot{α}}_{R} \\ \dot{φ} \end{matrix}] = [\begin{matrix} J^{- 1} \end{matrix}] [\begin{matrix} \dot{x} \\ \dot{y} \\ {\dot{θ}}_{p} \end{matrix}] .

(11)

In the above expression,

[J^{- 1}]

is the inverse of the previously computed Jacobian matrix, which can be calculated to obtain the matrix

[J^{- 1}] = [\begin{matrix} \frac{2 d_{1} cos θ_{c} + d_{2} sin θ_{c}}{2 R d_{1}} & \frac{2 d_{1} sin θ_{c} - d_{2} cos θ_{c}}{2 R d_{1}} & 0 \\ \frac{2 d_{1} cos θ_{c} - d_{2} sin θ_{c}}{2 R d_{1}} & \frac{2 d_{1} sin θ_{c} + d_{2} cos θ_{c}}{2 R d_{1}} & 0 \\ \frac{sin θ_{c}}{d 1} & - \frac{cos θ_{c}}{d 1} & 1 \end{matrix}] .

(12)

3.3. Passive degrees of freedom

To integrate the response of the caster assembly with the velocities of the other degrees of freedom of the robot, the Jacobian matrix is expanded, adding two lines to

[J]

. To produce this expanded Jacobian, Equations 6 and 7 must be expressed in terms of variables

{\dot{α}}_{L}

{\dot{α}}_{R}

, and

\dot{φ}

. From the rewritten expressions,

\dot{β}

and

{\dot{α}}_{c}

are isolated and the derivatives of their definitions incorporated into the expanded Jacobian,

[J_{d i r}]

[J_{d i r}] = [\begin{matrix} \frac{R cos θ_{c}}{2} + \frac{R d_{1} sin θ_{c}}{d_{2}} & \frac{R cos θ_{c}}{2} - \frac{R d_{1} sin θ_{c}}{d_{2}} & 0 \\ \frac{R sin θ_{c}}{2} - \frac{R d_{1} cos θ_{c}}{d_{2}} & \frac{R sin θ_{c}}{2} + \frac{R d_{1} cos θ_{c}}{d_{2}} & 0 \\ - \frac{R}{d_{2}} & \frac{R}{d_{2}} & 1 \\ - \frac{R (2 d_{3} - d_{2} cos β + 2 d_{1} sin β + 2 d_{4} sin β)}{2 d_{2} d_{3}} & \frac{R (2 d_{3} + d_{2} cos β + 2 d_{1} sin β + 2 d_{4} sin β)}{2 d_{2} d_{3}} & 0 \\ \frac{R (2 d_{1} cos β + 2 d_{4} cos β + d 2 sin β)}{2 R_{c} d_{2}} & - \frac{R (2 d_{1} cos β + 2 d_{4} cos β - d_{2} sin β)}{2 R_{c} d_{2}} & 0 \end{matrix}] .

(13)

The expanded Jacobian provides the expected values of velocities

\dot{β}

and

{\dot{α}}_{c}

[\begin{matrix} \dot{x} \\ \dot{y} \\ {\dot{θ}}_{p} \\ \dot{β} \\ {\dot{α}}_{c} \end{matrix}] = [\begin{matrix} J_{d i r} \end{matrix}] [\begin{matrix} {\dot{α}}_{L} \\ {\dot{α}}_{R} \\ \dot{φ} \end{matrix}] .

(14)

Notice that this Jacobian matrix is not square and thus no longer invertible. The expanded inverse Jacobian is obtained by repeating the previous process, this time using

[J^{- 1}]

as a starting point and expressing Equations 6 and 7 in terms of the task space variables:

\dot{x}

\dot{y}

, and

{\dot{θ}}_{p}

. The resulting matrix,

[J_{i n v}]

satisfies Equation (15), which produces the response of all the degrees of freedom of the system to a velocity command expressed in the task space,

[\begin{matrix} {\dot{α}}_{L} \\ {\dot{α}}_{R} \\ \dot{φ} \\ \dot{β} \\ {\dot{α}}_{c} \end{matrix}] = [\begin{matrix} J_{i n v} \end{matrix}] [\begin{matrix} \dot{x} \\ \dot{y} \\ {\dot{θ}}_{p} \end{matrix}],

(15)

with

\begin{matrix} [J_{i n v}] = \\ [\begin{matrix} \frac{2 d_{1} cos θ_{c} + d_{2} sin θ_{c}}{2 R d_{1}} & \frac{2 d_{1} sin θ_{c} - d_{2} cos θ_{c}}{2 R d_{1}} & 0 \\ \frac{2 d_{1} cos θ_{c} - d_{2} sin θ_{c}}{2 R d_{1}} & \frac{2 d_{1} sin θ_{c} + d_{2} cos θ_{c}}{2 R d_{1}} & 0 \\ \frac{sin θ_{c}}{d 1} & - \frac{cos θ_{c}}{d 1} & 1 \\ \frac{2 d_{1} cos (β + θ) + d_{4} cos (β + θ_{c}) - 2 d_{3} sin θ_{c} - d_{4} cos (β - θ_{c})}{2 d_{1} d_{3}} & \frac{2 d_{1} sin (β + θ_{c}) + d_{4} sin (β + θ_{c}) + 2 d_{3} cos θ_{c} + d_{4} sin (β - θ_{c})}{2 d_{1} d_{3}} & 0 \\ \frac{2 d_{1} sin (β + θ_{c}) + d_{4} sin (β + θ_{c}) - d_{4} sin (β - θ_{c})}{2 R_{c} d_{1}} & - \frac{2 d_{1} cos (β + θ_{c}) + d_{4} cos (β + θ_{c}) + d_{4} cos (β - θ_{c})}{2 R_{c} d_{1}} & 0 \end{matrix}] . \end{matrix}

(16)

4. Kinematic Behavior

The main phenomenon of interest is the instability described by Yun & Yamamoto [11]. It is most obvious when the machine is commanded to move with its actuated wheels in front, that is, with the wheels pulling the chassis rather than pushing it. In the cited analysis, the authors found that the robot has two equilibrium points. The first equilibrium point is the configuration in which the center of the robot and the midpoint of the axis of the active wheels are aligned in the direction of motion, with the wheels behind the center of the robot. This state can be called pure push, and it is a stable equilibrium point. If the robot is commanded to move in a straight line it will gradually reach this state.

Unlike the first first equilibrium point, the second equilibrium point is unstable. In this state, the wheels are ahead of the center of the robot. This unstable state can be called pure pull. With a minimal disturbance, the angle between the chassis and the direction of motion will grow until they are perpendicular; at that point, the robot will start pushing and eventually reach the pure push state, as shown in Figure 5.

An easy solution is to avoid driving from this unstable equilibrium point; however, for rough terrains, such as the agricultural ground, the pulling maneuver is advantageous. One easy way to see this is to consider the situation in which the robot has to climb a small obstacle with the caster wheel in front, which will create a jamming effect, as opposed to climbing with the active wheels in front.

Mathematically, the push-pull region of the velocity can be determined using the dot product of the current velocity and the direction of neutral steering. Assuming that the robot has a velocity of magnitude greater than zero, the cosine of

γ

in Equation (17) will be positive when the velocity is in the push region, negative when in the pull region, and zero in the specific case of neutral steering. The particular cases of pure push and pure pull will yield 1 and −1, respectively.

Figure 6. Regions and main directions of the robot. The compensation region is defined by the user and can even include part of the push region. The dark red arrow shows an example of a velocity in the push region.

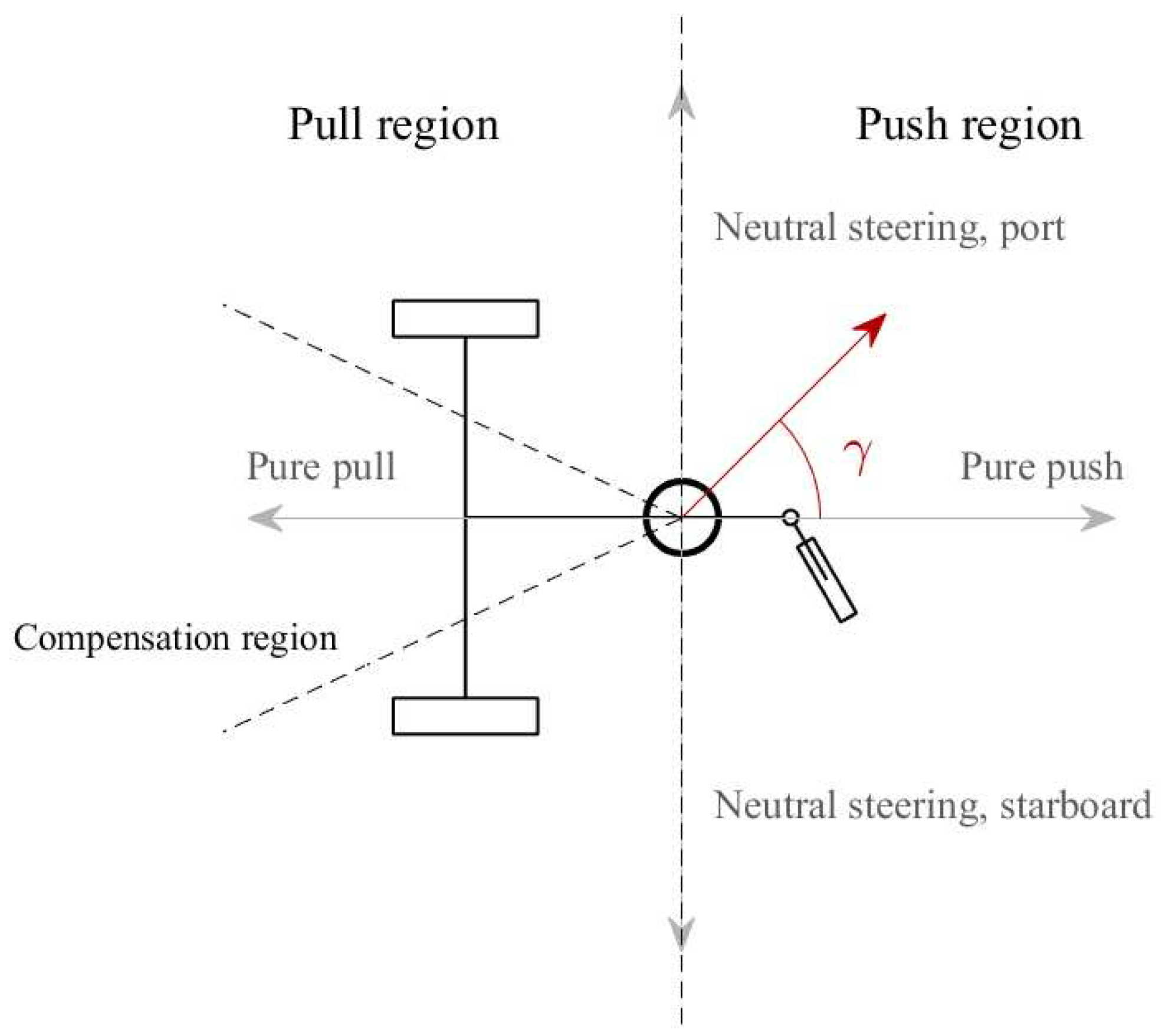
The name neutral steering is given to the two particular velocities perpendicular to pure push/pull. These directions are of special interest since they present the tightest possible continuous turn radius achievable without alternating regions. During such a turn, the instant center of rotation of the chassis will be located at the midpoint between the two actuated wheels. This will result in their velocities having the same magnitude but opposite directions.

cos γ = \frac{{([R o t (θ_{c})] [\begin{matrix} 1 \\ 0 \end{matrix}])}^{T} [\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}]}{c},

(17)

where

[\begin{matrix} R o t (θ) \end{matrix}] = [\begin{matrix} cos θ & - sin θ \\ sin θ & cos θ \end{matrix}] .

(18)

The speed at which the chassis approaches the pure push state when moving continuously in the positive x direction can be found through the relations defined by the inverse kinematics and the derivative of expression 10. The wheel speeds

{\dot{α}}_{L}

and

{\dot{α}}_{R}

expressed in terms of

\dot{x}

and

\dot{y}

are substituted in the velocity of the chassis,

{\dot{θ}}_{c} = \frac{R ({\dot{α}}_{R} - {\dot{α}}_{L})}{d_{2}} = - \frac{sin θ_{c}}{d_{1}} \dot{x} .

(19)

Assuming a situation in which the robot is reversing in a straight line, a more general case can be obtained expressing the desired velocity in a frame of reference aligned with the chassis,

\dot{γ} = - \frac{sin γ}{d_{1}} c,

(20)

where

γ

is the angle between the pure push direction and the direction of the desired velocity, and c is the magnitude of the velocity of the robot. Note that both sides of the expression can be divided by c, yielding

\frac{1}{R_{t u r n}} = - \frac{sin γ}{d_{1}},

(21)

which details the instant radius of turn of the robot during the reversal. This points to the trajectory being independent of the magnitude of the velocity.

If the robot is going in a straight line,

\dot{γ}

would ideally be zero. Assuming

d_{1}

is fixed and c is decided by the operator, the only way to influence

\dot{γ}

is by changing the angle between the chassis frame of reference and the desired velocity. Taking advantage of this, the velocity vector may simply be rotated so that it is aligned with the chassis frame of reference. This would stop the progress of the reversal. However, considering Equation (20), when the robot is in the push region with the same value of c, it is evident that the rate at which the spontaneous turn of the chassis accelerates is the same at which it slows down when approaching pure push. Using this knowledge, it becomes clear that there are velocities that can not only halt the progress of the turn, but reverse it. Therefore, it can be inferred that there is a value of

γ

that yields the opposite to the current value of

\dot{γ}

Considering only cases in the pull region,

γ \in (\frac{π}{2}, \frac{3 π}{2})

, the direction which corrects the attitude of the chassis is

- γ

. Thus, to rectify the orientation of the chassis, the velocity is mirrored along the x axis of the chassis frame of reference.

Because the correction is prescribed through modifying the task space velocities, it leads to inaccuracies in the trajectory. Ways of mitigating the error between corrected and planned trajectories are discussed in the following section.

The earlier the tendency to switch the chassis is corrected, the smaller is the change in trajectory. If the trend to push is continuously corrected, it will not proliferate provided that there are no significant unexpected forces involved. This was not the case in the simulation shown in Figure 7, in which

γ

was allowed to grow freely from the beginning of the motion to the red arrow.

Figure 7. Corrected motion of the chassis when reversing. The red arrow shows the point in the trajectory (dashed black line) where the correction starts being applied. The dashed green line shows the originally intended trajectory.

This approach can be extended to any trajectory by matching

\dot{γ}

to the instant angular velocity of the chassis. This generalization requires the introduction of an additional variable,

γ_{g o a l}

, which is the angle of the velocity with respect to the chassis when the robot is moving in a circular trajectory. It can be found using the relation

γ_{g o a l} = π - {sin}^{- 1} (\frac{d_{1} ω}{c}),

(22)

where

ω

is the angular velocity of the robot with respect to its instant center of rotation (positive is counter-clockwise). The corrected velocity vector is produced by mirroring the input velocity along an axis passing through the center of the robot with angle

γ_{g o a l}

with respect to the input velocity.

{[\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}]}_{c o r r e c t e d} = [R o t (θ_{c} + γ_{g o a l})] [\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}] {[R o t (θ_{c} + γ_{g o a l})]}^{T} {[\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}]}_{i n p u t}

(23)

The chosen approach, to mirror the direction of the velocity without changing its magnitude, returns the chassis to its target orientation at the same rate as it left it assuming that the change of region was purely kinematic. If the disturbance that initiated the reversal was dynamic in nature, the maximum torque that the motors can provide may prevent the robot from matching the growth of angular velocity. In that case, the robot will return to the desired configuration as rapidly as the motors allow attempting to maintaining the target speed.

To avoid returning to the pull region unnecessarily, a compensation region is defined, beyond which the compensation algorithm is not applied. The compensation region is unlike the other regions in the sense that its bounds can be set arbitrarily and change during the motion. For instance, if loss of traction on the wheels or tipping over are concerns, the compensation region may change depending on the velocity of the robot. An example of a possible compensation region can be seen in Figure 6.

To better observe the compensation algorithm in action, the simulation shown in Figure 8 introduces unanticipated forces in the shape of blows to the fork of the caster wheel. In the following simulation, the impact is simulated as a 4000 N force acting on the fork of the caster wheel during 25 ms. The direction of the force is perpendicular to the chassis and roughly towards the center of rotation.

As can be seen in Figure 8, the compensation only returns the chassis to the predetermined orientation. This is enough to prevent the spontaneous change of region, but getting the robot to go back to the path requires a recalculation of the trajectory to accommodate the merging back into the original path.

Looking further into expression 23 and introducing a definition for

γ_{e r r}

, which is the difference of

γ

and

γ_{g o a l}

, it is apparent that the same effect may be achieved by rotating the input velocity vector two times the opposite of

γ_{e r r}

. Note that, while the result of Eqs. 23 and 24 is the same, the transformations are not equivalent.

{[\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}]}_{c o r r e c t e d} = [R o t (- 2 γ_{e r r})] {[\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}]}_{i n p u t}

(24)

A more general expression can be written as shown in Equation (25), in which k determines the aggressiveness of the compensation, ranging from 0 (no compensation at all) through to 1 (only stopping the progress of the switch but not returning to the desired configuration) and from then returning to the desired configuration faster the higher the value of k. The compensation region should be smaller the higher the value of k to avoid ineffective compensation.

{[\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}]}_{c o r r e c t e d} = [R o t (- k γ_{e r r})] {[\begin{matrix} \dot{x} \\ \dot{y} \end{matrix}]}_{i n p u t}

(25)

5. Driving Strategy

The insight gained from the kinematic and dynamic analysis has been used to design maneuvers so that the robot will be in the pull region for extended periods of time. In order to avoid a region change, two rules have emerge from previous sections:

The trajectory must be smooth, that is, it must be continuous as well as continuously differentiable. This extends to the initial position of the robot. The vector analogous to the pure pull direction must be tangent to the velocity at the starting point; otherwise, significant compensation will be necessary to remain in the pull region long-term. If the first part of the path is curved, $γ$ and $γ_{g o a l}$ should be equal.
Turns with a radius smaller than $d_{1}$ are possible but should be avoided. While momentarily turning tightly does not guarantee a change in velocity region, sustained rotation with such a small radius will eventually result in a change of the direction of the chassis.

In addition to disturbances due to the terrain, the instability manifests inherently due to the fact that commands cannot be given to the motors in a perfectly continuous manner. Every slight change in desired turn radius will result in a small lateral shift, even if

γ_{g o a l}

and

γ

where equal in the previous instant. The lower the refresh rate and the more sudden the change in turn radius, the more deviation is to be expected. For this reason, the trajectory should be recalculated periodically to adapt to changes brought on by compensations during the motion. The more important precision is to the particular application, the more often trajectories should be amended to redress the lateral deviation caused by the compensation algorithm. These recalculations may concern only a small part of the path and lead the robot to rejoin the original route or entail the recomputation of the entire motion.

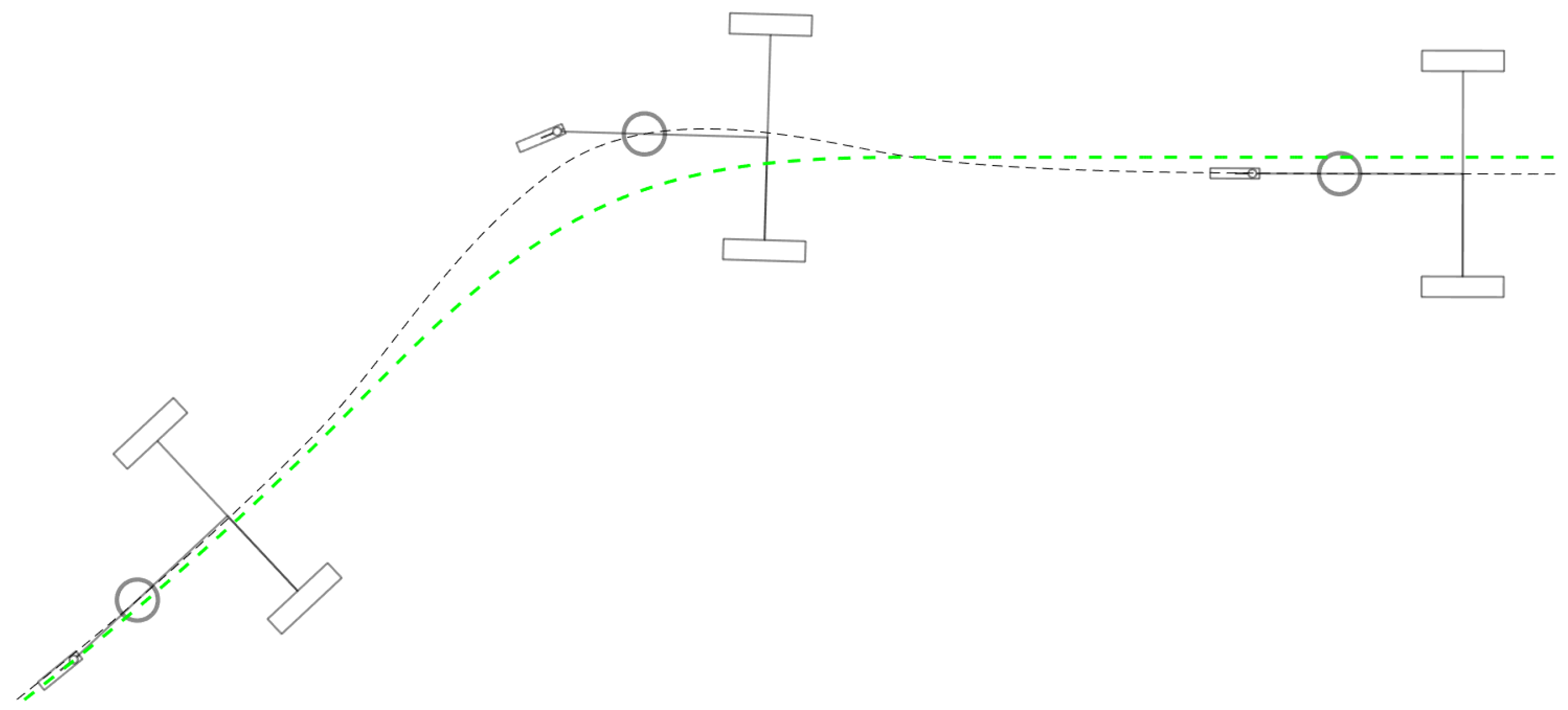
General trajectories with changing curvature will always exhibit unstable behavior, even on smooth, continuous motion. One easy way of defining a viable trajectory involves concatenating a series of arcs which are tangent to each other at the points where they meet. In this case, the first arc would need to be tangent to the direction of the robot at its starting point.

An interesting characteristic of the motion is that the progress of the switch in chassis orientation is independent of the velocity, as evidenced by Equation (21). This means that, absent any dynamic effects, the trajectories which are consistent with the first two rules can be executed at any speed allowed by the actuators.

Another kinematically viable strategy is to always keep the instant center of rotation on the axis of the actuated wheels of the previous instant. This is also accomplished by building a trajectory of concatenating arcs. This time, there is a discontinuity in the velocity each time a the robot passes from one arc to the next. Instead, what is kept track of is the orientation of the chassis and the direction of the center and radius of the turn is calculated so that

γ_{g o a l}

and

γ_{r e a l}

remain equal during the motion, absent any disturbances. This method solves the otherwise inherent need to compensate every time the radius of turn of the trajectory changes, at the cost of decreased maneuverability. Additionally, if the instant radius changes too suddenly, it will result in large on-the-spot wheel velocity variations. Such changes not only lead to spikes in needed torque, but may also cause the friction force between the tires and the ground to exceed the static friction threshold and slide. One last disadvantage of this method is that it only deals with the kinematic causes of the error of

γ

, meaning that other sources, such as external forces, remain.

Figure 10. Detail of the previous figure showing how tighter turns are prone to cause an increase in position error due to the discreet nature of the velocity commands.

6. Dynamic Model

MOBY’s dynamics were modelled using the Lagrangian formulation. To do so, a few more variables have been defined:

The mass $m_{c}$ and moment of inertia $I_{c}$ of the chassis (excluding the actuated wheels).
The mass $m_{W}$ and moments of inertia $I_{W}$ of the actuated wheels, which are assumed to be the same for both.

-

$I_{W, a x}$ is the moment of inertia of the wheel spinning through its axis

-

$I_{W, r a d}$ is the moment of inertia as it relates to the contribution of the wheel when the whole chassis is rotating. It is calculated as the moment of inertia of the wheel spinning about its radius plus the additional inertia brought about by the distance from the center of rotation of the chassis, which is taken into account through the parallel axis theorem.
The mass $m_{p}$ and moment of inertia $I_{p}$ of the platform.
The mass $m_{c f}$ and moment of inertia $I_{c f}$ of the castor fork.
The mass $m_{c w}$ and moments of inertia $I_{c w, a x}$ and $I_{c w, r a d}$ of the castor wheel.

The distance between the centers of mass of the actuated wheels is considered the same as the distance between the centers of their tires,

d_{2}

The present case involves the robot moving on flat, even ground, which makes the potential energy term of the Lagrangian null.

The mass matrix of the system, M, is calculated using the definition of the kinetic energy of the bodies like in [9]. The Coriolis matrix, C, was calculated using the Christoffel symbols of the first kind method [15]. The five constraints applied on the robot are written as Pfaffian constraints [16] such that:

A (q) \dot{q} = 0

(26)

Here,

A (q)

is a 5-by-8 constraint Jacobian and q is a vector containing the degrees of freedom of the system. q can be divided between active,

q_{A} = (α_{L}, α_{R}, φ)

, and passive variables,

q_{P} = (x, y, θ_{p}, β, α_{c})

. These vectors come together to form q, the 8-by-1 vector that contains all the variables in the order

q = (q_{A}, q_{P})

. This leads to Equation (27).

τ = M (q) \ddot{q} + C (q, \dot{q}) \dot{q} + A {(q)}^{T} λ

(27)

Where

λ

is a vector containing the Lagrange multipliers. From Equation (27), the forward dynamics are easily solved.

6.1. Forward dynamics

\ddot{q} = M^{- 1} (τ_{u} + τ_{f} + F_{e x t} - C \dot{q} - A^{T} λ)

(28)

Note that in the previous expression, the general force term

τ

has been replaced by a term containing the torque supplied by the three motors,

τ_{u}

, and a term outlining the dynamic contribution of friction on all the joints affected by it,

τ_{f}

. An additional force vector,

F_{e x t}

has also been included in order to introduce external forces on any of the degrees of freedom.

6.2. Inverse dynamics

As shown in [9], the calculation of the Lagrange multipliers can be conveniently bypassed in the inverse dynamics. Considering the nature of

τ_{u}

τ_{u} = [\begin{matrix} τ_{u, α_{L}} \\ τ_{u, α_{R}} \\ τ_{u, φ} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}] = [\begin{matrix} I_{3 \times 3} \\ 0_{5 \times 3} \end{matrix}] [\begin{matrix} τ_{u, α_{L}} \\ τ_{u, α_{R}} \\ τ_{u, φ} \end{matrix}] = T_{u} u,

(29)

the dynamic equilibrium equation can be rewritten as shown in Equation (30).

In the previous equation,

T_{u}

is the input tensor that maps the control variables, u, to the coordinates of the system [17]. Note that the external forces in Equation (30) include only those which can be anticipated.

u = [\begin{matrix} I_{3 \times 3} & 0_{3 \times 5} \end{matrix}] [\begin{matrix} T_{u} & - A^{T} \end{matrix}] (M \ddot{q} + C \dot{q} - τ_{f} - F_{e x t}) .

(30)

In the simulations, the friction on the joints of the robot is approximated using a viscous friction model,

τ_{f} = [\begin{matrix} c_{α_{L}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & c_{α_{R}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & c_{φ} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & c_{β} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & c_{α_{c}} \end{matrix}] \dot{q} .

(31)

7. Simulations

The dynamic model of the robot has been used to understand the impact of the kinematic instability of the robot on the torque needed to comply with the velocity commands. In addition the modelling of the caster wheel also allows for the analysis of its own contribution to the system.

Two simulations have been carried out to these ends, using the mass properties presented in [8] for comparison. Both start with the chassis of the robot anti-parallel to x and an angle

β = 0

. For the first simulation, the instability is allowed to progress freely. The second run applies the compensation algorithm since the beginning of the movement. The raw velocity commands are the same for both, constantly accelerating during the first quarter of the simulation, holding a velocity

c = 1.2 m / s

and decelerating at the same rate during the final part. The configuration of the robot during the first test can be seen in Figure 5.

For clarity, the simulations have been conducted without friction. The simulated total mass of the robot is around 130 kg, including

m_{c f} = 0.5 k g

of the caster fork and

m_{c w} = 0.7 k g

of the caster wheel. The moment of inertia of the chassis is

I_{c} = 1.3 k g m^{2}

. In addition, the moments of inertia of the actuated wheels and the components of the caster wheel are also considered for all directions in which they rotate.

In all simulations, the refreshing rate of the engines was 1000 Hz, as was the refreshing rate of the dynamics calculations. The time-integration scheme used was the forward Euler.

7.1. Dynamic implications of the spontaneous region switch

During the switch shown in Figure 5, the robot must quickly alter the velocity of its motors to maintain the velocity of the center. To do so, large torques need to be supplied to the actuated wheels, as can be seen in the left graph of Figure 11. Also note that, besides the effect of the caster wheel, the torque profile is the same when accelerating and slowing down. This is due to the chassis rotating 180º through the second stage of the motion.

When correcting the rotation of the chassis, the torques are those presented in the right graph of Figure 11. The three phases of the motion are plainly visible; acceleration, holding

c = 1.2 m / s

, and coming to a stop.

In the first simulation, the greatest torque required by any of the wheels was

τ_{u, α_{R}} = 12.38 N m

, whereas the same value for the second simulation was

τ_{u, α_{L}} = 5.22 N m

. In addition, the combined friction with the ground needed by all three wheels to execute the motion, shown in Figure 12 was much greater in the first run, reaching 225.1 N. Had there been no reversal, the maximum necessary static friction would have been 94.5 N.

This points to another issue as a consequence of the instability, the fact that the required force between the ground and tires may exceed the maximum stiction.

7.2. Dynamic effects of the caster wheel

The caster wheel presents an instability in some ways analogous to the offset differential drive. The main difference being that it is not active. As such, what dictates its behaviour is the movement of the point in the chassis connected to the caster fork with a revolute joint. This motion, through the constraints defined in Eqs. 6 and 7, informs the response of the constrained degrees of freedom

β

and

α_{c}

In the case of the previous simulations, the low velocity of the robot at the beginning of the motion means that the torques that the motors need to produce to make up for the increased resistance due to the position of the caster wheel are relatively small.

Nonetheless, there are cases in which the caster wheel can have a greater impact on the dynamics of the whole system. An example is the common case in which the robot is moving in the pure push direction and then is ordered to move in the pure pull direction. The caster wheel is then in an unstable equilibrium with a value of

β = - \frac{π}{2}

. Granted that there are no notable disturbances, the robot can reach significant speeds while the caster wheel remains in or close to the unstable equilibrium point.

Despite being far less massive, the instability of the caster wheel assembly may have an impact on the torques needed by the wheels comparable to that of the whole chassis. In the situation described in Figure 14, the caster fork stays in its unstable equilibrium point during the acceleration phase and suddenly comes out of it during the constant velocity stage. In this simulation, the peak torque is

τ_{u, α_{R}} = 12.38 N m

, which is supplied to the right wheel.

Another important consequence of the dynamics of the caster wheel is its potential to initiate a region switch. As long as the velocity commands are discrete, the response of the motors to the rotation of the caster wheel is always slightly off. If left uncorrected, the deviation induced by the caster wheel has the potential to greatly accelerate the progress of the region switch.

8. Experimental Results

Two experiments were conducted. In both, the robot depicted in Figure 2 was ordered to move forward 2 meters and then back. By doing so, it was ensured that the return half of the itinerary begins in the pull region. During the the journey back to its starting point, the robot is "hit" by two impulses of alternating direction. These simulated impacts are short velocity commands perpendicular to the motion of the robot.

In the first test, the robot is allowed to react naturally. In the second test, the compensation algorithm is implemented so that the robot may recover its original chassis orientation.

The distance between the center of the robot and the wheel axis in Figure 1 in the case of the real robot is

d_{1} = 0.145 m

. Commands are given to the real robot once every 4 ms.

8.1. Uncompensated pull-region motion

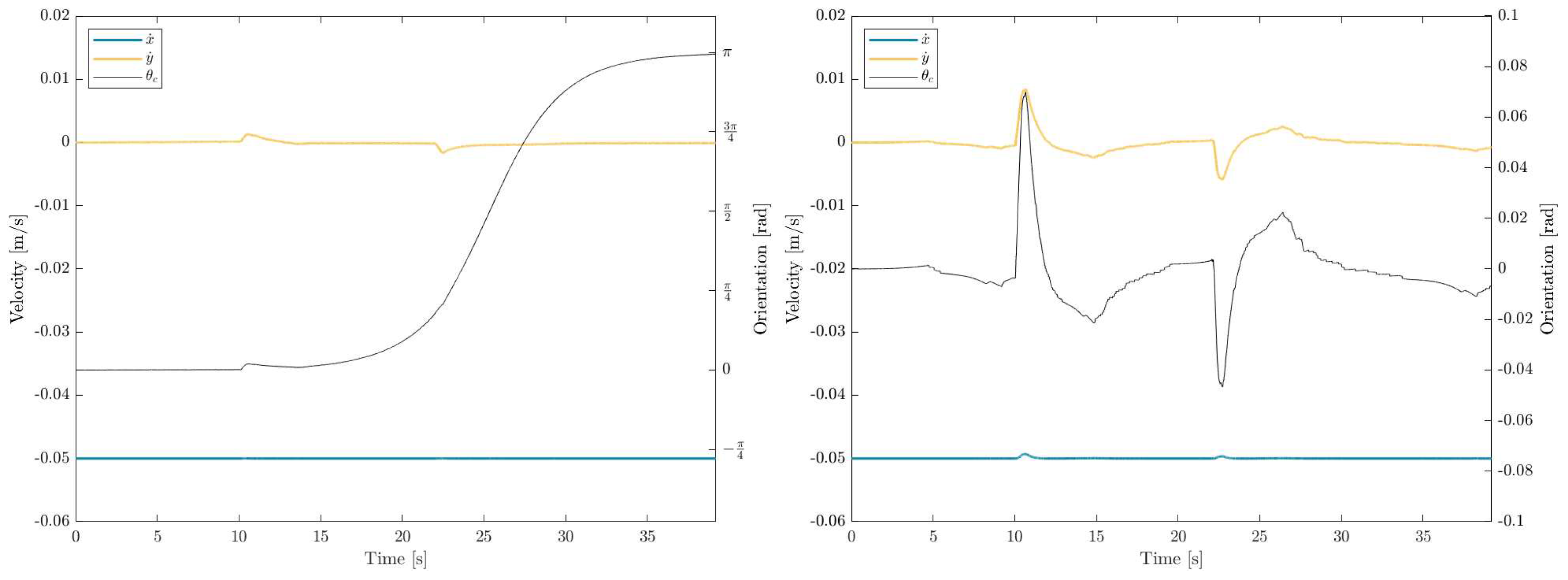
The robot was ordered to move forward 2 m at a velocity of

c = 0.05 m / s

. Then, the velocity is reversed. After 10 seconds, an order is given to add a perpendicular component of

0.5 m / s

to the velocity during 0.4 seconds. 22 seconds into the reverse motion, the same order is given but towards the other side.

As expected, the first disturbance was more than enough to initiate the turn.

8.2. Compensated pull-region motion

The previous experiment was repeated, this time with the compensation on. In addition, the duration of the "hits" was doubled to allow the perpendicular velocity to grow more than it had in the previous test.

In this run, the perpendicular velocities make the magnitude of

θ_{c}

increase as the robot gets shoved. However, as soon as the disturbance ceases, the chassis quickly recovers its original heading.

9. Conclusions

There are clear advantages to the use of the unstable pull region in the operation of offset differential drive robots. From simple increases in speed in certain situations, to reducing the risk of getting stuck while navigating difficult terrain. In the context of agricultural applications, advancing with the bigger actuated wheels in front makes soft and irregular ground easier to traverse. In these conditions, driving with the actuated wheels first is easier not only on account of their larger diameter, but also because they actually use the terrain to propel themselves, instead of just being pushed or pulled like passive wheels.

As shown in the simulations, the cost of allowing the robot to choose freely its velocity region can have detrimental effects on its odometry and precision of its movement. Often, this would mean to have to choose not only between precision and velocity, but also safety, as a loss of traction in the wheels can endanger the robot and its environment.

As a result of the instability inherent to the design, constant corrections are necessary to remain in the pull region. These corrections can be successfully applied using the methods described in this paper. These methods can be generalized to a broad range of trajectories, encompassing most situations. However, trajectories involving fast, tight turns and great variations in turning speed are susceptible to noticeable position error. In these circumstances, there is still a decision to be made between speed and precision, but the risks of losing traction or not having the adequate capacity to supply the necessary torque to the wheels are similar to those suffered by the robot in its pure pull (or equivalent) direction. If the robot is left unmonitored, there is the possibility of a region switch being produced at an unexpected point, greatly increasing the chance of failing to perform as called for.

Lastly, the dynamic effect of the caster wheel has been considered, opening the door to torque control for the offset differential drive robot structure. The inclusion of the caster wheel assembly in the dynamic model has proven especially relevant to understand the way it can contribute to the convergence to the stable equilibrium of the robot by accelerating it. For an accurate calculation of torques, knowing the orientation of the caster wheel, for instance with an encoder, may be necessary.

When it comes to avenues for future research, path planning and control algorithms that comply with the conditions outlined in Section 5 and return the robot to its original trajectory will be necessary for most applications that make use of the strategies described in this paper. The dynamic model can also serve as the basis for more research into issues that MOBY-like machines may run into, like loss of traction, tipping over when turning, driving up slopes, and getting wheels unstuck in agricultural settings.

Acknowledgments

This research was supported in part by award TED2021-131877B-I00 and award PDR 2014-2022.... The contents are solely the authors’ responsibility.

References

Jacobs, T. Omnidirectional Robot Undercarriages with Standard Wheels – A Survey. In Proceedings of the 25th IEEE International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Stuttgart, Germany, 20-22 November 2018. [Google Scholar] [CrossRef]
Taheri, H.; Zhao, C. Omnidirectional mobile robots, mechanisms and navigation approaches. Mechanism and Machine Theory 2020, 153, 103958. [Google Scholar] [CrossRef]
Ramirez-Serrano, A.; Kuzyk, R. Modified Mecanum Wheels for Traversing Rough Terrains. In Proceedings of the 2010 Sixth International Conference on Autonomic and Autonomous Systems; 2010; pp. 97–103. [Google Scholar] [CrossRef]
Chung, W.; Moon, C.; Jung, C.; Jin, J. Design of the Dual Offset Active Caster Wheel for Holonomic Omni-directional Mobile Robots. International Journal of Advanced Robotic Systems 2010, 7, 105–110. [Google Scholar] [CrossRef]
Nasu, S.; Wada, M. Mechanical Design of an Active-caster Robotic Drive with Dual-Wheel and Differential Mechanism. In Proceedings of the Annual Conference of the IEEE Industrial Electronics Society- IECON2015, Yokohama, Japan, 9-12 November 2015. [Google Scholar] [CrossRef]
You, Y.; Fan, Z.e.a. Design and Implementation of Mobile Manipulator System. In Proceedings of the Proc. International Conference on CYBER Technology in Automation, Control, and Intelligent Systems, Suzhou, China; 2019. [Google Scholar] [CrossRef]
Jung, M.J.; Shim, H-S; Kim, H.S.K.J.H. The miniature omni-directional mobile robot OmniKity-I (OK-I). In Proceedings of the Proc. IEEE International Conference on Robotics and Automation 1999 (ICRA’99), Detroit, MI, USA; 1999. [Google Scholar] [CrossRef]
Giro Perez, P. Dynamic modelling, parameter identification, and motion control of an omnidirectional tire-wheeled robot. Master’s thesis, Universitat Politecnica de Catalunya (UPC), Barcelona, Spain, 2021. [Google Scholar]
Giró, P.; Celaya, E.; Ros, L. The Otbot project: Dynamic modelling, parameter identification, and motion control of an omnidirectional tire-wheeled robot. arXiv, 2023; arXiv:cs.RO/2311.10834. [Google Scholar] [CrossRef]
Canuto Gil, J.; Domènech, C. Patent: Omnidirectional platform and omnidirectional conveyor. WO2019020861A2.
Yun, X.; Yamamoto, Y. Stability analysis of the internal dynamics of a wheeled mobile robot. Journal of Robotic Systems 1997, 14, 697–709. [Google Scholar] [CrossRef]
Shojaei, K.; Shahri, A.M.; Tarakameh, A.; Tabibian, B. Adaptive trajectory tracking control of a differential drive wheeled mobile robot. Robotica 2010, 1, 11–23. [Google Scholar] [CrossRef]
Shojaei, K.; Shahri, A.M.; Tabibian, B. Design and Implementation of an Inverse Dynamics Controller for Uncertain Nonholonomic Robotic Systems. Journal of Intelligent Robotic Systems 2013, 71, 65–83. [Google Scholar] [CrossRef]
Siegwart, R.; Nourbakhsh, I. Introduction to Autonomous Mobile Robots; The MIT Press, 2011. [Google Scholar]
Echeandia, S.; Wensing, P.M. Numerical Methods to Compute the Coriolis Matrix and Christoffel Symbols for Rigid-Body Systems. Journal of Computational and Nonlinear Dynamics 2021, 16. [Google Scholar] [CrossRef]
Murray, R.M.; Sastry, S.; Li, Z. A Mathematical Introduction to Robotic Manipulation. 1994.
Lynch, K.; Bloch, A.; Drakunov, S.; Reyhanoglu, M.; Zenkov, D., Control of Nonholonomic and Underactuated Systems; 2011; pp. 1–36. [CrossRef]

Figure 1. Structure of MOBY.

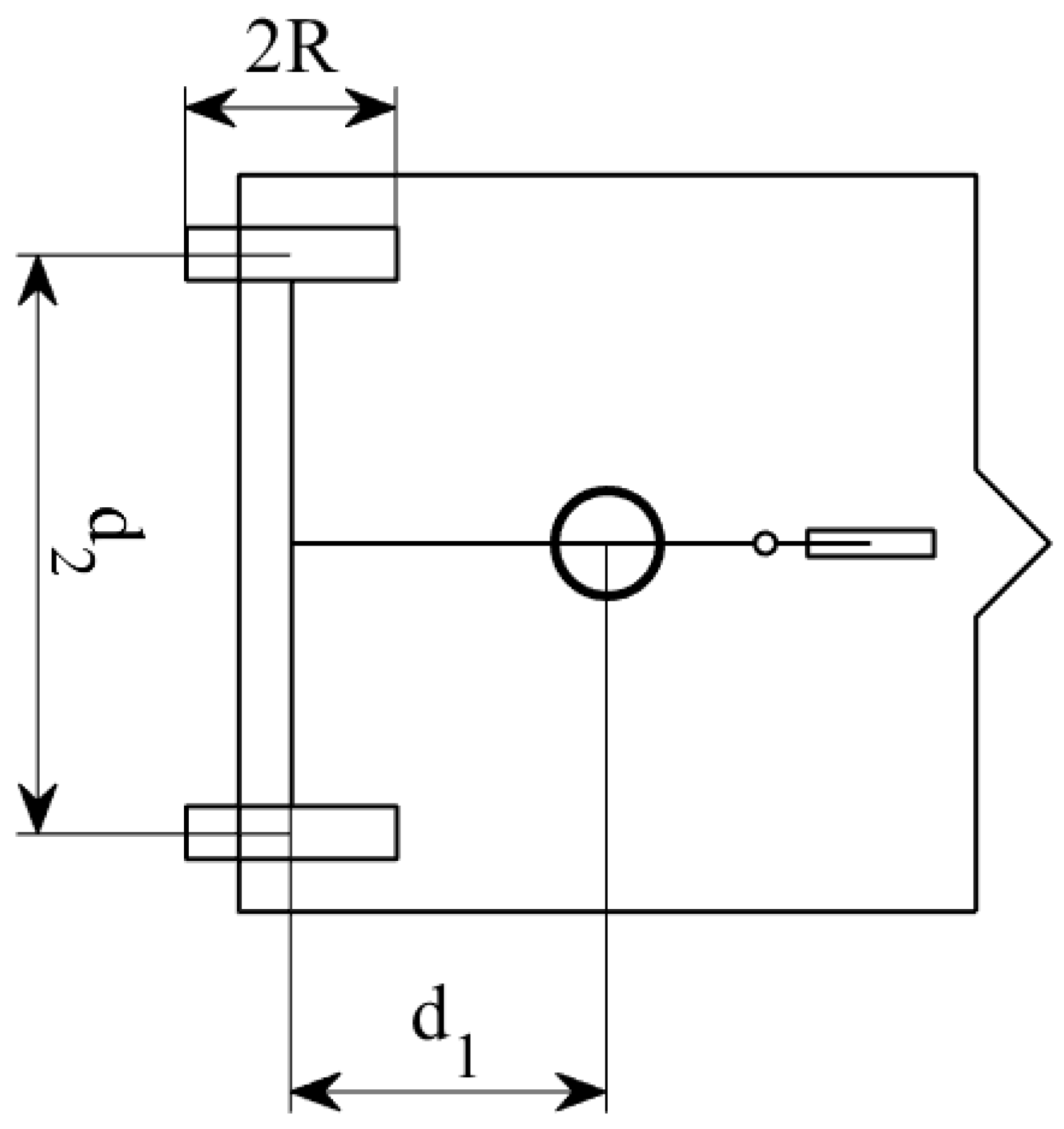
Figure 2. Real robot used for the experiments, MOBY.

Figure 3. The orientation of the robot as a function of the defined variables.

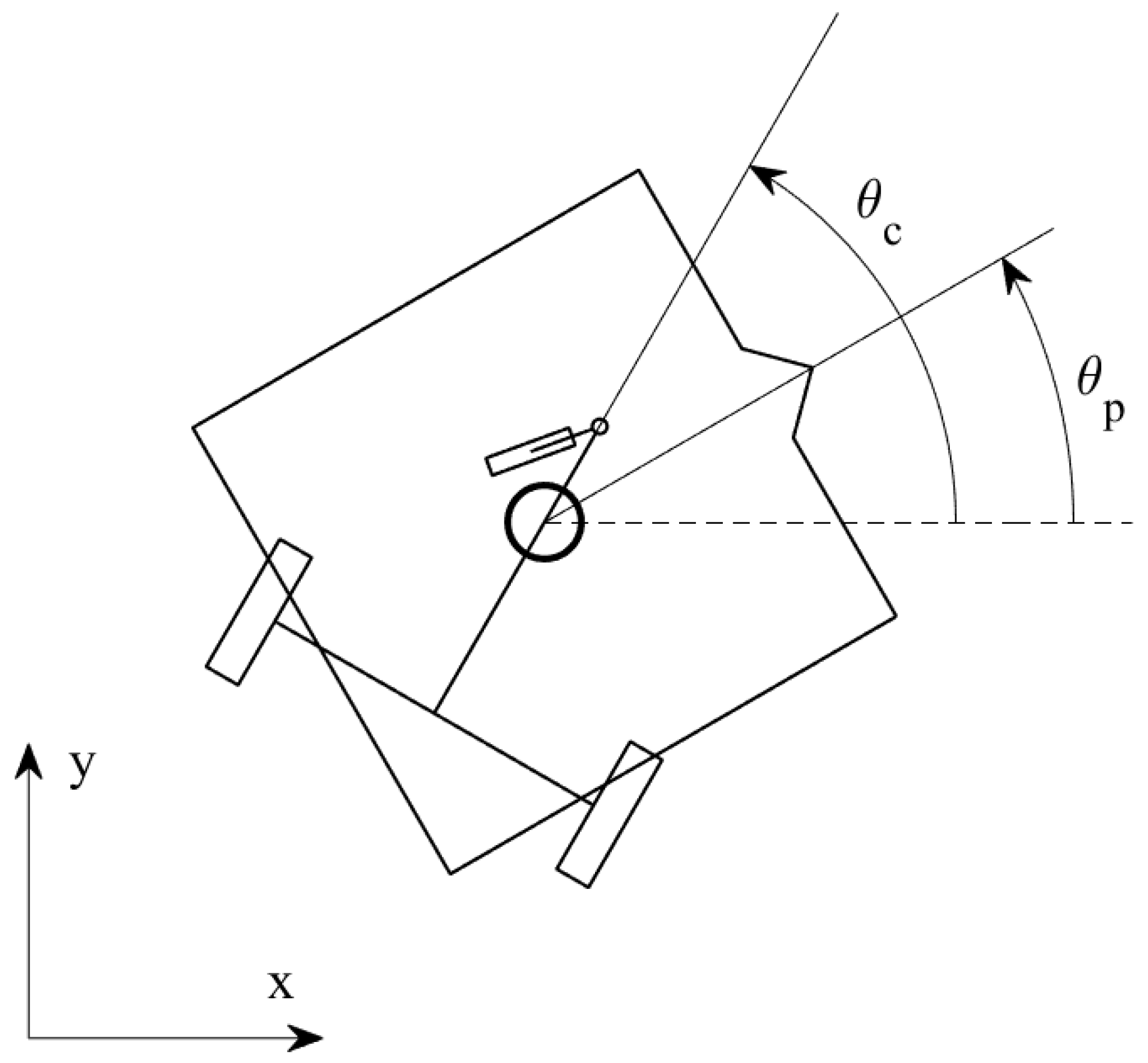
Figure 4. Variables defining the dimensions and configuration of the caster wheel assembly.

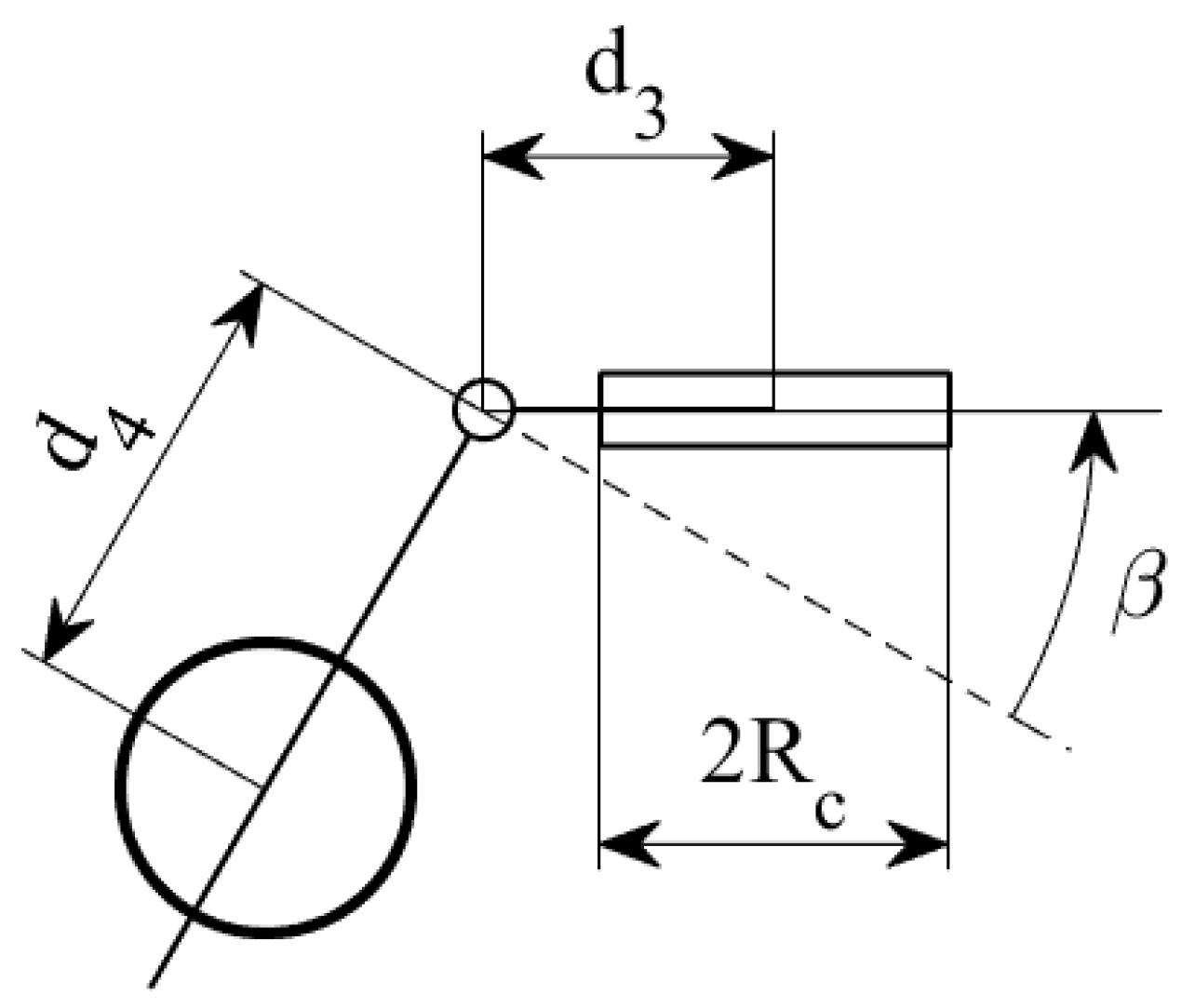
Figure 5. Simulation showing the reversal of the direction of the chassis. From left to right, the robot accelerates backwards, holds its speed, switches from pull to push, and comes to a stop.

Figure 8. Dynamic simulation of the response of the robot to an impact on the fork of the caster wheel. The blue arrow indicates the position of the center of the robot when the force is applied and its direction. The green dashed line shows the expected trajectory had there been no impact.

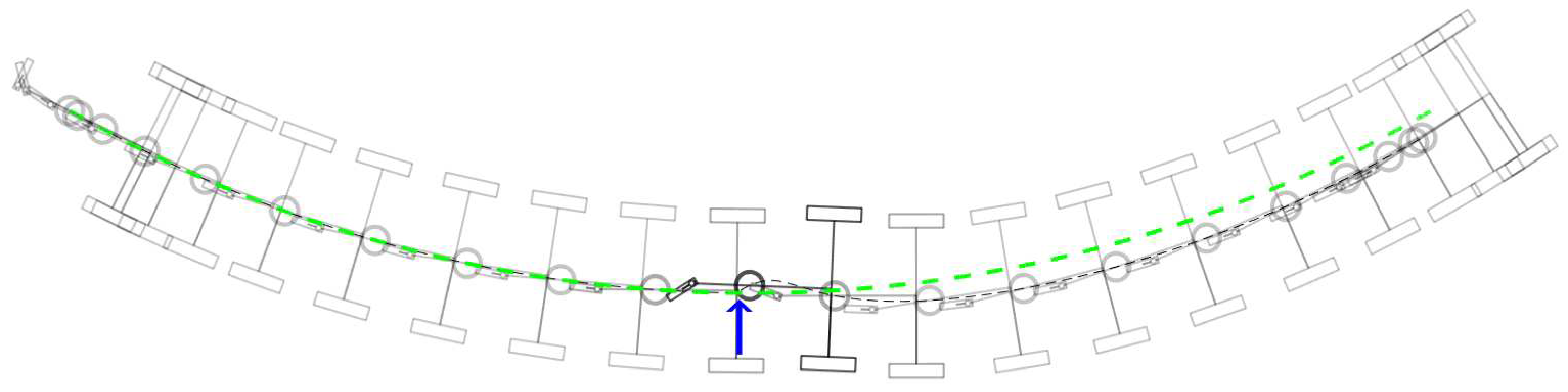
Figure 9. Trajectory built by concatenating arcs and a straight line. The dashed green line is the pre-defined trajectory. The path begins with a 60º arc with a radius of 5 m, then a 90º arc with a radius of 8 m, and finally a 5 m long straight line. The angular velocity changes uniformly in the stretches between arcs. The shapes of the chassis and wheels of the robot show the position and orientation of the robot at temporally evenly spaced instants.

Figure 11. Torques required on the actuated wheels to perform the motion in Figure 5. Left, uncompensated; right, applying the compensation at every instant.

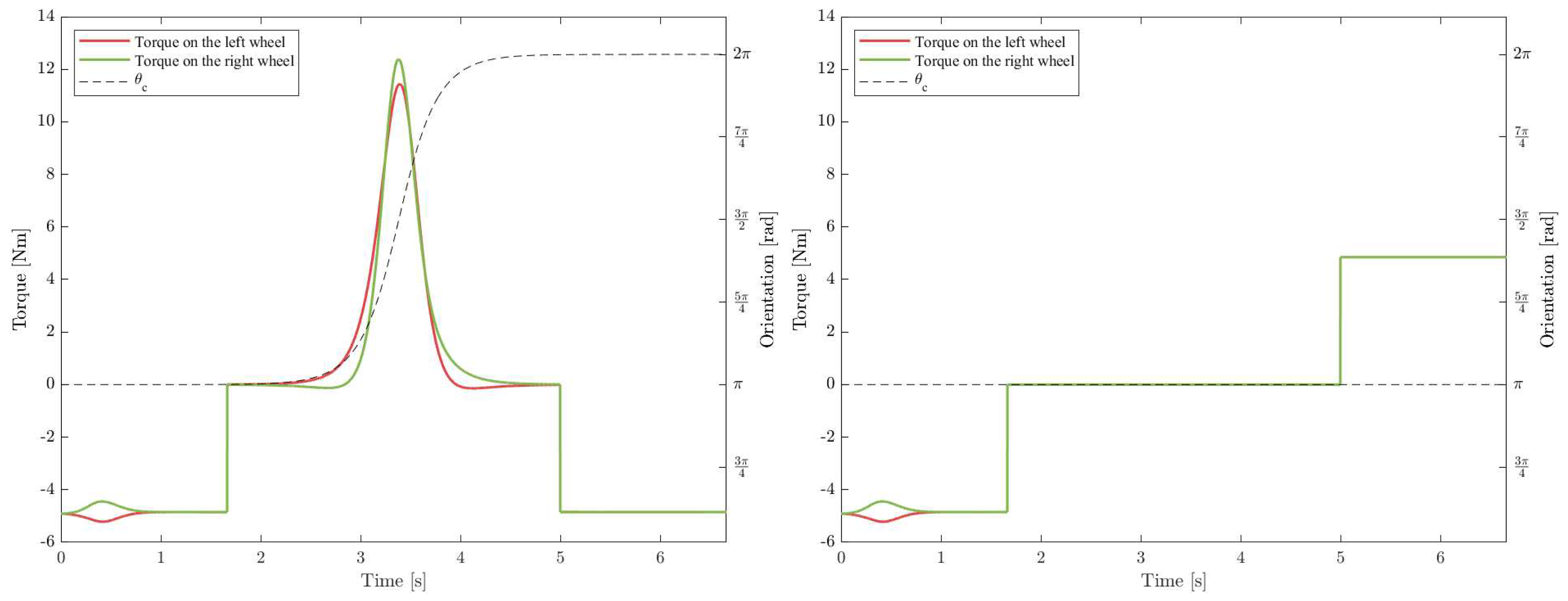
Figure 12. Magnitude of the friction with the ground needed by the robot to perform the motion in Figure 5.

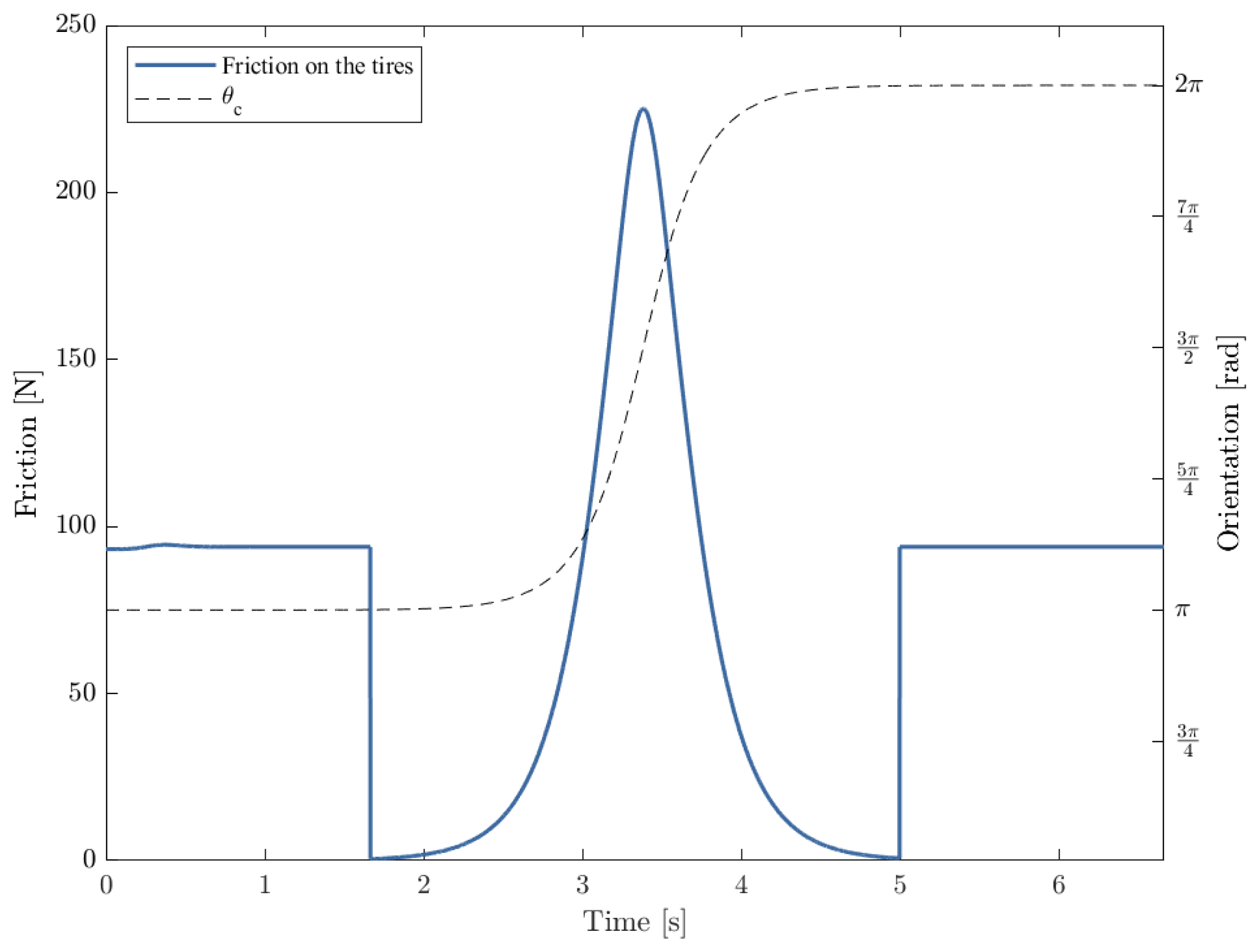
Figure 13. Detail showing the effect of the position of the caster wheel during the acceleration phase in the motion shown in Figure 5. The simulation is the same as the one shown in Figure 11 (right).

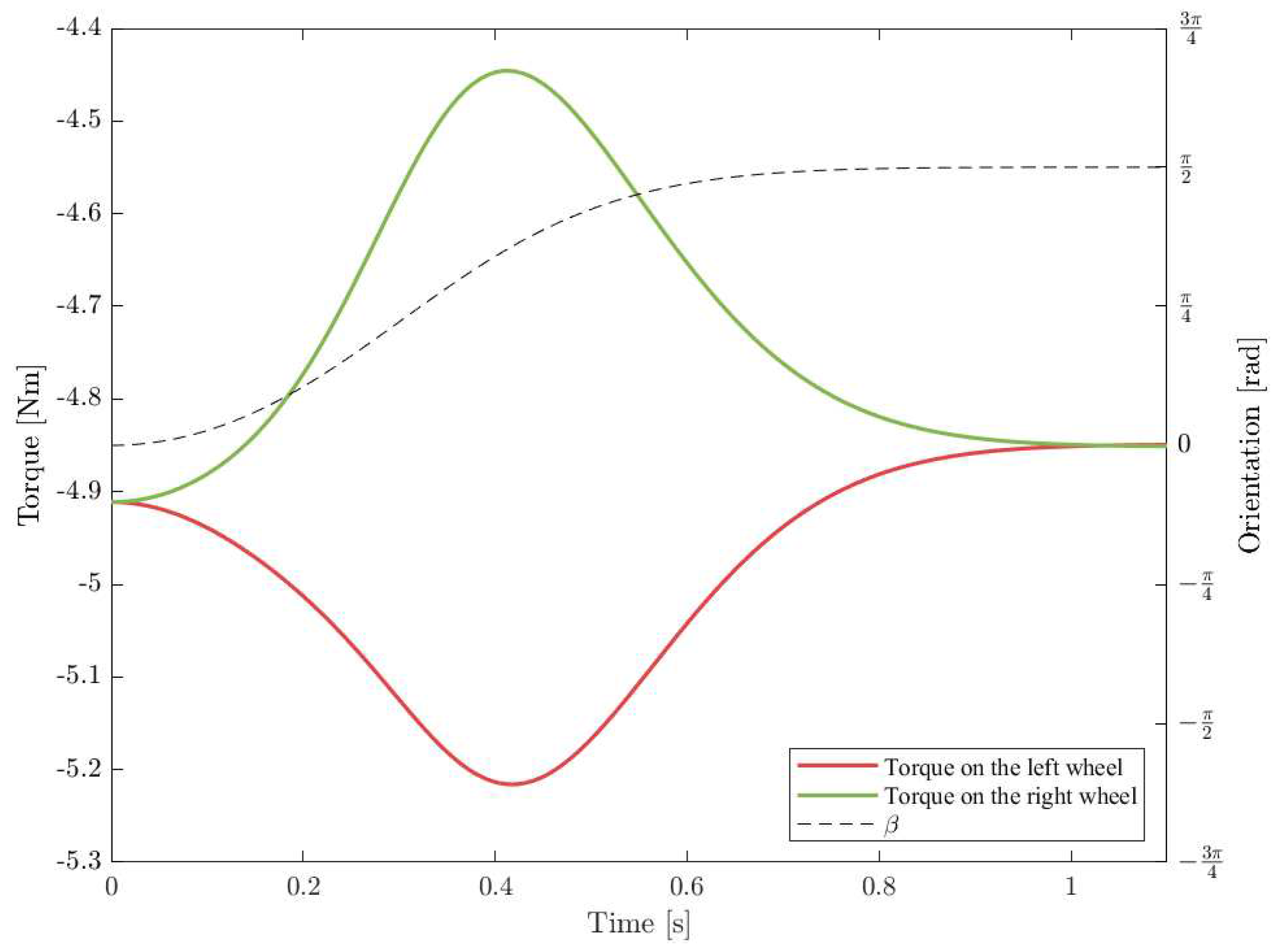
Figure 14. Dynamic effects of the caster wheel when it exits its unstable position during the second phase of the compensated motion.

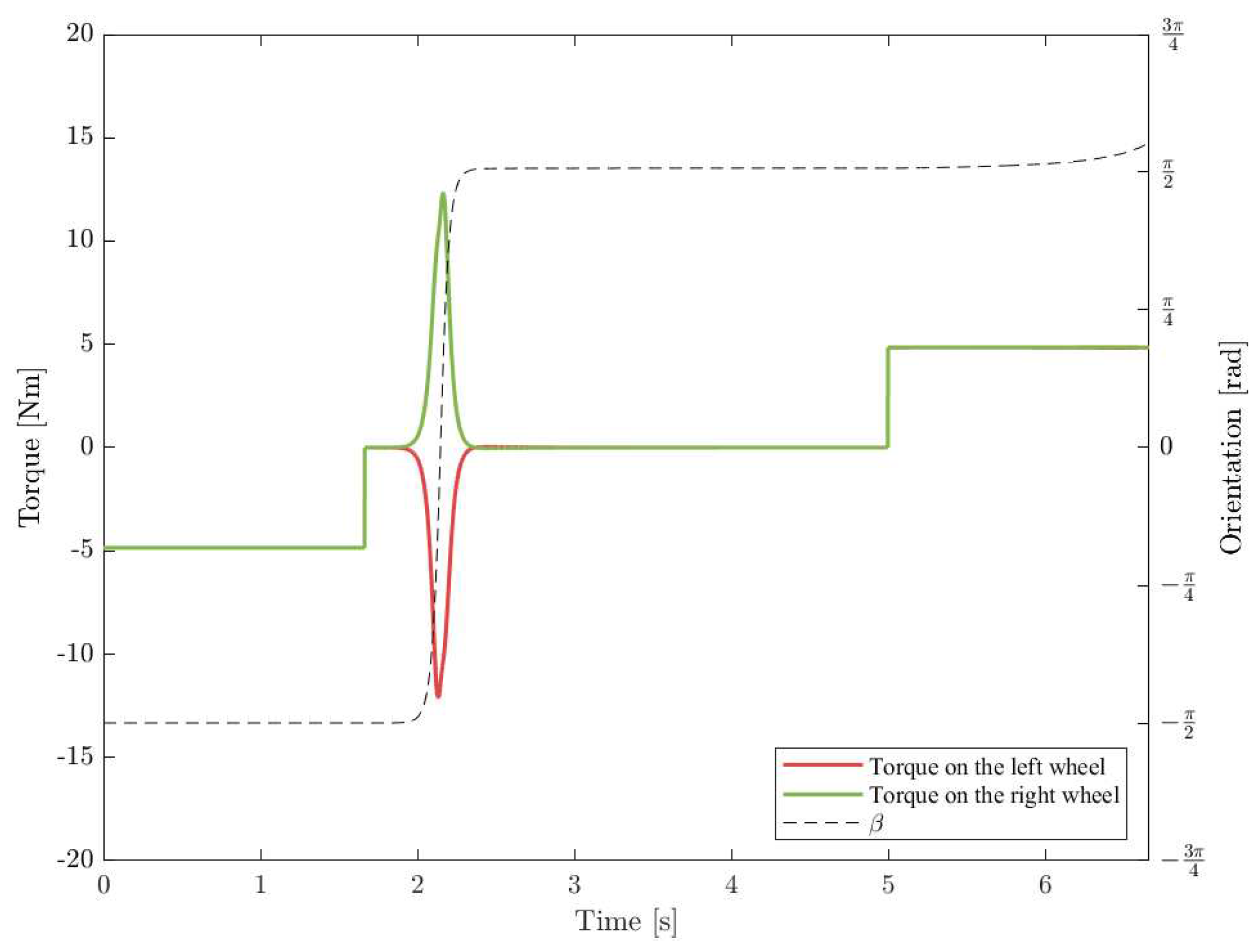
Figure 15. Velocities and chassis angle during the experiments: left, the first experiment and right, second (compensated) experiment.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Driving Strategies for Omnidirectional Mobile Robots with Offset Differential Wheels

Abstract

1. Introduction

2. Description of the Robot

3. Kinematic Analysis

3.1. Forward kinematics

3.2. Inverse kinematics

3.3. Passive degrees of freedom

4. Kinematic Behavior

5. Driving Strategy

6. Dynamic Model

6.1. Forward dynamics

6.2. Inverse dynamics

7. Simulations

7.1. Dynamic implications of the spontaneous region switch

7.2. Dynamic effects of the caster wheel

8. Experimental Results

8.1. Uncompensated pull-region motion

8.2. Compensated pull-region motion

9. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe