Prerpints.org logo
Preprint
Article

Power Loss Modelling and Performance Comparison of Three-Level GaN-Based Inverters Used for Electric Traction

Altmetrics

Downloads

190

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 December 2023

Posted:

19 December 2023

You are already at the latest version

Alerts
Abstract
The main aim of this work is to present a step-by-step procedure to model and analyze the power loss distribution of three-level Gallium Nitride (GaN) inverters. It has been applied to three distinct three-phase three-levels voltage source inverters utilized in electric traction drives: Active Neutral Point Clamped, Neutral Point Clamped and T-Type Neutral Point Clamped. The proposed analytical power loss modelling, combined to an equivalent representation of the electrical machine demonstrated to be a viable solution to achieve a time-saving and low computational burden simulation platform, leading to satisfying accuracy results. This has been confirmed by comparing the results carried out from the simulations of a 110kW permanent magnet synchronous motor drive and those determined by considering a simplified circuital representation based on the proposed analytical power loss modelling.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Nowadays, the significance of electric traction is widely acknowledged as fundamental for the advancement of society. Projections indicate substantial growth in the global electric vehicle (EV) market in the upcoming years, largely due to policy objectives aimed at reducing greenhouse gas emissions in transportation across numerous countries worldwide [1,2,3].
Currently, light-duty electric vehicles typically feature powertrains with rated power varying between 60kW and 200kW. These powertrains are mostly powered by lithium-ion battery packs with capacities ranging from 30kWh to 110kWh, resulting in estimated ranges mostly below 400km. This limited range stands as a significant barrier hindering the widespread adoption of EVs. Another substantial limitation is the lengthy recharging duration compared to equivalent internal combustion vehicles. Despite significant developments in recharging infrastructure, most charging points still operate at a peak power of 100kW [4]. Consequently, charging times for reaching 80% battery capacity using 100kW - 480V DC fast charging typically range from 30 minutes to 1 hour. Reducing charging times would alleviate the inconvenience posed by limited driving range. Therefore, higher charging power can considerably diminish battery refueling duration. For instance, increasing fast-charging power levels from 100 kW to 350 kW results in a significant reduction in charging time. However, maintaining the charging voltage at the typical value of 400V would necessitate increased current ratings for charging cables, leading to amplified system power losses. Some automotive manufacturers are exploring solutions involving an 800V DC bus to achieve faster battery charge times, [5,6,7,8,9]. However, this approach presents technical challenges related to current electric powertrain technologies, especially semiconductor technologies utilized in electric traction inverters.
Additionally, considering alternative power converter topologies could potentially enhance efficiency, reliability, and power density, while simultaneously reducing the cost and weight of power conversion processes.
Because of their notable efficiency and cost-effectiveness, the prevailing choice for most production EVs involves the utilization of Two-Level (2L) three-phase volage source inverters (VSIs). These inverters typically rely on insulated gate bipolar transistors (IGBTs), with only a few cases incorporating silicon-carbide based (SiC) power modules. IGBTs power devices still remain the primary choice for realizing common traction inverters over other available power device technologies. This preference stems from the technology's maturity, widespread availability, cost-effectiveness, and sufficient power-handling capabilities. IGBTs with blocking voltages ranging from 650V to 1200V are well-suited to manage the variable DC-link voltages of today's battery packs, which typically range from 300V to 450V. The VSI topology can be realized by compact power modules, each comprising multiple dies arranged in parallel to evenly distribute the high current load across the switches, to reach the appropriate power level. In commercial vehicle applications, most IGBT-based traction inverters demonstrate efficiencies below 94%. These systems operate at switching frequencies intentionally kept below 30kHz to limit power losses. Additionally, due to technological limitations inherent in power switches, the dead-time between complementary switches is generally set to at least 1μs. This practice is adopted to mitigate output current distortion and voltage error, which become more pronounced at higher rotational speeds, consequently impacting on the control performance [10,11,12,13]. A DC-link capacitor, denoted as Cdc, is commonly employed in the standard 2L topology to mitigate current and voltage fluctuations generated by Pulse Width Modulated (PWM) power devices. This capacitor serves to smoothen these fluctuations, curbing the adverse effects associated with high-frequency current harmonics. Figure 1 shows an example of a traditional IGBT-based traction inverter.
In the last ten years, Wide Band Gap (WBG) semiconductors like SiC and GaN have gained prominence in various power conversion applications, replacing silicon (Si) devices due to their superior physical attributes, as detailed in Table 1 [14]. Leveraging these superior properties allows for the creation of smaller-sized switching devices that possess higher breakdown voltages, lower on-resistance, and increased switching frequency capabilities [15]. The reduced dimensions of these devices facilitate the design of inverters significantly smaller in size, yet with equivalent ratings compared to traditional Si-based inverters. Furthermore, it aids in the integration of motor drives within the inverter design, particularly advantageous for GaN-based inverters, fostering the development of integrated modular motor drives, [16,17]. SiC-based power modules offer advantages like reduced switching and conduction losses, increased power density, and the ability to operate at higher temperatures. Some SiC inverters have demonstrated efficiency gains of up to +2% compared to their Si counterparts. However, the cost implications still constrain their widespread adoption in automotive traction.
Presently, 2L SiC-based inverters in traction systems operate at frequencies below 30kHz, with dv/dt values comparable to those of silicon IGBTs. This is to mitigate the adverse effects of PWM on the cable-motor system. Noteworthy issues encompass over-voltages at motor terminals, common mode currents, additional losses, and subsequent reduction in motor efficiency.
Although currently not extensively utilized in motor drives, GaN power switches hold promising potential for enhancing electric drives in traction systems, especially when paired with high-speed electrical machines and operating within GaN-based inverter topologies at elevated switching frequencies. In fact, GaN devices exhibit advantages such as reduced switching and conduction losses, heightened power density, and the capability for operation at higher temperatures, surpassing the performance of Si power switches. Furthermore, GaN devices claim fewer parasitic components, making them more suitable, particularly in hard-switched applications. Consequently, this technology presents an opportunity to develop traction electric drives characterized by compactness, high efficiency, robustness, and reduced weight—factors contributing to expanding a vehicle's range. The primary limitation of this technology lies in the rated blocking voltage, typically limited to 650V for most of the available products. Consequently, to harness the full potential of this technology in the upcoming generation of electric traction drives for electric vehicles, the implementation of a multilevel inverter configuration becomes imperative. This setup allows the GaN-based power inverter to effectively operate with DC bus voltages ranging between 800V and 1kV.
Multilevel inverters offer several advantages over the conventional two-level topologies commonly employed in today's vehicles [18]. These benefits encompass improved efficiency, superior thermal characteristics, optimized distribution of switching and conduction power losses, and reduced size of passive components. In low-voltage applications (<1.5kV), multilevel inverters leverage the advantageous traits of lower-voltage semiconductor switches, leading to decreased conduction and switching power losses. This results in the more efficient distribution of overall losses among multiple switches, effectively reducing junction temperatures compared to the conventional two-switch arrangement in each phase of a three-phase two-level power inverter.
Additional advantages associated with multilevel topologies include:
-
Reduced dv/dt stress on the electric load;
-
Reduced common mode voltages;
-
Enhanced freedom to control the output waveform;
-
Mitigation of Total Harmonic Distortions;
-
Lower stress on the power switches;
-
Improved fault tolerance capability.
Hence, GaN-based multilevel inverters emerge as an appealing solution for designing compact and highly efficient traction inverters, circumventing the breakdown voltage limits (650V) inherent in existing GaN technologies. Additionally, due to reduced output voltage steps, the utilization of multilevel converters proves effective in curbing voltage stress and subsequently reducing electrical aging in traction machines.
In literature several methods have been presented to compute the power losses of motor drive fed by inverter, including both the main electric motor (copper, iron and friction) and the power converter losses (conduction and switching) [19,20,21,22,23,24,25]. In [19,20,21] an IGBT-based 2L-VSI power converter is considered, and the related power losses are analytically evaluated, where the conduction ones are determined by computing the load RMS current, duty ratio and power factor. These models can be improved by taking into consideration the manufacturer’s curve fitting coefficients [20]; the switching losses are computed starting from the curve fitting of the energy curves provided in the datasheet in [19,20], whereas in [21] the energy switching losses are analytically evaluated taking into account physical aspects of the IGBT, such as transconductance, breakdown voltage and permittivity of the semiconductor. Furthermore, in [19,20] an analytical dynamic model of the induction motor (IM) drive is considered realized through an equivalent circuit model [19] and state space vector equivalent circuit [20], whereas in [21] per phase steady-state IM equivalent circuit model is used. In [22,23] the electric motor and relative power losses are developed by finite element analysis (FEA), IM and PMSM are both analyzed in [22] and in [23] only IM is considered. Despite similar approach in electric motor modelling, in [22] IGBT power losses are computed as in [19,21], while in [23] a look-up table-based approach is implemented. Differently from [19,21], in [24,25] the IGBT power losses are computed including the junction temperature function; about the electric motor model, [24] uses a similar qd-axis equivalent circuit model of [19], whereas in [25] a inductor load replaces the electric motor.
This paper introduces a systematic procedure for estimating power loss distributions in three distinct three-phase three-level voltage source GaN-based inverters employed within a PMSM-based traction drive. The power loss analysis spans a broad operational range of the drive, incorporating energy-saving control techniques like maximum torque per ampere (MTPA) and flux weakening (FW). The suggested approach combines analytical power loss modeling of the considered 3LIs with a simplified equivalent representation of the electrical machine. This integration offers a viable solution, enabling the creation of a simulation platform that saves time, reduces computational load, and yields accurate results.
The remaining part of the paper is organized as follows. Section II illustrates the traction drive unit under test, the inverter topologies that have been considered in this study and their corresponding modulation strategies. Section III details the static and dynamic characterizations of the GaN HEMT intended for use in the power inverters. Section IV describes the realization of the entire traction drive in PSIM (speed and current controls have been implemented in MATLAB/Simulink environment) including accurate loss modelling of power devices. Section V details the step-by-step procedure utilized to develop the analytical power loss models for the three level inverters (3LIs) examined in this study. Additionally, it necessitates determining an equivalent model of the PMSM across various operating conditions. In Section VI, the power loss distributions of the three examined 3LIs will be carried out by using both the proposed analytical approach and a detailed “inverter + electrical machine”-based circuit simulation modelling. Differences between these methodologies will be discussed. Finally, Section VII will provide concluding remarks.

2. Electric Traction Drive Description

The traction drive under examination in this study comprises a DC battery pack, represented as a constant voltage source VDC, which is linked to one of the considered 3LIs. These inverters are responsible for powering the PMSM, employing a rotor flux field-oriented control strategy, enabling an independent control of torque and flux by appropriately managing the two qd-axes stator current components: iq and id. This is achieved through a closed current loop, as depicted in Figure 2. Field orientation is possible thanks to suitable reference frame transformations abc/qd and qd/abc indicated in the same figure and in the modelling of the electrical machine. An external speed loop has been used to map the overall torque-speed operating range of the traction drive. Concerning the id current, its selection aims to minimize motor drive losses by employing established current vector profiles associated with the conditions of MTPA and FW.
Specifications of the interior permanent magnet synchronous motor (IPM) used for the considered traction drive are listed in Table 2, while motor parameters are given in Table 3, [26].
To thoroughly validate the proposed analytical modeling, the power conversion and motor control depicted in Figure 2 have been replicated in detail within a circuit simulation environment. This setup includes comprehensive models of power switches and the electrical machine. The PMSM has been mathematically modelled in a qd-axes synchronous reference frame aligned with the rotor flux position θre [27,28], including iron losses, Figure 3. The iron loss resistance Rc is determined by accounting for hysteresis and eddy current losses, further expressed in relation to the rotational frequency ωre [29].
The PMSM model is described by equations (1)-(4), encompassing both electrical and mechanical equations that govern the behavior of the electromechanical system, [30]. Specifically, the qd-axes air-gap current components ioq and iod are determined starting from the voltages and currents relationships (1), where Rs is the stator resistance, Rc is the iron losses equivalent resistance, Lq and Ld are the qd-axes inductances, λpm is the permanent magnet flux, p denotes time derivative d/dt, vq and vd are the qd-axes voltage components, and voq, vod are the qd-axes air-gap voltage components, defined in (2); while icq and icd are the qd-axes iron losses current components, iq and id are the qd-axes input current components, both defined in (3). The electromagnetic torque Te and the mechanical equation of motion for the PMSM are given by (4). Here, J represents the mechanical inertia, ωrm stands for the mechanical rotor speed, TL is mechanical torque load and B denotes the viscous friction coefficient. The electrical rotor speed ωre is obtained as ωre= ppωrm, where pp are the pole pairs. The rotor position θrm is determined by integrating the rotor speed ωrm, as illustrated in equation (4).
Preprints 93709 i001
Preprints 93709 i002
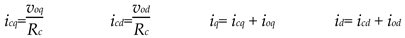
Preprints 93709 i003
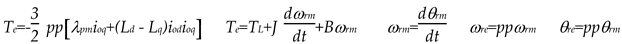
Preprints 93709 i004
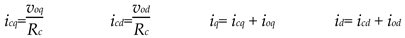
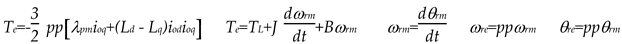
The PMSM is powered by one of three 3LI configurations: Active Neutral Point Clamped (ANPC), Neutral Point Clamped (NPC), and T-type Neutral Point Clamped (TNPC). To supply the electric drive's rated voltage at the rated speed, a DC bus voltage ranging 800V is necessary. The NPC topology consists of 4 switches and 2 diodes per phase [31], Figure 4a. Conversely, the ANPC topology substitutes the 2 diodes with identical switches [32], Figure 4b. As indicated by their names, both topologies clamp the midpoint of the capacitor to the neutral using diodes or switching devices. However, the NPC topology's primary drawback involves the need for a balancing circuit to maintain voltage equilibrium across the capacitors. On the other hand, the ANPC topology does not require this additional circuitry but necessitates extra components to control the switches clamping the neutral [33]. The conventional T-type inverter [34] consists of 2 switching devices in the main leg and 2 in the parallel leg. However, the voltage stress on the devices in the main leg is VDC, while in the parallel leg, it is VDC/2. Consequently, for the considered application the topology is modified by including 4 devices in the parallel leg, as depicted in Figure 4.c. This modification in the analyzed TNPC implements the serialization of power switches [35,36], posing challenges related to the simultaneous operation of devices functioning as a single switch. This challenge arises because individual switching devices might have differing turn-on and turn-off characteristics, necessitating an appropriate switching strategy for the efficient operation of both devices.
One significant advantage of employing 3LI topologies is the array of modulating strategies available for implementation. In this study, the level shifted PWM modulation technique is utilized across all three topologies [37,38]. Throughout each commutation cycle, the output voltage alternates between +VDC/2, 0, and -VDC/2. The voltage across the terminals of each GaN power MOSFET in these topologies is VDC/2, offering a significant advantage as the selected switching devices can be rated at half of the DC Bus Voltage. The modulation techniques employed for each topology are illustrated in Figure 5.
The realization of three-phase topologies involves adding two additional legs for the remaining two phases. The modulation strategies encompass two reference voltages phase-shifted by 2π/3 and 4π/3 to synthesize a symmetrical voltage set [33,36].
The modeling described above has been implemented within the PSIM simulation platform, specifically tailored for simulating power conversion systems and control algorithms. However, a major limitation of this approach arises due to substantial differences between the extremely rapid switching transients of GaN power MOSFETs and the dynamic response of the electrical machine. Consequently, if the objective is to assess the power loss distribution of the inverter's power devices, simulating the entire drive will demand a considerable computational load and result in prolonged times to achieve the steady-state condition in the simulated drive.
The aforementioned consideration has prompted the authors to devise an alternative methodology aimed at modeling the entire traction drive. In this approach, the power converters are implemented using ideal switches, while their conduction and switching power losses are determined through appropriate analytical models. Additionally, as the primary objective is to identify the power loss distribution among the GaN devices, the electrical machine is emulated with an equivalent three-phase RL load for each operating condition of the traction drive. By combining these two approaches, there is a substantial reduction in the computational load required for simulation, while maintaining a satisfactory level of accuracy in estimating 3LI power loss distribution. The efficacy of this approach is supported by the results outlined in the subsequent sections, which delve into the analysis of a 110kW traction drive as a case study.

3. Methodology for the Estimation of Power Loss Distribution in GaN-based 3LI

The authors executed the proposed procedure to identify power losses of each power switch in the inverter. They applied this methodology to a prototype with early-stage GaN technology power devices, considering the challenges of identifying parameters for power switches in a developmental stage.

3.1. Characterization of GaN MOSFETs

To accurately assess inverter performance, power devices parameters evaluation is essential. The SGT120R65AES, a prototype manufactured by STMicroelectronics, is the GaN power device being evaluated in this study. This transistor uses a PowerFLAT 5x6 package, shown in Figure 6, with separate Kelvin source and source terminals to isolate the driving loop from the power loop, improving packaging parasitics. Table 5 presents the primary specifications of the analyzed GaN MOSFET.
The GaN device's performance is evaluated based on switching and conduction losses. Hard-switching transients cause energy loss due to parasitic capacitances charging and discharging currents, while conduction losses depend on RDS(on). Proper evaluation requires static and dynamic characterization tests or can be derived from power MOSFET datasheets. In the case of utilizing datasheets for GaN devices, particularly in the early stages of technology development, the information provided might be rather generic, lacking in detailed characterization. This becomes a critical concern, especially when integrating these GaN devices across multiple dies connected in parallel to form power modules. The absence of comprehensive characterization data can pose significant challenges in the power loss estimation.

3.1.1. Static Characterization

Two curve tracers are used for static power device characterization: the Tektronix 370B for threshold voltage VGS(th) and the Tektronix 371A for static RDS(on) and output characteristics. The 370B provides high-resolution measurements and capability to set very low current value (about10-100μA) necessary for VGS(th) tests, while the 371A enables high-voltage and high-current sourcing. To measure VGS(th) using the 370B, the drain and gate terminals are shorted to ensure identical current flow (IDS = IGS), as shown in Figure 7a.
The GaN transistor conducts when a 2DEG is created between the AlGaN and GaN layers by the piezoelectric effect [39]. The voltage at which device conduction begins is determined by varying the IDS current at 500µA and 1mA across temperatures from 25°C to 150°C, as shown in Figure 7b. Assuming the more stable threshold voltage indication at IDS=1mA, it increases with temperature from 1.65V to 1.75V.
The 371A Curve Tracer was used to establish the output characteristics of the GaN MOSFETs. This involves setting a specified VGS and incrementally increasing VDS to obtain the v-i characteristics for that VGS. The output characteristics are also evaluated while varying the junction temperature (Tj), as shown in Figure 8.
The static assessment of the RDS(on) of the analyzed GaN HEMTs is conducted using the Tektronix 371A Curve Tracer. RDS(on) can be determined from the curve tracer as a ratio of VDS(on) to IDS at specific value of VGS. Figure 9 shows the evaluation of the RDS(on) as function of the junction temperature from 25°C to 150°C, for three different values of IDS at VGS=6V.
Threshold voltage, output characteristics and RDS(on), profiles are the main static parameters necessary but not sufficient to implement the proposed model.

3.1.2. Dynamic Characterization

Dynamic characterization aims to assess “dynamic” parameters of DUTs, which in this case are mainly dynamic on-resistance and switching losses (Eon and Eoff) using a specialized board shown in Figure 10 and the Tektronix TDS 5054 Oscilloscope with TPP0500B probes for data acquisition. The board minimizes parasitic inductance paths, while the higher probe bandwidth of 500MHz allows to correctly capture all dynamic signal response without impacting on its slew rate.
Dynamic RDS(on) issues is a well know research topic for GaN device and more information can be found in literature [40,41], while in this section it is provided a more detailed description of its experimental evaluation for its inclusion in the proposed model.
The assessment of dynamic RDS(on) relies on the ratio of measured VDS(on) and IDS. However, a standard voltage probe lacks the sensitivity required to measure VDS(on), which falls within the millivolt range during the GaN HEMT's turn-on phase starting the transient from VDD, that for the device under tests has typical value of hundred volt, primarily due to the equivalent input RC network of the probe. Consequently, a voltage clamping circuit has been implemented to clamp the voltage VDS(on) when the DUT is off, enabling the measurement of the actual VDS(on) during the device's turn-on phase [40]. By concurrently measuring the current flowing through the device using a current probe and VDS(on), it becomes feasible to determine the RDS(on). Figure 11 illustrates the electric scheme of the test bench and typical waveforms of a measurement of VDS(on) (blue trace) and IDS (green trace) for the determination of the dynamic RDS(on).
Measurements of dynamic RDS(on) have been conducted considering a switching commutation on resistive load applying a fixed number of pulses, typically 100, as function of VDD from 100V to 400V and case temperature from 25°C and 150°C. Due to the relation between the time and application of the “stressing” voltage, it is necessary to evaluate the dynamic RDS(on) at different time instant, and example of results for 400V, 5A at 25°C are reported in Table 6.
From Table 6, it apparent that RDS(on) decreases and stabilizes at a constant value over time. The relationship between RDS(on) variations concerning changes in temperature Tj and VDS is depicted in the results of Figure 12, confirming an increase in RDS(on) corresponding to the blocking time of the bus voltage [41].
Another significant source of losses occurring into the power devices is attributed to the switching losses. These can be identified by implementing classical double pulse tests. The circuit and the related switching energy losses estimation are given in Figure 13.
The estimation of Eon and Eoff is conducted at the rated voltage VDD = 400V while varying the current from 5A to 10A. The assessment involves varying parameters: Rg is modified while maintaining a constant case temperature Tcase, Figure 14, and case temperature is modified while keeping the gate resistance Rg constant, Figure 15.
The switching losses are recorded also with respect to the change in temperature from 25°C to 150°C. An increase in trend of the losses is observed due to the higher rise time of voltage and current at higher junction temperatures.
The GaN HEMTs have been modelled in PSIM by using a MOSFET model including all data relative to static and dynamic characterization: the variations of RDS(on) in forward and reverse conduction mode and energy losses Eon and Eoff. Moreover, RDS(on) dependance from junction temperature Tj, is considered by the following relationship:
R D S ( o n ) = R D S ( o n ) B 1 + K T ( T j − T j B )
where RDS(on)B is the on-resistance at the base junction temperature TjB (typically 25°C), while KT is the temperature coefficient.
Drain-source voltage and current flowing through the MOSFET model are obtained from the simulation for each instant. These last values are then used for the losses calculation. However, the value of RDS(on) is updated at each time step of the simulation, according to (5).

4. GaN-based Traction Drive Modelling in PSIM

To verify the effectiveness of the proposed mathematical based power loss analysis of power converters, the traction drive has been entirely realized in PSIM, Figure 16, including accurate loss modelling of power devices, Figure 17, determined according to the above-mentioned measurements and electrical machine. To achieve the proper current capability is supposed to connect 20 dies in parallel. As experienced in the technical literature [42,43], in a power system which contains power electronic devices, the time scale spans nanoseconds of the switching devices to several seconds or even minutes of the electrical machines.

5. Analytical Power Loss Modelling of Three-Level Inverters and Electrical Machine

An alternate and effective approach to simulate the performance of the 3LI is the proposed one, which involves utilizing power converters composed of ideal switches and exploiting analytical models to estimate power losses and approximating the electrical machine with an equivalent RL load for various torque-speed operating conditions of the traction drive.
For each GaN power device composing the 3LI the conduction losses Pcond are computed according to (6), where the root mean square (RMS) current is given by (6); we are assuming a sinusoidal load current I ( θ r e ) = I p s i n ( θ r e − φ ) and the duty cycle d(θre) of one phase of the PWM voltage waveform is defined as a quantity variable with the modulation index m and power factor cos(φ), [33,44]. The load current is identified by the peak value Ip and phase angle φ, while the angular position θre is given by ωret, where ωre is the angular frequency of the fundamental voltage harmonic.
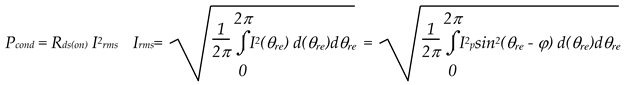
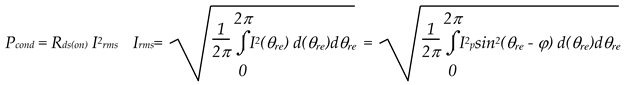
Preprints 93709 i006
The carrier-based modulation techniques feature a symmetrical behavior: Irms(S1)=Irms(S4), Irms(S2)=Irms(S3), Irms(S5)=Irms(S6), thus the conduction losses computation can be limited to the top half GaN devices of the power converter i.e. S1, S2 and S5, whereas in the case of NPC topology D1 is symmetric to D2. The computation of the RMS currents Irms (6) for each device are reported in Table 7. The computation has been carried out by considering the reverse conduction mechanism of GaN HEMT, thus considering the two current parallel paths for each device. The state of the generic jth power switch Sj associated to forward and reverse current conductions is indicated with SjF and SjR, respectively. Same approach can be extended even to other modulation strategies, such as the third harmonic injection PWM techniques.
The switching losses were analytically calculated starting from the measured Eon and Eoff, determined from devices characterization, which can be defined as the function of VDD, IDS and Rg. Under the assumption that VDS and Rg maintain constant values, the switching energies can be exclusively expressed as functions of IDS, (7). Their behavior can be depicted using a generic curve fitting mathematical tool. For the considered GaNs, the energy loss profiles are given by:
Preprints 93709 i007
The expression of the average switching power losses PSW(on) and PSW(off) over a fundamental period Tre = 2π/ωre are provided in (8), where n is the ratio between switching fSW and fundamental fre=1/Tre frequencies, equivalent to the number of commutations per fundamental period of the current, while n1 and n2 define the starting and final intervals in which each power device is PWM commutated. Starting from (7), the switching losses for each GaN device composing the 3LI can be expressed as a function of the output load current characteristics, in terms of peak value Ip and phase angle ϕ. Their expression for the considered GaNs are:
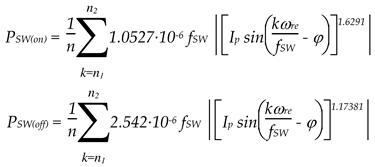
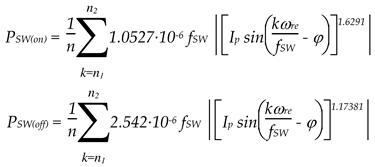
Preprints 93709 i008
Table 8 provides the values of n1 and n2 associated to each device used in the considered topologies.
Also, in the calculation of these switching losses, the symmetry is considered for the switches as the same case as for computing the RMS currents. According to the modulation strategy used in the ANPC, the switching loss power related to S2 and S3 is negligible compared to the other switches composing the 3LI, because of their lower number of commutations in the fundamental period.
To streamline the modeling process, an adaptive RL network is used to represent the electrical equivalent circuit of the AC motor. The network's values are chosen to be representative of the stator current for each operating torque-speed of the PMSM. The determination of both R and L parameter surfaces can be accomplished by conducting a series of simulations. These simulations involve supplying the controlled PMSM with sinusoidal voltages across the entire torque-speed map. This process is notably swift since it neglects the dynamics of the power converters, resulting in a significantly reduced execution time. The surfaces of the RL network for the considered PMSM are displayed in Figure 18 and Figure 19.

6. Analysis of Power Losses in the Case Study

The 110kW traction drive considered in this study has been simulated by using the two-modelling presented in the above sections. The power loss profiles for each GaN device and for the three considered 3LI topologies have been calculated using the proposed analytical approach and are illustrated in Figure 20.
The averaged conduction and switching power loss over a fundamental period are summarized in the Figure 21 and Figure 22, for three motor drive operating points.
Based on the power loss analysis, it is possible to generate efficiency maps for the three considered inverters, the results of which are depicted in Figure 23.
According to the above results, the 3LI topologies utilizing GaN technology exhibit high performance owing to their notably low switching losses. However, the efficiency declines at low speeds and high torque levels due to conduction losses. Furthermore, efficiency above the rated speed diminishes due to elevated d-axis current in the flux weakening region. Comparing the ANPC and NPC topologies, their efficiencies are nearly equivalent, with the ANPC offering slightly higher efficiency in the low-speed region. On the contrary, the TNPC demonstrates significantly lower efficiency compared to the other two topologies. This discrepancy is attributed to the series connection of GaN devices in the main leg, leading to increased overall conduction losses.
The power loss evaluation of the 3LIs using the combined mathematical modelling of converter power loss and the RL loads to simulate the electric traction drive offers a time-saving and efficient approach. However, in real-world scenarios, the impact of high-frequency components also needs consideration. Therefore, a comparison of the overall drive, incorporating the inverter along with the effects of high-frequency components, against the proposed approach have been conducted. This discrepancy is visually presented in Figure 24.
The higher error percentage is noticeable primarily at low load torque, specifically at low currents, attributed to the presence of high-frequency components. However, it's noteworthy that the error remains consistently below 2% at higher currents.
A comparison between the computational burdens associated with simulating the entire traction drive—encompassing both inverter and electrical machine dynamics—and the one achieved by the proposed approach has been conducted for various operating conditions. In both cases the simulation stop time has been set at 1s, while the execution time has been set at 0.1ns. In particular, both simulations have been conducted with a reference speed at ωrmR and varying the torque load with a step at 0.5s from no-load to rated torque load conditions. The results are summarized in Table 9, illustrating a notable and substantial reduction in simulation time with the proposed solution, about 68%, independently of the 3LI topology considered.

6. Conclusions

This work has introduced a systematic methodology to model and analyze power losses distribution for three different three-level GaN inverters devoted to traction drives. The proposed analytical power loss modeling, integrated with an equivalent representation of the electrical machine, proved to offer a viable solution capable to significantly reduce simulation times and computational load while delivering accurate results for a wide traction drive operating conditions. The methodology holds potential for extension to encompass various other topologies and modulation strategies, representing a promising area for future activities.

References

  1. S. P. Sathiyan et al., Comprehensive Assessment of Electric Vehicle Development, Deployment, and Policy Initiatives to Reduce GHG Emissions: Opportunities and Challenges, in IEEE Access, vol. 10, pp. 53614-53639, 2022. [CrossRef]
  2. Barbosa, W., Prado, T., Batista, C., Câmara, J.C., Cerqueira, R., Coelho, R., Guarieiro, L. Electric Vehicles: Bibliometric Analysis of the Current State of the Art and Perspectives. Energies 2022, 15, 395. [CrossRef]
  3. Ali, I.; Naushad, M. A Study to Investigate What Tempts Consumers to Adopt Electric Vehicles. World Electr. Veh. J. 2022, 13, 26. [Google Scholar] [CrossRef]
  4. H. Tu, H. Feng, S. Srdic and S. Lukic, Extreme Fast Charging of Electric Vehicles: A Technology Overview, in IEEE Transactions on Transportation Electrification, vol. 5, no. 4, pp. 861-878, Dec. 2019. [CrossRef]
  5. T. M. Jahns and H. Dai, The past, present, and future of power electronics integration technology in motor drives, in CPSS Transactions on Power Electronics and Applications, vol. 2, no. 3, pp. 197-216, Sept. 2017. [CrossRef]
  6. C. S. Goli, M. Manjrekar, S. Essakiappan, P. Sahu and N. Shah, Landscaping and Review of Traction Motors for Electric Vehicle Applications, 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 2021, pp. 162-168. [CrossRef]
  7. C. S. Goli, S. Essakiappan, P. Sahu, M. Manjrekar and N. Shah, Review of Recent Trends in Design of Traction Inverters for Electric Vehicle Applications, 2021 IEEE 12th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Chicago, IL, USA, 2021, pp. 1-6. [CrossRef]
  8. Aghabali, J. Bauman, P. J. Kollmeyer, Y. Wang, B. Bilgin and A. Emadi, 800-V Electric Vehicle Powertrains: Review and Analysis of Benefits, Challenges, and Future Trends, in IEEE Transactions on Transportation Electrification, vol. 7, no. 3, pp. 927-948, Sept. 2021. [CrossRef]
  9. Allca-Pekarovic, P. J. Kollmeyer, P. Mahvelatishamsabadi, T. Mirfakhrai, P. Naghshtabrizi and A. Emadi, Comparison of IGBT and SiC Inverter Loss for 400V and 800V DC Bus Electric Vehicle Drivetrains, 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 2020, pp. 6338-6344. [CrossRef]
  10. J. Reimers, L. Dorn-Gomba, C. Mak and A. Emadi, Automotive Traction Inverters: Current Status and Future Trends, in IEEE Transactions on Vehicular Technology, vol. 68, no. 4, pp. 3337-3350, April 2019. [CrossRef]
  11. Z. Tang and B. Akin, Suppression of Dead-Time Distortion Through Revised Repetitive Controller in PMSM Drives, in IEEE Transactions on Energy Conversion, vol. 32, no. 3, pp. 918-930, Sept. 2017. [CrossRef]
  12. S. Dai, J. Wang, Z. Sun and E. Chong, Deadbeat Predictive Current Control for High-Speed Permanent Magnet Synchronous Machine Drives With Low Switching-To-Fundamental Frequency Ratios, in IEEE Transactions on Industrial Electronics, vol. 69, no. 5, pp. 4510-4521, May 2022. [CrossRef]
  13. C. Oliveira, C. B. Jacobina and A. M. N. Lima, Improved Dead-Time Compensation for Sinusoidal PWM Inverters Operating at High Switching Frequencies, in IEEE Transactions on Industrial Electronics, vol. 54, no. 4, pp. 2295-2304, Aug. 2007. [CrossRef]
  14. Lidow, A., De Rooij, M., Strydom, J., Reusch, D. and Glaser, J., 2019. GaN transistors for efficient power conversion. John Wiley & Sons.
  15. J. Millán, P. Godignon, X. Perpiñà, A. Pérez-Tomás and J. Rebollo, A Survey of Wide Bandgap Power Semiconductor Devices, in IEEE Transactions on Power Electronics, vol. 29, no. 5, pp. 2155-2163, May 2014. [CrossRef]
  16. Morya, M. Moosavi, M. C. Gardner and H. A. Toliyat, Applications of Wide Bandgap (WBG) devices in AC electric drives: A technology status review, 2017 IEEE International Electric Machines and Drives Conference (IEMDC), 2017, pp. 1-8. [CrossRef]
  17. Y. Yang, L. Dorn-Gomba, R. Rodriguez, C. Mak and A. Emadi, Automotive Power Module Packaging: Current Status and Future Trends, in IEEE Access, vol. 8, pp. 160126-160144, 2020. [CrossRef]
  18. S. Foti et al., A novel Hybrid N-Level T-Type Inverter Topology, 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 2019, pp. 5507-5513. [CrossRef]
  19. Y. Liu and A. M. Bazzi, A comprehensive analytical power loss model of an induction motor drive system with loss minimization control, 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d'Alene, ID, USA, 2015, pp. 1638-1643. [CrossRef]
  20. F. L. Mapelli, D. Tarsitano and M. Mauri, Plug-In Hybrid Electric Vehicle: Modeling, Prototype Realization, and Inverter Losses Reduction Analysis, in IEEE Transactions on Industrial Electronics, vol. 57, no. 2, pp. 598-607, Feb. 2010. [CrossRef]
  21. S. S. Williamson, A. Emadi and K. Rajashekara, Comprehensive Efficiency Modeling of Electric Traction Motor Drives for Hybrid Electric Vehicle Propulsion Applications, in IEEE Transactions on Vehicular Technology, vol. 56, no. 4, pp. 1561-1572, July 2007. [CrossRef]
  22. L. Aarniovuori, L. I. E. Laurila, M. Niemela and J. J. Pyrhonen, Measurements and Simulations of DTC Voltage Source Converter and Induction Motor Losses, in IEEE Transactions on Industrial Electronics, vol. 59, no. 5, pp. 2277-2287, May 2012. [CrossRef]
  23. T. Nemeth, A. Bubert, J. N. Becker, R. W. De Doncker and D. U. Sauer, A Simulation Platform for Optimization of Electric Vehicles With Modular Drivetrain Topologies, in IEEE Transactions on Transportation Electrification, vol. 4, no. 4, pp. 888-900, Dec. 2018. [CrossRef]
  24. Stabile, J. O. Estima, C. Boccaletti and A. J. Marques Cardoso, Converter Power Loss Analysis in a Fault-Tolerant Permanent-Magnet Synchronous Motor Drive, in IEEE Transactions on Industrial Electronics, vol. 62, no. 3, pp. 1984-1996, March 2015. [CrossRef]
  25. D. Zhang, D. Cittanti, P. Sun, J. Huber, R. I. Bojoi and J. W. Kolar, Detailed Modeling and In-Situ Calorimetric Verification of Three-Phase Sparse NPC Converter Power Semiconductor Losses, in IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 11, no. 3, pp. 3409-3423, June 2023. [CrossRef]
  26. Choe, Y.Y., Oh, S.Y., Ham, S.H., Jang, I.S., Cho, S.Y., Lee, J. and Ko, K.C., 2012. Comparison of concentrated and distributed winding in an IPMSM for vehicle traction. Energy Procedia, 14, pp.1368- 1373. [CrossRef]
  27. Hassan, W. and Wang, B., 2012, June. Efficiency optimization of PMSM based drive system. In Proceedings of The 7th International Power Electronics and Motion Control Conference (Vol. 2, pp. 1027-1033). [CrossRef]
  28. G. Scelba et al., Combined Rotor Position Estimation and Temperature Monitoring in Sensorless Synchronous Motor Drives, 2018 IEEE 9th International Symposium on Sensorless Control for Electrical Drives (SLED), Helsinki, Finland, 2018, pp. 30-35. [CrossRef]
  29. Z. Qu, T. Tuovinen and M. Hinkkanen, Minimizing losses of a synchronous reluctance motor drive taking into account core losses and magnetic saturation, 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 2014, pp. 1-10. [CrossRef]
  30. C. Cavallaro, A. O. Di Tommaso, R. Miceli, A. Raciti, G. R. Galluzzo and M. Trapanese, Efficiency enhancement of permanent-magnet synchronous motor drives by online loss minimization approaches, in IEEE Transactions on Industrial Electronics, vol. 52, no. 4, pp. 1153-1160, Aug. 2005. [CrossRef]
  31. Gupta, K.K. and Bhatnagar, P., 2017. Multilevel inverters: conventional and emerging topologies and their control. Academic Press.
  32. M. Valente, F. Iannuzzo, Y. Yang and E. Gurpinar, Performance Analysis of a Single-phase GaN-based 3L-ANPC Inverter for Photovoltaic Applications, 2018 IEEE 4th Southern Power Electronics Conference (SPEC), Singapore, 2018, pp. 1-8. [CrossRef]
  33. S. Mita et al., Power Loss Modelling of GaN HEMT-based 3L-ANPC Three-Phase Inverter for different PWM Techniques, 2022 24th European Conference on Power Electronics and Applications (EPE'22 ECCE Europe), Hanover, Germany, 2022, pp. P.1-P.10.
  34. Schweizer, M. and Kolar, J.W., 2012. Design and implementation of a highly efficient three-level T-type converter for low-voltage applications. IEEE Transactions on Power Electronics, 28(2), pp.899- 907. [CrossRef]
  35. Jørgensen, A.B., Sønderskov, S.H., Beczkowski, S., Bidoggia, B. and Munk-Nielsen, S., 2020. Analysis of cascaded silicon carbide MOSFETs using a single gate driver for medium voltage applications. IET Power Electronics, 13(3), pp.413-419. [CrossRef]
  36. J. Roig et al., Series-connected GaN transistors for ultra-fast high-voltage switch (>1kV), 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 2017, pp. 3043-3048. [CrossRef]
  37. J. Rodriguez, Jih-Sheng Lai and Fang Zheng Peng, Multilevel inverters: a survey of topologies, controls, and applications, in IEEE Transactions on Industrial Electronics, vol. 49, no. 4, pp. 724-738, Aug. 2002. [CrossRef]
  38. S. Foti et al., A novel Hybrid N-Level T-Type Inverter Topology, 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 2019, pp. 5507-5513. [CrossRef]
  39. Yu, E.T., Dang, X.Z., Yu, L.S., Qiao, D., Asbeck, P.M., Lau, S.S., Sullivan, G.J., Boutros, K.S. and Redwing, J.M. Piezoelectric enhancement of Schottky barrier heights in GaN-AlGaN HFET structures. In 56th Annual Device Research Conference Digest (Cat. No. 98TH8373) (pp. 116-117), June 1998. [CrossRef]
  40. R. Gelagaev, P. Jacqmaer and J. Driesen, A Fast Voltage Clamp Circuit for the Accurate Measurement of the Dynamic ON-Resistance of Power Transistors, in IEEE Transactions on Industrial Electronics, vol. 62, no. 2, pp. 1241-1250, Feb. 2015. [CrossRef]
  41. G. Zulauf, M. Guacci and J. W. Kolar, Dynamic on-Resistance in GaN-on-Si HEMTs: Origins, Dependencies, and Future Characterization Frameworks, in IEEE Transactions on Power Electronics, vol. 35, no. 6, pp. 5581-5588, June 2020. [CrossRef]
  42. C. Schulte and J. Böcker, Co-simulation of an electric traction drive, 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 2013, pp. 974-978. [CrossRef]
  43. V. Ballestín-Bernad, J. Sergio Artal-Sevil and J. Antonio Domínguez-Navarro, Co-Simulation of a Two-Phase Axial-Gap Transverse Flux Machine, 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 2022, pp. 956-961. [CrossRef]
  44. G. Turrisi, L. D. Tornello, G. Scelba, M. Cacciato and G. Scarcella, Losses Evaluation in Current Source Inverter Topologies for Automotive Traction Applications, 2023 25th European Conference on Power Electronics and Applications (EPE'23 ECCE Europe), Aalborg, Denmark, 2023, pp. 1-11. [CrossRef]
Preprints 93709 g001
Figure 1. Standard IGBT-based 2L VSI topology used in the automotive industry.
Figure 1. Standard IGBT-based 2L VSI topology used in the automotive industry.
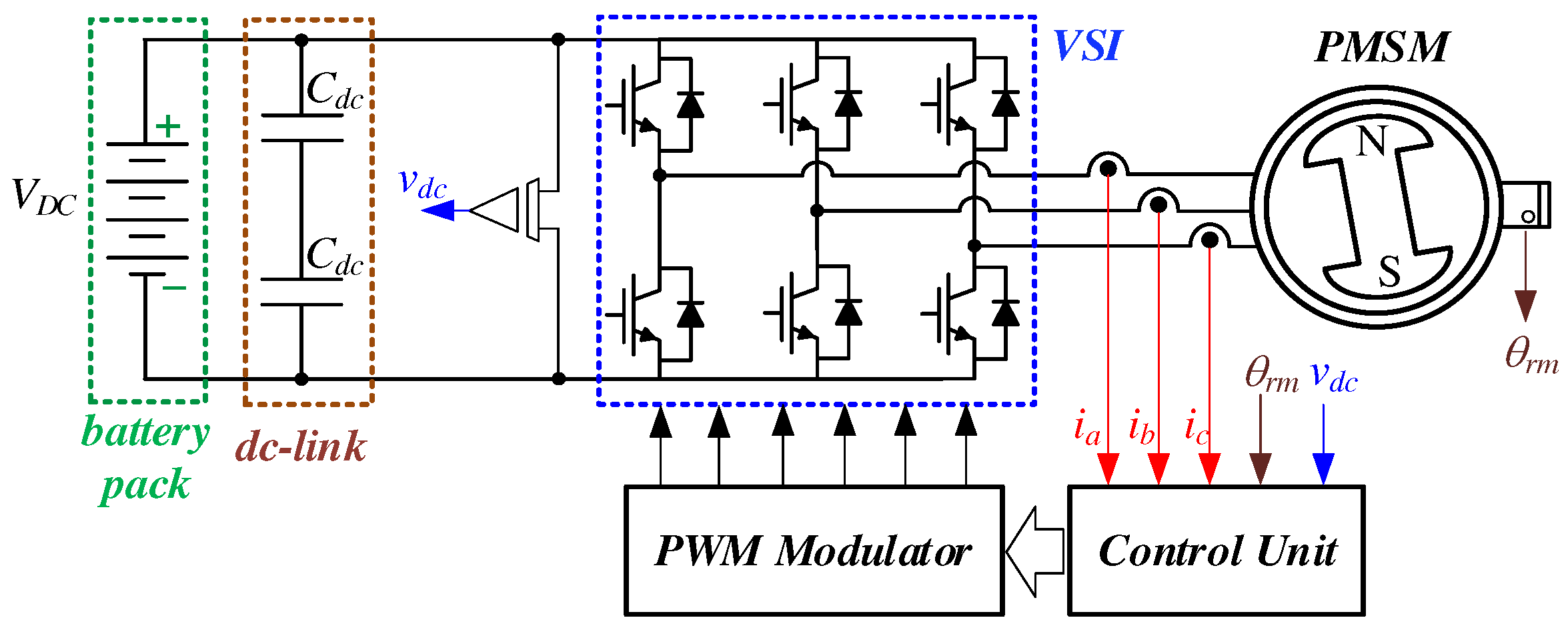
Preprints 93709 g001
Preprints 93709 g002
Figure 2. Closed loop implementation of traction drive.
Figure 2. Closed loop implementation of traction drive.
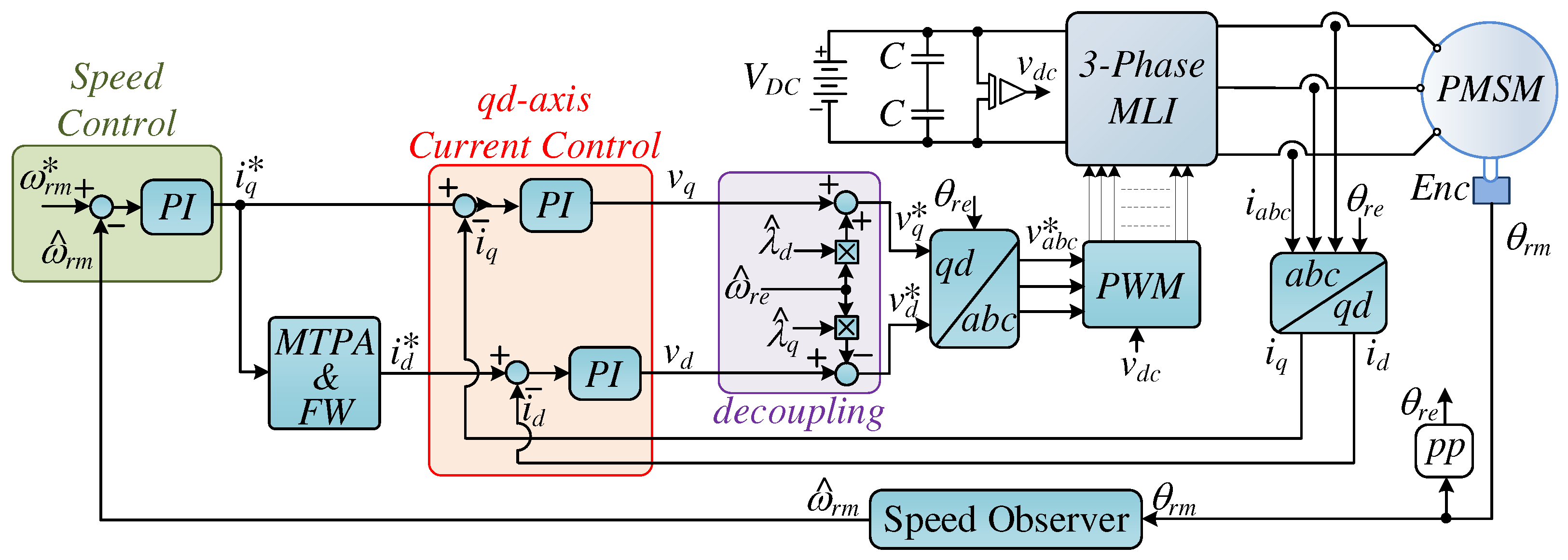
Preprints 93709 g002
Preprints 93709 g003
Figure 3. Dynamic Equivalent circuit of the IPM machine: (a) q-axis and (b) d-axis.
Figure 3. Dynamic Equivalent circuit of the IPM machine: (a) q-axis and (b) d-axis.
Preprints 93709 g003
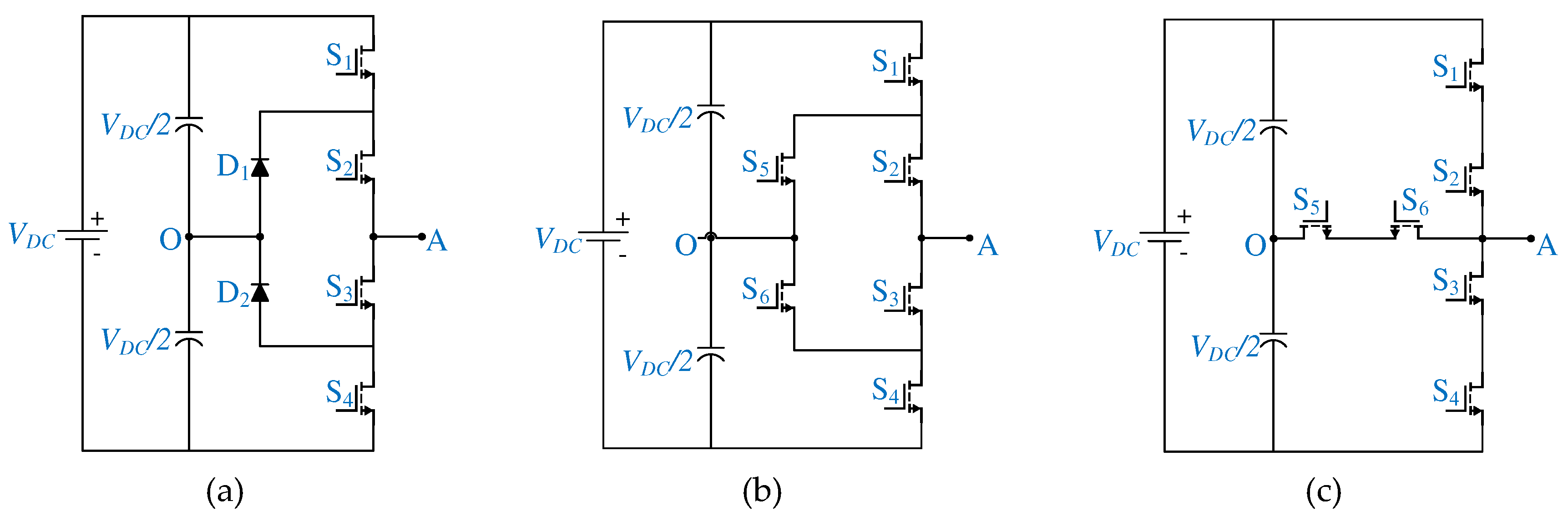
Preprints 93709 g004
Figure 4. MLI topologies considered (a) NPC (b) ANPC (c) TNPC.
Figure 4. MLI topologies considered (a) NPC (b) ANPC (c) TNPC.
Preprints 93709 g004
Preprints 93709 g005
Figure 5. Modulation schemes and corresponding switching pattern for (a)NPC and (b)ANPC (c)TNPC.
Figure 5. Modulation schemes and corresponding switching pattern for (a)NPC and (b)ANPC (c)TNPC.
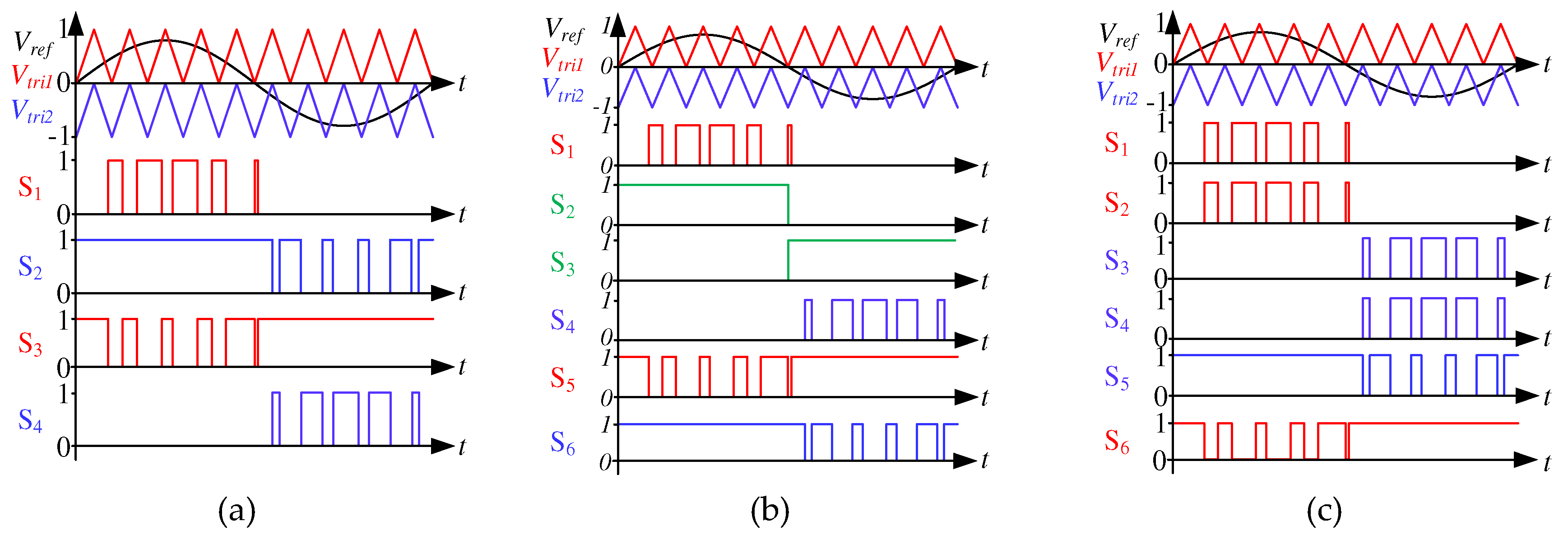
Preprints 93709 g005
Preprints 93709 g006
Figure 6. SGT120R65AES GaN MOSFET.
Figure 6. SGT120R65AES GaN MOSFET.
Preprints 93709 g006
Preprints 93709 g007
Figure 7. (a)Estimation of VGS(th) using the curve Tracer and (b) VGS(th) at different temperatures.
Figure 7. (a)Estimation of VGS(th) using the curve Tracer and (b) VGS(th) at different temperatures.
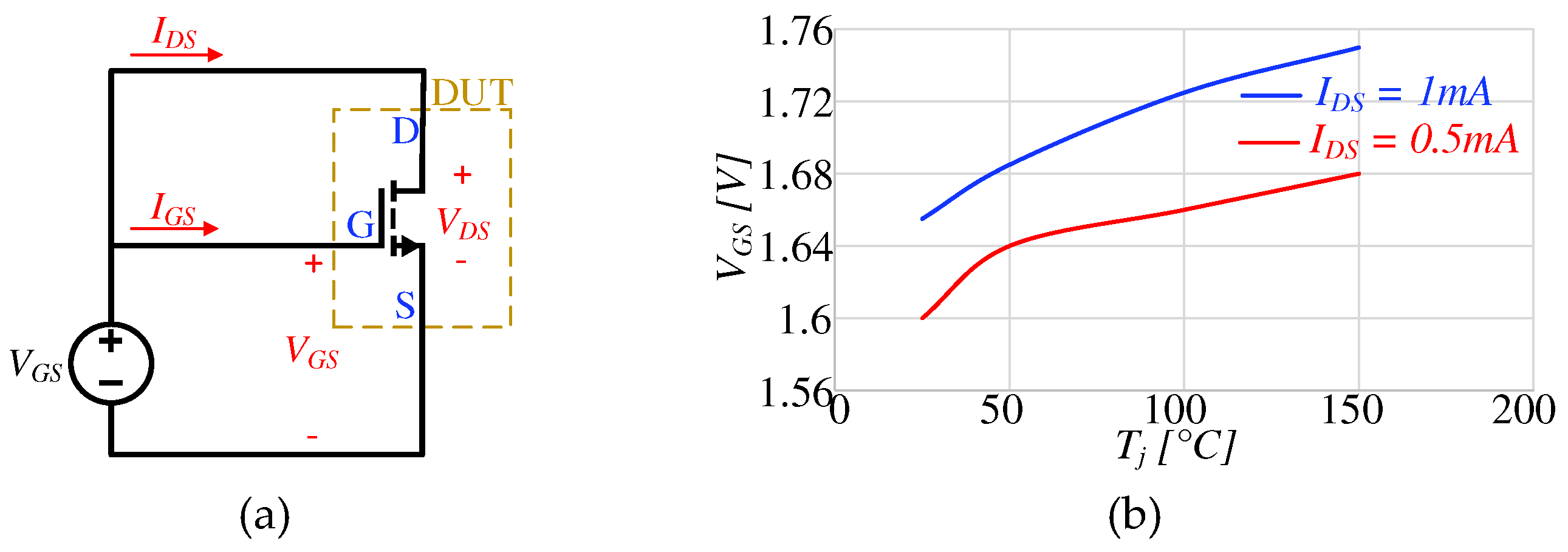
Preprints 93709 g007
Preprints 93709 g008
Figure 8. Output v-i characteristics at different junction temperature Tj and with VGS = 6V.
Figure 8. Output v-i characteristics at different junction temperature Tj and with VGS = 6V.
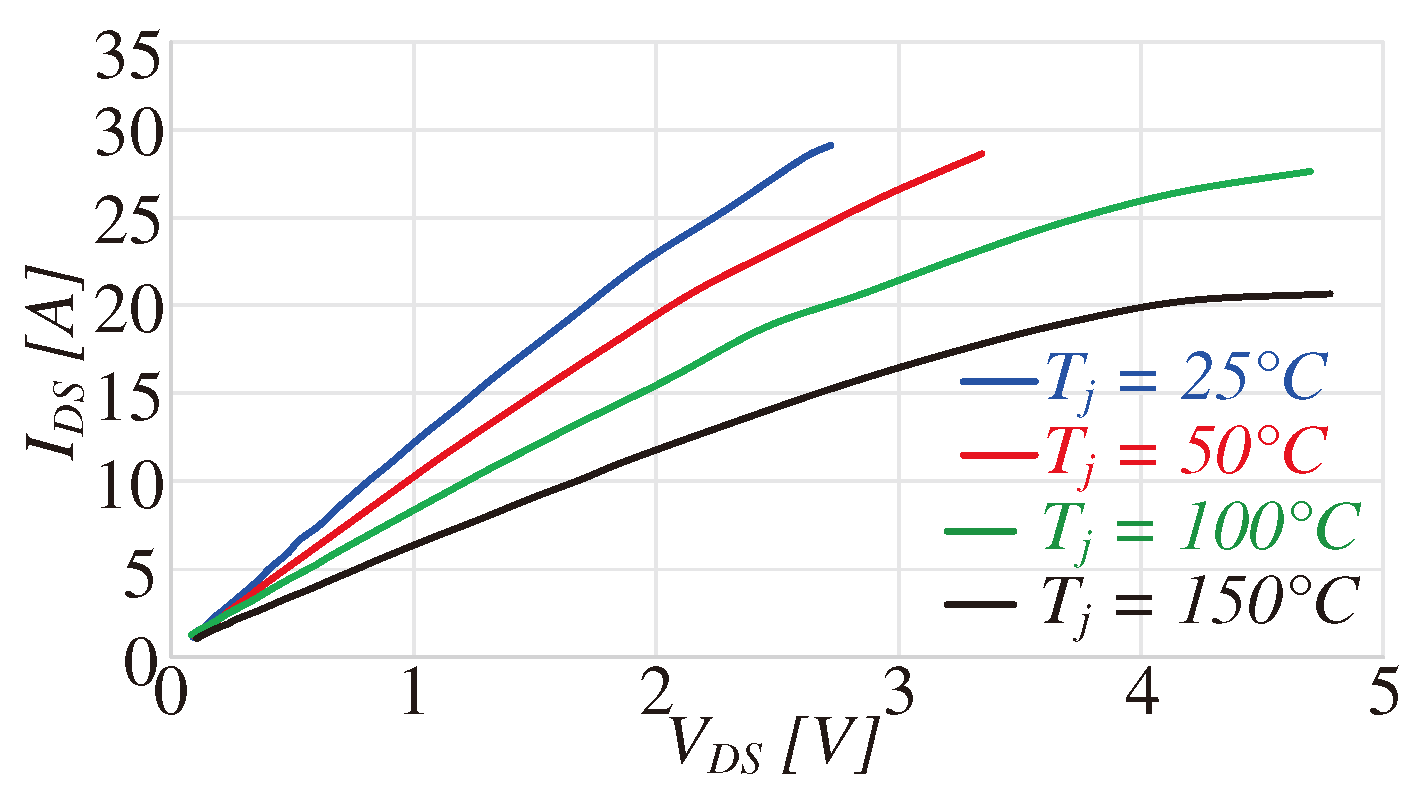
Preprints 93709 g008
Preprints 93709 g009
Figure 9. Static RDS(on) at different junction temperatures Tj and IDS.
Figure 9. Static RDS(on) at different junction temperatures Tj and IDS.
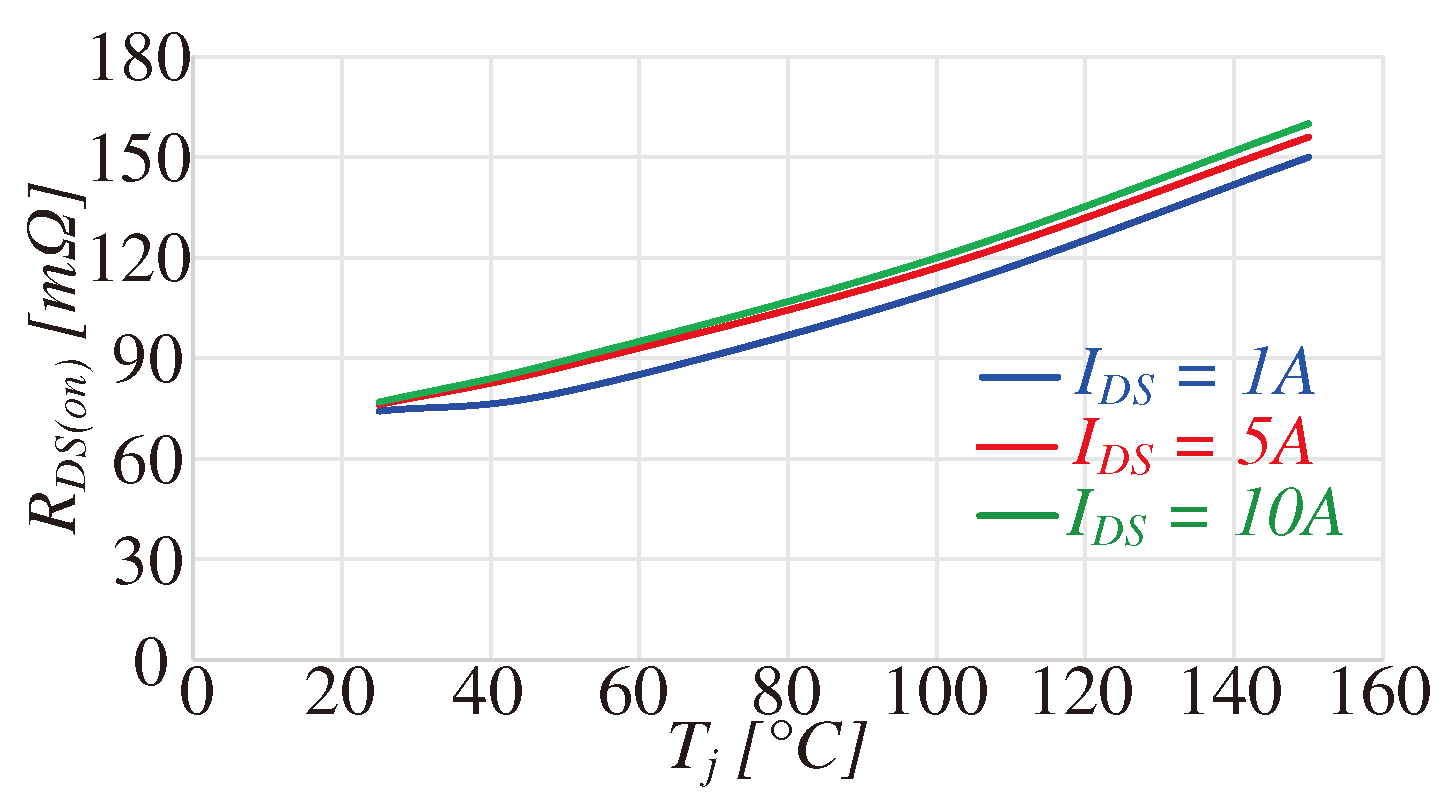
Preprints 93709 g009
Preprints 93709 g010
Figure 10. Characterization board used for the dynamic characterization of GaN HEMTs power devices.
Figure 10. Characterization board used for the dynamic characterization of GaN HEMTs power devices.
Preprints 93709 g010
Preprints 93709 g011
Figure 11. (a) Clamping circuit used to measure the VDS(on) (b) Evaluation of VDS(on) at VDD=100V and IDS=5A.
Figure 11. (a) Clamping circuit used to measure the VDS(on) (b) Evaluation of VDS(on) at VDD=100V and IDS=5A.
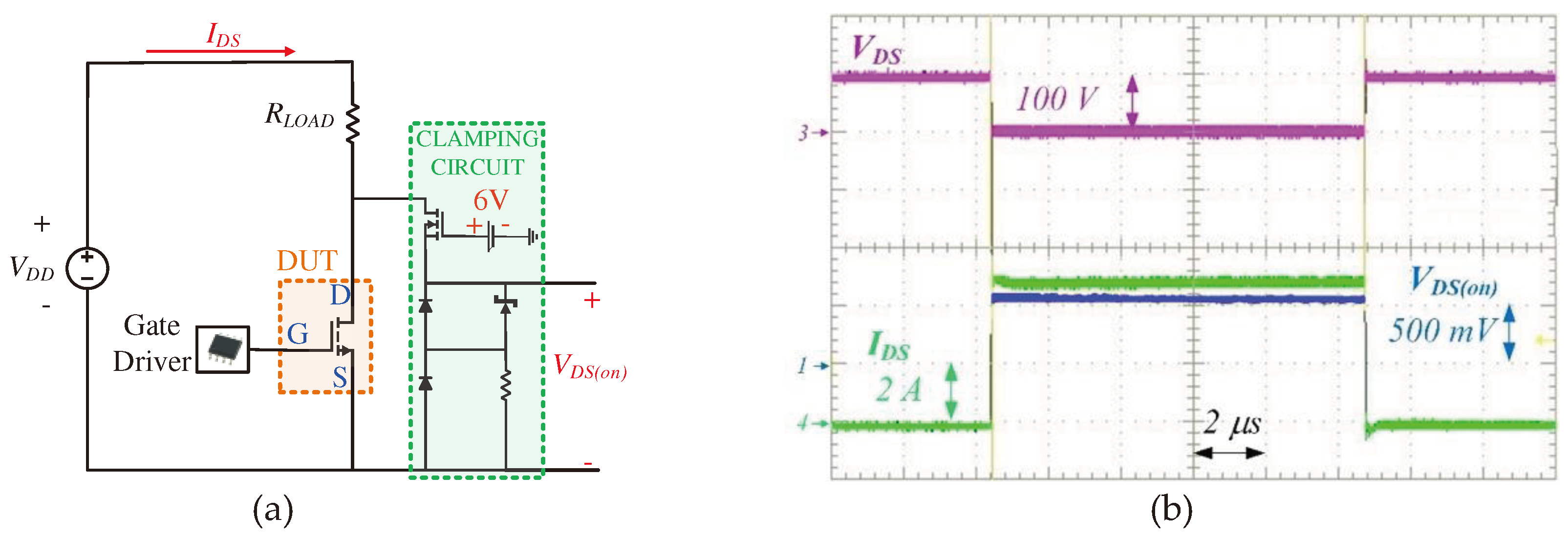
Preprints 93709 g011
Preprints 93709 g012
Figure 12. Measurement of RDS(on) at different VDS and Tj.
Figure 12. Measurement of RDS(on) at different VDS and Tj.
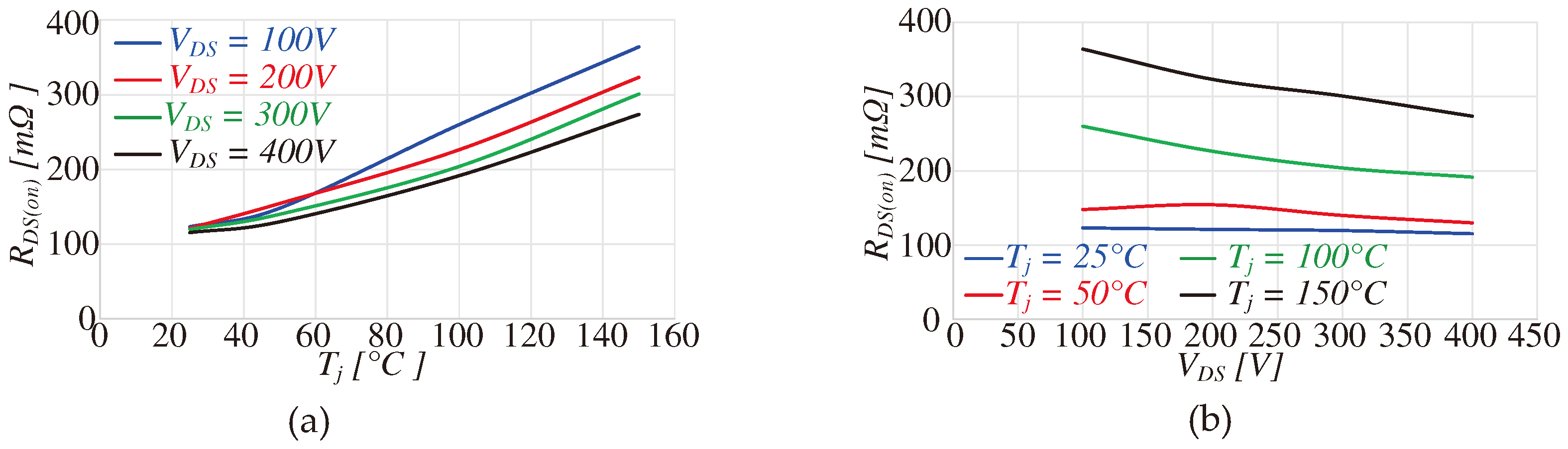
Preprints 93709 g012
Preprints 93709 g013
Figure 13. Double pulse tests: (a) electric scheme, (b) Eon estimation and (c) Eoff estimation.
Figure 13. Double pulse tests: (a) electric scheme, (b) Eon estimation and (c) Eoff estimation.
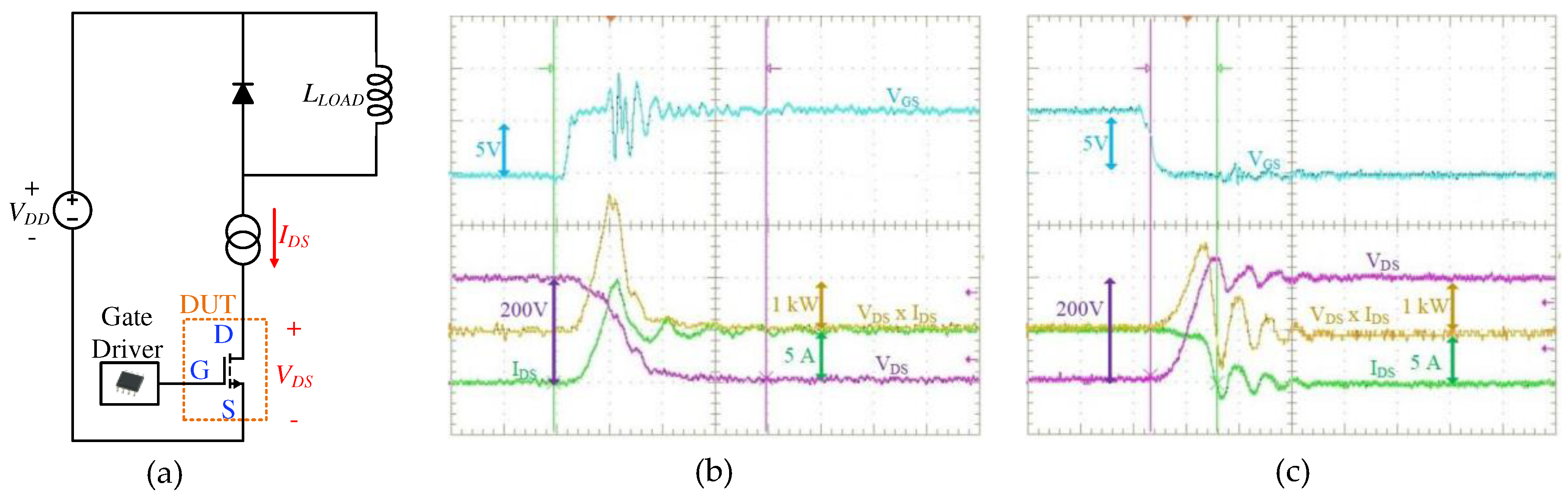
Preprints 93709 g013
Preprints 93709 g014
Figure 14. Switching energy losses evaluated at different IDS and Rg.
Figure 14. Switching energy losses evaluated at different IDS and Rg.
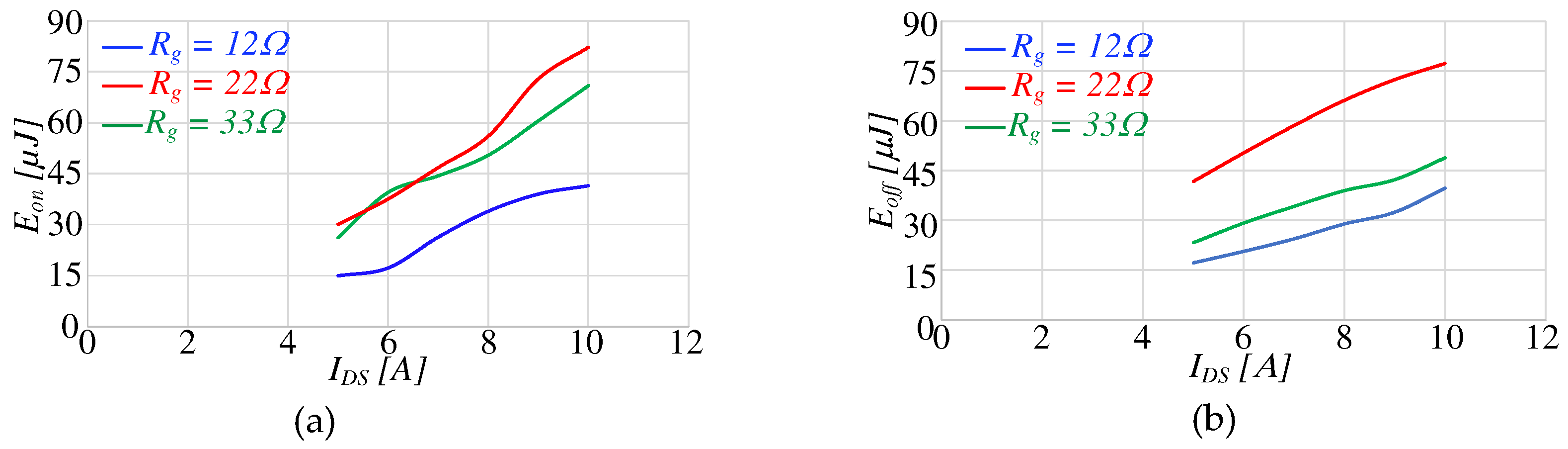
Preprints 93709 g014
Preprints 93709 g015
Figure 15. Switching energy losses with respect to change in the junction temperature.
Figure 15. Switching energy losses with respect to change in the junction temperature.
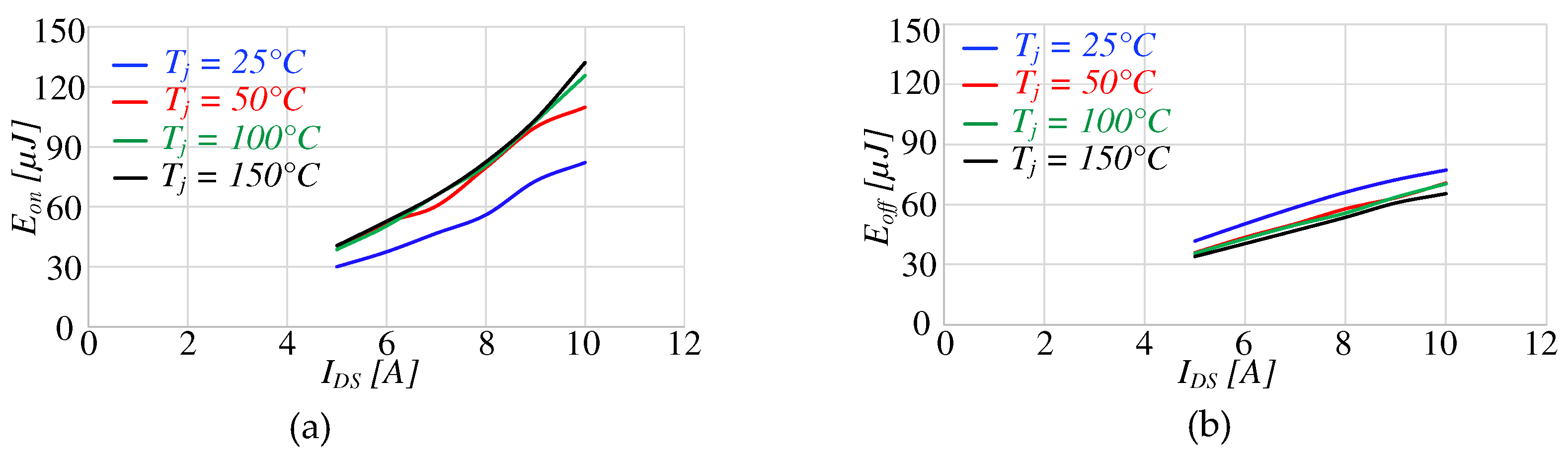
Preprints 93709 g015
Preprints 93709 g016
Figure 16. GaN HEMT PSIM MOSFET(Eon) model according to SGT120R65AES prototype.
Figure 16. GaN HEMT PSIM MOSFET(Eon) model according to SGT120R65AES prototype.
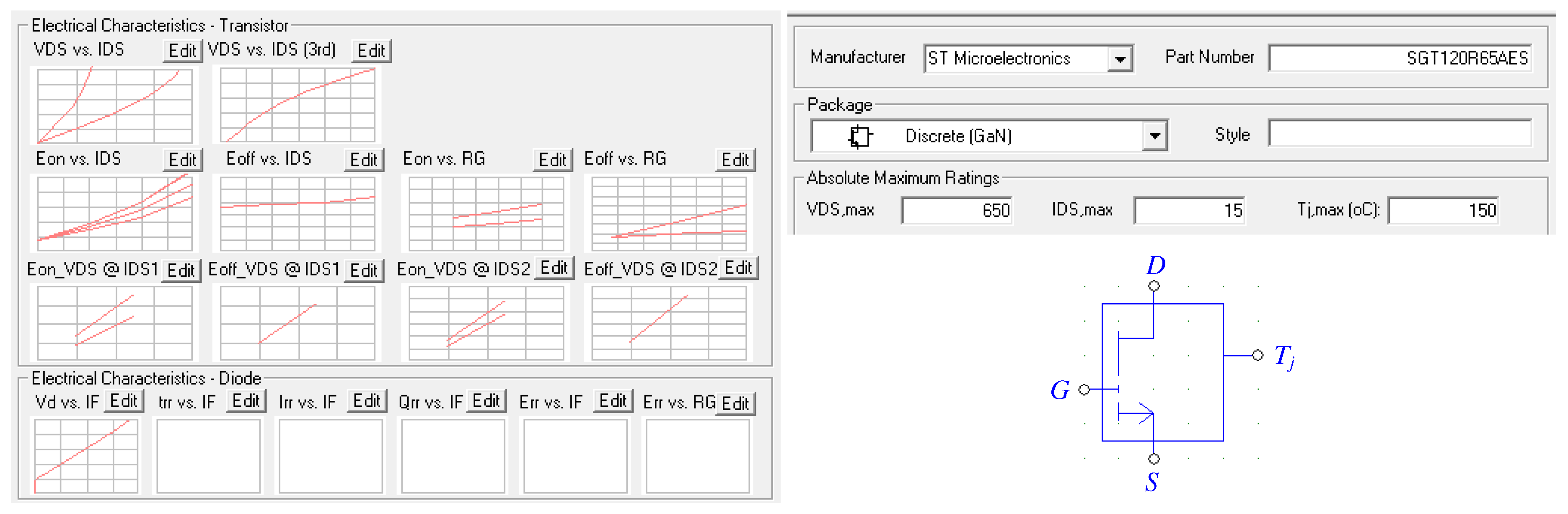
Preprints 93709 g016
Preprints 93709 g017
Figure 17. PSIM implementation of IPM motor drive.
Figure 17. PSIM implementation of IPM motor drive.
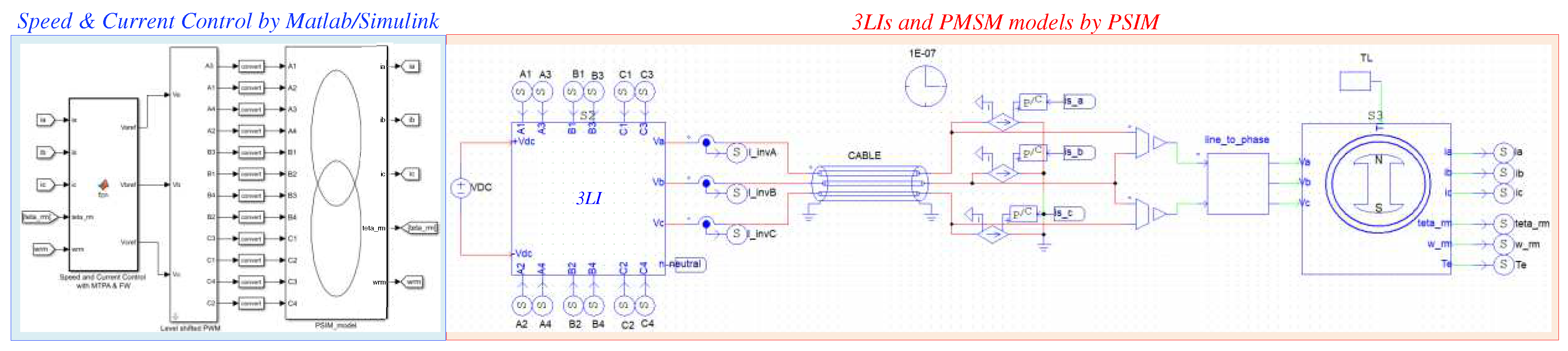
Preprints 93709 g017
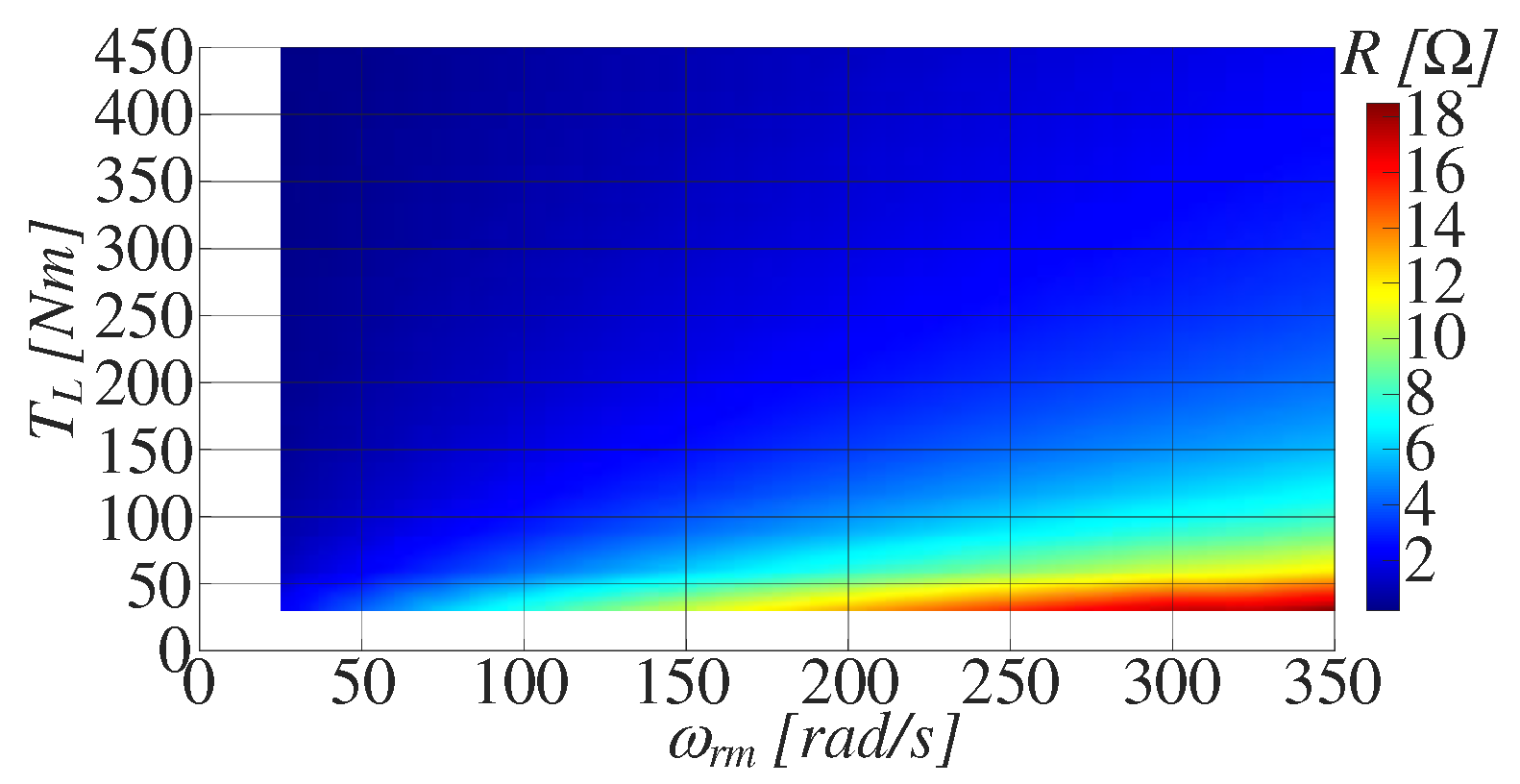
Preprints 93709 g018
Figure 18. Relationship between R and Te, ωrm.
Figure 18. Relationship between R and Te, ωrm.
Preprints 93709 g018
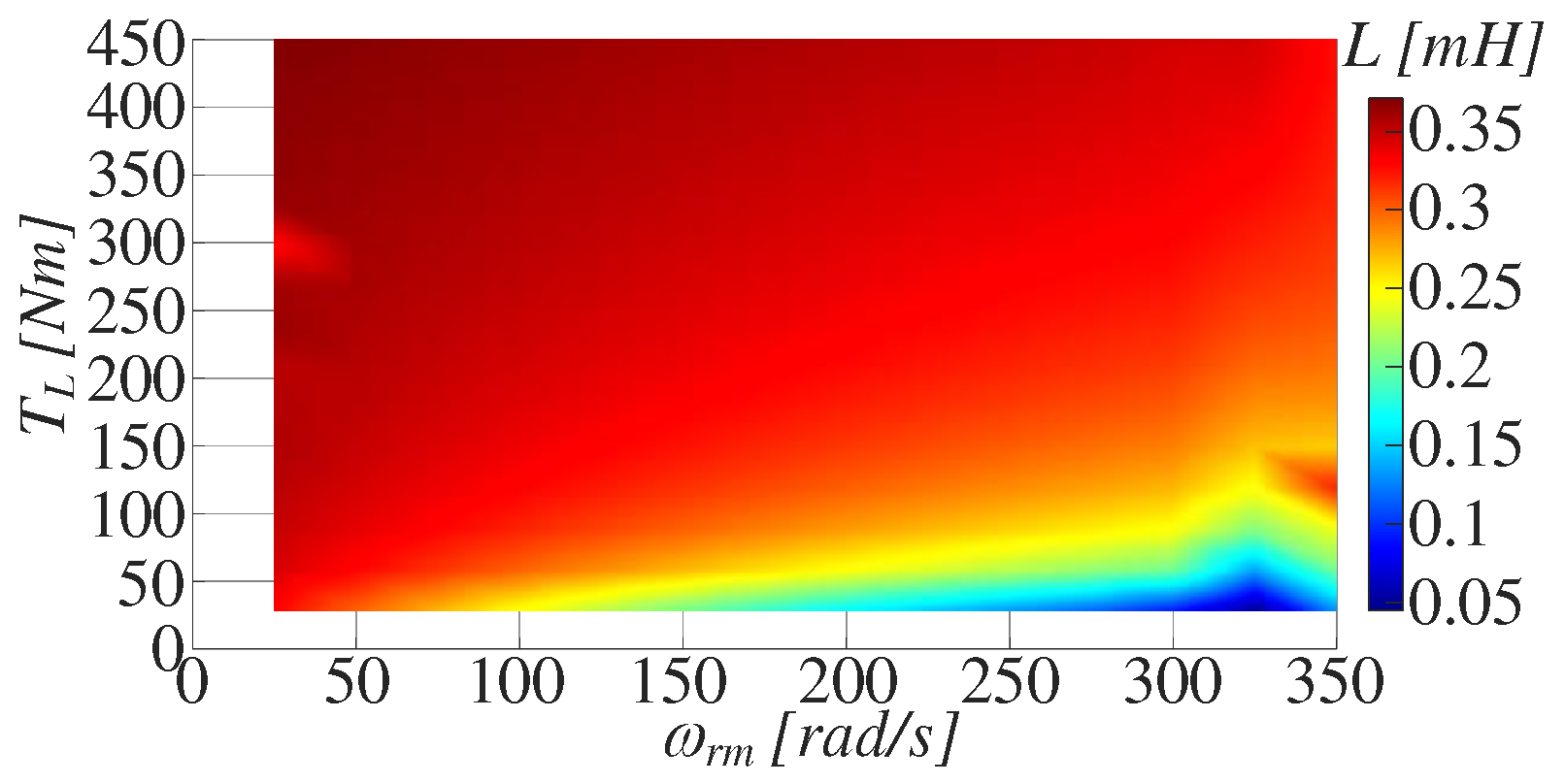
Preprints 93709 g019
Figure 19. Relationship between L and Te, ωrm.
Figure 19. Relationship between L and Te, ωrm.
Preprints 93709 g019
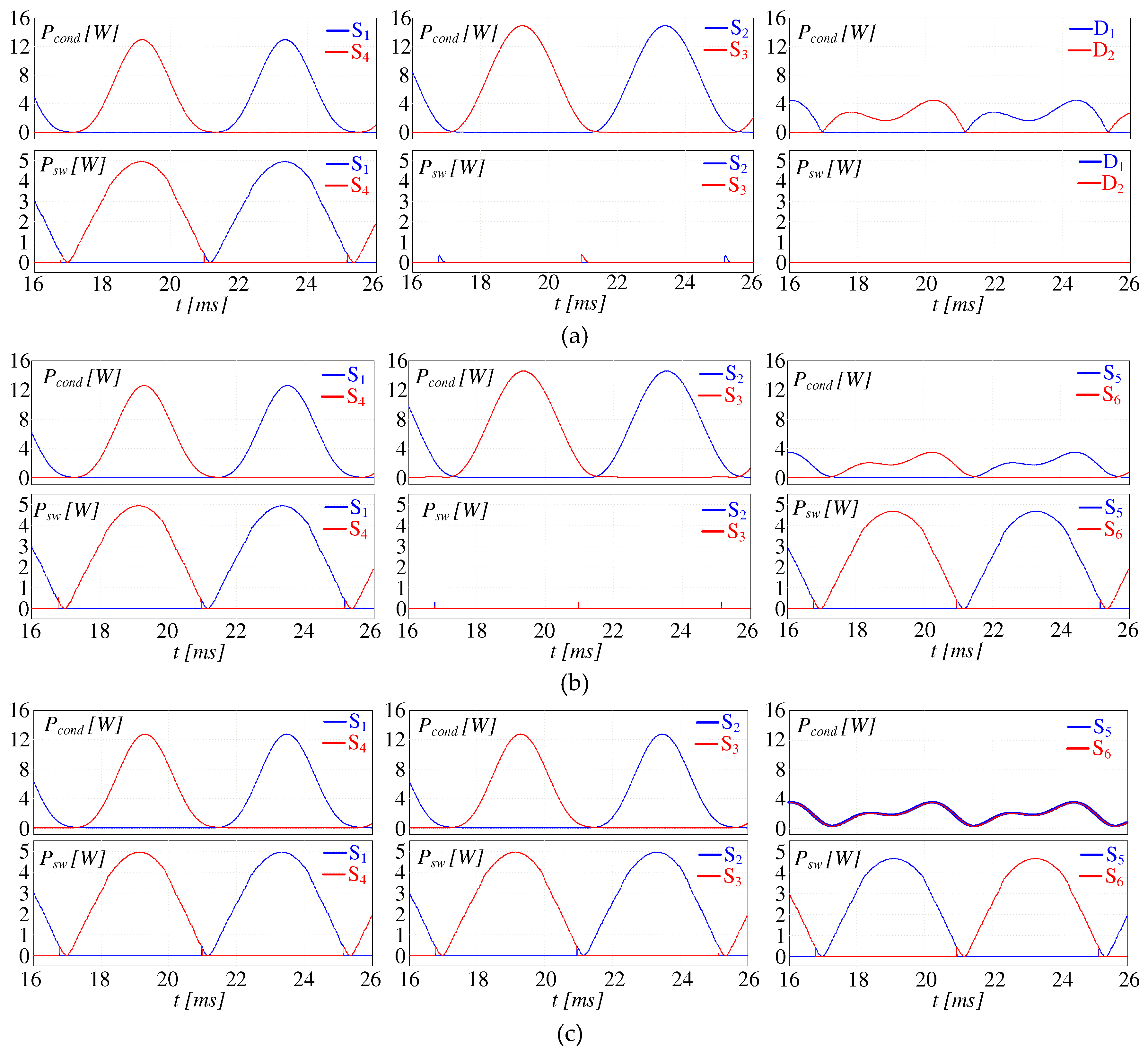
Preprints 93709 g020
Figure 20. Profile of power losses distribution across the switches composing the three 3LIs legs, averaged in each switching period: (a) NPC, (b) ANPC and (c) TNPC, with the drive operated at TL=450Nm and ωrm=250rad/s.
Figure 20. Profile of power losses distribution across the switches composing the three 3LIs legs, averaged in each switching period: (a) NPC, (b) ANPC and (c) TNPC, with the drive operated at TL=450Nm and ωrm=250rad/s.
Preprints 93709 g020
Preprints 93709 g021
Figure 21. Distribution of conduction losses in the considered 3LI topologies, at the following operating conditions: (a) TL=450Nm and ωrm=50rad/s, (b) TL=450Nm and ωrm=250rad/s and (c) TL=150Nm and ωrm=350rad/s.
Figure 21. Distribution of conduction losses in the considered 3LI topologies, at the following operating conditions: (a) TL=450Nm and ωrm=50rad/s, (b) TL=450Nm and ωrm=250rad/s and (c) TL=150Nm and ωrm=350rad/s.
Preprints 93709 g021
Preprints 93709 g022
Figure 22. Distribution of switching losses in the considered 3LI topologies, at the following operating conditions: (a) TL=450Nm and ωrm=50rad/s, (b) TL=450Nm and ωrm=250rad/s and (c) TL=150Nm and ωrm=350rad/s.
Figure 22. Distribution of switching losses in the considered 3LI topologies, at the following operating conditions: (a) TL=450Nm and ωrm=50rad/s, (b) TL=450Nm and ωrm=250rad/s and (c) TL=150Nm and ωrm=350rad/s.
Preprints 93709 g022
Preprints 93709 g023
Figure 23. Efficiency maps of the considered 3LIs: (a) NPC, (b) ANPC and (c) TNPC.
Figure 23. Efficiency maps of the considered 3LIs: (a) NPC, (b) ANPC and (c) TNPC.
Preprints 93709 g023
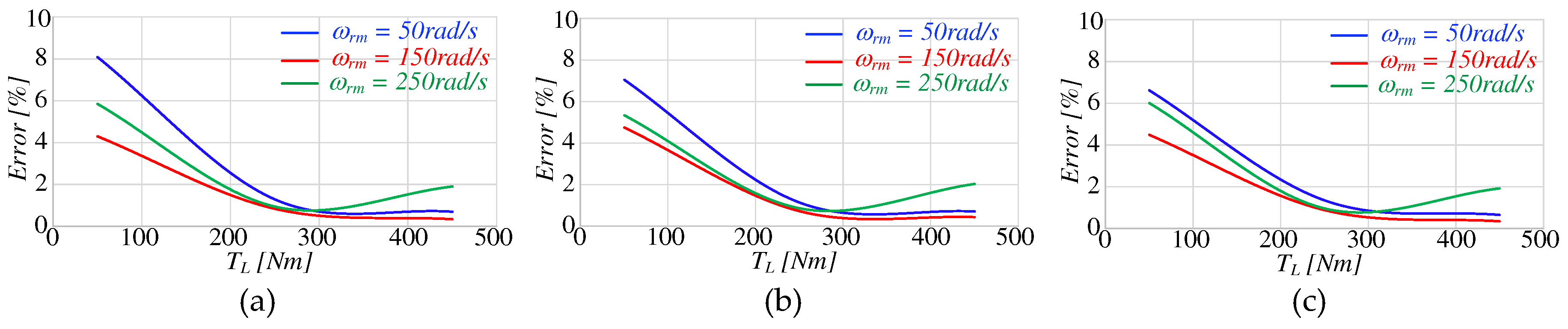
Preprints 93709 g024
Figure 24. Error percentage between model of traction drive and equivalent load modelled inverter.
Figure 24. Error percentage between model of traction drive and equivalent load modelled inverter.
Preprints 93709 g024
Table 1. Material Properties of Si, GaN and SiC.
Table 1. Material Properties of Si, GaN and SiC.
Parameter Unit Si GaN SiC
Band Gap (Eg) eV 1.12 3.39 3.26
Critical Field (Ecrit) MV/cm 0.23 3.3 2.2
Electron Mobility (µn) cm2/(V∙s) 1400 1500 950
Permittivity (ɛr) 11.8 9 9.7
Thermal Conductivity (λ) W/(cm∙K) 1.5 1.3 3.8
Table 2. IPM traction drive.
Table 2. IPM traction drive.
Parameter Value
Maximum Power 110kW
DC Bus Voltage 800V
Maximum torque @ rated speed 450Nm
Rated Speed (ωrmR) 250rad/s
Maximum Speed (ωrmax) 350rad/s
Table 3. IPM Motor Parameters.
Table 3. IPM Motor Parameters.
Parameter Symbol Value
Stator Resistance Rs 18.3mΩ
q-axis Inductance Lq 745μH
d-axis Inductance Ld 361.4μH
Permanent Magnet Flux λpm 0.45Wb
Iron Loss Resistance @ ωrmR Rc 50Ω
Table 5. Main Specifications of SGT120R65AES.
Table 5. Main Specifications of SGT120R65AES.
Parameter Value
Drain-source blocking voltage (V(BL)DSS) 650V
Continuous drain current (IDS) 15A @ Tcase=25°C
12A @ Tcase=100°C
Operating junction temperature (Tj) -50°C to +150°C
Table 6. Dynamic RDS(on) at VDS = 400V and IDS = 5A at Tj = 25 °C.
Table 6. Dynamic RDS(on) at VDS = 400V and IDS = 5A at Tj = 25 °C.
t [µs] 2.5 5 7.5 10
RDS(on) [mΩ] 121.3 117.8 115.5 115.5
Table 7. Modulation functions and RMS currents across the devices.
Table 7. Modulation functions and RMS currents across the devices.
Preprints 93709 i005
Table 8. Interval points for different topologies.
Table 8. Interval points for different topologies.
Topology Device n1 n2
NPC S1 0 n/2
S2 n/2 n ( π + φ ) / ( 2 π )
ANPC S1 0 n/2
S2 - -
S5 0 n/2
TNPC S1 0 n/2
S2 0 n/2
S5 n/2 N
Table 9. Simulation times of the proposed approach and traction drive model.
Table 9. Simulation times of the proposed approach and traction drive model.
Topology Traction Drive Model Proposed Analytical Approach + RL circuit Improvement
NPC, ANPC, TNPC ≈16min ≈5min ≈68%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated