Prerpints.org logo
Preprint
Article

Data-Driven ICS Network Simulation for Synthetic Data Generation

Altmetrics

Downloads

133

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 December 2023

Posted:

19 December 2023

You are already at the latest version

Alerts
Abstract
Industrial Control Systems (ICS) are integral to managing and optimizing processes in various industries, including manufacturing, power generation, and more. However, the scarcity of widely adopted ICS datasets hampers research efforts in areas like optimization and security. This scarcity arises due to the substantial cost and technical expertise required to create physical ICS environments. In response to these challenges, this paper presents a groundbreaking approach to generating synthetic ICS data through a data-driven ICS network simulation. We circumvent the need for expensive hardware by recreating the entire ICS environment in software. Moreover, rather than manually replicating the control logic of ICS components, we leverage existing data to autonomously generate control logic. The core of our method involves the stochastic setting of setpoints, which introduces randomness into the generated data. Setpoints serve as target values for controlling the operation of the ICS process. This approach enables us to augment existing ICS datasets and cater to the data requirements of machine learning-based ICS intrusion detection systems and other data-driven applications. Our simulated ICS environment employs virtualized containers to mimic the behavior of real-world PLCs and SCADA systems, while control logic is deduced from publicly available ICS datasets. Setpoints are generated probabilistically to ensure data diversity. Experimental results validate the fidelity of our synthetic data, emphasizing its ability to closely replicate temporal and statistical characteristics of real-world ICS networks. In conclusion, this innovative data-driven ICS network simulation offers a cost-effective and scalable solution for generating synthetic ICS data. It empowers researchers in the field of ICS optimization and security with diverse, realistic datasets, furthering advancements in this critical domain. Future work may involve refining the simulation model and exploring additional applications for synthetic ICS data.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

Industrial control system (ICS) is widely used to manage and control processes in industries such as manufacturing, power generation, communications, and chemicals. As ICS plays an increasingly core role in the industry, it has become the subject of various studies such as optimization [1,2] to improve process efficiency. These studies require datasets collected from actual ICS because they require process status information in many cases. SWaT[3] and HAI[4] are datasets collected from a test bed configured similarly to an actual ICS and are used in many data-driven studies.
While the need for and importance of ICS datasets is increasing, the number of widely adopted datasets is limited. There are two main reasons for this. 1) Building an ICS environment, including hardware, costs a lot of money. The ICS environment is largely implemented with supervisory control and data acquisition (SCADA) systems, distributed control systems (DCSs), programmable logic controllers (PLCs), human-machine interfaces (HMIs), and various sensors[5]. These devices require high reliability and performance to delicately control the process and are generally expensive. 2) Even if hardware devices are equipped, implementing the logic to control these devices requires the know-how of skilled workers.
Even if public datasets exist, more data may be required. For example, machine learning or deep learning-based ICS intrusion detection systems [21,22] require a large amount of learning data to be supplied to achieve high detection performance. For this purpose, augmentation of the dataset is necessary. The best way to augment data is to recreate the ICS environment where the dataset was collected, but this presents the following challenges: 1) In general, a network design that collects publicly available ICS data sets is presented, but the control logic of detailed components such as PLC is often not disclosed, making it difficult to reproduce. 2) In the ICS network, numerous components (or data points) interact. Therefore, even if well-known generative models such as generative adversarial networks (GAN)[6] or variational autoencoder (VAE)[7] are utilized, it is not appropriate to generate data independently for data points.
However, it is essential to acknowledge the limitations and challenges posed by existing methods for data augmentation in the context of Industrial Control Systems (ICS). While the need for additional data is evident, recreating the ICS environment to augment datasets presents its own set of issues:
Lack of Control Logic Disclosure: In many cases, publicly available ICS datasets do not provide comprehensive details regarding the control logic of intricate components like Programmable Logic Controllers (PLCs). This lack of disclosure hampers the ability to accurately reproduce the control strategies and behaviors of these critical components in a simulated environment.
Interconnected Data Points: Within an ICS network, numerous components and data points interact intricately. Unlike traditional data augmentation scenarios, where generative models like Generative Adversarial Networks (GANs) or Variational Autoencoders (VAEs) may be applied independently to generate data points, ICS data points are interdependent. Changes in one component can have ripple effects on others. Therefore, conventional generative models may not capture the complex interdependencies and correlations present in ICS networks effectively.
Addressing these challenges requires innovative approaches that can replicate not only the data but also the intricate control logic and interactions between components accurately. These challenges underscore the need for more specialized and data-driven methods tailored specifically to the unique characteristics of ICS environments.
Our insights for resolving the above challenges and generating ICS artificial data are as follows. 1) Instead of using expensive hardware equipment, the ICS environment is completely recreated in software. 2) Instead of completely reproducing the control logic of equipment such as PLC, the logic is reproduced based on data. 3) Probabilistically set setpoints to control or provide randomness to the generated data. Setpoint is a target value for the process value of the control system and is used to control the operation of the process.
Combining the above insights, in this paper, we propose a method to simulate the ICS network environment where data is collected for a given original ICS dataset and augment the data. First, we build a simulated ICS environment using virtualized containers containing PLCs or SCADA. Each PLC uses a software-virtualized hardware layer instead of actual hardware. Additionally, the control logic of the PLC is reproduced using the existing ICS dataset to operate identically to the actual PLC it is intended to imitate. SCADA controls PLC using setpoints, collects data generated from the network, and stores it in a database. Our experimental findings confirm that our simulated ICS environment successfully generates synthetic data that closely mimics the temporal patterns and statistical characteristics of real-world ICS network data. This approach holds promise for enhancing data availability in various ICS research applications, such as optimization and intrusion detection systems. At this time, setpoints are set stochastically to provide randomness to the collected data. The contributions of this paper are as follows.
  • For a given original ICS dataset, we reproduce the ICS network environment where the dataset was collected with a virtualized container.
  • Each container contains a PLC or SCADA, and the control logic of the PLC is regressed from the given ICS data set.
  • SCADA uses setpoints to control PLCs, and the values of setpoints are set probabilistically to ensure the randomness of the collected data sets.
The remainder of this paper is organized as follows. Chapter 2 presents research on actively used public ICS datasets and data generation. Chapter 3 describes the proposed simulated ICS environment architecture and data generation method. Chapter 4 presents experimental results, including a comparison of the similarity between the original and generated datasets. A summary of the proposal and future work are discussed in Chapter 5.

2. Related Work

In this section, we present the work related to our proposal. Chapter 2.1 introduces datasets popularly used in data-driven ICS research. Chapter 2.2 describes previously proposed machine learning-based data generation methods.

2.1. Public Datasets for ICS

SWaT[3] is an ICS testbed for large-scale modern water treatment systems. This testbed aims to design a secure cyber-physical system and is designed to be similar to a full-scale system. This system consists of six processes (P1-6): Raw water intake (P1), chemical disinfection (P2), ultrafiltration (P3), dichlorination using ultraviolet lamps (P4), purification by reverse osmosis (P5), and ultrafiltration membrane backwash and cleaning (P6). The SWaT dataset was collected for the purpose of studying cyber and physical attacks on these processes. This dataset consists of physical datasets such as network packet data and sensor/PLC data, and we are interested in physical datasets. SWaT’s physical dataset has 51 features and contains 946,772 samples.
HAI[4] is a dataset collected from a testbed that implements a steam-turbine power generation and pumped storage hydropower system. This testbed consists of four main processes (P1-P4): Boiler process (P1), turbine process (P2), water-treatment process (P3), and hardware-in-the-loop simulator (P4). This dataset was also collected to study cyberattacks in ICS environments. The most recently collected dataset has 86 features and contains 1,365,500 samples.
Tommy Morris et al. The five datasets presented by[8,9,10,11] are other datasets frequently employed in ICS research. These datasets were collected from the power, gas pipeline, and energy management systems. It is also used, like the other two datasets described above, to study cyber-attacks against ICS.

2.2. Synthetic Data Generation

Artificial data generation is a technique that creates data that is statistically similar to actual data collected in a real-world environment. This technique is frequently used in research where data collection is limited, or privacy must be considered. Tushar et al.[13] generated stochastic data from a smart grid for solar generation. This study divided the state of solar irradiance, which changes randomly throughout the day, into four categories. Then, we modeled transitions between states using a segmented first-order Markov chain and generated data from the learned model. Iftikhar et al.[14,16] proposed a data generation method that reflects statistical characteristics such as trends and patterns. This study used a moving average to control periodic variations such as morning/evening peak and predicted energy consumption data using periodic autoregressive (PAR). Zhang et al.[12] designed a GAN model to generate data for a smart grid. In order to effectively process time series data, this study introduced two distinct statistical characteristics: ‘level’, which is responsible for the mean and scale of the data, and ‘pattern’, which reflects individual activity. Zheng et al.[18] studied the generation of time series data by the phasor measurement unit (PMU) in the power system. GAN was used to learn the underlying physical model that affects the internal relationships of data. While many studies have adopted GANs for data generation, Razghandi et al.[20] proposed a model combining VAE and GAN to generate smart home synthetic time series data. This model learns the distribution of various data types in a smart home without prior knowledge and generates plausible samples. Additionally, by introducing VAE, the mode collapse problem, a common problem of GAN, was improved.
Due to its nature, research on medical data always involves patient privacy concerns. To solve this problem, synthetic data can be used instead of actual patient data. Esteban et al.[15] proposed a GAN-based medical data generation model to publish data without privacy concerns. Simulation-based medical training is frequently employed, but its configuration usually relies on hand-engineered rules. This study uses a data generation model to reproduce a variety of realistic intensive care unit (ICU) situations. Dahmen et al.[17] proposed a method of generating synthetic sensor data that reflects human behavior using a hidden Markov Model (HMM). The authors introduced similarity measures to compare and verify real data and synthetic data.
Additionally, accuracy was improved using the data generated for semi-supervised activity recognition, where only a small amount of annotated data was available. Imtiaz et al.[19] created smart healthcare records using Boundary-seeking GAN (BGAN). This study collected real-world smart healthcare data from geographically separated users and augmented the data to represent diversity in nutritional/behavioral patterns. Using this dataset and GAN, the authors generated time series data containing categorical and numerical values.

3. Proposal

In this chapter, we describe a simulation architecture that reproduces the original ICS environment from which a given ICS dataset was collected and a method for generating data from it. Chapter 3.1 introduces an overview of the ICS simulation environment built entirely in software. Section 3.2 presents a method to mimic the behavior of the control logic of the original PLC involved in a given dataset. Finally, in Section 3.3, we present a method to control newly generated synthetic data and provide randomness simultaneously.

3.1. Overview

Leave a space of one line before and after a figure or an image, i.e., one line between the main text and the top of the figure or image, and one line between the bottom of the figure or image and the caption. The caption has a default space of 12 pt after it so the main text can continue below the caption. If no text follows the figure caption, do not leave any space between the caption and the next headline (the headline has a default space).
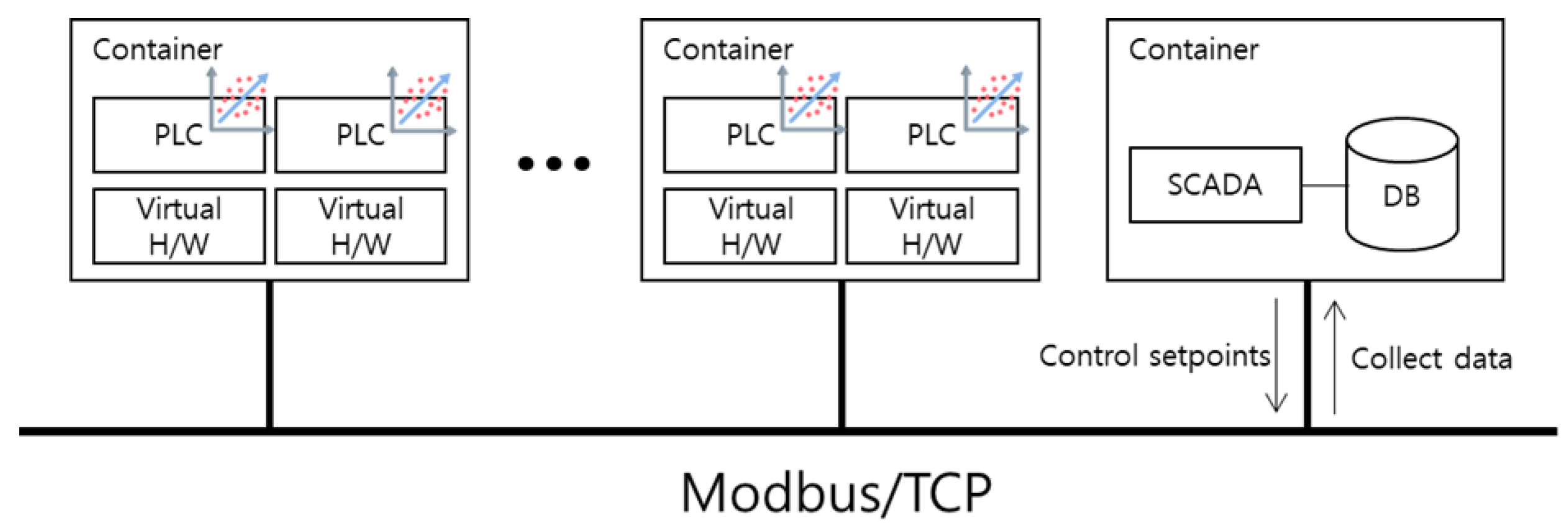
Figure 1 shows the architecture for the proposed simulated ICS environment. We employ virtualized containers to simulate the ICS environment entirely in software, without special hardware devices such as PLCs or sensors. One container contains the SCADA system and a database to collect and store the data generated. The remaining containers contain one or more PLCs, each operating on a virtualized hardware layer. To faithfully mimic a real ICS network, all containers are connected via Modbus/TCP protocol.

3.1.1. Containers for SCADA system

A typical ICS environment includes SCADA to control the system, HMI for monitoring, and a historian server to collect data. To reduce architecture complexity and simplify environment construction, we included the above functions into a single SCADA system and connected a database to store the collected data. We can obtain a synthetic dataset by exporting and refining this database. PLCs can also request control signals (setpoints) according to programmed logic. This SCADA system manually sets setpoints or generates them probabilistically and transmits them to PLCs.

3.1.2. Containers for PLCs

These containers contain PLCs. In an actual PLC, it receives status signals from various connected sensors and outputs signals to control devices such as valves or actuators. However, we introduce a virtualized hardware layer to avoid using hardware devices. The virtualized hardware layer imitates sensors or controlled devices in software. In other words, the container’s PLCs periodically scan sensor signals of the virtualized hardware layer and produce control signals according to logic. One thing that needs to be pointed out is the control logic installed in PLCs. We do not have access to the control logic of the actual PLC that produced the SWaT[3] or HAI datasets[4]. Therefore, we reproduce control logic that performs the same or similar actions from the publicly available ICS dataset in a data-driven manner.

3.2. Reproducing Control Logic for PLCs

PLCs are equipped with control logic written in programming languages such as ladder or structured text (ST). The SWaT[3] or HAI dataset[4] was collected from a network of multiple PLCs. If we can obtain the control logic of these PLCs, we can build a simulated ICS environment relatively easily. Additionally, by randomly generating data, it has the advantage of overcoming privacy protection issues and making testing more active. Unfortunately, publishers of these datasets provide technical details such as the ICS testbed’s network configuration but not the PLC’s control logic. Therefore, we abductively infer the control logic of PLCs using the input and output tags of PLCs specified in technical details and the publicly available ICS dataset.
According to our previous experiments, a high correlation was observed between the input and output of PLCs in SWaT or HAI testbeds. That means we can express the relationship between input and output signals through simple linear regression.
y i = ∑ j = 1 p w j i x j + w 0 i
Here, y i is the i ( ∈ 1 , … , n ) th output signal of the PLC with n outputs. x j and w j i are each the j ( ∈ 1 , … , p ) th input of the PLC and its weight. Linear regression models are trained with the traditional least square method (LSM). We write a linear regression model learned with ST or Laddar logic into the PLC’s control logic. The logic of the PLC reproduced in this way behaves equivalently to the PLC of SWaT or HAI.

3.3. Stochastic setpoint generation

In PLC, setpoints are reference values to compare measured values from sensors or other inputs. This value ensures that the system operates within acceptable parameters. Typically, a programmer or operator controls the system by manually or automatically determining setpoints. To fully simulate the ICS environment in software, it is necessary to automatically generate setpoints values. Since the setpoint value is determined according to the state of the control system, it inevitably has time series characteristics. There are various machine learning models for modeling time series data, such as autoregressive (AR), moving average (MA), and autoregressive integrated moving average (ARIMA). However, although these models show high prediction performance for training data, they are unsuitable for artificially generating new data. Therefore, we model setpoints stochastically using a hidden Markov model (HMM)[23]. HMM is a probabilistic model to describe a system where Markovian is assumed without explicit observation of the system’s state.
For instance, let’s consider a hypothetical PLC in a water treatment system. The HMM model, as illustrated in Figure 2, could represent different states such as ’Normal Operation,’ ’Low Flow,’ or ’High Contaminant Levels.’ Figure 2 illustrates an HMM model for the setpoint of an arbitrary PLC. We assume that the setpoint of the PLC is emitted from N hidden states, denoted as Q = { q 1 , q 2 , … , q N } , and observed as a sequence of observations O = o 1 o 2 … o T . Our HMM model is parameterized as λ = ( A , B ) . Here A = a 11 a 12 … a i j … a N N is the transition probability matrix between states, B = b 1 ( o 1 ) … b i ( o t ) … b N ( o T ) is the emission probability. The element a i j of A is the probability of transition from state q i to q j . The element b i ( o t ) of B is the probability that the setpoint value o t comes from state q i . We assume the emission probability b i ( o t ) to be Gaussian distributed. That is, state q i is defined by mean μ i ∈ R and standard deviation σ i ∈ R . Then, based on this definition, we define forward probability α t ( j ) and backward probability β t ( j ) (Eq. 2 and 3).
α t ( j ) = P ( o 1 , o 2 , … , o t , Q t = q i | λ ) = ∑ i = 1 N α t − 1 ( i ) × a i j × b j ( o t )
β t ( j ) = P ( o t + 1 , o t + 2 , … , o T , Q t = q j | λ ) = ∑ i = 1 N a i j × b j ( o t + 1 ) × β t + 1 ( j )
Forward probability α t ( j ) is the probability of observing the first t setpoints and being in a specific state q j . Backward probability β t ( j ) , on the other hand, is the probability of observing T − t + 1 setpoints starting from timestep t + 1 , assuming that the system is in state q j at timestep t. As expressed in Eq 2 and 3, obviously, α 1 ( j ) and β T ( j ) are defined recursively, and dynamic programming is used for efficient calculation. At this time, α 1 ( j ) and β T ( j ) are defined as π j × b j ( o 1 ) and 1, respectively ( π = ( π 1 π 2 … π N ) is the probability for the initial state). Based on the above definition, we learn the HMM model for the PLC’s setpoint using the standard Baum-Welch algorithm. This algorithm is a type of expectation-maximization (EM) algorithm, and as a learning result, we obtain σ = ( A , B ) , the parameter of the HMM model (Algorithm 1).
With the learned HMM model λ = ( A , B ) , we probabilistically generate artificial setpoint values. First, the initial state Q 1 is drawn from the probability distribution Π for the initial state. Once the initial state is determined, a new setpoint o 1 is sampled from the emission distribution for that state. We use a Gaussian distribution as the emission distribution, as mentioned above. Then, the next state, Q 2 , is determined using the potential probability matrix A. o 2 is generated from the emission distribution for Q 2 . Repeating the above process creates as many setpoint values as necessary. Once this setpoint is set in the SCADA system, it is passed to the PLC to simulate the ICS environment. Algorithm 2 is an algorithm for creating an artificial setpoint.
Preprints 93775 i001
Preprints 93775 i002

4. Evaluation of Simulated ICS

We implemented the fully software-simulated ICS environment proposed in section 3. In this chapter, we generate artificial ICS data with the simulated ICS proposed in section 3 and compare it with the benchmark ICS dataset. Section 4.1 describes details about building a simulated ICS environment. Section 4.2 describes the benchmark ICS dataset used in the evaluation. Finally, in section 4.3, we conduct a multi-faceted comparative analysis of the benchmark dataset and the data generated from the simulated ICS.

4.1. Implementation

The simulated ICS environment proposed in Section 3 consists of several containers. This container is a lightweight software package that contains everything needed to run an application, including code, system tools, libraries, and runtime. Containers are isolated from the host operating system and other containers running on the same host, providing a secure and consistent application runtime environment. Among several popular container software, we used Docker[24] to configure a simulated ICS environment. Each container contains a PLC or SCADA system. We used OpenPLC[28] to implement PLC and adopted ScadaBR[25] for SCADA. OpenPLC is an open-source programmable logic controller that can be used to control various industrial processes. OpenPLC supports several hardware devices to drive PLC logic, such as Arduino[26] or Raspberry Pi[27], among which we used the Python submodule. ScadaBR is an open-source SCADA system that can be used to monitor and control industrial processes.
The PLC of Simulated ICS includes a linear regression model learned in the manner described in section 3.2. This model was implemented in ST or Laddar logic. SCADA monitors the PLC’s variable values and controls the PLC by setting setpoints. Setpoints have values artificially generated by the HMM model, as described in section 3.3. An important note is that since control systems typically operate for very long periods, numerical issues can easily arise during calculating the HMM model (i.e., floating-point over/under-flow). To solve this problem, we calculated the probability values that appear in the calculation process in log space and scaled the forward/backward probability at each timestep.

4.2. Benchmark datasets on ICS

The simulated ICS environment proposed in Section 3 consists of several containers. This container is a lightweight software package that contains everything needed to run an application, including code, system tools, libraries, and runtime. Containers are isolated from the host operating system and other containers running on the same host, providing a secure and consistent application runtime environment. Among several popular container software, we used Docker[24] to configure a simulated ICS environment. Each container contains a PLC or SCADA system. We used OpenPLC[28] to implement PLC and adopted ScadaBR[25] for SCADA. OpenPLC is an open-source programmable logic controller that can be used to control various industrial processes. OpenPLC supports several hardware devices to drive PLC logic, such as Arduino[26] or Raspberry Pi[27], among which we used the Python submodule. ScadaBR is an open-source SCADA system that can be used to monitor and control industrial processes.
The PLC of Simulated ICS includes a linear regression model learned in the manner described in section 3.2. This model was implemented in ST or Laddar logic. SCADA monitors the PLC’s variable values and controls the PLC by setting setpoints. Setpoints have values artificially generated by the HMM model, as described in section 3.3. An important note is that since control systems typically operate for very long periods, numerical issues can easily arise during calculating the HMM model (i.e., floating-point over/under-flow). To solve this problem, we calculated the probability values that appear in the calculation process in log space and scaled the forward/backward probability at each timestep.

4.3. Experimental Results

This section presents the rigorous evaluation of our data-driven ICS network simulation framework, designed to assess its effectiveness in generating realistic synthetic data. We conducted comprehensive experiments utilizing the SWaT dataset, a meticulously curated resource capturing network traffic from a real-world ICS network consisting of 51 sensors and actuators over 11 days. The dataset’s meticulous annotation with ground truth labels, differentiating normal and abnormal system behavior, served as a valuable benchmark for measuring the fidelity and effectiveness of our synthetic data generation approach.

4.3.1. Model Creation

To comprehensively evaluate the performance of our simulated ICS environment, we created several dedicated models leveraging the SWaT dataset. These models, designated P1-CC, P1-FC, P1-TC, P1-PC, and P2-SC, were specifically tailored to replicate the behavior of distinct processes and components within the real-world ICS network captured by the SWaT dataset. This model-based approach ensured focused evaluation of the simulation’s ability to accurately reproduce the nuanced behavior of individual network elements.

4.3.2. Evaluation Metrics

To rigorously assess the quality of the synthetic data generated by our simulation, we employed a multifaceted approach encompassing quantitative metrics and temporal analysis. Our primary evaluation indicators included:
  • Dynamic Time Warping (DTW): This powerful technique measures the similarity between two-time series sequences, accounting for temporal distortions and misalignments. We utilized DTW to compare the temporal patterns and dynamics between the generated synthetic data and the benchmark SWaT dataset, ensuring our simulation accurately captures the temporal aspects of real-world network traffic.
  • Statistical Analysis: We further compared the statistical properties of the generated data with those of the SWaT dataset. This included analyzing key statistical moments such as mean, variance, and higher-order moments to validate that the synthetic data accurately reflects the overall statistical distribution of the real-world network traffic.

4.3.3. Analysis of Dynamic Time Warping (DTW)

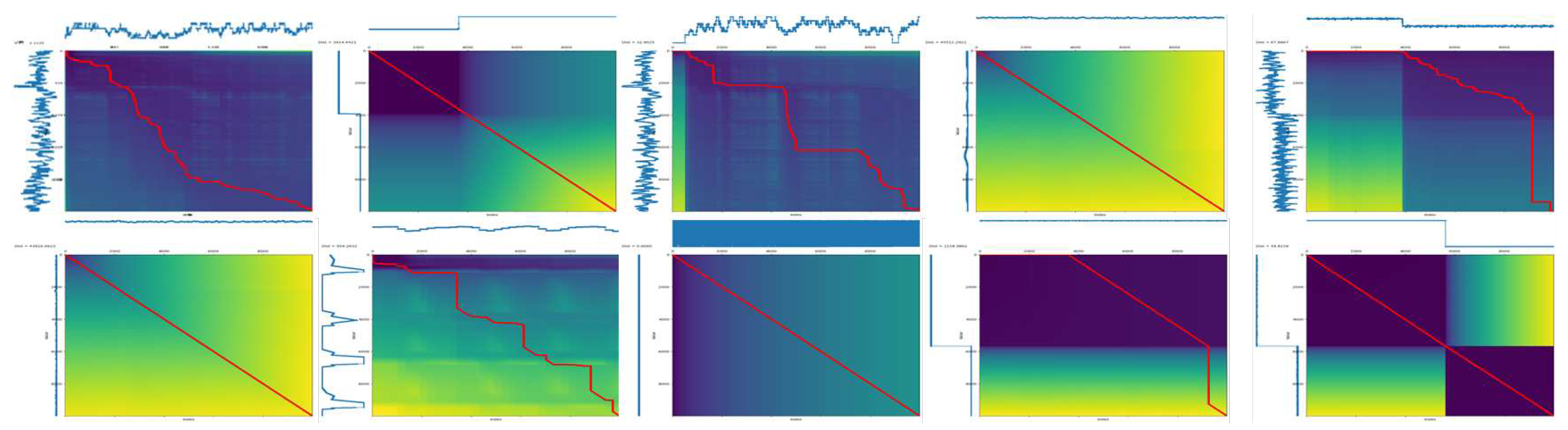
Figure 3 presents the results of a Dynamic Time Warping (DTW) analysis comparing the temporal patterns of our synthetically generated ICS network data with those of the benchmark SWaT dataset. DTW is a powerful technique for measuring the similarity between time series data, even when they exhibit temporal shifts or distortions. In this context, a lower DTW distance signifies a closer resemblance in the underlying temporal dynamics between the compared datasets.
Figure 3 displays each generated model’s mean and variance values. The x-axis represents the different models (P1-CC, P1-FC, P1-TC, P1-PC, and P2-SC), while the y-axis represents the mean and variance values.
Our analysis reveals that the synthetic data generated by our proposed method demonstrates remarkable similarity to the real-world data captured in the SWaT dataset. As evident in the figure, the DTW distances between our synthetic data and the SWaT data for each model are consistently lower compared to other baseline approaches. This observation strongly suggests that our synthetic data faithfully reproduces the time-dependent characteristics of the real-world ICS network data.
This finding is significant for several reasons:
  • Validation of synthetic data generation: It confirms the effectiveness of our proposed method in generating realistic and representative synthetic ICS network data. This paves the way for its use in various research and development tasks related to ICS security analysis and anomaly detection.
  • Improved model performance: By providing realistic training data, our synthetic data can potentially lead to the development of more robust and generalizable models for anomaly detection and other tasks in the domain of ICS cybersecurity.
  • Reduced reliance on real-world data: The availability of accurate synthetic data can alleviate the dependence on scarce and sensitive real-world ICS network data for training and evaluation purposes. This can be particularly beneficial for security-sensitive applications or situations where access to real-world data is limited.

4.3.4. Statistical Analysis

In addition to DTW analysis, we computed the mean and variance values of the synthetic data models and compared them to those of the benchmark SWaT dataset. These statistics provide insights into whether the synthetic data captures the central tendency and variability observed in the real-world ICS network data.
  • Mean Analysis. The mean values of the synthetic data models closely align with those of the benchmark dataset. This suggests that our simulation successfully replicates the central tendencies observed in the real-world ICS network data.
  • Variance Analysis. Similarly, the variance values of the synthetic data models exhibit similarities to the benchmark dataset. The variance reflects the degree of data dispersion, and our synthetic data captures this dispersion effectively.
Overall, the results from the DTW analysis and the mean and variance analysis collectively demonstrate that our simulated ICS environment generates synthetic data that closely resembles the temporal and statistical characteristics of the benchmark SWaT dataset. This underscores the capability of our approach to produce realistic and data-driven synthetic ICS data. In conclusion, the experimental results validate the effectiveness of our data-driven ICS network simulation method for synthetic data generation. By replicating both the temporal patterns and statistical characteristics of real-world ICS network data, our approach provides a valuable resource for researchers in the field of ICS optimization, security, and data-driven studies.

5. Conclusion

In conclusion, this paper presented a novel data-driven method for generating realistic synthetic data for Industrial Control System (ICS) networks. This approach eliminates the need for expensive hardware by simulating the entire ICS environment in software. We replicated the control logic of PLCs based on existing data and employed stochastic setpoint generation to introduce natural variability into the collected data. This simulated environment, built on virtualized containers, mimics the behavior of real ICS components like PLCs and SCADA systems, ensuring the generated data’s fidelity to real-world scenarios.
Our experiments validated the effectiveness of our approach, demonstrating the generated data’s close resemblance to actual ICS network characteristics. Comparisons with benchmark datasets confirmed the similarity in key statistical properties, such as mean and variance. This success paves the way for utilizing our synthetic data in various data-driven ICS research, including optimization and security studies.
Our work offers a valuable solution to the challenges of cost, hardware, and control logic complexity in ICS data generation. This software-based method empowers researchers to access diverse and realistic datasets, ultimately contributing to advancements in ICS research and ultimately, improved system optimization and security.

Abbreviations

The following abbreviations are used in this manuscript:
ICS Industrial control system
SCADA Supervisory control and data acquisition
DCS Distributed control system
PLC Programmable logic controller
HMI Human-machine interfaces
GAN Generative adversarial networks
VAE Variational autoencoder
PAR Periodic autoregressive
PMU Phasor measurement unit
HMM Hidden Markov model
BGAN Boundary-seeking GAN
ST Structured text
LSM Least square method
AR Autoregressive
MA Moving average
ARIMA Autoregressive integrated moving average
HMM Hidden Markov model

References

  1. Subramanian, D., Murali, P., Zhou, N., Ma, X., Cesar Da Silva, G., Pavuluri, R., & Kalagnanam, J. (2019). A prediction-optimization framework for site-wide process optimization. Proceedings - 2019 IEEE International Congress on Internet of Things, ICIOT 2019 - Part of the 2019 IEEE World Congress on Services. [CrossRef]
  2. Min, Q., Lu, Y., Liu, Z., Su, C., & Wang, B. (2019). Machine Learning based Digital Twin Framework for Production Optimization in Petrochemical Industry. International Journal of Information Management, 49. [CrossRef]
  3. Mathur, A. P., & Tippenhauer, N. O. (2016). SWaT: A water treatment testbed for research and training on ICS security. 2016 International Workshop on Cyber-Physical Systems for Smart Water Networks, CySWater 2016. [CrossRef]
  4. Shin, H. K., Lee, W., Yun, J. H., & Kim, H. C. (2020). HAI 1.0: HIL-based augmented ICS security dataset. CSET 2020 - 13th USENIX Workshop on Cyber Security Experimentation and Test, Co-Located with USENIX Security 2020.
  5. Craggs, B., Rashid, A., Hankin, C., Antrobus, R., Serban, O., & Thapen, N. (2019). A reference architecture for IIoT and industrial control systems testbeds. IET Conference Publications, 2019(CP756). [CrossRef]
  6. Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., & Bengio, Y. (2014). Generative adversarial nets. Advances in Neural Information Processing Systems.
  7. Kingma, D. P., & Welling, M. (2014). Auto-encoding variational bayes. 2nd International Conference on Learning Representations, ICLR 2014 - Conference Track Proceedings.
  8. Beaver, J. M., Borges-Hink, R. C., & Buckner, M. A. (2013). An evaluation of machine learning methods to detect malicious SCADA communications. Proceedings - 2013 12th International Conference on Machine Learning and Applications, ICMLA 2013, 2. [CrossRef]
  9. Morris, Tommy. Industrial Control System (ICS) Cyber Attack Datasets. Available online: https://sites.google.com/a/uah.edu/tommy-morris-uah/ics-data-sets (accessed on 20 January 2023).
  10. Morris, T., & Gao, W. (2014). Industrial control system traffic data sets for intrusion detection research. IFIP Advances in Information and Communication Technology, 441. [CrossRef]
  11. Morris, T. H., Thornton, Z., & Turnipseed, I. (2015). Industrial Control System Simulation and Data Logging for Intrusion Detection System Research. Seventh Annual Southeastern Cyber Security Summit.
  12. Zhang, C., Kuppannagari, S. R., Kannan, R., & Prasanna, V. K. (2018). Generative Adversarial Network for Synthetic Time Series Data Generation in Smart Grids. 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids, SmartGridComm 2018. [CrossRef]
  13. Tushar, W., Huang, S., Yuen, C., Zhang, J. A., & Smith, D. B. (2015). Synthetic generation of solar States for smart grid: A multiple segment Markov chain approach. IEEE PES Innovative Smart Grid Technologies Conference Europe, 2015-January (January). [CrossRef]
  14. Iftikhar, N., Liu, X., Nordbjerg, F. E., & Danalachi, S. (2016). A Prediction-Based Smart Meter Data Generator. NBiS 2016 - 19th International Conference on Network-Based Information Systems. [CrossRef]
  15. Esteban, C., Hyland, S. L., & Rätsch, G. (2017). Real-valued (Medical) Time Series Generation with Recurrent Conditional GANs. ArXiv:1706.02633v2. [CrossRef]
  16. Iftikhar, N., Liu, X., Danalachi, S., Nordbjerg, F. E., & Vollesen, J. H. (2017). A scalable smart meter data generator using spark. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 10573 LNCS. [CrossRef]
  17. Dahmen, J., & Cook, D. (2019). SynSys: A synthetic data generation system for healthcare applications. Sensors (Switzerland), 19(5). [CrossRef]
  18. Zheng, X., Wang, B., & Xie, L. (2019). Synthetic dynamic PMU data generation: A generative adversarial network approach. 2019 International Conference on Smart Grid Synchronized Measurements and Analytics, SGSMA 2019. [CrossRef]
  19. Imtiaz, S., Arsalan, M., Vlassov, V., & Sadre, R. (2021). Synthetic and Private Smart Health Care Data Generation using GANs. Proceedings - International Conference on Computer Communications and Networks, ICCCN, 2021-July. [CrossRef]
  20. Razghandi, M., Zhou, H., Erol-Kantarci, M., & Turgut, D. (2022). Variational Autoencoder Generative Adversarial Network for Synthetic Data Generation in Smart Home. ArXiv:2201.07387v1. [CrossRef]
  21. Ayodeji, A., Liu, Y. kuo, Chao, N., & Yang, L. qun. (2020). A new perspective towards the development of robust data-driven intrusion detection for industrial control systems. In Nuclear Engineering and Technology (Vol. 52, Issue 12). [CrossRef]
  22. Ling, J., Zhu, Z., Luo, Y., & Wang, H. (2021). An intrusion detection method for industrial control systems based on bidirectional simple recurrent unit. Computers and Electrical Engineering, 91. [CrossRef]
  23. Ghahramani, Z. (2001). An introduction to hidden Markov models and Bayesian networks. International Journal of Pattern Recognition and Artificial Intelligence, 15(1). [CrossRef]
  24. Docker, Inc. Docker, Inc. https://www.docker.com/, Access date: 2023-03-08. Available online: https://www.docker.com/ (accessed on 08 March 2023).
  25. SCADA-BR. Available online: https://www.scadabr.com.br/ (accessed on 08 March 2023).
  26. Arduino. Available online: https://www.arduino.cc/ (accessed on 09 March 2023).
  27. Raspberry, Pi. Available online: https://www.raspberrypi.com/ (accessed on 09 March 2023).
  28. Alves, T., & Morris, T. (2018). OpenPLC: An IEC 61,131–3 compliant open-source industrial controller for cyber security research. Computers and Security, 78. [CrossRef]
Preprints 93775 g001
Figure 1. Overview of simulated ICS architecture.
Figure 1. Overview of simulated ICS architecture.
Preprints 93775 g001
Preprints 93775 g002
Figure 2. Hidden Markov model for a setpoint of PLC.
Figure 2. Hidden Markov model for a setpoint of PLC.
Preprints 93775 g002
Preprints 93775 g003
Figure 3. Dynamic Time Warping (DTW) result.
Figure 3. Dynamic Time Warping (DTW) result.
Preprints 93775 g003
Table 1. Mean and variance values.
Table 1. Mean and variance values.
P1-CC (P1_PP04SP) P1-CC (P1_PP04) P1-FC (P1_B3005) P1-FC (P1_FCV03D) P1-TC (P1_B4022) P1-TC (P1_FCV01D) P2-SC (P2_AutoSD) P2-SC (P2_SCO) P1-PC (P1_B2016) P1-PC (P1_PCV01D)
Original Mean 27.418 29.4 993.211 49.044 30.971 18.872 113.989 54747.254 1.109 30.723
Predicted Mean 27.528 24.058 1010.991 49.043 30.951 18.874 118.053 54747.22 1.111 472.913
Original Variance 0.061 103.586 912.649 2.143 0.435 246.328 116.114 3216.688 0.013 11.322
Predicted Variance 0.08 4.018 440.815 1.34 0.446 229.671 94.342 3215.406 0.011 107.278
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated