Semi-Structured Complex Numbers:Extending the Cauchy–Riemann Equations and developing Semi-Structured Complex Analytic Functions

Preprint

Article

Semi-Structured Complex Numbers:Extending the Cauchy–Riemann Equations and developing Semi-Structured Complex Analytic Functions

Altmetrics

Downloads

Views

Comments

Peter Jean Paul^*,Shanaz Wahid

This version is not peer-reviewed

Submitted:

18 December 2023

Posted:

19 December 2023

You are already at the latest version

Alerts

Abstract

Real and complex analytic functions are largely studied in the field of complex analysis and are seen as very useful tools in solving problems in mathematics, physics and engineering. Real and complex numbers are a subset of semi-structured complex numbers (a new number set created to algebraically solve division by zero). Nevertheless, the properties of analytic functions made up of semi-structured complex variables (called semi-structured complex analytic functions) is yet to be explored. This limits the range of possible problems that can be resolved using analytic functions). In this regard, the aim of this paper was to expound upon the properties of semi-structured complex analytic functions and show their application in solving engineering problems. The results of this paper included (1) developing a full set of Cauchy–Riemann Equations for the semi-structured complex -space; (2) define sufficient and necessary conditions for a semi-structured complex function to be analytic; (3) determine the relationship between semi-structured complex analytic functions, Laplace’s Equations and Poisson’s Equations; and (5) provide an example of the use of these functions.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

1.1. Analytic Functions and their Importance

Analytic functions, are mathematical functions that can be represented by a power series expansion. Formally, a function is said to be an analytic function if and only if its Taylor series expansion about some point

x_{0}

converges to the function under investigation in some neighbourhood for every

x_{0}

in the function’s domain.

According to the current framework of complex analysis, analytic functions can be categorised into two different types: (1) Real Analytic Functions and (2) Complex Analytic Functions. A function

f (x)

is said to be a real analytic function in the domain D of the function on the real line if for any

x_{0} \in D

, then:

f (x) = \sum_{n = 0}^{\infty} a_{n} {(x - x_{0})}^{n} = a_{0} + a_{1} {(x - x_{0})}^{1} + a_{2} {(x - x_{0})}^{2} + \dots

(1)

where the coefficients

a_{0}, a_{1}, a_{2}, \dots

are the real numbers and also the series is convergent to the function

f (x)

for

x

in the neighbourhood of

x_{0}

On the other hand, a function

f (z)

is said to be a complex analytic function in the domain D of the function in the complex plane if for any

z_{0} \in D

, then:

f (z) = \sum_{n = 0}^{\infty} a_{n} {(z - z_{0})}^{n} = a_{0} + a_{1} {(z - z_{0})}^{1} + a_{2} {(z - z_{0})}^{2} + \dots

(2)

where the coefficients

a_{0}, a_{1}, a_{2}, \dots

are the real numbers and also the series is convergent to the function

f (z)

for

z

in the neighbourhood of

z_{0}

Complex differentiability has several important consequences, such as the existence of power series expansions and the satisfaction of the Cauchy–Riemann equations. Power series expansions such as the one shown in Equation (2) permits complicated complex functions to be evaluated using the four basic operations of arithmetic. Power series representations of complex analytic functions also allows these functions to be complex differentiable facilitating rigorous mathematical analysis, approximations, and manipulations of complex functions. This makes complex analytic functions valuable in many areas of mathematics and physics.

In physics, they are used to describe various phenomena, such as electromagnetic fields, fluid flow, and quantum mechanics. In engineering, analytic functions are employed in the design and analysis of systems, signal processing and control theory, and conformal mapping. Aside from having a power series expansion representation, complex analytic functions also have the property of satisfying the Cauchy-Riemann equations.

1.2. The Cauchy–Riemann Equations and Analytic Functions

The Cauchy-Riemann equations are a set of partial differential equations that establish a necessary condition for a complex-valued function to be differentiable.

Let's consider a complex-valued function

f (z) = u (x, y) + i v (x, y)

, where

z = x + i y

is a complex variable, and

u (x, y)

and

v (x, y)

are real-valued functions of the real variables

x

and

y

. The Cauchy-Riemann equations state that for

f (z)

to be differentiable at a point

z = x + i y

, the following conditions must hold:

\{\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x} \end{matrix}

(3)

The Cauchy-Riemann equations provide a powerful tool for studying the properties of complex functions, such as holomorphicity, conformal mappings, and the construction of harmonic functions. Unfortunately, Cauchy–Riemann equations can only be used in the context of complex numbers. If they were to be applied to larger number sets (number sets for which complex numbers are a subset) they would very likely need to be modified to accommodate analysis on these larger sets. One such number set is semi-structured complex numbers, a new set created to algebraically solve division by zero.

1.3. Semi-structured Complex Numbers: a recent development in division by zero

Recently there has been a range of research involving division by zero. The problem of division by zero can simply be stated as: What is

\frac{a}{0}

where “a” is any complex number. Table A1, Appendix 1, shows sample research conducted on “division by zero”.

There have been several solutions to the problem the most recent being the invention of the semi-structured complex number set

H

[1]. The first attempt at creating this number set was riddled with issues [1], however, a second paper [2], written to reformulate and strengthen the theory of semi-structured complex numbers, produced several grounded and profound results. Table 1 shows the major results (pertinent to this research) developed in paper [2].

Table 1. Major results from paper [2].

Result 1	Semi-structured complex number set can be defined as follows: A semi-structured complex number is a three-dimensional number of the general form $h = x + y i + z p;$ that is, a linear combination of real (1), imaginary ( $i$ ) and unstructured ( $p$ ) units whose coefficients $x, y, z$ are real numbers. The number $h$ is called semi-structured complex because it contains a structured complex part $(x + y i)$ and an unstructured part $(z p)$ .
Result 2	The unstructured number $p$ was redefined as: $p^{n} = \frac{\sqrt{2} \times \cos (\frac{π}{2} n - \frac{π}{4})}{f^{n} (1)}$ (4) where $f^{n} (c)$ is a composite function such that $f (c) = 1 - c$ . Integer powers of $p$ yield the following cyclic results: $p^{1} = \frac{1}{0}$ $p^{2} = - 1$ $p^{3} = - p$ $p^{4} = 1$ $p^{5} = \frac{1}{0}$ $p^{6} = - 1$ $p^{7} = - p$ $\dots$
Result 3	$p$ does not belong to the set of complex numbers $C$ (that is, $p \notin C$ ), but belongs to a higher order number set $H$ called the set of semi-structured complex numbers such that the set of complex numbers is a subset of $H$ (that is, $C \subset H$ ).
Result 4	The field of semi-structured complex numbers was defined, and proof was given that this field obeys the field axioms. This implies (1) the number set can easily be used in everyday algebraic expressions and can be used to solve algebraic problems, (2) the number set can be used to form more complicated structures such as vector spaces and hence solve more complex problems that may involve “division by zero”.
Result 5	Semi-structured complex number set $H$ does not form an ordered field. For the objects in a field to have an order, operations such as greater than or less than can be applied to these objects. This is because in an ordered field the square of any non-zero number is greater than 0; this is not the case with semi-structured complex numbers.
Result 6	Semi-structured complex numbers can be represented by points in a 3-dimensional Euclidean $x y z$ -space. The xyz-space consist of three perpendicular axes: the real $x$ -axis, the imaginary y-axis, and the unstructured $z$ -axis. These axes form three perpendicular planes: the real-imaginary $x y$ -plane, the real-unstructured $x z$ -plane, and the imaginary-unstructured $y z$ -plane.
Result 7	The unit $p$ was used to find a viable solution to the logarithm of zero. The logarithm of zero was found to be: $\log 0 = - p (\frac{π}{2} + 2 k π)$ (5) where k is some integer value.
Result 8	The new definition of $p$ provided an unambiguous understanding that $\frac{0}{0} = n$ simply represents $90^{°}$ clockwise rotation of the vector $n p$ from the positive unstructured z-axis to $n$ on the positive real x-axis along the real-unstructured $x z$ -plane. Note that $n$ is any real number.
Result 9	Semi-structured complex numbers have both a 3D and 4D representation in the form: $h = x + y i + z p$ (3D form) $h = A + B i + C p + D i p$ (4D form) where: $x, y, z, A, B, C, D$ are real numbered scalars and $i, p$ are semi-structured basis units.
Result 10	Two new Euler formulas were developed. When combined with the original Euler formula describes the relationship between trigonometric, hyperbolic, and exponential functions for the entire semi-structured complex Euclidean $x y z$ -space.
Result 11	Semi-structured complex numbers can be used to resolve singularities that may arise in engineering and science equations (because of division by zero) to develop reasonable conclusions in the absence of experimental data.
Result 12	From Result 10 semi-structured complex numbers can present in four forms as given below:
Result 13	The zeroth root of a number h can be found using the equation $\sqrt[0]{h} = h^{p} = e^{p \ln h} = \cos (\ln h) + p \sin (\ln h)$
Result 14	Since $p^{1} = \frac{1}{0}$ this implies that $\frac{1}{p} = 0$ which further implies that $- p = 0$
Result 15	Any real number with the semi-structured unit $p$ attached to it is not a physically measurable quantity. That is, $k p$ where $k$ is a real number is not physically measurable (however, $k$ can be calculated given enough information)
Result 16	If $a$ and $b$ measure different (but quantitatively related) aspects of the same object, where $a$ is physically measurable but $b$ is not, then $a$ and $b$ can be combined into one equation in the form $a + b p$

The foundational results found in Table 1 potentially pave the way to understanding the properties of analytic functions constructed from semi-structured complex numbers and variables. It has already been shown in complex analysis the profound importance of complex analytic functions (made from complex numbers and variables). It has also been shown (from Table 1) that complex numbers form a subset of semi-structured complex numbers. It only stands to reason that if the framework of complex analysis was expanded to examine the properties of functions made from semi-structured complex numbers and variables, this would potentially yield results that could be used to tackle a wide range of mathematical problems. From this standpoint the idea of semi-structured complex analysis to examine semi-structured complex analytic functions cannot be ignored.

1.4. Major contributions

Given the potential importance of developing an understanding of the properties of semi-structured analytic functions, the aim of this paper was:

To use the features of semi-structured complex numbers and the characteristics of analytic functions to develop the properties and explore the applications of semi-structured complex analytic functions.

In the process of fulfilling the stated aim, this paper makes five major contributions:

Develop an extension to the Cauchy–Riemann equations to include three other conditions for a semi-structured complex function to be analytic in the semi-structured complex $x y z$ -space.
Used the extension to the Cauchy–Riemann equations to define a semi-structured complex analytic function along the real-imaginary $x y$ -plane, the real-unstructured $x z$ -plane, the imaginary-unstructured $y z$ -plane and within the semi-structured complex $x y z$ -space.
Defined sufficient and necessary conditions for a semi-structured complex function to be analytic along the real-imaginary $x y$ -plane, the real-unstructured $x z$ -plane, the imaginary-unstructured $y z$ -plane and within the semi-structured complex $x y z$ -space.
Determined the relationship between semi-structured complex analytic functions, Laplace’s equations and Poisson’s equations.
Provided a simple example where semi-structured complex analytic functions can be used to solve problems in engineering.

The rest of this paper is devoted to showing how achieving the main aim of the paper led to these major contributions.

2. Extensions to the Cauchy–Riemann Equations

Before the properties of semi-structured complex analytic functions can be defined, the Cauchy–Riemann equations (the basis for defining analytic functions) needed to be modified so that it can be used in the context of semi-structured complex functions.

To do this, the semi-structured complex

x y z

-space was divided into three planes, real-imaginary plane (

x y

-plane), real-unstructured plane (

x z

-plane) and the imaginary-unstructured plane (

y z

-plane). Since, the Cauchy–Riemann equations were already derived for functions that reside in the real-imaginary plane (

x y

-plane) (that is the complex plane), the same process of derivation was used to contain a set of Cauchy–Riemann equations for the real-unstructured plane (

x z

-plane), the complex-unstructured plane (

y z

-plane) and the entire semi-structured complex

x y z

-space. Once these equations had been derived the properties of semi-structured complex analytic functions were defined.

2.1. Cauchy–Riemann Equations for the $x y$

-plane or complex plane

The Cauchy–Riemann Equations for the real-imaginary plane (

x y

-plane or complex plane) are given in Equation (6). Incidentally, Equations (6) is the original Cauchy–Riemann equations. Derivation of Equation (6) as well as an example on how to use these equations is provided in Appendix 2.

Proposition 1: Let $f (h_{x y})$ be a complex function that can be written as $f (h_{x y}) = u (x, y) + i v (x, y)$ , where $u (x, y)$ and $v (x, y)$ are real functions of two real inputs and $h_{x y}$ is a complex number. If $f (h_{x y})$ is complex-differentiable at a given $h_{x y} = x + y i$ , then $u (x, y)$ and $v (x, y)$ have valid first-order partial derivatives and these derivatives have the following relationship:
$\{\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \\ \frac{\partial v}{\partial x} = - \frac{\partial u}{\partial y} \end{matrix}$	(Cauchy-Riemann equations for $x y$ -plane)	(6)

2.2. Cauchy-Riemann Equations for the $x z$ -plane

Additionally, the Cauchy-Riemann equations for the real-unstructured plane (

x z

-plane) is given in Equations (7). Proof of Equations (7) as well as an example on how to use these equations is provided in Appendix 3.

Proposition 2: Let $f (h_{x z})$ be a complex function that can be written as $f (h_{x z}) = u (x, z) + p w (x, z)$ , where $u (x, z)$ and $w (x, z)$ are real functions of two real inputs. If $f (h_{x z})$ is complex-differentiable at a given $h_{x z} = x + p z$ , then $u (x, z)$ and w $(x, z)$ have valid first-order partial derivatives and these derivatives have the following relationship:
$\{\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial w}{\partial z} \\ \frac{\partial u}{\partial z} = \frac{\partial w}{\partial x} \end{matrix}$	(Cauchy-Riemann equations for $x z$ -plane)	(7)

2.3. Cauchy–Riemann Equations for the $y z$ -plane

Moreover, the Cauchy–Riemann Equations for the complex-unstructured plane (

y z

-plane) is given in Equations (8). Proof of Equations (8) as well as an example on how to use these equations is provided in Appendix 4.

Proposition 3: Let $f (h_{y z})$ be a complex function that can be written as $f (h_{y z}) = i v (y, z) + p w (y, z)$ , where $v (y, z)$ and $w (y, z)$ are real functions of two real inputs. If $f (h_{y z})$ is complex-differentiable at a given $h_{y z} = y i + z p$ , then $u (y, z)$ and $w (y, z)$ have valid first-order partial derivatives and these derivatives have the following relationship:
$\{\begin{matrix} \frac{\partial v}{\partial y} = \frac{\partial w}{\partial z} \\ \frac{\partial v}{\partial z} = \frac{\partial w}{\partial y} \end{matrix}$	(Cauchy-Riemann equations for $y z$ -plane)	(8)

2.4. Cauchy-Riemann Equations for the $x y z$ -space

Finally, considering the full set of semi-structured complex numbers, an extension of the Cauchy–Riemann equations for the

x y z

-space is given in Equations (9). Proof of Equations (9) as well as an example on how to use these equations is provided in Appendix 5.

Proposition 4: Let $f (h)$ be a complex function that can be written as $f (h) = u (x, y, z) + i v (x, y, z) + p w (x, y, z)$ , where $u (x, y, z)$ , $v (x, y, z)$ and $w (x, y, z)$ are real functions of two real inputs. If $f (h)$ is complex-differentiable at a given $h = x + y i + p z$ , then $u (x, y, z)$ , $v (x, y, z)$ and $w (x, y, z)$ have valid first-order partial derivatives and these derivatives have the following relationship:
$\{\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} = \frac{\partial w}{\partial z} \\ \frac{\partial v}{\partial x} = - \frac{\partial u}{\partial y} \\ \begin{matrix} \frac{\partial w}{\partial x} = - \frac{\partial u}{\partial z} \\ \frac{\partial w}{\partial y} = \frac{\partial v}{\partial z} \end{matrix} \end{matrix}$	(Cauchy-Riemann equations for $x y z$ -space)	(9)

3. Semi-structured Complex Analytic Functions

Now that the extended Cauchy–Riemann Equations for semi-structured complex functions have been properly outlined, the next step was to use these equations to define the properties of Semi-structured Complex Analytic Functions.

3.1. Semi-structured Complex Analytic Functions along the $x y$ -plane

The following definitions and observations hold for semi-structured complex analytic functions

f (h_{x y})

along the

x y

-plane:

Definition 1:

A function

f (h_{x y}) = u (x, y) + i v (x, y)

is said to be analytic in a region

R

of the complex plane if

f (h_{x y})

is single valued and has a derivative at each point of

R

From definition 1, a single valued function simply means that every input to the function produces one and only one output (that is, a single valued function is a one-to-one function).

Definition 2:

A function

f (h_{x y}) = u (x, y) + i v (x, y)

is said to be analytic at a point

h_{x y}

h_{x y}

is an interior point of some region where

f (h_{x y})

is analytic.

Hence the concept of analytic function at a point implies that the function is analytic in some circle with center at this point.

The necessary and sufficient conditions for the function

f (h_{x y})

to be analytic are as follows:

Necessary Condition:	For the function $f (h_{x y})$ , the four partial derivatives of the real and imaginary parts $\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial v}{\partial x}, \frac{\partial v}{\partial y}$ exist and satisfy the Cauchy-Riemann Equations given in Equation (6).
Sufficient Condition:	For the function $f (h_{x y})$ , the four partial derivatives of the real and imaginary parts $\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial v}{\partial x}, \frac{\partial v}{\partial y}$ exist and are continuous.

3.2. Semi-structured Complex Analytic Functions along the $x z$ -plane

The following definitions and observations hold for semi-structured complex analytic functions

f (h_{x z})

along the

x z

-plane:

Definition 1:

A function

f (h_{x z}) = u (x, z) + p w (x, z)

is said to be analytic in a region

R

of the

x z

-plane if

f (h_{x z})

is single valued and has a derivative at each point of

R

From definition 1, a single valued function simply means that every input to the function produces one and only one output (that is, a single valued function is a one-to-one function).

Definition 2:

A function

f (h_{x z}) = u (x, z) + i w (x, z)

is said to be analytic at a point

h_{x z}

h_{x z}

is an interior point of some region where

f (h_{x z})

is analytic.

Hence the concept of analytic function at a point implies that the function is analytic in some circle with center at this point.

The necessary and sufficient conditions for the function

f (h_{x z})

to be analytic are as follows:

Necessary Condition:	For the function $f (h_{x z})$ , the four partial derivatives of the real and unstructured parts $\frac{\partial u}{\partial x}, \frac{\partial u}{\partial z}, \frac{\partial w}{\partial x}, \frac{\partial w}{\partial z}$ exist and satisfy the Cauchy-Riemann Equations given in Equation (7).
Sufficient Condition:	For the function $f (h_{x z})$ , the four partial derivatives of the real and unstructured parts $\frac{\partial u}{\partial x}, \frac{\partial u}{\partial z}, \frac{\partial w}{\partial x}, \frac{\partial w}{\partial z}$ exist and are continuous.

3.3. Semi-structured Complex Analytic Functions along the $y z$ -plane

The following definitions and observations hold for semi-structured complex analytic functions

f (h_{y z})

along the

y z

-plane:

Definition 1:

A function

f (h_{y z}) = i v (y, z) + p w (y, z)

is said to be analytic in a region

R

of the

y z

-plane if

f (h_{y z})

is single valued and has a derivative at each point of

R

From definition 1, a single valued function simply means that every input to the function produces one and only one output (that is, a single valued function is a one-to-one function).

Definition 2:

A function

f (h_{y z}) = i v (y, z) + p w (y, z)

is said to be analytic at a point

h_{y z}

h_{y z}

is an interior point of some region where

f (h_{y z})

is analytic.

Hence the concept of analytic function at a point implies that the function is analytic in some circle with centre at this point.

The necessary and sufficient conditions for the function

f (h_{y z})

to be analytic are as follows:

Necessary Condition:	For the function $f (h_{y z})$ , the four partial derivatives of the real and unstructured parts $\frac{\partial v}{\partial y}, \frac{\partial v}{\partial z}, \frac{\partial w}{\partial y}, \frac{\partial w}{\partial z}$ exist and satisfy the Cauchy-Riemann Equations given in Equation (8).
Sufficient Condition:	For the function $f (h_{y z})$ , the four partial derivatives of the real and unstructured parts $\frac{\partial v}{\partial y}, \frac{\partial v}{\partial z}, \frac{\partial w}{\partial y}, \frac{\partial w}{\partial z}$ exist and are continuous.

3.4. Semi-structured Complex Analytic Functions within the $x y z$ -space

The following definitions and observations hold for semi-structured complex analytic functions

f (h)

within the

x y z

-plane:

Definition 1:

A function

f (h) = u (x, y, z) + i v (x, y, z) + p w (x, y, z)

is said to be analytic in a region

R

of the

x y z

-space if

f (h)

is single valued and has a derivative at each point of

R

From definition 1, a single valued function simply means that every input to the function produces one and only one output (that is, a single valued function is a one-to-one function).

Definition 2:

A function

f (h) = u (x, y, z) + i v (x, y, z) + p w (x, y, z)

is said to be analytic at a point

h

h

is an interior point of some region where

f (h)

is analytic.

Hence the concept of analytic function at a point implies that the function is analytic in some circle with centre at this point.

The necessary and sufficient conditions for the function

f (h)

to be analytic are as follows:

Necessary Condition:

For the function

f (h)

, the four partial derivatives of the real and unstructured parts

\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial u}{\partial z}, \frac{\partial v}{\partial x}, \frac{\partial v}{\partial y}, \frac{\partial v}{\partial z}, \frac{\partial w}{\partial x}, \frac{\partial w}{\partial y}, \frac{\partial w}{\partial z}

exist and satisfy the Cauchy-Riemann Equations given in Equation (9).

Sufficient Condition:

For the function

f (h)

, the four partial derivatives of the real and unstructured parts

\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial u}{\partial z}, \frac{\partial v}{\partial x}, \frac{\partial v}{\partial y}, \frac{\partial v}{\partial z}, \frac{\partial w}{\partial x}, \frac{\partial w}{\partial y}, \frac{\partial w}{\partial z}

exist and are continuous.

4. Semi-structured Complex Analytic Functions, Laplace and Poisson Equations

Having defined semi-structured analytic functions along the

x y

-plane,

x z

-plane,

y z

-plane and within the

x y z

-space, it is important to consider the relationship between semi-structured analytic functions and the Laplace and Poisson equations.

Laplace’s equation, is a second-order partial differential equation that widely used in physics because the solution to the equation are used to resolve problems in topic such as electric, magnetic, and gravitational potentials, steady-state temperatures, and hydrodynamics. Laplace’s equation takes the form shown in Equation (10).

\frac{\partial^{2} ϕ}{\partial x^{2}} + \frac{\partial^{2} ϕ}{\partial y^{2}} = 0

(10)

Solutions of Laplace's equation are called harmonic functions; they are all analytic within the domain where the equation is satisfied. Establishing a relationship between Laplace’s equation and analytic functions is one of the major achievements of complex analysis. Therefore, in extending the theory of complex analysis to semi-structured complex numbers it is necessary to establish the relationship between Laplace’s equation and semi-structured complex analytic functions.

The same line of reasoning holds for Poisson’s equation. Poisson’s equation takes the form shown in Equation (11).

\frac{\partial^{2} φ}{\partial x^{2}} + \frac{\partial^{2} φ}{\partial z^{2}} = ϕ

(11)

4.1. Semi-structured Complex Analytic Functions along the $x y$ -plane and Laplace’s Equations

The relationship between a semi-structured complex function along the

x y

-plane and Laplace’s equation is given by Proposition 5. Proof of Proposition 5 is given in Appendix 6.

Proposition 5: if $f (h_{x y}) = u (x, y) + i v (x, y)$ , is an analytic function along the $x y$ -plane, where $u (x, y)$ and $v (x, y)$ are real functions, then the real part $u (x, y)$ and imaginary part $v (x, y)$ of $f (h_{x y})$ satisfy Laplace’s Equations. That is:
$\begin{matrix} \frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} = 0 \\ \frac{\partial^{2} v}{\partial x^{2}} + \frac{\partial^{2} v}{\partial y^{2}} = 0 \end{matrix}$	(12)

Since the real and imaginary parts of the semi-structured complex analytic function are solutions to Laplace equation and satisfy the Cauchy–Riemann equations given by Equation (6), they are called harmonic conjugate functions.

4.2. Semi-structured Complex Analytic Functions along the $x z$ -plane and Laplace’s Equations

The relationship between a semi-structured complex function along the

x z

-plane and Laplace’s Equations is given by Proposition 6. Proof of Proposition 6 is given in Appendix 7.

Proposition 6: if $f (h_{x z}) = u (x, z) + p w (x, z)$ , is an analytic function along the $x z$ -plane, where $u (x, z)$ and $w (x, z)$ are real functions, then the real part $u (x, z)$ and unstructured part $w (x, z)$ of $f (h_{x z})$ satisfy Laplace’s Equations. That is:
$\begin{matrix} \frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial z^{2}} = 0 \\ \frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{2} w}{\partial z^{2}} = 0 \end{matrix}$	(13)

Since the real and unstructured parts of the semi-structured complex analytic function are solutions to Laplace equation and satisfy the Cauchy–Riemann equations given by Equation (7), they are called harmonic conjugate functions.

4.3. Semi-structured Complex Analytic Functions along the $y z$ -plane and Poisson’s Equations

The relationship between a semi-structured complex function along the

x z

-plane and Poisson’s Equations is given by Proposition 7. Proof of Proposition 7 is given in Appendix 8.

Proposition 7: if $f (h_{y z}) = i v (y, z) + p w (y, z)$ , is an analytic function along the $y z$ -plane, where $v (y, z)$ and $w (y, z)$ are real functions, then the imaginary part $v (x, z)$ and unstructured part $w (x, z)$ of $f (h_{y z})$ satisfy Poisson’s Equations. That is:
$\begin{matrix} \frac{\partial^{2} v}{\partial y^{2}} + \frac{\partial^{2} v}{\partial z^{2}} = ϕ_{1} \\ \frac{\partial^{2} w}{\partial y^{2}} + \frac{\partial^{2} w}{\partial z^{2}} = ϕ_{2} \end{matrix}$	(14)

In Equation (14),

ϕ_{1}

and

ϕ_{2}

are all functions.

4.4. Semi-structured Complex Analytic Functions within the $x y z$

-space and Poisson’s Equations

The relationship between a semi-structured complex function within the

x y z

-space and Poisson’s Equations is given by Proposition 8. Proof of Proposition 8 is given in Appendix 9.

Proposition 8:
if

f (h) = u (x, y, z) + i v (x, y, z) + p w (x, y, z)

, is an analytic function within the

x y z

-space, where

u (x, y, z),

v (x, y, z)

and

w (x, y, z)

are real functions, then the real part

u (x, y, z),

imaginary part

v (x, y, z)

and unstructured part

w (x, y, z)

f (h)

all satisfy Poisson’s Equations. That is:

\begin{matrix} \frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} + \frac{\partial^{2} u}{\partial z^{2}} = ϕ_{3} \\ \frac{\partial^{2} v}{\partial x^{2}} + \frac{\partial^{2} v}{\partial y^{2}} + \frac{\partial^{2} v}{\partial z^{2}} = ϕ_{4} \\ \frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{2} w}{\partial y^{2}} + \frac{\partial^{2} w}{\partial z^{2}} = ϕ_{5} \end{matrix}

(15)

In Equation (14),

ϕ_{3}, ϕ_{4}

and

ϕ_{5}

are all functions.

5. Applications of Semi-structured Complex Analytic Functions

Having defined semi-structured complex analytic functions and exploring some of their properties, it is instructive to consider the application of these functions. Here one example (for illustration) was provided.

Example 1: The position vector of a point in the fluid field of a fluid flowing around a sphere is defined by the semi-structured complex analytic function A. Given this position vector, find the velocity field of the fluid flowing near the surface of a sphere of radius “a” centered at the origin of the semi-structured complex

x y z

-space.

Consider the semi-structured complex analytic function:

A = (1 + \frac{a^{3}}{2 r^{3}}) x + (\frac{1}{2} + \frac{a^{3}}{2 r^{3}}) i y + (\frac{1}{2} + \frac{a^{3}}{2 r^{3}}) p z

where

r = {(x^{2} + y^{2} + z^{2})}^{\frac{1}{2}}

.
"A" represents the position vector of a point in the fluid field of a fluid flowing near the surface of the sphere as shown in Figure 1.

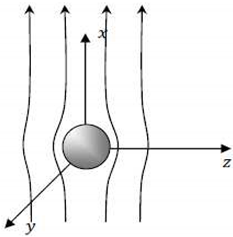Figure 1. Fluid flowing around a sphere.

To get the velocity field

v

of the fluid flowing near the surface of the sphere of radius “a” cantered at the origin of the semi-structured

x y z

-space simply use the nabla operator

\partial

on the real part of the position vector. Hence:

v = \partial [R e (A)] = (\frac{\partial}{\partial x} - i \frac{\partial}{\partial y} - p \frac{\partial}{\partial z}) (x + \frac{a^{3} x}{2 r^{3}}) = 1 + \frac{a^{3}}{2 r^{3}} - (\frac{3 a^{3} x}{2 r^{5}}) z^{*}

where

z^{*} = x - i y - p z

.
The velocity field

v

of the fluid is given by

v = (v_{x}, v_{y}, v_{z})

where:

v_{x} = 1 + \frac{a^{3}}{2 r^{3}} - \frac{3 a^{3} x^{2}}{2 r^{5}}

v_{y} = - \frac{3 a^{3} x y}{2 r^{5}}

v_{z} = - \frac{3 a^{3} x z}{2 r^{5}}

Hence the velocity field is represented by the semi-structured complex vector

v = v_{x} + i v_{y} + p v_{z}

In the Example 1, semi-structured complex functions were used to represent the problem of fluid flow in 3-dimensional space. This may seem trivial as any 3-dimensional coordinate system can be used to solve 3-dimensional problems in engineering. However, it is important to note that semi-structured complex analytic functions are based on semi-structured complex numbers and variables. Some 3-dimensional problems may contain singularities because of division by zero. These singularities can be resolved using the unstructured part of the semi-structured complex analytic function.

6. Discussion

There are a few points to highlight in this research. First, the general definitions associated with complex analytic functions can be applied to semi-structured complex analytic functions. For example, a semi-structured complex analytic function is said to be analytic in a region R if it is differentiable at each point of R, except possibly at a finite number of exceptional points called the singularities of the function. Whilst in complex analysis these singularities may be due to division by zero and or the fact that the function may not be complex differentiable, with semi-structured complex analysis these singularities are due to semi-structured complex analytic functions not being complex differentiable at a point. This is due to the fact that semi-structured complex functions are well defined at points that result in division by zero. If no point in the region R is a singularity of the analytic function, then the analytic function is described as a regular analytic function in R.

Additionally, a function is said to be analytic at a point if it is analytic in some neighborhood of that point. If in the neighborhood of a point (no matter how small this neighborhood is) a function is analytic and single-valued, then the function is said to be holomorphic at that point. An analytic function is said to be holomorphic in a domain if it is holomorphic in each point of that domain. These definitions apply not just to complex analytic functions but also semi-structured complex analytic functions.

As shown previously, semi-structured complex analytic functions can be used to describe 3-dimensional potentials and flows in physics and engineering. Beyond this, any 2-dimensional engineering problem that uses complex numbers and has a 3-dimensional equivalent that potentially has singularities resulting from division by zero, this 3-dimensional equivalent can potentially be assessed using semi-structured complex analytic functions. Singularities in such problems can be resolved using the unstructured part of the semi-structured complex analytic function.

7. Conclusion

It was observed that there was very little literature on the properties of analytic functions made up of semi-structured complex variables. Therefore, the aim of this research paper was to use the features of semi-structured complex numbers and the characteristics of analytic functions to develop the properties and explore the applications of semi-structured complex analytic functions.

Based on the stated aim, this paper made the following five major contributions: (1) developed an extension to the Cauchy–Riemann equations to include three other conditions for a semi-structured complex function to be analytic in the semi-structured complex

x y z

-space; (2) used the extension to the Cauchy–Riemann Equations to define a semi-structured complex analytic function along the real-imaginary

x y

-plane, the real-unstructured

x z

-plane, the imaginary-unstructured

y z

-plane and within the semi-structured complex

x y z

-space; (3) defined sufficient and necessary conditions for a semi-structured complex function to be analytic along the real-imaginary

x y

-plane, the real-unstructured

x z

-plane, the imaginary-unstructured

y z

-plane and within the semi-structured complex

x y z

-space; (4) determined the relationship between semi-structured complex analytic functions, Laplace’s Equations and Poisson’s Equations; and, (5) provided a simple example where semi-structured complex analytic functions can be used to solve problems in engineering. These results provide a firm basis to explore the field of semi-structured complex analysis.

Appendix 1. Research conducted on division by zero

Table A1. Research conducted on division by zero from 2018 to 2022.

Research	Research Aim
[3,4,5]	Explores the application of division by zero in calculus and differentiation
[6]	Uses classical logic and Boolean algebra to show the problem of division by zero can be solved using today’s mathematics
[7]	Develops an analogue to Pappus Chain theorem with Division by Zero
[8]	This paper proposes that the quantum computation being performed by the cancer cell at its most fundamental level is the division by zero. This is the reason for the insane multiplication of cancer cells at its most fundamental scale.
[9]	Explores evidence to suggest zero does divide zero
[10]	Considered using division by zero to compare incomparable abstract objects taken from two distinct algebraic spaces
[11]	Show recent attempts to divide by zero
[12]	Generalize a problem involving four circles and a triangle and consider some limiting cases of the problem by division by zero.
[13]	Paper considers computing probabilities from zero divided by itself
[14,15]	Considers how division by zero is taught on an elementary level
[16]	Develops a method to avoid division by zero in Newton’s Method
[17]	This work attempts to solve division by zero using a new form of optimization called Different-level quadratic minimization (DLQM)

Appendix 2. Proof of the extended Cauchy–Riemann Equations for the $x y$ -plane

To provide proof of the theorem which states that

f

being semi-structured complex-differentiable implies the extended Cauchy-Reiman equations, let us suppose the function

f

is semi-structured complex differentiable at some point

h_{x y}

. Suppose there exist a derivative

f^{'} (h_{x y})

defined as:

f^{'} (h_{x y}) = \lim_{δh \to 0} \frac{f (h_{x y} + δ h_{x y}) - f (h_{x y})}{δ h_{x y}}

(16)

whose value is independent of the argument that we take for the infinitesimal

δ h_{x y}

. If we take this to be real, that is,

δ h = δ x \in R

, the expression for the derivative can be written as:

f^{'} (h_{x y}) = \lim_{δx \to 0} \frac{f (x + δ x + i y) - f (x + i y)}{δ x} f^{'} (h_{x y}) = \lim_{δx \to 0} \frac{[u (x + δ x, y) + i v (x + δ x, y)] - [u (x, y) + i v (x, y)]}{δ x} f^{'} (h_{x y}) = \lim_{δx \to 0} \frac{[u (x + δ x, y) - u (x, y)] + i [v (x + δ x, y) - v (x, y)]}{δ x} f^{'} (h_{x y}) = [\lim_{δx \to 0} \frac{u (x + δ x, y) - u (x, y)}{δ x}] + i [\lim_{δx \to 0} \frac{v (x + δ x, y) - v (x, y)}{δ x}]

(17)

On the last line, the quantities in square brackets are the real partial derivatives of

u

and

v

(with respect to

x

). Therefore, those partial derivatives are well-defined, and can be simplified to Equation (18).

f^{'} (h_{x y}) = \frac{\partial u}{\partial x} + i \frac{\partial v}{\partial x}

(18)

On the other hand, we could also take an infinitesimal displacement in the imaginary direction, by setting

δ h = i δ y \in R

. Then the expression for the derivative is:

f^{'} (h_{x y}) = \lim_{δy \to 0} \frac{f (x + i y + i δ y) - f (x + i y)}{i δ y} f^{'} (h_{x y}) = \lim_{δy \to 0} \frac{[u (x, y + i δ y) + i v (x, y + i δ y)] - [u (x, y) + i v (x, y)]}{i δ y} f^{'} (h_{x y}) = \lim_{δy \to 0} \frac{[u (x, y + i δ y) - u (x, y)] + i [v (x, y + i δ y) - v (x, y)]}{i δ y} f^{'} (h_{x y}) = [\lim_{δy \to 0} \frac{u (x, y + i δ y) - u (x, y)}{i δ y}] + i [\lim_{δy \to 0} \frac{v (x, y + i δ y) - v (x, y)}{i δ y}]

(19)

On the last line, the quantities in square brackets are the real partial derivatives of

u

v

(with respect to y). Therefore, those partial derivatives are well-defined, and can be simplified to Equation (20).

f^{'} (h_{x y}) = - i \frac{\partial u}{\partial y} + \frac{\partial v}{\partial y}

(20)

Since

f (h)

is semi-structured complex differentiable, Equations (18) and Equations (20) must be equal so that:

\frac{\partial u}{\partial x} + i \frac{\partial v}{\partial x} = - i \frac{\partial u}{\partial y} + \frac{\partial v}{\partial y}

(21)

Noting that

u

, and

v

, we can take the real and imaginary parts of the equations separately. This yields as a set of real equations as shown Equations (22).

\{\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \\ \frac{\partial v}{\partial x} = - \frac{\partial u}{\partial y} \end{matrix}

(22)

Example of application of Equations (22):

Problem: Prove that

f (h_{x y}) = x + i y

is semi-structured complex differentiable in along the

x y

-plane.

Solution: It is sufficient to show that the function satisfies the Cauchy-Riemann equations for the

x y

-plane. Given the function the partial derivatives of the function are:

$\frac{\partial u}{\partial x} = 1$	$\frac{\partial v}{\partial y} = 1$	$\to \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}$
$\frac{\partial v}{\partial x} = 0$	$\frac{\partial u}{\partial y} = 0$	$\to \frac{\partial v}{\partial x} = - \frac{\partial u}{\partial y}$

Hence the function

f (h_{x y}) = x + i y

is semi-structured complex differentiable in along the

x y

-plane since it satisfies the Cauchy-Riemann equations for the

x y

-plane.

Appendix 3. Proof of the extended Cauchy–Riemann Equations for the $x z$ -plane

To provide proof of the theorem which states that

f

being semi-structured complex-differentiable implies the extended Cauchy-Reiman equations, let us suppose the function

f

is semi-structured complex differentiable at some point

h_{x z}

. Suppose there exist a derivative

f^{'} (h_{x z})

defined as:

f^{'} (h_{x z}) = \lim_{δh \to 0} \frac{f (h_{x z} + δ h_{x z}) - f (h_{x z})}{δ h_{x z}}

(23)

whose value is independent of the argument that we take for the infinitesimal

δ h_{x z}

. If we take this to be real, that is,

δ h_{x z} = δ x \in R

, the expression for the derivative can be written as:

f^{'} (h_{x z}) = \lim_{δx \to 0} \frac{f (x + δ x + p z) - f (x + p z)}{δ x} f^{'} (h_{x z}) = \lim_{δx \to 0} \frac{[u (x + δ x, z) + p w (x + δ x, z)] - [u (x, z) + p w (x, z)]}{δ x} f^{'} (h_{x z}) = \lim_{δx \to 0} \frac{[u (x + δ x, z) - u (x, z)] + p [w (x + δ x, z) - w (x, z)]}{δ x} f^{'} (h_{x z}) = [\lim_{δx \to 0} \frac{u (x + δ x, z) - u (x, z)}{δ x}] + p [\lim_{δx \to 0} \frac{v (x + δ x, z) - v (x, z)}{δ x}]

(24)

On the last line, the quantities in square brackets are the real partial derivatives of

u

and

w

(with respect to

x

). Therefore, those partial derivatives are well-defined, and can be simplified to Equation (25).

f^{'} (h_{x y}) = \frac{\partial u}{\partial x} + p \frac{\partial w}{\partial x}

(25)

On the other hand, we could also take an infinitesimal displacement in the imaginary direction, by setting

δ h = p δ z \in R

. Then the expression for the derivative is:

f^{'} (h_{x z}) = \lim_{δz \to 0} \frac{f (x + p z + p δ z) - f (x + p z)}{p δ z} f^{'} (h_{x z}) = \lim_{δz \to 0} \frac{[u (x, z + p δ z) + p w (x, z + p δ z)] - [u (x, z) + p w (x, z)]}{i δ y} f^{'} (h_{x z}) = \lim_{δz \to 0} \frac{[u (x, z + p δ z) - u (x, z)] + p [w (x, z + p δ z) - w (x, z)]}{p δ z} f^{'} (h_{x z}) = [\lim_{δz \to 0} \frac{u (x, z + p δ z) - u (x, z)}{p δ z}] + p [\lim_{δz \to 0} \frac{w (x, z + p δ z) - w (x, z)}{p δ z}]

(26)

On the last line, the quantities in square brackets are the real partial derivatives of

u

w

(with respect to y). It is also important to note that

\frac{1}{p} = \frac{- p^{2}}{p} = - p

. Therefore, those partial derivatives are well-defined, and can be simplified to Equation (27).

f^{'} (h_{x z}) = - p \frac{\partial u}{\partial z} + \frac{\partial w}{\partial z}

(27)

Since

f (h)

is semi-structured complex differentiable, Equations (25) and Equations (27) must be equal so that:

\frac{\partial u}{\partial x} + p \frac{\partial w}{\partial x} = - p \frac{\partial u}{\partial z} + \frac{\partial w}{\partial z}

(28)

Noting that

u

, and

v

, we can take the real and imaginary parts of the equations separately. This yields as a set of real equations as shown in Equations (29).

\{\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial w}{\partial z} \\ \frac{\partial w}{\partial x} = - \frac{\partial u}{\partial z} \end{matrix}

(29)

Example of application of Equations (29):

Problem: Prove that

f (h_{x z}) = \frac{1}{x + p z}

is semi-structured complex differentiable in along the

x z

-plane.

Solution: It is sufficient to show that the function satisfies the Cauchy-Riemann equations for the

x z

-plane. Now

f (h_{x z}) = \frac{1}{x + p z} = \frac{x}{x^{2} + z^{2}} - p \frac{z}{x^{2} + z^{2}}

. Given the function the partial derivatives of the function are:

$\frac{\partial u}{\partial x} = \frac{- x^{2} + z^{2}}{x^{2} + z^{2}}$	$\frac{\partial w}{\partial z} = \frac{- x^{2} + z^{2}}{x^{2} + z^{2}}$	$\to \frac{\partial u}{\partial x} = \frac{\partial w}{\partial z}$
$\frac{\partial w}{\partial x} = \frac{2 x z}{x^{2} + z^{2}}$	$\frac{\partial u}{\partial z} = \frac{- 2 x z}{x^{2} + z^{2}}$	$\to \frac{\partial u}{\partial y} = - \frac{\partial w}{\partial x}$

Hence the function

f (h_{x z}) = \frac{1}{x + p z}

is semi-structured complex differentiable in along the

x z

-plane since it satisfies the Cauchy-Riemann equations for the

x z

-plane.

Appendix 4. Proof of the extended Cauchy–Riemann Equations for the $y z$ -plane

To provide proof of the theorem which states that

f

being semi-structured complex-differentiable implies the extended Cauchy-Reiman equations, let us suppose the function

f

is semi-structured complex differentiable at some point

h_{y z}

. Suppose there exist a derivative

f^{'} (h_{y z})

defined as:

f^{'} (h_{y z}) = \lim_{δh \to 0} \frac{f (h_{y z} + δ h_{y z}) - f (h_{y z})}{δ h_{y z}}

(30)

whose value is independent of the argument that we take for the infinitesimal

δ h_{y z}

. If we take this to be real, that is,

δ h_{y z} = i δ y \in R

, the expression for the derivative can be written as:

f^{'} (h_{y z}) = \lim_{δy \to 0} \frac{f (i y + i δ y + p z) - f (i y + p z)}{i δ y} f^{'} (h_{y z}) = \lim_{δy \to 0} \frac{[v (y + i δ y, z) + p w (y + i δ y, z)] - [v (y, z) + p w (x, z)]}{i δ y} f^{'} (h_{y z}) = \lim_{δy \to 0} \frac{[v (y + i δ y, z) - v (y, z)] + p [w (y + i δ y, z) - w (y, z)]}{i δ y} f^{'} (h_{y z}) = i [\lim_{δy \to 0} \frac{v (y + i δ y, z) - v (y, z)}{i δ y}] + p [\lim_{δy \to 0} \frac{w (y + i δ y, z) - w (y, z)}{i δ y}]

(31)

On the last line, the quantities in square brackets are the real partial derivatives of

v

and

w

(with respect to

y

). Therefore, those partial derivatives are well-defined, and can be simplified to Equation (32).

f^{'} (h_{y z}) = \frac{\partial v}{\partial y} + \frac{p}{i} . \frac{\partial w}{\partial y}

(32)

On the other hand, we could also take an infinitesimal displacement in the imaginary direction, by setting

δ h = p δ z \in R

. Then the expression for the derivative is:

f^{'} (h_{y z}) = \lim_{δz \to 0} \frac{f (i y + p z + p δ z) - f (i y + p z)}{p δ z} f^{'} (h_{y z}) = \lim_{δz \to 0} \frac{[v (y, z + p δ z) + p w (y, z + p δ z)] - [v (y, z) + p w (y, z)]}{p δ z} f^{'} (h_{y z}) = \lim_{δz \to 0} \frac{[v (y, z + p δ z) - v (x, z)] + p [w (y, z + p δ z) - w (y, z)]}{p δ z} f^{'} (h_{y z}) = i [\lim_{δz \to 0} \frac{v (y, z + p δ z) - v (y, z)}{p δ z}] + p [\lim_{δz \to 0} \frac{w (y, z + p δ z) - w (y, z)}{p δ z}]

(33)

On the last line, the quantities in square brackets are the real partial derivatives of

v

w

(with respect to

z

). It is also important to note that

\frac{i}{p} = \frac{p}{i}

. Therefore, those partial derivatives are well-defined, and can be simplified to Equation (34).

f^{'} (h_{x z}) = \frac{p}{i} . \frac{\partial v}{\partial z} + \frac{\partial w}{\partial z}

(34)

Since

f (h)

is semi-structured complex differentiable, Equations (32) and Equations (34) must be equal so that:

\frac{\partial v}{\partial y} + \frac{p}{i} . \frac{\partial w}{\partial y} = \frac{p}{i} . \frac{\partial v}{\partial z} + \frac{\partial w}{\partial z}

(35)

Noting that

u

, and

w

, we can take the real and imaginary parts of the equations separately. This yields as a set of real equations as shown Equations (36).

\{\begin{matrix} \frac{\partial v}{\partial y} = \frac{\partial w}{\partial z} \\ \frac{\partial w}{\partial y} = \frac{\partial v}{\partial z} \end{matrix}

(36)

Example of application of Equations (36):

Problem: Prove that

f (h) = (i . \sin y . \cos z + p . \sin z . \cos y)

is semi-structured complex differentiable in along the

y z

-plane.

Solution: It is sufficient to show that the function satisfies the Cauchy-Riemann equations for the

y z

-plane. Given the function the partial derivatives of the function are:

$\frac{\partial v}{\partial y} = \cos z . \cos y$	$\frac{\partial w}{\partial z} = \cos z . \cos y$	$\to \frac{\partial v}{\partial y} = \frac{\partial w}{\partial z}$
$\frac{\partial v}{\partial z} = - \sin y . \sin z$	$\frac{\partial w}{\partial y} = - \sin z . \sin y$	$\to \frac{\partial v}{\partial z} = \frac{\partial w}{\partial y}$

Hence the function

f (h) = (i . \sin y . \cos z + p . \sin z . \cos y)

is semi-structured complex differentiable in along the

x z

-plane since it satisfies the Cauchy-Reimann equations for the

y z

-plane.

Appendix 5. Proof of the extended Cauchy–Riemann Equations for the $x y z$ -space

To provide proof of the theorem which states that

f

being semi-structured complex-differentiable implies the extended Cauchy-Reiman equations, let us suppose the function

f

is semi-structured complex differentiable at some point

h

. Suppose there exist a derivative

f^{'} (h)

defined as:

f^{'} (h) = \lim_{δh \to 0} \frac{f (h + δ h) - f (h)}{δ h}

(37)

whose value is independent of the argument that we take for the infinitesimal

δ h

. If we take this to be real, that is,

δ h = δ x \in R

, the expression for the derivative can be written as:

f^{'} (h) = \lim_{δx \to 0} \frac{f (x + δ x + i y + p z) - f (x + i y + p z)}{δ x} f^{'} (h) = \lim_{δx \to 0} \frac{[u (x + δ x, y, z) + i v (x + δ x, y, z) + p w (x + δ x, y, z)] - [u (x, y, z) + i v (x, y, z) + p w (x, y, z)]}{δ x} f^{'} (h) = \lim_{δx \to 0} \frac{[u (x + δ x, y, z) - u (x, y, z)] + i [v (x + δ x, y, z) - v (x, y, z)] + p [w (x + δ x, y, z) - w (x, y, z)]}{δ x} f^{'} (h) = [\lim_{δx \to 0} \frac{u (x + δ x, y, z) - u (x, y, z)}{δ x}] + i [\lim_{δx \to 0} \frac{v (x + δ x, y, z) - v (x, y, z)}{δ x}] + p [\lim_{δx \to 0} \frac{w (x + δ x, y, z) - w (x, y, z)}{δ x}]

(38)

On the last line, the quantities in square brackets are the real partial derivatives of u, v and w (with respect to

x

). Therefore, those partial derivatives are well-defined, and can be simplified to Equation (39).

f^{'} (h) = \frac{\partial u}{\partial x} + i \frac{\partial v}{\partial x} + p \frac{\partial w}{\partial x}

(39)

On the other hand, we could also take an infinitesimal displacement in the imaginary direction, by setting

δ h = i δ y \in R

. Then the expression for the derivative is:

f^{'} (h) = \lim_{δy \to 0} \frac{f (x + i y + i δ y + p z) - f (x + i y + p z)}{i δ y} f^{'} (h) = \lim_{δy \to 0} \frac{[u (x, y + i δ y, z) + i v (x, y + i δ y, z) + p w (x, y + i δ y, z)] - [u (x, y, z) + i v (x, y, z) + p w (x, y, z)]}{i δ y} f^{'} (h) = \lim_{δy \to 0} \frac{[u (x, y + i δ y, z) - u (x, y, z)] + i [v (x, y + i δ y, z) - v (x, y, z)] + p [w (x, y + i δ y, z) - w (x, y, z)]}{i δ y} f^{'} (h) = [\lim_{δy \to 0} \frac{u (x, y + i δ y, z) - u (x, y, z)}{i δ y}] + i [\lim_{δy \to 0} \frac{v (x, y + i δ y, z) - v (x, y, z)}{i δ y}] + p [\lim_{δy \to 0} \frac{w (x, y + i δ y, z) - w (x, y, z)}{i δ y}]

(40)

On the last line, the quantities in square brackets are the real partial derivatives of

u

v

and

w

(with respect to

y

). Therefore, those partial derivatives are well-defined, and can be simplified to Equation (41).

f^{'} (h) = - i \frac{\partial u}{\partial y} + \frac{\partial v}{\partial y} + \frac{p}{i} . \frac{\partial w}{\partial y}

(41)

Finally, we could also take an infinitesimal displacement in the imaginary direction, by setting

δ h = p δ z \in R

. Then the expression for the derivative is:

f^{'} (h) = \lim_{δz \to 0} \frac{f (x + i y + p z + p δ z) - f (x + i y + p z)}{p δ z} f^{'} (h) = \lim_{δz \to 0} \frac{[u (x, y, z + p δ z) + i v (x, y, z + p δ z) + p w (x, y, z + p δ z)] - [u (x, y, z) + i v (x, y, z) + p w (x, y, z)]}{p δ z} f^{'} (h) = \lim_{δz \to 0} \frac{[u (x, y, z + p δ z) - u (x, y, z)] + i [v (x, y, z + p δ z) - v (x, y, z)] + p [w (x, y, z + p δ z) - w (x, y, z)]}{p δ z} f^{'} (h) = [\lim_{δz \to 0} \frac{u (x, y, z + p δ z) - u (x, y, z)}{p δ z}] + i [\lim_{δz \to 0} \frac{v (x, y, z + p δ z) - v (x, y, z)}{p δ z}] + p [\lim_{δz \to 0} \frac{w (x, y, z + p δ z) - w (x, y, z)}{p δ z}]

(42)

On the last line, the quantities in square brackets are the real partial derivatives of u, v and w (with respect to y). Therefore, those partial derivatives are well-defined, and can be simplified to Equation (43).

f^{'} (h) = - p \frac{\partial u}{\partial z} + \frac{i}{p} . \frac{\partial v}{\partial z} + \frac{\partial w}{\partial z}

(43)

Since

f (h)

is semi-structured complex differentiable, Equations (39), Equations (41) and Equations (43) must be equal so that:

\frac{\partial u}{\partial x} + i \frac{\partial v}{\partial x} + p \frac{\partial w}{\partial x} = - i \frac{\partial u}{\partial y} + \frac{\partial v}{\partial y} + \frac{p}{i} . \frac{\partial w}{\partial y} = - p \frac{\partial u}{\partial z} + \frac{i}{p} . \frac{\partial v}{\partial z} + \frac{\partial w}{\partial z}

(44)

Noting that

u

v

and

w

are real functions, and

\frac{p}{i} = \frac{i}{p}

, we can take the real, imaginary, and unstructured parts of the equations separately. This yields as a set of real equations as shown Equations (45).

\{\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} = \frac{\partial w}{\partial z} \\ \frac{\partial v}{\partial x} = - \frac{\partial u}{\partial y} \\ \begin{matrix} \frac{\partial w}{\partial x} = - \frac{\partial u}{\partial z} \\ \frac{\partial w}{\partial y} = \frac{\partial v}{\partial z} \end{matrix} \end{matrix}

(45)

Example of application of Equations (45):

Problem: Prove that

f (h) = e^{x + i y + p z}

is semi-structured complex differentiable in along the

y z

-plane.

Solution: It is sufficient to show that the function satisfies the Cauchy-Riemann equations for the

x y z

-plane. Firstly,

f (h) = e^{x + i y + p z} = e^{x} . (\cos y + i . \sin y) . (\cos z + p . \sin z)

= e^{x} . \cos y . \cos z + i e^{x} . \sin y . \cos z + p e^{x} . \cos y . \sin z

The partial derivatives of the given function are:

$\frac{\partial u}{\partial x} = e^{x} . \cos y . \cos z$	$\frac{\partial u}{\partial y} = - e^{x} . \sin y . \cos z$	$\frac{\partial u}{\partial z} = - e^{x} . \cos y . \sin z$
$\frac{\partial v}{\partial x} = e^{x} . \sin y . \cos z$	$\frac{\partial v}{\partial y} = e^{x} . \cos y . \cos z$	$\frac{\partial v}{\partial z} = - e^{x} . \sin y . \sin z$
$\frac{\partial w}{\partial x} = e^{x} . \cos y . \sin z$	$\frac{\partial w}{\partial y} = - e^{x} . \sin y . \sin z$	$\frac{\partial w}{\partial z} = e^{x} . \cos y . \cos z$

Clearly from the partial derivatives Equations (45) holds. Hence the function

f (h) = e^{x + i y + p z}

is semi-structured complex differentiable in along the

x z

-plane since it satisfies the Cauchy-Reimann equations for the

x y z

-space.

Appendix 6. Proof of Proposition 5

Let the function

f (h_{x y}) = u (x, y) + i v (x, y)

be analytic in some domain D, then the Cauchy–Riemann Equations for this function is:

\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} & a n d & \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x} \end{matrix}

(46)

Assume that the second order partial derivatives of

u (x, y)

and

v (x, y)

exist and are continuous functions of

x

and

y

, then from Equations (46),

\begin{matrix} \frac{\partial^{2} u}{\partial x^{2}} = \frac{\partial v}{\partial x \partial y} & a n d & \frac{\partial^{2} u}{\partial y^{2}} = - \frac{\partial v}{\partial y \partial x} \end{matrix}

(47)

So that

\frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} = 0

(48)

Similarly, it can be shown that:

\frac{\partial^{2} v}{\partial x^{2}} + \frac{\partial^{2} v}{\partial y^{2}} = 0

(49)

From Equations (48) and (49), it is clear that functions

u (x, y)

and

v (x, y)

satisfy Laplace’s Equations which is of the form given in Equation (50):

\frac{\partial^{2} ϕ}{\partial x^{2}} + \frac{\partial^{2} ϕ}{\partial y^{2}} = 0

(50)

Appendix 7. Proof of Proposition 6

Let the function

f (h_{x z}) = u (x, z) + p w (x, z)

be analytic in some domain D, then the Cauchy–Riemann Equations for this function is:

\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial w}{\partial z} & a n d & \frac{\partial u}{\partial z} = - \frac{\partial w}{\partial z} \end{matrix}

(51)

Assume that the second order partial derivatives of

u (x, z)

and

w (x, z)

exist and are continuous functions of

x

and

z

, then from Equations (51),

\begin{matrix} \frac{\partial^{2} u}{\partial x^{2}} = \frac{\partial w}{\partial x \partial z} & a n d & \frac{\partial^{2} u}{\partial z^{2}} = - \frac{\partial w}{\partial z \partial x} \end{matrix}

(52)

So that

\frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial z^{2}} = 0

(53)

Similarly, it can be shown that:

\frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{2} w}{\partial z^{2}} = 0

(54)

From Equations (53) and (54), it is clear that functions

u (x, z)

and

w (x, z)

satisfy Laplace’s Equations which is of the form given in Equation (55):

\frac{\partial^{2} ϕ}{\partial x^{2}} + \frac{\partial^{2} ϕ}{\partial z^{2}} = 0

(55)

Appendix 8. Proof of Proposition 7

Let the function

f (h_{y z}) = i v (y, z) + p w (y, z)

be analytic in some domain D, then the Cauchy–Riemann Equations for this function is:

\begin{matrix} \frac{\partial v}{\partial y} = \frac{\partial w}{\partial z} & a n d & \frac{\partial v}{\partial z} = \frac{\partial w}{\partial y} \end{matrix}

(56)

Assume that the second order partial derivatives of

v (y, z)

and

w (y, z)

exist and are continuous functions of

y

and

z

, then from Equations (56),

\begin{matrix} \frac{\partial^{2} v}{\partial y^{2}} = \frac{\partial w}{\partial y \partial z} & a n d & \frac{\partial^{2} v}{\partial z^{2}} = \frac{\partial w}{\partial z \partial y} \end{matrix}

(57)

So that

\frac{\partial^{2} v}{\partial y^{2}} + \frac{\partial^{2} v}{\partial z^{2}} = 2 \frac{\partial w}{\partial z \partial y} = ϕ_{1}

(58)

Similarly, it can be shown that:

\frac{\partial^{2} w}{\partial y^{2}} + \frac{\partial^{2} w}{\partial z^{2}} = 2 \frac{\partial v}{\partial z \partial y} = ϕ_{2}

(59)

From Equations (58) and (59), it is clear that functions

v (y, z)

and

w (y, z)

satisfy Poisson’s Equations which is of the form given in Equation (60):

\frac{\partial^{2} φ}{\partial x^{2}} + \frac{\partial^{2} φ}{\partial z^{2}} = ϕ

(60)

Appendix 9. Proof of Proposition 8

Let the function

f (h) = u (x, y, z) + i v (x, y, z) + p w (x, y, z)

be analytic in some domain D, then the Cauchy–Riemann Equations for this function is:

\begin{matrix} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} = \frac{\partial w}{\partial z} & a n d & \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x} \end{matrix} \begin{matrix} \frac{\partial u}{\partial z} = - \frac{\partial w}{\partial x} & a n d & \frac{\partial v}{\partial z} = \frac{\partial w}{\partial y} \end{matrix}

(61)

Assume that the second order partial derivatives of

u (x, y, z)

v (x, y, z)

and

w (x, y, z)

exist and are continuous functions of

x, y

and

z

, then from Equations (61),

\begin{matrix} \frac{\partial^{2} u}{\partial x^{2}} = \frac{\partial v}{\partial x \partial y} = \frac{\partial w}{\partial x \partial z} & a n d & \begin{matrix} \frac{\partial^{2} u}{\partial y^{2}} = - \frac{\partial v}{\partial y \partial x} & a n d & \frac{\partial^{2} u}{\partial z^{2}} = - \frac{\partial w}{\partial z \partial x} \end{matrix} \end{matrix}

(62)

So that

\frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} + \frac{\partial^{2} u}{\partial z^{2}} = \frac{\partial w}{\partial x \partial z} - \frac{\partial v}{\partial y \partial x} - \frac{\partial w}{\partial z \partial x} = - \frac{\partial v}{\partial y \partial x} = ϕ_{3}

(63)

Similarly, it can be shown that:

\frac{\partial^{2} v}{\partial x^{2}} + \frac{\partial^{2} v}{\partial y^{2}} + \frac{\partial^{2} v}{\partial z^{2}} = - \frac{\partial u}{\partial x \partial y} + \frac{\partial u}{\partial y \partial x} + \frac{\partial w}{\partial z \partial y} = \frac{\partial w}{\partial z \partial y} = ϕ_{4}

(64)

\frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{2} w}{\partial y^{2}} + \frac{\partial^{2} w}{\partial z^{2}} = - \frac{\partial u}{\partial x \partial z} + \frac{\partial v}{\partial y \partial z} + \frac{\partial u}{\partial z \partial x} = \frac{\partial v}{\partial y \partial z} = ϕ_{5}

(65)

From Equations (64) and (65), it is clear that functions

u (x, y, z)

v (x, y, z)

and

w (x, y, z)

satisfy Poisson’s Equations which is of the form given in Equation (66):

\frac{\partial^{2} φ}{\partial x^{2}} + \frac{\partial^{2} φ}{\partial y^{2}} + \frac{\partial^{2} φ}{\partial z^{2}} = ϕ

(66)

References

P. Jean Paul and S. Wahid, "Unstructured and Semi-structured Complex Numbers: A Solution to Division by Zero.," Pure and Applied Mathematics Journal, vol. 10, no. 2, p. 49, 2021. [CrossRef]
P. Jean Paul and S. Wahid, "Reformulating and Strengthening the theory of Semi-strucutred Complex Numbers," International Journal of Applied Physics and Mathematics, 2022.
S. Pinelas and S. Saitoh, "Division by Zero Calculus and Differential Equations," in Differential and Difference Equations with Applications: ICDDEA, Amadora, Portugal, 2018. [CrossRef]
S. Saitoh, "Introduction to the division by zero calculus," in Scientific Research Publishing, Inc, USA, 2021.
H. Okumura, "The arbelos in Wasan geometry: Atsumi’s problem with division by zero calculus," Sangaku Journal of Mathematics, vol. 5, pp. 32-38, 2021.
I. Barukčić, "Classical logic and the division by zero," International Journal of Mathematics Trends and Technology IJMTT, vol. 65, no. 7, pp. 31-73, 2019. [CrossRef]
H. Okumura, "An Analogue to Pappus Chain theorem with Division by Zero," In Forum Geom, vol. 18, pp. 409-412, 2018.
M. P. Lobo, "Cancer: Division by Zero," Open Journal of Mathematics and Physics, vol. 2, no. 73, p. 5, 2020. [CrossRef]
M. P. Lobo, "Does zero divide zero," Open Journal of Mathematics and Physics, vol. 2, no. 69, p. 3, 2020. [CrossRef]
J. Czajko, "On unconventional division by zero," World Scientific News, vol. 99, pp. 133-147, 2018.
H. Okumura, "Is It Really Impossible To Divide By Zero," J Appl Math, vol. 27, no. 2, pp. 191-198, 2018. [CrossRef]
H. Okumura, "A four circle problem and division by zero," Sangaku Journal of Mathematics, vol. 4, pp. 1-8, 2020.
W. Mwangi, "Definite Probabilities from Division of Zero by Itself Perspective," Asian Journal of Probability and Statistics, vol. 6, no. 2, pp. 1-26, 2020. [CrossRef]
J. Dimmel and E. Pandiscio, "When it’s on zero, the lines become parallel: Preservice elementary teachers’ diagrammatic encounters with division by zero," The Journal of Mathematical Behavior, vol. 58, pp. 1-27, 2020. [CrossRef]
F. Karakus and B. Aydin, "Elementary Mathematics Teachers’specialized Content Knowledge Related To Division By Zero," Malaysian Online Journal of Educational Sciences, vol. 7, no. 2, pp. 25-40, 2019.
I. Abdulrahman, "A Method to Avoid the Division-by-Zero or Near-Zero in Newton-Raphson Method," Feburary 2022. [Online]. Available: https://www.researchgate.net/publication/358857049_A_Method_to_Avoid_the_Division-by-Zero_or_Near-Zero_in_Newton-Raphson_Method. [Accessed 28 April 2022].
Y. Zhang, Y. Ling, M. Yang and M. Mao, "Exemplar Different-Level Quadratic Minimization,," in The 2018 5th International Conference on Systems and Informatics, 2018. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Semi-Structured Complex Numbers:Extending the Cauchy–Riemann Equations and developing Semi-Structured Complex Analytic Functions

Abstract

1. Introduction

1.1. Analytic Functions and their Importance

1.2. The Cauchy–Riemann Equations and Analytic Functions

1.3. Semi-structured Complex Numbers: a recent development in division by zero

1.4. Major contributions

2. Extensions to the Cauchy–Riemann Equations

2.1. Cauchy–Riemann Equations for the x y

2.2. Cauchy-Riemann Equations for the x z -plane

2.3. Cauchy–Riemann Equations for the y z -plane

2.4. Cauchy-Riemann Equations for the x y z -space

3. Semi-structured Complex Analytic Functions

3.1. Semi-structured Complex Analytic Functions along the x y -plane

3.2. Semi-structured Complex Analytic Functions along the x z -plane

3.3. Semi-structured Complex Analytic Functions along the y z -plane

3.4. Semi-structured Complex Analytic Functions within the x y z -space

4. Semi-structured Complex Analytic Functions, Laplace and Poisson Equations

4.1. Semi-structured Complex Analytic Functions along the x y -plane and Laplace’s Equations

4.2. Semi-structured Complex Analytic Functions along the x z -plane and Laplace’s Equations

4.3. Semi-structured Complex Analytic Functions along the y z -plane and Poisson’s Equations

4.4. Semi-structured Complex Analytic Functions within the x y z

5. Applications of Semi-structured Complex Analytic Functions

6. Discussion

7. Conclusion

Appendix 1. Research conducted on division by zero

Appendix 2. Proof of the extended Cauchy–Riemann Equations for the x y -plane

Appendix 3. Proof of the extended Cauchy–Riemann Equations for the x z -plane

Appendix 4. Proof of the extended Cauchy–Riemann Equations for the y z -plane

Appendix 5. Proof of the extended Cauchy–Riemann Equations for the x y z -space

Appendix 6. Proof of Proposition 5

Appendix 7. Proof of Proposition 6

Appendix 8. Proof of Proposition 7

Appendix 9. Proof of Proposition 8

References

MDPI Initiatives

Important Links

Subscribe

2.1. Cauchy–Riemann Equations for the $x y$

2.2. Cauchy-Riemann Equations for the $x z$ -plane

2.3. Cauchy–Riemann Equations for the $y z$ -plane

2.4. Cauchy-Riemann Equations for the $x y z$ -space

3.1. Semi-structured Complex Analytic Functions along the $x y$ -plane

3.2. Semi-structured Complex Analytic Functions along the $x z$ -plane

3.3. Semi-structured Complex Analytic Functions along the $y z$ -plane

3.4. Semi-structured Complex Analytic Functions within the $x y z$ -space

4.1. Semi-structured Complex Analytic Functions along the $x y$ -plane and Laplace’s Equations

4.2. Semi-structured Complex Analytic Functions along the $x z$ -plane and Laplace’s Equations

4.3. Semi-structured Complex Analytic Functions along the $y z$ -plane and Poisson’s Equations

4.4. Semi-structured Complex Analytic Functions within the $x y z$

Appendix 2. Proof of the extended Cauchy–Riemann Equations for the $x y$ -plane

Appendix 3. Proof of the extended Cauchy–Riemann Equations for the $x z$ -plane

Appendix 4. Proof of the extended Cauchy–Riemann Equations for the $y z$ -plane

Appendix 5. Proof of the extended Cauchy–Riemann Equations for the $x y z$ -space