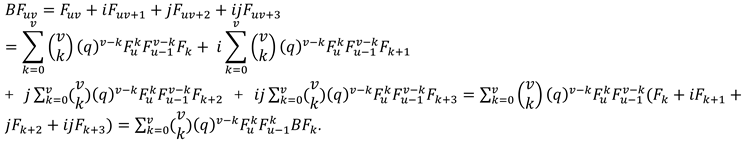Prerpints.org logo
Preprint
Article

On Bicomplex (p,q)-Fibonacci Quaternions

Altmetrics

Downloads

117

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 December 2023

Posted:

19 December 2023

You are already at the latest version

Alerts
Abstract
Here, we describe the bicomplex (p,q)- Fibonacci numbers and the bicomplex (p,q)- Fibonacci quaternions that are based on these numbers and give some of their equations, including the Binet formula, generating function, Catalan, Cassini, d’Ocagne’s identities, and some summation formulas for both of them. Finally, we create a matrix for bicomplex (p,q)- Fibonacci quaternions, and we obtain a determinant of a special matrix that gives the terms of that quaternion.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics

MSC:  11B39; 11R52; 20G20

1. Introduction

A generalization of the second-order sequences is the p , q − Fibonacci sequence. Suvarnamani and Tatong [2] defined p , q − Fibonacci sequence, { F n p , q } n = 0 ∞ , that has initial terms 0 and 1 , and for n ≥ 2 , holds the following recurrence relation:
F n + 2 p , q = p F n + 1 p , q + q F n p , q ,
where p and q are nonzero real numbers such that p 2 + 4 q > 0 .
The first few p , q − Fibonacci numbers are
F 0 p , q = 0 , F 1 p , q = 1 , F 2 p , q = p , F 3 p , q = p 2 + q , F 4 p , q = p 3 + 2 p q , F 5 p , q = p 4 + 3 p 2 q + q 2 .
The characteristic equation of (1) is
σ 2 − p σ − q = 0 .
Binet’s formula of the F n p , q is as follow
F n p , q = β n − θ n β − θ ,
where β and θ are roots of (2) [2].
Furthermore, there are many more articles on p , q − Fibonacci sequence [2,3,4,5,6,7,8].
Quaternions have become a popular subject of study by researchers, especially in recent years. In 1843, Hamilton [9] introduced quaternions that extended complex numbers. In addition, a set of quaternions is defined by Hamilton as follows:
H = { h = 1 h 0 + e 1 h 1 + e 2 h 2 + e 3 h 3 :   h 0 ,   h 1 , h 2 ,   h 3   ∈ R }
where R is the set of real numbers,
e 1 2 = e 2 2 = e 3 2 = − 1 , e 1 e 2 = − e 2 e 1 = e 3 , e 2 e 3 = − e 3 e 2 = e 1 , e 3 e 1 = − e 1 e 3 = e 2 .
The quaternions can be thought of as four-dimensional vectors, just as complex numbers can be thought of as two-dimensional vectors [9] because the quaternions are extensions of complex numbers into a four-dimensional space.
In addition, new quaternions can be defined by combining quaternions and different number sequences. For example, nth  p , q − Fibonacci quaternions [4] are defined as follows:
Q F n p , q = F n p , q + e 1 F n + 1 p , q + e 2 F n + 2 p , q + e 3 F n + 3 p , q ,
where F n p , q is the n t h   p , q − Fibonacci number. Also, the imaginary quaternion units e 1 , e 2 ,   and e 3 have the rules in (4). There are many more works on quaternions in literature (see, for example, [2,6,7,10,11,12,13,14,15,16,17,18,19,20]).
Another popular number sequence is the bicomplex numbers. In 1892, it is defined bicomplex numbers [21] by four base elements 1 , i , j , i j where
i 2 = j 2 = − 1   and   i j = j i .
In that case, any bicomplex number b c can be written as follows:
b c = b c 0 + i b c 1 + j b c 2 + i j b c 3 = b c 0 + i b c 1 + j ( b c 2 + i b c 3 )
where b c 0 , b c 1 , b c 2 , b c 3 ∈ R and R is the set of real numbers. Let b c = b c 0 + i b c 1 + j b c 2 + i j b c 3 and b c ' = b c ' 0 + i b c ' 1 + j b c ' 2 + i j b c ' 3 are two bicomplex numbers. Then, it is written the addition, subtraction, and multiplication of the bicomplex numbers in the following form:
b c + b c ' = ( b c 0 + b c ' 0 ) + ( b c 1 + b c ' 1 ) i + ( b c 2 + b c ' 2 ) j + ( b c 3 + b c ' 3 ) i j , b c − b c ' = ( b c 0 − b c ' 0 ) + ( b c 1 − b c ' 1 ) i + ( b c 2 − b c ' 2 ) j + ( b c 3 − b c ' 3 ) i j , b c × b c ' = ( b c 0 b c ' 0 − b c 1 b c ' 1 − b c 2 b c ' 2 + b c 3 b c ' 3 ) + ( b c 0 b c ' 1 + b c 1 b c ' 0 − b c 2 b c ' 3 + b c 3 b c ' 2 ) i + ( b c 0 b c ' 2 + b c 2 b c ' 0 − b c 1 b c ' 3 + b c 3 b c ' 1 ) j + ( b c 0 b c ' 3 + b c 3 b c ' 0 − b c 1 b c ' 2 + b c 2 b c ' 1 ) i j ,
respectively.
Moreover, there are three different conjugations of the bicomplex numbers as follows:
b c i ¯ = b c 0 − i b c 1 + j b c 2 − i j b c 3 , b c j ¯ = b c 0 + i b c 1 − j b c 2 − i j b c 3 , b c i j ¯ = b c 0 − i b c 1 − j b c 2 + i j b c 3 .
For more information on bicomplex numbers, refer to the resources in [7,8,14,18,19,22,23,24,25,26,27].
There are also studies in which bicomplex numbers and number sequences and bicomplex numbers and quaternion sequences are used together [8,14,15,18,19,20,23,25,26,27].
Here, we obtain a generalization of second-order bicomplex number and bicomplex quaternion sequences. We give some of their equations, including the Binet formula, generating function, Catalan, Cassini, d’Ocagne’s identities, and summation formulas for bicomplex p , q − Fibonacci numbers and bicomplex p , q − Fibonacci quaternions. In addition, we describe a matrix that we call N-matrix of type 4 × 4 for bicomplex p , q − Fibonacci quaternions whose terms are bicomplex p , q − Fibonacci numbers. Then, we obtained that the bicomplex p , q − Fibonacci quaternions can be expressed as the 8 × 8 real matrices. Finally, we create a special matrix for bicomplex p , q − Fibonacci quaternions, we obtain some equations about the matrix, and we obtain the determinant of a special matrix that gives the terms of that quaternion.

2. Bicomplex p , q − Fibonacci Numbers

Here, we describe the bicomplex p , q − Fibonacci numbers. Some equations and summation formulas about bicomplex p , q − Fibonacci number sequence are given. In addition, the generating function, Binet’s formula, Catalan, Cassini, and d’Ocagne’s identities are obtained for these number sequences.
Definition 1. 
The bicomplex p , q − Fibonacci numbers are introduced by
B F u p , q = F u + i F u + 1 + j F u + 2 + i j   F u + 3 ,
where  F u  is the  u t h   p , q − Fibonacci number and  i , j  are bicomplex units that provide (5).
In the remainder of the study, F u will be considered as u t h   p , q − Fibonacci number.
The first few terms of bicomplex p , q − Fibonacci sequence are the following:
B F 0 p , q = i + p j + p 2 + q i j , B F 1 p , q = 1 + p i + p 2 + q j + p 3 + 2 p q i j , B F 2 p , q = p + p 2 + q i + p 3 + 2 p q j + p 4 + 3 p 2 q + q 2 i j , B F 3 p , q = p 2 + q + p 3 + 2 p q i + p 4 + 3 p 2 q + q 2 j + p 5 + 4 p 3 q + 3 p q 2 i j , B F 4 p , q = p 3 + 2 p q + ( p 4 + 3 p 2 q + q 2 ) i + p 5 + 4 p 3 q + 3 p q 2 j + p 6 + 5 p 4 q + 6 p 2 q 2 + q 3 i j .
For u ≥ 2 , it is given the following identity with simple calculation
B F u p , q = p B F u − 1 p , q + q B F u − 2 p , q .
Thus, the characteristic equation of (8) is
φ 2 − p φ − q = 0 .
Let any two bicomplex p , q − Fibonacci numbers be B F u p , q = F u + i F u + 1 + j F u + 2 + i j F u + 3 and B F v p , q = F v + i F v + 1 + j F v + 2 + i j F v + 3 . The addition, subtraction, and multiplication for them are written as follows:
B F u p , q ± B F v p , q = ( F u ± F v ) + ( F u + 1 ± F v + 1 ) i + ( F u + 2 ± F v + 2 ) j + ( F u + 3 ± F v + 3 ) i j , B F u p , q × B F v p , q = ( F u F v − F u + 1 F v + 1 − F u + 2 F v + 2 + F u + 3 F v + 3 ) +   F u F v + 1 + F u + 1 F v − F u + 2 F v + 3 + F u + 3 F v + 2 i + ( F u F v + 2 + F u + 2 F v − F u + 1 F v + 3 + F u + 3 F v + 1 ) j + ( F u F v + 3 + F u + 3 F v − F u + 1 F v + 2 + F u + 2 F v + 1 ) i j .
The multiplication of a bicomplex p , q − Fibonacci number by the real scalar μ is described as the following:
μ B F u p , q = μ F u + i μ F u + 1 + j μ F u + 2 + i j   μ F u + 3 .
Furthermore, bicomplex p , q − Fibonacci numbers have three different conjugations, which can be written as follows:
B F u p , q i ¯ = F u − i F u + 1 + j F u + 2 − i j F u + 3 ,
( B F u p , q ) j ¯ = F u + i F u + 1 − j F u + 2 − i j F u + 3 ,
( B F u p , q ) i j ¯ = F u − i F u + 1 − j F u + 2 + i j F u + 3 .
Theorem 1. 
Let B F u and B F v be two bicomplex p , q − Fibonacci numbers. In that case, it can be given the following for bicomplex p , q − Fibonacci numbers about the different three conjugates of these numbers:
B F u B F v i ¯ = B F u i ¯   B F v i ¯ =   ( B F v ) i ¯   ( B F u ) i ¯ B F u B F v j ¯ = B F u j ¯   B F v j ¯ =   B F v j ¯   B F u j ¯ B F u B F v i j ¯ = ( B F u ) i j ¯   ( B F v ) i j ¯ =   ( B F v ) i j ¯   ( B F u ) i j ¯
Proof. 
By using (10)-(12), these identities can be obtained with simple mathematical calculations. □
Theorem 2. 
Binet’s formula of the bicomplex p , q − Fibonacci numbers { B F u p , q }  is given in the following equation for  u ≥ 0  ( u  is any integer),
B F u =   τ _ τ u −   ω _ ω u τ − ω
where  τ  and  ω  are roots of (9).
  τ _ = 1 + i   τ + j τ 2 + i j τ 3   ω _ = 1 + i   ω + j ω 2 + i j ω 3
Proof. 
By using (8) and (4), we have following equation:
B F u p , q = τ u − ω u τ − ω + i τ u + 1 − ω u + 1 τ − ω + j τ u + 2 − ω u + 2 τ − ω + i j τ u + 3 − ω u + 3 τ − ω .
Thus, Binet’s formula of the bicomplex p , q − Fibonacci numbers is easily given with some simple computation. □
In the remainder of the study, B F u will be considered as u t h bicomplex p , q − Fibonacci number.
Theorem 3. 
The generating function of the bicomplex  p , q − Fibonacci numbers { B F u }  is
G B F t = B F 0 + B F 1 − p B F 0 t 1 − p t − q t 2 = B F 0 + 1 + q j + p 3 + p 2 − q i j t 1 − p t − q t 2 _ .
Proof. 
To find the generating function of { B F u } , we will first use the following equation.
G B F t = ∑ u = 0 ∞ B F u t u .
In that case
G B F t = B F 0 + B F 1 t + B F 2 t 2 + … + B F m t m + … .
Thus,
− p t G B F t = − p B F 0 t − p B F 1 t 2 − p B F 2 t 3 − … − p B F m t m + 1 + … . − q t 2 G B F t = − q B F 0 t 2 − q B F 1 t 3 − q B F 2 t 4 − … − q B F m t m + 2 + … .
We obtain that
1 − p t − q t 2 G B F t = B F 0 + B F 1 − p B F 0 t + ( B F 2 − p B F 1 − q B F 0 ) t 2         + … + ( B F m + 1 − p B L e m − q B F m − 1 ) t m + 1 + … .
Using (9) and initial conditions, we have
G B F t = B F 0 + B F 1 − p B F 0 t 1 − p t − q t 2 = B F 0 + 1 + q j + p 3 + p 2 − q i j t 1 − p t − q t 2 _ . □
Theorem 4. 
The exponential generating function of the bicomplex   p , q − Fibonacci numbers { B F u }  is
E B F t =   τ _ e τ u −   ω _ e ω u τ − ω .
Proof. 
To find the exponential generating function of { B F u } , firstly, we will use the following equation:
E B F t = ∑ u = 0 ∞ B F u t u u ! .
By using (14) and e t = ∑ u = 0 ∞ t u u ! , the exponential generating function of B F u is obtained
E B F t = ∑ u = 0 ∞   τ _ τ u −   ω _ ω u τ − ω t u u ! =   τ _ e τ u −   ω _ e ω u τ − ω . □
Theorem 5. 
For u ≥ v , Catalan identity for bicomplex p , q − Fibonacci numbers is as follows:
B F u − v B F u + v − B F u 2 = −   τ _     ω _ − q u − v τ v − ω v 2 p 2 + 4 q
where  u  and  v  are positive integers.
Proof.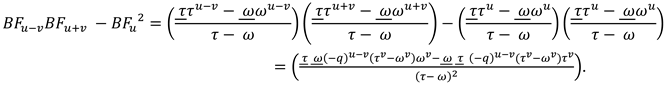 
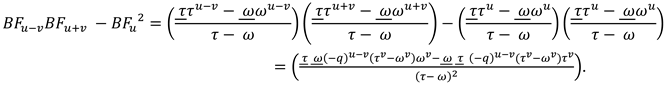
Preprints 93694 i001
Because τ and ω are roots of (10), τ ω = ( − q ) and τ _ = 1 + i τ + j τ 2 + i j τ 3 and ω _ = 1 + i ω + j ω 2 + i j ω 3 , we obtain
  τ _     ω _ = 1 + q − q 2 − q 3 + i p − p q 2 + j p 2 + 2 q + p 2 q + 2 q 2 + i j p 3 + 2 q p =   ω _     τ _ .
Thus, we obtain = −   τ _     ω _ − q u − v τ v − ω v 2 τ − ω 2 = −   τ _     ω _ − q u − v τ v − ω v 2 p 2 + 4 q _ . □
If v = 1 in the Catalan identity, Cassini identity is obtained as follows:
Corollary 1. 
For u ≥ 1 , Cassini identity for bicomplex p , q − Fibonacci numbers is as follows:
B F u − 1 B F u + 1 − B F u 2 = −   τ _     ω _ − q u − 1
where  u  is an integer.
Theorem 6. 
D’Ocagne’s identity for bicomplex p , q − Fibonacci numbers is as follows:
B F u B F v + 1 − B F u + 1 B F v =   τ _     ω _ − q v τ u − v − ω u − v p 2 + 4 q .
Proof. 
                                B F u B F v + 1 − B F u + 1 B F v =   τ _ τ u −   ω _ ω u τ − ω   τ _ τ 1 + v −   ω _ ω 1 + v τ − ω −   τ _ τ u + 1 −   ω _ ω u + 1 τ − ω   τ _ τ v −   ω _ ω v τ − ω =   τ _     ω _ τ u ω v ( τ − ω ) −   ω _     τ _     ω u τ v ( τ − ω ) τ − ω 2   τ _     ω _ =   ω _     τ _     u ≥ v   and   τ ω = − q =   τ _     ω _ − q v τ u − v − ω u − v ( τ − ω ) =   τ _     ω _ − q v τ u − v − ω u − v p 2 + 4 q   . □
Now, we give some identities about summations of terms in the bicomplex p , q − Fibonacci numbers.
Theorem 7. 
For k , l  are natural number, the summation formula of bicomplex  p , q − Fibonacci numbers is
∑ k = 1 l B F k = B F l + 1 + q B F l − B F 1 − q B F 0 p + q − 1                                     p + q ≠ 1   q B F l + B F 1 + l − 1 ( 1 + i + j + i j ) 1 + q _                           p + q = 1 .
Proof. 
Firstly, we assume that p + q ≠ 1 . In this situation,
∑ k = 1 l B F k = ∑ k = 1 l F k + i ∑ k = 1 l F k + 1 + j ∑ k = 1 l F k + 2 + i j ∑ k = 1 l F k + 3
In addition, we know that from the equ (13) in [5]
∑ k = 1 l F k = F l + 1 + q F l − F 1 − q F 0 p + q − 1 _
With simple calculations, we obtain
∑ k = 1 l F k + 1 = p ∑ k = 1 l F k + q ∑ k = 1 l F k − 1 = F l + 2 + q F l + 1 − F 2 − q F 1 p + q − 1 _ , ∑ k = 1 l F k + 2 = F l + 3 + q F l + 2 − F 3 − q F 2 p + q − 1 _ , ∑ k = 1 l F k + 3 = F l + 4 + q F l + 3 − F 4 − q F 3 p + q − 1 _ .
Thus,
∑ k = 1 l B F k = F l + 1 + q F l − F 1 − q F 0 p + q − 1 + i F l + 2 + q F l + 1 − F 2 − q F 1 p + q − 1 _ + j F l + 3 + q F l + 2 − F 3 − q F 2 p + q − 1 + i j ( F l + 4 + q F l + 3 − F 4 − q F 3 p + q − 1 _ ) = B F l + 1 + q B F l − B F 1 − q B F 0 p + q − 1   .
Now, let p + q = 1 ,
We obtain that from the equ (13) in [5], ∑ k = 1 l F k = q F l + ( l − 1 ) + F 1 1 + q _ . Moreover, we have
∑ k = 1 l F k + 1 = p ∑ k = 1 l F k + q ∑ k = 1 l F k − 1 = q F l + 1 + l − 1 + F 2 1 + q _ ,
So we can write
∑ k = 1 l F k + 2 = q F l + 2 + l − 1 + F 3 1 + q _ ,
∑ k = 1 l F k + 3 = q F l + 3 + l − 1 + F 4 1 + q _ . Thus,
∑ k = 1 l B F k = q F l + ( l − 1 ) + F 1 1 + q _ + i q F l + 1 + l − 1 + F 2 1 + q _ + j q F l + 2 + l − 1 + F 3 1 + q _ + i j ( q F l + 3 + l − 1 + F 4 1 + q _ ) = q B F l + l − 1 1 + i + j + i j + B F 1 1 + q _   .
□
Theorem 8. 
For u , v ≥ 0 ,
B F u v = ∑ k = 0 v ( v k ) q v − k F u k F u − 1 v − k B F k   .
Proof. 
According to the lemma in [17] for p , q − Fibonacci numbers, we know that
F m n + r = ∑ j = 0 n ( n j ) q n − j F m j F m − 1 n − j F j + r ,
Using (7) and (15),
Preprints 93694 i002
□

3. Bicomplex p , q − Fibonacci Quaternions

Here, we describe the bicomplex p , q − Fibonacci quaternions. Some equations and summation formulas about bicomplex p , q − Fibonacci quaternion sequence are given. In addition, the generating function, Binet’s formula, Catalan, Cassini, and d’Ocagne’s identities are obtained for these quaternions.
Definition 2. 
The bicomplex p , q − Fibonacci quaternions are defined by
B C Q F u p , q = Q F u p , q + i   Q F u + 1 p , q + j Q F u + 2 p , q + i j   Q F u + 3 p , q ,
where  Q F u p , q = F u e 0 + F u + 1 e 1 + F u + 2 e 2 + F u + 3 e 3  is the  u t h   p , q − Fibonacci quaternion,  i 2 = j 2 = − 1 ,  i j = j i .
Thus, bicomplex p , q − Fibonacci quaternion with four bicomplex components can be written as
B C Q F u p , q = ( F u + i F u + 1 + j F u + 2 + i j   F u + 3 ) + ( F u + 1 + i F u + 2 + j F u + 3 + i j   F u + 4 )   e 1 + ( F u + 2 + i F u + 3 + j F u + 4 + i j   F u + 5 )   e 2 + ( F u + 3 + i F u + 4 + j F u + 5 + i j   F u + 6 )   e 3 .
By using (8), we obtain the following equation
B C Q F u p , q = B F u + B F u + 1 e 1 + B F u + 2 e 2 + B F u + 3 e 3 .
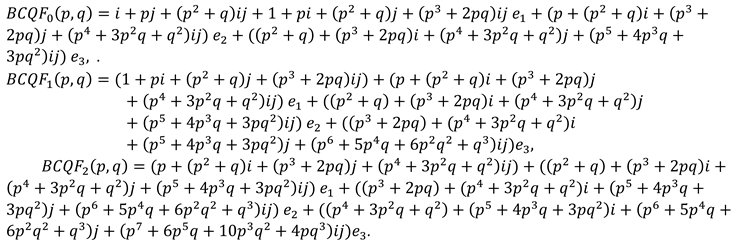
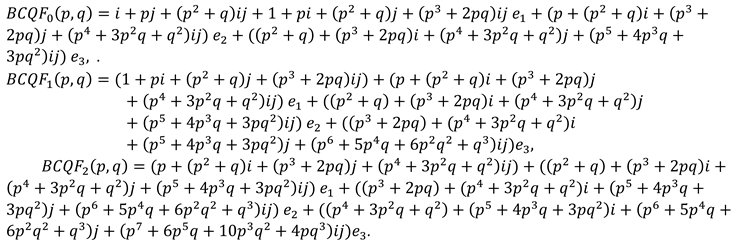
Thus, the first few terms of the bicomplex p , q − Fibonacci quaternions are Preprints 93694 i003
Therefore, any bicomplex p , q − Fibonacci quaternion occurs of a scalar part and vectorial part expressed as follows;
S B C Q F u = K 0 = B F u p , q = F u + i F u + 1 + j F u + 2 + i j   F u + 3 , V B C Q F u = K = B F u + 1 p , q   e 1 + B F u + 2 p , q e 2 + B F u + 3 p , q   e 3 .
Here, the set of bicomplex p , q − Fibonacci quaternions will be denoted by H B C Q F p , q . And in the remainder of the study, B C Q F u and Q F u will be considered as u t h bicomplex p , q − Fibonacci and p , q − Fibonacci quaternion, respectively.
Let B C Q F u = K 0 + K a n d B C Q F v = L 0 + L be two bicomplex p , q − Fibonacci quaternions. The addition and the subtraction of them are
B C Q F u ∓ B C Q F v = ( B F u ∓ B F v ) + ( B F u + 1 ∓ B F v + 1 ) )   e 1 + ( B F u + 2 ∓ B F v + 2 )   e 2 + ( B F u + 3 ∓ B F v + 3 )   e 3 .
The multiplication of a bicomplex p , q − Fibonacci quaternion by the real scalar λ is described as follows:
λ B C Q F u = λ Q F u + i   λ Q F u + 1 + j λ Q F u + 2 + i j   λ Q F u + 3 .
The product of any two bicomplex p , q − Fibonacci quaternions B C Q F u and B C Q F v
B C Q F u = K 0 + K   and   B C Q F v =   L 0 + L is B C Q F u B C Q F v = ( K 0 + K ) ( L 0 + L ) = K 0 L 0 + K 0 L + L 0 K − K . L + K × L ,
where K . L and K × L represent the dot product and the cross product of K and L , respectively. The conjugate operation in H B C F p , q is
B C Q F u * = S B C Q F u − V B C Q F u =   B F u p , q − B F u + 1 p , q   e 1 − B F u + 2 p , q e 2 − B F u + 3 p , q   e 3 ,
whereas the bicomplex conjugates are
( B C Q F u ) i ¯ = ( S B C Q F u ) i ¯ + ( V B C Q F u ) i   ¯ = ( B F u p , q ) i ¯ + ( B F u + 1 p , q ) i ¯ e 1 + ( B F u + 2 p , q ) i ¯ e 2 + ( B F u + 3 p , q ) i ¯ e 3 ( B C Q F u ) j ¯ = ( S B C Q F u ) j ¯ + ( V B C Q F u ) j ¯ = ( B F u p , q ) j ¯ + ( B F u + 1 p , q ) j ¯ e 1 + ( B F u + 2 p , q ) j ¯ e 2 + ( B F u + 3 p , q ) j ¯ e 3 ( B C Q F u ) i j ¯ = ( S B C Q F u ) i j ¯ + ( V B C Q F u ) i j ¯ = ( B F u p , q ) i j ¯ + ( B F u + 1 p , q ) i j ¯ e 1 + ( B F u + 2 p , q ) i j ¯ e 2 + ( B F u + 3 p , q ) i j ¯ e 3 .
The features of quaternion algebra are adapted to bicomplex quaternions as well as to complex quaternions. In this situation, some key properties in bicomplex quaternions change. Because the norm of a real quaternion h = ( h 0 , h 1 , h 2 , h 3 ) is defined by h = h 0 2 + h 1 2 + h 2 2 + h 3 2 , the norm is positive definite and real. But, we consider the complex quaternion; the norm is described according to the inner product of a complex quaternion with itself. That is, for a complex quaternion c h = ( c h 0 , c h 1 , c h 2 , c h 3 ) , the norm of c h can be written as c h = c h 0 2 + c h 1 2 + c h 2 2 + c h 3 2 .
Since the components of c h are complex numbers, the norm of c h has a complex value. In [15], the norm of a complex Fibonacci quaternion can be given as follows;
R = C n 2 + C n + 1 2 + C n + 2 2 + C n + 3 2 .
In addition, we described the norm of any bicomplex quaternion, in terms of the inner product of a bicomplex quaternion with itself as in the definition of a complex quaternion. Then for any bicomplex quaternion b c h = ( b c h 0 , b c h 1 , b c h 2 , b c h 3 ) , the norm of b c h can be written as b c h = b c h 0 2 + b c h 1 2 + b c h 2 2 + b c h 3 2 . In this situation, the norm of a bicomplex p , q − Fibonacci quaternion can be given as follows;
B C Q F = B F u 2 + B F u + 1 2 + B F u + 2 2 + B F u + 3 2 .
Also, we obtained that there are four different conjugates of bicomplex p , q − Fibonacci quaternion, whereas there are three different conjugates of bicomplex p , q − Fibonacci numbers. Furthermore, the following inequalities get about four different conjugations of bicomplex p , q − Fibonacci quaternion.
Theorem 9. 
Let B C Q F u  and B C Q F v  be two bicomplex p , q − Fibonacci quaternion. In that case, we obtain the following inequalities about the four conjugates of them:
( ( B C Q F u ) ( B C Q F v ) )   * ≠ ( B C Q F u )   *   ( B C Q F v )   * ( B C Q F u ) ( B C Q F v ) i ¯   ≠ ( B C Q F u ) i ¯     ( B C Q F v ) i ¯ ( B C Q F u ) ( B C Q F v ) j ¯   ≠ ( B C Q F u ) j ¯     ( B C Q F v ) j ¯ ( B C Q F u ) ( B C Q F v ) i j ¯   ≠ ( B C Q F u ) i j ¯     ( B C Q F v ) i j ¯
Proof. 
Using conjugate operations in H B C Q F and (16), the above identities can be easily proved.□
The following equation for the elements of B C Q F is easily obtained using (16)
B C Q F u + 2 = p B C Q F u + 1 + q B C Q F u .
Thus, the characteristic equation of (18) is
γ 2 − p γ − q = 0 .
Theorem 10. 
Binet’s formula of the bicomplex  p , q − Fibonacci quaternions { B C Q F u }  is given by the following equation for u ≥ 0 ,
B C Q F u =   δ _ δ ´ δ u −   ρ _ ρ   ´ ρ u δ − ρ
where  δ  and  ρ  are roots of (19) and
  δ _ = 1 + i   δ + j δ 2 + i j δ 3   ρ _ = 1 + i   ρ + j ρ 2 + i j ρ 3 δ ´ = 1 + δ e 1 +   δ 2 e 2 + δ 3   e 3 , ρ ´ = 1 + ρ e 1 + ρ 2 e 2 + ρ 3 e 3 ,
Proof. 
By using (16) and (13), we have the following equation:
B C Q F u =   δ _ δ u −   ρ _ ρ u δ − ρ + (   δ _ δ u + 1 −   ρ _ ρ u + 1 δ − ρ ) e 1 + (     δ _ δ u + 2 −   ρ _ ρ u + 2 δ − ρ ) e 2 + (   δ _ δ u + 3 −   ρ _ ρ u + 3 δ − ρ )   e 3 .
Thus, Binet’s formula of the bicomplex p , q − Fibonacci quaternion is easily found with some simple computation. □
Theorem 11. 
The generating function of the bicomplex p , q − Fibonacci quaternions { B C Q F u }  is determined by
G B C Q F t = B C Q F 0 + B C Q F 1 − p B C Q F 0 t 1 − p t − q t 2 _ .
Proof. 
To obtain the generating function of { B C Q F u } u = 0 ∞ , we use power series representation of { B C Q F u } .
G B C Q F t = ∑ u = 0 ∞ B C Q F u t u .
That is,
G B C Q F t = B C Q F 0 + B C Q F 1 t + B C Q F 2 t 2 + … + B C Q F m t m + … .
Thus,
− p t G B C Q F t = − p B C Q F 0 t − p B C Q F 1 t 2 − p B C Q F 2 t 3 − … − p B C Q F m t m + 1 + … . − q t 2 G B C Q F t = − q B C Q F 0 t 2 − q B C Q F 1 t 3 − q B C Q F 2 t 4 − … − q B C Q F m t m + 2 + … .
We obtain that
1 − p t − q t 2 G B C Q F t = B C Q F 0 + B C Q F 1 − p B C Q F 0 t + ( B C Q F 2 − p B C Q F 1 − q B C Q F 0 ) t 2         + … + ( B C Q F m + 1 − p B C Q F m − q B C Q F m − 1 ) t m + 1 + … .
Using (18) and initial conditions, we have
G B C Q F t = B C Q F 0 + B C Q F 1 − p B C Q F 0 t 1 − p t − q t 2 .
□
Theorem 12. 
The exponential generating function of the bicomplex   p , q − Fibonacci quaternions { B C Q F u }  is
E B C Q F t =   δ _     δ ´   e δ u −   ρ   _   ρ ´   e ρ u δ − ρ .
Proof. 
To obtain the exponential generating function of { B C Q F u } u = 0 ∞ , we use the power series representation of { B C Q F u } .
E B C Q F t = ∑ u = 0 ∞ B C Q F u t u u ! ,
Using (20) and e t = ∑ u = 0 ∞ t u u ! , we have
E B C Q F t = ∑ u = 0 ∞   δ _ δ ´ δ u −   ρ _     ρ ´ ρ u δ − ρ t u u ! =   δ _     δ ´   e δ u −   ρ   _   ρ ´   e ρ u δ − ρ . □
Theorem 13. 
For u ≥ v , Catalan identity for bicomplex p , q − Fibonacci quaternions is as follows:
B C Q F u − v B C Q F u + v − B C Q F u 2 =   δ _     ρ _   − q u − v δ v − ρ v ( δ   ρ ´ ´ ρ v − ρ ´ δ ´ δ v ( p 2 + 4 q )
where  u  and  v  are positive integers.
Proof. 
B C Q F u − v B C Q F u + v – B C Q F u 2 = δ _ δ u − v δ ´ − ρ _ ρ u − v ρ ´ δ − ρ δ _ δ u + v δ ´ − ρ _ ρ u + v ρ ´ δ − ρ − δ _ δ u δ ´ − ρ _ ρ u ρ ´ δ − ρ δ _ δ u δ ´ − ρ _ ρ u ρ ´ δ − ρ =   δ _     ρ _   δ ρ ´ ´ − q u − v δ v − ρ v ρ v −   ρ _     δ _     ρ ´ δ ´ − q u − v δ v − ρ v δ v δ − ρ 2
Because δ and ρ are roots of (19),
  δ ρ = − q ,   δ _ = 1 + i   δ + j δ 2 + i j δ 3   and   ρ _ = 1 + i   ρ + j ρ 2 + i j ρ 3 , we obtain   δ _     ρ _ = 1 + q − q 2 − q 3 + i p − p q 2 + j p 2 + 2 q + p 2 q + 2 q 2 + i j p 3 + 2 q p                                 =   ρ _     δ _ .
Thus, we obtain
B C Q F u − v B C Q F u + v   – B C Q F u 2 =   δ _     ρ _   − q u − v δ v − ρ v ( δ ρ ´ ´ ρ v − ρ ´ δ ´ δ v δ − ρ 2 =   δ _     ρ _   − q u − v δ v − ρ v ( δ ρ ´ ´ ρ v − ρ ´ δ ´ δ v ( p 2 + 4 q ) □
If v = 1 in the Catalan identity, Cassini identity is obtained as follows:
Corollary 2. 
For u ≥ 1 , Cassini identity for bicomplex p , q − Fibonacci quaternions is as follows:
B C Q F u − 1 B C Q F u + 1 − B C Q F u 2 =   δ _     ω _   − q u − 1 ( δ ρ ρ ´ ´ − ρ δ δ ´ ´ ( p 2 + 4 q )
where  u  is an integer.
Theorem 14. 
D’ocagne’s identity of bicomplex  p , q − Fibonacci quaternions for u ≥ v  is as follows:
B C Q F u B C Q F v + 1 − B C Q F u + 1 B C Q F v =   δ _     ρ _   δ   ´ ρ ´ − q v δ   ´ ρ ´ δ u − v − ρ ´   δ ´ ρ u − v p 2 + 4 q .
Proof. 
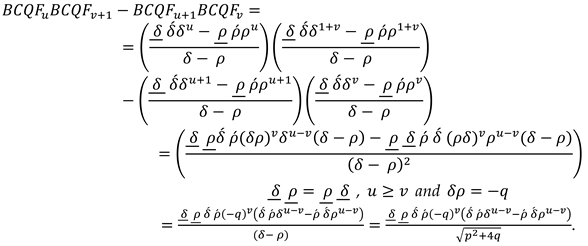
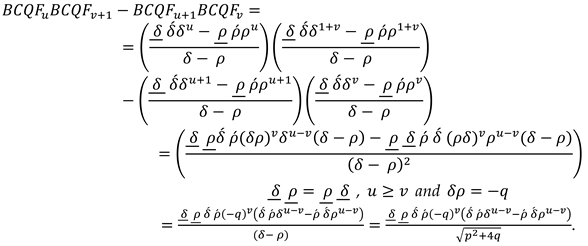
Preprints 93694 i004
□
Now, we give some identities about summations of terms in the bicomplex p , q − Fibonacci quaternions.
Theorem 15. 
For k , l  are natural number, the summation formula of bicomplex   p , q − Fibonacci quaternions is
∑ k = 1 l B C Q F k = B C Q F l + 1 + q B C Q F l − B C Q F 1 − q B C Q F 0 p + q − 1                                                           p + q ≠ 1   q B C Q F l + B C Q F 1 + l − 1 ( 1 + e 1 + e 2 + e 3 ) 1 + i + j + i j 1 + q                       p + q = 1 .
Proof. 
Firstly, we assume that p + q ≠ 1 . In this situation, ∑ k = 1 l B C Q F k = ∑ k = 1 l Q F k + i ∑ k = 1 l Q F k + 1 + j ∑ k = 1 l Q F k + 2 + i j ∑ k = 1 l Q F k + 3 . In addition, we obtain that by using the equ (13) in [5], ∑ k = 1 l Q F k = Q F l + 1 + q Q F l − Q F 1 − q Q F 0 p + q − 1 _ . With simple calculations, we get
∑ k = 1 l Q F k + 1 = p ∑ k = 1 l Q F k + q ∑ k = 1 l Q F k − 1 = Q F l + 2 + q Q F l + 1 − Q F 2 − q Q F 1 p + q − 1 _ , ∑ k = 1 l Q F k + 2 = Q F l + 3 + q Q F l + 2 − Q F 3 − q Q F 2 p + q − 1 _ , ∑ k = 1 l Q F k + 3 = Q F l + 4 + q Q F l + 3 − Q F 4 − q Q F 3 p + q − 1 _ .
Thus,
∑ k = 1 l B C Q F k = Q F l + 1 + q Q F l − Q F 1 − q Q F 0 p + q − 1 _ + i Q F l + 2 + q Q F l + 1 − Q F 2 − q Q F 1 p + q − 1 _ + j Q F l + 3 + q Q F l + 2 − Q F 3 − q Q F 2 p + q − 1 _ + i j ( Q F l + 4 + q Q F l + 3 − Q F 4 − q Q F 3 p + q − 1 _ ) = B C Q F l + 1 + q B C Q F l − B C Q F 1 − q B C Q F 0 p + q − 1 _ .
Now, we assume that p + q = 1 . We obtain that by using the equ (13) in [5], ∑ k = 1 l Q F k = q Q F l + ( l − 1 ) ( 1 + e 1 + e 2 + e 3 ) + Q F 1 1 + q . Moreover, we have
∑ k = 1 l Q F k + 1 = p ∑ k = 1 l Q F k + q ∑ k = 1 l Q F k − 1 = q Q F l + 1 + ( l − 1 ) ( 1 + e 1 + e 2 + e 3 ) + Q F 2 1 + q _ , ∑ k = 1 l Q F k + 2 = q Q F l + 2 + ( l − 1 ) ( 1 + e 1 + e 2 + e 3 ) + Q F 3 1 + q _ , ∑ k = 1 l Q F k + 3 = q Q F l + 3 + ( l − 1 ) ( 1 + e 1 + e 2 + e 3 ) + Q F 4 1 + q _ .
So we can write
∑ k = 1 l B C Q F k = ∑ k = 1 l Q F k + i ∑ k = 1 l Q F k + 1 + j ∑ k = 1 l Q F k + 2 + i j ∑ k = 1 l Q F k + 3 ∑ k = 1 l B C Q F k = q Q F l + ( l − 1 ) ( 1 + e 1 + e 2 + e 3 ) + Q F 1 1 + q _ + i q Q F l + 1 + ( l − 1 ) ( 1 + e 1 + e 2 + e 3 ) + Q F 2 1 + q + j q Q F l + 2 + ( l − 1 ) ( 1 + e 1 + e 2 + e 3 ) + Q F 3 1 + q + i j ( q Q F l + 3 + l − 1 1 + e 1 + e 2 + e 3 + Q F 4 1 + q _ )   . = q B C Q F l + l − 1 ( 1 + e 1 + e 2 + e 3 ) 1 + i + j + i j + B C Q F 1 1 + q _ .
□
Theorem 16. 
For u , v ≥ 0 ,
B C Q F u v = ∑ k = 0 v ( v k ) q v − k F u k F u − 1 k B C Q F k   .
Proof. 
Using (7) and (17), B F u v = ∑ k = 0 v ( v k ) q v − k F u k F u − 1 v − k B F k
B C Q F u v = B F u v + B F u v + 1 e 1 + B F u v + 2 e 2 + B F u v + 3 e 3 = ∑ k = 0 v v k q v − k F u k F u − 1 v − k B F k + ∑ k = 0 v v k q v − k F u k F u − 1 v − k B F k + 1 e 1 + ∑ k = 0 v v k q v − k F u k F u − 1 v − k B F k + 2 e 2 + ∑ k = 0 v v k q v − k F u k F u − 1 v − k B F k + 3 e 3 = ∑ k = 0 v v k q v − k F u k F u − 1 v − k ( B F k + B F k + 1 e 1 + B F k + 2 e 2 + B F k + 3 e 3 ) = ∑ k = 0 v ( v k ) q v − k F u k F u − 1 k B C Q F k . □

4. Matrix Representation of Bicomplex p , q − Fibonacci Quaternions and an Application in This Representation for Them

Firstly, we will use the matrix that generates { F u ( p , q ) } , which we define to obtain the N-matrix, which is similar to the definition of the S-Matrix defined in [11]. We know that
F u + 1 F u = p q 1 0 u F 1 F 0 ,
By using (21), The N-matrix is defined as
N u = p q 1 0 u = F u + 1 q F u F u q F u − 1 _ ,
where F − 2 = − p q _ 2 , F − 1 = 1 q .
Here, we will define the B C Q F N -matrix that we called the bicomplex p , q − Fibonacci quaternion matrix as follows:
B C Q F N = B C Q F 3 q B C Q F 2 B C Q F 2 q B C Q F 1 _ .
Now, we can give the following theorem about the B C Q F N -matrix.
Theorem 17. 
If B C Q F u  be the u t h  bicomplex p , q − Fibonacci quaternion. Then, for u ≥ 0
B C Q F N .   p q 1 0 u = B C Q F u + 3 q B C Q F u + 2 B C Q F u + 2 q B C Q F u + 1 _ .
Proof. 
To do this, we apply induction on l . If u = 0 , it is clear that (23) holds. Now, we suppose that (23) is hold for u = v , that is, B C Q F N .   p q 1 0 v = B C Q F v + 3 q B C Q F v + 2 B C Q F v + 2 q B C Q F v + 1 _ .
Using the Eq. (18), for v ≥ 0 , B C Q F v + 2 = p B C Q F v + 2 + q B C Q F v . Then, by induction,
B C Q F N . N v + 1 = ( B C Q F N . N v ) N = B C Q F v + 3 q B C Q F v + 2 B C Q F v + 2 q B C Q F v + 1 _ . p q 1 0 = p B C Q F v + 3 + q B C Q F v + 2 q B C Q F v + 3 p B C Q F v + 2 + q B C Q F v + 1 q B C Q F v + 2     = B C Q F v + 4 q B C Q F v + 3 B C Q F v + 3 q B C Q F v + 2 _ .
Thus the Eq. (23) holds for all u ≥ 0 . □
Corollary 3. 
For u ≥ 0 ,
B C Q F u + 2 = B C Q F 2 F u + 1 + ( q B C Q F 1 ) F u .
Proof. 
The proof can be easily seen by the coefficient (2, 1) of the matrix B C Q F N . N u and the Eq. (22). □
Theorem 18. 
For u ≥ 1 , ( u  is an integer) and v ∈ { 0,1 } . Then
B C Q F 2 u + v B C Q F 2 ( u − 1 ) + v B C Q F 2 ( u + 1 ) + v B C Q F 2 u + v = B C Q F 2 + v B C Q F v B C Q F 4 + v B C Q F 2 + v p 2 + 2 q 1 − q 2 0 u − 1 .
Proof. 
We prove the theorem by induction on u . If u = 1 then the result is clear. Now we assume that, for any integer d such as 1 ≤ d ≤ u ,
B C Q F 2 d + v B C Q F 2 ( d − 1 ) + v B C Q F 2 ( d + 1 ) + v B C Q F 2 d + v = B C Q F 2 + v B C Q F v B C Q F 4 + v B C Q F 2 + v p 2 + 2 q 1 − q 2 0 d − 1 .
Then for u = d + 1 , we obtain
B C Q F 2 + v B F v B C Q F 4 + v B F 2 + v p 2 + 2 q 1 − q 2 0 d = B F 2 + v B F v B F 4 + v B F 2 + v p 2 + 2 q 1 − q 2 0 d − 1 p 2 + 2 q 1 − q 2 0 = B F 2 d + v B F 2 ( d − 1 ) + v B F 2 ( d + 1 ) + v B F 2 d + v p 2 + 2 q 1 − q 2 0 = B F 2 ( d + 1 ) + v B F 2 d + v B F 2 ( d + 2 ) + v B F 2 ( d + 1 ) + v .
where v ∈ { 0,1 } . Therefore, the proof is completed. □
In [15], it is obtained the complex Fibonacci quaternions are shown by the 8 × 8 real matrices. First, we obtained the matrix form of a bicomplex p , q − Fibonacci quaternion B C Q F u with the aid of 4 × 4 matrix representations and produced a new 8 × 8 type bicomplex quaternion matrix similarly. We can define the following matrices.
E 0 = α 0 0 α , E 1 = i Γ 0 0 − i Γ   ,   E 2 = 0 α − α 0 ,   E 3 = 0 j ζ j ζ 0
where
α = 1 0 0 1     Γ = 0 − i i 0 ,   ζ = 0 − j j 0 , and   i 2 = − 1 ,   j 2 = − 1 , i j 2 = 1 , i j = j i .
Using the matrices α ,   Γ and ζ , we obtain   E 0 2 = I 4 and   E 1 2 =   E 2 2 =   E 3 2 = − I 4 , where I 4 is the 4 × 4 identity matrix. Furthermore, it satisfies the following equations:
E 1 E 2 = − E 2 E 1 = E 3 , E 3 E 1 = − E 1 E 3 = E 2 ,   E 2 E 3 = − E 3 E 2 = E 1 , E 1 E 2 E 3 = − I 4 .
The bicomplex p , q − Fibonacci quaternion B C Q F is also expressed by the 4×4 matrix with these new matrices. By the bicomplex p , q − Fibonacci number, we can write
B C Q F u = B F u E 0 + B F u + 1   E 1 + B F u + 2 E 2 + B F u + 3   E 3                     B C Q F = B F u − B F u + 1 − B F u + 2 B F u + 1       B F u B F u + 3 − B F u + 3 − B F u + 2 B F u + 2 − B F u + 3 B F u B F u + 3 B F u + 2 − B F u + 1   B F u + 1 B F u _ .
Theorem 19. 
For u ≥ 0 , the u t h  term of the bicomplex p , q − Fibonacci quaternion sequence with the determinant of a special matrix can be obtained as follows:
B C Q F u = B C Q F 0 − 1 0 B C Q F 1 0 − 1 B C Q F 2 0     0       0                 0       …   0               0       … − 1             0         …             0             0             0   0             0             0 0             0             0 0                     0           q ⋮                     ⋱             ⋱ 0                   0             0 0 0 0                   0 0 0               0 0 0               p         − 1           … ⋱               ⋱           ⋱ 0 0 0 0                   0 0 0 0           ⋱ ⋱ ⋱ ⋱             0         0     0     ⋱       ⋱     ⋮ − 1 p q 0             0 − 1 p             q       0 0 − 1     p u + 1 × u + 1 .
Proof. 
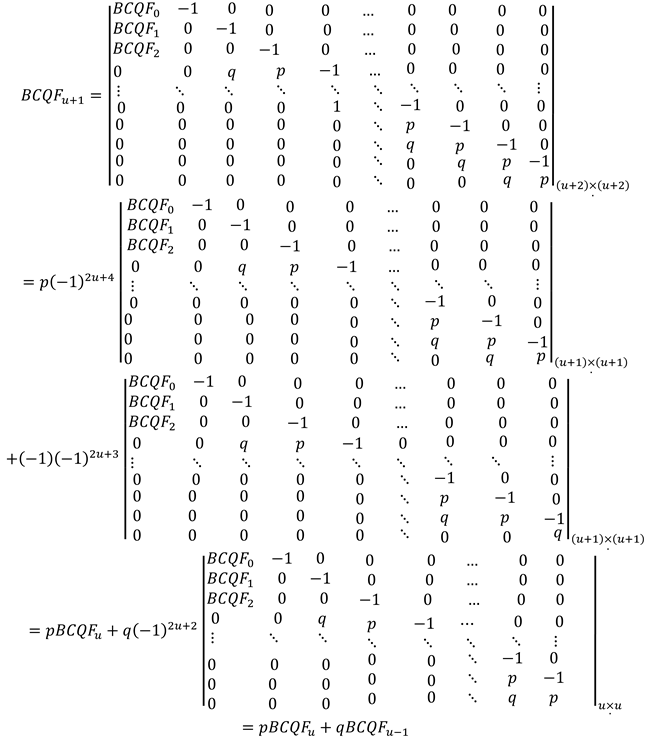
For the proof, we use the induction method on u . It is clear that equality holds for u = 0,1 . Now, suppose that the equality is true for 2 ≤ k ≤ u . Then, we can verify it for u + 1 as follows: Preprints 93694 i005
Thus, the proof is completed. □

5. Conclusions

Here, we investigated p , q − Fibonacci numbers, quaternions, bicomplex numbers, and bicomplex quaternions. And we introduced bicomplex p , q − Fibonacci numbers and bicomplex p , q − Fibonacci quaternions based on these numbers. That is, we obtain a generalization of second-order bicomplex number and bicomplex quaternion sequences. Furthermore, some of their equations include the Binet formula, generating function, Catalan, Cassini, and d’Ocagne’s identities, and some summation formulas for both of them.
In addition, we describe a matrix that we call N-matrix of type 4 × 4 for bicomplex p , q − Fibonacci quaternions whose terms are bicomplex p , q − Fibonacci numbers. Then, we obtained that the bicomplex p , q − Fibonacci quaternions can be expressed as the 8 × 8 real matrices. With the help of the new four matrices we defined in 4 × 4 type, we obtained { E 0 ,   E 1 , E 2 ,   E 3 } which is used as the basic elements of real quaternions { 1 ,   e 1 , e 2 ,   e 3 } . Also, we obtained that the bicomplex p , q − Fibonacci quaternion can also be expressed with a new matrix of type 4 × 4, whose elements consist of bicomplex p , q − Fibonacci numbers.
Finally, we create a matrix for bicomplex p , q − Fibonacci quaternions, and we obtain a determinant of a special matrix that gives the terms of that quaternion.

Author Contributions

All authors contributed equally to this work. All authors read and approved the final manuscript.

Funding

This research received no external funding.

Acknowledgments

The authors would like to express their sincere gratitude to the referees for their valuable comments, which have significantly improved the presentation of this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Koshy, T. Fibonacci and Lucas Numbers with Applications; A Wiley Inter science publication, U.S.A, 2001.
  2. Suvarnamani, A.; Tatong, M. Some properties of (p,q)-Fibonacci numbers. Progress in Applied Science and Technology 2015, 5, 17–21. [Google Scholar]
  3. Diskaya, O.; Menken, H. On the (p,q)-Fibonacci N-dimensional recurrences. Bulletin of the International Mathematical Virtual Institute. 2022, 12, 205–212. [Google Scholar]
  4. İpek, A. On (p, q)-Fibonacci quaternions and their Binet formulas, generating functions and certain binomial sums. Advances in Applied Clifford Algebras. 2017, 27, 1343–1351. [Google Scholar] [CrossRef]
  5. Liu, L. On the spectrum and spectral norms of r-circulant matrices with generalized-Horadam numbers entries. International Journal of Computational Mathematics. 2014, 2014, 795175. [Google Scholar] [CrossRef]
  6. Patel, B. K.; Ray, P. K. On the properties of (p, q)-Fibonacci and (p, q)-Lucas quaternions. Mathematical Reports. 2019, 21, 15–25. [Google Scholar]
  7. Yağmur, T. A note on hyperbolic (p, q)-Fibonacci quaternions. Communications Faculty of Sciences University of Ankara Series A1 Mathematics and Statistics. 2020, 69, 880–890. [Google Scholar] [CrossRef]
  8. Yazlık, Y.; Köme, S.; Köme, C. Bicomplex generalized k-Horadam quaternions. Miskolc Mathematical Notes. 2019, 20, 1315–1330. [Google Scholar] [CrossRef]
  9. Hamilton, W. R. Elements of quaternions; Green, & Company, London: Longmans 1866.
  10. Horadam, A.F. Complex Fibonacci Numbers and Fibonacci Quaternions. American Math. Monthly. 1963, 70, 289–291. [Google Scholar] [CrossRef]
  11. Cerda-Morales, G. On a generalization for Tribonacci quaternions. Mediterranean Journal of Mathematics. 2017, 14, 1–12. [Google Scholar] [CrossRef]
  12. Akyiğit, M.; Kösal, H. H.; Tosun, M. Split Fibonacci quaternions. Advances in applied Clifford algebras. 2013, 23, 535–545. [Google Scholar] [CrossRef]
  13. Flaut, C.; Shpakivskyi, V. On generalized Fibonacci quaternions and Fibonacci-Narayana quaternions. Advances in Applied Clifford Algebras. 2013, 23, 673–688. [Google Scholar] [CrossRef]
  14. Gül, K. Dual bicomplex Horadam quaternions. Notes on Numbers Theory and Discrete Mathematics. 2022, 26, 187–205. [Google Scholar] [CrossRef]
  15. Halici, S. On complex Fibonacci quaternions. Advances in Applied Clifford Algebras. 2013, 23, 105–112. [Google Scholar] [CrossRef]
  16. Halici, S.; Karataş, A. On a generalization for Fibonacci quaternions. Chaos, Solitons & Fractals. 2017, 98, 178–182. [Google Scholar]
  17. Iar, Z. S.; Keskin, R. Some new identities concerning generalized Fibonacci and Lucas numbers. Hacet. J. Math. Stat. 2013, 42, 211–222. [Google Scholar]
  18. Kızılateş, C.; Catarino, P.; Tuğlu, N. On the bicomplex generalized Tribonacci quaternions. Mathematics. 2019, 7, 80. [Google Scholar] [CrossRef]
  19. Tan, E.; Yilmaz, S.; Sahin, M. On a new generalization of Fibonacci quaternions. Chaos, Solitons and Fractals. 2016, 82, 1–4. [Google Scholar] [CrossRef]
  20. Yağmur, T. On generalized bicomplex k-Fibonacci numbers. Notes Number Theory Discrete Math. 2019, 25, 132–133. [Google Scholar] [CrossRef]
  21. Segre, C. Le rappresentazioni reali delle forme complesse e gli enti iperalgebrici. Mathematische Annalen. 1892, 40, 413–467. [Google Scholar] [CrossRef]
  22. Elizarrarás-Luna, M.E.; Shapiro, M.; Struppa, M.; Vajiac, A.D.C. The bicomplex numbers. In Bicomplex Holomorphic Functions; Frontiers in Mathematics, Birkhuser: Cham, Switzerland, 2015; pp. 5–28. [Google Scholar]
  23. Halıcı, S. On Bicomplex Fibonacci Numbers and Their Generalization, Models and Theories in Social Systems, 179, 509-524, Springer, 2019.
  24. Luna-Elizarraras, M.E.; Shapiro, M.; Struppa, D.C.; Vajiac, A. Bicomplex numbers and their elementary functions. Cubo. 2012, 14, 61–80. [Google Scholar] [CrossRef]
  25. Nurkan, S.K.; Güven, I. A, A note on bicomplex Fibonacci and Lucas numbers. Internat. J. Pure Appl. Math. 2018, 120, 365–377. [Google Scholar]
  26. Rochon, D.; Shapiro, M. On algebraic properties of bicomplex and hyperbolic numbers. An. Univ. Oradea Fasc. Mat. 2004, 11, 71–110. [Google Scholar]
  27. Torunbalcı Aydın, F. Bicomplex Fibonacci quaternions. Chaos Solutions and Fractals. 2018, 106, 147–153. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated