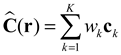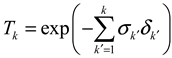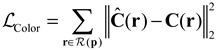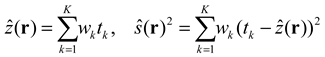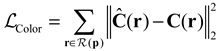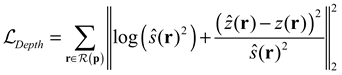1. Introduction
Up to the present, state-of-the-art methods for novel view synthesis, which involves using captured images to recover a three-dimensional representation that can be rendered from previously unobserved viewpoints, are primarily based on Neural Radiance Fields (NeRF). By modeling a scene as a continuous volumetric function parameterized by a multilayer perceptron (MLP), NeRF is capable of generating photorealistic renderings that exhibit detailed geometry and view-dependent effects.
NeRF, despite its remarkable achievements, has certain limitations. When the scene is captured from a limited number of sparsely-distributed viewpoints, NeRF’s ability to accurately represent intricate geometry and appearance may lead to the presence of several artifacts arising from an imperfect density distribution. The underlying reason is that NeRF relies solely on RGB values from input images to determine the relationships among input views. Therefore, obtaining high-quality rendering results requires feeding adequate images with diverse perspectives. Training NeRF is notoriously time-consuming, and may take up to 10-12 hours to complete using an NVIDIA RTX 3060 on a regular room-sized scene, becoming a significant bottleneck to NeRF’s robust adoption. Moreover, NeRF runs the risk of overfitting when not provided with enough input views. In such instances, NeRF can only render the surface color of an object, but is incapable of precisely capturing the depth information of the scene.
DoNeRF [
1] introduces an Oracle network to predict ideal sampling positions for the ray-tracing shading network, significantly reducing inference time. However, it doesn’t substantially improve training speed, leaving the NeRF training duration issue unresolved. EfficientNeRF [
2] proposes a different approach to the sampling strategy by advocating for effective and critical sampling at both coarse and fine stages. It also utilizes NeRFTree to efficiently represent 3D scenes, leading to faster caching and querying, improving rendering speed. Nonetheless, EfficientNeRF does not eliminate the problem of color and geometry mismatches resulting from overfitting.
This study addresses the mentioned challenges by proposing a method to supervise NeRF using both color and depth information. Additionally, it introduces a novel sampling approach that effectively reduces training time without compromising rendering quality. Since the depth maps generated by consumer-grade RGB-D cameras often suffer from noise, missing data, and holes, we deploy a depth completion technique to generate dense and accurate depth maps for feeding into NeRF. Depth completion endeavors to densify sparse depth maps by predicting depth values on a per-pixel level. It holds a crucial position in several domains, including 3D reconstruction, autonomous driving, robot navigation and augmented reality. Deep learning-based approaches have emerged as the predominant solutions for this task, demonstrating notable achievements in recent advancements. Considering the substantial computational resources required by NeRF, the utilization of deep learning-based methods is not viable. This study employs the OpenCV-based depth completion algorithm, which capable of running in real-time on a CPU with comparable accuracy to mainstream deep learning-based methods for depth completion. Furthermore, our approach to utilizing depth information is entirely different from the methods mentioned earlier. we utilize coordinate transformation to convert the depth map into a point cloud, obtaining the coordinates of each point in the world coordinate system. Rays are cast from the camera coordinate center towards these 3D points, theoretically terminating at these 3D points. We apply a depth loss to encourage the termination distribution of the rays to be consistent with the 3D points in space.
In summary, this study introduces an RGB-D neural radiance field that incorporates color and depth measurements, employing an implicit occupancy representation. The introduction of depth information demonstrates a notable positive influence on the rendering quality, surpassing the performance achieved through training with RGB data alone. Moreover, we propose a novel dynamic sampling approach, which utilizes depth information for more precise sampling. By reducing unnecessary sampling points, the dynamic sampling technique significantly accelerates the training process and lowers the computational load compared to the original NeRF.
The main contributions of this study are as follows:
Introducing depth completion to NeRF to provide dense and accurate depth maps.
Enhancing the sampling efficiency by utilizing dense depth information.
Introducing RGB and depth supervision in NeRF to enhance rendering quality, improve accuracy, and ensure consistent scene depth.
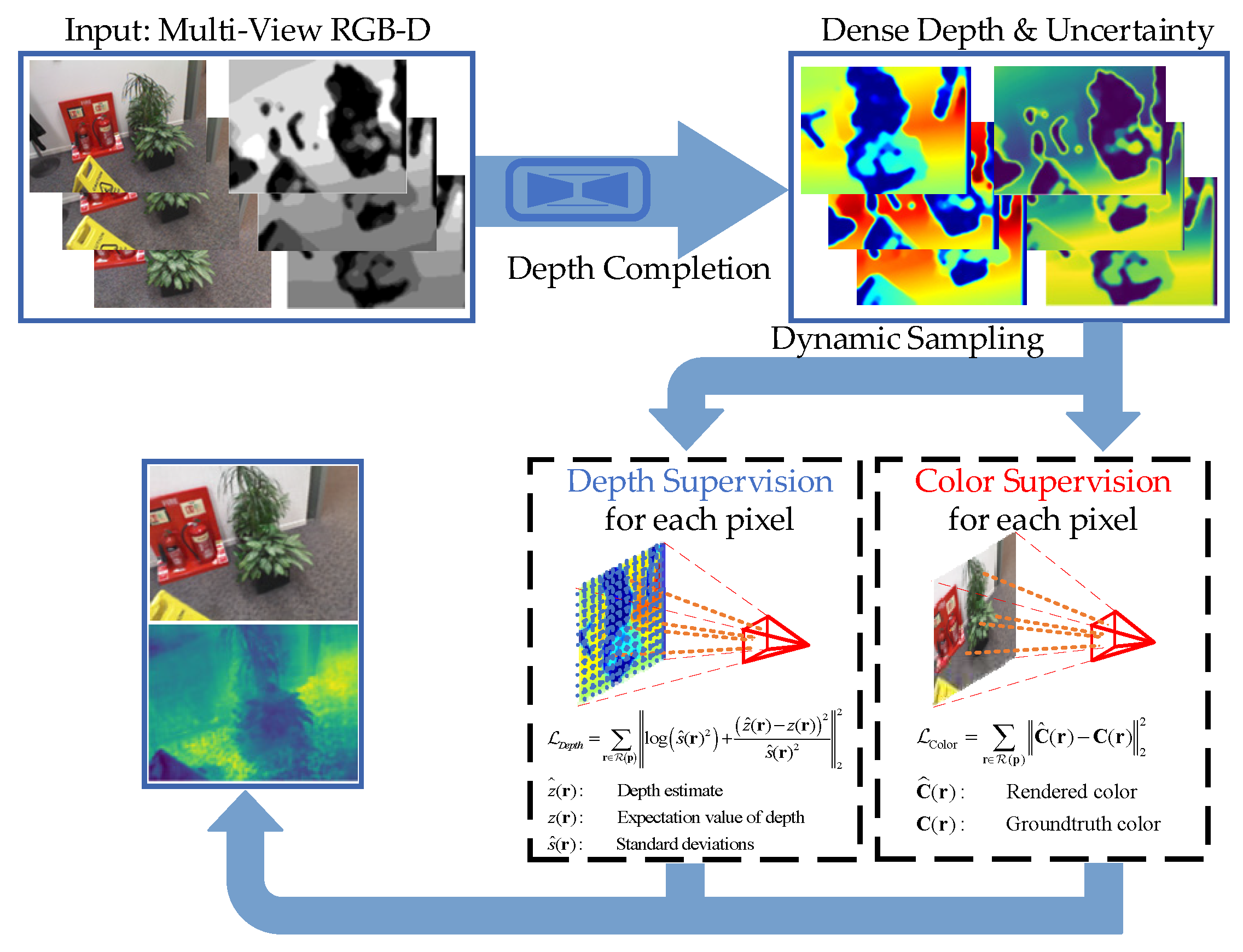
Figure 1.
Method overview.
Figure 1.
Method overview.
2. Related Work
Our proposed Depth-NeRF utilizes a series of RGB-D images as input, and trains an MLP to acquire a comprehensive volumetric scene representation from the observed data. The depth information is utilized to supervise NeRF training and determine the distribution of sampling points in order to accurately capture the depth at which a ray terminates using fewer sampling points. In the following sections, we will discuss related work pertaining to this research.
2.1. Neural Volume Rendering
The well-known NeRF [
3] has achieved impressive results using a simple approach. An MLP takes 3D points and view direction as input and generates density and color values as output. However, NeRF has some drawbacks, including long training and rendering times, the need for separate models for each scene, and its limitation to static scenes. The problem of static scenes is addressed in [
4,
5,
6]. NeRF models have been extended and generalized in [
7,
8,
9,
10] by incorporating fully convolutional image features, utilizing generator-discriminator architectures, and leveraging meta-learning techniques. These advancements have enhanced their ability to handle a wider range of scenes and produce more realistic renderings. In [
11], a CNN-based encoder and an MLP-based decoder are employed to compute density and color values for each point in space, enabling the creation of realistic and visually appealing images. [
12] use data-driven methods to train a deep network for predicting volumetric representations and employ alpha-compositing to render photographs from novel viewpoints. [
13] has explored the optimization of a hybrid approach that combines convolutional networks with scene-specific voxel grids. This combination effectively addresses the discretization artifacts resulting from the use of low-resolution voxel grids. [
14] employs neural networks to address gaps and enhance the overall quality of a textured geometric representation. BakedSDF [
15] and MonoSDF [
16] both utilize signed distance function (SDF) to represent scene geometry. Neuralangelo [
17] leverages the representation capabilities of 3D hash grids in combination with neural surface rendering.
2.2. Neural radiance field with depth
Prior researches have delved into the application of depth information in view synthesis and NeRF training. In the NerfingMVS [
18], a monocular depth network is adapted to the specific scene by fine-tuning it on a sparse Structure from Motion (SfM) combined with Multi-view Stereo (MVS) reconstruction. The adjusted depth priors are subsequently utilized to steer the sampling procedure during volume rendering. The adapted depth priors are subsequently employed to guide and supervise the sampling process of volume rendering. Meanwhile, DS-NeRF[
19] introduces improvements to NeRF by incorporating a direct supervision mechanism for its density function. This is accomplished through the utilization of a specific loss function that encourages the alignment of ray termination depth distribution with a given 3D keypoint. DONeRF[
1] reduces inference costs by employing a depth oracle network that computes sample points’ locations in a single evaluation. This replaces NeRF’s MLP-based raymarching with a compact local sampling strategy, which prioritizes crucial samples near surfaces. The primary objective is to improve efficiency and prioritize relevant information during rendering. In addition, [
20] incorporates depth information within the Mip-NeRF [
21] framework and models depth uncertainty to enhance geometry accuracy, reduce artifacts, and improve the efficiency of both training and prediction. The integration of depth information with NeRF for enhanced reconstruction, as presented in [
22], involves the utilization of a truncated signed distance function (TSDF) instead of density. This approach incorporates two networks that have an impact on both the training and prediction time.
2.3. NeRF training acceleration
[
23,
24,
25] addressed the issue of lengthy inference time in NeRF by employing a compact MLP and an enhanced sampling approach. The Neural Scene Representation (NSVF) [
26] was introduced as a solution for efficient and high-fidelity rendering. To capture local characteristics within each voxel, NSVF employs a collection of implicit fields bounded by voxels, which are organized within a sparse voxel octree structure. This sparse voxel octree arrangement facilitates the rapid generation of new perspectives by disregarding voxels that do not contain relevant scene information. This method overcomes the limitations of traditional voxel-based rendering methods by modeling the underlying surface with a continuous signed distance function, which ensures high-quality rendering even for complex scenes. “bakes”NeRF [
27] enables real-time rendering on commodity hardware. It reformulates NeRF’s architecture using sparse voxel grids with learned feature vectors, enabling efficient rendering without the need for original training data. EfficientNeRF [
2] proposes effective sampling in both rough and fine stages to improve sampling efficiency. Additionally, the method incorporates a new caching mechanism that stores the entire scene, significantly accelerating rendering speed during testing. Moreover, to enhance model robustness during inference, randomization of camera position and direction is employed during training. These improvements, along with the introduction of a novel data structure for scene caching, contribute to a substantial increase in rendering speed and overall efficiency. MVSNeRF [
28] utilizes MVSNet [
29] to generate a feature volume for NeRF, enabling the synthesis of high-quality images with just 15 minutes of finetuning. However, the testing time for these methods still remains as long as that of the original NeRF.
2.4. Limitation of Existing Methods
Despite the significant progress made by these methods in view synthesis and NeRF training, they still have certain limitations. DS-NeRF[
19] requires a set of 3D keypoints generated by COLMAP [
30]. A prerequisite for the successful initialization of COLMAP is that there needs to be a sufficiently large translational movement of the relative poses between the photos, and the operation of DS-NeRF relies on COLMAP. This limitation prevents DS-NeRF from functioning properly in some scenarios. DONeRF [
1] requires an additional depth oracle network during training, which could increase the computational time and make training more challenging. Most NeRF methods that use depth information only apply a depth loss to constrain the rendered depth values. In contrast, our approach starts from the principles of volume rendering and introduces a completely new way of generating rays, ensuring that the ray termination distribution aligns with the scene surface. This effectively reduces depth errors and allows for more accurate rendering of geometric information in the scene. EffiecientNeRF [
2] requires scene caching during testing, which may not be feasible for large-scale scenes or devices with limited memory. Moreover, appropriate sampling is sensitive to the initial view direction, and training with a limited set of initial views may introduce bias towards those views. For surface rendering, the precise identification of an accurate surface is crucial to ensure consistent colors across different views. However, this task presents significant challenges that impede training convergence and result in undesirable blurring effects in the rendered images. In contrast, volume rendering methods require sampling a large number of points along the rays to accurately capture colors and achieve high-quality rendering. However, NeRF’s evaluation of each sampled point along the ray is inefficient. It takes approximately 22 seconds to use NeRF on an NVIDIA RTX 3060 to generate a 640×480 image.
Our primary observation is that it is crucial to limit the sampling of points in empty spaces. By guiding with depth information, we can accurately identify the surface position of the current scene and perform sampling near the object surface, significantly reducing the quantity of sample points required and improving the training speed of NeRF. Depth information can also be employed to supervise NeRF, ensuring that the termination distribution of each light ray closely matches the actual position of the object.
3. Method
By integrating depth information into the traditional NeRF method, we achieved a termination distribution of rays that closely approximates the surface of the real scene. This effectively addresses the problem of shape-radiance ambiguity in traditional NeRF. We begin by revisiting the volumetric rendering technique, followed by an analysis of depth completion. Next, we analyze the location of sampling points guided by depth information. Finally, we conclude by discussing optimization with the depth constraint.
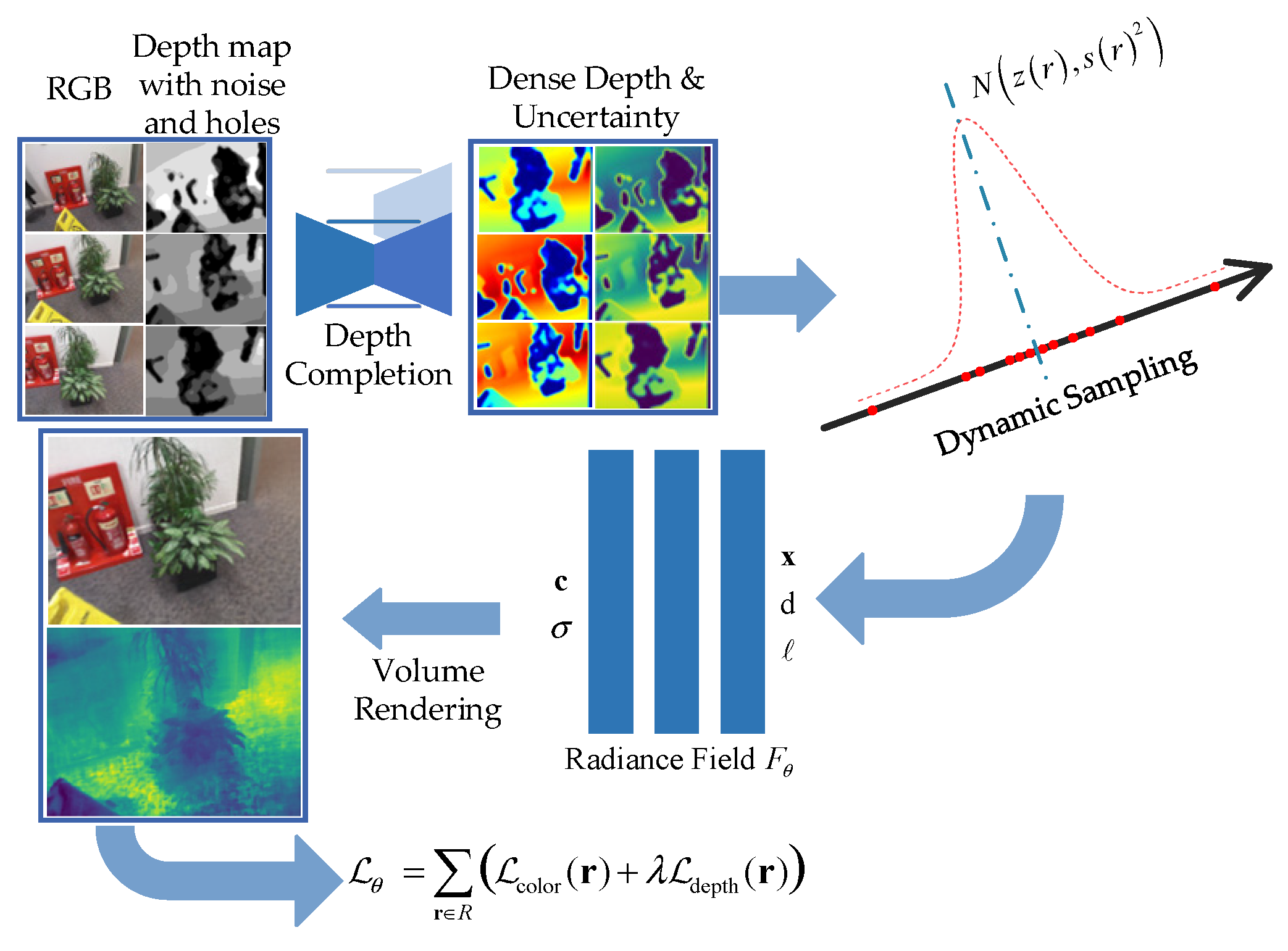
Figure 2.
Overview of our radiance field optimization pipeline.
Figure 2.
Overview of our radiance field optimization pipeline.
3.1. Volume Rendering with Radiance Fields
NeRF is a deep learning method that reconstructs 3D scenes from 2D images. It encodes a scene as a volume density and emitted radiance by employing a model called the neural radiance field, which represents density and color information within the 3D scene. It employs a model called the neural radiance field to represent density and color information within the 3D scene. This model comprises a feed-forward neural network that takes positions and orientations in 3D space as input and produces the corresponding density and color values at those positions. More specifically, for a given 3D point and a specific direction , NeRF provides a function to estimate the volume density and RGB color :.
When NeRF renders an image with a given pose
, a series of rays is cast from the
’s center of projection
in the direction
. Since the rays have a fixed direction, the propagation distance can be parameterized by time:
. We sample multiple points along each ray and input these sample points into the NeRF network, obtaining voxel density
and radiance
for each sample point. By integrating the implicit radiance field along the ray, we estimate the color of the object surface from viewing direction
.
where
.
is transmittance, which checks for occlusions by integrating the differential density between 1 to
.
describes the contribution of each sampled point along the ray to the radiance. NeRF assumes that the scene exists within a range
, and to ensure the sum of
is equal to 1, a non-transparent wall is introduced at
. The final loss function of NeRF is as follows:
where
represents a series of rays emitted from a fixed pose
.
3.2. Depth Completion with Uncertainty
Depth maps captured by RGB-D cameras in consumer devices often suffer from noise, holes, and missing regions. To address this issue, we employ depth completion algorithms to fill in the missing information and generate a complete depth image. We utilize OpenCV-based depth completion method, which is designed to run efficiently on CPU and provide real-time performance. The problem of depth completion can be described as follows.
Given an image
, and a sparse depth map
,find
that approximates a true function
where
. The problem can be formulated as:
Here, is the output dense depth map with missing data replaced by their depth estimates.
Due to the input source originates from a LIDAR sensor and its suitability limited to large-scale outdoor scenes, we have made improvements to the IP_Basic [
31] algorithm, tailoring it to better suit indoor scenarios, and it now supports RGB-D input. Specifically, we have implemented critical adjustments in the calculation methods for the near-plane mask and far-plane mask. These modifications have enabled our algorithm to effectively segment indoor scenes into distinct close-range and far-range areas. By accurately dividing the scene based on proximity, our enhanced algorithm delivers more precise and reliable results for indoor applications. The partitioning of these two areas significantly affects the accuracy of depth completion.
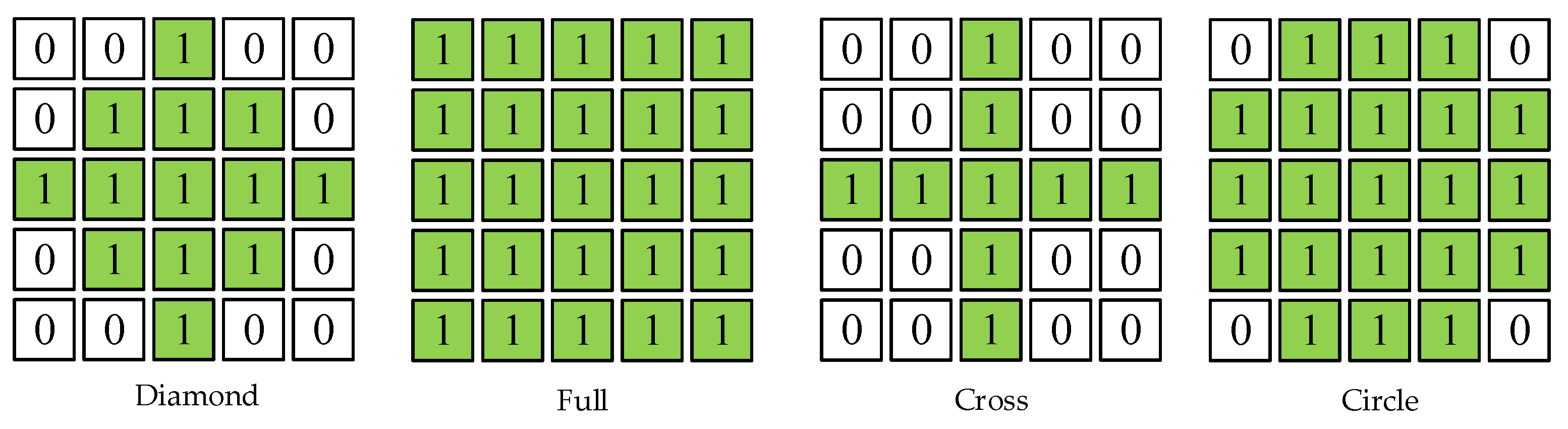
The algorithm follows a series of steps to process the depth map effectively. First, we begin with preprocessing the depth map. Our dataset primarily consists of indoor scenes with depth values ranging from 0 to 20 meters. However, some empty pixels have a value of 0, necessitating preprocessing before utilizing OpenCV operations. To address this issue, we invert the depths of valid (non-empty) pixels according to
, creating a buffer zone between valid and empty pixels. In the subsequent steps, we employ OpenCV’s dilation operation to process the image. This operation can result in the blurring of nearby object edges. Another benefit of inverting the depth is to prevent such blurring. Next, we consider that the depth values of adjacent pixels in the depth map generally change smoothly unless near object edges. To tackle this, we start by filling empty pixels closest to valid pixels. We use OpenCV’s dilation operation, which involves sliding a kernel over the input image. At each kernel position, the dilate operation checks if at least one pixel under the kernel is non-zero. If it finds at least one non-zero pixel under the kernel, it sets the center pixel of the kernel to a non-zero value in the output image. The kernel’s design ensures that pixels with similar values are dilated to a common value. We assessed the effects of different kernel sizes and shapes, as shown in
Table 1. Unlike IP_Basic [
31], we found that a 4×4 kernel size produces the best results, and we use a 4×4 diamond kernel to dilate all valid pixels.
After the initial dilation operation, there may still be gaps in the depth map. We observe that adjacent sets of dilated depth values can be connected to establish object edges. To address this, we apply a 5×5 full kernel to close minor gaps in the depth map. Furthermore, to address any remaining gaps, we perform a dilation operation with a 7×7 kernel. This process selectively fills empty pixels while leaving the previously computed valid pixels unchanged. In the next step, we address larger gaps in the depth map that may not have been completely filled in the previous steps. Similar to the previous operations, we use a dilation operation with a 20×20 full kernel to fill any remaining empty pixels while ensuring that valid pixels remain unaltered. Following the preceding dilation operations, certain outliers may emerge. To eliminate these outliers, we employ a 5×5 kernel median blur. Subsequently, we use a 5×5 Gaussian blur to enhance the smoothness of local surfaces and soften the sharp edges of objects. Finally, the last step involves reverting back to the original depth according to
Figure 4 clearly shows that our modified IP_Basic algorithm outperforms the original version in indoor scenes. The original algorithm considered tall objects like trees, utility poles, and buildings that extend beyond LIDAR points. It extrapolated the highest column values to the top of the image for a denser depth map, but this could lead to noticeable errors when applied in indoor settings. As seen in
Figure 4(b) and
Figure 4(c), our approach effectively rectifies errors in the depth values at the top of the depth map.
Figure 3.
Using different kernel to process depth images.
Figure 3.
Using different kernel to process depth images.
Figure 4.
Comparison of depth completion effects. (a) Raw depth map with noise and holes. (b) IP_Basic (c) Modified IP_Basic.
Figure 4.
Comparison of depth completion effects. (a) Raw depth map with noise and holes. (b) IP_Basic (c) Modified IP_Basic.
3.3. Depth-Guided Sampling
In 3D space, there are many empty (unoccupied) regions. Traditional NeRF methods tend to oversample these empty regions during training, resulting in significant computational overhead for NeRF. To tackle this problem, our proposed approach introduces a sampling strategy that leverages depth information to guide the sampling process effectively. For each pixel in each image of the training dataset, a ray is emitted. If the object surface is completely opaque, the ray will terminate at the object surface. We have access to the depth map corresponding to each frame, where each pixel represents the distance between the object and the camera in camera coordinates. After applying the necessary coordinate transformations to this depth value, we obtain the depth value of the object in world coordinates. We then perform sampling around this depth value. Specifically, each pixel
is associated with a corresponding depth value
in the image
. We denote the positions of the sampling points as
and ensure that they follow a Gaussian distribution with a mean of
and a standard deviation of
. Therefore, the random variable
follows the Gaussian distribution:
The sampled points are distributed around the depth value depth, which prevents excessive sampling in empty space and conserves computational resources. The sampling space is determined by the depth value of the object corresponding to the current pixel in the world coordinate system. Merely increasing the sampling range as in the original NeRF approach would inevitably lead to ineffective sampling. This is one of the key reasons for the time-consuming nature of NeRF.
3.4. Optimization with Depth Constrain
To optimize the neural radiance field, the color
of the object surface corresponding to each pixel is computed using Eq (1). In addition to the predicted color of a ray, the NeRF depth estimate
and standard deviation
are required to provide supervision to the radiance field based to the depth prior.
By minimizing the loss function
, we can obtain the optimal network parameter
.
consists of depth-related loss function
and color-related loss function
. Here,
is a hyperparameter used to adjust the weights of
and
.
The discrete forms of
and
are given as follows:
By adopting this approach, NeRF is incentivized to terminate rays within a range close to the most confident surface observation based on the depth prior. Simultaneously, NeRF still retains a degree of flexibility in allocating density to effectively minimize color loss. Differing from other methods that compute depth loss, we utilize coordinate transformation to restore the depth map into a point cloud, obtaining the coordinates of each point in the world coordinate system. Rays are cast from the camera coordinate center towards these 3D points, theoretically terminating at these 3D points. We apply a depth loss to encourage the termination distribution of the rays to be consistent with the 3D points in space.
4. Experiments
In this section, we compared our method to recently proposed approaches. Additionally, we conducted ablation experiments to verify the necessity of depth completion and depth-guided sampling. Finally, we compared the training speed of our algorithm under the same conditions with that of NeRF.
4.1. Experimental Setup
We use the Adam optimizer with a learning rate of 6 × 10-4 to process rays in batches of 1024. The radiance fields are optimized for 50k iterations. To simulate a scenario involving the partial absence of depth information, we introduce random perturbations to the depth data in the dataset.
To quantitatively compare different view synthesis methods, we calculate the peak signal-to-noise ratio (PSNR), the Structural Similarity Index Measure (SSIM)[
32], and the Learned Perceptual Image Patch Similarity (LPIPS)[
33] on the RGB of new views. Moreover, we compute the root-mean-square error (RMSE) between the rendered depth maps generated by different methods and the depth information recorded by the sensor.
4.2. Basic Comparison
We compare our method with NeRF [
3], Depth-Supervised NeRF [
19], and NerfingMVS [
18]. The results of the experiment in
Table 2 demonstrate that our method achieves better performance than the baselines across all evaluation criteria.
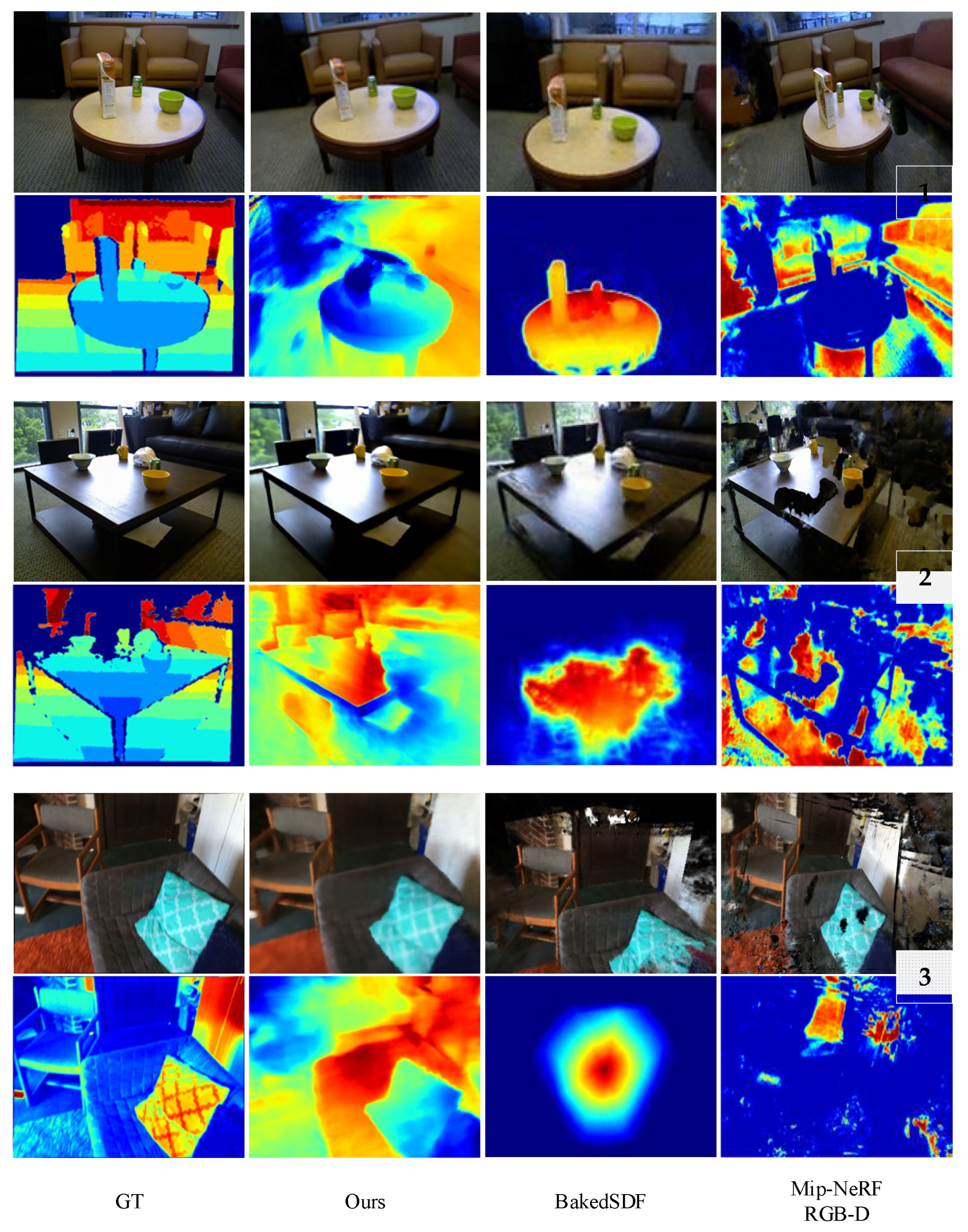
The application of NeRF approaches in scenarios characterized by a limited number of input views often gives rise to artifacts. However, our proposed method addresses this issue by integrating dense depth priors accompanied by uncertainty. This incorporation leads to a remarkable reduction of artifacts compared to conventional baseline methods. Additionally, our approach achieves significantly enhanced accuracy in depth output and finer granularity in color representation. A notable example illustrating the efficacy of our method can be observed in example 1, as depicted in
Figure 5. The images generated by our approach exhibit distinctly sharper edges for both the table and objects, when contrasted with the output obtained using NeRF. The lack of depth supervision in NeRF poses considerable challenges in establishing a reliable correspondence between images, particularly when relying solely on RGB values. This challenge is further amplified in scenarios where the number of available images is limited, resulting in the proliferation of artifacts in the synthesized output.
Despite the limitations of sparse 3D point utilization[
19], our method’s integration of dense depth priors and uncertainty estimation achieves remarkable results. It emerges as a highly promising solution for diverse scenarios. Our approach effectively mitigates artifacts, improves depth accuracy, and enhances color fidelity. Supervising depth information from both RGB data and 3D points enables us to establish reliable image correspondence and reduce artifacts. Our method outperforms traditional NeRF approaches, making it a promising solution for scenarios.
Our method demonstrates robustness against outliers found in the sparse depth input. For instance, in the case of erroneous SfM points located in the cabinets area (as shown in example 4,
Figure 5), alternative approaches suffer more significantly in terms of geometric and color fidelity compared to our proposed method. The NerfingMVS employs COLMAP [
30] initially to acquire depth information and subsequently trains a monocular depth network tailored to the specific scene. The depth map predicted by this monocular depth network is then utilized to guide the learning process of NeRF. Ensuring the accuracy of the predicted depth map is pivotal in guaranteeing the production of artifact-free and consistent final rendered images. In
Figure 6, we compared our approach with two of the popular methods, BakedSDF [
15] and Mip-NeRF RGB-D [
34]. BakedSDF optimize a hybrid neural volume-surface scene representation designed to have well-behaved level sets that correspond to surfaces in the scene. This refined representation is subsequently embedded into a high-quality triangle mesh, enhanced by a streamlined and rapid view-dependent appearance model rooted in spherical Gaussians. BakedSDF excels in capturing fine details, as demonstrated in examples 1
Figure 6, where it can capture more high-frequency details. However, BakedSDF comes with a higher requirement for the number of input views. In comparison to an equal number of input views, our method delivers superior overall performance, as illustrated in example 3
Figure 6. Mip-NeRF RGB-D uses conical frustums instead of rays for volume rendering, allows one to account for the varying area of a pixel with distance from the camera center. In bounded environments, this design does not exhibit a clear advantage. In our method, we utilize a depth supervision mechanism, which enables us to concentrate exclusively on samples near the scene’s surface. This selective approach proves to be advantageous during the rendering phase, as we synthesize depth information for the new viewpoint by making use of the available depth information. By promoting the alignment of a ray’s termination distribution with the surface of the scene, we achieve a significant reduction in artifacts compared to the baseline methods. The outcome of this refinement process is evident in the form of a more precise depth output and a richer representation of colors, as explicitly demonstrated in
Figure 6. These improvements are a result of our method’s ability to effectively handle outliers, its tailored training approach, and the selective utilization of depth information during the rendering process. Together, these advancements contribute to the production of high-quality rendered images with improved fidelity and visual appeal.
4.3. Ablation Study
To verify the impact of the added components, we performed ablation experiments on the ScanNet[
35] and 3DMatch[
36] datasets. The quantitative results (refer to
Table 3) demonstrate that the complete version of our method achieves superior performance in terms of image quality and depth estimation. These findings are consistent with the qualitative results depicted in
Figure 7.
Without Completion The exclusion of depth completion significantly impacts the accuracy of both depth estimation and color reproduction, primarily due to the presence of artifacts in areas lacking depth input. Moreover, even in regions characterized by low confidence in depth values, the outcomes exhibit inferior sharpness compared to those regions with higher confidence in depth values.
Without Dynamic Sampling In the absence of dynamic sampling guided by depth information, the termination depth of each ray may deviate from the actual scene conditions. By employing a dynamic sampling strategy that concentrates a majority of sampling points near the surface of the scene, the accuracy of depth is greatly enhanced. As depicted in
Figure 7, significant improvements in RGB image quality are not observed after the addition of dynamic sampling. However, a notable enhancement has been observed in the quality of the depth map.
Without Depth Loss Lack of deep supervision leads to shape-radiance ambiguity. Despite the generation of high-quality RGB images from new perspectives, an accurate representation of the scene’s geometry remains unattainable. Merely a fraction of the generated depth map provides accurate depth information, as the differences in depth across the remaining areas are negligible, rendering it inadequate for portraying the actual scene depth.
4.4. Training Speed
To quantify the speed improvements in NeRF training, we conducted a comparative analysis between training Depth-NeRF and NeRF under appropriate settings. The evaluation of view synthesis quality on training views was performed using PSNR, considering varying numbers of input views obtained from the 3DMatch dataset[
36]. To assess the training speed performance, we plotted the PSNR values on training views against the number of training iterations, as shown in
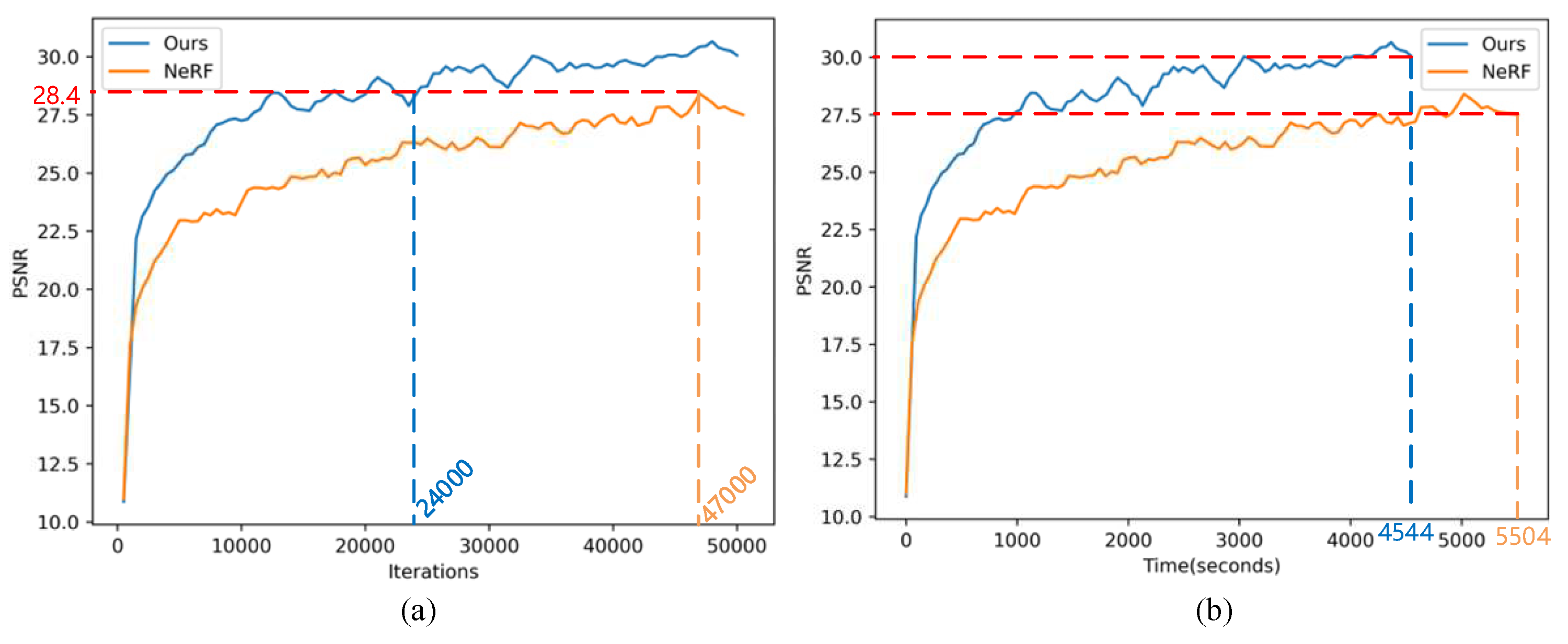
Figure 8.
We trained Depth-NeRF and NeRF models under the same training conditions, and the results showed that Depth-NeRF achieves comparable peak PSNR quality to NeRF, but with considerably fewer iterations. From
Figure 8, Our method exhibits superior performance to NeRF concerning iteration count and training time.
Figure 8(a) shows that our method achieves a higher PSNR than NeRF after 50k iterations. Notably, our method reaches the maximum PSNR of NeRF after only 24k iterations, representing a 51% reduction in iteration count compared to NeRF. These results, initially presented in terms of training iterations, can be translated into tangible improvements in wall time. For instance, when utilizing a single NVIDIA RTX 4090 GPU, Depth-NeRF took approximately ∼ 90.8 ms per iteration, while NeRF required around ∼ 110.1 ms per iteration. Consequently, as shown in
Figure 8(b), our method completes the same 50k iterations in 4544 seconds, whereas NeRF requires 5504 seconds, resulting in an 18% reduction in time compared to NeRF.
5. Conclusions
In this study, we proposed a novel view synthesis method that utilizes neural radiance fields and dense depth priors. Our method utilizes depth completion on scene depth maps to provide dense and accurate depth information for NeRF training and efficient sample collection. This allows for improved rendering quality and more accurate, continuous representations of scene depth. We demonstrate that our dense depth information with uncertainty effectively guide the NeRF optimization, resulting in considerably improved image quality for novel views and more precise depth estimates compared to alternative approaches. Furthermore, our approach exhibits a notable reduction of 18% in the training time required by NeRF.
Although our approach demonstrates advantages across various datasets, there is still the potential for further enhancement. The current positional encoding method has room for improvement, especially in representing high-frequency details, and future research can focus on finding more suitable positional encoding approaches. Additionally, our method has a relatively high demand for GPU memory, which may pose challenges in specific application scenarios. To reduce memory requirements, future work can concentrate on optimizing the network structure of NeRF. Overall, we perceive our method as a meaningful progression towards making NeRF reconstructions more accessible and applicable in common settings.
Author Contributions
Conceptualization, Bojun Wang and Danhong Zhang; methodology, Bojun Wang; software, Bojun Wang; validation, Bojun Wang, Danhong Zhang and Yixin Su; formal analysis, Bojun Wang and Yixin Su; investigation, Bojun Wang and Huajun Zhang; resources, Bojun Wang; data curation, Bojun Wang.; writing—original draft preparation, Bojun Wang; writing—review and editing, Bojun Wang and Danhong Zhang; visualization, Bojun Wang and Danhong Zhang; supervision, Huajun Zhang; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest.
References
- Neff, T., Stadlbauer, P., Parger, M., Kurz, A., Mueller, J.H., Chaitanya, C.R.A., Kaplanyan, A., Steinberger, M.: DONeRF: Towards Real-Time Rendering of Compact Neural Radiance Fields using Depth Oracle Networks. Comput. Graph. Forum. 40, 45–59 (2021). [CrossRef]
- Hu, T., Liu, S., Chen, Y., Shen, T., Jia, J.: EfficientNeRF: Efficient Neural Radiance Fields, http://arxiv.org/abs/2206.00878, (2022).
- Mildenhall, B., Srinivasan, P.P., Tancik, M., Barron, J.T., Ramamoorthi, R., Ng, R.: NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis, http://arxiv.org/abs/2003.08934, (2020).
- Gafni, G., Thies, J., Zollhofer, M., Niesner, M.: Dynamic Neural Radiance Fields for Monocular 4D Facial Avatar Reconstruction. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). pp. 8645–8654. IEEE, Nashville, TN, USA (2021).
- Tretschk, E., Tewari, A., Golyanik, V., Zollhofer, M., Lassner, C., Theobalt, C.: Non-Rigid Neural Radiance Fields: Reconstruction and Novel View Synthesis of a Dynamic Scene From Monocular Video. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV). pp. 12939–12950. IEEE, Montreal, QC, Canada (2021).
- Pumarola, A., Corona, E., Pons-Moll, G., Moreno-Noguer, F.: D-NeRF: Neural Radiance Fields for Dynamic Scenes. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). pp. 10313–10322. IEEE, Nashville, TN, USA (2021).
- Tancik, M., Mildenhall, B., Wang, T., Schmidt, D., Srinivasan, P.P., Barron, J.T., Ng, R.: Learned Initializations for Optimizing Coordinate-Based Neural Representations. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). pp. 2845–2854. IEEE, Nashville, TN, USA (2021).
- Chan, E.R., Monteiro, M., Kellnhofer, P., Wu, J., Wetzstein, G.: pi-GAN: Periodic Implicit Generative Adversarial Networks for 3D-Aware Image Synthesis. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). pp. 5795–5805. IEEE, Nashville, TN, USA (2021).
- Yu, A., Ye, V., Tancik, M., Kanazawa, A.: pixelNeRF: Neural Radiance Fields from One or Few Images, http://arxiv.org/abs/2012.02190, (2021).
- Schwarz, K., Liao, Y., Niemeyer, M., Geiger, A.: GRAF: Generative Radiance Fields for 3D-Aware Image Synthesis, http://arxiv.org/abs/2007.02442, (2021).
- Lombardi, S., Simon, T., Saragih, J., Schwartz, G., Lehrmann, A., Sheikh, Y.: Neural volumes: learning dynamic renderable volumes from images. ACM Trans. Graph. 38, 1–14 (2019). [CrossRef]
- Henzler, P., Rasche, V., Ropinski, T., Ritschel, T.: Single-image Tomography: 3D Volumes from 2D Cranial X-Rays. Comput. Graph. Forum. 37, 377–388 (2018). [CrossRef]
- Sitzmann, V., Thies, J., Heide, F., NieBner, M., Wetzstein, G., Zollhofer, M.: DeepVoxels: Learning Persistent 3D Feature Embeddings. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). pp. 2432–2441. IEEE, Long Beach, CA, USA (2019).
- Martin-Brualla, R., Pandey, R., Yang, S., Pidlypenskyi, P., Taylor, J., Valentin, J., Khamis, S., Davidson, P., Tkach, A., Lincoln, P., Kowdle, A., Rhemann, C., Goldman, D.B., Keskin, C., Seitz, S., Izadi, S., Fanello, S.: LookinGood: Enhancing Performance Capture with Real-time Neural Re-Rendering, http://arxiv.org/abs/1811.05029, (2018).
- Yariv, L., Hedman, P., Reiser, C., Verbin, D., Srinivasan, P.P., Szeliski, R., Barron, J.T., Mildenhall, B.: BakedSDF: Meshing Neural SDFs for Real-Time View Synthesis, http://arxiv.org/abs/2302.14859, (2023).
- Yu, Z., Peng, S., Niemeyer, M., Sattler, T., Geiger, A.: MonoSDF: Exploring Monocular Geometric Cues for Neural Implicit Surface Reconstruction.
- Li, Z., Müller, T., Evans, A., Taylor, R.H., Unberath, M., Liu, M.-Y., Lin, C.-H.: Neuralangelo: High-Fidelity Neural Surface Reconstruction, http://arxiv.org/abs/2306.03092, (2023).
- Wei, Y., Liu, S., Rao, Y., Zhao, W., Lu, J., Zhou, J.: NerfingMVS: Guided Optimization of Neural Radiance Fields for Indoor Multi-view Stereo. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV). pp. 5590–5599. IEEE, Montreal, QC, Canada (2021).
- Deng, K., Liu, A., Zhu, J.-Y., Ramanan, D.: Depth-supervised NeRF: Fewer Views and Faster Training for Free. In: 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). pp. 12872–12881. IEEE, New Orleans, LA, USA (2022).
- Dey, A., Ahmine, Y., Comport, A.I.: Mip-NeRF RGB-D: Depth Assisted Fast Neural Radiance Fields. J. WSCG. 30, 34–43 (2022). [CrossRef]
- Barron, J.T., Mildenhall, B., Tancik, M., Hedman, P., Martin-Brualla, R., Srinivasan, P.P.: Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV). pp. 5835–5844. IEEE, Montreal, QC, Canada (2021).
- Azinovic, D., Martin-Brualla, R., Goldman, D.B., Niebner, M., Thies, J.: Neural RGB-D Surface Reconstruction. In: 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). pp. 6280–6291. IEEE, New Orleans, LA, USA (2022).
- Garbin, S.J., Kowalski, M., Johnson, M., Shotton, J., Valentin, J.: FastNeRF: High-Fidelity Neural Rendering at 200FPS, http://arxiv.org/abs/2103.10380, (2021).
- Reiser, C., Peng, S., Liao, Y., Geiger, A.: KiloNeRF: Speeding up Neural Radiance Fields with Thousands of Tiny MLPs, http://arxiv.org/abs/2103.13744, (2021).
- Yu, A., Li, R., Tancik, M., Li, H., Ng, R., Kanazawa, A.: PlenOctrees for Real-time Rendering of Neural Radiance Fields, http://arxiv.org/abs/2103.14024, (2021).
- Liu, L., Gu, J., Lin, K.Z., Chua, T.-S., Theobalt, C.: Neural Sparse Voxel Fields, http://arxiv.org/abs/2007.11571, (2021).
- Hedman, P., Srinivasan, P.P., Mildenhall, B., Barron, J.T., Debevec, P.: Baking Neural Radiance Fields for Real-Time View Synthesis. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV). pp. 5855–5864. IEEE, Montreal, QC, Canada (2021).
- Chen, A., Xu, Z., Zhao, F., Zhang, X., Xiang, F., Yu, J., Su, H.: MVSNeRF: Fast Generalizable Radiance Field Reconstruction from Multi-View Stereo. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV). pp. 14104–14113. IEEE, Montreal, QC, Canada (2021).
- Yao, Y., Luo, Z., Li, S., Fang, T., Quan, L.: MVSNet: Depth Inference for Unstructured Multi-view Stereo. In: Ferrari, V., Hebert, M., Sminchisescu, C., and Weiss, Y. (eds.) Computer Vision – ECCV 2018. pp. 785–801. Springer International Publishing, Cham (2018).
- Schonberger, J.L., Frahm, J.-M.: Structure-from-Motion Revisited. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). pp. 4104–4113. IEEE, Las Vegas, NV, USA (2016).
- Ku, J., Harakeh, A., Waslander, S.L.: In Defense of Classical Image Processing: Fast Depth Completion on the CPU, http://arxiv.org/abs/1802.00036, (2018).
- Wang, Z., Bovik, A.C., Sheikh, H.R., Simoncelli, E.P.: Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 13, 600–612 (2004). [CrossRef]
- Zhang, R., Isola, P., Efros, A.A., Shechtman, E., Wang, O.: The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 586–595. IEEE, Salt Lake City, UT (2018).
- Dey, A., Ahmine, Y., Comport, A.I.: Mip-NeRF RGB-D: Depth Assisted Fast Neural Radiance Fields. J. WSCG. 30, 34–43 (2022). [CrossRef]
- Dai, A., Chang, A.X., Savva, M., Halber, M., Funkhouser, T., Niessner, M.: ScanNet: Richly-Annotated 3D Reconstructions of Indoor Scenes. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). pp. 2432–2443. IEEE, Honolulu, HI (2017).
- Zeng, A., Song, S., Niessner, M., Fisher, M., Xiao, J., Funkhouser, T.: 3DMatch: Learning Local Geometric Descriptors from RGB-D Reconstructions. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). pp. 199–208. IEEE, Honolulu, HI (2017).
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).