Prerpints.org logo
Preprint
Article

Improved Dynamic Performance of Average-Value Modelled Active Front-End Rectifiers

Altmetrics

Downloads

90

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 December 2023

Posted:

20 December 2023

You are already at the latest version

Alerts
Abstract
Active front-end (AFE) rectifiers have been becoming widely employed in power systems to achieve unity power factor and harmonic mitigations. The typical modeling approaches applied for AFE rectifiers in the literature mostly relied on two baselines named the detailed model and the time average model. The former approach deals with the switching element model (SEM) leads to significant harmonics in currents with distorted waveforms. The latter approach uses the average-value model (AVM) to overcome the currents’ harmonics as well as provide fast responses. However, even the AVM baseline has contained problems during the starting stage (lack of control signals) and over the dead-time periods which causes serious issues in the implementation process. This paper presents an improved dynamic AVM for AFE rectifiers by precisely considering the issues mentioned above along with the practical starting procedure and desirable initialization. The studied AFE rectifier is developed using the voltage-oriented control (VOC) technique based on the different modeling methodologies including SEM, Conventional AVM, and the proposed AVM. The performance of all models is analyzed and compared using simulation results with MATLAB/Simulink R2023a Function blocks for all the algorithm parts and SimScape elements for the electrical circuit model. The simulation results illustrate that the performance of the proposed AVM approach can closely resemble the behavior of the SEM baseline with low harmonic distortion.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Nowadays, the power system has endured a huge transformation due to the development of power converters and renewable energy resources [1]. Power quality challenges, the widespread employing of high-order filters, and the overall decrease in the impact of the power grid due to distributed generation are the main changes that have caused this transition [2,3]. To address these challenges, enormous solutions have been reported to guarantee the proper control and operation of power systems equipped with power converters. Among these solutions, smart transformers that are also called the power electronics transformers has been widely applied to interface medium- and low-voltage systems through fully controllable power electronics devices [4]. In a similar manner, the power electronics transformations have played a key role in the on-board systems for transportation applications, aircraft, and shipboard [5,6]. Active rectifiers, as a first stage in those kinds of grid represents, have been becoming the most attractive approaches towards the smart power systems.
Active front-end (AFE) rectifiers have been widely used in medium-to-high-power adjustable speed drives, high-voltage DC systems, electric vehicles, and traction battery chargers to achieve regenerative operation and meet energy efficiency and harmonic requirements. In many applications, where improved harmonic distortion is demanded, conventional front-end devices have been replaced by AFE rectifiers [7]. In addition, the AFE rectifiers can improve the reactive power balance by operating at a near unity power factor or by compensating the inductive/capacitive impact of other loads in the vicinity. Moreover, the fast transient feature of the new generation of AFE rectifiers enables superior ride-through capability during system disturbances [8].
Several marine vessels have utilized DC power systems for their simple controllability, high efficiency, and high reliability based on AFE rectifiers and synchronous generators [9,10]. AFE rectifiers have retained impetus as the key device for high-power electric vehicles (EVs) charging equipment that is growing exponentially. AFE rectifiers reduce the distortions produced via the operation of the EV charging infrastructures by minimizing harmonic disturbances and operating close to the unity power factor (PF) [11,12]. In [13], an AFE rectifier equipped with a PF correction (PFC) is proposed for power quality improvement in telecom applications using a sensorless voltage control strategy to tackle harmonic issues and boost overall performance. Modular multilevel converter-based AFE rectifier topology is studied in [14] under unbalanced power grid conditions to improve the steady-state performance of the system that feeds the variable-speed motor drive. Variable-speed motor drives are a massive part of the grid-connected loads in distribution networks that use either conventional diode-bridge rectifiers or AFE rectifiers to adjust the operating frequency [15]. Recently, modular power converters with AFE rectifiers have been extensively employed by motor drives to improve their harmonic characteristics and raise the overall power quality. In [16], a modular AFE rectifier with a common DC link is extended for multidrive configuration to mitigate harmonic distortions based on the electronic phase shifting technique. To elevate the modular AFE rectifier behavior, it is useful to separate the rectifier module from the drive unit and consider it as the main interface circuit between the AC power grid and the motor drive system's DC link and deploy a robust and feasible control strategy.
The typical control techniques developed for the AFE rectifiers are voltage-oriented control (VOC) [17], virtual-flux-based strategies [18], and direct power control (DPC) [19]. Several other control approaches have been proposed for the dynamic model of the AFE converters including predictive hybrid pulse-width-modulation (PWM) [20], predictive duty cycle control [21], multicarrier-based PWM [22], synchronous space-vector modulation [23], proportional-integral (PI) controller with anti-windup scheme [24], and digital control with multi-loop tuning approaches [25]. Dynamic transient simulation of AFE rectifiers is a powerful item that is widely developed by many researchers to evaluate the effect of switched loads on power grids. Although several transient simulation tools with extensive elements can be willingly used to develop a detailed switching model of the AFE converter, such detailed schemes are computationally vigorous and may cause long simulation times for large distribution networks with enormous interfaced loads. Dynamic modeling, particularly, the average-value model (AVM) is a powerful method that averages or mitigates the high-order harmonics of the AFE rectifier while maintaining the capability to precisely estimate the system's dynamic behavior [26].
For AVM of AFE rectifiers that operate based on conventional PWM strategies, the models are typically performed by rotating reference frame operators [27,28,29]. In [30] the double Fourier series of PWM was studied to figure out the dead-time effect by inserting a correction value. These results extended to clarify the dead time impact on the band-limited PWM signals [31]. However, all these approaches can only be performed in a switching function baseline and cannot be employed in a time-average model. In [32] an improved dynamic model of an AFE converter is studied using the calculation of the duty cycle impact and considering the distortion by modeling the voltage drop on the semiconductor switching devices as an error of the duty cycle. However, those methods ignore the effect of duty cycle distortion over the zero crossing points of current when they are being altered to null. Moreover, this voltage drop on the switching devices does not directly distort the DC link current and, consequently should not be considered as duty cycle distortion. Another technique presented in [33] for modeling a motor drive by adding the effect of the dead time to the modulation space vectors, however, this approach did not consider the impact of voltage drops on switching devices.
This article provides improved AVM (IAVM) for the AFE rectifiers based on the VOC approach to enhance the performance of the time average simulation using several dynamic case studies including startup and load variations. To validate the accuracy of the studied time average approach, the result of the proposed IAVM simulation was compared with the standard AVM (SAVM) and the switching element model (SEM) simulations based on the same control strategy. While some SAVM-based AFE rectifiers have been developed to overcome the aforementioned issues related to the converters, some challenges have remained unsolved such as starting stage without command signals from the controllers, the impact of inrush currents, the effect of dead-time distortion, and fully considering the voltage drop on switching devices. To address these issues, an improved AVM distortion model is proposed that contains the following merits:
  • Built practical SEM, SAVM, and IAVM simulation models for the AFE rectifiers.
  • Appropriate initialize the AFE rectifiers in case of lack of command control signals.
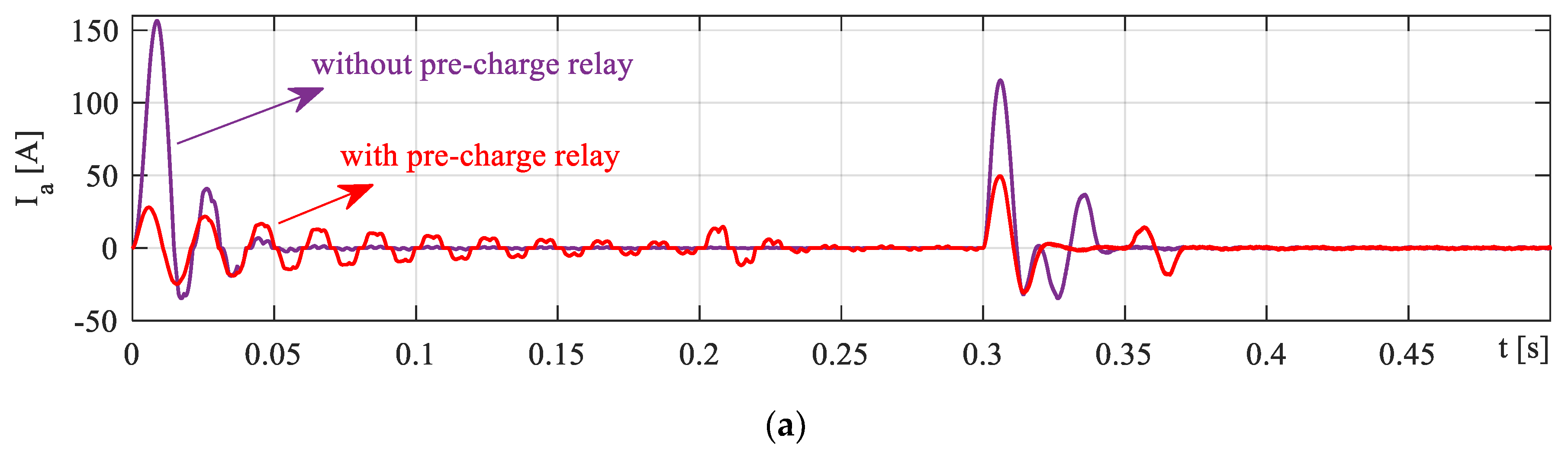
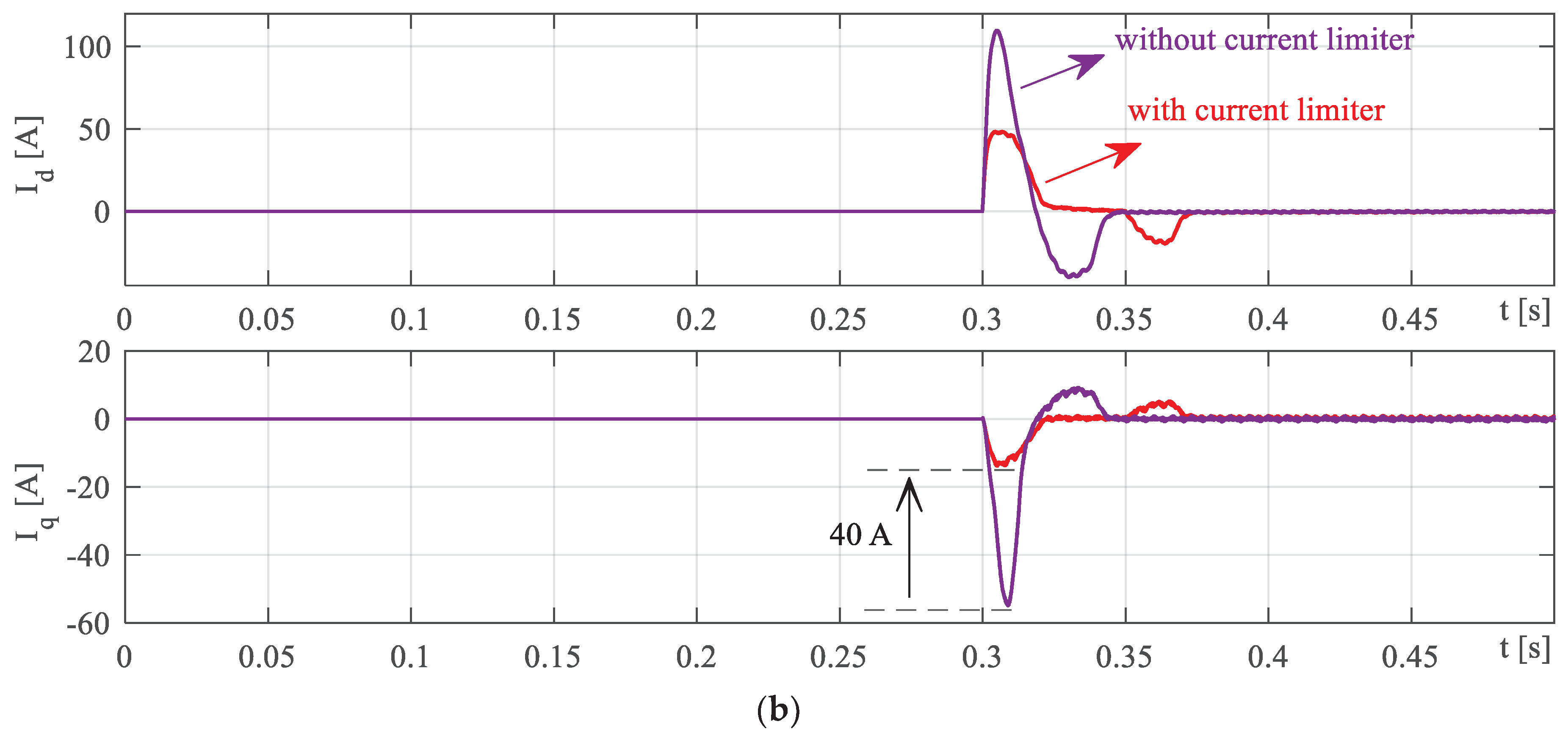
  • Limit the inrush current during the starting period using a pre-charge circuit.
  • Provide a robust close-loop control strategy with a unit power factor.
  • Improve the dead-time impact on the rectifier using the proposed advanced AVM.
  • Fully consider the effect of switching devices’ voltage drops in the models.
  • Compare the performance of the models to verify the proposed IAVM operation.
Section 2 describes different topologies for a three-phase AFE rectifier. Section 3 discusses the proposed time average model for the AFE topology besides its VOC implementation. Section 4 illustrates the simulation results of the case studies. Section 5 concludes this research work and the outlooks in AFE rectifiers.

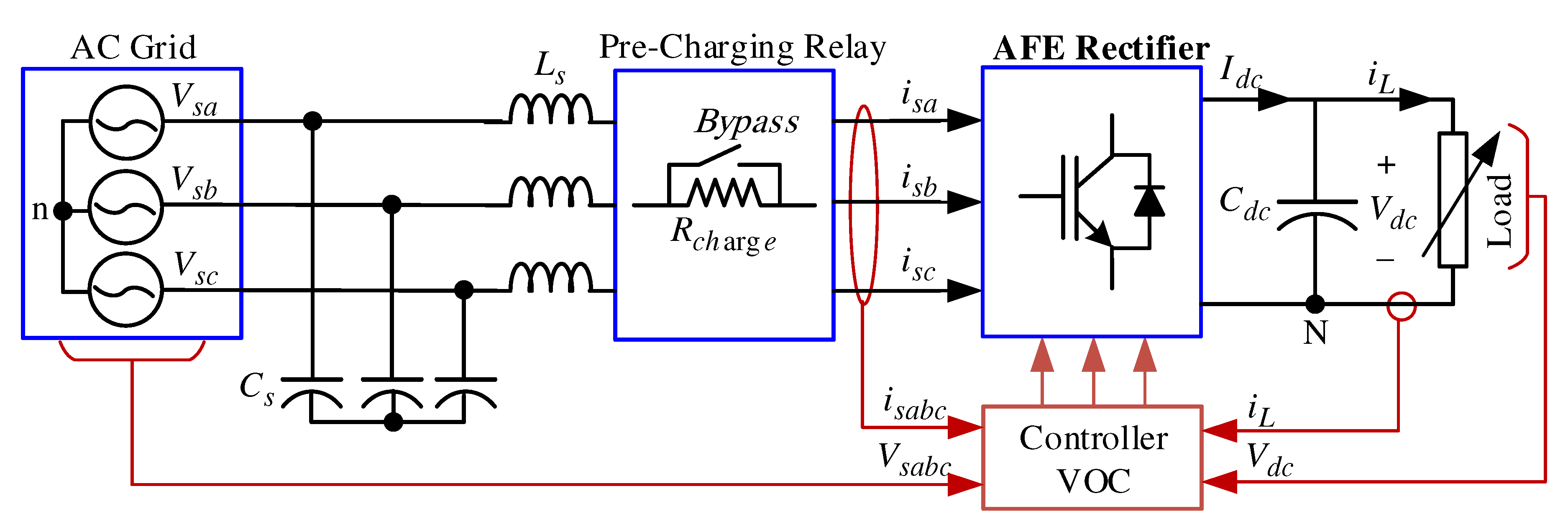
2. AFE Rectifier Models

As explained in Section 1, three-phase rectifiers are widely utilized in power system applications as front-end converters due to their reliability and simplicity. Therefore, this section explores the mathematical model of the AFE rectifiers with both a switched model based on PWM switching strategies and a dynamic time average model.

2.1. Switched (PWM) Model

Figure 1 depicts the physical topology of the three-phase AFE rectifier, i.e. SEM model, based on the VOC scheme. The control strategy can be implemented whether by hardware tools in digital processors with related requirements including A/D and D/A converters or by software-based function modules. The dynamic performance of the AFE rectifier topology is practically measured by a dynamic signal analyzer to verify the responses of the rectifier. As shown in Figure 1b, an AFE rectifier, regardless of the switching model or average-value model, utilizes a cascaded control approach with outer and inner close loops. The VOC scheme, as one of the common cascade control methods, uses the outer control loop to regulate the rectifier DC link voltage value via a classic PI controller. The DC link PI’s output produces a current signal in the d-axis which is required to maintain the AFE rectifier output DC voltage at a desired value. To achieve unity PF, another control loop is required to keep the q-axis current at zero. Accordingly, these DC signals, as d- and q-axis current references, are delivered to the inner voltage control loops to regulate the rectifier d-q axis voltages using the appropriate power balance equations.
In the SEM approach, the semiconductor switching devices of the AFE rectifier are considered to be switched to on/off states to connect or disconnect the switches based on the controlled time discontinuous signals that originate from the VOC system. The ac-side dynamic requirements of the AFE rectifier with the SEM approach can be developed by Kirchhoff’s voltage law (KVL) equations [34] as follows
[ V s a V s b V s c ] = L s d d t [ i s a i s b i s c ] + [ S a S b S c ] V d c − [ v n N v n N v n N ]
v n N = 1 3 ( S a + S b + S c ) V d c
S a i s a + S b i s b + S c i s c = C d c d V d c d t + i L
where V s a , V s b , and V s c are the AC side phase voltages, i s a , i s b , and i s c represent the line currents. S a , S b , and S c denote the switching states of the upper switching devices, i.e. S a H , S b H , and S c H based on Figure 1a, which are equal to 1 when the switch is closed and 0 when the switch is open. The lower switches of the rectifier legs, i.e. S a L , S b L , and S c L are switched in a complementary with a specific amount of dead-time applied to gating signals of the upper and lower switches in the same leg. The DC link voltage and capacitor are expressed by V d c and C d c respectively, and i L is the current consumed by the load on the DC side of the AFE rectifier.
To employ the VOC scheme, Equations (1) and (3) are transformed into the d-q reference frame as follows
d d t i q = 1 L s ( V q − S q V d c − ω s L s i d )
d d t i d = 1 L s ( V d − S d V d c + ω s L s i q )
d d t V d c = 1 C d c [ 3 2 ( S q i q + S d i d ) − i L ]
where V d and V q represent the phase voltages in the d-q frame, i d and i q are the line currents in the d-q frame, S d and S q are the switching states in the d-q frame, and ω s is the power grid angular frequency that is synchronized to the utility by a software phase-locked loop (PLL).
To acquire the desired DC link voltage V d c , the switching states S d and S q should be determined properly which then be passed on three-phase values and transformed into the space vector PWM (SVPWM) module. To achieve this goal, according to Figure 1b, the power grid voltages in the d-q axis are added to the output signals of the current controllers, V q * and V d * , along with decoupling terms to provide reference switching states, S q * and S d * , as follows
S q * = V q − ω s L s i d − V q *
S d * = V d + ω s L s i q − V d *
It should be noted that the VOC scheme requires three AC current sensors, two AC voltage sensors, and one DC voltage sensor. In addition, a PLL is demanded to attain the power grid voltage angle which is used in the Parke transformation.

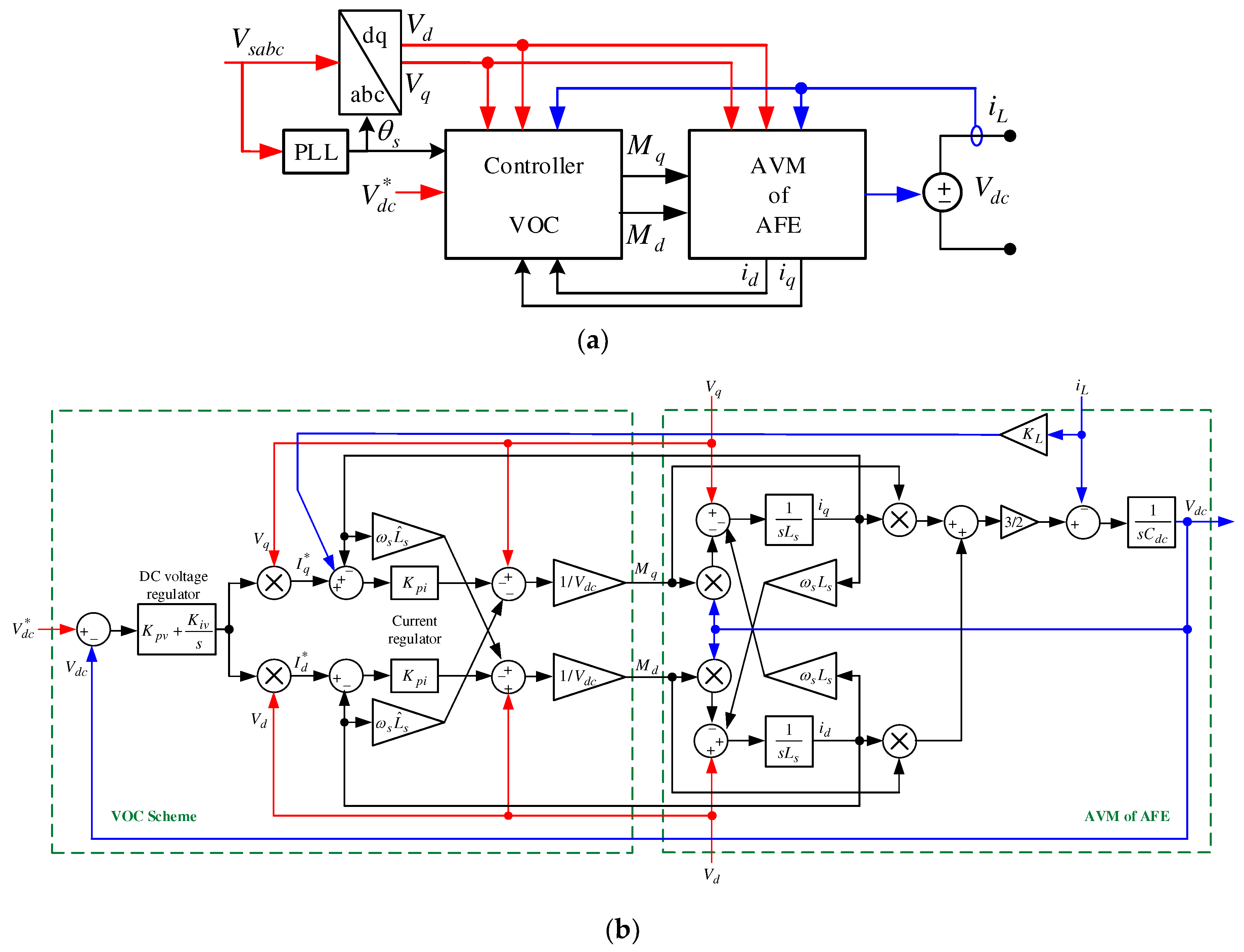
2.2. Dynamic Average-Value Model

The standard dynamic average-value model, i.e. SAVM, of the AFE rectifier includes controlled current sources to replace the switching elements and modulation indexes ranging from 0 to 1 instead of switching states. The dynamic model of the AFE rectifier under the synchronous reference frame can be obtained by replacing the time-discontinuous switch states S d and I d c with time-continuous functions named modulation indexes M d and M q in Equations (4) to (6) as follows
d d t i q = 1 L s ( V q − M q V d c − ω s L s i d )
d d t i d = 1 L s ( V d − M d V d c + ω s L s i q )
d d t V d c = 1 C d c [ 3 2 ( M q i q + M d i d ) − i L ]
where these time-continuous modulation indexes are namely the duty cycles of the phases’ switching devices and can be expressed as follows
M x = 1 T s w ∫ t − T s w t S x ( τ ) d τ   ,   x ∈ { a , b , c }
wherein T s w is the one switching period.
Figure 2 shows the overall block diagram of the SAVM for the AFE rectifiers along with their controller structure. The dynamics explained in Equations (9) to (11) are developed on the right-hand side of Figure 2b with the SAVM of the AFE rectifier block diagram. The DC link voltage regulation and the d-q axis currents’ control are implemented by the VOC block diagrams which is illustrated on the left-hand side of Figure 2b. The difference amount between the desired DC link voltage V d c * and the actual one V d c as error command is fed into a PI regulator to control the DC link voltage using the well-known control function as K p v + K i v s . To maintain the DC link voltage in a desired level as well as receive power from the AC grid at unity PF, the output of the DC voltage PI regulator is multiplied by the grid voltages in the d-q axis to accordingly produce the current references in the d-q terms I d * and I q * which are in perfect match with the grid phase currents. To precise consider the load impact on the dynamic model, the load current i L is multiplied by a load coefficient K L , which is determined by the type and magnitude of the output load, and then is applied to the q-axis current control loop as a feedforward term. The current control loops employed the proportional (P) regulator with a gain K p i to generate the modulation indexes in d-q axis M d and M q as the switching duty cycles as expressed below
M q = ( V q − ω s L ^ s i d − ( I q * − i q ) ) / V d c
M d = ( V d + ω s L ^ s i q − ( I d * − i d ) ) / V d c
where L ^ s is the approximated value of the grid side filter inductor L s , multiplied by the grid angular frequency and current terms to compensate the cross-coupling terms of ω s L s i q and ω s L s i d in the AFE rectifier dynamic model on the right-hand of Figure 2b. In order to perfect decouple of the current control loops as well as simplify the overall controller implementation, L ^ s value can be considered as equal as the L s practical amount [35].

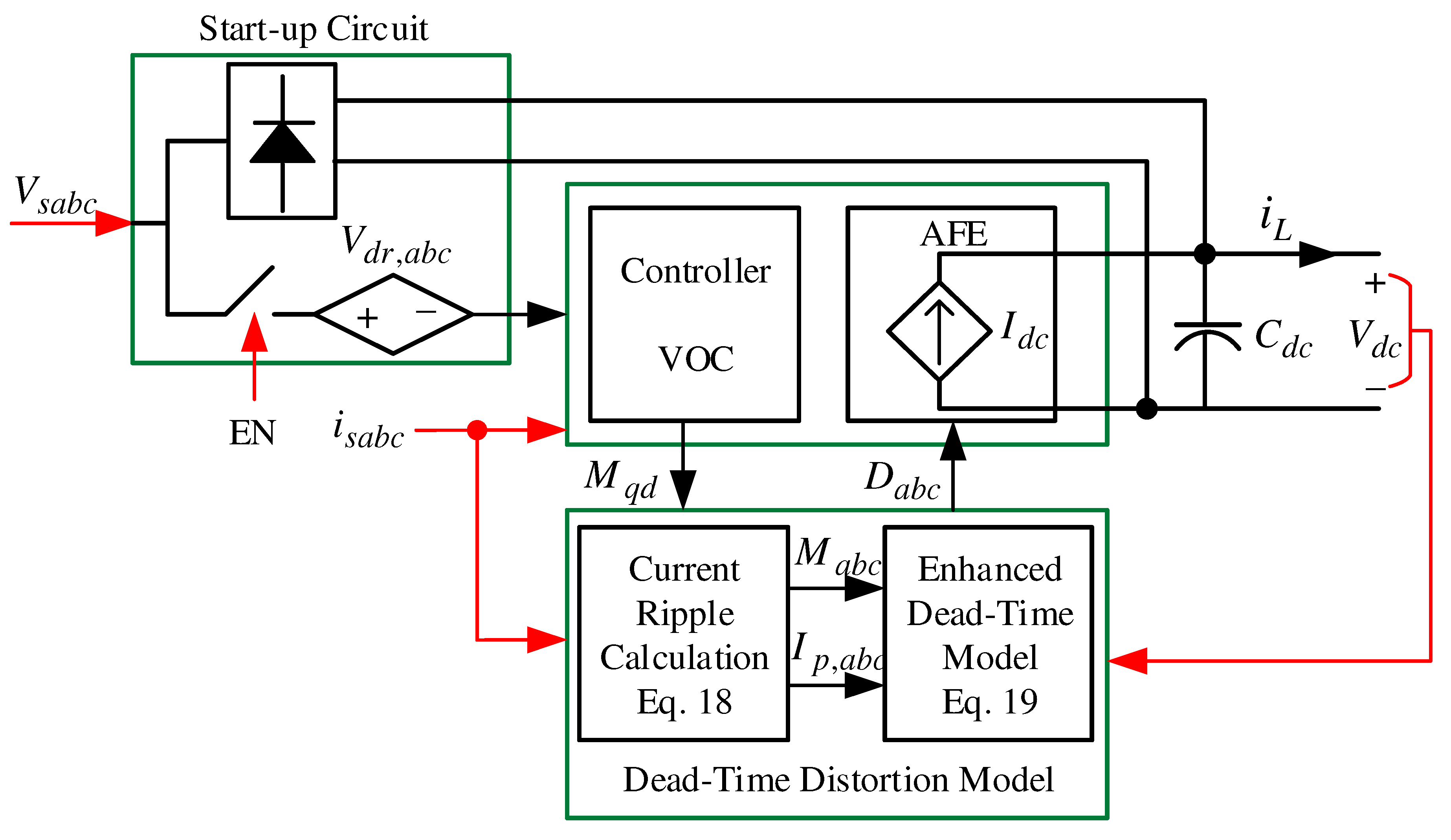
3. Proposed Improved AVM

As discussed before, the AVM based AFE rectifiers provides quick simulation debugging time with less memory usage. However, as discussed in earlier, employing linear equations for modeling and integrated them with ideal switching process lead to non-practical ideal voltage and current waveform with zero distortions. Another drawback of the AVM approach in comparison with the SEM baseline is the lack of ability for startup procedure of simulation because it cannot offer the switching signals in the off status prior to enabling the controller module. To address those issues, an improved AVM, IAVM, is proposed for AFE rectifiers to mitigate the dead-time impacts on total harmonic distortion (THD) of currents and precise starting the simulation with an auxiliary circuit model. Figure 3 illustrates the complete structure of the proposed IAVM including enhanced distortion model to reduce the dead-time harmonics and auxiliary circuit for the startup process. In this approach, the AFE rectifier is modeled as a controlled current source I d c , which is calculated as
I d c ( t ) = D a b c T × I s a b c = [ D a ( t )     D b ( t )     D c ( t ) ] [ i s a ( t ) i s b ( t ) i s c ( t ) ]
where D a b c is the proposed enhanced phase duty cycles. Accordingly, the V d c can be obtained as
d d t V d c = 1 C d c ( I d c − i L )
Each block of the proposed IAVM approach along with D a b c will be clarified in the following subsections.

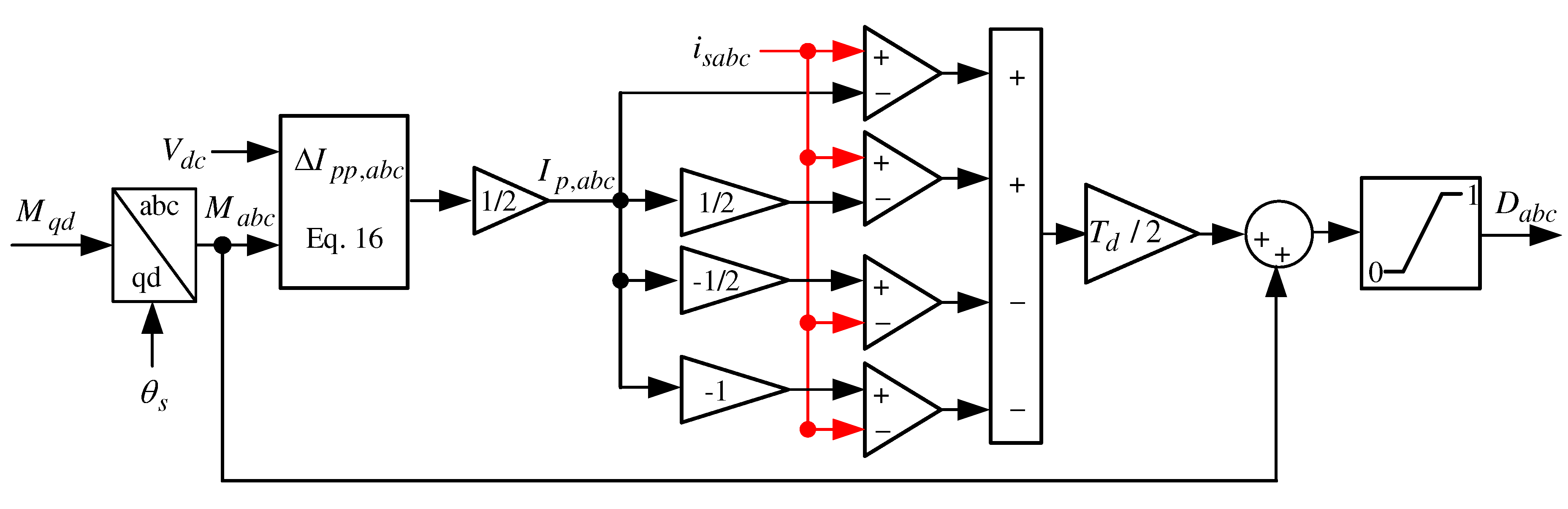
3.1. Enhanced Dead-Time Distortion Model

Dead-time of switching devices causes zero crossing distortion on phase currents’ waveforms of the three-phase AFE rectifiers due to its impact on the deviation of the duty cycle of phase voltages (namely D a b c ) from the command duty cycles produced by controller output ( M a b c in Equation 12). This deviation is a result of phase currents’ signs that compel rectifier leg output voltages to be equal to either DC link voltage or zero during dead-time ( t d ) narrow intervals, correspondingly leading to differ D a b c from the command duty cycle M a b c as follows
D x = { M x − t d / T s w   ,   i s x > 0 M x + t d / T s w   ,   i s x < 0   ,   x ∈ { a , b , c }
The duty cycle definition in Equation 17 is a general one known as the two-level distortion model causes a high amount of harmonics on phase currents as well as high THD. To enhance the definition of the dead-time distortion, one effective solution is dividing the D a b c into more levels than two general levels to tackle the current zero crossing distortions. This target can be achieved by considering a ripple current to allocate relevant duty cycles instead of zero. To estimate the ripple current ( I p ) for each rectifier phase leg, the difference between peak-to-peak ripples ( Δ I p p ) is demanded to be precisely calculated based on the AFE rectifier parameters and variables as follows [36]
Δ I p p , x = V d c T s w 2 L s × M x 3   ,   x ∈ { a , b , c }
here, the modulation index M x is considered in the range of 0 to 1 / 3 due to utilizing SVPWM scheme instead of sinusoidal PWM. From Δ I p p , the ripple current I p for each phase current can be approximated as Δ I p p / 2 .
According to the ripple current, an improved duty cycle based on enhanced dead-time distortion model which is approximated in five-level is defined to reduce the THD of IAVM as follow
D x = { M x − T d   ,         i s x > I p M x − 0.5 T d   ,   0.5 I p ≤ i s x ≤ I p M x ,           − 0.5 I p ≤ i s x ≤ 0.5 I p M x + 0.5 T d   ,   − I p ≤ i s x ≤ − 0.5 I p M x + T d   ,       i s x < − I p   ,   x ∈ { a , b , c }
where T d is the total time delay over the T s w for each switching period based on the IGBTs turn-on time ( t o n ) and turn-off time ( t o f f ) which can be calculated as
T d = ( t d + t o n − t o f f ) / T s w
To avoid gradient transition between turning ON and OFF of duty cycle levels introduced in Equation 15 by the active switching devices, additional three levels are presented in this study using ± 0.5 I p in order to mitigate the dead-time distortion on currents. Since the dead-time intervals are too short in practice, these half-point values are feasible approximations. To better view, the studied five-level dead-time distortion model is illustrated in Figure 4 which integrates the ripple current calculator with the enhanced duty cycle model. A limiter is also added to the model to maintain the outputs of duty cycles D a b c in a range between 0 and 1.

3.2. Improved Startup Procedure

The practical startup circuit model, as the main part of this IAVM approach, is implemented to enhance the proposed IAVM performance by precisely taking into account the voltage drops of the switching devices (e.g. IGBTs and the freewheeling diodes) and employing a standard three-phase diode rectifier with an enable switch.
According to Figure 3, the total voltage drop ( V d r ) of each phase leg of the AFE rectifier on the IGBTs ( V S ) and diodes ( V D ) is implemented as a controlled voltage source. To accurately calculate the V d r as a function of voltages duty cycles D a b c and phase currents polarities, the forward voltage of the IGBT switches ( V f S ) and diodes ( V f D ) are required along with their internal resistances r S and r D , respectively. Consequently, the total voltage drop of each phase V d r , x can be calculated as [37]
V d r , x = { D x V D + ( 1 − D x ) V S   ,             i s x > 0 − D x V S − ( 1 − D x ) V D   ,       i s x < 0
where
{ V s = r s | i s x | + V f S V D = r D | i s x | + V f D
As the last part of the IAVM approach, the three-phase standard diode rectifier is added along with the enable switch (shown by the EN switch in Figure 3) to simulate the AFE rectifier before connecting to the VOC controller. The reason behind this is that during the AVM-based rectifier startup for real hardware test of AFE, there are no control signals to enable the IGBT switches ON and OFF. In other words, IAVM will short-circuit the three phases during startup. To avoid this issue, an enabled switch will disconnect the IAVM circuit before the VOC controller is initiated. As a result, the proposed IAVM baseline operation is similar to the SEM before the controller is connected which is verified by the simulation results in the following section.

4. Results

To verify the performance of the proposed methodologies, a grid-connected AFE rectifier system with PFC module, whose nominal circuit parameters as well as controller gains are listed in Table 1, is considered to implementation. Simulation studies are conducted by MATLAB/Simulink R2023a environment to demonstrate the validity of detailed switching model along with the electrical circuit utilized in all mentioned approaches including SEM, SAVM, and IAVM. The proposed IAVM baseline and SAVM are implemented by MATLAB S-Functions for all the blocks and the SimScape Tools for the all electrical circuits employed in the SEM baseline. The tested AFE rectifier topology is shown in Figure 5 wherein a pre-charging relay is used to soft starting the system.
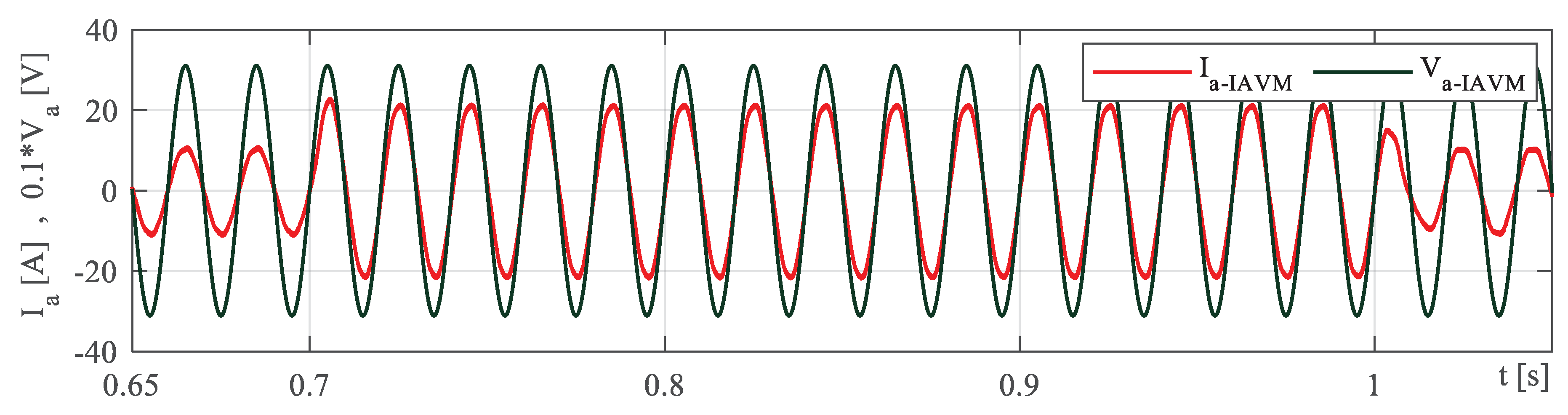
Several case studies are implemented to compare the operation of the proposed IAVM with the other two algorithms in the conditions of startup and transients’ behaviors that are discussed in the following subsections.

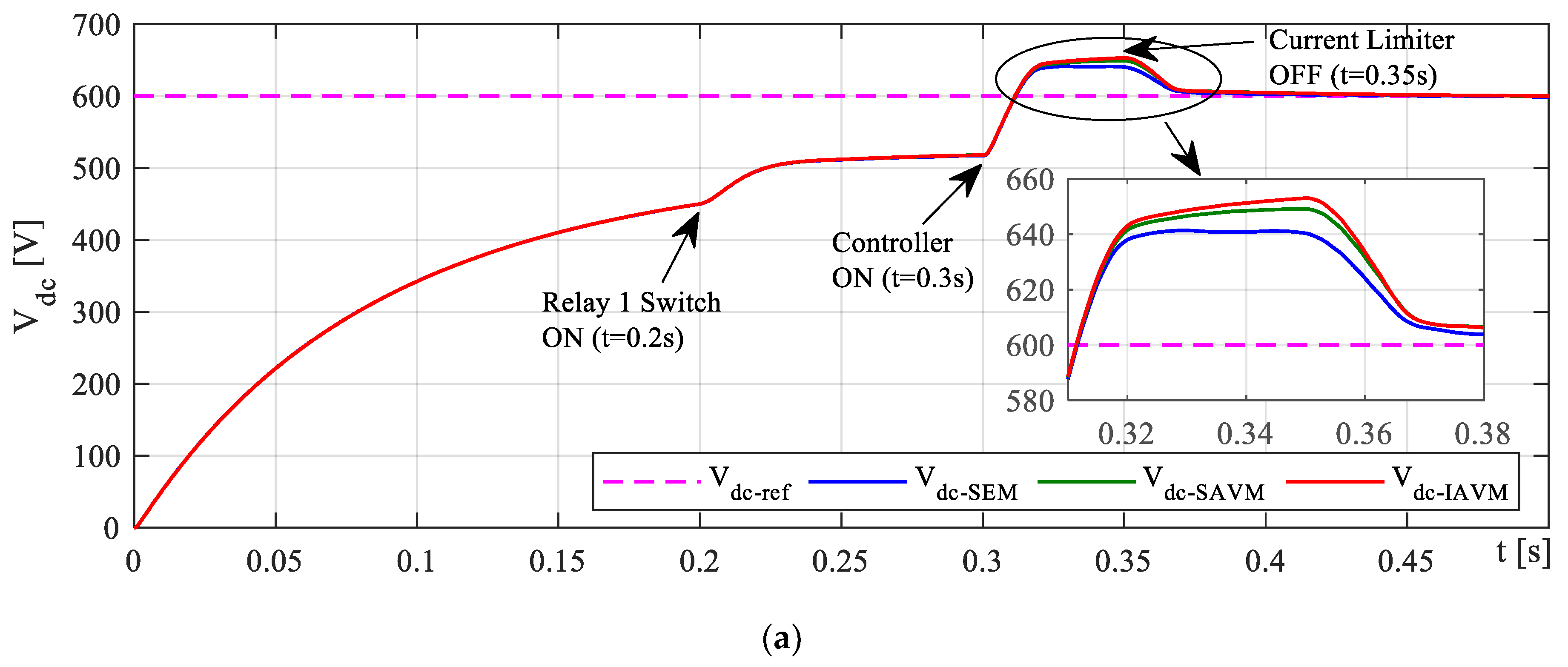
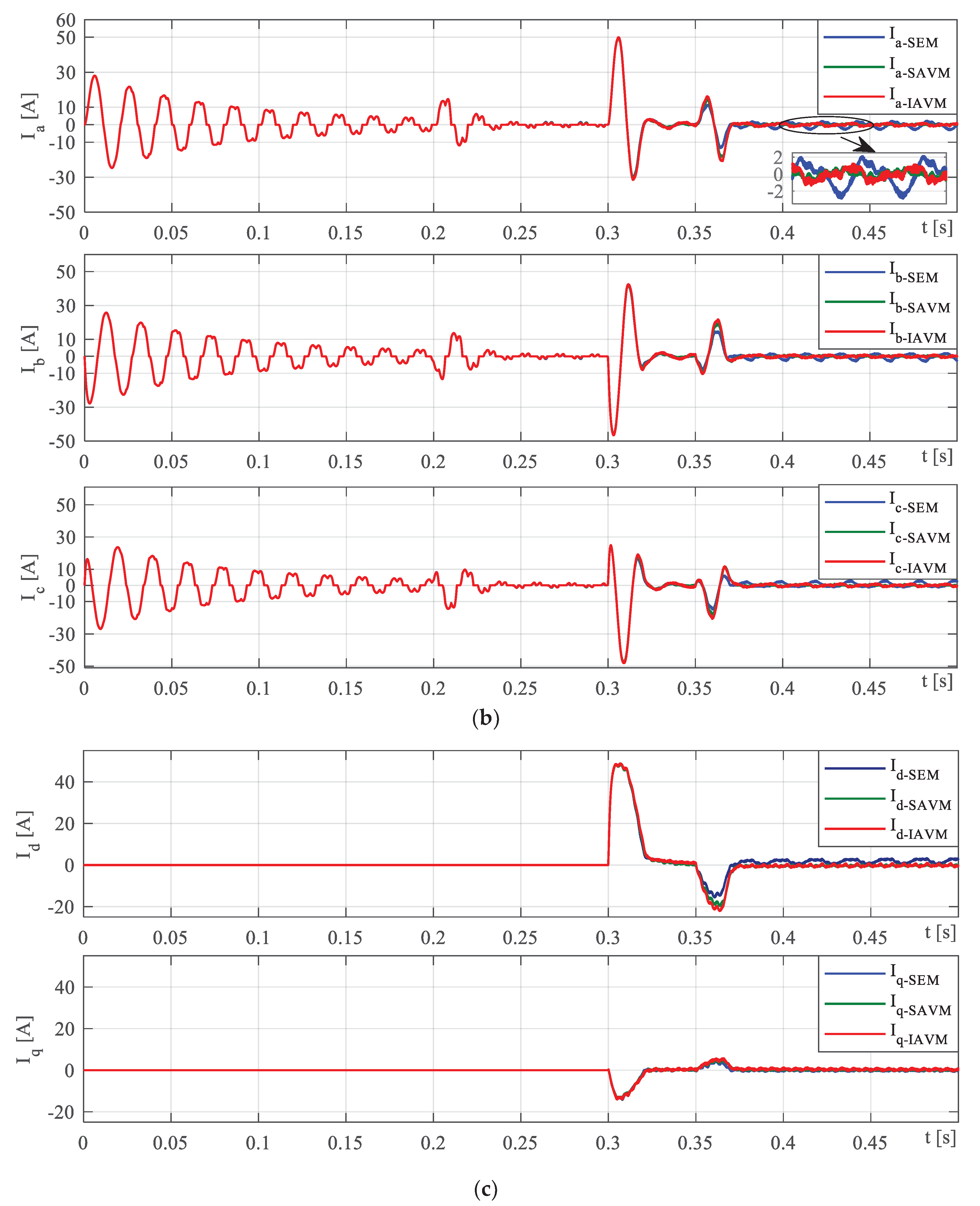
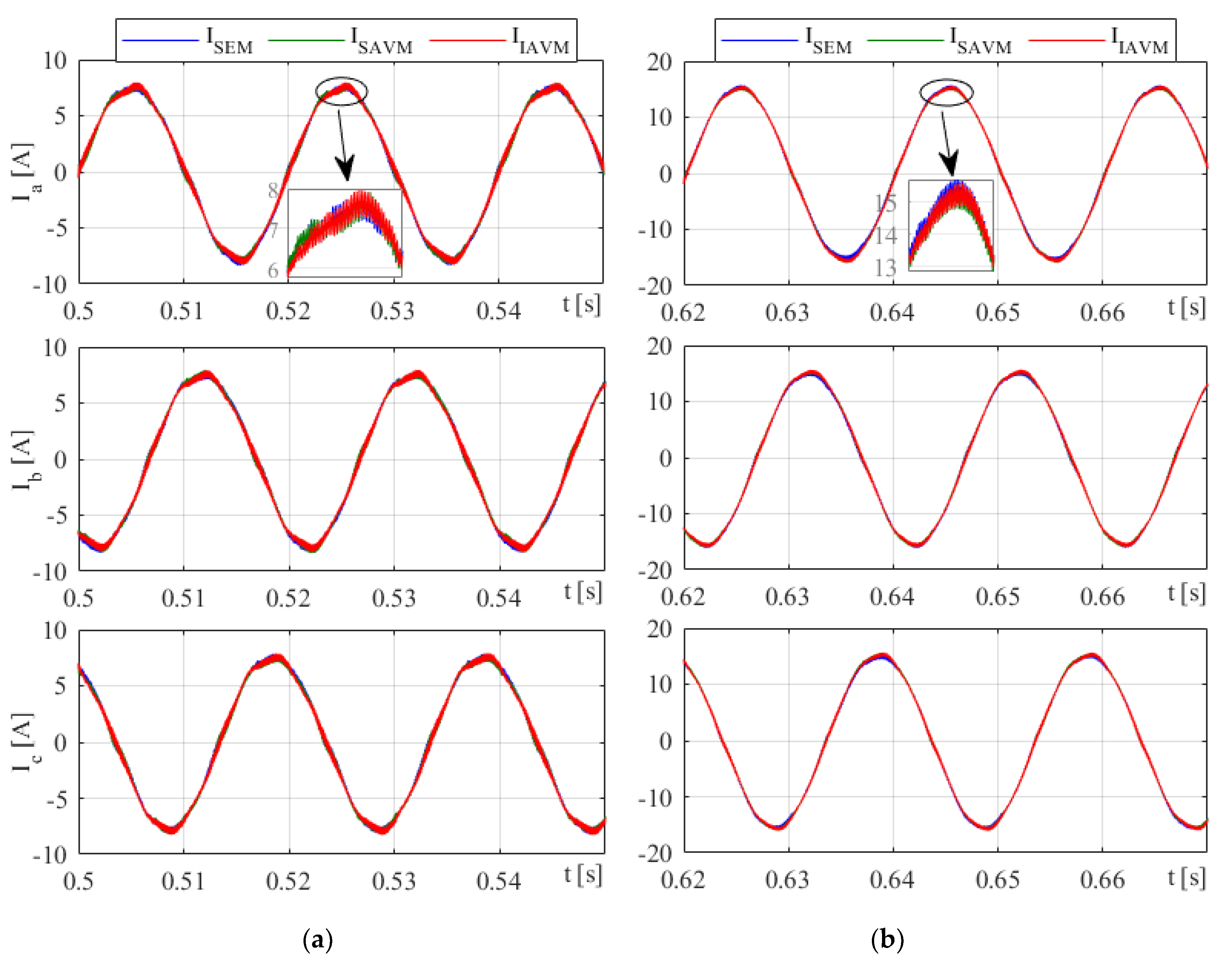
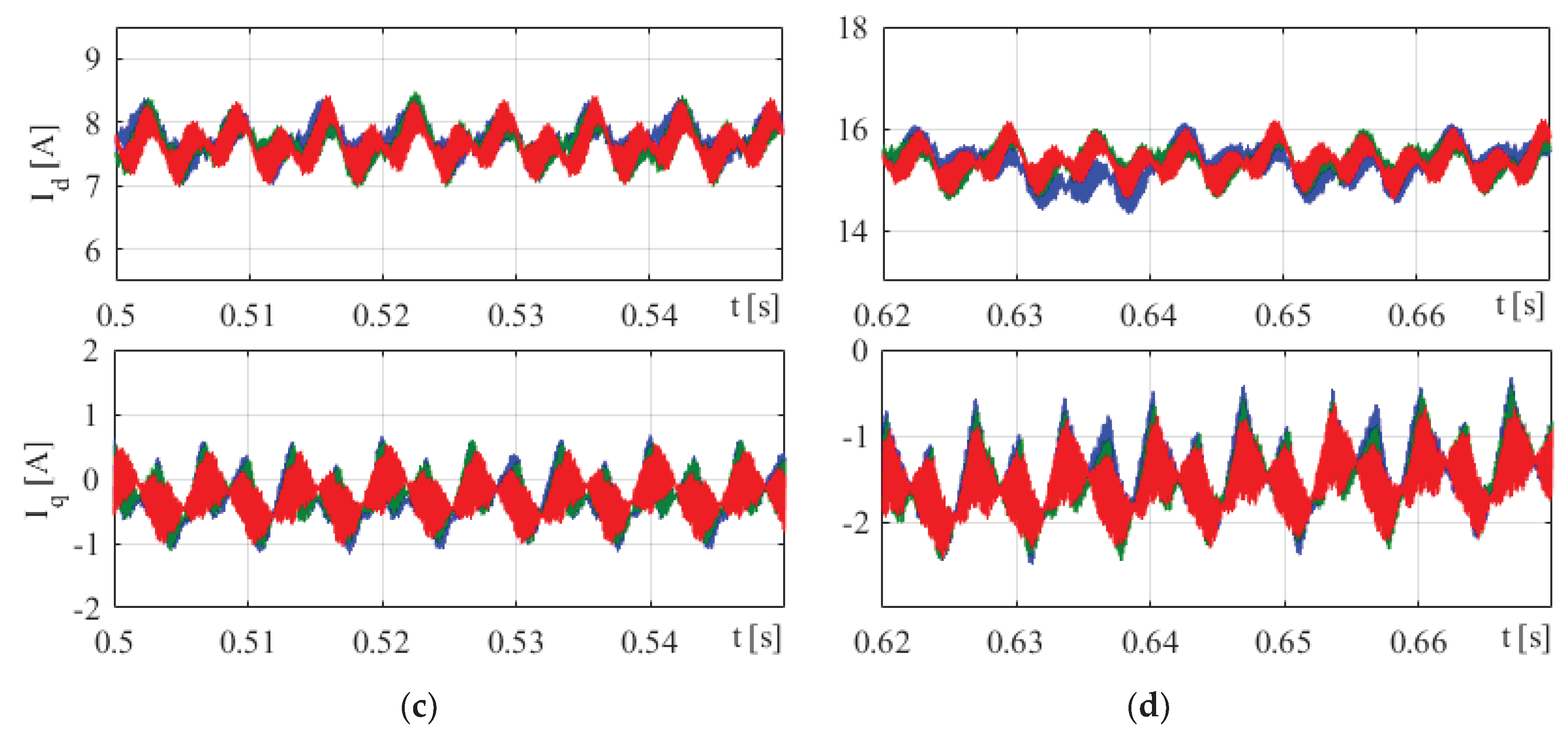
4.1. Case 1: Startup Performance

In this study, the transient behavior of the IAVM is tested during the startup conditions under the zero load (open circuit output) to validate the starting procedure performance in comparison to the SAVM and SEM approaches. Figure 6 shows the simulation results under startup transient to start and bring the AFE rectifier DC link voltage from 0 to the desired value 600 V with zero active power, and consequently zero phase currents. The operation procedure of this Case study includes four stages. During the first stage (from starting to 0.2 s as shown in Figure 6a), so called the pre-charging stage, the DC link capacitor C d c is slowly charged from 0 to a safe limit around 80% of the peak value of input line to line grid voltage 2 V g r i d ( L − L ) (here is around 440 V) through three pre-charge resistors for each phases. All IGBT devices are OFF during this stage and pre-charging resistors in series with the boost inductors L s are connected the output capacitor C d c via auxiliary three-phase diode rectifier to limit the current. During the second stage, from 0.2 s to 0.3 s, the bypass relay 1 short-circuits the pre-charging resistors, then the capacitor C d c is normally charged to 2 V g r i d ( L − L ) using the inductors L s and the auxiliary diode rectifier. It should be noted that during these two stages, the VOC controller are not connected to the AFE rectifier, thus control signals are not applied yet to the rectifier. When C d c voltage is reached to more than 85% of the desired DC link voltage (600 V), the VOC controller is switched ON and starts the third stage. In the third stage, the auxiliary diode rectifier is disconnected and the controller is connected to the AFE rectifier by considering the total voltage drop V d r in IAVM algorithm. During this stage, the controlled d-q axis currents are restricted to 50 A for soft starting and then at the fourth stage (here at 0.35 s), the current upper limit is set to 80 A, allowing a nominal current to flow. According to Figure 6a, by considering this four-stage procedure, the DC link voltage can be safely reached to its desired value without producing huge inrush current. The simulation waveform of V d c for all three baselines are closely matches each other except some differences among them during the third stage when the first current limiter is disabled. The simulation results of three-phase grid currents in Figure 6b illustrates the operational differences between the proposed IAVM and other two approaches as current ripples during no-load conditions. It is clearly observed that the IAVM based AFE rectifier has low ripples than the SAVM baseline and very low than the SEM baseline. This is because of developing enhanced duty cycles for the IAVM to reduce the zero crossing current ripples as also shown in Figure 6c in upper waveform for d-axis current.
To better reveal the studied startup performance differences, some simulations are carried out without startup stages as shown in Figure 7. From Figure 7a, the phase current peak value is very high when there is not pre-charge relay, however, using that relay is limited the starting current to lower than the nominal current. In addition, without pre-charging procedure, the controlled d-q axis currents contain excessive overshoot and undershoot which is more than 40 A for q-axis current undershoot.

4.2. Case 2: Load Responces

The AFE rectifier steady-state current waveforms for the three mentioned baselines are illustrated in Figure 8 for operating power of 3.6 kW and 7.2 kW. In spite of the Case 1 where the two AVM baselines have similar current waveforms, this case discovers different current results especially at lower power level because of longer range of the ripple current ± I p . Form Figure 8a, for output power 3.6 kW, the current waveform for the SEM approach depicts significant ripples due to switching elements at high switching frequency, for the SAVM approach some ripples are still shown because of using the conventional two-level duty cycle, however, the IAVM baseline shows better current waveforms where such significant ripples no longer exist. These variances are precisely shown in Figure 8c by their d-axis currents. Similar behaviors are also illustrated by the current waveforms at output power of 7.2 kW, although the ripple distortions in this study are not as significant as the pervious study with power level of 3.6 kW.
Table 2 summarized the harmonic distortion results of this case study for both output power level with THD %, reporting that the IAVM current waveforms include the lowest harmonic distortion for both power rates. It is depicted that at high power rate, the harmonic distortion is decreased dramatically for all the models, and THD evaluation is almost the same for the SEM and IAVM baselines. Therefore, the best performance of the proposed IAVM approach can be obtained for the applications with low and/or medium power demands.

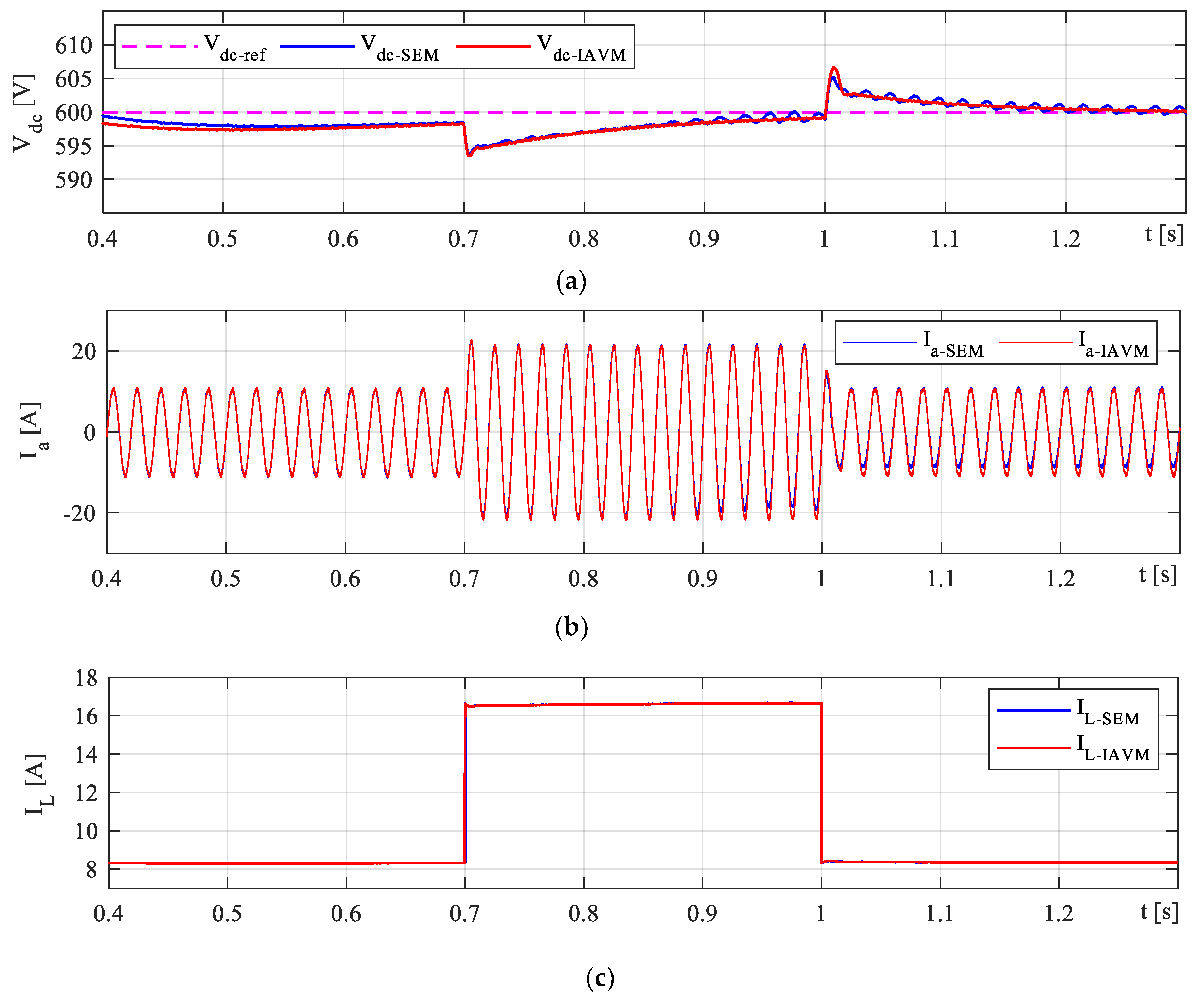
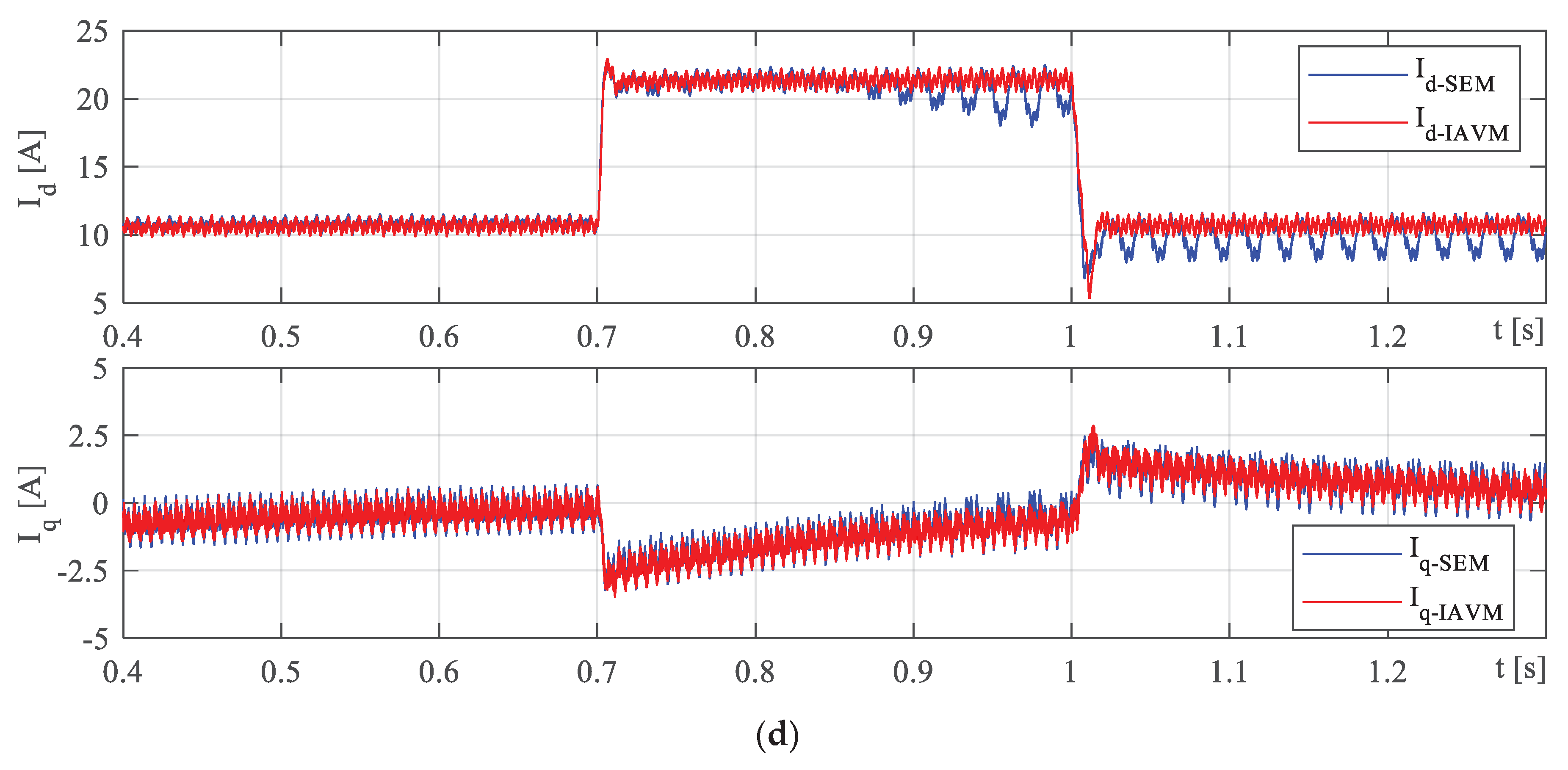
4.3. Case 3: Transient Performance

This study deals with performance comparisons between the physical SEM and time average model IAVM AFE rectifier during load changes and step transient conditions. Figure 9 shows the rectifier responses for the mentioned baselines during step changes in output resistive loads to ensure the proposed model smooth operation. From Figure 9a, for a fixed DC link voltage reference 600 V, it depicted that both baselines track the desired voltage, although the SEM contains some fluctuations than the IAVM. However, the main difference is illustrated by the controlled d-q axis currents, especially with d-axis current ripples as shown in Figure 9d. Those significant fluctuations in d-axis current for the SEM baseline causes more harmonic distortions as well as high switching losses.
Finally, to verify the unity PF, A-phase voltage and current are simulated for different load amounts using the IAVM baseline as shown in Figure 10. It is clear that both voltage and current waveforms are in perfect angle match which leads to proper PFC over low and high output powers.

5. Conclusions

This article presents a useful methodology to implement dynamic AVM of AFE rectifiers under VOC-based controllers. Unlike the SEM baselines, the use of AVM approaches can significantly decrease the computational burden (which is about 200 times faster than a SEM baseline) while maintaining the transient performance of these topologies. An enhanced AVM baseline is proposed by precisely considering the dead-time distortions and total voltage drops on switching devices during various operating circumstances. Based on the comparative studies, it has been illustrated that such an improved model includes less harmonic distortions and lower current ripples. One decent part of the proposed model is practical startup circuit which leads to the smoothest operation of AFE rectifier. In addition, it is depicted that the IAVM has low THD rate because of employing the enhanced duty cycle scheme by splitting the dead-time over a ripple current. It is obviously observed that in some cases the proposed IAVM resembles the actual SEM-based AFE rectifier which can be used in industries for the aim of software developing. Furthermore, the proposed model can be a viable device for the plug-in electric vehicle battery chargers due to its quick response and lower harmonics.

Acknowledgments

The author would like to thank Dr. Hamed Hashemi-Dezaki with the Optics11 company for his careful help during the simulations and also appreciate the kind clarifications of Mr. Petr Kadanik with the AMP X company around the project challenges.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Buticchi, G.; Lam, C.-S.; Xinbo, R.; Liserre, M.; Barater, D.; Benbouzid, M.; Gomis-Bellmunt, O.; Pamos-Paja, C.A.; Kumar, C.; Zhu, R. The role of renewable energy system in reshaping the electrical grid scenario. IEEE Open J. Ind. Electron. 2021, 2, 451–468. [Google Scholar] [CrossRef]
  2. Ebadpour, M. A Multiport Isolated DC-DC Converter for Plug-in Electric Vehicles Based on Combination of Photovoltaic Systems and Power Grid. In Proceedings of the 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran; 2021. [Google Scholar]
  3. Guerrero, J.M.; Blaabjerg, F.; Zhelev, T.; Hemmes, K.; Monmasson, E.; Jemei, S.; Comech, M.P.; Granadino, R.; Frau, J.I. Distributed generation: toward a new energy paradigm. IEEE Ind. Electron. Mag. 2010, 4, 52–64. [Google Scholar] [CrossRef]
  4. Esenboğa, B.; Demirdelen, T. Soft-Switching Smart Transformer Design and Application for Photovoltaic Integrated Smart City Power Distribution. Sustainability 2023, 15, 32. [Google Scholar] [CrossRef]
  5. Ebadpour, M.; Sharifian, M.B.B. Cascade H-Bridge Multilevel Inverter with Low Output Harmonics for Electric/Hybrid Electric Vehicle Applications. Int. Rev. Electr. Eng. (IREE) 2012, 7, 3248–3256. [Google Scholar]
  6. Planès, T.; Delbecq, S.; Pommier-Budinger, V.; Bénard, E. Modeling and Design Optimization of an Electric Environmental Control System for Commercial Passenger Aircraft. Aerospace 2023, 10, 260. [Google Scholar] [CrossRef]
  7. Alduraibi, A.; Yaghoobi, J.; Solatialkaran, D.; Zare, F. A Modular Power Converter With Active Front-End System to Mitigate Harmonics in Distribution Networks. IEEE Trans. Emerg. Sel. Topics Power Electron. 2021, 9, 1725–1735. [Google Scholar] [CrossRef]
  8. Sannino, A.; Bollen, M.H.J.; Svensson, J. Voltage tolerance testing of three-phase voltage source inverters. IEEE Trans. Power Deliv. 2005, 20, 1633–1639. [Google Scholar] [CrossRef]
  9. Gao, F.; Bozhko, S. Modeling and impedance analysis of a single DC bus-based multiple-source multiple-load electrical power system. IEEE Trans. Transp. Electrific. 2016, 2, 335–346. [Google Scholar] [CrossRef]
  10. Kim, Y.-W.; Sul, S.-K. Stability Analysis of Active Front End and Permanent Magnet Synchronous Generator with Back EMF-Based Sensorless Control for DC Marine Vessels. IEEE Trans. Power Electron. 2023, 38, 5411–5421. [Google Scholar] [CrossRef]
  11. Zhaksylyk, A.; Rasool, H.; Abramushkina, E.; Chakraborty, S.; Geury, T.; El Baghdadi, M.; Hegazy, O. Review of Active Front-End Rectifiers in EV DC Charging Applications. Batteries 2023, 9, 150. [Google Scholar] [CrossRef]
  12. Bagheri, N.; Alipour, H.; Mohammadian, L.; Beiza, J.; Ebadpour, M. A Multiport Isolated Resonant LLC Converter for Grid-Tied Renewable Energy Powered Bidirectional EV Charger. Int. J. Ind. Electron. Control. Optim. 2023, 6, 37–48. [Google Scholar]
  13. Prakash P, P.; Kalpana, R.; Singh, B.; Bhuvaneswari, G. Design and Implementation of Sensorless Voltage Control of Front-End Rectifier for Power Quality Improvement in Telecom System. IEEE Trans. Ind. Appl. 2018, 54, 2438–2448. [Google Scholar] [CrossRef]
  14. Gong, Z.; Wu, X.; Dai, P.; Zhu, R. Modulated Model Predictive Control for MMC-Based Active Front-End Rectifiers under Unbalanced Grid Conditions. IEEE Trans. Ind. Electron. 2018, 66, 2398–2409. [Google Scholar] [CrossRef]
  15. Zhang, Z.; Wei, L.; Yi, P.; Cui, Y.; Murthy, P.S.; Bazzi, A.M. Conducted Emissions Suppression of Active Front End (AFE) Drive Based on Random Switching Frequency PWM. IEEE Trans. Ind. APPL. 2020, 56, 6598–6607. [Google Scholar] [CrossRef]
  16. Zare, F.; Davari, P.; Blaabjerg, F. A Modular Active Front-End Rectifier With Electronic Phase Shifting for Harmonic Mitigation in Motor Drive Applications. IEEE Trans. Ind. Appl. 2017, 53, 5440–5450. [Google Scholar] [CrossRef]
  17. Malinowski, M.; Kazmierkowski, M.P.; Trzynadlowski, A.M. A comparative study of control techniques for PWM rectifiers in ac adjustable speed drives. IEEE Trans. Power Electron. 2003, 18, 1390–1396. [Google Scholar] [CrossRef]
  18. Malinowski, M.; Kazmierkowski, M.P.; Hansen, S.; Blaabjerg, F.; Marques, G. Virtual-flux-based direct power control of three-phase PWM rectifiers. IEEE Trans. Ind. Appl. 2001, 37, 1019–1027. [Google Scholar] [CrossRef]
  19. Cano, J.M.; Jatskevich, J.; Norniella, J.G.; Davoudi, A.; Wang, X.; Martinez, J.A.; Mehrizi-Sani, A.; Saeedifard, M.; Aliprantis, D.C. Dynamic Average-Value Modeling of Direct Power-Controlled Active Front-End Rectifiers. IEEE Trans. Power Deliv. 2014, 29, 2458–2466. [Google Scholar] [CrossRef]
  20. Gendrin, M.; Gauthier, J-Y.; Lin-Shi, X. A Predictive Hybrid Pulse-Width-Modulation Technique for Active-Front-End Rectifiers. IEEE Trans. Power Electron. 2017, 32, 5487–5496. [Google Scholar] [CrossRef]
  21. Song, Z.; Tian, Y.; Chen, W.; Zou, Z.; Chen, Z. Predictive Duty Cycle Control of Three-Phase Active-Front-End Rectifiers. IEEE Trans. Power Electron. 2016, 31, 698–710. [Google Scholar] [CrossRef]
  22. Hou, C-C. A Multicarrier PWM for Parallel Three-Phase Active Front-End Converters. IEEE Trans. Power Electron. 2013, 28, 2753–2759. [Google Scholar] [CrossRef]
  23. Wiechmann, E.P.; Burgos, R.P.; Holtz, J. Active Front-End Converter for Medium-Voltage Current-Source Drives Using Sequential-Sampling Synchronous Space-Vector Modulation. IEEE Trans. Ind. Electron. 2003, 50, 1275–1289. [Google Scholar] [CrossRef]
  24. Divakar, Dwivedi, P.; Bose, S.; Pandey, S. Comparative Analysis of PI Control with Anti-Windup Schemes for Front-end Rectifier. In Proceedings of the IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC), Nagpur, India, 2020.
  25. Cittanti, D.; Gregorio, M.; Bossotto, E.; Mandrile, F.; Bojoi, R. Full Digital Control and Multi-Loop Tuning of a Three-Level T-Type Rectifier for Electric Vehicle Ultra-Fast Battery Chargers. Electronics 2021, 10, 1453. [Google Scholar] [CrossRef]
  26. Chiniforoosh, S.; Jatskevich, J.; Yazdani, A.; Sood, V.; Dinavahi, V.; Martinez, J.; Ramirez, A. Definitions and applications of dynamic average models for the analysis of power systems. IEEE Trans. Power Deliv. 2010, 25, 2655–2669. [Google Scholar] [CrossRef]
  27. Yazdani, A.; Iravani, R. A unified dynamic model and control for the voltage-source converter under unbalanced grid conditions. IEEE Trans. Power Deliv. 2006, 21, 1620–1629. [Google Scholar] [CrossRef]
  28. Ebadpour, M.; Radmand, F. Hyper-plane sliding mode control of non-minimum phase grid-connected zeta converter. In Proceedings of the 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 2021.
  29. Nikkhajoei, H.; Iravani, R. Dynamic model and control of ac-dc-ac voltage-source converter system for distributed resources. IEEE Trans. Power Deliv. 2007, 22, 1169–1178. [Google Scholar] [CrossRef]
  30. Lau, W.H.; Zhou, B.; Chung, H.S.H. Compact analytical solutions for determining the spectral characteristics of multicarrier-based multi-level PWM. IEEE Trans. Circuits Syst. I, Reg. Papers. 2004, 51, 1577–1585. [Google Scholar] [CrossRef]
  31. Chierchie, F.; Stefanazzi, L.; Paolini, E.E.; Oliva, A.R. Frequency analysis of PWM inverters with dead-time for arbitrary modulating signals. IEEE Trans. Power Electron. 2014, 29, 2850–2860. [Google Scholar] [CrossRef]
  32. Ahmed, S.; Boroyevich, D.; Wang, F.; Burgos, R. Development of a new voltage source inverter (VSI) average model including low-frequency harmonics. In Proceedings of the 25th Annual IEEE Appl. Power Electron. Conf. Expo. (APEC), California, USA; 2010. [Google Scholar]
  33. Guha, A.; Narayanan, G. Average modeling of a voltage source inverter with dead-time in a synchronous reference frame. In Proceedings of the IEEE Innov. Smart Grid Technol.-Asia (ISGT Asia), Bangalore, India; 2013. [Google Scholar]
  34. Banerji, A.; Patil, A.; Patil, S.; Pakhare, A.; Ugale, R.T. Design, analysis and fast tuning of active front end rectifier controller with comparative performance evaluation. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India; 2022. [Google Scholar]
  35. Hou, C-C. ; Cheng, P-T. Experimental verification of the active front-end converters dynamic model and control designs. IEEE Trans. Power Electron. 2011, 26, 1112–1118. [Google Scholar] [CrossRef]
  36. Grandi, G.; Loncarski, J. Evaluation of current ripple amplitude in three-phase PWM voltage source inverters. In Proceedings of the International Conference-Workshop Compatibility and Power Electronics, Ljubljana, Slovenia; 2013. [Google Scholar]
  37. Ebadpour, M.; Jamshidi, M.; Talla, J.; Hashemi-Dezaki, H.; Peroutka, Z. Digital Twin Model of Electric Drives Empowered by EKF. Sensors 2023, 23, 2006. [Google Scholar] [CrossRef]
Preprints 93833 g001
Figure 1. AFE rectifier topology. (a) SEM configuration. (b) VOC scheme.
Figure 1. AFE rectifier topology. (a) SEM configuration. (b) VOC scheme.
Preprints 93833 g001
Preprints 93833 g002
Figure 2. Dynamic SAVM for the AFE rectifier with VOC. (a) overall rectifier configuration. (b) block diagram of the dynamic structure.
Figure 2. Dynamic SAVM for the AFE rectifier with VOC. (a) overall rectifier configuration. (b) block diagram of the dynamic structure.
Preprints 93833 g002
Preprints 93833 g003
Figure 3. The overall scheme of the proposed IAVM for AFE rectifiers.
Figure 3. The overall scheme of the proposed IAVM for AFE rectifiers.
Preprints 93833 g003
Preprints 93833 g004
Figure 4. Block diagram of the enhanced dead-time distortion model.
Figure 4. Block diagram of the enhanced dead-time distortion model.
Preprints 93833 g004
Preprints 93833 g005
Figure 5. AFE rectifier with control methodology for test verification.
Figure 5. AFE rectifier with control methodology for test verification.
Preprints 93833 g005
Preprints 93833 g006aPreprints 93833 g006b
Figure 6. AFE rectifier no-load startup waveforms for the SEM, SAVM, and IAVM based on the proposed startup procedure: (a) Rectifier DC link voltage; (b) AC-side currents; (c) D-q currents.
Figure 6. AFE rectifier no-load startup waveforms for the SEM, SAVM, and IAVM based on the proposed startup procedure: (a) Rectifier DC link voltage; (b) AC-side currents; (c) D-q currents.
Preprints 93833 g006aPreprints 93833 g006b
Preprints 93833 g007aPreprints 93833 g007b
Figure 7. No-load startup procedure waveforms for the IAVM baseline: (a) AC-side A-phase currents; (b) D-q currents.
Figure 7. No-load startup procedure waveforms for the IAVM baseline: (a) AC-side A-phase currents; (b) D-q currents.
Preprints 93833 g007aPreprints 93833 g007b
Preprints 93833 g008aPreprints 93833 g008b
Figure 8. Load responses of AFE rectifier for the SEM, SAVM, and IAVM baselines: (a) AC-side currents for 3.6 kW load; (b) AC-side currents for 7.2 kW load; (c) D-q currents during 3.6 kW load; (d) D-q currents during 7.2 kW load.
Figure 8. Load responses of AFE rectifier for the SEM, SAVM, and IAVM baselines: (a) AC-side currents for 3.6 kW load; (b) AC-side currents for 7.2 kW load; (c) D-q currents during 3.6 kW load; (d) D-q currents during 7.2 kW load.
Preprints 93833 g008aPreprints 93833 g008b
Preprints 93833 g009aPreprints 93833 g009b
Figure 9. AFE rectifier transient waveforms for the SEM, and IAVM based on the VOC technique: (a) Rectifier DC link voltage; (b) AC-side A-phase current; (c) Load current; (d) D-q currents.
Figure 9. AFE rectifier transient waveforms for the SEM, and IAVM based on the VOC technique: (a) Rectifier DC link voltage; (b) AC-side A-phase current; (c) Load current; (d) D-q currents.
Preprints 93833 g009aPreprints 93833 g009b
Preprints 93833 g010
Figure 10. PF studies for the AFE rectifier during transient operation for the proposed IAVM.
Figure 10. PF studies for the AFE rectifier during transient operation for the proposed IAVM.
Preprints 93833 g010
Table 1. Main parameters of the studied AFE rectifier.
Table 1. Main parameters of the studied AFE rectifier.
AFE parameters
IGBT Module Vdc [V] Vf (IGBT || D) [V] Cdc [mF] Tsw [s] td [s]
Fs400R07A1E3 600 1.5 4.7 1e-4 2e-6
Ac side parameters
Vgrid (L-L) [Vrms] Fs [Hz] Ls [mH] Cs [ μ F] Vout [V]
380 50 10 5 600
Controller gains
DC voltage controller Kp = 2.6 || Ki = 20.8
d-axis current controller Kp = 31.72 || Ki = 157.44
q-axis current controller Kp = 31.72 || Ki = 157.44
Table 2. Harmonic comparisons for the AFE rectifier models during the steady-state operation.
Table 2. Harmonic comparisons for the AFE rectifier models during the steady-state operation.
AFE Rectifier Model SEM SAVM IAVM
THD% for 3.6 kW load 5.14 4.96 4.78
THD% for 7.2 kW load 2.55 2.78 2.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated