Computing Offloading for Energy Conservation in UAV-Assisted Mobile Edge Computing

Preprint

Article

Computing Offloading for Energy Conservation in UAV-Assisted Mobile Edge Computing

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

19 December 2023

Posted:

20 December 2023

You are already at the latest version

Alerts

Abstract

The rapid growth of equipment tasks in 5G large-scale machine-type communication scenarios presents challenges due to user equipment’s (UE) limited computing power and power constraints. To address these limitations, task offloading to unmanned aerial vehicles (UAVs) has gained attention. However, traditional cloud computing centres far from the UE fail to meet latency requirements. Mobile Edge Computing (MEC) emerges as a solution by deploying computing servers at the edge of the cellular network to enhance service responsiveness. However, traditional MEC solutions need more flexibility. This paper explores the advantages of UAVs, including flexibility and rapid deployment, and considers UAV power constraints. It proposes a joint optimization approach for user offloading strategies and UAV trajectories to minimize the overall energy consumption of UE. By leveraging the benefits of UAVs and MEC, the proposed method aims to improve task execution efficiency in energy-constrained 5G machine-type communication scenarios.

Keywords:

Subject: Computer Science and Mathematics - Computer Networks and Communications

1. Introduction

This thesis addresses IoT end devices’ computing power and battery capacity limitations in the context of mobile edge computing (MEC) [1,2]. IoT devices and base stations are essential in disaster relief scenarios, where the need to build a network for personnel collection quickly arises. However, due to the complex nature of task calculations and the energy limitations of user equipment (UE) [3], tasks often need to be offloaded for computation. The traditional approach of uploading tasks to distant cloud computing centres fails to meet the stringent delay requirements. Therefore, this research investigates using Unmanned Aerial Vehicles (UAV) in MEC scenarios to overcome the challenges posed by remote areas with damaged infrastructure.

By leveraging the mobility of UAVs, the channel conditions of communication with UEs can be altered, thereby influencing the channel transmission rate [4]. The introduction of MEC brings the computing server closer to the edge, usually by adding a computing server at the base station of the cellular network. This significantly reduces the distance between the base station and UES, enhancing the responsiveness of the service. However, the traditional MEC solution needs more flexibility, prompting an exploration of the advantages of UAVs in recent years. UAVs exhibit flexible and rapid deployment capabilities, enabling them to adapt to diverse real-world situations [5].

Nonetheless, UAVs possess a limitation in the form of a limited battery-powered energy supply. To address this constraint, this research aims to jointly optimize the user unloading strategy and the trajectory of the UAV while considering energy constraints. The ultimate objective is to minimize UE’s energy consumption, ensuring efficient resource utilization in MEC scenarios. By developing and analyzing efficient task offloading techniques and UAV trajectory planning algorithms, this study seeks to enhance IoT networks’ overall performance and energy efficiency in disaster relief scenarios [6,7,8].

2. Related Work

Compared with the data processing model of traditional cloud computing, mobile edge computing offloads the computing tasks of user devices to edge servers close to the user for calculation, alleviating the computing pressure on the cloud centre and reducing the total system latency and energy consumption. However, in mobile edge computing scenarios, the task offloading strategy of user equipment determines the allocation relationship of tasks, which indirectly affects the latency and energy consumption of task calculations and ultimately affects the entire system’s performance. Furthermore, MEC needs to adapt to various scenarios, so it places specific requirements on the flexibility of edge servers. Drones have received widespread attention due to their high manoeuvrability and low deployment costs, and they can be used as edge computing servers. The following will introduce the current research status from the offloading strategy and drone-assisted MEC.

In the literature [9], for high-performance virtual reality video transmission scenarios, the autonomous perception capability in VR video transmission supported by MEC is focused on, and a computing offloading algorithm based on deep deterministic policy gradient is designed. The algorithm first models the optimization problem as a Markov decision-making problem, uses a deep Q network to solve the problem, and finally simulates a VR video transmission scenario to verify the effectiveness of the proposed algorithm. Literature [10] focuses on balancing the energy consumption and time delay of computing tasks. By deploying energy harvesting modules for edge servers, a non-convex optimization that minimizes the energy consumption of all terminal devices is proposed while satisfying the time delay constraints. Question. Based on this problem, the article presents an algorithm based on Lyapunov optimization using the long-term average energy consumption and discard rate of computing tasks as quantitative indicators. Finally, simulation experiments are conducted with algorithms such as all local calculations, all offloaded calculations, and random partial offloaded calculations. Comparative results show the superiority of the proposed algorithm. Literature [11] considers that end users can preprocess tasks before requesting computing offloading instead of offloading the computing tasks to edge servers for calculation immediately after generating them. This can reduce the time delay caused by task transmission. This article first defines personal utility, and then, to maximize benefits, a computational offloading game based on the queuing model is established to describe the strategic interaction between user devices.

UAVs have attracted attention due to their high mobility, and after extensive research, UAVs have been widely used in assisting wireless communication networks. Literature [12] considers drones’ limited computing power and energy and studies a multi-drone collaborative mobile edge computing system. By jointly optimizing the UAV’s flight trajectory, computing task offloading allocation, and communication resource allocation, task computing experiments and energy consumption are minimized. To solve the non-convex optimization problem proposed for this problem, a multi-agent cooperation deep reinforcement learning framework is proposed based on the double-delay deep deterministic policy gradient algorithm for high-dimensional continuous action space. Literature [13] considers the safety of the task and the energy consumption of UAVs and designs a UAV-assisted mobile edge computing system with an energy collection function. The system uses a full-duplex protocol to receive data, while the UAV Broadcast control signalling is intended to act as artificial interference. Literature [14] considers the entry and exit problems of user equipment in mobile edge computing scenarios and proposes a computing resource allocation model based on cooperative evolution to solve the problem of terminal equipment access across wireless networks. A multi-layer data stream processing system is also proposed to powerfully utilize the entire system’s computing. The top layer of the system contains the cloud centre, the middle layer includes the UAV-assisted MEC server, and the bottom layer contains the user equipment.

3. System Model and Problem Formulation

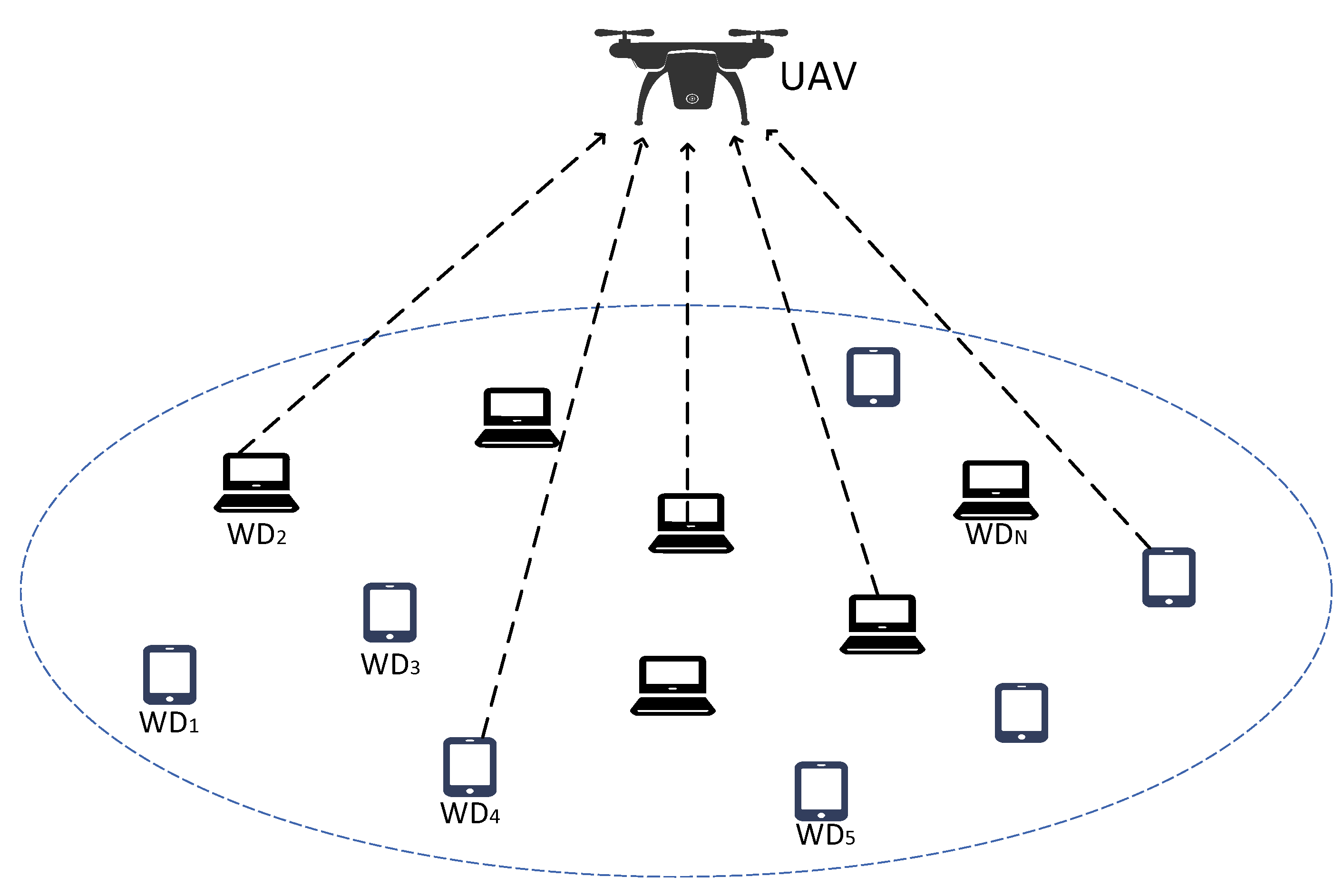
This paper studies the energy consumption optimization problem in a single UAV-assisted edge computing scenario. It minimizes the total energy consumption of UE by optimizing the trajectory of the UAV and the unloading ratio of UE. This paper considers a UAV-assisted mobile edge computing scenario, which consists of N UE and a UAV with computing capabilities, and each UE has a task to be calculated. The scene modelling is shown in Figure 1. The content of the research is to minimize the total energy consumption of UE by optimizing the trajectory of the UAV and the unloading ratio of the terminal equipment [15].

The calculation task of the nth UE can be expressed as the following form.

D_{n} = 〈S_{n}, C_{n}, T_{n}〉, n \in N

(1)

Among them,

S_{n}

represents the size of the task to be calculated, and the unit is bit;

C_{n}

represents the number of CPU cycles required to calculate each bit of data, and

T_{n}

represents the tolerable delay.

All tasks are completed within time T.

T = max \{T_{1}, T_{2}, . . ., T_{N}\}

(2)

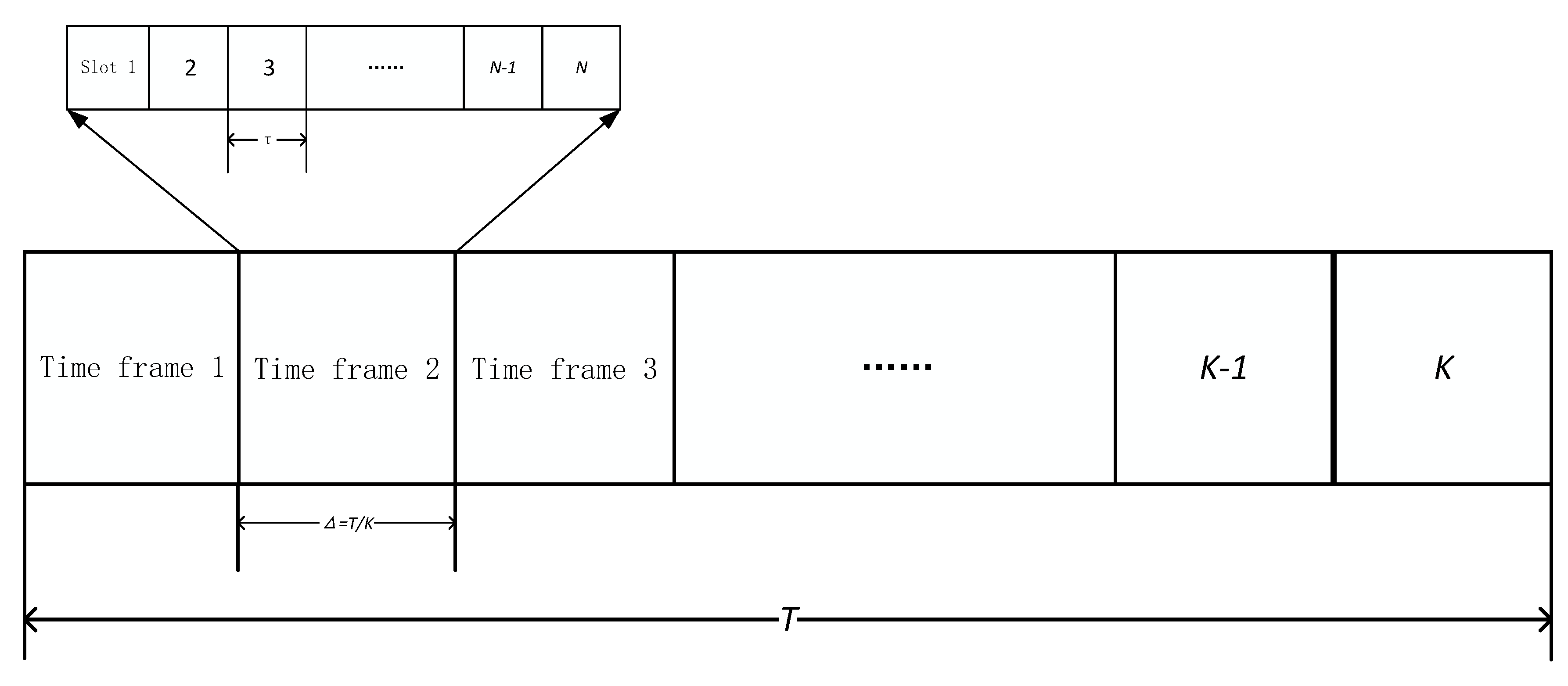
Divide the duration T into K time frames with a duration of

Δ

Δ = T / K

(3)

Figure 2 shows the time frame division. Since the duration

Δ

of each frame is small enough, the position of the UAV can be approximately regarded as unchanged within one frame, and the change of the position of the UAV within the entire duration T is its trajectory.

Assuming that the UAV is flying at a fixed height, H, the position at the kth time frame, is expressed as follows.

w_{u} (k) = (x_{u} (k), y_{u} (k), H)

(4)

The position of UE is fixed and does not change with the change in the time frame. In reality, it corresponds to the IoT device in the IoT scenario. The position of the nth UE is expressed as follows.

w_{n} = (x_{n}, y_{u}, 0)

(5)

3.1. Communication Model

The communication method between WD and UAV adopts TDMA. The time frame

δ

is divided into N time slots according to the number of UE. Figure 2 shows the time slot division diagram. Only one UE can maintain communication with the UAV in each time slot. The maximum time that a WD can communicate within a time frame is expressed as follows:

τ = \frac{τ}{N} = \frac{T}{K N}

(6)

Assuming that the wireless channel between the UAV and the UE is a line-of-sight channel, then the channel gain between the nth UE and the UAV can be expressed as:

h_{n} (k) = \frac{β_{0}}{{(x_{n} (k) - x_{n})}^{2} + {(y_{n} (k) - y_{n})}^{2} + H^{2}}

(7)

Among them,

β_{0}

represents the channel gain at a reference distance of 1m.

When

U E_{n}

offloads computing tasks to UAVs, the uplink data transmission rate can be calculated by the formula 8.

R_{n} (k) = B {log}_{2} (1 + \frac{h_{n} (k) p_{n}^{o f f}}{σ^{2}})

(8)

Where B is the channel bandwidth,

σ^{2}

is the noise power, and

p_{n}^{o f f}

represents the power of

{UE}_{n}

during the transmission task. Changes in the transmission rate

R_{n}

due to changes in position between the UAV and the WD. When using the TDMA communication method, one WD can monopolize the entire bandwidth for communication in one time slot.

At the same time, considering that the communication between the UAV and the UE may be interrupted when the link capacity cannot meet the required user rate, the UE cannot upload the computing task. The following equation represents the break condition:

I_{n} (k) = \{\begin{matrix} 0, R_{n} (k) < R_{n, t h r e s h o l d} \\ 1, R_{n} (k) > R_{n, t h r e s h o l d} \end{matrix}\}

(9)

Among them,

R_{n, t h r e s h o l d}

represents the minimum data transmission rate required for

{WD}_{n}

to communicate with the UAV.When the minimum transmission rate that the actual channel conditions can provide is less than this value, the communication between the terminal device and the UAV will be interrupted.

The occurrence of interruption conditions can ensure that devices that are far away from the UAV cannot be served, and it is closer to the actual scene, so that the UAV can ensure that all devices in the environment can be served by changing its position.

3.2. Local Computational model

A WD has a task to be computed. There are two options for how WD calculates tasks: local calculation and offloaded calculation.Two choices can be made at the same time, that is, within a time frame, a part of the computing tasks can be selected to be calculated locally, and a part of the computing tasks can be selected to be offloaded to the UAV for calculation. The following formula can express the calculation decision for the kth time frame:

a_{n} (k) = 〈a_{n, l o c} (k), a_{n, U A V} (k)〉

(10)

Among them,

a_{n, l o c} (k)

represents the amount of task data that

{WD}_{n}

chooses to calculate locally in the kth time frame, and

a_{n, U A V} (k)

represents the amount of task data that is offloaded.

According to the calculation amount

a_{n, l o c} (k)

of a time frame task and the calculation frequency

f_{n}

of WD, the local calculation time of a time slot can be obtained:

t_{n}^{l o c} (k) = \frac{a_{n, l o c} (k) C_{n}}{f_{n}}

(11)

Then you can get the energy consumed by the local calculation:

E_{n}^{l o c} (k) = p_{n}^{l o c} t_{n}^{l o c} = \frac{p_{n}^{l o c} a_{n, l o c} (k) C_{n}}{f_{n}}

(12)

Among them,

p_{n}^{l o c}

represents the power of the WD numbered n when calculating the task.Among them,

p_{n}^{l o c}

and

f_{n}

are fixed for a WD, so the variable to be optimized is the unloading decision variable

a_{n, l o c} (k)

3.3. Offloading Computational model

f_{U A V}

indicates the CPU calculation frequency of UAV.

a_{n, U A V} (k)

is the amount of tasks offloaded. The offloading calculation is divided into three steps:

1) WD uploads the calculation task to UAV;

2) UAV calculates the task;

3) UAV returns the task calculation result to WD.

According to the transmission rate

R_{n} (k)

obtained in the communication model, the transmission delay can be obtained as follows:

t_{n}^{o f f} (k) = \frac{a_{n, U A V} (k)}{R_{n} (k)}

(13)

Then the energy consumption of the WD transmission task can be obtained:

E_{n}^{o f f} (k) = p_{n}^{o f f} t_{n}^{o f f} (k)

(14)

According to the CPU calculation frequency

f_{U A V}

of UAV, the time consumption of offloading calculation can be obtained:

t_{n}^{c a l} (k) = \frac{a_{n, U A V} (k) C_{n}}{f_{U A V}}

(15)

In turn, the energy consumed by the UAV computing task can be obtained:

E_{n}^{c a l} (k) = p_{U A V}^{c a l} t_{n}^{c a l} (k)

(16)

Usually, the calculation result data volume of the task is small, and the transmission delay is negligible compared with the other two steps. Combining the above three steps, the delay of WD in a time frame can be obtained as follows:

t_{n}^{u a v} (k) = t_{n}^{o f f} (k) + t_{n}^{c a l} (k)

(17)

3.4. Problem Formulation

The research content of this paper is to minimize the calculation energy consumption sum of all WDs by jointly optimizing the unloading decision of WD and the trajectory of UAV and considering the constraints such as the time delay of calculation tasks and the energy consumption of UAVs.Therefore, the optimization problem can be expressed as:

\begin{matrix} min_{a_{n} (k), w_{u} (k)} & \sum_{k = 1}^{K} \sum_{n = 1}^{N} (E_{n}^{l o c} (k) + E_{n}^{o f f} (k)) \end{matrix}

(18a)

\begin{matrix} s . t . & C 1 : \sum_{k = 1}^{T_{n} / Δ} (a_{n, l o c} (k) + a_{n, uav} (k)) = S_{n} \end{matrix}

(18b)

\begin{matrix} C 2 : E_{f l y}^{uav} + \sum_{k = 1}^{K} \sum_{n = 1}^{N} E_{n}^{c a l} (k) \leq E \end{matrix}

(18c)

\begin{matrix} C 3 : t_{n}^{u a v} (k) + t_{n}^{o f f} (k) \leq τ, n \in N, k \in K \end{matrix}

(18d)

\begin{matrix} C 4 : a_{n, u a v} (k) = 0 | I_{n} (k) = 0, \forall n, k \end{matrix}

(18e)

\begin{matrix} C 5 : w_{u} (0) = w_{u, S}, w_{u} (K) = w_{u, E} \end{matrix}

(18f)

\begin{matrix} C 6 : \frac{||w_{u} (k + 1) - w_{u} (k)||}{Δ} \leq V_{m a x}, k \in K \end{matrix}

(18g)

\begin{matrix} C 7 : a_{n, l o c} (k) \geq 0, a_{n, u a v} (k) \geq 0, n \in N, k \in K \end{matrix}

(18h)

Among them, E represents the energy the UAV can provide, and F represents the computing frequency that the UAV can provide. The C1 constraint represents the delay constraint of the computing task; the C2 constraint represents the energy consumption constraint of the UAV; the C3 constraint represents that When WD chooses calculation offloading, the task calculation time in a time slot should not exceed the length of the time slot; C4 constraint indicates that an interruption will occur when the communication condition between the UE and the UAV does not meet the minimum sending rate; C5 constraint represents the take-off position and landing position of the UAV; C6 constraint represents the flight speed constraint of the UAV, and

V_{m a x}

represents the maximum flight speed of the UAV. C7 constraint indicates that the task volume of the offloading decision must be greater than zero.

4. IOECA Algorithm Based on DDPG

4.1. Markov Process Modeling

If you want to use reinforcement learning to solve optimization problems, you need to express the optimization problem as a Markov decision process[16,17].

4.1.1. State Space

Corresponding to the Markov decision process, in the scenario studied in this paper, the state of each time frame only depends on the state of the previous time frame.The state space represents all possible states of a time frame, jointly determined by The UAV and N UEs. At the kth time frame, the state space of the system is defined as follows:

s_{k} = (E_{u a v} (k), w_{u} (k), Q_{1} (i), . . ., Q_{n} (i), I_{1} (i), . . ., I_{n} (i), R_{1} (i), . . ., R_{n} (i))

(19)

Among them,

E_{u a v} (k)

represents the remaining power of the UAV,

w_{u} (k)

the position of the UAV, and

Q_{n} (k)

represents the remaining waiting time of the UE numbered n in the kth time frame Calculate the size of the task,

I_{n} (k)

represents the situation where the communication between the UAV and the UE is interrupted, and

R_{n} (k)

represents the data transmission rate of the channel environment of different UEs.

4.1.2. Action Space

Action refers to the need to do some actions from a certain state and then change to the next state, then the action space refers to all the actions that can be selected.

The scenario studied in this paper is to minimize energy consumption by jointly optimizing the trajectory of the UAV and the task offloading strategy, so the agents that can take action are the UAV and the UE. Based on the current state of the system, the action space of the agent at the kth time frame can be expressed as follows:

A_{k} = (β_{u a v} (k), v_{u a v} (k), a_{1} (k), . . ., a_{n} (k))

(20)

Among them, where

β_{u a v} (k)

represents the flight angle of the UAV,

v_{u a v} (k)

represents the flight speed of the UAV, and

a_{n} (k)

represents the unloading decision of the UE.

4.2. Algorithm

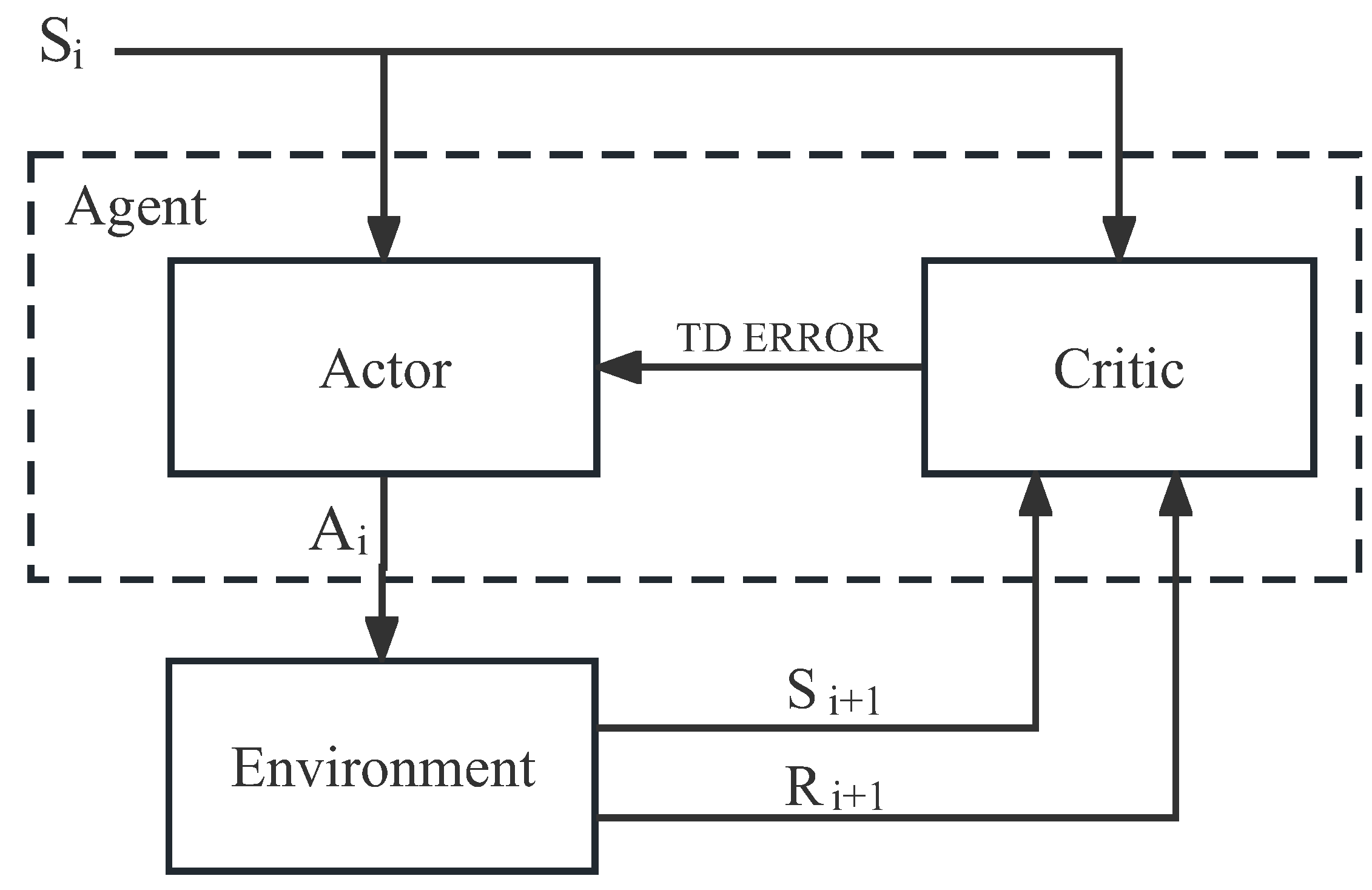
Deep Deterministic Policy Gradient (DDPG) is a deep reinforcement learning algorithm capable of outputting a continuous action space, consisting of two neural networks, Actor and Critic [18,19]. The Actor chooses behaviour according to a certain probability, and then Critic scores the behaviour made by the Actor, and finally, Actor chooses the highest-scoring behaviour output according to Critic’s score. The network structure is shown in Figure 3.

DDPG outputs a continuous action, so it is suitable for scenarios where variables are continuously optimized. The Actor network uses a strategy function to input the current statu

S_{i}

to obtain a probability distribution.Usually, Gaussian distribution and other methods are used to ensure that the output is an effective probability distribution, and then the appropriate action

A_{i}

is selected according to the probability, and the next state is obtained through the feedback of the environment. Critic uses the value function to input the current state

S_{i}

and the next state

S_{i + 1}

, and two values can be obtained through the value function of Critic. The parameters of the Actor and Critic network are updated by the difference TD ERROR. When updating the Actor network, the method of policy gradient is usually used for updating, such as DDPG.

DDPG is also a single-step update strategy network Figure 3. Compared with the round update strategy network, it is more suitable for the problem model proposed in this chapter. Based on the defined state space and action space, this paper designs a DDPG-based iterative optimization of energy consumption algorithm. The detailed steps of IOECA are shown in Algorithm 1.

Algorithm 1: Iterative Optimizing Energy Consumption Algorithm Based on DDPG

Input:: Number of iterations, Number of UEs, Task size
Output:: UE offload decision, UAV trajectory, UE energy consumption
1:: Initialize the environment
2:: Initialize Actor and Critic network in DDPG
3:: for $i = 1, 2, . . ., E p i s o d e$ do
4:: Initialize environment parameters
5:: for $j = 1, 2, . . ., S t e p$ do
6:: Acording to $s_{i}$ , obtain $a_{i}$ through DDPG
7:: Put $a_{i}$ into the environment, get $r_{i}$ and $s_{i + 1}$
8:: Store ( $a_{i}$ , $r_{i}$ , $s_{i}$ , $s_{i + 1}$ ) in the memory bank
9:: Update the current state to $s_{i + 1}$
10:: if $j = S t e p$ or is Finished then
11:: Record result
12:: break
13:: end if
14:: end for
: Update parameters of the Actor and Critic networks
15:: end for
16:: Return convergence result

4.3. Reward Function

The behavior of the agent is based on rewards, and designing an appropriate reward function plays a crucial role in problem convergence. The goal of reinforcement learning is to maximize the return, and the goal of this article is to minimize the return.

In IOECA, the environment must generate the next state

s_{(} i + 1)

and

r_{i}

according to the input action

a_{i}

. In this process,

r_{i}

is obtained through the reward function. The purpose of designing the reward function is to speed up the convergence speed of the algorithm. The reward function in this paper is designed as follows:

r_{k} = - (a \times n o r m a l (T a s k) + b \times n o r m a l (E))

(21)

The reward function is a weighted sum normalized by the number of computing tasks and energy consumption. Dynamically change the weight value to change the focus of each stage in the task execution process. The early stage of the algorithm focuses on completing the task, and the later stage of the algorithm pays more attention to the energy consumption of execution. Therefore, with the calculation of the task, the weight value of the energy consumption part increases, and the task weight value of the quantity part decreases accordingly. The following constraints need to be satisfied:

a + b = 1

(22)

The purpose of designing the weighted sum of two parts is that if only the first part of the energy is considered, the unloading ratio will be too low due to excessive pursuit of low energy consumption, making the task unable to be completed within the specified time. Therefore, consider adding the second part of the energy to balance the too-low. In the case of the unloading ratio, only when the unloading ratio is as high as possible within the constraints can a higher reward be obtained. At the same time, the value of the weight factor can be controlled so that the algorithm can achieve a faster convergence speed.

When DDPG trains the actor network and critical network, the input parameters of each layer will change as the output parameters of the previous layer change. Since the physical meaning of each parameter value is different, for example, the power of the drone can reach 2000J, and the location range of the drone is only 300m in space, each parameter needs to be normalized. The normalization algorithm is shown in Algorithm 2.

Algorithm 2: State Normalization Algorithm

Input:: $E_{u a v} (k), w_{u} (k), Q_{n} (i)$
Output:: $E_{u a v}^{'} (k), w_{u}^{'} (k), Q_{n}^{'} (i)$
1:: $E_{u a v}^{'} (k) = E_{u a v} (k) / E_{m a x}$
2:: $x_{u}^{'} (k) = x_{u} (k) / x_{m a x}$
3:: $y_{u}^{'} (k) = y_{u} (k) / y_{m a x}$
4:: $Q_{n}^{'} (i) = Q_{n} (i) / Q_{m a x}$
5:: Return $E_{u a v}^{'} (k), w_{u}^{'} (k), Q_{n}^{'} (i)$

5. Performance Evaluation

5.1. Parameter Settings

The simulation area is a square area of 100m×100m, the flying height of the UAV is kept at 100m, the maximum flying speed of the UAV is 8m/s. The experimental scene consists of a UAV and N UEs. The starting and ending positions of the UAV are located in the centre of the area. Each UE randomly generates a computing task with a size between 10M and 30M. The communication between the UE and the UAV is a line-of-sight channel. Table 1 shows the relevant parameters of the simulation.

5.2. Numerical Results

In this section, the proposed algorithm is simulated. The algorithm’s performance is mainly analyzed from four aspects: algorithm convergence, performance of the algorithm with the growth of the task size, performance of the algorithm with the growth of the number of terminal devices, and optimization of the algorithm for UAV trajectory Analysis of results. Among them, the analysis of the algorithm performance in the first three aspects introduces the algorithms in three other papers for comparison, and the algorithms are introduced as follows:

1) LocalOnly algorithm: The tasks of the UE are all calculated locally, and the tasks are no longer offloaded to the UAV;

2) DQN-based optimization algorithm [20]: using the algorithm DQN based on discrete action space, when the agent selects an action, the action is divided into equivalent intervals within the range of optional intervals [21].

3) Two-step iterative optimization algorithm(TIOA) based on block coordinate descent: the optimization problem of one iteration is divided into two steps to solve; the first step assumes that the UAV trajectory is fixed and optimizes to obtain the unloading ratio of the lowest energy consumption; the second part is obtained according to the first step The unloading ratio is optimized to obtain the UAV trajectory with the lowest energy consumption.

5.2.1. Algorithm Convergence Analysis

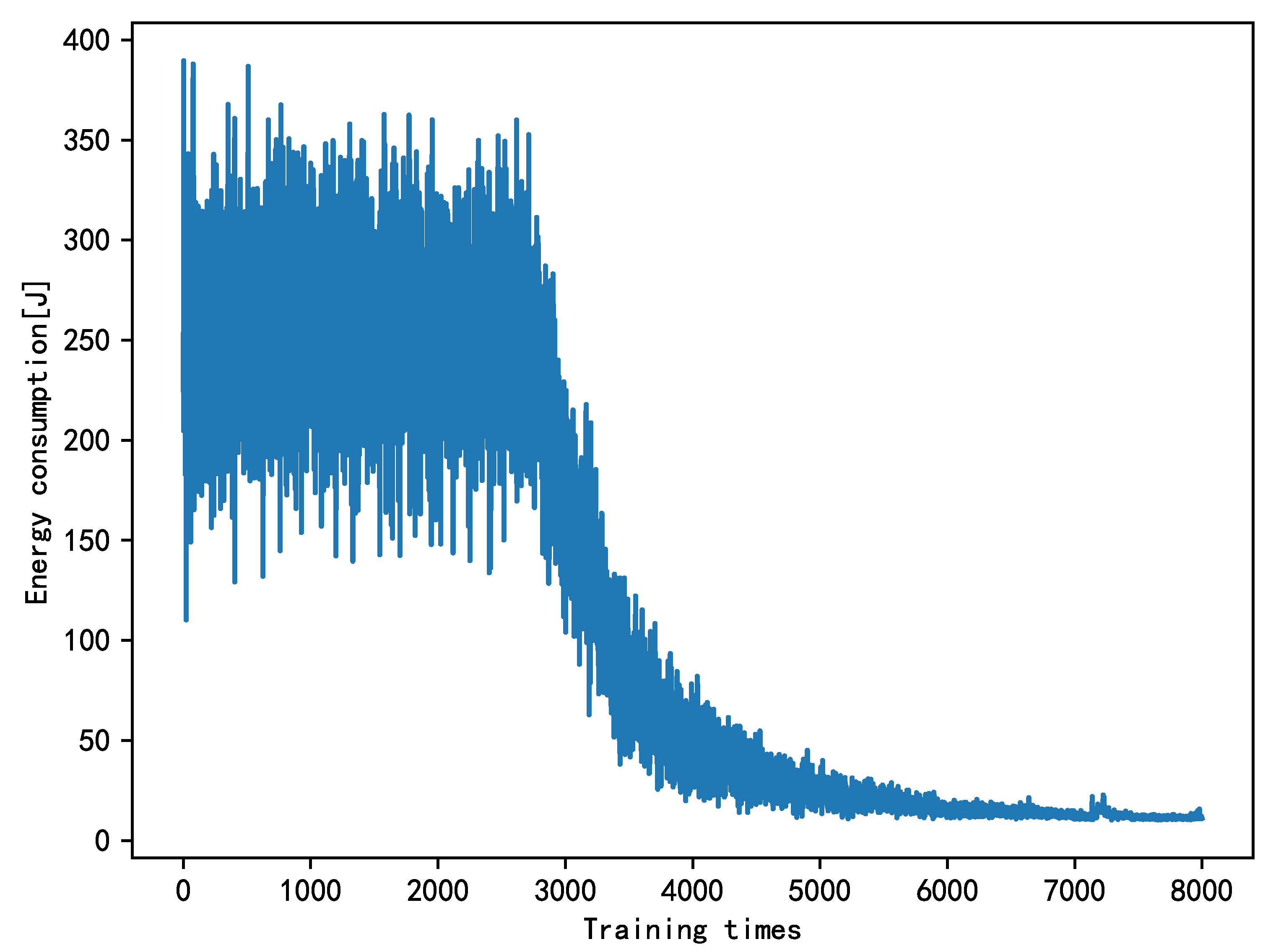
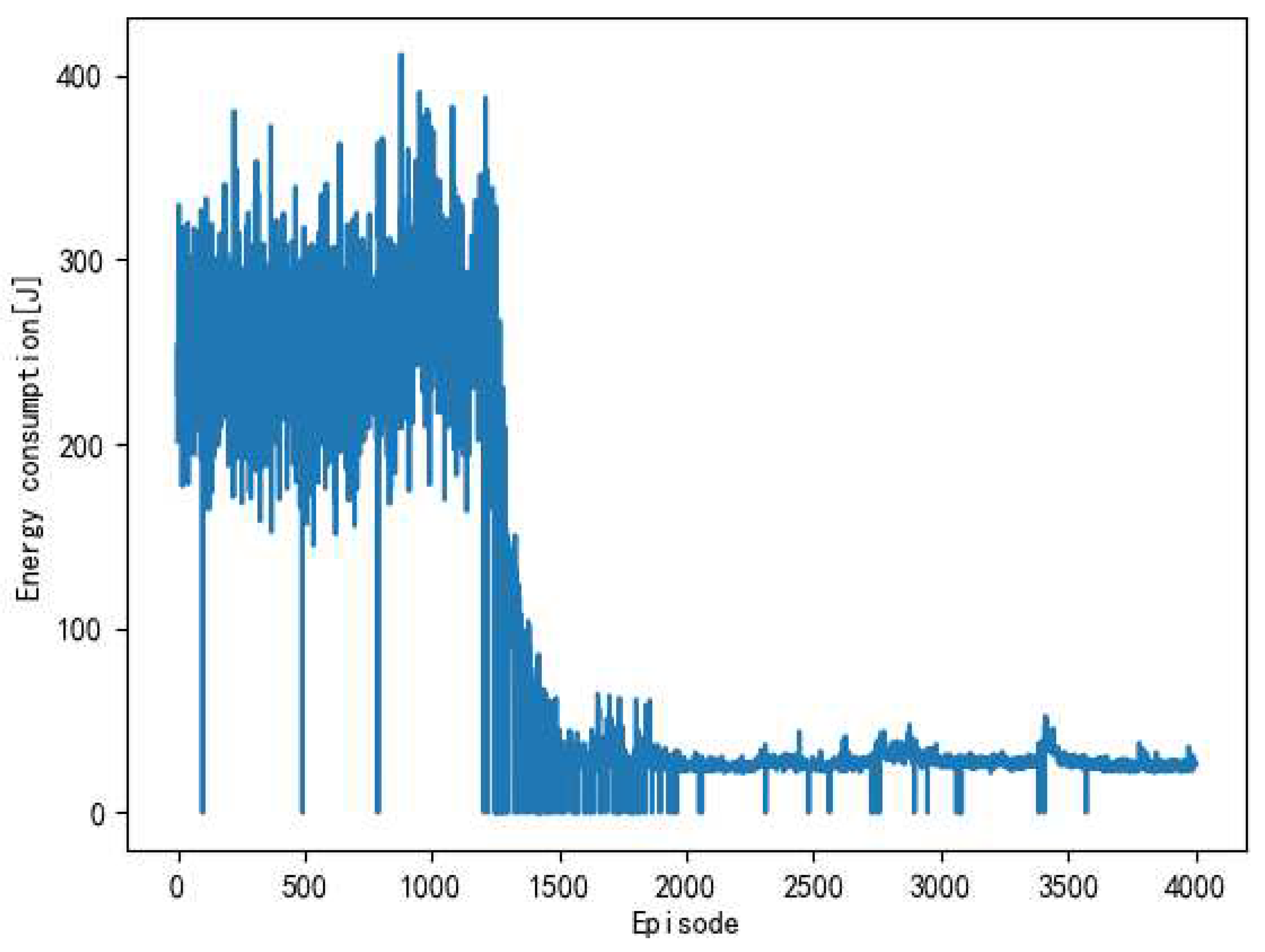
As seen from Figure 4, 3000 times belonged to the exploration period of the algorithm. At this time, the data was stored in the memory bank. After 3000 iterations, the model starts training, and as the number of iterations increases, the energy consumption begins to decrease, and the algorithm converges after about 6000 iterations.

In Figure 5, the total energy consumption of some rounds in DQN is 0, which means that the calculation of tasks in the system has not been completed in this round, and there is a protrusion in the convergence graph of DQN, and is At the end of the exploration period, it should be that the direction of exploration at the beginning is opposite to the optimal solution, and the feedback of rewards will continue to approach the optimal solution until it converges to obtain the lowest total energy consumption. At the same time, it can be seen that the action space of DQN is discrete, so The process of convergence is more tortuous.

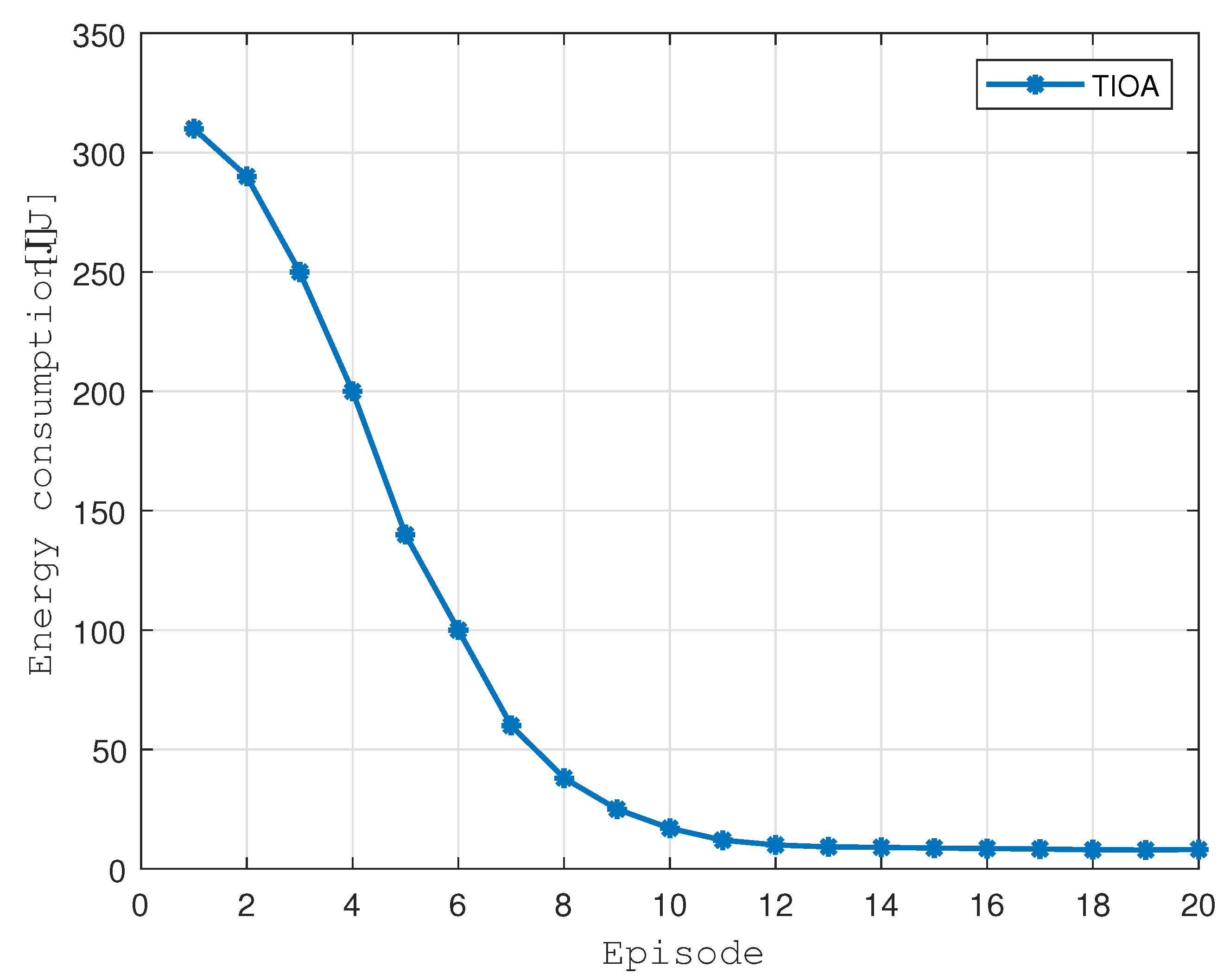
Figure 6 shows the convergence process of the two-step iterative optimization algorithm. The termination condition of the algorithm is that the difference between the total energy consumption of the terminal equipment between the two iterations is less than a given threshold

ε

, and the algorithm has gone through 15 times Convergence is achieved by iterating left and right. In the first 8 iterations, the energy consumption of the terminal decreases rapidly. Therefore, it is concluded that the algorithm is characterized by a fast convergence speed, but the disadvantage is that this method belongs to the traditional optimization method, and it converges when the number of terminal devices is large. Performance will drop dramatically.

5.2.2. UE Quantity Analysis

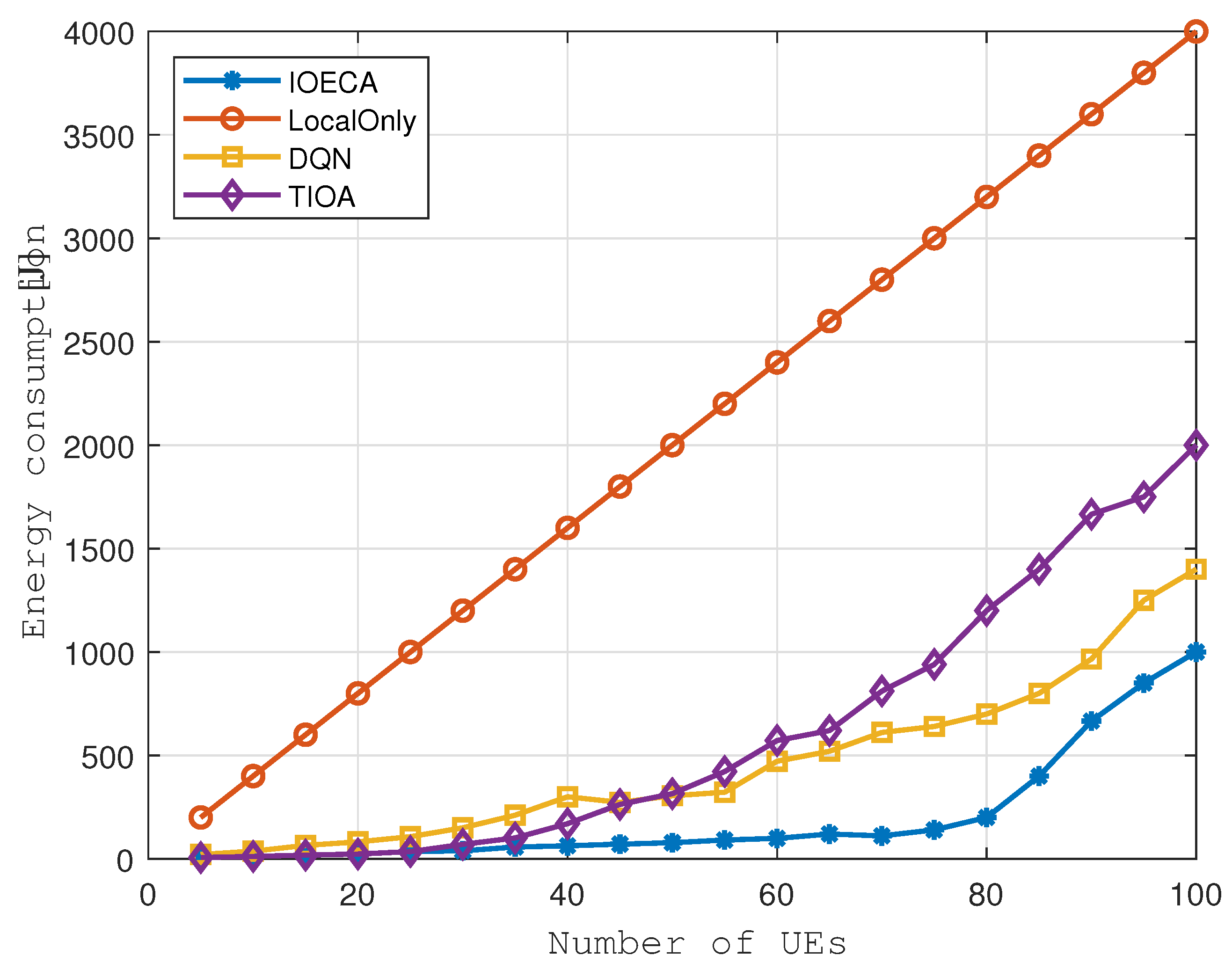
It can be seen from Figure 7 that as the number of UE increases, the total energy consumption of UEs in the system continues to increase. When the number of interruptions reaches about 80, the carrying capacity of the UAV reaches the limit. If the number of devices is increased, the newly added tasks can only be calculated locally, and the growth rate of the total energy consumption of the UE is also accelerated. Since DQN can only output discrete actions, there is a specific error in the total energy consumption calculation value, resulting in large fluctuations in the curve. The TIOA algorithm can maintain high performance when the number of UE is small. As the number increases, the massive amount of calculations generated makes it difficult for the algorithm to converge.

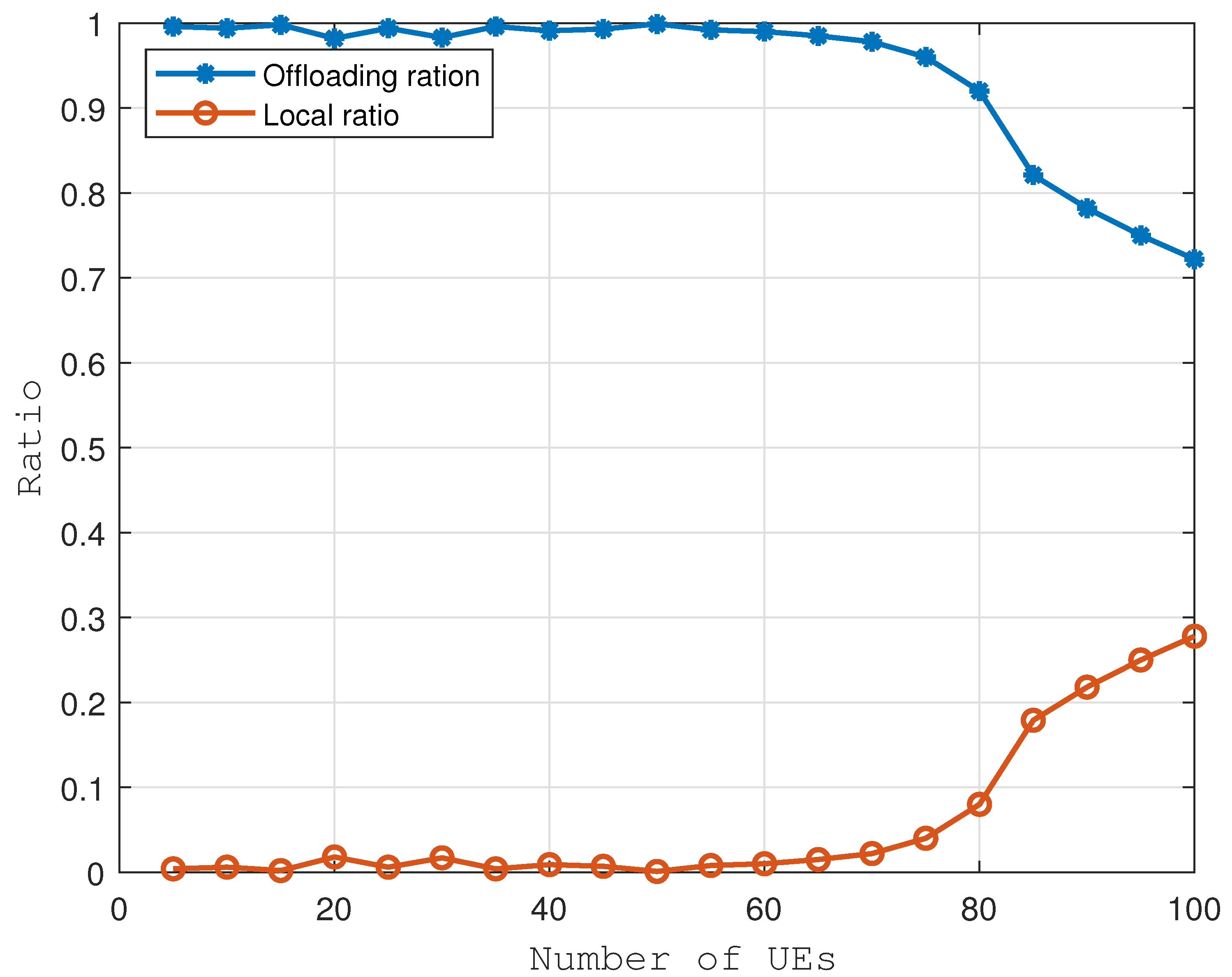
It can be seen from Figure 8 that when the number of UEs is small, the proportion of task offloading is high. When the number of UEs reaches 80, the tasks uploaded by UEs reach the computing bottleneck of the UAV, so the proportion of task offloading begins to decrease.

5.2.3. Task Size Analysis

Figure 9 is a simulation result in a scenario where the number of UEs is 10. Increase the task size of the UE. With the increase of the total task volume, when the computing bottleneck of the UAV is exceeded, the energy consumption of the UAV begins to increase. The performance of the TIOA algorithm is the best because the number of UEs is small and the amount of calculation is not large, and the traditional optimization algorithm can achieve faster convergence speed. The IOECA algorithm has a similar performance to the TIOA algorithm. Since DQN can only output discrete actions, it cannot cover the continuous action space, so it cannot reach the optimal solution. The LocalOnly algorithm does not utilize UAV computing resources, so the total energy consumption is much higher than other algorithms.

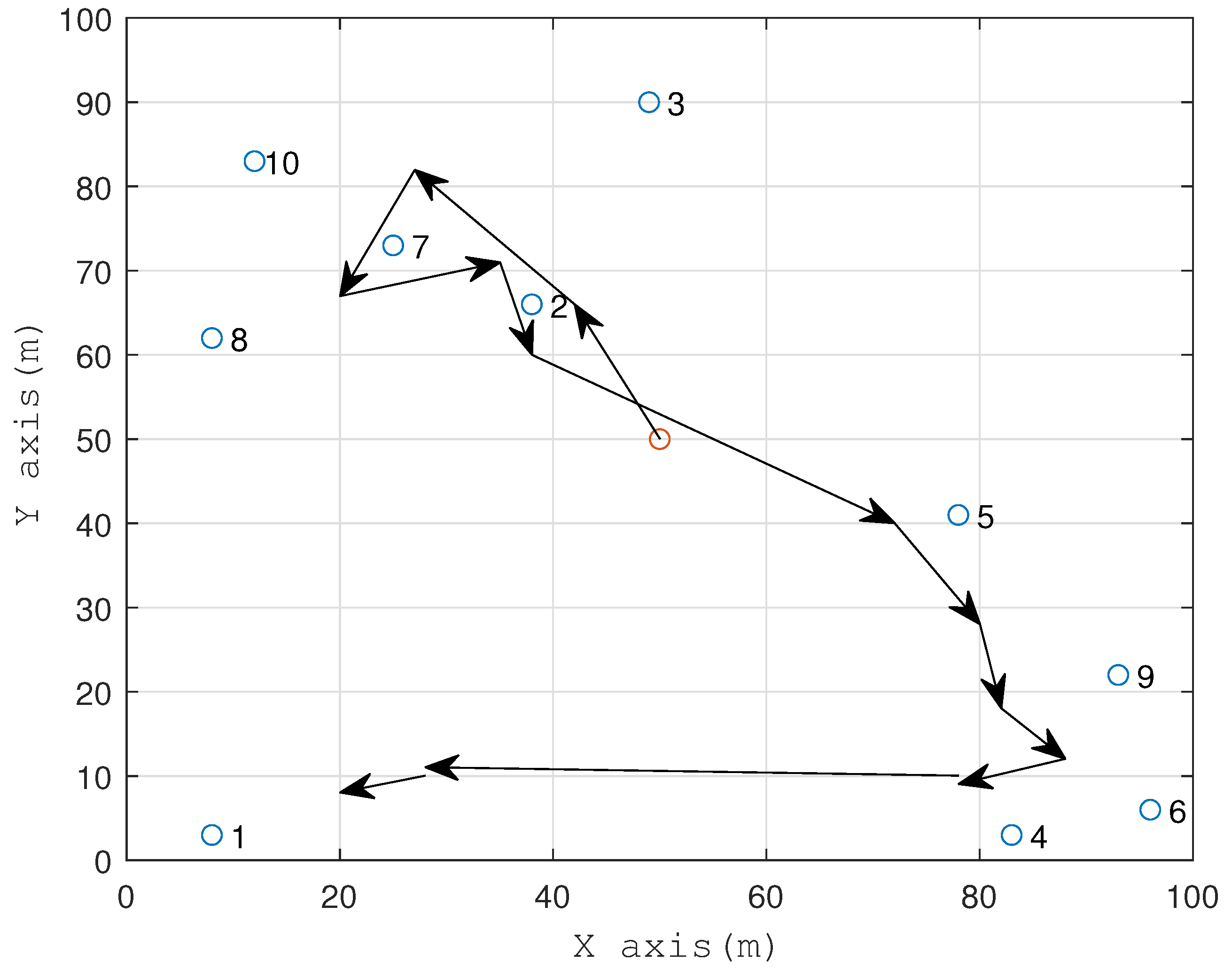
5.2.4. UAV Trajectory Analysis

The maximum flight speed of the UAV is 8m/s. It can be seen from the simulation results in Figure 10 that the UAV first flies to the place where UEs are densely populated to perform task calculations. It can also be seen from the sequence of UE task completion that the UE in the upper right corner completes the task calculation first, and then the UAV Fly to the next task-intensive area for task offloading calculations. The UAV affects the data transmission rate by changing its position with the UE, so it will constantly change its position between time frames to get closer to the UE [22].

6. Conclusions

This chapter studies the task offloading problem in single UAV-assisted mobile edge computing. Each UE has a computing task, and the UAV is responsible for providing computing services for the UE. The research goal of this chapter is to minimize the total energy consumption of UE by optimizing the unloading ratio of UE tasks and the flight trajectory of UAVs. Through problem modelling, a nonlinear programming problem is obtained, the IOECA algorithm is designed based on the DDPG algorithm, and the optimal solution can be obtained by convergence through multiple iterations. At the same time, a normalization algorithm is proposed in the iterative process to speed up the algorithm’s convergence. Finally, the proposed IOECA algorithm is compared with other algorithms, and the simulation proves that the proposed algorithm has better performance.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided.

Funding

This research was funded by NAME OF FUNDER grant number XXX.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are avaliable on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

Siriwardhana, Y.; Porambage, P.; Liyanage, M.; Ylianttila, M. A Survey on Mobile Augmented Reality With 5G Mobile Edge Computing: Architectures, Applications, and Technical Aspects. IEEE Communications Surveys & Tutorials 2021, 23, 1160–1192. [Google Scholar] [CrossRef]
Sharma, A.; Diwaker, C.; Nadiyan, M. Analysis of Offloading Computation in Mobile Edge Computing (MEC): A Survey. 2022 Seventh International Conference on Parallel, Distributed and Grid Computing (PDGC), 2022, pp. 280–285. [CrossRef]
Li, M.; Cheng, N.; Gao, J.; Wang, Y.; Zhao, L.; Shen, X. Energy-Efficient UAV-Assisted Mobile Edge Computing: Resource Allocation and Trajectory Optimization. IEEE Transactions on Vehicular Technology 2020, 69, 3424–3438. [Google Scholar] [CrossRef]
Nie, J.; Mu, J.; Zhou, Q.; Jing, X. Offloading Strategy for UAV-Assisted Mobile Edge Computing with Computation Rate Maximization. 2023 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), 2023, pp. 1–6. [CrossRef]
Zhang, T.; Xu, Y.; Loo, J.; Yang, D.; Xiao, L. Joint Computation and Communication Design for UAV-Assisted Mobile Edge Computing in IoT. IEEE Transactions on Industrial Informatics 2020, 16, 5505–5516. [Google Scholar] [CrossRef]
Chen, Y.; Zhang, N.; Zhang, Y.; Chen, X.; Wu, W.; Shen, X. Energy Efficient Dynamic Offloading in Mobile Edge Computing for Internet of Things. IEEE Transactions on Cloud Computing 2021, 9, 1050–1060. [Google Scholar] [CrossRef]
Xu, C.; Zhan, C.; Liao, J.; Gong, J. Computation Throughput Maximization for UAV-Enabled MEC with Binary Computation Offloading. ICC 2022 - IEEE International Conference on Communications, 2022, pp. 4348–4353. [CrossRef]
Chen, Z.; Lei, L.; Song, X. Multi-agent DDPG Enpowered UAV Trajectory Optimization for Computation Task Offloading. 2022 IEEE 22nd International Conference on Communication Technology (ICCT), 2022, pp. 608–612. [CrossRef]
Xu, X.; Song, Y. A Deep Reinforcement Learning-Based Optimal Computation Offloading Scheme for VR Video Transmission in Mobile Edge Networks. IEEE Access 2023, 11, 122772–122781. [Google Scholar] [CrossRef]
Guo, M.; Wang, W.; Huang, X.; Chen, Y.; Zhang, L.; Chen, L. Lyapunov-Based Partial Computation Offloading for Multiple Mobile Devices Enabled by Harvested Energy in MEC. IEEE Internet of Things Journal 2022, 9, 9025–9035. [Google Scholar] [CrossRef]
Yuan, Y.; Yi, C.; Chen, B.; Shi, Y.; Cai, J. A Computation Offloading Game for Jointly Managing Local Pre-Processing Time-Length and Priority Selection in Edge Computing. IEEE Transactions on Vehicular Technology 2022, 71, 9868–9883. [Google Scholar] [CrossRef]
Zhao, N.; Ye, Z.; Pei, Y.; Liang, Y.C.; Niyato, D. Multi-Agent Deep Reinforcement Learning for Task Offloading in UAV-Assisted Mobile Edge Computing. IEEE Transactions on Wireless Communications 2022, 21, 6949–6960. [Google Scholar] [CrossRef]
Gu, X.; Zhang, G.; Wang, M.; Duan, W.; Wen, M.; Ho, P.H. UAV-Aided Energy-Efficient Edge Computing Networks: Security Offloading Optimization. IEEE Internet of Things Journal 2022, 9, 4245–4258. [Google Scholar] [CrossRef]
Goudarzi, S.; Soleymani, S.A.; Wang, W.; Xiao, P. UAV-Enabled Mobile Edge Computing for Resource Allocation Using Cooperative Evolutionary Computation. IEEE Transactions on Aerospace and Electronic Systems 2023, 59, 5134–5147. [Google Scholar] [CrossRef]
Zhang, Y.; Mao, Z. Computation Offloading Service in UAV-Assisted Mobile Edge Computing: A Soft Actor-Critic Approach. 2023 International Conference on Ubiquitous Communication (Ucom), 2023, pp. 373–378. [CrossRef]
Li, Y.; Yang, C.; Deng, M.; Tang, X.; Li, W. A Dynamic Resource Optimization Scheme for MEC Task Offloading Based on Policy Gradient. 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), 2022, Vol. 6, pp. 342–345. [CrossRef]
Zhou, S.; Fei, S.; Feng, Y. Deep Reinforcement Learning based UAV-Assisted Maritime Network Computation Offloading Strategy. 2022 IEEE/CIC International Conference on Communications in China (ICCC), 2022, pp. 890–895. [CrossRef]
Huang, L.; Bi, S.; Zhang, Y.J.A. Deep Reinforcement Learning for Online Computation Offloading in Wireless Powered Mobile-Edge Computing Networks. IEEE Transactions on Mobile Computing 2020, 19, 2581–2593. [Google Scholar] [CrossRef]
Zhou, H.; Jiang, K.; Liu, X.; Li, X.; Leung, V.C.M. Deep Reinforcement Learning for Energy-Efficient Computation Offloading in Mobile-Edge Computing. IEEE Internet of Things Journal 2022, 9, 1517–1530. [Google Scholar] [CrossRef]
Wang, Y.; Fang, W.; Ding, Y.; Xiong, N. Computation offloading optimization for UAV-assisted mobile edge computing: a deep deterministic policy gradient approach. Wireless Networks 2021, 27, 2991–3006. [Google Scholar] [CrossRef]
Yu, L.; Zheng, J.; Wu, Y.; Zhou, F.; Yan, F. A DQN-based Joint Spectrum and Computing Resource Allocation Algorithm for MEC Networks. GLOBECOM 2022 - 2022 IEEE Global Communications Conference, 2022, pp. 5135–5140. [CrossRef]
Lu, W.; Ding, Y.; Gao, Y.; Hu, S.; Wu, Y.; Zhao, N.; Gong, Y. Resource and Trajectory Optimization for Secure Communications in Dual Unmanned Aerial Vehicle Mobile Edge Computing Systems. IEEE Transactions on Industrial Informatics 2022, 18, 2704–2713. [Google Scholar] [CrossRef]

Figure 1. Single UAV with multiple wireless devices

Figure 2. Time frame and time slot division

Figure 3. The IOECA structure composition

Figure 4. Convergence of the IOECA when the number of UEs is 10

Figure 5. Convergence of the DQN when the number of UEs is 10

Figure 6. Convergence of the TIOA when the number of UEs is 10

Figure 7. Energy consumption varies with the number of UEs

Figure 8. Offloading ratio vary with the number of UEs

Figure 9. Energy consumption varies with task size when N = 10

Figure 10. The flight path of UAV

Table 1. Simulation parameters.

Parameter	definition	Default
H	UAV flying height	100m
K	Number of slots	40
$α_{0}$	Channel gain at a reference distance of 1m	-50dB
B	Transmission bandwidth	1MHz
$p_{n}^{o f f}$	UE Task sending power	10W
$p_{n}^{l o c}$	UE task computing power	10W
$p_{n}^{s l e e p}$	UE standby power	1W
$f_{n}$	UE CPU calculation frequency	0.2GHz
$p_{U} A V^{c a l}$	UAV computing power	40W
$p_{U} A V^{f l y}$	UAV flight power	10W
$f_{U} A V$	UAV CPU calculation frequency	3GHz
E	UAV power	2000J

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Computing Offloading for Energy Conservation in UAV-Assisted Mobile Edge Computing

Abstract

1. Introduction

2. Related Work

3. System Model and Problem Formulation

3.1. Communication Model

3.2. Local Computational model

3.3. Offloading Computational model

3.4. Problem Formulation

4. IOECA Algorithm Based on DDPG

4.1. Markov Process Modeling

4.1.1. State Space

4.1.2. Action Space

4.2. Algorithm

4.3. Reward Function

5. Performance Evaluation

5.1. Parameter Settings

5.2. Numerical Results

5.2.1. Algorithm Convergence Analysis

5.2.2. UE Quantity Analysis

5.2.3. Task Size Analysis

5.2.4. UAV Trajectory Analysis

6. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe