Physics-Based Aircraft Dynamics Identification Using Genetic Algorithms

Preprint

Article

Physics-Based Aircraft Dynamics Identification Using Genetic Algorithms

Altmetrics

Downloads

179

Views

Comments

A peer-reviewed article of this preprint also exists.

Raymundo Peña-García

Rodolfo Daniel Velázquez-Sánchez

Cristian Gómez-Daza-Argumedo,

Jonathan Omega Escobedo-Alva,

Ricardo Tapia-Herrera,

Jesús Alberto Meda-Campaña^*

Raymundo Peña-García

Rodolfo Daniel Velázquez-Sánchez

Cristian Gómez-Daza-Argumedo,

Jonathan Omega Escobedo-Alva,

Ricardo Tapia-Herrera,

Jesús Alberto Meda-Campaña^*

This version is not peer-reviewed

Submitted:

19 December 2023

Posted:

20 December 2023

You are already at the latest version

Alerts

Abstract

This work proposes a physics-based identification technique based on genetic algorithms. The main objective is to obtain a parametric matrix A that describes the time-invariant linear model of the longitudinal dynamics of an aircraft. This is achieved by proposing a fitness function based on the properties of the transition matrix and taking advantage of some of the capabilities of the genetic algorithm, mainly those of restricting the search ranges of the unknowns. In this case, such unknowns are related to the type of aircraft and flight conditions that are considered during the identification process. The proposed identification method is validated with a reliable nonlinear model that can be found in the literature, as well as with the calculation of the trim condition and linearization generally used in aircraft dynamics. In summary, this study suggests the genetic algorithm provided with the adequate fitness function, could be an appealing alternative for aircraft model identification, even when only a limited amount of data is available. Furthermore, in some cases, linearization using genetic algorithm can be more efficient than classical methods.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

1.1. Motivation

One of the fundamental pursuits in the scientific domain is the development of mathematical models that accurately represent physical systems. A fundamental criterion for evaluating such models is their usefulness. This may involve the ability to predict crucial aspects of the behavior of a physical system or to provide critical information to the design process through model parameters. In all cases, the mathematical model must achieve a balance between simplicity to be of practical use, and complexity to describe the most important characteristics of the system being modeled.

A long-standing need in aeronautics has been that of obtaining reliable and accurate models for aircraft dynamics. This goes beyond aircraft design and flight simulation, it involves the implementation and validation of control systems. In the current era, because of the impressive development of Unmanned Aerial Vehicles (UAVs), the search for control systems have become more demanding, both in civil and military applications. The arrive of high-reliability, low-cost sensors and sophisticated control systems has broken down previous barriers. Small aircraft can now reach higher altitudes, higher speeds and longer ranges. This provides the opportunity to implement cutting-edge algorithms, which are both smarter and more efficient [1].

However, the effort to identify an optimal model for advanced control system design objectives remains a costly and complex task. Given this reality, it is imperative to reevaluate the identification process, seeking an innovative approach that is simple, fast and effective. It is crucial to avoid heuristic models and costly experiments, recognizing that the simplest option is often the most prudent. Several compelling and direct examples can be found in [2]. Over the past two decades, the identification in aeronautics, particularly for manned airplanes, has been vigorously explored by prominent civil-military and government entities such as the Deutsches Zentrum für Luft-und Raumfahrt (DLR) and NASA [3].

A correct identification system incorporates experimental data and undergoes validation in flight. Presently, a hugh amount of information on experimental identification and validation processes can be obtained from various technical reports and manuals [4], affording insights into many facets of authentic identification procedures. Recent research [3] offers an excellent overview of the state-of-the-art in this field. Tools for the time domain are comprehensively examined in [5], with additional contributions from the German Aerospace Center featured in [6]. Furthermore, system identification techniques for aircraft dynamics in the frequency domain have been given in [7].

In [3], it is noted that advances in machine learning have yet to yield substantial benefits for aircraft system identification, primarily due to the absence of a physics-based model. This limitation becomes evident when employing neural networks to represent dynamics [8] or aircraft dynamics as a black box [9], or when resorting to genetic algorithms in pursuit of a heuristic model [10]. There are also published works where two techniques are combined, for instance in [11], genetic algorithms are part of a hybrid identification system originally based on optimization, and in [12], the blend of neural networks and fuzzy systems is considered to obtain the longitudinal model of an aircraft.

When artificial intelligence is judiciously integrated with a comprehension of physics-based aircraft models, alongside the aforementioned state-of-the-art knowledge, we can impose parametric constraints that facilitate swift convergence algorithms. This approach circumvents the conventional issue of infinite solutions in computational algorithms and yields more cost-effective results compared to relying solely on artificial intelligence or physics-based algorithms [13]. As we shall demonstrate, this robust identification methodology proves invaluable not only for linear dynamics identification but also for linearization under diverse trim conditions, providing a simple, effective, and tailored solution to the formidable challenges of today’s aerospace industry.

On the other hand, a notable disadvantage of the application of genetic algorithms in obtaining mathematical models from real or simulated data is that during the evaluation of the fitting function, the model obtained must be simulated in each iteration to determine the error between the data and the response of the intermediate model. This causes a very high computational cost that may be out of the reach of researchers with limited budgets. To reduce this computational cost, and considering that the linear system is sufficient to describe the longitudinal dynamics of an aircraft, in this work the transition matrix [14,15] is considered instead of the complete simulation of the intermediate model in each iteration of the genetic algorithm.

1.2. Contribution

Therefore, the main goal of the current work, is that of presenting a fitness function based on the transition matrix, such that, when the fitness function is included in the genetic algorithm, the matrix A, involved in the linear approximation of the aircraft, is promptly obtained, and only a relatively small amount of data is needed.

1.3. Manuscript Organization

The rest of this note is organized as follows: In Section 2, the nonlinear model of the aircraft is presented. Section 3 describes the trim condition considered. In Section 4 the traditional linearization of the nonlinear model is performed. Below, Section 5 presents a concise analysis of the parameters included in the matrix A. The main result, i.e., the linearization achieved by the genetic algorithm, is discussed in detail in Section 6. Finally, in Section 7 some conclusions are presented.

1.4. Notation and Definitions

Nomenclature

A	Matrix for LTI longitudinal dynamics
$\hat{A}$	Jacobian matrix of nonlinear equations with respect to the state variables
B	Input Matrix for LTI system
$\hat{B}$	Jacobian matrix of nonlinear equations with respect to inputs
$c (\cdot)$	Cosine function
C	Matrix for output definition in state form
E	Jacobian matrix of Nonlinear equations with respect to the first-order state variables
$F^{b}$	Force vector in body frame
$\hat{F}$	Jacobian matrix of nonlinear equations with respect to the first-order state variables
h	Step size for numerical derivative, $h = x (t_{k + 1}) - x (t_{k})$
$\bar{h}$	Aircraft flying height
H	Weight diagonal matrix for optimization criteria
$H (Φ)$	Transformation matrix of angular rates from body axes to the inertial system
$J^{b}$	Inertial tensor of body center of gravity
m	Aircraft mass.
$M^{b}$	Moment vector in body axes
$M_{q}$	Moment due to pitch rate
$M_{u}$	Moment due to horizontal velocity in body axes
$M_{w}$	Moment due to vertical speed in body axis
p	Roll rate in x body axis
$\dot{p}$	Angular acceleration in the x-axis in body frame
$P_{E}$	Aircraft displacement to the east direction (navigation frame)
$P_{N}$	Aircraft displacement to north direction (navigation frame)
q	Pitch rate in y body axis
$\dot{q}$	Angular acceleration in the y-axis in body frame
r	Yaw rate in body axes
$\dot{r}$	Angular acceleration on the z-axis in body frame
$s (\cdot)$	Sine function
T	Step size for Genetic Algorithm
u	Flight velocity in x-axes in body frame from the equilibrium state (cruise flight)
U	Input vector control
$\dot{u}$	Flight acceleration in x-axes in the body frame and from the equilibrium state (cruise flight)
$U_{e}$	Input vector control for equilibrium condition
$u_{0}$	Input for equilibrium condition in the linear system
v	Lateral component for flight speed from equilibrium condition, in body frame
$V_{c m / e}^{b}$	Aircraft velocity from the center of mass to earth axes,super-index b indicates body frame
$V_{e}$	Flight velocity in trim condition
$\dot{v}$	Lateral component for acceleration from equilibrium point, in body frame
w	Vertical component for flight velocity from equilibrium condition, in body frame
$\dot{w}$	Vertical component for acceleration from equilibrium condition, in body frame
X	Twelve dimensional state vector
x	x displacement on body frame
$x_{0}^{n l}$	Initial condition for non linear model
$X_{e}$	Vector state in trim condition
$X_{θ}$	Forces in x body axis due to pitch angle
$x_{0}$	State values in equilibrium point for the linear system definition
$\dot{x_{0}}$	First order state values in equilibrium point for the linear system definition
$\dot{X}$	First order vector state
$x_{N L}$	Matrix containing the values of the nonlinear states
$X_{q}$	Forces in x body axis due to pitch rate

$X_{u}$	Forces in the x-body axis due to velocity in the x-axis of the body frame
$X_{w}$	Forces in the x-body axis due to velocity in the z-axis of the body frame
y	Lateral displacement in body axis
z	Vertical displacement in body axis
$Z_{θ}$	Forces in z body axis due to pitch angle
$Z_{q}$	Forces in z body axis due to pitch rate
$Z_{u}$	Forces in the z-body axis due to velocity in the x-axis of the body frame
$Z_{w}$	Forces in the z-body axis due to velocity in the z-axis of the body frame
$γ$	Longitudinal flight path angle
$θ$	Pitch angle
$θ_{e}$	Pitch angle for trim condition
$\dot{θ}$	Pitch rate
$\dot{Φ}$	Vector of Euler angle rates, angular rates of aircraft respect to the inertial system
$ϕ$	Roll angle
$\dot{ϕ}$	Roll rate
$Φ (t - t_{0})$	Transition matrix $Φ (t - t_{0}) = e^{A (t - t_{0})}$
$Φ (t, 0)$	Transition matrix with initial condition $x (0) = 0$
$ψ$	Yaw angle
$\dot{ψ}$	Yaw rate
$ω_{b / e}^{b}$	Angular rate vector in body axis
${\dot{ω}}_{b / e}^{b}$	Angular acceleration vector in body axis

2. Nonlinear 6-DOF dynamic model of a research aircraft

The principal function of the nonlinear model is to ensure the applicability of the methodology presented above. Although we only excite the longitudinal dynamics, it is necessary to pay attention to the complete dynamics. Next, we express in a synthetic form the non-linear model we used in the analysis and validation of the genetic algorithm identification process. This complete and validated model was extracted from [16], which is an excellent summary of [17].

In accordance with rigid body dynamics and classical approximation from Newton-Euler, we present the next equations:

Translation equation on body axes:

{\dot{V}}_{c m / e}^{b} = \frac{1}{m} F^{b} - ω_{b / e}^{b} \times V^{b},

(1)

where m is the mass, the sub-index

c m / e

means from the center of mass to earth axes and super-index b indicates body frame, this nomenclature comes from kinematics equations deduction, see [18].

{\dot{V}}_{c m / e}^{b} = {[\dot{u} \dot{v} \dot{w}]}^{T}

is the linear acceleration vector,

V_{c m / e}^{b} = {[u v w]}^{T}

is the linear velocity vector,

F^{b}

are the external forces,

{\dot{ω}}_{b / e}^{b} = {[\dot{p} \dot{q} \dot{r}]}^{T}

is the angular acceleration and

ω_{b / e}^{b} = {[p q r]}^{T}

is the angular rate.

Rotational equations on body axes:

{\dot{ω}}_{b / e}^{b} = {(J^{b})}^{- 1} [M^{b} - ω_{b / e}^{b} \times J^{b} ω_{b / e}^{b}]

(2)

where

J^{b}

is the inertial matrix,

M^{b}

are external moments.

Kinematic Euler Equation:

It’s important to consider a transformation of angular rates from body axes to the general frame Euler system (inertial).

\dot{Φ} = H (Φ) {\dot{ω}}_{b / e}^{b},

(3)

where

\dot{Φ} = {[\dot{ϕ} \dot{θ} \dot{ψ}]}^{T}

is the vector of Euler angles rate and:

H (Φ) = [\begin{matrix} 1 & s e n (ϕ) t a n (θ) & c o s (ϕ) t a n (θ) \\ 0 & c o s (ϕ) & - s e n (ϕ) \\ 0 & s e c (θ) s e n (ϕ) & c o s (ϕ) s e c (θ) \end{matrix}] .

The non-linear complete model is considered non-autonomous, and it depends on the complete state (even forces and moments are direct functions of states) and control inputs. Constructing the general form we have:

\dot{X} = f (X, U) .

(4)

With the next states.

\begin{matrix} X & = & {[\begin{matrix} x_{1} & . . . & x_{12} \end{matrix}]}^{T} = {[u v w p q r ϕ θ ψ P_{N} P_{E} \bar{h}]}^{T}, \end{matrix}

where

P_{N}

P_{E}

and

P_{D}

are the

x - y - z

aircraft displacements on North-East-Down navigation frame system and

\bar{h} = - P_{D}

As mentioned above external forces and moments are functions of states and control inputs:

F^{b} (X, U),

M^{b} (X, U),

finally:

\begin{matrix} [\begin{matrix} {\dot{x}}_{1} \\ {\dot{x}}_{2} \\ {\dot{x}}_{3} \\ {\dot{x}}_{4} \\ {\dot{x}}_{5} \\ {\dot{x}}_{6} \\ {\dot{x}}_{7} \\ {\dot{x}}_{8} \\ {\dot{x}}_{9} \\ {\dot{x}}_{10} \\ {\dot{x}}_{11} \\ {\dot{x}}_{12} \end{matrix}] = [\begin{matrix} \frac{1}{m} F^{b} (X, U) - [\begin{matrix} x_{4} \\ x_{5} \\ x_{6} \end{matrix}] \times [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \end{matrix}] \\ {(J^{b})}^{- 1} [M^{b} (X, U) - [\begin{matrix} x_{4} \\ x_{5} \\ x_{6} \end{matrix}] \times J^{b} [\begin{matrix} x_{4} \\ x_{5} \\ x_{6} \end{matrix}]] \\ H (Φ) [\begin{matrix} x_{4} \\ x_{5} \\ x_{6} \end{matrix}] \\ C S (ϕ, θ, ψ) [\begin{matrix} u \\ v \\ w \end{matrix}] \end{matrix}] \end{matrix} .

(5)

In Eq. (5),

C S (ϕ, θ, ψ)

is the body to navigation axis transformation:

[\begin{matrix} c θ c ψ & (- c ϕ s ψ + s ϕ s θ c ψ) & (s ϕ s ψ + c ϕ s θ c ψ) \\ c θ s ψ & (c ϕ c ψ + s ϕ s θ s ψ) & (- s ϕ c ψ + c ϕ s θ s ψ) \\ - s θ & s ϕ c θ & c ϕ c θ \end{matrix}],

(6)

where

c (\cdot)

and

s (\cdot)

are

c o s i n e

and

s i n e

function respectively.

3. Trim Condition

In this case for identification, the trim condition will be the wings-level, non-sideslipping steady state flight [18]. The determination of the equilibrium point in a coupled, nonlinear, and multivariable system like Eq. (9) is not trivial, and a special algorithm is required [19]. Before linearization, we must choose a trim condition such that for the general form

\dot{X} = f (X, U)

f (X_{e}, U_{e}) = 0 .

(7)

In accordance to Eq. (5), ignoring navigation variables,

X_{e} \in R^{9}

and

U_{e} \in R^{5}

. That means we need

\dot{u} = \dot{v} = \dot{w} = \dot{p} = \dot{q} = \dot{r} = 0

for steady state flight. We use a convenient methodology presented in [18]. The problem statement is:

min_{X \in Ω} \hat{f} (X) = f (X) + C^{T} H C,

(8)

where H is a weight diagonal matrix, and

C \in R^{9 + 1}

is the restriction vector. Next, the process is performed with minimization search Nelder and Mead Simplex algorithm, using fminsearch() MATLAB command, which is a non-linear programming solver to find the minimum of an unconstrained multivariable function using the derivative-free method. We need the cost function and initial search values. In our case, all functions equal to zero defined in C are:

C = [{\dot{x}}_{1} \dots {\dot{x}}_{9} (| V_{c m / e}^{b} | - V_{e}) γ x_{2} x_{7} x_{9}],

(9)

in Eq. (9),

V_{e}

is the required operation speed in trim condition,

| V_{c m / e}^{b} | = \sqrt{x_{1}^{2} + x_{2}^{2} + x_{3}^{2}}

γ = x_{8} - a t a n (x_{3} / x_{1})

is the flight path angle. The weight matrix was defined like

H = d i a g (3)

after a trial and error process resulting in affordable results.

The final function cost is

\hat{f} (X) = C^{T} H C

Using fminsearch() with the function cost defined above, after 9 iterations and with a minimization error of

1 \times 10^{- 19}

the trim condition

X_{e}

obtained is:

x_{1} = 110 m / s

x_{3} = - 2.0882 m / s

x_{8} = - 0.0634 r a d

, all remaining states are zero.

4. Linearization

For the coefficient identification process, we need to obtain the Linear Time-Invariant Systems on the equilibrium point

X_{e}

. Let the equations be defined like Eq. (4) and

\dot{x} \in R^{n}, x \in R^{n}, u \in R^{m}

and

f : R^{n + m} ⟶ R^{n}

In an implicit form:

F (\dot{x}, x, u) = \dot{x} - f (x, u) = 0,

(10)

where

f : R^{2 n + m} ⟶ 0^{n}

Linearizing Eq. (10) by Taylor expansion series on equilibrium point and considering only low order terms (linear):

\begin{matrix} F (\dot{x}, x, u) = F ({\dot{x}}_{0}, x_{0}, u_{0}) + \frac{\partial F}{\partial \dot{x}} ({\dot{x}}_{0}, x_{0}, u_{0}) (\dot{x} - {\dot{x}}_{0}) \\ + \frac{\partial F}{\partial x} ({\dot{x}}_{0}, x_{0}, u_{0}) (x - x_{0}) + \frac{\partial F}{\partial u} ({\dot{x}}_{0}, x_{0}, u_{0}) (u - u_{0}), \end{matrix}

(11)

Evaluating equilibrium condition:

F ({\dot{x}}_{0}, x_{0}, u_{0}) = 0,

(12)

then from Eq. (12) and Eq. (10)

\dot{x} = {\dot{x}}_{0}, x = x_{0}, u = u_{0}

and the partial derivatives are defined as:

\frac{\partial F}{\partial \dot{x}} ({\dot{x}}_{0}, x_{0}, u_{0}) = E,

(13)

\frac{\partial F}{\partial x} ({\dot{x}}_{0}, x_{0}, u_{0}) = \hat{A},

(14)

\frac{\partial F}{\partial u} ({\dot{x}}_{0}, x_{0}, u_{0}) = \hat{B},

(15)

and simplifying Eq. (11) we obtain:

\begin{matrix} 0 = E δ \dot{x} + \hat{A} δ x + \hat{B} δ u \end{matrix},

(16)

solving for

δ \dot{x}

δ \dot{x} = A δ x + B δ u,

(17)

where:

A = - \frac{\hat{A}}{E},

(18)

B = - \frac{\hat{B}}{E} .

(19)

After the process, it should therefore be made clear that the LTI system

\dot{x} = A x + B u

conforming for Eq. (18) and Eq. (19) matrices will give values of perturbations (

δ x

) from an initial equilibrium condition

X_{e}

, as in the case of the control inputs.

The next step is to obtain the partial derivatives on Eq. (13) - Eq. (15). In accordance with [20] we can obtain more precise results using a numerical algorithm with finite differential approximation. This is feasible in simulation because we have control over the confiability and integrability of data. The process is relatively easy and we must be aware of numerical error, which can be avoided with values of h not too small. In literature is well known that central differentiation is more accurate than one-sided difference formula [21,22]. Then for any partial derivatives, we have:

\frac{\partial F (t_{k})}{\partial x (t_{k})} = \frac{F (x (t_{k + 1})) - F (x (t_{k - 1}))}{2 h},

(20)

where

h = x (t_{k + 1}) - x (t_{k})

. We used this method for the

\hat{E}

\hat{A}

, and

\hat{B}

determination, column by column.

\begin{matrix} E_{i, j} = \frac{F_{i} ({\dot{x}}_{j} (t_{k + 1})) - F_{i} ({\dot{x}}_{j} (t_{k - 1}))}{2 h_{j}}, \\ {\hat{A}}_{i, j} = \frac{F_{i} (x_{j} (t_{k + 1})) - F_{i} (x_{j} (t_{k - 1}))}{2 h_{j}}, \\ {\hat{B}}_{i, j} = \frac{F_{i} (u_{j} (t_{k + 1})) - F_{i} (u_{j} (t_{k - 1}))}{2 h_{j}} . \end{matrix}

(21)

In order to obtain data and calculate the matrices in Eq. (21), we use as perturbations initial condition and input signals. For example, to produce a response in all states of the nonlinear model without input signal, we choose initial conditions for

x {(0)}_{1} = 10 m / s

and

x {(0)}_{2} = 5 m / s

, these values are additional to trim condition. After an increment of the state variable

x_{j}

h_{j} = 1 \times 10^{- 12}

we calculate for the function

F_{i}

against every state

x_{j}

the partial derivatives conforming matrices as in Eq. (21). In accordance with Eq. (18) and Eq. (19), we obtain the state-space matrices of all 6 DOF linear dynamics.

\dot{x} = A x + B u, x \in R^{9}

and

u \in R^{5}

, nevertheless we can separate the longitudinal dynamics as in the next reduced system:

A = [\begin{matrix} - 0.052 & - 0.0011 & 6.852 & - 9.7903 \\ - 0.2333 & - 0.9104 & 107.9602 & 0.6215 \\ - 0.0044 & - 0.0431 & - 1.4537 & 0 \\ 0 & 0 & 1 & 0 \end{matrix}],

(22)

B = [\begin{matrix} 0 & - 0.8022 & 0 & 9.8100 & 9.8100 \\ 0 & - 12.6387 & 0 & 0 & 0 \\ 0 & - 5.0424 & 0 & 0.3924 & 0.3924 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}] .

(23)

This matrix A has a direct relation with Eq. (24) and, therefore is considered parametric, which means, with physical meaning.

5. Parameters

The matrix coefficient in a state space form, has an analytic form well known in flight dynamics. In this case, we take into account only longitudinal dynamics. A is a square matrix with the vector state

x = {[u w q θ]}^{T}

. Each coefficient has a special nomenclature, defining moments and forces in the function of state variables.

A = [\begin{matrix} X_{u} & X_{w} & X_{q} & X_{θ} \\ Z_{u} & Z_{w} & Z_{q} & Z_{θ} \\ M_{u} & M_{w} & M_{q} & 0 \\ 0 & 0 & 1 & 0 \end{matrix}] .

(24)

In Eq. (24)

X_{θ}

and

Z_{θ}

are linearized forces projections due to gravity on body axes, are direct functions from trim condition defined by

θ_{e}

, M is referring moments on body axes (moment controlling pitch ). We can find data for common coefficient range parameters and their physical interpretation in several sources, for example in [18,23,24], and [25]. These valuable values depend on aircraft and flight conditions.

6. Main result: Linearization by means of the genetic algorithm (GA)

In this section, we utilize the nonlinear model introduced in Section 2 as the benchmark for evaluating the performance of the linearization methods presented in Section 4 and the genetic algorithm-based linearization approach.

The nonlinear model, as defined by equations Eq. (1)-Eq. (6), is simulated to capture the longitudinal behavior of the aircraft, with initial condition

x_{0}^{n l} = {[10 5 0.2094 0]}^{T}

, over a duration of

t = 180 s

using a sampling time of

T = 0.05 s

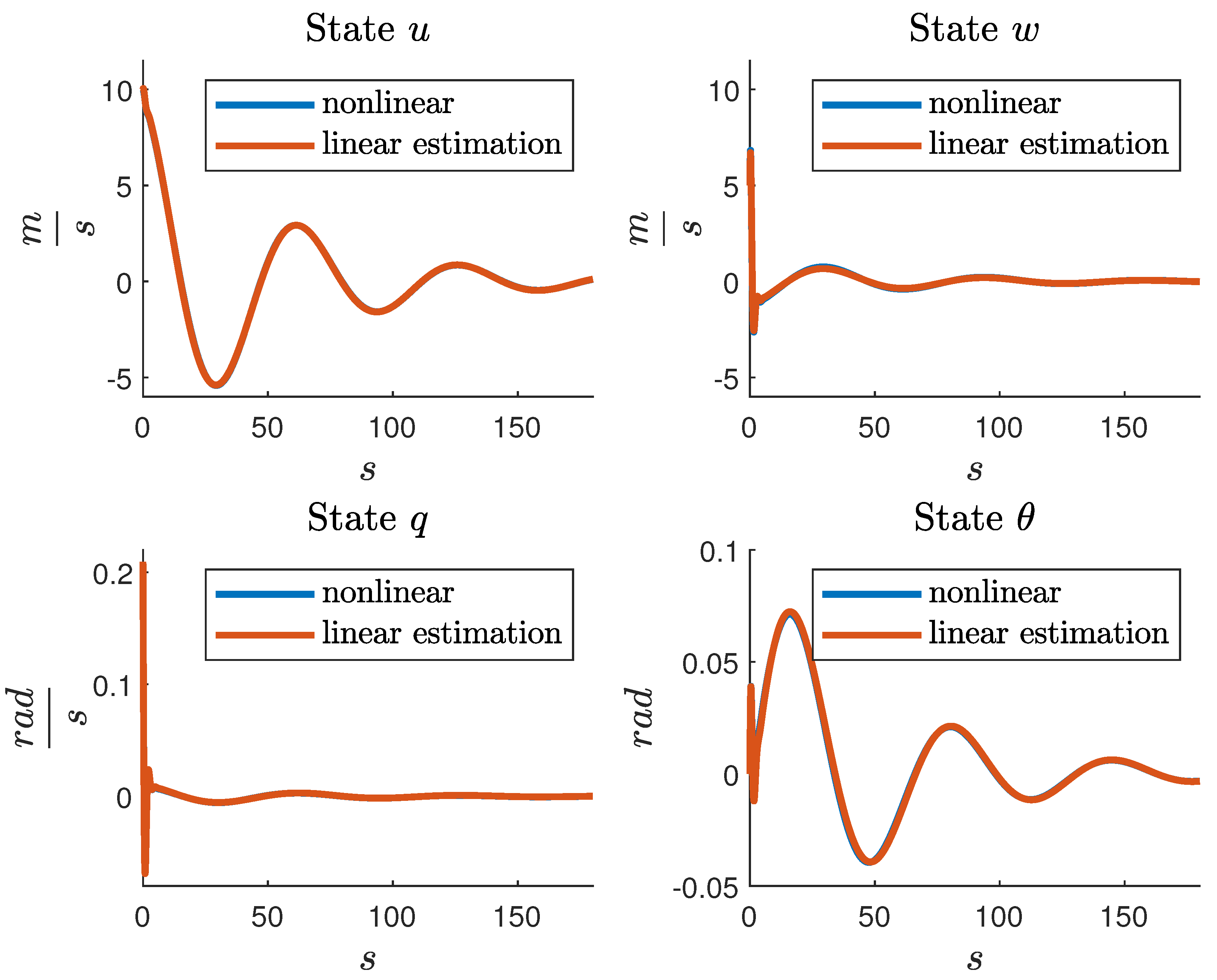
Then, to provide a reference for comparing the GA linearization, the linear system with matrix A, obtained through the linearization procedure described in Section 4 and represented by equation Eq. (22), is simulated under identical conditions. The numerical results are depicted in Figure 1, and the mean squared error (MSE) between the linear states and their corresponding nonlinear counterparts is calculated to be

0.0034

Next, we linearize the nonlinear system using a genetic algorithm. However, before presenting the results, we provide a brief description of the genetic algorithm.

6.1. Genetic algorithm (GA)

A genetic algorithm (GA) is an optimization technique that mimics the processes of evolution and natural selection. Usually, it is applied to solve complex optimization problems.

In a genetic algorithm, a potential solution to the problem is represented as a chromosome, typically as a binary string, but other representations are also possible, depending on the problem at hand. A population is a collection of such chromosomes. The size of the population is a user-defined parameter. The fitness function evaluates how well each chromosome in the population solves the problem. It assigns a fitness score to each chromosome based on the goal of the problem. The fitness function is problem-specific and provided by the user.

Chromosomes with higher fitness scores have a greater chance of being selected for reproduction. The most common selection methods include roulette wheel selection and tournament selection. Crossover is the process of combining two parent chromosomes to create one or more offspring. Various crossover operators are used, such as one-point, two-point, and uniform crossover. The crossover rate (probability of crossover) is a user-defined parameter. Mutation involves randomly changing some bits in a chromosome with a low probability. It introduces genetic diversity into the population. The mutation rate (probability of mutation) is another user-defined parameter. Genetic algorithms terminate when a stopping criterion is met. Common termination conditions include a maximum number of generations, reaching a satisfactory fitness level, or a time limit.

A typical genetic algorithm operates in a loop, which includes selection, crossover, mutation, and replacement of the old population with the new one. This process continues for a predefined number of generations [26,27,28,29,30]. It is important to mention that the GA has been successfully used to solve a number of problems in aeronautics. For instance, a methodology involving a multiobjective genetic algorithm for exploring parametrized microstructures is presented in [31]. In [32], the authors investigate the aerodynamics of desert locust tandem wings through computational fluid dynamics (CFD) simulations. Using 2D and 3D Navier–Stokes equations, they explore wing interactions and corrugation effects. Optimization with genetic algorithms and Nash game theory improves gliding performance by at least 77%. In [33], an automated framework for developing interpolatable aeroelastic reduced-order models (AE ROMs) across diverse flight conditions is presented. By combining system identification, state-consistency enforcement (SCE), and a genetic algorithm (GA), the approach addresses the issue of state inconsistency in ROMs.

In MATLAB, optimization via Genetic Algorithm (GA) can be performed using the function ga, which is part of the Global Optimization Toolbox. The syntax is as follows:

x = g a (f u n, n v a r s, A, b, A e q, b e q, l b, u b, n l c o n, o p t s),

(25)

where

f u n

is the fitness function to be optimized; x is the vector of variables included in the fitness function;

n v a r s

is the dimension of the vector x; the pair

(A, b)

defines the inequality restrictions in the form of

A \cdot x \leq b

; the pair

(A e q, b e q)

defines the equality restrictions in the form of

A e q \cdot x = b e q

; the vectors

l b

and

u b

, both of dimension

n v a r s

, define the lower and upper limits for the search of x, respectively;

n l c o n

defines the nonlinear constraints;

o p t s

allows the user to modify parameters such as tolerance, the type of plot to be depicted, the maximal number of generations, etc. For more details, please refer to [34].

An essential challenge when working with GA is the need to define an appropriate fitness function. This is a crucial factor as the fitness function plays a critical role in evaluating how effectively a solution addresses the specific problem. The selection of the fitness function can significantly influence the overall performance of the algorithm and the quality of the solutions it produces.

With this in mind, we introduce a simple yet practical fitness function in the following sections. This function is designed to derive a parametric matrix A that characterizes the longitudinal dynamics of an aircraft. It utilizes data obtained from the simulation of the highly reliable nonlinear aircraft model described in Section 2.

6.2. Linearization via GA

In this section, we aim to find a matrix A in the form of equation Eq. (24) to linearize the longitudinal dynamics of the aircraft described in equations Eq. (1)–Eq. (6) using Genetic Algorithms (GA). To accomplish this, a fitness function is derived in a practical manner. The unknowns

x^{'} s

to be determined by the GA are organized in the matrix

A_{G A}

as follows:

A_{G A} = [\begin{matrix} x (1) & x (4) & x (7) & - 9.7903 \\ x (2) & x (5) & 107.9602 & x (9) \\ x (3) & x (6) & x (8) & 0 \\ 0 & 0 & 1 & 0 \end{matrix}],

(26)

where the constants appearing in Eq. (26) are fixed values dependent on the characteristics of the modeled aircraft. In other words, only 9 of the 16 elements of the matrix Eq. (26) need to be determined.

We propose that the fitness function evaluates the matrix described in equation Eq. (26) in each iteration, comparing the linear states with their corresponding nonlinear states at arbitrary sample instants. To minimize computational load, we consider the inclusion of the transition matrix in this process.

6.2.1. Transition matrix

The transition matrix, denoted as

Φ (t - t_{0}) = e^{A (t - t_{0})}

, describes the evolution of a time-invariant linear system over time, considering a given initial condition

x (t_{0})

. It shows how the state of the system at an initial time

t_{0}

is transformed to the state at a later instant t. For continuous-time systems described by

\dot{x} (t) = A x (t)

, the transition matrix can be used to obtain

x (t)

from the initial condition

x (t_{0})

(with

t_{0} = 0

) as follows:

x (t) = Φ (t, 0) x (0) .

(27)

Please refer to [14] and [15] for further details. In MATLAB, the transition matrix can be computed using the function

e x p m ()

, and its application in this work is explained below.

6.2.2. Fitness function

To optimize computational resource utilization, we propose applying the fitness function to a reduced set of samples. Instead of using the entire set of simulated data, which consists of 3601 data points collected over a duration of 180 seconds with a sampling interval of

T = 0.05 s

, we concentrate on a smaller subset where the linear approximation is desired to closely match the nonlinear data.

Taking this into account, from the simulation of the nonlinear model Eq. (1)–Eq. (6) and based on the transition matrix mentioned above, the following algorithm describes the fitness function used to linearize the nonlinear dynamics of the aircraft.

Explanation:

Line 1: The name of the function is $f i t n e s s$ , and the argument $x \in R^{9}$ is the vector of the variables to be found by the GA in order to minimize this function.
Line 2: Global variables $n d a t a$ , $x_{N L}$ , $x_{0}$ , and t are used in this function, where $n d a t a$ is the number of samples considered during the linearization, $x_{N L} \in R^{n d a t a \times 4}$ is a matrix containing the values of the nonlinear states $u, w, q, θ$ , from the numerical simulation at desired instants, $x_{0}$ represents the vector of initial conditions, and $t \in R^{n d a t a}$ is a vector with the corresponding time instants at which the matrix $x_{N L}$ has been obtained.
Line 3: Matrix $A_{G A}$ is constructed from elements of vector x from a previous iteration.
Line 4: Matrix $x_{L} \in R^{n d a t a \times 4}$ is initialized as a matrix of zeros with $n d a t a$ rows (number of samples) and 4 columns (states $u, w, q, θ$ ).
Lines 5-7: A loop iterates over the elements of t, using the exponential matrix operation to compute the states of $x_{L}$ at each one of the time instants included in vector t.
Lines 8-11: Squared errors $s q e_{i}$ for each state, with $i = 1, \dots, 4$ .
Line 12: The total error f is computed as the square root of the sum of squared errors.
Line 13: The function returns f as the result of the fitness evaluation.

6.3. Numerical experiments

In this section, we present the results of two linearizations using the Genetic Algorithm (GA). These experiments were performed on a personal computer with the following specifications: Intel(R) Core(TM) i5-10500H CPU @ 2.50GHz, 16GB of RAM, running MATLAB 2019b.

6.3.1. Experiment 1: GA linearization using 31 Samples

In this case, we consider the samples obtained during the first 3 seconds of the nonlinear simulation with a sampling interval of

T = 0.1 s

. This involves selecting every other sample from the nonlinear simulation, resulting in a total of 31 samples. In this example, according to the fitness function outlined in Algorithm 1, we have

n d a t a = 9

x_{N L} \in R^{31 \times 4}

x_{0} = {[10 5 0.2094 0]}^{T}

, and

t \in R^{31}

During the execution of the GA in MATLAB, neither inequality nor equality restrictions nor nonlinear constraints are considered. However, due to the limitations of the available computer resources, we have decided to search for the solution around the values obtained by the linearization procedure explained in Section 4.

Therefore, the GA in MATLAB was executed using the following three lines of code:

\begin{matrix} o p t s = o p t i m o p t i o n s (^{'} g a^{'},^{'} P l o t F c n^{'}, @ g a p l o t b e s t f) \\ f u n = @ f i t n e s s \\ x = g a (f u n, 9, [], [], [], [], l b, u b, [], o p t s) \end{matrix}

(28)

with

\begin{matrix} l b = [- 0.06, - 0.3, - 0.005, - 0.002, - 1, - 0.05, 5.5, - 2, 0] \\ u b = [0, 0, 0, 0, 0, 0, 7, 0, 0.7], \end{matrix}

(29)

It is worth mentioning that the options chosen in Eq. (28) are primarily intended for monitoring the GA’s behavior during execution, which may lead to a higher consumption of computer resources. A more refined selection of these parameters could potentially yield more efficient results. For a comprehensive description of MATLAB’s function

g a

, interested readers are referred to [34].

The elapsed time was 355.863055 seconds, and the matrix obtained by the GA is:

A_{G A 1} = [\begin{matrix} - 0.0572 & - 0.0020 & 5.5 & - 9.7903 \\ - 0.2367 & - 0.9198 & 107.9602 & 0.0001 \\ - 0.005 & - 0.05 & - 1.5393 & 0 \\ 0 & 0 & 1 & 0 \end{matrix}] .

(30)

Then, matrix Eq. (30) is used to simulate the linear system for 180 seconds with a sampling time of

T = 0.05 s

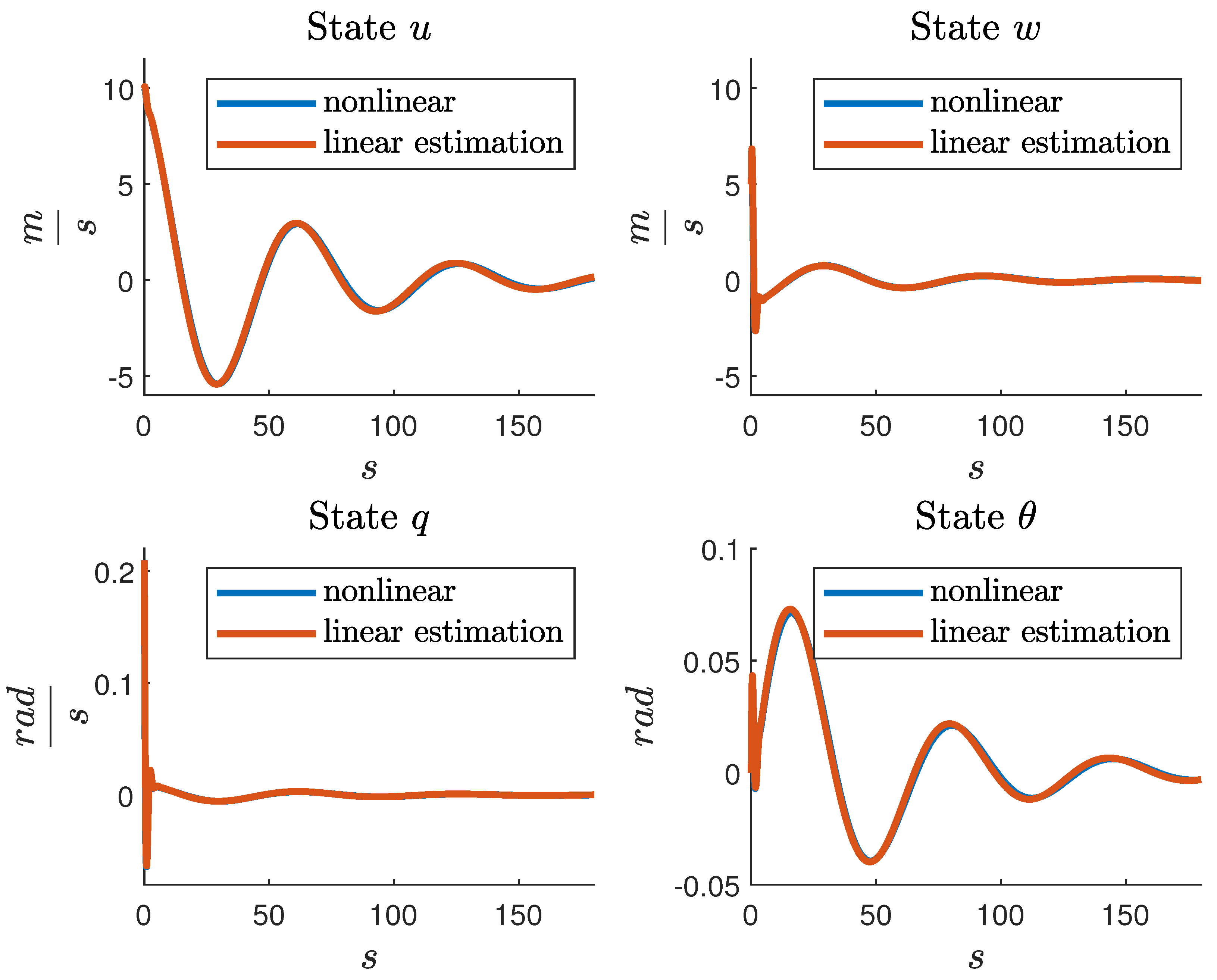
, in order to compare the states of the linear identified system with the nonlinear ones. The results are presented in Figure 2. The overall Mean Square Error (MSE) between the nonlinear states and their linear approximations is 0.0167.

Notice that the MSE obtained in this experiment is greater than the one obtained by the linearization of Section 4, but the GA has been executed considering only 31 samples. In the next experiment, a larger set of samples is considered.

6.3.2. Experiment 2: GA linearization using 66 Samples

Now, we consider the samples that occurred during the initial 3 seconds of the nonlinear simulation with a sampling time of

T = 0.1 s

, along with samples taken from the remainder of the signal with

T = 5 s

, resulting in a total of 66 samples. Therefore, we have

n d a t a = 9

x_{N L} \in R^{66 \times 4}

x_{0} = {[10 5 0.2094 0]}^{T}

, and

t \in R^{66}

. The execution of the GA in MATLAB is exactly the same as presented in Eq. (28)-Eq. (29). The elapsed time was 1304.814475 seconds, and the matrix obtained by the GA is:

A_{G A 2} = [\begin{matrix} - 0.0549 & - 0.0019 & 6.1047 & - 9.7903 \\ - 0.2209 & - 0.9005 & 107.9602 & 0.0001 \\ - 0.0046 & - 0.0499 & - 1.5690 & 0 \\ 0 & 0 & 1 & 0 \end{matrix}] .

(31)

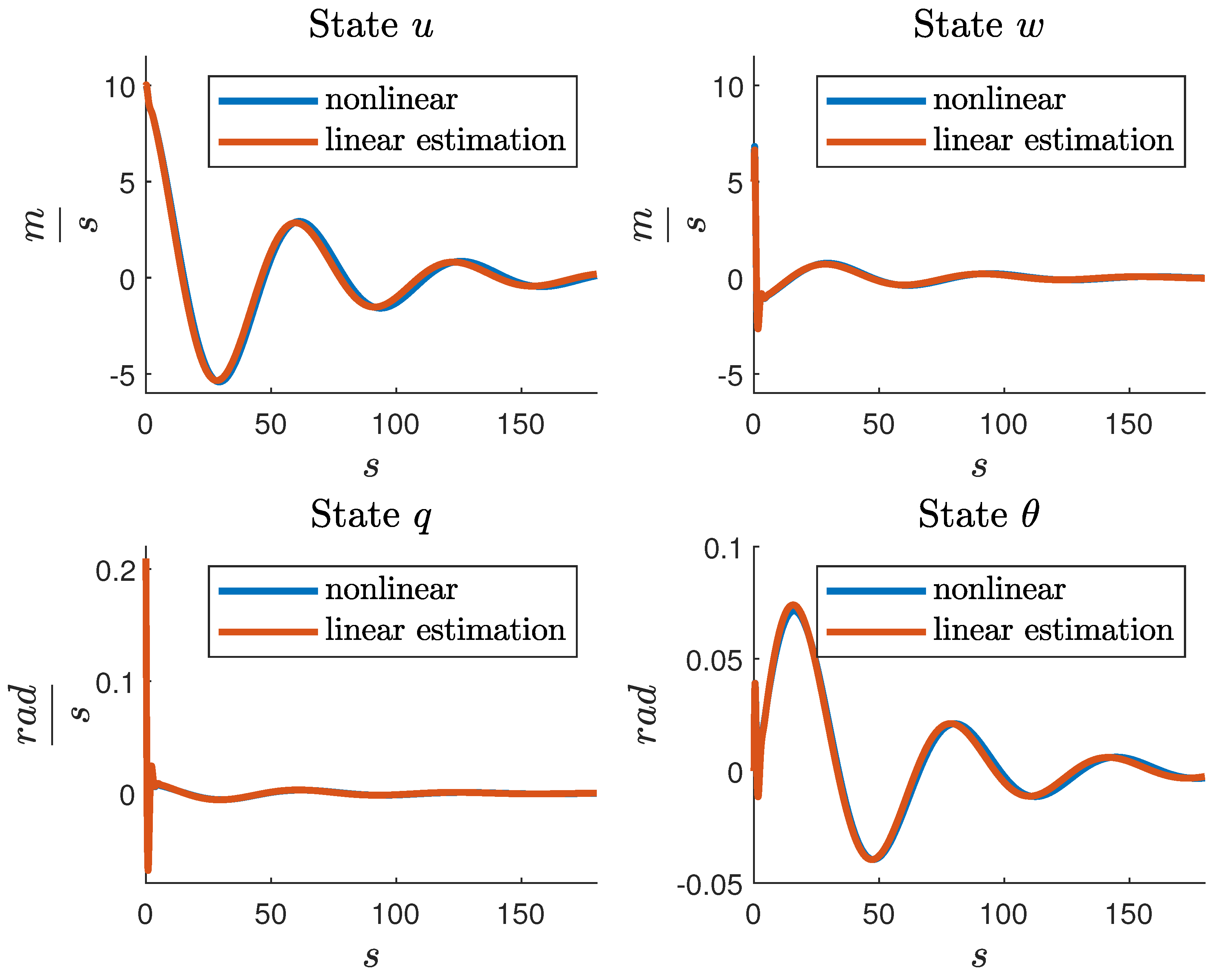
As before, the linear system with state matrix Eq. (31) is simulated for 180 seconds with a sampling time of

T = 0.05 s

, and the comparisons with the nonlinear states are depicted in Figure 3. The overall Mean Square Error (MSE) between the nonlinear states and their linear approximations is notably smaller:

4.3984 \times 10^{- 4}

, but the execution time is larger than in the previous case. This analysis is summarized in Table 1.

7. Conclusions

The traditional linearization algorithm is based on the idealized assumption of perfectly clean and complete data (typically considering

h = 1 \times 10^{- 12}

), which often makes it impractical for real-world experimental data. However, our study demonstrates that GA not only produces matrices with clear physical interpretations, but also exhibits the essential robustness required for reliable experimental identification and that the linearization process can be automated. Furthermore, in situations where computational resources are limited and it is not possible to apply GA from scratch to linearize nonlinear dynamics because the search ranges are completely unknown but, if measurements of the nonlinear system are available, then the GA approach based on proposed transition matrices proves to be a valuable post-processing tool, since, as has been demonstrated, it is capable of improving the results obtained through the traditional linearization method.

Author Contributions

Conceptualization, J. O. E.-A. and J. A. M.-C.; formal analysis, R. P.-G., R. D. V.-S., C. G.-D.-A., J. O. E.-A. and R. T.-H.; investigation, J. O. E.-A., R. T.-H. and J.A.M.-C.; methodology, J. O. E.-A., R. T.-H. and J.A.M.-C.; project administration, J. A. M.-C.; writing—original draft, J. O. E.-A. and J. A. M.-C.; writing— review and editing, J. A. M.-C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

This work was supported in part by Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONAHCYT), through the Scholarship Sistema Nacional de Investigadores (SNI); in part by Instituto Politécnico Nacional through Research Project under Grant 20230023 and 20231126; in part by the Scholarship Estímulo al Desempeño de los Investigadores (EDI); in part by the Scholarship Comisión de Operación y Fomento de Actividades Académicas (COFAA); and in part by the Scholarship Beca de Estímulo Institucional de Formación de Investigadores (BEIFI)..

Conflicts of Interest

The authors declare no conflict of interest.

References

Martinez, O.A.; Cardona, M. State of the Art and Future Trends on Unmanned Aerial Vehicle. 2018 International Conference on Research in Intelligent and Computing in Engineering (RICE), 2018, pp. 1–6. [CrossRef]
Brunton, S.L.; Proctor, J.L.; Kutz, N.J. Discovering Governing Equations From Data by Sparse Identification of Nonlinear Dynamical Systems. Proceedings of the National Academy of Sciences of the United States of America 2016, 113, 3932–3937. [Google Scholar] [CrossRef]
Grauer, J.A.; Morelli, E.A. Introduction to the Advances in Aircraft System Identification from Flight Test Data Virtual Collections. Journal of aircraft 2023, 60, 1329. [Google Scholar] [CrossRef]
Hosseini, B.; Steinert, A.; Hofmann, R.; Fang, X.; Steffensen, R.; Holzapfe, F. Advancements in the Theory and Practice of Flight Vehicle System Identification. Journal of Aircraft 2023, 6, 1419–1436. [Google Scholar] [CrossRef]
Jategaonkar, R.V. Flight Vehicle System Identification: A Time-Domain Methodology; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, 2015. [Google Scholar] [CrossRef]
Deiler, C.; Mönnich, W.; Seher-Wei, S.; Wartmann, J. Retrospective and Recent Examples of Aircraft and Rotorcraft System Identification at DLR. Journal of Aircraft 1996, 33, 1–26. [Google Scholar] [CrossRef]
Tischler, M.B.; Remple, R. System Identification. Engineering Methods with Flight Test Examples; AIIA Educ: Virginia, 2006. [Google Scholar]
Cedillo, S.G.T.; Bonello, P. Empirical identification of the inverse model of a squeeze-film damper bearing using neural networks and its application to a nonlinear inverse problem. Journal of Vibration and Control 2018, 24, 357–378. [Google Scholar] [CrossRef]
Kirkpatrick, K.; J., M.; Valasekz, J. Aircraft System Identification Using Artficial Neural Networks. 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition; , 2013; pp. 1–12.
Ulinowicz, M.; Narkiewicz, J. Aircraft parameter Identification Using Genetic Algorithm. 29th Congress of the International Council of the Aeronautical Sciences;, 2014; pp. 317–334.
Bruce, P.; Kellett, M. Maximum likelihood identification of linear aircraft dynamics using a hybrid genetic algorithm. 36th AIAA Aerospace Sciences Meeting and Exhibit, 1998, pp. 357–378.
Roy, A.G.; Peyada, N.K. Longitudinal Aircraft Parameter Estimation Using Neuro-Fuzzy and Genetic Algorithm Based Method. AIAA Atmospheric Flight Mechanics Conference, 2017, pp. 1–12.
Anderson, M.B. Genetic Algorithms in Aerospace Design: Substantial Progress, Tremendous Potential. Technical report, Sverdrup Technology Inc./TEAS Group, 2002.
Kailath, T.; Sayed, A.H.; Hassibi, B. Linear Estimation; Prentice Hall: Englewood Cliffs, 2000. [Google Scholar]
Ogata, K. Modern Control Engineering; Pearson Education: Saddle River, 2010. [Google Scholar]
Lambrechts, P.; Bennani, S.; Looye, G.; Moormann, D. The RCAM design challenge problem description. Robust Flight Control; Magni, J.F., Bennani, S., Terlouw, J., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 1997; pp. 149–179. [Google Scholar]
Lambrechts, P.F. Technical Publication TP-088-3, GARTEUR-FM(AG08). Technical report, Group for Aeronautical Research and technology in Europe (GARTEUR)., 1997.
Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation; Wiley: New Jersey, 2016. [Google Scholar]
Hong-Gi, L. Linearization of Nonlinear Control Systems; Springer: Singapore, 2022. [Google Scholar]
Lum, C. Aircraft Control and Simulation; Wiley: New Jersey, 2023. [Google Scholar]
Kiusalaas, J. Numerical Methods in Engineering with MATLAB®, 3 ed.; Cambridge University Press, 2015. [CrossRef]
Miller, G. Numerical Analysis for Engineers and Scientists; Cambridge University Press, 2014. [CrossRef]
Roskam, J. Airplane Flight Dynamics and Automatic Flight Controls; DAR Corporation: Kansas, 2003. [Google Scholar]
Blakelock, J.H. Automatic Control of Aircraft and Missiles; Wiley: Nueva York, 1991. [Google Scholar]
McLean, D. Automatic Flight Control Systems; Prentice Hall: New York, 1990. [Google Scholar]
Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Cambridge, MA, 1975. [Google Scholar]
Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Boston, MA, 1989. [Google Scholar]
Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, 1998. [Google Scholar]
Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms; John Wiley & Sons: Hoboken, New Jersey, 2004. [Google Scholar] [CrossRef]
López-González, A.; Meda-Campaña, J.A.; Hernández-Martínez, E.G.; Paniagua-Contro, P. Multi robot distance based formation using Parallel Genetic Algorithm. Applied Soft Computing 2020, 86, 105929. [Google Scholar] [CrossRef]
Liu, S.; Acar, P. Parameter Space Exploration of Cellular Mechanical Metamaterials Using Genetic Algorithms. AIAA Journal 2023, 61, 3633–3643. [Google Scholar] [CrossRef]
Isakhani, H.; Yue, S.; Xiong, C.; Chen, W. Aerodynamic Analysis and Optimization of Gliding Locust Wing Using Nash Genetic Algorithm. AIAA Journal 2021, 59, 4002–4013. [Google Scholar] [CrossRef]
Shu, J.I.; Wang, Y.; Brown, A.; Kaminsky, A. Genetic-Algorithm-Guided Development of Parametric Aeroelastic Reduced-Order Models with State-Consistence Enforcement. AIAA Journal 2023, 61, 3976–3994. [Google Scholar] [CrossRef]
MathWorks. Genetic Algorithm Options (Global Optimization Toolbox; Mathworks, 2023. Accessed: October 24, 2023. [Google Scholar]

Figure 1. Linearization achieved via the procedure presented in Section 4.

Figure 2. Linearization achieved via GA using the first three seconds of nonlinear simulated data, sampled at

T = 0.1 s

Figure 2. Linearization achieved via GA using the first three seconds of nonlinear simulated data, sampled at

T = 0.1 s

Figure 3. Linearization achieved using a GA using the initial three seconds of nonlinear simulated data, sampled at

T = 0.1 s

, followed by

T = 5 s

for the rest of the nonlinear data.

Figure 3. Linearization achieved using a GA using the initial three seconds of nonlinear simulated data, sampled at

T = 0.1 s

, followed by

T = 5 s

for the rest of the nonlinear data.

Table 1. MSE and execution time

Linearization via:	MSE	Execution time
Section 4	$0.0034$	—–
GA (31 samples)	$0.0167$	$355.86 s$
GA (66 samples)	$4.3984 \times 10^{- 4}$	$1304.81 s$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Physics-Based Aircraft Dynamics Identification Using Genetic Algorithms

Abstract

1. Introduction

1.1. Motivation

1.2. Contribution

1.3. Manuscript Organization

1.4. Notation and Definitions

2. Nonlinear 6-DOF dynamic model of a research aircraft

3. Trim Condition

4. Linearization

5. Parameters

6. Main result: Linearization by means of the genetic algorithm (GA)

6.1. Genetic algorithm (GA)

6.2. Linearization via GA

6.2.1. Transition matrix

6.2.2. Fitness function

6.3. Numerical experiments

6.3.1. Experiment 1: GA linearization using 31 Samples

6.3.2. Experiment 2: GA linearization using 66 Samples

7. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe