Preprint
Article
Cognitive Semantics: From Sensations to Contrast, Opposition and Numbers
Altmetrics
Downloads
116
Views
21
Comments
0
This version is not peer-reviewed
Submitted:
19 December 2023
Posted:
21 December 2023
You are already at the latest version
Alerts
Abstract
Cognitive linguistics is founded on the assumption that language is a reflection of universal cognitive principles, implying that all cognitive processes share a common origin. This assumption is known as the 'Cognitive Commitment.' The present article examines the sensory schema hypothesis, which traces all forms of expression back to sensations. This theoretical framework integrates the physicality of the body with sensations that underlie human experiences and their linguistic and non-linguistic expressions. By challenging the traditional dichotomy between mind and body, it provides a more integrated understanding.
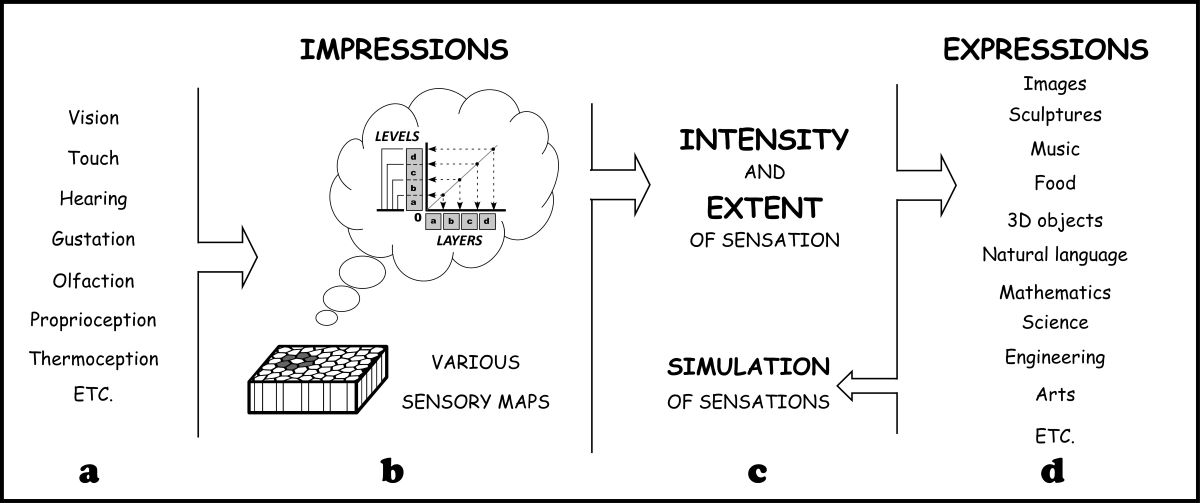
Keywords:
Subject: Social Sciences - Cognitive Science
1. Introduction
Language goes beyond mere words; it opens the door to our embodied experiences and sensory impressions. In the field of cognitive linguistics, which has transformed our understanding of language and human cognition, scholars have challenged traditional notions and embraced fresh perspectives. This framework, known as cognitive linguistics, has revolutionized our understanding of grammar, knowledge frames, and metaphors, as well as vital areas of research such as categorization, embodiment, and cognition.
However, to fully grasp the intricate relationship between language and cognition, it is important to explore theories that establish a conceptual link between sensations and more complex processes such as perceptions and conceptualizations. In this article, I will provide a concise overview of sensory schema theory, its origins, and its applications in natural language and cognition. By understanding how intensity and extent are combined within the elements of sensory schema, we can gain deeper insights into the cognitive processes underlying our language use.
Figure 0.
A representation of sensory mapping experiences (Deviantart DA10526884).

1.1. Many Ways of Understanding Cognition
I will make no attempt to convince you other theories are wrong—in fact, I assume that most of them are partially right.(Feldman 2006: xiv)
The article provides a concise overview of the sensory schema theory, including its origins and some applications in natural language and cognition in general (The article introduces several notions based on the concept of the sensory schema. To aid understanding and avoid obfuscation, the overview of literature in the article has been kept to a minimum.). One of the main objectives of this schema is to establish a conceptual link between sensations and more complex processes. The previous articles by Raykowski (2019, 2022) have characterized the sensory schema as a generalization of topographic/topological sensory maps within the human brain. The basic premise is that spatial patterns in these maps are formed through variations in the intensity of neuronal activation.
It is important to note that the sensory schema, as outlined in Raykowski's work (2013, 2014, 2015, 2018, 2019, 2022), does not seek to replace alternative theories but rather complements them. Therefore, I fully agree with the sentiment expressed in the quote at the beginning of this section. In the spirit of that statement, the ideas presented in this article should be seen not as fully established concepts, but rather as foundational intuitions that contribute meaning to concepts used in higher levels of cognition.
1.2. Materiality of Communication
… language merely provides prompts for the construction of a conceptualisation which is far richer and more elaborate than the minimal meanings provided by language.(Evans and Green 2006: 8)
I hope the readers agree that it is practically impossible to directly experience the sensations and feelings of another being. In order for this to occur, both organisms would need to share the same body and sensory system, which is highly unlikely (Conduit metaphor (Reddy 1979) suggests a non-physical answer to this issue.). This raises a valid question:
How can one individual effectively communicate their thoughts, experiences, feelings, ideas, and intentions to another individual?
To address this question, let's consider two individuals looking at the same chair in front of them. If they are standing close to each other, it is likely that they will have similar, if not identical, visual sensations associated with the chair. In a way, they "share" the sensory experience of that object. (The common sensory experiences do not necessarily lead to identical perceptions.)
Now, imagine that one of the individuals has created the chair as a means to publicly express his or her private experience of sitting in a chair. In order to do this, the individual must physically alter the shared space by constructing and displaying a chair. This process involves acquiring timber, building the object, and painting it. Once the chair is ready, the viewer can be invited to engage with it by sitting in it. Due to its shape, the chair ‘deforms’ the body and, in turn, the molecular structure of specialized receptors, whose neurons are organized into sensory maps in the brain. When integrated, the sensations associated with the chair become multimodal percepts (sensations recognized as a chair), contributing to the object's meaning. (The argument shows how important the physical aspect of communication is. Limiting investigation to natural language and neglecting other forms of human expression is short sighted.)
It is worth noting that there are alternative ways to express private sensations. One example is pointing at or reaching towards an existing chair or its photograph, which provide quicker but less precise alternatives to creating the actual object. (The expressions may also include a person interacting with the object of expression.) Similarly, writing the word "chair" or uttering the sound /tʃɛː/ (In the case of sound, the medium subjected to modification is the air. The human ear responds to temporal variations in pressure.) can evoke associations with the sensory experience of a chair for some of us. However, these expressions differ significantly from the sensations of actually sitting in the chair. While photographs and drawings may capture certain aspects of the original object, such as its shape, sounds and words cannot. They can only serve as symbolic prompts to access meaning elsewhere, which will be discussed in the next section.
1.3. Sensory Schema Origins
The concept of the sensory schema originated from research conducted on contrast in fine art, where the notion of intensity plays a significant role. When considering painting, one method of creating contrast is by juxtaposing areas of the same color but different intensity (e.g., high intensity against a background of low or no intensity). This observation led to the realization that nearly all color expressions in painting convey a sense of intensity combined with extent. (Intensity is used here as a general term for various nested properties of sensation, e.g., private brightness and public lightness of a color.) In fact, it is impossible to express one without the other. Further investigations into expressions in music, technology, mathematics, and science have revealed that they all share this same design, in which intensity is associated with extent. Curiously, natural language appears to be the only exception to this pattern (Raykowski, 2019).
A detailed analysis of color mixtures, such as tints, tones, and shades of a hue (In this article, paint serves as a public and material expression of the private experience of various hues. Both pure black and pure white lack hue altogether. Pure black is formulated to absorb light, while pure white is designed to maximize light intensity. Tint is a mixture of pure colors with added white, shade involves mixing pure colors with black, and tone entails a combination of pure colors with gray.), demonstrated that the extents of their properties are additive, while adding intensities (and similar attributes of a property) is idempotent (more details are provided in Section 3). This analysis drew attention to the nested and private nature of intensity, which depends entirely on a unit, much like a water column depends on a container. Since all units possess an extent, their collections are likely to convey a sense of space that is uniform and public in character. When arranged in two-dimensional surfaces, these units form map-like arrays capable of displaying spatial patterns by varying the activation of their individual elements (see an example in Section 2).
By examining linguistic expressions used to reason about intensity, grades, degrees, ranks, scales, scores, and similar concepts, it was suggested that a column of water in a regular container could be the most suitable way to publicly express the intuition behind the sensory schema. This approach allows for the covert interactions between the intensity and extent of sensations to be publicly expressed and reasoned about in terms of levels, layers, and containers filled with water-like content. The schema enables the grading of all properties and attributes, including abstract ones, by reinterpreting them as substances (see Raykowski 2022). These topics, along with related issues, are further discussed in Section 4. The subsequent subsection delves into the issue of cortical maps.
1.4. Reality of Sensory Maps
One of the most profound findings in neuroscience is that nervous systems exploit topological and topographic organization.(Mark Johnson and Tim Rohrer 2007: 7)
It is essential to keep in mind that the concept of sensory maps originated from studies of human expressions, rather than biology. As a result, this article presents a simplified and idealized top-down model of sensory maps, which may not be confined to a specific region of the brain or a particular function. (The underlying idea is to interpret physiological processes as they are experienced, conceptualized, and publicly expressed by individuals. It is based on the belief that cognition serves as a means to interact with the physical environment.) In previous articles, hypothetical sensory maps in the brain were described as resembling typical sensor-based arrays. The activation of receptors distributed across various surfaces of the human body is mirrored in the brain through topological and topographic arrangements. These initial patterns undergo further processing to extract and enhance various contrasts, ultimately forming the final shape of objects and the direction of their movement. The integration of information from maps of different modalities is utilized in the planning and control of bodily movements.
However, there exists a significant disparity between biological sensory maps and those proposed in the articles. Actual sensory maps are not confined to cortices; they tend to be multilayered, highly interconnected, fractured, overlapping, and malleable. Thus, they differ greatly from the regularity and simplicity of artificial sensors like charge-coupled devices (CCDs). Nonetheless, the most significant distinction lies in the complete absence of any means to directly communicate sensations to the public. For instance, a typical camera possesses both a CCD sensor and a monitor for displaying images. In contrast, sensory maps in the brain serve as both the ‘sensor’ and the ‘display’, making the patterns of sensations accessible solely to the map's owner. In order to express private experiences, sentient beings must physically modify the external environment using their own bodies, as explained in Section 1.2.
While the reality of sensory maps is widely acknowledged, their role in cognition remains underappreciated. The significance of sensory maps arises from the necessity to coordinate voluntary movement. From this perspective, the brain can be interpreted as a large neural network that is topologically not dissimilar, at least in this conceptualization, to electrical circuits. For the information from such networks to be implemented in voluntary movement, stimuli from adjacent areas of the body must reach the brain (e.g., cortices) nearly simultaneously. Achieving this is straightforward in electrical circuits but challenging in biological networks. Compared to signal transmission in wires, the speed of signal propagation along neurons is extremely slow, which may hinder the formation of representations. To ensure the simultaneous arrival of related action potentials, neurons from adjacent areas of the body must have similar lengths. All arrangements exhibiting these properties can be referred to as sensory maps, and concurrent signals can be considered sensory representations. From this perspective, sensory maps can be viewed as a type of network in slow transmission systems (Raykowski 2019). Before delving into the issue of representation in Section 2, it is necessary to revisit the theory of embodied cognition.
1.5. Embodied Cognition
In order to begin this examination, then, I here say, in the first place, that there is a great difference between mind and body, inasmuch as body is by nature always divisible, and the mind is entirely indivisible.(Descartes 1641: 1-31)
The private nature of mental processes is a topic often missing from discussions about embodied cognition. For example, in a 2002 article, Margaret Wilson lists several claims about the embodiment of cognition (Cognition is situated; cognition is time-pressured; we offload cognitive work onto the environment; the environment is part of the cognitive system; cognition is for action; offline cognition is bodily based.), none of which deals with the privacy of thought processes. So far, this subject has been of little interest to researchers, even though most of them would likely agree that no one can experience the sensations and thoughts of other people directly (Most discussions about communication revolve around the conduit metaphor, wherein mental content is transferred between people through a conduit-like means. Unfortunately, this metaphor inadvertently reinforces the idea that thoughts and sensations can be accessed directly.). How human individuals feel and what they think can only be inferred from their overt behavior, with natural language being one example. Therefore, addressing the privacy of thought processes is an important issue that has the potential to redefine natural language as a biological and physical phenomenon. (The schema refers to the processes at lower scales as 'private' in the sense that they cannot be accessed directly from higher scales. For example, sensations experienced by the individual (lower scale) cannot be experienced publicly (higher scale or scales). To make them accessible at the higher scales, they need to be expressed publicly.)
Section 1.2 of the current article describes a simple cognitive strategy in which private sensations and feelings can be expressed by physically modifying the surrounding environment to create material 'expression objects' with which the public can physically engage to experience the intended sensations. The diagram below depicts only a few main stages of such a process:
(Private sensory simulation) individual 1 → (physical modification to public space) individual 1 → (engagement with public expressions) individual 2 → (private sensory impressions) individual 2
Creating expressions by modifying the outside environment is possible only because the body, unlike the mind, is an integral part of its physical surroundings.
To conceptualize cognition fully, any prospective schema has to take into account the public and divisible nature of the physical body and the hidden and inaccessible nature of the mind, which presents itself as a single indivisible and private whole. The proposed sensory schema does exactly that: It connects the nested and private activation levels confined to a sensory unit with a public collection of such units that are concatenated, hence additive and divisible (It also connects the smaller scale of the mind with the larger scale of the body; the indivisible unit with a divisible collection of units; state with process; intensity with extent; content with container; internal with external; additive with idempotent; private with public, and so on.). To interpret sensory maps, the schema refers to a conceptual metaphor of a water container, which makes thinking about abstract concepts possible in terms of the interaction between container(s), levels, and layers of the content.
As a synthetic construct, the schema can be reduced to its 'components,' which explains at least some of the claims made by Wilson (2002) and others. For example, by focusing on extent, one can interpret cognition as being situated and extended, and see the environment as a part of the cognitive system. Emphasizing the nested aspect of the schema, on the other hand, can explain the privacy of the mind and its offline simulations. Only when both aspects are considered together does the sensory schema have a chance to advance human understanding of natural language and cognition in general as biological phenomena.
While the sensory schema offers an innovative perspective on understanding human experiences and their expressions, it also acknowledges the historical context of dualistic thinking, such as Cartesian dualism. However, the theory provides a nuanced approach that goes beyond the strict dichotomy of mind and body, offering a more integrated understanding. It combines the physicality of the body with the physicality of private sensory processes, thereby bridging the ‘gap’ between the subjective and objective realms. (Sensations and expressions are physical processes. Sensation privacy occurs at a lower level than public expression.) In this sense, the theory can be seen as a departure from strict dualism, proposing a more comprehensive framework that accounts for the interconnectedness of physical experiences and the privacy of subjective sensations.
To discuss multifactorial relationships that are difficult or impossible to express with words, the article resorts to the use of diagrams and images. For example, the next section discusses artwork to reveal the structure and workings attributed in this article to sensory maps.
2. Sensory Maps
The non-reflective surfaces of the wood are able to reflect an image because the computer manipulates them to cast back different amounts of light as they tilt toward or away from the light source.(Rozin 1999: artist statement)
In everyday situations, maps are used to depict spatial relations between symbols representing countries, cities, roads, buildings, and other physical features of land and sea. However, sensory maps differ from cartographical charts as they do not utilize symbols. They also differ from mirrors in the conventional sense. To understand the functioning of sensory maps in the brain, we can refer to the artwork "Mechanical mirror (2014)" created by Daniel Rozin, depicted in Figure 1. For the purpose of this analysis, we will overlook programming and technical details and focus solely on the underlying concept of the artwork.
The first striking feature is the large size of the artwork, consisting of 784 identical wooden tiles. Each tile occupies a distinct area, and when combined, they contribute to the overall size of the artwork. This extent can be represented using brackets as ( )( )( )( )... where each pair of brackets represents one tile.
The artwork is uniformly illuminated from above. Due to the identical illumination of all tiles, no discernible image can be observed. Therefore, it is not possible to create images using permanently fixed tiles or a single tile. To create spatial patterns, the illumination of individual tiles must be allowed to vary. One way to achieve this is by rotating the tiles away from the lighting source. Since mechanical rotation is continuous, the degree of tile illumination can be continuously adjusted. Unlike the extent, the illumination of tiles is nested, meaning that higher levels of illumination contain lower levels, eventually leading to no illumination. This nesting can be represented using nested brackets as ((((...)))).
Varying the illumination across an array of tiles generates low-resolution patterns against a well-lit background. These patterns serve to express the spatial relations between the elements. These relations contribute to pattern recognition, which, in this case, is the shape of a human head. For instance, in Figure 1, the head demonstrates that the nose is positioned above the mouth, and the distance between the ears is greater than that between the eyes. The head becomes visible due to the contrast created by areas with different levels of illumination. To achieve this contrast, the artist has employed various materials for the tiles in the past, including wood, rusted metal, plastic, penguin toys, soft pom-poms, and even discarded trash, among others. This demonstrates that contrast relies not on the specific materials used but rather on the capacity of all the pictorial elements to reflect variation. Conversely, the resolution of the image depends on the number of tiles employed in the artwork. It is important to note that this artwork can be used not only to create impressions but also to express and simulate both static and dynamic images. (Impressions are captured by a camera, processed, and then displayed on a panel. Expressions, on the other hand, involve displaying images stored in computer memory. In this context, simulation refers to internally replaying video images without overt/public display.)
Numerous similarities can be drawn between the artwork and sensory maps in the brain. It is my hope that the analysis of "Wooden Mirror 2014" will aid the reader in visualizing the intricate relationship between intensity, extent, contrast, and patterns in sensory maps within the brain. These maps are crucial for enabling human beings to plan their movements. (Sensory maps are integral to multicellular organisms, but they are not essential for reflex-based movement in bacteria and lower-level multicellular organisms.) To move purposefully, organisms must possess an awareness of both the external and internal spatial relations of their bodies (Raykowski 2019), and sensory maps facilitate this awareness. However, before delving into these topics, it is imperative to revisit the concept of orthogonals, which will be explored in the subsequent section.
3. Additive and Idempotent Aspects of Sensations
If you are collecting money and have accumulated $15, then you also have $10.(Johnson 1987: 122)
In the preceding section, the terms "intensity of illumination/brightness" and "extent of intensity" were described as representing two distinct yet related aspects of cognition. These aspects can be visualized using brackets as (((…))) for intensity and ( )( )( )( )... for extent. These two ways of thinking can be categorized as pairs of orthogonyms, and their relationship can be considered orthogonal (Raykowski, 2019). In the context of cognition, orthogonality implies more than just perpendicularity. To grasp this concept, let's consider the notion of value.
For something to possess value, there must be a human being capable of experiencing its significance and expressing it publicly, such as through coins in the case of money. Value can be seen as existing at a private level, which resides beneath the level of its public expression as coins (See also the argument by Raykowski 2018: 122-123). As these levels exist in different spaces, the concept of value and its extent are orthogonal to each other. This is distinct from concepts like north and east, which are perpendicular but not orthogonal since they pertain to the same space. Other examples of orthogonal pairs include the intensity of a hue and its area, the pitch of a sound and its duration, the intensity of pain and its extent, the sweetness of a food and its quantity, as well as the power of feeling and its breadth, the potency of a medication and its dosage, and so on (adapted from Raykowski, 2019: 203).
Idempotence is a concept related to orthogonality. (In this example, the area, typically interpreted as additive, is used to demonstrate the non-additive application of the sensory schema template. The gray color of the rectangles is solely employed to create visual contrast. The example shows that the template can be applied to any property irrespective of its typical classification.) To understand it, let's consider a rectangular area Z in Figure 2a. If the nested rectangles a, b, and c are superimposed on Z (as shown in Figure 2b), there are two possible interpretations of this arrangement. The more familiar one, called an extensive/additive interpretation, is depicted in Figure 2c1, where the sum of the areas a + b + c equals Z. This sum represents an additive relationship, which can be expressed using brackets as ( )( )( ).
Visualizing the diagram (((...))) in Figure 2c2 is more challenging as it involves the intricacies of nesting. For the areas to sum up to Z, rectangle a must be interpreted as already encompassed by b and c, and rectangle b as already contained within c. This implies that (a + a + a) + (b + b) + c equals (a + b + c), resulting in Z as shown in Figure 2b. Only then are the images in Figure 2c2 and Figure 2b equivalent. This arrangement represents an intensive/idempotent interpretation, and the transition from the left to the right of the above equation is referred to as cognitive idempotence, signifying that the entities that are part of themselves are non-additive (adding a to itself remains a). However, if the rectangles in Figure 2c2 are interpreted as three separate and unrelated areas of identical color intensity, their total would exceed Z. In such a case, the areas a, b, and c behave as additive extents.
The interaction between additive and non-additive (idempotent) properties can be observed in both scientific and everyday situations. For example, adding a solution of a certain concentration to another solution of the same concentration increases the overall amount of the solution without changing its concentration. Similarly, adding 5 cars traveling at a speed of 100 km/hour to 5 cars already traveling at that speed is an idempotent action as it doesn't alter the overall speed but doubles the number of cars. This principle applies to various scenarios, such as when water of a certain temperature is added to water of identical temperature, or when red paint of a particular intensity is mixed with red paint of the same intensity (Raykowski 2014, 2018, 2019).
As demonstrated by the examples above, idempotence defines the concept of addition. To add two entities, they must possess not only identical properties but also the same intensity of those properties, though not necessarily the same extent. This distinction is crucial for a proper understanding of addition versus mixing, which will be discussed in Section 5. However, before delving into that topic, it is necessary to revisit and examine the concept of sensory schema in greater detail.
4. The Sensory Schema
It is often assumed that complex concepts emerge late in cognitive processes or that they are socially created. One reason why this might not always be the case is that human intuition of intensity and extent already exists at the level of sensations.(Raykowski 2022: 245)
In Section 1.1 of this article, the concept of sensory schema is presented as an extension of sensory maps within the human brain. Interestingly, the proposal of the schema originated not from the field of biology but from linguistics, as discussed in Section 1.3. A perplexing discrepancy emerged when comparing expressions in science, visual arts, and technology with those in natural language. While non-linguistic expressions fully specify properties in terms of intensity, extent, and similar concepts, natural language often falls short in this regard. This issue was carefully examined (Rajkowski, 2013; Raykowski, 2014, 2018, 2019, 2022), revealing that most, if not all, non-linguistic expressions are either directly derived from sensations or incorporate sensory experiences. This observation emphasizes the biological interpretation of the sensory schema.
The issue with the biological perspective is that sensations are often regarded in many scientific fields as raw data without inherent meaning (e.g., see Evans and Green, 2006), and therefore they are not expected to possess any internal structure that can be inherited (The matter is further complicated by the use of undefined cluster terms such as sensory experience, sensory perception, sensory input, sensory-perceptual experience, and sensory information/data.). However, not everyone subscribes to this interpretation. I have been developing a theory that sensations are not only meaningful but also universally influential in cognition. Since "everything we know about the world comes to us through our senses" (Fain, 2003: 1), it is expected that the intensity-extent relationship exists in all forms of expression, including natural language. Given their ubiquity, these aspects of sensation are likely crucial factors in governing language and cognition in general.
Beyond their widespread influence, the significance of intensity and extent lies in the fact that they represent two distinct yet closely related intuitions. Intensity captures the nested aspect of properties, while extent exemplifies the repetition of units containing those properties. The sensory schema merges these different modes of thinking into a unified concept that cannot be separated, as both aspects are necessary for viable expressions. Several examples of such combinations include intensity combined with extent, nesting with concatenation, value with range, magnitude with multitude, quality with quantity, amplitude with period, rank with range, degree with scope/interval, pitch with duration, rise with run, velocity with time, density with volume, force with displacement, pressure with area, mass with velocity, cardinals with ordinals, and more broadly, levels with layers/containers. It is important to note that the schema is designed to handle one attribute at a time, and when associated with other attributes, it creates a sense of an object or process.
4.1. Layers, Levels, and the Water Column
Whether derived from sensory-map studies or rooted in language, the sensory schema is an intuitive concept. In order to engage in reasoning about this intuition with others, it is necessary to express it publicly, and the most effective means of doing so is by invoking a routine experience of handling water (Raykowski, 2018). Figure 3a illustrates the accumulation of water in a container. The different stages of pouring water can be represented using brackets:
( ) for stage one, ( )( ) for stage two, ( )( )( ) for stage three, and ( )( )( )( ) for the final stage. Each pair of brackets represents a single layer. Thus, the process of pouring water and its accumulation in the container are inherently additive.
On the other hand, levels represent a nested arrangement, which can be visualized using brackets as follows: ( ) for the first stage, (( )) for the second stage, ((( ))) for the third stage, and (((( )))) for the final stage. Unlike layers, levels exhibit idempotence, making them nonadditive (refer to Section 3 for further details). Layers and levels are intricately linked: Every time a water layer is added, the water level in the container rises. It is important to note that the water must be added using the same cup. This aspect is critical for conceptualizing the schema, which will be further elaborated in the subsequent section.
4.2. Sensory Schema Expressions
The water column depicted in Figure 3a combines both levels and layers into a unified concept. Since levels and layers are orthogonal concepts, they can be represented using two perpendicular axes. (To avoid any association with Cartesian coordinates, the lines are deliberately devoid of arrows.) This visual representation, as shown in Figure 3b, helps to highlight the relationship between levels and layers. The 45-degree diagonal line, which represents the points where layers intersect with levels, aids in visualizing this relationship. The nested levels are depicted on the vertical axis, while the horizontal axis represents the repetition of discrete layers. Unlike layers, which contribute to a sense of space, levels represent a non-spatial relationship.
Due to their non-spatial nature, there can be infinitely many nested diagrams of levels that illustrate identical relationships, potentially leading to ambiguity in expressions. To eliminate ambiguity, it is necessary for all layers to be identical. This is achieved by adding water to the container using the same cup, ensuring that the relationship remains independent of layer thickness (refer to Raykowski, 2018: 112-118 for further details). The layers on the horizontal “axis” are not only identical through unit repetition, but they are also concatenated, meaning that there are no spatial gaps between them. Examples of this repetitive nature of layers include steps in walking or running, centimeter units on a measuring tape, periods of sound, degree intervals on a thermometer, and so on—all of which have the potential for endless repetition.
4.3. Reciprocal Relationship Between Levels and Layers
Layers and levels are intricately connected through the sensory schema, influencing each other in significant ways. New levels are created by adding layers first. Layers impose their characteristics of regularity, discreteness, and a sense of progression, as well as their spatial and kinetic nature, onto static levels. By imposing repetition onto nested levels, an impression is created that the differences between subsequent levels are identical and equal to the thickness of the layers.
On the other hand, levels project their sense of nested order and confinement, along with their static and finite nature, onto the potentially infinite repetition of layers. For instance, when the containment associated with levels is applied to the repetition of layers, it generates a perception of the process being halted, terminated, and bounded.
Conceptual duality is another example of reciprocity observed in most properties. For instance, one can describe the container in Figure 3 as having three cups of water, which is an interpretation based on layers, or as a four-level container that is three-quarters full, which is an interpretation based on levels. Continuity is another concept that demonstrates reciprocity. There are two interpretations of continuity: one related to layers, where continuity implies concatenation without spatial gaps between subsequent extents, and the other related to nesting, where continuity refers to indivisible units. Since nesting cannot be divided without losing its essence, such units are perceived as internally continuous.
Reciprocity can be observed in various domains, including temperature, time, distance, area, volume, mass, numerosity, as well as abstract concepts like monetary value, poverty, health, luck, importance, and death. All of these concepts can be interpreted in terms of unit repetition and nested arrangements. For instance, we can express that half of a tree is dead, representing an extensive interpretation, or that the tree has a fifty percent chance of returning to full health, representing a nested interpretation. Another example is the concept of real numbers, which involves nested interpretation, and positive integers, which involve concatenated interpretation.
Due to limited space, a detailed analysis of the interactions between levels and layers will be presented through the examination of practical applications of the sensory schema. These applications include cognitive products and the concept of contrast, which will be explored in relation to absolute, relative, binary, and opposition.
5. Cognitive Sums and Products
Whether we are aware of it or not, the sensory schema is employed in our everyday interactions with money. In this section, I will utilize this cognitive framework to shed light on the operations of addition, multiplication, and mixing as they are understood within the context of the sensory schema. Money, given its widespread use and the distinct separation between values and their physical representations, serves as the ideal candidate for examination.
Figure 4 shows a small collection of units depicted as containers along the horizontal axis. The vertical axis represents values, a property attributed to money by humans. Similar to intensity, values in the context of money exhibit a nested structure as explained in Section 4.1. When it comes to money, the individual perception of value is typically conveyed publicly through coins and paper bills, symbolized by the containers on the horizontal axis. These three elements—the container-like property, values, and their physical expressions—are intricately linked in a consistent manner: while specific aspects of the sensory schema may vary, their overall relationship remains unchanged.
To demonstrate these concepts, let's consider the scenario of making a payment amounting to $12. There are various ways to achieve this, limited only by the available denominations, which, in Australia, include coins such as ¢10, ¢20, ¢50, $1, $2, and bills of $5 and $10. Please refer to the example below:
[1] $12 = ($2 value ∙ 6 multiple) = ($1 value ∙ 12 multiple) = (¢50 value ∙ 24 multiple) = (¢20 value ∙ 60 multiple) = (¢10 value ∙ 120 multiple) = PRODUCT
Each of the five forms of payment, which combine a private intuition of monetary value with public coins, can be described as sensory/cognitive products that are equal and equivalent, though not identical. These products provide a flexible means of human expression, allowing for payments to be made using any agreed denomination.
While there are numerous configurations of products, three of them hold particular significance in terms of cognition. The first configuration involves the accumulation of layers within a single container, as depicted in Figure 4a. This representation, known as the intensive representation of products, emphasizes the nested arrangement of levels. It functions as an indivisible unit that cannot be divided or multiplied by a fraction (Raykowski 2019). The intensive representation of products finds use not only in grading adverbs, adjectives, and other properties (Raykowski, 2022), but also in multiplication and comparisons between units sharing the same property.
Figure 4b illustrates extensive accumulation, which involves a product with a value of $1, the lowest denomination in the example. In this configuration, the accumulation contributes to a sense of space occupied by the coins. This aspect of the schema epitomizes the intuition of addition, sum, and space.
The square representation depicted in Figure 4c represents yet another significant concept, with its value being ‘identical’ to multitude, thus explaining its name. The significance of this representation is discussed in Raykowski (2018).
To further illustrate the above topics, let's examine a few examples. Consider the formula ($2 value ∙ 6 multiple) in [2]. This formula represents a product with six two-level nested brackets. (The brackets (((( in (((( )))) can be replaced with a single bracket ( or with [, both of which represent the empty container. To maintain simplicity, I refrain from using notations ( )))) or [ )))) in this article.) Which can be converted to 12 single-level brackets. The extensive representation of products redefines addition as concatenation and division as the reverse process of concatenation, as discussed in Subsection 5.1.
[2] $12 = $2 value ∙ 6 multiple = (())(())(())(())(())(()) product =()()()()()()()()()()()() extensive product
[3] $12 = $12 value ∙ 1 multiple = (((((((((((( )))))))))))) intensive product = { } unit
Twelve dollars can also be depicted using a single "container" as shown in [3]. Depending on the need, one can switch between various representations and forms of accumulation due to the flexibility of products. Apart from using coins, one can pay $12 using bills, as depicted in example [4]. However, there is a distinction: despite the "+" sign suggesting addition, the operation cannot be completed unless the ten-dollar banknote is converted into two-dollar or one-dollar coins (not shown) (Similarly, expressions of decimal numbers (e.g., 158 = 100x1 + 10x5 + 1x8) cannot be added unless they are all converted to the same magnitude, typically the unit of one.)
[4] $12 = ($10 value ∙ 1 multiple) + ($2 value ∙ 1 multiple)
Example [5] demonstrates another application of product representations in repeated multiplication. Let's consider multiplying a one-dollar coin by four, and then multiplying the resulting product by three:
[5] $1 ∙ 4 ∙ 3 = ($1 ∙ 4) extensive ∙ 3 multiple = ($4 ∙ 1) intensive ∙ 3 multiple = $12
The task of multiplying becomes easier if the extensive representation is converted into intensive representation.
The sensory schema can also be utilized to derive powers. Let's consider the example of 25 (two raised to the power of five). If 2 is represented extensively, it needs to be converted to the intensive representation before being repeated twice: 2intensive ∙ 2extensive = 4extensive. The resulting product of 4 needs to be converted to the intensive representation and then repeated twice: 4intensive ∙ 2extensive = 8extensive. Again, the resulting product of 8 must be converted to the intensive representation to be multiplied twice, and so on, until we obtain 32. Multiplication involving fractions and negative numbers is discussed in Raykowski (2018).
5.1. Cognitive Concatenation and Division
Cognitive addition differs slightly from mathematical addition because it is defined in the context of sensory maps visualized as arrays of containers. Take the example in [6]:
[6] ()()()()()() _ _ _ ()()() = ()()()()()() ()()() _ _ _
Adding, or more accurately, concatenating, involves removing three empty containers (marked with underscores) between the addends. It's important to note that the underscores are moved to the right (or left) of the array, so the overall size of the array remains unchanged. (Space can be represented without fully empty containers as long as a clear contrast between objects and the background space is maintained.) Division, on the other hand, reverses the process by inserting empty containers between elements of the product. (Division in this framework does not always involve equal parts.) As depicted in [7], this process can be applied to the addition of multilevel products as long as their levels are identical. A similar approach is employed to represent movement across maps.
To summarize, the cognitive interpretation of addition and division involves map-like sensory arrays that can vary the activity, intensity, value, and other properties of their elements. This implies that not everything can be added together: Only expressions with the same property and identical levels of that property can be concatenated. In cases where the property is the same but the value is different, we are not dealing with addition but rather a process of mixing, which will be addressed in the next section.
5.2. Cognitive Mixing
Cognitive products can be found everywhere as there can be no interpersonal communication without a product of private meaning and public expression of it. Some experiences are naturally private (love, hate, importance, force, effort, pain, etc.) while others are derived. Out of many likely examples, consider concentration defined as the mass/ volume/ amount of a constituent divided by the volume or mass. Concentration can be dimensionless, expressed as a number, ratio, fraction, or percentage. The notion is already discussed in primary schools. Let's consider a typical word problem involving the addition of volumes of orange juice with different concentrations. Let's start with drinks of the same concentration, 20%:
[7] (400 ml) 20% + (1500 ml) 20% = (400 ml + 1500 ml) 20% = (1900 ml) 20%
As discussed earlier, adding products of the same concentration results in an increase in volume, not in the concentration level itself. However, adding drinks of different concentrations is not additive in the way just described, as it leads to a mixture with a different concentration: (The concentration of the mixture in [8] is calculated as follows: (400 ml) 20% + (1500 ml) 10% is converted to the respective volumes of pure juice, which are 80 ml + 150 ml, resulting in a total of 230 ml. The total drink volume is 400 ml + 1500 ml, equaling 1900 ml. Therefore, the resulting drink concentration is approximately (230 ml / 1900 ml) % = 12.1%, hence (400 ml) 20% + (1500 ml) 10% = (1900 ml) 12.1 %)
[8] (400 ml) 20% + (1500 ml) 10% = (1900 ml) 12.1 %
Without mixing, it would be impossible to achieve harmony or contrasts by altering the tint or shade of paints, adjusting the sweetness or taste of drinks, changing the consistency of food, modifying the concentration of medication, creating concrete with specific strength, adjusting the temperature of a mixture, and so on.
The argument presented in Section 5 can be extended to include other concepts, such as the intensity of sensation, color perception, love, importance, or levels of education, to name a few. This way of expressing sensations as sensory products is a part of cognitive processes. It is also common for humans to transform highly variable experiences into static products characterized by constant intensity or value, which makes their identification, processing, and simulation faster. To make products easier to identify, the background they are set against needs to exhibit contrasting levels of intensity. The role of contrast in cognition will be explored further in the subsequent section.
6. Concepts of Contrast
Contrast refers to the noticeable differences between two or more levels, elements or aspects of a property or properties, qualities, and characteristics. It manifests across diverse domains, including sensory experiences, language, music, art, and more. Contrast serves to highlight differences, draw attention, create emphasis, and improve clarity. In its most basic form, contrast refers to noticeable differences observed among levels of sensory experiences. According to the sensory schema outlined in Section 2, contrasts can only be created within large arrays comprising identical elements capable of incremental activation. In the case of single property, contrast can be analyzed by exploring nested levels within a single container.
6.1. Absolute Contrast
In context of the sensory schema, absolute contrast is a difference between the activation levels of a pattern and its background of lesser or no activation. The strongest contrast occurs when the background activation is zero (e.g., a bright star in the background of a black sky). While contrast sensitivity can vary with age and among individuals, there is always a threshold below which the detection of activation becomes impossible. It is the existence of this zero level that establishes the nested structure, giving rise to the concept of absolute contrast derived from it.
Figure 5a depicts absolute contrast between a pattern and its background, represented by a single cell of a large array dedicated to wealth. The cell activation is nested in the sense that the 100% level of activation already contains the 80% level, which contains the 60% level, and so on. At the bottom of each nest is a 0% level (referred to as an absolute zero), which, in this case, stands for the total absence of wealth (destitution).
If generalized, container schema can represent not only individual sensory domains such as touch, vision, and pain but also a host of concrete and abstract properties, such as wet-ness, full-ness, good-ness, etc., in which negations (not wet, not full, not good) are understood as the absence of the respective content. Examples of absolute scale in physics include Kelvin temperature scale and measures of the International System of Units (SI).
To grasp the concept of contrast fully, a solid understanding of nesting is essential. When comparing two or more levels it is crucial that they coexist in the same temporal and spatial context. This implies that they represent an internal state of independent units, unaffected by external influences or constraints. Due to their private nature, and boundedness, all absolute scales can be described as universal, unconditional, complete, and internally consistent. For those reasons, they are often used in natural language as an intensifier, as in "absolutely certain", which means the absence of any doubt; or to describe an unlimited disposition (e.g., absolute power, absolute monarchy, absolute truth, etc.).
In summary, absolute contrast represents the most basic experience. There is no room for ambiguity in the case of absolute scales: they express a single property, hence there is only one zero, and each layer is associated with only one level. Importantly, there is only one direction of accumulation, and, as a result, there is only one way in which accumulation can be undone. In light of all of these characteristics, the absolute scales should be viewed as the most basic cognitive mechanism used to conceptualize all other scales and associated contrasts, including relative contrasts discussed in the next section.
6.2. Relative Contrasts
The sensory schema is a template-like arrangement from which different concepts and processes can be derived. One such concept is a relative scale and, based on it, contrast. Let's consider the scale of wealth shown in Figure 5b. Unlike the grading in Figure 5a, where poverty is synonymous with destitution, Figure 5b presents poverty grading as wealth below the 40% level of the wealth scale. The relative zero on the absolute scale defines two asymmetrical concepts: a below-zero range (e.g., poor), positioned between absolute and relative zeros, and the range above relative zero (rich).
The concept of negation in relative grading is complex as it encompasses the entire sub-range of poverty, rather than just one level as observed in absolute contrast. For example, the statement "He is not rich" could imply that the person is destitute (with no assets) or possesses assets ranging from 0 to 40 percent of the maximum wealth. Contrast also becomes more intricate: while absolute contrast is between a specific level and absolute zero, relative contrast can encompass any range between 0% and 40% (lower bound) and 100% (upper bound) of the wealth scale. The notions of relative contrast are subject to interpretation by individuals, making them subjective.
The direction of accumulation is not clear because both subscales rely on the absolute scale as a reference. Consequently, relative concepts are often susceptible to misinterpretation. For instance, pairs such as 'rich and poor,' 'long and short,' 'high and low,' and 'hot and cold' are frequently interpreted as binary oppositions. However, in the context of relative scales, this interpretation is incorrect because both subscales are juxtaposed not against each other, but against the absolute scale. As a result, they cannot be considered in opposition, as they refer to the same absolute property and are merely different ranges of that property. Furthermore, these subscales are asymmetrical in that the below-relative-zero range is limited, while the range above it is not. (The relationship between two temperature ranges, such as above and below relative zero, where they appear to oppose each other, can be described as "complementary" or "contrasting.")
Relative scales are widely used and typically associated with expressions of status, ranks, ratings, scores, marks, gradings, and ordering, among others. In addition to the examples mentioned earlier, relative scales also encompass constructions that refer to minimum levels of various aspects, such as minimum wages, protection, proficiency, energy intake, competence, inventory, training, taxation, and more. These examples all share a common structure in which levels of relative properties are referenced in relation to the absolute scale of that property. A similar framework is applied in concepts like relative temperature scales (e.g., Celsius and Fahrenheit scales), the concept of distance above and below sea level, and the concept of the future and the past, with the latter bounded by the beginning of time.
6.3. Binary Contrast
In various logical constructs, intermediate gradation levels are intentionally disregarded or excluded, leading to binary or bivalent relations. This concept is exemplified in Figure 5c, where only two levels, 0 (false, or off) and 1 (true, or on), are present. Unlike the arrangement depicted in Figure 5b, where an individual with 40% of wealth could still be considered poor, Figure 5c illustrates a binary distinction between being rich and not being rich. Classical logic adheres to the "principle of excluded middle," (Łukasiewicz 1951) which limits the relationship to these two nested levels of a property. The nature of binary logic intensifies the sense of contrast, reinforcing and solidifying the relationship between contrasting expressions.
Note that in the context of the sensory schema, '1' represents a level of a property, while '0' signifies the absence of that property. Therefore, the zero level, or an empty container, denotes the negation of the property. In non-mathematical reasoning, distinct names are often assigned to these levels (such as on-off, true-false, rich-poor, open-closed, wet-dry, etc.), which might suggest an opposition between two properties rather than the negation of one property. However, it is important to observe that the statement 'the switch is either on or off' (opposition) does not have exactly the same meaning as 'the switch is either on or not on' (negation). In logic, since it deals with one attribute at a time, negation cannot be interpreted as a different property, and logical expressions should not be perceived as an opposition between two properties. There are other inconsistencies associated with oppositions, which will be further discussed in the next section.
7. Generalized-Opposition Contrast
The concept of opposition is often misconstrued as relative scales, which are typically defined in relation to a single property. For instance, short and long are usually understood in relation to the absolute property of length. These terms represent different length ranges defined by a relative zero point. However, to truly embody opposition, both short and long must be interpreted as distinct absolute properties depicted by two sensory schema diagrams, as shown in Figure 6. According to this interpretation, opposition arises from the contrast between two absolute properties within the same category.
Oppositions, such as friendly and unfriendly, always involve two distinct and absolute properties that can be independently graded. However, this is not the case with negations. For instance, the negation of the word friendly is not friendly, which means the absence of friendliness altogether. Negations always refer to the property they negate.
As an illustration of opposition, let's consider in greater detail the properties of debit (property X) and credit (property Y), depicted in Figure 6 with diagrams facing away from each other. In order for properties X and Y to establish a quantifiable relationship, they must pertain to the same category (e.g., money), share a common zero level (representing their containers), and utilize an identical unit of accumulation (e.g., a dollar coin). Consequently, the values assigned to both properties align, allowing for the reconciliation of their respective balances.
In the case of both debit and credit, the accumulation process typically begins with an empty container (at moment ta). The content levels increase with each added layer at tb, tc, … to te. Changes in value levels only occur through the addition or removal of layers. Since non-existing layers cannot be physically removed, the process of reversing accumulation can only be carried out from the last step (at moment tf) until the container reaches an empty state (zero level). It is important to note that both debt and credit accumulations are independent, potentially infinite, and symmetrical in this conceptualization. (The apostrophe (' ) is used to distinguish the timing between properties X and Y.) As absolute properties, they can be added or removed independently.
Contrast in the context of generalized opposition refers to the difference between the levels of two absolute properties. In the realm of money, contrast denotes the disparity between credit and debit levels. For example, the contrast between $100 of debt and $160 of credit is not simply the account balance of $60 credit, but rather the "sum" of two absolute values, $100 and $160, understood as layers publicly expressed through coins and/or bills. This is depicted in Figure 6 as a 'distance' B-0-D, often described as the total distance from the common zero.
Generalized opposition, being a way of thinking, can occasionally lead to unrealistic conceptualizations. For instance, in the case of negative temperature within generalized opposition, the extension can be endless, despite the well-known fact that the cold part of the Celsius scale cannot go below −273⁰C, which corresponds to 0⁰K. Similar situations arise with other relative pairs, such as poverty, shortness, lowness, or dryness, which can be conceptualized as unlimited absolute properties.
A generalized version of opposition is a highly productive approach. It is often employed in literary techniques to compare and contrast ideas, individuals, subjects, objects, and events. It is important to remember that, within the context of the sensory schema, all these entities are experienced as associations of properties that can be reduced to sensations. For example, the opposites man/woman, masculinity/ femininity, teacher/student, and Christian/non-Christian are compared based on their respective properties, rather than as contrasting terms defined against each other.
This concludes the analysis of contrasts discussed in the context of the sensory schema. The next section introduces an example of the sensory schema's application, which is important for understanding natural language: integers and a number line.
8. From Opposition to Number Line
The previous section's discussion highlights the crucial role of accumulation in the formation of opposition. The independent nature of debt and credit arises from their distinct directions of accumulation. Consequently, reversing the accumulation direction of one property has the potential to unify the opposing properties into a cohesive system. This rationale is depicted in Figure 7.
8.1. Semi-Opposition
Consider a scenario where fulfilling obligations, such as paying off a mortgage for a house or car, significantly improves a person's financial situation. From a credit perspective, the act of debt repayment can be viewed as accumulating credit. This interpretation can be achieved by reversing the direction of debt accumulation and aligning it with the accumulation of credit, as shown in Figure 7. The resulting construct represents a transformation of two opposing properties (two containers) into a single property (one container), with ranges determined by the position of the zero-point. The unified accumulation is depicted in Figure 7 with a sequence of white arrows on a black background.
As a consequence of this unified accumulation, the addition of layers for property X occurs prior to the accumulation of property Y: t1 → t2 → t3 → t4 → t5 → t6 and so on. It is important to note that this does not imply that debit is less than zero; it simply indicates that any step to the left of a given point occurs earlier. It is worth mentioning that numbers are used here for reference purposes only. The resulting concept bears some resemblance to generalized opposition in certain aspects, and to a relative scale with a relative zero but no absolute one in other aspects.
… --------------------- 0 ---------------------->
Property Property Y
The construct derived through this process suggests the simultaneous presence of absolute zero and its absence. For this reason, I refer to this concept as semi-opposition. Similar to generalized opposition, contrast in semi-opposition is the difference between the levels of two absolute properties, which can be described as the sum of the distances B-0 and 0-D. The significance of this conceptualization lies in its potential to derive mathematical notions such as integers, number lines, absolute values, scales, dimensions, and their equivalents in natural language.
8.2. Integer Schema
The concept of semi-opposition, as outlined in the previous subsection, may offer an answer. By reinterpreting debt repayments as credit, the opposing concepts can be unified through the common direction of their accumulation. However, one issue still remains: should we invert the values of property X when its accumulation is reversed?
The transformation described can be seen in Figure 8, where nested values of property X (e.g., debt) are depicted below the accumulation line, while values of property Y (credit) are shown above it. Similar arrangements can be observed in expressions such as temperature below/above zero, elevation below/above sea level, wages below/above average, and so on. This arrangement necessitates the adoption of distinct names to differentiate magnitudes below and above zero. Values above the horizontal line are generally interpreted as positive (e.g., pleasant), while values below the line are considered negative (unpleasant). In natural language, positive properties are typically unmarked, while negatives are marked by adding a prefix. Similarly, in mathematics, negative numbers are denoted by a minus sign, while positive numbers remain typically unmarked. Symbolically, the diagram can be represented using inequalities as
… -5 < -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5 …, with symbols to the left of zero referred to as negatives and those to the right as positives.
In the context of the Figure 8 diagram, the direction of the 'greater than' sign indicates an increase in value from left to right. It's important to note that the diagram represents an extended version of the sensory schema and should not be confused with Cartesian coordinates, which are discussed in the next subsection.
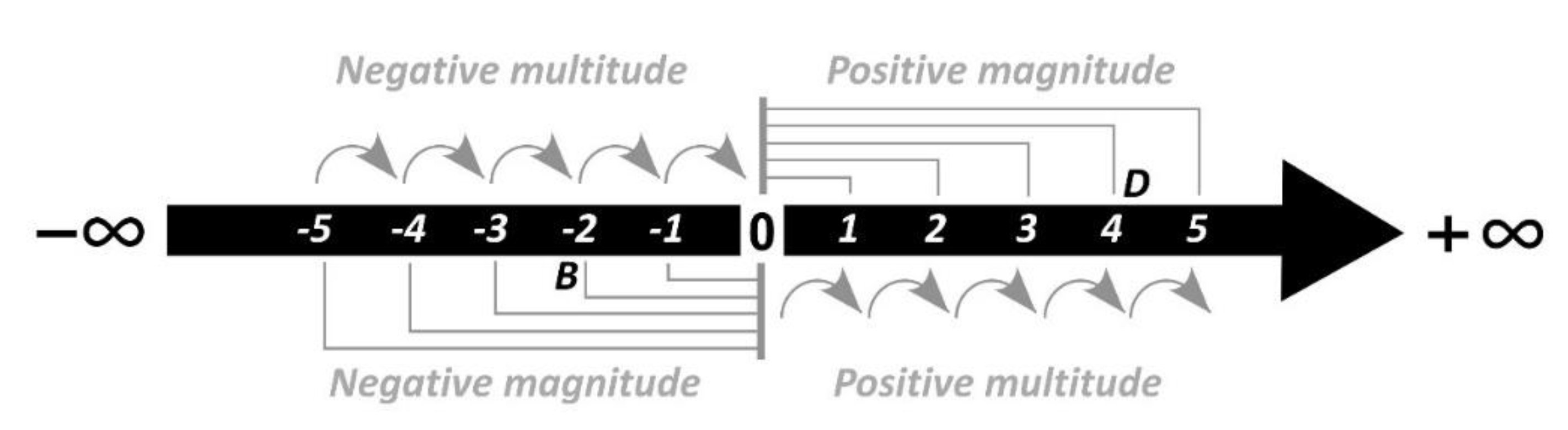
8.3. Number Line Concept
One form of the diagram in Figure 8 is commonly known to most users as the 'number line'. Its diagram is created by rotating the vertical magnitude line around the zero point towards the horizontal multitude line (as shown by the broken-line arrows in Figure 8) until they merge into a single axis in Figure 9.
The number line is represented by a black arrow, and its conceptual structure is depicted in grey. It illustrates a common direction of accumulation and two distinct value systems: negative and positive magnitudes. Because it combines nested magnitudes with concatenated multitudes, the number line can be considered as a dimension from which multidimensional (coordinate) systems can be constructed. Examples of such constructions include two- or three-dimensional Cartesian coordinate systems, vectors, and various scales.
The number line finds relevance not only in mathematics but also in everyday situations. Take walking as an example. If we consider the starting point as the zero point, each step taken accumulates distance away from it (positive valence). Walking back involves undoing the original action, and going further than the starting point can be interpreted as missing the target (negative valence). This example demonstrates that the concept of the number line can be applied not only in mathematics but also to everyday life.
Due to its broad applicability, the number line serves as a foundation for a wide range of expressions, extending beyond mathematics into natural language. Its generality allows it to underpin various linguistic and cognitive constructs (The PATH image schema (Johnson, 1987) and its derivatives reflect the structure of a number line, highlighting the intuitive understanding of sequential progression.), which include factive motion (She ran/walked from the suburbs to the city), fictive motion (The road/path/track winds through the mountains), emotional intensity (Her anger escalated gradually), degree of agreement (I partially agree with your statement), levels of difficulty (The exam was more difficult than I thought), intensity of pain (The pain level gradually eased), to mention a few.
The relationship between the number line and natural language is not coincidental. According to cognitive linguistics, these two forms of reasoning are grounded in the same cognitive processes, resulting in comparable structures in their expressions. This can be demonstrated by examining conceptual metaphors such as "MORE IS UP; LESS IS DOWN," "HAPPY IS UP; SAD IS DOWN," and other metaphors relying on the spatial orientation of up and down (Lakoff and Johnson, 1980: 15). The consistent association of these concepts with the up-down orientation may initially appear puzzling. In my view, both the number line and these metaphors are rooted in a shared experience. They represent different manifestations of the sensory schema and, consequently, of the number line. While the up-down orientation is a crucial aspect of the number line, it is just one facet of its broader concept.
9. Conclusions
Biological senses play a crucial role in shaping our understanding of the world. The shared structural similarities among sensory organs contribute to a consistent sensory experience across all modalities, implying a fundamental relationship between different features of sensations. To uncover and elucidate these relationships, semantics must broaden its scope beyond natural language to include all forms of human expression. Only through such a comprehensive approach can we realize the goals of the 'Cognitive Commitment.'
The sensory schema exemplifies this endeavor by addressing the commitments and assumptions of cognitive linguistics and exploring the embodiment thesis to clarify its meaning. Due to its complexity and prelinguistic origins, the sensory schema can be publicly expressed through conceptual diagrams. By gaining insights into the structure, organization, and manifestation of sensory experiences, we can deepen our understanding of the foundational concepts that underlie human comprehension and reasoning. Additionally, the schema holds potential for practical applications in linguistics, communication, education, design, technology, and interdisciplinary collaborations. It is important to note that research on the sensory schema is still in its early stages, requiring an interdisciplinary effort. (Musical notation, for example, provides a vast treasure trove of sensory expressions that still awaits systematic exploration.)
In summary, the sensory schema offers not only a theoretical framework for understanding human sensations and their expressions but also practical benefits. Although still in its early stages, the exploration of the sensory schema holds promise for advancing various fields of study.
References
- Descartes, René. 1641. Meditations on First Philosophy. In Internet Encyclopedia of Philosophy, 1996. This file is of the 1911 edition of The Philosophical Works of Descartes (Cambridge University Press), translated by Elizabeth S. Haldane.
- Evans, Vyvyan and Melanie Green. 2006. Cognitive Linguistics: An Introduction. Lawrence Erlbaum Associates, Publishers. London.
- Fain, Gordon. 2003. Sensory Transduction. Sunderland: Sinauer Associates, Inc.
- Feldman, Jerome A. 2006. From Molecule to Metaphor: A Neural Theory of Language. A Bradford Book. The MIT Press.
- Johnson, Mark. 1987. The Body in the Mind: The Bodily Basis of Meaning, Imagination, and Reason. Chicago: University of Chicago Press.
- Johnson, Mark and Tim Rohrer. 2007. We Are Live Creatures: Embodiment, American Pragmatism, and the Cognitive Organism. In Body, Language, and Mind, vol. 1, 17-54. Zlatev, Jordan; Ziemke, Tom, Frank, Roz, Eds.; Dirven, René (eds.). Berlin: Mouton de Gruyter, 2007. [Google Scholar]
- Lakoff, George and Mark Johnson. 1980. Metaphors We Live By. Chicago and London: The University of Chicago Press.
- Łukasiewicz, J. (1951). Aristotle’s Syllogistic from the Standpoint of Modern Formal Logic. Clarendon Press.
- Rajkowski, Wieslaw (Wes). 2013. Conceptualising Experience: What Human Expressions Suggest about Cognition. Doctor of Philosophy thesis.
- Raykowski, Wes. 2014, Conceptual Understructure of Human Experience: Volume 1 (Thesis). CreateSpace, North Charleston, South Carolina.
- Raykowski, Wes. 2015. Conceptual Duality of Mathematical Expressions.
- Raykowski, Wes. 2018. Layers and Levels: What a Column of Water Tells Us About Human Cognition. Cognitive Semantics, 4(1): 104–134.
- Raykowski, Wes. 2019. Is There Such a Thing as Orthogonyms? Cognitive Semantics, 5(2): 201–223.
- Raykowski, Wes. 2022. Sensory Schema: From Sensory Contrasts to Antonyms. 2: Cognitive Semantics 8 (2022), 2022.
- Reddy, M. J. (1979). The conduit metaphor: A case of frame conflict in our language about language. In A. Ortony (Ed.), Metaphor and Thought (pp. 284–310). Cambridge: Cambridge University Press.
- Rozin, Daniel. 1999: Artist statement. Wooden Mirror 1999 / 2013. Photo credit Bitforms Gallery. https://history.siggraph.org/artwork/daniel-rozin-wooden-mirror/ accessed on July 1, 2023.
- Wilson, Margaret. 2002. Six views of embodied cognition. In Psychonomic Bulletin & Review 9(4): 625-636.
Figure 1.
Daniel Rozin (Wooden Mirror 1999 / 2013) Photo credit Bitforms Gallery. 28x28=784 tiles.

Figure 2.
Additive and idempotent properties of sensations.
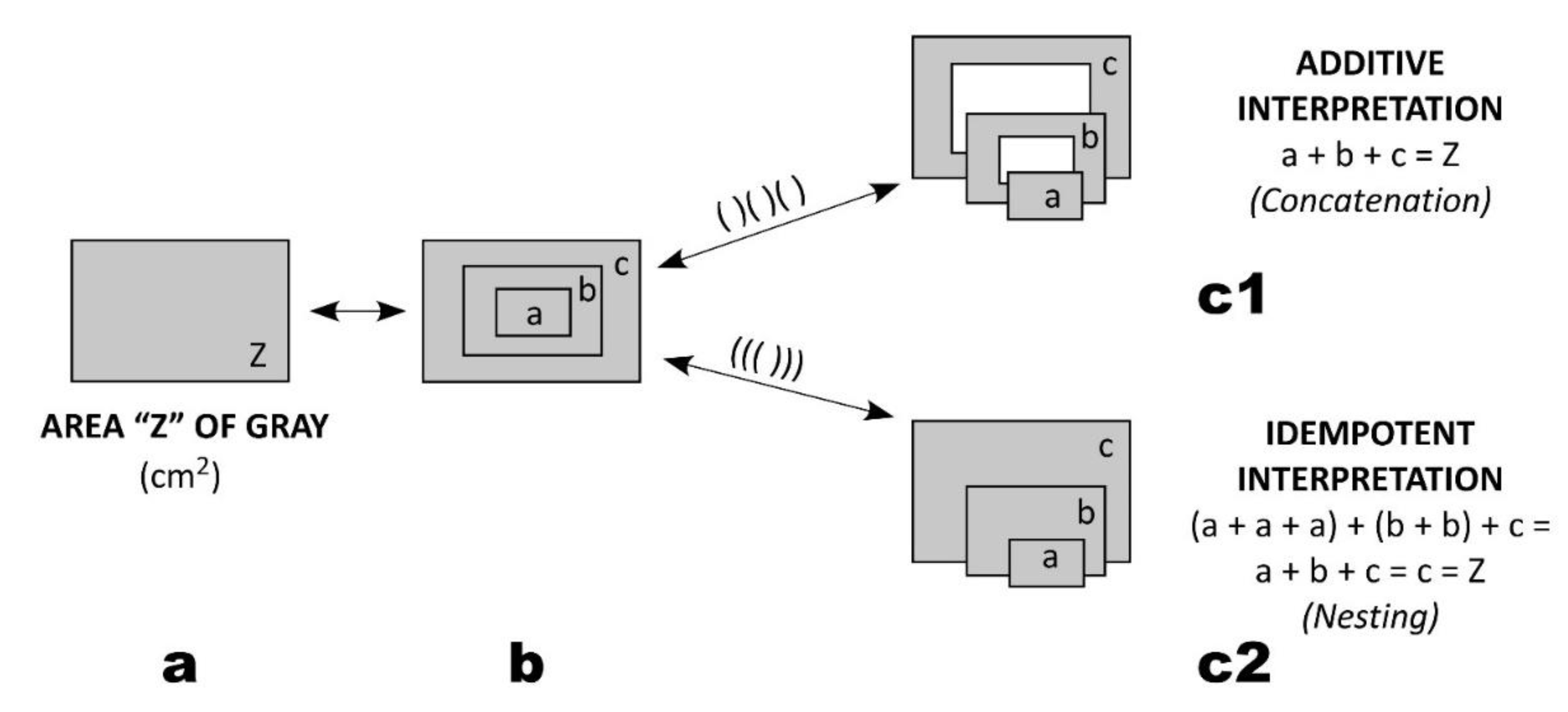
Figure 3.
Expression of sensory schema intuition. (a) Column of liquid in a container. (b) Unfolded representation of the column.
Figure 3.
Expression of sensory schema intuition. (a) Column of liquid in a container. (b) Unfolded representation of the column.
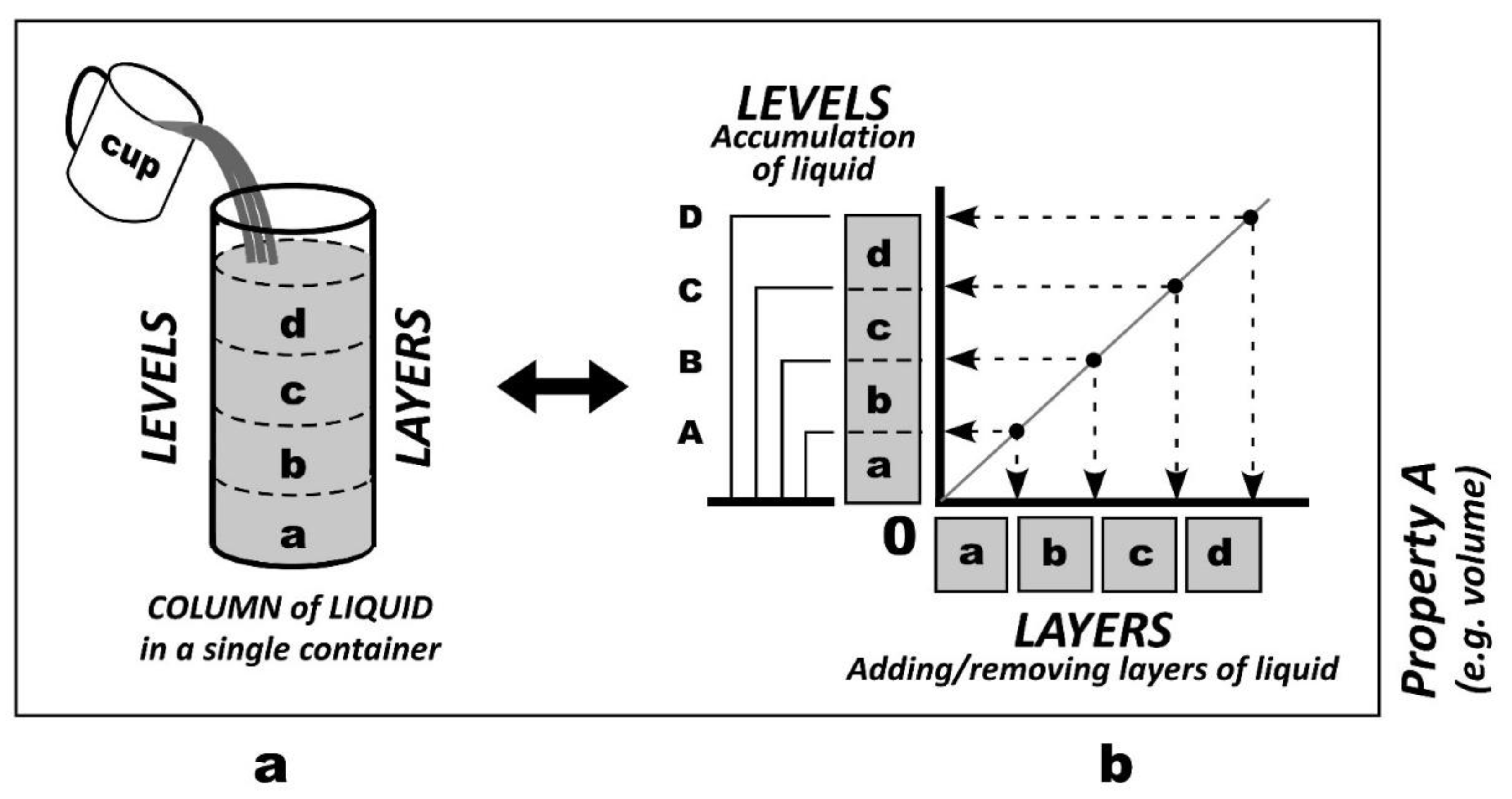
Figure 4.
Some concepts based on the sensory schema intuition. (a) intensive representation, (b) extensive representation, and (c) square representation.
Figure 4.
Some concepts based on the sensory schema intuition. (a) intensive representation, (b) extensive representation, and (c) square representation.
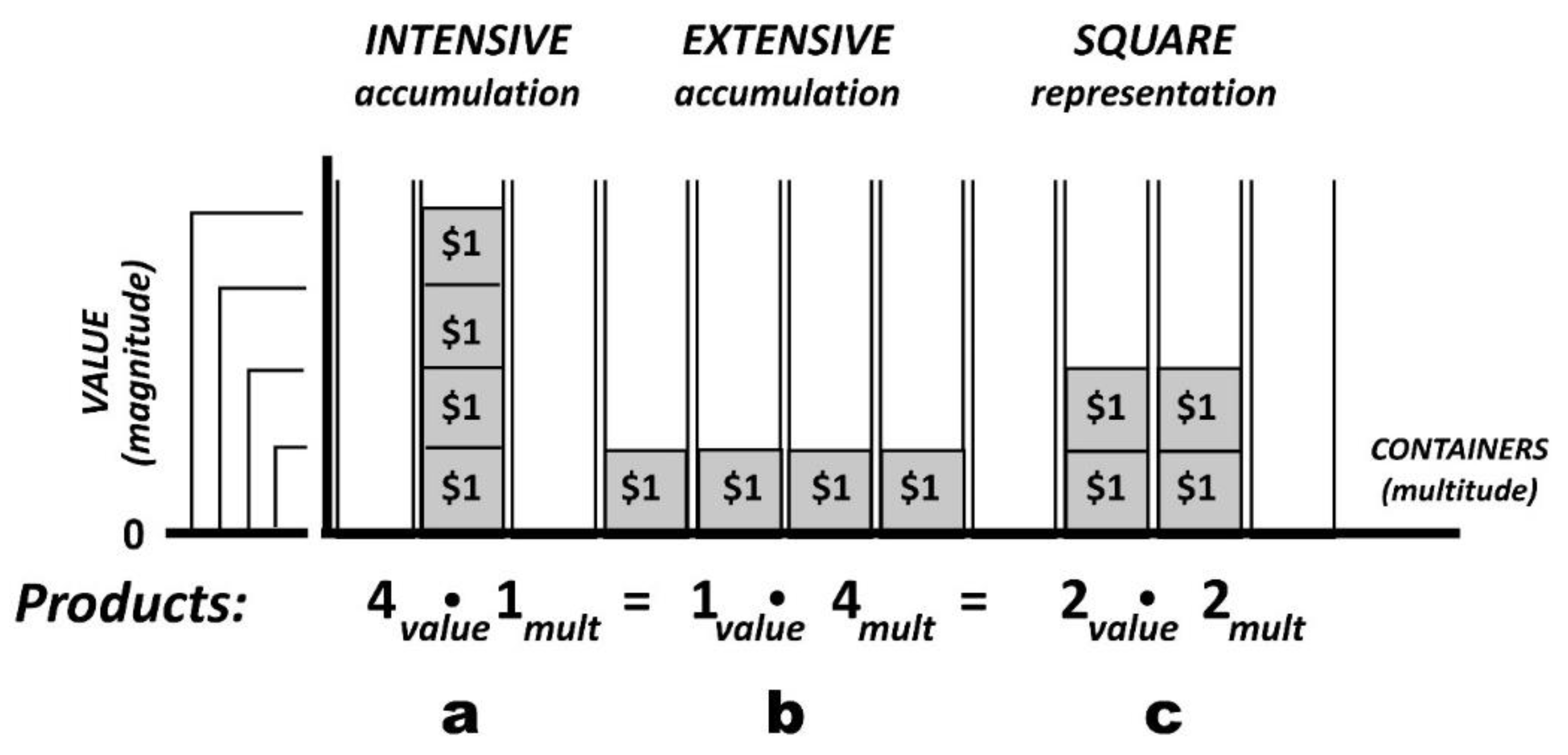
Figure 5.
Contrasts based on the sensory schema intuition: (a) absolute contrast, (b) relative contrast, (c) binary contrast.
Figure 5.
Contrasts based on the sensory schema intuition: (a) absolute contrast, (b) relative contrast, (c) binary contrast.
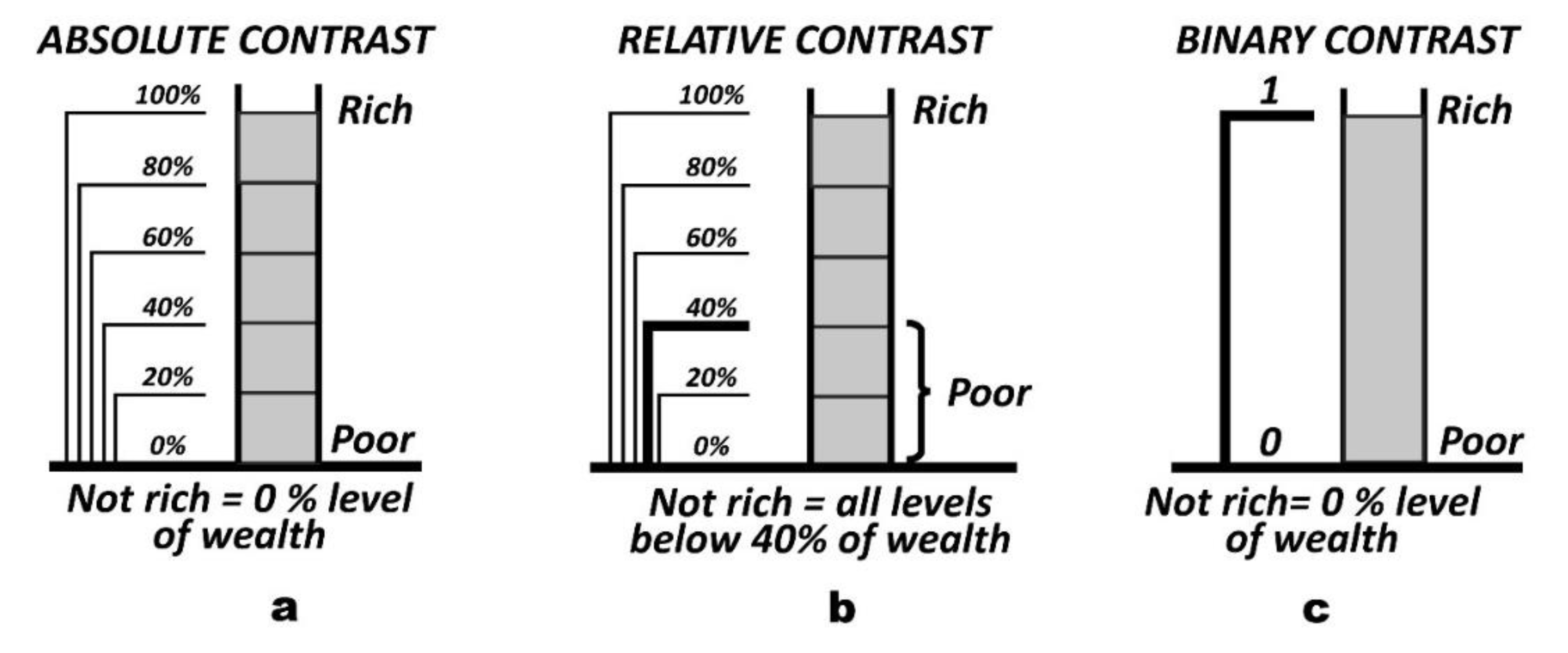
Figure 6.
Generalized opposition contrast of two properties X and Y.
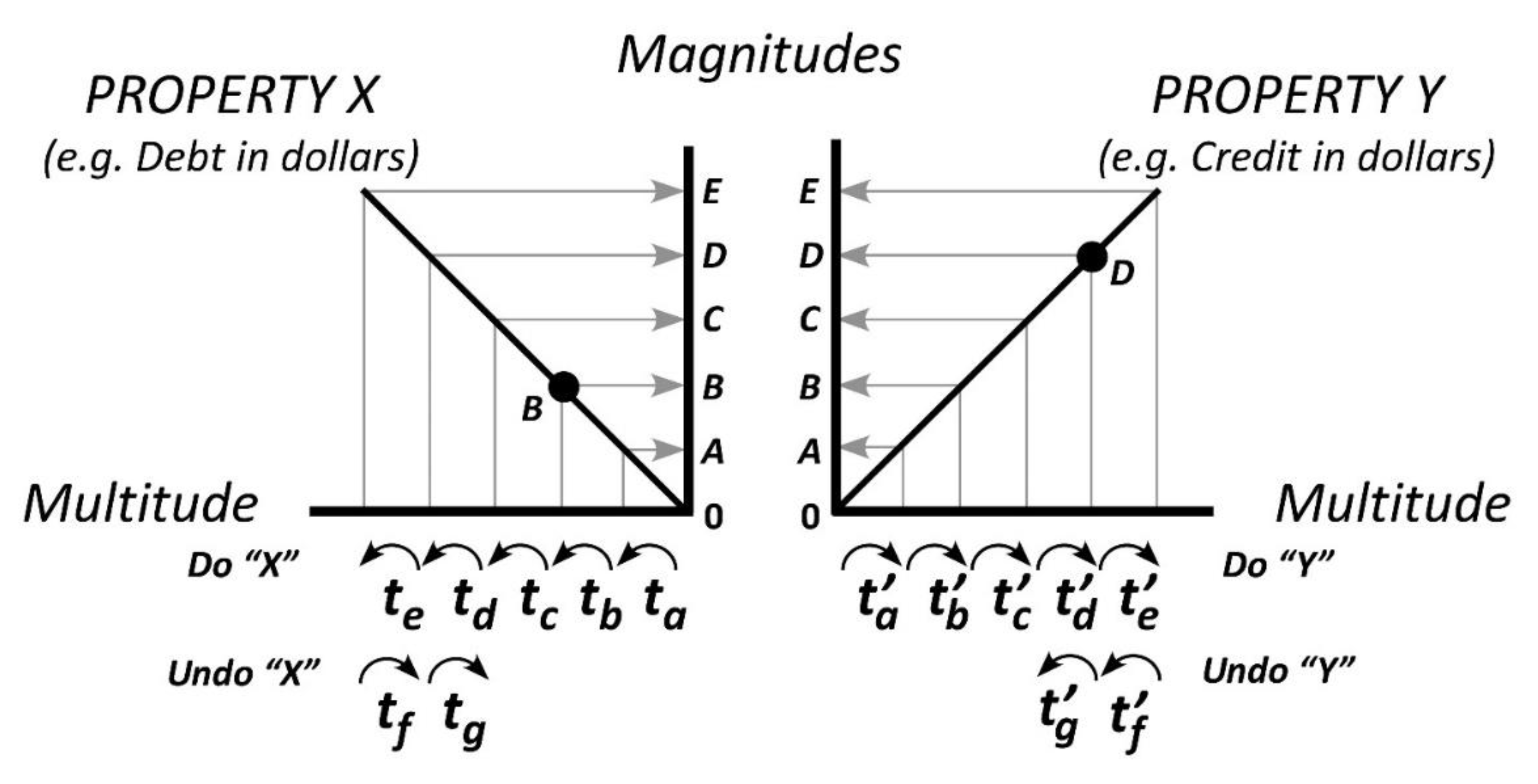
Figure 7.
Semi-opposition contrast. Take note of the reversal in the direction of accumulation.
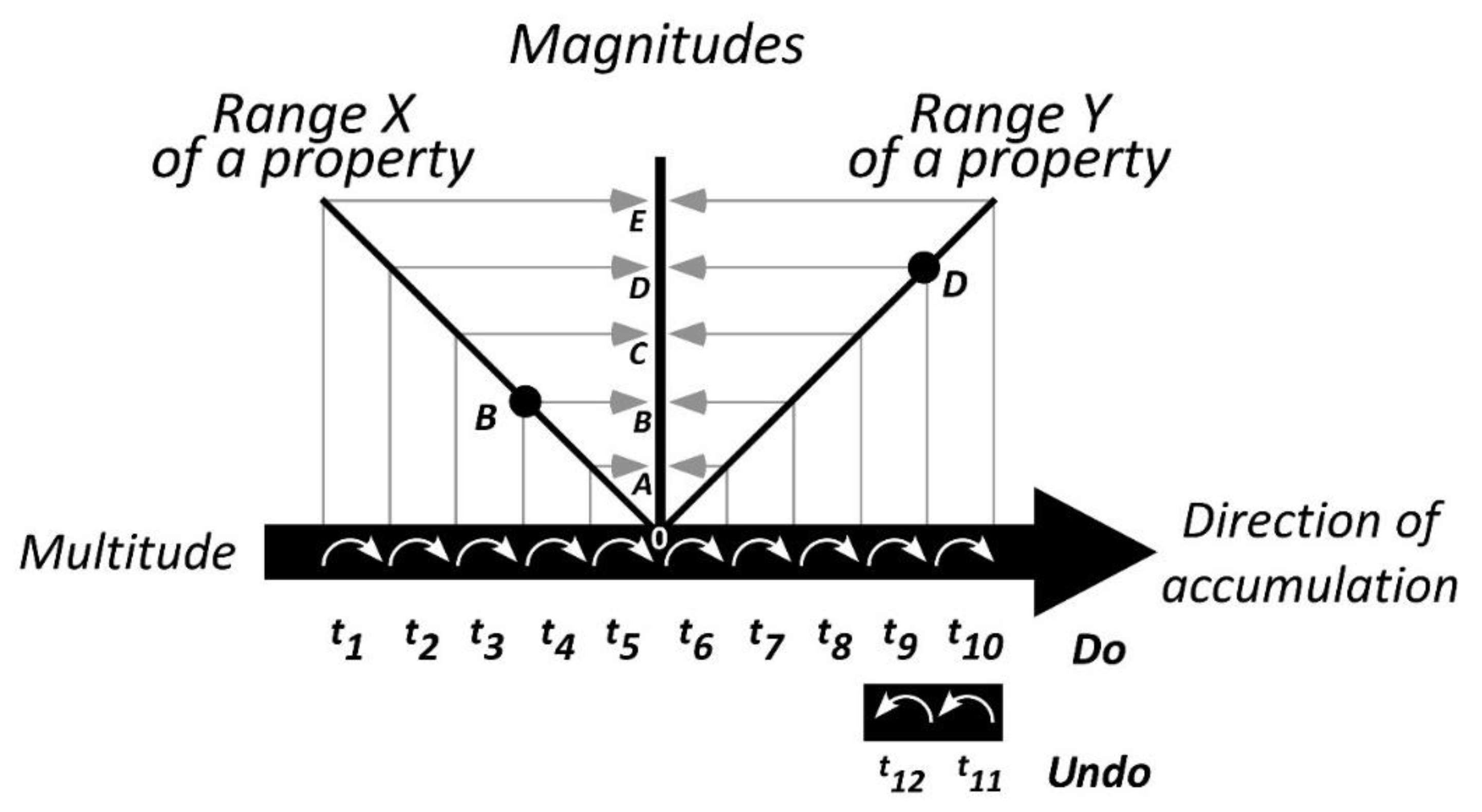
Figure 8.
Concept of integer line.
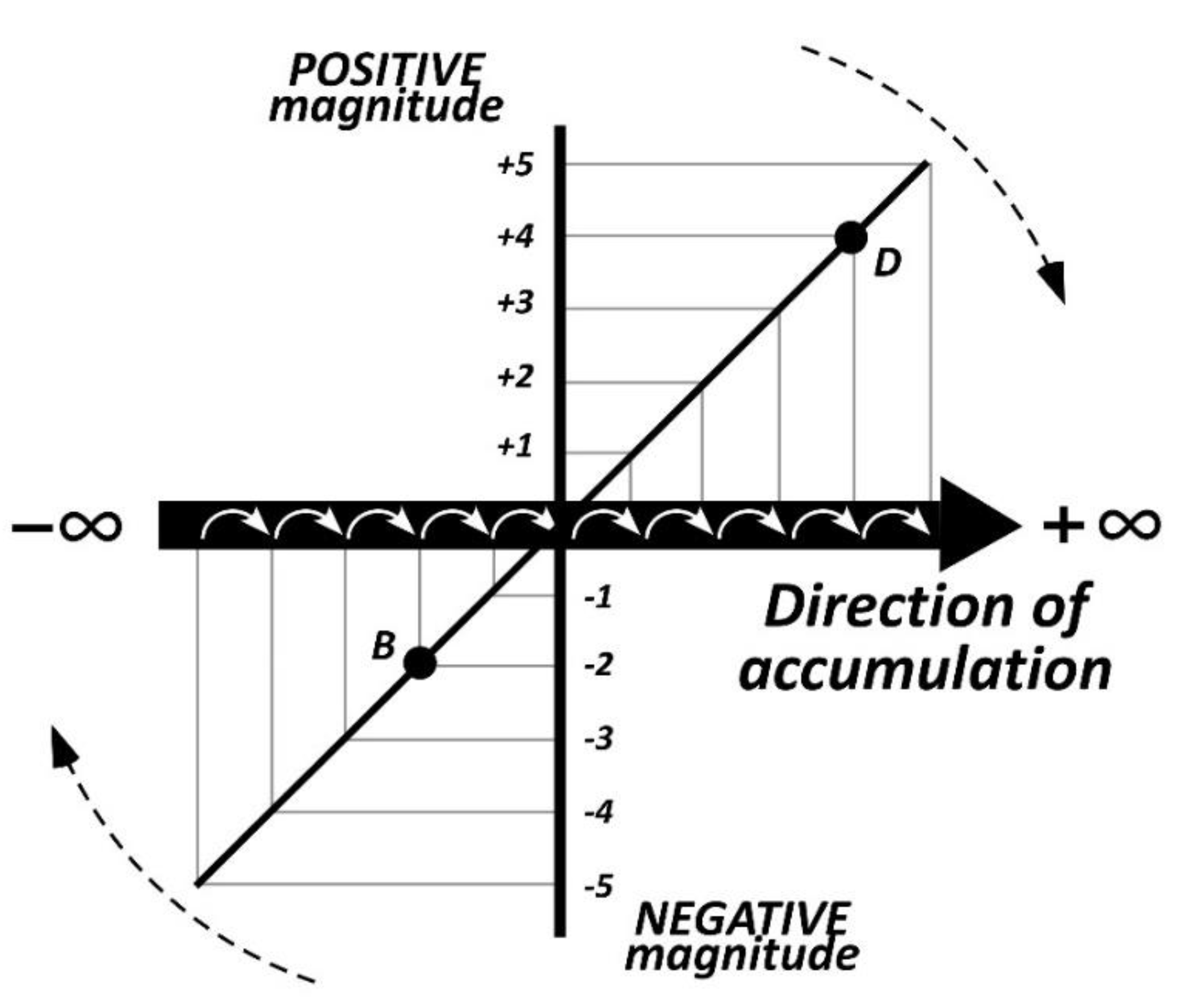
Figure 9.
Number line concept.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




