Submitted:
20 December 2023
Posted:
21 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
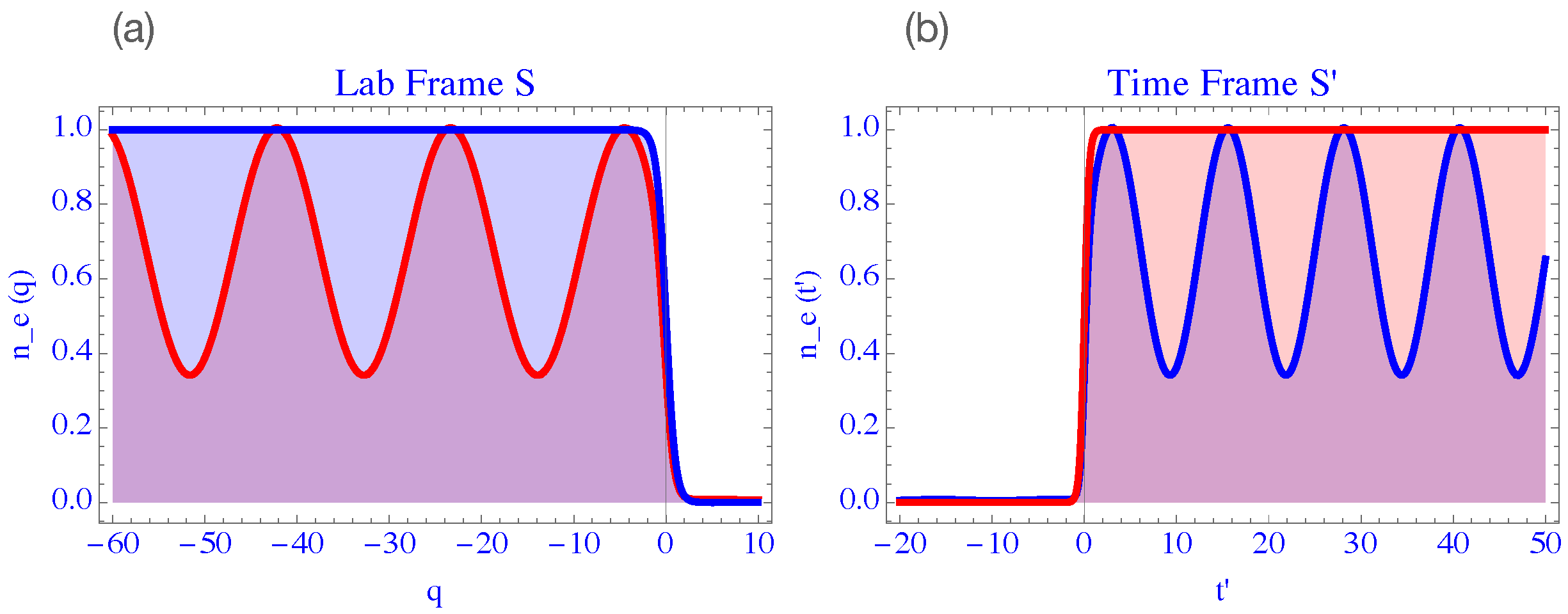
2. Time Frame
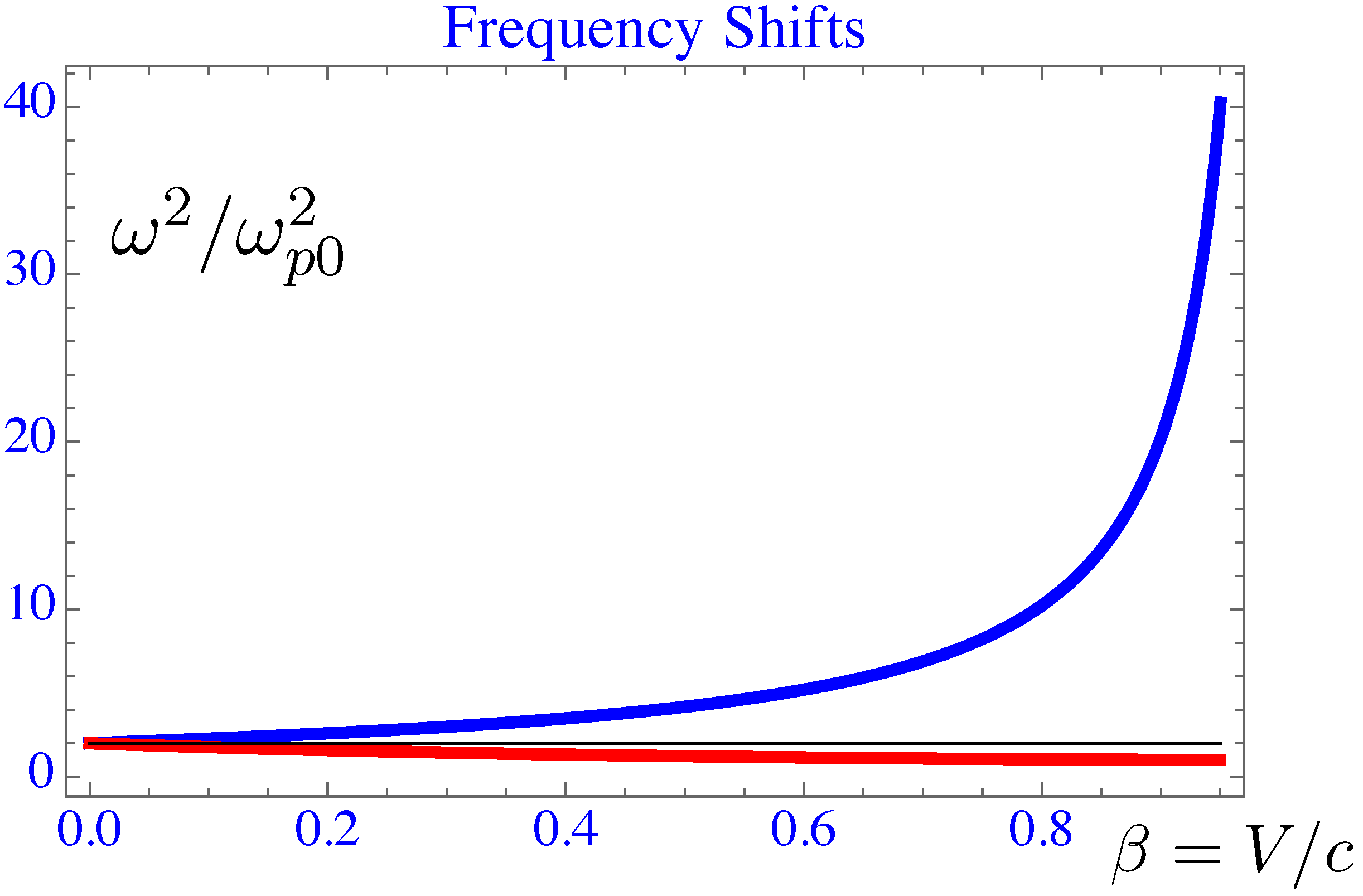
3. Frequency shifts
4. Field Transformations
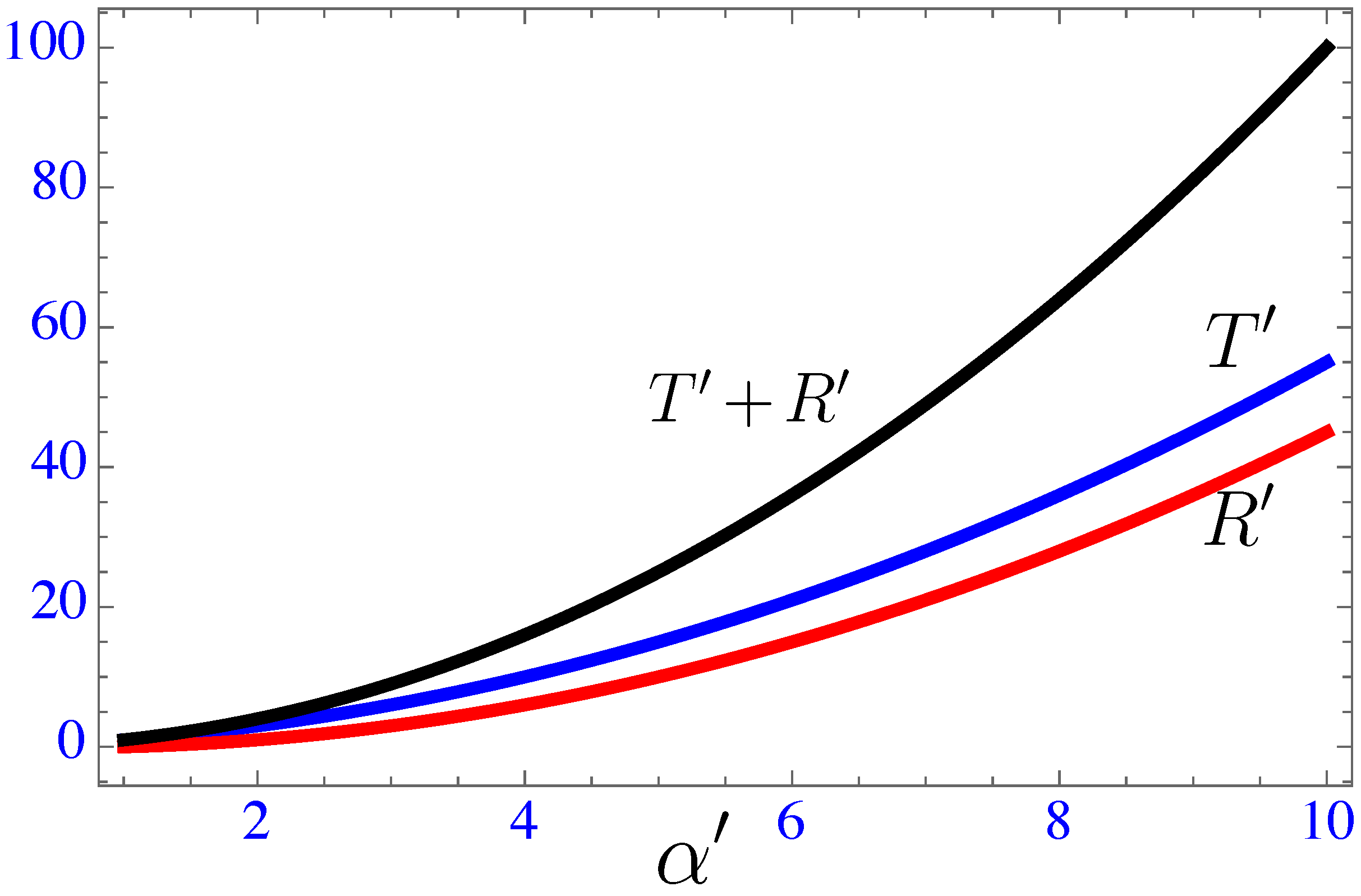
5. Modulated fronts
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Semenova, V.I. "Reflection of Electromagnetic Waves from an Ionization Front", Sov. Radiophys. Quantum Electron. 1967; 10, 599. [Google Scholar] [CrossRef]
- Lampe, M.; Ott, E. ; J.H. Walker, J.H. 1978, "Interaction of Electromagnetic Waves with a Moving Ionization Front", Phys. Fluids 21, 42. [CrossRef]
- Mendonça, J.T. 1979, "Nonlinear Interaction of Wavepackets", J. Plasma Phys. 22, 15. [CrossRef]
- Wilks, S. C, et al. 1989, "Photon Accelerator", Phys. Rev. Lett. 62, 2600. [CrossRef]
- Mendonça, J.T. Theory of Photon Acceleration, Institute of Physics Publishing, Bristol, 2001.
- Boyd, R.W. Nonlinear Optics, Academic Press, San Diego, 1992.
- Silva, L.O.; Mendonça, J.T. 2001, "Photon Kinetic Theory of Self-Phase Modulation", Opt. Commun. 196, 285. [CrossRef]
- Alfano, R.R. editor, Ths Supercontinuum Laser Source, Springer Nature, Switzerland; 4th edition, 2022.
- Silva, L.O.; Mendonça, J.T. 1996, "Photon Acceleration in Superluminous and Accelerated Ionization Fronts", IEEE Trans. Plasma Sci. 24, 316. [CrossRef]
- Savage Jr., R. L.; Joshi, C.; Mori, W.B. 1992, "Frequency upconversion of electromagnetic radiation upon transmission into an ionization front", Phys. Rev. Lett. 68, 946. [CrossRef]
- Dias, J.M. et al. 1997, "Experimental Evidence of Photon Acceleration of Ultrashort Laser Pulses in Relativistic Ionization Fronts", Phys. Rev. Lett. 78, 4773. [CrossRef]
- Mendonça, J.T.; Shukla, P.K. 2002,"Time Refraction and Time Reflection: Two Basic Concepts", Phys. Scr. 65,. 160. [CrossRef]
- Plansinis, B.W.; Donaldson, W.R.; Agrawal, G.P. 2015, "What is the temporal analog of reflection and refraction of optical beams", Phys. Rev. Lett. 115, 183901. [CrossRef]
- Dias, J.M. et al. 2002, "Photon Acceleration of Ultrashort Laser Pulses by Relativistic Ionization Fronts", Phys. Rev. E 66, 056406. [CrossRef]
- Malaca, B. et al. 2023, "Coherence and Superradiance from a Plasma-Based Quasiparticle Accelerator", Nat. Photon. [CrossRef]
- Mendonça, J.T. The Quantum Nature of Light, Institute of Physics Publishing, Bristol 2022.
- Lopes, N. C, et al. 2004, "Laser Pulse Frequency Up-shifts by Relativistic Ionization Fronts", EuroPhys. Lett. 66, 371. [CrossRef]
- Sainte-Marie, A.; Gobert, O.; Quéré, F. 2017, "Controlling the Velocity of Ultrashort Light Pulses in Vacuum through Spatio-temporal Couplings", Optica 4, 1298. [CrossRef]
- Froula, D.H. et al. 2018, "Spatiotemporal Control of Laser Intensity"", Nature Photon 12, 262. [CrossRef]
- Franke, P. et al. 2019, "Measurement and Control of Large Diameter Ionization Waves of Arbitrary Velocity", Opt. Express 27, 31978. [CrossRef]
- Li, Z.; Liu, Y.; Leng, Y.; Li, R. 2022, "Investigating Group-Velocity-Tunable Propagation-Invariant Optical Wave-Packets", Sci. Rep. 12, 16102. [CrossRef]
- Agarwal, K.; Bhatt, R.N.; Sondhi, S.L. 2018, "Fast Preparation of Critical Ground States using Superluminal Fronts", Phys. Rev. Lett. 120, 210604. [CrossRef]
- Mendonça, J.T.; Guerreiro, A.; Martins, A.M. 2000, "Quantum Theory of Time Refraction", Phys. Rev. A 62, 033805. [CrossRef]
- Mendonça, J.T.; Martins, A. M; Guerreiro, A. 2003, "Temporal Beam Splitter and Temporal Interference", Phys. Rev. A 68, 043801. [CrossRef]
- Mendonça, J.T. 2021, "Temporal Klein Model for Particle-Pair Creation", Symmetry 13, 1361. [CrossRef]
- Mendonça,J.T. 2023, "Particle-pair creation by high-harmonic laser fields", Phys. Src. 98, 125606. [CrossRef]
- J.T. Mendonça, J.T.; Guerreiro, A. 2005, "Time Refraction and the Quantum Properties of Vacuum", Phys. Rev. A 72, 063805. [CrossRef]
- Ginzburg, V.L. , Propagation of Electromagnetic Waves in Plasmas, Gordon and Breach, New Your 1961.
- Kline, M. ; I.W. Kay, I.W., Electromagnetic Theory and Geometric Optics, John Wiley & Sons, New York 1965.
- M.R. Shcherbakov et al., M.R. 2019, "Time-Variant Metasurfaces Enable Tunable Spectral Bands of Negative Extinction", Optica 6, 1441. [CrossRef]
- Liu, C. et al. 2021, "Photon Acceleration Using a Time-Varying Epsilon-Near-Zero Metasurface", ACS Photonics 8, 716. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




