Preprint
Article
Harnessing Multistability: A Novel Approach to Optical Logic Gate Construction Using Erbium-Doped Fiber Lasers
Altmetrics
Downloads
98
Views
24
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
20 December 2023
Posted:
21 December 2023
You are already at the latest version
Alerts
Abstract
We present an innovative method harnessing multistability within a diode-pumped erbium-doped fiber laser to construct logic gates. Our approach involves manipulating the intensity of external noise to regulate the probability of transitioning among four concurrent attractors. In this manner, we facilitate the realization of OR, AND, NOT, and NOR logic operations, aligning with the coexisting period-1, period-3, period-4, and period-5 orbits. Employing detrended fluctuation analysis, we establish equilibrium in the probability distributions of these states. The obtained results denote a substantial advancement in the field of optical logic gate development, representing a pivotal stride toward the seamless integration of an all-optical logic gate within laser oscillator-based systems.
Keywords:
Subject: Physical Sciences - Optics and Photonics
1. Introduction
Systems exhibiting multiple coexisting attractors have been identified across various scientific disciplines and in natural phenomena [1]. Among many dynamical systems displaying coexisting attractors, the laser marked a pivotal milestone as the first system where multistability was experimentally observed [2]. Fiber lasers, in particular, have garnered significant attention owing to their crucial applications in optical communications, reflectometry, sensing, and medicine [3]. Notably, erbium-doped fiber lasers (EDFLs) stand out for their versatility, characterized by compact dimensions, high damage threshold, excellent heat dissipation, and superior efficiency. In addition to its practical applications, EDFLs hold significance in the realm of nonlinear systems. They exhibit susceptibility to external perturbations, facilitating the emergence of chaotic dynamics and the coexistence of multiple attractors. This dual nature of practical utility and inherent nonlinear complexity renders the EDFL an intriguing subject for research and exploration in diverse scientific domains [4,5,6,7].
Multistability is an intriguing phenomenon not only from a scientific standpoint but also due to its important applications, including advancements in cognitive neuroscience [8,9,10], generation of giant pulses [11], secure communications [12], and digital computing [13,14,15]. Highlighting the last mentioned advancements, it is noteworthy that experimental implementations of logic gates, rooted in a triple-well potential, have been successfully implemented in electronic systems [13] and cavity magnonic systems [14]. The intrinsic versatility of a triple-well potential system is demonstrated further, as it enables the attainment of all six logic operations through the combination of various states [15]. Moreover, the exploration of logic gates has been extended to EDFLs [16,17,18]. In contrast to earlier logic gate implementations that relied on perturbing the laser with a digital signal, our current research delves into the influence of external noise. This enhancement streamlines the process, paving the way for the realization of four distinct logic operations. The convergence of diverse scientific domains, encompassing both attractor dynamics and logical operations, underscores the broad-reaching implications and interdisciplinary significance of these multifaceted systems.
The formulation of digital functions for characterizing logic gates within dynamical systems typically involves the integration of hybrid systems, where signals generated in a computer are translated into analog signals. The concept of "chaos computing" has gained considerable traction, leveraging the dynamic properties of chaotic systems. This approach predominantly relies on employing an analog chaotic oscillator that emulates the behavior of multiple logic gates. This unique feature enables seamless transitions between different modes of operation, facilitating the resolution of specific arithmetic operations [7]. The seminal work of Sinha et al. [19], introducing an SR (Set-Reset) flip-flop based on NOR gates implemented by a Chua circuit, marked the inception of extensive research and development in chaotic logic gates [16,17,20,21,22,23]. Noteworthy among these efforts are shared challenges, namely: (i) the utilization of systems with coexisting attractors, and (ii) the incorporation of the sum of two digital decorrelated and periodless signals as input to the dynamical system for generating the truth table associated with the logic gate. These commonalities form the foundational basis for exploring the potential and limitations of chaos-driven computing in logic gate applications.
In this study, we introduce a novel approach to implementing logic gates using noise-induced multistate intermittency (or attractor hopping) in a laser system. Our work represents the first exploration of logic gate functionality controlled by external noise in such a system. Specifically, through comprehensive numerical simulations, we demonstrate the feasibility of realizing logic gates in a noisy EDFL coupled with a Low-Pass Filter (LPF). In our system, each logic operation is uniquely associated with a specific periodic orbit. Notably, in the laser system featuring four coexisting periodic orbits, we assign the period 1 (P1) to OR operation, period 3 (P3) to AND, period 4 (P4) to NOT, and period 5 (P5) to NOR. The conceptual representation of the potential well for such a system is illustrated in Figure 1.
The introduction of noise in this system destabilizes coexisting attractors making the system metastable and inducing transitions between them. This offers a dynamic and adaptable foundation for logic gate operations. In the presence of noise, a laser system featuring coexisting attractors undergoes multistate intermittency, wherein the laser switches between various coexisting states [24].
The subsequent sections of this paper are structured as follows. Section 2 provides an overview of the laser system employed, outlining its diverse behaviors and elucidating the method employed to induce attractor hopping within the system. In Section 3, we present the results achieved by equalizing the probability of occurrence for each coexisting period in the laser. This section also delves into the process of constructing a digital signal by activating logic operations when the EDFL exhibits equiprobable multistate intermittency. The final section encapsulates the conclusions drawn from this work and offers a platform for discussions on its implications and potential future directions.
2. Numerical Model of Erbium-Doped Fiber Laser
The dynamics of an EDFL is described by two differential equations [25,26,27]
where P is the power of the laser in the cavity, is the mean value of the upper level of the laser potential, where is the refractive index of the cold core of the erbium-doped fiber, and indicate the relationship between the effective cross sections and the fundamental absorption state, and is the upper level in the z coordinate (propagation direction of the laser emission). The element is the total time required for a photon to travel through the cavity, is the absorption coefficient of the erbium-doped fiber, is the threshold loss counter of the laser cavity, is the lifetime of an excited erbium ion and is the quantity that determines how closely the fundamental mode of the laser and the volume of the erbium-doped core coincide. The spontaneous emission in the laser basic regime is described by
where is the wavelength of the laser emission at 1.5 m. The pump power
is periodically modulated as follows
where m and are the modulation depth and frequency, respectively, is the dimensionless pumping power at the fiber inlet, and p is the constant power without modulation.
The system in Eq. (1) is normalized to get the following dimensionless form [25,26]:
where a, b, c, and d are coefficients given in Table 1.
These equations can be solved numerically by modulating the pump current of the laser diode with a periodic signal and analyzing the response of the laser to changes in modulation frequency and amplitude. Figure 2 shows the bifurcation diagram of the local maxima of the laser intensity obtained by varying modulation frequency for fixed modulation depth . The frequency was changed in steps of 1 kHz, and a random initial condition was used for each change. The region of multistability explored in this paper are marked in red. One can see that at kHz, the laser exhibits the coexistence of four stable periodic orbits (P1, P3, P4, P5).
Remark
(1). In this paper, we use the term "period" to denote the duration of a periodic orbit within the laser system. This refers to the repetitive oscillations induced by the harmonic modulation of the pump power. The numerical representation of the period aligns with the count of periods of the pump function in the EDFL emission.
- If the laser oscillates in period 1, the modulation frequency is .
- If the laser oscillates in period 3, the modulation frequency is .
- If the laser oscillates in period 4, the modulation frequency is .
- If the laser oscillates in period 5, the modulation frequency is .
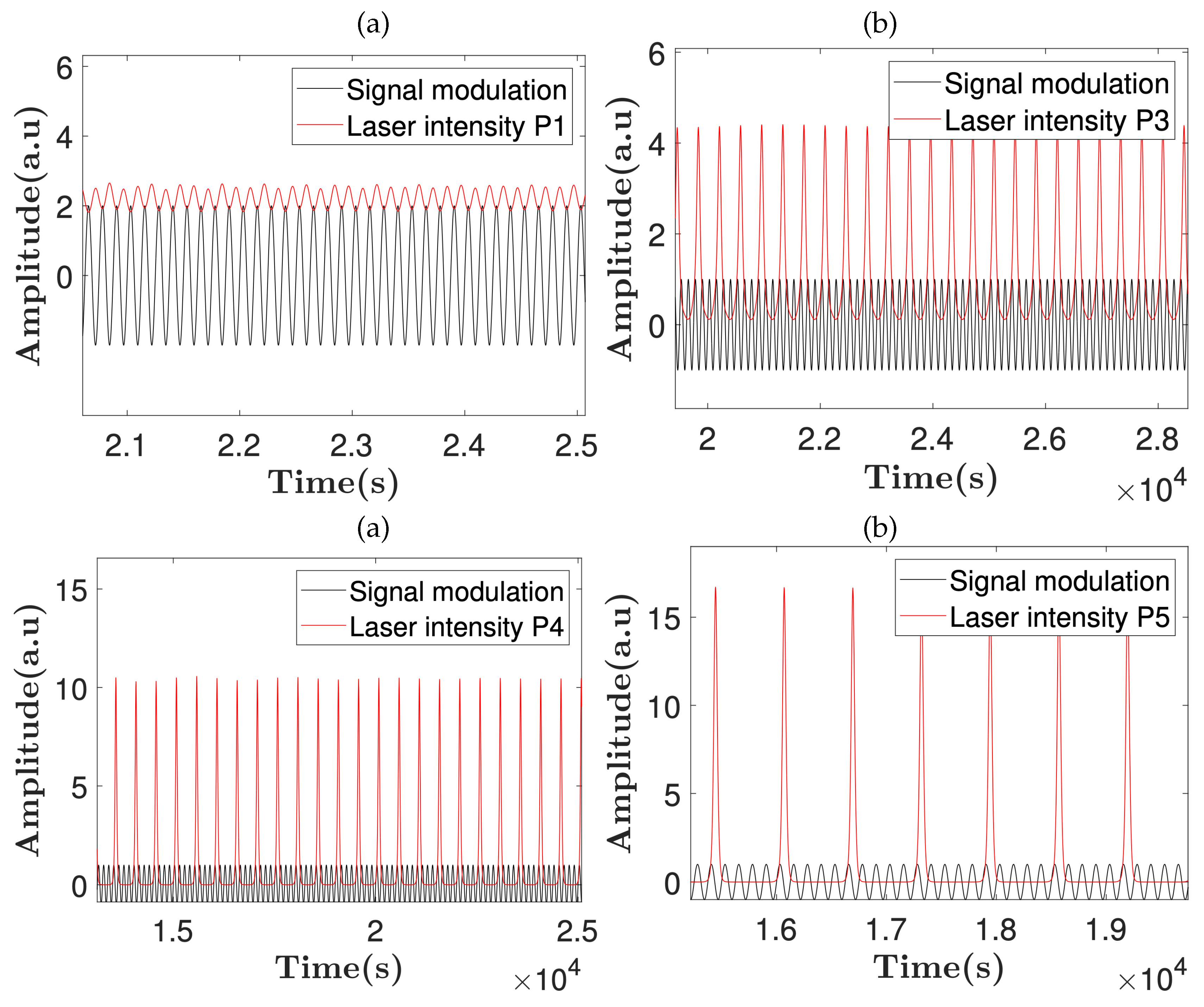
This relationship between the pumping frequency and the periodic response of the EDFL is illustrated with the time series in Figure 3.
2.1. System under noise addition
When the system described by Eq. (5) is subjected to periodic modulation, the laser manifests a remarkably intricate dynamics, as illustrated in Figure 2 and Figure 3. However, adding a stochastic component to Eq. (4) we get
where is the noise amplitude and is the noise function with zero mean between a random number and the frequency is the low-pass filtered (LPF) noise (white noise is filtered with a discrete fifth-order low-pass Butterworth filter). In the multistability region, noise triggers multistate intermittency, also known as attractor hopping, wherein the laser alternates among the coexisting states.
Figure 3.
Time series of the laser intensity corresponding to (a) P1, (b) P3, (c) P4, and (d) P5 coexisting periodic orbits for modulation depth and frequency kHz.
Figure 3.
Time series of the laser intensity corresponding to (a) P1, (b) P3, (c) P4, and (d) P5 coexisting periodic orbits for modulation depth and frequency kHz.
The diagram in Figure 4 displays the regions of various intermittency regimes experimentally observed in the EDFL in the parameter space of the modulation frequency and input noise intensity [24]. One can note the appearance of new intermittency attractors as the input noise intensity is increased. These attractors represent the mixture of P1 and P3 states; P1, P3, P4; and P1, P3, P4, P5; each state has different frequency as indicated in Remark (1).
Remark
(2). While the findings presented in Figure 2 and Figure 4 are derived from our earlier work [24], it is important to clarify that these results do not constitute the primary focus of this paper. Rather, they serve as foundational insights crucial for comprehending the contributions of the current study. As such, these results are retained within Remark (1) to provide essential context and background for the subsequent developments in this work.
2.2. Problem Statement
As discussed in the preceding sections, the development of logic gates within dynamical systems has garnered increasing attention due to its potential advantages in information processing speed, surpassing current achievements. This approach also enables the integration of various logic gates within a single oscillator. To accomplish this, existing systems rely on decorrelated digital signals as triggers to characterize system responses and construct associated truth tables for obtained logic gates. Typically, these digital signals are generated computationally, translated into analog signals, and then injected into chaotic dynamical systems, a paradigm known as chaos computing [23].
In this paper we take a distinctive approach by generating random signals derived from an optical system, such as the EDFL, operating in the regime of multistate intermittency. By stabilizing the probability of occurrence for each coexisting state within this intermittency region, the laser signal exhibits amplitude variations characteristic of each period of oscillations. This variation is leveraged to activate and randomly deactivate logic operations, facilitating the creation of digital signals implementable in optical-system-based logic gates, as demonstrated by Afanador et al. [23].
3. Results
Upon the addition of a filtered noisy signal, we observe multistate intermittency previously described in Ref. [24]. This phenomenon unfolds as the external noise is gradually increased. Figure 5 represent the time series of P1 (Figure 5(a)) and intermittent attractors (Figures 5(b-d)) illustrating switches between various coexisting states, derived from the LPF featuring a 60-Hz cut frequency.
While without noise () the laser stays in one of the coexisting attractors depending on the initial conditions, say P1 (Figure 5(a)), increasing noise intensity induces first into two-state intermittency (switches between P1 and P3), then tri-state intermittency (switches between P1, P3, and P4), and finally multistate intermittency (switches between P1, P3, P4, and P5 [24]. To facilitate the identification of distinct periodic states in the intermittent dynamics shown in Figure 5, Table 2 provides information about noise intensity for each intermittent state.
An analysis of multistate intermittency induced in the EDFL system under both periodic and stochastic modulation reveals an uneven distribution in the probability of attractor occurrences across varying noise levels. To address this discrepancy and align with the primary objective of the study — the random activation of logical operations through the laser system’s hopping between coexisting states — an investigation into the system’s response is undertaken for different noise values. This exploration aims to identify a parameter range wherein the probability of occurrence for coexisting states is comparable. By achieving a balanced distribution, any preferential bias in logic operation activation is eliminated, facilitating the generation of decorrelated digital signals by an optical system.
Remark
(3). The assignment of logical operations to each of the coexisting states of the system is as follows.
- If the system has oscillations of P1 type, the logical OR operation is performed.
- If the system has oscillations of P3 type, the logical AND operation is performed.
- If the system has oscillations of P4 type, the logical NOT operation is performed.
- If the system has oscillations of P5 type, the logical NOR operation is performed.
Figure 6 illustrates the assessment of each coexistent state in the EDFL for varying the noise intensity on the abscissa and LPF value on the ordinate. As outlined in Remark (3), the graphs in Figures 6(a-d) hold different logic gates. Notably, when the applied filter value is below 20 kHz, the observed behavior exhibits minimal variation compared to the system without LPF, consistent with previous observations [28].
Figure 7 presents the calculated probability of occurrence for each defined gate (period) based on each analyzed time series, with the color bar indicating the likelihood of a specific gate occurring in the time series for a given () combination.
Upon identifying the optimal range for "stabilizing" the probabilities of occurrence for different periods in the system, each period is then assigned a logic operation. This assignment triggers the activation of the corresponding operation, leading to the generation of a digital signal, intricately associated with the EDFL dynamics. The operations allocated to each period, along with their respective truth tables, are detailed in Table 3.
The depicted behavior in Figure 7 reveals that, for specific combinations of noise intensity and particular LPF frequency, achieving a comparable probability of activating different logic gates is attainable. In light of this, we incorporate Detrended Fluctuation Analysis (DFA). Initially introduced by Peng et al. [29], DFA elucidates long-range power-law correlations, offering insights into the statistical self-affinity of specific behaviors. This method proves valuable for analyzing time series indicative of long-memory processes, characterized by correlations in dynamical nonlinear actions (e.g., power-law decaying autocorrelation functions). Importantly, DFA helps circumvent the inadvertent detection of spurious long-range correlations stemming from nonstationarity.
The DFA analysis employs fluctuation function , adhering to the power-law scaling relation:
where the time series is segmented into s pieces, each with length . The scaling exponent or slope delineates distinct regimes, offering valuable insights into the laser dynamics, as follows.
- : anti-correlated behavior,
- : uncorrelated behavior or white noise,
- : correlated behavior,
- : -noise or pink noise,
- : non-stationary or unbounded behavior,
- : Brownian motion.
Figure 8 presents the DFA results obtained for all analyzed time series across various noise intensity variations and applied LPF frequencies. The findings affirm that the diverse combinations of amplitude noise and LPF application reflect a correlated behavior among the different interacting states within the system. Additionally, certain regions indicate proximity to pink noise behavior, suggesting nuanced dynamics in specific conditions.
As an illustrative example of diverse applications, the upper trace in Figure 9 displays 300 red points that define a Local Maximum Vector (LMV) derived from EDFL time series with LPF at kHz and noise intensity . Each point on the LMV corresponds to the amplitude of possible pulses (gates), as outlined in Remark 3. Two red-square time series (Pulse I1 and Pulse I2) (middle traces) depict randomly generated digital signals, while the black-square time series (lower trace) represents the response to a Logic Operation (LO) between I1 and I2, defined by the LMV. To elaborate further, consider the time moment near 200 marked by a vertical blue line in Figure 9. At this moment, the value of LMV corresponds to an AND gate, indicating the operation for I1 and I2 . As expected, the result is 0, as demonstrated by the black time series of the LO in the lower trace. This example showcases the practical application of the proposed approach in executing logic operations based on the laser dynamics.
4. Conclusion
In this study, we numerically explored the potential of harnessing noise-induced multistate intermittency in a multistable erbium-doped fiber laser to realize logic gates. The manipulation of noise intensity allowed for the attainment of specific logical operations. Additionally, employing a low-pass filter for each noise variation enabled an examination of how filters can influence the probability of a particular state’s occurrence. This activation of operations facilitated the generation of uncorrelated binary signals with variable periods, offering possibilities for implementation in logic gate generation schemes based on optical media.
Through the application of detrended fluctuation analysis, we revealed the correlated behavior resulting from various noise intensities combined with specific low-pass filters. This finding underscores the potential to achieve a more balanced equilibrium between different states exhibiting hopping intermittency in temporal series. Such equilibrium is valuable for applications, including encryption systems, where the generation of a pseudo-random number embedded in an optical system depends on a low-pass filter, offering enhanced security and unpredictability.
Author Contributions
Safara Bibi: Writing - Review & Editing, Resources. José Luis Echenausía Monroy: Writing - Review & Editing, Visualization, Conceptualization. Rider Jaimes Reátegui: Supervision, Funding acquisition, Writing - Review & Editing, Resources. Juan Hugo García López: Writing - Review & Editing, Resources, Project administration. Guillermo Huerta Cuellar: Writing - Original Draft, Writing - Review & Editing, Methodology, Software, Validation, Data Curation, Visualization, Project administration. Alexander N. Pisarchik: Writing - Review & Editing, Supervision.
Funding
This project was supported by CONACYT under project number 320597.
Acknowledgments
J.L.E.M. thanks CONACYT for financial support (CVU-706850, project: A1-S-26123, and project: 320597). R.J.R. thanks CONACYT for financial support, project No. 320597.
Conflicts of Interest
The authors certify that they have NO affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers’ bureaus; membership, employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or non-financial interest (such as personal or professional relationships, affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript.
References
- Pisarchik, A.N.; Hramov, A.E. Multistability in Physical and Living Systems: Characterization and Applications; Springer: Cham, 2022. [Google Scholar]
- Arecchi, F.T.; Meucci, R.; Puccioni, G.; Tredicce, J. Experimental evidence of subharmonic bifurcations, multistability, and turbulence in a Q-switched gas laser. Phys. Rev. Lett. 1982, 49, 1217–1220. [Google Scholar] [CrossRef]
- Digonnet, M. (Ed.) Rare Earth Doped Fiber Lasers and Amplifiers; Marcel Dekker: New York, 1993. [Google Scholar]
- Pisarchik, A.N.; Barmenkov, Y.O.; Kir’yanov, A.V. Experimental characterization of the bifurcation structure in an erbium-doped fiber laser with pump modulation. IEEE J. Quantum Electron. 2003, 39, 1567–1571. [Google Scholar] [CrossRef]
- Saucedo-Solorio, J.M.; Pisarchik, A.N.; Kir’yanov, A.V.; Aboites, V. Generalized multistability in a fiber laser with modulated losses. J. Opt. Soc. Am. B 2003, 20, 490–496. [Google Scholar] [CrossRef]
- Sevilla-Escoboza, R.; Pisarchik, A.N.; Jaimes-Reátegui, R.; Huerta-Cuellar, G. Selective monostability in multi-stable systems. Proc. Royal Soc. A 2015, 471, 20150005. [Google Scholar] [CrossRef]
- Meucci, R.; Marc Ginoux, J.; Mehrabbeik, M.; Jafari, S.; Clinton Sprott, J. Generalized multistability and its control in a laser. Chaos 2022, 32, 083111. [Google Scholar] [CrossRef] [PubMed]
- Maksimenko, V.A.; Frolov, N.S.; Hramov, A.E.; Runnova, A.E.; Grubov, V.V.; Kurths, J.; Pisarchik, A.N. Neural interactions in a spatially-distributed cortical network during attentional tasks. Front. Behav. Neurosci. 2019, 13, 220. [Google Scholar] [CrossRef] [PubMed]
- Hramov, A.E.; Maksimenko, V.A.; Koronovskii, A.A.; Runnova, A.E.; Zhuravlev, M.O.; Pisarchik, A.N.; Kurths, J. Percept-related EEG classification using machine learning approach and features of functional brain connectivity. Chaos 2019, 29, 093110. [Google Scholar] [CrossRef]
- Maksimenko, V.A.; Kuc, A.; Frolov, N.S.; Khramova, M.V.; Pisarchik, A.N.; Hramov, A.E. Dissociating cognitive processes during ambiguous information processing in perceptual-decision making. Front. Behav. Neurosci. 2020, 14, 95. [Google Scholar] [CrossRef]
- Jaimes-Reátegui, R.; Esqueda de la Torre, J.O.; García-López, J.H.; Huerta-Cuellar, G.; Aboites, V.; Pisarchik, A.N. Generation of giant periodic pulses in the array of erbium-doped fiber lasers by controlling multistability. Opt. Commun. 2020, 477, 126355. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Jaimes-Reátegui, R.; Rodríguez-Flores, C.; García-López, J.H.; Huerta-Cuellar, G.; Martín-Pasquín, F.J. Secure chaotic communication based on extreme multistability. J. Frank. Inst. 2021, 358, 2561–2575. [Google Scholar] [CrossRef]
- Ashokkumar, P.; Aravindh, M.S.; Venkatesan, A.; Lakshmanan, M. Realization of all logic gates and memory latch in the SC-CNN cell of the simple nonlinear MLC circuit. Chaos 2012, 31, 063119. [Google Scholar] [CrossRef] [PubMed]
- Shen, R.C.; Wang, Y.P.; Li, J.; Zhu, S.Y.; Agarwal, G.S.; You, J.Q. Long-time memory and ternary logic gate using a multistable cavity magnonic system. Phys. Rev. Lett. 2021, 127, 183202. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Y.; Xu, W.; Li, X. Logical stochastic resonance in triple-well potential systems driven by colored noise. Chaos 2012, 22, 043130. [Google Scholar] [CrossRef] [PubMed]
- Jaimes-Reátegui, R.; Afanador-Delgado, S.; Sevilla-Escoboza, R.; Huerta-Cuellar, G.; García-López, J.H.; López-Mancilla, D.; Pisarchik, A. Optoelectronic flexible logic gate based on a fiber laser. Eur. Phys. J. Spec. Top. 2014, 223, 2837–2846. [Google Scholar] [CrossRef]
- García-López, J.H.; Jaimes-Reátegui, R.; Afanador-Delgado, S.M.; Sevilla-Escoboza, R.; Huerta-Cuéllar, G.; López-Mancilla, D.; Chiu-Zarate, R.; Castañeda-Hernández, C.E.; Pisarchik, A.N. Experimental and numerical study of an optoelectronics flexible logic gate using a chaotic doped fiber laser. In Recent Development in Optoelectronic Devices; Srivastava, R., Ed.; IntechOpen, 2018; pp. 97–114. [Google Scholar]
- Delgado, S.M.A.; Monroy, J.L.E.; Cuellar, G.H.; García López, J.H.; Jaimes Reátegui, R. Numerical and experimental data of the implementation of logic gates in an erbium-doped fiber laser (EDFL). Data 2022, 8, 7. [Google Scholar] [CrossRef]
- Sinha, S.; Ditto, W.L. Dynamics based computation. Phys. Rev. Lett. 1998, 81, 2156. [Google Scholar] [CrossRef]
- Munakata, T.; Sinha, S.; Ditto, W.L. Chaos computing: implementation of fundamental logical gates by chaotic elements. IEEE Trans. Circuits Syst. I 2002, 49, 1629–1633. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Chaos-based SR flip–flop via Chua’s circuit. Intern. J. Bifurc. Chaos 2006, 16, 1521–1526. [Google Scholar] [CrossRef]
- Murali, K.; Sinha, S.; Ditto, W.L.; Bulsara, A.R. Reliable logic circuit elements that exploit nonlinearity in the presence of a noise floor. Phys. Rev. Lett. 2009, 102, 104101. [Google Scholar] [CrossRef]
- Delgado, A.; Mardoqueo, S.; Echenausía Monroy, J.L.; Huerta Cuellar, G.; García López, J.H.; Jaimes Reátegui, R. Implementation of logic gates in an erbium-doped fiber laser (EDFL): Numerical and experimental analysis. Photonics 2022, 9, 977. [Google Scholar] [CrossRef]
- Huerta-Cuellar, G.; Pisarchik, A.N.; Barmenkov, Y.O. Experimental characterization of hopping dynamics in a multistable fiber laser. Phys. Rev. E 2008, 78, 035202. [Google Scholar] [CrossRef] [PubMed]
- Reategui, R.; Kir’yanov, A.; Pisarchik, A.; Barmenkov, Y.O.; Il’ichev, N. Experimental study and modeling of coexisting attractors and bifurcations in an erbium-doped fiber laser with diode-pump modulation. Laser Phys. 2004, 14, 1277–1281. [Google Scholar]
- Pisarchik, A.N.; Kir’yanov, A.V.; Barmenkov, Y.O.; Jaimes-Reátegui, R. Dynamics of an erbium-doped fiber laser with pump modulation: theory and experiment. J. Opt. Soc. Am. B 2005, 22, 2107–2114. [Google Scholar] [CrossRef]
- Huerta-Cuellar, G.; Pisarchik, A.; Kir’yanov, A.; Barmenkov, Y.O.; del Valle Hernández, J. Prebifurcation noise amplification in a fiber laser. Phys. Rev. E 2009, 79, 036204. [Google Scholar] [CrossRef]
- Pisarchik, A.; Jaimes-Reátegui, R.; Sevilla-Escoboza, R.; Huerta-Cuellar, G. Multistate intermittency and extreme pulses in a fiber laser. Phys. Rev. E 2012, 86, 056219. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Hypothetical potential well for a system featuring four coexisting attractors (P1, P3, P4, P5), with noise-induced transitions between them indicated by the arrows.
Figure 1.
Hypothetical potential well for a system featuring four coexisting attractors (P1, P3, P4, P5), with noise-induced transitions between them indicated by the arrows.
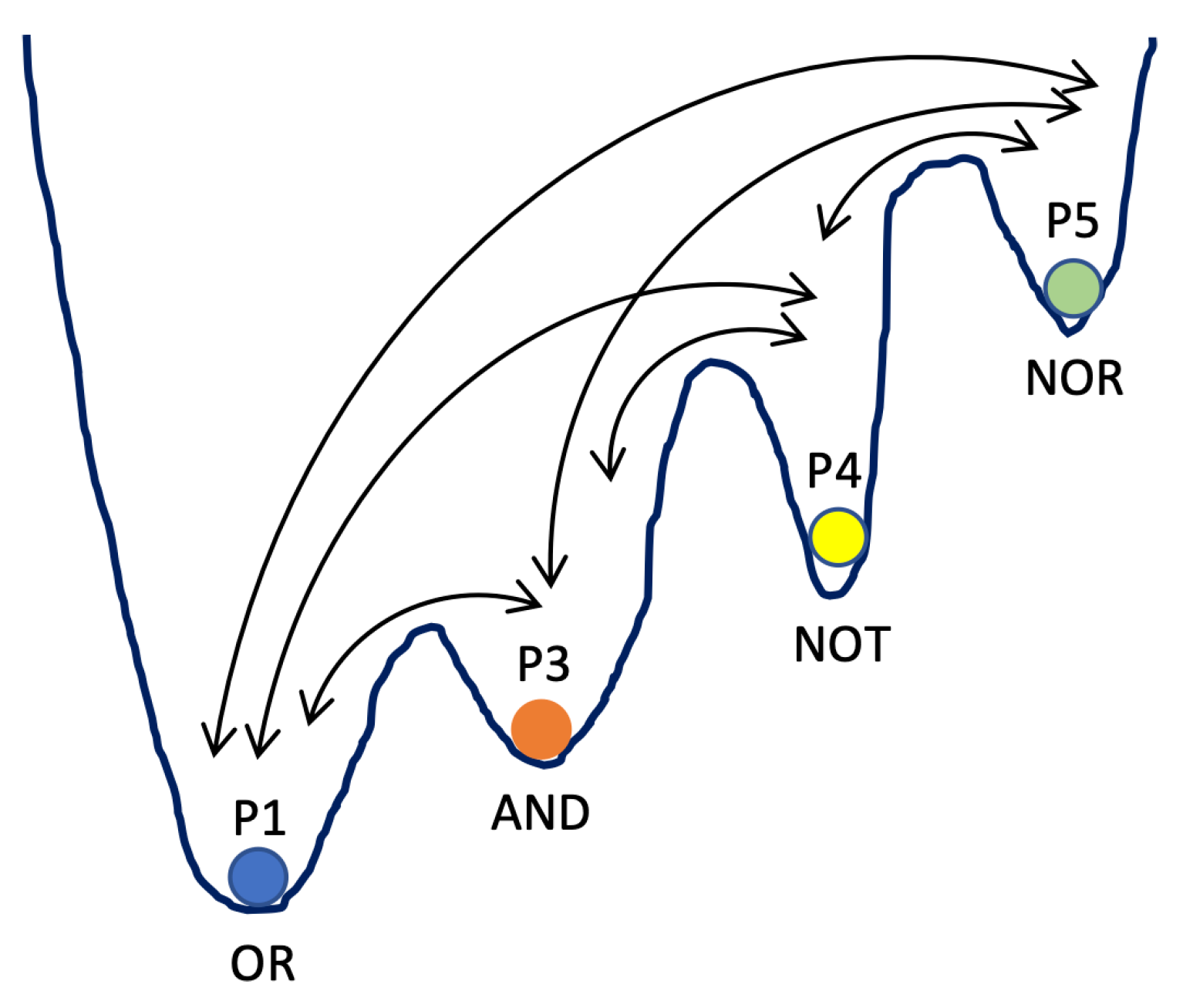
Figure 2.
Numerical bifurcation diagram of Eq. (5) with respect to modulation frequency for . The red rectangle indicates the modulation frequency explored in this work.
Figure 2.
Numerical bifurcation diagram of Eq. (5) with respect to modulation frequency for . The red rectangle indicates the modulation frequency explored in this work.
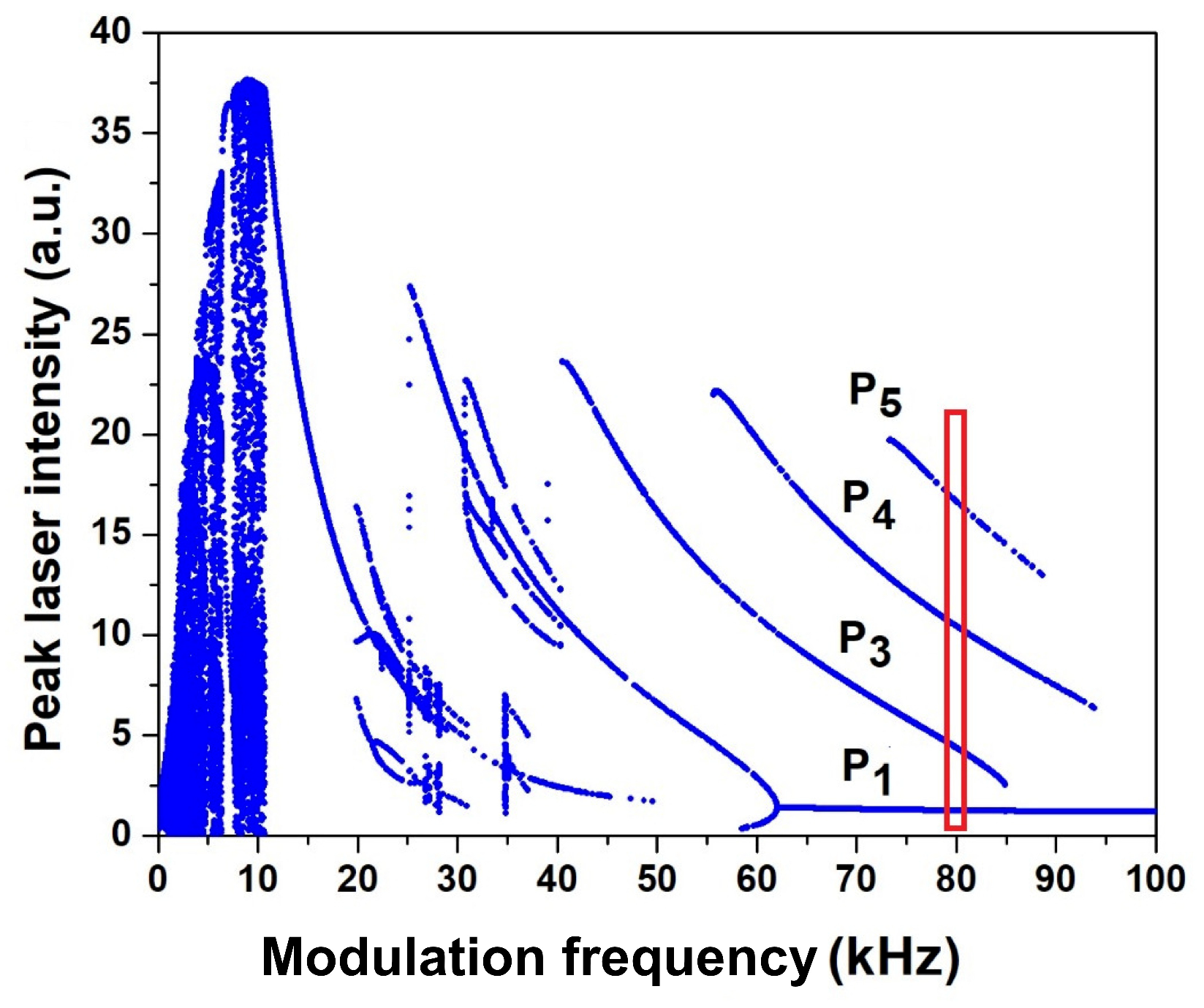
Figure 4.
State diagram of the EDFL in the parameter space of modulation frequency and noise intensity . Different colors represent different periodic and metaperiodic states.
Figure 4.
State diagram of the EDFL in the parameter space of modulation frequency and noise intensity . Different colors represent different periodic and metaperiodic states.
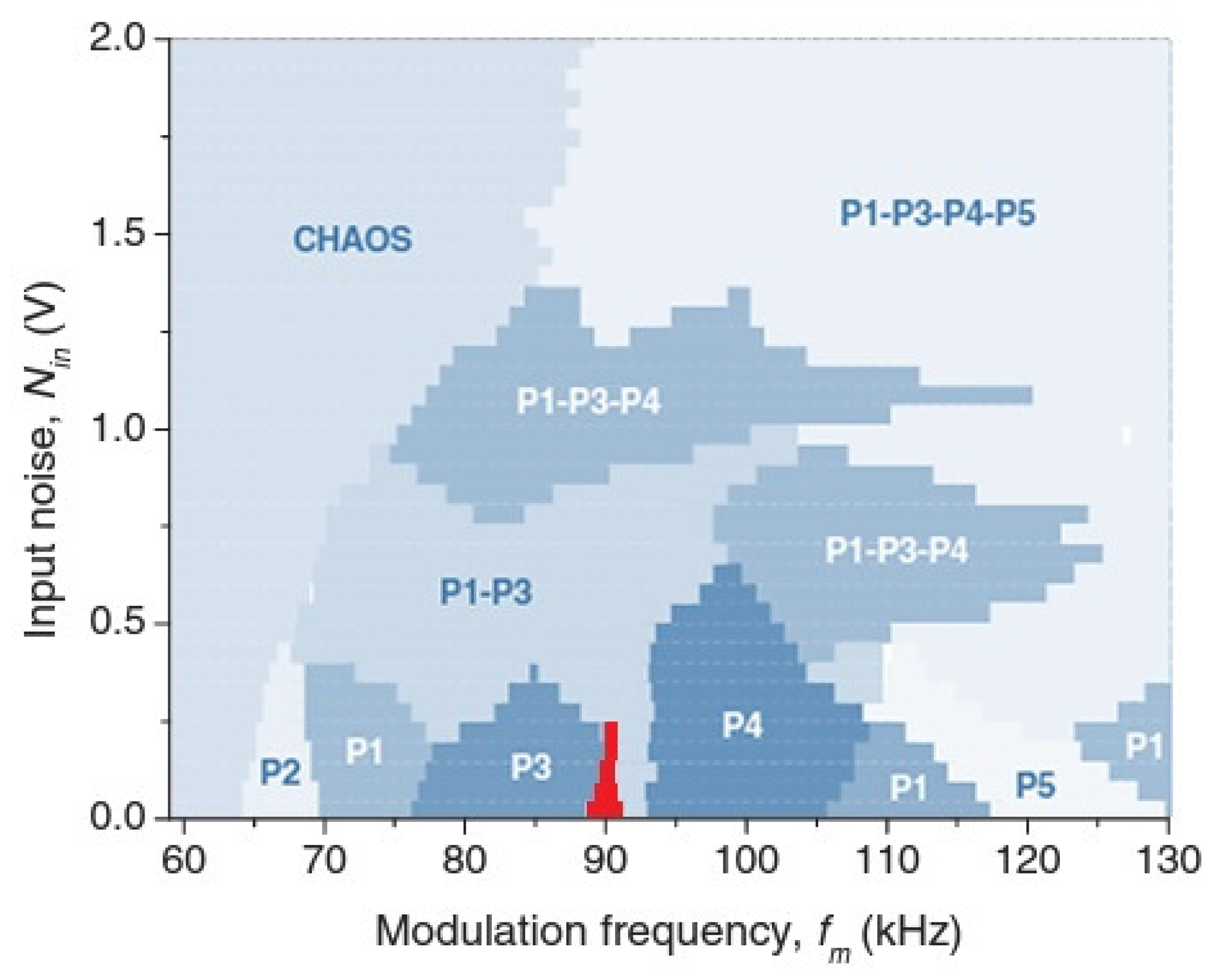
Figure 5.
Time series of laser intensity after low-pass filtering at =60 kHz for noise intensities (a) =0, (b) =30, (c) =60, and (d) =80.
Figure 5.
Time series of laser intensity after low-pass filtering at =60 kHz for noise intensities (a) =0, (b) =30, (c) =60, and (d) =80.
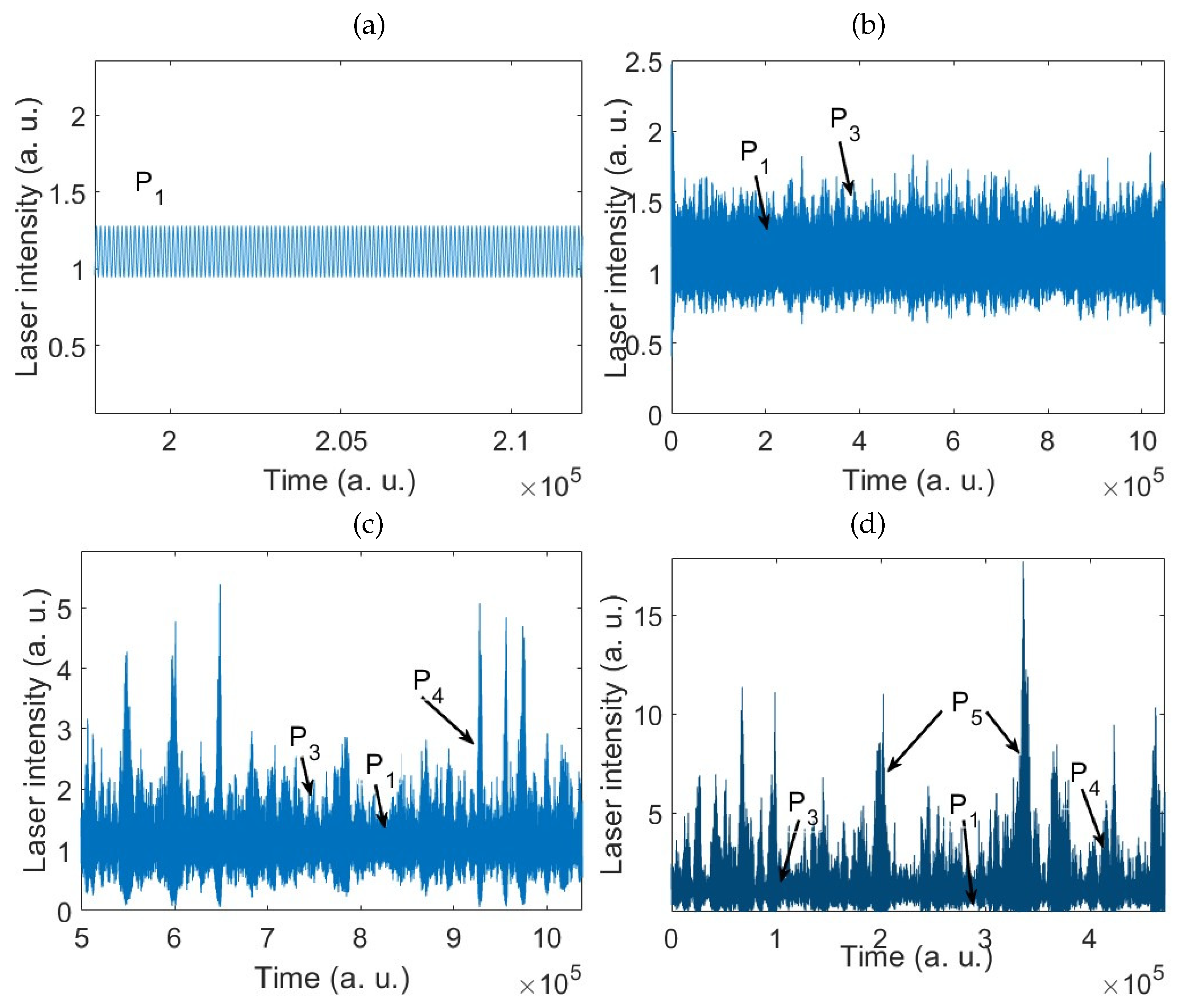
Figure 6.
Number of occurrences of (a) P1, (b) P3), (c) P4, and (d) P5 in the multistate intermittency regime versus noise intensity for different LPF values. kHz, .
Figure 6.
Number of occurrences of (a) P1, (b) P3), (c) P4, and (d) P5 in the multistate intermittency regime versus noise intensity for different LPF values. kHz, .
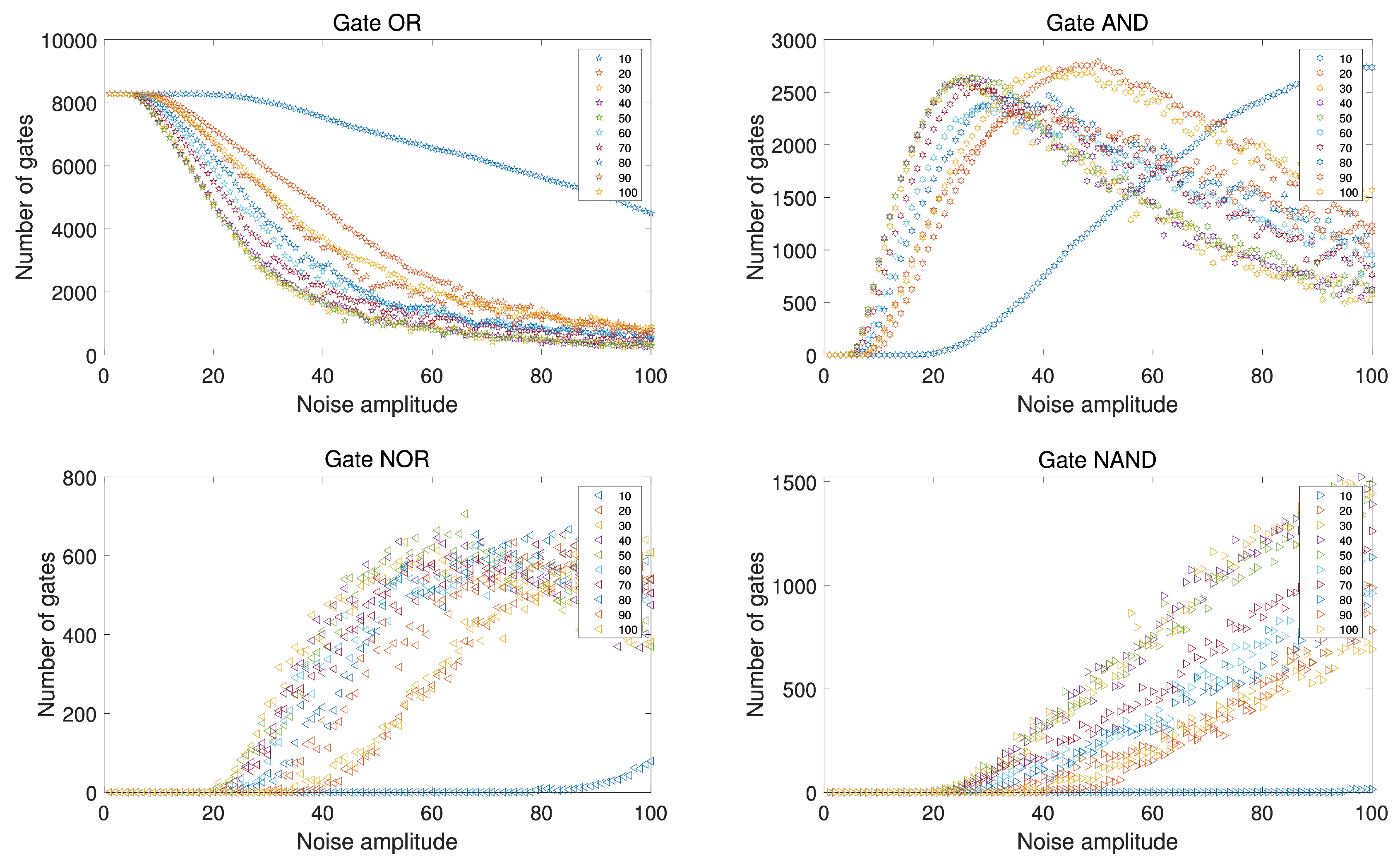
Figure 7.
Probability maps of occurrence of each of the periods in the multistate intermittency regime as a function of noise intensity and LPF frequency kHz.
Figure 7.
Probability maps of occurrence of each of the periods in the multistate intermittency regime as a function of noise intensity and LPF frequency kHz.
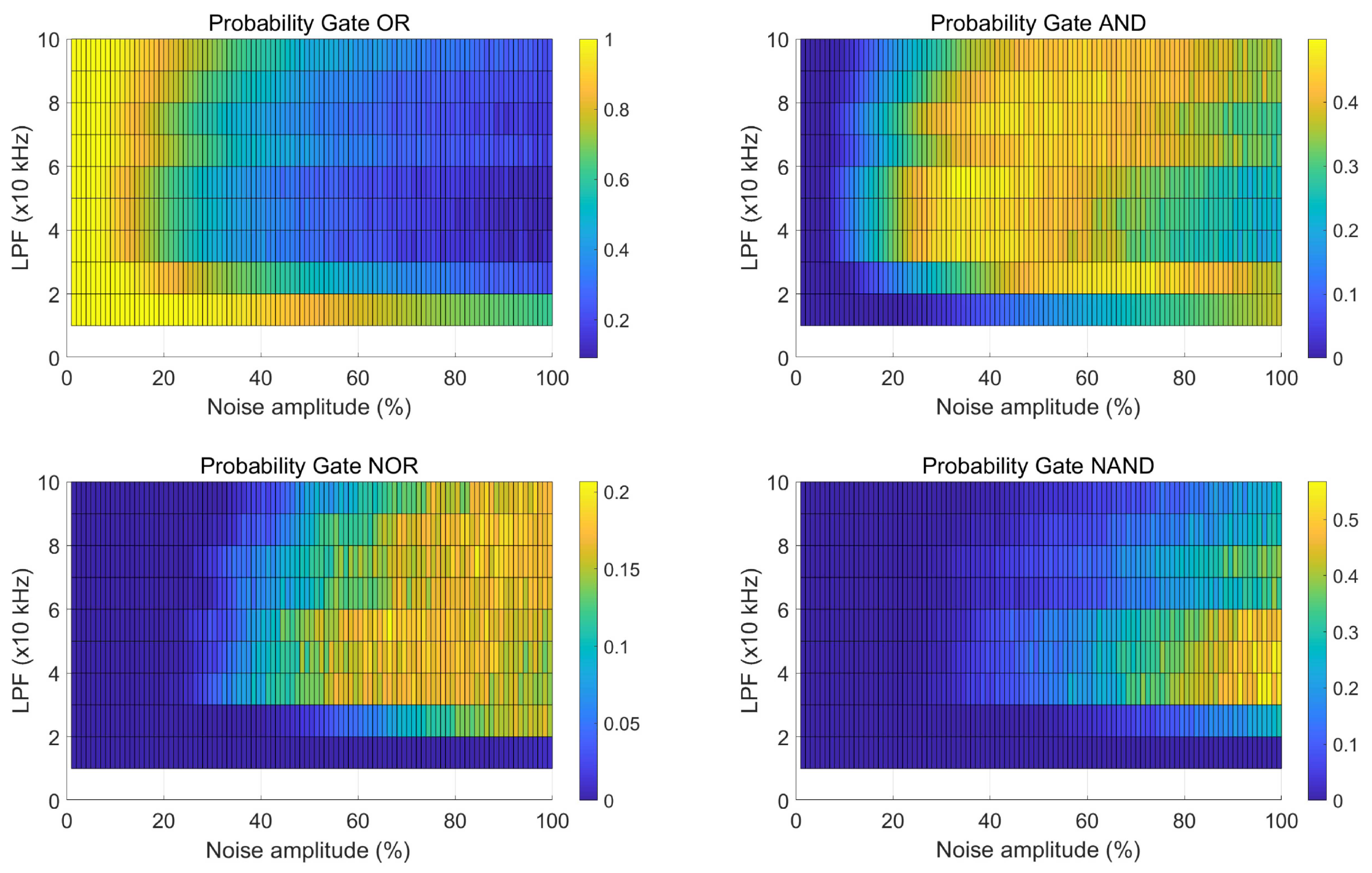
Figure 8.
Map of DFA slope for each combination of noise intensity and LPF frequency. When a correlated behavior between P1, P3, P4, and P5 states is observed.
Figure 8.
Map of DFA slope for each combination of noise intensity and LPF frequency. When a correlated behavior between P1, P3, P4, and P5 states is observed.

Figure 9.
Logic operations are defined by the local maxima of time series (upper trace) defining a logic gate. The squared red time series (middle traces) are two logic random signals and the black squared signal (lower trace) results from the operation defined by the laser-filtered noisy signal.
Figure 9.
Logic operations are defined by the local maxima of time series (upper trace) defining a logic gate. The squared red time series (middle traces) are two logic random signals and the black squared signal (lower trace) results from the operation defined by the laser-filtered noisy signal.
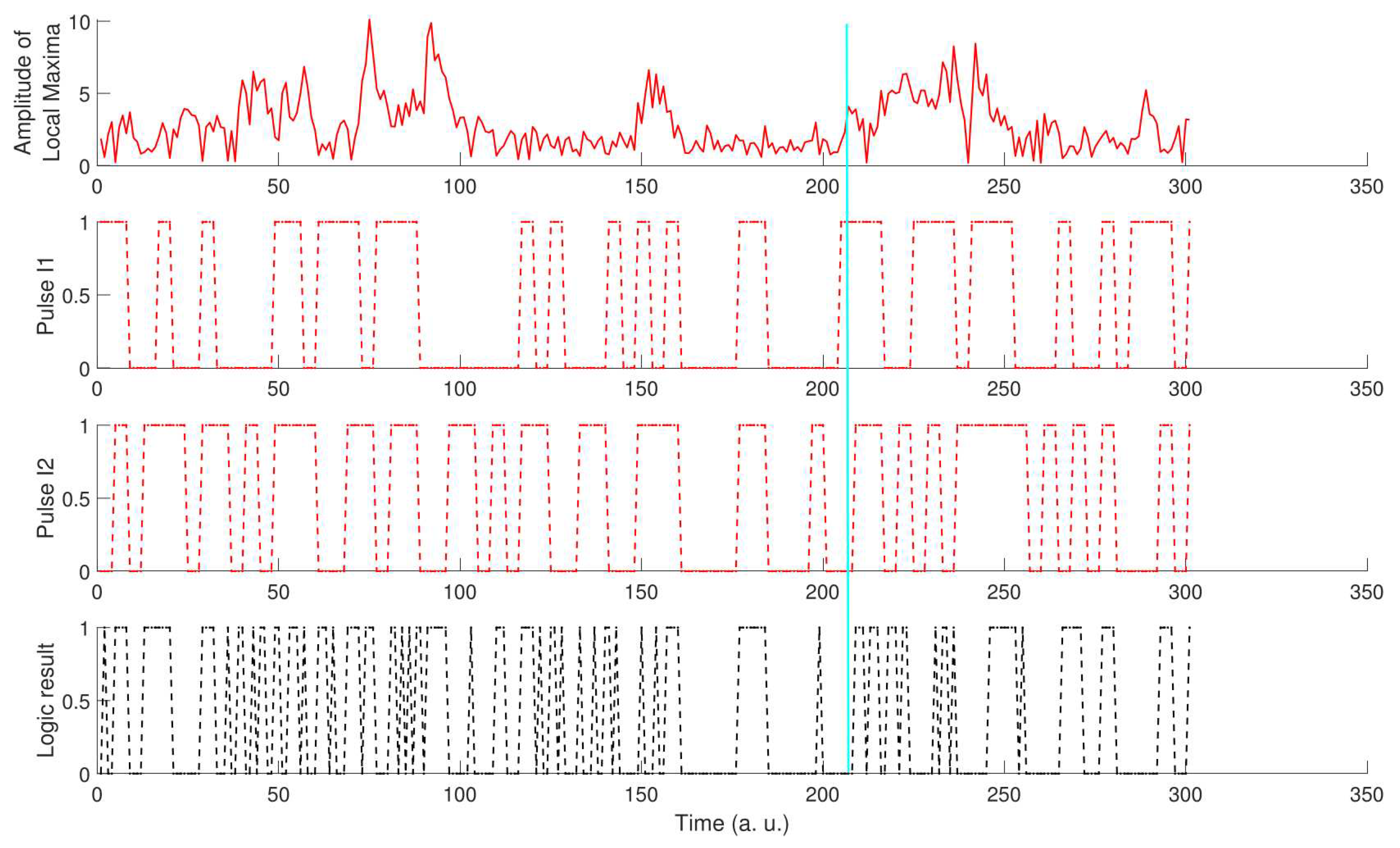
Table 1.
Parameter values of the normalized system in Eq. 5 for numerical simulations of the EDFL.
Table 1.
Parameter values of the normalized system in Eq. 5 for numerical simulations of the EDFL.
| Parameter | Value | Parameter | Value |
| a | b | ||
| c | 0.016 | d | |
| e | 506 | 0.307 | |
| 0.615 | -18 |
Table 2.
Noise intensities for intermittent regimes depicted in Figure 5.
Table 2.
Noise intensities for intermittent regimes depicted in Figure 5.
| State | Noise Intensity (a.u.) |
| 1.5 | |
| 4 | |
| 8 | |
| < 8 |
Table 3.
Logic operations associated with each of the coexisting periods in multistate intermittency.
Table 3.
Logic operations associated with each of the coexisting periods in multistate intermittency.
| Inputs | OR | AND | NOT | NOR |
| 0,0 | 0 | 0 | 0 | 1 |
| 1,0 | 1 | 0 | 0,1 | 0 |
| 0,1 | 1 | 0 | 1,0 | 0 |
| 1,1 | 1 | 1 | 0,0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated










