Preprint
Article
Two-Timescale Design for RIS-Aided Multicell MIMO Systems with Transceiver Hardware Impairments
Altmetrics
Downloads
72
Views
16
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
21 December 2023
Posted:
22 December 2023
You are already at the latest version
Alerts
Abstract
This paper investigates the reconfigurable intelligent surface (RIS)-aided uplink multicell massive multiple-input multiple-output (mMIMO) communication system with transceiver hardware impairments (THWIs), and the practical and feasible two-timescale scheme is used to design the phase shifts of RIS. We consider the Rician channel model and use maximal-ratio combining (MRC) technology to process the received signal at BS. The expression of the uplink achievable rate is derived and analyzed. Besides, genetic algorithm (GA) is used to optimize the phase shifts of RIS to maximize the data rate. Finally, the accuracy of the derived results is verified. The simulation results show that appropriately increasing the number of RIS’s reflecting elements can compensate for the performance loss caused by inter-cell interference and THWIs, and reduce the demand for the number of BS antennas, which can significantly reduce the hardware costs at the BS.
Keywords:
Subject: Engineering - Telecommunications
1. Introduction
The explosive growth of mobile data, as well as the emergence of innovative technologies such as virtual reality and holographic communication, require future wireless communication systems with extremely high data rates, seamless coverage, and ultra-high reliability. Fortunately, Reconfigurable Intelligent Surface (RIS) can enable future wireless communication systems to meet these requirements [1–3]. Therefore, RIS has been widely studied.
The authors in [4] focus on an RIS-aided multicell multiple-input single-output (MISO) system and maximize the minimum weighted signal-to-interference-plus-noise ratio (SINR) through jointly optimizing the transmit beamforming vectors at the base stations (BS) and the reflective beamforming vector of the RIS. The authors in [5] investigate a RIS backscatter-based uplink coordinated transmission strategy and aim to maximize the weighted sum rate (WSR). In [6], the authors suggest RIS be deployed at the boundaries of multiple cells to mitigate inter-cell interference and assist cell-edge users in communicating with BS, aiming to maximize the WSR by jointly optimizing the phase shifts of RIS and the precoding matrix at the BS. In [7], the authors consider the phase shifts design of RIS and joint user scheduling in RIS-aided multicell downlink systems. The authors in [8] study an intelligent omni-surface-aided multicell MIMO communication system and design a distributed hybrid beamforming scheme to maximize the sum rate. In [9], besides considering the joint beamforming problems for a RIS-aided multicell MISO system, authors further consider the SINR balancing beamforming design to enhance the fairness of users by maximizing the minimum SINR among all users.
However, the transceiver hardware impairments (THWIs) in the scenario of RIS-aided multicell massive MIMO system have not been considered. Therefore, we investigate an RIS-aided multicell mMIMO system with THWIs. More importantly, the phase optimization of RIS is based on the more practical and feasible two-timescale design scheme. Specifically, the phase shifts of the RIS are designed based on the statistical channel state information (CSI). In contrast, while the beamforming at the BS is designed based on the instantaneous CSI, which can significantly reduce the frequency of reconfiguring RIS [10]. We first derive and analyze the expression of uplink achievable data rate. Then, we use a genetic algorithm (GA) to optimize the phase shifts of RIS to maximize the sum and minimum user rates. Finally, we verify the accuracy of derivation through Monte Carlo (MC) simulation. The simulation shows that in the RIS-aided multicell mMIMO system with THWIs, appropriately increasing the number of RIS’s reflecting elements can compensate for the performance loss caused by inter-cell interference and THWIs, and also reduce the demand for the number of BS antennas, which can significantly reduce the hardware costs at the BS.
2. System Model
As shown in Figure 1, we consider an RIS-aided uplink multicell mMIMO communication system. The number of cells is L, and the RIS comprises N reflecting elements. The base station (BS) in each cell is equipped with M receiving antennas, both the BS and RIS adopt the uniform square planar array. In each cell, the direct link between users and BS is blocked by obstacles, K single-antenna users can only communicate with BS through RIS, and both the transmitters and receivers have hardware impairments.
The phase shifts matrix of RIS is , where , , represents the phase shift of element n. In the l-th cell, the channel from the users to the RIS is denoted by , , where represents the channel from the k-th user to the RIS. The channel from the RIS to the BS is denoted by . The expressions of and are
where and are large scale path loss factors, and are Rician factors, and are the none-line-of-sight (NLoS) components of the channel whose elements are independent and identical distribution (i.i.d.) random variables following . and are LoS components of channel, and the expressions are
where , respectively represent the arrival azimuth and elevation angles from RIS to the BS in the l-th cell. , respectively represent the departure azimuth and elevation angles from the RIS to the BS in the l-th cell. , respectively represent the arrival azimuth and elevation angles from user k to the RIS in the l-th cell. In addition, the expressions of is
where , d represents the elements spacing, represents wavelength.
Based on the above definitions, the cascaded channel in the l-th cell can be denoted by , where .
In the l-th cell, the transmit distortion of users is denoted by , where represents the transmit distortion of the user k. The receive distortion of BS is denoted by .
Therefore, the signal received by the BS of the l-th cell is
where is the transmit power of users. is the signal vector of users, and . represents the additive white Gaussian noise (AWGN). The transceiver distortions are described in terms of conditional distributions with respect to the channel realizations as and , where and represent the severity of the residual impairments of the transceiver.
Then, we employ the MRC technology, and the received signal at the BS can be expressed as
Therefore, in the l-th cell, the k-th user’s signal received by the BS can be expressed as
3. Analysis of Uplink Achievable Rate
The uplink data rate of user k can be denoted by , where is the signal-to-interference-plus-noise ratio (SINR) of the user k in l-th cell. The expression of is given as
Theorem 1.
In the RIS-aided uplink multicell mMIMO communication system with THWIs, by using Lemma 1, can be approximated as , where
where , , , , and .
The expressions of , , , and are respectively given by (11)-(15), where , , is the m-th element of ,
Proof of Theorem 1.
Please refer to Appendix A. □
By observing (10), We find that the phase shift term is always related to the Rician factors , , , . We can conclude that if the channel in this system is fully Rayleigh channel, namely , , the performance of this system will be independent of the phase shifts and only depends on the number of RIS elements N and BS antennas M. Hence, it is important to reveal the relation between the system performance and the number of RIS elements N and BS antennas M.
Corollary 1.
In the RIS-aided uplink multicell mMIMO communication system with THWIs, when and the phase shifts of RIS are random, we can approximate the rate as , where
where
Proof of Corollary 1.
Similar to the derivation method in [11] Corollary 3, we can remove the terms that are not on the order of when . Besides, it is noted that the phase shift terms such as can be replaced as its expectation. □
It can be seen that the noise term is not included in equation (19) and the rate will tend to be a constant. This shows that in the RIS-aided uplink multicell mMIMO communication system with THWIs when and the phase shifts of RIS are random, we can eliminate the effect of noise.
Corollary 2.
In the RIS-aided uplink multicell mMIMO communication system with THWIs, when , we can approximate the rate as , where
where
Proof of Corollary 2.
Similar to the derivation of Corollary 1, we can remove the terms that are not on the order of . □
As same as Corollary 1, when the number of BS antennas M tends to be infinite, the rate of this system will tend to a constant too. Besides, the effect of noise can be ignored.
4. Phase Shifts Optimization
By observing (10), we found that the rate only depends on statistical CSI including the Rician factors, LoS components of the channel and path loss coefficients. Therefore, we can optimize the phase shifts of RIS based on statistical CSI.
Specifically, we respectively formulate two optimization problems the sum rate maximization problem to guarantee overall system performance and the minimum user rate maximization problem to guarantee fairness between users as (27), (28).
where is given in (10).
Due to the complexity of the rate expression, the existing gradient descent method and convex optimization method cannot solve this problem. The genetic algorithm (GA) does not need to calculate the first-order derivative of the objective function as the conventional gradient descent method does. Instead, we only need to calculate the objective function in each iteration, so we use GA. The detailed steps of the algorithm are as follows
Initialize population: Generate S individuals, and each individual has N chromosomes randomly generated from , corresponding to the phase shifts matrix of RIS.
Calculate fitness: In the current population, we first calculate the fitness of each individual through the objective function of the optimization problem (32) or (33). Then, we sort them in descending order according to fitness.
Select elite: We select the top individuals as elites and pass them to the next generation.
Mutation: We select the last individuals as parents and mutate them with a probability of 0.1 to generate offspring. The mutation algorithm is shown as follows.
Crossover: We use stochastic universal sampling to generate parents from the remaining individuals. Then, we use the two-points crossover method to generate offspring from parents. The two-points crossover method is shown as follows.
Finally, we combine elites and offspring to generate the next generation population. When the change value of average fitness is less than the preset value or the number of iterations reaches the preset maximum number of iterations, the algorithm stops. In the current population, the chromosome of the individual with the highest fitness corresponds to the optimal phase shifts of RIS.
| Algorithm 1: Mutation Algorithm |
| 1. for do; |
| 2. for do; |
| 3. ; |
| 4. if then ; |
| 5. The n-th chromosome of individual mutates to ; |
| 6. end if |
| 7. end for |
| 8. end for |
| Algorithm 2: Two-Points Crossover Algorithm |
| 1. Initialize ; |
| 2. for do; |
| 3. Select the c-th and -th parents from the parents; |
| 4. Randomly generate integers from and satisfy ; |
| 5. Generate the s-th offspring, and the N chromosomes of the s-th offspring are the chromosomes of the c-th parent, the chromosomes of the -th parent, the chromosomes of the c-th parent. |
| 6. |
| 7. end for |
5. Simulation Result
In this section, we provide simulation results to validate the derived expressions and analyze various system parameters. The parameter settings were referred to [6] and [12]. Unless otherwise stated, we set it as follows: dBm, dBm, . We assume that the distance from RIS to BS is , users are distributed on a circle with RIS as the center and a radius of . Therefore, , . In addition, the element spacing of is set to avoid spatial correlation. The various angles at BS and RIS are randomly generated from and fixed after initial generation.
As shown in Figure 2, we plot the achievable rate obtained from optimization problems (32) and (33) and carry out MC simulation for verification. The MC simulation results are consistent with the derived results, which shows the accuracy of the derived results.
In Figure 3, we verified that the optimization problem (33) can ensure users’ fairness. The relationship between the two vertical coordinates is four times, and the two curves coincide with each other, while the number of users , means that the minimum user rate reaches the average user rate, i.e., all users have the same rate.
Figure 4 depicts the achievable rate in different scenarios. As shown in Figure 4, scheme ’, Sum rate by max-sum’ is superior to scheme ’, Sum rate by random phase’, and as N increases, the performance gap between the two will become larger. This is consistent with our Corollary 2 that the rate will tend to be a constant when BS antennas .
Besides, it indicates that it is necessary to optimize the phase shifts of RIS.
In Figure 5, we plot the achievable rate versus the Rician factor of the RIS-BS channel. As increases, the sum and minimum user rates decrease. This is because, with the increase of , the channels between users have a stronger correlation, which reduces the spatial multiplexing gain and also increases the interference between users.
In Figure 6, we plot the achievable rate with different THWIs coefficients. As the transmit power increases, the sum rate and minimum user rate gradually increase and tend towards a limit value. In addition, with the increase of power, the performance gap between the two THWIs scenarios also widens because the THWIs are tightly coupled with the transmitted signal and become stronger as the THWIs coefficients increase.
Figure 7 depicts the achievable rate under different schemes. Through comparison, we find that the rate performance of scheme ’, ’ is the same as that of scheme ’’. This means that we can significantly reduce the demand for the number of BS antennas by appropriately increasing the number of RIS’s reflecting elements, effectively reducing the hardware cost at BS.
To ensure the accuracy of scheme comparison, we further draw Figure 8. As shown in Figure 8, the scheme ’’ is superior to the scheme ’, ’ in different THWIs and power scenarios, which shows the accuracy of the scheme comparison.
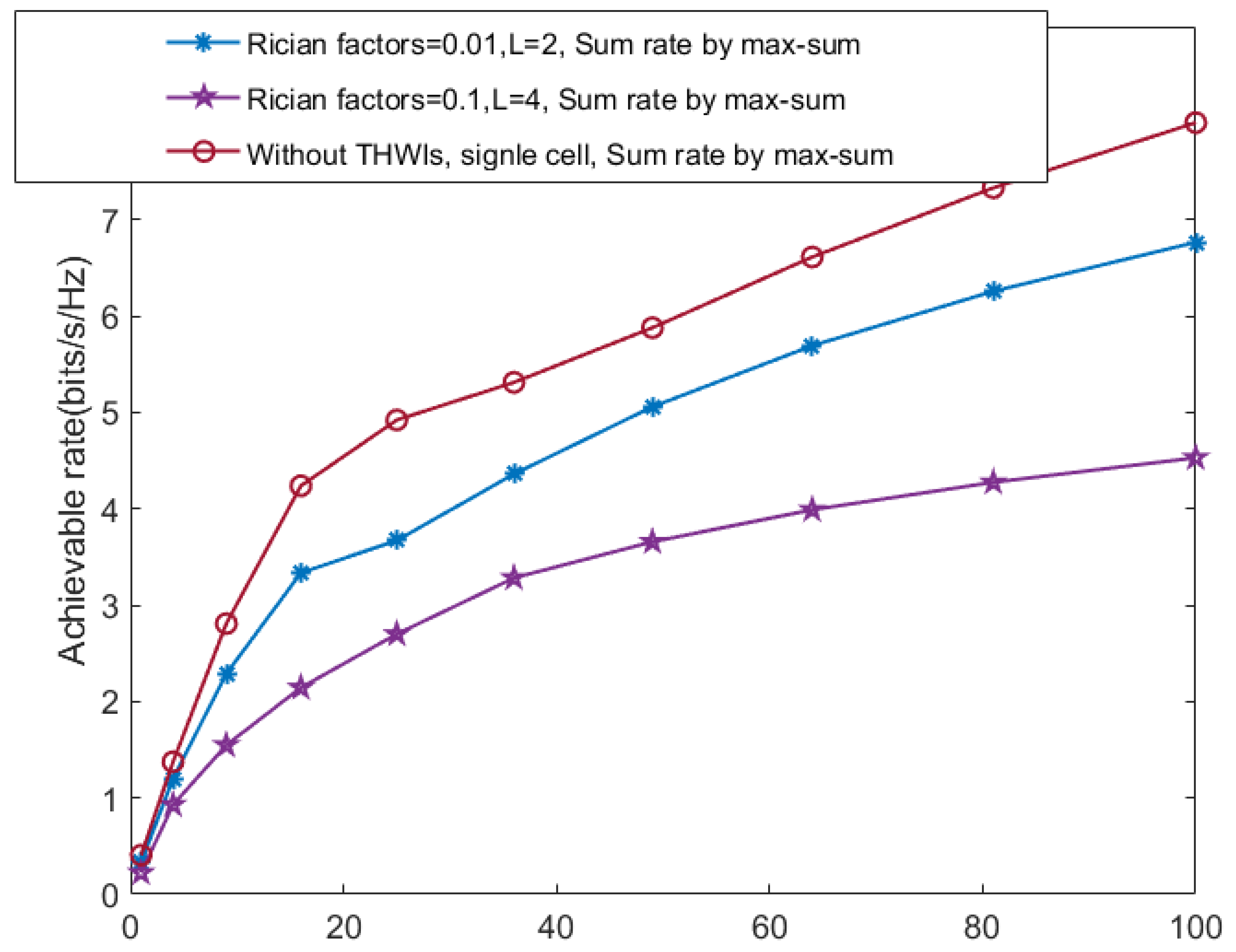
In Figure 9, we plot the sum rate for three scenarios. In scenario , Sum rate by max-sum’, the impact of inter-cell interference and THWIs can be compensated by increasing the number of components. This is meaningful because increasing N is more cost-effective and practical compared to replacing transceivers and reducing the number of cells.
6. Conclusion
This paper has focused on an RIS-aided uplink multicell mMIMO communication system with THWIs. We have derived and analyzed the achievable rate expression, and the phase shifts of RIS have been optimized based on the two-time scale design scheme. Through simulation, the correctness of the derived expression has been verified, and the following conclusion has been obtained. In RIS-aided uplink multicell mMIMO communication system with THWIs, we can compensate for the performance loss caused by inter-cell interference and THWIs by appropriately increasing the number of RIS’s reflecting elements, and also significantly reduce the demand for the number of BS receiving antennas, which will effectively reduce the hardware cost at the BS.
Author Contributions
Conceptualization, S.Z. and F.Z.; methodology, S.Z.; software, S.Z.; validation, S.Z., W.G. and J.D.; formal analysis, W.G.; investigation, W.G.; resources, W.G.; data curation, J.D.; writing—original draft preparation, F.Z.; writing—review and editing, S.Z.; visualization, S.Z.; supervision, S.Z.; project administration, W.G.; funding acquisition, W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology on Information Systems Engineering Laboratory (No.05202101) and the open research fund of National Mobile Communications Research Laboratory, Southeast University (No. 2023D03).
Data Availability Statement
The data presented in this study are available on request from the lead author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
have been given in [11]. The derivations of can refer to . Besides, can be expanded as
is obtained by removing the zero terms, can be found in [11]. Therefore, we only need to derive and .
Substituting (1)-(3) into . Then, we can express as
where is the m-th element of , , and are respectively the n-th element of , and , is the -th element of . The expression of can be obtained in the same way.
Hence, we have
where is obtained by removing the zero terms.
We will calculate the terms in (A3) one by one. The first term can be calculated directly
Besides, assume that
Substituting (A5) into (A3) and after some simplifications, the second item can be derived as (A6). Accordingly, the remaining items can be derived as
References
- C. Huang et al., "Holographic MIMO Surfaces for 6G Wireless Networks: Opportunities, Challenges, and Trends," in IEEE Wireless Communications, vol. 27, no. 5, pp. 118-125, October 2020. [CrossRef]
- Wang, H. Wang, Y. Han, S. Jin and X. Li, "Joint Transmit Beamforming and Phase Shift Design for Reconfigurable Intelligent Surface Assisted MIMO Systems," in IEEE Transactions on Cognitive Communications and Networking, vol. 7, no. 2, pp. 354-368, June 2021. [CrossRef]
- M. Di Renzo et al., "Smart Radio Environments Empowered by Reconfigurable Intelligent Surfaces: How It Works, State of Research, and The Road Ahead," in IEEE Journal on Selected Areas in Communications, vol. 38, no. 11, pp. 2450-2525, Nov. 2020. [CrossRef]
- H. Xie, J. Xu and Y. -F. Liu, "Max-Min Fairness in IRS-Aided Multi-Cell MISO Systems via Joint Transmit and Reflective Beamforming," ICC 2020 - 2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 2020, pp. 1-6. [CrossRef]
- S. Xu, C. Chen, Y. Du, J. Wang and J. Zhang, "Intelligent Reflecting Surface Backscatter Enabled Uplink Coordinated Multi-Cell MIMO Network," in IEEE Transactions on Wireless Communications. [CrossRef]
- C. Pan et al., "Multicell MIMO Communications Relying on Intelligent Reflecting Surfaces," in IEEE Transactions on Wireless Communications, vol. 19, no. 8, pp. 5218-5233, Aug. 2020. [CrossRef]
- L. Jiang, X. Li, M. Matthaiou and S. Jin, "Joint User Scheduling and Phase Shift Design for RIS Assisted Multi-Cell MISO Systems," in IEEE Wireless Communications Letters, vol. 12, no. 3, pp. 431-435, March 2023. 23. [CrossRef]
- Y. Zhang, B. Di, H. Zhang, Z. Han, H. V. Poor and L. Song, "Meta-Wall: Intelligent Omni-Surfaces Aided Multi-Cell MIMO Communications," in IEEE Transactions on Wireless Communications, vol. 21, no. 9, pp. 7026-7039, Sept. 2022. [CrossRef]
- J. Qiu, J. Yu, A. Dong and K. Yu, "Joint Beamforming for IRS-Aided Multi-Cell MISO System: Sum Rate Maximization and SINR Balancing," in IEEE Transactions on Wireless Communications, vol. 21, no. 9, pp. 7536-7549, Sept. 2022. [CrossRef]
- A. Abrardo, D. Dardari and M. Di Renzo, "Intelligent Reflecting Surfaces: Sum-Rate Optimization Based on Statistical Position Information," in IEEE Transactions on Communications, vol. 69, no. 10, pp. 7121-7136, Oct. 2021. [CrossRef]
- K. Zhi, C. Pan, H. Ren and K. Wang, "Power Scaling Law Analysis and Phase Shift Optimization of RIS-Aided Massive MIMO Systems With Statistical CSI," in IEEE Transactions on Communications, vol. 70, no. 5, pp. 3558-3574, May 2022. [CrossRef]
- K. Zhi, C. Pan, H. Ren and K. Wang, "Statistical CSI-Based Design for Reconfigurable Intelligent Surface-Aided Massive MIMO Systems With Direct Links," in IEEE Wireless Communications Letters, vol. 10, no. 5, pp. 1128-1132, May 2021. [CrossRef]
Figure 1.
An RIS-aided uplink multicell mMIMO communication system.

Figure 2.
Sum rate and minimum user rate versus N.
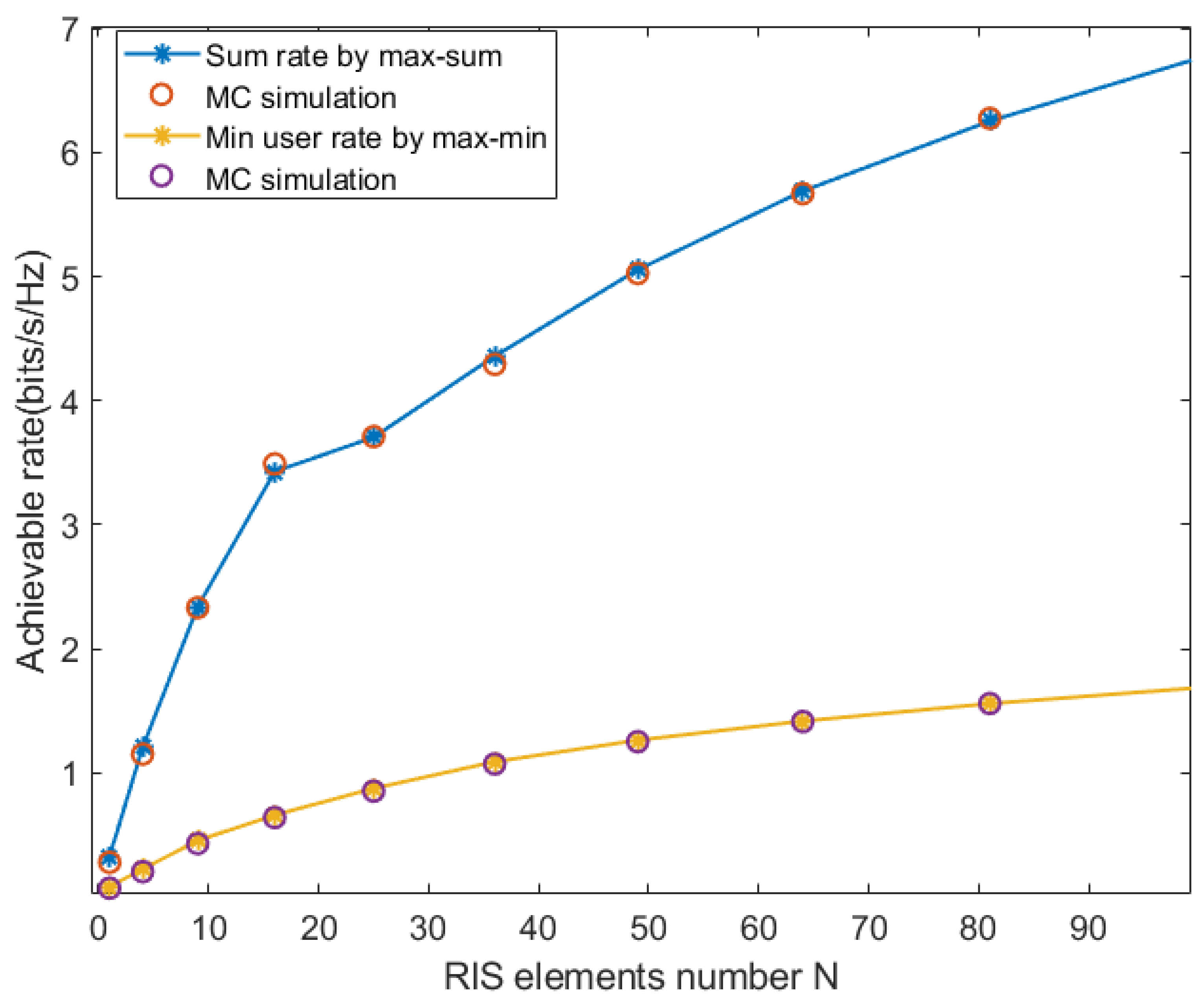
Figure 3.
max min-rate to ensure users’ fairness.
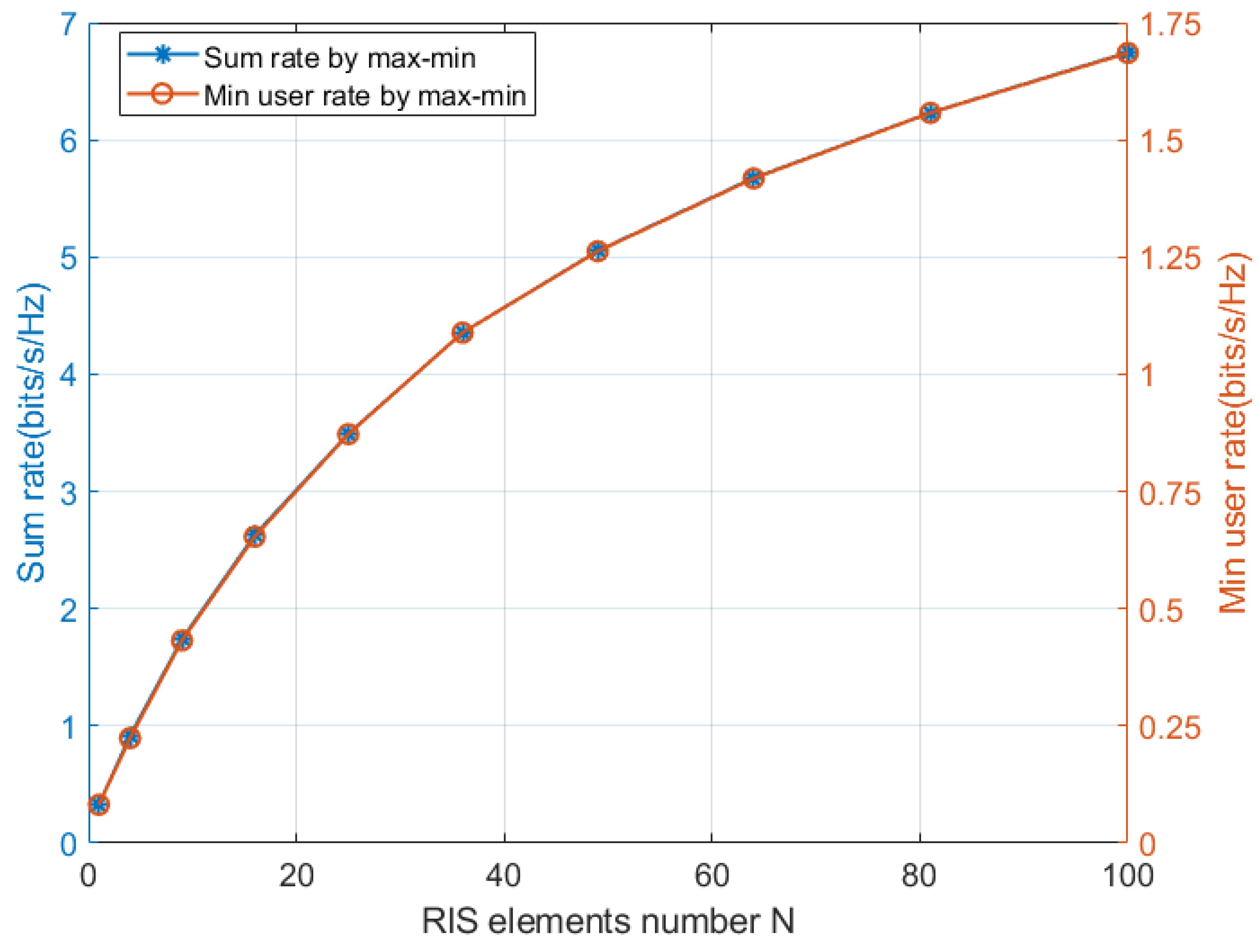
Figure 4.
Sum rate versus M.
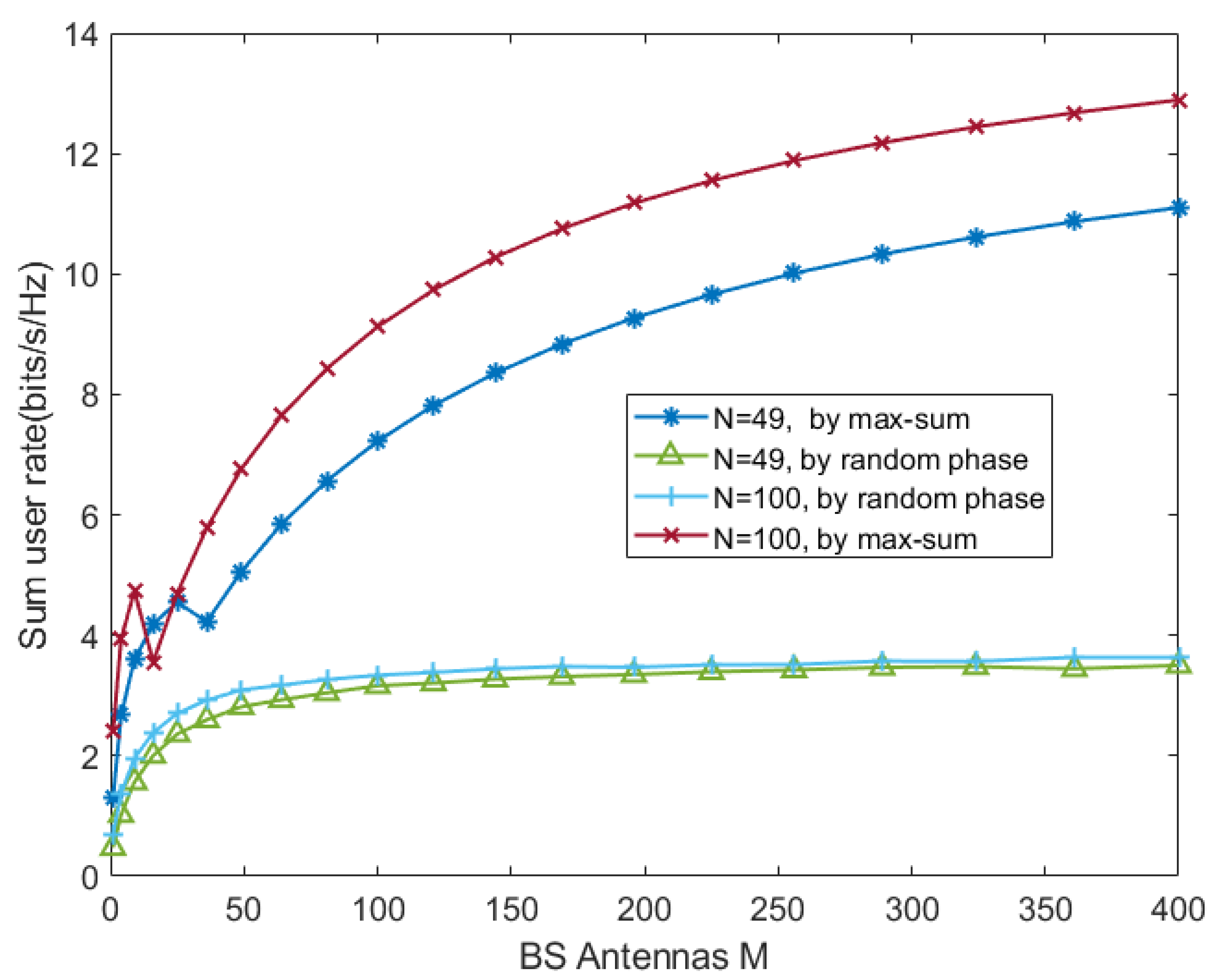
Figure 5.
Achievable rate versus the Rician factor of RIS-BS.
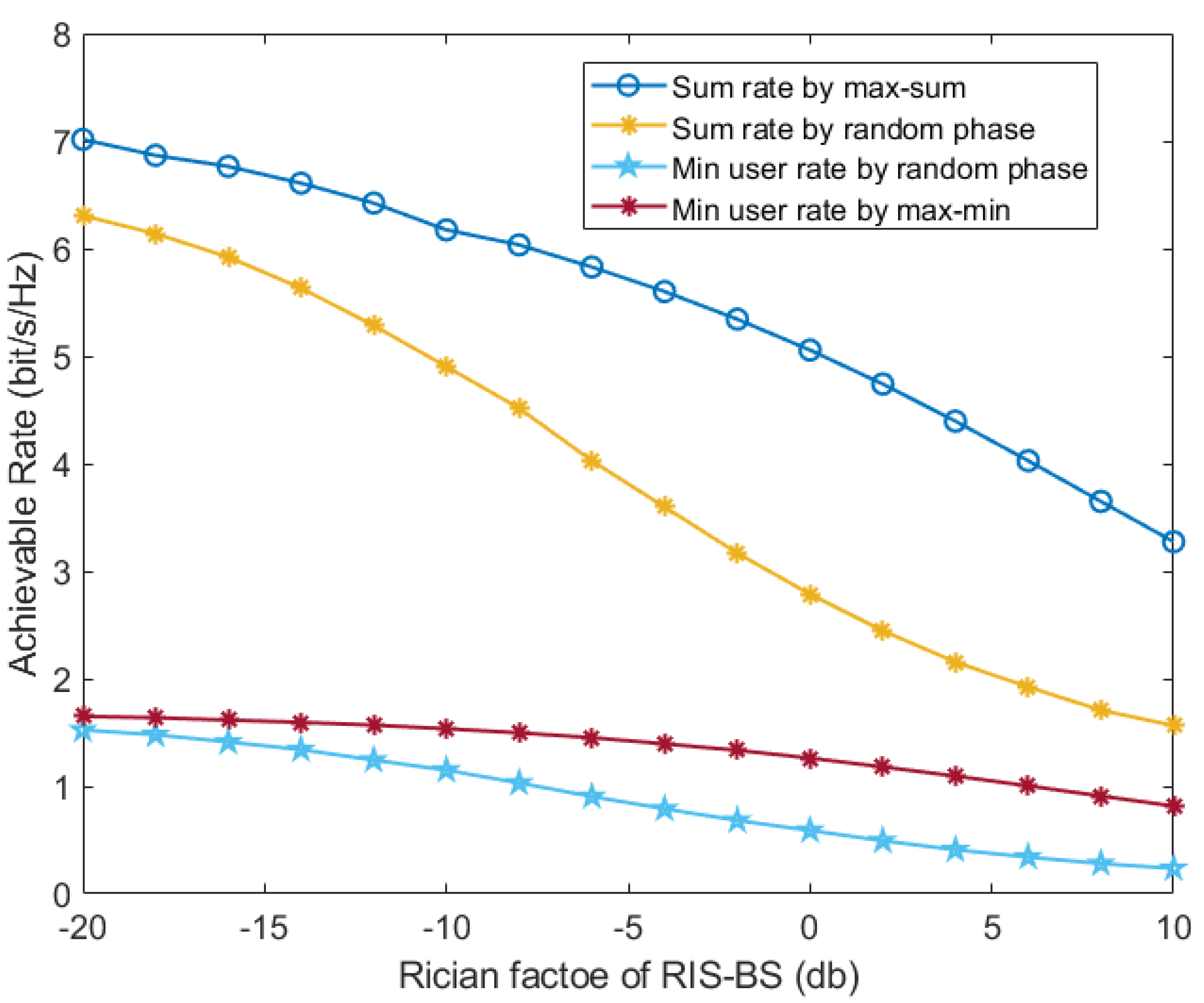
Figure 6.
Sum rate and minimum user rate versus transmit power.
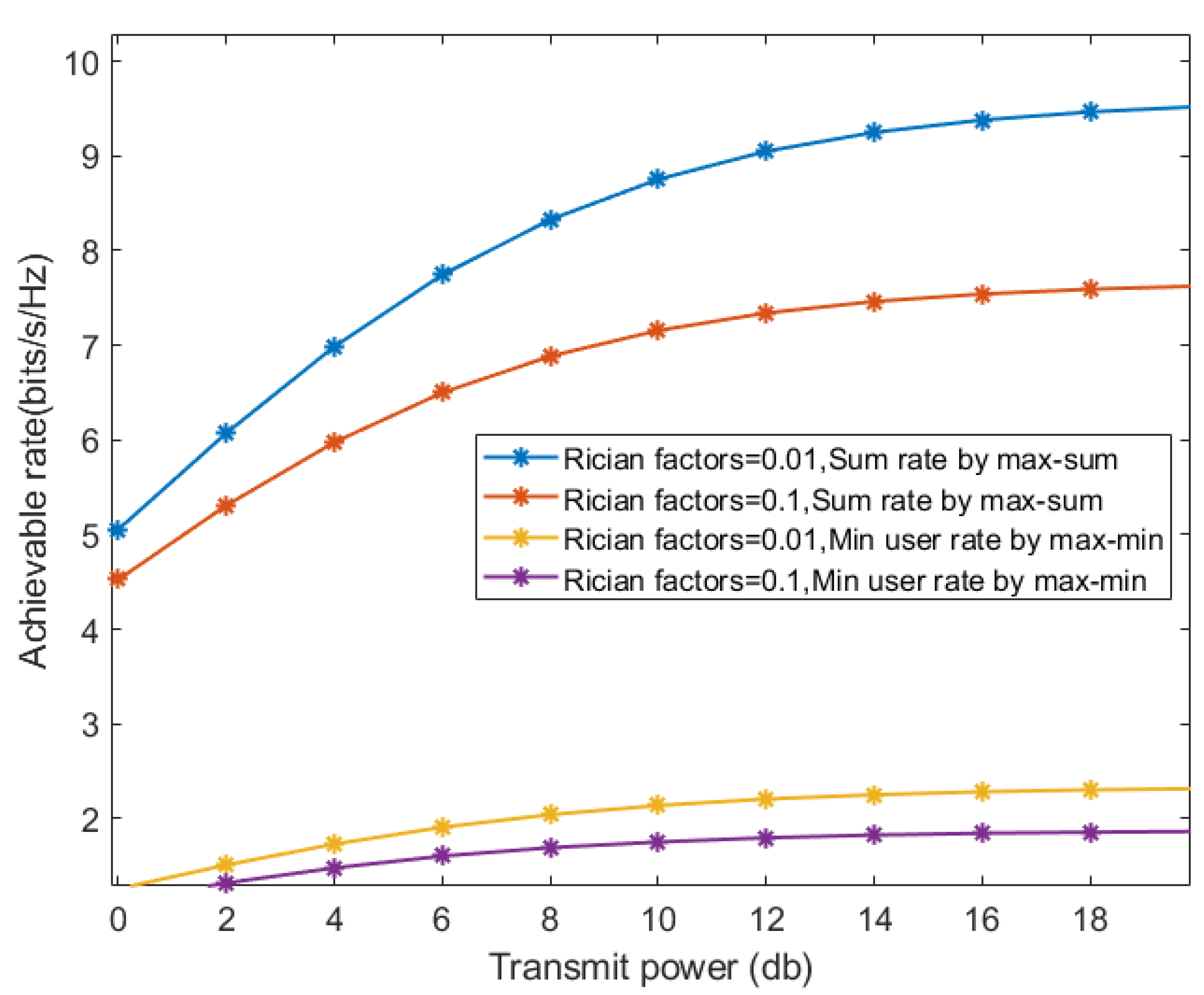
Figure 7.
Sum rate and minimum user rate versus N under different schemes.
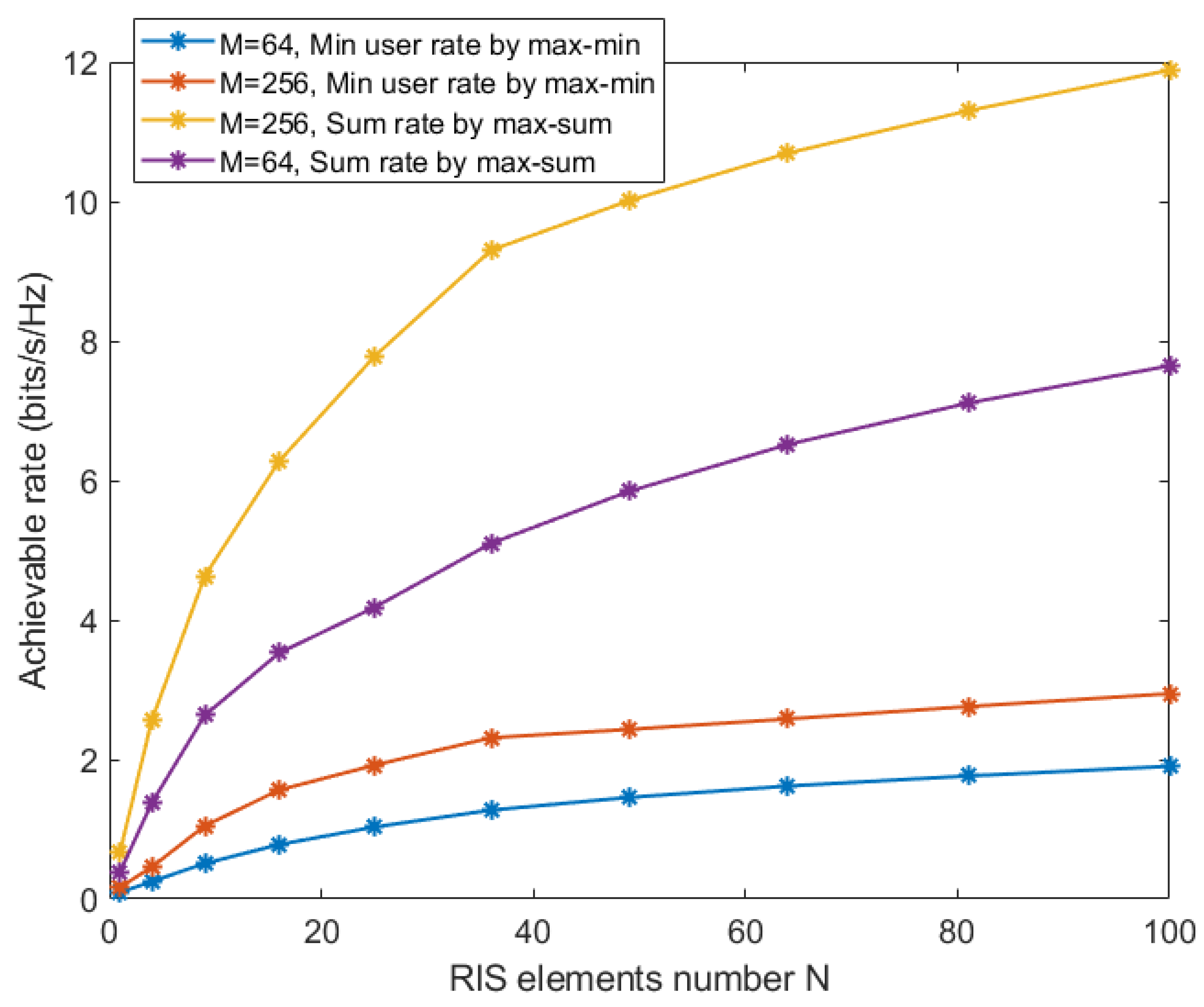
Figure 8.
Comparison of rate performance under different schemes.
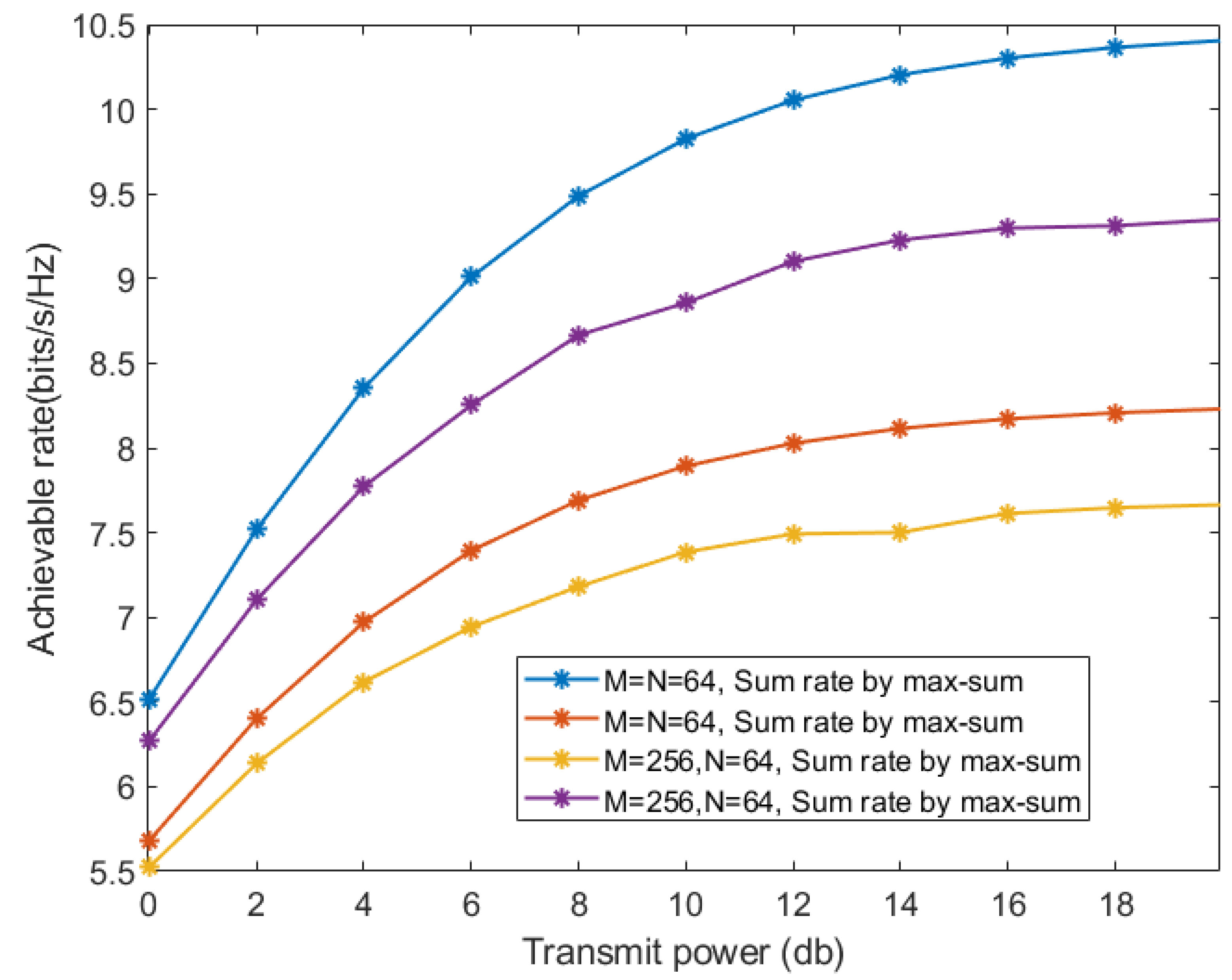
Figure 9.
Sum rate versus N in different scenarios.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





