Prerpints.org logo
Preprint
Communication

The Theoretical Dose That Exerts the Maximum Hormesis Effect Is 20 mSv When the Risk Is Approximately Proportional to Dose above 100 mSv.

Altmetrics

Downloads

108

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (353.85KB )

This version is not peer-reviewed

Submitted:

22 December 2023

Posted:

22 December 2023

You are already at the latest version

Alerts
Abstract
To date, radiation adaptation response has been reported as a low-dose related phenomenon and has been associated with radiation hormesis. Well-known cancers are caused by non-radiation active reactants, in addition to radiation. A model of suppression for radiation-specific cancers was previously reported, but the model did not target radiation-nonspecific cancers. In this paper, we describe kinetic models of radiation-induced suppressors for general radiation non-specific cancers, estimating the dose that induces the maximum hormesis effect while satisfying the condition that the risk is approximately proportional to dose above 100 mSv. It was found that the radiation hormesis effect is maximal at about 20 mSv when the rate constant for generation is the same as the rate constant for decomposition. When the two rate constants are different, the dose at which the radiation hormesis effect is maximized depends on both rate constants, but the dose increases as the two rate constants approach each other, reaching a maximum of about 20 mSv. This conclusion may lead to the discovery of unknown cancer suppressors at low doses and the development of cancer suppression methods in the future.
Keywords: 
Subject: Public Health and Healthcare  -   Public, Environmental and Occupational Health

1. Introduction.

Radiation can ionize DNA in vivo, and causes various types of DNA damage, including double-strand breaks, which in turn cause gene mutations, such as ras oncogenes and p53 tumor-suppressor genes, ultimately resulting in cancerous cells. Radiation safety management is based on the linear non-threshold (LNT) hypothesis, which states that the probability of carcinogenesis is proportional to radiation dose below 100 mSv. The LNT hypothesis is based on the result that excess relative risk is proportional to dose above 100 mSv [1]. However, if Sv is considered the same as Gy, a sample size of 6200 persons at 100 mSv, approximately 620,000 persons at 10 mSv, and approximately 61.8 million persons at 1 mSv would be needed to make the data statistically significant. Therefore, it is difficult to statistically evaluate the probability of cancer occurrence at doses below 100 mSv, so whether the risk is increased or decreased is not known [2,3,4,5,6,7,8,9,10]. Radiation adaptation responses have been reported as a phenomenon associated with low doses [11,12,13,14,15,16,17,18,19] and are closely related to radiation hormesis [20,21,22,23,24,25,26,27,28], the hypothesis that low-dose radiation is beneficial to an organism. Thus, biological findings and mathematical models at the molecular-cellular level have been studied to unravel the mysteries of low-dose exposure [20,29,30,31,32,33,34,35,36,37], and we have previously proposed a linear-hormesis coupling theory.
Our theory is based on the hypothesis that radiation risk is approximately proportional to dose above 100 mSv and that a hormesis effect occurs below 100 mSv [38,39,40]. If we assume that cancer is caused solely by radiation, then the radiation risk at 0 mSv must be zero [38]. Furthermore, when a risk-reducing factor depends solely on radiation, the amount of this factor at 0 mSv must be zero [38]. To satisfy both conditions, the graph of the increase/decrease in the amount of the risk-reducing factor needs to be a peak with two inflection points [38]. In our previous paper, we mathematically proved that the risk-reducing factor is generated in the second step by using the concept of chemical reaction kinetics [40].
On the other hand, ordinary cancers are caused by radiation and active substances other than radiation such as reactive oxygen species [16,17]. Therefore, even at 0 mSv, the risk is not zero, due to active substances other than radiation that make it positive [24,38,40,41,42,43]. For example, it is estimated that the percentage of deaths due to cancer in Japan is ~30% at 0 mSv, according to the official website of the Ministry of the Environment, Japan [44], and increases by 0.5% at a cumulative radiation dose of 100 mSv [1,45]. Defining the radiation dose as x and the risk as D(x), the risk can be expressed as in equation 1. In this paper, we consider a linear-hormesis coupling theory for the case of positive risk at 0 mSv, based on the chemical reaction kinetics previously considered.
D x = 30 + 0.005 x

2. Methods

When values could not be solved for analytically, approximate values were obtained through numerical calculations using the graphing program Grapher 2.5 that is included in Mac OS 10.10.5. Specifically, this software was used to solve equations 12 and 25 and to draw the graphs of equations 13, 27 and 43 as Figure 1, Figure 2 and Figure 4. It was also used to draw the graph of equation 42 (Figure 3) to find the maximum value of X and the value of t. The figures were created using Mac OS desktop pictures.

3. Results and Discussion

A linear-hormesis coupling theory for the case of positive risk at 0 mSv
The amount of the risk-reducing factor is denoted by Q(x). Considering the risk-reducing factor, equation 2 can be obtained from equation 1. Note that D(x) ≥ 0 is always satisfied, since risk is non-negative. The positive value k is a proportionality constant and combines D(x) and Q(x) into a single equation.
D x = 30 + 0.005 x − k Q x
First, let us consider what kind of continuous function Q(x) should be. From equation 1, the risk is 30% at 0 mSv. This is also true for equation 2, so Q(0) is zero when a risk-reducing factor depends solely on radiation. As the radiation dose increases, the risk-reducing factor increases, but as the radiation dose increases further, the factor is inactivated by radiation and decreases. To have a hormesis region in equation 2, Q(x) need not have an inflection point in the increasing region, but only one inflection point in the decreasing region. The shape of this graph is not new; a hunchback graph has been proposed in the past as a factor involved in radiation adaptation response [46,47,48].

3.1. A sequential model reaction when the two rate constants are the same

Considering function Q(x), as in the previous paper [40], given that the dose rate is constant and the dose x is proportional to time, each component quantity can be expressed as a function of the dose x in reaction kinetics using differential equations. The raw material P decomposes to produce Q, and Q decomposes to another substance (Scheme 1). When two rate constants are the same and the rate constant a is positive, the function Q(x) is obtained as equation 3, where P(0) is the initial component amount of component P. This equation gives a hunchback graph.
Q x = P 0 a x e − a x
From equations 2 and 3 and the new definition K = kP(0), equation 4 is obtained.
D x = 30 + 0.005 x − K a x e − a x
From this, the new function q(x) is defined as in equation 5.
q x = K a x e − a x
Ignoring the 0.5% increase from 0 mSv to 100 mSv, equation 4 implies equation 6.
D x ≈ 30 − K a x e − a x
When x is alpha, suppose D is at its minimum, 0, and q is at its maximum, 30 (equations 7 and 8).
α = 1 / a
q ( α ) = 30
Then, K is 30e and q(x) takes the following form:
q x = 30 e a x e − a x
When x is 100 mSv, the following equation is obtained:
q 100 = 3000 e a e − 100 a
When we allow an error of 10%, 30.5 is multiplied by 0.9 to get 27.45 as D(100). Therefore, subtract 27.45 from 30 to get 2.55 as q(100). Now, since alpha is greater than 0 and less than 100, a is greater than 0.01. When 100a is defined as A (A > 1), equation 10 gives the following equation:
q 100 = 30 e A e − A = 2.55
Therefore, equation 12 is obtained.
A e − A = 3.127 × 10 − 2
Solving equation 12 using Grapher 2.5, we obtain that A is 5.093, so a is 5.093 × 10 − 2 . From equation 7, alpha is 19.63 mSv. Therefore, equation 4 implies equation 13, which is graphed in Figure 1. From the above, it can be determined that the dose at which the hormesis effect is maximized is approximately 20 mSv.
D x = 30 + 0.005 x − 4.1533 x e − 0.05093 x
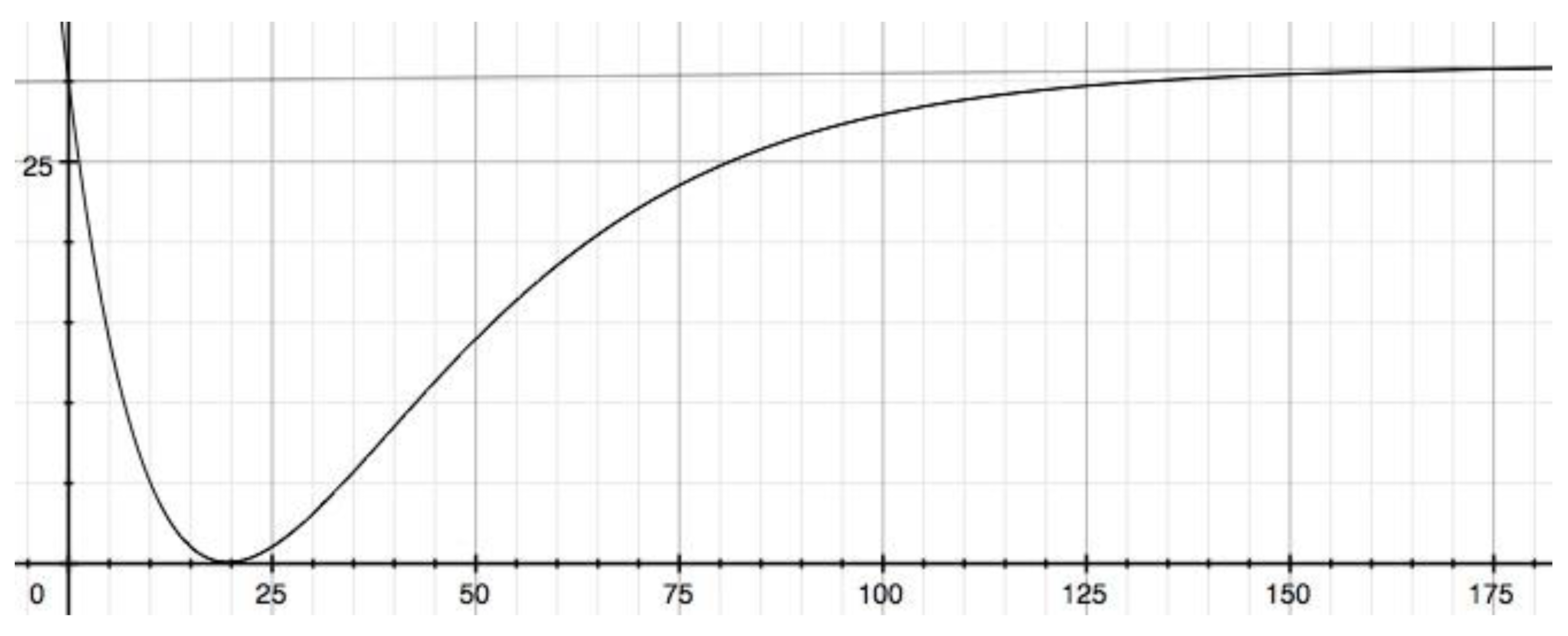
Preprints 94206 g001
Figure 1. Graph of equation 13, with x (mSv) on the horizontal axis and D(x) (%) on the vertical axis.
Figure 1. Graph of equation 13, with x (mSv) on the horizontal axis and D(x) (%) on the vertical axis.
Preprints 94206 g001

3.2. Not ignoring the 0.5% increase from 0 mSv to 100 mSv

In the approximation in Section 3.1 using equations 4 to 6, the increment of 0.5 for 0 mSv to 100 mSv was ignored. In the current section, equation 4 is used without neglecting this increment. We allow an error of 0.1, so 30.5 is multiplied by 0.9 to get 27.45 as D(100). Substituting this value into equation 4 yields equation 14, which when reorganized becomes equation 15.
27.45 = 30 + 0.5 − 100 K a e − 100 a
K a = 0.0305 e 100 a
Substituting equation 15 into equation 4 gives equation 16.
D x = 30 + 0.005 x − 0.0305 x e a 100 − x
As the definition of alpha, when x is alpha, the value of D is its minimum, 0 (equation 17). Differentiating equation 16 gives equation 18. Since equations 17 and 19 both hold, equations 20 and 21 follow.
D α = 0
d D d x = 0.005 − 0.0305 1 − a x e a 100 − x
d D d x α = 0
30 + 0.005 α − 0.0305 α e a 100 − α = 0
0.005 − 0.0305 1 − a α e a 100 − α = 0
From equations 20 and 21, eliminating the exponential term gives equation 22.
30 + 0.005 α = 0.005 α 1 − a α
This equation can be rearranged into equation 23, which is quadratic in alpha. Furthermore, solving equation 23 yields equation 24.
a α 2 + 6000 a α − 6000 = 0
α = 3000 1 + 1 1500 a − 3000
Substituting equation 24 into equation 21 establishes equation 25, using the new definition given in equation 26 and recalling that 100a = A (A > 1).
e A − 30 A β = 0.1639 1 1 − 30 A β
β = 1 + 1 15 A − 1
Using equations 25 and 26, we can find A using Grapher 2.5. Note that since alpha is greater than 0 and less than 100, beta is less than 1/30, and from equation 26, A is greater than 0.9836.
The result shows that A is 4.873, implying that a is 0.04873. Using equation 24, we obtain that alpha is 20.45 mSv. Equation 16 can thus be expressed as equation 27, which was graphed using Grapher 2.5 to obtain the value of D(20.45) as 0.0055, which is almost zero (Figure 2).
D x = 30 + 0.005 x − 3.9867 x e − 0.04873 x
The dose at which the hormesis effect is maximized is approximately 20 mSv, which is the same dose as in Section 3.1 when considering two significant digits. This indicates that the increase from 0 mSv to 100 mSv can be disregarded.
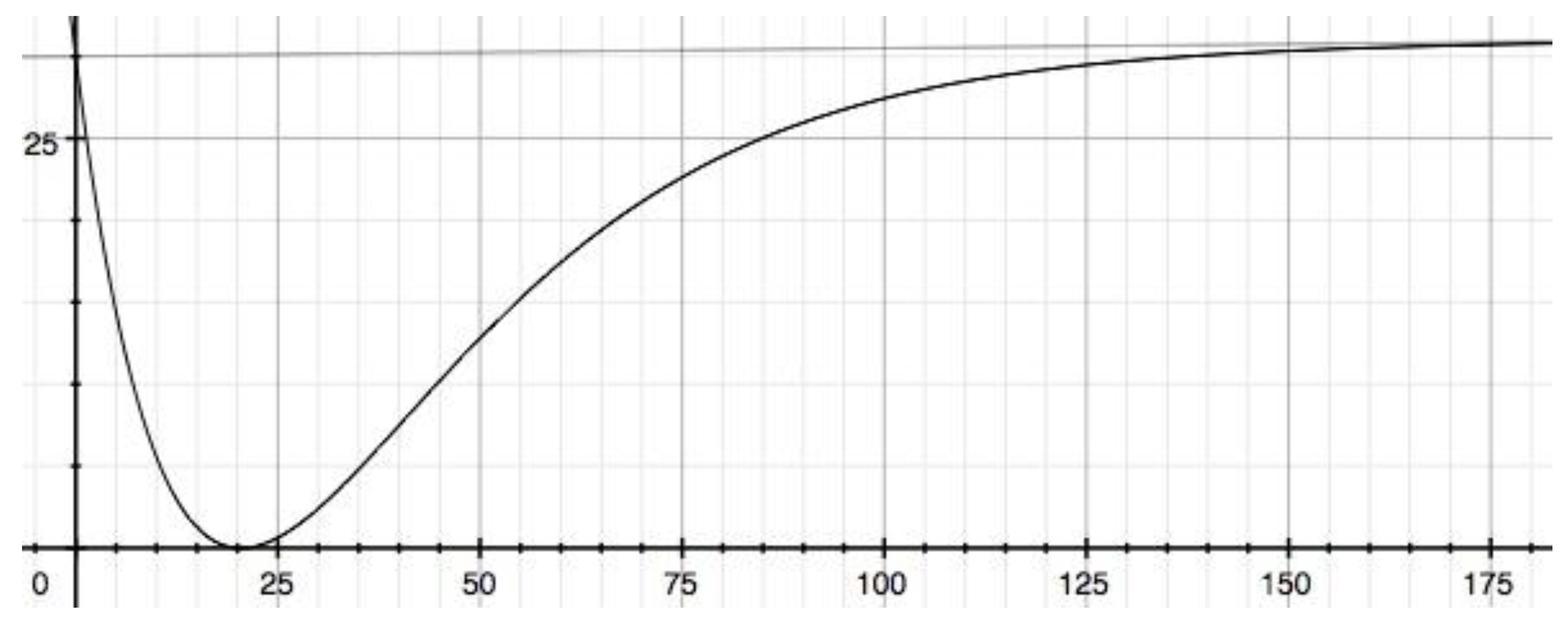
Preprints 94206 g002
Figure 2. Graph of equation 27, with x (mSv) on the horizontal axis and D(x) (%) on the vertical axis.
Figure 2. Graph of equation 27, with x (mSv) on the horizontal axis and D(x) (%) on the vertical axis.
Preprints 94206 g002

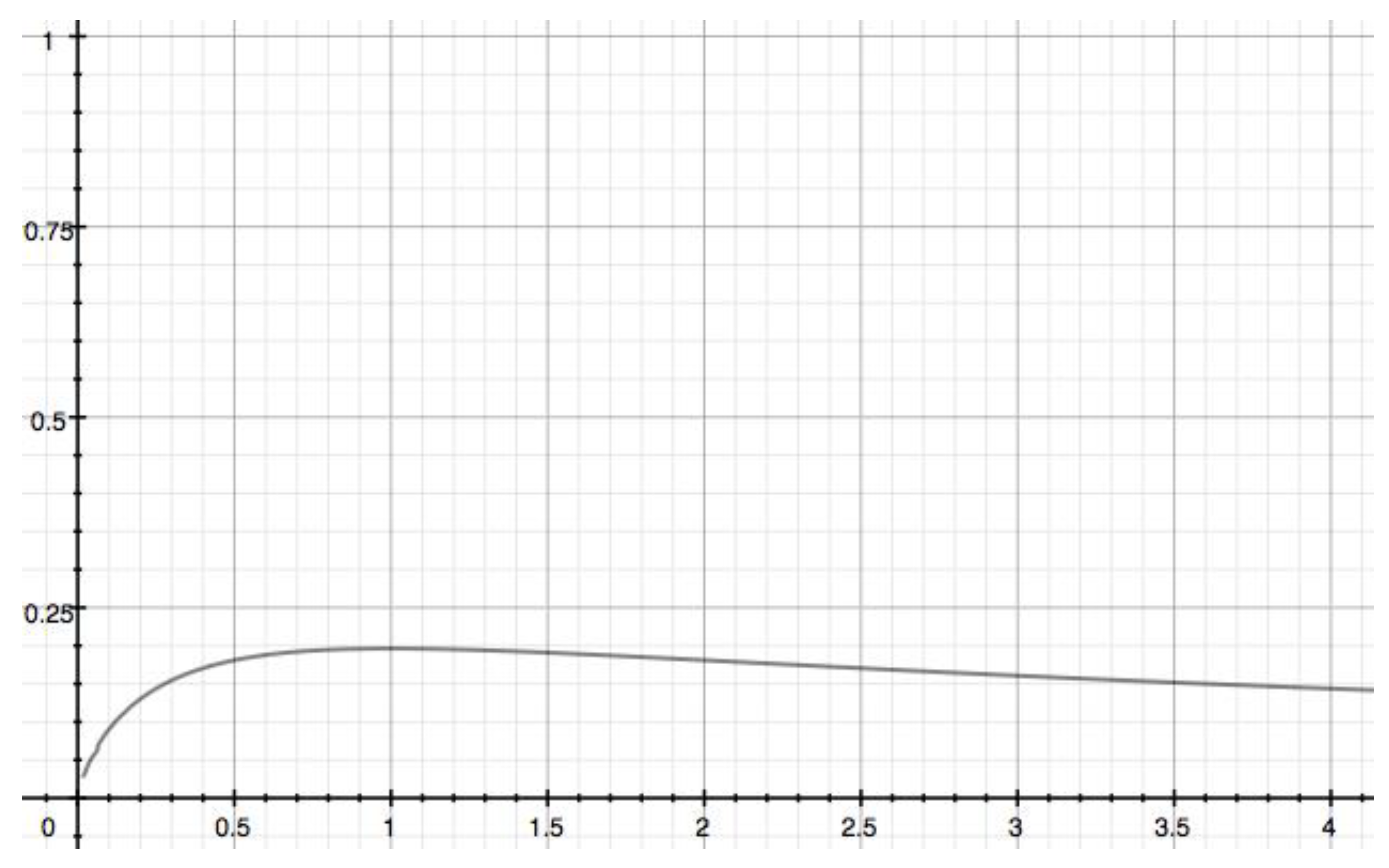
3.3. A sequential general model reaction when the two rate constants are different

In Section 3.1, we showed that the component Q in scheme 1 obeys equation 3. However, it is not common for two reaction rate constants to be the same. Therefore, we considered a general model in which the two reaction constants are different (Scheme 2). Following a general differential equations textbook, we obtain equation 28, where P(0) is the initial component amount of component P and the rate constants a and b are positive. This equation gives a hunchback graph.
Q x = P 0 a b − a e − a x − e − b x
From equations 2 and 28 and the definition K = kP(0), equation 29 is obtained.
D x = 30 + 0.005 x − K a b − a e − a x − e − b x
As shown in Section 3.2, the increase in risk from 0 mSv to 100 mSv can be ignored. Therefore, equation 29 may be approximated by equation 30, similar to as in Section 3.1.
D x = 30 − K a b − a e − a x − e − b x
Here, the new function q(x) is defined by equation 31.
q x = K a b − a e − a x − e − b x
Like in Section 3.1, when x is alpha, the value of q is its maximum, 30. Following a calculus textbook, alpha is solved for as follows.
α = l n b − l n a b − a                             0 < α < 100
Here, the value obtained by dividing b by a is defined as t (t > 0). Equation 32 can be rewritten as equation 33, and the value of q when x is alpha can be found as shown by the sequence of steps in equation 34.
α = l n t a t − 1
q α = K 1 t − 1 e − a α − e − a t α = K 1 t − 1 e − l n t t − 1 − e − t l n t t − 1 = K 1 t − 1 t − 1 t − 1 − t − t t − 1 = K 1 t − 1 t − 1 t − 1 1 − t − 1 = K t − t t − 1
When x is alpha, the value of q is 30 and the following equation is obtained.
K t − t t − 1 = 30
As in Section 3.1, q(100) is 2.55, so equation 36 can be derived as shown from equation 31 and the definition of t.
q 100 = K 1 t − 1 e − 100 a − e − 100 a t = 2.55
By eliminating K using equation 35, equation 37 can be derived.
t t t − 1 1 t − 1 e − 100 a − e − 100 a t = 0.085
Recalling that 100a = A (A > 0), equation 37 becomes equation 38.
t t t − 1 1 t − 1 e − A − e − A t = 0.085
To make it easier to interpret the graph that will be described later, we newly define X as the value obtained by dividing alpha by 100 (0 < X < 1). From equation 33 and the definition of A, X becomes as shown in equation 39. From equation 39, A is expressed in terms of X and t as shown in equation 40.
X = l n t 100 a t − 1 = l n t A t − 1
A = l n t X t − 1
From equations 38 and 40, B is newly defined as in equation 41, and equation 42 is derived. Figure 3 shows equation 41 given equation 42 plotted using Grapher 2.5.
B = : − 1 X t − 1
t t t − 1 1 t − 1 t B − t B t = 0.085
Preprints 94206 g003
Figure 3. Graph of equation 42, with t on the horizontal axis and X on the vertical axis.
Figure 3. Graph of equation 42, with t on the horizontal axis and X on the vertical axis.
Preprints 94206 g003
By definition, t represents the relationship between a and b, and X is 1/100 of the dose alpha at which the hormesis effect is maximized. From the results in Figure 3, we can see that as the relationship between a and b changes, the dose at which the hormesis effect is maximized changes. What we are most interested in next is how large the dose can be. From the results in Figure 3, when t is 1, X reaches its maximum of 0.1963. Therefore, alpha is 19.63 mSv. Although not surprising, this value is the same as the conclusion in Section 3.1. From the graph, in the range where t is greater than 0.9471 and less than 1.0559, X is 0.1963. When t is 0.9471, a is 0.05233 and b is 0.04956. When t is 1.0559, a is 0.04956 and b is 0.05233. Thus, when the first rate constant a is almost the same as the second rate constant b, the factor generating the first step can effectively cause radiation hormesis at about 20 mSv.

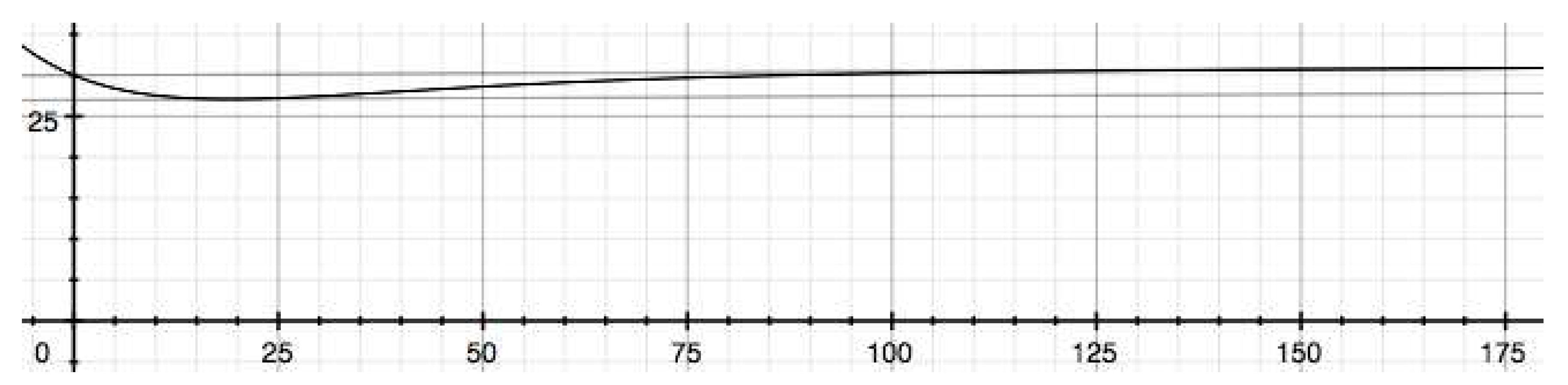
4. Conclusion and Implications

We had previously reported a model that suppresses radiation-specific cancer development [38,39,40]. In this paper, we considered reaction kinetic models that suppress radiation-nonspecific cancer. With the first reaction kinetic model (Section 3.1), we considered the case in which the rate constant for the formation of the risk suppressor is the same as the rate constant for its degradation, and furthermore, we ignored the 0.5% increase from 0 mSv to 100 mSv. As a result, the calculations led to a maximum effect of radiation hormesis at 19.63 mSv.
With the next model (Section 3.2), which does not neglect the 0.5% increase, it was estimated that radiation hormesis is a maximum at 20.45 mSv. When considering two significant digits, it was found that the dose that maximizes radiation hormesis is 20 mSv in both cases, and so the 0.5% increase can be ignored.
With the last model (Section 3.3), we considered the case where the rate constants for production and decomposition are different and neglected the increase of 0.5% from the second conclusion. As a result, it was theoretically determined that the dose at which the effect of radiation hormesis is maximized depends on the relationship between the rate constant for production and the rate constant for decomposition, and that the dose increases as the values of the two rate constants approach each other. In this case, the dose reached a maximum of about 20 mSv when the relationship was near identity.
The weakness of the above conclusion is, of course, that this article is only hypothetical. Equation 13 has the largest hormesis effect as the result of adjusting for k, which links the risk to the risk-reducing factor in equation 2, and the initial raw material amount P(0) in equation 28. For the hormesis effect to be buried in a linear increase, we must first allow a 10% error in equation 1 at 19.63 mSv and D(19.63) must be at least 27.09%. Applying a = 0.05093 and D(19.63) = 27.09% to equation 4, equation 43 (Figure 4) is obtained. From Figure 4, equation 43 shows that the risk increases linearly with dose when a 10% error is allowed in D(x).
D x = 30 + 0.005 x − 0.4165 x e − 0.05093 x
Equation 43 is the case where k and P(0) in equation 13 are very small. In future, if k or P(0) can be increased, a hormesis effect will appear at low doses. For example, if an unknown factor is found that is maximal at 20 mSv, that factor may be a risk-reducing factor, and overexpression of that factor in vivo would reduce risk, then the model proposed in this paper is justified. Thus, the exploration and overexpression of such risk-reducing factors may lead to the development of cancer-reducing therapeutic modalities. If cancer suppression by such factors is achieved, it is expected that the perspective on low doses will change. These factors may be found by exploring unknown substances present in radioresistant bacterium [49], radiotolerant hyperthermophilic archaea [50], and radiotolerant tardigrades [51].
Preprints 94206 g004
Figure 4. Graph of equation 43, with x (mSv) on the horizontal axis and D(x) (%) on the vertical axis.
Figure 4. Graph of equation 43, with x (mSv) on the horizontal axis and D(x) (%) on the vertical axis.
Preprints 94206 g004

Funding

The idea described in this manuscript was obtained on the basis of my other studies supported by research grants from Radiation Effects Association, from the Nakatomi Foundation, from KAKENHI, and from the Japan Prize Foundation; I am grateful to the foundations.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article.

Acknowledgments

Thank you to the clerks at Tokushima Bunri Univ. The author thanks FORTE Science Communications (https://www.forte-science.co.jp/) for English language editing.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Preston, D.L.; Ron, E.; Tokuoka, S.; Funamoto, S.; Nishi, N.; Soda, M.; Mabuchi, K.; Kodama, K. Solid cancer incidence in atomic bomb survivors: 1958–1998. Radiat. Res. 2007, 168, 1–64. [Google Scholar] [CrossRef] [PubMed]
  2. ICRP. Low-Dose Extrapolation of Radiation-Related Cancer Risk. ICRP Publication 99. International Commission on Radiological Protection; Elsevier Oxford: Amsterdam, The Netherlands, 2006. [Google Scholar]
  3. UNSCEAR. Summary of Low-Dose Radiation Effects on Health. UNSCEAR 2010 Report; United Nations Publications: New York, NY, USA, 2010. [Google Scholar]
  4. Tubiana, M.; Arengo, A.; Averbeck, D.; Masse, R. Low-dose risk assessment. Radiat. Res. 2007, 167, 742–744. [Google Scholar] [CrossRef] [PubMed]
  5. Mossman, K.L. Economic and policy considerations drive the LNT debate. Radiat. Res. 2008, 169, 245. [Google Scholar] [CrossRef] [PubMed]
  6. Leonard, B.E. Common sense about the linear no-threshold controversy-give the general public a break. Radiat. Res. 2008, 169, 245–246, Erratum in Radiat. Res. 2008, 169, 606. [Google Scholar] [CrossRef] [PubMed]
  7. Tubiana, M.; Aurengo, A.; Averbeck, D.; Masse, R. Low-dose risk assessment: The debate continues. Radiat. Res. 2008, 169, 246–247. [Google Scholar] [CrossRef]
  8. Feinendegen, L.E.; Paretzke, H.; Neumann, R.D. Two principal considerations are needed after low doses of ionizing radiation. Radiat. Res. 2008, 169, 247–248. [Google Scholar] [CrossRef] [PubMed]
  9. Mothersill, C.; Seymour, C. Low dose radiation mechanisms: The certainty of uncertainty. Mutat. Res. Genet. Toxicol. Environ. Mutagen. 2022, 876–877, 503451. [Google Scholar] [CrossRef]
  10. Boice, J.D.J. The linear nonthreshold (LNT) model as used in radiation protection: An NCRP update. Int. J. Radiat. Biol. 2017, 93, 1079–1092. [Google Scholar] [CrossRef]
  11. Olivieri, G.; Bodycote, J.; Wolff, S. Adaptive response of human lymphocytes to low concentrations of radioactive thymidine. Science 1984, 223, 594–597. [Google Scholar] [CrossRef]
  12. Wolff, S. The adaptive response in radiobiology: Evolving insights and implications. Environ. Health Perspect. 1998, 106 (Suppl. S1), 277–283. [Google Scholar]
  13. Azzam, E.I.; Raaphorst, G.P.; Mitchel, R.E. Radiation-induced adaptive response for protection against micronucleus formation and neoplastic transformation in C3H 10T1/2 mouse embryo cells. Radiat. Res. 1994, 138, S28–S31. [Google Scholar] [CrossRef] [PubMed]
  14. Shadley, J.D. Chromosomal adaptive response in human lymphocytes. Radiat. Res. 1994, 138, S9–S12. [Google Scholar] [CrossRef] [PubMed]
  15. Thierens, H.; Vral, A.; Barbé, M.; Meijlaers, M.; Baeyens, A.; Ridder, L.D. Chromosomal radiosensitivity study of temporary nuclear workers and the support of the adaptive response induced by occupational exposure. Int. J. Radiat. Biol. 2002, 78, 1117–1126. [Google Scholar] [CrossRef] [PubMed]
  16. Tapio, S.; Jacob, V. Radioadaptive response revisited. Radiat. Environ. Biophys. 2007, 46, 1–12. [Google Scholar] [CrossRef] [PubMed]
  17. Guéguen, Y.; Bontemps, A.; Ebrahimian, T.G. Adaptive responses to low doses of radiation or chemicals: Their cellular and molecular mechanisms. Cell Mol. Life Sci. 2019, 76, 1255–1273. [Google Scholar] [CrossRef] [PubMed]
  18. Devic, C.; Ferlazzo, M.L.; Foray, N. Influence of individual radiosensitivity on the adaptive response phenomenon: Toward a mechanistic explanation based on the nucleo-shuttling of atm protein. Dose-Response 2018, 16, 1559325818789836. [Google Scholar] [CrossRef]
  19. Agathokleous, E.; Calabrese, E.J.; Barcelo, D. Environmental hormesis: new developments. Sci. Total Environ. 2024, 906, 167450. [Google Scholar] [CrossRef] [PubMed]
  20. Socol, Y.; Dobrzynski, L.; Doss, M.; Feinendegen, L.E.; Janiak, M.K.; Miller, M.L.; Sanders, C.L.; Scott, B.R.; Ulsh, B.; Vaiserman, A. Commentary: Ethical issues of current health-protection policies on low-dose ionizing radiation. Dose Response 2014, 12, 342–348. [Google Scholar] [CrossRef]
  21. Luckey, T.D. Radiation Hormesis; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
  22. Sanders, C.L. Radiation Hormesis and the Linear-No-Threshold Assumption; Springer: Berlin, Germany, 2010. [Google Scholar]
  23. Feinendegen, L.E.; Bond, V.P.; Sondhaus, C.A. The dual response to low-dose irradiation: induction vs. prevention of DNA damage. In: Yamada, T.; Mothersill, C.; Michael, B.D.; Potten, C.S. Biological effects of low dose radiation. Excerpta Medica. International Congress Series 1211. Elsevier: Amsterdam, The Netherlands, 2000; pp. 3–17. [Google Scholar]
  24. Sutou, S. A message to Fukushima: nothing to fear but fear itself. Genes Environ. 2016, 38, 12. [Google Scholar] [CrossRef]
  25. Sutou, S. The 10th anniversary of the publication of genes and environment: memoir of establishing the Japanese environmental mutagen society and a proposal for a new collaborative study on mutagenic hormesis. Genes Environ. 2017, 39, 9. [Google Scholar] [CrossRef]
  26. Sutou, S. Low-dose radiation from A-bombs elongated lifespan and reduced cancer mortality relative to un-irradiated individuals. Genes Environ. 2018, 40, 26. [Google Scholar] [CrossRef] [PubMed]
  27. Sutou, S.; Koeda, A.; Komatsu, K.; Shiragiku, T.; Seki, H.; Yamakage, K.; Niitsuma, T.; Kudo, T.; Wakata, A. Collaborative study of thresholds for mutagens: proposal of a typical protocol for detection of hormetic responses in cytotoxicity tests. Genes Environ. 2018, 40, 20. [Google Scholar] [CrossRef] [PubMed]
  28. Rattan, S.I.S.; Bourg, E.L. Hormesis in health and disease.; CRC Press, Inc.: Boca Raton, USA, 2014. [Google Scholar]
  29. UNSCEAR. Sources and Effects of Ionizing Radiation. United Nations Scientific Committee on the Effects of Atomic Radiation. UNSCEAR 2000 Report; United Nations Publications: New York, NY, USA, 2000. [Google Scholar]
  30. NCRP. Evaluation of the Linear-Nonthreshold Dose-Response Model for Ionizing Radiation; NCRP Report No. 136; National Council on Radiation Protection and Measurements: Bethesda, MD, USA, 2001. [Google Scholar]
  31. Uchinomiya, K.; Yoshida, K.; Kondo, M.; Tomita, M.; Iwasaki, T. A mathematical model for stem cell competition to maintain a cell pool injured by radiation. Radiat. Res. 2020, 194, 379–389. [Google Scholar] [CrossRef]
  32. Kim, S.B.; Sanders, N. Model averaging with AIC weights for hypothesis testing of hormesis at low doses. Dose Response 2017, 15, 1559325817715314. [Google Scholar] [CrossRef] [PubMed]
  33. Kim, S.B.; Bartell, S.M.; Gillen, D.L. Inference for the existence of hormetic dose-response relationships in toxicology studies. Biostatistics 2016, 17, 523–536. [Google Scholar] [CrossRef] [PubMed]
  34. Esposito, G.; Campa, A.; Pinto, M.; Simone, G.; Tabocchini, M.A.; Belli, M. Adaptive response: Modelling and experimental studies. Radiat. Prot. Dosim. 2011, 143, 320–324. [Google Scholar] [CrossRef] [PubMed]
  35. Wodarz, D.; Sorace, R.; Komarova, N.L. Dynamics of cellular responses to radiation. PLoS Comput. Biol. 2014, 10, e1003513. [Google Scholar] [CrossRef]
  36. Socol, Y.; Shaki, Y.Y.; Dobrzyński, L. Damped-oscillator model of adaptive response and its consequences. Int. J. Low Rad. 2020, 11, 186–206. [Google Scholar] [CrossRef]
  37. Smirnova, O.A.; Yonezawa, M. Radioprotection effect of low level preirradiation on mammals: Modeling and experimental investigations. Health Phys. 2003, 85, 150–158. [Google Scholar] [CrossRef]
  38. Kino, K. The prospective mathematical idea satisfying both radiation hormesis under low radiation doses and linear non-threshold theory under high radiation doses. Gene Environ. 2020, 42, 4. [Google Scholar] [CrossRef]
  39. Kino, K.; Ohshima, T.; Takeuchi, H.; Kobayashi, T.; Kawada, T.; Morikawa, M.; Miyazawa, H. Considering existing factors that may cause radiation hormesis at <100 mSv and obey the linear no-threshold theory at ≥100 mSv. Challenges 2021, 12, 33. [Google Scholar] [CrossRef]
  40. Kino, K. The radiation-specific components generated in the second step of sequential reactions have a mountain-shaped function. Toxics 2023, 11, 301. [Google Scholar] [CrossRef] [PubMed]
  41. Calabrese, E.J.; Shamoun, D.Y.; Hanekamp, J.C. Cancer risk assessment: Optimizing human health through linear dose-response models. Food Chem. Toxicol. 2015, 81, 137–140. [Google Scholar] [CrossRef] [PubMed]
  42. Lampe, N.; Breton, V.; Sarramia, D.; Sime-Ngando, T.; Biron, D.G. Understanding low radiation background biology through controlled evolution experiments. Evol. Appl. 2017, 10, 658–666. [Google Scholar] [CrossRef] [PubMed]
  43. Scott, B.R. Residential radon appears to prevent lung cancer. Dose Response 2011, 9, 444–464. [Google Scholar] [CrossRef] [PubMed]
  44. Ministry of the Environment, Japan. Uniform basic information on health effects of radiation, etc. 2016 edition ver.2017001. Available online: https://www.env.go.jp/chemi/rhm/h28kisoshiryo/h28kiso-03-07-03.html (accessed on 13 December 2023).
  45. ICRP. The 2007 Recommendations of the International Commission on Radiological Protection. ICRP Publication 103.; Elsevier Oxford: Amsterdam, The Netherlands, 2007. [Google Scholar]
  46. Feinendegen, L.E. Evidence for beneficial low level radiation effects and radiation hormesis. Br. J. Radiol. 2005, 78, 3–7. [Google Scholar] [CrossRef] [PubMed]
  47. Feinendegen, L.E. Low doses of ionizing radiation: Relationship between biological benefit and damage induction. A synopsis. World J. Nucl. Med. 2005, 4, 21–34. [Google Scholar]
  48. Agathokleous, E.; Kitao, M.; Calabrese, E.J. Environmental hormesis and its fundamental biological basis: Rewriting the history of toxicology. Environ. Res. 2018, 165, 274–278. [Google Scholar] [CrossRef] [PubMed]
  49. Sadowska-Bartosz, I.; Bartosz, G. Antioxidant defense of Deinococcus radiodurans: how does it contribute to extreme radiation resistance? Int. J. Radiat. Biol. 2023, 99, 1803–1829. [Google Scholar] [CrossRef]
  50. Ranawat, P.; Rawat, S. Radiation resistance in thermophiles: mechanisms and applications. World J. Microbiol. Biotechnol. 2017, 33, 112. [Google Scholar] [CrossRef]
  51. Kasianchuk, N.; Rzymski, P.; Kaczmarek, Ł. The biomedical potential of tardigrade proteins: A review. Biomed Pharmacother. 2023, 158, 114063. [Google Scholar] [CrossRef] [PubMed]
Preprints 94206 sch001
Scheme 1. Sequential reaction when two rate constants are the same.
Scheme 1. Sequential reaction when two rate constants are the same.
Preprints 94206 sch001
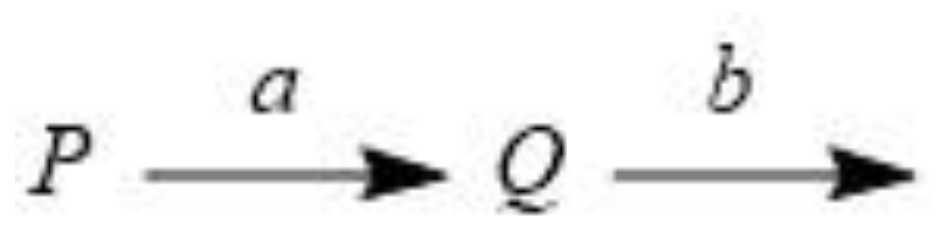
Preprints 94206 sch002
Scheme 2. Sequential reaction when then two rate constants are different.
Scheme 2. Sequential reaction when then two rate constants are different.
Preprints 94206 sch002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Dose-Dependent Shift in Relative Contribution of Homologous Recombination to DNA Repair after Low-LET Ionizing Radiation Exposure: Empirical Evidence and Numerical Simulation

Oleg Belov

et al.

,

2023

The Optimal Radiation Dose to Induce Robust Systemic Anti-Tumor Immunity

Jan Poleszczuk

et al.

,

2018

Hydrogen and Vitamin C Combination Therapy: A Novel Method of Radioprotection

Michiko Miyakawa

et al.

,

2023

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated