Preprint
Article
A Fuzzy-based System for Autonomous UAV Ship Deck Landing
Altmetrics
Downloads
98
Views
29
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
22 December 2023
Posted:
22 December 2023
You are already at the latest version
Alerts
Abstract
This paper introduces a fuzzy logic-based autonomous ship-deck landing system for fixed-wing Unmanned Aerial Vehicles (UAVs). The ship is assumed to maintain a constant course and speed. The aim of this fuzzy logic landing model is to simplify the task of landing UAVs on moving ships in challenging maritime conditions, relieving operators from this demanding task. The designed UAV ship-deck landing model is based on a fuzzy system comprised of three interconnected subsystems. Each subsystem consists of three inputs and one output incorporating various fuzzy rules to account for external factors during ship-deck landings. Specifically, the Fuzzy Logic System (FLS) takes inputs such as the airspeed, the relative wind direction and speed, the range from the deck and the UAV's flight altitude. The FLS outputs provide data on the Speed of the UAV relative to the ship’s velocity, the Bank Angle, and the Angle of Descent of the UAV. The performance of the designed intelligent ship-deck landing system is evaluated using the standard configuration of MATLAB Fuzzy Toolbox.
Keywords:
Subject: Engineering - Control and Systems Engineering
1. Introduction
Nowadays, the utilization of drones in the maritime domain is rapidly increasing. Their use for civil missions, as well as military operations vary greatly. Regarding the civil sector, from transporting spare parts, documents, medicine, etc. between land and ships at sea or between ships at sea only [1], to controlling traffic and the emission of pollutants from ships or even preventing illegal activities such as piracy, smuggling and illegal fishing [2], drones – and especially Unmanned Aerial Vehicles (UAVs) - are used. The underlying reason for this fact lies in the drone’s numerous sensing capabilities and interchangeable payload equipment [3], combined with the reduced risk, time and cost that the UAVs provide in a wide range of missions [1].
On the other hand, in the military/security domain, another vast range of missions is covered solely from UAVs, both in peacetime and in wartime periods. Drones provide unparalleled surveillance capabilities for border security, facilitating real-time monitoring of large areas with minimal risk to individuals on the ground, combining also the ability to deploy easily and respond immediately to any potential threat or emergency [2]. Furthermore, drones are used for Search And Rescue (SAR) missions, improving response times and limiting exposure to dangerous conditions or even by dropping flotation devices for lifeguarding purposes [3]. Additionally, UAVs are mostly used in maritime surveillance operations to uphold the safety and security of maritime traffic, while concurrently thwarting illicit activities. UAVs are also used as moving targets during military exercises of naval forces.
Lastly, in wartime, the operation capabilities of modern maritime military UAVs experience further augmentation. Depending on the payload and the equipment of the UAV, a drone is able to undertake strategic missions. Recognizing the value of utilizing UAVs in the maritime domain, the US Navy, as well as the UK Royal Navy [1], have integrated a variety of different drones in their arsenal, leading the way in modern warfare and naval research technology.
Landing, one of the most critical parts in the flight of a drone, is a topic slightly researched by the academic community. Even today, most UAV landings are performed manually by their operators, from inside the drone’s ground station, depriving the drone pilot of the peripheral vision, the instinctive senses and the space perception during the procedure. As a result, the majority of UAV’s crashes happen due to human errors, during take offs and landings, which constitute the most dangerous parts of a drone’s flight [4].
More specifically, during ship-deck landings, the difficulty of manually guiding the UAV to touchdown increases exponentially, demanding even more experience and skill from the drone pilot. The unpredictable nature of the maritime environment, characterized by low visibility, strong wings, high humidity and noticeable waves, in combination with the dynamic motion of the landing platform of the ship in the sea with its limited dimensions, pose a great, sometimes even impossible, challenge for the drone pilot. Consequently, the imperative arises for the development of an autonomous landing system, crucially contributing to the progression of drone technology within the maritime sector.
Concerning the operation of UAVs, relevant literature exists that studies autonomous flight navigation. The work of [4] presents an extensive review of landing techniques of various landing techniques using a number of control and vision-based techniques for different types of aircraft. In [5], the control of the landing and descent simulation of a Boeing 747, employing its linearized landing configuration model, is governed by fuzzy logic controllers (FLCs). The rule bases defining the FLCs are formulated as functions of the linearized model’s inputs, specifically the vertical velocity and altitude of the Boeing 747. The outputs are the elevator and throttle deflections.
In [6], a control system for autonomous flight and landing based on fuzzy logic is introduced. The system consists of three fuzzy logic controllers for autonomous navigation in UAVs and three additional fuzzy logic modules are created within the primary landing system. These modules control the horizontal and vertical positions of the aircraft relative to the runway under a Tactical Air Navigation approach. The work in [7] introduces a technique for auto-landing using fuzzy logic-based position and speed control. This system utilizes position and velocity data to regulate the attitude of a quadcopter UAV. The velocity control algorithm is designed to facilitate a secure landing, preventing the quadcopter from impacting the ground at high speeds. Simultaneously, the position control component assesses altitude, ensuring a smooth and rapid landing. The integration of position and speed control enhances efficiency by minimizing landing time and offers increased safety assurances compared to conventional controllers.
The authors in [8] present a proposed fuzzy logic framework for intelligent aircraft landing decision systems. Various factors influencing the required aircraft landing decisions are incorporated in this approach, encompassing wind velocity, wind direction, visibility, and pilot experience. The landing decision process is categorized into three classes: feasible, cautious, and not feasible. In [9], a decision support system is introduced utilizing fuzzy logic to aid pilots of Boeing 747-100 aircraft. The research aims to mitigate accidents associated with the aircraft landing assistance system and conduct a speed analysis of the Boeing 747-100. To prevent aviation accidents, factors such as aircraft landing speed, braking force, rolling resistance, distance to obstacles, and runway length are meticulously considered.
This paper focuses on the concluding stages of UAV operations, specifically the final approach and touch-down periods. It introduces a fuzzy logic-based autonomous ship-deck landing system for fixed-wing UAVs as a proposed solution to most of the complex problems previously mentioned. The proposed strategy is based on the development of an intelligent ship-deck landing system based on a fuzzy logic approach.
The paper is organized as follows: Section 2 presents the fundamental concepts for autonomous ship-deck landing. Section 3 provides a concise overview of the main characteristics of the landing as well as the sensors used for a successful landing process. Section 4 analyzes the developed fuzzy ship-deck landing system comprised of three fuzzy sub-systems and the simulation results are presented in Section 5. Finally, conclusions and directions for further research are drawn in Section 6.
2. Fundamental terms for autonomous ship-deck landing
This Section introduces fundamental terms related to the autonomous ship-deck landing system providing a comprehensive clarification of essential concepts and information.
2.1. Indicated Airspeed (IAS)
Indicated airspeed (IAS) is the speed of the UAV relative to the body of air through which it is flying [13]. It is measured using an airspeed sensor and it is expressed in knots. In other terms, the IAS is “the speed of an aircraft as shown on its pitot static airspeed indicator, calibrated to reflect standard atmosphere adiabatic compressible flow at sea level, uncorrected for airspeed system errors” [14]. Basically, IAS represents the dynamic pressure upon the airspeed sensor, as the aircraft moves through a body of air. It is a function of the dynamic pressure experienced by the UAV and the atmospheric density of air surrounding the drone at a certain altitude. In practice, however, it is considered that air density is independent of the attitude due to the very low heights during landing. As a result, air density is considered to be constant, so there is no need for a dynamic pressure sensor to compute airspeed [10]. IAS is calculated by an airspeed sensor.
IAS is the most important speed of the pilot from an aerodynamic point of view, especially when controlling the aircraft during take-offs or landings. It differs completely from the ground speed, which is the actual aircraft speed in relation to the ground. For fixed-wing aircrafts, such as the UAVs, it is the IAS that guarantees lift - not ground speed. So, for example, if airspeed is minimum, then stability conditions are severe, and the maneuvering abilities are limited [6].
2.2. Azimuth Angle of Wind and Relative Wind Speed (AAW)
The Azimuth Angle of Wind (AAW) is the direction from which the wind is blowing, measured in degrees clockwise from North on an azimuth circle. An azimuth circle consists of 360 degrees [11]. Traditionally, wind direction is reported as one of eight compass points (N, NE, E, SE, S, SW, W, NW) [15], which depicts certain degrees in the azimuth circle.
The AAW is either True or Relative depending on the North used as a reference. True North corresponds to the direction indicated by a gyroscopic compass and is represented on a map as the line of longitude which converges on the North Pole [16]. Conversely, Relative Wind is calculated using a Relative North as a reference (Figure 1). In the case of a fixed-wing UAV, the Relative North is the nose of the UAV. Consequently, the Relative AAW signifies the wind direction relative to the UAV. In the FLS later, we utilize only the Relative AAW.
The Speed of the Wind (WS) [17] is also characterized as True WS and Relative WS. True WS (Ground Wind) “is the actual speed of the wind as it passes over land or the surface of the sea” [18]. Relative or Apparent Wind Speed (RWS) is the wind that a body (aircraft, UAV, ship etc) “feels” as it moves through space. The AAW as well as the WS are measured by an anemometer providing their relative values.
2.3. Range from Landing Deck (RLD)
The Range of the UAV from the Landing Deck of the ship (RLD) is measured in meters by a Time Difference Of Arrival (TDOA) based localization mechanism. The working principle of the TDOA system is as follows: A modulated signal is transmitted from the UAV and this signal is captured at three or more probes placed in different locations around the landing deck. Then, the signal captured at each receiver is shifted in time to locate a position of maximum correlation and this time delay is later multiplied by the speed of light, calculating the distance difference between each probe. Afterwards, the distance difference is plotted as a set of hyperbolic lines between the pairs of the probes (Figure 2) and lastly the intersection of the lines indicates the location of the emitting drone [19].
To determine the drone’s distance from the ship, precise knowledge of the UAV’s location in the 2D plane is essential (Figure 3). This localization necessitates the deployment of a three-node TDOA-based system. In the context of this paper, however, a four-node TDOA system is employed to pinpoint the UAV within three-dimensional space (Figure 4). This configuration allows for the determination of both the RLD and altitude of the UAV, as elaborated upon in subsequent sections.
Furthermore, since the times of arrival of the signal are measured by different receivers in the TDOA based localization mechanism, precise synchronization between all these nodes is essential [20]. Also, TDOA is vulnerable to the time-delay as the system’s measurements are based on the assumption that the signal travels the shortest path from the source (the emitting UAV) to the receiver (node) [21].
2.4. Altitude
The altitude of the UAV is the distance from the surface of the sea. It is measured in feet (ft) by a barometric altimeter, which measures atmospheric pressure to estimate altitude, combined with the 3D TDOA based localization system. However, weather conditions can affect atmospheric pressure and that is why altimeters are often calibrated at the takeoff site. Also, to increase the accuracy of the height value, a four-node TDOA based mechanism is utilized [22], providing the position of the UAV in 3D space, during the entire phase of the landing.
2.5. Relative Speed of the Drone (RSD)
The Relative Speed of the Drone (RSD) is the speed of the UAV in reference with the speed of the ship. More specifically, during the landing phase, it represents the difference between the Speed Over Ground (SOG) of the UAV and the SOG of the Ship, as the UAV approaches the landing deck of the ship, measured in knots. In the context of this paper, where the ship moves in front of the drone, it is calculated by subtracting the constant SOG of the ship from the SOG of the UAV.
2.6. Bank Angle (BA)
The Bank Angle (BA) is the angle of turn in the azimuth plane of an aircraft and is measured in degrees (°) [23]. In other terms, it is the angle between the aircraft’s normal, or vertical, axis and the earth’s vertical plane containing the aircraft’s longitudinal axis. The BA of an aircraft is measured from 0° to 179° port or starboard (left or right) [24]. When an aircraft makes a turn, it banks to one side, and the bank angle is the amount by which the aircraft is tilted. It is dependent on the forces of lift and weight that are acted upon the UAV.
2.7. Angle of Descent (AOD)
The Angle of Descent (AOD) is the angle between the aircraft’s horizontal axis and the earth’s horizontal plane. It indicates how steep the “dive” of the aircraft is during the landing or the take-off phase and it is measured in degrees.
3. The Autonomous Landing Strategy
3.1. Ship characteristics and Sensors
The ship’s Course Over Ground (COG) and Speed Over Ground (SOG) is considered to be constant during the landing phase of the drone. Due to the limited dimensions of the helidecks on most ships, the most successful landing of a fixed-wing UAV would involve the use of a vertical rope or a net to “catch” the flying drone. In this context, “SkyHook” [25] is proposed as a capture system onboard the helideck of the ship. Also, we consider the height level of the ship’s landing deck from sea surface to be 8 meters (Figure 6).
Additionally, four spatially-separated nodes of the time difference of arrival (TDOA) based localization mechanism are planted in different positions on the landing deck in order to track the UAV’s position in the three-dimensional space during its approach to the ship [26]. The ultimate goal of the autonomous landing system is to present an alternative navigation approach that operates independently of a GPS, providing a robust and self-reliant solution in a contested electromagnetic environment.
For even better accuracy and precision during the last phase of the landing procedure, in a RLD less than 20 meters, the use of a passive Ultra High Frequency (UHF) Radio Frequency Identification (RFID) based UAV positioning system is proposed [19]. The best candidate RFID for this role is the MilliSign guidance system based on a batteryless tag to support UAVs in poor visibility and all-weather conditions [27]. A corner reflector (CR) array based chipless RFID tag and a one-shot slant range reading procedure with Commercial Off-The-Shelf (COTS) mmWave radar constitute the MilliSign system, as shown in Figure 7. The RFID tag is placed vertically in the longitudinal axis of the landing deck, right behind the receiver rope of the “Skyhook” capture system. This placement is designed to facilitate the alignment of the fixed-wing UAV with the “catch rope” in the final meters of its flight. (Figure 8). The chipless tag is a conventional high radar cross-section (RCS) scatterer, with retro-reflective attributes for 3D incident wave and provides a wide 3D read range so that it can be read by the UAV’s UHF radar from a distance of more than 10 meters, with a viewing angle of more than 30 in elevation and azimuth. The tag is covered by a radome, as it is sensitive against debris such as dust, sand, mud, and water (rain), which can enter and deteriorate the backscattering RCS of the tag. The RFID Reader (mmWave radar), on the other hand, is deployed on the UAV and the communication between the reader and the tag is much more efficient in LOS.
Lastly, as a general observation, the majority of merchant ships often cruise at 18 to 25 knots. However, warships are capable of operating at speeds approximately 32 knots. In this particular context, the designated maximum speed for the ship during the landing phase is stipulated as 30 knots. Subsequently, this value serves as the basis for determining the maximum Relative Speed of the Drone (RSD).
3.2. UAV Characteristics and Sensors
The fixed-wing UAV that is investigated in this paper is a Small – Medium Size/Class drone (Figure 9) capable of reaching a maximum speed of 70 knots during the landing phase of its mission. Also, the BA of the UAV is considered to be a maximum of 60 degrees, indicative of a highly agile military UAV capable of executing sharp and steep turns. However, the ability of the UAV to turn at such degrees is immediately dependent on the IAS, which strongly affects the aerodynamics of the UAV.
Additionally, to enable precise landing, the UAV necessitates an array of sensors and equipment. The sensors of the fixed-wing UAV gather the information around the environment of the drone and send it to the microcontroller of the UAV. For the purpose of the autonomous ship-deck landing proposed in this paper, the UAV should be equipped with the following sensors:
- An Anemometer
- An Airspeed Sensor
- A Barometric Altimeter
- An Inertial Navigation System (INS)
- A Radio Frequency (RF) Transmitter for the TDOA based localization system
- A mmWave radar (RFID Reader)
Regarding the RFID Reader deployed on the UAV, its small size, lightweight design and cost effectiveness, as well as its minimal power requirements contribute to enhancing the UAV’s autonomous capabilities [22].
All these sensors constitute the essential equipment of a fixed-UAV to conduct a successful autonomous ship-deck landing as described in this work. The deliberate omission of a GPS sensor during the landing phase is driven by the necessity for the UAV to exhibit resistance against Electronic Warfare interference (see Section 3.5).
3.3. The Main Attributes of Landing
The scope of this paper is the design of a precise autonomous landing system utilizing fuzzy logic, in order to be used by fixed-wing UAVs during ship-deck landings. For a successful landing to take place, three variables must be taken into consideration [4]. First of all, the speed of the UAV is of the most importance and especially the RSD, in relation to the ship’s SOG. The ship’s data (COG & SOG) are inserted manually and sent to the UAV from the ground station, so that the drone is aware of the ship’s fixed SOG and COG values. The UAV’s relative speed indicates the rate at which it converges toward the ship’s landing deck. Furthermore, for the effective operation of the landing system, the RSD must be a minimum of 5 knots, ensuring that the clips on the drone’s wings can securely engage with the landing rope.
Τhe lateral position of the fixed-wing UAV with reference to the longitudinal axis of the deck of the ship is undeniably a noteworthy attribute during the landing phase of the drone. The scope of the landing system is to guide the UAV on the lateral middlepoint of the helideck, where the SkyHook’s rope will be hanging, ready to “catch” the UAV. To achieve this part of the “outer loop” control [5], the BA of the UAV is modified, thereby modifying the angle of turn in the azimuth plane of the drone. In that way, the autonomous landing system guides the UAV along the desired trajectory rejecting external disturbances such as wind [5].
The final factor to be considered for a fixed-wing UAV during the execution of a landing on a ship’s deck is the vertical position of the drone, expressed alternatively as its altitude. To reach the desired landing altitude, the UAV must “dive” gradually with a specific rate of descent. This is achieved by controlling the AOD of the fixed-wing drone. Nevertheless, for a successful landing, the UAV must maintain a minimum altitude of approximately 5 meters from the landing platform (13 meters from the sea surface) to mitigate the risk of the drone colliding with the helideck.
3.4. The Landing Process
The small-medium size fixed-wing UAV has completed its mission and is Returning To Base (RTB). When in range of the TDOA based UAV localization system, the drone takes its starting position 100 meters behind the ship, along the axis of equal distance, where the time difference of arrival and the difference in distance between three of the four nodes in the 2D x-y plane are zero (Figure 3). The short distance of 100 meters between the ship and the UAV when the landing phase begins is deliberately chosen so that smaller errors occur in the absence of a GPS [5]. At the same time, the data regarding the ship’s constant SOG and COG are transferred via a telecommunication link to the UAV and the drone adjusts its own speed and course accordingly, utilizing the INS component.
As the drone follows the landing path with the same course and speed as the ship, the landing phase begins as the fuzzy logic-based autonomous ship-deck landing system is enabled. During the approach of the UAV to the landing deck, the FLS controls the three main attributes of landing that are mentioned above in order to ensure a successful landing, against external factors such as the wind:
- The RSD must always be greater than the velocity of the ship, so that it is able to approach the landing deck.
- The lateral movement of the UAV needs to be mitigated by controlling the drone’s BA to ensure that the UAV will follow the landing path.
- The altitude of the UAV must decrease progressively by controlling the drone’s angle of descent. This is essential to attain a specified height ranging between 5 to 15 meters above the landing deck (13 to 23 meters above the surface of the sea) facilitating the UAV’s engagement with the “SkyHook” retrieval system’s rope.
Around 20 meters from the capture rope, the MilliSign RFID guidance system is enabled and utilized in order to increase the precision of the autonomous landing system. The UAV then aligns with the batteryless chipless CR tag and navigates with pinpoint accuracy on the “SkyHook” system. Subsequently, at a relative speed exceeding 5 knots concerning the ship, the UAV maneuvers towards the landing rope and hooks on it.
3.5. Electronic Warfare Resistant Landing
Considerable attention has been paid to the Electronic Warfare (EW) Resistance of the fuzzy logic-based autonomous ship-deck landing system, particularly in military applications in order to guide the UAV in a safe and successful landing under a harsh and dense electromagnetic environment. The Global Positioning System (GPS) stands as an important component within the equipment on a UAV, serving as a sophisticated localization mechanism. Its primary function is to provide the drone with vital data regarding its precise position, speed, and height level. However, this pivotal system is susceptible to spoofing and jamming [10]. Lessons learned from the Israel-Hamas conflict prove that EW and more specifically GPS jamming, affects all kinds of civil GPSs, and consequently, counters the drone attacks from Hezbollah and Hamas military organizations [11]. Considering that civil GPSs are utilized much more frequently than military GPS units in UAVs due to their cost, it is easily understandable that the vulnerability of the autonomous UAV systems is real. In the Ukraine – Russian War, EW technics, such as jamming and spoofing, are utilized from the Russian Army to take down Ukrainian UAVs [12]. To counter these modern warfare operational tactics, this paper proposes the integration of Inertial Navigation System (INS) sensors with altimeters, anemometers, TDOA based localization systems and more equipment onboard UAVs. This integration aims to enhance the estimation of the vehicle’s state and position, even in a hostile electromagnetic environment.
4. The Designed Fuzzy System for Ship-Deck Landing
Fuzzy logic “is intended to model logical reasoning with vague or imprecise statements” [28]. Fuzzy set theory provides a framework for dealing with classes of objects where the boundaries are not precisely defined. Instead of strict, absolute, binary membership (either true or false) [5], fuzzy sets allow for degrees of membership, acknowledging the gradual transition between the two aspects [8].
To construct the fuzzy logic-based autonomous ship-deck landing system, five input variables are imported: the Indicated Airspeed, the Azimuth Angle of Wind and the Speed of the Wind, the Altitude and the Horizontal Distance from the Landing Deck. The input data is received by the airspeed sensor, the anemometer, the barometric altimeter and the TDOA based localization system, respectively. Then, the fuzzy logic based autonomous landing system determines three output variables: the Relative Speed of the Drone, the Angle of Descent and the Bank Angle of the UAV by controlling the drone’s throttle and ailerons.
For the FLS, Mamdani fuzzy inference system is used that outputs the Relative Speed of the Drone, the BA and the AOD of the fixed-wing UAV. The fuzzy logic based autonomous ship-deck landing system utilizes the input data provided by the range of sensors in order to calculate the corrective maneuvers of the drone by using three fuzzy logic components. Figure 10 depicts the Ship-Deck Landing Architecture with an overall presentation of the FLS, where three fuzzy subsystems are interconnected. Each subsystem consists of three inputs and one output; totally five inputs and three outputs are involved. In the next Subsections, an analytical description of these three subsystems is presented.
4.1. Speed Component
The first fuzzy subsystem block is the speed component, with three inputs: AAW, WS and RLD from the Landing Deck and one output: the RSD with respect to the ship’s velocity. The RLD is fuzzified using linguistic values: On Top (ON_TOP), Close (CLOSE), Medium Distance (MED_DIST), Far (FAR), Very Far (VERY_FAR) and the membership functions of RLD are depicted in (Figure 11). The RLD is calculated by the TDOA based positioning system.
The AAW is fuzzified using linguistic values: North (N1 and N2), North East (NE), East (E), South East (SE), South (S), South West (SW), West (W), North West (NW), shown in Figure 12.
RWS is fuzzified using linguistic values: No Wind, Low Wind, Medium Wind, High Wind and Very High Wind and their membership functions are shown in Figure 13. WS, as well as the AAW are calculated by an anemometer.
The output (RSD) of the fuzzy subsystem is fuzzified using linguistic values as Min, Slow, Medium, Fast and Max and their membership functions are shown in Figure 14. To control the variable above, the FLS regulates the throttle of the drone.
The total number of the fuzzy rules is 185 and 15 of them are indicatively presented in Figure 15.
4.2. Lateral Motion Component
The second fuzzy subsystem block is the lateral motion component with three inputs: AAW, RWS and IAS and one output: the BA of the UAV. IAS is fuzzified using linguistic values as shown in Figure 16.
The output of the fuzzy subsystem is the BA of the UAV and is fuzzified as shown in Figure 17. To control the variable above, the FLS regulates the ailerons of the drone’s wings.
IAS, AAW and RWS are directly related. When the wind is stronger, then the molecules of air around the body of the vehicle will move faster, depending also on the angle that these molecules will slam the UAV’s airspeed sensor. For example, if the wind is blowing against the drone’s course, then the IAS will increase, as the mass of air that slams the body of the UAV will move faster. For the construction of the fuzzy subsystem, a total number of 82 fuzzy rules are generated (Figure 18).
4.3 Altitude Component
The third fuzzy subsystem block is the altitude component with three inputs: RLD, Altitude and IAS and one output: the AOD of the UAV. The Altitude is fuzzified using the depicted in Figure 18.
The output of the component is the AOD of the UAV is fuzzified as shown in Figure 20. To control this variable, the FLS regulates both the ailerons of the drone’s wings, either up or down.
A total number of 105 fuzzy rules are generated and some of them are shown in Figure 21.
The vertical control and airspeed of a UAV exhibit a reciprocal relationship—when the UAV pitches upward, its speed decreases proportionally, and conversely, pitching downward leads to an increase in speed [4]. Notably, in this study, it is considered that there is no interdependency between airspeed and vertical control.
5. Simulation Results for Autonomous Landing
To verify the effectiveness of the proposed fuzzy system, a test case is presented separately for each component in the following subsections. This test case involves certain values for the input variables and provides certain values for the three outputs of the fuzzy control system.
5.1. Speed Component Results
For the test case of a UAV at a distance of 27 meters from the landing deck, with winds blowing from 108 degrees at a speed of 40 knots, the required RSD in relation to the ship’s velocity will be 12.8 knots in order to land effectively onboard the ship. Figure 22 presents the fuzzy rules that are fired by these input data values. Figure 23 shows the surface plots between RSD and the inputs.
5.2. Lateral Motion Component Results
Figure 24 illustrates the case of a UAV flying with an IAS of 70 knots, with winds blowing from 108 degrees at an RSD of 40 knots. As a result, during the turn that the UAV will make to correct its course, a BA of 36.3 degrees will be executed. Figure 25 shows the surface plots between the BA and the inputs.
5.3. Altitude Component
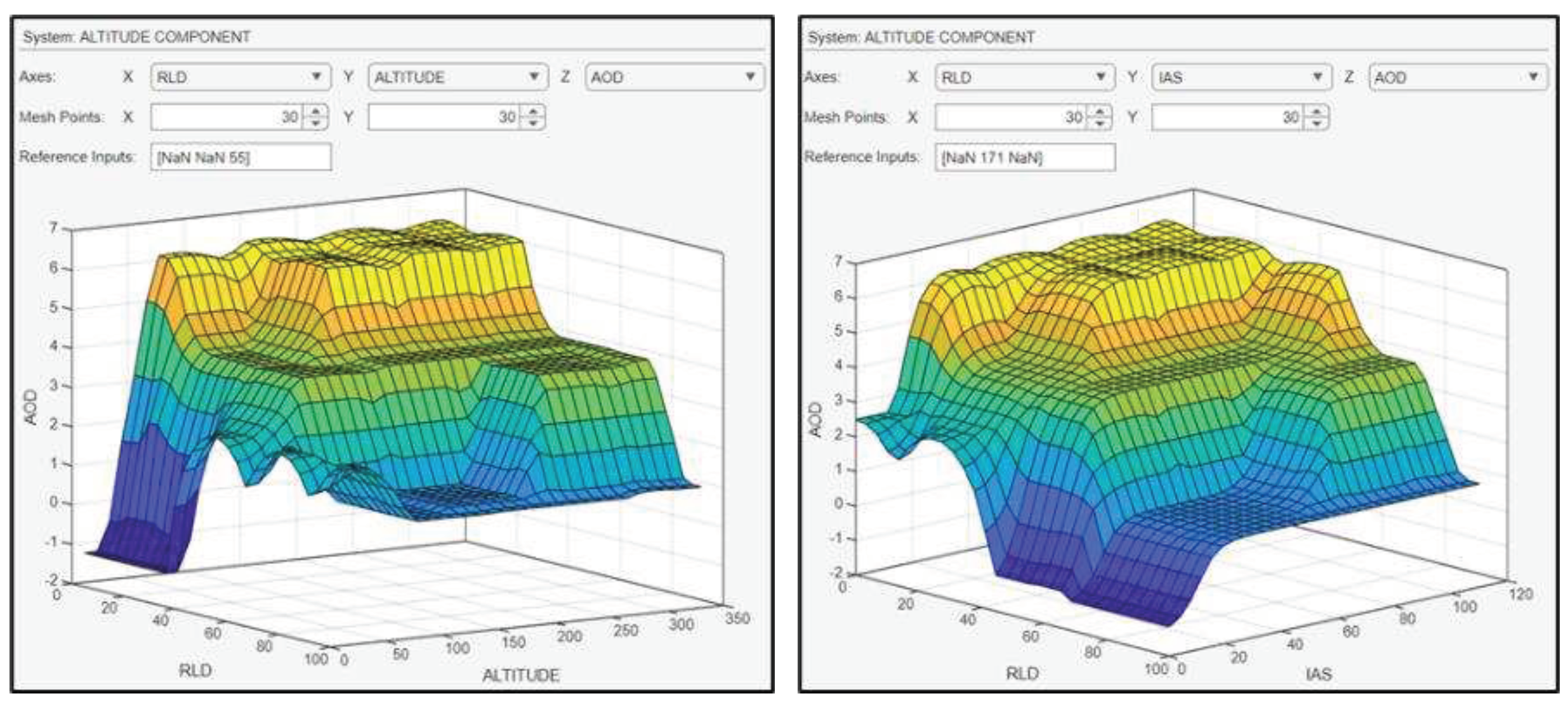
The UAV flies with an IAS of 70 knots, at a range of 27m from the landing deck, at a height level (altitude) of 120 feet. Consequently, the AOD of the UAV is yielded equal to 4.23 degrees (Figure 26), ensuring a sufficient altitude for a successful landing on the “SkyHook” capture system. Figure 27 shows the surface plots between the AOD and the inputs.
Figure 32 illustrates the surface of the Angle of Descent, on the x axis the Range from the Landing Deck is shown (in meters) and on the y axis is the Airspeed (in knots).
In conclusion, in the case of a UAV operating at a distance of 27 meters from the landing deck, at an altitude of 120 feet, with winds blowing from 108 degrees at a speed of 40 knots and an IAS of 70 knots, the required RSD in relation to the ship’s velocity will be 12.8 knots, during the turn that will be executed the UAV will have a BA of 36.3 degrees and the AOD will have a value of 4.23 degrees.
6. Conclusions
The primary aim of this research is to design a fuzzy logic-based autonomous ship-deck landing system specifically tailored for medium/small class fixed-wing UAVs. This system aims to alleviate maritime UAV operators from the demanding and challenging task of landing a drone on a moving ship. A variety of sensors onboard the UAV and also onboard the ship has been utilized including RF localization systems such as RFID and TDOA based mechanisms, anemometers, altimeters and airspeed sensors. However, a key objective of this study is to reduce the requisite number of sensors and equipment, with a dual focus on cost-effectiveness and diminished system complexity. Additionally, particular attention has been given to the deliberate exclusion of GPS, enhancing the UAV’s resistance to long range EW jamming and spoofing techniques.
The purpose of the autonomous ship-deck landing system is to control the UAV’s movement in the three-dimensional space, ensuring precise positional control during the final approach. The wind, being an external factor that directly influences drone landing, particularly at sea, is integrated into the fuzzy logic-based system along with the airspeed of the UAV, altitude, and the distance from the landing platform. This integration is facilitated through the UAV’s sensors. The FLS in return, provides as outputs: the RSD in relation with the speed of the ship, the angle of descent and the bank angle of the drone, or else the azimuth angle of turn, in order to control the UAV’s movement. As a result, the simulation results are generally satisfactory, affirming the reliability of the autonomous fuzzy logic landing system.
Lastly, future suggestions would involve searching for more optimal membership function parameters and rule base, by incorporating the knowledge and the experience of maritime UAV operators, in combination with those of maritime helicopter pilots, who undeniably excel in harsh, all-weather landings onboard ships, utilizing polls or other statistic methods. Research could also explore additional input variables or parameters, such as humidity or visibility (particularly relevant when utilizing computer vision algorithms for landing). These factors significantly impact UAV navigation and control during the final stage of flight, where environmental conditions and the drone’s aerodynamics differ significantly from the usual phases of UAV flight.
Author Contributions
Conceptualization, I.T. and P.Z.; methodology, I.T. and P.Z.; writing—original draft preparation, I.T. and P.Z.; writing—review and editing, I.T. and E.X.; supervision, E.X. and M.P. All authors have read and agreed to the published version of the manuscript.”
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krystosik-Gromadzińska, A. The use of drones in the maritime sector – areas and benefits, Scientific Journals of the Maritime University of Szczecin, Szczecin, Poland, 2021.
- Chukwube, M. The Role of UAVs in Border Security and Maritime Surveillance, readwrite, 3 April 2023. [Online]. Available: https://readwrite.com/the-role-of-uavs-in-border-security-and-maritime-surveillance/.
- Flyability, “WHAT IS A MARITIME DRONE?, Flyability, [Online]. Available: https://www.flyability.com/maritime-drone.
- Gautam, A.; Sujit, P.B.; Saripalli, S. A Survey of Autonomous Landing Techniques for UAVs, International Conference on Unmanned Aircraft Systems (ICUAS), May 27-30, 2014. Orlando, FL, USA.
- McLauchlan, L. L. L. Fuzzy Logic Controlled Landing of a Boeing 747, International Conference on Intelligent Robots and Systems, St. Louis, USA, 2009.
- Cetin, O.; Kurnaz, S., Kaynak O. Fuzzy Logic Based Approach to Design of Autonomous Landing System for Unmanned Aerial Vehicles. J of Intell Robot Sys 2011, 61, 239–250. [CrossRef]
- Talha, M.; Asghar, F.; Rohan, A.; Rabah, M.; Kim, S.H. Fuzzy Logic-Based Robust and Autonomous Safe Landing for UAV Quadcopter. Arab J Sci Eng 2019, 44, 2627–2639. [Google Scholar] [CrossRef]
- Pratiwi, W.; Sofwan, A.; Setiawan, I. Implementation of fuzzy logic method for automation of decision making of Boeing aircraft landing, IAES International Journal of Artificial Intelligence (IJ-AI) 2020, Diponegoro University, Indonesia.
- Seitbattalov, Z. Y.; Atanov, S. K.; Moldabayeva, Z. S. An Intelligent Decision Support System for Aircraft Landing Based on the Runway Surface, IEEE Smart Information Systems and Technologies (SIST) 2021, 28-30 April, Nur-Sultan, Kazakhsta.
- Valavanis, K. P.; Vachtsevanos, G. J. Handbook of Unmanned Aerial Vehicles, 2014.
- Sieger, J. Electronic warfare: Israel ramps up GPS jamming to counter Hamas drone attacks," FRANCE 24, 17 October 2023. [Online]. Available: https://www.france24.com/en/tv-shows/science/20231017-electronic-warfare-israel-ramps-up-gps-jamming-to-counter-hamas-drone-attacks.
- Mozur, P. and Krolik, A. The Invisible War in Ukraine Being Fought Over Radio Waves, The New York Times, 19 November 2023. [Online]. Available: https://www.nytimes.com/2023/11/19/technology/russia-ukraine-electronic-warfare-drone-signals.html.
- SKYbrary, SKYbrary, 2021. [Online]. Available: https://skybrary.aero/articles/air-speed-indicator.
- IVAO Documentation Library, “IVAO Documentation Library,” 29 April 2023. [Online]. Available: https://wiki.ivao.aero/en/home/training/documentation/Airspeed_definition.
- NWCG National Wildfire Coordinating Group, “NWCG National Wildfire Coordinating Group,” [Online]. Available: https://www.nwcg.gov/course/ffm/location/62-azimuths#:~:text=However%2C%20plots%20of%20wind%20and,the%20southeast%20(135%C2%B0).
- Barcelona Field Studies Center, Google Maps Compass Application, Set Compass, [Online]. Available: https://setcompass.com/TypesofNorth.htm.
- Wijaya, R. F.; Tondang, Y. M.; Utama Siahaan, A. P. Take Off and Landing Prediction Using Fuzzy Logic. International Journal of Recent Trends in Engineering and Research 2016, 127–134.
- RYA Training Center, “Jolly Parrot Sailing,” [Online]. Available: https://jollyparrot.co.uk/blog/the-difference-between-true-and-apparent-wind-speed-480#:~:text=True%20wind%20speed%2C%20sometimes%20known,on%20you%20as%20you%20sail.
- Anritsu Advancing Beyond, “Time Difference of Arrival (TDOA),” Anritsu Americas Sales Company, Allen, USA, 2022.
- Yang, B.; Yang, E. A Survey on Radio Frequency based Precise Localisation Technology for UAV in GPS-denied Environment. J Intell Robot Syst 2021, 103/38. [Google Scholar]
- O’Keefe, B. Techniques, Finding Location with Time of Arrival and Time Difference of Arrival, Department of Electrical and Computer Engineering, 2017.
- Dogancay, K.; Hmam, H. 3D TDOA Emitter Localization Using Conic Approximation. Sensors, 2023; 23, 6254. [Google Scholar]
- Ostler, J. N.; Bowman, W. J.; Snyder, D.O.; McLain, T. W. Performance Flight Testing of Small Electric Powered Unmanned Aerial Vehicles, BYU ScholarsArchive, Brigham Young University, 2009.
- AGENCIA NACIONAL DE AVIACAO CIVIL, “ANACPEDIA,” [Online]. Available: https://www2.anac.gov.br/anacpedia/ing-por/tr686.htm#:~:text=to%3A%20%22B%22-,bank%20angle,starboard%20(left%20or%20right).
- PowerNationTV, “PowerNationTV, 3 May 2017. [Online]. Available: https://www.powernationtv.com/post/how-to-land-a-drone-aircraft-with-no-runway-the-skyhook-recovery-system.
- MathWorks, “Object Tracking Using Time Difference of Arrival (TDOA), MathWorks, 2021. [Online]. Available: https://www.mathworks.com/help/fusion/ug/object-tracking-using-time-difference-of-arrival.html.
- Iizuka, T.; Sasatani, T.; Nakamura, T.; Kosaka, N.; Hisada, M.; Kawahara, Y. MilliSign: mmWave-Based Passive Signs for Guiding UAVs in Poor Visibility Conditions, ACM MobiCom ’23: Proceedings of the 29th Annual International Conference on Mobile Computing and Networking, no.50, Tokyo, Japan, 2023.
- Stanford Encyclopedia of Philosophy, Fuzzy Logic, Stanford Encyclopedia of Philosophy, 15 November 2016. [Online]. Available: https://plato.stanford.edu/entries/logic-fuzzy/.
Figure 1.
Wind Calculator App.
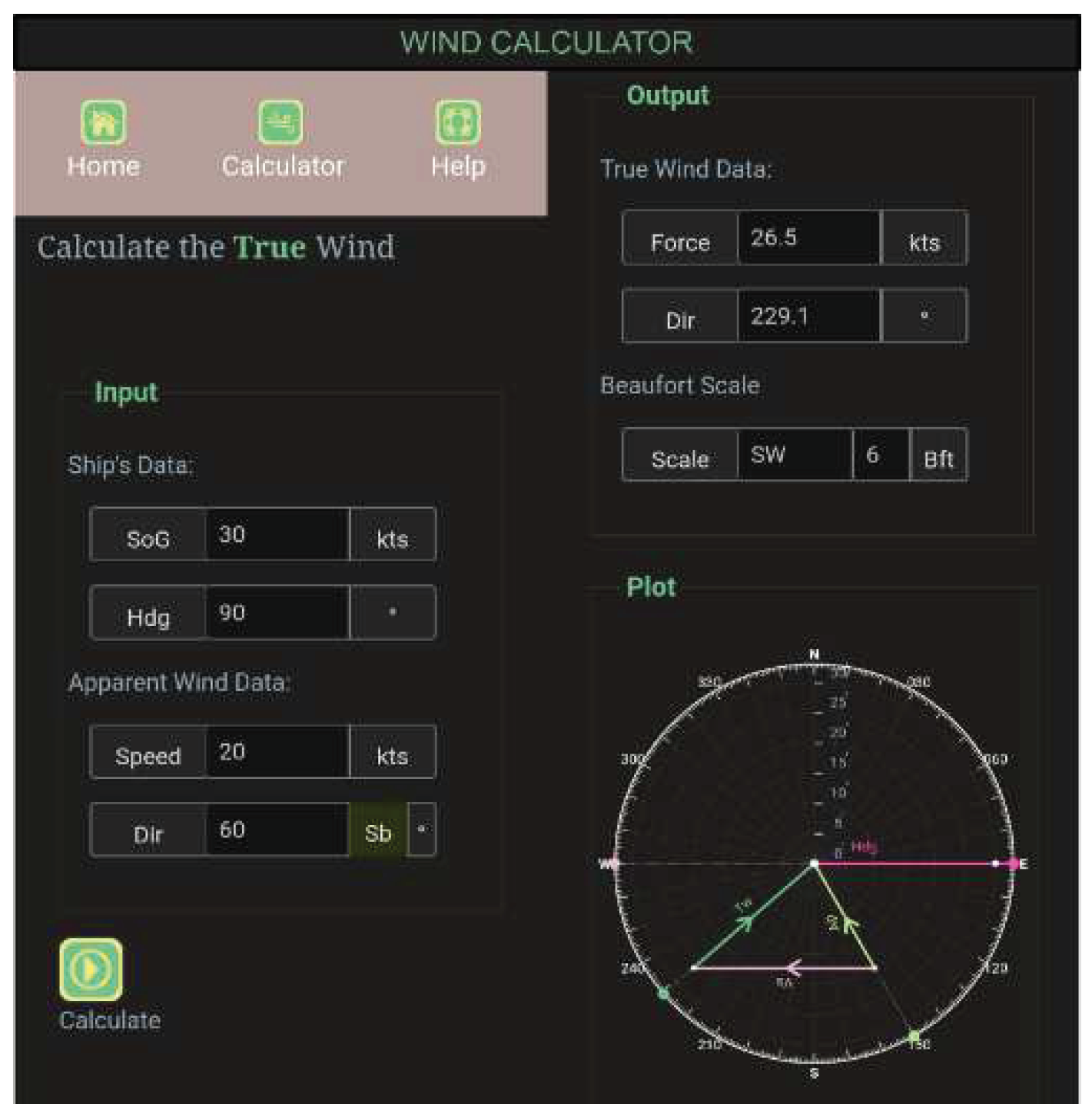
Figure 2.
A TDOA based localization mechanism with two nodes.
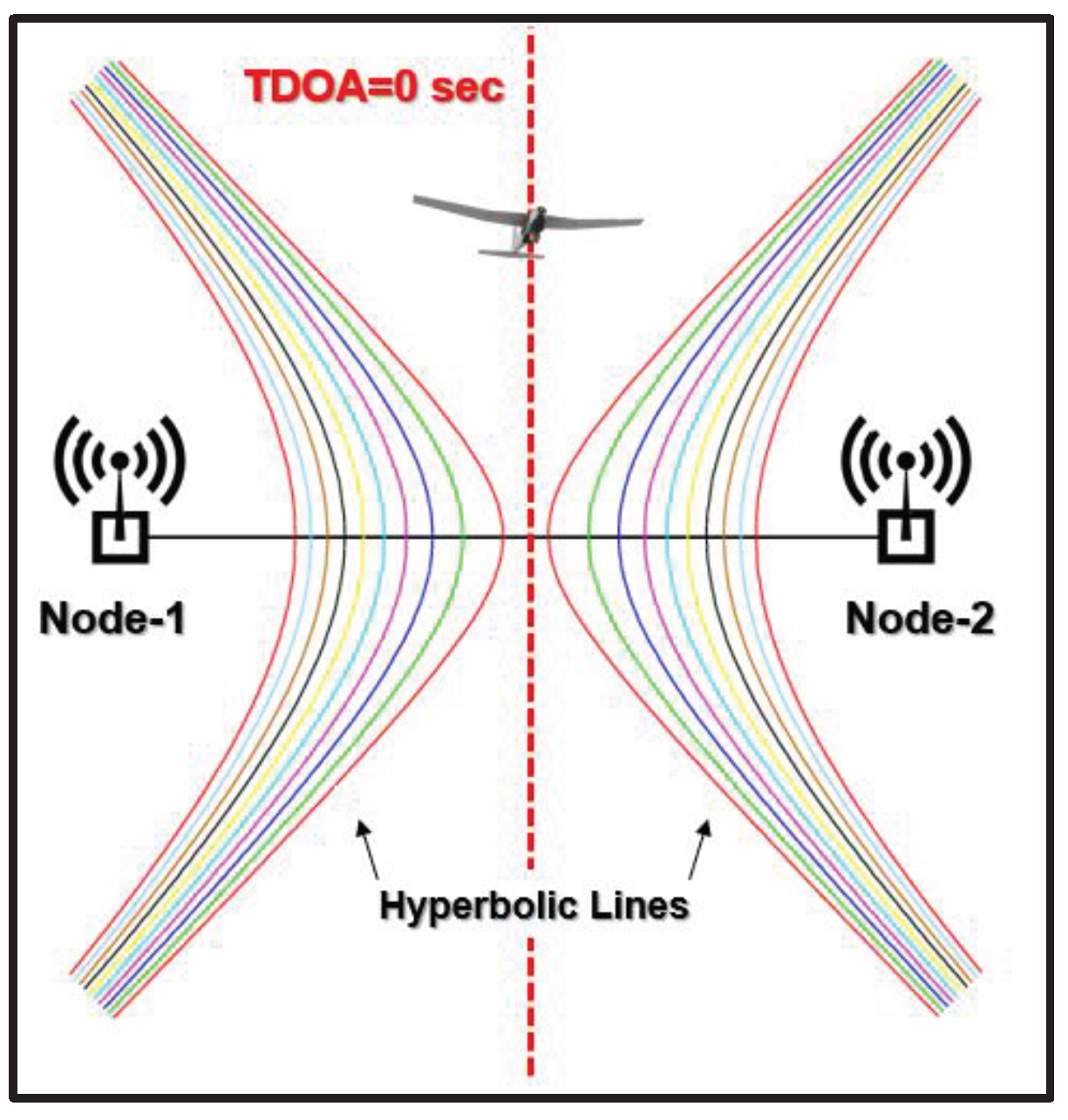
Figure 3.
TDOA based three-node system to calculate the distance of the UAV in the 2D space.
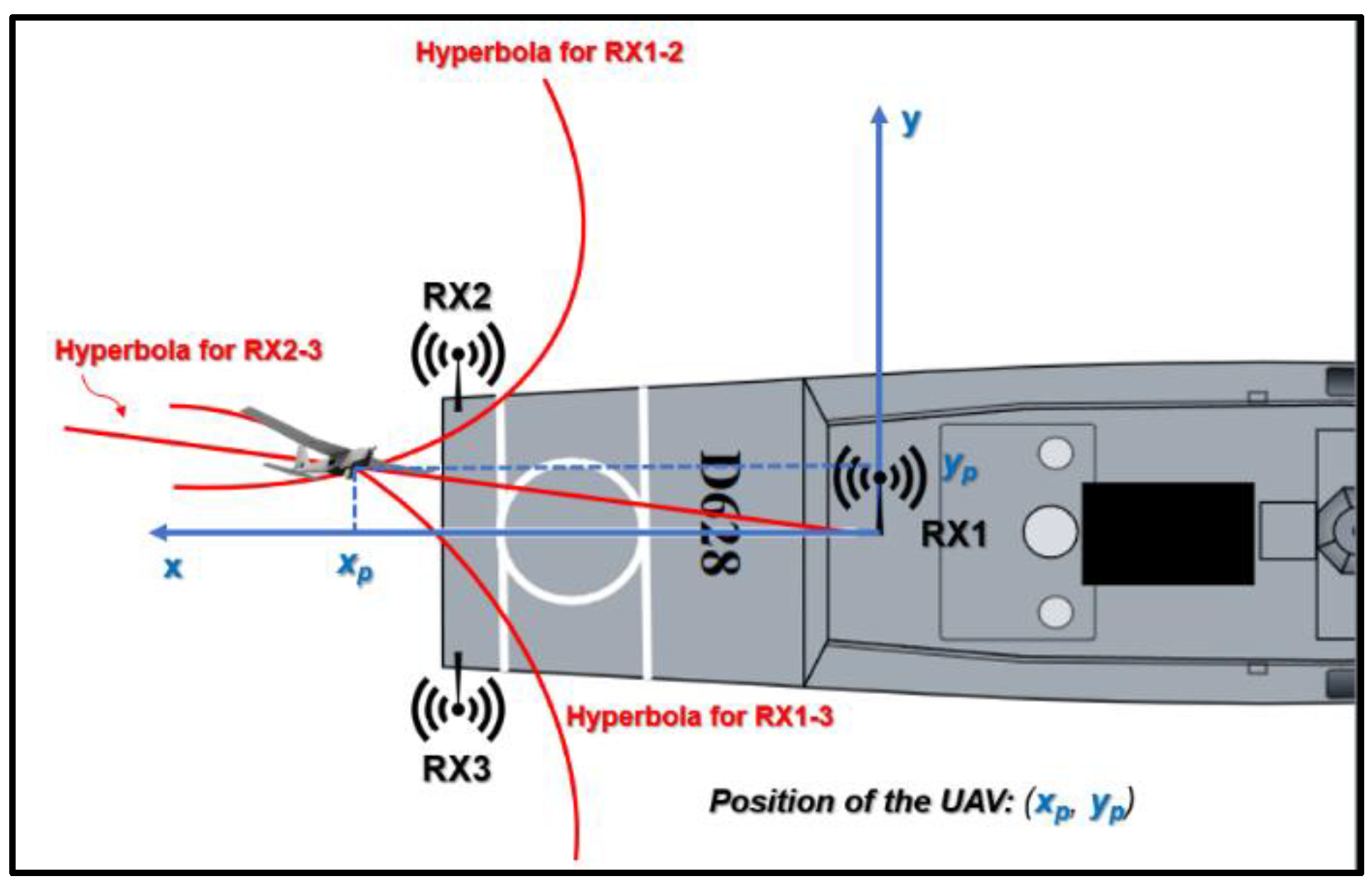
Figure 4.
The TDOA based localization four-node system.
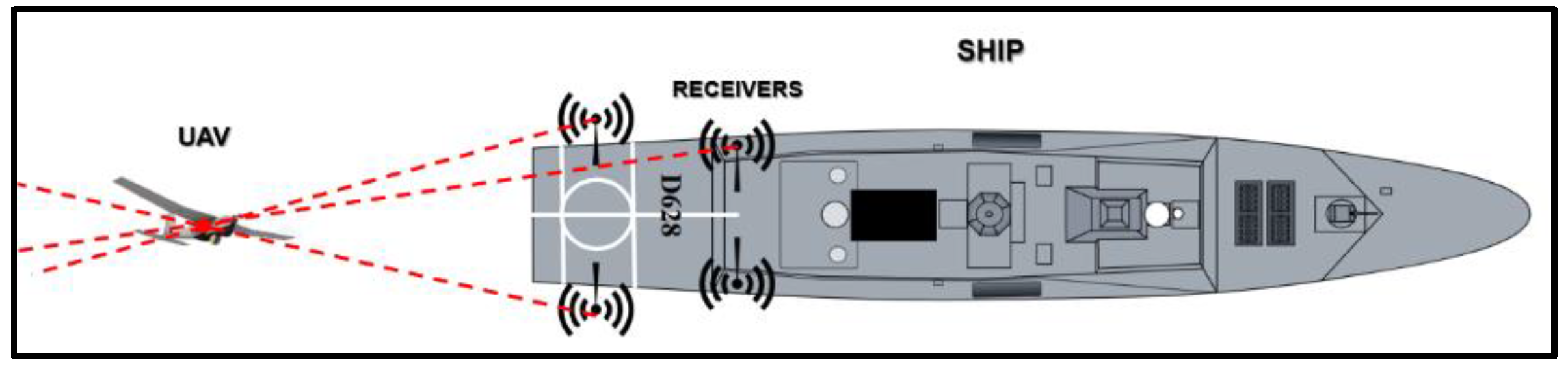
Figure 6.
Different Heights used for the Landing System.
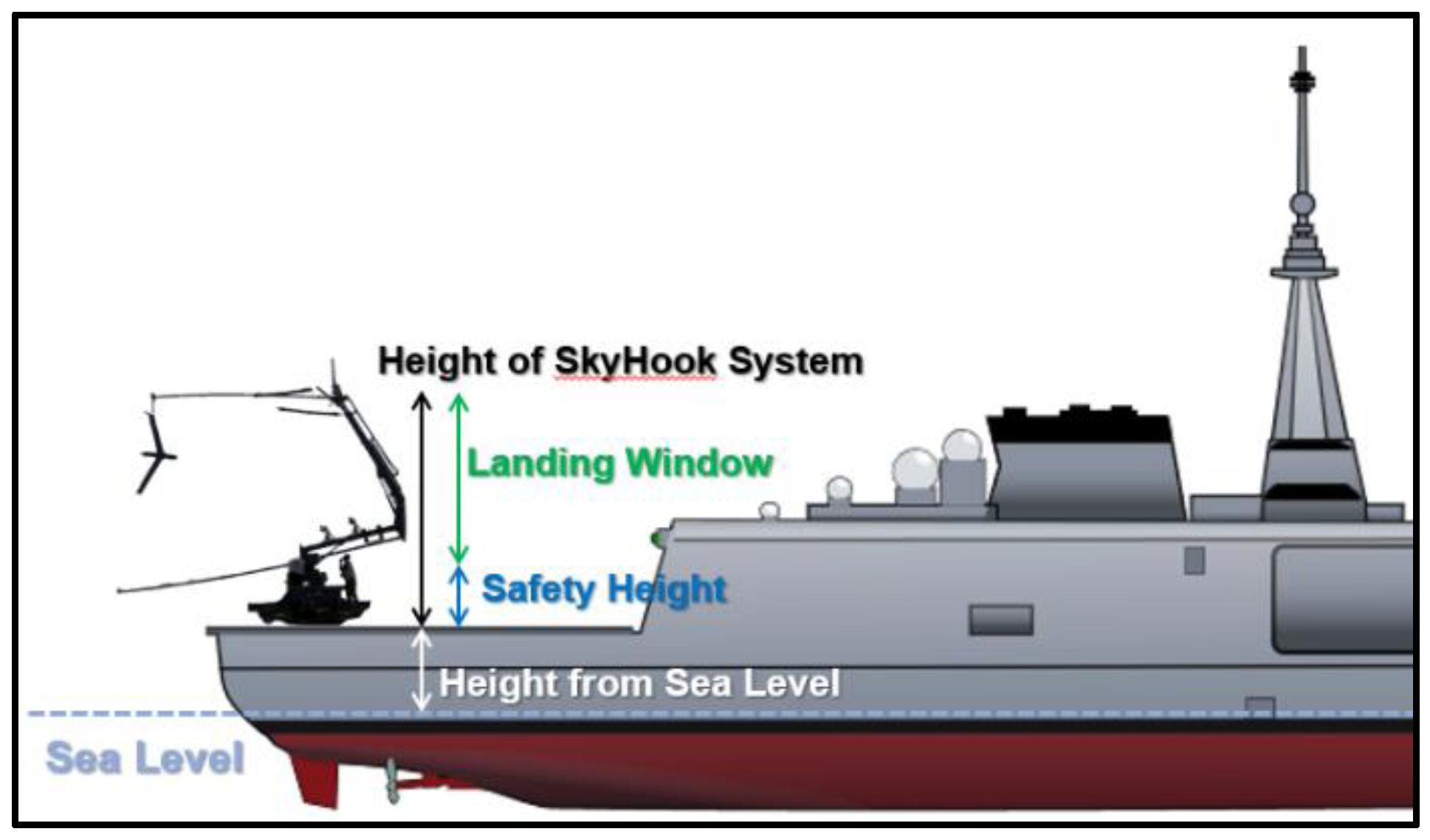
Figure 7.
The chipless RFID tag used in the MilliSign System [20].
Figure 7.
The chipless RFID tag used in the MilliSign System [20].

Figure 8.
The chipless RFID tag on a tripod stand behind the SkyHook Landing System.
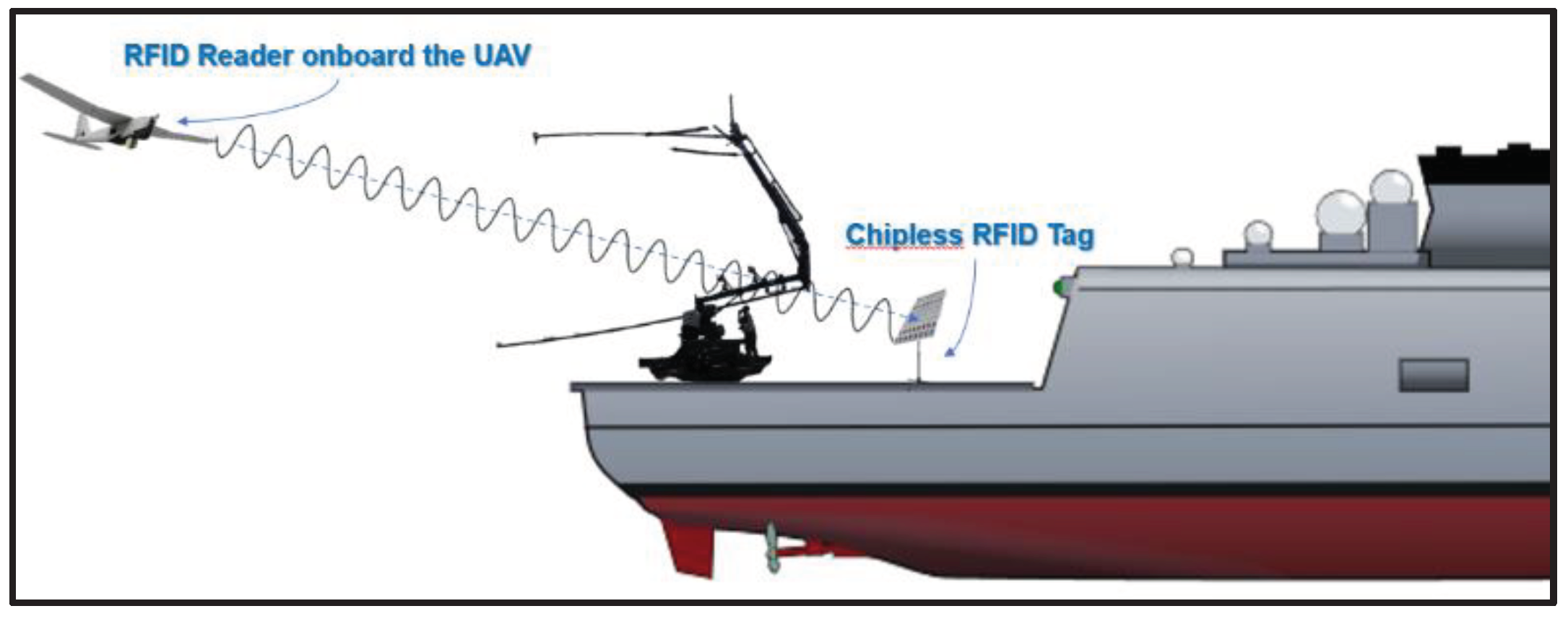
Figure 9.
Examples of Small – Medium Size/Class UAVs.

Figure 10.
The Ship-Deck Landing Architecture.
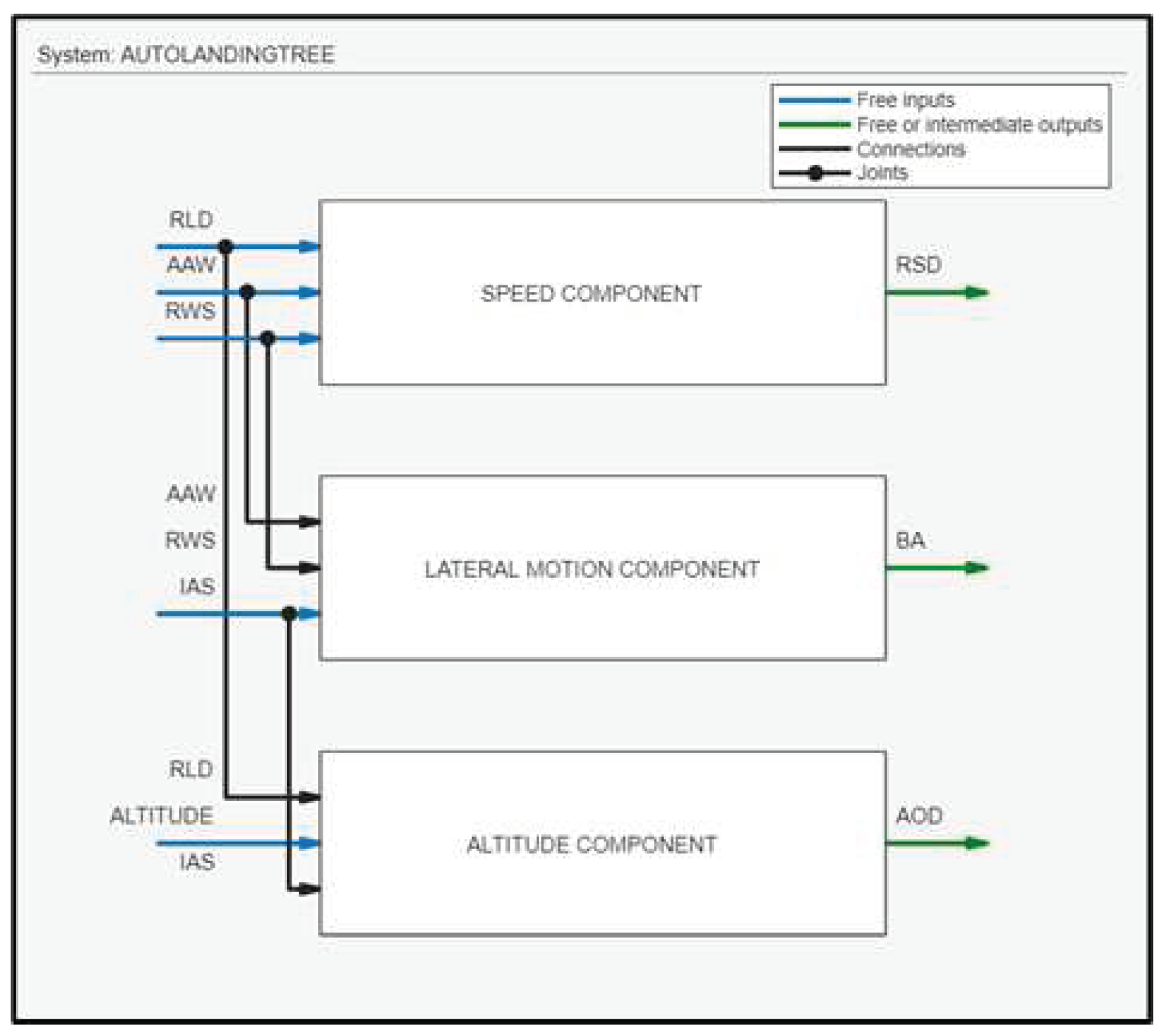
Figure 11.
Membership Functions for RLD.
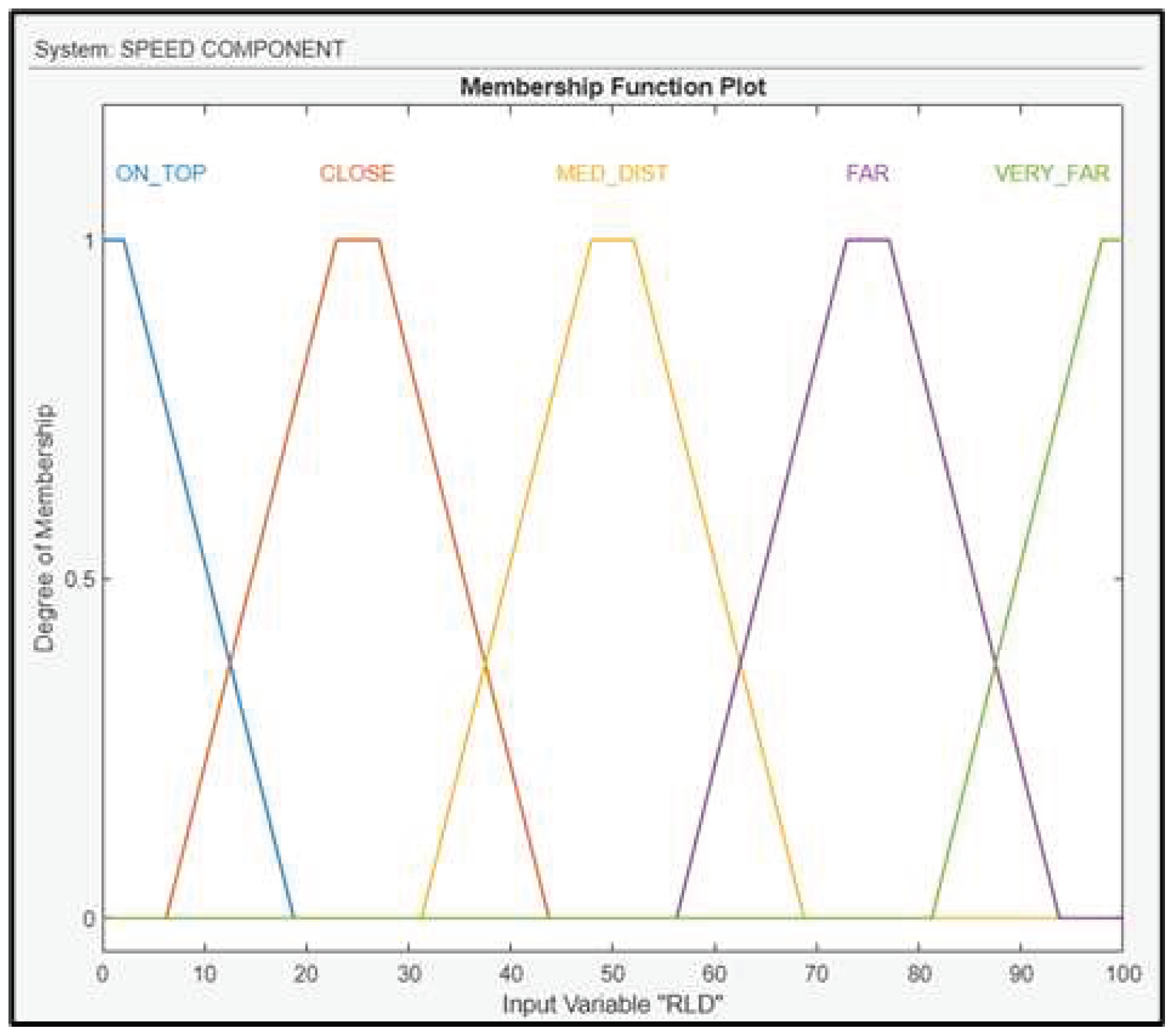
Figure 12.
Membership Functions for AAW.
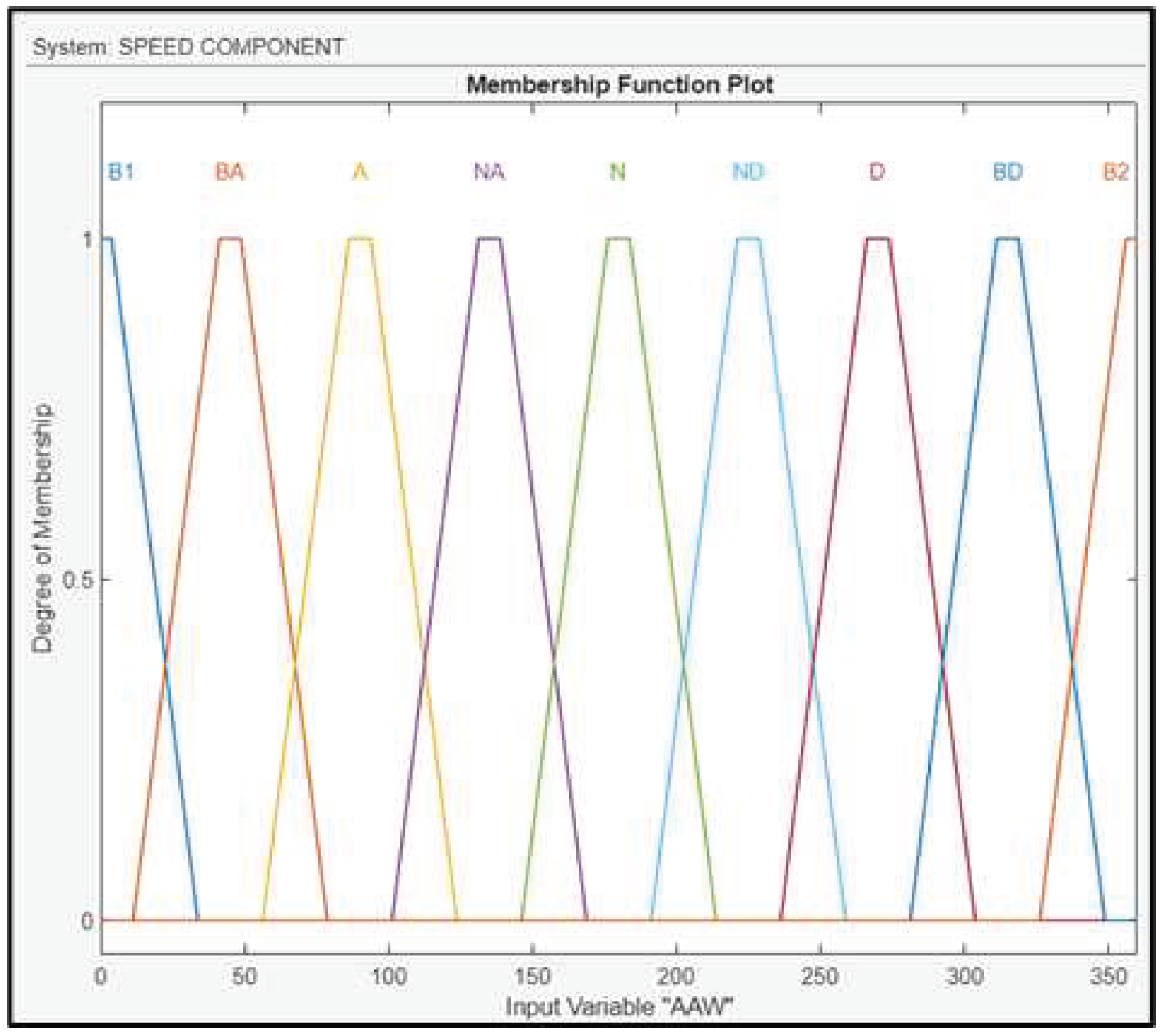
Figure 13.
Membership Functions for RWS.
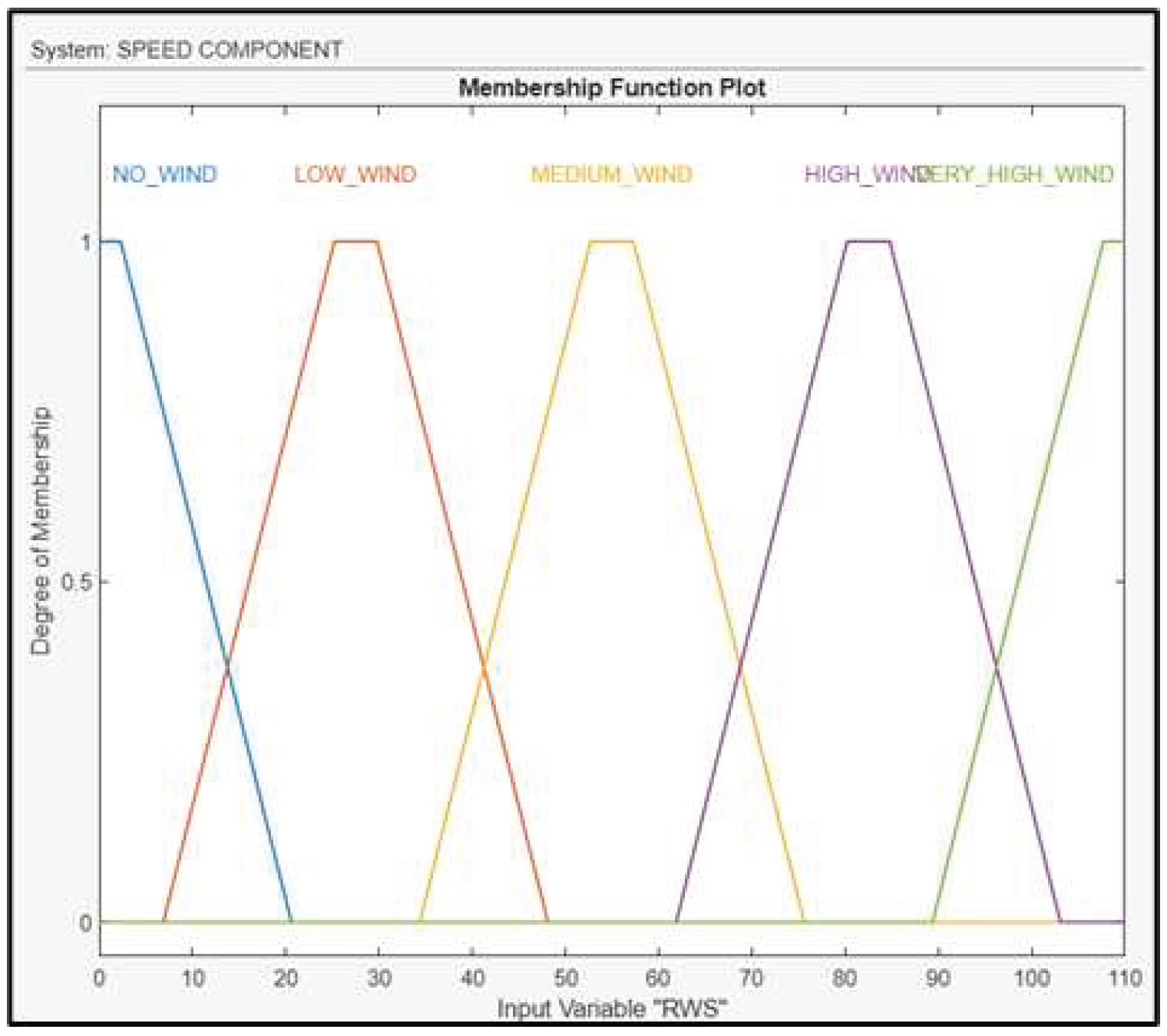
Figure 14.
Membership Functions for RSD.
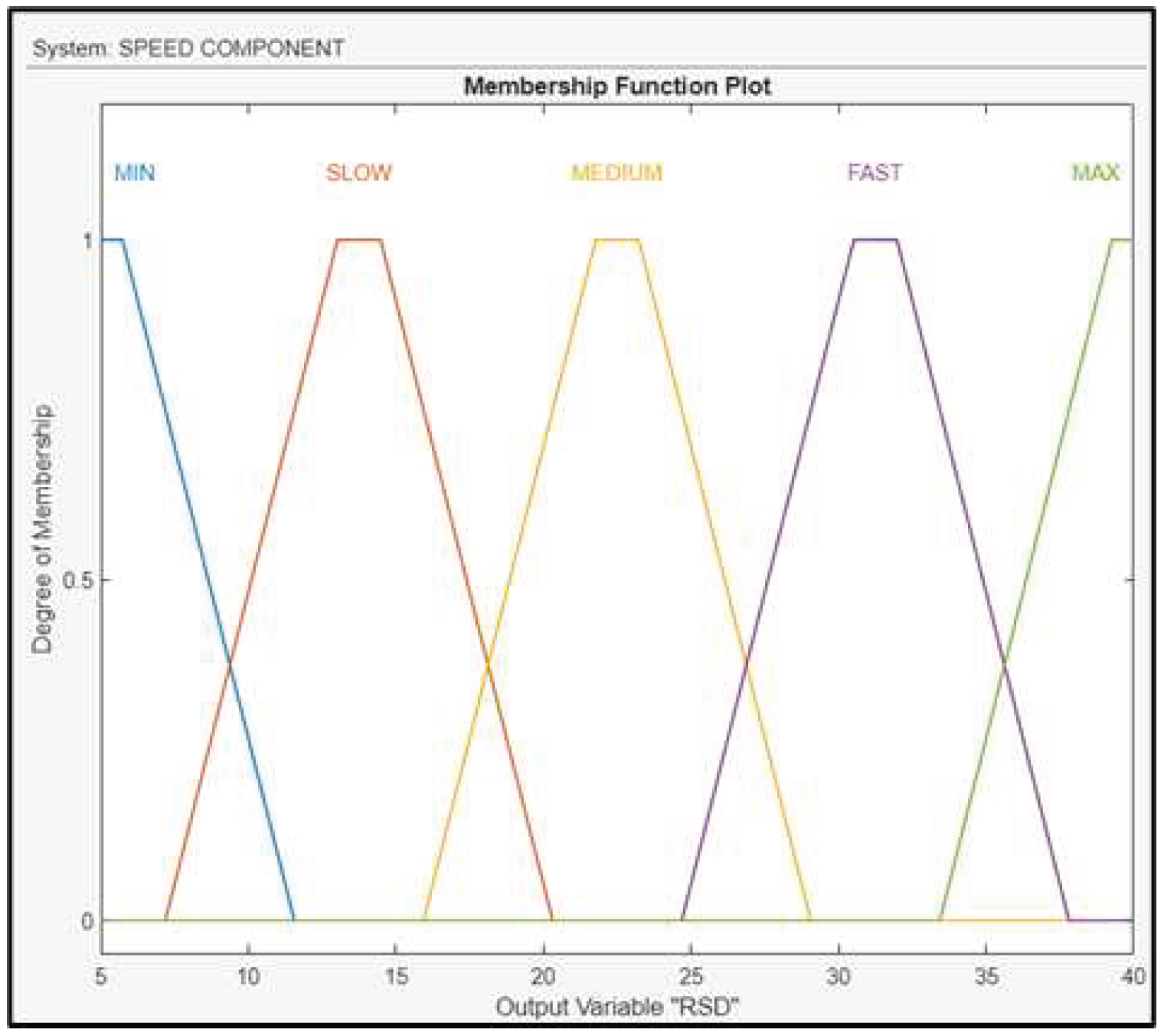
Figure 15.
Fuzzy rules for the Speed Component.
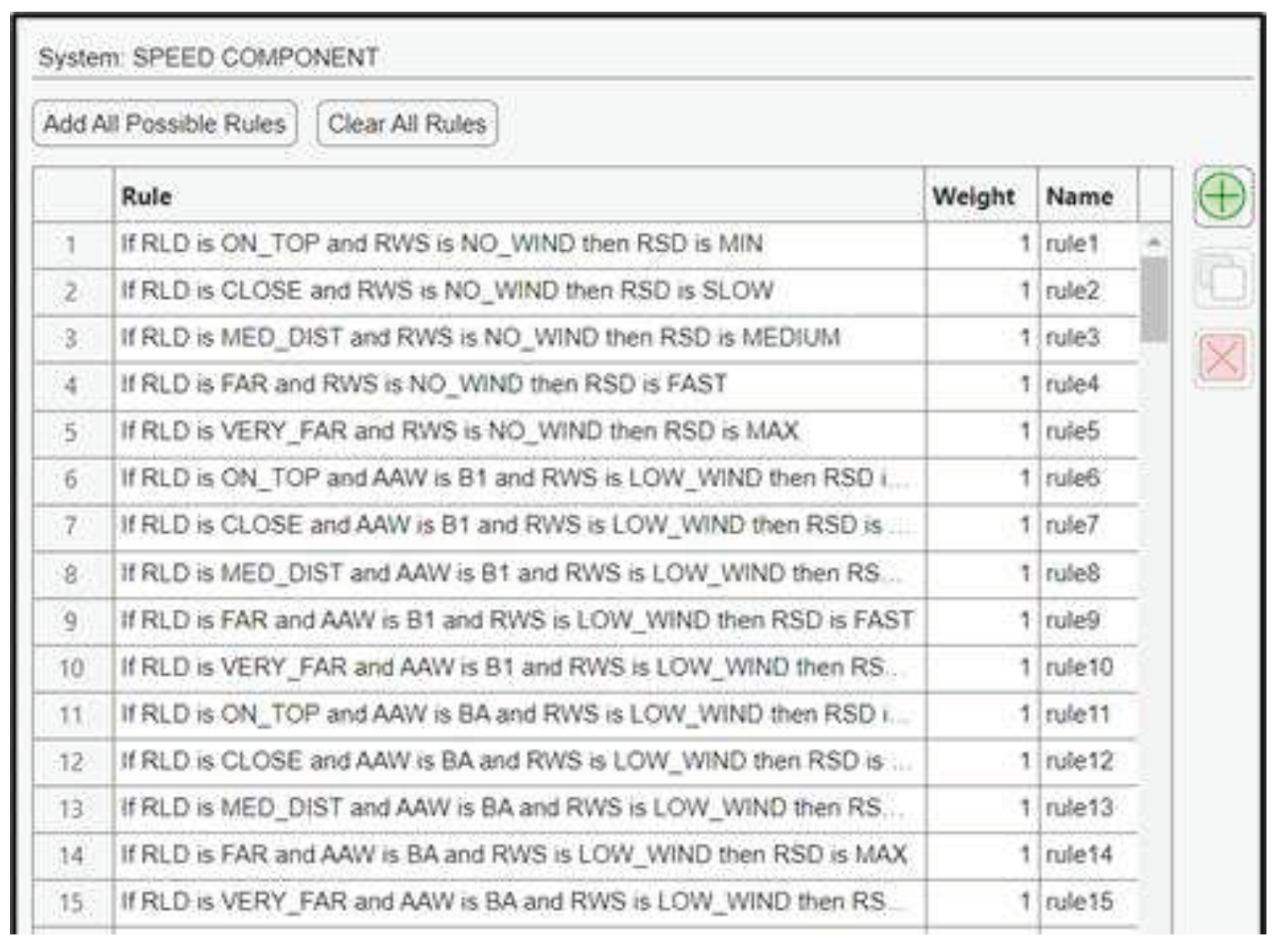
Figure 16.
Membership Functions for IAS.
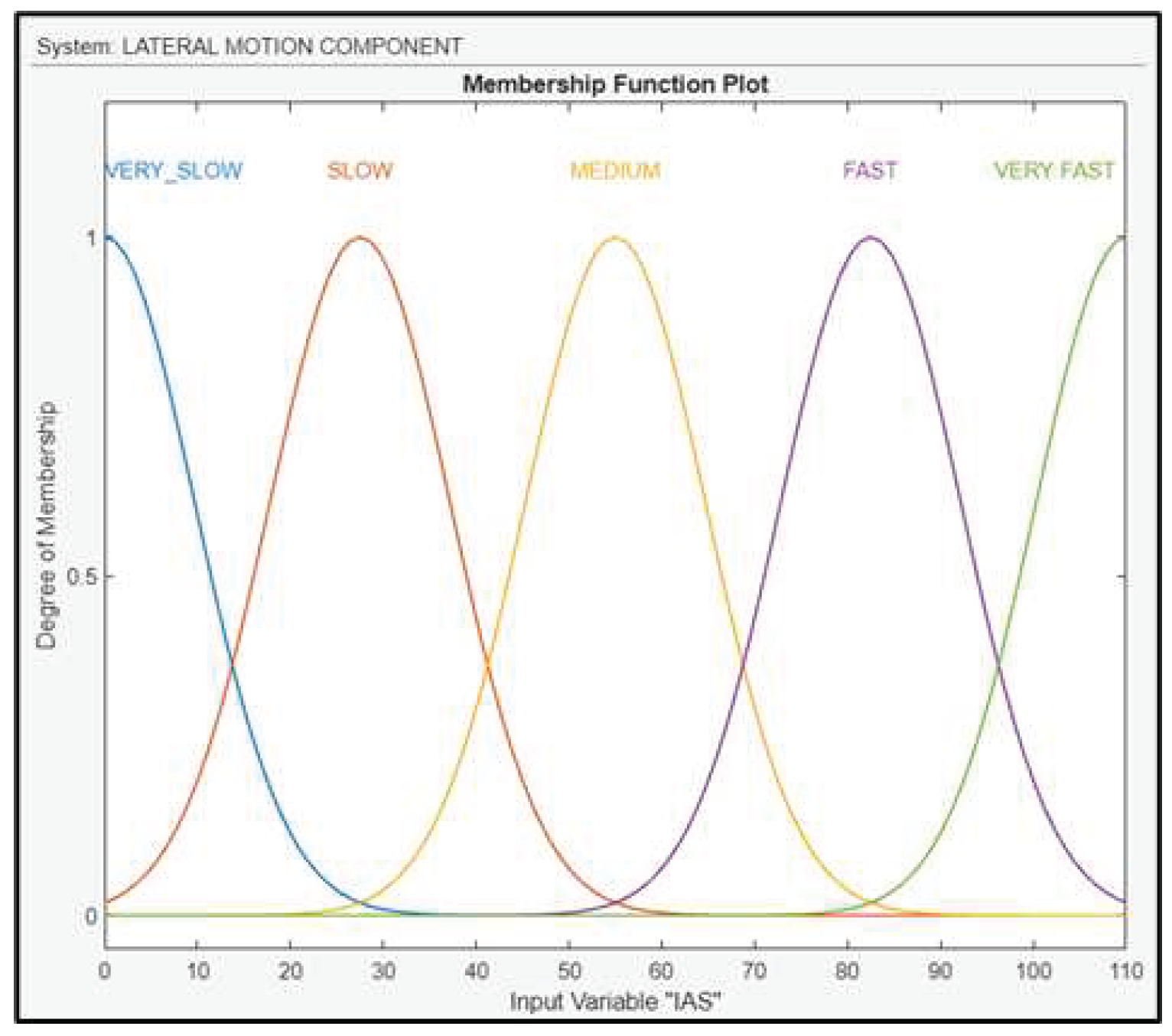
Figure 17.
Membership Functions for BA.
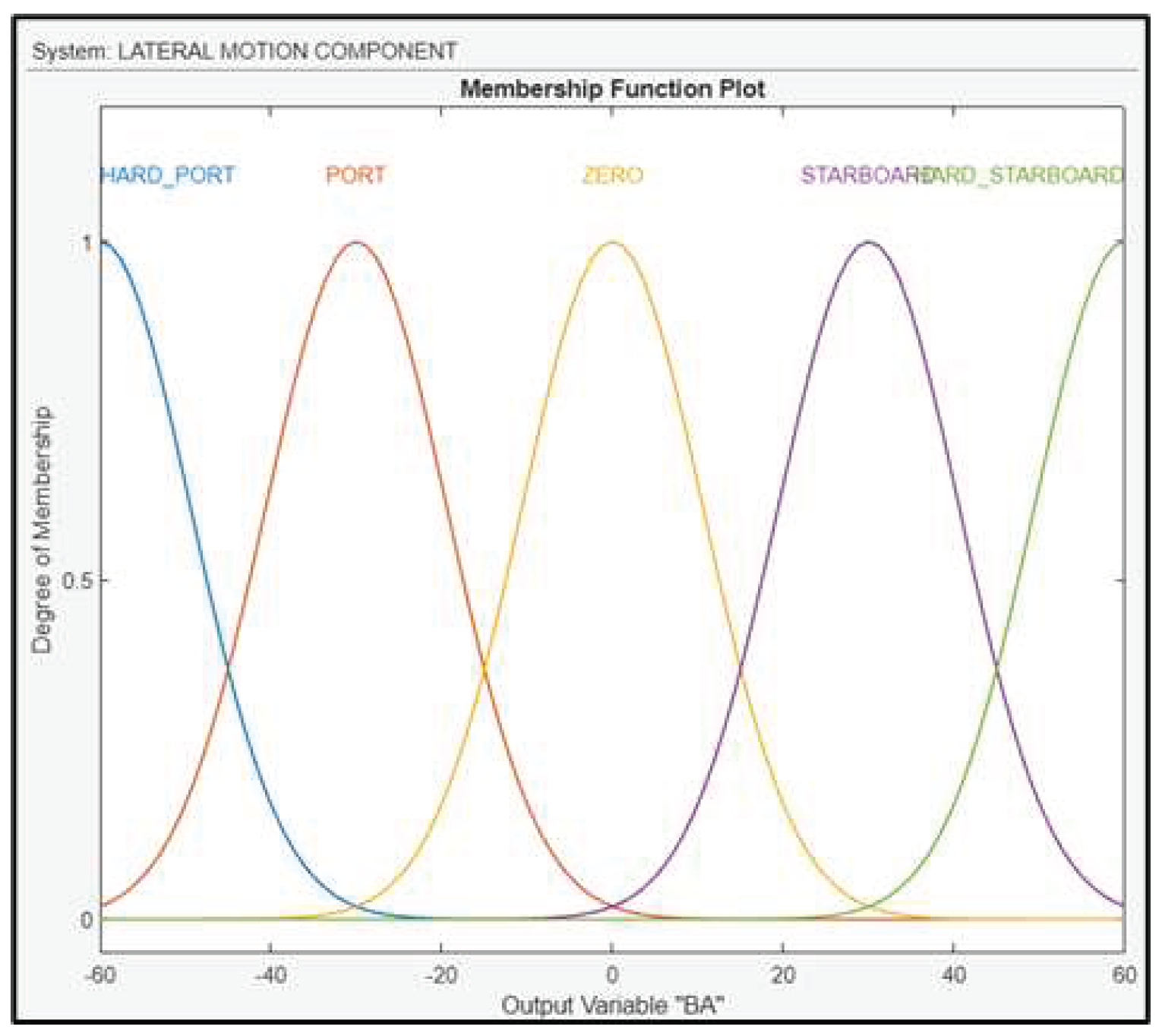
Figure 18.
Fuzzy rules for the Lateral Motion Component.
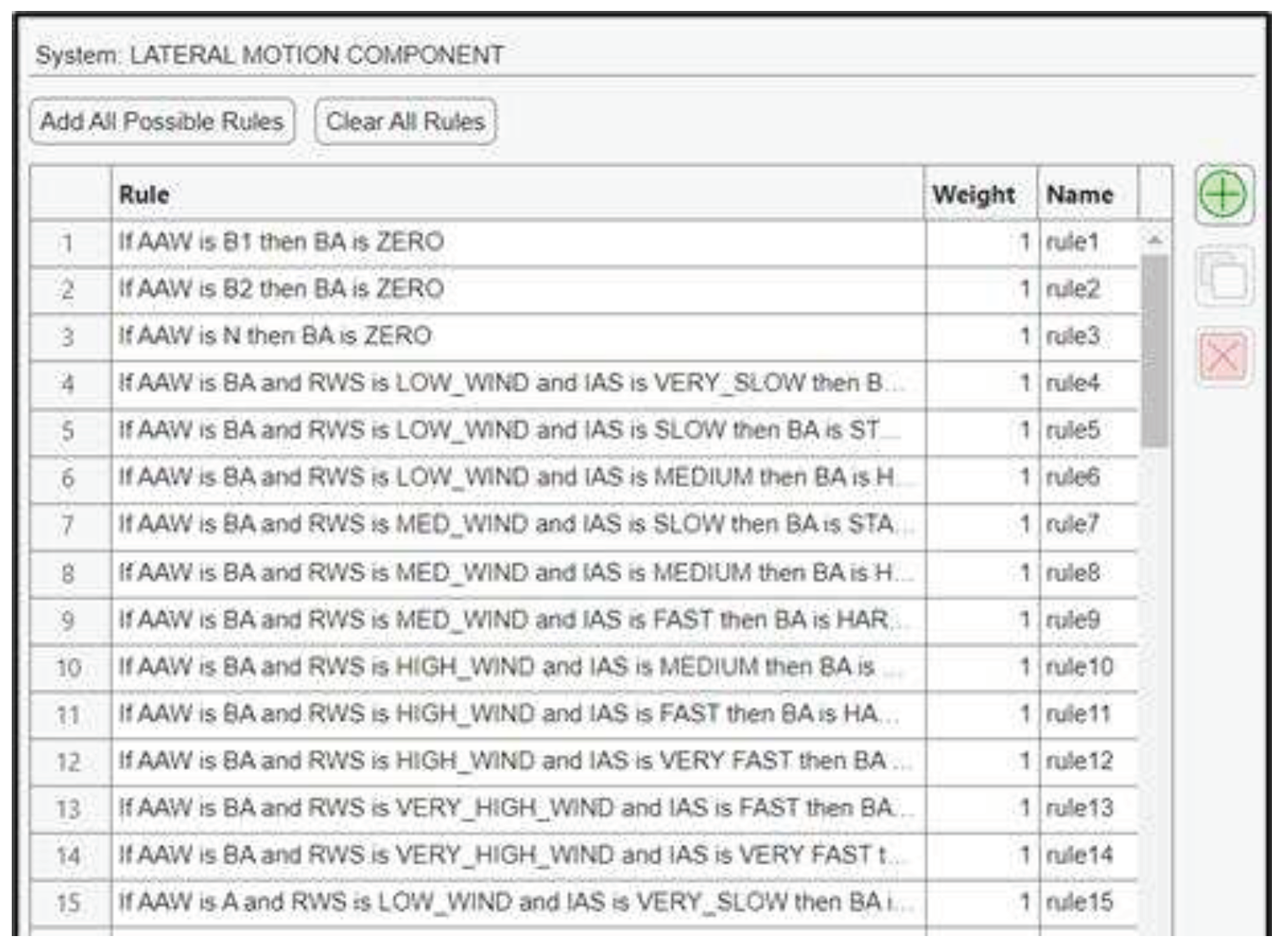
Figure 19.
Membership Functions for Altitude.
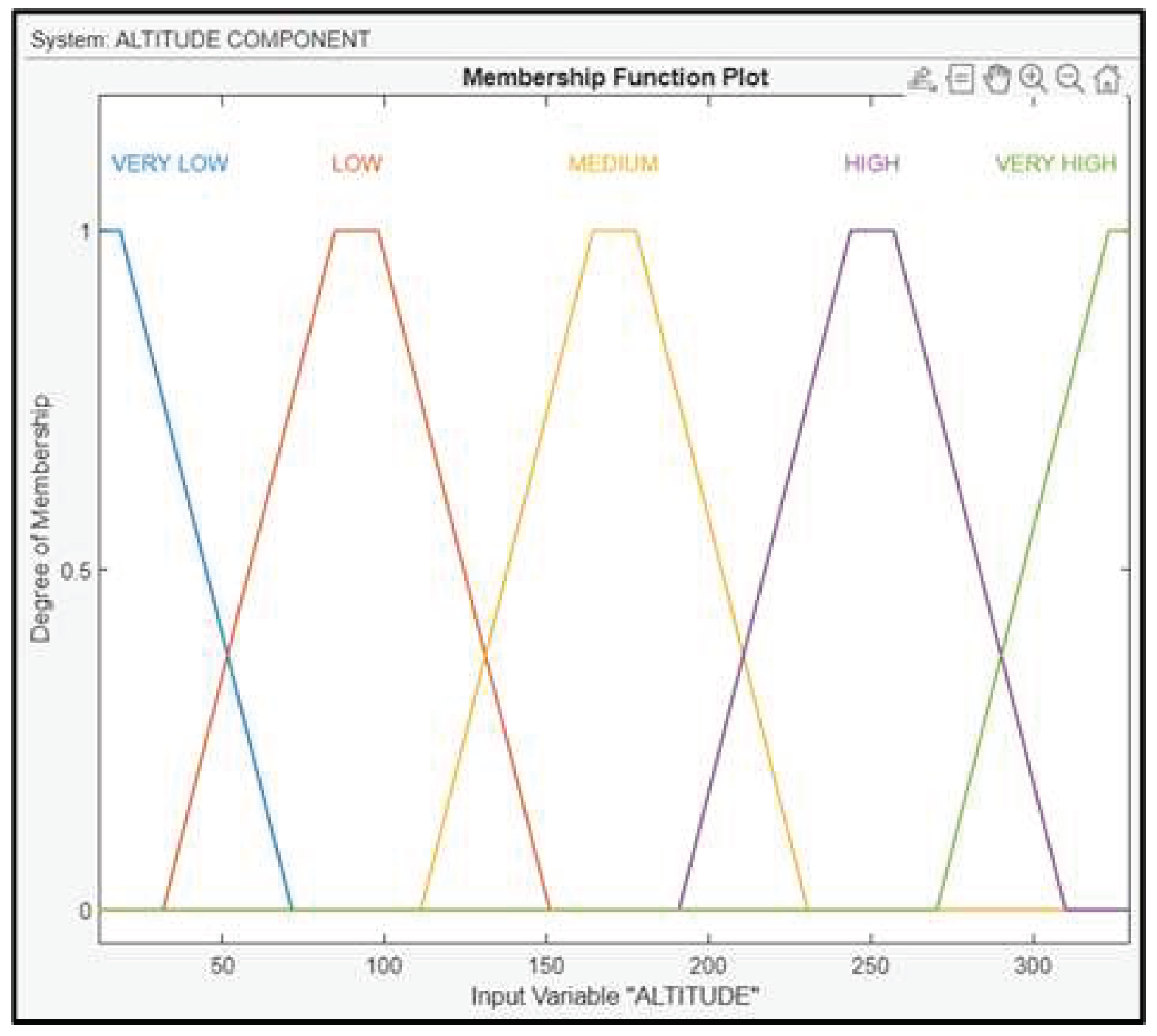
Figure 20.
Membership Functions for AOD.
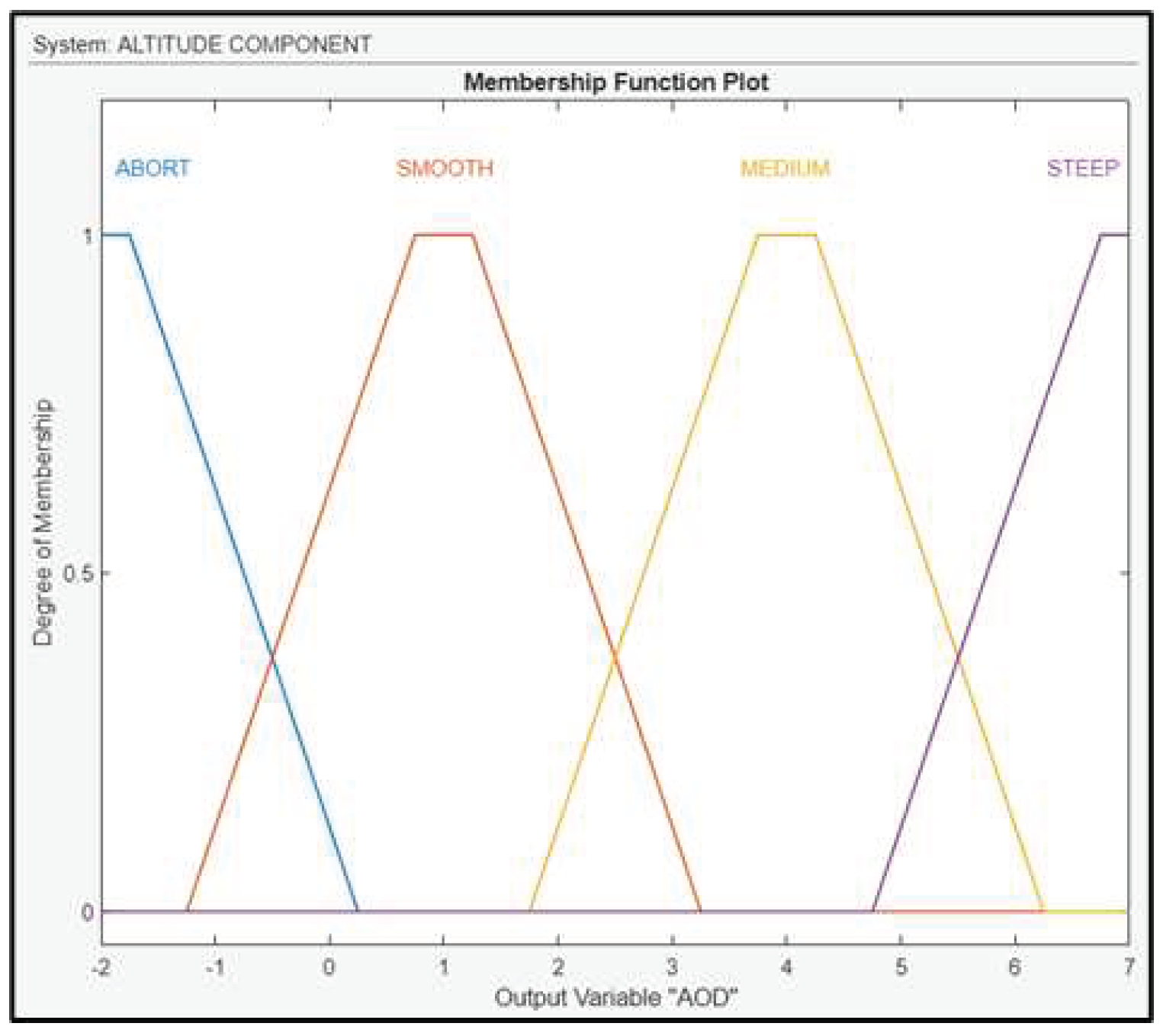
Figure 21.
Fuzzy rules for the Altitude Component.
Figure 22.
Fuzzy rules activation for the Speed Component.
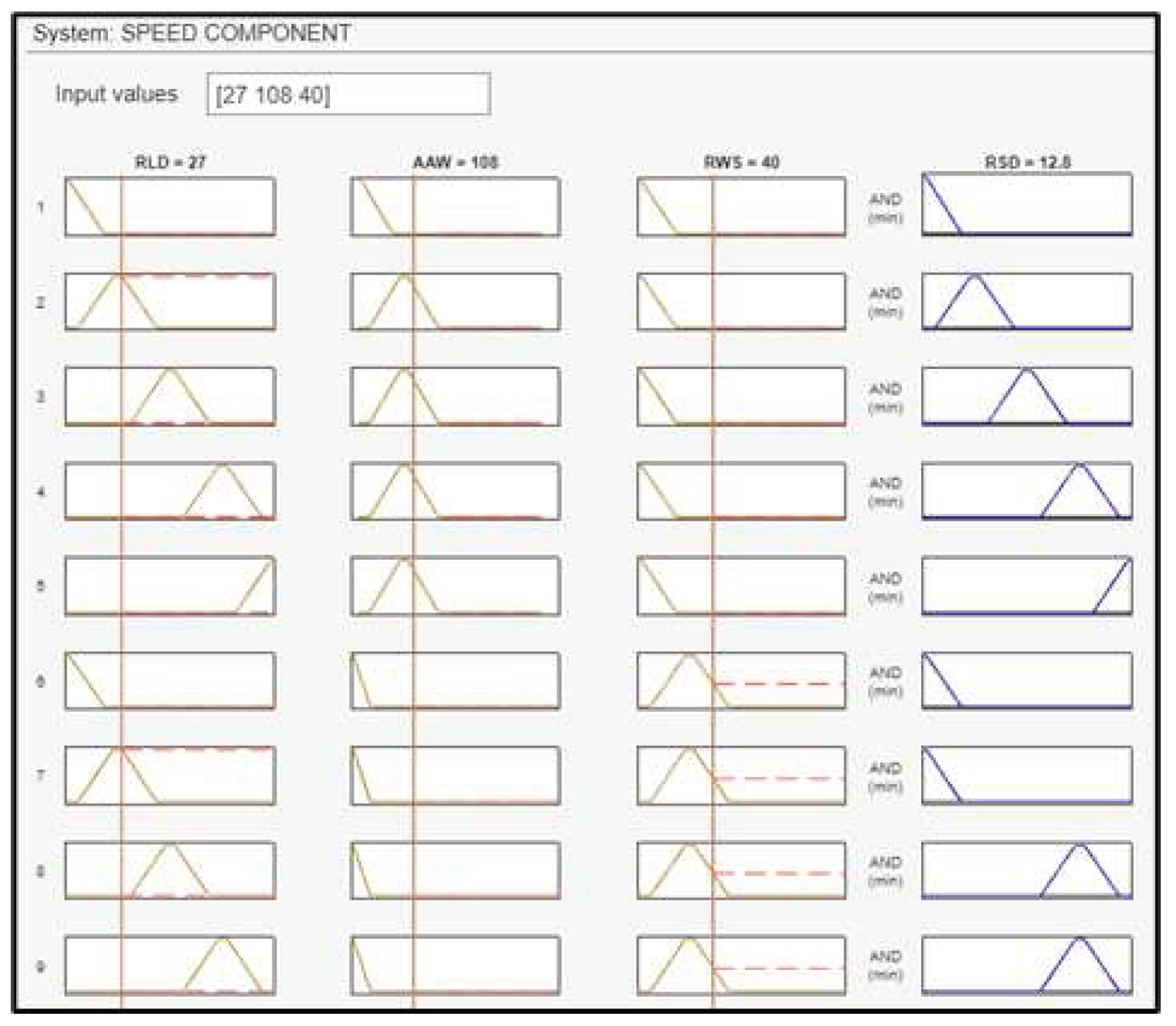
Figure 23.
Surface plots indicative of the relationship between the inputs and the RSD.
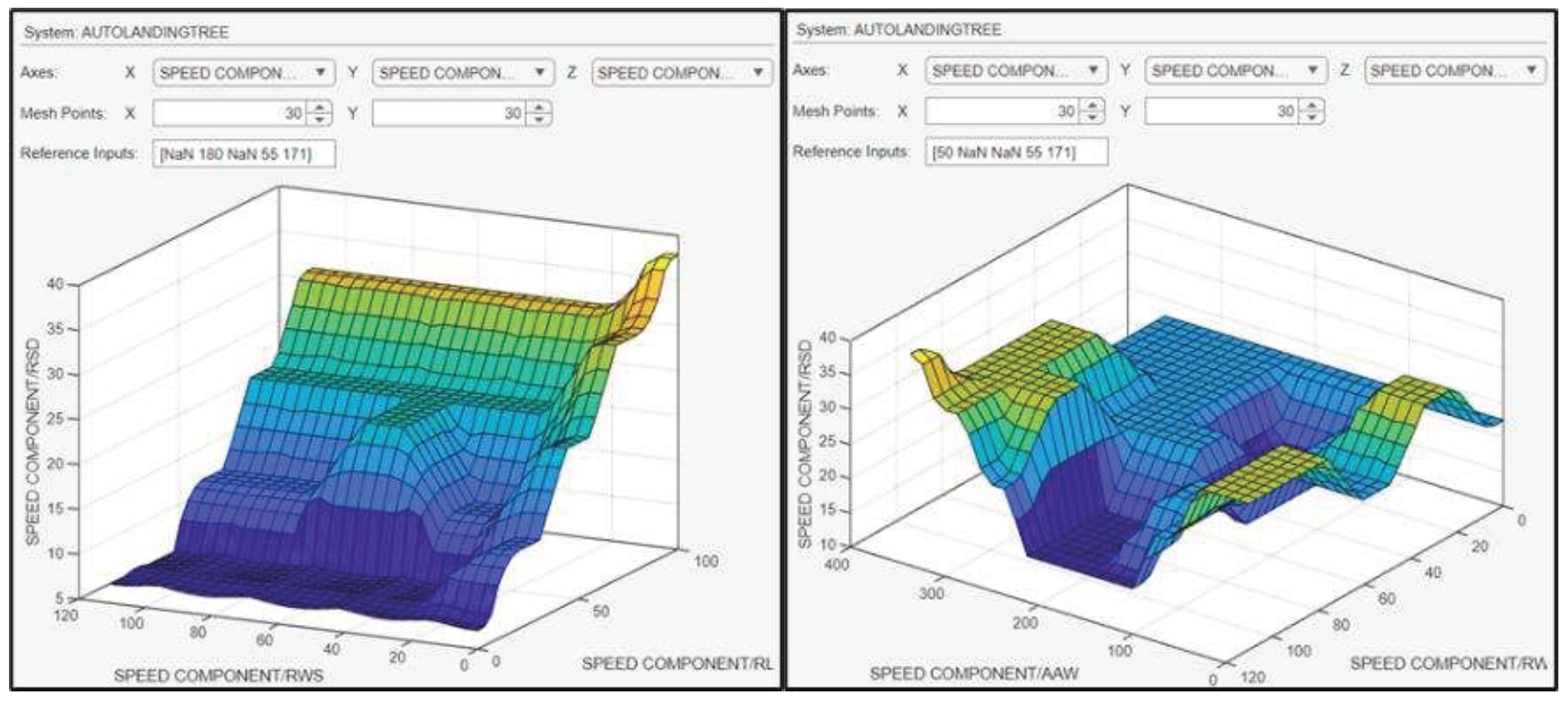
Figure 24.
Fuzzy rules activation for the Lateral Motion Component.
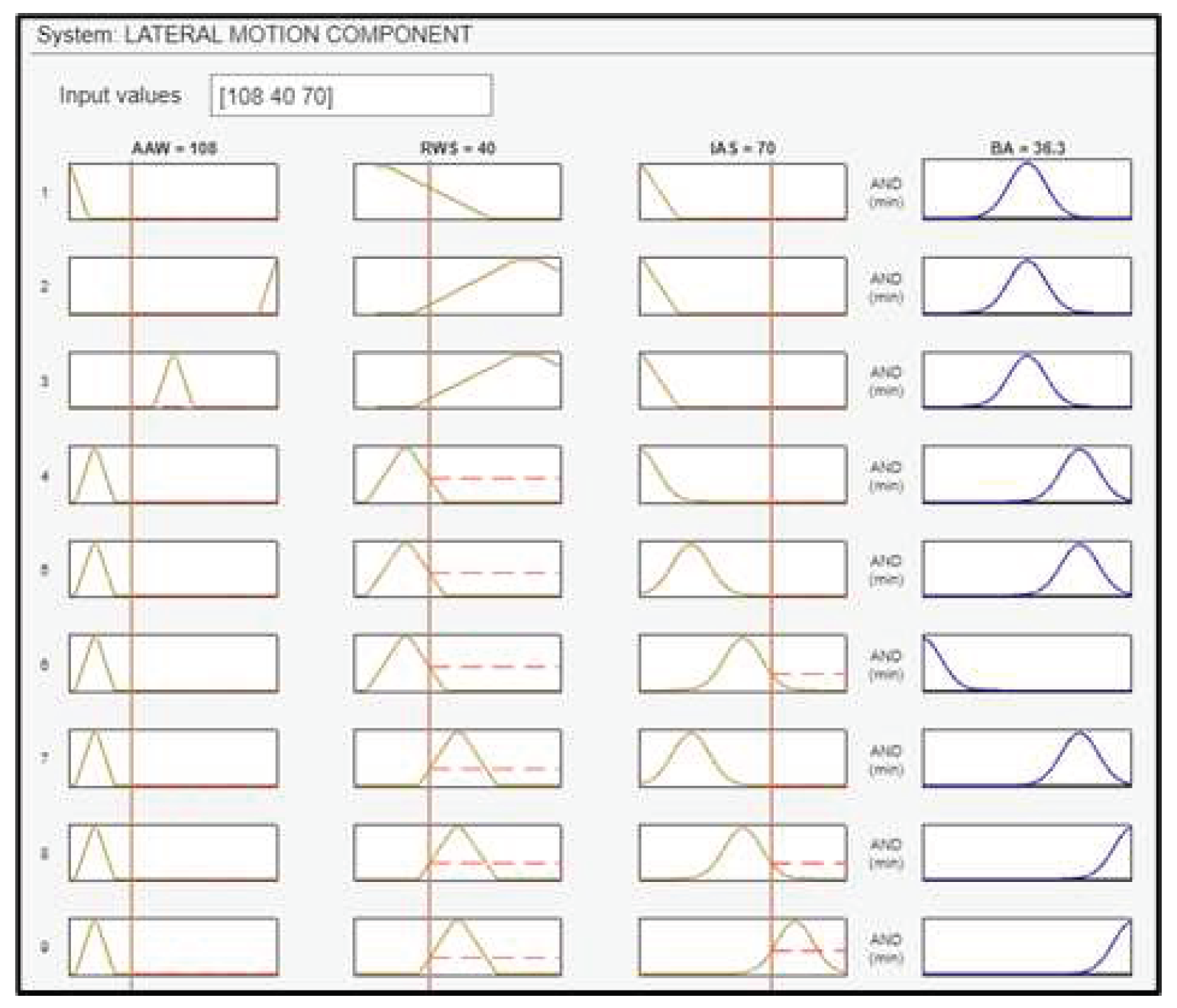
Figure 25.
Surface plots indicative of the relationship between the inputs and the BA.
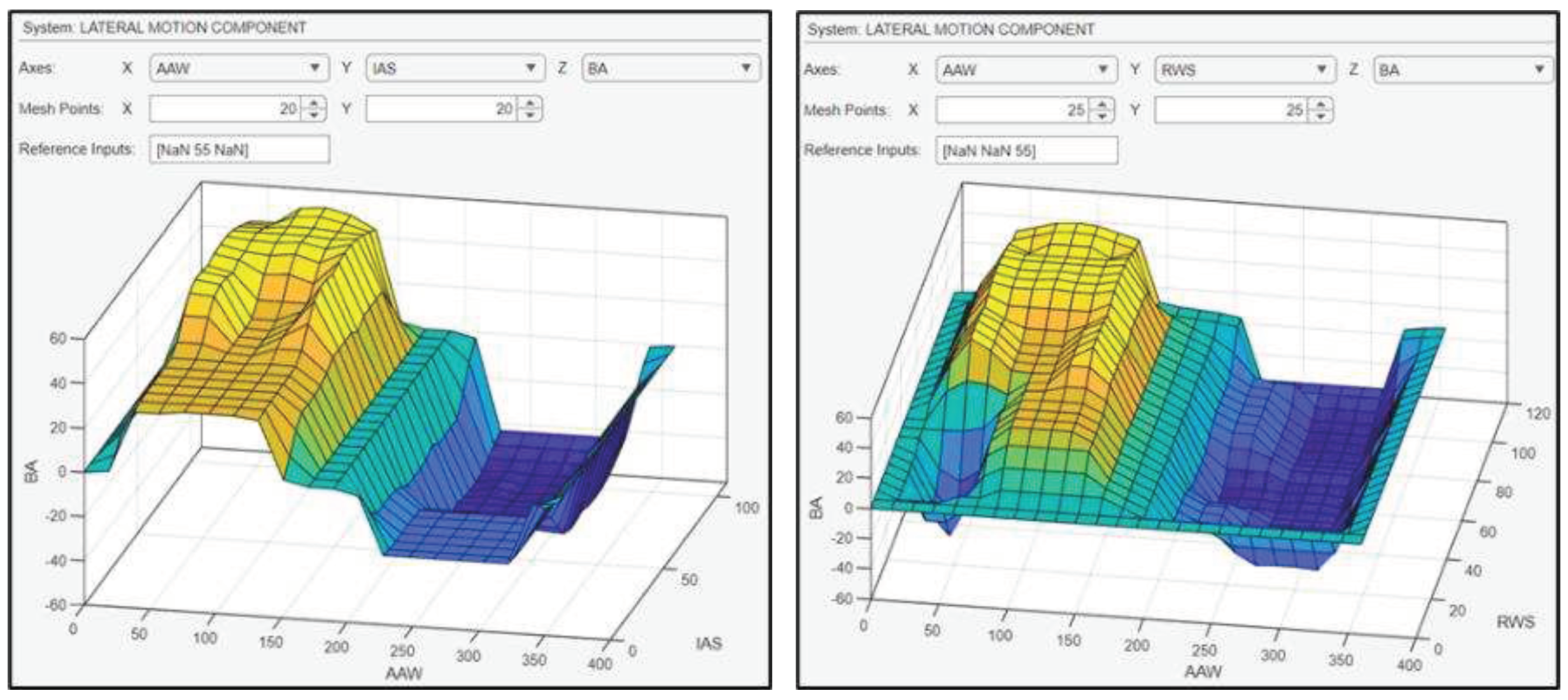
Figure 26.
Fuzzy rules activation for the Altitude Component.
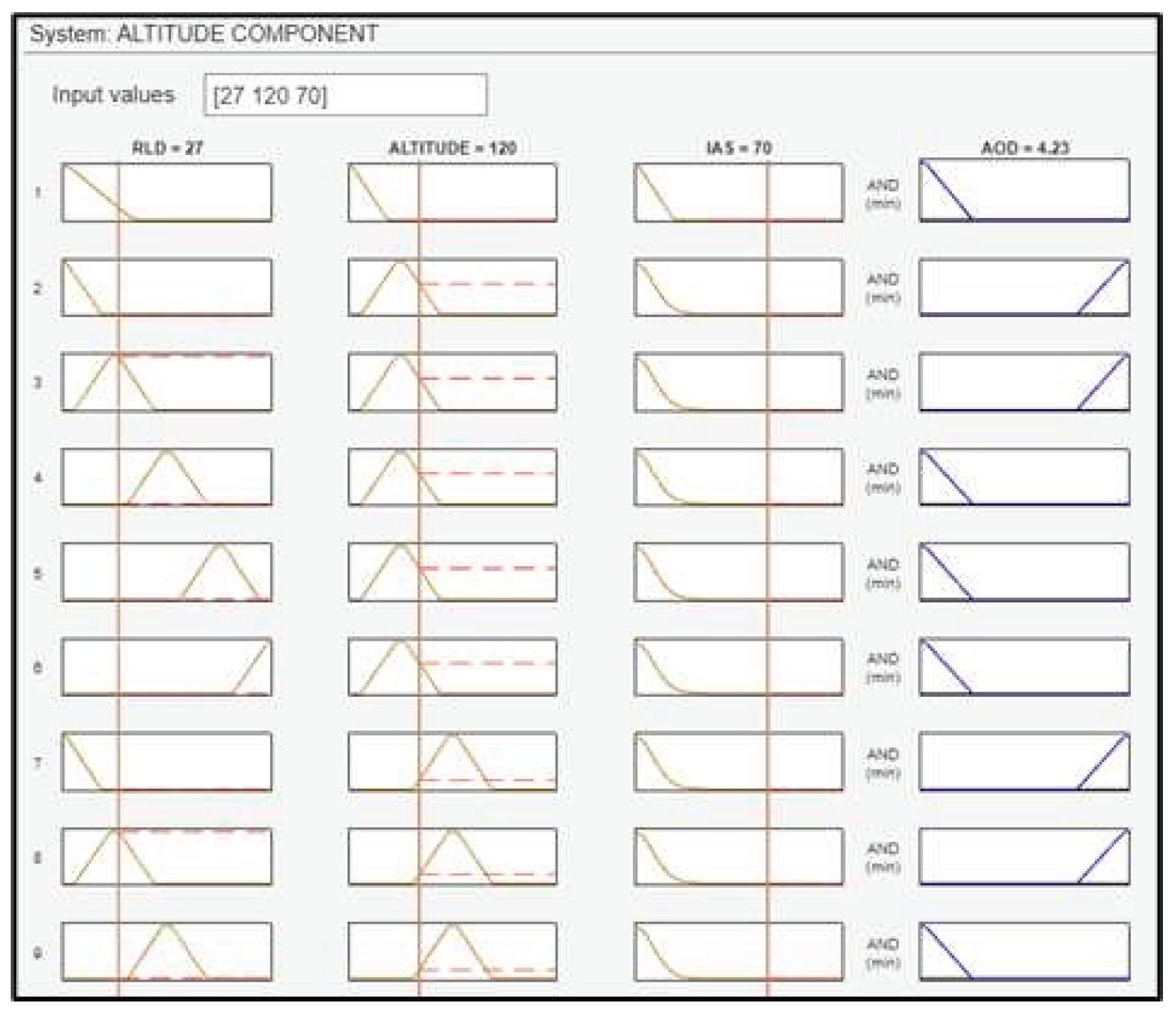
Figure 27.
Surface plots indicative of the relationship between the inputs and the AOD.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






