Prerpints.org logo
Preprint
Article

A generative approach to person reidentification

Altmetrics

Downloads

101

Views

64

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 December 2023

Posted:

25 December 2023

You are already at the latest version

Alerts
Abstract
Person Re-identification is the task of recognizing comparable subjects across a network of nonoverlapping cameras. This is typically achieved by extracting from the source image a vector of characteristic features of the specific person captured by the camera. Learning a good set of robust, invariant and discriminative features is a complex task, often leveraging contrastive learning. In this article, we explore a different approach, learning the representation of an individual as the conditioning information required to generate images of the specific person starting from random noise. In this way we decouple the identity of the individual from any other information relative to a specific instance (pose, background, etc.), allowing interesting transformations from one identity to another. As generative models, we use the recent diffusion models that have already proven their sensibility to conditioning in many different contexts. The results presented in this article serve as a proof-of-concept. While our current performance on common benchmarks is lower than state-of-the-art techniques, the approach is intriguing and rich of innovative insights, suggesting a wide range of potential improvements along various lines of investigation.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

The challenge of Person Re-identification lies in recognizing comparable subjects across a network of non-overlapping cameras, a common scenario in multi-camera surveillance systems [1]. In its typical formulation, the Person Re-ID task aims to identify a specific individual from an extensive collection of person images, known as the gallery, by utilizing a query image [2]. While this task falls under the framework of image retrieval problems, its unique objective of determining the identity of the person within a query image, typically expressed by a distinctive ID label, introduces intriguing peculiarities.
At its core, Person Re-ID involves acquiring knowledge about distinct characteristics of individuals, enabling the differentiation between images depicting the same person and those featuring different individuals. The difficulty of this task stems from substantial variations in viewpoint, pose, lighting, and image quality across diverse cameras in real-world scenarios. In such situations, individuals may appear in multiple cameras across various locations, thereby intensifying the challenge of feature acquisition [3].
The typical approach to the Re-ID task involves a two-phase process: a representation learning phase, where interesting and distinctive features of individuals are extracted, and a metric learning phase, where training objectives are designed using various loss functions or sampling strategies. This process aims to shape the embedding space in a way suitable for searching and retrieval.
Both phases are complex and very interesting. For feature extraction, modern approaches leverage deep learning techniques, exploiting Convolutional networks [4,5], Generative Adversarial Networks [6,7,8,9], Visual Transformers [10,11,12,13,14], and different kinds of attention mechanisms [15,16,17,18]. Features can be enhanced exploiting part-based methods, focusing on extracting features from specific regions of interest [10,19,20], pretraining [21,22] and multitasking [23] via a suitable set of pretext tasks.
Metric Learning is typically based on some form of contrastive learning [24], either using contrastive loss [25,26,27,28] or, more frequently, triplet loss [29,30,31,32,33,34,35,36]. Both approaches aim to encourage similar examples to be close in the feature space and dissimilar examples to be separated.
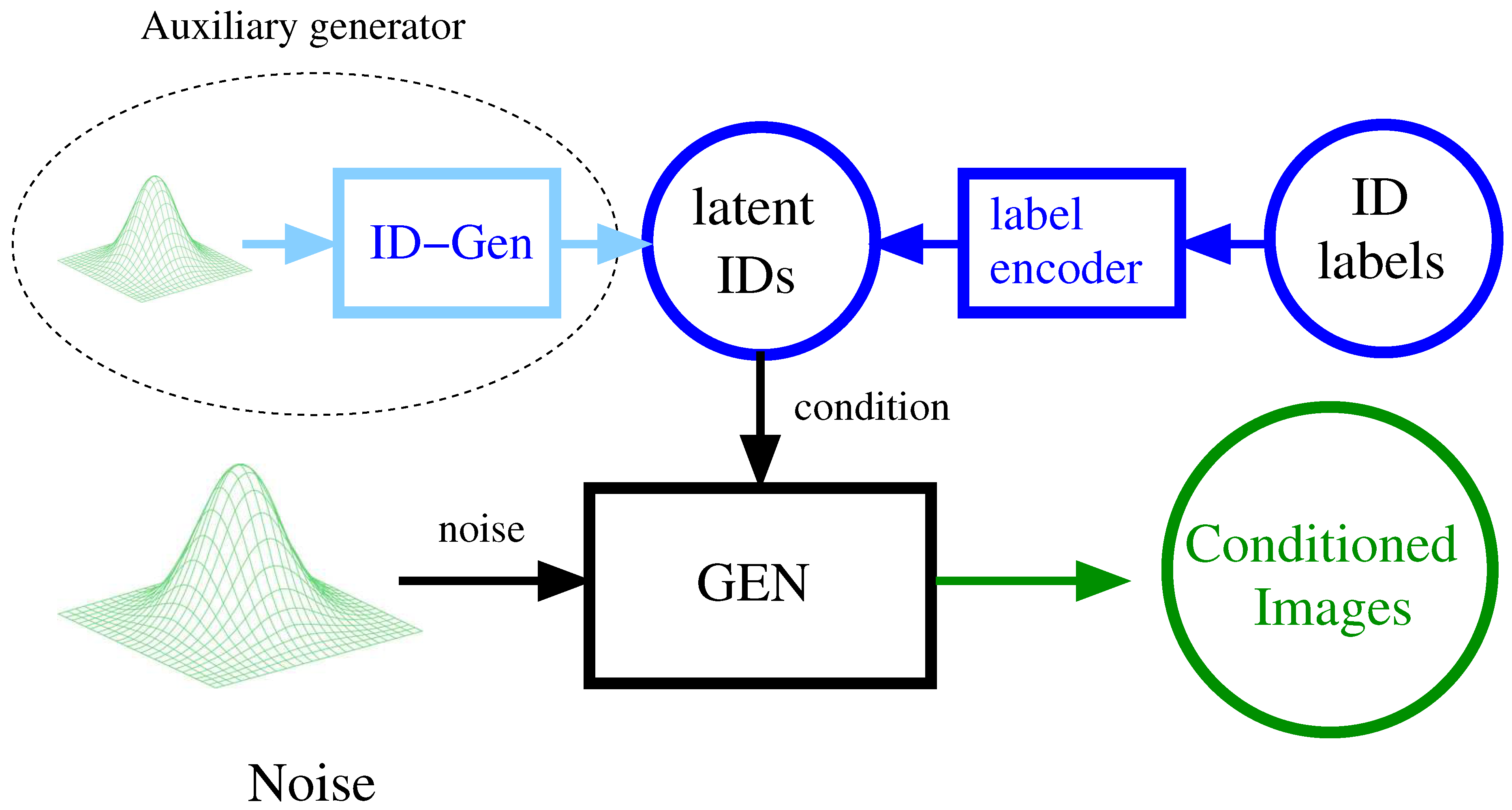
We adopt a different approach by associating a singular latent representation with each identity. This representation is learned as the conditioning information necessary to generate samples of the particular person from random Gaussian noise. By inverting the generator, we can derive, from an individual’s image, its most probable embedding, along with the "noise" containing all information unrelated to the specific identity, such as background, pose, etc. The former information is then utilized to retrieve samples from the gallery. The overall structure of the generative model is depicted in Figure 1.
Since we do not know the distribution of the latent representation of the identities in their latent space, this need to be learned, and we use an auxiliary small generative model for this purpose.
As generative model, we employ an instance of the recent diffusion models [37,38] due to their remarkable sensitivity to conditioning, coupled with unbiased sampling capabilities and excellent expressiveness. Examples of generation of images conditioned on the individual identity are given in Figure 2.
The generative quality is not perfect, and can be probably improved. In particular, for this prototyping work, we used a low resolution version of the dataset, with images of dimension 64 × 32 (instead of the usual 128 × 64 ). The embedding space for identities has 32 dimensions. In spite of being so small, conditioning seems to work well, as exemplified in Figure 2.
The results presented in this article are just a preliminary investigation in the direction described above. They are essentially intended as a proof-of-concept, testing the feasibility of the approach. The current performance, measured on standard benchmark like Market1051 is encouraging, even if below different state-of-the-art approaches.
The article is structured in the following way. In Section 2, we discuss Related Work. Section 3 is devoted to introduce the particular class of generative models that we use, namely Denoising Diffusion Models, and a specific subclass know as Implicit Models. The methodology is described in Section 4, where we address the inversion of the Generative network A detailed description of the Neural Networks is given in Section 5. Section 6 gives a short summary of our results. In Section 7, we explore the latent space of identities, considering the spatial organization of latent representations, and the meaning of the different factors of variation. Section 8 is devoted to ablation studies, and alternative solutions that have been tested and finally rejected. Concluding remarks and directions for future investigations are given in Section 9.

2. Related work

Generative techniques in the field of person re-identification have been mostly used for data augmentation and unsupervised domain adaptation (UDA). Almost all works make use of Generative Adversarial Networks, that only in recent years have been challenged by the emerging Diffusion models.
Domain adaptation methods employ style transformation techniques to adapt a source domain to a target domain. This transformation produces images that retain the content of the source domain while adopting the visual style of the target domain. Following this procedure, images resembling the target domain are generated and paired with label annotations from the source images. These newly created images are then used to fine-tune the network parameters. GAN-based image style transfer has immediately gained popularity as an effective method for transferring knowledge between the source and target domains in the context of unsupervised cross-domain person Re-ID [6,7,39,40]. In [9,41], CycleGANs are used to this purpose. In the former work, the target encoder was employed to acquire a discriminative mapping of target images to the transformed source feature space by deceiving a domain discriminator. The discriminator’s task is to differentiate between the features of the target domain and those of the transformed source domain. In refGAN6 the goal is to exchange source and target environment features to create cross-domain images that maintain identity-related features linked to the source (or target) background features. This process is then reversed to reconstruct the original input image, enabling a self-supervised cyclic generation.
In [8], GANs serve a dual purpose. They leverage CycleGAN and Siamese networks to transfer image styles between domains while preserving pedestrian identities, followed by iterative self-training using GANs to enhance global and local features in the target domain, contributing to robust feature learning in unlabeled data.
In [42], the PCDS-GAN model is introduced to synthesize source-labeled images with domain-specific backgrounds, addressing the domain gap and aiding in more efficient domain adaptation. This is achieved by disentangling pedestrian images into foreground, background, and style features. To transfer the background between different domains a U-Net based Hole-Filling-Module (HFM) is used, in charge of filling the pixels of the scene occupied by the source foreground. These are used to generate person images with diverse target domain backgrounds.

3. Denoising Diffusion Models

Denoising Diffusion Models (DDM) [37] represent a cutting-edge advancement in the realm of deep generative modeling, challenging the traditional dominance of Generative Adversarial Networks [43]. The technique has been successfully used in many recent and well known applications, such as [44,45,46]. The distinctive properties that contribute to its prominence include exceptional generation quality, high sensitivity and ease of conditioning, diverse and robust sampling capabilities, stable training dynamics, and commendable scalability.
A fundamental characteristic of this generative paradigm is its robust probabilistic foundation. However, a formal exploration of the underlying theory behind denoising diffusion models exceeds the scope of this article. We direct the reader to the extensive available literature for a deeper theoretical understanding [37,38]. In this section, we provide a more operationally focused description of the denoising model, easily comprehensible independent of its theoretical background.
In very rough terms, a diffusion model trains a single network to denoise images with a parametric amount of noise. This network is then used to generate new samples in an iterative way, starting from a purely “noisy” image, and progressively removing a decreasing amount of noise.
This process is traditionally called reverse diffusion since it is meant to “invert” the direct diffusion process consisting in iteratively adding noise (see Figure 3).
We focused on a specific subclass of Diffusion models, namely Implicit Diffusion models [38], which we extensively employed in numerous prior works. One crucial characteristic of these models is their fully deterministic reverse diffusion process, a vital aspect for those interested in embedding the output into its latent representation [48]. Another noteworthy property is their tendency to require a minimal number of iterations (usually around 10, as seen in [49,50]), in stark contrast to alternative techniques that often demand thousands of iterations. Lastly, we observed their remarkable conditioning capabilities in the context of precipitation forecasting [47], where our objective is to predict a probability distribution of a specific atmospheric parameter conditioned on recent weather conditions.

3.1. The denoising network

The only trainable component of the reverse diffusion process is a denoising network  ϵ θ ( x t , α t , c ) , which takes as input a noisy image x t , a signal rate α t , possibly a condition c, and tries to guess the noise present in the image. The model is trained is a completely supervised way. The main steps are the following:
  • pick a random image x 0 from the train set, coherent with the condition c;
  • select a random step t of the process; to each step t is associated a signal rate α t defined by a suitable noise scheduling (more in the sampling section);
  • sample a random gaussian noise ϵ ;
  • create a corrupted image as a weighted combination of x 0 and ϵ :
    x t = α t x 0 + 1 − α t ϵ
  • train the network to properly guess the amount of noise present in x t , by minimizing the distance between ϵ ( x t , α t , c ) and ϵ
The previous steps are summarized in the pseudocode of Algorithm 1, where q ( x 0 | c ) denotes the distribution of training data, relative to the condition c.
Algorithm 1 Training
1:
repeat
2:
     x 0 ∼ q ( x 0 | c )                 ▹ take a sample coherent with c
3:
     t ∼ Uniform(1,..,T)                     ▹ choose a timestep
4:
     ϵ ∼ N ( 0 ; I )                  ▹ create random gaussian noise
5:
     x t = α t x 0 + 1 − α t ϵ         ▹ corrupt the sample with signal rate α t
6:
    Take a gradient descent step on | | ϵ − ϵ θ ( x t , α t , c ) | | 2   ▹ backpropagate the loss
7:
until converged
The previous form of conditional training was formally investigated in [51]. The article suggest to mix conditional and unconditional generation, and some authors found that this was indeed beneficial for training, but we didn’t observe sensible improvements.
An alternative way to address conditioning is by means of an auxiliary classifier [43], similar, in spirit, to AC-GANs [52]). This technique involves training a classifier f ϕ ( c | x t ) on a noisy image x t to predict its class c. The gradient ∇ x log f ϕ ( c | x t ) can then be used to guide the diffusion sampling process to generate samples better reflecting the condition. We did not yet experiment with this technique, that is one of the possible directions for improvements.
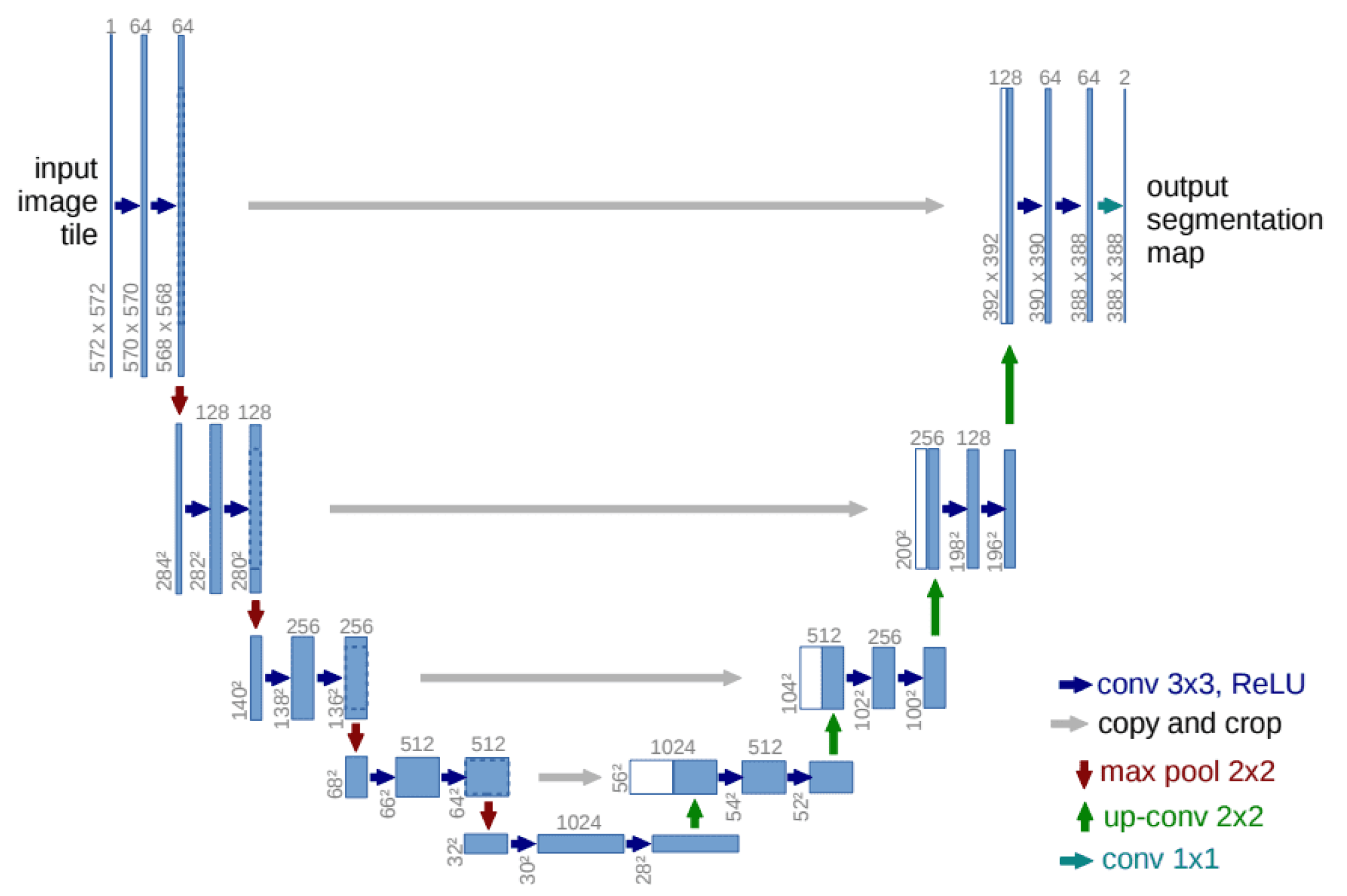
The usual architecture for the denoising network is that of a U-Net [53], structured with a downsampling sequence of layers followed by an upsampling sequence, with skip connections added between the layers of the same size. We added conditioning to all downsampling layers.
To improve the sensibility of the network to the signal rate α t , this value is frequently embedded using an ad-hoc sinusoidal transformation, splitting it into a set of frequencies, in a way similar to positional encodings in Transformers [54].

3.2. Sampling

Sampling is an iterative process. Starting from a purely noisy image x T , we progressively remove noise by calling the denoising network. Specifically, if the error predicted by the network at timestep t is ϵ = ϵ ( x t , α t , c ) , then the corresponding denoising prediction is
x 0 ^ = 1 α t ( x t − 1 − α t ϵ )
The noise ϵ is then re-injected into the network at signal rate α t − 1 , obtaining the next noisy image
x t − 1 = α t − 1 x ˜ 0 + 1 − α t − 1 ϵ
The pseudocode of the sampling process is given in Algorithm 2
Algorithm 2 Sampling
1:
x T ∼ N ( 0 , I )
2:
for  t = T , . . . , 1  do
3:
     ϵ = ϵ θ ( x t , α t , c )                        ▹ predict noise
4:
     x ˜ 0 = 1 α t ( x t − 1 − α t ϵ )                ▹ compute denoised result
5:
     x t − 1 = α t − 1 x ˜ 0 + 1 − α t − 1 ϵ             ▹ re-inject noise at rate α t − 1
6:
end for
A major aspect of the reverse diffusion process involves the scheduling of the diffusion noise { α t } t = 1 T . In [37], the authors suggested employing linear or quadratic schedules. However, this selection results in a too rapid decline in the initial time steps, leading to issues during generation. The literature proposes alternative scheduling functions with a more gradual decrease, such as the "cosine" or "continuous cosine" schedule [55,56]. Opting for a milder scheduler not only addresses problems during generation but also enables a reduction in the number of iterations. For our specific objectives, we implemented a generator with 10 diffusion steps.

4. Methodology

As already described in the introduction, the main idea is to associate each identity with a unique latent representation, which is learned as the conditioning information required for generating samples of that specific individual from random Gaussian noise. The general architecture of the generative model is illustrated in Figure 1. The generative model is an instance of a diffusion model, discussed in the previous section.
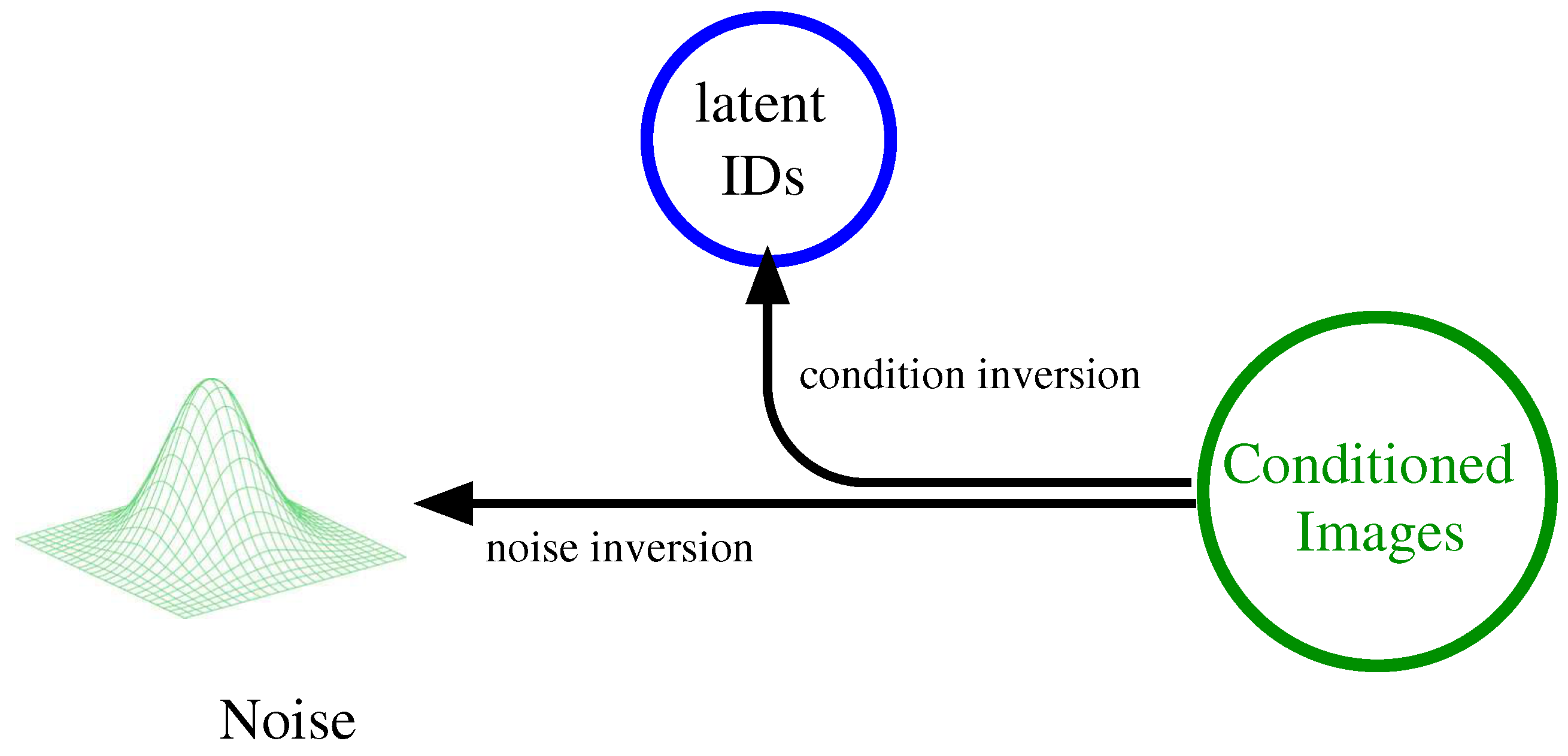
The next step consist in reversing the generative model, as illustrated in Figure 4.
This allows us to obtain, starting from the image of an individual, the latent representation of his identity, and a noise encompassing all non-identity-related details like background and pose. The latent identity is the relevant information for person re-identification, since by comparing it with the latent representations of samples from the gallery we can retrieve the most similar identities.
We already explored the possibility to invert diffusion models by means of suitably trained neural networks in many of our previous works. The overall idea was introduced in [48]; the technique was used in [49] for the "reification" of artistic portraits, by embedding a portrait into a latent space of human faces, and reconstructing the closest real approximation. In [50], the inverse of the diffusion was used to define a trajectory in the latent space inducing a smooth rotation effect on human faces.
In the case of this work, after a few attempts, we opted for training two distinct models, one going from images to latent identities, and another one producing the noise. After all, the two models extract orthogonal features from the source image, so there is no major reason to share layers between them.
The are a few different possibilities for training the inversion model. The general idea is to start from a random noise ϵ , a "random" latent identity i d , use the generator to produce an image x = G e n ( ϵ , i d ) , and then train the networks to respectively reconstruct i d and ϵ starting from x. The main difficulty of the previous approach is that we do not know the distribution of identities in the latent space, that could be arbitrary, and so we have no way to pick a random identity. We could possibly start from random choices of the train set identities, considering their latent representations, but this leads to overfitting and does not generalize well.
Our solution is to use an auxiliary id-generator, learning the distribution of identities in the latent space, and allowing us to sample in this space.
The resulting system is extremely robust, since in principle is able to derive the internal representation of an arbitrary individual, in an arbitrary context, with the only proviso that individuals and contexts must be similar to those provided in the training set.

5. Neural Networks architectures

In Section 3, it was elucidated that the sole trainable element within a diffusion model is the denoising network ϵ θ ( x t , α t ) . This network takes as input a noise rate α t , an image x t corrupted with a corresponding level of noise, and endeavors to predict the noise present in the image. This problem aligns with the conventional image-to-image paradigm, and the denoising network is typically implemented using the well-known U-net architecture [53] depicted in Figure 5.
The U-net has an encoder-decoder structure with skip connections linking corresponding layers in the encoder and decoder. This design enables the network to assimilate both global and local structures within the image, rendering it well-suited for the requirements of the diffusion model. The U-Net is usually parameterized by specifying the number of downsampling blocks, and the number of channels for each block; the upsampling structure is symmetric. For our implementation we considered for downsampling blocks, with respective dimensions [48, 96, 192, 384].
We recall that we work with images at resolution 64 × 32 ; for 128 × 64 images an additional g layer is probably required.
The input relative to the noise variance α t is typically embedded using sinusoidal position embeddings. Then, this information is vectorized and concatenated to each residual block of the network, along with the conditioning information.
Also the inversion networks are esentially inspired by the U-Net. The Inv-Id network just uses the encoder part of the U-Net, completing the processing through a small sequence of dense layers.
Results of the inversion process are shown in Figure 6. The reconstruction is good, even if not perfect. Some details are lost, that could be a problem for Person Re-ID. In case you are curios, we also show the noise extracted from the picture, that should in principle contain all the information not pertaining to the specific individual (middle row). The noise (that should have a Gaussian shape) has been clipped in the interval [-2.5,2.5] and renormalized to [0,1] before plotting.

6. Evaluation

The current performance of our technique is somewhat below the state-of-the-art. On a standard benchmark like Market1501, we achieve a mean average precision (MAP) of 73%, whereas state-of-the-art techniques attain a MAP of 96% in the supervised setting and around 90% in the unsupervised setting. Nevertheless, we believe that our approach is interesting, instructive, and could foster significant developments. The next section will present intriguing investigations into the organization of the latent space of identities.
Visually, results are good, and the errors made by the model are quite understandable: at the low resolution we are using, differentiating between some identities is really problematic. Some examples are given in Figure 7.

7. Latent space exploration

In our apporach, latent representations are synthesized as the features of each individual able to shape the generation of distinctive images of the person under different noises. As typical of generative processes, this should naturally produce a highly informed and well structured latent space, where similar persons should result in similar encodings.
Some examples are provided Figure 8: in the first column we have some identities, and in the corresponding row we show the 5 different individuals whose latent representation are closer, in terms of euclidean distance, to the representation of the given id. Images are taken from the traditional Market1501 dataset [57], that we used for most of our experiments. Let us also observe the strong similarity between different identities, making the reidentification problem far from trivial.
In Figure 9 we show the two closest identities, at a minimum distance of .14, and the two more apart from each other, at a maximum distance of .99. The average euclidean distance is around .6.
Another interesting operation consists in deciphering how the the different explanatory factors of variation behind the data are captured in the latent representation, similarly as we try to understand the meaning of nucleotide sequences in a genome. The problem is that these factors can be more or less entangled together, so that a visible effect may depend on a combination of latent variables, more than a single one.
Our studies in this direction are very preliminary. As an example, in Figure 10 we show the effect on generation of modifying a single variable in the latent space of identities.
Let us observe as the modification of a single variable may correspond to a sensibly different identity.
The investigation of interesting semantic trajectories inside the latent space can also be used to synthesize new and distinctive identities to be used, e.g. for data augmentation purposes.

8. Ablation and alternatives

Many different versions of the previous architecture have been tested.
Before attempting to learn the distribution of the latent variables through an auxiliary generator, we tried to regularize its shape in various ways. This included simple methods such as using BatchNormalization layers, or injecting a light amount of noise. We eventually explored a full variational model, compelling the latent space to adopt a Gaussian shape through Kullback-Leibler regularization. However, a drawback of the latter approach is that the signal influencing the definition of latent representations is relatively weak. This makes it challenging to balance with the KL-component, as highlighted in [58]. The KL-component could easily prevail, leading to the well-known variable collapse phenomenon [59].
The use of an auxiliary generator can be essentially understood as a two-stage generative model [58,60]. For the implementation of the auxiliary generator, our first experiments have been with a variational autoencoder. However, this attempt resulted in an elevated reconstruction loss, associated with a corresponding loss of variance in generated data [61]. In this case too, a diffusion model seems to learn the distribution in a much better way.
Along a different line of research, we tried to increase the distance between different latent representation by means of a "repulsive" loss, proportional to the inverse of their distance in the space (a sort of magnetic repulsion). This was coupled with a weak attractive loss forcing points to stay close to the origin and centering the latent space around it. While we retained the former, the repulsive loss does not seem to improve performance, and could also be detrimental. Our explanation is that the loss mainly affects latent variables with low significance, attempting to separate them for different subjects. The separation is artificial and semantically unpredictable, therefore not reconstructible from the input images.
We also made several experiments on the Embedding module for identities. In the current implementation, it is a single Keras Embedding layer, that is a layer first expanding labels to their categorical encoding and then mapping them to a latent space of the desired dimension trough a single dense layer. A priori, this should not be restrictive since, starting from a categorical description, any embdedding can be potentially learned. However, what is not so clear is the flexibility of the model to change and improve encodings during training, along with the acquisition of additional knowledge. For this reason, we also experimented with more complex embedding modules, that however did not seem to bring any benefit.

9. Conclusions

The work presented in this article is first of all a divertissment: we were interested to test, in a complex scenario, the conditional capabilities of generative diffusion models. Specifically, we learn the latent representation of different individuals as the common information required to condition the generation of images of the given person starting from different noise. In this way, we achieve the separation of individual’s identity from other specific instance-related information (such as pose, background, etc.) expressed as part of the noise.
The work can be improved along many different directions. Both the generator and the network used for its inversion can be improved. A natural reserach direction consist in repeating the work with images at the original 128x68 spatial resolution, possibly enlarging the dimension of the latent space. A detailed investigation of the kind of errors made in the process of re-identification may also lead to interesting discoveries and potential improvements. Leveraging the generator for smart and focused data-augmentation is another intriguing possibility.
A weak point of the approach is its supervised nature: in order to train the conditional generator we need to have many instances of the same identity in different poses and contexts. Understanding if the methodology can be extended in an unsupervised scenario is a complex and interesting challenge. It is not excluded that the typical approaches used for unsupevised Person ReID, mosly based on clustering, centroids, and pseudo-labels [62,63,64] might be adapted to our approach.

Funding

This research was partially funded by the Future AI Research (FAIR) project of the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.3 funded from the European Union - NextGenerationEU.

Data Availability Statement

The application described in this paper is open source. The software can be downloaded from the following github repository: https://github.com/asperti/GenerativePersonReID.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bukhari, M.; Yasmin, S.; Naz, S.; Maqsood, M.; Rew, J.; Rho, S. Language and vision based person re-identification for surveillance systems using deep learning with LIP layers. Image and Vision Computing 2023, 132. [Google Scholar] [CrossRef]
  2. Kim, K.; Kim, M.J.; Kim, H.; Park, S.; Paik, J. Person Re-identification Method Using Text Description Through CLIP. 2023 International Conference on Electronics, Information, and Communication (ICEIC), 2023, pp. 1–4. [CrossRef]
  3. Ming, Z.; Zhu, M.; Wang, X.; Zhu, J.; Cheng, J.; Gao, C.; Yang, Y.; Wei, X. Deep learning-based person re-identification methods: A survey and outlook of recent works. Image and Vision Computing 2022, 119, 104394. [Google Scholar] [CrossRef]
  4. Chen, J.; Wang, Y.; Tang, Y.Y. Person Re-identification by Exploiting Spatio-Temporal Cues and Multi-view Metric Learning. IEEE Signal Processing Letters 2016, 23, 998–1002. [Google Scholar] [CrossRef]
  5. Chung, D.; Tahboub, K.; Delp, E.J. A Two Stream Siamese Convolutional Neural Network for Person Re-identification. 2017 IEEE International Conference on Computer Vision (ICCV), 2017, pp. 1992–2000. [CrossRef]
  6. Wei, L.; Zhang, S.; Gao, W.; Tian, Q. Person Transfer GAN to Bridge Domain Gap for Person Re-Identification 2018. pp. 79–88. [CrossRef]
  7. Liu, X.; Tan, H.; Tong, X.; Cao, J.; Zhou, J. Feature preserving GAN and multi-scale feature enhancement for domain adaption person Re-identification. Neurocomputing 2019, 364, 108–118. [Google Scholar] [CrossRef]
  8. Li, Y.; Chen, S.; Qi, G.; Zhu, Z.; Haner, M.; Cai, R. A GAN-Based Self-Training Framework for Unsupervised Domain Adaptive Person Re-Identification. J. Imaging 2021, 7, 62. [Google Scholar] [CrossRef] [PubMed]
  9. Tang, G.; Gao, X.; Chen, Z.; Zhong, H. Unsupervised adversarial domain adaptation with similarity diffusion for person re-identification. Neurocomputing 2021, 442, 337–347. [Google Scholar] [CrossRef]
  10. Li, Y.; He, J.; Zhang, T.; Liu, X.; Zhang, Y.; Wu, F. Diverse part discovery: Occluded person re-identification with part-aware transformer. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 2898–2907.
  11. Cao, G.; Jo, K.H. Unsupervised Person Re-Identification with Transformer-based Network for Intelligent Surveillance Systems. 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE). IEEE, 2021, pp. 1–6.
  12. Chen, Y.; Xia, S.; Zhao, J.; Zhou, Y.; Niu, Q.; Yao, R.; Zhu, D.; Liu, D. ResT-ReID: Transformer block-based residual learning for person re-identification. Pattern Recognition Letters 2022, 157, 90–96. [Google Scholar] [CrossRef]
  13. Chen, X.; Xie, S.; He, K. An empirical study of training self-supervised vision transformers. Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 9640–9649.
  14. Perwaiz, N.; Shahzad, M.; Fraz, M. Ubiquitous vision of transformers for person re-identification. Machine Vision and Applications 2023, 34, 27. [Google Scholar] [CrossRef]
  15. Zhou, S.; Wang, F.; Huang, Z.; Wang, J. Discriminative Feature Learning With Consistent Attention Regularization for Person Re-Identification. 2019 IEEE/CVF International Conference on Computer Vision (ICCV), 2019, pp. 8039–8048. [CrossRef]
  16. Huang, Y.; Lian, S.; Hu, H.; Chen, D.; Su, T. Multiscale Omnibearing Attention Networks for Person Re-Identification. IEEE Transactions on Circuits and Systems for Video Technology 2021, 31, 1790–1803. [Google Scholar] [CrossRef]
  17. Huang, Y.; Peng, P.; Jin, Y.; Li, Y.; Xing, J. Domain Adaptive Attention Learning for Unsupervised Person Re-Identification. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; pp. pp. 11069–11076. [Google Scholar] [CrossRef]
  18. Saber, S.; Meshoul, S.; Amin, K.; Pławiak, P.; Hammad, M. A Multi-Attention Approach for Person Re-Identification Using Deep Learning. Sensors 2023 2023, 23. [Google Scholar] [CrossRef]
  19. Somers, V.; De Vleeschouwer, C.; Alahi, A. Body Part-Based Representation Learning for Occluded Person Re-Identification. Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, 2023, pp. 1613–1623.
  20. Wu, J.J.; Chang, K.H.; Lin, I.C. Generalizable person re-identification with part-based multi-scale network. Multimedia Tools and Applications, 2023; 1–28. [Google Scholar]
  21. Fu, D.; Chen, D.; Bao, J.; Yang, H.; Yuan, L.; Zhang, L.; Li, H.; Chen, D. Unsupervised Pre-Training for Person Re-Identification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2021, virtual, 19–25 June 2021; pp. 14750–14759. [Google Scholar] [CrossRef]
  22. Yang, Z.; Jin, X.; Zheng, K.; Zhao, F. Unleashing Potential of Unsupervised Pre-Training with Intra-Identity Regularization for Person Re-Identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2022, New Orleans, LA, USA, 18–24 June 2022; pp. 14278–14287. [Google Scholar] [CrossRef]
  23. Chen, W.; Xu, X.; Jia, J.; Luo, H.; Wang, Y.; Wang, F.; Jin, R.; Sun, X. Beyond Appearance: A Semantic Controllable Self-Supervised Learning Framework for Human-Centric Visual Tasks. 2023, 15050–15061. [Google Scholar] [CrossRef]
  24. Le-Khac, P.H.; Healy, G.; Smeaton, A.F. Contrastive Representation Learning: A Framework and Review. IEEE Access 2020, 8, 193907–193934. [Google Scholar] [CrossRef]
  25. Hadsell, R.; Chopra, S.; LeCun, Y. Dimensionality Reduction by Learning an Invariant Mapping. 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), 2006, Vol. 2, pp. 1735–1742. [CrossRef]
  26. Wang, M.; Lai, B.; Huang, J.; Gong, X.; Hua, X.S. Graph-Induced Contrastive Learning for Intra-Camera Supervised Person Re-Identification. IEEE Access 2021, 9, 20850–20860. [Google Scholar] [CrossRef]
  27. Hu, S.; Zhang, X.; Xie, X. Decoupled Contrastive Learning for Intra-Camera Supervised Person Re-identification. 2022 26th International Conference on Pattern Recognition (ICPR), 2022, pp. 2628–2665. [CrossRef]
  28. Shi, X.; Liu, H.; Shi, W.; Zhou, Z.; Li, Y. Boosting Person Re-Identification with Viewpoint Contrastive Learning and Adversarial Training. ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2023, pp. 1–5. [CrossRef]
  29. Wang, J.; Song, Y.; Leung, T.; Rosenberg, C.; Wang, J.; Philbin, J.; Chen, B.; Wu, Y. Learning Fine-Grained Image Similarity with Deep Ranking. 2014 IEEE Conference on Computer Vision and Pattern Recognition, 2014, pp. 1386–1393. [CrossRef]
  30. Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 815–823.
  31. Hermans, A.; Beyer, L.; Leibe, B. In defense of the triplet loss for person re-identification. arXiv 2017, arXiv:1703.07737. [Google Scholar]
  32. Wang, Y.; Wang, L.; You, Y.; Zou, X.; Chen, V.; Li, S.; Huang, G.; Hariharan, B.; Weinberger, K.Q. Resource Aware Person Re-identification Across Multiple Resolutions. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 8042–8051. [CrossRef]
  33. Chang, X.; Hospedales, T.M.; Xiang, T. Multi-level Factorisation Net for Person Re-identification. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 2109–2118. [CrossRef]
  34. Zhang, S.; Zhang, Q.; Wei, X.; Zhang, Y.; Xia, Y. Person Re-Identification With Triplet Focal Loss. IEEE Access 2018, 6, 78092–78099. [Google Scholar] [CrossRef]
  35. Si, T.; Zhang, Z.; Liu, S. Compact Triplet Loss for person re-identification in camera sensor networks. Ad Hoc Networks 2019, 95, 101984. [Google Scholar] [CrossRef]
  36. Hu, S.; Wang, K.; Cheng, J.; Tan, H.; Pang, J. Triplet Ratio Loss for Robust Person Re-identification. Pattern Recognition and Computer Vision; Springer International Publishing: Cham, 2022; pp. 42–54. [Google Scholar] [CrossRef]
  37. Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual; Larochelle, H.; Ranzato, M.; Hadsell, R.; Balcan, M.; Lin, H., Eds., 2020.
  38. Song, J.; Meng, C.; Ermon, S. Denoising Diffusion Implicit Models. 9th International Conference on Learning Representations, ICLR 2021, Virtual Event, Austria, May 3-7, 2021. OpenReview.net, 2021.
  39. Deng, W.; Zheng, L.; Ye, Q.; Kang, G.; Yang, Y.; Jiao, J. Image-Image Domain Adaptation with Preserved Self-Similarity and Domain-Dissimilarity for Person Re-identification 2018. [CrossRef]
  40. Yanbei, C.; Zhu, X.; Gong, S. Instance-Guided Context Rendering for Cross-Domain Person Re-Identification 2019.
  41. Verma, A.; Subramanyam, A.; Wang, Z.; Satoh, S.; Shah, R.R. Unsupervised Domain Adaptation for Person Re-Identification Via Individual-Preserving and Environmental-Switching Cyclic Generation 2021. [CrossRef]
  42. Zhu, Y.; Deng, C.; Cao, H.; Wang, H. Object and background disentanglement for unsupervised cross-domain person re-identification 2020. [CrossRef]
  43. Dhariwal, P.; Nichol, A.Q. Diffusion Models Beat GANs on Image Synthesis. Advances in Neural Information Processing Systems 34: Annual Conference on Neural Information Processing Systems 2021, NeurIPS 2021, December 6-14, 2021, virtual; Ranzato, M.; Beygelzimer, A.; Dauphin, Y.N.; Liang, P.; Vaughan, J.W., Eds., 2021. 8780–8794.
  44. Ramesh, A.; Dhariwal, P.; Nichol, A.; Chu, C.; Chen, M. Hierarchical Text-Conditional Image Generation with CLIP Latents. ArXiv, 2022; abs/2204.06125. [Google Scholar]
  45. Saharia, C.; Chan, W.; Saxena, S.; Li, L.; Whang, J.; Denton, E.; Ghasemipour, S.K.S.; Ayan, B.K.; Mahdavi, S.S.; Lopes, R.G.; Salimans, T.; Ho, J.; Fleet, D.J.; Norouzi, M. Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding. CoRR 2022, abs/2205.11487. [Google Scholar] [CrossRef]
  46. Ho, J.; Salimans, T.; Gritsenko, A.; Chan, W.; Norouzi, M.; Fleet, D.J. Video diffusion models. arXiv 2022, arXiv:2204.03458. [Google Scholar]
  47. Asperti, A.; Merizzi, F.; Paparella, A.; Pedrazzi, G.; Angelinelli, M.; Colamonaco, S. Precipitation nowcasting with generative diffusion models. arXiv 2023, arXiv:2308.06733. [Google Scholar]
  48. Asperti, A.; Evangelista, D.; Marro, S.; Merizzi, F. Image Embedding for Denoising Generative Models. arXiv 2022, arXiv:2301.07485. [Google Scholar]
  49. Asperti, A.; Colasuonno, G.; Guerra, A. Portrait Reification with Generative Diffusion Models. Applied Sciences 2023, 13. [Google Scholar] [CrossRef]
  50. Asperti, A.; Colasuonno, G.; Guerra, A. Head Rotation in Denoising Diffusion Models. arXiv 2023, arXiv:2308.06057. [Google Scholar]
  51. Ho, J.; Salimans, T. Classifier-Free Diffusion Guidance. CoRR, 2022; abs/2207.12598. [Google Scholar] [CrossRef]
  52. Odena, A.; Olah, C.; Shlens, J. Conditional Image Synthesis with Auxiliary Classifier GANs. Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, NSW, Australia, 6-11 August Proceedings of Machine Learning Research. Vol. 70, 2642–2651.
  53. Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention. Springer, 2015, pp. 234–241.
  54. Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, 2017. 5998–6008.
  55. Kingma, D.; Salimans, T.; Poole, B.; Ho, J. Variational diffusion models. Advances in neural information processing systems 2021, 34, 21696–21707. [Google Scholar]
  56. Nichol, A.Q.; Dhariwal, P. Improved denoising diffusion probabilistic models. International Conference on Machine Learning. PMLR, 2021, pp. 8162–8171.
  57. Chen, M.; Wang, Z.; Zheng, F. Benchmarks for Corruption Invariant Person Re-identification, 2021. [CrossRef]
  58. Asperti, A.; Trentin, M. Balancing Reconstruction Error and Kullback-Leibler Divergence in Variational Autoencoders. IEEE Access 2020, 8, 199440–199448. [Google Scholar] [CrossRef]
  59. Asperti, A.; Evangelista, D.; Piccolomini, E.L. A Survey on Variational Autoencoders from a Green AI Perspective. SN Comput. Sci. 2021, 2, 301. [Google Scholar] [CrossRef]
  60. Dai, B.; Wipf, D.P. Diagnosing and enhancing VAE models. Seventh International Conference on Learning Representations (ICLR 2019), May 6-9, New Orleans, 2019.
  61. Asperti, A. Variance Loss in Variational Autoencoders. Machine Learning, Optimization, and Data Science - 6th International Conference, LOD 2020, Siena, Italy, September 10-13, 2020, July 19-23, 2020, Proceedings. Springer, 2020, Vol. To appear, Lecture Notes in Computer Science.
  62. Fan, H.; Zheng, L.; Yang, Y. Unsupervised Person Re-identification: Clustering and Fine-tuning 2017.
  63. Wang, S.; Zhang, L.; Chen, W.; Wang, F.; Li, H. Refining pseudo labels for unsupervised Domain Adaptive Re-Identification 2021.
  64. Yan, T.; Zhu, K.; guo, H.; Zhu, G.; Tang, M.; Wang, J. Plug-and-Play Pseudo Label Correction Network for Unsupervised Person Re-identification 2022. [CrossRef]
Preprints 94216 g001
Figure 1. Conditional model. We train a diffusion generative model conditioned on people’s identity. The embedding of Identity labels into their latent representation is learned along with the generator. Since the distribution of the embedded identities is not known, we use a small additional model to learn their distribution. Reverting the conditional generator, we obtain a model able to split the image into the identity of the person, and all contextual information (pose, background, an so on) mapped back to the noise.
Figure 1. Conditional model. We train a diffusion generative model conditioned on people’s identity. The embedding of Identity labels into their latent representation is learned along with the generator. Since the distribution of the embedded identities is not known, we use a small additional model to learn their distribution. Reverting the conditional generator, we obtain a model able to split the image into the identity of the person, and all contextual information (pose, background, an so on) mapped back to the noise.
Preprints 94216 g001
Preprints 94216 g002
Figure 2. Conditional generation. On the left, three sample identities taken from the Market1501 dataset. We sample 5 random noises, and for each of them we generate an image conditioned by the given identity; the noise in each column is always the same.
Figure 2. Conditional generation. On the left, three sample identities taken from the Market1501 dataset. We sample 5 random noises, and for each of them we generate an image conditioned by the given identity; the noise in each column is always the same.
Preprints 94216 g002
Preprints 94216 g003
Figure 3. Direct and Reverse diffusion. Picture from [47]
Figure 3. Direct and Reverse diffusion. Picture from [47]
Preprints 94216 g003
Preprints 94216 g004
Figure 4. Caption
Figure 4. Caption
Preprints 94216 g004
Preprints 94216 g005
Figure 5. The U-net architecture. Source [53].
Figure 5. The U-net architecture. Source [53].
Preprints 94216 g005
Preprints 94216 g006
Figure 6. Reconstrution examples. . In the fist row we have original gallery images, in the middle row the noise synthesized by inversion, and in the third row the reconstructed images.
Figure 6. Reconstrution examples. . In the fist row we have original gallery images, in the middle row the noise synthesized by inversion, and in the third row the reconstructed images.
Preprints 94216 g006
Preprints 94216 g007
Figure 7. Person re-identification. In each row, the first image is the query, and the successive images are the 5 best matchings in the gallery.
Figure 7. Person re-identification. In each row, the first image is the query, and the successive images are the 5 best matchings in the gallery.
Preprints 94216 g007
Preprints 94216 g008
Figure 8. Inherent clustering of the latent space. For every id in the initial column, we display five distinct individuals whose latent representations are closer, in terms of Euclidean distance, to the representation of the specified id.
Figure 8. Inherent clustering of the latent space. For every id in the initial column, we display five distinct individuals whose latent representations are closer, in terms of Euclidean distance, to the representation of the specified id.
Preprints 94216 g008
Preprints 94216 g009
Figure 9. On the left we have the two closest identities in the latent space of Market1501; on the right, the two more distant ones.
Figure 9. On the left we have the two closest identities in the latent space of Market1501; on the right, the two more distant ones.
Preprints 94216 g009
Preprints 94216 g010aPreprints 94216 g010b
Figure 10. Effect of latent variables on generation. In each row we keep a same random noise and vary a given variable in a predefined range. The specific variable and its value are indicated above the generated image.
Figure 10. Effect of latent variables on generation. In each row we keep a same random noise and vary a given variable in a predefined range. The specific variable and its value are indicated above the generated image.
Preprints 94216 g010aPreprints 94216 g010b
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated