Prerpints.org logo
Preprint
Article

The Hubble Sphere, Gravitational Fluid, Fluid Mechanics and the Planck Scale

Altmetrics

Downloads

76

Views

25

Comments

0

This version is not peer-reviewed

Submitted:

23 December 2023

Posted:

25 December 2023

You are already at the latest version

Alerts
Abstract
We will apply Pascal’s hydrostatic pressure law to black holes and also to the Hubble sphere. Haug has recently demonstrated how hydrostatic pressure in water can be utilized to determine the Planck length. One can conceptualize the energy in the Hubble sphere as a type of superfluid, and if this is correct, then Blaise Pascal’s hydrostatic pressure formula may also be applicable to such a superfluid, even within the Hubble sphere. By employing the same method on the Hubble sphere and considering it as a Schwarzschild black hole with the critical Friedmann mass, we can estimate the Planck length based on its hypothetical hydrostatic pressure.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Background on Hydrostatic Pressure and the Planck Scale

Blaise Pascal’s law gives us the well known hydrostatic pressure formula (see Granger [1]):
p = ρ g d
where p is the pressure, ρ is the liquid density of an “incompressible" fluid and d is the height of the liquid column, and g is the gravitational acceleration. As g = G M r 2 , we can rewrite this as:
p = ρ G M r 2 d
Further, Haug [2] has recently shown that the Planck length is given by:
l p = r c p λ ¯ ρ d
where λ ¯ is the reduced Compton [3] wavelength of the gravitational mass. By simply using manometers to measure the hydrostatic pressure in a water column, Haug [2] has demonstrated that one can find the Planck length from hydrostatic pressure.
In this paper, we will demonstrate that the hydrostatic pressure method can remarkably be applied to the Hubble sphere when treating it as a gigantic black hole, with all the energy being a type of perfect gravity fluid. The idea that parts of gravity can be modeled as a perfect fluid dates back at least to Benjamin’s paper [4] in 1968 and has been discussed in many subsequent papers. Black hole cosmological models can be traced back to Pathera in 1972 [5] and later to Stucky in 1994 [6]. These models treat the Hubble sphere as a black hole, as the Schwarzschild radius appears to perfectly align with the Hubble radius.
In the critical Friedmann universe, the critical mass is given by
M c = c 2 R h 2 G
where R h = c H 0 is the Hubble radius and H 0 is the Hubble parameter. However, we can solve this equation for the Hubble radius, yielding
R h = 2 G M c c 2
Which is identical to the Schwarzschild radius. This idea of a black hole universe, despite being in conflict with the Λ -CDM model, continues to be a topic of ongoing discussion, as evidenced by recent publications such as [7,8,9,10]. However there are many types of black holes depending on the metric one study, the best known is the Schwarzschild metric, but we also have for example the Reissner-Nordström [11,12] metric, the Kerr [13] metric, the Kerr-Newman [14,15] metric and Haug-Spavieri [16] metric. We will here concentrate on the critical Friedmann solution.

2. Hubble Sphere Hydrostatic Pressure in the Critical Friedmann Universe

In the critical Friedmann [17] univers the gravitational acceleration at the Hubble radius distance must be:
g = G M c r H 2 = G c 3 2 G H 0 r H 2 = c H 0 2 ≈ 3.25 × 10 − 10 m / s 2
The kilogram density in the Hubble sphere is for the critical Friedmann universe given by
ρ M = M c 4 3 π r H 3 = M c 4 3 π r s 3 = 3 H 0 2 8 π G
The energy density is given by
ρ E = M c c 2 4 3 π r H 3 = M c c 2 4 3 π r s 3 = 3 H 0 2 c 2 8 π G
The hydrostatic pressure of the Hubble sphere is given by
p = ρ M G M c r H 2 r H = 3 H 0 2 8 π G c H 0 2 r H = 3 H 0 2 c 2 8 π G 1 2 = ρ E 1 2
This is exactly half of the energy density in the critical Friedmann universe. Next, the Planck length should be given by:
l p = r c p λ ¯ c ρ M d = r H c p λ ¯ c ρ M r H = 1 H 0 3 H 0 2 c 2 8 π G 1 2 λ ¯ c 3 H 0 2 8 π G r H = 1 H 0 λ ¯ c H 0 c 2
where λ ¯ c is the reduced Compton wavelength of the critical Friedmann mass. It is given by the Compton [3] wavelength formula, but now applied to the critical Friedmann mass: λ ¯ c = ℏ M c c . This way to find the reduced Compton wavelength of the mass in the Hubble sphere requires knowledge of G as the critical Friedamnn mass is given by M c = c 3 2 G H 0 . However, Haug has recently demonstrated that the reduced Compton wavelength of the critical mass in the Hubble sphere is given by
λ ¯ c = H 0 3 T C M B 4 ℏ 4 c k b 4 512 π 4 ≈ 3.79 × 10 − 96 m
where T C M B is the cosmic microwave background temperature now, approximately 2.725 K, and k b is the Boltzmann constant, and ℏ is the Planck constant. This means we can find the Planck length totally independent of knowledge of G from the cosmic scale. The reason is, in our view, that gravity is clearly linked to the Planck scale, and we can extract it also from the Hubble sphere with no knowledge of G. This we have already demonstrated in multiple papers; what is new here is that we can apply basic fluid mechanics to the Hubble sphere, and it leads to the conclusion that we get the Planck length.
l p = 1 H 0 λ ¯ c H 0 c 2 l p = 1 H 0 H 0 3 T C M B 4 ℏ 4 c k b 4 512 π 4 H 0 c 2 l p = H 0 ℏ 2 c T C M B 2 k b 2 32 π 2
We have not derived the Planck length from the pressure formula applied to the Hubble sphere to get a more accurate predictions of the Planck length than known from before, but to demonstrate that the Planck length indeed can be extracted from observations from the Hubble sphere without having to go through G. This implies a direct link between the CMB temperature, the Hubble constant, and the Planck length. What is remarkable in this paper is that we have demonstrated that this can also be derived by assuming the energy in the Hubble sphere is some kind of superfluid and then using standard hydrodynamics to deduce the Planck length. Figure 1 summarizes our findings.

3. Conclusion

The energy in the Hubble sphere can be modeled as a gravitational superfluid, where standard fluid mechanics can be applied, including Blaise Pascal’s law and hydrostatic pressure. This, once again, can be used to extract the Planck length independent of any knowledge of G.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. R. A., Granger. Fluid Mechanics; Dover: New York, 1995. [Google Scholar]
  2. E. G., Haug. Planck scale fluid mechanics: Measuring the Planck length from fluid mechanics independent of G. URL Open Journal of Fluid Dynamics 2023, 13, 250. [Google Scholar]
  3. A. H., Compton. A quantum theory of the scattering of x-rays by light elements. Physical Review 1923, 21, 483. [Google Scholar] [CrossRef]
  4. Benjamin T., B. Gravity currents and related phenomena. Journal of Fluid Mechanics 1968, 31, 209. [Google Scholar] [CrossRef]
  5. R. K., Pathria. The universe as a black hole. Nature 1972, 240, 298. [Google Scholar] [CrossRef]
  6. W. M., Stuckey. The observable universe inside a black hole. American Journal of Physics 1994, 62, 788. [Google Scholar] [CrossRef]
  7. E. T. Tatum, U. V. S. Seshavatharam, and S. Lakshminarayana. The basics of flat space cosmology. International Journal of Astronomy and Astrophysics 2015, 5, 16. [Google Scholar] [CrossRef]
  8. N., Popławski. The universe in a black hole in einstein–cartan gravity. The Astrophysical Journal 2016, 832, 96. [Google Scholar] [CrossRef]
  9. O., Akhavan. The universe creation by electron quantum black holes. Acta Scientific Applied Physics 2022, 2, 34. Available online: https://actascientific.com/ASAP/pdf/ASAP-02-0046.pdf.
  10. C. H. Lineweaver and V. M., Patel. All objects and some questions. American Journal of Physics 2023, 91. [Google Scholar]
  11. H., Reissner. Über die eigengravitation des elektrischen feldes nach der einsteinschen theorie. Annalen der Physics 1916, 355, 106. [Google Scholar] [CrossRef]
  12. G., Nordström. On the energy of the gravitation field in Einstein’s theory. Koninklijke Nederlandsche Akademie van Wetenschappen Proceedings 1918, 20, 1238. [Google Scholar]
  13. R. P., Kerr. Gravitational field of a spinning mass as an example of algebraically special metrics. Physical Review Letters 1963, 11, 237. [Google Scholar] [CrossRef]
  14. E. Newman, E. Couch, K. Chinnapared; Exton, A. Prakash, and R. Torrence. Metric of a rotating, charged mass. Journal of Mathematical Physics 1965, 6, 918. [Google Scholar] [CrossRef]
  15. E. T. Newman and A. I., Janis. Note on the Kerr spinning-particle metric. Journal of Mathematical Physics 1965, 6, 915. [Google Scholar] [CrossRef]
  16. E. G. Haug and G., Spavieri. Mass-charge metric in curved spacetime. International Journal of Theoretical Physics 2023, 62, 248. [Google Scholar] [CrossRef]
  17. A., Friedmann. Über die krüng des raumes. Zeitschrift für Physik 1922, 10, 377. [Google Scholar] [CrossRef]
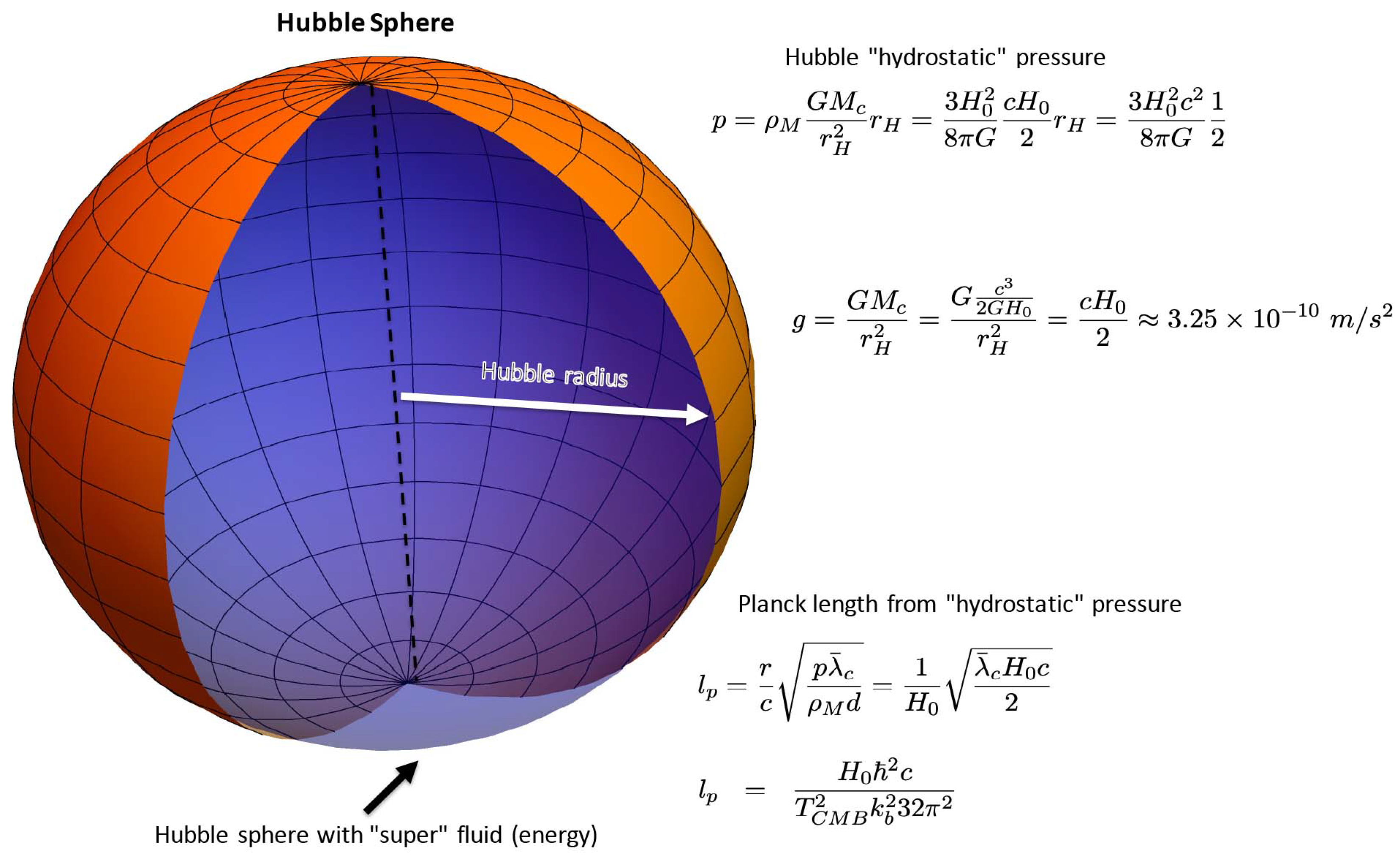
Preprints 94311 g001
Figure 1. The figure illustrates how we can model certain aspects of the Hubble sphere as simply a sphere filled with super fluid (energy of the Hubble sphere) and how this leads to a hydrostatic pressure that we can find the Planck length from without knowledge of G.
Figure 1. The figure illustrates how we can model certain aspects of the Hubble sphere as simply a sphere filled with super fluid (energy of the Hubble sphere) and how this leads to a hydrostatic pressure that we can find the Planck length from without knowledge of G.
Preprints 94311 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated