Prerpints.org logo
Preprint
Article

Urban–Rural Boundary Delineation Based on Population Spatialization: A Case Study of Guizhou Province, China

Altmetrics

Downloads

79

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 December 2023

Posted:

27 December 2023

You are already at the latest version

Alerts
Abstract
Rational delineation of urban–rural boundaries is a foundational prerequisite for holistic urban and rural development planning and rational resource allocation. However, the results of division of urban–rural boundaries extracted using a single data source are non-comprehensive. To address this problem, the present study proposes a method for using multiple sources such as population data, nighttime light data, land use, and points of interest (POI) data to extract urban–rural boundaries. Considering Guizhou Province for a case study, we here present a two-step method for identifying urban–rural boundaries. First, the random forest model was combined with the dasymetric mapping method to obtain the population spatialization data with a 30-m resolution in the studied province. Second, using the breaking point method, we extracted the urban–rural boundary for Guizhou Province in 2020 based on the spatialized population. This method fully integrated the benefits of various data and judiciously extracted the boundaries of the main urban areas and small- and medium-sized towns of each city in the study province at the same spatial scale. The stratified random sampling method revealed that the average overall accuracy was 88.05%. The method proposed has certain universality and application value and allows identifying the urban–rural boundaries more accurately and practically.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

The rapidly advancing urbanization and the implementation of the urban–rural integration development strategy have gradually extended the mutual nesting and influence between urban and rural areas1. The urban fringe area, which is located between built-up and rural areas, has steadily become the most dynamic zone for urban development, diffusion, and sprawl2. Under the influence of both urban and rural areas3, problems such as man–land contradictions and land use conflicts have emerged in these urban fringe areas. These issues have led to several other problems such as chaotic urban and rural planning, resource misallocation, and unbalanced public service4. Therefore, identifying the spatial identification method of urban and rural fringe areas and reasonably delineating the urban–rural spatial boundary for the overall planning of urban and rural development, rational resource distribution, and promotion of coordinated development of these areas are of great significance[5,6].
The urban–rural fringe area is affected by factors such as population, urban size, and economy3, which make its spatial form dynamic that is constantly undergoing changes. Therefore, most studies have been conducted from the perspectives of population characteristics[7,8,9] and urban spatial morphological changes[10,11]. Population, as one of the key factors for the evolution of urban–rural boundaries, is a crucial indicator for measuring the spatial structure of cities. Previous research methods have mostly focused on the qualitative demarcation of urban–rural boundaries based on population density [12,13] from the perspective of administrative or natural regions. Subsequently, various indicators closely related to human activities, such as commuting levels[7,13], socio-economic linkages14, and infrastructure services[15,16], were used for delineating these boundaries. Some recent studies have attempted to demarcate urban–rural boundaries by using spatial positioning data such as points of interest (POI)[17,18], takeaway data19, and locations of new residential buildings in suburbs20.
Advancement of remote sensing technology has resulted in increasing research on the methods for determining urban spatial morphological change. These methods are combined with quantitative methods such as the breaking point method21, information entropy method22, and mutation detection23for identifying the spatial boundaries of cities. The urban–rural boundary is principally obtained by extracting the relevant indicators of land spatial morphology, such as the impervious surface index and landscape disorder degree24,25. The extent of urban built-up at the global [26,27] and urban scales [10,28,29] was determined. The remote sensing image data used included Landsat-TM images30, nighttime light data 26, Sentinel[11,19,31], and other sources. Convolutional11and deep neural network models32have also been used for studying urban–rural boundaries. However, being a complex socio-economic polyhedron, the formation of this urban–rural boundary is affected by various factors. When delineating boundaries, the urban fringe zone often cannot rely solely on some types of indicators such as territorial units or a given population range3.
To compensate for the lack of comprehensive data from a single data source, some scholars have attempted to use nighttime light data33 combine two types of indicators related to population and land, and employ an empirical threshold method or classification method34to obtain the urban boundary range. These studies have preferred to construct composite indices for unifying data types. However, obtaining unified data at the spatial scale is difficult because of the availability of various spatial data sources, which then reduces those methods’ applicability35. By contrast, population spatialization fits population data to spatial locations by establishing relationships between the population and influencing factors. It presents the geographical distribution characteristics of the population as grid cells36 can display more refined spatial information in the statistical population data. To some extent, population spatialization can "bridge" spatial scale differences between different data.
Therefore, considering Guizhou Province as the study area, this study first integrated various data including those of land use, nighttime light, demographic features, POI, and topography. Using the population spatialization method and the random forest model, the multi-source data were then uniformly mapped to the grid data with a 30-m resolution to achieve the fusion of multi-source data at the same scale. Using the breaking point method, the urban–rural boundary for Guizhou Province (GZURB) was extracted based on the spatialized population. This study offers a new approach for demarcating urban boundaries.

2. Materials and Methods

2.1. Study Area

Guizhou Province (Figure 1) is situated in the southwestern region of China, spanning coordinates 24°37′–29°13′N latitude and 103°36′–109°35′E longitude. This province comprises nine municipal-level and 88 county-level administrative divisions. Its total land area is approximately 176,167 km². Of the total land area, approximately 61.7% is mountainous terrain, 31.1% is hilly, and only 7.5% comprises the mountainous Pingba region. The karst landform area accounts for approximately 62% of the total area of the province. Guizhou Province is a typical mountainous region.
Over the past three decades, the urbanization rate in the study province has increased significantly. It was 23.87% in 2000, which increased to 33.81% by 2010 and reached 53.15% in 2020. In comparison, the overall urbanization rate of China increased from 36.2% in 2000 to 49.7% in 2010, which further accelerated to 63.9% in 2020. Notably, although the urbanization rate of the study province has not yet reached the overall level of China, its urbanization growth rate has far exceeded that of China (Figure 2). Because Guizhou Province is located in the transportation hub of southwest China and is a crucial part of the Yangtze River Economic Belt, the coordination and optimization of urban and rural spatial layouts in this province have been the research focus in related regions. Therefore, considering this province as the study area, the present study analyzed the urban–rural boundary with a decentralized distribution pattern, which is favorable for comprehending the development and change characteristics of southwest China, especially in karst landform regions.

2.2. Research Method

2.2.1. Overall Framework

This paper proposes an urban–rural boundary delineation method that includes four steps: data collection and preprocessing, population spatial representation, urban–rural boundary determination, and accuracy verification (Figure 3). First, various data such as NPP/VIIRS, land use, and POI data were collected and preprocessed to construct a characteristic factor database. Second, a random forest regression model coupled with dasymetric mapping was used to generate the population spatialization data with 30-m spatial resolution in the study province. Then, the population spatialization result was considered as the index factor, and the urban–rural boundary was extracted using the breaking point method. Finally, stratified random sampling and comparative analysis were used to verify whether the boundary division results were accurate.

2.2.2. Population Spatialization Methods

The spatial interpolation method36and multiple linear regression models[37,38] have often been used in the population spatialization studies. Although the spatial interpolation method can, to some extent, eliminate the influence of administrative boundaries, accurately expressing the true characteristics of the spatial distribution of a population within administrative units is difficult. Multiple linear regression models can more accurately fit the spatial distribution of the population but are relatively less effective when addressing data collinear problems. By contrast, the random forest model can construct complex nonlinear relationships between the population and its auxiliary variables, leading to a high-precision spatial distribution of the population[39-41]. Therefore, in recent years, the random forest model has been extensively used in the spatial expression of populations. This 2001’s Bierman model [42] is a decision tree-based ensemble learning algorithm that involves introducing the bagging algorithm for multiple random sampling into decision trees and combining the extracted multiple decision trees to complete integrated model construction [43].
Population data, POI data, and other characteristic factors constituted the foundational database. The random forest model was employed for training to predict population weight values for different factors. Leveraging dasymetric mapping [44], the actual area’s total population was spatially assigned based on the aforementioned predicted weight values to achieve a spatial representation of population quantities. The calculation formula is as follows:
P i = S j / D j × D i
where Pi represents the final population count for grids; Sj denotes the total statistical population of the city where grid j is located; Dj is the total weighted value of the estimated grid i in the city (autonomous prefecture), and Di denotes the raster value of the estimated grid i.

2.2.3. Methods of Urban–Rural Boundary Delimitation

Methods such as information entropy, mutation detection, and breaking point analysis[45,46] have been widely used for delineating urban–rural boundaries. The information entropy method requires that a reasonable threshold is selected and exposed to some subjectivity22. The mutation detection method focuses on a single factor, whereas the breaking point method offers a clear inflection point for outlining urban–rural boundaries3. Hence, the breaking point analysis method was adopted in this study for identifying these boundaries. The breaking point theory47, proposed by P.D. Converse in 1949, postulates that the population size of and distance between two cities determine the attraction between those cities. The fundamental principle involves identifying the distance decay mutation peak for each element in the same direction as the breaking point by using the following formula:
d A = D A B 1 + P B / P A
where dA is the distance from the breaking point to the city, DAB represents the distance between two cities, and PA and PB are the population size values of the two cities, respectively.
The fracture point is determined by calculating the maximum distance attenuation value as follows:
D i = max ( x i j − x i ( j + 1 ) ∑ x i j − x i ( j + 1 ) / N )
where Di is the maximum distance attenuation value on the ith profile line, xij is the jth sequence eigenvalue on the ith profile line, and xi(j+1) is the (j+1)th sequence eigenvalue on the ith profile line.

2.2.4. Accuracy Verification Methods

The accuracy of both population spatialization and urban–rural boundary delineation was evaluated in this study. Because population spatialization results directly impact urban–rural boundary delineation, we conducted an error analysis of population spatialization by employing three evaluation indicators: root mean square error (RMSE), relative root means square error (%RMSE), and mean absolute error (MAE). Population spatialization results were compared and analyzed with datasets such as WorldPop and LandScan to assess the accuracy of the results. The accuracy of urban–rural boundary demarcation was verified using stratified random sampling and comparative analysis.

3. Data Sources and Processing

We here used a comprehensive array of data sources, including land use data, administrative divisions, normalized difference vegetation index (NDVI), digital elevation model (DEM), NPP/VIIRS and DMSP/OLS nighttime light remote sensing data, demographic statistics, meteorological information (including precipitation and temperature data), POI data, road networks, river data, and population datasets from WorldPop and LandScan. Table 1 presents data information and their sources.
Because of the diversity of data sources, different data types were first standardized to the Lambertian projection uniformly and then resampled to a 30-m resolution. The primary data processing steps are as follows:
1. Nighttime Light Data: Using the constant target area method48NPP/VIIRS and DMSP/OLS images were subjected to oversaturation correction, continuity correction, and outlier processing, along with mutual substitution between continuous year images. Following logarithmic transformation49, a function relationship was established for DN values between the two images to ensure consistency in the correction results for nighttime light data of Guizhou Province in 2020 (Figure 4).
(1)
Land use data: Using the GlobeLand30 dataset, land use data for Guizhou Province were extracted, and the proportions of various land cover types in each district were evaluated. These results allowed us to calculate the cultivated land index, grassland index, shrubland index, forest index, water index, and artificial surface index.
(2)
Urban Nighttime Light Index and Human Settlements Index: We constructed the corrected urban nighttime light index VANUI 50and the human settlements index (HSI) by comprehensively using nighttime light data and the NDVI vegetation index.
(3)
DEM: We applied the moving window method and the mean variation point method 51for identifying the optimal statistical unit for topographic relief in the study area. Additionally, the proportion factor of a flat land area in the study area 52was incorporated to calculate topographic relief.
(4)
Meteorological data: ArcGIS software was used to query, screen, and calculate the annual average precipitation and temperature for each district in the study province.
(5)
POI: Fourteen types of POI data were obtained from the open API platform of Amap for 2020, and kernel density analyses were performed to calculate the average kernel density for each district.
(6)
River and road data: Leveraging existing datasets and the Euclidean distance method, we computed the straight-line distance between each point and the nearest river and road and determined Euclidean distance mean values.
(7)
NDVI: Based on MOD13Q1 data, the administrative division data of Guizhou Province were used to crop the NDVI image data for each time period. Subsequently, the average values of NDVI images in 2020 were calculated using a raster calculator.
To alleviate the impact of different scales and dimensions, the Min-Max data standardization method was applied to normalize various indicators and compile a database of population spatialization characteristic factors (Table 2).

4. Results and Discussion

4.1. Results of Population Spatialization

By referring to the database of population spatialization characteristic factors, statistical mean data were correlated with the districts in the study province by using ArcGIS software. To construct a fundamental dataset, the population density data from the 2020 census for each district were used as the dependent variable, whereas the database of characteristic factors was used as the independent variable. The corresponding random forest model was constructed using the R programming language. The data were categorized into training (70%) and test (30%) sets (Table 3).
Initially, the model for the relationship between independent variables and population density was established. The model was then applied to the characteristic factor data at a 30-m grid scale, which yielded the initial population grid data on the basis of the random forest model prediction, known as the grid weight eigenvalue. To ensure that the grid data align with the actual district population, dasymetric mapping was performed to allocate the actual city population based on weight values. Subsequently, the total number of weight values in each city or state was tallied, and the grid's population count was computed using the ratio of actual population data to the total number of weight layers, which resulted in the final population spatialization outcome (Figure 5).
The population spatialization results (Figure 5) were achieved by integrating multi-source data, including nighttime light, land use, and POI data. These results revealed a population distribution pattern, characterized by a high population density in the primary urban areas and a relatively low density in the surrounding regions, in the study province. Of note, the population was concentrated in the central and northwest parts of Guizhou Province, with eastern and southern areas exhibiting sparser populations. Population was significantly concentrated in major urban areas within cities, with Guiyang City, the provincial capital, being the primary center.

4.2. Accuracy of Population Spatialization Data

We extracted corresponding data for our study area from the WorldPop and LandScan datasets and comparatively assessed the population spatialization dataset, with MAE, RMSE, and %RMSE values as index factors (Table 4). The simulation accuracy of the WorldPop dataset, LandScan dataset, and the population spatialization method applied in this study were 79.71%, 78.54%, and 93.34%, respectively, which indicated relatively high accuracy of the population spatialization method.

4.3. Identification of Urban–Rural Boundaries Based on Population Spatialization

We here adopted the urban–rural fringe boundary as the urban–rural boundary. Leveraging population spatialization data and the breaking point theory, the population density of the study province in 2020 was computed and the spatial boundary between urban and rural populations within the province was successfully delineated.
Once the population spatialization data met the required accuracy standards, our next objective was to locate the urban–rural boundary. To achieve this objective, we initiated a meticulous process as outlined below.
Considering the unique characteristics of each city in Guizhou Province, the geometric center point of each city was selected as the reference origin. Starting from the east, we drew 360 cross-sectional lines at 1° intervals, thereby encircling the city's perimeter. These lines intersected with the urban–rural division index factor, thus yielding 360 cross-sectional data columns containing population data. We then calculated the maximum distance attenuation value from these columns (Figure 6).
Next, the distance attenuation value from the cross-sectional line to the corresponding spatial grid was linked through attribute fields for identifying the grid position of the breaking point. Considering the distance between the breaking point and the city center, we excluded any anomalous mutation values and connected the breaking points. Finally, the urban–rural boundary delineation was determined for the nine cities in the study province (Figure 7).
The extraction results (Figure 7) unveiled that this approach can precisely extract urban boundaries of the nine cities and effectively identify small towns with dispersed distributions within each city. Moreover, this approach shows enhanced recognition of the core areas. An analysis of the spatial distribution of the provincial population revealed that the development of urban population spatial boundaries in each city follows a pattern characterized by a central core and multiple sub-cores.

4.4. Discussion on the Accuracy of GZURB

4.4.1. Accuracy Validation Based on the Stratified Random Sampling Method

The Landsat 8 OLI_TIRS remote sensing images from 2020 (https://www.gscloud.cn/) were used as the foundational map. A random sampling method was applied to assess the accuracy of the extracted boundary data. In total, 1000 sample points were randomly selected from the GZURB-designated urban and non-urban areas in the urban–rural boundary dataset of the study province. The GZURB accuracy was verified by calculating the sample point number in urban and non-urban areas. The number of random sampling points falling within the urban and non-urban areas was recorded for constructing a confusion matrix. Four indicators, namely overall accuracy (OA), kappa coefficient, producer accuracy (PA), and user accuracy (UA), were used to assess whether the classification results were accurate and consistent.
As shown in Table 5, the proposed method achieved a UA and PA of 96.69% and 78.80%, respectively, for the urban area and 82.11% and 97.30%, respectively, for the non-urban area. The OA of GZURB reached 88.05%, and the kappa coefficient was 0.761, which indicated a high classification accuracy of the dataset.

4.4.2. Accuracy of Superimposed Remote Sensing Image Data

To further assess the accuracy of GZURB, a comparative analysis was conducted using World Imagery (WB_2020_R01) for ascertaining the consistency of the study dataset. Data from the seventh national population census revealed that Guiyang, Zunyi, and Bijie were the top three most populous cities within Guizhou Province, having permanent populations of 5.987, 6.6067, and 6.8996 million, respectively. Consequently, these cities were selected as focal points for a detailed evaluation of the extraction performance of GZURB, and a comprehensive urban–rural boundary division map was employed.
The primary urban zones along with certain dispersed small towns within the study area were successfully identified and delineated (Figure 8). This approach enabled effective delineation between urban and non-urban areas on the basis of distinctions arising from varying spatial configurations of urban boundaries. In the heart of Guiyang, which has a relatively dense population (Figure 8a), the method proposed could accurately identify the urban–rural demarcation despite the complexity of the urban boundary. Specifically, in the intricate urban periphery, the proposed methodology exceled in conveying the intricate spatial nuances of this region. Despite the scattered distribution of Zunyi and Bijie, which primarily comprise small towns, the boundary identification approach advocated here also yielded remarkable outcomes for the peripheries of these smaller municipalities (Figure 8b, Figure 8c).
On analyzing the accuracy of urban boundary extraction in the study province, we noted that the boundary delineation results for the main urban areas were superior to those for the small towns. To delve into this phenomenon, the significance of different characteristic factors in population spatialization for each city (prefecture) in the study area was ranked (Figure 9), which indicated that POI data hold the highest feature importance of 25.300%. The results further indicated that POI data are crucial in delineating urban boundary, particularly in urban core recognition, whereas factors such as slope, rainfall, and shrubland data have relatively limited impact.
The POI data encompass various sectors, including retail, education, and healthcare, and offer noteworthy advantages in reflecting the spatial distribution characteristics of urban structures. Figure 10 presents the distribution of the POI kernel density in Guizhou Province in 2020. As depicted, the POI distribution in the core areas of each city was relatively dense. The POI density decreased considerably near the boundaries of built-up areas and small towns, with the number of POI points declining from urban centers to urban edges and rural areas. The higher POI data density in the primary urban areas positively correlated with the finer urban–rural boundary division results, which contributed to highly accurate boundary recognition. This result aligns perfectly with previous research findings [8,18].
In summary, the urban–rural boundary delineation method proposed here was more accurate in recognizing boundaries in the key urban areas of Guizhou Province. This delineation effectively captured the study area’s boundary range, thereby offering an accurate reflection of the spatial boundary between the urban and rural populations in the study province in 2020.

5. Conclusions

The method proposed in this study comprehensively considers data from different sources and spatializes them into a unified grid unit to extract the urban–rural boundary. Considering Guizhou Province in China as the research area, we included multi-source data, such as POI data, nighttime light data, and population data. By applying the random forest model and dasymetric mapping method, a spatial distribution model of Guizhou Province's population in 2020 was constructed and the spatial data of the population with a 30-m resolution were obtained. The stratified random sampling method exhibited that the OA of the proposed urban–rural boundary extraction method was 88.05%, with a kappa coefficient of 0.761. This method can effectively extract the spatial boundary range of urban and rural populations and strongly support urban and rural planning and resource management. However, obtaining a more detailed spatial distribution of the city population is not possible because of the low spatial resolution of nighttime light data. In future, we intend to use higher resolution data for a more accurate reflection of the dynamics of population spatial changes, which can provide more precise urban–rural boundary delineations.

Author Contributions

Conceptualization, H.W. and X.Y.; methodology, H.W. and R.L.; data curation, L.L and X.Y.; writing—original draft preparation, X.Y. and H.W.; writing—review and editing, X.Y. and H.W.; funding acquisition, R.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China, grant number 42171354.

Data Availability Statement

The urban–rural boundary dataset in this study (GZURB) in 2020 can be obtained from wanghong@hubu.edu.cn.

Acknowledgments

The authors would like to gratefully acknowledge data providers. Thank you to Yueyue Zhao for her exploratory work in the early stage.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gu, C. A study of the fringe areas of China's large cities; Science Press: Beijing, China, 1995. [Google Scholar]
  2. Peng, J.; Ma, J.; Yuan, Y. Research progress and prospect on the identification of urban fringe. Prog. Geogr. 2014, 33, 1068–1077. [Google Scholar] [CrossRef]
  3. Zhou, X. Spatial identification and evolution of urban fringe: A case study of Xi'an city, China. Master thesis, Northwest University, Xi’an, CN, 2018.
  4. Lu, D. Urbanization process and spatial sprawl in China. Urban Plan. Forum 2007, 2007, 47–52. [Google Scholar]
  5. Gu, C.; Xiong, J. On urban fringe studys. Geogr. Res. 1989, 1989, 95–101. [Google Scholar] [CrossRef]
  6. Yi, X.; Dong, W.; Zhang, H. Methods and evolution of US urban area delineation with its enlightenment to China. Urban Plan. Int. 2021, 36, 69–75. [Google Scholar] [CrossRef]
  7. Andrea, D.M.; Marc, B.; Alessandro, C.; Alessandro, V. The Structure of Interurban Traffic: A Weighted Network Analysis. Environ. Plan. B: Plan. Des. 2007, 34, 905–924. [Google Scholar] [CrossRef]
  8. Xu, Z.; Gao, X. Boundary recognition method of urban built-up area based on electronic map interest points. Acta Geogr. Sin. 2016, 71, 928–939. [Google Scholar] [CrossRef]
  9. Henderson, J.V.; Nigmatulina, D.; Kriticos, S. Measuring urban economic density. J. Urban Econ. 2021, 125, 103188. [Google Scholar] [CrossRef]
  10. Zhu, J.; Lang, Z.; Yang, J.; Wang, M.; Zheng, J.; Na, J. Integrating spatial heterogeneity to identify the urban fringe area based on NPP/VIIRS nighttime light data and dual spatial clustering. Remote Sens. 2022, 14, 6126. [Google Scholar] [CrossRef]
  11. Bramhe, V.S.; Ghosh, S.K.; Garg, P.K. Extraction of built-up areas using convolutional neural networks and transfer learning from sentinel-2 satellite images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 79–85. [Google Scholar] [CrossRef]
  12. Friedmann, J.; Miller, J. The urban field. J. Am. Inst. Plan. 1965, 31, 312–320. [Google Scholar] [CrossRef]
  13. Sharp, J.S.; Clark, J.K. Between the country and the concrete: Rediscovering the rural-urban fringe. City Community 2008, 7, 61–79. [Google Scholar] [CrossRef]
  14. Ren, R.; Zhang, H. A study on the methods of defining urban-rural fringe. Urban Probl. 2008, 2008, 40–48. [Google Scholar] [CrossRef]
  15. Gao, S.; Janowicz, K.; Couclelis, H. Extracting urban functional regions from points of interest and human activities on location-based social networks. Trans. GIS 2017, 21, 446–467. [Google Scholar] [CrossRef]
  16. Chen, Y.; Chen, X.; Liu, Z.; Li, X. Understanding the spatial organization of urban functions based on co-location patterns mining: A comparative analysis for 25 Chinese cities. Cities 2020, 97, 102563. [Google Scholar] [CrossRef]
  17. Dong, Q.; Qu, S.; Qin, J.; Yi, D.; Liu, Y.; Zhang, J. A method to identify urban fringe area based on the industry density of POI. ISPRS Int. J. Geo-Inf. 2022, 11, 128. [Google Scholar] [CrossRef]
  18. Wang, Q.; Wang, R.; Liu, X. An empirical study on boundary identification of urban built-up area based on POI of retail business. Mod. Urban Res. 2022, 2022, 59–64. [Google Scholar] [CrossRef]
  19. Zhou, C.; He, X.; Wu, R.; Zhang, G. Using food delivery data to identify urban -rural areas: A case study of Guangzhou, China. Front. Earth Sci. 2022, 10, 860361. [Google Scholar] [CrossRef]
  20. LeSage, J.P.; Charles, J.S. Using home buyers’ revealed preferences to define the urban-rural fringe. J. Geogr. Syst. 2008, 10, 1–21. [Google Scholar] [CrossRef]
  21. Du, N. Realization of extraction technology of urban-rural junction based on night-light data—taking Beijing as an example. Master thesis, Chongqing Jiaotong University, Chongqing, CN, 2020. [CrossRef]
  22. Cai, D.; Li, M.; Chen, Z.; Wei, W.; Hu, W. Digital image atlas quality control analysis based on fuzzy comprehensive evaluation model. Sci. Surv. Mapp. 2010, 35, 106–109. [Google Scholar] [CrossRef]
  23. Ma, J.; Li, Q.; Ying, W. Identification of a rural-urban fringe based on wavelet transform-A case study of Wuhan. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 235–241. [Google Scholar] [CrossRef]
  24. Yin, X.; Wei, H.; Li, Y. Identification and spatio-temporal variation of county towns' built-up area of China based on impervious surface dataset. Geogr. Res. 2023, 42, 1492–1505. [Google Scholar] [CrossRef]
  25. Cheng, J.; Hu, P.; Yuan, Z. Analysis of temporal and spatial changes of the central plains urban agglomeration based on luminous remote sensing data. Bull. Surv. Mapp. 2022, 2022, 39–44. [Google Scholar] [CrossRef]
  26. Li, X.; Gong, P.; Zhou, Y.; Wang, J.; Bai, Y.; Chen, B.; Hu, T.; Xiao Y.; Xu, B.; Yang, J.; etc. Mapping global urban boundaries from the global artificial impervious area (GAIA) data. Environ. Res. Lett. 2020, 15, 094044. [CrossRef]
  27. Shi, K.; Wu, Y.; Liu, S.; Chen, Z.; Huang, C.; Cui, Y. Maping and evaluating global urban entities (2000-2020): A novel perspective to delineate urban entities based on consistent nighttime light data. GIScience Remote Sens. 2023, 60, 2161199. [Google Scholar] [CrossRef]
  28. Zhao, H.; Zhu, Y.; Wu, K.; Hu, X. Study on the method for the demarcation of urban-rural fringe based on land use dynamic indicator. China Land Sci. 2012, 26, 60–65. [Google Scholar] [CrossRef]
  29. Sun, J.; Sun, Z.; Guo, H.; Wang, J.; Jiang, H.; Gao, J. A dataset of built-up areas of Chinese cities in 2020. China Sci. Data 2022, 7, 190–204. [Google Scholar] [CrossRef]
  30. Zhang, W.; Fang, X.; Zhang, L. Method to identify the urban-rural fringe by TM images. Natl. Remote Sens. Bulletin, 1999, 3, 199–202. [Google Scholar] [CrossRef]
  31. Li, X.; Zheng, K.; Qin, F.; Wang, H.; Zhao, C. Deriving urban boundaries of Henan province, China, based on Sentinel-2 and Deep Learning methods. Remote Sens. 2022, 14, 3752. [Google Scholar] [CrossRef]
  32. Liu, X. Research in the definition of urban fringe area based on Deep Neural Network. Master thesis, Guangzhou University, Guangzhou, CN, 2020. [CrossRef]
  33. Li, C.; Wang, X.; Wu, Z.; Dai, Z.; Yin, J.; Zhang, C. An improved method for urban built-up area extraction supported by multi-source data. Sustain. 2021, 13, 5042. [Google Scholar] [CrossRef]
  34. Dou, Y.; Liu, Z.; He, C.; Yue, H. Urban land extraction using VIIRS nighttime light data: An evaluation of three popular methods. Remote Sens. 2017, 9, 175. [Google Scholar] [CrossRef]
  35. Bai, Z.; Wang, J.; Yang, F. Research progress in spatialization of population data. Prog. Geogr. 2013, 32, 1692–1702. [Google Scholar] [CrossRef]
  36. Dong, N.; Yang, X.; Cai, H. Research progress and perspective on the spatialization of population data. J. Geo-Inf. Sci. 2016, 18, 1295–1304. [Google Scholar] [CrossRef]
  37. Li, H.; Zhang, H.; Wang, M. A comparative study of population spatialization based on NPP/VIIRs and LJ1-01 night light data: taking Beijing for an example. Remote Sens. Inf. 2021, 36, 90–97. [Google Scholar] [CrossRef]
  38. Zeng, C.; Zhou, Y.; Wang, S.; Yan, F.; Zhao, Q. Population spatialization in China based on night-time imagery and land use data. Int. J. Remote Sens. 2011, 32, 9599–9620. [Google Scholar] [CrossRef]
  39. Zhou, Y.; Ma, M.; Shi, K.; Peng, Z. Estimating and interpreting fine-scale gridded population using random forest regression and multisource data. ISPRS Int. J. Geo-Inf. [CrossRef]
  40. Li, K.; Chen, Y.; Li, Y. The random forest-based method of fine-resolution population spatialization by using the international space station nighttime photography and social sensing data. Remote Sens. 2018, 10, 1650. [Google Scholar] [CrossRef]
  41. He, M.; Xu, Y.; Li, N. Population spatialization in Beijing city based on machine learning and multisource remote sensing data. Remote Sens. 2020, 12, 1910. [Google Scholar] [CrossRef]
  42. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  43. Breiman, L. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
  44. Jia, P.; Gaughan, A.E. Dasymetric modeling: A hybrid approach using land cover and tax parcel data for mapping population in Alachua County, Florida. Appl. Geogr. 2016, 66, 100–108. [Google Scholar] [CrossRef]
  45. Rao, J.; Ding, H.; Xu, P. Extraction of Built-Up Area in Shanghai Based on Luojia-1. Jiangxi Sci. 2023, 41, 261–265. [Google Scholar] [CrossRef]
  46. Chen, Y. On the urban and rural ecotone and its characteristics and functions. Econ. Geogr. 1996, 1996, 27–31. [Google Scholar] [CrossRef]
  47. Xu, X.; Zhou, Y.; Ning, Y. Urban geography,2nded.; Higher Education Press: Beijing, CN, 2009; ISBN 9787040255393. [Google Scholar]
  48. Cao, Z.; Wu, Z.; Mi, S.; Yang, K. A method for classified correction of stable DMSP/OLS nighttime light imagery across China. J. Geo-inf. Sci. 2020, 22, 246–257. [Google Scholar] [CrossRef]
  49. Guan, J.; Li, D.; Wang, Y.; Wang, X. DMSP-OLS and NPP-VIIRS night light image correction in China. Bull. Surv. Mapp. 2013, 129, 32–41. [Google Scholar] [CrossRef]
  50. Zhang, Q.; Schaaf, C.; Seto, K.C. The Vegetation Adjusted NTL Urban Index: A new approach to reduce saturation and increase variation in nighttime luminosity. Remote Sens. Environ. 2013, 129, 32–41. [Google Scholar] [CrossRef]
  51. Zhang, J.; Zhu, W.; Zhu, L.; Cui, Y.; He, S.; Ren, H. Topographical relief characteristics and its impact on population and economy: A case study of the mountainous area in western Henan, China. J. Geogr. Sci. 2019, 29, 598–612. [Google Scholar] [CrossRef]
  52. Feng, Z.; Tang, Y.; Yang, Y.; Zhang, D. The relief degree of land surface in China and its correlation with population distribution. Acta Geogr. Sin. 2007, 62, 1073–1082. [Google Scholar] [CrossRef]
Preprints 94203 g001
Figure 1. Study area.
Figure 1. Study area.
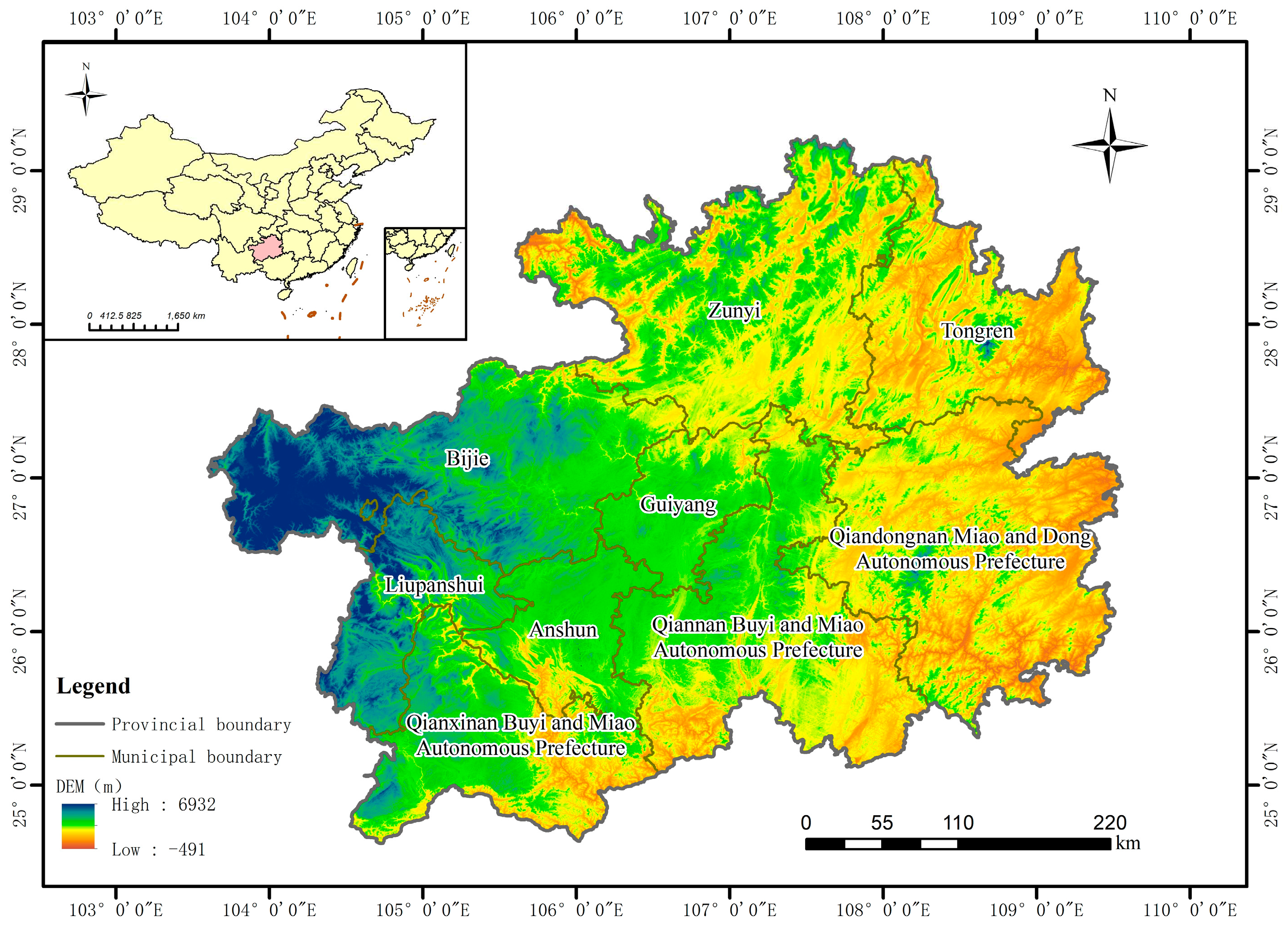
Preprints 94203 g001
Preprints 94203 g002
Figure 2. Urbanization change rate from 2000 to 2020.
Figure 2. Urbanization change rate from 2000 to 2020.
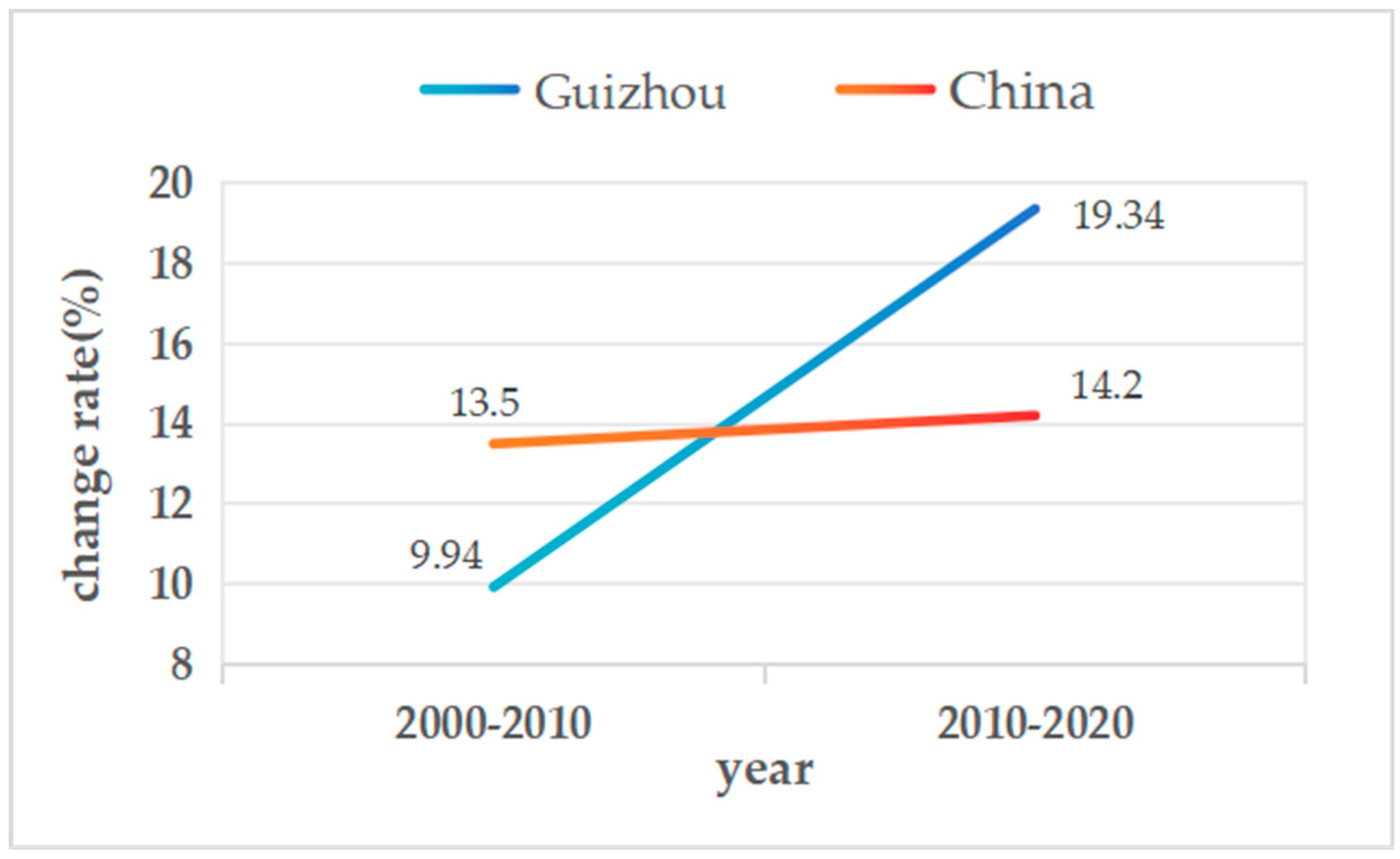
Preprints 94203 g002
Preprints 94203 g003
Figure 3. Flow chart of delimiting urban boundary divisions.
Figure 3. Flow chart of delimiting urban boundary divisions.
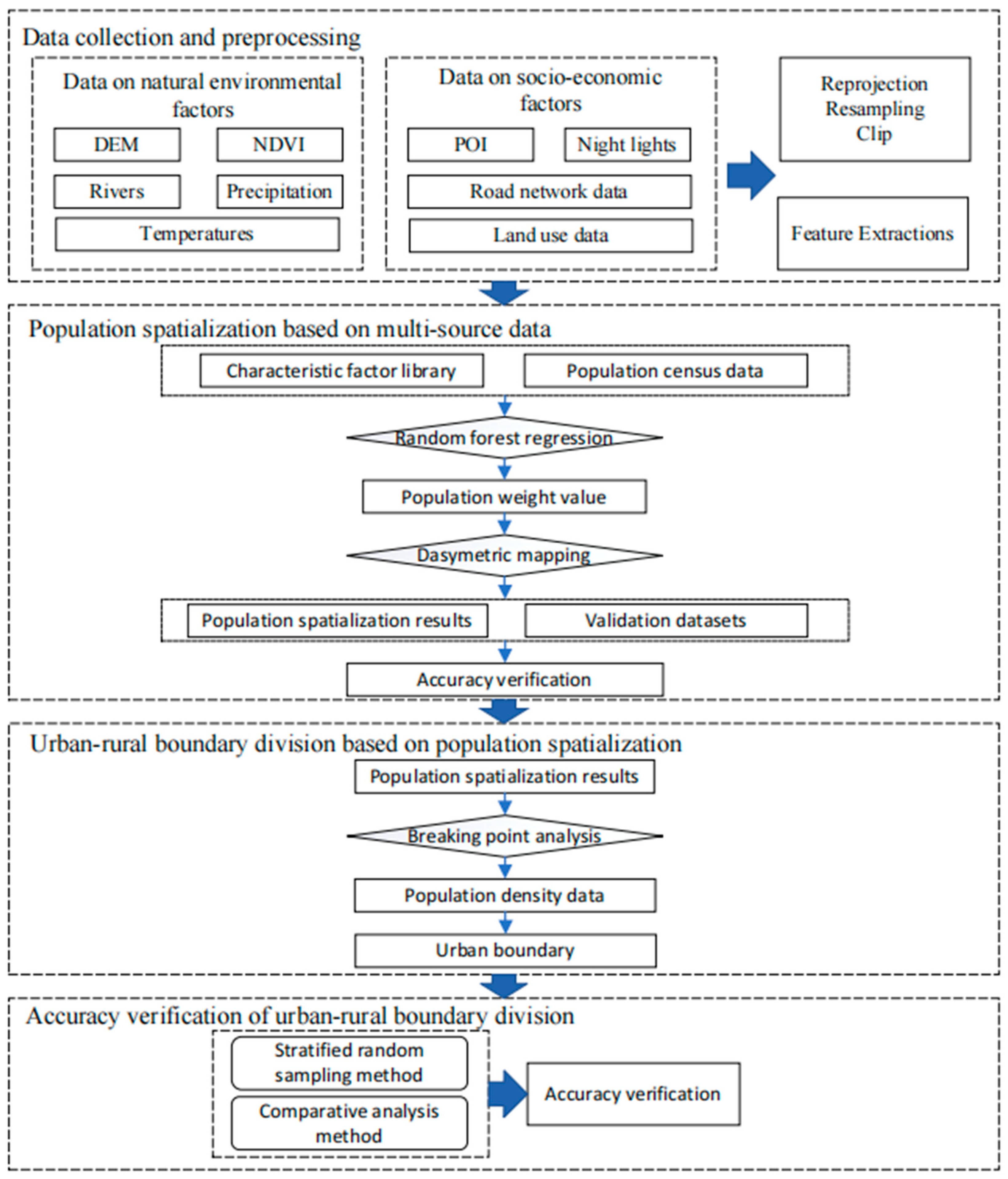
Preprints 94203 g003
Preprints 94203 g004
Figure 4. Correction results of nighttime light image consistency.
Figure 4. Correction results of nighttime light image consistency.
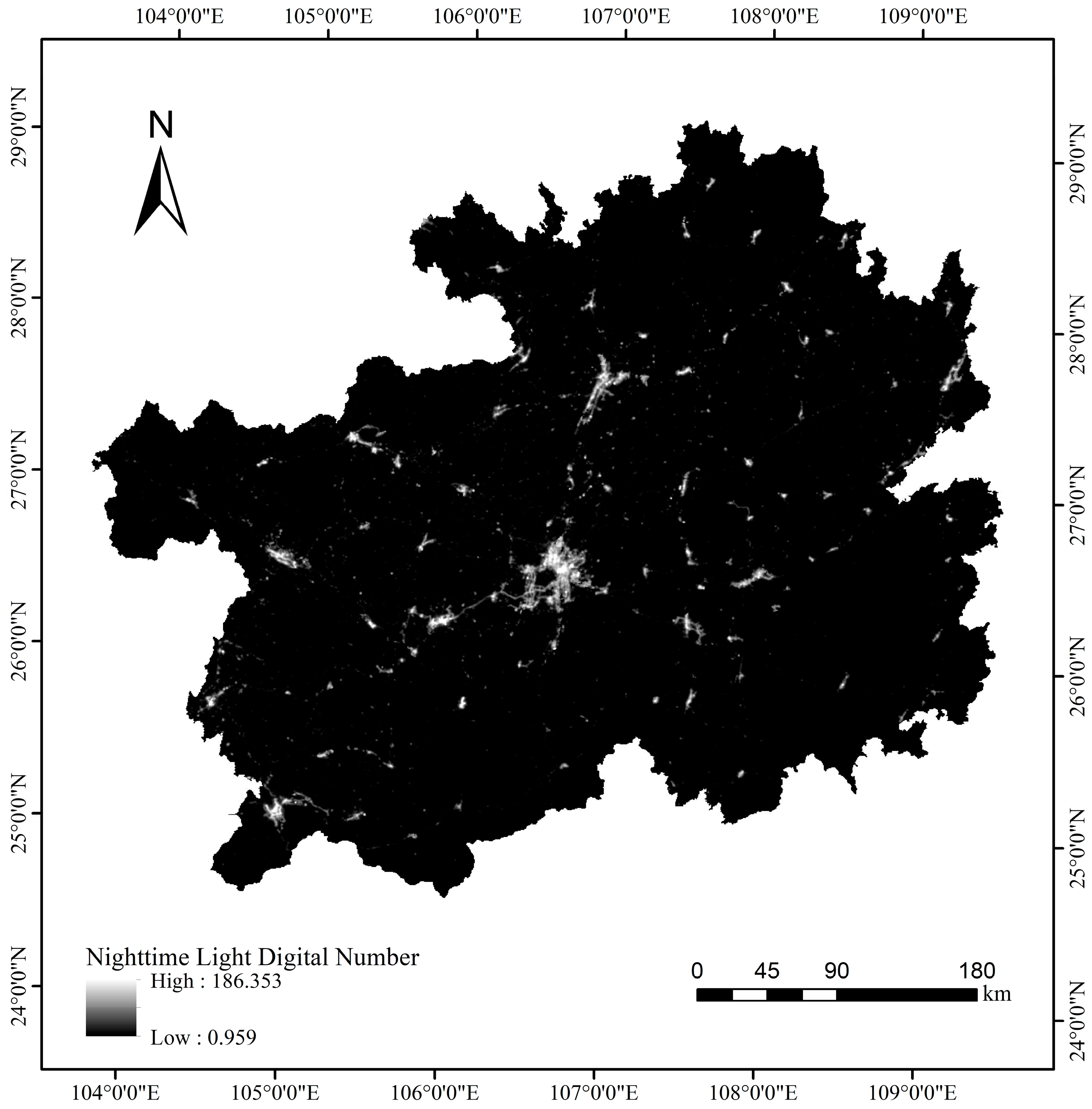
Preprints 94203 g004
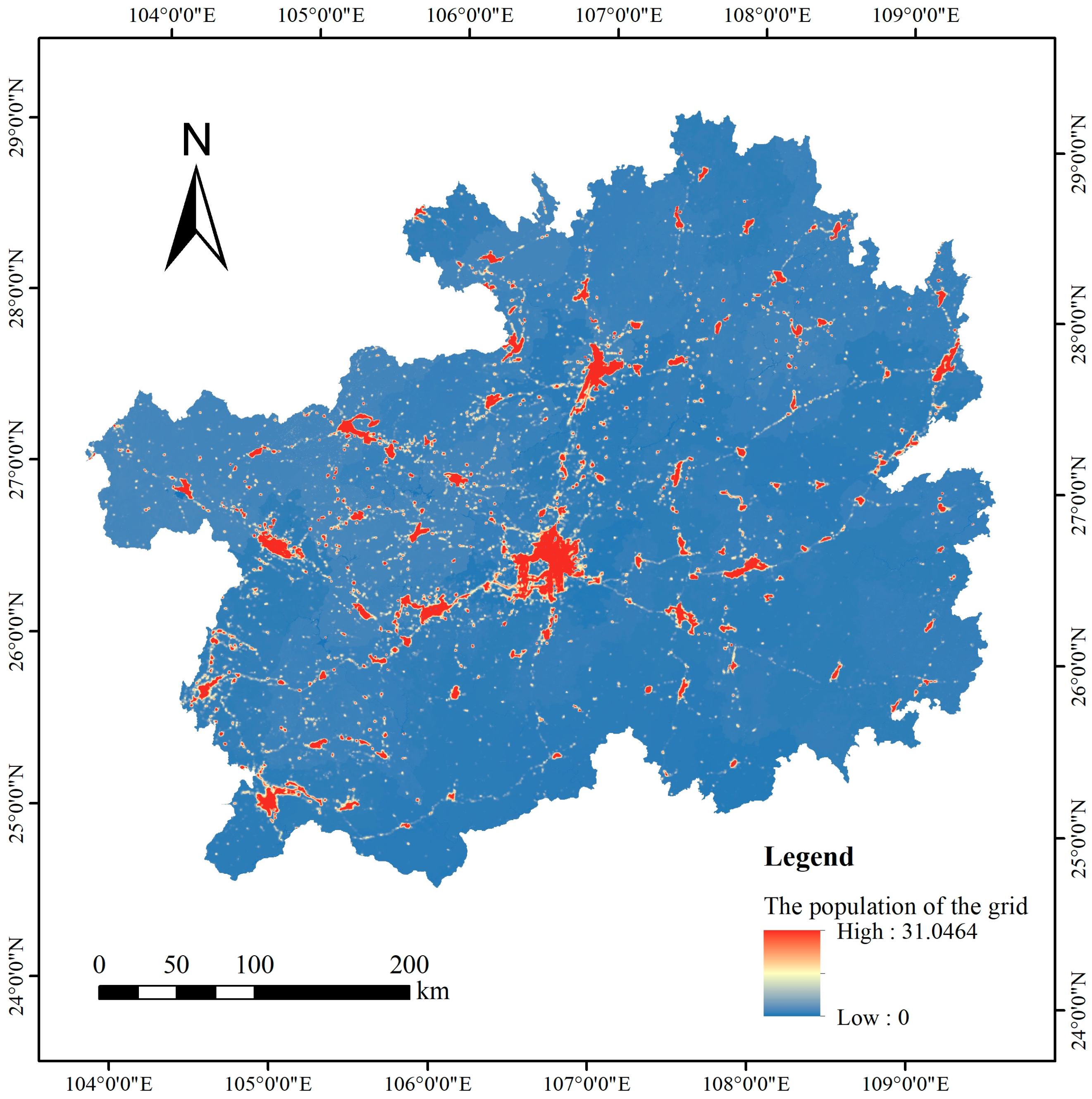
Preprints 94203 g005
Figure 5. Population spatialization results of Guizhou Province.
Figure 5. Population spatialization results of Guizhou Province.
Preprints 94203 g005
Preprints 94203 g006
Figure 6. Sketch of profile line (Guiyang City).
Figure 6. Sketch of profile line (Guiyang City).
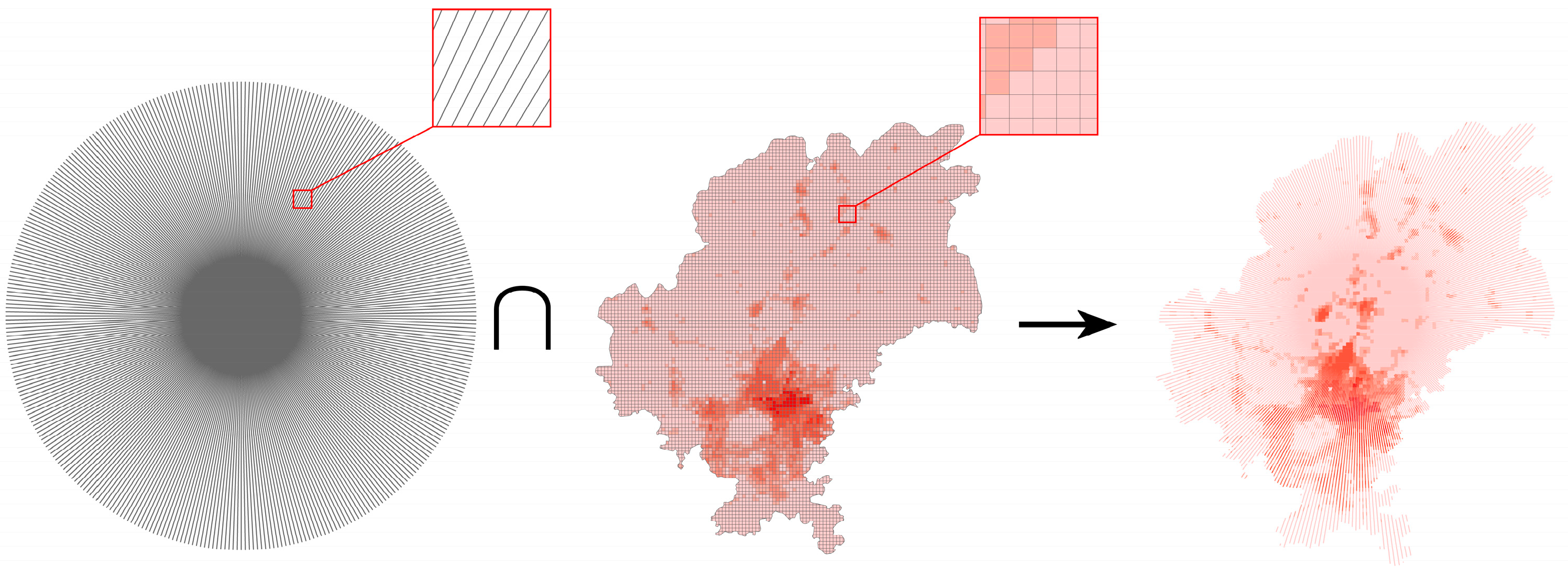
Preprints 94203 g006
Preprints 94203 g007aPreprints 94203 g007b
Figure 7. Results of urban boundary delimitation of various cities/autonomous prefectures in Guizhou Province.
Figure 7. Results of urban boundary delimitation of various cities/autonomous prefectures in Guizhou Province.
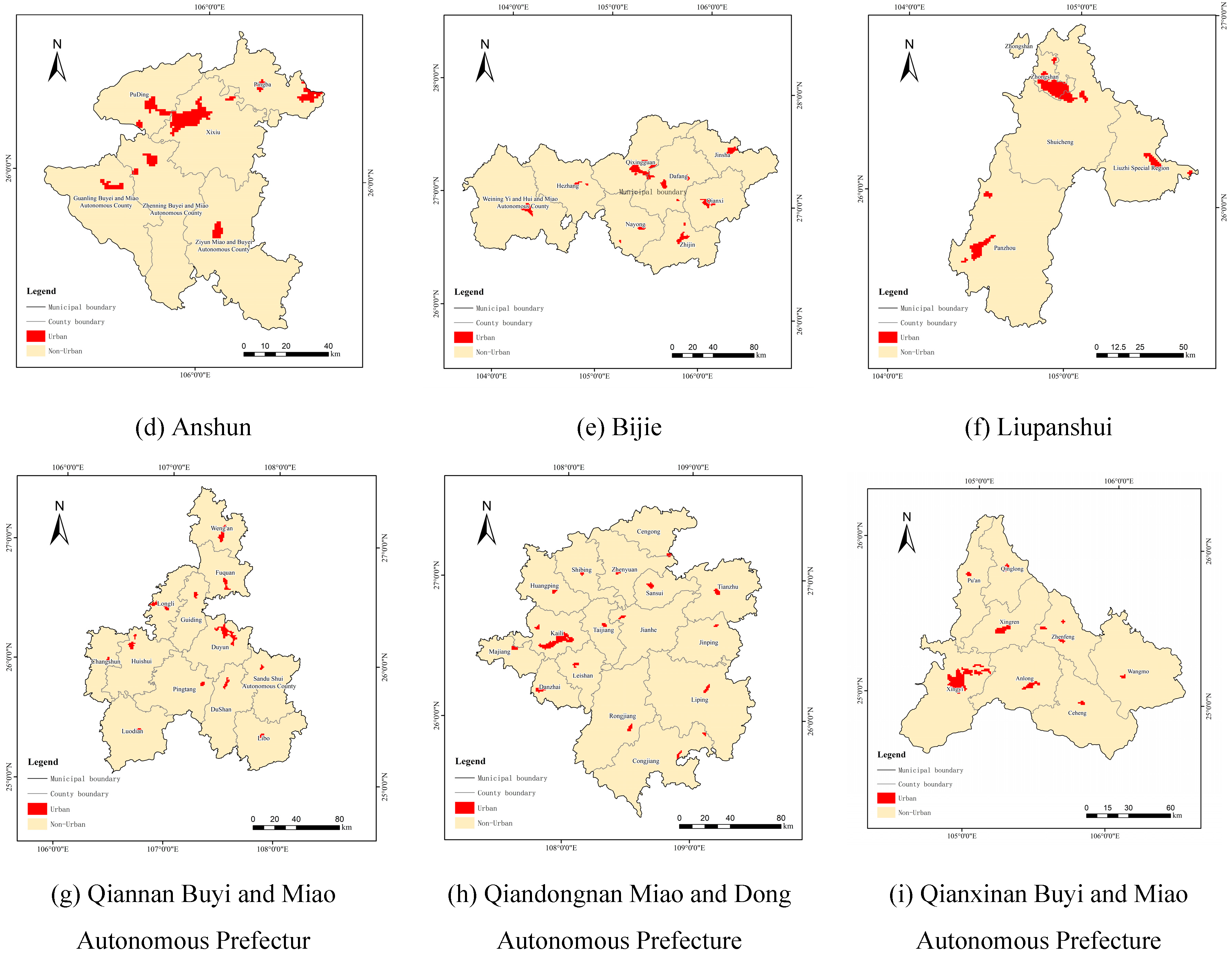
Preprints 94203 g007aPreprints 94203 g007b
Preprints 94203 g008
Figure 8. Overlay of UZURB and World Imagery.
Figure 8. Overlay of UZURB and World Imagery.
Preprints 94203 g008
Preprints 94203 g009
Figure 9. Importance ranking of feature factors.
Figure 9. Importance ranking of feature factors.
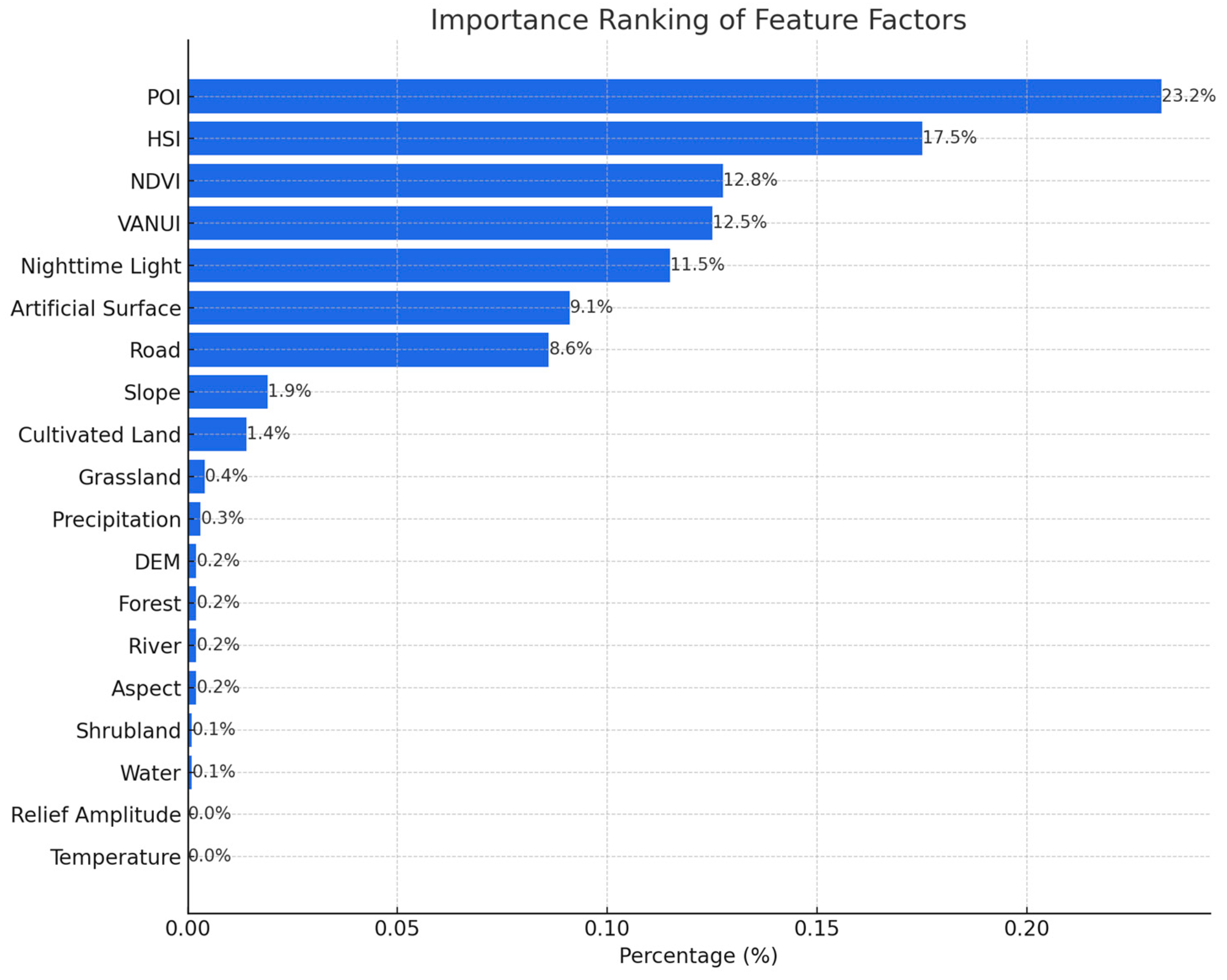
Preprints 94203 g009
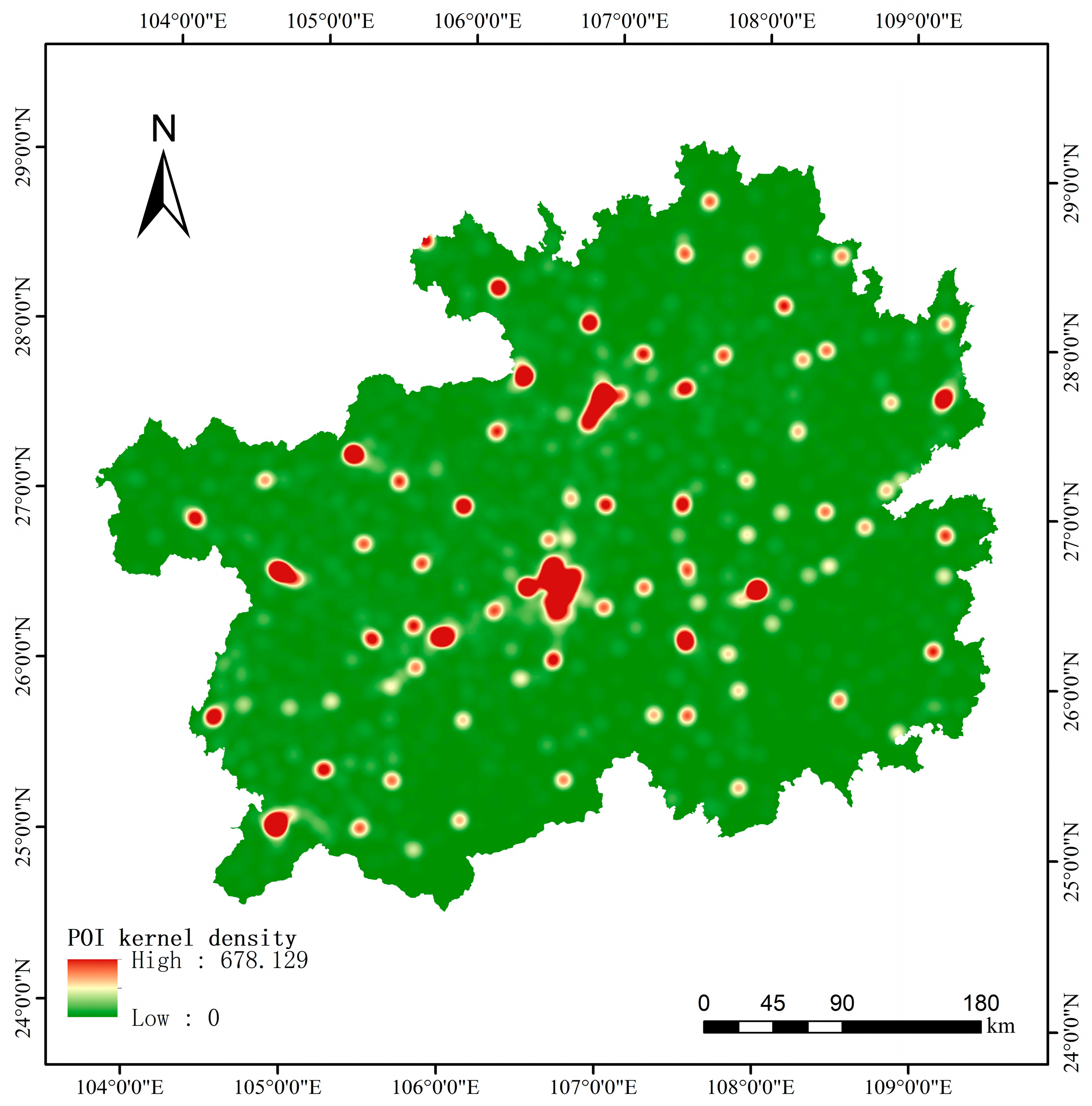
Preprints 94203 g010
Figure 10. Kernel density map of POI data.
Figure 10. Kernel density map of POI data.
Preprints 94203 g010
Table 1. Data information and sources.
Table 1. Data information and sources.
Data Type Data Name Data Year Scale/Resolution Data Sources
Vector data GlobeLand30 2020 30 m https://www.webmap.cn
Administrative division data 2019 1:1,000,000 https://www.webmap.cn
Rivers 2019 1:1,000,000 https://www.webmap.cn
Roads 2020 1:1,000,000 https://www.openstreetmap.org
POI data 2020 - https://lbs.amap.com
Raster data DEM 2020 30 m https://www.gscloud.cn
Meteorological data 2020 1 km https://data.tpdc.ac.cn
NDVI 2020 Spatial resolution: 250m
Temporal resolution: 16 days		 https://ladsweb.modaps.eosdis.nasa.gov
NPP/VIIRS 2020 500 m https://www.ngdc.noaa.gov/eog/dmsp.html
DMSP/OLS 2020 1 km https://payneinstitute.mines.edu
WorldPop 2020 100 m https://www.worldpop.org
LandScan 2020 1000 m https://landscan.ornl.gov
Statistical data Population census data 2020 - http://www.stats.gov.cn
https://www.guizhou.gov.cn
Table 2. Database of population spatialization characteristic factors.
Table 2. Database of population spatialization characteristic factors.
Source of the Characteristic Factor Name of the Characteristic Factor
GlobeLand30 Cultivated land index
Forest index
Grassland index
Shrubland index
Water index
Artificial surface index
Nighttime light data Average brightness of night lights
NDVI Average value of
NDVI index
NDVI and nighttime light data VANUI
HSI
DEM DEM
Slope
Aspect
relief amplitude
River and road data Distance from the road
Distance from the river
Meteorological data Annual average temperature
Annual average precipitation
POI data Kernel density of POI data
Table 3. Parameter setting of the random forest model.
Table 3. Parameter setting of the random forest model.
Parameter Name Parameter Value
Number of decision trees 100
Maximum number of features during partitioning Auto
Minimum number of samples for leaf nodes 1
Maximum depth of the tree 10
Sampling rule With replacement
Out of bag estimation Yes
Table 4. Precision comparison of population spatialization results.
Table 4. Precision comparison of population spatialization results.
Data Year Dataset MAE RMSE %RMSE
2020 Population spatialization 6675.60 29294.23 6.66
WorldPop 53795.71 89286.58 20.29
LandScan 46776.30 94433.72 21.46
Table 5. Accuracy verification of GZURB.
Table 5. Accuracy verification of GZURB.
Urban Nonurban Total UA
Urban 788 27 815 96.69%
Non-urban 212 973 1185 82.11%
Total 1000 1000 2000 -
PA 78.80% 97.30% - -
OA 88.05%
kappa 0.716
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated