Prerpints.org logo
Preprint
Article

Circumventing the Uncertainties of Liquid Phase in the Compositional Control of VLS III-V Ternary Nanowires Based on Group V Intermix

Altmetrics

Downloads

60

Views

6

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 December 2023

Posted:

26 December 2023

You are already at the latest version

Alerts
Abstract
Control over the composition of III-V ternary nanowires grown by the vapor-liquid-solid (VLS) method is essential for bandgap engineering in such nanomaterials and fabrication of functional nanowire heterostructures for a variety of applications. From the fundamental viewpoint, III-V ternary nanowires based on group V intermix (InSbxAs1-x, InPxAs1-x, GaPxAs1-x and many others) present the most difficult case, because the concentrations of highly volatile group V atoms in a catalyst droplet are beyond the detection limit of any characterization technique and therefore principally unknown. Here, we present a model for the vapor-solid distribution of such nanowires, which fully circumvents the uncertainties that remained in the theory so far, and link the nanowire composition to the well-controlled parameters of vapor. The unknown concentrations of group V atoms in the droplet do not enter the distribution, despite of the fact that a growing solid is surrounded by the liquid phase. The model fits quite well the available data on the vapor-solid distributions of VLS InSbxAs1-x, InPxAs1-x and GaPxAs1-x nanowires grown with different catalyst. Even more importantly, it provides a basis for the compositional control of III-V ternary nanowires based on group V intermix, and can be extended over other material systems where two highly volatile elements enter a ternary solid alloy through a liquid phase.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Control over the composition of III-V ternary materials has been a subject of extensive research for decades [1,2]. More recently, III-V ternary nanowires (NWs) and NW-based heterostructures attracted great interest due their fundamental properties and potential applications in Si-integrated optoelectronics and other fields [2,3,4,5,6]. Most III-V NWs are grown by different epitaxy techniques by the VLS method with a catalyst droplet, often Au [7], which can be replaced with a group III metal (Ga) in the self-catalyzed VLS approach [8]. From the fundamental viewpoint, the VLS growth of a ternary AxB1-xC NW is a complex process where the vapor phase containing A, B and C species condenses in a quaternary liquid phase consisting of A, B, C and Au atoms (in the case of Au catalyst) and then crystallizes into a ternary AxB1-xC NW [9,10,11,12,13,14,15,16,17]. The composition of a quaternary liquid in a catalyst droplet is described by three independent variables, for example, (i) the fraction of A atoms in liquid,
y = χ A χ A + χ B ,
where χ A and χ B are the atomic concentrations of A and B atoms in liquid, (ii) the total concentration of A and B atoms in liquid, χ t o t = χ A + χ B , and (iii) the concentration of atoms C in liquid χ C , with χ A u = 1 − χ C − χ t o t . In the self-catalyzed VLS growth, the droplet is a ternary alloy, and the number of independent variables is reduced to two in view of χ A u = 0 . The vapor phase producing three atomic fluxes of A, B and C atoms I A , I B and I C can be described by the fraction of A atoms in vapor,
z = I A I A + I B .
the total flux of A and B atoms I t o t = I A + I B , and the flux ratio ( I A + I B ) / I C . The liquid-solid distribution x ( y ) links the solid and liquid composition, whereas the vapor-solid distribution x ( z ) links the solid and vapor composition [10,12].
Most models for the composition of VLS III-V ternary NWs developed so far treat the liquid-solid growth and hence the liquid-solid distributions, considering liquid as an isolated mother phase without any material exchange with vapor [11,12,13,14,15,16,17]. Here, we study VLS ternary NWs based on group V intermix, with A and B atoms belonging to group V and C atoms belonging to group III. In this case, the liquid-solid growth occurs under group III rich conditions, because the total concentration of highly volatile group V atoms in the droplet χ A + χ B   is always much smaller than χ C . According to Ref. [10], this yields the kinetic liquid-solid distribution of III-V ternary NWs based on group V intermix, given by
y = x + g ( x ) c l + 1 − c l x ,   g x = 1 − x x Γ l c l e ω ( 1 − x ) 2 − β l e ω x 2 ,
c l = D A D B e ψ A − ψ B ,
β l = e μ A l , 0 − μ A C s , 0 − ( μ B l , 0 − μ B C s , 0 ) + ψ A − ψ B = e ∆ μ A C 0 − ∆ μ B C 0 + ψ A − ψ B
Γ l = 1 ( χ A + χ B ) χ C e − ( μ A l , 0 + μ C l , 0 − μ A C s . 0 ) − ψ A − ψ C = 1 ( χ A + χ B ) χ C e − ∆ μ A C 0 − ψ A − ψ C .
Here, ω is the pseudo-binary interaction parameter of AC and BC pairs in solid in thermal units, D k are the diffusion coefficients of k = A, B atoms in liquid, ψ k are the interaction terms in the chemical potentials of A and B atoms in liquid,
μ A l = μ A l , 0 + l n χ A + ψ A ,   μ B l = μ B l , 0 + l n χ B + ψ B ,
μ k l , 0 are the chemical potentials of pure k = A, B and C liquids, and μ k C s , 0 are the chemical potentials of pure solid binaries AC and BC. The expressions for the parameters β l and Γ l in Eqs. (3) are given in the two equivalent forms, with ∆ μ A C 0 = μ A l , 0 + μ C l , 0 − μ A C s . 0 and ∆ μ B C 0 = μ B l , 0 + μ C l , 0 − μ B C s . 0 as the chemical potential differences for pure binaries.
The functional form of the kinetic liquid-solid distribution given by Eqs. (3) is the same as the kinetic vapor-solid distribution for III-V ternary materials based on group III intermix, which are grown under group V rich conditions without any droplet [18]. However, the coefficients in Eqs. (3) are modified and contain the parameters of liquid rather than vapor. While the interaction terms ψ k depend only on χ C with neglect of small corrections containing χ A and χ B (see Ref. [10] for a detailed discussion), the Γ l term is inversely proportional to χ t o t = χ A + χ B . Unfortunately, the very low concentrations of group V elements in the droplet (~0.01 or even less [9]) are below the detection limit of any characterization technique and cannot be measured during or after growth. Furthermore, there is almost no chance that the value of χ A + χ B is kept constant under varying vapor fluxes I A and I B during the VLS growth of a ternary NW, which is why even the use of χ A + χ B as a fitting constant cannot be justified. This uncertainty was not circumvented in Ref. [10], where the obtained vapor-solid distribution contained χ A + χ B . This uncertainty makes the liquid-solid distribution given by Eqs. (3) almost useless for the compositional control over VLS ternary NWs based on group V intermix.
In Ref. [19], a rather general approach was developed which resulted in the analytic vapor-solid distribution of III-V ternary materials:
z ≅ x ε + 1 − 1 ε 1 1 + f 2 x ,
f x = β g ( 1 − x ) x e ω ( 2 x − 1 ) .
This vapor-solid distribution is the sum of the purely kinetic ( z = x ) and equilibrium ( z = 1 / [ 1 + f 2 ( x ) ] ) distributions, whose weighs are regulated by the effective atomic V/III ratio ε related to ( I A + I B ) / I C . Thermodynamic function f x   contains the pseudo-binary interaction constant and the affinity parameter β g which will be given below. When ε is close to unity, the growth of a ternary is kinetically controlled, whereas at ε ≫ 1 the growth occurs under C-poor conditions and the vapor-solid distribution becomes close-to-equilibrium (or nucleation-limited [14,15]). This expression fits very well the compositional data on InSbxAs1-x [2] and AlSbxAs1-x [20] epi-layers as well as Au-catalyzed VLS InSbxAs1-x NWs [21], although no droplet on the NW top was considered in the model of Ref. [19]. In Ref. [21], Borg and coauthors fitted the VLS data using the numerical model of Biefeld [2], which is based on similar considerations as the model of Ref. [19]. Due to the additional diffusion flux of group III (C) atoms from the NW sidewalls to the droplet, the fitting values of the V/III ratios obtained in Refs. [21] and [19] are much smaller than the V/III ratios in vapor. This fundamental observation will be used in this work.
The compositions of VLS III-V ternary NWs based on group V intermix were experimentally studied in many material systems including InSbxAs1-x [21,22,23,24], GaSbxAs1-x [25], InPxAs1-x [26,27], and GaPxAs1-x [28,29,30,31,32], using different epitaxy techniques such as Au-catalyzed metal-organic vapor phase epitaxy (MOVPE) [21,22,25,27], Au-catalyzed chemical beam epitaxy (CBE) [26], Ag-catalyzed [26] and self-catalyzed [23,28,29,30,31] molecular beam epitaxy (MBE) on different substrates, or even the substrate-free Au-catalyzed aerotaxy by MOVPE [32] (see Refs. [11,12] for comprehensive reviews). A limited number of the measured vapor-solid distributions, for example, Au-catalyzed InPxAs1-x [26] and self-catalyzed GaPxAs1-x [29] followed the simplest kinetic Langmuir-McLean shape (see below), with only one parameter describing the different incorporation rates of A and B atoms into a droplet. The comprehensive experimental study of Borg and coauthors [21] revealed the transition from linear z ( x ) dependence of Au-catalyzed InSbxAs1-x NWs at low V/III ratios to a non-linear close-to-equilibrium shape at high V/III ratios. Such a transition was observed much earlier by Biefeld in InSbxAs1-x epi-layers [2] and predicted to be a general phenomenon in Ref. [19] (see Eq. (5)). However, the models of Refs. [2] and [19] considered the vapor-solid growth without any droplet, and their use for modeling the compositions of VLS NWs requires a justification.
Overall, the achieved level of the growth and compositional modeling of VLS III-V ternary NWs based on group V intermix is insufficient for quantitative comparison with the data and even for qualitative understanding of some compositional trends. The principally unknown parameters of the liquid phase should be either fully eliminated or expressed through the known parameters of vapor in the final expressions. Consequently, here we develop a fully self-consistent growth model of such NWs which, under rather general assumptions, leads to the vapor-solid distributions with the circumvented uncertainties in the infinitely low group V concentrations in the droplet. It will be shown that, using some reasonable simplifications, the vapor-solid distribution can be reduced to an approximation which is very close to Eq. (5), where the parameter ε accounts for surface diffusion of group III atoms. The model fits quite well the available compositional data for different VLS NWs based on group V intermix. It justifies the use of the vapor-solid distribution similar to Eq. (5) for VLS NWs [21] and provides a basis for modeling and the compositional tuning of such NWs in general.

2. Model

We consider the steady-state VLS growth of an AxB1-xC NW based on group V intermix under the following assumptions. First, we neglect desorption of group III atoms C from the droplet. This is usual in modeling the VLS growth by MBE [9,33] and MOVPE [34], and supported by the data of Ref. [35] showing that group III atoms can re-emit from a masked surface but not from the NW sidewalls or droplet. As a result, a NW ensemble of sufficient volume is able to collect all group III atoms sent from vapor. The absence of group III desorption from the droplet is also supported by the measured vapor-solid distributions of III-V ternary NWs based on group III intermix, whose shape is close to the Langmuir-McLean shape in most cases [10]. Second, we assume that the droplet volume does not change with time, at least after a certain incubation stage where the measured NW composition can be different from its steady-state value. This assumption is usual in modeling of Au-catalyzed VLS growth [9,33,34]. Self-catalyzed VLS growth is different, because the droplet serves as a non-stationary reservoir of group III atoms which can either swell or shrink depending on the effective V/III ratio [36,37]. However, the droplet volume should self-equilibrate to a steady-state value corresponding to equal group III and group V flows and stay constant after that [36,37,38]. Third, we assume that group V atoms are not diffusive and enter NWs only through their droplets [8,36,37,38,39]. Fourth, we consider that the arriving group V species are A2 and B2 dimers, as usual in MBE [39]. This assumption is not critical. The model can be re-arranged, for example, for A4 and B4 tetramers or group V precursors containing only one group V atom, such as AsH3 or PH3. However, these precursors most probably decompose in vapor before reaching the droplet surface, resulting in the fluxes of V2 dimers or V4 tetramers depending on the growth temperature.
Under these assumptions, the steady-state VLS growth of a ternary NW based on group V intermix is described by the two equations:
x σ C I C = 2 σ A I A 2 − I A d e s ,
( 1 − x ) σ C I C = 2 σ B I B 2 − I B d e s .
Here, σ A and σ B are the vapor-liquid incorporation rates or, more precisely, the effective adsorption coefficients giving the ratio of the number A or B atoms entering the droplet over the total number of these atoms impinging onto the droplet surface. They account for a possible difference in A and B beam angles in the directional deposition techniques such as MBE. These σ A and σ B in our notation do not include desorption. Similarly, σ C is the effective collection efficiency of group III atoms on the droplet surface, NW sidewalls and possibly the substrate surface. For III-V NWs, σ C may be much larger than σ A and σ B , because most group III atoms are collected by the droplet from solid surfaces surrounding the droplet [9,21,26,33,34,35,36,37]. The I A 2 and I B 2 denote the vapor fluxes of A2 and B2 dimers, brining 2 group V atoms each, whereas I A d e s and I B d e s denote the desorption fluxes of A and B atoms. The vapor composition for the fluxes of group V dimers is given by
z = I A 2 I A 2 + I B 2 ,
which is the same as Eq. (2) due to I A = 2 I A 2 and I B = 2 I B 2 .
Equations (6) are similar to the ones considered in Ref. [10], However, there is one important difference. In Ref. [10], we used the unknown NW growth rate G instead of I C in the left-hand-side, which was then eliminated by dividing one equation to the other. This did not allow us to circumvent the uncertainty in the unknown total concentration of group V atoms in the droplet, which remained in the vapor-solid distribution. Now, Eqs. (6) contain the known group III flux σ C I C , which determines the NW growth rate in the absence of desorption. It equals the total influx of A and B atoms minus their total desorption fluxes. This follows from summing up the two Eqs. (6). Our aim is to express the unknown group V concentrations in the droplet χ A and χ B (or, equivalently, y and χ t o t = χ A + χ B ) through the vapor fluxes. To do that, we need to find the desorption fluxes as functions of χ A and χ B . We define the desorption fluxes as the vapor fluxes which are at equilibrium with liquid at a given composition, like in Ref. [39] for a binary III-V NW. The vapor-liquid equilibrium corresponds to
μ A 2 g = 2 μ A l ,   μ B 2 g = 2 μ B l ,
where μ A 2 g and μ B 2 g are the chemical potentials of A2 and B2 dimers in vapor.
Considering that vapor is a mixture of perfect gases, the chemical potentials of A2 and B2 dimers are logarithmic functions of the fluxes
μ A 2 g = 2 μ A l , 0 + l n I A 2 σ A I A 2 0 ,   μ B 2 g = 2 μ B l , 0 + l n I B 2 σ B I B 2 0 .
Here, we prefer to use the reference states of A2 and B2 vapors corresponding to the fluxes σ A I A 2 0 and σ B I B 2 0 that are at equilibrium with pure A and B liquids (having the chemical potentials μ A l , 0 and μ B l , 0 ). We choose the reference fluxes with the same incorporation rates σ A and σ B as for a quaternary droplet. It will be shown later that using the reference fluxes I A 2 e q = σ A I A 2 0 and I B 2 e q = σ B I B 2 0 (corresponding to σ A = σ B = 1 ) does not affect the final result.
Using Eqs. (9) and Eqs. (4) for the chemical potentials μ A l and μ B l in Eqs. (8), we obtain the desorption fluxes in the form
I A d e s = 2 I A 2 d e s = 2 σ A I A 2 0 e 2 ψ A χ A 2 ,   I B d e s = 2 I B 2 d e s = 2 σ B I B 2 0 e 2 ψ B χ B 2 .
According to these expressions, the desorption fluxes are proportional to the squared concentrations of A and B atoms in liquid, because group V atoms always desorb in the form of dimers [39,40]. Substitution of these desorption fluxes into Eqs. (6), along with the definitions for y given by Eq. (1) and z by Eq. (7), leads to
I A 2 0 e 2 ψ A ( χ A + χ B ) 2 y 2 I A 2 + I B 2 = z − σ C I C 2 σ A I A 2 + I B 2 x ,
I B 2 0 e 2 ψ B χ A + χ B 2 ( 1 − y ) 2 I A 2 + I B 2 = 1 − z − σ C I C 2 σ B I A 2 + I B 2 ( 1 − x ) .
This gives two equations for the two unknowns χ A + χ B and y which contain, however, the vapor composition z and the solid composition x . Summing up Eqs. (11) and (12), we find
χ A + χ B 2 = I A 2 + I B 2 − ( σ C / 2 σ A ) I C [ x + c g ( 1 − x ) ] I A 2 0 e 2 ψ A y 2 + I B 2 0 e 2 ψ B ( 1 − y ) 2 ,
with
c g = σ A σ B
as the ratio of the vapor-liquid condensation rates of A and B atoms. Importantly, χ A + χ B is independent of the vapor composition z . However, it depends on the liquid composition y and the solid composition x , becoming x -independent only when c g = 1 .
Inferring ( 1 − z ) / z from Eqs. (11) and (12), we get
z = 1 1 + F ,   F = σ C / 2 σ B I C 1 − x + I B 2 0 e 2 ψ B χ A + χ B 2 ( 1 − y ) 2 σ C / 2 σ A I C x + I B 2 0 e 2 ψ B χ A + χ B 2 ( 1 − y ) 2 .
Using Eq. (13), after some simple manipulations we obtain the main result of this work in the form
z = x ε + 1 − x + c g ( 1 − x ) ε 1 1 + ζ [ ( 1 − y ) / y ] 2 ,
with the parameters
ε = 2 σ A ( I A 2 + I B 2 ) σ C I C ,
ζ = I B 2 0 I A 2 0 e 2 ( ψ B − ψ A ) .
Clearly, the parameter   ε determines the effective ratio of the total flux of group V atoms over the flux of group III atoms entering the droplet. In the simplest model for surface diffusion of group III adatoms [9], the σ A / σ C   ratio is given by σ A / σ C = 1 / ( 1 + a λ 3 / R ) , where λ 3 is the diffusion length of group III adatoms on the NW sidewalls, R is the NW radius and a is a constant related to the droplet contact angle and the epitaxy technique. Therefore,
ε = F 53 1 + a λ 3 / R
in III-V NWs is largely reduced with respect to the atomic V/III flux ratio in vapor F 53 , particularly for thin NWs with λ 3 / R ≫ 1 .

3. Results and discussion

In our model, the effective V/III ratio is allowed to vary in the range x + c g ( 1 − x ) ≤ ε ≤ ∞ to preserve the steady-state VLS growth conditions with a constant droplet volume. At ε = x + c g ( 1 − x ) , the incoming group V and III fluxes equal each other and all the arriving atoms are incorporated into the NW, meaning that the group V desorption fluxes are negligible. In this kinetic VLS regime, the vapor-solid distribution given by Eq. (16) is reduced to the one-parametric Langmuir-McLean formula
z = x x + c g ( 1 − x ) .
For larger ε , a fraction of A2 and B2 dimers must desorb from the droplet surface. In this case, the vapor-solid distribution is described by Eq. (16), in which the liquid composition y should be calculated using Eqs. (3). The previously unknown χ A + χ B in the parameter Γ l is now given by Eq. (13). Therefore, Γ l becomes a function of y and x . Inferring the explicit dependence y x from Eq. (13) requires the solution of a quadratic equation for y . Substitution of the obtained y ( x ) into Eq. (16) yields the analytic vapor-solid distribution z ( x ) . This z ( x ) is a function of vapor fluxes and the parameters of the liquid phase which depend only on χ C . Therefore, the general vapor-solid distribution at intermediate ε contains a parametric dependence on χ C , which can be measured during [41] or after [9] growth.
This complicated procedure is not required for practical purposes. We now show that the parameters of liquid can be fully circumvented in the following approximation. The limiting behavior at ε → ∞ corresponds to no-growth conditions where the arriving fluxes of A2 and B2 atoms are equalized by the desorption fluxes. In this case, AC and BC pairs in liquid should also be at equilibrium with solid. The liquid-solid equilibrium in a ternary system corresponds to [13]
μ A l + μ C l = μ A C s ,   μ B l + μ C l = μ B C s ,
where μ A C s and μ B C s are the composition-dependent chemical potentials of AC and BC pairs in solid. Using Eqs. (4) and the same expression for C atoms, μ C l = μ C l , 0 + l n χ C + ψ C , along with the regular solution model for the chemical potentials in solid, μ A C s = μ A C s , 0 + l n x + ω ( 1 − x ) 2 and μ B C s = μ B C s , 0 + l n ⁡ ( 1 − x ) + ω x 2 (Refs. [10,11,12,13,14,15,16,17,18,19]), Eqs. (21) are equivalent to
( χ A χ c ) e q = e − ( μ A l , 0 + μ C l , 0 − μ A C s . 0 ) − ψ A − ψ C x e ω ( 1 − x ) 2 ,
( χ B χ c ) e q = e − ( μ B l , 0 + μ C l , 0 − μ B C s . 0 ) − ψ B − ψ C ( 1 − x ) e ω x 2 .
Upon substitution of these expressions into Eqs. (3), the simple calculation shows that the kinetic liquid-solid distribution is reduced to the equilibrium one [10,13,14,15]:
y e q = 1 1 + β l ( 1 − x ) e ω ( 2 x − 1 ) / x ,
where β l is the same as in Eq. (3). For the equilibrium liquid-solid distribution, we have
1 1 + ζ [ ( 1 − y e q ) / y e q ] 2 = 1 1 + f 2 ( x ) ,
where the equilibrium function f ( x ) is the same as in Eq. (5), and the affinity parameter is given by
β g = I B 2 0 I A 2 0 e ∆ μ A C 0 − ∆ μ B C 0 .
Using the approximation y = y e q in Eq. (16), the analytic vapor-solid distribution is obtained in the form:
z ≅ x ε + 1 − x + c g ( 1 − x ) ε 1 1 + f 2 ( x ) ,
f x = β g ( 1 − x ) x e ω ( 2 x − 1 ) ,
where c g is given by Eq. (14) and β g is given by Eq. (25). At c g = 1 , it is reduced to the result of Ref. [19] given by Eq. (4). If we re-write Eqs. (9) as
μ A 2 g = 2 μ A l , 0 + l n I A 2 I A 2 e q ,   μ B 2 g = 2 μ B l , 0 + l n I B 2 I B 2 e q ,
with I A 2 e q = σ A I A 2 0 and I B 2 e q = σ B I A 2 0 as the equilibrium fluxes at σ A = σ B = 1 , all the results remain, with β g modified to
β g = c g I B 2 e q I A 2 e q e ∆ μ A C 0 − ∆ μ B C 0 .
Thus, the analytic vapor-solid distribution of VLS III-V ternary NWs based on group V intermix is given by Eq. (26) and is very close to the vapor-solid distribution for III-Vx-V1-x materials grown in the vapor-solid mode without any droplet [19]. The main difference is in the ε parameter, which equals the atomic V/III flux ratio in vapor for the vapor-solid growth, while for VLS NWs it accounts for the fact that a catalyst droplet is able to collect much more group III atoms from the surrounding surfaces (as given, for example, by Eq. (19)). The other difference is in the parameter c g that describes the effect of different condensation rates of A2 and B2 dimers into the droplet. These rates are usually assumed equal for the vapor-solid growth, corresponding to c g = 1 . The obtained result is similar to Ref. [42], where it was shown that the vapor-solid distribution of VLS III-V ternary NWs based on group III intermix is kinetic, despite of the fact that the corresponding liquid-solid distribution is close-to-equilibrium [10]. Equation (26) is approximate, because it uses the equilibrium shape of the liquid-solid distribution at intermediate ε which, strictly speaking, is valid only under no-growth conditions at ε → ∞ . Similar approximation was used in Ref. [19] for obtaining Eq. (3).
The shape of the vapor-solid distribution given by Eq. (26) is determined by the two thermodynamic parameters ω and β g , and the two kinetic parameters c g and ε . The effective V/III ratio can easily be changed in the VLS growth experiments. The other parameters are independent of ε in the first approximation and determined primarily by the material system, growth catalyst and temperature. Figure 1 shows the vapor-solid distributions obtained from Eq. (26) for a model system with a fixed ω = 1.6, β g = 0.3, c g = 2 and different ε . Although the miscibility gap is absent ( ω < 2 ), the equilibrium distribution and the distribution at a large ε = 20 are non-linear. They are shifted to the right due to a small β g = 0.3 , meaning that obtaining a noticeable fraction of AC pairs in a NW requires a much larger fraction of A atoms in vapor. As the effective V/III ratio decreases, the curves get closer to the kinetic Langmuir-McLean shape, which favors the vapor-liquid incorporation of A atoms with respect to B atoms at c g = 2. In principle, any vapor-solid distribution between the equilibrium and kinetic curves is possible, and can be achieved by tuning the total V/III ratio at a fixed temperature (for example, by changing the total group V flux at a fixed group III flux).
Such a behavior was observed in InSbxAs1-x epi-layers [2], AlSbxAs1-x epi-layers [20], and more recently in Au-catalyzed VLS InSbxAs1-x NWs [21]. These NWs were grown by MOVPE on InAs(111)B substrates at 450 oC using TMIn, TMSb and AsH3 precursors, with 50 nm diameter colloidal Au nanoparticles as the VLS growth seeds. The total V/III flux ratio in vapor F 53 was set to 15, 27 and 56 by varying group V fluxes at a constant TMIn flux. These vapor-solid distributions were analyzed in our recent work [19]. Here, we extend the analysis by considering the vapor-solid distributions of InSbxAs1-x NWs together with epi-layers that were grown concomitantly with the NWs [21]. Figure 2 shows the measured vapor-solid distributions of InSbxAs1-x NWs and epi-layers. The ω value at 450 oC is well-known and equals 1.566 [19,43]. The vapor-solid growth of epi-layers at a high F 53 of 27 must yield a close-to-equilibrium shape of the corresponding distribution. This allows us to choose a β g value of 0.34, which is close to the equilibrium constant of 0.429 given in Ref. [1] and used for modeling in Ref. [21]. The kinetic curve, obtained for NWs at F 53 = 15 , is linear. This should correspond to c g = 1 , that is, equal incorporation rates of Sb and As into the droplet. Assuming that β g is the same for epi-layers and NWs (which is not guaranteed in the general case), the different behaviors of the vapor-solid distributions in Figure 2 are entirely due to different ε values in Eq. (26). For epi-layers, the fitting value of ε = 27 is the same as F 53 is vapor. For NWs, the fitting values of ε   are 11-16 times smaller than F 53 is vapor, which is explained by the additional fluxes of diffusive In adatoms from the surrounding surfaces as compared to the surrounding vapor. This observation was made in the original work [21].
Before discussing the data on VLS InPxAs1-x and GaPxAs1-x NWs, we note that the parameter β g given by Eq. (25) or Eq. (28) contains the exponential of the well-known difference of chemical potentials for pure binaries ∆ μ A C 0 − ∆ μ B C 0 [44,45,46], while the pre-exponential factor (for example, [ c g I B 2 e q / I A 2 e q ] 1 / 2 in Eq. (28)) is less obvious. It is different from what is usually considered in the equilibrium constants for surface reactions [1,2,20]. These constants describe the equilibrium of binary or more complex vapors with binary solids, while our I A 2 e q and I B 2 e q are the equilibrium fluxes for pure group V liquids. Our β g also includes the unknown parameter c g . An accurate analysis of these factors is beyond the scope of this work. In what follows, we will use β g as a fitting value, but taking into account the thermodynamic trend that follows from the exponential factor e x p ⁡ ( ∆ μ A C 0 − ∆ μ B C 0 ) in the affinity parameter.
Figure 3 shows the vapor-solid distributions of Au-catalyzed InPxAs1-x NWs obtained by Persson and coauthors [26]. These NWs were grown by CBE on InAs(111)B substrates using 50 nm diameter colloidal Au droplets, which resulted in ~ 60 nm diameter NWs. The growth started with InAs NW stems and continued with InPxAs1-x sections grown at three different temperatures of 390 oC, 405 oC and 435 oC. The total V/III flux ratio in vapor during growth of InPAs sections was in the range from 30 to 45. It is seen that the values of z are systematically larger than x , meaning that the incorporation of P atoms is lower than for As atoms. The authors fitted the data using the kinetic Langmuir-McLean Eq. (20) with the low c g values that increased from 0.105 at 390 oC to 0.175 at 435 oC (dashed lines in Figure 3). The values of e x p ⁡ ( ∆ μ I n P 0 − ∆ μ I n A s 0 ) equal 0.233 at 390 oC, 0.2375 at 405 oC, and 0.244 at 435 oC [44,45,46]. This shows a thermodynamic trend for having a smaller fraction of P atoms in vapor than in solid in the whole temperature domain studied in Ref. [26]. Very high V/III flux ratios employed in this work should lead to desorption of the excessive P and As atoms from the droplet surface, as in the previous case of InSbxAs1-x NWs. Therefore, we fit the data using the general equation Eq. (26), using the ε values that are noticeably larger than unity. They appear close to InSbAs NWs under similar V/III flux ratios in vapor. The best fits are obtained with β g = 0.1   at 390 oC, 0.13 at 405 oC, and 0.2 at 435 oC, and c g = 1 in all cases (solid lines in Figure 3). These curves provide slightly better fits than the Langmuir-McLean formula.
It is interesting to note that these fitting values are very close to the effective ratios of the P over As incorporation rates obtained in Ref. [26]. This is most probably explained by relatively weak interactions of InP and InAs pairs in solid, corresponding to the low ω values given in Table 1. In this case, the equilibrium distribution in Eq. (26) is close to the Langmuir-McLean shape. This property follows directly from Eq. (26) for f ( x ) at ω → 0 . Therefore, fitting the vapor-solid distributions of III-V ternary NWs with low pseudo-binary interaction parameters ω by the one-parametric Langmuir-McLean formula is entirely possible [13,14,15,47]. The effective ratio of the incorporation rates of different group V atoms must, however, include the differences in the desorption rates and the dependence on the total V/III flux ratio, as in our model.
GaPAs is another example of a ternary material with low ω , which are in the range from 0.64 to 0.7 in the typical growth temperature window of 550-630 oC (see Table 1). In contrast to InPAs, the difference of chemical potentials ⁡ ∆ μ G a P 0 − ∆ μ G a A s 0 is positive, yielding the values of e x p ⁡ ( ∆ μ G a P 0 − ∆ μ G a A s 0 ) ranging from 1.849 at 550 oC to 1.782 at 630 oC [44,45]. This should favor faster incorporation of P atoms relative to As atoms and, consequently, a larger P fraction in vapor relative to solid in close-to-equilibrium growth regimes under high V/III flux ratios. Figure 4 show the compilation of the vapor-solid distributions of VLS GaPxAs1-x NWs from the four works. Metaferia and coauthors grew the NWs by Au-catalyzed MOVPE using the substrate-free aerotaxy at 550 oC, under a low total V/III flux ratios in vapor from 0.82 to 1.64 [32]. Other GaPxAs1-x NWs [28,30] or GaPxAs1-x sections in GaP NWs [31] were grown by the self-catalyzed MBE (with Ga droplets) on Si(111) substrates. Himwas and coauthors [28] grew the NWs at 610 oC under the total V/III flux ratios ranging from 10 to 12. Zhang and coauthors [30] and Bolshakov and coauthors [31] grew the NWs at 630 oC under higher total V/III ratios, ranging from 40 to 80 in Ref. [30] and from 16 to 32 in Ref. [31]. Different procedures for preparation of Ga droplets were used and resulted in different NW surface densities, diameters and lengths. The vapor-solid distribution of the NWs grown by aerotaxy at low V/III ratios corresponds to a lower incorporation rate of P atoms, while the other NWs grown at much higher V/III ratios exhibit the opposite trend. The vapor-solid distributions obtained by Zhang and coauthors [30] and Bolshakov and coauthors [31] at 630 oC are very close to each other.
Figure 4 (a) shows the fits to the whole set of data obtained from Eq. (26) with different ε . The data of Ref. [32] at low F 53   are fitted with a minimum ε corresponding to the Langmuir-McLean shape at c g = 0.27 , as in the original work. The MBE data of Refs. [28], [30] and [31] are fitted with large ε of 1.8, 2.97 and 4.5, using the same parameter β g = 3.1 in the equilibrium distribution and the same c g = 0.27 . The value of c g   is not critical for these fits. The MBE data can be well-fitted using, for example, c g = 1 using slightly different ε values. This figure shows the same trend as in Figs. 1 and 2, that is, transitioning of the kinetic distribution to the equilibrium shape with increasing the total V/III ratio. Figure 4 (b) shows that the equally good fits can be obtained using the Langmuir-McLean formula with different c g for all the data. The fitting value of the effective ratio of the incorporation rates of P over As atoms increases from 0.27 to 4.05 (the fitting value of 2.97 was obtained by Zhang and coauthors in Ref. [30] for their data). It would be difficult to explain this trend without considering desorption of the excessive group V atoms in MBE growths under very high V/III ratios. As in the previous case, the Langmuir-McLean shapes provide the excellent fits due to a low ω values in this material system.

4. Conclusions

In summary, we have shown that the uncertainty in the unmeasurable group V concentrations in a catalyst droplet can be fully circumvented by considering the growth kinetics of VLS III-V ternary NWs based on group V intermix in the entire VLS growth process rather than in the liquid-solid growth alone. The self-consistent vapor-solid distribution of VLS III-V NWs is close to the shape obtained earlier for the vapor-solid growth without any droplet. The simple analytic form of the distribution is useful for the analysis of the data, and fits well the available data on InSbxAs1-x, InPxAs1-x and GaPxAs1-x NWs grown by different epitaxy techniques at different temperatures and with different metal catalysts.
This works presents the first attempt to obtain a general vapor-solid distribution of VLS III-V ternary NWs based on group V intermix beyond the common one-parametric Langmuir-McLean approach. This enables us to model and explain some compositional trends which are inaccessible in the common approach, in particular, the strong dependence of the vapor-solid distribution on the total V/III flux ratio. We have used several approximations in deriving the final result. The most important approximation is the effective absence of desorption, or downward diffusion of group III atoms from the droplet. This process may become important at higher temperatures. If such sink of group III atoms is present, the governing equations should include the outgoing flux of group III atoms, which depends on the group III concentration in the droplet. We plan to consider this refinement in a forthcoming work. It will be interesting to test the model against the data on VLS NWs of ternary III-V materials with the miscibility gaps at a growth temperature, for example, GaSbxAs1-x or AlSbxAs1−x NWs, where the miscibility gaps can be suppressed by tuning the V/III flux ratio. Overall, this simple model for the complex ternary material system should be useful for understanding and tuning the compositions of different III-V NWs based on group V intermix, and may be extended to other material systems with highly volatile growth species.

Funding

This research was supported by the research grant of St. Petersburg State University (ID 94033852).

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Panish, M. B.; Ilegams, M. Progress in solid state chemistry, v. 7, Pergamon Press, New York, 1972.
  2. Biefeld, R. M. The preparation of InSb and InAs1−xSbx by metalorganic chemical vapor deposition. J. Cryst. Growth 1986, 75, 255. [Google Scholar] [CrossRef]
  3. McIntyre, P. C.; Fontcuberta i Morral, A. Semiconductor nanowires: to grow or not to grow? Mater. Today Nano 2020, 9, 100058. [Google Scholar] [CrossRef]
  4. Hyun, J. K.; Zhang, S.; Lauhon, L. J. Nanowire heterostructures. Ann. Rev. Mater. Research 2013, 43, 451. [Google Scholar] [CrossRef]
  5. Boras, G.; Yu, X.; Liu, H. III–V ternary nanowires on Si substrates: growth, characterization and device applications. J. Semicond 2019, 40, 101301. [Google Scholar] [CrossRef]
  6. Martelli, F. III-V ternary nanowires, In: Advances in III-V Semiconductor Nanowires and Nanodevices, Li, J., Wang, D., LaPierre, R.R., Eds.; Bentham Science: Sharjah, United Arab Emirates, 2011; pp. 105–128.
  7. Wagner, R. S.; Ellis, W. C. Vapor-liquid-solid mechanism of single crystal growth. Appl. Phys. Lett. 1964, 4, 89. [Google Scholar] [CrossRef]
  8. Colombo, C.; Spirkoska, D.; Frimmer, M.; Abstreiter, G.; Fontcuberta i Morral, A. Ga-assisted catalyst-free growth mechanism of GaAs nanowires by molecular beam epitaxy. Phys. Rev. B 2008, 77, 155326. [Google Scholar] [CrossRef]
  9. Dubrovskii, V. G.; Glas, F. Vapor–liquid–solid growth of semiconductor nanowires, In: N. Fukata, R. Rurali (eds) Fundamental Properties of Semiconductor Nanowires. Springer, Singapore, 2020. [CrossRef]
  10. Dubrovskii, V. G. Liquid-solid and vapor-solid distributions of vapor-liquid-solid III-V ternary nanowires. Phys. Rev. Materials 2023, 7, 096001. [Google Scholar] [CrossRef]
  11. Ghasemi, M.; Leshchenko, E. D.; Johansson, J. Assembling your nanowire: an overview of composition tuning in ternary III–V nanowires. Nanotechnology 2021, 32, 072001. [Google Scholar] [CrossRef] [PubMed]
  12. Leshchenko, E. D.; Dubrovskii, V. G. An overview of modeling approaches for compositional control in III–V ternary nan-owires. Nanomaterials 2023, 13, 1659. [Google Scholar] [CrossRef]
  13. Glas, F. Comparison of modeling strategies for the growth of heterostructures in III–V nanowires. Cryst. Growth Des. 2017, 17, 4785. [Google Scholar] [CrossRef]
  14. Dubrovskii, V. G.; Koryakin, A. A.; Sibirev, N. V. Understanding the composition of ternary III-V nanowires and axial nanowire heterostructures in nucleation-limited regime. Mater. Design 2017, 132, 400. [Google Scholar] [CrossRef]
  15. Johansson, J.; Ghasemi, M. Composition of gold alloy seeded InGaAs nanowires in the nucleation limited regime. Cryst. Growth Des. 2017, 17, 1630–1635. [Google Scholar] [CrossRef]
  16. Johansson, J.; Ghasemi, M. Kinetically limited composition of ternary III-V nanowires. Phys. Rev. Materials 2017, 1, 040401(R). [Google Scholar] [CrossRef]
  17. Leshchenko, E. D.; Johansson, J. Role of thermodynamics and kinetics in the composition of ternary III-V nanowires. Nanomaterials 2020, 10, 2553. [Google Scholar] [CrossRef] [PubMed]
  18. Dubrovskii, V. G.; Leshchenko, E. D. Kinetically controlled composition of III-V ternary nanostructures. Phys. Rev. Materials 2023, 7, 056001. [Google Scholar] [CrossRef]
  19. Dubrovskii, V. G.; Leshchenko, E. D. Composition of III-V ternary materials under arbitrary material fluxes: the general approach unifying kinetics and thermodynamics. Phys. Rev. Materials 2023, 7, 074603. [Google Scholar] [CrossRef]
  20. Chen, W.-K.; Chin, M.-T. Influence of thermodynamic factors on growth of AlAs1-xSbx Alloys. Jpn. J. Appl. Phys. 1994, 33, 1370. [Google Scholar] [CrossRef]
  21. Borg, B. M.; Dick, K. A.; Eymery, J.; Wernersson, L.-E. Enhanced Sb incorporation in InAsSb nanowires grown by metalorganic vapor phase epitaxy. Appl. Phys. Lett. 2011, 98, 113104. [Google Scholar] [CrossRef]
  22. Namazi, L.; Ghalamestani, S. G.; Lehmann, S.; Zamani, R. R.; Dick, K. A. Direct nucleation, morphology and compositional tuning of InAs1−xSbx nanowires on InAs (111)B substrates. Nanotechnology 2017, 28, 165601. [Google Scholar] [CrossRef]
  23. Zhuang, Q. D.; Alradhi, H.; Jin, Z. M.; Chen, X. R.; Shao, J.; Chen, X.; Sanchez, A. M.; Cao, Y. C.; Liu, J. Y.; Yates, P.; Durose, K.; Jin, C. J. Optically-efficient InAsSb nanowires for silicon-based mid-wavelength infrared optoelectronics. Nanotechnology 2017, 28, 105710. [Google Scholar] [CrossRef]
  24. Wen, L.; Pan, D.; Liu, L.; Tong, S.; Zhuo, R.; Zhao, J. Large-composition-range pure-phase homogeneous InAs1–xSbx nanowires. J. Phys. Chem. Lett. 2022, 13, 598. [Google Scholar] [CrossRef] [PubMed]
  25. Yuan, X.; Caroff, P.; Wong-Leung, J.; Tan, H. H.; Jagadish, C. Controlling the morphology, composition and crystal structure in gold-seeded GaAs1−xSbx nanowires. Nanoscale 2015, 7, 4995. [Google Scholar] [CrossRef]
  26. Persson, A.I.; Bjork, M.T.; Jeppesen, S.; Wagner, J.B.; Wallenberg, L.R.; Samuelson, L. InAs1-xPx nanowires for device engineering. Nano Lett. 2006, 6, 403. [Google Scholar] [CrossRef] [PubMed]
  27. Mandl, B.; Keplinger, M.; Messing, M.E.; Kriegner, D.; Wallenberg, R.; Samuelson, L.; Bauer, G.; Stangl, J.; Holy, V.; Deppert, K. Self-seeded axio-radial InAs-InAs1-xPx nanowire heterostructures beyond “common” VLS growth. Nano Lett. 2018, 18, 144. [Google Scholar] [CrossRef]
  28. Himwas, C.; Collin, S.; Rale, P.; Chauvin, N.; Patriarche, G.; Oehler, F.; Julien, F.H.; Travers, L.; Harmand, J.C.; Tchernycheva, M. In situ passivation of GaAsP nanowires. Nanotechnology 2017, 28, 495707. [Google Scholar] [CrossRef]
  29. Zhang, Y.; Sanchez, A.M.; Sun, Y.; Wu, J.; Aagesen, M.; Huo, S.; Kim, D.; Jurczak, P.; Xu, X.; Liu, H. Influence of droplet size on the growth of self-catalyzed ternary GaAsP nanowires. Nano Lett 2016, 16, 1237. [Google Scholar] [CrossRef]
  30. Zhang, Y.; Aagesen, M.; Holm, J. V.; Jørgensen, H. I.; Wu, J.; Liu, H. Self-catalyzed GaAsP nanowires grown on silicon substrates by solid-source molecular beam epitaxy. Nano Lett. 2013, 13, 3897. [Google Scholar] [CrossRef]
  31. Bolshakov, A. D.; Fedorov, V. V.; Sibirev, N. V.; Fetisova, M. V.; Moiseev, E. I.; Kryzhanovskaya, N. V.; Koval, O. Yu.; Ubyivovk, E. V.; Mozharov, A. M.; Cirlin, G. E.; Mukhin, I. S. Growth and characterization of GaP/GaPAs nanowire heterostructures with controllable composition. Phys. Stat. Sol. RRL 2019, 13, 1900350. [Google Scholar] [CrossRef]
  32. Metaferia, W.; Persson, A.R.; Mergenthaler, K.; Yang, F.; Zhang, W.; Yartsev, A.; Wallenberg, R.; Pistol, M.E.; Deppert, K.; Samuelson, L.; Magnusson, M. H. GaAsP nanowires grown by aerotaxy. Nano Lett 2016, 16, 5701. [Google Scholar] [CrossRef]
  33. Plante, M. C.; LaPierre, R. R. Analytical description of the metal-assisted growth of III–V nanowires: Axial and radial growths. J. Appl. Phys. 2009, 105, 114304. [Google Scholar] [CrossRef]
  34. Borg, M.; Johansson, J.; Storm, K.; Deppert, K. Geometric model for metalorganic vapour phase epitaxy of dense nanowire arrays. J. Cryst. Growth 2013, 366, 15. [Google Scholar] [CrossRef]
  35. Oehler, F.; Cattoni, A.; Scaccabarozzi, A.; Patriarche, G.; Glas, F.; Harmand, J. C. Measuring and modeling the growth dynamics of self-catalyzed GaP nanowire arrays. Nano Lett. 2018, 18, 701. [Google Scholar] [CrossRef]
  36. Schroth, P.; Köhl, M.; Hornung, J.-W.; Dimakis, E.; Somaschini, C.; Geelhaar, L.; Biermanns, A.; Bauer, S.; Lazarev, S.; Pietsch, U.; Baumbach, T. Evolution of polytypism in GaAs nanowires during growth revealed by time-resolved in situ x-ray diffraction. Phys. Rev. Lett. 2015, 114, 055504. [Google Scholar] [CrossRef] [PubMed]
  37. Tersoff, J. Stable self-catalyzed growth of III-V nanowires. Nano Lett. 2015, 15, 6609. [Google Scholar] [CrossRef] [PubMed]
  38. Plissard, S.; Dick, K. A.; Larrieu, G.; Godey, S.; Addad, A.; Wallart, X.; Caroff, P. Gold-free growth of GaAs nanowires on silicon: arrays and polytypism. Nanotechnology 2010, 21, 385602. [Google Scholar] [CrossRef]
  39. Glas, F.; Ramdani, M. R.; Patriarche, G.; Harmand, J. C. Predictive modeling of self-catalyzed III-V nanowire growth. Phys. Rev. B 2013, 88, 195304. [Google Scholar] [CrossRef]
  40. Glas, F.; Panciera, F.; Harmand, J. C. Statistics of nucleation and growth of single monolayers in nanowires: towards a deterministic regime. Phys. Stat. Solidi RRL 2022, 16, 2100647. [Google Scholar] [CrossRef]
  41. Sjokvist, R.; Jacobsson, D.; Tornberg, M.; Wallenberg, R.; Leshchenko, E.D.; Johansson, J.; Dick, K.A. Compositional correlation between the nanoparticle and the growing Au-assisted I(xGa1-xAs nanowire. J Phys Chem Lett 2021, 12, 7590. [Google Scholar] [CrossRef] [PubMed]
  42. Dubrovskii, V. G. Composition of vapor-liquid-solid III-V ternary nanowires based on group III intermix. Nanomaterials 2023, 13, 2532. [Google Scholar] [CrossRef]
  43. Martins, J. L.; Zunger, A. Bond lengths around isovalent impurities and in semiconductor solid solutions. Phys. Rev. B 1984, 30, 6217. [Google Scholar] [CrossRef]
  44. Ansara, I.; Chatillon, C.; Lukas, H. L.; Nishizawa, T.; Ohtani, H.; Ishida, K.; Hillert, M.; Sundman, B.; Argent, B. B.; Watson, A.; Chart, T.; Anderson, T. A binary database for III–V compound semiconductor systems. Calphad 1994, 18, 177. [Google Scholar] [CrossRef]
  45. Dinsdale, A. T. SGTE unary database ver. 4.4. Calphad 1991, 15, 317. [Google Scholar] [CrossRef]
  46. Glas, F. Chemical potentials for Au-assisted vapor-liquid-solid growth of III-V nanowires. J. Appl. Phys. 2010, 108, 073506. [Google Scholar] [CrossRef]
  47. Zhang, Y.; Velichko, A. V.; Fonseka, H. A.; Parkinson, P.; Gott, J. A.; Davis, G.; Aagesen, M.; Sanchez, A. M.; Mowbray, D.; Liu, H. Defect-free axially-stacked GaAs/GaAsP nanowire quantum dots with strong carrier confinement. Nano Lett. 2021, 21, 5722. [Google Scholar] [CrossRef]
Preprints 94404 g001
Figure 1. Transformation of the vapor-solid distribution from the equilibrium shape at ε → ∞ to the purely kinetic Langmuir-McLean shape at ε = x + c g ( 1 − x ) . Any distribution between the equilibrium and kinetic curves is possible, and is regulated by the single parameter ε .
Figure 1. Transformation of the vapor-solid distribution from the equilibrium shape at ε → ∞ to the purely kinetic Langmuir-McLean shape at ε = x + c g ( 1 − x ) . Any distribution between the equilibrium and kinetic curves is possible, and is regulated by the single parameter ε .
Preprints 94404 g001
Preprints 94404 g002
Figure 2. Vapor-solid distributions of Au-catalyzed VLS InSbxAs1-x NWs and epi-layers grown by MOVPE at 450 oC [21] (symbols), fitted by Eq. (26) with the parameters given in Table 1 (solid lines). Dashed line shows the equilibrium distribution.
Figure 2. Vapor-solid distributions of Au-catalyzed VLS InSbxAs1-x NWs and epi-layers grown by MOVPE at 450 oC [21] (symbols), fitted by Eq. (26) with the parameters given in Table 1 (solid lines). Dashed line shows the equilibrium distribution.
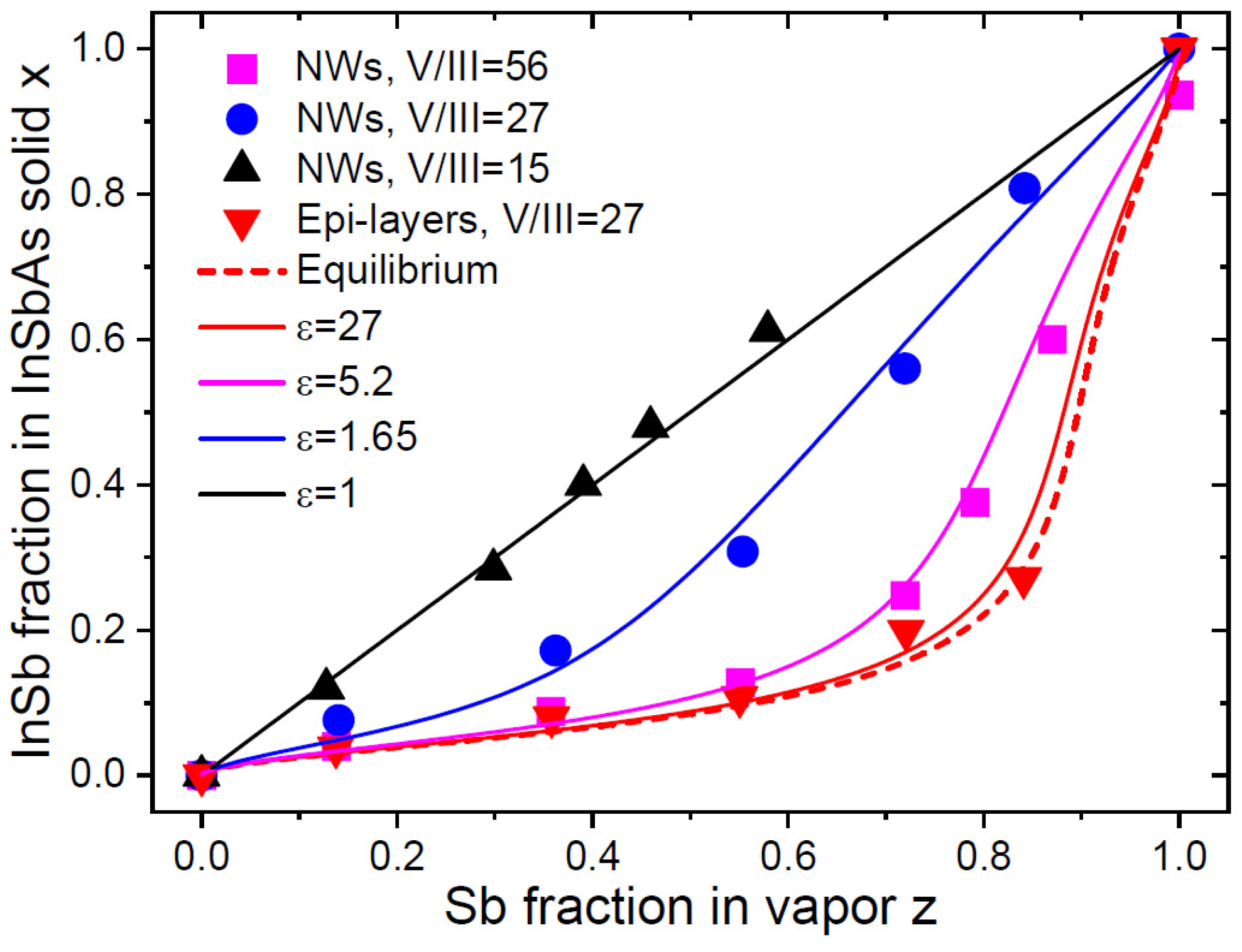
Preprints 94404 g002
Preprints 94404 g003
Figure 3. Vapor-solid distributions of Au-catalyzed VLS InPxAs1-x NWs grown by CBE on InAs NW stems at 390 oC, 405 oC and 435 oC [21] (symbols). Solid lines are the fits obtained from Eq. (26) with the parameters listed in Table 1. Dashed lines show the fits by Eq. (20) with different parameters c g given in the legend.
Figure 3. Vapor-solid distributions of Au-catalyzed VLS InPxAs1-x NWs grown by CBE on InAs NW stems at 390 oC, 405 oC and 435 oC [21] (symbols). Solid lines are the fits obtained from Eq. (26) with the parameters listed in Table 1. Dashed lines show the fits by Eq. (20) with different parameters c g given in the legend.
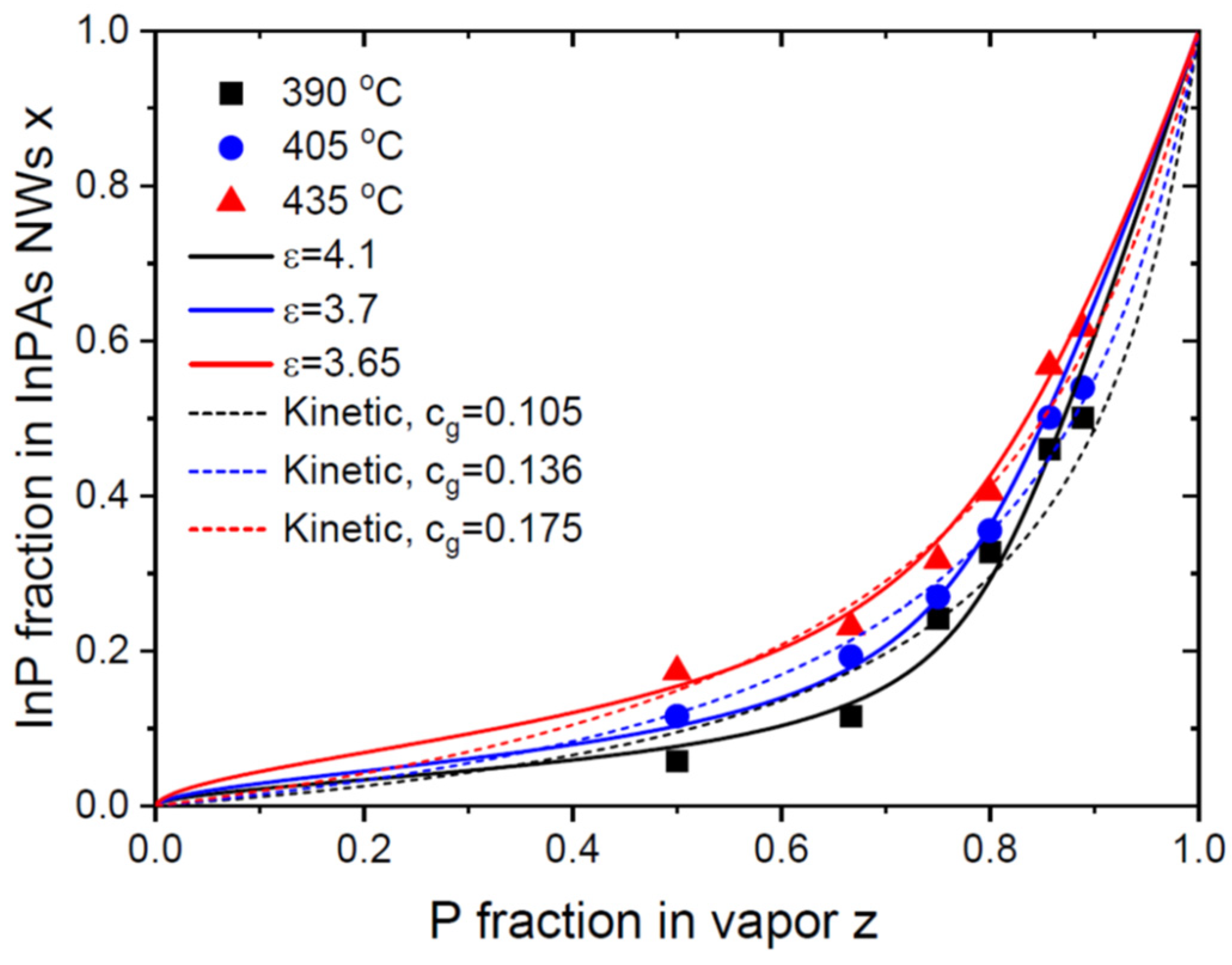
Preprints 94404 g003
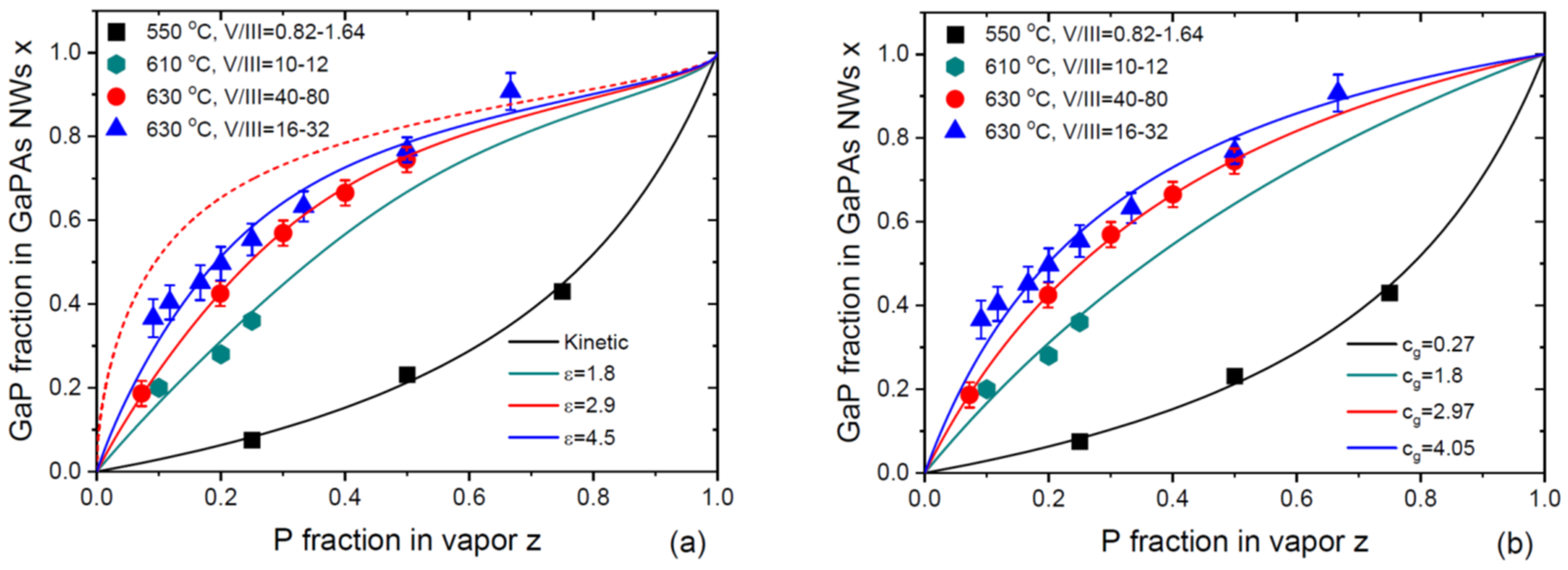
Preprints 94404 g004
Figure 4. Vapor-solid distributions of VLS GaPxAs1-x NWs grown by the substrate-free Au-catalyzed aerotaxy at 550 oC at low V/III flux ratios in vapor F 53   ~ 1 [32], Ga-catalyzed MBE on Si(111) substrates at 610 oC at F 53   = 10-12 [28], 630 oC at F 53   = 40-80 [30], and 630 oC at F 53   = 16-32 [31]. Solid lines are the fits by Eq. (26) with the parameters given in Table 1. Dashed line shows the equilibrium distribution at 630 oC, which is almost indistinguishable from the one at 610 oC. The data of Ref. [32] are fitted by the Langmuir-Mclean Eq. (20) with c g = 0.27. (b) Same data as in (a), fitted by Eq. (20) with different c g given in the legend.
Figure 4. Vapor-solid distributions of VLS GaPxAs1-x NWs grown by the substrate-free Au-catalyzed aerotaxy at 550 oC at low V/III flux ratios in vapor F 53   ~ 1 [32], Ga-catalyzed MBE on Si(111) substrates at 610 oC at F 53   = 10-12 [28], 630 oC at F 53   = 40-80 [30], and 630 oC at F 53   = 16-32 [31]. Solid lines are the fits by Eq. (26) with the parameters given in Table 1. Dashed line shows the equilibrium distribution at 630 oC, which is almost indistinguishable from the one at 610 oC. The data of Ref. [32] are fitted by the Langmuir-Mclean Eq. (20) with c g = 0.27. (b) Same data as in (a), fitted by Eq. (20) with different c g given in the legend.
Preprints 94404 g004
Table 1. Parameters of III-V ternary epi-layers and VLS NWs based on group V intermix.
Table 1. Parameters of III-V ternary epi-layers and VLS NWs based on group V intermix.
Material Catalyst T
(oC)		 V/III ratio in vapor F 53 ε ω β g c g
InSbxAs1-x epi-layers [21] - 450 27 27 1.566 0.34 1

InSbxAs1-x NWs [21]
Au
450		 56 5.2
1.56
0.34
1
27 1.65
15 1

InPxAs1-x NWs [26]
Au		 390
30-45		 4.1 0.546 0.1 1
405 3.7 0.534 0.13 1
430 3.65 0.515 0.2 1
GaPxAs1-x NWs [32] Au 550 0.82-1.64 Min 0.703 - 0.27
GaPxAs1-x NWs [28] Ga 610 10-12 1.8 0.656 3.1 0.27
GaPxAs1-x NWs [30] Ga 630 40-80 2.9 0.641 3.1 0.27
GaPxAs1-x NWs [31] Ga 630 16-32 4.5 0.641 3.1 0.27
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated