Prerpints.org logo
Preprint
Article

Game Models for Ordering and Channel Decisions of New and Differentiated Remanufactured Products in a Closed-Loop Supply Chain

Altmetrics

Downloads

87

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 December 2023

Posted:

26 December 2023

You are already at the latest version

Alerts
Abstract
Environmental responsibility and economic benefits have promoted the development of closed-loop supply chain (CLSC), and shortages and channels are considered to be two important issues in CLSC. This paper explores ordering and channel decisions in CLSC with new and differentiated remanufactured products, and considers the price and sales effort-dependent demands, as well as the proportion of emergency orders determined by emergency order costs and backorder losses, and establishes an integrated and decentralized CLSC game models. We introduce a stochastic sales effort, which affects two types of products. Numerical results show that sales effort and the order quantity of new and remanufactured products exhibit concave and convex functions, respectively. Wherein, the upper limit of sales effort has a greater impact on supply chain decisions. High sales efforts can serve as a means of coordinating dispersed supply chains. Moreover, in different cases, decisions of integrated channel are better than those of decentralized channel. Finally, whether the supply chain adopts an emergency order strategy depends on the relative cost of emergency orders and out of stock costs. According to the research in this article, some management insights are also provided.
Keywords: 
Subject: Business, Economics and Management  -   Econometrics and Statistics

MSC:   

1. Introduction

In recent years, the quantity of end-of-life products has increased sharply, resulting in environmental pressures and waste of resources, which leads to the development of closed-loop supply chain (CLSC). Through CLSC, recycling and remanufacturing not only help reduce environmental pollution, but also enable resource recycling and saving, and promote a circular economy [1]. Remanufacturing after recycling of waste tires, electronic products and automobile engines can effectively save more than 30% of raw materials and reduce energy consumption by more than 15%. Apple reduced carbon emissions per dollar of revenue by 15.4% through remanufacturing; Canon and Xerox saved millions of dollars by recycling and remanufacturing [2]. Both economic and non-economic factors promote the implementation of recycling and remanufacturing, while economic benefits may be the key factor that attracts enterprises [3].
In a CLSC, besides producing new products, manufacturers also remanufacture using re-manufacturable end-of-life products. Some consumers strongly agree that they tend to buy socially responsible and environmentally friendly products [4]. However, most consumers are skeptical and wait-and-see about remanufactured products. Sales efforts, such as advertising, commitment and promoting, can increase the demand for remanufactured products through changing consumers' cognition degree to remanufactured products, helping consumers identify environmental values of remanufactured products [5]. Thus, sales efforts are crucial to increase the market share of remanufactured products.
On the other hand, due to the demand uncertainty and information asymmetry, CLSC is more likely to experience shortages. In a CLSC, remanufacturing begins with the recovery of end-of-life products which are full of great uncertainty. Furthermore, consumers' preference for the two types of products and sales efforts for remanufactured products increase the uncertainty of demand. All mentioned above are reasons that emphasized on shortage issues in CLSC to avoid profit and non-profit loss caused by shortage. In this paper, we will explore the ordering and channel decision of CLSC members under different supply chain structures, in which sales effort of the remanufactured products affects the market demand for the remanufactured and new product. Further, we consider models without and with emergency order to deal with the shortage problem. In the models without emergency order, backlogged demands are lost. While in the models with emergency order, backlogged demands could be met through emergency order, but in a certain proportion, which is related to the cost of emergency order and the cost of out-of-stock loss.
This paper explores a two-echelon CLSC with one manufacturer and one retailer, where the market demand is related to retail price and sales efforts. Game theoretic models of integrated CLSC and decentralized CLSC without and with emergency order are established to answer the following questions:
What are the optimal order quantities for the two types of products in different channel structures?
What is the influence of sales effort and costs of emergency order and losses of out-of-stock on channel strategies and profits?
Whether emergency order have a positive impact on order quantity and profit in a CLSC with sales effort?
The remainder of this paper is organized as follows. Section 2 reviews the related literature. In Section 3, the model description is expanded. Section 4 presents and analyzed different CLSC models. Section 5 provides numerical examples to examine the propositions. Section 6 discusses optimal results with the impact of sales effort and emergency order strategy. Section 7 concludes the study and outlines the future research directions. Some implications are also discussed in this section.

2. Literature Review

This paper presents a literature review in four areas: competition between new products and remanufactured products, sales efforts for remanufactured products, emergency order, and centralized and decentralized CLSC structure.

2.1. Competition between new products and remanufactured products

In CLSC, a part of literature assumed that remanufactured and new products are not distinguishable[2, 6], while some others hold that remanufactured products are different from new products [7, 8]. In either case, especially the latter, according to the product cannibalization, remanufactured products will lead to a reduction in the sales volume, sales revenue, or market share of new products. Considering remanufactured products competing with new products, Jian et al. [9] studied how manufacturers and remanufacturers can benefit each other, taking into account patent protection and carbon emissions. Dai et al. [10] analyzed the impact of different CSR ratios on product pricing and profits from the perspective of product differential pricing. Souza [1] found that the remanufacturing decision of products would bring about two results: market expansion effect, that was, remanufactured products would help to expand market share; cannibalization effect, that was, remanufactured products entering the market would reduce the sales of new products of the same type or model. Based on the cannibalization effect of remanufactured products, we analyze the supply chain management of the impact of sales effort on the demand for remanufactured and new products.

2.2. Sales efforts for remanufactured products

In practice, consumers may have different preferences for new products and remanufactured products. For example, some consumers are psychologically biased towards remanufactured products and will not buy them no matter how cheap they are [11]. Michaud and Llerena [12] found that when consumers were informed of the significance of remanufactured products for environmental protection, they would have a friendly attitude towards remanufactured products. Therefore, sales effort is necessary to promote consumers' perception of remanufactured products. Literature have confirmed the important role of sales efforts in improving consumers’ acceptance of remanufactured products [4]. In recent years, Mondal and Giri [3] constructed a two-cycle green closed-loop supply chain model in which market demand depends on selling price, greenization level and sales effort, and studied the effects of green innovation, sales effort and waste product recovery rate on closed-loop supply chain. Yang et al. [13] discussed whether and how the level of sales effort of retailers affects the economic performance and sustainability of remanufacturing. Sane Zerang et al. [14] studied the effects of sales effort and recovery rate on decision variables, and demonstrated the superiority of manufacturer-led closed-loop supply chain. Taleizadeh et al. [15] explored pricing and reverse channel selection decisions in CLSC. The demand depends on retail prices and advertising efforts. Khorshidvand et al. [16] developed a new demand function based on price elasticity, cross sensitivity, product green quality, and advertising level, providing a two-stage approach to model and solve a sustainable CLSC. Ma et al. [17] studied the combined effects of marketing efforts and recycling rates on the profitability of retailers, manufacturers and CLSCs. Zhang et al.[18] considered that manufacturers will pay attention to the fairness of profit distribution when making sales efforts. We studied a green closed-loop supply chain (CLSC) that considers manufacturer sales efforts and fairness concerns.
Most of the above literature assume that sales effort is a definite variable. In this paper, considering the sales effort will change with industry and time, we assume that it is a random variable subject to uniform distribution. And it also affects the demands for two types of products, that is, the demand for remanufactured products will increase with the deepening of sales effort; on the contrary, the demand for new products will decrease due to the cannibalizing effect.

2.3. Emergency order

When the inventory is out of stock or under some special circumstances, emergency orders can be used as a supplement to the regular order, which can reduce the loss and cost [19]. Models with emergent order have been studied extensively [20, 21]. Zhang et al. [22] compared two different ways to deal with excess demand. One was excess demand loss and shortage penalty; the other was that excess demand can be met by emergency ordering. Which way is better depends on the comparison of emergency ordering cost and sales price plus the shortage penalty under the demand loss system. When the possibility of an emergency order exists, it is necessary to consider emergency ordering costs. Poormoaied and Demirci [23] studied an inventory strategy described by a continuous-time Markov chain model, in which emergency orders could be issued based on stock levels prior to the disruption. And the results showed that with high cost of sales losses, long break periods and a low percentage of supplier availability, providing emergency ordering opportunities in the event of disruption could lead to significant cost savings. Emergency orders affect the social and environmental sustainability goals of the supply chain, in addition to affecting profits. Because remanufactured products are made from recycled waste products, and the demand for remanufactured products is not independent of the demand for new products. There is little literature on this aspect.

2.4. The centralized and decentralized CLSC structure

Many researchers have examined integrated and decentralized game structure in CLSC from various perspectives: for example, recycling decisions [24]; pricing decisions [3] and ordering strategies [25]. Maiti and Giri [26] explored the effect of channel power structures on the pricing strategy, the collection rate, the quality, and the profits, showing that the integrated policy is always better. In this paper, we focus on ordering decisions. He et al. [27] investigated three possible channel structures for manufacturer with government subsidy. Solaleh et al. [28] studied the behavior of a two-stage decentralized channel CLSC. Zhou et al. [29] studied the channel leadership and performance in a three-echelon CLSC.

3. Problem Definition

We consider a CLSC composed of one retailer and one hybrid manufacturer that provides remanufactured products using end-of-products and manufactures new products from raw materials. We assume that all the recycled products can be remanufactured. The manufacturer provides the two types of products with unit wholesale prices wn, wr (wn > wr) to the retailer. The retailer is responsible for selling both types of products at different prices pn, pr (pn>pr), basing that the remanufactured products are clearly different from the new product [1,2]. In order to enhance the perception of remanufactured products and positively influence the market demand, the retailer pay a certain amount of sales effort, such as advertising, promotion, service commitment. Let s denote the level of a composite index of sales effort input. The retailer's investment in the level of sales effort s is assumed as a convex function, defined as 1 2 g s 2   [3]. The sales effort s can vary across industries, consumer groups and change over time. Therefore, we assume s to be a random variable following a uniform distribution in the range of [c, d] (0 =< c< d; c is the lowest limit and d is the upper limit. If the sales effort exceeds d, the cost paid may be greater than the benefit gained, thus there will be no economic benefit). The effect of the sales effort on demand is to change the marketing share of the two types of products. In addition, both demands are functions of individual prices. The demand function of each product type is expressed as:
D n = a ( 1 − b 1 − ⅇ − s θ − α ) − ξ p n
        D r = a ( b ( 1 − ⅇ − s θ ) + α ) − ξ p r
where, index “n” stands for the new product, and index “r” refers to the remanufactured product. a represents the initial market potential. ξ is the sensitivity of demand to price. b 1 − ⅇ − s θ symbolizes the increased demand share of remanufactured product from sales effort. θ   a n d   b   ( 0 < b < 1 ) are influence coefficients of the sales effort on demand. α   is a positive parameter measuring the initial quota of the demand of the remanufactured product when the sales effort is 0.
In manufacturing, the unit production cost of new product cn is more costly than the unit remanufacturing cost of used product cr, i.e., cn >cr. In retailing, the retailer decides how much to order for both types of products according to market demand, defined as Qn and Qr. If the quantity ordered exceeds the demand, the remainder is disposed of as a salvage value, recorded as Vn, Vr (Vn >Vr). On the other hand, if the order quantity is lower than the demand, the unmet demand is lost in the case that emergency orders are not allowed, and the out-of-stock is recorded as loss, denoted as Bn, Br, (Bn > Br) respectively. When an emergency order is allowed, a proportion of emergency order shall be determined according to the relative relationship between emergency order cost and shortage loss. Many literatures believe that the cost of emergency order is borne by retailers [3]. In fact, it is more possibly borne by manufacturers. Therefore, we analyze the impact of emergency order cost borne by manufacturers. Costs of emergency order are recorded as kn, kr (kn < kr) respectively. The reason for the high cost of emergency orders for the remanufactured product is the uncertainty of the recovery process. Table 1 summarizes the major notations in our following model development.

4. Model Formulation and Solution

In this section, the CLSC and channel members’ profit functions are formulated and optimal decisions on Qn, Qr, wn and wr in each scenario are derived. Concavity of profit functions is proved, and closed-form relations for decision variable Qn and Qr are extracted in both decentralized and integrated scenarios under the situation without and with emergency orders.

4.1. Models under different channel power structures without emergency order

4.1.1. Integrated scenario

In the integrated scenario, in order to maximize the benefit of the CLSC, the members of the CLSC make decisions under the promotion of the central decision maker. The profit function of the integrated scenario model is:
π I N ( Q n , Q r ) = p n ( D n ∧ Q n ) + V n ( Q n - D n ) + - B n ( D n - Q n ) + - c n Q n + p r ( D r ∧ Q r ) + V r ( Q r - D r ) + - B r ( D r - Q r ) + - c r Q r − 1 2 g s 2
where x ^ y = min {x, y}, (x - y) + = max {x - y, 0}
According to the properties of the demand function, the expected profit function is described as follows:
E I N ( Π ( Q n , Q r ) ) = p n ( ∫ z n d D n f ( s ) d s + ∫ c z n Q n f ( s ) d s ) + V n ∫ z n d ( Q n − D n ) f ( s ) d s − B n ∫ c z n ( D n − Q n ) f ( s ) d s - c n Q n + p r ( ∫ c z r D r f ( s ) d s + ∫ z r d Q r f ( s ) d s ) + V r ∫ c z r ( Q r − D r ) f ( s ) d s − B r ∫ z r d ( D r − Q r ) f ( s ) d s - c r Q r − 1 8 g ( d + c ) 2
where z n = l n [ a b − a + a b + a α + ξ p n + Q n ] θ ; z r = l n [ a b a b + a α − ξ p r − Q r ] θ
Proposition 1. Under the integrated scenario without emergency order, the expected profit function E I N ( ∏ ( Q n , Q r ) )   is concave with respect to Qn and Qr; hence there is a unique optimal combination of decision variables ( Q N I * n ,   Q N I * r ) that maximizes E I N ( ∏ ( Q n , Q r ) ) and the optimal production quantities of the two types of products are:
Q N I * n = a + a b − 1 + e − θ c B n + − c + d c n + c p n − d V n B n + p n − V n − a α − ξ p n
Q N I * r = a ( b − b e − θ ( d B r + ( c − d ) c r + d p r − c V r ) B r + p r − V r + α ) − ξ p r      
  • Proof. To prove concavity, Hessian matrix of E I N ( ∏ ( Q n , Q r ) ) is calculated:
B n + p n − V n ( c − d ) θ ( a ( − 1 + b + α ) + ξ p n + Q n ) 0 0 − B r + p r − V r ( c − d ) θ ( − a ( b + α ) + ξ p r + Q r )
It's obvious that ( a ( − 1 + b + α ) + ξ p n + Q n ) = a b e   − θ   s > 0 and − a b + α + ξ p r + Q r = − a b e   − θ   s < 0 . Since all parameters are positive, the first principal minor B n + p n − V n c − d θ a − 1 + b + ξ p n + Q n is negative and the second principal minor B n + p n − V n ( c − d ) θ ( a ( − 1 + b + α ) + ξ p n + Q n ) * B r + p r − V r ( c − d ) θ ( − a ( b + α ) + ξ p r + Q r ) is positive. Thus, the Hessian matrix is negative definite and E I N ( ∏ ( Q n , Q r ) ) is concave in all decision variables. Solving ∂ E I N ( ∏ ( Q n , Q r ) ) ∂ Q n = 0   a n d   ∂ E I N ( ∏ ( Q n , Q r ) ) ∂ Q r = 0   , Equation (1) and (2) are obtained.
Corollary 1. In the integrated model , the optimal order quantities Q N I * n   is convex and Q N I * r is concave with respect to the lower and upper bound of sales effort c and d.
Proof. Since ∂ 2 Q N I * n   ∂ c 2   = a b e − θ ( c ( B n + p n ) − d V n + ( − c + d ) c n ) B n + p n − V n θ 2 ( B n + p n − c n ) 2 ( B n + p n − V n ) 2 > 0 ;   ∂ 2 Q N I * n   ∂ d 2   = a b e − θ ( c B n + c p n − d V n + ( − c + d ) c n ) B n + p n − V n θ 2 ( − V n + c n ) 2 ( B n + p n − V n ) 2 > 0 ;   ∂ 2 Q N I * r   ∂ c 2   = − a b e − θ d B r + d p r − c V r + c − d c r B r + p r − V r θ 2 V r − c r 2 B r + p r − V r 2 < 0   ;   ∂ 2 Q N I * r   ∂ d 2   = − a b e − θ d B r + c − d c r + d p r − c V r B r + p r − V r θ 2 B r − c r + p r 2 B r + p r − V r 2 < 0       then the optimal order quantity   Q N I * n   is convex and Q N I * r is concave in c and d.

4.1.2. Decentralized scenario

In the decentralized CLSC, each channel member makes decision independently to maximize their own profits. The manufacturer act as a Stackelberg leader and decides the wholesale price. The retailer, according to its own profit function, determines order quantities based on the manufacturer's decisions. Backward induction is adopted in pursuit of equilibrium decisions.
The retailer’s profit in general form can be expressed as:
π R N ( Q n , Q r ) = p n ( D n ∧ Q n ) + V n ( Q n - D n ) + - B n ( D n - Q n ) + - w n Q n + p r ( D r ∧ Q r ) + V r ( Q r - D r ) + − w r Q r - B r ( D r - Q r ) + − 1 2 g s 2
Similarly, the expected profit function of the retailer is described as follows:
E R N ( Π ( Q n , Q r ) ) = p n ( ∫ z n d D n f ( s ) d s + ∫ c z n Q n f ( s ) d s ) + V n ∫ z n d ( Q n − D n ) f ( s ) d s − B n ∫ c z n ( D n − Q n ) f ( s ) d s - w n Q n + p r ( ∫ c z r D r f ( s ) d s + ∫ z r d Q r f ( s ) d s ) + V r ∫ c z r ( Q r − D r ) ) f ( s ) d s − B r ∫ z r d ( D r − Q r ) f ( s ) d s - w r Q r − 1 8 g ( d + c ) 2
Proposition 2. Under the decentralized scenario without emergency order, the expected retailer’s profit function E R N ( ∏ ( Q n , Q r ) )   is concave with respect to Qn and Qr; hence there is a unique optimal combination of decision variables ( Q N R * n ,   Q N R * r ) that maximizes E R N ( ∏ ( Q n , Q r ) )     and the optimal production quantities of the two products are:
Q N R * n = a + a b ( − 1 + e − θ ( c B n + ( − c + d ) w n + c p n − d V n ) B n + p n − V n ) − a α − ξ p n
Q N R * r = a ( b − b e − θ ( d B r + ( c − d ) w r + d p r − c V r ) B r + p r − V r + α ) − ξ p r        
Proof. To prove concavity, Hessian matrix of E R N ( ∏ ( Q n , Q r ) )     is calculated as follows:
B n + p n − V n ( c − d ) θ ( a ( − 1 + b + α ) + ξ p n + Q n ) 0 0 − B r + p r − V r ( c − d ) θ ( − a ( b + α ) + ξ p r + Q r )
The proof process is the same as Proposition 1.
Corollary 2. In the decentralized model, the optimal order quantities Q N R * n   is convex and Q N R * r is concave with respect to the lower and upper bound of sales effort c and d.
Proof. Since ∂ 2 Q N I * n   ∂ c 2   = a b e − θ ( c ( B n + p n ) − d V n + ( − c + d ) w n ) B n + p n − V n θ 2 ( B n + p n − w n ) 2 ( B n + p n − V n ) 2 > 0 ;   ∂ 2 Q N I * n   ∂ d 2   = a b e − θ ( c B n + c p n − d V n + ( − c + d ) w n ) B n + p n − V n θ 2 ( − V n + w n ) 2 ( B n + p n − V n ) 2 > 0 ；   ∂ 2 Q N I * r   ∂ c 2   = − a b e − θ ( d B r + d p r − c V r + ( c − d ) w r ) B r + p r − V r θ 2 ( V r − w r ) 2 ( B r + p r − V r ) 2 < 0   ;   ∂ 2 Q N I * r   ∂ d 2   = − a b e − θ d B r + c − d w r + d p r − c V r B r + p r − V r θ 2 B r − w r + p r 2 B r + p r − V r 2 < 0 ,   then the optimal order quantity   Q N R * n   is convex and Q N R * r is concave in c and d.
The manufacturer’s profit function is formulated as:
E M N ( Π ( w n , w r ) ) = w n Q n - c n Q n + p r Q r - c r Q r
Proposition 3. Under the decentralized scenario without emergency order, the expected manufacturer profit function E M N ( ∏ ( w n , w r ) )   is concave with respect to wn and wr if 2 B n + p n − V n − d − c θ − c n + w n > 0 .
Proof. To prove concavity, Hessian matrix of E M N ( ∏ ( w n , w r ) )   is calculated as follows:
a b ( c − d ) e − θ ( c ( B n + p n ) − d V n + ( − c + d ) w n ) B n + p n − V n θ ( X n + ( c − d ) θ ( − c n + w n ) ) ( B n + p n − V n ) 2 0 0 a b ( c − d ) e − θ ( d B r + d p r − c V r + ( c − d ) w r ) B r + p r − V r θ ( X r + ( c − d ) θ ( c r − w r ) ) ( B r + p r − V r ) 2
where X i = 2 B i + 2 p i − 2 V i ( i = n , r )
The first principal minor is negative, and the second principal minor is positive if:
2 B n + p n − V n − d − c θ − c n + w n > 0      
By holding Condition (5) the Hessian matrix is negative definite and E M N ( ∏ ( w n , w r ) )   is concave in both wn and wr. Hence there is a unique optimal combination of decision variables ( w N * n ,   w N * r ) that maximizes E M N ( ∏ ( w n , w r ) ) . To obtain the optimal values of the decision variables, ∂ E M N ( ∏ ( w n , w r ) ) ∂ w n = 0   a n d   ∂ E M N ( ∏ ( w n , w r ) ) ∂ w r = 0   need to be solved. That is:
a + a b ( − 1 + e − θ ( c B n + c p n − d V n + ( − c + d ) w n ) B n + p n − V n ) − a α − ξ p n − a b ( − c + d ) e − θ ( c B n + c p n − d V n + ( − c + d ) w n ) B n + p n − V n θ ( − c n + w n ) B n + p n − V n = 0      
a ( b − b e − θ ( d B r + d p r − c V r + ( c − d ) w r ) B r + p r − V r + α ) − ξ p r + a b ( c − d ) e − θ ( d B r + d p r − c V r + ( c − d ) w r ) B r + p r − V r θ ( − c r + w r ) B r + p r − V r = 0
Equation (6) and (7) are transcendental equation, numerical method needs to be used. We discuss the results using numerical examples in Section 5 and Section6.
Corollary 3. The order quantity of the two products in the centralized channel is higher than that in the decentralized channel : Q N I * n > Q N R * n ; Q N I * r > Q N R * r .
Proof. Q N I * n − Q N R * n = a b e − θ c B n + − c + d c n + c p n − d V n B n + p n − V n − e − θ c B n + p n − d V n + − c + d w n B n + p n − V n > 0 ; Q N I * r − Q N R * r = a b − e − θ d B r + c − d c r + d p r − c V r B r + p r − V r + e − θ d B r + d p r − c V r + c − d w r B r + p r − V r > 0 .

4.2. Models under different channel power structures with emergency order

In the case with emergency ordering, not all the unmet demands to be satisfied will be satisfied by emergency ordering. When the cost of emergency ordering is high, emergency ordering is actually uneconomical. While if the loss of stock is high, the company will allow emergency ordering. Therefore, we consider the ratio of emergency order cost to backorder loss to determine the proportion of emergency order, denoted as β i :
β i = 1 − k i B i     k i < B i         i = n , r

4.2.1. Integrated scenario

When the emergency order is allowed, a part of the demand exceeding the regular order quantity is satisfied by the emergency order, the supply chain obtains additional revenue from the emergency order, and the backorder loss is reduced. The profit function of the integrated scenario model is:
π I Y ( Q n , Q r ) = p n ( D n ∧ Q n ) + V n ( Q n - D n ) + + β n ( p n − k n ) ( D n - Q n ) + - B n ( 1 − β n ) ( D n - Q n ) + - c n ( Q n + β n ( D n - Q n ) + ) + p r ( D r ∧ Q r ) + V r ( Q r - D r ) + + （ p r − k r ) β r ( D r - Q r ) + - B r ( 1 − β r ) ( D r - Q r ) + - c r ( Q r + β r ( D r - Q r ) + ) − 1 2 g s 2
The expected profit function is described as follows:
E I Y ( Π ( Q n , Q r ) ) = p n ( ∫ z n d D n f ( s ) d s + ∫ c z n Q n f ( s ) d s ) + V n ∫ z n d ( Q n − D n ) f ( s ) d s + ( p n − k n ) ∫ c z n β n ( D n − Q n ) f ( s ) d s − B n ∫ c z n ( 1 − β r ) ( D n − Q n ) f ( s ) d s - c n ( Q n + ∫ c z n β n ( D n − Q n ) f ( s ) d s ) + p r ( ∫ c z r D r f ( s ) d s + ∫ z r d Q r f ( s ) d s ) + V r ∫ c z r ( Q r − D r ) f ( s ) d s + ( p r − k r ) ∫ z r d β r ( D r − Q r ) f ( s ) d s − B r ∫ z r d ( 1 − β r ) ( D r − Q r ) f ( s ) d s - c r ( Q r + ∫ z r d β r ( D r − Q r ) f ( s ) d s ) − 1 8 g ( d + c ) 2
Proposition 4. Under the integrated scenario with emergency order, the expected supply chain profit function E I Y ( ∏ ( Q n , Q r ) )   is concave with respect to Qn and Qr if k i ( B i + p i ) − B i V i > 0 ; hence there is a unique optimal combination of decision variables ( Q Y I * n ,   Q Y I * r ) that maximizes E I Y ( ∏ ( Q n , Q r ) ) a n d   the optimal production quantities of the two products are:
Q Y I * n = a b e − θ ( c k n p n + B n ( c k n + ( − c + d ) c n − d V n ) ) k n ( B n + p n ) − B n V n − a ( − 1 + b + α ) − ξ p n
Q Y I * r = a ( b − b e − θ ( d k r p r + B r ( d k r + ( c − d ) c r − c V r ) ) k r ( B r + p r ) − B r V r + α ) − ξ p r  
Proof. To prove concavity, hessian matrix of E I Y ( ∏ ( Q n , Q r ) )   calculated as follows:
k n ( B n + p n ) − B n V n ( c − d ) θ B n ( a ( − 1 + b + α ) + ξ p n + Q n ) 0 0 − k r ( B r + p r ) − B r V r ( c − d ) θ p r ( − a b + α + ξ p r + Q r )
By holding the condition k i ( B i + p i ) − B i V i > 0 , the first principal minor k n ( B n + p n ) − B n V n ( c − d ) θ B n ( a ( − 1 + b + α ) + ξ p n + Q n ) is negative. The second principal minors k n ( B n + p n ) − B n V n ( c − d ) θ B n ( a ( − 1 + b + α ) + ξ p n + Q n ) * − k r ( B r + p r ) − B r V r ( c − d ) θ p r ( − a b + α + ξ p r + Q r ) is positive. Thus, the Hessian matrix is negative definite and E I Y ( ∏ ( Q n , Q r ) ) is concave in all decision variables. ∂ E I Y ( ∏ ( Q n , Q r ) ) ∂ Q n = 0   a n d   ∂ E I Y ( ∏ ( Q n , Q r ) ) ∂ Q r = 0   result in Equation (8) and (9).
Corollary 4. In the integrated model with emergency order, the optimal order quantities Q Y I * n   is convex and Q Y I * r is concave with respect to the lower and upper bound of sales effort c and d.
Proof. Since ∂ 2 Q Y I * n   ∂ c 2   = a b e − θ ( c k n p n + B n ( c k n + ( − c + d ) c n − d V n ) ) k n ( B n + p n ) − B n V n ( θ k n ( B n + p n ) − θ B n c n ) 2 ( k n ( B n + p n ) − B n V n ) 2 > 0 ;   ∂ 2 Q Y I * n   ∂ d 2   = a b e − θ ( c k n p n + B n ( c k n + ( − c + d ) c n − d V n ) ) k n ( B n + p n ) − B n V n θ 2 B n 2 ( c n − V n ) 2 ( k n ( B n + p n ) − B n V n ) 2 > 0 ;   ∂ 2 Q Y I * r   ∂ c 2   = − a b e − θ ( d k r p r + B r ( d k r + ( c − d ) c r − c V r ) ) k r ( B r + p r ) − B r V r θ 2 B r 2 ( c r − V r ) 2 ( k r ( B r + p r ) − B r V r ) 2 < 0   ;   ∂ 2 Q Y I * r   ∂ d 2   = − a b e − θ ( d k r p r + B r ( d k r + ( c − d ) c r − c V r ) ) k r ( B r + p r ) − B r V r ( θ k r ( B r + p r ) − θ B r c r ) 2 ( k r ( B r + p r ) − B r V r ) 2 < 0       then the optimal order quantity   Q Y I * n   is convex and Q Y I * r is concave in c and d.

4.2.2. Decentralized scenario

In the decentralized scenario, the retailer issues an emergency order when it is out of stock, and the manufacturer makes supplies for the emergency order and pays the emergency order cost. Remanufacturing takes recycled products as materials, and the recycling process is usually more uncertain, so the reaction cost is higher than that of new products.
The retailer’s profit in general form can be expressed as:
π Y R ( Q n , Q r ) = p n ( D n ∧ Q n ) + V n ( Q n - D n ) + + p n β n ( D n - Q n ) + - B n ( 1 − β n ) ( D n - Q n ) + - w n ( Q n + β n ( D n - Q n ) + ) + p r ( D r ∧ Q r ) + V r ( Q r - D r ) + + p r β r ( D r - Q r ) + w r ( Q r + β r ( D r - Q r ) + ) - B r ( 1 − β r ) ( D r - Q r ) + − 1 2 g s 2
The expected profit function of the retailer is described as follows.
E R Y ( Π ( Q n , Q r ) ) = p n ( ∫ z n d D n f ( s ) d s + ∫ c z n Q n f ( s ) d s ) + V n ∫ z n d ( Q n − D n ) f ( s ) d s + p n ∫ c z n β n ( D n − Q n ) f ( s ) d s − B n ∫ c z n ( 1 − β n ) ( D n − Q n ) f ( s ) d s - w n ( Q n + ∫ c z n β n ( D n − Q n ) f ( s ) d s ) + p r ( ∫ c z r D r f ( s ) d s + ∫ z r d Q r f ( s ) d s ) + V r ∫ c z r ( Q r − D r ) ) f ( s ) d s + p r ∫ z r d β r ( D r − Q r ) f ( s ) d s − B r ∫ z r d ( 1 − β r ) ( D r − Q r ) f ( s ) d s - w r ( Q r ∫ z r d β r ( D r − Q r ) f ( s ) d s ) − 1 8 g ( d + c ) 2
Proposition 5. Under the decentralized scenario with emergency order, the expected retailer’s profit function E R Y ( ∏ ( Q n , Q r ) )   is concave with respect to Qn and Qr if k i ( B i + p i ) − B i V i > 0 ; hence there is a unique optimal combination of decision variables ( Q Y R * n ,   Q Y R * r ) that maximizes E R Y ( ∏ ( Q n , Q r ) )       and the optimal production quantities of the two products are:
Q Y R * n = a b e − θ ( c k n p n + B n ( c k n + ( − c + d ) w n − d V n ) ) k n ( B n + p n ) − B n V n − a ( − 1 + b + α ) − ξ p n
Q Y R * r = a ( b − b e − θ ( d k r p r + B r ( d k r + ( c − d ) w r − c V r ) ) k r ( B r + p r ) − B r V r + α ) − ξ p r      
Proof. To prove concavity, hessian matrix of E R Y ( ∏ ( Q n , Q r ) )     calculated as follows:
k n ( B n + p n ) − B n V n ( c − d ) θ B n ( a ( − 1 + b + α ) + ξ p n + Q n ) 0 0 − k r ( B r + p r ) − B r V r ( c − d ) θ p r ( − a b + α + ξ p r + Q r ) The proof process is the same as Proposition 4.
Corollary 5. In the integrated model with emergency order, the optimal order quantities Q Y R * n   is convex and Q Y R * r is concave with respect to the lower and upper bound of sales effort c and d.
Proof. Since ∂ 2 Q Y I * n   ∂ c 2   = a b e − θ ( c k n p n + B n ( c k n + ( − c + d ) w n − d V n ) ) k n ( B n + p n ) − B n V n ( θ k n ( B n + p n ) − θ B n w n ) 2 ( k n ( B n + p n ) − B n V n ) 2 > 0 ;   ∂ 2 Q Y I * n   ∂ d 2   = a b e − θ ( c k n p n + B n ( c k n + ( − c + d ) w n − d V n ) ) k n ( B n + p n ) − B n V n θ 2 B n 2 ( w n − V n ) 2 ( k n ( B n + p n ) − B n V n ) 2 > 0 ;   ∂ 2 Q Y I * r   ∂ c 2   = − a b e − θ ( d k r p r + B r ( d k r + ( c − d ) w r − c V r ) ) k r ( B r + p r ) − B r V r θ 2 B r 2 ( w r − V r ) 2 ( k r ( B r + p r ) − B r V r ) 2 < 0   ;   ∂ 2 Q Y I * r   ∂ d 2   = − a b e − θ ( d k r p r + B r ( d k r + ( c − d ) w r − c V r ) ) k r ( B r + p r ) − B r V r ( θ k r ( B r + p r ) − θ B r w r ) 2 ( k r ( B r + p r ) − B r V r ) 2 < 0     then the optimal order quantity   Q Y I * n   is convex and Q Y I * r is concave in c and d.
The manufacturer’s profit function is formulated as:
E M Y ( Π ( w n , w r ) ) = ( w n - c n ) Q n + ( w n - c n − k n ) ∫ c z n β n ( D n − Q n ) f ( s ) d s + ( w r - c r ) Q r + ( w r - c r − k r ) ∫ z r d β r ( D r − Q r ) f ( s ) d s
Proposition 6. Under the decentralized scenario without emergency order, the expected manufacturer profit function E M Y ( ∏ ( w n , w r ) )   is concave with respect to wn and wr if:
2 k n p n + 2 B n k n − 2 B n V n + B n ( c − d ) θ ( − c n + w n ) > 0
Proof. To prove concavity, hessian matrix of E M Y ( ∏ ( w n , w r ) )     calculated as follows:
⁠ a b ( c − d ) e − θ ( c k n p n + B n ( c k n − d V n + ( − c + d ) w n ) ) k n ( B n + p n ) − B n V n θ B n ( Y n + B n ( c − d ) θ ( − c n + w n ) ) ( k n ( B n + p n ) − B n V n ) 2 0 0 a b ( c − d ) e − θ ( d k r p r + B r ( d k r − c V r + ( c − d ) w r ) ) k r ( B r + p r ) − B r V r θ B r ( Y i + B r ( c − d ) θ ( c r − w r ) ) ( k r ( B r + p r ) − B r V r ) 2 where Y i = 2 k i p i + 2 B i k i − 2 B i V i ( i = n , r )
By holding Condition (12), the first principal minor is negative and the second principal minor. Therefore, Hessian matrix is negative definite. To obtain the optimal values of the decision variables, ∂ E M Y ( ∏ ( w n , w r ) ) ∂ w n = 0   a n d   ∂ E M Y ( ∏ ( w n , w r ) ) ∂ w r = 0   need to be solved. That is:
a b e − θ ( c k n p n + B n ( c k n − d V n + ( − c + d ) w n ) ) k n ( B n + p n ) − B n V n − a ( − 1 + b + α ) − ξ p n − a b ( − c + d ) e − θ ( c k n p n + B n ( c k n − d V n + ( − c + d ) w n ) ) k n ( B n + p n ) − B n V n θ B n ( − k n − c n + w n ) k n ( B n + p n ) − B n V n = 0  
a ( b − b e − θ ( d k r p r + B r ( d k r − c V r + ( c − d ) w r ) ) k r ( B r + p r ) − B r V r + α ) − ξ p r + a b ( c − d ) e − θ ( d k r p r + B r ( d k r − c V r + ( c − d ) w r ) ) k r ( B r + p r ) − B r V r θ B r ( − k r − c r + w r ) k r ( B r + p r ) − B r V r = 0        
Equation (13) and (14) are transcendental equation, numerical method needs to be used. We discuss the results using numerical examples in Section 5.
Corollary 6. The order quantity of the two products in the centralized channel is higher than that in the decentralized channel with emergency order : Q Y I * n > Q Y R * n ; Q Y I * r > Q Y R * r .
Proof. Q Y I * n − Q Y R * n = a b ( e − θ ( c k n p n + B n ( ( − c + d ) c n + c k n − d V n ) ) k n ( B n + p n ) − B n V n − e − θ ( c k n p n + B n ( c k n − d V n + ( − c + d ) w n ) ) k n ( B n + p n ) − B n V n ) > 0 ; Q N I * r − Q N R * r = a b ( − e − θ ( d k r p r + B r ( ( c − d ) c r + d k r − c V r ) ) k r ( B r + p r ) − B r V r + e − θ ( d k r p r + B r ( d k r − c V r + ( c − d ) w r ) ) k r ( B r + p r ) − B r V r ) > 0 . Corollary 7. Under the two channel structures, the difference of product order quantity of the two products with or without urgent order depends on the difference of their respective out-of-stock losses and the cost of emergency orders.
Proof. Q N R n − Q Y R n = a b e − θ c B n + p n − d V n + − c + d w n B n + p n − V n − e − θ c k n p n + B n c k n − d V n + − c + d w n k n B n + p n − B n V n ; Q N R r − Q Y R r = a b ( − e − θ ( d B r + d p r − c V r + ( c − d ) w r ) B r + p r − V r + e − θ ( d k r p r + B r ( d k r − c V r + ( c − d ) w r ) ) k r ( B r + p r ) − B r V r ) . It is similar under the integrated structures.

5. Analysis of equilibrium results

5.1. Numerical examples datasets

In this section, numerical examples are taken to analyze the decision results in different models. The datasets are consistent with the data in the study [5] and satisfies all assumptions. Datasets are shown in Table 2. Mathematica 12 is used to solve the models.
Table 2. Numerical examples datasets.
Table 2. Numerical examples datasets.
pn pr Bn Br Vn Vr cn cr kn
8 6 3 2 1.5 1 4 1.5 1.75
a α θ c d b g ξ kr
50 0.015 1.7 0 5 0.25 0.005 2 1.85

5.2. Results of order quantities and profits

For the given datasets, the corresponding decision variables, and members’ profits under integrated and decentralized models under different cases are shown in Table 3.
According to Table 3, the order quantity of both product types in the decentralized scenario is lower than that in the integrated scenario. Moreover, under the emergency ordering strategy, the order quantity of both integrated and decentralized scenarios decreases, while the total profit of the CLSC increases. As expected, the total channel profit in the integrated scenario is higher than that in the decentralized scenario. And that proves that the performance of CLSC in integrated scenario is better [4]. This conclusion is independent of the presence or absence of an emergency order strategy. Under the emergency order case, emergency ordering does not increase profits for both manufacturer and retailer. Instead, it makes the retailer more profitable and the manufacturer less profitable[5]. And the profit gap between the manufacturer and the retailer decreases. The manufacturer's revenue decreases for that it bears the emergency ordering cost.

5.3. Impact of sales effort

In this part, the influence of sales efforts under different channel structures on the decision variables and profits will be presented and analyzed. Sales effort s has been defined as a random variable subject to uniform distribution, where c and d are the lower and the upper bound. Profits and order quantities vary with different combinations of c and d as shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11.
Preprints 94387 g001
Figure 1. Order quantity of new product in integrated and decentralized scenarios without emergency order.
Figure 1. Order quantity of new product in integrated and decentralized scenarios without emergency order.
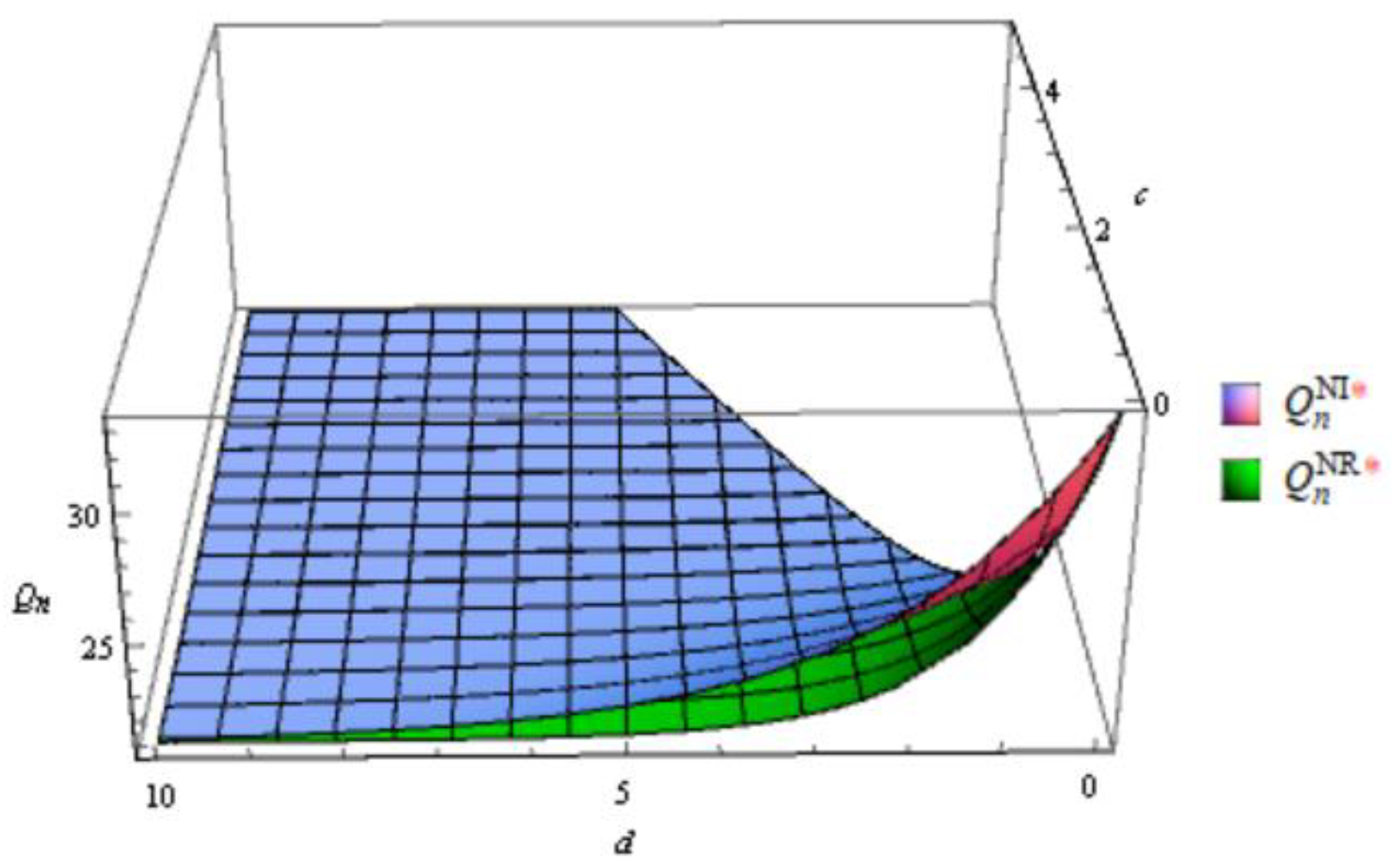
Preprints 94387 g001
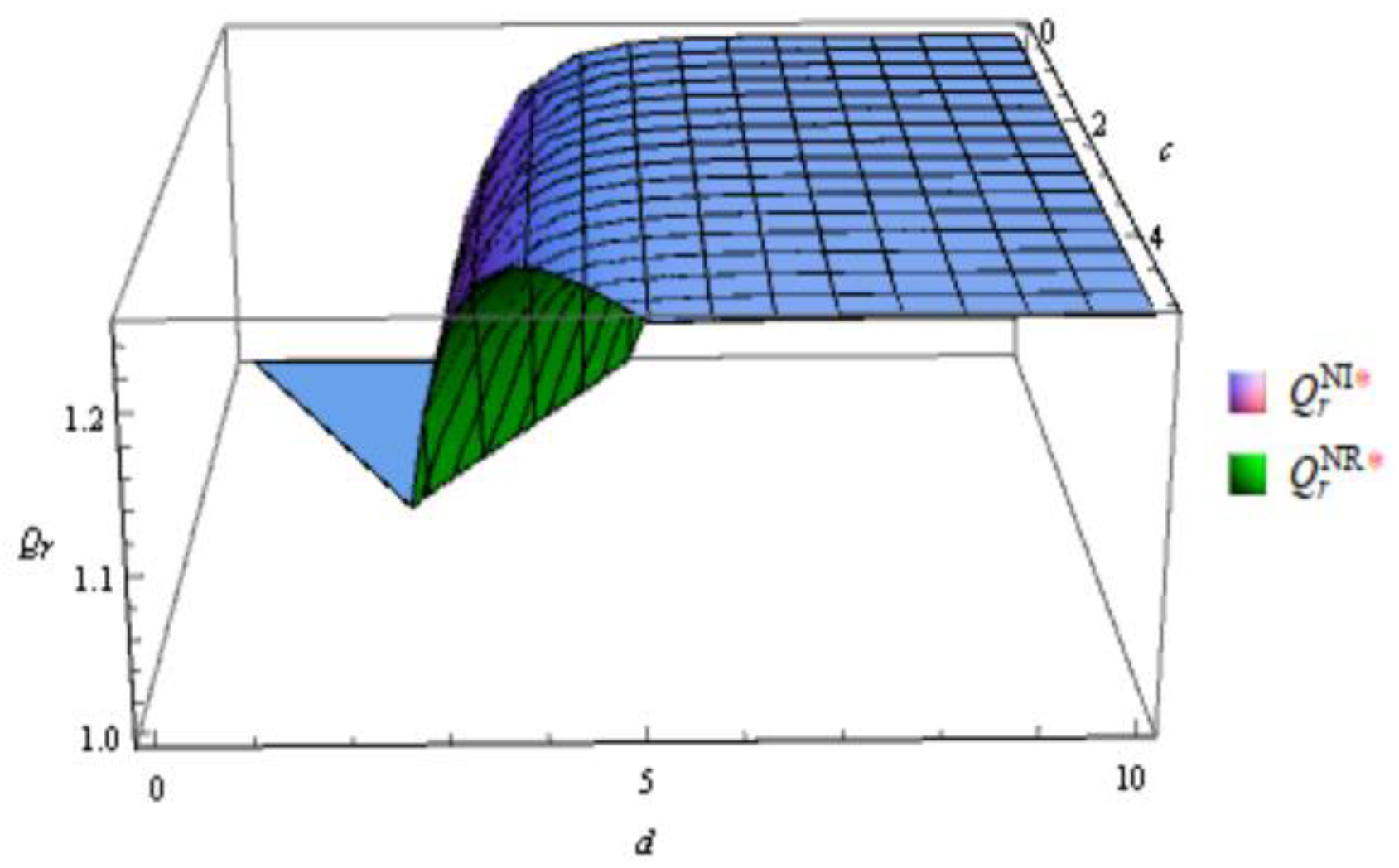
Preprints 94387 g002
Figure 2. Order quantity of remanufactured product in integrated and decentralized scenarios without emergency order.
Figure 2. Order quantity of remanufactured product in integrated and decentralized scenarios without emergency order.
Preprints 94387 g002
Preprints 94387 g003
Figure 3. Order quantity of new product without and with emergency order in the integrated scenario.
Figure 3. Order quantity of new product without and with emergency order in the integrated scenario.
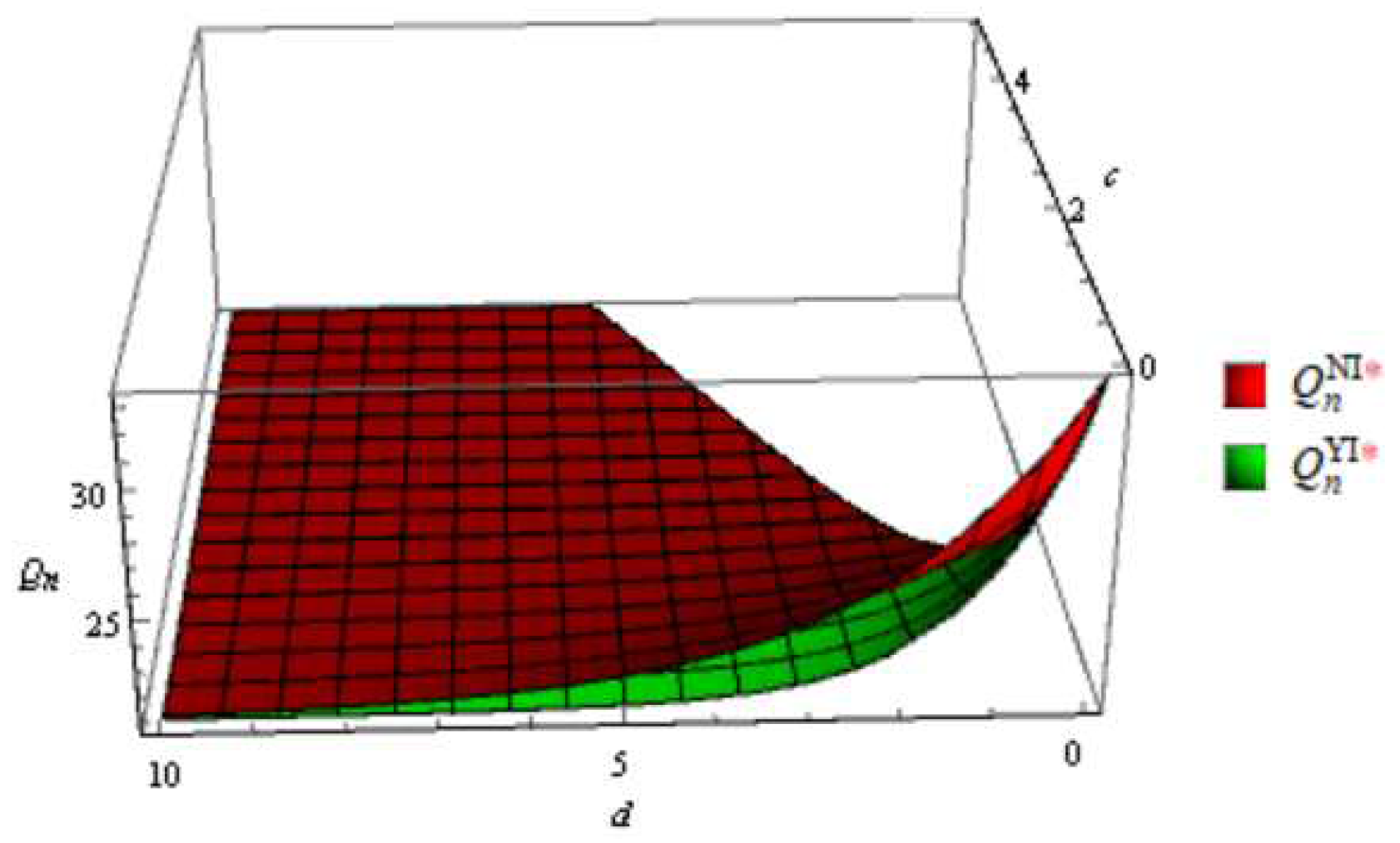
Preprints 94387 g003
Preprints 94387 g004
Figure 4. Order quantity of remanufactured product without and with emergency order in the integrated scenario.
Figure 4. Order quantity of remanufactured product without and with emergency order in the integrated scenario.
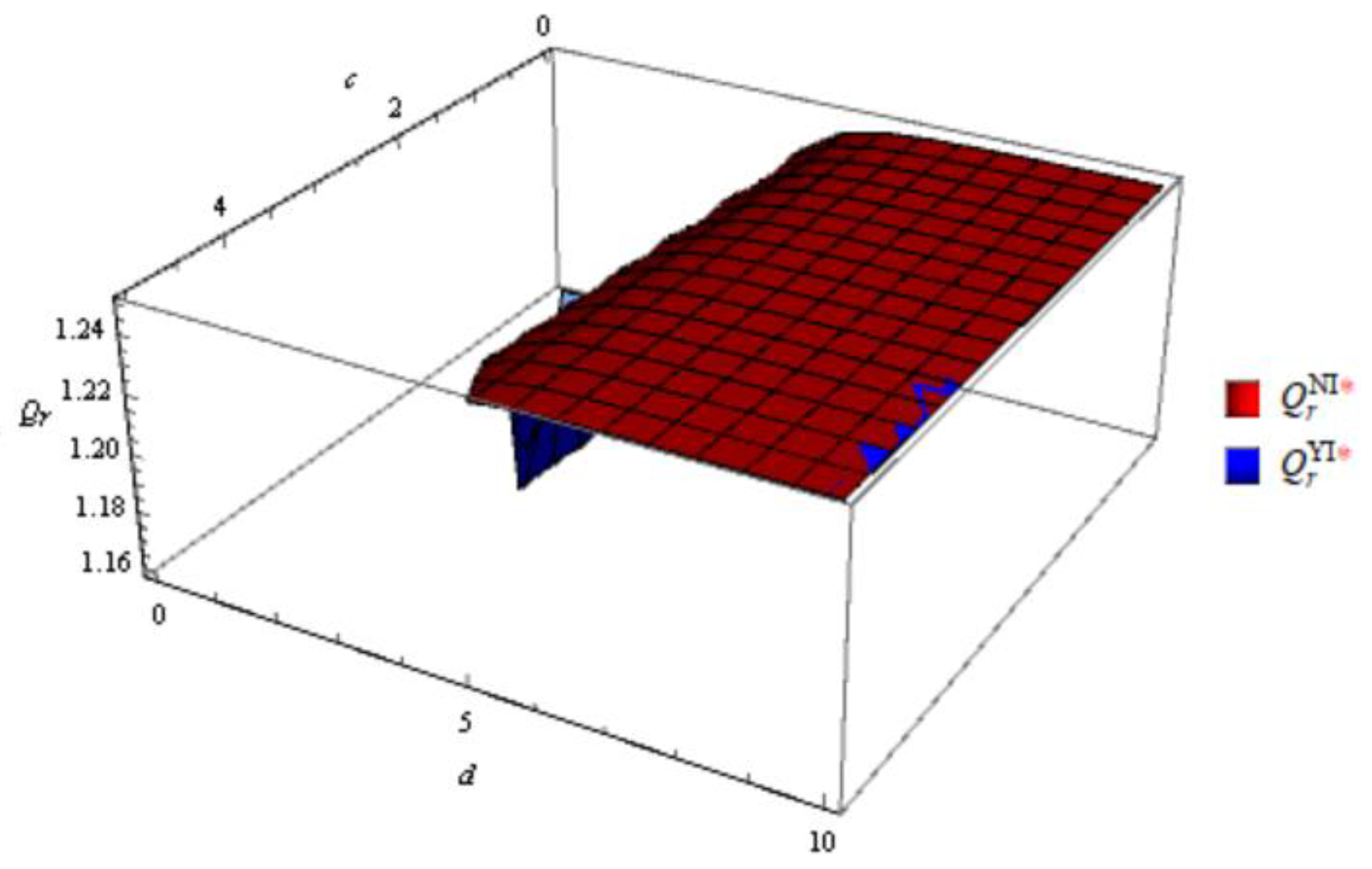
Preprints 94387 g004
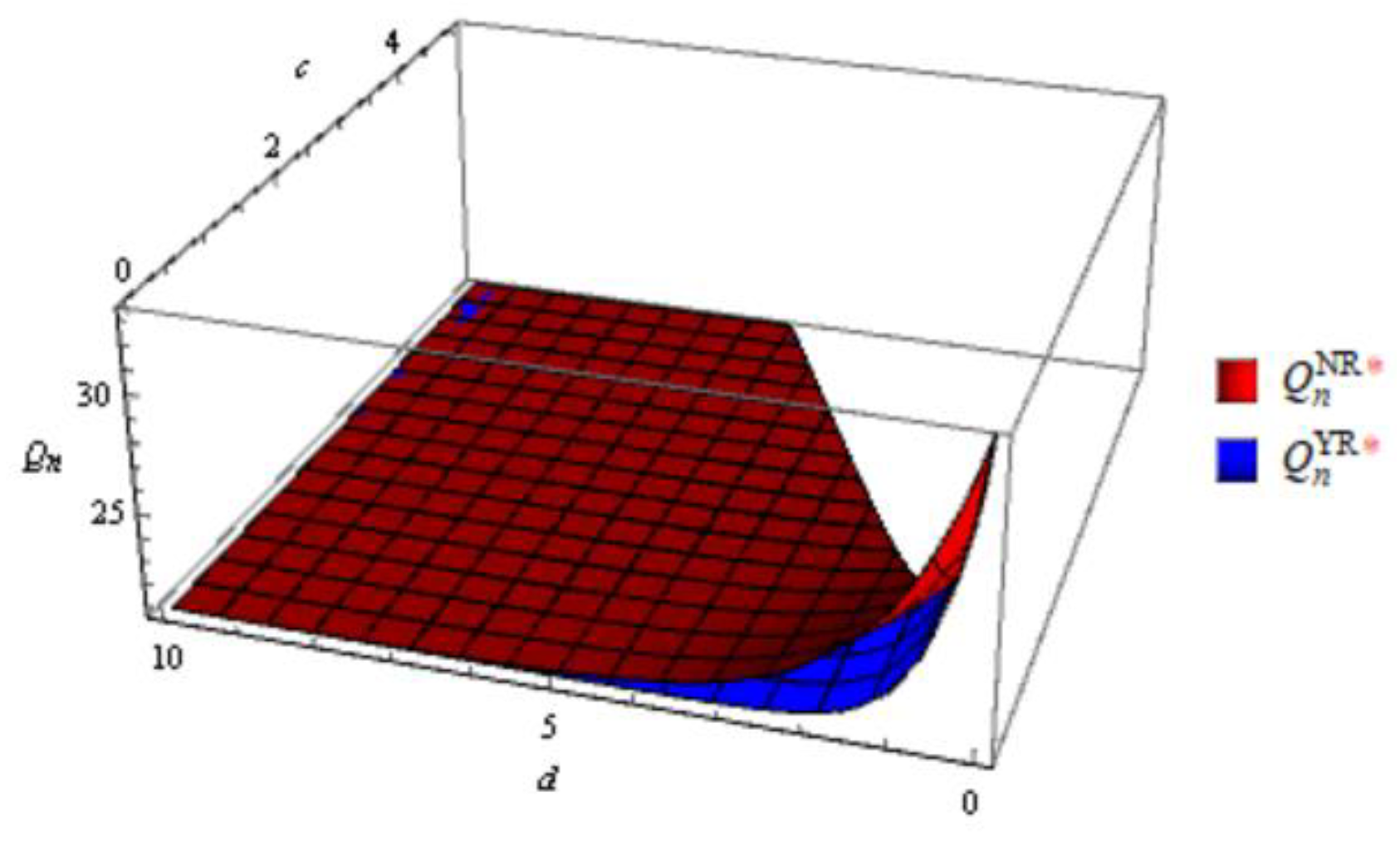
Preprints 94387 g005
Figure 5. Order quantity of new product without and with emergency order in the decentralized scenario.
Figure 5. Order quantity of new product without and with emergency order in the decentralized scenario.
Preprints 94387 g005
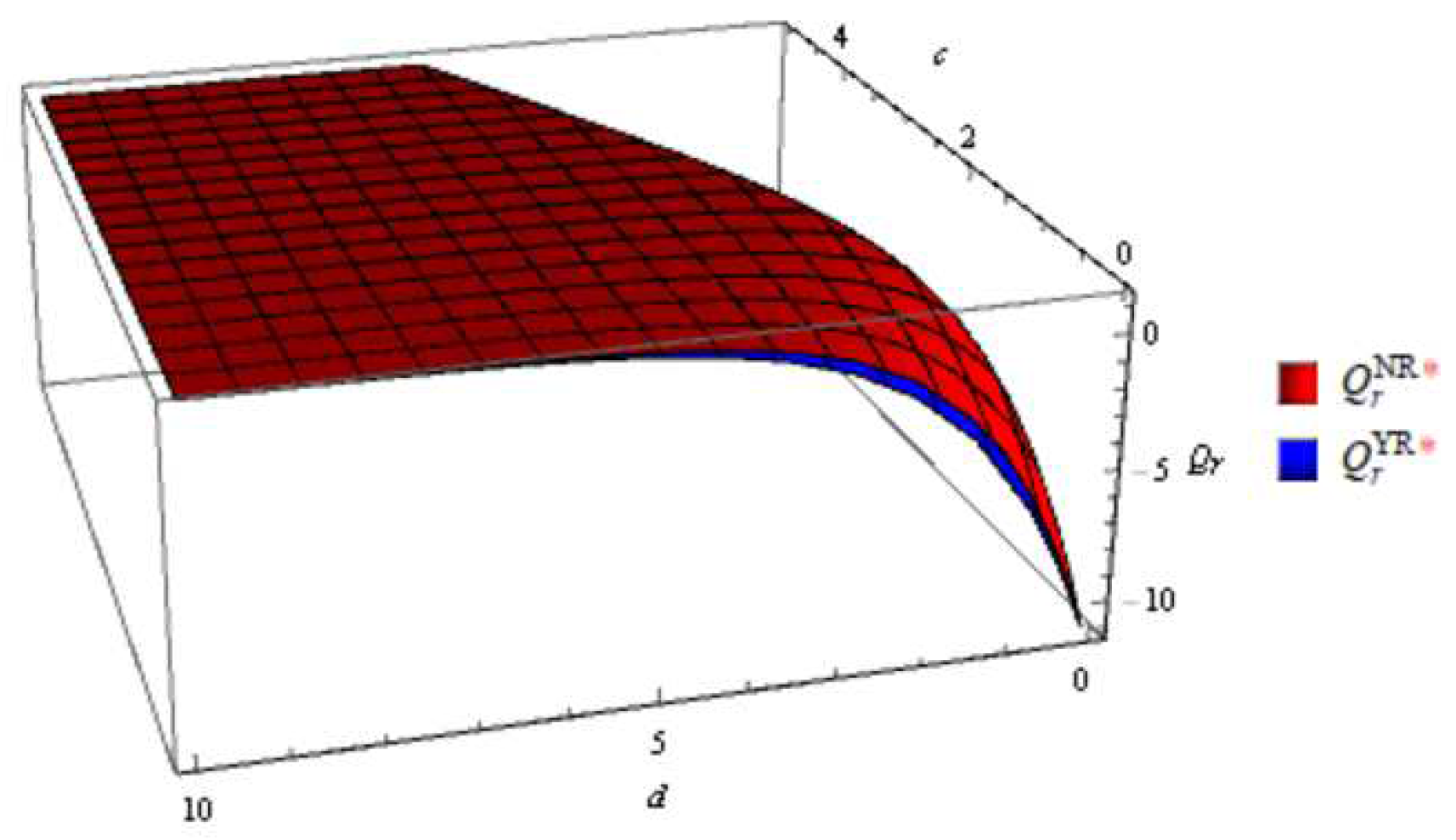
Preprints 94387 g006
Figure 6. Order quantity of remanufactured product without and with emergency order in the decentralized scenario.
Figure 6. Order quantity of remanufactured product without and with emergency order in the decentralized scenario.
Preprints 94387 g006
Preprints 94387 g007
Figure 7. Order quantity of new product in integrated and decentralized scenarios with emergency order.
Figure 7. Order quantity of new product in integrated and decentralized scenarios with emergency order.
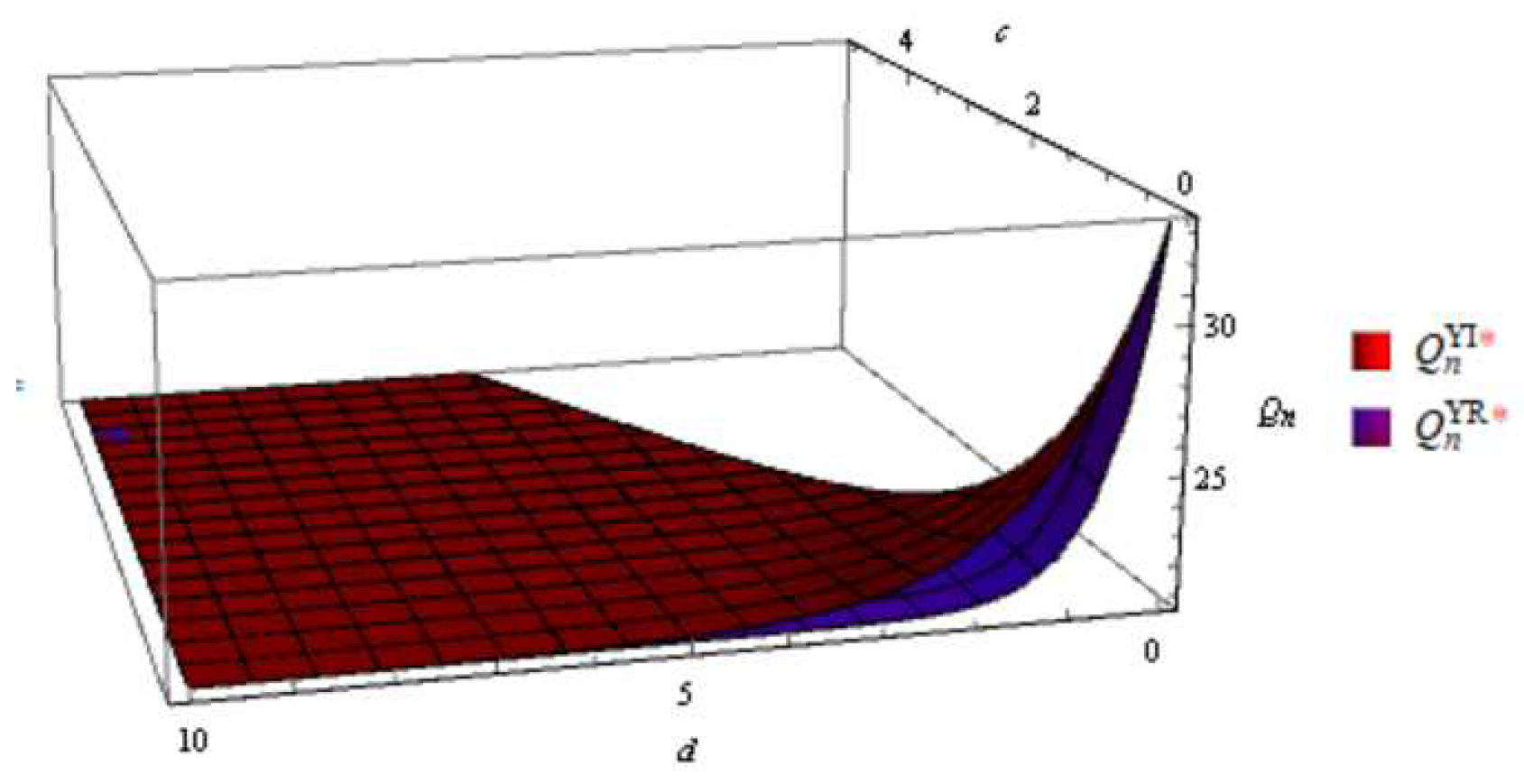
Preprints 94387 g007
Preprints 94387 g008
Figure 8. Order quantity of remanufactured product in integrated and decentralized scenarios with emergency order.
Figure 8. Order quantity of remanufactured product in integrated and decentralized scenarios with emergency order.
Preprints 94387 g008
According to the Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, In general, the order quantity of new products has a convex function relationship with both c and d, and the order quantity of remanufactured products is concave function with sales effort c and d. This result is consistent with Corollary 1, 2 and Corollary 4, 5. Moreover, when d approaches to 0, meaning that retailers do not make sales efforts for the sale of remanufactured products, the order quantity for remanufactured products is significantly lower. However, when sales efforts begin to take effect, the impact is greater in the early stages. And when d is large enough, the gap in channel order quantity gradually decreases.
From the channel structure aspect, consistent with Corollary 3 and Corollary 6, it is illustrated that the order quantities are generally higher in the integrated scenario than in the decentralized scenario both with and without emergency order. Moreover, the order quantity of remanufactured product is not sensitive to the channel structure under different sales efforts. The possible reason is that the market share of remanufactured products is relatively small. In addition, high sales efforts will reduce channel differences in order quantity.
Comparing the order quantities of two types of products with and without emergency orders, it was found that the order quantities with emergency orders were lower than those without emergency orders. This conclusion is in line with the actual situation.

5.4. Impact of emergency order costs and loss of out-of-stock

As it can be seen in Figure 9, the integrated CLSC profit with emergency order is higher than without emergency order upon most occasions, which is consistent with Table 3. And in some cases, the opposite is true. As shown in Figure 10, except in a few cases, emergency orders will also bring more profits to the manufacturer. While Figure 11. illustrates that the retailer will always benefit from emergency ordering. Comparing Figure 10 with Figure 11, it is found that the manufacturer obtains a larger part of the profit of the CLSC. It indicates that the manufacturer has more power in the CLSC.
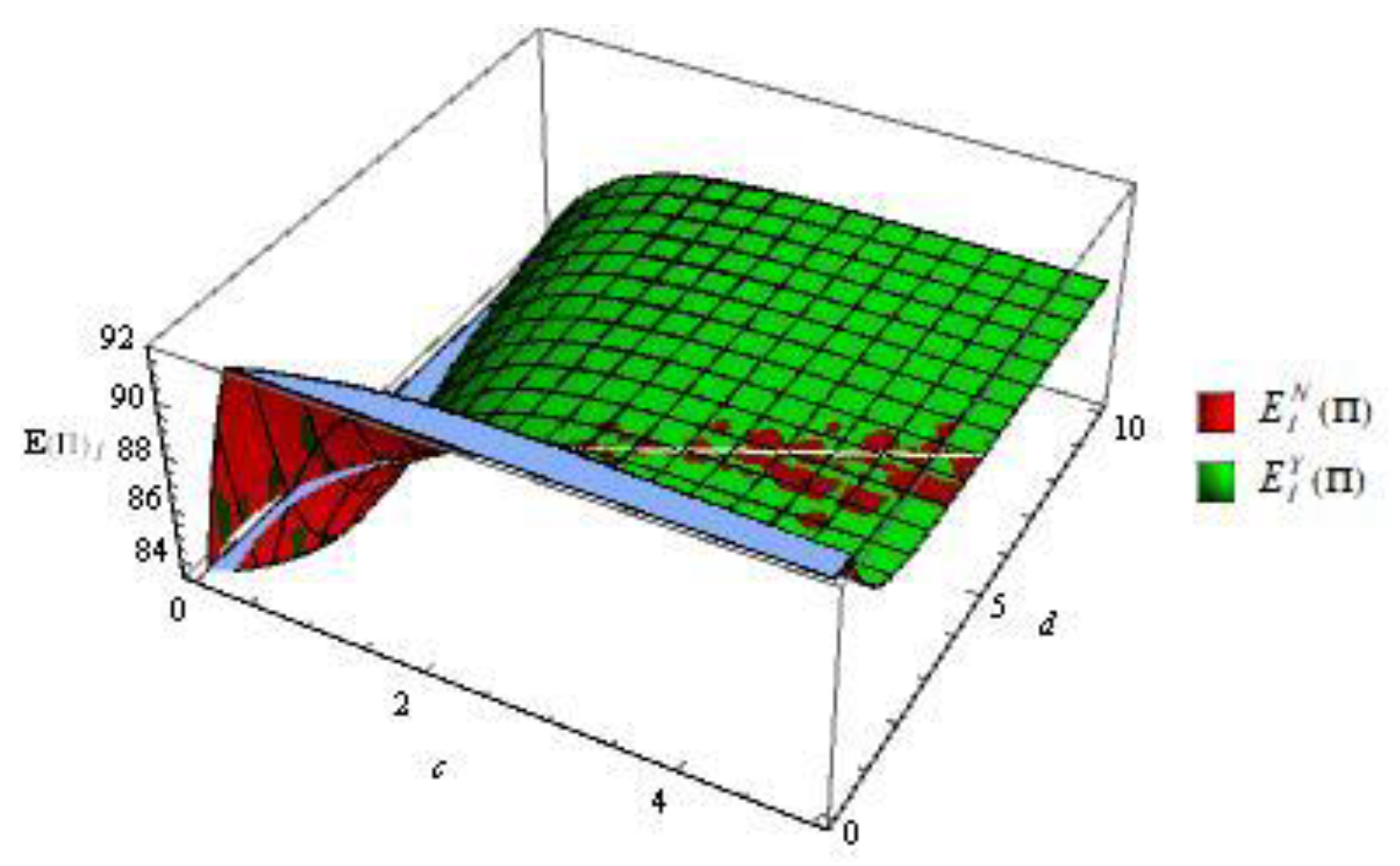
Preprints 94387 g009
Figure 9. Profit of the CLSC without and with emergency order in the integrated scenario.
Figure 9. Profit of the CLSC without and with emergency order in the integrated scenario.
Preprints 94387 g009
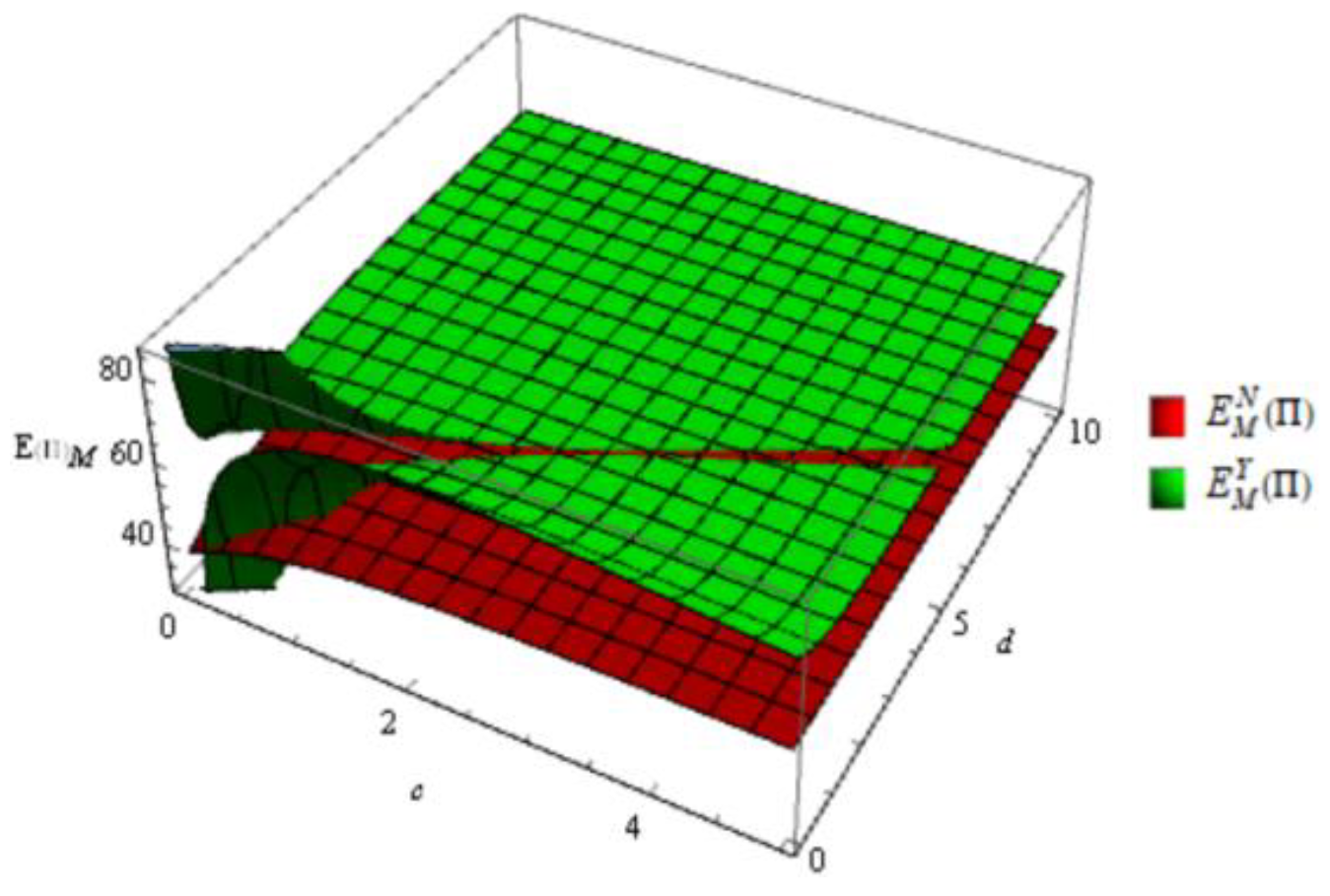
Preprints 94387 g010
Figure 10. Profit of the manufacturer without and with emergency order in the decentralized scenario.
Figure 10. Profit of the manufacturer without and with emergency order in the decentralized scenario.
Preprints 94387 g010
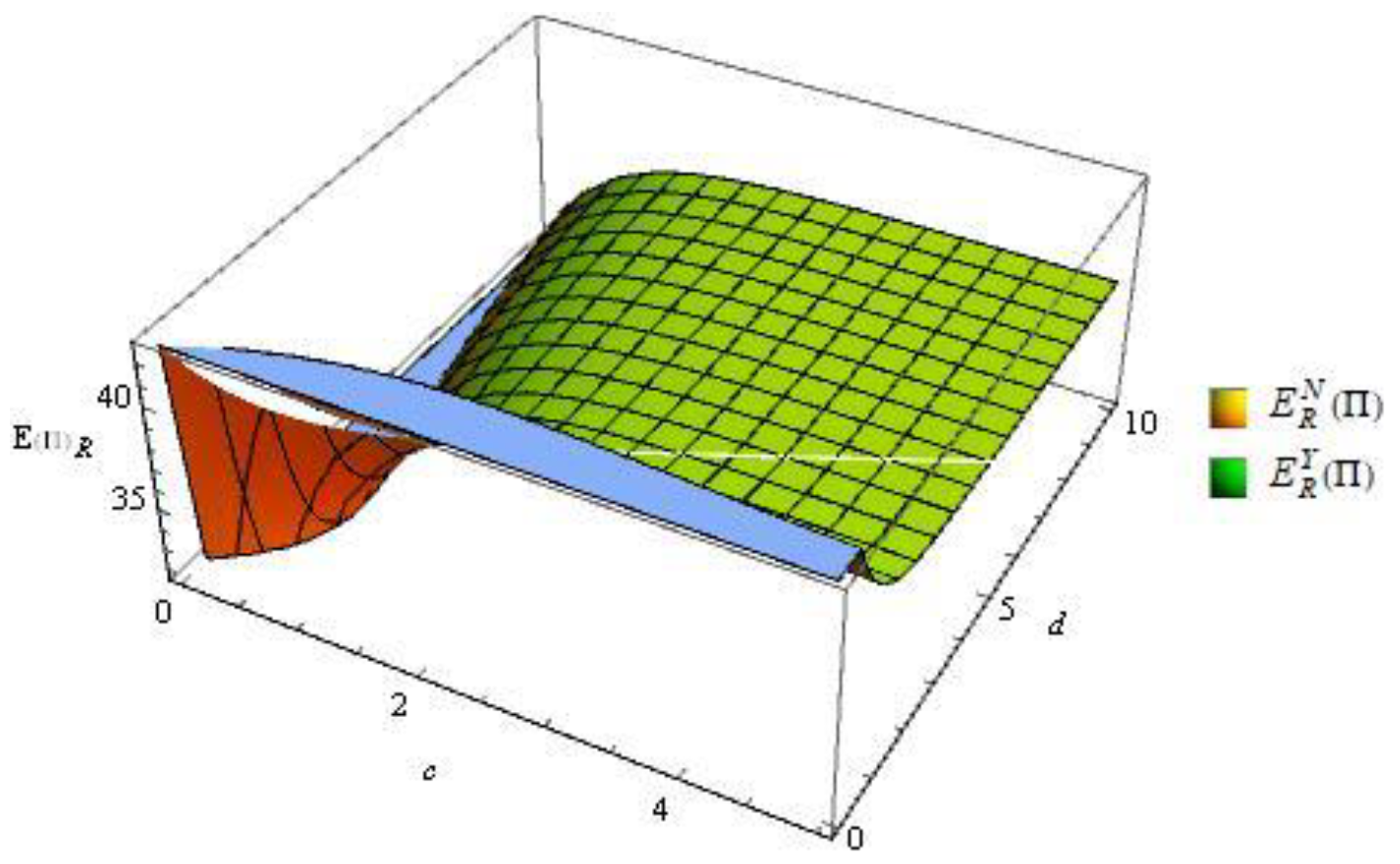
Preprints 94387 g011
Figure 11. Profit of the retailer without and with emergency order in the decentralized scenario.
Figure 11. Profit of the retailer without and with emergency order in the decentralized scenario.
Preprints 94387 g011
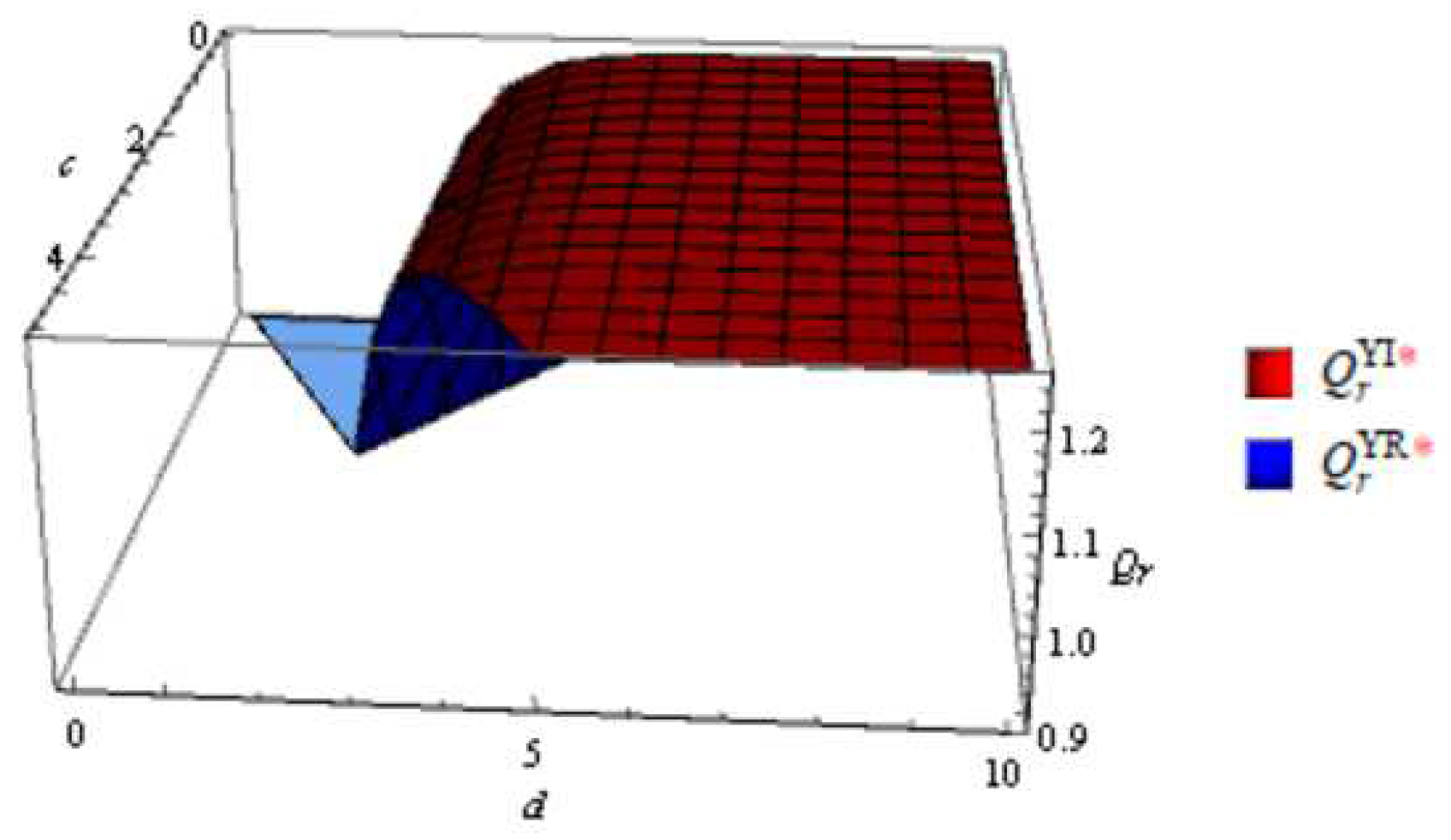
Figure 12 shows that as kn increases, Qn also increases, while Qn decreases with the increase of Bn. Furthermore, from the perspective of the proportion of emergency order, when kn is pretty small and Bn is relatively large, that is, the proportion of emergency order is higher, the impact of the ratio (kn /Bn) on Qn is almost not obvious. Moreover, the order quantity of new products in the high ratio case is higher than that of the low ratio case. What causes this phenomenon is that the retailer will increase the order quantity at the time of the original order when emergency order is costly.
According to Figure 13, the results of the impact of emergency order on the order quantity of the remanufactured product are a bit different from those of new product. Specifically, an increase in both kr and Br will result in an increase in Qr. And compared to integrated structures, in a decentralized supply chain structure, the variation in the order quantity of remanufactured products is greater. In addition, it can be inferred that when kr /Br decreases, that is, the proportion of emergency order increases, and the order quantity for remanufactured products decreases.
According to Figure 14, Figure 15, Figure 16, the emergency ordering costs and out of stock costs of new and remanufactured products both affect the profits of the manufacturer, the retailer, and the CLSC. When ki is rather small, the profits of the CLSC and members are not sensitive to the ratio (ki/Bi). And in the case of the implementation of emergency ordering, the emergency ordering of the new product makes the manufacturer's profit lower with kn increasing (see Figure 15a). When Bn is relatively small, the impact of the ratio kn on the profit of the CLSC depends on kn, causing the lowest profit. In addition, the profit of the CLSC decreases with the kn increasing (see Figure 14a). For the retailer, if the loss of stock shortage Bn is small, emergency ordering is not necessary, because it will cause a large reduction in profits, as shown in Figure 16a. As kr increases, the profit of the CLSC and the retailer decreases (see Figure 14b and Figure 16b).

6. Conclusions

Environmental awareness, resource conservation and economic benefits have promoted the development of closed-loop supply chains, and remanufactured products are gradually appearing in the market with new products. Relative to new products, the acceptance of remanufactured products in consumers’ perception is more influenced by sales effort, especially in the initial stage. On the other hand, sales effort also makes the market share of new products vary. There have been some studies on sales effort in closed supply chains, and most of them are based on the assumption of linear relationship between sales effort and demand. In this study, a CLSC with one manufacturer and one retailer, in which sales effort, as a random variable, affects market share of two types of products, the optimal ordering decision and wholesale price are explored by establishing game theoretic models of centralized CLSC and decentralized CLSC without and with emergency order. All models are evaluated using numerical experiments. Managerial insights from the proposed model can be summarized as:
(1)
In general, the order quantity of new products usually has a convex function with sales effort, while the order quantity of remanufactured products has a concave function with sales effort. And the sales effort has a higher impact on the order quantity of new product than remanufactured product. Wherein, the upper bound of sales effort has a greater impact on the order quantity of the two types of products, rather than the lower bound.
(2)
In most cases, the emergency order will increase the profit of the CLSC and its members. In addition, the order quantity and profit in the CLSC are both affected by the relative ratio between the cost of emergency ordering and the cost of out-of-stock, rather than solely one of them.
(3)
The profits and order quantities of the integrated closed-loop supply chain is higher than that of the decentralized scenario, which indicates that the integrated supply chain performs better than the decentralized one whether there is an emergency ordering strategy.
(4)
A certain degree of sales effort will narrow the difference in product order quantity between decentralized and integrated channels.
The management recommendations that can be derived from the research results are:
(1)
Retailers need to establish appropriate sales effort limits to avoid excessive resource investment leading to diminishing marginal returns, and to focus on the overall revenue. Additionally, it is necessary for managers to take measures to ensure effective response to the sales challenges of new and remanufactured products, and to ensure that sales efforts are maximally translated into an increase in order volume.
(2)
For the impact of emergency orders on the supply chain, a cost-benefit analysis can be conducted for each product or product category to determine the economic benefits of using emergency orders in different situations. Moreover, retailers and manufacturers can establish close cooperative relationships to better respond to emergency situations. This may include sharing information, collaborating to solve problems, and ensuring the reliability and stability of the supply chain.
(3)
A closed-loop supply chain can take the sales effort strategy for remanufactured products as a means to coordinate a decentralized supply chain, ensuring that sales efforts generate more consistent order volumes across various channels, thereby improving overall sales performance and customer satisfaction. For example, integrate sales strategies and train sales teams to better achieve synergies between channels.
In this paper, it is assumed that the manufacturer directly remanufactures the recycled products; this assumption can be relaxed and the behavior of CLSC including the recycling process can be explored in the future. Moreover, multi-echelons CLSC points to an interesting future research. The proportion of emergency orders related to the out-of-stock quantity is also a direction that can be studied. Or the CLSC management with other forms of backorder compensation strategies. There are many aspects of closed-loop supply chain management that need to be explored.

Author Contributions

Conceptualization, Y.T-J. and N.G.; methodology, N.G.; software, N.G.; validation, J.H. and L.C-Q.; formal analysis, N.G.; investigation, N.G.; resources, Y.T-J.; data curation, Y.T-J.; writing—original draft preparation, N.G.; writing—review and editing, Y.T-J.; visualization, N.G.; supervision, J.H.; project administration, L.C-Q.; funding acquisition, Y.T-J. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Social Science Fund Project "Mechanism and Path Optimization of Digitalization Empowering High-quality Development of Shipping Service Industry"(23BJY130).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The authors would like to thank feedbacks from professors for this work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Souza, G. Closed-loop supply chains: A Critical Review, and Future Research. Dec. Sci. 2012, 44, 7–38. [Google Scholar] [CrossRef]
  2. Gu, Y.; Xue, M.; Zhao, M.; Long, Y. Optimal Government Subsidy Decision and Its Impact On Sustainable Development Of A Closed-Loop Supply Chain. Systems 2023, 11, 378. [Google Scholar] [CrossRef]
  3. Mondal, C.; Giri, B. C. Optimizing Price, Quality and CSR Investment under Competing Dual Recycling Channels In A Sustainable Closed-Loop Supply Chain. CIRP J. Man. Sci. Tech. 2021, 35, 193–208. [Google Scholar] [CrossRef]
  4. Li, G.; Lu, M.; Lai, S.; Li, Y. Research on Power Battery Recycling in the Green Closed-Loop Supply Chain: An Evolutionary Game-Theoretic Analysis. Sustainability 2023, 15, 10425. [Google Scholar] [CrossRef]
  5. Zhang, L.; Wang, J.; You, J. Consumer Environmental Awareness and Channel Coordination with Two Substitutable Products. Eur. J. Op. Res. 2015, 241, 63–73. [Google Scholar] [CrossRef]
  6. Modak, N. M.; Kazemi, N.; Cárdenas-Barrón, L. E. Investigating Structure of a Two-Echelon Closed-Loop Supply Chain Using Social Work Donation as A Corporate Social Responsibility Practice. Int. J. Prod. Ec. 2019, 207, 19–33. [Google Scholar] [CrossRef]
  7. Lee, D.-H.; Park, E.-H. Decision Making in a Closed-Loop Supply Chain with A Waste Management Program: Manufacturers’ Take-Back Activity and Governmental Subsidies for Remanufacturing. Processes 2023, 11, 3132. [Google Scholar] [CrossRef]
  8. Feng, Z.; Xiao, T.; Robb, D. J. Environmentally Responsible Closed-Loop Supply Chain Models with Outsourcing and Authorization Options. J Clean Prod. 2021, 278, 123791. [Google Scholar] [CrossRef]
  9. Jian, J.; Wang, G.; Hu, H.; Su, J. Decision-making Models And Coordination in a Closed-Loop Supply Chain Considering Patent Protection for DfR. Systems 2023, 11, 127. [Google Scholar] [CrossRef]
  10. Dai, L.; Shu, T.; Chen, S.; Wang, S.; Lai, K. K. CSR Remanufacturing Supply Chains under WTP Differentiation. Sustainability. 2020, 12, 2197. [Google Scholar] [CrossRef]
  11. Atasu, A.; Guide, V. D. R.; Van Wassenhove, L. N. So What If Remanufacturing Cannibalizes My New Product Sales? Cal. Man. Rev. 2010, 52, 56–76. [Google Scholar] [CrossRef]
  12. Michaud, C.; Llerena, D. Green Consumer Behavior: An Experimental Analysis of Willingness to Pay for Remanufactured Products. Bus. Strat. En. 2010, 20, 408–420. [Google Scholar] [CrossRef]
  13. Yang, D.; Zhang, L.; Wu, Y.; Guo, S.; Zhang, H.; Xiao, L. A Sustainability Analysis on Retailer’s Sales Effort in A Closed-Loop Supply Chain. Sustainability. 2019, 11, 8. [Google Scholar] [CrossRef]
  14. Sane Zerang, E.; Taleizadeh, A. A.; Razmi, J. Analytical Comparisons in A Three-Echelon Closed-Loop Supply Chain with Price and Marketing Effort-Dependent Demand: Game Theory Approaches. Env. Dev. Sus. 2016, 20, 451–478. [Google Scholar] [CrossRef]
  15. Taleizadeh A. A.; Mamaghan K. M.; Torabi A, S. A Possibilistic Closed-Loop Supply Chain: Pricing, Advertising and Remanufacturing Optimization. Neur. Com. App. 2020, 32, 1195–1215. [CrossRef]
  16. Behrooz K.; Hamed S.; Soheil S. et al. Developing a Two-Stage Model for A Sustainable Closed-Loop Supply Chain with Pricing and Advertising Decisions. J. Clean. Prod. 2021, 309, 127165.
  17. Ma P.; Li K.; Jing Z. W. Pricing Decisions in Closed-Loop Supply Chains with Marketing Effort and Fairness Concerns. Int. J. Prod. Econ. 2017, 55, 6710–6731. [CrossRef]
  18. Zhang H.; Wang Z.J.; Hong X.P.et. al. Fuzzy Closed-Loop Supply Chain Models with Quality and Marketing Effort-Dependent Demand. Exp. Sys. Appl. 2022, 207, 118081. [CrossRef]
  19. Poormoaied, S.; Demirci, E. Z. Analysis of An Inventory System with Emergency Ordering Option at the Time of Supply Disruption. Or Spec. 2021, 43, 1007–1045. [Google Scholar] [CrossRef]
  20. Ghiami, Y.; Beullens, P. Planning for Shortages? Net Present Value analysis for A Deteriorating Item with Partial Backlogging. IJPE. 2016, 178, 1–11. [Google Scholar] [CrossRef]
  21. Huang, J.; Wu, G.; Wang, Y. Retailer’s Emergency Ordering Policy When Facing an Impending Supply Disruption. Sustainability. 2021, 13, 7041. [Google Scholar] [CrossRef]
  22. Zhang, W.; Li, J.; Zhang, R. et. al. Impact of Emergency Order in Price-Dependent Newsvendor Problems. Asia-Pac. J. Op. Res. 2017, 34, 1750001. [Google Scholar] [CrossRef]
  23. Poormoaied, S.; Atan, Z.; de Kok, T. et. al. Optimal Inventory and Timing Decisions for Emergency Shipments. IISE Trans. 2020, 52, 904–925. [Google Scholar] [CrossRef]
  24. Yin, J.; Fang, Y.; Zhang, H.; Wang, T.; Cai, S. Pricing and Coordinating the Lease-Oriented Closed-Loop Supply Chain for Construction Machinery in the Era of Carbon Tax. Buildings 2023, 13, 2145. [Google Scholar] [CrossRef]
  25. Shi, J.; Zhang, G.; Sha, J. Optimal Production and Pricing Policy for A Closed Loop System. Res. Con. Rec. 2011, 55, 639–647. [Google Scholar] [CrossRef]
  26. Maiti, T.; Giri, B.C. A Closed Loop Supply Chain under Retail Price and Product Quality Dependent Demand. J. Man. Sys. 2015, 37, 624–637. [Google Scholar] [CrossRef]
  27. He, P.; He, Y.; Xu, H. Channel Structure and Pricing in a Dual-Channel Closed-Loop Supply Chain with Government Subsidy. J. Prod. Econ. 2019, 213, 108–123. [Google Scholar] [CrossRef]
  28. Solaleh, K.; Esmaeili, M.; Barrón, L.; Sunil, T.; Shaikh, A. A Sustainable Closed-Loop Supply Chain in A Two-Period: A Game Theory Approach. Eur. J. Ind. Eng. 2021, 15, 226–249. [Google Scholar]
  29. Zhou Y.Y.; Zhang Y.L.; Wahab M.I.M. et. al. Channel Leadership And Performance For A Closed-Loop Supply Chain Considering Competition. Tran. Res. Part E: Log. Tran. Rev. 2023, 175, 103151.
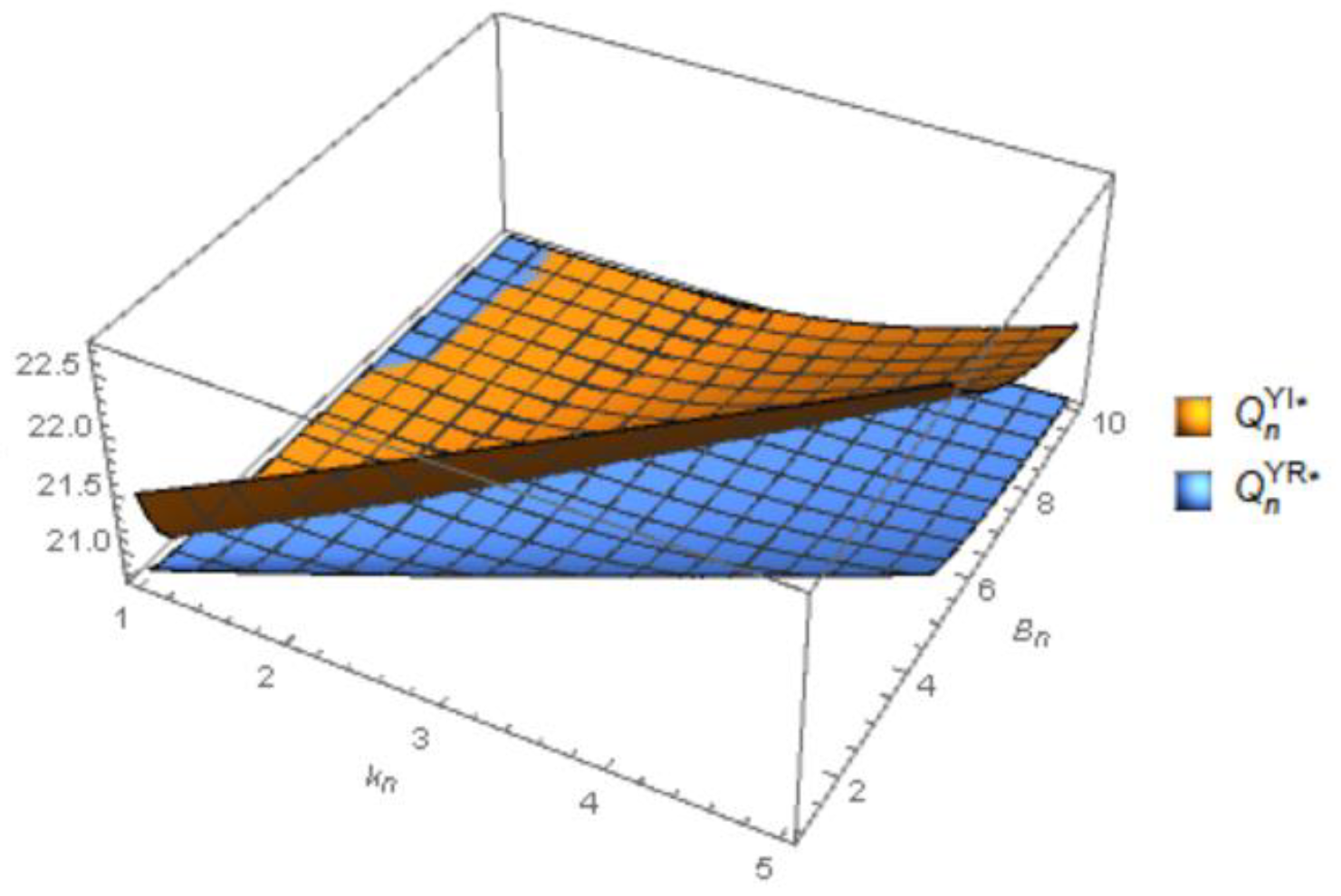
Preprints 94387 g012
Figure 12. Order quantity of new product in the integrated and decentralized scenario with emergency order.
Figure 12. Order quantity of new product in the integrated and decentralized scenario with emergency order.
Preprints 94387 g012
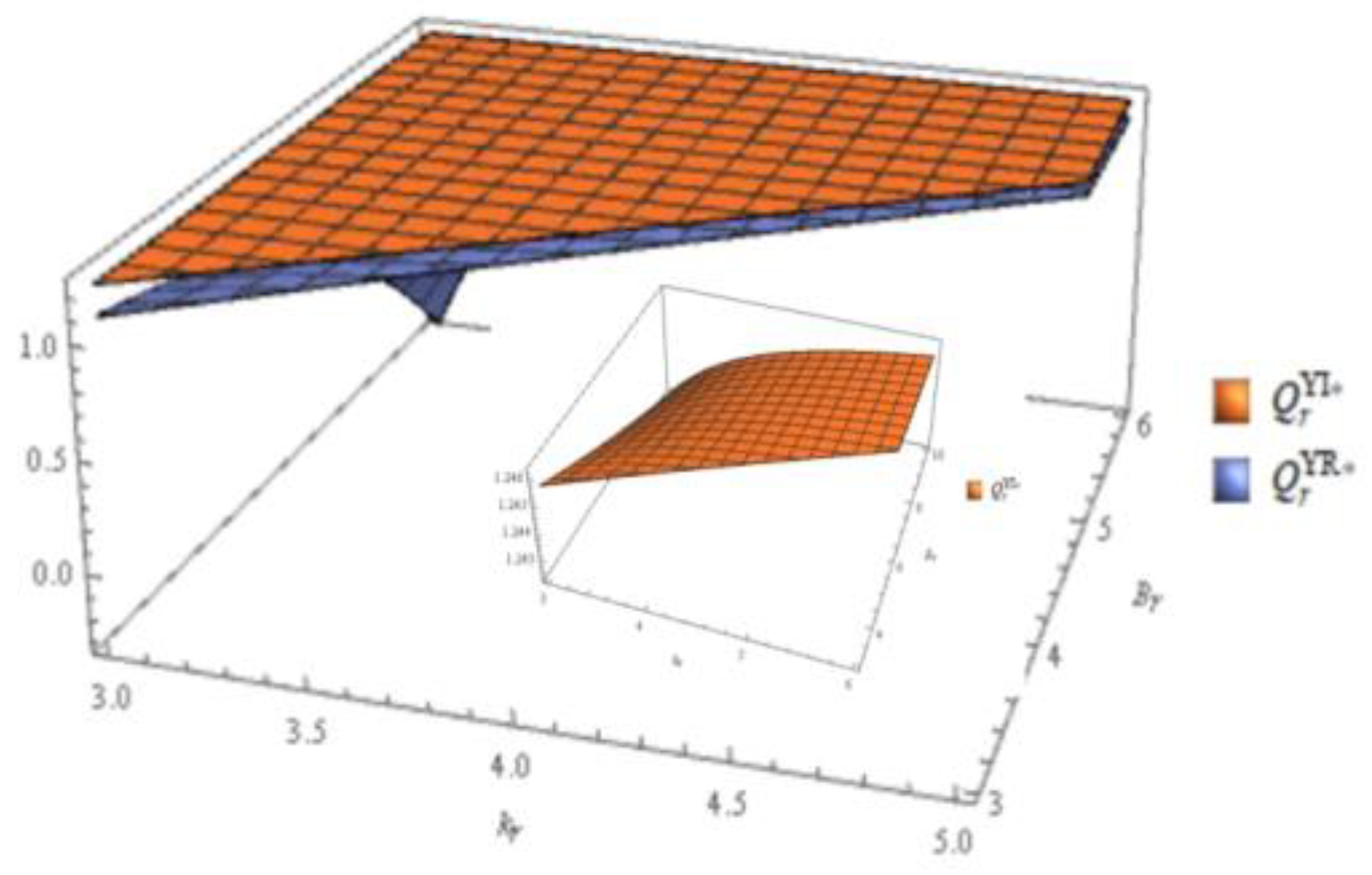
Preprints 94387 g013
Figure 13. Order quantity of remanufactured product in the integrated and decentralized scenario with emergency order.
Figure 13. Order quantity of remanufactured product in the integrated and decentralized scenario with emergency order.
Preprints 94387 g013
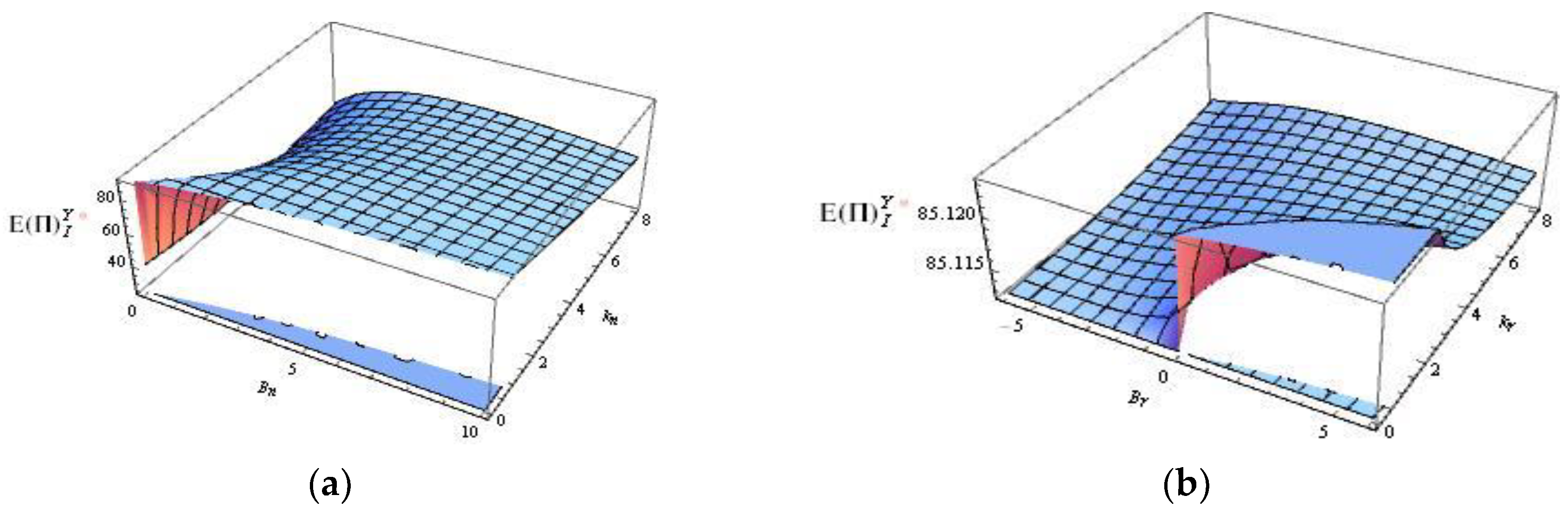
Preprints 94387 g014
Figure 14. Profit of the CLSC in the integrated scenario with emergency order.
Figure 14. Profit of the CLSC in the integrated scenario with emergency order.
Preprints 94387 g014
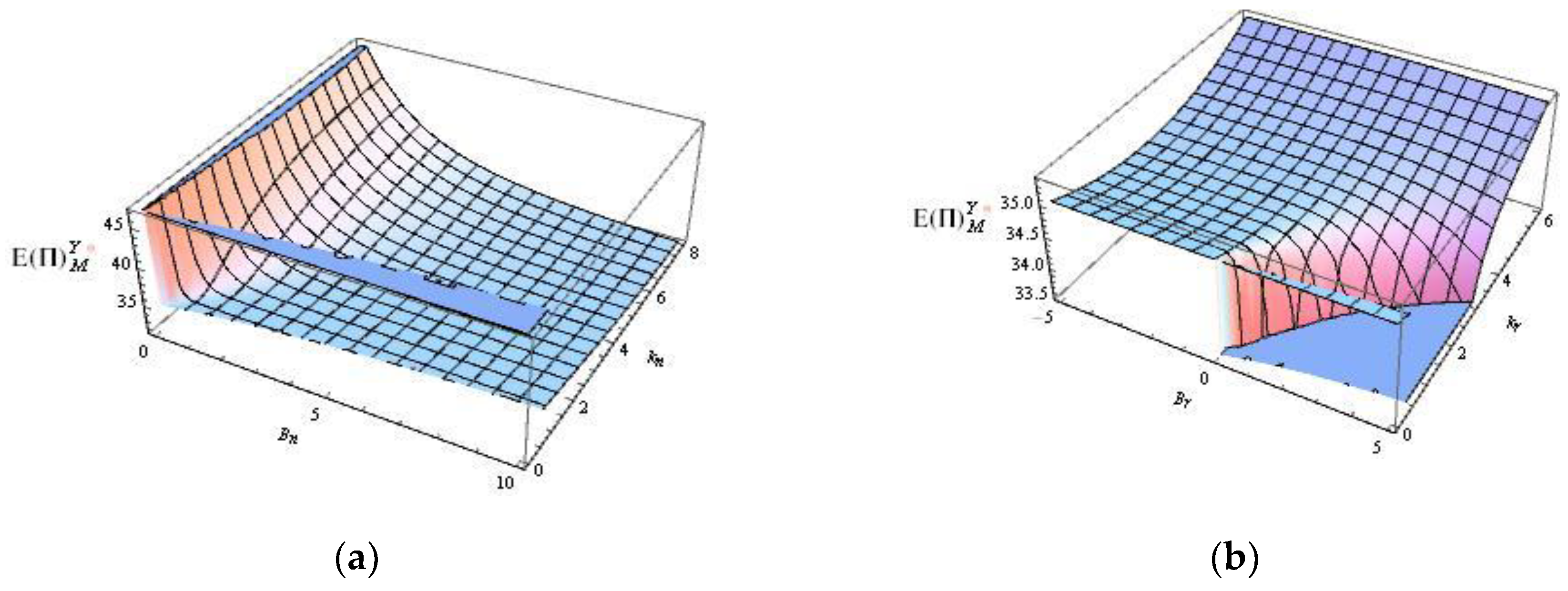
Preprints 94387 g015
Figure 15. Profit of the manufacturer in the decentralized scenario with emergency order.
Figure 15. Profit of the manufacturer in the decentralized scenario with emergency order.
Preprints 94387 g015
Preprints 94387 g016
Figure 16. Profit of the retailer in the decentralized scenario with emergency order.
Figure 16. Profit of the retailer in the decentralized scenario with emergency order.
Preprints 94387 g016
Table 1. Model parameters and decision variables.
Table 1. Model parameters and decision variables.
Model parameters:
a initial market potential
ξ price elasticity coefficient of demand
θ   a n d   b influence coefficients of sales effort on demand
α initial quota of remanufactured product
s sales effort level for remanufactured product
c the low bound on sales effort
d the up bound on sales effort
g sales-effort investment coefficient
pn, pr unit selling prices of new product and remanufactured product
cn, cr unit costs of production or remanufacturing of new product and remanufactured product
Bn, Br unit shortage costs of new product and remanufactured product
Vn, Vr unit salvage values of new product and remanufactured product
kn, kr unit extra costs of the emergency order
Decision variables:
wn, wr unit wholesale prices of new product and remanufactured product
Qn, Qr order quantities of new product and remanufactured product
Table 3. Decision variables and profits in different scenarios.
Table 3. Decision variables and profits in different scenarios.
Integrated CLSC Decentralized CLSC
Q*n Q*r E(πI)* Q*n Q*r E(πR)* E(πM)*
Without emergency order 22.0849 1.2453 78.338 20.9307 0.999 26.7704 50.0612
With emergency order 20.9159 1.2451 84.7575 20.8106 0.996 32.1299 49.4988
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated