Preprint
Article
Modeling Blood Vessels Lumen from 3D Images with the Use of Deep Learning and B-Splines
Altmetrics
Downloads
143
Views
69
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
25 December 2023
Posted:
26 December 2023
You are already at the latest version
Alerts
Abstract
Accurate geometric modeling of blood vessels lumen given their 3D images is a basis for vessel quantification in support of cardiovascular diseases diagnosis, treatment and monitoring. Unlike other approaches, which assume circular or elliptical vessel cross-section, the proposed method employs parametric B-splines combined with the image formation system equations to accurately localize the highly curved lumen boundaries. No image segmentation is involved which might reduce the localization accuracy in effect of spatial discretization. It is shown that the model parameters can be reliably identified by a feedforward neural network which, driven by the cross-section images, predicts the parameter values many times faster than a reference least-squares (LS) model fitting algorithm. Two example applications: modeling the lower extremities artery-vein complexes visualized in steady-state contrast-enhanced magnetic resonance images (MRI) and the coronary arteries pictured in computed tomography angiograms (CTA), are presented and discussed to demonstrate the method potential. Besides application to medical diagnosis, blood-flow simulation and vessel-phantom design, it can serve as a tool for automated annotation of image datasets required to train machine-learning algorithms.
Keywords:
Subject: Computer Science and Mathematics - Computer Vision and Graphics
1. Introduction
Vascularity diseases, characterized by either blocked or excessive blood supply to organs and tissues, are among the most serious health problems [1]. They may lead to life-threatening conditions, like stroke or heart attack, and are accompanied by the presence of abnormalities in blood-vessels lumen geometry, such as stenoses caused by pathological deposition of atherosterotic plaque inside the vessel. Diagnosis and treatment of cardiovascular diseases require accurate lumen geometry quantification, in a non-invasive way where possible. Three-dimensional imaging is the main technique used to acquire quantitative information about the vasculature. Example modalities include magnetic resonance angiography (MRA) which can be blood-flow-dependent [time-of-flight (TOF) or phase contrast angiography (PCA)] or flow-independent. An invasive alternative is computed tomography angiography (CTA). The vasculature images can be contrast-enhanced (CE) or nonenhanced, which is obtained by injecting a contrastive substance into the blood circulatory system.
Parametric evaluation of the shape of blood vessels lumen requires identification and quantification of 3D image regions that represent the relevant part of the circulatory system. This certainly is not a trivial task, for many reasons. The vasculature exhibits a complex tree-like structure of highly curved, different-diameter branches. Their diameter may change from 50 mm for the aorta to 50 m for venules and arterioles. At the same time, imaging systems spatial resolution is limited, say to cuboids (voxels) having the shortest sidelength of 0.2 mm for clinical scanners. Thus the thin vessels’ regions are heavily blurred in the image and thinnest of them are not visible. In search of the resolution increase, the voxel volume is reduced using various technical solutions, but this causes the decrease of the signal collected from this volume, so random noise becomes a significant component of the image intensity. Its presence increases the uncertainty of the intensity evaluation inside the lumen, vessel wall and in the background and adversely affects the lumen geometry measurements. Image artefacts make the situation even worse.
Typically, the vessels of interest are closely surrounded by other arteries, veins and tissues. Thus the background region features uneven image intensity, and the spatially blurred signals from different regions overlap. Moreover, the intensity inside the vessel walls is not constant − the plaque depositions, especially those calcified, exhibit different properties to the blood or to the contrastive medium, e.g. [2]. Classical, numerically efficient segmentation-through-thresholding becomes highly inaccurate in these conditions. The pointed out factors make the task of vessel quantification in 3D images especially challenging for radiologists. Manual vessel delineation in 3D images is tedious, time-consuming and error-prone [3]. Its adequacy depends much on the readers experience and their level of fatigue. There is a strong need to develop automated techniques for accurate, fast and objective vascularity evaluation from volumetric image data [4].
There have been numerous methods of lumen segmentation and quantification proposed for the last few decades [3,4,5]. The research in this area has been further intensified with the advent of deep learning as an approach to image segmentation [6,7]. One can identify two main approaches to vascular structures segmentation and quantification in 3D images [8,9]:
- Volumetric lumen segmentation;
- 2D cross-sectional characterization along an approximate centerline.
The result of direct 3D image segmentation is another image. In its basic form it is a grid having the same spatial resolution as the original volume whose nodes (e.g. centers of the voxels) are attributed binary intensity values. Some of these voxels are marked by a label indicating they represent the lumen, all the others are assigned the label of the background. The boundary of the lumen region, which otherwise is smooth and continuous in the physical space, thus becomes discretized. For random boundary location in space, the variance of the discretization error could only be reduced by decreasing the voxel sidelength, always at the price of increased noise. Thus the lumen surface, when visualized, would exhibit a stair-like, or voxelized form. It would need additional spatial smoothing for visualization or for building a geometric model for blood flow simulation. However, part of the information about the actual course of this continuous surface, needed for faithfull reconstruction, had been lost in the binary segmentation step, in which the continuous intensities got replaced by two-level values. From this point of view, image segmentation, although intuitive, is an unnecessary processing step. Yet another disadvantage of some of the segmentation algorithms are the time-consuming iterative calculations [10,11].
We focus on the second approach to estimate the lumen geometry parameters from 3D image cross-sections. These cross-sections are computed as 2D images on planes perpendicular to the vessel centerline, approximated by a smooth curve in 3D space beforehand [12]. This is less troublesome than volumetric segmentation of the lumen; various algorithms are available [13,14]. Normal vectors to the centerline define the cross-section planes. The cross-section images are obtained through the 3D discrete image interpolation and resampling. The center of the cross-section image grid is usually set to lie on the vessels centerline. Then, lumen contours are delineated in these images, either semi-manually [15] or automatically [12]. For automated contour delineation, a 2D image formation model is defined. It accounts for image smoothing by an equivalent scanner impulse response, either one-dimensional along radial lines [12,16] or two-dimensional over the image plane [17], as well as for the random noise. The model is fitted with the use of the least-squares (LS) algorithm. This involves long-lasting iterative minimization of a nonlinear error function and is likely to get stuck in its local minima, depending on the initial parameter values. We will use the LS fitting as a reference method, and apply the convolutional neural network driven by 2D cross-section images for fast estimation of the model parameters [17,18]. The contours found at predefined increments along the centerline arc are lofted to build the geometric models. Lofting is a technique used in computer-assisted-design programs to create 3D surfaces or solid objects [15]. They are formed from sequences of cross-section curves − contours of the lumen in our case.
The past works that followed the modeling approach incorporate circular or elliptical cylinders as the abstract geometric objects that represent the vessels’ lumen in the image space. In fact, the actual shape of the lumen contours significantly deviate from this idealized figures. This happens in particular in the vessels narrowed by atherosclerotic plaque [19]. The novelty of our method is in using B-splines as part of the image formation model − the parameterised curves that accurately represent the natural lumen shapes in normal and pathological vasculature. Although B-splines were used for blood-vessel contouring [20], they were fitted to the approximate surface extracted from the 3D image. In our approach, the fitting process takes place in the image intensity instead of the spatial domain. No cross-section image preprocessing is performed. Innovatively, lumen contour parameters are estimated by a neural network with increased speed and robustness compared to LS fitting. Moreover, the usage of B-splines makes our method compatible with the isogeometric approach [21] to image analysis, test objects (physical phantoms) design and computational blood flow simulation.
2. Materials and Methods
To illustrate the properties and capabilities of the proposed lumen modeling method, real-life and synthetic images were used. They include:
- Lower-extremities MRA volumes available within the PAVES Grand Challenge [22];
- Computer-synthesized cross-section images generated within this project.
These datasets will be characterized in the following subsections.
2.1. PAVES MR dataset
Steady-state MR contrast-enhanced volumes, available as part of the PAVES dataset, are high spatial resolution images which, in principle, allow evaluation of the shape of arteries’ lumen, e.g. in search for stenosis. However, these images take several minutes to acquire. During this rather long time both arteries and veins become filled with the gadolinium-based contrast medium. In effect, the intensity of these regions shows similar values, making the arterial regions difficult to identify and to distinguish from the neighbouring veins. The arteries are of smaller diameter, and their cross-section is close to circular, except for pathological stenosed vessels featuring wall-thickening. On the other hand, veins typically have oval shape and are located in pairs next to an artery. Thus the cross-section of artery-vein complexes do not exhibit circular shape − it is non-circular, although its boundaries are smooth. As highlighted in [24], veins can be used by surgeons to introduce a „bypass” to a blocked artery, provided they are of correct diameter and length. Therefore, delineating veins and arteries in the high-resolution GdCE (gadolinium contrast-enhanced) MR images is a valid medical image processing task, formulated as a Grand Challenge [22].
The research problem defined in this example is to evaluate suitability of the proposed method to delineate boundaries of the veins and arteries given their steady-state GdCE MR volume. The PAVES dataset No. 5 was selected for the purpose, as the clinical significance of its properties was characterized in [24]. To obtain the cross-sections, centerlines of the blood-vessel regions were extracted and smoothly approximated by application of the following 3D image preprocessing steps [12]:
- Vesselness map thresholding to obtain binary lumen representation;
- Binary regions thinning to produce their skeleton;
- Skeleton parsing [27] to identify the blood-vessel tree branches between bifurcations;
- Approximating the skeleton branches by a differentiable function in 3D (to initialize their centerline).
Tangent vectors to the smooth vessel centerline curve were computed at a number of consecutive points, separated by about 0.5 mm from each other. Together with the binormal vectors, they define the Frenet-Serret frame at each point. This frame often gets rotated around the tangent vector, causing undesirable twist of the elongated objects surface. A rotation minimizing frame algorithm [28] was then used to compute the vessel local coordinate systems 0xy, in which 2D lumen cross-sections were calculated by resampling the MR volume. The above image preprocessing and analysis algorithms were implemented both in (version R2022B) and (version 3.10.13). The codes will be made available to the interested readers on request.
Examples of such cross-sections are presented in Figure 1B, in a form of the mosaic of 15×15 pixel images, where the pixel size is 1.0 mm×1.0 mm. The consequtive lumen cross-sections show a minimal twist. These images were obtained in result of applying the above-outlined algorithm to segment b14 of the tibial artery whose binary skeleton is pictured in Figure 1D, among other vessel-tree branches, enumerated by the skeleton parsing algorithm. Basically, a cross-section contains a dark background where there is no tissue filled with blood, a medium-intensity vein region and a bright artery blob of highest concentration of the contrastive medium. As shown in upper two rows of Figure 1B, the healthy arteries feature circle-like cross-sections. However, the atherosclerotic occlusions cause narrowing of the vessel lumen (row 3, left part) and reduce the intensity of the artery region. In effect of collateral blood circulation, the width of the artery lumen may be restored down the vessel, as can be seen in rows 4, 5, and 6, Figure 1B.
2.2. CAT08 coronary CTA dataset
We applied the proposed lumen modeling method to 3D images of the training set available from Rotterdam Coronary Algorithm Evaluation Framework [23,29,30]. It was designed for development of algorithms of lumen segmentation, detection and quantification of coronary arteries stenoses, and provided in the MICCAI 2008 Coronary Artery Tracking Challenge (CAT08). There are 48 datasets available in the Rotterdam Challenge data repository. Anatomical segments of the arteries (specified in [29], visualized in the images, are manually annotated by three experts for 18 of them. These 18 sets constitute the CAT08 training set. For 78 of the training-set segments, expert-annotated contours of the arteries cross-sections are available. We used this information, together with the corresponding 3D images, for the CNN estimator training and as a reference for its testing. It is worth noting the three observers needed approximately 300 hours to complete annotation of this data [23].
The CT images of the Rotterdam dataset were acquired with different scanners over one year, for a number of patients who underwent a cardiac examination. The average voxel size for the whole dataset is 0.32 mm×0.32 mm×0.4 mm. We clipped the CT volumes intensity to HU and normalized it to . The volumes were resampled on the planes of marked contours to obtain lumen cross-sections centered at the centerline points.
Figure 2 shows examples of cross-sections of a few segments in the CAT08 dataset, computed for the sampling interval of 0.45 mm. Segments and are consecutive anatomical parts of the right coronary artery (RCA). The sections of these segments presented in Figure 2 belong to different datasets, though. Their appearance is quite different. The contrast of the 25 images of is much higher and the area of its lumen region does not change as much as that of the 33 sections of . Thresholding would not be useful for the lumen region segmentation in . Lumen diameter apparently decreases along the 20 sections of (from left to right, row by row) and approaches subpixel values in the bottom row. At the same time, bright regions are present in the background, actually dominating the image content. The contrast of images in is good, the lumen region is well defined, its shape is close to circular. However, it shows a significant blur, similarly to all other images. This property, originating in limited spatial resolution of the CT scanners, leads to high uncertainty of lumen boundaries localization, especially in noisy images. Segments and form consecutive parts of the left anterior descending artery (LAD). First section (the leftmost in the upper row) of is closet to the heart, last section (rightmost in the lower row) is the immediate neighbour of the first section in . The sections in the upmost row of exhibit a reduced lumen area and bright image spots in the sixth and seventh section, apparently caused by an atherosclerotic plaque. If they become part of the lumen model in result of image analysis, postprocessing is needed to detect and quantify them. is the first obtuse marginal artery (OM1). Its lumen is well distinguished from immediate background, however, significant part of its sections is occupied by black (triangular shape) regions where the normalized intensity is close to zero (-300 HU or less in the scanner-acquired CT volumes). Typical cross-section shape of the vessels lumen marked by observers is neither circular nor elliptical, Figure 3.
All the image nonidealities pointed out in the previous paragraph make the lumen modeling task difficult. In our numerous experiments, the LS model fitting method failed in too many cases of the CAT08 arterial branches, being attracted by background regions of locally higher intensity than the lumen. On the other hand, the proposed parameterized B-spline lumen contour model can be robustly identified by a feedforward CNN, which will be demonstrated in the section.
2.3. Image formation model
We assumed the blood-vessel cross-section image centered at any point in the 3D space is a convolution of the function , which represents the lumen and its background, with − the imaging system effective impulse response (point spread function PSF)
where are image coordinates on the cross-section plane. The function in (1) combines the effects of the 3D image scanner impulse response and interpolation necessary for computing the cross-section intensity from the 3D image via resampling. This assumption, though idealized, is relevant to most practical situations [31].
Further, we assume the function is constant within the lumen region, surrounded by the background of different, but also constant intensity. These expectations are, in turn, often not met, as it was mentioned before with regard to the coronary artery CE CTA images. We will demonstrate in the section that CNN-based lumen geometry restoration features robustness to image intensity variations in the regions of interest.
We considered equidistant sampling on a Cartesian grid of points (although other sampling strategies are possible to tune the estimator properties)
where denotes the sampling interval. The cross-section image size is . The image intensity at is the sampled convolution (1) multiplied by lumen intensity step b and added to the background intensity a:
The lumen section boundary at each centerline point , is described in this paper by a closed (periodic) B-spline curve which encloses the higher-intensity lumen region in
The in-plane blur in our model is assumed isotropic Gaussian [31,32,33] where w is a parameter
The lumen contour is approximated by a parameterized curve lying on a plane of the vessel cross-section. The concept of B-spline curve [34,35] was chosen here. B-spline is a smooth, piecewise polynomial allowing stable, locally controlled approximation of real-world data. To define a curve of this kind, one has to specify a sequence of , , real numbers, the knots
which define the curve segments boundaries, , and n is the B-spline degree. At the boundaries (internal knots), the segments are joined together to satisfy continuity constraints. The third-degree polynomials are used in our work, meaning first and second derivatives are continuous along the curve arclength.
The closed B-spline of degree n is controlled by points , such that the first control point overlaps with the last one in their sequence. For any t within the B-spline segments, the curve points can be computed as [36]
The B-spline (7) is a linear combination of degree n basis B-splines . Those can be defined recursively with the de Boor algorithm [34]
To compute a cross-section model intensity (3), one needs to specify the boundary of the lumen region in (4). It is described by a B-spline curve controlled by a sequence of points which have to be defined. In our approach, the control points, for a cross-section centered at the vessel centerline, are located on the radial lines extruding from the image center at D angles
The distance in the physical space from the image center to the ith control point is , . R is a scale factor (fixed for the image of given size) and a vector of adjustable B-spline parameters. The coordinates of the control points are computed as
It follows from our experience with blood-vessel images of various modalities that the w parameter of the PSF in (5) does not change significantly within an image. Then a constant value of w is assumed, measured separately e.g. via analysis of appropriate edge blur. Then, there are altogether adjustable parameters . Combining expressions from (1) to (11), one obtains
where given by (1) is multiplied by the parameter b (the intensity pulse corresponding to the lumen region) and added to the background intensity a. The lumen is represented in (4) by a set of points of unit intensity (the shaded area in Figure 4B), surrounded by the background points having the intensity equal to zero (the white area in Figure 4B).
2.4. Least-squares model fitting for the PAVES dataset
The aim is to find the estimate of the parameter vector , given an acquired 2D digital image of the lumen cross-section of known R, w and . This image is the input to the CNN which approximates the mapping from the image space to the parameter space. We will compare the performance of two approaches to the parameter vector estimation – a least-squares (LS) model fitting and the prediction by convolutional neural network [17]. Using the former method, the lumen contour parameters can be estimated by minimizing the sum of squared differences between the acquired and modeled image samples
The (version 1.11.4) module was used to perform the minimization of the sum-of-squares in (13).
2.5. Quantitative evaluation of contours (dis)similarity
The lumen contour is defined by a closed continuous curve on the cross-section plane in the physical space. For numerical analysis, it is represented by a finite set of discrete points − vertices of a polygon chosen to approximate this curve. We will use the term contour to refer to its discrete version. We applied two measures to evaluate the discrepancy between contours. Consider the contours A and B comprised of respectively and points, resampled respectively to and . The mean distance of them is defined as
where is a set of Euclidean distances between a given point x and each of the points in set Y. In our experiments, we interpolated the contours being compared such that the cardinality of them was = = 100 and = = 500.
The second measure was the Dice Similarity Coefficient (DSC), computed for the sets and , which denote all the points of a common contours’ plane, that lie inside the contour A and B, respectively. It is defined as
In our numerical experiments, the sets and were approximated by all the points of a high-resolution image (e.g. 800×800 points, coplanar with the contours), which were lying inside a polygon defined, respectively, by the points of A and B.
2.6. CNN-based model parameter estimation
A neural network was trained to predict the B-spline parameter vector d. The architecture is shown in Figure 5. Three 2D convolution layers are followed by a flattening layer and by four fully-connected layers. The three convolutional layers feature 3x3 kernels, with kernel number equal to 8 for each layer, ‘same’ input padding type and ReLU nonlinear activation function. The flattening layer transforms the multichannel 2D feature maps into vectors. The latter are then processed by three fully-connected layers with 64, 32 and 16 neurons, respectively, and ReLU activation. The output layer estimates the 10 elements of vector d and features a linear activation function. In total, the network has 119 290 trainable parameters and was implemented in keras (version 2.13.1).
Network training was performed with the mean squared error as the cost function, optimized using the Adam algorithm. Mini-batches of 64 examples were used during training. The maximum number of training epochs was set to 500, but an early stopping algorithm was employed to stop training before overfitting occurred. The early stopping patience parameter was set to 15 epochs.
The synthetic dataset of 10000 examples was used to train the network for prediction on the PAVES dataset. 10% of data was excluded for the test set, which yielded 9 000 examples in the training set. The validation set used in the early stopping algorithm was extracted from the training set as its 20% fraction. The synthetic dataset was considered in two versions: noiseless and noisy. The noise addition procedure is described in further sections.
The CAT08 dataset used for neural network training, validation and testing has 652 examples. 66 of them (10%) were excluded for the test set, and the rest was split into training and validation sets in the same proportion, 90:10. Targets in the form of B-spline-approximated expert contour annotations constitute three separate sets, each for one expert. The training procedure was repeated for each expert’s target set, yielding three trained models.
In summary, five models were trained: two for the PAVES (noiseless and noisy) and three for the CAT08 datasets. Evaluation of these models is described in the Results.
3. Results
3.1. PAVES dataset
3.1.1. LS model fitting to PAVES data
Prior to delineating blood-vessel contours in the PAVES images with the CNN-based technique, the performance of the LS model fitting was evaluated. A twelve-parameter image formation model (12) model was chosen heres. The adjustable parameters vector comprised (a, b, ) entries, whereas the others were fixed at =1.0mm, R=11, =0.65. The solutions were searched in the range [0,0.3] for a, [0.1,0.5] for b and [-0.3,1.0] for each element of the vector . [A negative value of indicates that the corresponding control point is located on a radial line at the angle (), cf. (10), (11).]
The Scipy method was used which allowed imposing bounds on the estimated model parameter values. Estimation of the lumen model parameters for all 113 cross-sections (spaced by a distance of 0.5 mm between each other) of the example vessels branch b14 took about 3 hours on an Intel Core i5 PC computer. The results are shown in Figure 6. One can note a high level of consistency in the contour shape when moving between the consecutive cross-sections. Apparently, no significant local minima were encountered in this optimization experiment, although a robust starting point range for the elements of was found after a few attempts, being [0.2,0.4] for the collection of images at hand.
The sections presented in Figure 6 feature relatively flat background. In contrast, the intensity of the foreground representing both arteries and veins varies significantly within an image. Nevertheless, the model fitting resulted in stable values of the parameters a and b, with mean (standard deviation) equal to 0.10(0.009) and 0.18(0.017), respectively.
The parameters spanned the range [-0.1,1.0]. Negative values were found for parameter in sections 12-18 only, where the contour closely approaches the image center. An example illustration is shown in Figure 7, for section No. 14. The angle of the radial line for takes the value of -36°, while it would be 216° for positive values of this parameter. The fitting experiment was repeated a few times for different values of R. In the case of images where the lumen region was completely included in the image, with a reasonable margin in the background, e.g. nos. 35-55, the values of linearly scaled with . An increase in R causes a proportional decrease in all the elements of . This property is not observed in areas where the lumen region goes beyond the image edge, such as in sections 97-112, e.g. in the neighbourhood of the vessel bifurcations.
Scatter plots of pairs of vector elements are presented in Figure 8. Only those involving occupy the range of values close to 0 or slightly negative. Apparently, the plots demonstrate an existence of correlation between the parameters. Also, some visual patterns can be identified, suggesting possibility of using these parameters as features for classification of contour shapes. Figure 9 shows lumen surface visualizations of branch b14 in PAVES data, LS-estimated with B-splines and circular-cross-sections image formation models. Apparently, the circularity assumption is not right in the case of PAVES data. It is, however, applicable and gives accurate lumen quantification in the case of artificially designed objects, such as physical phantoms for blood-flow simulation [17].
3.1.2. Generation of synthetic images for CNN training
To train the neural network for estimation of lumen contour parameters for the PAVES data, we computed synthetic images. The 12-parameter model (12) was used for the task. The parameter values were randomly drawn from a uniform distribution over [0,0.2] for a and [0.2,0.3] for b. The 10 parameters in were drawn from the range [0.0,1.0] and, treated as a circular sequence, smoothed with a simple lowpass filter [0.15, 0.7, 0.15]. This step introduces correlation into the vector, to simulate their bonds to the contour shape. The value of one in ten parameters was randomly drawn from the range [-0.2,0.1], with probability 0.25 (corresponding to the observed rate of negative values in PAVES data). This takes account of concave contours. Ten thousand images were generated for the CNN transfer training. Examples are shown in Figure 10.
3.1.3. CNN-estimated B-spline model for PAVES data
The neural network was first trained on synthesized noiseless images comprised in the training set. Figure 11 demonstrates the histogram of the error in B-spline parameters estimation over the test set. This error has a normal distribution and its mean is practically zero − the network does not introduce any bias. This applies to individual parameters as well. The standard deviation was about 0.02.
Figure 12 contains example images from the noiseless synthetic test set with two lines superimposed on them. The turquoise line is a randomly generated contour used for image computing with the use of expressions from (1) to (12), whereas the red curve represents the contour corresponding to B-spline parameters predicted by the CNN. The input to the CNN was the corresponding image in each case. As one can see, the two lines overlap basically, indicating an excellent accuracy of the CNN predictions. This was confirmed by very small values of and practically unit values of measures applied to the two contours, over the synthetic test set.
The CNN trained on the synthesized noiseless images was applied to the cross-sections of branch b14 visualized in PAVES MR volumes. For each cross-section, the network predicted a set of B-spline parameters which was used to compute coordinates of the estimated lumen contour points. Example results are shown in Figure 13A. There is generally a good agreement between the contours obtained via these two methods. However, spurious bright objects present in the background, e.g. in the rightmost image in the upper row, "attract" the CNN contour. In effect, it departs from the LS-identified curve. This effect is a results of training the CNN on idealized images, having constant values of intensity inside the lumen region and in the background. During such training, the network has not acquired any information about possible spatial variations of image intensity. More realistic training examples are then needed.
To accomodate image intensity variations over the training dataset, we added patch samples of random fractal-like texture to the synthesized noiseless images. The texture patterns and its intensity were chosen to visually resemble the properties of PAVES cross-sections, Figure 14. Thus created noisy images were collected to constitute the synthesized noisy training and test sets (10 000 examples in total).
The neural network was trained on synthesized fractal-noise images training set. Figure 15 demonstrates the histogram of the error in B-spline parameters estimation over the synthesized noisy test set. Similar to the noiseless case, this error has a normal distribution and its mean value is close to zero, cf. Figure 11. However, its standard deviation is a few times larger for the noisy case. At this expense, the contours are less dependent on the intensity variations and, visually, approximate the true boundaries better, see Figure 13B where the CNN trained on noisy dataset was used to predict contour parameters of PAVES sections.
Unfortunately, the PAVES dataset does not contain any reference information. No radiologists’ annotations are available, so there are no ground-truth contours to compare with those related to B-spline parameters found in the course of LS model fitting or CNN-based prediction. Still, the dataset was useful to demonstrate that the proposed lumen quantification approach, based on image formation model, can be successfully applied to highly non-circular blood vessel cross-sections. Moreover, we demonstrated the possibility of obtaining reasonable contours for real-life MR images with the use of transfer-trained CNN, and making the CNN predictions robust to spatial intensity variations by adding fractal texture patterns to the training images. We leave the topic of optimizing the augmentation strategy for future research.
A ground-truth reference is available within the CAT08 dataset quantified with our method as described in the next subsection.
3.2. CNN-based modeling of arteries lumen in CAT08 dataset
Our first attempt to finding the lumen contour of the blood vessels visualized in the CAT08 images involved LS-fitting of the image formation model by numerical minimization of the goal function (13). The parameter vector comprised twelve elements: a and b, respectively for background and lumen intensities, and =(, ..., ) for description of the contour shape. Despite numerous trials of tuning the meta-parameters of the optimization routine, no satisfactory result was obtained. After long-lasting computations, the optimized contours were located far from the observers marking. Then this approach to CAT08 non-circular lumen quantification was abandoned.
To train the CNN for contour shape quantification, we assumed the parameters a and b of the image formation model will not be estimated (although they could be if needed [17]). The natural variation of background and lumen intensities in the training cross-section images was then treated as a factor, which the CNN was trained to ignore. The training examples comprised pairs of 2D cross-section images (with their middle points positioned at the geometrical centers of contours marked by the three observers on the common plane), and the B-spline parameters of the marked contours.
A contour marked by an observer is available in CAT08 dataset as a set of () coordinates, of discrete points, where Q is their count, varying for different contours. To obtain the B-spline parameters for such contour, we used numerical minimization of the mean distance (14) where A was a contour by observer and B denoted a B-spline curve whose course was controlled by the entries of the parameter vector . This process took a fraction of a second per contour executed wiyh (version 1.8.0) library installed on an Apple iPad Pro tablet (11inch, 3rd generation, iPadOS 17.2), resulting typically in at optimum values of . Figure 16 shows two of the few worst results (the left and middle plots); still, the contours similarity is excellent for the task at hand.
Slightly better results in terms of lower values were obtained with NURBS contours [34,35], mainly for highly curved lines such as the ones shown in Figure 16 on the left and in the middle. This was achieved with the use of geomdl library (version 5.3.1) at the expense of an increased number of model parameters (the node weights). No significant fit accuracy was observed for most, rather smooth lumen contours extracted from low-resolution images. The use of NURBS was then not justified in the case of data explored within our project.
For each observer, the artery cross-section images were applied to the CNN input and the B-spline parameters found for observer-marked contour were the target in the training process characterized in the paper section. Thus three CNNs were trained on CAT08 dataset. A typical histogram of the parameters estimation error over the training set, obtained after training, is shown in Figure 17, for observer no. 1. It is similar to the already presented error distributions noticed for CNN trained on synthesized images.
Figure 18 shows graphical representation of typical mean values and standard deviations of the mean absolute error (MAE) of the CNN-predicted vector elements over the test set. The mean values of MAE oscillate around 0.035. The scale factor chosen for this experiment was and the sampling interval was mm. Then the mean values of over the test set are approximately equal to 0.16mm, and their standard deviations are less than 0.20mm. The distance of B-spline control points from the common centerpoint can then be determined with a subpixel accuracy.
The contours marked by the observers and CNN-identified ones are depicted in Figure 19 which shows an example of respective cross-sections sampled from the test set. Despite variations in the contours shape and size within these samples, one can note consistency in visual similarity between the curves marked by each observer and identified by the corresponding CNN. Another observation is the shape of observer-marked contours on a given image differs between the experts in some cases, see e.g. slices nos. 11 and 12 (fourth and fifth from the left in lower rows). Figure 20 illustrates the differences for section no.11. The mean distance (14), Dice similarity coefficient (15), and the image area inside contours were computed to quantify similarities and differences, Table 1. These measures are complementary. reflects smallest absolute distances between contour points and does not depend on their number or contour size. expresses overlap of the areas enclosed by the contours, divided by the sum of the areas. As such it can take large values for small-area lumen sections which are deformed or shifted only. The area is an absolute measure of contour size and does not reflect its shape.
The entries of Table 1 indicate that CNN was in a better agreement with observer no. 3 than with the other experts, featuring almost two times smaller, larger by ca 0.03, and the contour area different by about 14% compared to 20% and 23%, respectively for observers no. 1 and no. 2. On the other hand, the average area for observer no. 3 and its neural network model makes 60% only of the average of those marked by the other two experts and the CNNs trained on their data. Interestingly, following the observers’ choice, all three CNNs learned to recognize a lower-intensity region close to a bright spot as the lumen area, see e.g. cross-section no. 11 in Figure 19. This is not incidental, there are other cross-sections featuring this appearance in the test set which were correctly delineated by the CNN in this way.
3.2.1. Analysis of experimental results for CAT08 dataset
The values of and coefficients were computed for all 66 images in the test set. Figure 21 shows their violin plots for each observer-observer pair. Statistical distribution of this data is not normal which was confirmed by D’Agostino and Pearson’s normality test applied to all six samples presented in the figure. The median values, listed in Table 2, were marked on the plots with horizontal lines.
In the case of and coefficients computed for contours marked by different observers on the same image sections, Figure 21, the paired samples Wilcoxon test rejected the hypothesis ("The paired samples represent the same distribution.") for all six combinations of the samples. Most likely each sample comes from different distribution and the distributions of samples are also different from each other. These tests indicate significant differences between the observers with regard to inferring the lumen contour shape from cross-section images. The corresponding sample median and mean values are listed in Table 2.
The paired samples Wilcoxon test applied to observer-CNN failed to reject the hypotheses that the samples - paired with - come from the same distribution, as well as - paired with - come from the same distribution. It rejected the (p-value=0.013 at the significance level of ) for - paired with -. The Wilcoxon test did not reject the hypothesis in the case of all paired - samples of the Dice coefficient . Then, one of six tests only indicated a significant difference between the sample distributions of the discrepances between the CNN-predicted and observer-delineated contours.
Considering the median values (and mean values likewise), smaller for observer-CNN (Table 3) than for the observer-observer contour shape comparisons (Table 2), one can conclude that the average distance of the CNN-predicted contours to the contours marked by the observers is statistically smaller than the distance between contours marked by different observers on the same image. Similarly, the median (mean as well) values of are larger in (Table 3) than, respectively, in Table 2. In conclusion, the shape of contours drawn by an observer was closer to the shape of curves predicted by its corresponding CNN than to the shape of contours delineated by any other observer.
Figure 23 show violin plots for and contour descriptors. The sample median and mean values of them are listed in Table 4. Table 5 presents results of related paired Wilcoxon tests. The p-values for inter-samples tests (first three rows of the table) show very similar pattern. The hypothesis was rejected for paired with and the test failed to reject it for paired with . This concerns both observer-marked contours and the CNN-produced ones. The test for paired with failed with regard to observer contours and rejected the for the CNN contours. However, the p-values of the two tests (second row in Table 5) are close to the significance threshold =0.05.
Rows from four to six in Table 5, containing p-values for paired tests of CNN and observer contours, indicate that the tests rejected the hypothesis that the samples of the coefficients and were drawn from the same distribution. Indeed, the Bland-Altman plots (see an example for paired with , Figure 24) show that mean values of the differences are substantial, even if detrending options are applied, Table 6.
The contour shape is encoded in B-spline parameters (subsection 2.3). As expected, the area inside the contour carries additional information about the contour size. This information should be explicitly included in the goal function of the CNN training. This task, a part of optimization of the CNN architecture and training strategy, extends beyond the scope of this contribution and will be accounted for in our future research.
4. Discussion
Using the examples of two publicly available datasets, PAVES and CAT08, it is demonstrated that incorporation of B-spline-approximated lumen contours in the image formation model can be used to quantify non-circular shape of blood vessels with a subvoxel accuracy. Such an accuracy is not available with the use of existing circular or elliptical approximations.
The experimental results obtained for PAVES dataset demonstrate a good agreement between the B-spline parameters estimated by the CNN and those computed with the use of LS model fitting. It was shown that the differences can be reduced by proper augmentation of the synthesized images used for the CNN transfer training. Further study is planned on the design of training datasets, involving realistic texture synthesis to simulate spurious image intensity variations and noise in real-life images.
There is a significant difference between the CNN and LS algorithms in terms of the computation time needed. When implemented on a moderate-performance PC (Intel Core i5 plus NVIDIA GeForce 1050), the CNN predicts the contour parameters in microseconds per image, compared to ca s for the iterative nonlinear LS program. Moreover, the estimation task can be successfully executed with the use of rather simple CNN architecture having a modest number of adjustable weights, Figure 5. Time needed for its training is short, in order of 2 minutes.
Due to the complexity of CT images content in the case of coronary artery cross-sections, the LS model fitting does not offer the expected stability. Even with the use of troublesome constrained optimization it finds local minima too often and the fitting results depend much on the initialization points. On the contrary, the CNN can be trained to ignore the image noidealities (e.g. bright objects in the background) and produce lumen contours which are consistent with the observers’ delineations. It is, of course, much faster than human experts. Its application to image annotation would relieve the radiologist of this task.
Our experiments show the CNN can be trained to mimick the individual observers’ style of contour marking. Indeed, there is a good agreement between the shapes of CNN- and observer-produced contours. The CNN reproduces the interobserver variability very well. This raises the question of the ground truth. Future work is planned to design and implement realistic digital and physical phantoms of known tubular geometry and blood distribution, simulate and acquire their images respectively, present them to radiologists and CNNs, and quantitatively compare respective contour delineations with the phantom properties.
Author Contributions
Conceptualization, A.M. and J.J.; methodology, A.M. and J.J.; software, A.M. and J.J.; validation, A.M. and J.J.; formal analysis, A.M. and J.J.; investigation, A.M. and J.J.; resources, A.M. and J.J.; data curation, A.M. and J.J.; writing—original draft preparation, A.M.; writing—review and editing, A.M. and J.J.; visualization, A.M. and J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available in publicly accessible repositories.
- PAVES: https://paves.grand-challenge.org/ (accessed on 1 Feb 2019).
- CAT08: http://www.coronary.bigr.nl/stenoses/ (accessed on 14 Feb 2020).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CE | Contrast Enhanced |
| CNN | Convolutional Neural Network |
| CTA | Computed Tomography Angiography |
| DSC | Dice Similarity Coefficient |
| MAE | Mean Absolute Error |
| MRA | Magnetic Resonance Angiography |
| NURBS | Non-Uniform Rational B-splines |
References
- Tsao, C.W.; et al. Heart Disease and Stroke Statistics – 2022 Update. Circulation 2022, 145, e153–-e639. [CrossRef]
- Maffei E.; Martini, C.; Arcadi, T.; Clemente, A.; Seitun, S.; Zuccarelli, A.; Torri, T; Mollet, N.R.; Rossi, A.; Catalano, O.; Messalli, G.; Cademartiri, F. Plaque imaging with CT coronary angiography: Effect of intra-vascular attenuation on plaque type classification. World J Radiol. 2012, 4, 265–272, . [CrossRef]
- Lesage, D.; Angelini, D.E.; Bloch I.; Funka-Lea G. A review of 3D vessel lumen segmentation techniques: models, features and extraction schemes. Medical Image Analysis 2009, 13, 819–845, . [CrossRef]
- Li, H.; Tang, Z.; Nan, Y.; Yang, G. Human tree-like tubular structure segmentation: A comprehensive review and future perspectives. Computers in Biology and Medicine 2022, 151, 106241, . [CrossRef]
- Moccia, S.; De Momi, E.; El Hadji, S.; Mattos, L.S. Blood vessel segmentation algorithms - Review of methods, datasets and evaluation metrics. Computer Methods and Programs in Biomedicine 2018, 158, 71–91.
- Liu, Y.; Kwak, H.S.; Oh, I.S. Cerebrovascular Segmentation Model Based on Spatial Attention-Guided 3D Inception U-Net with Multidirectional MIPs. Applied Sciences, 2022, 12, 2288, . [CrossRef]
- Dong, C.; Xu, S.; Dai, D.; Zhang, Y.; Zhang, C.; Li, Z. A novel multi-attention multi-scale 3D deep network for coronary artery segmentation. Medical Image Analysis 2022, 85, 102745.
- Cheng, C.P. Geometric Modeling of Vasculature. Handbook of Vascular Motion 2019, 45-66, Academic Press, . [CrossRef]
- Choi, G.; Cheng, C.P.; Wilson, N.M.; Taylor, C.A. Methods for Quantifying Three-Dimensional Deformation of Arteries due to Pulsatile and Nonpulsatile Forces: Implications for the Designs of Stents and Stent Grafts. Annals of Biomedical Engineering bf 2009, 37(1), 14–33, . [CrossRef]
- Sethian, J.A. Level Set Methods and Fast Marching Methods, 2nd ed.; Cambridge University Press: Cambridge, England, 2002.
- Luo, L.; Liu, S.; Tong, X.; Jiang, P.; Yuan, C.; Zhao, X.; Shang, F. Carotid artery segmentation using level set method with double adaptive threshold (DATLS) on TOF-MRA images. Magnetic Resonance Imaging 2019, 63, 123–130.
- Materka, A.; Kociński, M.; Blumenfeld, J.; Klepaczko, A.; Deistung, A.; Serres, B.; Reichenbach, J.R. Automated modeling of tubular blood vessels in 3D MR angiography images. In Proceedings of the IEEE 9th Int. Symp. On Image and Signal Processing and Analysis, Zagreb, Croatia, ISPA 2015, Vol. 1, pp. 56–61, . [CrossRef]
- Frangi, A.F.; Niessen, W.J.; Vincken, K.L.; Viergever, M.A. Multiscale Vessel Enhancement Filtering. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention – MICCAI’98, 1998, Wells, M.W.; Colchester, A.; and Delp, S.L. (Eds.), LNCS 1496, pp. 130-137, . [CrossRef]
- Wolterink, J.M.; van Hamersvelt, R.W; Viergever, M.A.; Leiner, T.; Išgum, I. Coronary artery centerline extraction in cardiac CT angiography using a CNN-based orientation classifier. Medical Image Analysis 2019, 51, 46–60, . [CrossRef]
- Updegrove, A.; Wilson, N.M.; Merkow, J.; Lan, H.; Marsden, A.L.; Shadden, S.C. SimVascular - An open source pipeline for cardiovascular simulation. Annals of Biomedical Engineering 2016, 45, 525–-541, . [CrossRef]
- La Cruz, A.; Straka, M.; Kochl, A.; Sramek, M.; Groller, E.; Fleischmann, D. Non-linear model fitting to parameterize diseased blood vessels. IEEE Visualization 2004, 393–400, . [CrossRef]
- Materka, A.; Jurek, J.; Kociński, M.; Klepaczko, A. CNN-Based Quantification of Blood Vessels Lumen in 3D Images. In: Mikyska, J.; de Mulatier, C.; Paszynski, M.; Krzhizhanovskaya, V.V.; Dongarra, J.J.; Sloot, P.M. (eds) Computational Science. ICCS 2023. LNCS 14074. Springer, Cham, Switzerland, pp. 653–-661, . [CrossRef]
- Materka, A.; Mizushina, S. Parametric signal restoration using artificial neural networks. IEEE Transactions on Biomedical Engineering 1996, 43, 357–372, . [CrossRef]
- Camarasa, R.; Kervadec, H.; Kooi, M.E.; Hendrikse, J.; Nederkoorn, P.J.; Bos, B.; de Bruijne, M. Nested star-shaped objects segmentation using diameter annotations. Medical Image Analysis 2023, 90, 102934, . [CrossRef]
- Zhang, Y.; Bazilevs, Y.; Goswami, S.; Hughes, T.J.R. Patient-specific vascular NURBS modeling for isogeometric analysis of blood flow. Computer Methods in Applied Mechanics and Engineering 2007, 196, 2943–2959, . [CrossRef]
- Cottrell, J. A.; Hughes, T.J.R.; Bazilevs, Y. Isogeometric analysis. Towards integration of CAD and FEA. Wiley: Chichester, England, 2009.
- PAVES - Peripheral Artery: Vein Enhanced Segmentation. An SMRA 2018/19 Image Processing Challenge. Available online: https://paves.grand-challenge.org/ (accessed on 1 Dec 2023).
- Schaap, M.; Metz, C.T.; van Walsum, T.; van der Giessen, A.G.; Weustink, A.C.; Mollet, N.R.; Bauer, C.; Bogunović, H.; Castro, C.; Deng, X.; Dikici, E.; O’Donnell, T.; Frenay, M.; Friman, O.; Hernández Hoyos, M.H.; Kitslaar, P.H.; Krissian, K.; Kühnel, C.; Luengo-Oroz, M.A.; Orkisz, M.; Smedby, O.; Styner, M.; Szymczak, A.; Tek, H.; Wang, C.; Warfield, S.K.; Zambal, S.; Zhang, Y.; Krestin, G.P.; Niessen, W.J. Standardized evaluation methodology and reference database for evaluating coronary artery centerline extraction algorithms. Medical Image Analysis 2009, 13, 701–-714, . [CrossRef]
- Douglas, P. PAVES Challenge Additional information and instructions. Available online: https://paves.grand-challenge.org/Rules/ (accessed on 1 Dec 2023).
- Jerman, T.; Pernus, F.; Likar, B.; Spiclin Z. Enhancement of vascular structures in 3D and 2D angiographic images. IEEE Transactions on Medical Imaging 2016, 35, 2107-–2118, . [CrossRef]
- Lamy, J.; Merveille, O.; Kerautret, B.; Passat, N.; Vacavant, A. Vesselness Filters: A Survey with Benchmarks Applied to Liver Imaging. 2020 25th International Conference on Pattern Recognition (ICPR) Milan, Italy, Jan 10-15, 2021, pp. 3528–3535.
- Kollmannsberger, P.; Kerschnitzki, M.; Repp1, F.; Wagermaier1, W.; Weinkamer1, R.; Fratzl, P. The small world of osteocytes: connectomics of the lacuno-canalicular network in bone. New Journal of Physics 2017, 19, 073019, . [CrossRef]
- Wang, W.; Juettler, B.; Zheng, D.; Liu, Y. Computation of rotation minimizing frames. ACM Transactions on Graphics 2008, 27, 2:1–2:17, . [CrossRef]
- Kirişli, H. A.; et al. Standardized evaluation framework for evaluating coronary artery stenosis detection, stenosis quantification and lumen segmentation algorithms in computed tomography angiography. Medical Image Analysis 2013, 17, 859–876, . [CrossRef]
- Kirişli, H. A. et al.: Rotterdam Coronary Artery Algorithm Evaluation Framework, http://www.coronary.bigr.nl/stenoses/. Last accessed on 14 Feb 2020.
- Chen, Z.; Ning, R.: Three-dimensional point spread function measurement of cone-beam computed tomography system by iterative edge-blurring algorithm. Physics in Medicine and Biology 2004, 49, 1865–1880, . [CrossRef]
- Wörz S.: 3D Model-Based Segmentation of Biomedical Images. In Hlineny et al. (Eds.), MEMICS 2014, LNCS 8934, pp. 40–46, . [CrossRef]
- Chen Z.; Contijoch, F.; Schluchter, A.; Grady, L.; Schaap, M.; Stayman, W.; Pack, J.; McVeigh E. Precise measurement of coronary stenosis diameter with CCTA using CT number calibration. Medical Physics 2019, 46, 5514–5527, . [CrossRef]
- de Boor, C. A Practical Guide to Splines, Revised edition; Springer: New York, Berlin, Heidelberg, 2001.
- Beer, G.; Advanced Numerical Simulation Methods. From CAD Data Directly to Simulation Results; CRC Press: Boca Raton, London, New York, 2015, . [CrossRef]
- Racine, J.S. A Primer on regression splines. Available online: https://cran.r-project.org/web/packages/crs/vignettes/spline_primer.pdf (accessed on 3 Dec 2023).
- Bland-Altman plots for Python. Available online: https://pypi.org/project/pyCompare/ (accessed on 21.12.2023).
Figure 1.
() Coronal slice of a gadolinium contrast-enhanced (GdCE) MR 3D image (PAVES, dataset no. 2) of the lower part of a volunteer right leg. The arrow marks a pair of veins (gray ovals) on the left and right side of an artery (brighter circular blob). () Maximum intensity projection of the PAVES dataset no. 5 TWIST (subtracted time-resolved acquisition) volume on the axial plane, left volunteer extremity. The arrow indicates a stenosis in the anterior tibial artery. () A mosaic of 113 coronal cross-sections of the tibial artery, taken at 0.5-mm intervals along its centerline. () Binary skeleton of the blood vessels, after parsing. The tibial artery branch was assigned a code of b14.
Figure 1.
() Coronal slice of a gadolinium contrast-enhanced (GdCE) MR 3D image (PAVES, dataset no. 2) of the lower part of a volunteer right leg. The arrow marks a pair of veins (gray ovals) on the left and right side of an artery (brighter circular blob). () Maximum intensity projection of the PAVES dataset no. 5 TWIST (subtracted time-resolved acquisition) volume on the axial plane, left volunteer extremity. The arrow indicates a stenosis in the anterior tibial artery. () A mosaic of 113 coronal cross-sections of the tibial artery, taken at 0.5-mm intervals along its centerline. () Binary skeleton of the blood vessels, after parsing. The tibial artery branch was assigned a code of b14.
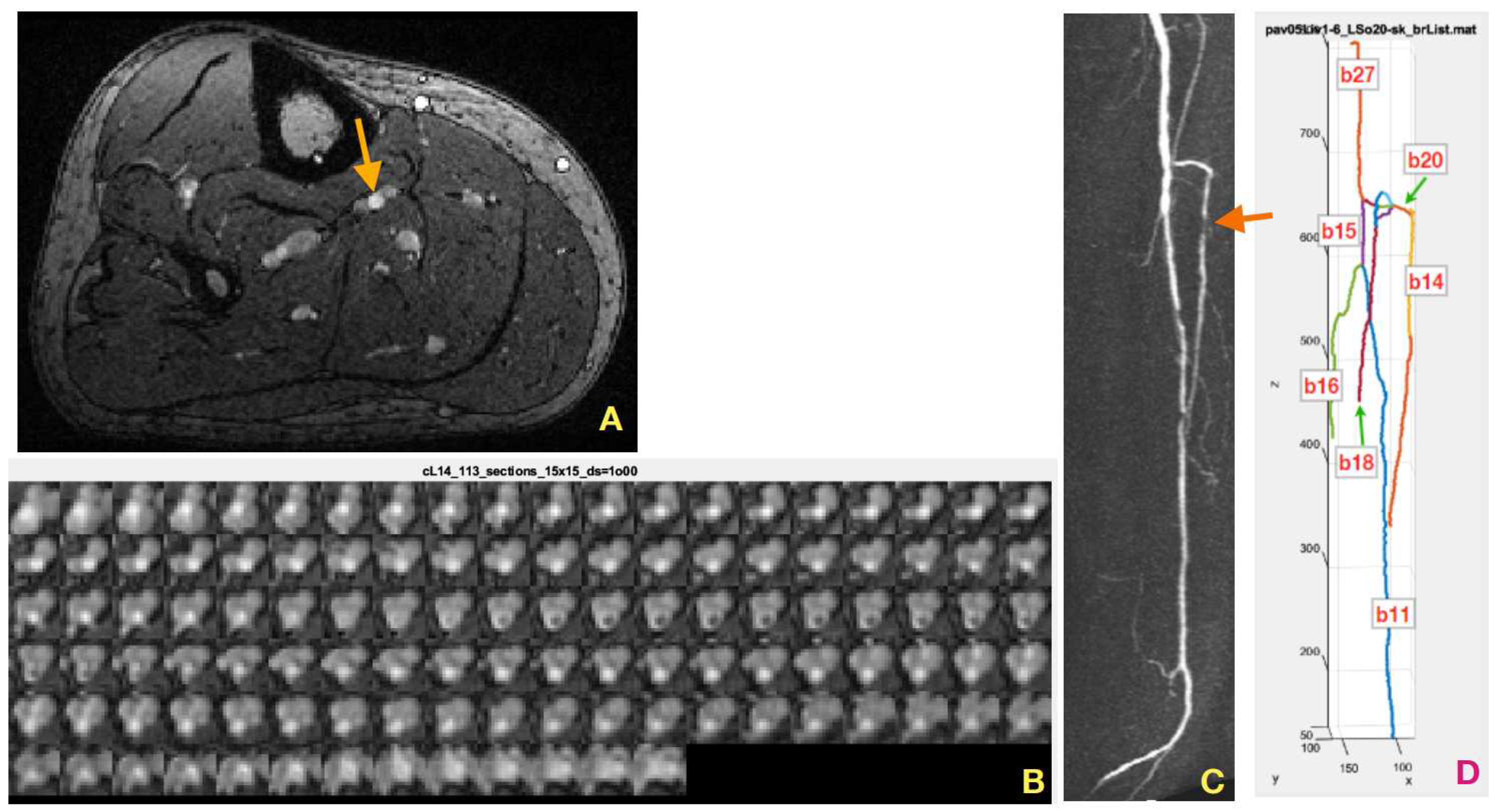
Figure 2.
Example 15×15-pixel cross-sections of coronary artery segments in CAT08, pixel size: 0.45×0.45 mm.
Figure 2.
Example 15×15-pixel cross-sections of coronary artery segments in CAT08, pixel size: 0.45×0.45 mm.

Figure 3.
Example contours marked by the three observers on coronary artery sections in CAT08 dataset. Cross-sections were interpolated to pixel resolution to make their appearance similar to the example shown in Fig. 4 of [23]. Pseudocolor palette was used to enhance visibility of the intensity variations.
Figure 3.
Example contours marked by the three observers on coronary artery sections in CAT08 dataset. Cross-sections were interpolated to pixel resolution to make their appearance similar to the example shown in Fig. 4 of [23]. Pseudocolor palette was used to enhance visibility of the intensity variations.
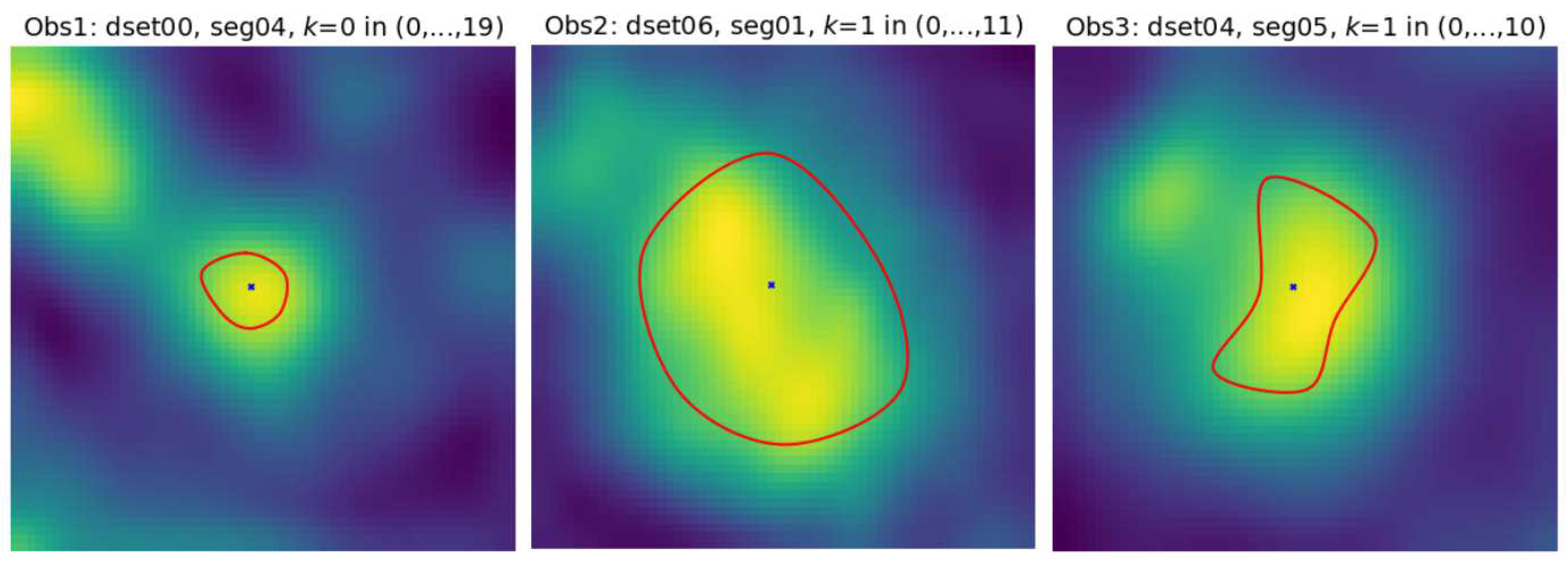
Figure 4.
() Geometry of an eight-parameter B-spline curve normalized to the scale factor R. () Ideal lumen region in the cross-section image space. The shaded area represents the constant-intensity lumen region . () Low-resolution noiseless image of the lumen on its background.
Figure 4.
() Geometry of an eight-parameter B-spline curve normalized to the scale factor R. () Ideal lumen region in the cross-section image space. The shaded area represents the constant-intensity lumen region . () Low-resolution noiseless image of the lumen on its background.
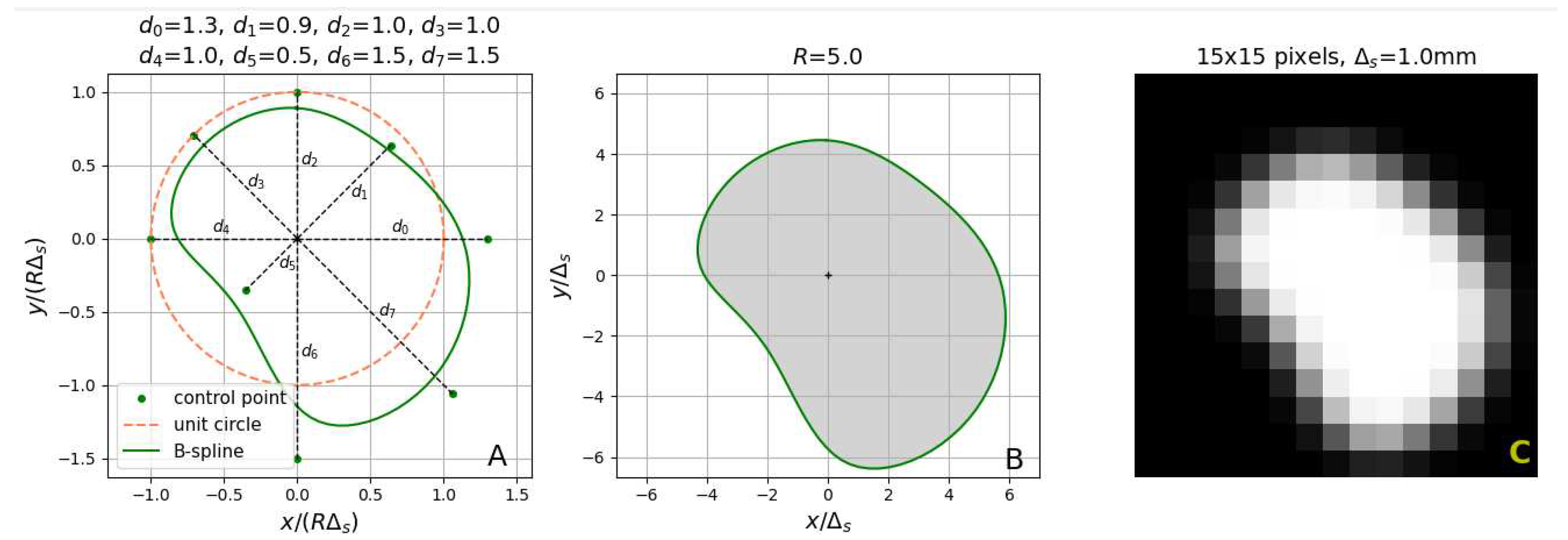
Figure 5.
The neural network architecture used in the described experiments.
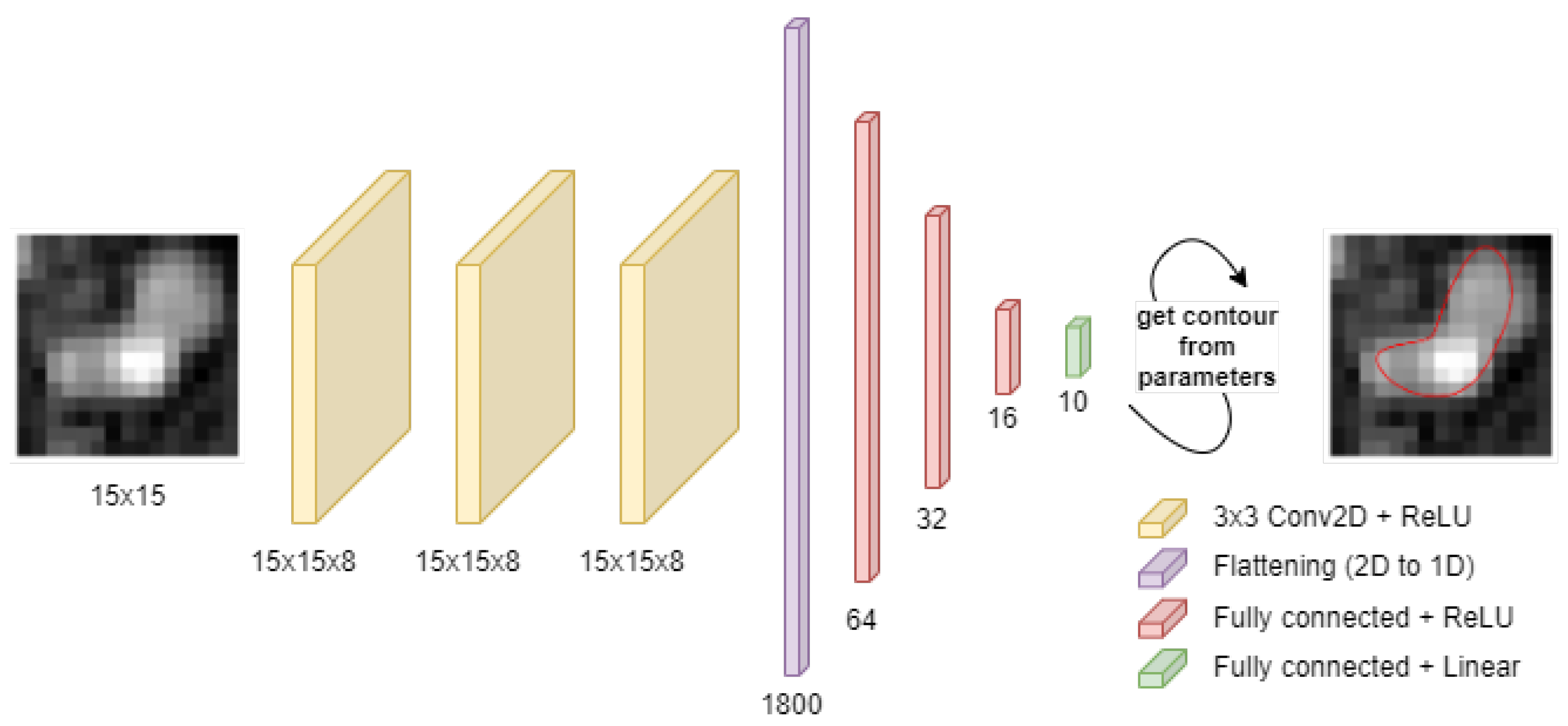
Figure 6.
Example contours (lightgreen lines) of the veins-artery lumen obtained in result of LS model fitting to -pixel odd-numbered (1,3,...) sections of branch b14 in the PAVES 05 dataset. Twelve-parameter (a, b, ) B-spline lumen model, =1.0mm, R=11, =0.65. The points marked by a blue „x” symbol indicate the approximate centerline location.
Figure 6.
Example contours (lightgreen lines) of the veins-artery lumen obtained in result of LS model fitting to -pixel odd-numbered (1,3,...) sections of branch b14 in the PAVES 05 dataset. Twelve-parameter (a, b, ) B-spline lumen model, =1.0mm, R=11, =0.65. The points marked by a blue „x” symbol indicate the approximate centerline location.

Figure 7.
() B-spline contour example for section no. 14 of branch b14 in PAVES 05. () B-spline geometry and synthesized image. The control points are marked by numbered red dots. Control point is located on the radial line at angle -36° (instead of 216°) which indicates negative value of . Indeed, the LS-identified vector for this image is (0.5,0.23,0.50,0.25,0.58, 0.54,-0.08,0.40,0.77,0.57).
Figure 7.
() B-spline contour example for section no. 14 of branch b14 in PAVES 05. () B-spline geometry and synthesized image. The control points are marked by numbered red dots. Control point is located on the radial line at angle -36° (instead of 216°) which indicates negative value of . Indeed, the LS-identified vector for this image is (0.5,0.23,0.50,0.25,0.58, 0.54,-0.08,0.40,0.77,0.57).
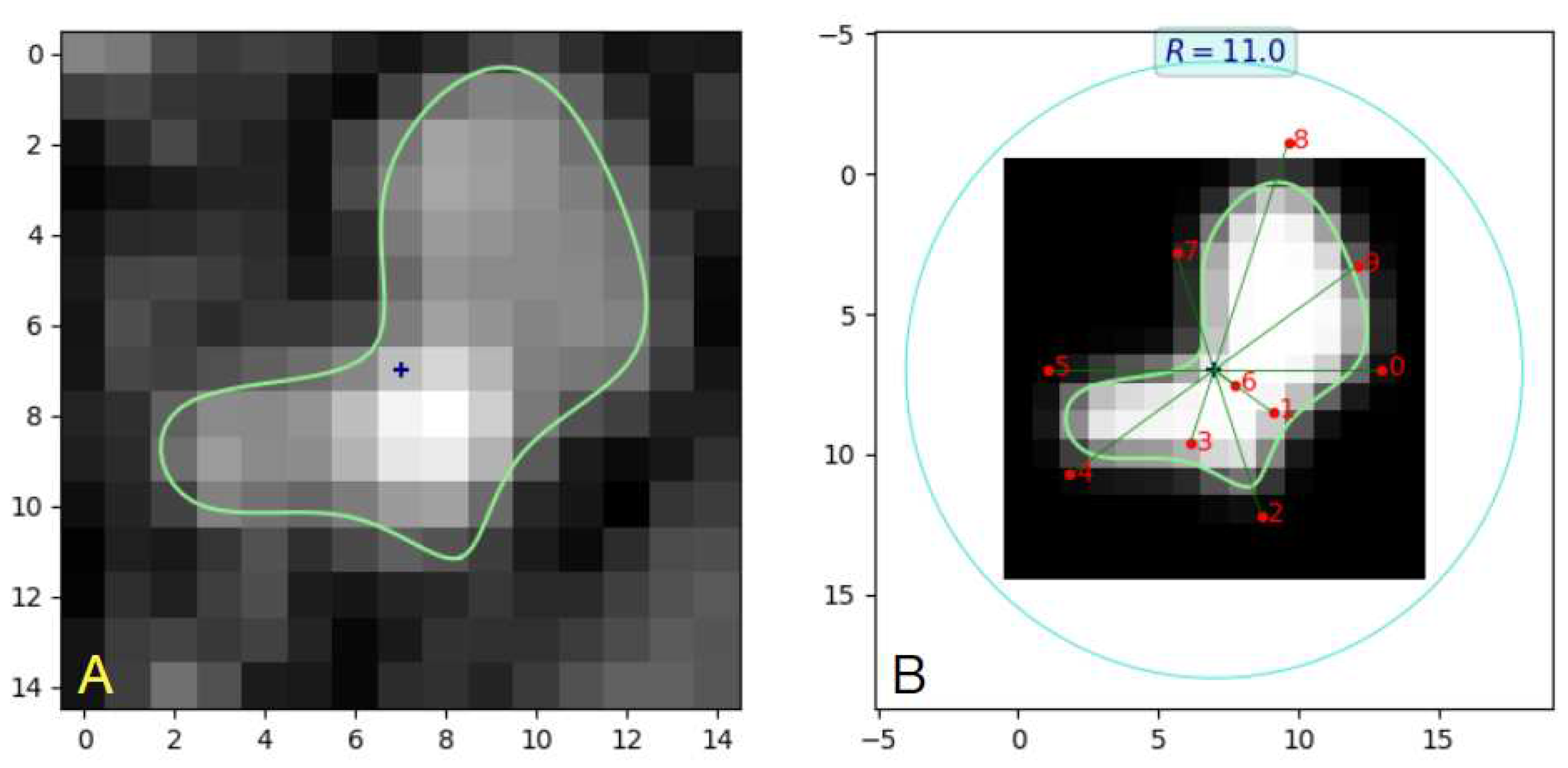
Figure 8.
Scatter plots for LS-estimated B-spline contour parameters for all branch b14 cross-sections in PAVES 05. Each subplot is annotated with a "" text meaning and are its horizontal and vertical coordinates, respectively.
Figure 8.
Scatter plots for LS-estimated B-spline contour parameters for all branch b14 cross-sections in PAVES 05. Each subplot is annotated with a "" text meaning and are its horizontal and vertical coordinates, respectively.
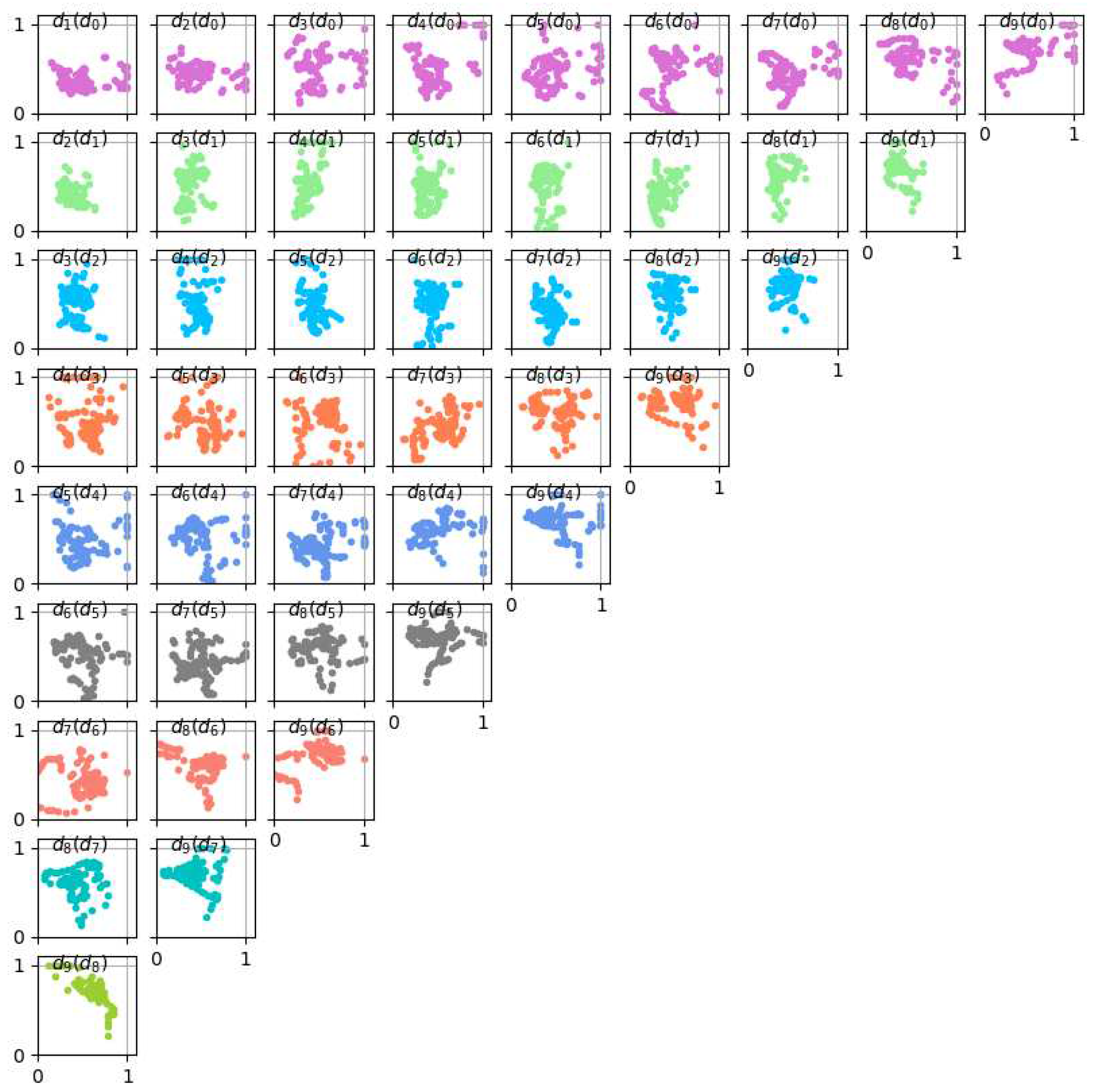
Figure 9.
Visualization of the PAVES b14 branch of vein-artery lumen based on contours obtained with different LS-identified image formation models, () B-spline contours, () circular lumen boundaries, () union of the surfaces in () and ().
Figure 9.
Visualization of the PAVES b14 branch of vein-artery lumen based on contours obtained with different LS-identified image formation models, () B-spline contours, () circular lumen boundaries, () union of the surfaces in () and ().
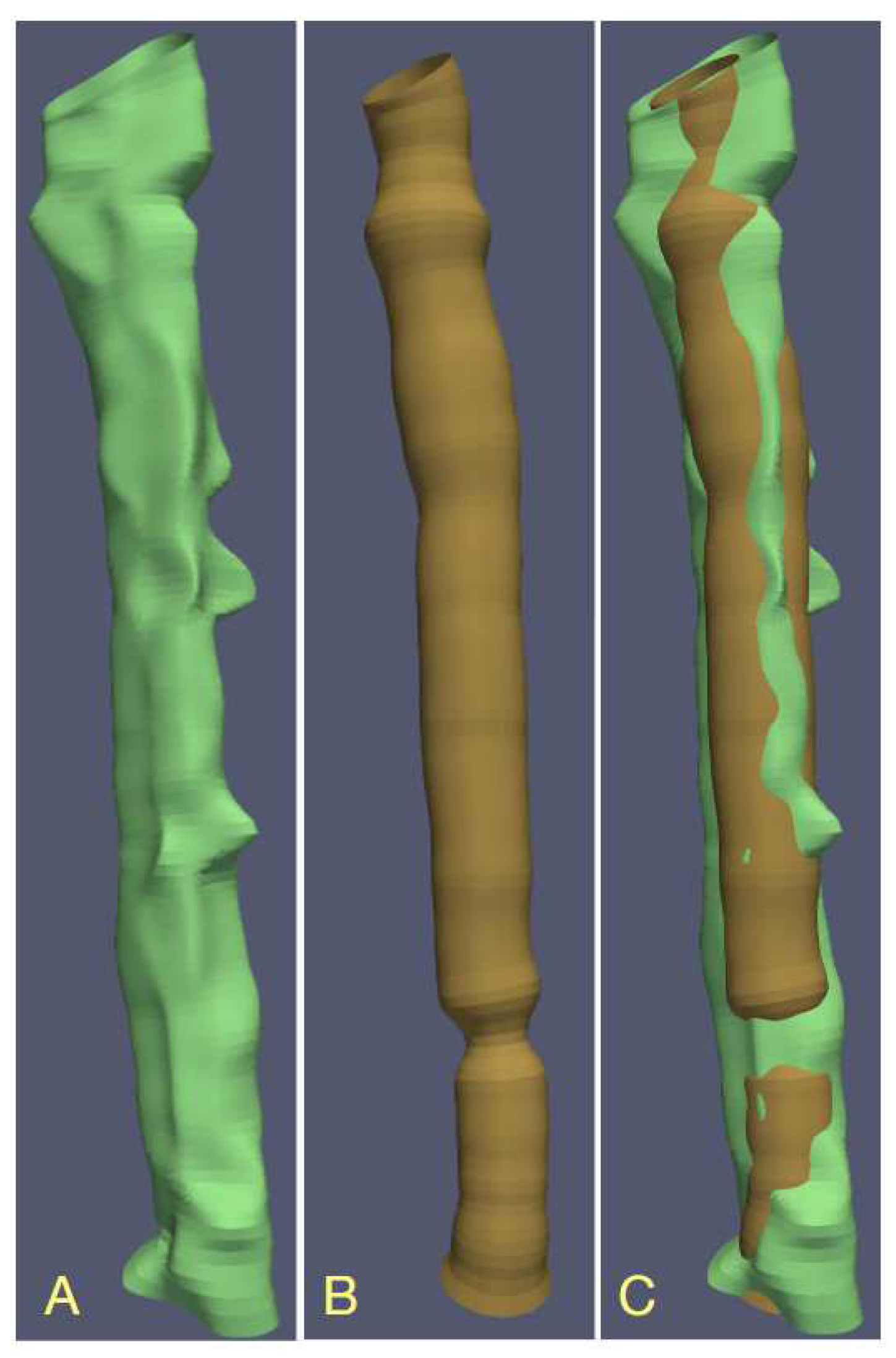
Figure 10.
Examples of computer-simulated noiseless images for CNN transfer training.
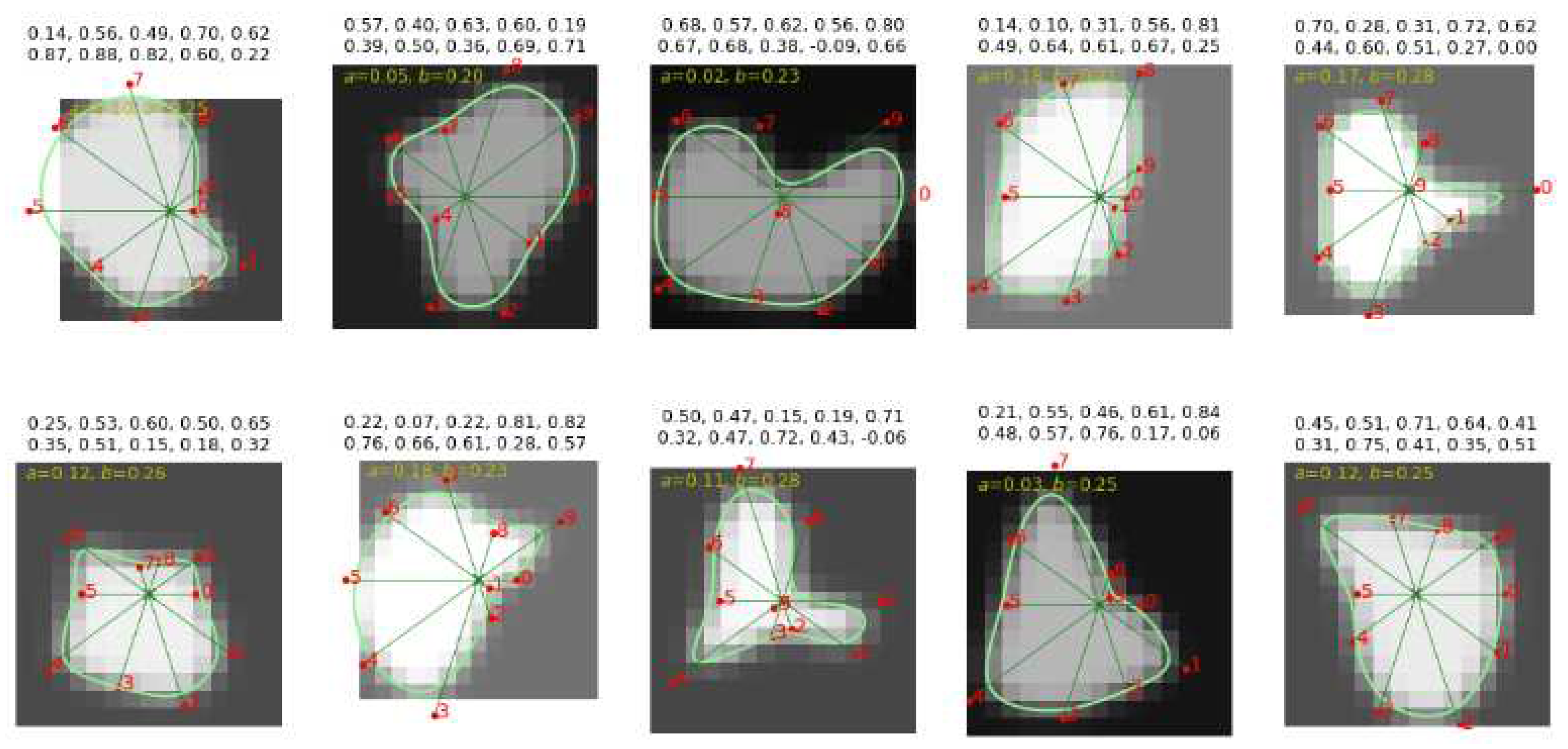
Figure 11.
Histogram of the differences between CNN-estimated and true values of B-spline parameters for the noiseless test set.
Figure 11.
Histogram of the differences between CNN-estimated and true values of B-spline parameters for the noiseless test set.
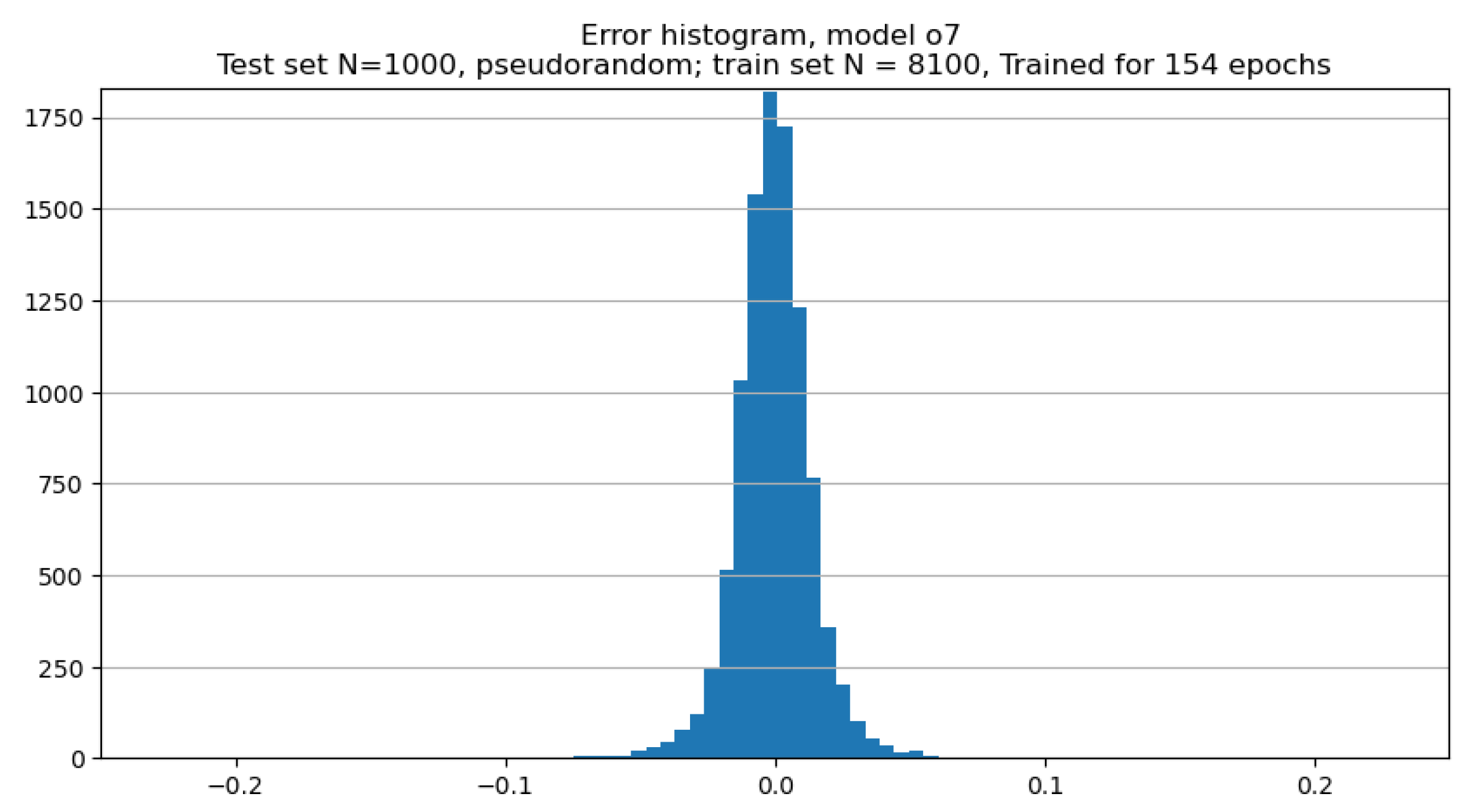
Figure 12.
Examples of noiseless images of the test set, synthesized with the use of randomly generated B-spline parameters (turquoise lines). Red lines mark contours computed with the use of CNN-predicted B-spline parameters.
Figure 12.
Examples of noiseless images of the test set, synthesized with the use of randomly generated B-spline parameters (turquoise lines). Red lines mark contours computed with the use of CNN-predicted B-spline parameters.
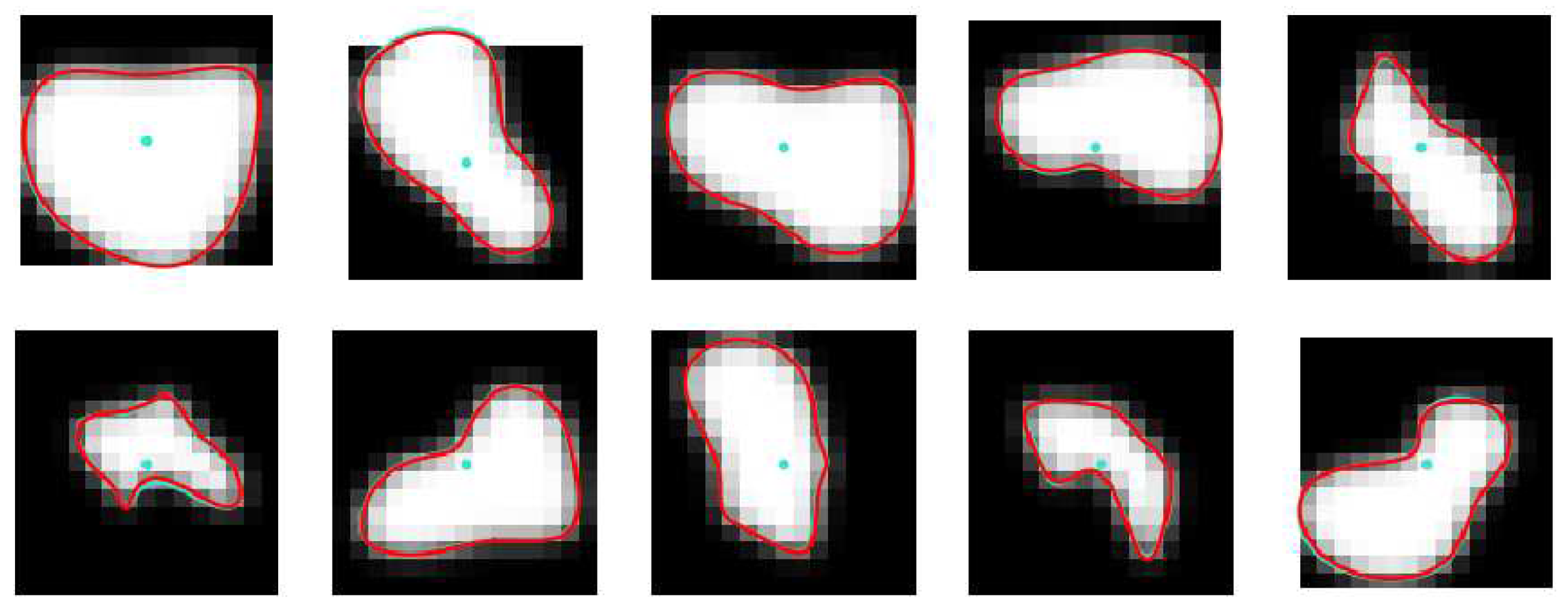
Figure 13.
Example sections of PAVES b14 branch, taken at random. Turquoise lines: lumen contours obtained via LS modeling. Red lines: contours computed with the use of B-spline parameters predicted by the CNN trained on synthesized noiseless images (A) and noisy images (B).
Figure 13.
Example sections of PAVES b14 branch, taken at random. Turquoise lines: lumen contours obtained via LS modeling. Red lines: contours computed with the use of B-spline parameters predicted by the CNN trained on synthesized noiseless images (A) and noisy images (B).
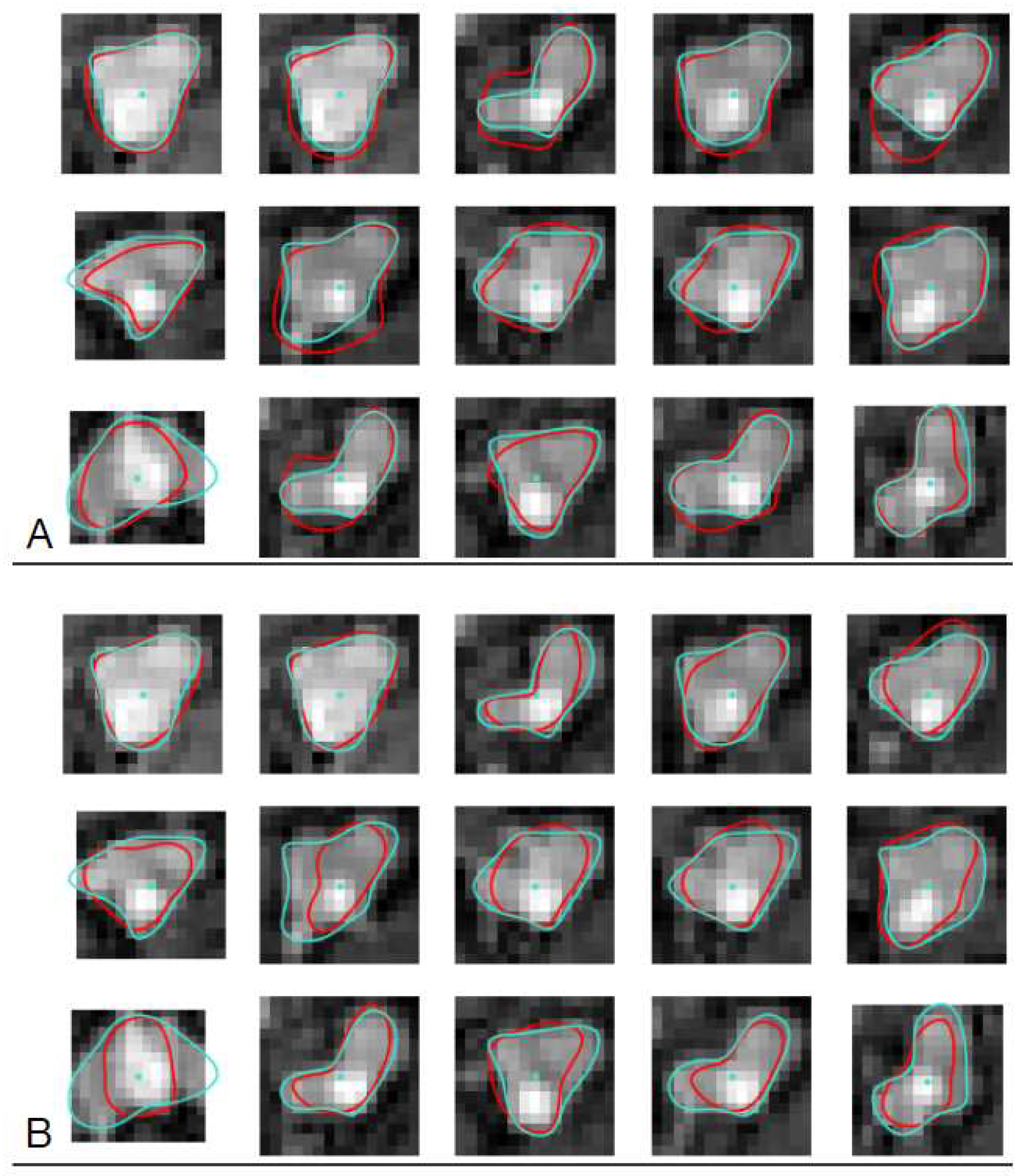
Figure 14.
(A) Example section no. 27 of PAVES b14 branch with LS-predicted lumen contour. One can note random intensity variations. (C) Sample of GIMP-generated fractal-like texture, visually similar to patterns observed in the PAVES data. (B) The image in (C) added to a noiseless image synthesized with the use of contour marked by the lightgreen line.
Figure 14.
(A) Example section no. 27 of PAVES b14 branch with LS-predicted lumen contour. One can note random intensity variations. (C) Sample of GIMP-generated fractal-like texture, visually similar to patterns observed in the PAVES data. (B) The image in (C) added to a noiseless image synthesized with the use of contour marked by the lightgreen line.
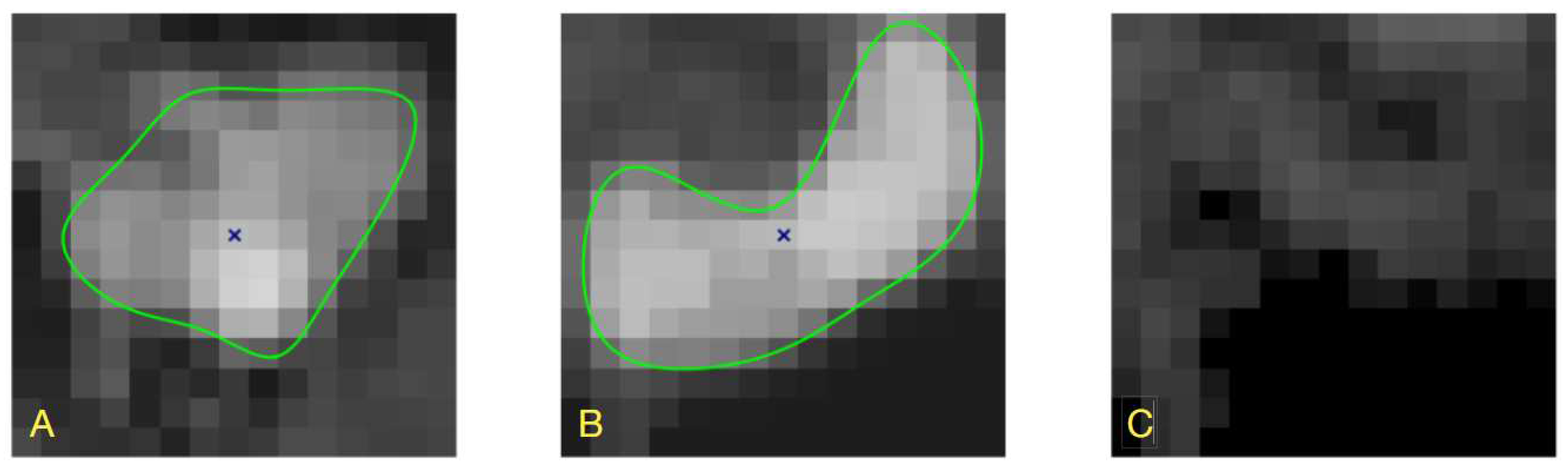
Figure 15.
Histogram of the differences between CNN-estimated and true values of B-spline parameters for the noisy test set.
Figure 15.
Histogram of the differences between CNN-estimated and true values of B-spline parameters for the noisy test set.
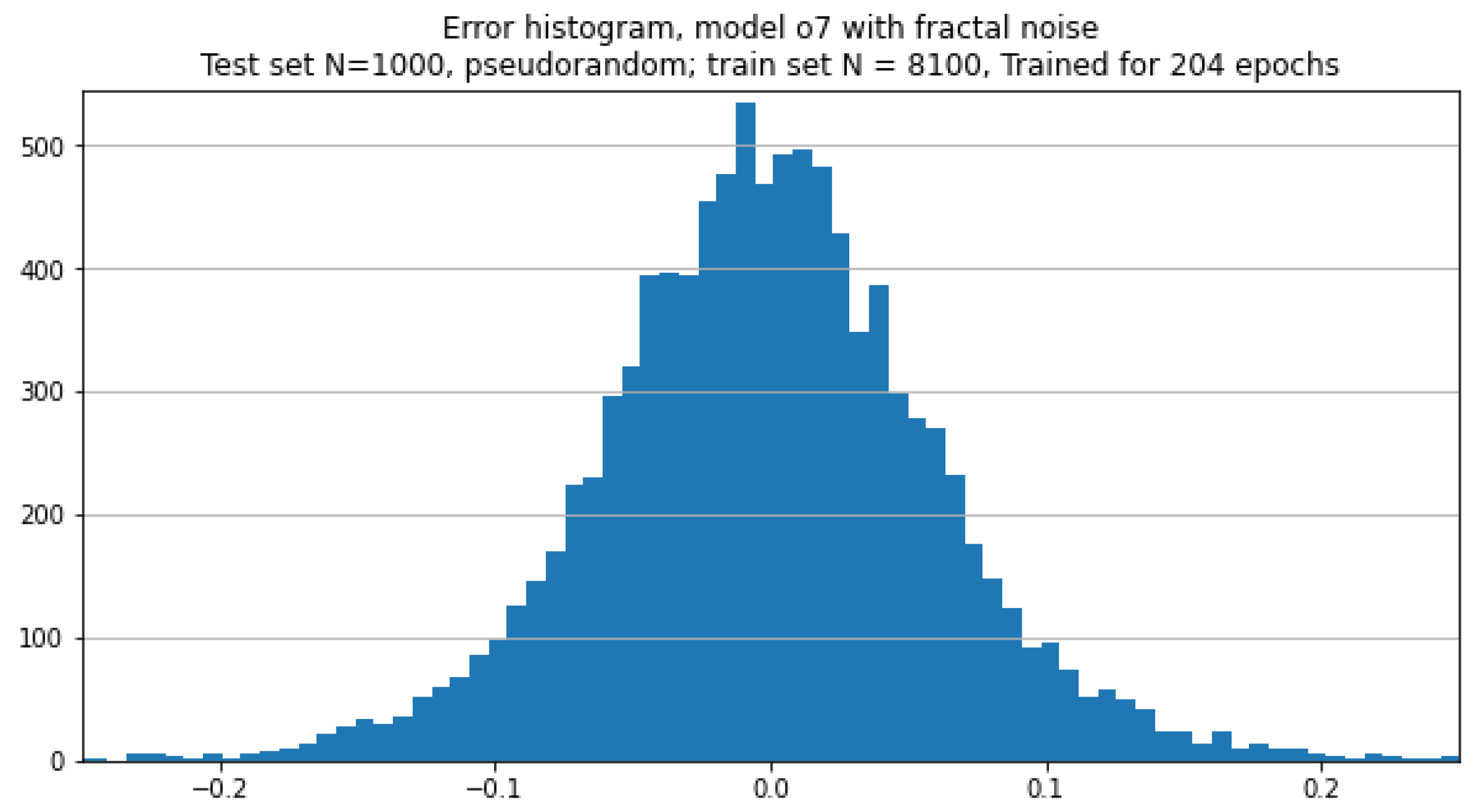
Figure 16.
Three examples of fitting B-spline curves to observer-marked contours (CAT08 data), to find B-spline parameters for CNN training. Dashed red line: contour marked by an observer, green line: B-spline curve. The numbers in boxes indicate the corresponding value.
Figure 16.
Three examples of fitting B-spline curves to observer-marked contours (CAT08 data), to find B-spline parameters for CNN training. Dashed red line: contour marked by an observer, green line: B-spline curve. The numbers in boxes indicate the corresponding value.
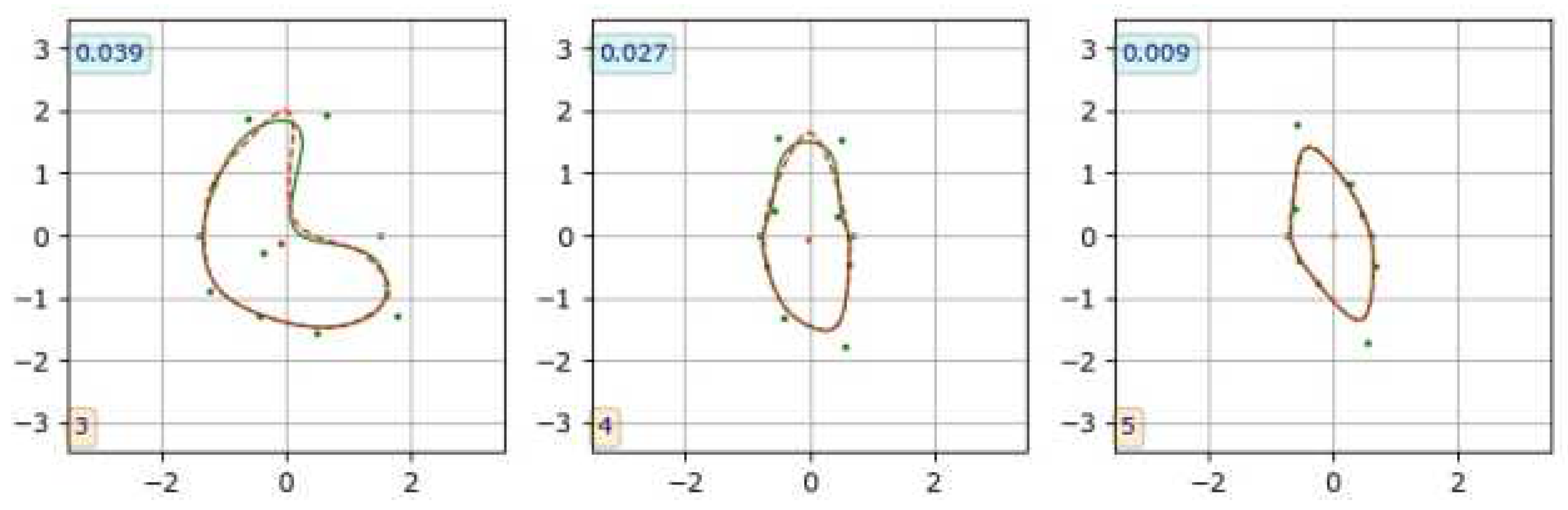
Figure 17.
Histogram of the differences between CNN-estimated and observer-contour-related values of B-spline parameters for the training set (CAT08 data).
Figure 17.
Histogram of the differences between CNN-estimated and observer-contour-related values of B-spline parameters for the training set (CAT08 data).
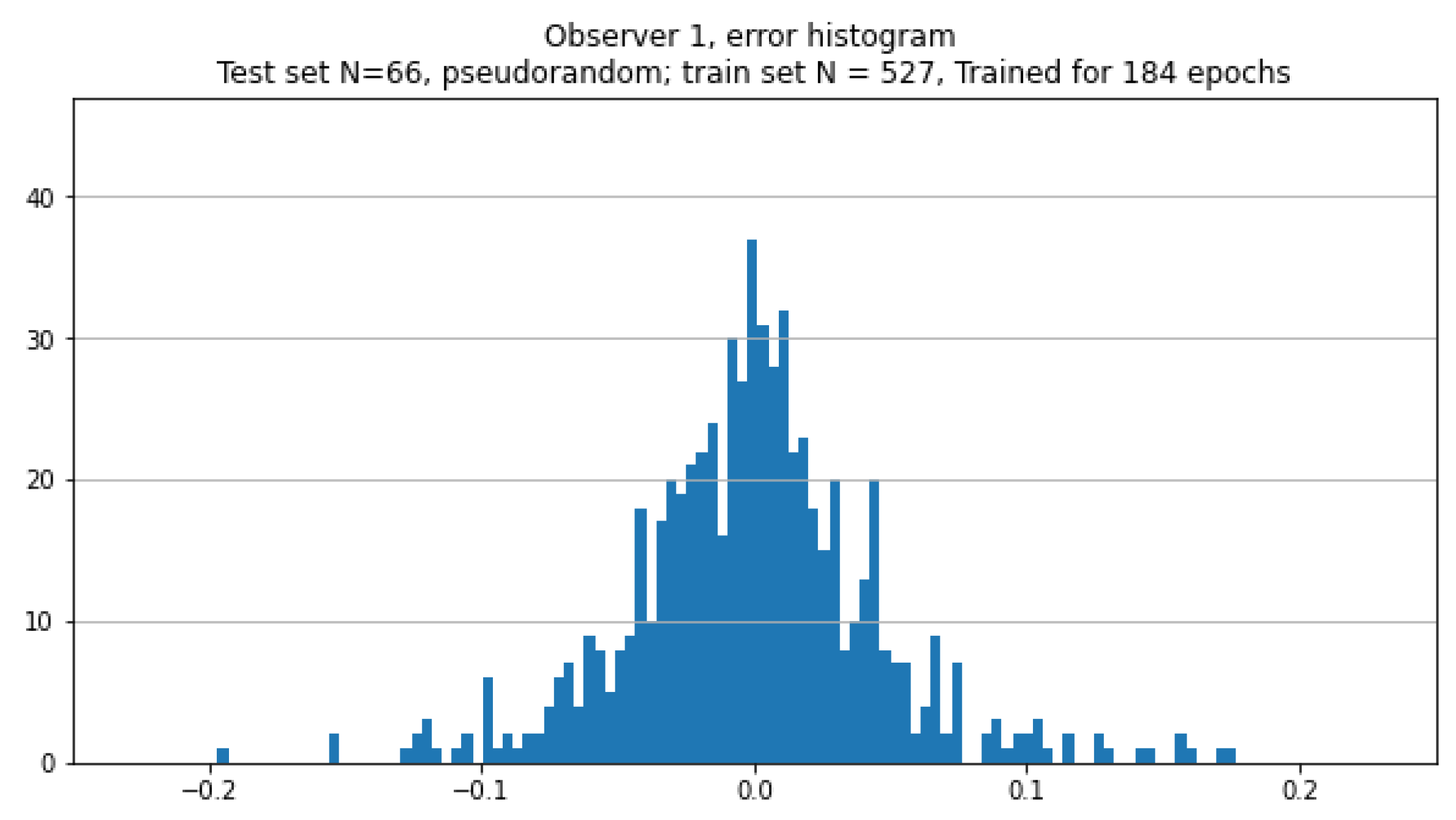
Figure 18.
Plot of the mean values and standard deviations of mean absolute differences between CNN-estimated and observer-contour-related B-spline parameters over the test set (CAT08 data).
Figure 18.
Plot of the mean values and standard deviations of mean absolute differences between CNN-estimated and observer-contour-related B-spline parameters over the test set (CAT08 data).
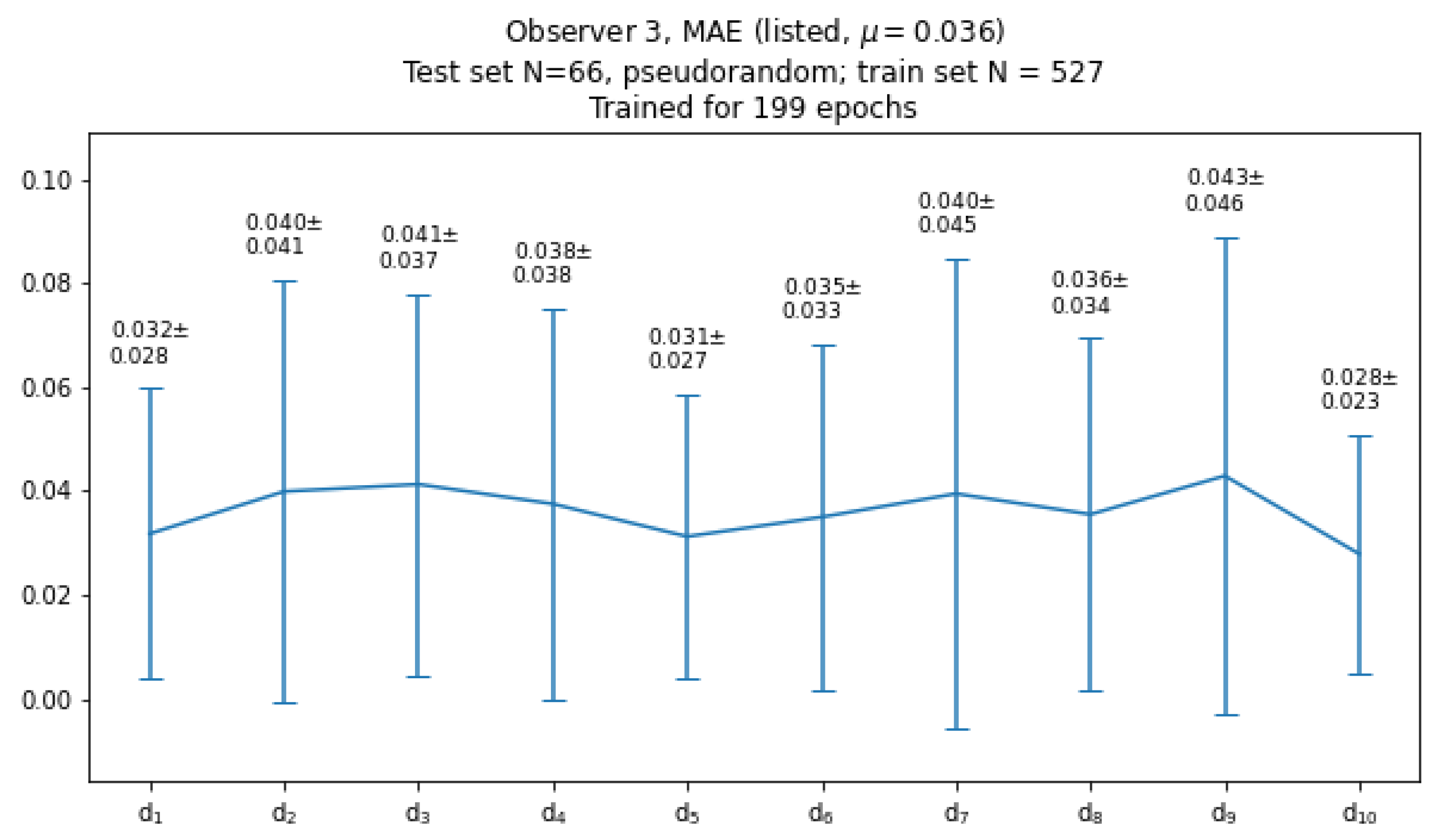
Figure 19.
Example forty eight images of the test set from CAT08 data. Red line: contours marked by observer, green line: CNN-predicted contours. (A) observer no. 1, (B) observer no. 2, (C) observer no. 3.
Figure 19.
Example forty eight images of the test set from CAT08 data. Red line: contours marked by observer, green line: CNN-predicted contours. (A) observer no. 1, (B) observer no. 2, (C) observer no. 3.

Figure 20.
Left column: Comparison of contours marked by the three observers and computed with the corresponding CNN-predicted B-spline parameters for cross-section No. 11 in the test set (CAT08 dataset 05, segment 07, section No. 5). () observer No. 1, () observer No. 2, () observer No. 3. Middle column: Geometric illustration of calculation. Right column: Image regions used to compute the .
Figure 20.
Left column: Comparison of contours marked by the three observers and computed with the corresponding CNN-predicted B-spline parameters for cross-section No. 11 in the test set (CAT08 dataset 05, segment 07, section No. 5). () observer No. 1, () observer No. 2, () observer No. 3. Middle column: Geometric illustration of calculation. Right column: Image regions used to compute the .
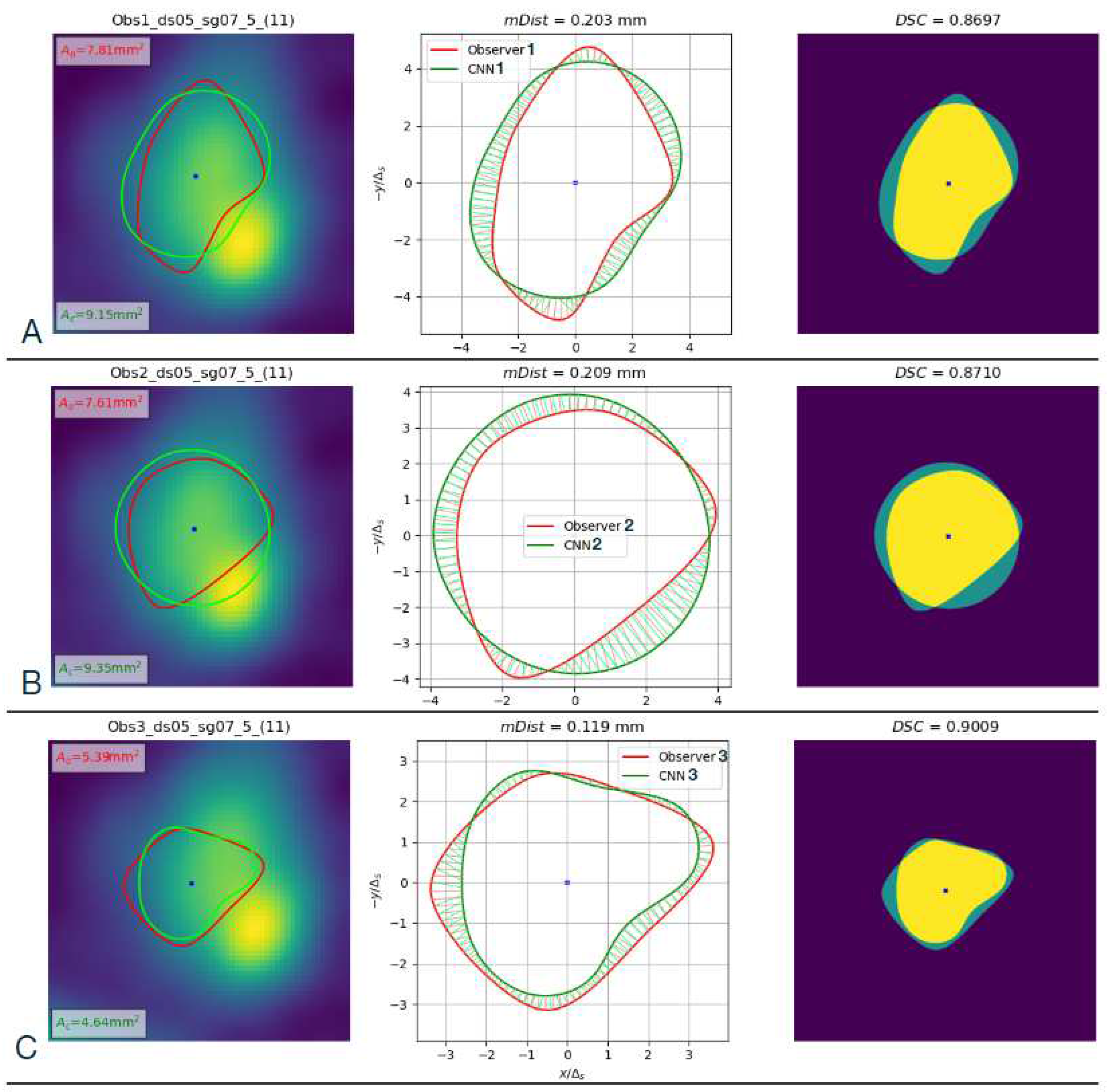
Figure 21.
Violin plots of and descriptors of differences between contours marked by different observers on CAT08 images (interobserver differences).
Figure 21.
Violin plots of and descriptors of differences between contours marked by different observers on CAT08 images (interobserver differences).
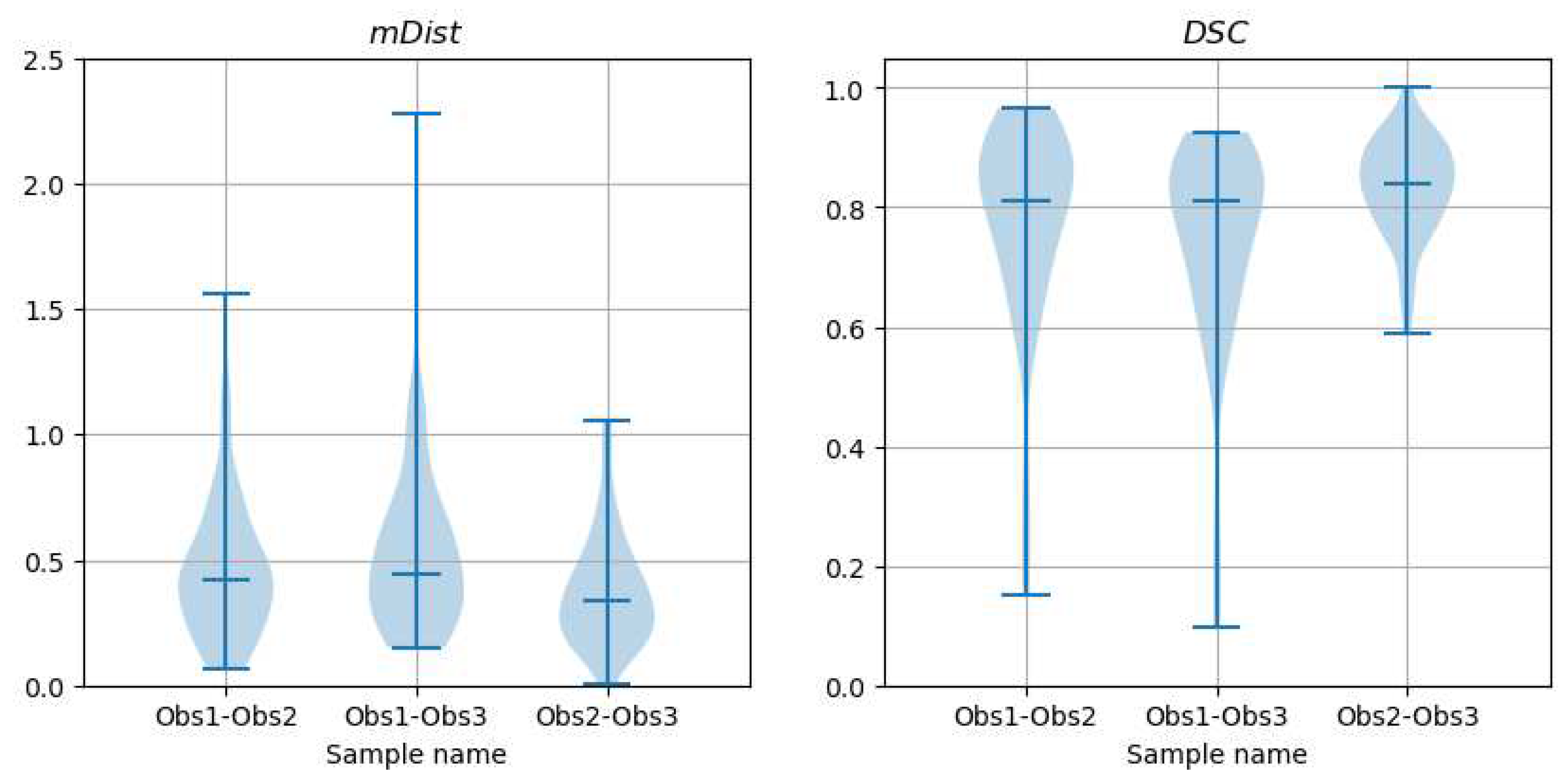
Figure 22.
Violin plots of and descriptors of differences between contours marked by observers on CAT08 images and those computed from CNN predictions (trained on the corresponding observer data), over the test set.
Figure 22.
Violin plots of and descriptors of differences between contours marked by observers on CAT08 images and those computed from CNN predictions (trained on the corresponding observer data), over the test set.
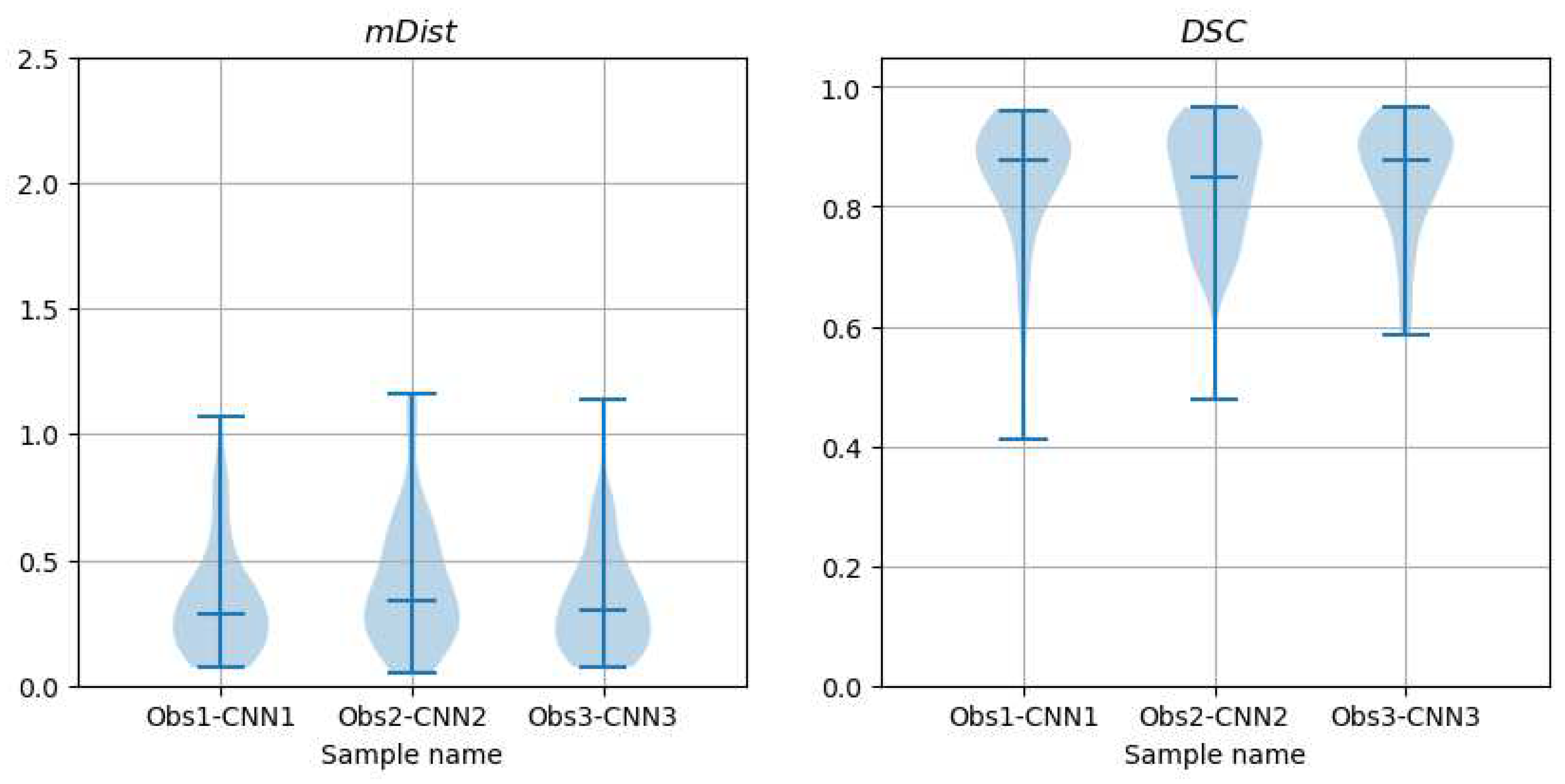
Figure 23.
Violin plots of and for the test set.
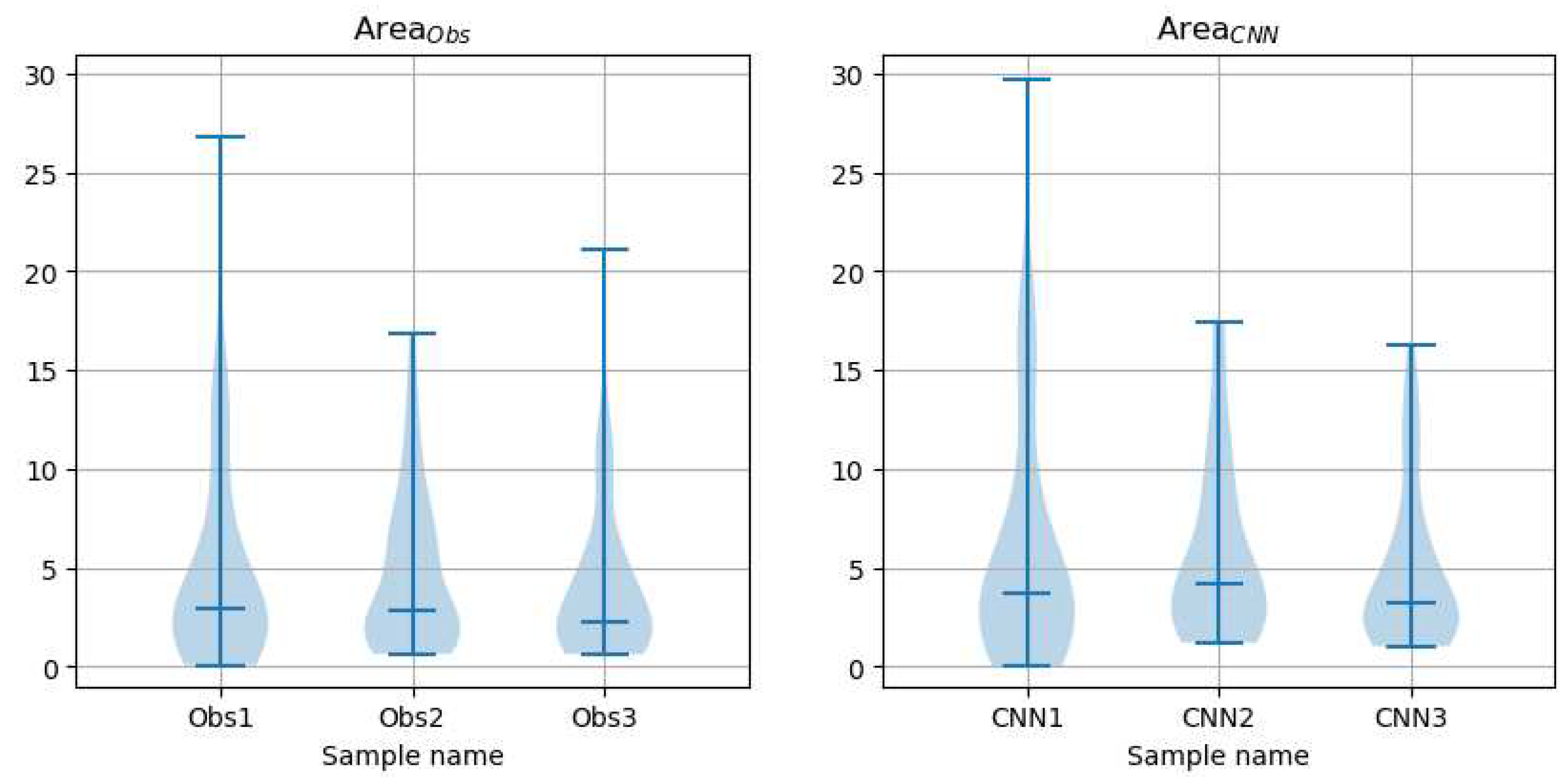
Figure 24.
Bland-Altman plot for and over the test set. Computed with ’ODR’ option of [37] to "model and remove a multiplicative offset between each assay by orthogonal distance regression".
Figure 24.
Bland-Altman plot for and over the test set. Computed with ’ODR’ option of [37] to "model and remove a multiplicative offset between each assay by orthogonal distance regression".
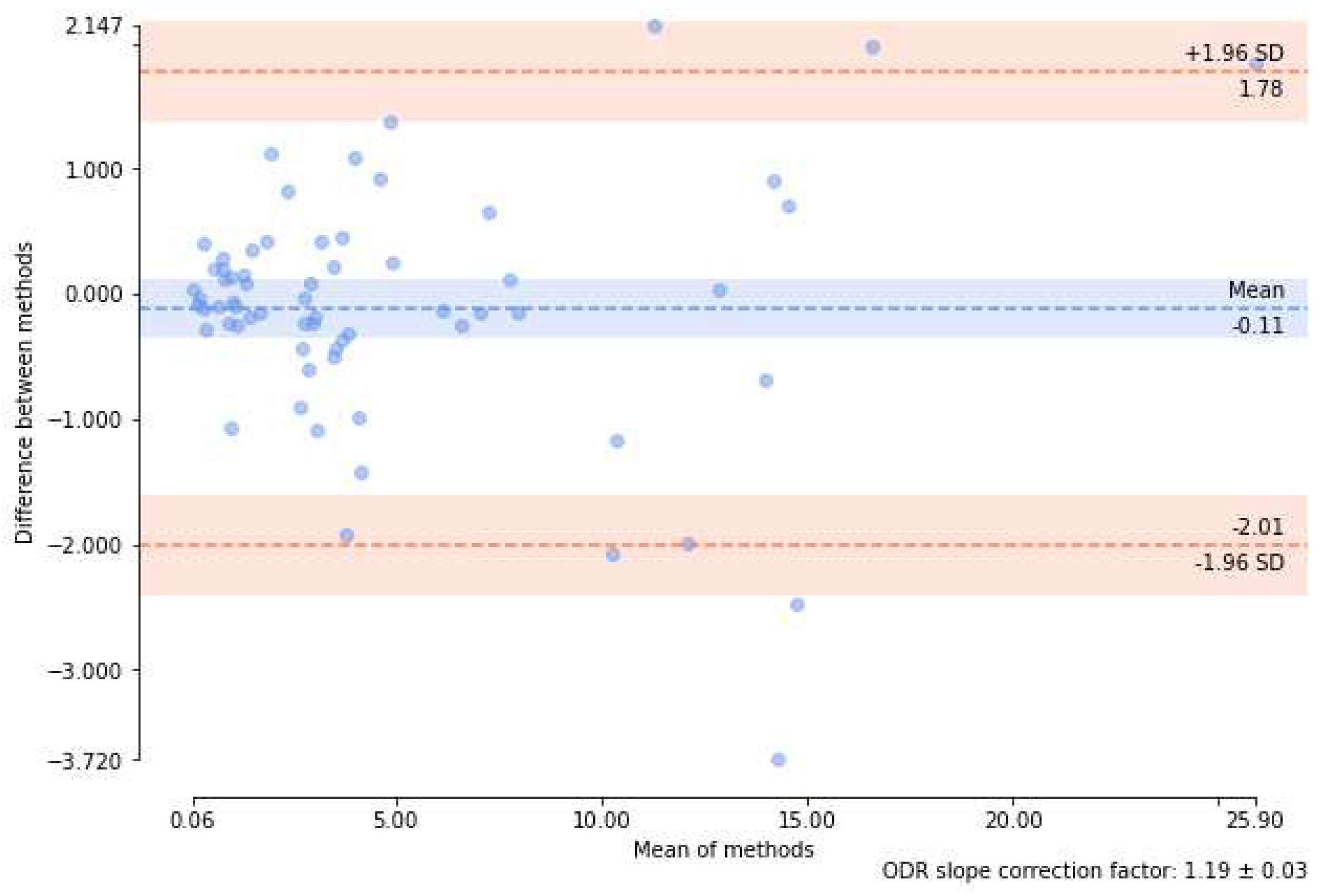
Table 1.
Descriptors of observers-marked and CNNs-predicted contours in Figure 20. †: Obs1 vs CNN1, ‡: Obs2 vs CNN2, *: Obs3 vs CNN3.
Table 1.
Descriptors of observers-marked and CNNs-predicted contours in Figure 20. †: Obs1 vs CNN1, ‡: Obs2 vs CNN2, *: Obs3 vs CNN3.
| Obs 1 | Obs 2 | Obs3 | |
|---|---|---|---|
| , mm | |||
| , − | |||
| , mm2 | 7.81 | 7.61 | 5.39 |
| , mm2 | 9.15 | 9.35 | 4.64 |
Table 2.
Median/mean values of and descriptors of shape differences between contours marked by different observers on the same images in CAT08, over the test set.
Table 2.
Median/mean values of and descriptors of shape differences between contours marked by different observers on the same images in CAT08, over the test set.
| Obs1 vs Obs2 | Obs1 vs Obs3 | Obs2 vs Obs3 | |
|---|---|---|---|
| , mm | 0.422/0.462 | 0.440/0.527 | 0.334/0.380 |
| , − | 0.813/0.771 | 0.809/0.743 | 0.841/0.832 |
Table 3.
Median/mean values of and descriptors of shape differences between observers-marked and CNNs-predicted contours for CAT08 images, over the test set.
Table 3.
Median/mean values of and descriptors of shape differences between observers-marked and CNNs-predicted contours for CAT08 images, over the test set.
| Obs1 vs CNN1 | Obs2 vs CNN2 | Obs3 vs CNN3 | |
|---|---|---|---|
| , mm | 0.284/0.333 | 0.336/0.405 | 0.298/0.335 |
| , − | 0.876/0.844 | 0.849/0.837 | 0.878/0.851 |
Table 4.
Median/mean values of the area of contours marked by observers and predicted by CNNs , over the test set drawn from CAT08 repository.
Table 4.
Median/mean values of the area of contours marked by observers and predicted by CNNs , over the test set drawn from CAT08 repository.
| Obs 1 | Obs 2 | Obs 3 | |
|---|---|---|---|
| , mm2 | 2.90/4.79 | 2.83/4.71 | 2.23/4.12 |
| , mm2 | 3.73/5.83 | 4.18/5.68 | 3.26/4.82 |
Table 5.
p-values of the paired Wilcoxon test for and coefficients, over the test set drawn from CAT08 repository.
Table 5.
p-values of the paired Wilcoxon test for and coefficients, over the test set drawn from CAT08 repository.
| Observer | CNN | Observer vs CNN | |
|---|---|---|---|
| Obs1 vs Obs2 | 0.775 | 0.751 | − |
| Obs1 vs Obs3 | 0.085 | 0.034 | − |
| Obs2 vs Obs3 | 3.5e-5 | 1.9e-5 | − |
| Obs1 vs CNN1 | − | − | 1.4e-8 |
| Obs2 vs CNN2 | − | − | 1.2e-7 |
| Obs3 vs CNN3 | − | − | 9.7e-9 |
Table 6.
Mean values (in mm2) of the differences between paired and coefficients, over the test set drawn from CAT08 repository. Columns ’None’, ’Linear’, and ’ODR’ correspond to detrending options available in function used to compare the distributions [37].
Table 6.
Mean values (in mm2) of the differences between paired and coefficients, over the test set drawn from CAT08 repository. Columns ’None’, ’Linear’, and ’ODR’ correspond to detrending options available in function used to compare the distributions [37].
| ’None’ | ’Linear’ | ’ODR’ | |
|---|---|---|---|
| Obs1 vs CNN1 | -1.04 | -0.20 | -0.11 |
| Obs2 vs CNN2 | -0.98 | -0.76 | -0.33 |
| Obs3 vs CNN3 | -0.70 | -0.93 | -0.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






