Research on the Wood Density Measurement in Standing Trees though the Micro Drilling Resistance Method

To achieve a micro-destructive and rapid measurement of the wood density of standing trees, this study investigated the feasibility of using the micro-drilling resistance method, formulated a mathematical model, explored the potential for a unified model across multiple tree species, and analyzed the influence of moisture content on measurement accuracy. First, 231 tree cores and drill resistance data were sampled from Pinus massoniana, Cunninghamia lanceolate, and Cryptomeria fortunei. The basic density and moisture content of each core were measured, and the average value of each resistance data record was calculated. Second, the average drill resistance, the natural logarithm of average drill resistance, and absolute moisture content were used as independent variables, while the wood basic density was used as the dependent variable. Third, the total model of the three tree species and sub-model for each tree species were established through a stepwise regression method. Finally, the accuracy of each model was compared and analyzed with that of using the average basic density of each tree species as an estimated density. The results revealed that the estimation accuracy of the sub-model for each tree species was 1.670 percentage points higher than the average value of each tree species used as the density estimation value for these tree species. Additionally, except for Cryptomeria fortunei, the natural logarithm of drill resistance significantly influenced the wood density model at a significance level of 0.05. Moreover, moisture content significantly affected the total model and sub-models of Pinus massoniana at a significance level of 0.05. The estimation accuracy of the total mathematical model was 2.125 percentage points lower than that achieved using the average basic density of each tree species to predict their density. The results indicated the feasibility of using the micro-drilling resistance method to measure the wood density of standing trees. Moreover, the relationship between wood density and drill resistance did not follow a linear pattern, and moisture content slightly influenced the drill needle resistance. Furthermore, the establishment of a mathematical model for each tree species was deemed essential. This study provides valuable guidance for measuring the wood density of standing trees through the micro-drilling resistance method.

Keywords:

Subject: Biology and Life Sciences - Forestry

1. Introduction

Wood density is the mass of wood per unit volume at a specific moisture content. This parameter is considered the most reliable predictor of wood quality [1,2,3]. Wood density exhibits a strong correlation with other wood qualities, such as strength and stiffness, and plays a significant role in determining wood suitability for different end uses [4]. Wood density is influenced by both genetic factors [5,6,7] and the growth environment of trees [8,9,10,11]. Therefore, wood density serves as a vital evaluation parameter in studies related to tree genetic breeding and forest management methods. With the development of human society, the demand for wood products has gradually increased [12,13,14,15], while the availability of wood resources has significantly decreased. Improving the efficiency of timber use emerges as an effective measure to address the imbalance between wood supply and demand [16]. Accurate measurement of wood density forms the basis for enhancing the efficiency of timber use. Forest managers and wood processors use wood density to effectively match raw materials with final products [17]. Additionally, wood density is a vital important factor in forest carbon measurement [18,19,20,21]. Improving the accuracy of measuring wood density can contribute to the enhanced precision in estimating forest carbon. Wood density exhibits significant variability among individual trees in forests [22,23]. Therefore, promoting sustainable human development requires the advancement of rapid, accurate, and non-destructive methods for assessing wood density in standing trees.

The traditional approach for measuring wood density is the volume method [24]. Although the volume method can accurately measure wood density, its dependence on sampling from the tested object leads to significant specimen damage. Moreover, the sampling and measurement processes are time-consuming and labor-intensive. The X-ray method indirectly measures wood density based on the intensity of X-rays absorbed by substances with different densities [25,26]. Moreover, this method accurately measures the density of wood in small areas and enables the assessment of average density in tree rings, early-wood density, and late-wood density. However, X-ray instruments for measuring density are expensive, and the method also requires sampling from the tested object. Therefore, the X-ray method is costly, time-consuming, and labor-intensive. In contrast, the Pilodyn method indirectly measures wood density by inserting a fixed specification of a fine needle into the wood using a preloaded spring and then gauging the depth of the needle penetration into the wood [27,28]. Despite the convenience of this instrument, it only measures the average density of the outer wood surface. The micro drill resistance instrument uses a motor to control the constant-speed penetration of the drill needle into wood and indirectly measures wood density through real-time drill resistance [29,30,31,32,33,34,35,36]. The resistance drilling method can effectively reflect the changes in the density of small wood areas. The resistance drilling method has considerable advantages over other methods, including minimal tree damage, faster operation, and higher measurement sensitivity, making it a highly promising method for measuring wood density [37].

Currently, scholars have mainly used linear models to investigate the relationship between drill resistance and wood density. For example, Rinn established a linear model with a correlation of r² = 0.943 between drill resistance and wood density [29]. Isik et al. measured the drill resistance and wood density of 11-years-old loblolly pine trees (Pinus taeda) from 14 full-sib families in four-4-plots. The results revealed strong correlations between average drilling resistance values and wood density, indicating strong genetic control at the family level. However, individual phenotypic correlations were observed to be relatively weak [38]. Downes et al. measured the resistance data and wood density of eucalyptus trees (mostly Eucalyptus globulus with a few Eucalyptus nitens) across nine sample plots. The study revealed determination coefficients of the linear models between the average drill resistance and wood density of each tree in various plots ranging from 0.662 to 0.868 [39]. Tomczak et al. measured the radial basic density of nine oak trees with increment corer and IML (Instrumenta Mechanik Labor) power drill. The results indicated that the determination coefficient of the linear model between the average drill resistance and wood density was 0.396 [40].

Owing to significant differences in parameters and determination coefficients across various linear models, the universal applicability of linear models is limited. Presently, researchers typically need to establish specific linear models for different tree species when using micro drill resistance instruments to measure wood density. Establishing a unified mathematical model for multiple tree species poses a challenge. Additionally, the relationship between drill resistance and wood density not follow a linear pattern. Numerous scholars have shown that the relationship between various wood mechanical properties and wood density can be expressed by a k-th parabolic equation:

s = αρ^k

(1)

where s represents a wood strength value; α denotes the proportional constant; k is the density index, shaping the relationship curve between wood strength and wood density. Certain wood strength properties exhibit exponential variations with changes in wood density. For example, the density index of flexural strength is 1.25, while the density index of transverse compressive strength and hardness is 2.25 [41]. Therefore, an exponential variation may occur between drill resistance and wood density.

Additionally, the moisture content of wood has a certain influence on its strength [42,43,44]. Therefore, the moisture content also affects drill resistance. Lin et al. found that drill resistance values typically decreased with decreasing moisture content, transitioning from a water-saturated condition to air-dried status for Taiwania cryptomerioides lumber [42]. Sharapov et al. reported that the impact of moisture content on drill needle resistance and drill feeding force depended on the rotational speeds and rates of the drill [43]. Ukrainetz et al. found that density prediction by drill resistance was influenced by tree moisture content [44]. Owing to significant differences in moisture content among different tree species, locations, and times, further research is needed to investigate the impact of moisture content on measuring the basic density of standing trees.

To measure the wood density of a standing tree, this study investigated the feasibility of using the micro-drilling resistance method, determined the mathematical model form, explored the potential unified modeling of multiple tree species, and analyzed the influence of moisture content on measurement accuracy. First, we sampled 231 tree cores and recorded drill resistance data from three tree species. Second, the basic density and moisture content of each core were measured, and the average value of each resistance data record was calculated. Subsequently, the average drill resistance, the natural logarithm of average drill resistance, and absolute moisture content were used as independent variables, while the wood basic density served as the dependent variable. Third, a comprehensive model for the three tree species and sub-models of each tree species were established through a stepwise regression method. Finally, we calculated the measurement accuracy, estimated standard deviation of each model, and compared and analyzed the tested accuracy of each model with that of using the average basic density of each tree species as an estimate.

2. Materials and Methods

2.1. Core sampling and drill resistance measurements

In October 2023, increment cores and drill resistance data were obtained from 10 plots of Pinus massoniana and 10 mixed forests plots of Cunninghamia lanceolate and Cryptomeria fortunei in Jigongshan Nature Reserve (114°01′ - 114°06′ E, 31°46′ - 31°52′ N), Xinyang City, Henan Province, China. Each plot measured 20 m × 20 m and was divided into 4 small quadrats of 10 m × 10 m. In each quadrat, one dominant tree, one moderate tree, and one suppressed tree were selected as test trees. Among the 40 Pinus massoniana quadrats, the number of Pinus massoniana trees in three quadrats was below 3. Therefore, no test tree was selected in these three quadrats, and the number of test Pinus massoniana trees was 111. In 10 mixed forests of Cunninghamia lanceolate and Cryptomeria fortunei, 60 Cunninghamia lanceolate trees and 60 Cryptomeria fortunei trees were selected as test trees. Each test tree has a core sampled in the north-south direction using an increment corer with an inner diameter of 5.15 mm at a height of 1.3 m. Moreover, the drill needle resistance was sampled using a Resistograph 650-s in the same direction. To minimize the difference in wood density between the cores and the drilled wood and prevent the overlapping sampling paths of increment corer and Resistograph 650-s, the distance between the sampling points of the two instruments was maintained at 3-5 cm. The sampling method is shown in Figure 1.

2.2. Basic density and moisture content measurements of the cores

After extracting the core from the increment corer, we first removed the bark at both ends of the core. Subsequently, the length (l) of the core was measured using a ruler, and the mass (m₀) of the core was calculated using an electronic balance. The inner diameter of the increment core was 5.15 mm, and the diameter of the core was 5.15 mm. The volume of fresh cores was calculated using the following formula.

V = 3.141 × (5.15/2)²l

(2)

where V represents the volume of fresh cores (cm³), and l denotes the length of the fresh core (cm).

In the laboratory, the cores were first fixed in the wood core groove and then subjected to baking in an oven until they reached an absolutely try state. Finally, the absolute dry mass of every core (m₁) was measured using an electronic balance. The basic density of the core was calculated using the following formula.

ρ = m₁/V

(3)

where ρ is the basic density of cores (g/cm³), and m₁ is the mass of the dry core (g). The moisture content of the cores was calculated using the following formula.

w = (m₀-m₁)/m₁

(4)

where w denotes the moisture content of cores (%).

2.3. Calculation method for average drill resistance of each test tree

The drill geometry of the Resistograph is shown in Figure 2 [29].

The width of the tip was twice the diameter of the drill shaft, and the drill resistance was mainly concentrated on the tip. However, some friction still occurred between the needle shaft and the drilling hole. The drill needle penetrated the tree after advancing ~1 cm in the drill needle socket. During this 1 cm displacement, the drill needle remained unloaded, both the drill bit resistance and drill needle shaft friction were negligible (~0), and the primary source of drill resistance was mainly the energy consumed by the motor. As the drill needle advanced ~2 cm out of the tree, it withdrew from the tree. During the withdrawal phase, as the drill needle exited the tree, the resistance of the drill bit was reduced to 0, and the remaining drill resistance was mainly attributed to the drill shaft friction and the energy consumed by the motor. Therefore, the difference between the average drill resistance after the drill exited the tree and the average drill resistance before the drill penetrated the tree represents the friction of the drill shaft. We assumed that the drill shaft friction was proportional to the drilling depth. Therefore, the resistance of each data point after eliminating drill shaft friction is calculated using the following formula.

F_{1 =}F₀-(f₀ - f_i)L₀/L

(5)

where F₁ is the drill resistance after removing drill shaft friction, F₀ denotes the original drill resistance, f₀ represents the average drill resistance after the drill exited the tree, f_i is the average drill resistance before the drill penetrated the tree, L₀ is the real-time drilling depth, L denotes the total drilling depth. The complete drill needle resistance curve and the schematic of removing the drill shaft friction are shown in Figure 3.

2.4. Statistical analysis, modeling, and testing

The average drill resistance, the wood basic density, and the absolute moisture content of each tree were considered as one data record, resulting in 231 data records. First, the box plot method was used to eliminate abnormal data for each parameter of each tree species. Subsequently, 2/3 of the data for each tree species were randomly selected as the modeling dataset. The average drill resistance, the natural logarithm of average drill resistance, and absolute moisture content were used as independent variables, while the wood basic density served as the dependent variable. The basic density regression models for the three tree species and each tree species were established through the stepwise linear regression method. Finally, the remaining 1/3 of the data was used as the test dataset. The estimated accuracy and standard deviation of each model were calculated using formulas (6) and (7):

ξ = \frac{\sum_{i = 1}^{n} (1 - \frac{|ŷ_{i} - y_{i}|}{y_{i}})}{n}

(6)

σ = \sqrt{\frac{{\sum_{i = 1}^{n} (ŷ_{i} - y_{i})}^{2}}{n - 2}}

(7)

where

ξ

is the estimated accuracy, n is the number of the total test data, ŷ_i is the estimated value of the ith data, y_i is the true value of the ith data, σ is the standard deviation.

The measurement accuracy and estimated standard deviation of each model were compared. To verify the practical value of micro drill resistance method for measuring wood basic density, the estimated results of micro drill resistance method were compared with the average wood density of the modeling dataset for each tree species.

3. Results

3.1. Results of removing outliers

The confidence level of the box plot was set at 95%. Figure 4 shows the box plots of the average drill resistance, the wood basic density, and the absolute moisture content of each tree.

The data with a confidence level above 95% were considered abnormal. Figure 4 reveals 18 outliers. Owing to the presence of two outliers in the same record data, 17 data records were deleted. The overview of the data is shown in Table 1.

3.2. Modeling results

3.2.1. Mathematical model for the three tree species

The complete set of modeling data was used to establish a linear model relating wood basic density the average drill resistance, the natural logarithm of the average drill resistance, and the absolute moisture content. The p-values of each parameter are shown in Table 2.

Owing to the highest p-value of the average drill resistance and its significant impact on the model at a significance level of 0.05, the average drill resistance can be removed from the independent variables. After excluding the average resistance of the drill needle, the parameters of the linear model for the basic density of the wood are shown in Table 3.

The p-values of each parameter were all below 0.05, indicating that each parameter significantly influenced the wood basic density at a significance level of 0.05 (Table 3). Therefore, the linear model between wood basic density, the natural logarithm of the average drill resistance, and the absolute moisture content was used as the mathematical model for measuring the wood basic density of these three tree species. The adjusted coefficient of determination for this model was 0.779.

3.2.2. Mathematical model for each tree species

(1) Mathematical model for Pinus massoniana

The modeling data of Pinus massoniana were used to develop a linear model correlating wood basic density with the average drill resistance, the natural logarithm of the average drill resistance, and the absolute moisture content. The p-values of each parameter are shown in Table 4.

Owing to the highest p-value of the average drill resistance and its negligible influence on the model at a 0.005 significance level, the average drill resistance can be excluded from the independent variables. After removing the average resistance of the drill needle, the parameters of the linear model for wood basic density are shown in Table 5.

The p-values of each parameter were all below 0.05, indicating that each parameter considerably influenced the wood basic density at a significance level of 0.05 (Table 5). Therefore, the mathematical model used to calculate the wood basic density of Pinus massoniana incorporated a linear relationship among the wood basic density, the natural logarithm of the average drill resistance, and the absolute moisture content. The adjusted coefficient of determination for this model was 0.588.

(2) Mathematical model for Cunninghamia lanceolate

The modeling data of Cunninghamia lanceolate were used to construct a linear model correlating wood basic density with the average drill resistance, the natural logarithm of the average drill resistance, and the absolute moisture content. The p-values of each parameter are shown in Table 6.

Owing to the highest p-value of the absolute moisture content and its negligible impact on the model at a significance level of 0.05, the absolute moisture content can be excluded from the independent variables. After removing absolute moisture content, the parameters of the linear model for wood basic density are shown in Table 7.

Owing to the highest p-value of the average drill resistance and its negligible impact on the model at a 0.05 significance level, the average drill resistance can be removed from the independent variables. After excluding the average resistance of the drill needle, the parameters of the linear model for wood basic density are presented in Table 8.

Owing to the highest p-value of the intercept and its negligible impact on the model at a significance level of 0.05, the intercept can be excluded from the model. After excluding the intercept, the parameters of the linear model for wood basic density are shown in Table 9.

The p-values of the natural logarithm of average drill resistance were less than 0.05, indicating that the natural logarithm of average drill resistance significantly affected the wood basic density at a significance level of 0.05 (Table 9). Therefore, the mathematical model for calculating the wood basic density of Cunninghamia lanceolate incorporated the linear relationship between wood basic density and the natural logarithm of the average drill resistance. The adjusted coefficient determination of this model was 0.994.

(3) Mathematical model for Cryptomeria fortunei

The modeling data of Cryptomeria fortunei were used to establish a linear model correlating wood basic density with the average drill resistance, the natural logarithm of the average drill resistance, and the absolute moisture content. The p-values of each parameter are shown in Table 10.

Owing to the highest p-value associated with the natural logarithm of average drill resistance and its negligible impact on the model at a significance level of 0.05, the natural logarithm of average drill resistance can be excluded from the independent variables. After the removal of the natural logarithm of average drill resistance, the parameters of the linear model for the wood basic density are shown in Table 11.

Owing to the highest p-value of the absolute moisture content and its insignificant impact on the model at a significance level of 0.05, the absolute moisture content can be excluded from the independent variables. After removing absolute moisture content, the parameters of the linear model for the wood basic density are shown in Table 12.

The p-values of average drill resistance were below 0.05, indicating a significant influence of average drill resistance on wood basic density at a significance level of 0.05 (Table 12). Therefore, the mathematical model for calculating the wood basic density of Cryptomeria fortunei incorporated the linear relationship between wood basic density and the average drill resistance. The adjusted coefficient of determination for this model was 0.347.

3.3. Test results

Using the test data set, the average accuracy, standard deviation of the total model estimate, sub-tree model estimate, and average basic density for each tree species in the modeling data were calculated and used as the estimated basic density for the respective tree species. The test results are shown in Table 13.

The mathematical model for each tree species exhibited the highest estimation accuracy, while the total model for the three tree species featured the lowest estimation accuracy (Table 13).

4. Discussion

Higher wood density indicates stronger wood strength and an increased energy demand for drilling through the wood. Therefore, drill resistance serves as an estimate for wood density. Currently, researchers have mainly used linear models, such as Rinn [29], Todoroki [44], and Fundova [2], to estimate wood density based on drill resistance. However, owing to the exponential relationship between wood strength and wood density, the relationship between drill resistance and wood density does not follow a linear pattern. The results of this study revealed that except for Cryptomeria fortunei, the natural logarithm of drill resistance significantly influenced the wood density model. Figure 5 shows a comparison between the linear and logarithmic fitting curves of the average drill resistance and wood density on the modeling dataset. Table 14 displays the linear and logarithmic fitting equations of the average drill resistance and wood density.

The logarithmic models exhibited higher fitting accuracy than linear models, except for Cryptomeria fortunei (Table 14).

Moisture content significantly influences the mechanical properties of wood [42-44], thereby affecting drill resistance. The results of this study revealed that moisture content significantly influenced the total model and sub-model of Pinus massoniana. Thus, measuring the moisture content of wood is challenging. Therefore, when using the micro drill resistance method for measuring wood density, most users do not measure the moisture content of wood. Therefore, to measure the wood density of standing trees, it is advisable to sample the drill resistance in a consistent environment to minimize the influence of moisture content on drill resistance.

From a macro perspective, higher wood density corresponded to greater drill resistance. However, the mathematical model established using data from multiple tree species featured lower test accuracy, even lower than predicting the density of each tree species based on the average basic density of each tree species. This difference may be attributed to the relationship between wood strength and density, which can be influenced by fiber length, cell wall thickness, resin content, and other factors. Thus, species with similar densities can still differ from each other in wood anatomical structure and resin content. Therefore, establishing a mathematical model for each tree species is vital.

The sub-model for each tree species exhibited higher estimation accuracy than the average value of each tree species used as the density estimation value. This confirmed the feasibility of using the micro drilling resistance method to measure the wood density of standing trees. However, the estimated accuracy of the total test data for each sub-model was only 1.670 percentage points higher than the average of each tree species used as the density estimate. This difference may be attributed to the following reasons. First, the thin and long structure of the drill needle led to significant vibration amplitude during high-speed rotation, resulting in the formation of noise signals in the resistance measurement. Second, the operator’s actions, such as breathing, trembling, and movement, can introduce vibrations in the micro drill resistance meter, thereby affecting the drill resistance measurements [45]. Future research should focus on improving the mechanical strength of the drill needle to reduce vibrations and designing a bracket to stabilize the micro drill resistance instrument and mitigate the impact of the operator’s movements on the accuracy of drill resistance measurements.

5. Conclusion

The efficient utilization of wood is crucial for sustainable human development. The rapid and non-destructive measurement of wood density forms the foundation for optimizing wood utilization. The micro-drilling resistance method is a highly promising approach for measuring wood density. This study investigated the feasibility of using the micro-drilling resistance method to measure the wood density of a standing tree. Moreover, the investigation included formulating a mathematical model, exploring the potential for unified modeling of multiple tree species, and analyzing the impact of moisture content on measurement accuracy. First, we sampled 231 tree cores and recorded the drill needle resistance data from three tree species. Second, the basic density and moisture content of each core were measured, and a comprehensive model for the three tree species and sub-models of each tree species were established through a stepwise regression method. Finally, the accuracy of each model was tested. From the research and analyses conducted by the authors, the following conclusions are drawn:

1. The use of the micro drilling resistance method for measuring the wood density of standing trees was feasible.

2. The relationship between wood density and drill resistance did not follow a linear pattern; in some tree species, this relationship exhibited a logarithmic pattern.

3. Moisture content slightly influenced drill needle resistance. Therefore, to measure the wood density of standing trees, it is recommended to sample the drill resistance in a consistent environment to minimize the influence of moisture content on drill resistance.

4. The establishment of a mathematical model for each tree species was considered essential.

This study provides valuable guidance for measuring the wood density of standing trees through the micro-drilling resistance method. However, owing to the inconsistent effect of the natural logarithm of average drill resistance and moisture content on some sub-models, further research in these two aspects is required in the future.

Author Contributions

Conceptualization, J.Y. and J.L.; methodology, J.Y. ,Y. Z. , H. L. and Z.W.; data sampling and processing, J.Y. and Y.S.; validation, Y.Z.; formal analysis, Z.L.; investigation, J.Y. and Z.L.; resources, J.Y. and Z.L.; data curation, Y. Z. , H. L. and Z.W.; writing—original draft preparation, Y.S.; writing—review and editing, J.Y. and J.L.; visualization, J.Y. and Z.L.; supervision, J.Y.; project administration, J.Y.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Key R&D Program of China (Grand No. 2021yfd2200404) and the Natural Science Foundation of Henan Province (232300421167), Key Scientific Research Projects of Universities in Henan Province (22A220002), Xinyang Academy of Ecological Research Open Foundation(2023XYQN04),Xinyang Academy of Ecological Research Open Foundation(2023XYZD02） Natural Science Foundation of Henan Province(222300420274),Academic Degrees & Graduate Education Reform Project of Henan Province (2021SJGLX057Y),and Postgraduate Education Reform and Quality Improvement Project of Henan Province (YJS2023SZ23).

Acknowledgments

Shouzheng Tang, an academician of the Chinese Academy of Forestry, provided guidance on topic selection; Xiangdong Lei, a researcher of the Chinese Academy of Forestry, provided the Resistograph 650-SC instrument.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

References

Martínez, R.D.; Balmori, J.A.F.; Llana, D.; Bobadilla, I. Wood density determination by drilling chips extraction in ten softwood and hardwood species. Forests 2020, 11, 383. [Google Scholar] [CrossRef]
Fundova, I.; Funda, T.; Wu, H.X. Non-destructive wood density assessment of Scots pine (Pinus sylvestris L.) using Resistograph and Pilodyn. PLoS ONE 2018, 13, e0204518. [Google Scholar] [CrossRef] [PubMed]
Jakubowski, M.; Dobroczyński, M. Allocation of wood density in european oak (Quercus robur L.) trees grown under a canopy of scots pine. Forests 2021, 12, 712. [Google Scholar] [CrossRef]
Vega, M.; Hamilton, M.; Downes, G.; Harrison, P.A.; Potts, B. Radial variation in modulus of elasticity, microfibril angle and wood density of veneer logs from plantation-grown Eucalyptus nitens. Ann. For. Sci. 2020, 77, 65. [Google Scholar] [CrossRef]
Kimberley, M.O.; Moore, J.R.; Dungey, H.S. Modelling the effects of genetic improvement on radiata pine wood density. New Zealand J. For. Sci. 2016, 46, 8. [Google Scholar] [CrossRef]
Soro, A.; Lenz, P.; Hassegawa, M.; Roussel, J.R.; Bousquet, J.; Achim, A. Genetic influence on components of wood density variation in white spruce. Forestry 2022, 95, 153–165. [Google Scholar] [CrossRef]
Rashidi-Jouybari, I.; Lenz, P.; Beaulieu, J.; Nadeau, S.; Bousquet, J.; Achim, A. Multi-trait selection for improved solid wood physical and flexural properties in white spruce. For. Int. J. For. Res. 2022, 95, 492–503. [Google Scholar] [CrossRef]
Castro, V.R.; Chambi-Legoas, R.; Tommasiello Filho, M.; Surdi, P.G.; Zanuncio, J.C.; Zanuncio, A.J.V. Retraction Note: The effect of soil nutrients and moisture during ontogeny on apparent wood density of Eucalyptus grandis. Sci. Rep. 2021, 11, 11590. [Google Scholar] [CrossRef] [PubMed]
Kerfriden, B.; Bontemps, J.D.; Leban, J.M. Variations in temperate forest stem biomass ratio along three environmental gradients are dominated by interspecific differences in wood density. Plant Ecol. 2021, 222, 289–303. [Google Scholar] [CrossRef]
Nabais, C.; Hansen, J.K.; David-Schwartz, R.; Klisz, M. , López, R.; Rozenberg, P. The effect of climate on wood density: what provenance trials tell us? For. Ecol. Manag. 2018, 408, 148–156. [Google Scholar] [CrossRef]
Pompa-García, M.; Hevia, A.; Camarero, J.J. Minimum and maximum wood density as proxies of water availability in two Mexican pine species coexisting in a seasonally dry area. Trees 2021, 35, 597–607. [Google Scholar] [CrossRef]
Eggers, J.; Lindner, M.; Zudin, S. , Zaehle, S.; Liski, J. Impact of changing wood demand, climate and land use on European forest resources and carbon stocks during the 21st century. Glob. Change Biol. 2008, 14, 2288–2303. [Google Scholar] [CrossRef]
Shmulsky, R.; Jones, P.D. Forest products and wood science: an introduction. Aust. For. 2007, 70, 209–212. [Google Scholar]
Sikkema, R.; Steiner, M.; Junginger, M.; Hiegl, W.; Hansen, M.T.; Faaij, A. The European wood pellet markets: current status and prospects for 2020. Biofuels, Bioprod. Bioref. 2011, 5, 250–278. [Google Scholar] [CrossRef]
Wu, T.; Zhang, B.; Cao, Y.; Sun, P. Impact of multi-dimensional and dynamic distance on China’s exports of wooden forest products to countries along the “Belt and Road”. Sustainability 2020, 12, 3339. [Google Scholar] [CrossRef]
Li, Q.; Chen, S.; Zhao, R. Study on evaluation of timber security in china based on the PSR conceptual model. Forests 2020, 11, 517. [Google Scholar] [CrossRef]
Todoroki, C.L.; Lowell, E.C.; Filipescu, C.N. Wood density estimates of standing trees by micro-drilling and other non-destructive measures. New Zealand J. For. Sci. 2021, 51, 6. [Google Scholar] [CrossRef]
Phillips, O.L.; Sullivan, M.J.; Baker, T.R.; Monteagudo Mendoza, A.; Vargas, P.N.; Vásquez, R. Species matter: wood density influences tropical forest biomass at multiple scales. Surv. Geophys. 2019, 40, 913–935. [Google Scholar] [CrossRef] [PubMed]
Ershov, A.E.; Stroganova, T.S. Structure and properties of biomorphic carbon scaffolds based on pressed birch and alder wood. Carbon Trends 2023, 13, 100312. [Google Scholar] [CrossRef]
Clough, B.J.; Curzon, M.T.; Domke, G.M.; Russell, M.B.; Woodall, C.W. Climate-driven trends in stem wood density of tree species in the eastern United States: Ecological impact and implications for national forest carbon assessments. Glob. Ecol. Biogeogr. 2017, 26, 1153–1164. [Google Scholar] [CrossRef]
Flores, O.; Coomes, D.A. Estimating the wood density of species for carbon stock assessments. Methods Ecol. Evol. 2011, 2, 214–220. [Google Scholar] [CrossRef]
Francis, E.J.; Muller-Landau, H.C.; Wright, S.J.; Visser, M.D.; Iida, Y.; Fletcher, C.; Hubbell, S.P.; Kassim, A.R. Quantifying the role of wood density in explaining interspecific variation in growth of tropical trees. Glob. Ecol. Biogeogr. 2017, 26, 1078–1087. [Google Scholar] [CrossRef]
Fajardo, A. Wood density is a poor predictor of competitive ability among individuals of the same species. For. Ecol. Manag. 2016, 372, 217–225. [Google Scholar] [CrossRef]
Gao, S.; Wang, X.; Wiemann, M.C.; Brashaw, B.K.; Ross, R.J. A critical analysis of methods for rapid and nondestructive de-termination of wood density in standing trees. Ann. For. Sci. 2017, 74, 77. [Google Scholar] [CrossRef]
Freyburger, C.; Longuetaud, F.; Mothe, F.; Constant, T.; Leban, J.M. Measuring wood density by means of X-ray computer tomography. Ann. For. Sci. 2009, 66, 804. [Google Scholar] [CrossRef]
Mannes, D.; Lehmann, E.; Cherubini, P.; Niemz, P. Neutron imaging versus standard X-ray densitometry as method to measure tree-ring wood density. Trees 2007, 21, 605–612. [Google Scholar] [CrossRef]
Cown, D.J. Comparison of the Pilodyn and Torsiometer methods for the rapid assessment of wood density in standing trees. New Zealand J. For. Sci. 1978, 8, 384–391. [Google Scholar]
Greaves, B.L.; Borralho, N.; Raymond, C.A.; Farrington, A. Use of a Pilodyn for the indirect selection of basic density in Eucalyptus nitens. Can. J. For. Res. 1996, 26, 1643–1650. [Google Scholar] [CrossRef]
Rinn, F. Basics of Micro-resistance Drilling for Timber Inspection. Holztechnologie 2012, 53, 24–29. [Google Scholar]
Rinn, F.; Schweingruber, F.-H.; Schär, E. Resistograph and X-ray Density Charts of Wood. Comparative Evaluation of Drill Resistance Profiles and X-ray Density Charts of Different Wood Species. Holzforschung 1996, 50, 303–311. [Google Scholar] [CrossRef]
Szewczyk, G.; Wasik, R.; Leszczyński, K.; Podlaski, R. Age Estimation of Different Tree Species Using a Special Kind of an Electrically Recording Resistance Drill. Urban For. Urban Green. 2018, 34, 249–253. [Google Scholar] [CrossRef]
Rinn, F. Practical Application of Micro-resistance Drilling for Timber Inspection. Holztechnologie 2013, 54, 32–38. [Google Scholar]
Guller, B.; Guller, A.; Kazaz, G. Is Resistograph an Appropriate Tool for the Annual Ring Measurement of Pinnus Brutia? In Proceedings of the NDE for Safety/Defektoskopie 2012, 42nd International Conference, Seč, Czech Republic, 30 October–1 November 2012; pp. 89–94. [Google Scholar]
Hu, X.; Zheng, Y.; Liang, H.; Zhao, Y. Design and Test of a Microdestructive Tree-ring Measurement System. Sensors 2020, 20, 3253. [Google Scholar] [CrossRef]
Hu, X.; Zheng, Y.; Xing, D.; Sun, Q. Research on tree ring micro-destructive detection technology based on digital micro-drilling resistance method. Forests 2022, 13, 1139. [Google Scholar] [CrossRef]
Oh, J.; Seo, J.; Kim, B. Determinate the number of growth rings using Resistograph with tree-ring chronology to investigate ages of big old trees. J. Korean Wood Sci. Technol. 2019, 47, 700–708. [Google Scholar] [CrossRef]
Wang, X. Recent advances in nondestructive evaluation of wood: in-forest wood quality assessments. Forests 2021, 12, 949. [Google Scholar] [CrossRef]
Isik, F.; Li, B. Rapid Assessment of Wood Density of Live Trees Using the Resistograph for Selection in Tree Improvement Programs. Can. For. Res. 2003, 33, 2426–2435. [Google Scholar] [CrossRef]
Downes, G.M.; Lausberg, M.; Potts, B.M.; Pilbeam, D.L.; Bird, M.; Bradshaw, B. Application of the Iml Resistograph to the Infield Assessment of Basic Density in Plantation Eucalypts. Aust. For. 2018, 81, 177–185. [Google Scholar] [CrossRef]
Tomczak, K.; Tomczak, A.; Jelonek, T. Measuring Radial Variation in Basic Density of Pendulate Oak: Comparing Increment Core Samples with the IML Power Drill. Forests 2022, 13, 589. [Google Scholar] [CrossRef]
Liu, Y.; Zhao, G. Wood Scence, 2nd ed.; China Forestry Publishing House: Beijing, China, 2019; pp. 226–228. [Google Scholar]
Lin, C.J.; Wang, S.Y.; Lin, F.C.; Chiu, C.M. Effect of moisture content on the drill resistance value in Taiwania plantation wood. Wood Fiber Sci. 2003, 35, 234–238. [Google Scholar]
Sharapov, E.; Brischke, C.; Militz, H.; Smirnova, E. Combined effect of wood moisture content, drill bit rotational speed and feed rate on drilling resistance measurements in Norway spruce (Picea abies (L.) Karst.). Wood Mater. Sci. Eng. 2018, 15, 198–204. [Google Scholar] [CrossRef]
Ukrainetz, N.K.; O’Neill, G.A. An analysis of sensitivities contributing measurement error to Resistograph values. Can J Res. 2010, 40, 806–811. [Google Scholar] [CrossRef]
Yao, J.; Wu, Z.; Zheng, Y.; Rao, B.; Li, Z.; Hu, Y.; Nie, B. Design of a tree micro drill instrument to improve the accuracy of wood density estimation. Forests 2023, 14, 2071. [Google Scholar] [CrossRef]

Figure 1. Schematic of sampling method.

Figure 2. Drill geometry of Resistograph.

Figure 3. Drill resistance curve.

Figure 4. Box plots.

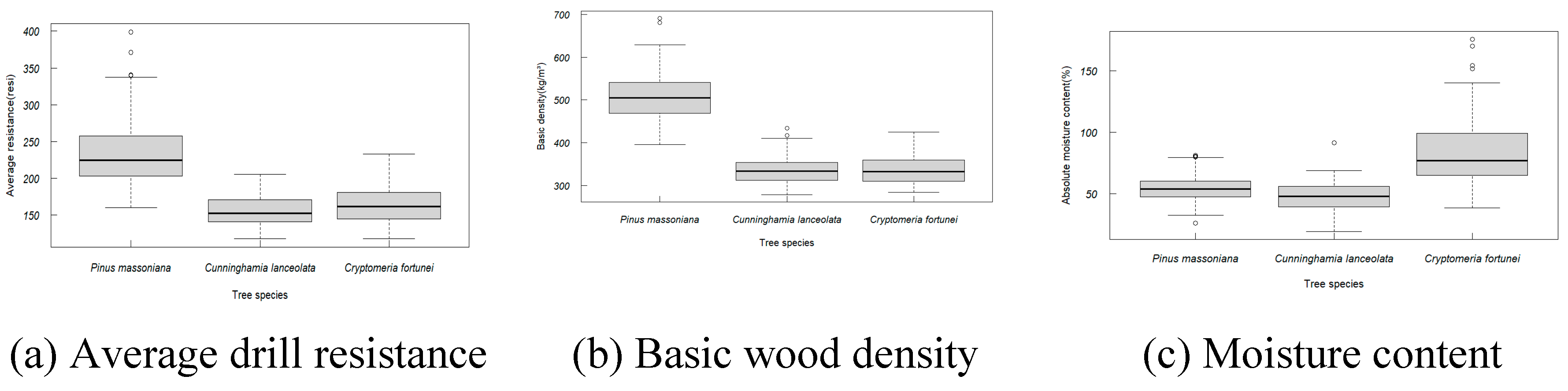
Figure 5. Comparison between the linear and logarithmic fitting curves of the average drill resistance and wood density.

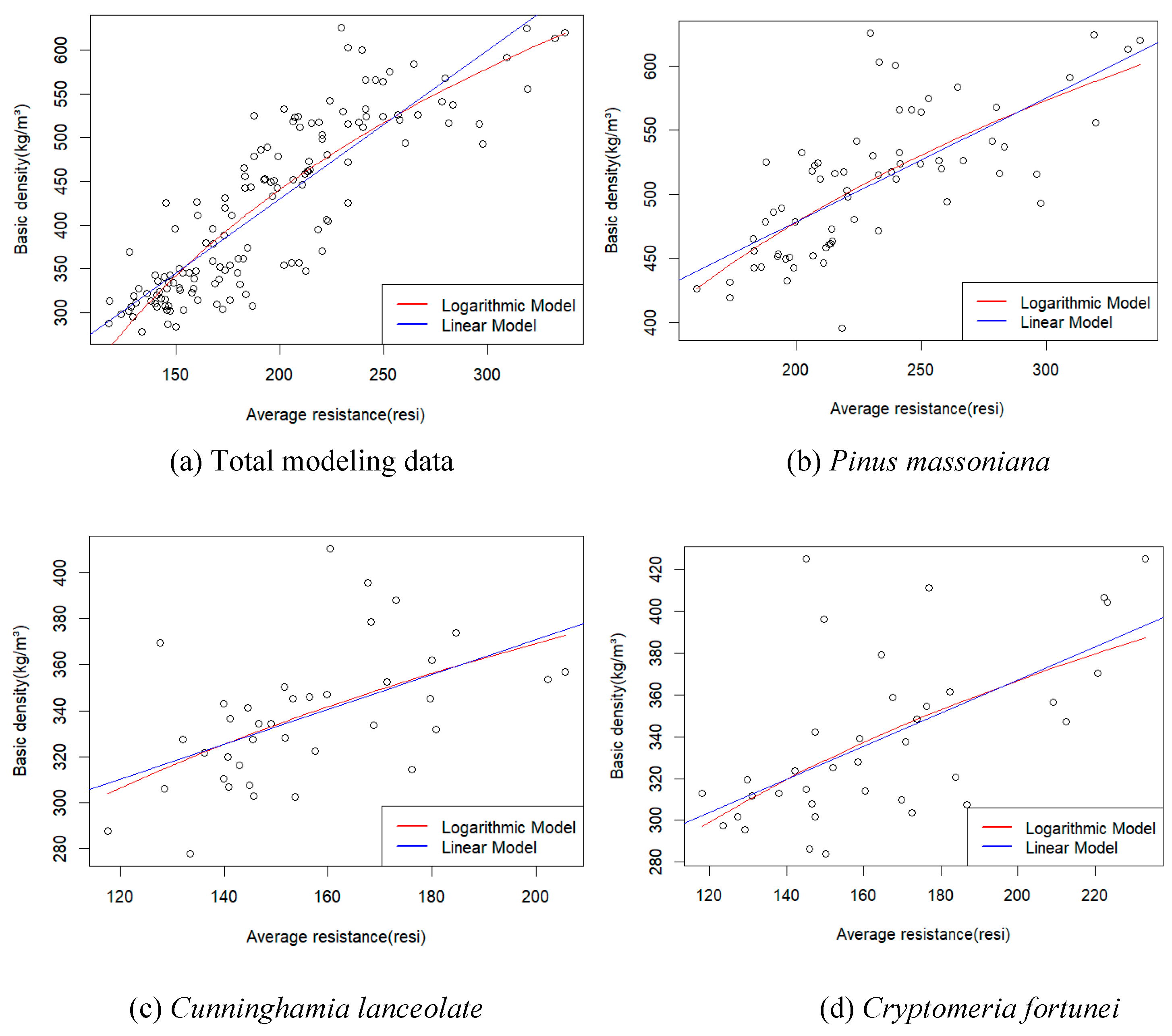
Table 1. Overview of the data.

Species	The number of original data records	The number of data records removed outliers
Pinus massoniana	111	101
Cunninghamia lanceolate	60	57
Cryptomeria fortunei	60	56
Total	231	214

Table 2. P-values of each parameter in the linear model for wood basic density, average drill resistance, the natural logarithm of the average drill resistance, and absolute moisture content.

Parameter	Parameter value	p-value
Intercept	-1346.218	0.006
average drill resistance	-0.079	0.887
the natural logarithm of average drill resistance	351.030	0.002
absolute moisture content	-97.673	<0.001

Table 3. P-values of each parameter in the linear model for wood basic density, the natural logarithm of the average drill resistance, and absolute moisture content.

Parameter	Parameter value	p-value
intercept	-1279.480	<0.001
the natural logarithm of average drill resistance	335.320	<0.001
absolute moisture content	-97.400	<0.001

Table 4. P-values of each parameter in the linear model for Pinus massoniana, involving wood basic density, average drill resistance, the natural logarithm of the average drill resistance, and absolute moisture content.

Parameter	Parameter value	p-value
intercept	-1420.179	0.218
average drill resistance	-0.71639	0.502
the natural logarithm of average drill resistance	400.351	0.121
absolute moisture content	-146.144	0.001

Table 5. P-values of each parameter in the linear model for Pinus massoniana, involving wood basic density, the natural logarithm of the average drill resistance, and absolute moisture content.

Parameter	Parameter value	p-value
intercept	-656.000	<0.001
the natural logarithm of average drill resistance	229.190	<0.001
absolute moisture content	-147.320	0.001

Table 6. P-values of each parameter in the linear model for Cunninghamia lanceolate, including wood basic density, average drill resistance, the natural logarithm of the average drill resistance, and absolute moisture content.

Parameter	Parameter value	p-value
intercept	-2119.289	0.224
average drill resistance	-2.892	0.286
the natural logarithm of average drill resistance	574.777	0.181
absolute moisture content	21.163	0.595

Table 7. P-values of each parameter in the linear model for Cunninghamia lanceolate, involving wood basic density, average drill resistance, and the natural logarithm of the average drill resistance.

Parameter	Parameter value	p-value
intercept	-1930.803	0.252
average drill resistance	-2.569	0.325
the natural logarithm of average drill resistance	529.414	0.203

Table 8. P-values of each parameter in the linear model for Cunninghamia lanceolate, involving wood basic density and the natural logarithm of the average drill resistance.

Parameter	Parameter value	p-value
intercept	-283.580	0.088
the natural logarithm of average drill resistance	123.220	<0.001

Table 9. P-values of each parameter in the linear model for Cunninghamia lanceolate, involving wood basic density and the natural logarithm of the average drill resistance without intercept.

Parameter	Parameter value	p-value
the natural logarithm of average drill resistance	66.958	<0.001

Table 10. P-values of each parameter in the linear model for Cryptomeria fortunei, involving wood basic density, average drill resistance, the natural logarithm of the average drill resistance, and absolute moisture content.

Parameter	Parameter value	p-value
intercept	478.751	0.712
average drill resistance	1.173	0.526
the natural logarithm of average drill resistance	-59.400	0.850
absolute moisture content	-39.303	0.140

Table 11. P-values of each parameter in the linear model for Cryptomeria fortunei, involving wood basic density, average drill resistance, and absolute moisture content.

Parameter	Parameter value	p-value
intercept	234.352	<0.001
absolute moisture content	-40.280	0.118
average drill resistance	0.827	<0.001

Table 12. P-values of each parameter in the linear model for Cryptomeria fortunei, involving wood basic density and average drill resistance.

Parameter	Parameter value	p-value
intercept	208.746	<0.001
average drill resistance	0.791	<0.001

Table 13. Test results.

Spieces	Total model		Sub model		Average basic density of each tree species
Spieces	Estimated standard error /(kg∙m^-3)	Mean estimated accuracy (%)	Estimated standard error /(kg∙m^-3)	Mean estimated accuracy (%)	Estimated standard error /(kg∙m^-3)	Mean estimated accuracy (%)
Pinus massoniana	58.646	91.401	47.393	93.248	47.669	92.639
Cunninghamia lanceolate	46.505	88.491	27.062	93.263	31.138	92.260
Cryptomeria fortunei	44.238	89.337	18.087	95.540	36.172	91.360
Total	50.599	90.070	35.639	93.865	39.776	92.195

Table 14. Linear and logarithmic fitting equations of the average drill resistance and wood density.

Species	Linear model		Logarithmic model
Species	Equation	Adjusted R²	Equation	Adjusted R²
Pinus massoniana	y=285.499+0.965x	0.506	y=-766.910+234.970lnx	0.521
Cunninghamia lanceolate	y=219.332+0.759x	0.256	y=-283.580+123.220lnx	0.270
Cryptomeria fortunei	y=208.746+0.791x	0.347	y=-335.230+132.510lnx	0.336
Total	y=91.366+1.692x	0.733	y=-1370.740+341.840lnx	0.746

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer