Distributed Sequential Detection for Cooperative Spectrum Sensing in Cognitive Internet of Things

Considering the spectrum shortage problem of IoT devices, we introduce a collaborative spectrum sensing (CSS) framework in this paper to identify available spectrum resources, so that IoT devices can access it and meanwhile avoid causing harmful interference to the normal communication of the primary user (PU). However, in the process of the PU’s signal detection in IoT devices, the issue about the stopping time and decision cost arises. To this end, we propose a distributed cognitive IoT model, which includes two IoT devices independently using sequential decision rules to detect the PU. On this basis, we define the stopping time and cost function for IoT devices, and formulate an average cost optimization problem in CSS. To solve this problem, we further regard the optimal stopping time problem as a finite horizon problem, and solve the threshold of the optimal decision rule by dynamic programming. At last, numerical simulation results demonstrate the correctness of our proposal in terms of the global false alarm and miss detection probability, and it always achieves minimal average cost under various cost of each observation taken and thresholds.

Keywords:

Subject: Computer Science and Mathematics - Computer Networks and Communications

1. Introduction

As wireless communication technology rapidly develops, spectrum resources cannot meet the growing number of internet of thing (IoT) devices and their applications. However, the frequency spectrum by primary users (PUs) still lies in insufficient state in the time or space domain. To address this concern, cognitive radio (CR) is regarded as a prospective technology to identify available spectrum resources and allow IoT devices to opportunistically access it [1,2], without causing harmful interference to PUs [3]. But spectrum sensing behaviors of the single IoT device is susceptible to inherent factors of wireless propagations. Consequently, cooperative spectrum sensing (CSS) paradigm is formulated to exploit spatial diversity and then improve the sensing accuracy of the PU signal through the observations of spatially positioning IoT devices. However, IoT architectures differ from traditional network architectures, which imply a high degree of reconfigurability, adaptability, mobility, and heterogeneity, and present some insurmountable challenges to spectrum sensing. Traditional spectrum sensing techniques must be carefully redesigned for use in complex and scalable IoT systems [4].

In the past, there are some researchers to investigate spectrum sensing for IoT systems. An energy-efficient reliable decision transmission in Zhu et al. to was proposed to decrease packet error and packet loss in industrial IoT [5]. At a low signal-to-noise ratio (SNR) environment, to minimize the energy consumption and sensing time, Ansere et al. proposed a dynamic spectrum sensing algorithm [6]. Wan et al. proposed an energy-efficient CSS scheme to reduce the negative impact of spatial correlation [7]. Since the previous energy detector is usually limited by the noise-uncertain, Miah et al. also proposed an energy efficient CSS in based CR-enabled IoTs network under the interference constraint [8]. Considering that battery-limited IoT devices are densely interconnected, Dao et al. optimized the sensing efficiency to leverage a lightweight but effective adaptive medium learning method [9]. Long et al. developed a harvesting-sensing-transmission tradeoff problem based cognitive IoT to take the diversity of energy harvesting efficiency, spectrum sensing performance and quality-of-service (QoS) of data transmission into consideration [10]. In order to enhance spectrum utilization in a 5G-based IoT, Abbas et al. proposed a hybrid mode of underlay and interweave enabled scheme [11]. Gharib et al. proposed a heterogeneous multi-band multi-user CSS scheme to realize secondary users’ scheduling to sense a subset of channel in heterogeneous distributed CR networks [12]. Ejaz et al. presented multiband CSS and resource allocation framework in a CR-enabled IoT 5G network to minimize the energy consumption under the performance requirement [13]. To maximize the effective throughput, Zhang et al. jointly optimized the sensing time and packet error rate in cognitive IoT [14]. Miah et al. presented a CSS technique in a noise-uncertain environment to comprise the use of the Kullback-Leibler divergence in CR-based IoT [15]. To encourage the spectrum sharing among unlicensed IoT devises, Lu et al. integrated the incentive mechanism into orthogonal frequency division multiplexing (OFDM)-based cognitive IoT network with multiple unlicensed IoT devises in the context of incomplete information [16]. In the CSS of high real-time scene of IoTs, Gao et al. considered an improved CSS scheme to decrease the latency and increase low throughput, where each cognitive node performs truncated sequential probability ratio test (SPRT) over each observation vector [17]. Wu et al. achieved CSS between micro-sensing slots in cognitive unmanned aerial vehicle networks and approximated the error probability and the stopping time [18].

Most of these efforts are focused on CR-enabled IoT, considering issues such as the achievable throughput, energy efficiency, frequency efficiency, or joint optimization with spectrum resource allocation algorithm. These issues are also common in traditional CR networks. However, they did not take into account the cost issues in cognitive IoT, such as the sensing/stopping time cost, the cost of incorrect decisions, especially when considering CSS among multiple IoT devices. Because only by achieving low-cost detection of the PU while ensuring spectrum sensing performance) can efficient spectrum sensing and resource allocation be achieved. Therefore, this article considers the optimal decision rule in cognitive IoT from the perspective of cost. To this end, a distributed cognitive IoT model is first established, including a pair of IoT devices for CSS and sequential detection, on the basis of which the stopping time and decision cost are defined, and the joint optimization problem between them is proposed. The optimal stopping time and threshold are analyzed by dynamic programming to obtain the optimal decision rule.

The remainder of this article is organized as follows. The local spectrum sensing model and sequential detection for CSS in a cognitive IoT are presented in Section 2. The optimal stopping time and decision rule based on distributed sequential detection is proposed and analyzed in Section 3. Comprehensive simulation result analyses and discussions are discussed in Section 4, and Section 5 draws a conclusion about this article.

2. Materials and Methods

2.1. Spectrum Sensing Model

In a cognitive IoT without a centralized fusion center (FC), there is a PU and a pair of IoT devices participating in CSS, as shown in Figure 1. To protect the PU’s normal operation from detrimental interference, each of IoT devices

S_{1}

and

S_{2}

individually exploits spectrum sensing technology to sense the PU at the sensing slot, and then derives a final local decision about the PU’s presence through a predetermined combination rule through observations of the PU activity information at each multiple micro-sensing slot. According to the global decisions of IoT devices, a distributed CSS algorithm is adopted to derive a global decision after the sensing slot to decide whether to allow IoT devices to access the channel. At last, a pair of IoT devices are allowed to utilize the free spectrum band via a predetermined spectrum resources algorithm during the transmitting slot if the PU is declared as absence.

The energy detection is usually utilised as a local sensing technology because it is easy to implemented and compatible to the PU network. In an energy detector, suppose that the hypothesis

H_{0}

and

H_{1}

represent the PU’s absence and presence, respectively, then the attenuated received PU signal at the

k

-th micro-sensing slot of a IoT device is expressed as [19]

y_{k} (m) = \{\begin{array}{l} n_{k} (m), H_{0} \\ h_{k} s_{k} (m) + n_{k} (m), H_{1} \end{array},

(1)

where

m

is the PU signal sampling,

n_{k} (m)

is the circularly symmetric complex Gaussian (CSCG) noise,

s_{k} (m)

is the complex-valued phase shift keying (PSK) signal at the PU,

n_{k} (m)

and

s_{k} (m)

are independent each other,

h_{k}

is the channel gain. Then, the test static

E_{k}

of energy detector is expressed by

E_{k} = \frac{1}{M} \sum_{m = 1}^{M} {|y_{k} (m)|}^{2},

(2)

where

M

is the sampling number of the received PU signal.

Following (2), we evaluate the local performance via a pre-determined detection threshold

λ_{k}

. Under the hypothesis

H_{0}

, the probability density function (PDF)

p_{0} (l)

of the test static

E_{k}

follows Chi-square distribution, the local false alarm probability is obtained by

P_{f, k} = P (r_{k} = 1 | H_{0}) = P (E_{k} > λ_{k} | H_{0}) = \int_{λ_{k}}^{\infty} p_{0} (l) d l,

(3)

where

r_{k}

is the sensing sample.

Suppose

M

is large enough, PDF of

E_{k}

is approximated as a Gaussian distribution where the mean

μ_{0} = σ_{n}^{2}

, the variance

σ_{0}^{2} = [E {|n_{k} (m)|}^{4} - σ_{n}^{4}] / M

. Because

n_{k} (m)

is CSCG,

E {|n_{k} (m)|}^{4} = 2 σ_{n}^{4}

, thus

σ_{0}^{2} = σ_{n}^{4} / M

. The sampling frequency is

f_{s}

, the duration time for the

k

-th micro-sensing slot is

τ_{k}

, for simplicity of denotation,

M = τ_{k} f_{s}

. Therefore, the local false alarm probability is given by

P_{f, k} = Q ((\frac{λ_{k}}{σ_{n}^{2}} - 1) \sqrt{τ_{k} f_{s}}),

(4)

where

Q (l) = \frac{1}{\sqrt{2 π}} \int_{λ_{k}}^{\infty} e x p (- \frac{t^{2}}{2}) d l .

(5)

Under the hypothesis

H_{1}

, PDF of

E_{k}

is denoted by

p_{1} (l)

, the local detection probability can be expressed by

P_{d, k} = P (r_{k} = 1 | H_{1}) = P (E_{k} > λ_{k} | H_{1}) = \int_{λ_{k}}^{\infty} p_{1} (l) d l .

(6)

Since PDF of

E_{k}

is also regarded as a Gaussian distribution where the mean

μ_{1} = (1 + λ_{k}) σ_{n}^{2}

, the variance

σ_{1}^{2} = [E {|h_{k} s_{k} (m)|}^{4} + E {|n_{k} (m)|}^{4} - {(h_{k}^{2} s_{k}^{2} (m) - σ_{n}^{2})}^{2}] / M = [(1 + γ_{k}) σ_{n}^{4}] / M

, where

γ_{k}

is the received SNR at the

k

-th micro-sensing slot, the local detection probability can be given by

P_{d, k} = Q ((\frac{λ_{k}}{σ_{n}^{2}} - γ_{k} - 1) \sqrt{\frac{τ_{k} f_{s}}{1 + 2 γ_{k}}}) .

(7)

2.2. Sequential Detection

Building on the above spectrum sensing model in a cognitive IoT, we further present a sequential detection framework for CSS and make the following assumptions and descriptions. The IoT device

S_{i}

receives a sequence of observations

\{Z_{k}^{i}\}

, and

\{Z_{k}^{i}\}

is i.i.d. and are independent of one another at a hypothesis,

i = 1, 2

. Under hypothesis

H_{j}

, the observations from the

i

-th IoT device follows a marginal probability density function

q_{j}^{(i)}

. In addition, the probability of hypotheses

H_{0}

and

H_{1}

are

1 - ρ

and

ρ

, respectively, a probability space is assumed to be

(Ω, F) = (ℝ^{\infty} \times ℝ^{\infty}, B^{\infty} \times B^{\infty})

equipped with the probability measure

P = ρ P_{1} + (1 - ρ) P_{0}

, where

P_{1} = P_{1}^{(1)} P_{1}^{(2)}

and

P_{0} = P_{0}^{(1)} P_{0}^{(2)}

P_{j}^{(1)}

and

P_{j}^{(2)}

denote the restrictions of

P_{j}

to the corresponding filtrations

\{F_{k}^{(i)}\}

with

F_{k}^{(i)} = σ \{Z_{1}^{(i)}, \dots, Z_{k}^{(i)}\}

. Each IoT devices

S_{i}

devises a sequential decision rule [20],

T^{(i)}

is the time of stopping sampling, and

θ^{(i)}

takes the value 0 or 1 to declare whether one of two hypotheses is accepted.

3. Disributed Sequential Detection

According to the above model, we delve into the distributed sequential detection for a cognitive IoT in this section, including the optimal stopping time and the optimal sequential detection.

3.1. Problem Formulation

To study the cost problem of a distributed sequential detection, we define a cost function

Δ (θ^{(1)}, θ^{(2)}; H)

indicates the cost of error decision in any one or both of the decisions made by a pair of IoT devices. To be specific,

Δ (0, θ^{(2)}; H_{1}) \geq Δ (1, θ^{(2)}; H_{1})

Δ (1, θ^{(2)}; H_{0}) \geq Δ (1, θ^{(2)}; H_{1})

Δ (1, θ^{(2)}; H_{0}) \geq Δ (0, θ^{(2)}; H_{0})

, and

Δ (0, θ^{(2)}; H_{1}) \geq Δ (0, θ^{(2)}; H_{0})

. Similarly, the inequalities apply to

θ^{(1)}

. From these inequalities, each additional sample of an IoT device also incurs a cost of

c

. Combining the time of stopping sampling and the cost function, there is a following decision problem, such as,

\inf_{\{(T^{(i)}, θ^{(i)})\}} E \{c T^{(1)} + c T^{(2)} + Δ (θ^{(1)}, θ^{(2)}; H)\} .

(8)

3.2. Preliminary Analysis

Since a positive cost

c

correlates with each additional time step taken by IoT devices in (8), the person-by-person optimization (PBPO) approach is applied to distributed sequential detection to address the problem of (8) [21]. Fixing

(T^{(2)}, θ^{(2)})

, a stochastic optimization problem is described as

J (ρ) = \inf_{\{(T^{(1)}, δ^{(1)})\}} E \{c T^{(1)} + c T^{(2)} + Δ (θ^{(1)}, θ^{(2)}; H)\} .

(9)

In (9), there is a special case, i.e.,

Δ (θ^{(1)}, θ^{(2)}; H) = Δ (θ^{(1)}, H) + Δ (θ^{(2)}, H)

, which is a classical sequential detection problem. Additionally, the cost function may be coupled between the two IoT devices.

Before solving (9), a sufficient statistic is preset as

ρ_{k}^{(1)} = P (H = H_{1} | F_{k}^{(2)}),

(10)

and the recursion result from Bayes’ formula can be expressed as

ρ_{k + 1}^{(1)} = \frac{ρ_{k}^{(1)} q_{1}^{(1)} (x)}{ρ_{k}^{(1)} q_{1}^{(1)} (x) + (1 - ρ_{k}^{(1)}) q_{0}^{(1)} (x)} P (H = H_{1} | F_{k}^{(2)}),

(11)

with

ρ_{0}^{(1)} = ρ

. Obviously,

\{ρ_{k}^{(1)}\}

forms a Markov process about the filtration

\{F_{k}^{(1)}\}

Considering the finite horizon problem, IoT device

S_{1}

discontinues sampling and derives a decision not later than time

τ

. Let

J_{k}^{τ}

denote the minimal expected cost at the

k

-th micro-sensing slot, a dynamic programming equation

(1): When $\{T^{(1)} = τ\}$ , we have

$J_{T^{(1)}}^{τ} (ρ_{T^{(1)}}^{(1)}) = \inf \{E \{Δ (0, θ^{(2)}; H) | F_{T^{(1)}}^{(1)}\}, E \{Δ (1, θ^{(2)}; H) | F_{T^{(1)}}^{(1)}\}\} .$

(12)
(2): When $\{T^{(1)} = k\}$ , $k = 1, \dots, τ - 1$ , we have

$J_{T^{(1)}}^{τ} (ρ_{T^{(1)}}^{(1)}) = \inf \{E \{Δ (0, θ^{(2)}; H) | F_{T^{(1)}}^{(1)}\}, E \{Δ (1, θ^{(2)}; H) | F_{T^{(1)}}^{(1)}\}, c + Δ_{k}^{τ} (ρ_{k}^{(1)})\},$

(13)

where $Δ_{k}^{τ} (ρ_{k}^{(1)}) = E \{J_{k + 1}^{τ} (ρ_{k + 1}^{(1)}) | F_{k}^{(1)}\}$ .

Since

J_{0}^{τ}

is the minimal expected cost of the finite horizon problem, (12) and (13) provide the dependence of the minimal expected cost on the sufficient statistic

ρ_{k}^{(1)}

. It can be clearly seen from the right-hand side of unfolding (12), according to

E \{Δ (0, θ^{(2)}; H) | F_{T^{(1)}}^{(1)}\} = \sum_{d = 0}^{1} \sum_{j = 0}^{1} P_{j} (θ^{(2)} = d) Δ (0, d; H_{j}) \times P (H = H_{j} | F_{T^{(1)}}^{(1)})

E \{Δ (1, θ^{(2)}; H) | F_{T^{(1)}}^{(1)}\} = \sum_{d = 0}^{1} \sum_{j = 0}^{1} P_{j} (θ^{(2)} = d) Δ (1, d; H_{j}) \times P (H = H_{j} | F_{T^{(1)}}^{(1)})

, and using (8). The same holds true for (13), then we have

E \{J_{k + 1}^{τ} (ρ_{k + 1}^{(1)}) | F_{k}^{(1)}\} = \int J_{k + 1}^{τ} (ρ_{k + 1}^{(1)}) [ρ_{k}^{(1)} q_{1}^{(1)} (x) + (1 - ρ_{k}^{(1)}) q_{0}^{(1)} (x)] d x

In addition, we define a function with respect to

ρ_{k}^{(1)}

f (ρ_{k}^{(1)}) = \min \{E \{Δ (0, θ^{(2)}; H) | F_{T^{(1)}}^{(1)}\}, E \{Δ (1, θ^{(2)}; H) | F_{T^{(1)}}^{(1)}\}\}

, for all

k = 0, \dots τ

, there are inequalities about

f (0)

and

f (1)

which follow their respective definitions, i.e.,

f (0) < c + Δ_{k}^{τ} (0),

(14)

and

f (1) < c + Δ_{k}^{τ} (0) .

(15)

Moreover, the monotonicity results of

J_{k}^{τ} (ρ)

can be given by

J_{k}^{τ} (ρ) \leq J_{k + 1}^{τ} (ρ), 0 \leq π \leq 1,

(16)

and

J_{k}^{τ} (ρ) \leq Δ_{k + 1}^{τ} (ρ), 0 \leq π \leq 1,

(17)

since each of the left-hand quantities is a hypo-mundum, on a larger set of stopping times than the corresponding right-hand quantity.

3.3. Optimal Stopping Time

To solve problem (9), we consider the limit

τ \to \infty

, the pointwise limit of

J_{k}^{τ}

exists and is independent of

k

. More specifically, we have

J (ρ) = \lim_{τ \to \infty} J_{k}^{τ} (ρ) = \lim_{τ \to \infty} J_{k}^{τ} (ρ), 0 \leq ρ \leq 1 .

(18)

Theorem 1.

The minimal expected cost on

J (ρ)

satisfies the Bellman equation

J (ρ) = \min \{E \{Δ (0, θ^{(2)}; H)\}, E \{Δ (1, θ^{(2)}; H)\}, c + Δ_{J} (ρ)\}, 0 \leq ρ \leq 1,

(19)

where

Δ_{J} (ρ) = E \{J (ρ_{1})\}, 0 \leq ρ \leq 1

The optimal stopping time is

T_{o p t} = \inf \{k | ρ_{k}^{(1)} \notin (ξ_{L}^{(1)}, ξ_{U}^{(1)})\},

(20)

where a pair of thresholds

(ξ_{L}^{(1)}, ξ_{U}^{(1)})

are described as

ξ_{L}^{(1)} = \sup \{0 \leq ρ \leq \frac{1}{2} | c + Δ_{J} (ρ) = E \{Δ (0, θ^{(2)}; H)\}\},

(21)

and

ξ_{U}^{(1)} = \inf \{1 / 2 \leq ρ \leq 1 | c + Δ_{J} (ρ) = E \{Δ (1, θ^{(2)}; H)\}\},

(22)

Proof of Theorem 1.

Taking the limit of (13) and using (18), (19) follows. The concavity of

J

derives from the limit of concave functions. Inequalities like (14) and (15) also hold. Utilizing these inequalities, the concavity of

Δ_{J}

, and

J (ρ)

, the optimal stopping time is the threshold type, as shown in (20), where the threshold is determined by □

c + Δ_{J} (ξ_{L}^{(1)}) = E \{Δ (0, θ^{(2)}; H)\} |_{\{ρ = ρ_{L}^{(1)}\}},

(23)

and

c + Δ_{J} (ξ_{U}^{(1)}) = E \{Δ (1, θ^{(2)}; H)\} |_{\{ρ = ρ_{U}^{(1)}\}} .

(24)

This establishes the proposition.

3.4. Optimal Decision Rule

Similar to an argument used in the proof of Proposition 7.4 [20], the uniqueness of the limit value function for (9) follows. Moreover, since the optimal thresholds

ξ_{L}^{(1)}

and

ξ_{U}^{(1)}

are coupled from (14) and (15), two simultaneous dynamic programming equations should be solved.

Given a value of

Δ (T^{(2)}, θ^{(2)})

, the optimal local decision rule of the IoT device

S_{1}

is derived, vice versa. That is to say, when two IoT devices achieve their respective optimal decisions for each other’s optimal decision rule. As a result, the global optimal decision rules can be iteratively implemented by continuously fixing the threshold of one IoT device and optimizing the threshold of the other by Theorem 1.

Finally, there are following process at the optimal decision rule of the IoT devices

S_{i}

i = 1, 2

, such as, (1) if

ρ_{k}^{(i)} \leq ξ_{L}^{(i)}

, the decision rule accepts

H_{0}

; (2) if

ρ_{k}^{(i)} \geq ξ_{U}^{(i)}

, the decision rule accepts accept

H_{1}

; (3) if

ξ_{L}^{(i)} \leq ρ_{k}^{(i)} \leq ξ_{U}^{(i)}

, the decision rule continues sampling, where a pair of thresholds

(ξ_{L}^{(i)}, ξ_{U}^{(i)})

at the per-IoT device are obtained by

ξ_{L}^{(i)} = \frac{{\bar{P}}_{m}^{(i)}}{1 - {\bar{P}}_{f}^{(i)}},

(25)

and

ξ_{U}^{(i)} = \frac{1 - {\bar{P}}_{m}^{(i)}}{{\bar{P}}_{f}^{(i)}},

(26)

where

{\bar{P}}_{m}^{(i)}

and

{\bar{P}}_{f}^{(i)}

are the tolerable miss detection probability and the tolerable false alarm probability, respectively.

A similar method can be utilised for the quickest detection problem. In such a problem, each of the IoT devices

S_{j}

sequentially receives observations

\{Z_{k}^{(j)}\}

, then there exists a change point

t

following a geometric distribution with a mass at 0, and correspondingly there is a known marginal density

q_{0}^{(j)}

for

k = 1, \dots, t - 1

and

q_{1}^{(j)}

for

k = t, \dots

. Given the change point, IoT device observations are assumed to be conditionally independent and it is valid within IoT devices and across IoT devices. Now, in order to quickly detect the change point and control the false alarm probability, each IoT device needs to optimally select stopping times

T^{(i)}

(each measurable with respect to their own filtrations

F^{(i)}

) with aim of minimizing

E \{Δ (T^{(1)}, T^{(2)}; t)\}

, where

Δ (T^{(1)}, T^{(2)}; t) = 1_{\{T^{(1)} < t\}} 1_{\{T^{(2)} < t\}} + c_{1} (T^{(1)} - t) 1_{\{T^{(1)} \geq t\}} + + c_{2} (T^{(2)} - t) 1_{\{T^{(2)} \geq t\}}

. Therefore, the optimal solution can be given by

T^{(1)} = \inf \{k | P (t \leq k | F_{k}^{(1)}) \geq ξ_{1}^{*}\},

(27)

and

T^{(2)} = \inf \{k | P (t \leq k | F_{k}^{(2)}) \geq ξ_{2}^{*}\},

(28)

where a pair of optimal thresholds

ξ_{1}^{*}

and

ξ_{2}^{*}

are coupled via a system of two dynamic programming equations. The term

1_{\{T^{(1)} < t\}} 1_{\{T^{(2)} < t\}}

appears in the cost function that couples the solution.

4. Simulation results

In this section, simulation results are introduced to corroborate the correctness and effectiveness of our proposal with respect to the global performance and the average cost from a IoT device. To this end, in 10⁶ spectrum sensing frames, unless otherwise specified, some parameter settings are considered as follows: the number of micro-sensing slots is 20, the probability

ρ

of the hypothesis

H_{1}

is 0.5, the local detection probability and the local false alarm probability are set to be 0.6 and 0.4, respectively. Both of the tolerable false alarm probability and the tolerable false alarm probability varies from 0.01 to 0.3 within an interval of 0.01.

Figure 2 illustrates the relationship of the global false alarm probability

Q_{f}

and the tolerable false alarm probability

{\bar{P}}_{f}

under various tolerable miss detection probabilities. First of all, it can be seen that as the tolerable false alarm probability becomes more relaxed, the global false alarm probability shows a stepwise increase, and the larger the tolerable false alarm probability, the larger the gradient of the step. This is because for a fixed probability, an increase in the tolerable false alarm probability leads to a decrease in the upper threshold

ξ_{U}

, and the sequential detection rule is easier to accept

H_{1}

, which in turn results in an increase in the global false alarm probability. Meanwhile, it is worth noting that on the steps before the global false alarm probability jumps, although the tolerable false alarm probability continues to increase, the global false alarm probability remains unchanged. At this point, an increase in the initial stopping time does not bring about a change in the global false alarm probability, that is, an increase in observation does not bring about a change in the global false alarm probability, and the initial stopping time is the optimal stopping time.

Moreover, the impact of the tolerable miss detection probability on the global false alarm probability can be neglectable at the beginning. That is to say, the thresholds

(ξ_{L}, ξ_{U})

of the sequential detection rule is still not satisfied. But as the tolerable false alarm probability increases, the impact of the tolerable miss detection probability is becoming more and more obvious. To be specific, the larger the tolerable miss detection probability, the faster the global false alarm probability jumps. Apparently, the large the tolerable miss detection probability, the larger the upper threshold

ξ_{U}

, resulting in a more acceptable

H_{1}

Under various tolerable miss detection probabilities, the relationship of the global miss detection probability

Q_{m}

and the tolerable false alarm probability

{\bar{P}}_{f}

is shown in Figure 3. In contrast to Figure 2, the tolerable false alarm probability has a greater effect on the global miss detection probability than the global false alarm probability and the effect is positive. In details, when the tolerable false alarm probability increases from 0.01 to 0.3, correspondingly, the global miss detection probability basically goes down from 0.95 to 0.22. Since the lower threshold

ξ_{L}

increases as the tolerable false alarm probability increases according to (25), the sequential detection rule is prone to accept

H_{0}

, resulting in a decrease of the global miss detection probability. Furthermore, in such an environment, the global miss detection probability of a large tolerable miss detection probability decreases first because it increases the lower threshold

ξ_{L}

, i.e.,

{\bar{P}}_{m} = 0.2

Figure 2. The global false alarm probability vs the tolerable false alarm probability.

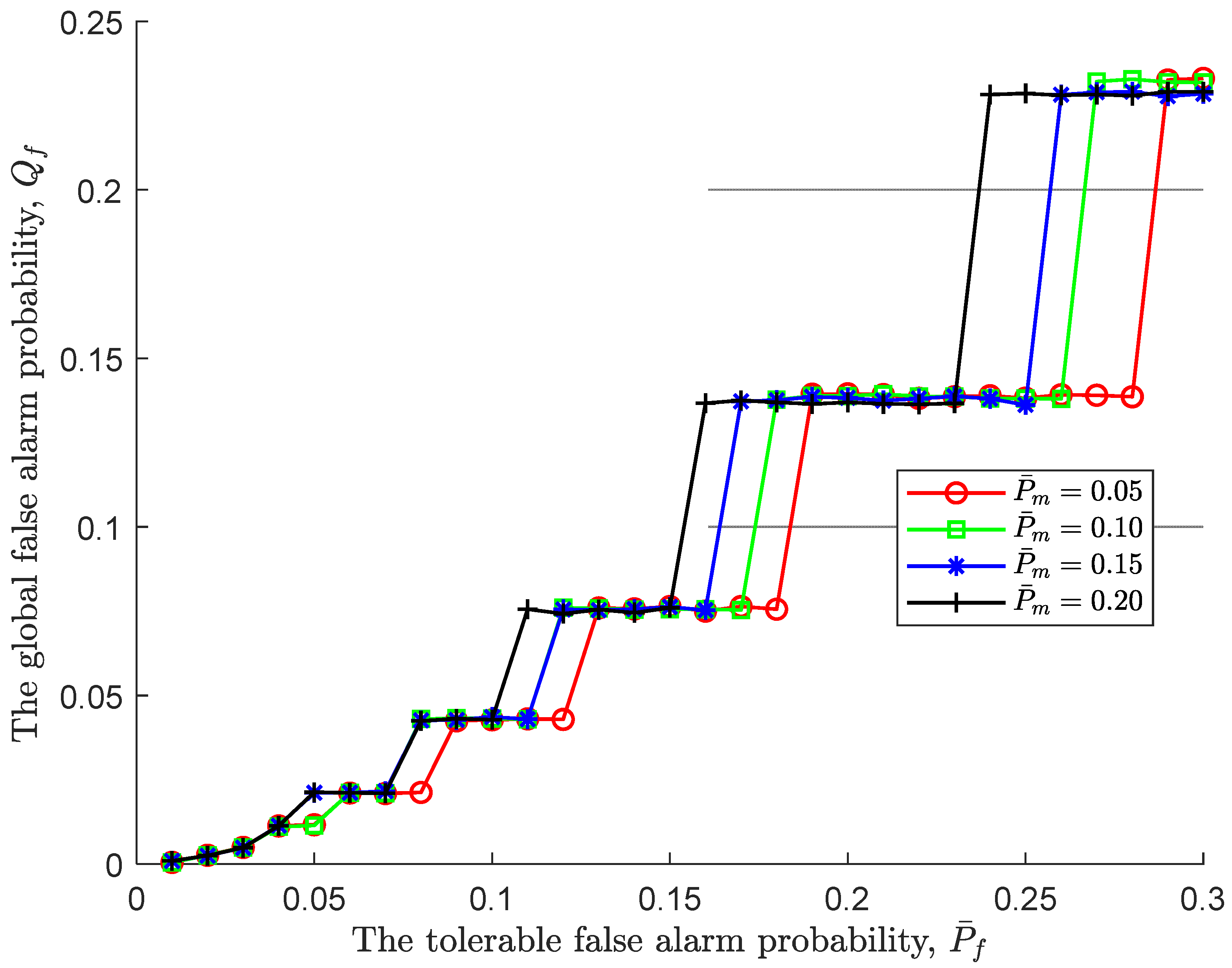
Figure 3. The global miss detection probability vs the tolerable false alarm probability.

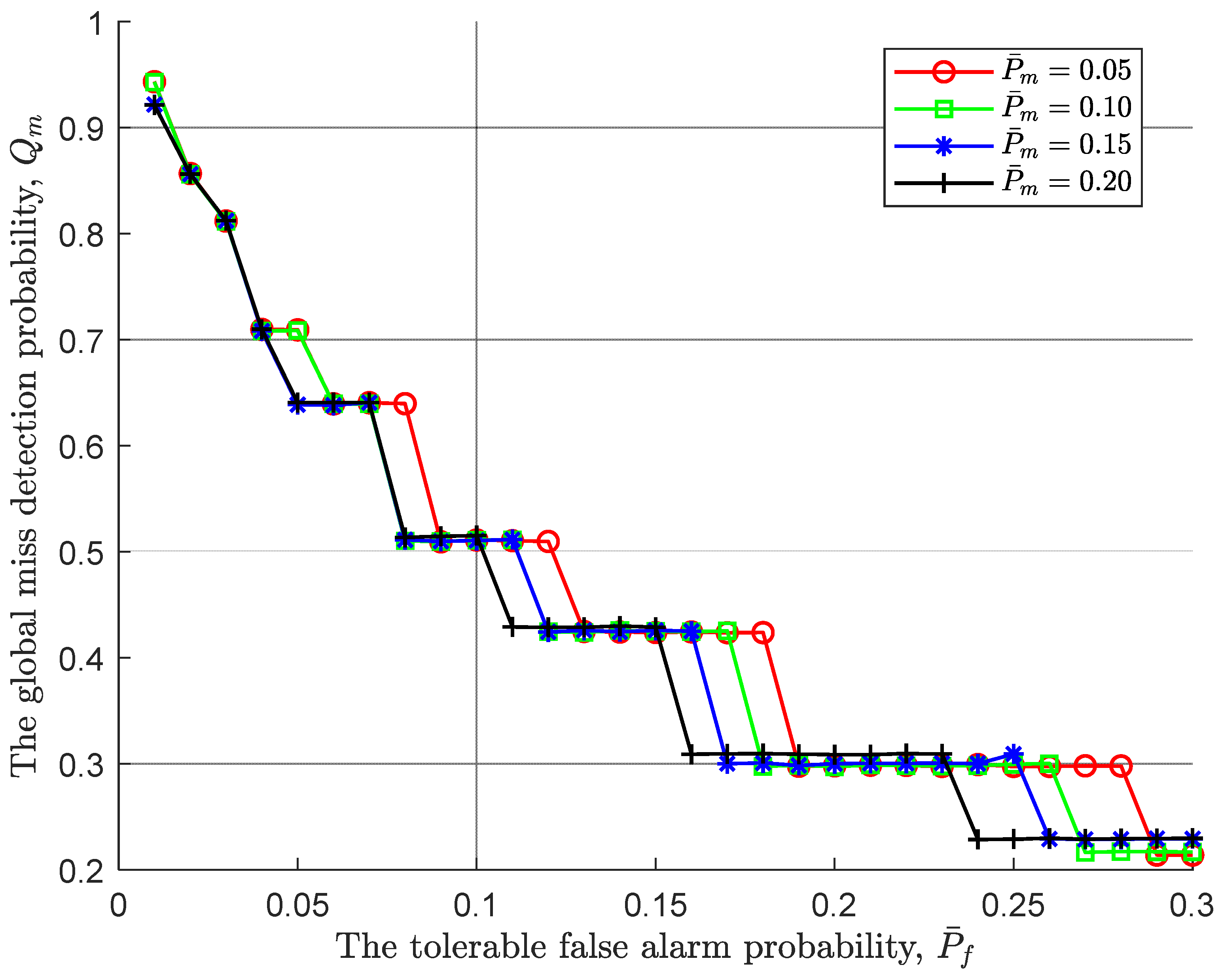
In addition, similar to Figure 2, the steps before the global miss detection probability jumps, although the tolerable false alarm probability continues to increase, the global false alarm probability remains unchanged. At this point, an increase in the initial stopping time does not bring about a change in the global miss detection probability, that is, an increase in observation does not bring about a change in the global miss detection probability, and the initial stopping time is the optimal stopping time.

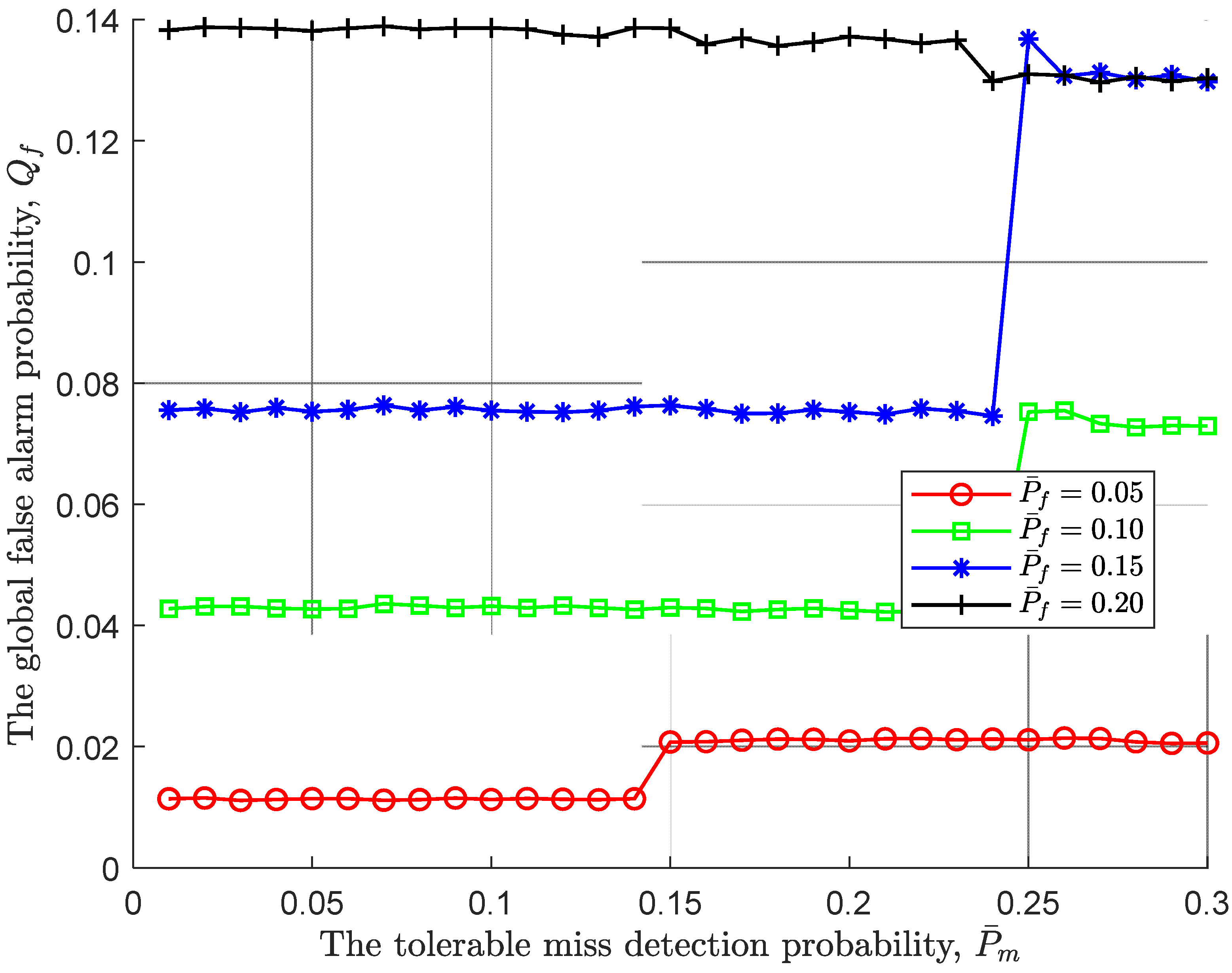
Next, we further take the impact of the tolerable miss detection probability on the global performance given a fixed tolerable false alarm probability into consideration. As displayed in Figure 4, regardless of the tolerable miss detection probability, it is obvious that a large tolerable false alarm probability leads to a low upper threshold

ξ_{U}

, therefore being prone to accept

H_{1}

. However, it also should be noted that as the tolerable miss detection probability increases, the global false alarm probability under different tolerable false alarm has jitter at different positions, such as jitter up at

{\bar{P}}_{f} = 0.05, 0.1, 02

and jitter down when

{\bar{P}}_{f} = 0.2

. This is not surprise, and is a direct of that a pair of tolerable probabilities simultaneously change, and the decision condition is reached within a certain stopping time.

Figure 4. The global false alarm probability vs the tolerable miss detection probability.

Similar to the global miss detection probability of Figure 4, given the tolerable false alarm probability, the positive impact of the tolerable miss detection probability is illustrated in Figure 5. In particular, the trend of the global miss detection probability is exactly the opposite to that of the global false alarm probability and the change interval is larger. There is no doubt that, the tolerable miss detection probability makes the lower threshold

ξ_{L}

smaller so that

H_{1}

is easier to accept.

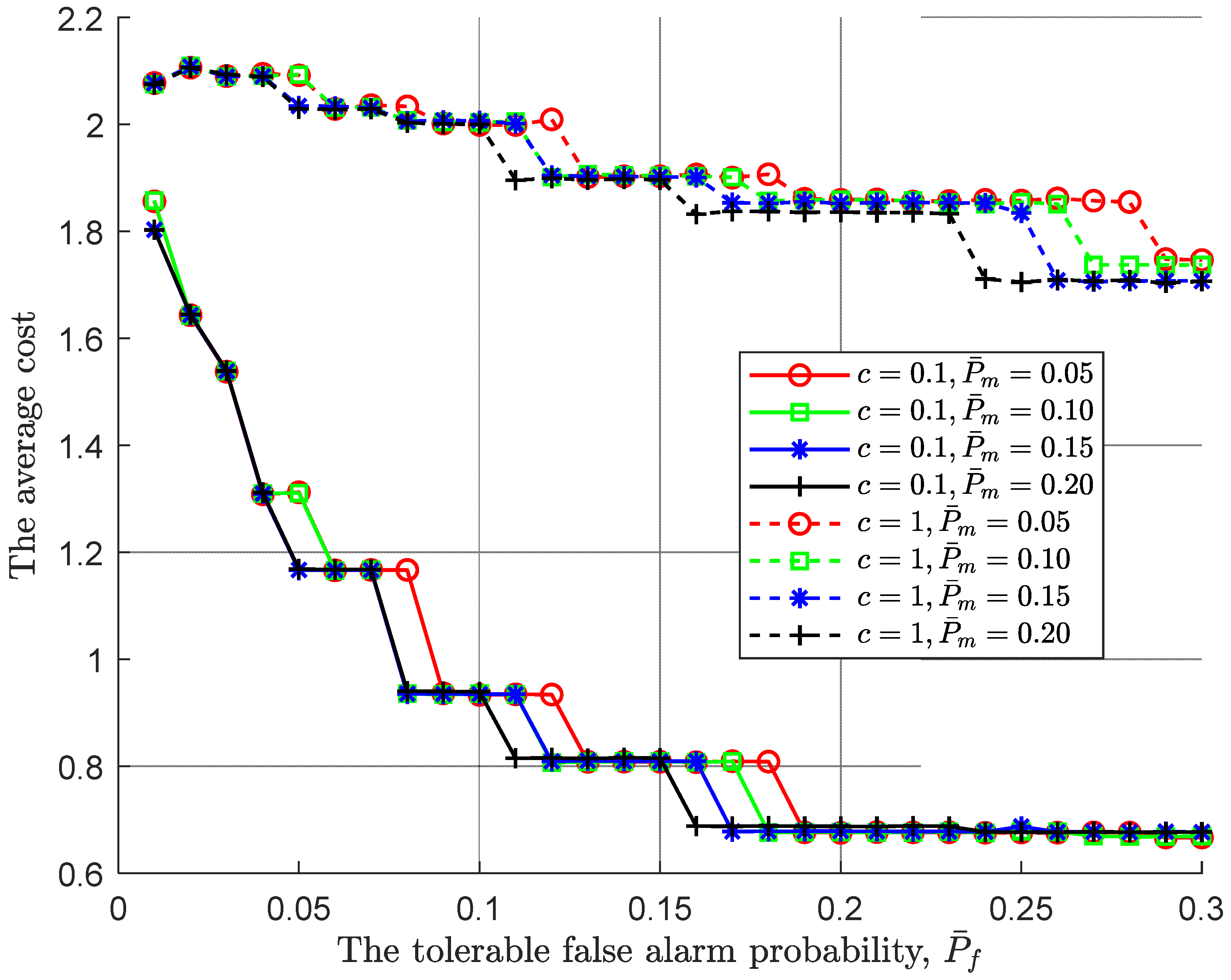
Following the joint impact of the tolerable performance metrics on the global performance, we further simulate the optimal cost of the tolerable performance under various costs of each observation taken, where the cost of each observation taken

c

is set to be 0.1 and 1. As shown in Figure 6, for a pair of fixed tolerable performance, the larger cost of each observation taken

c

, the larger the average cost. Moreover, as the tolerable false alarm probability increases, the average cost decreases. This is to say, an increasing tolerable false alarm probability makes the lower/upper threshold larger/smaller, resulting in that the global decision is difficult to be made. Consequently, the stopping time increases. However, the increasing tolerable false alarm probability also makes the global miss detection probability decrease, as shown in Figure 3. As a result, the global miss detection probability dominates the average cost because the cost about the miss detection decreases.

Figure 5. The global miss detection probability vs the tolerable miss detection probability.

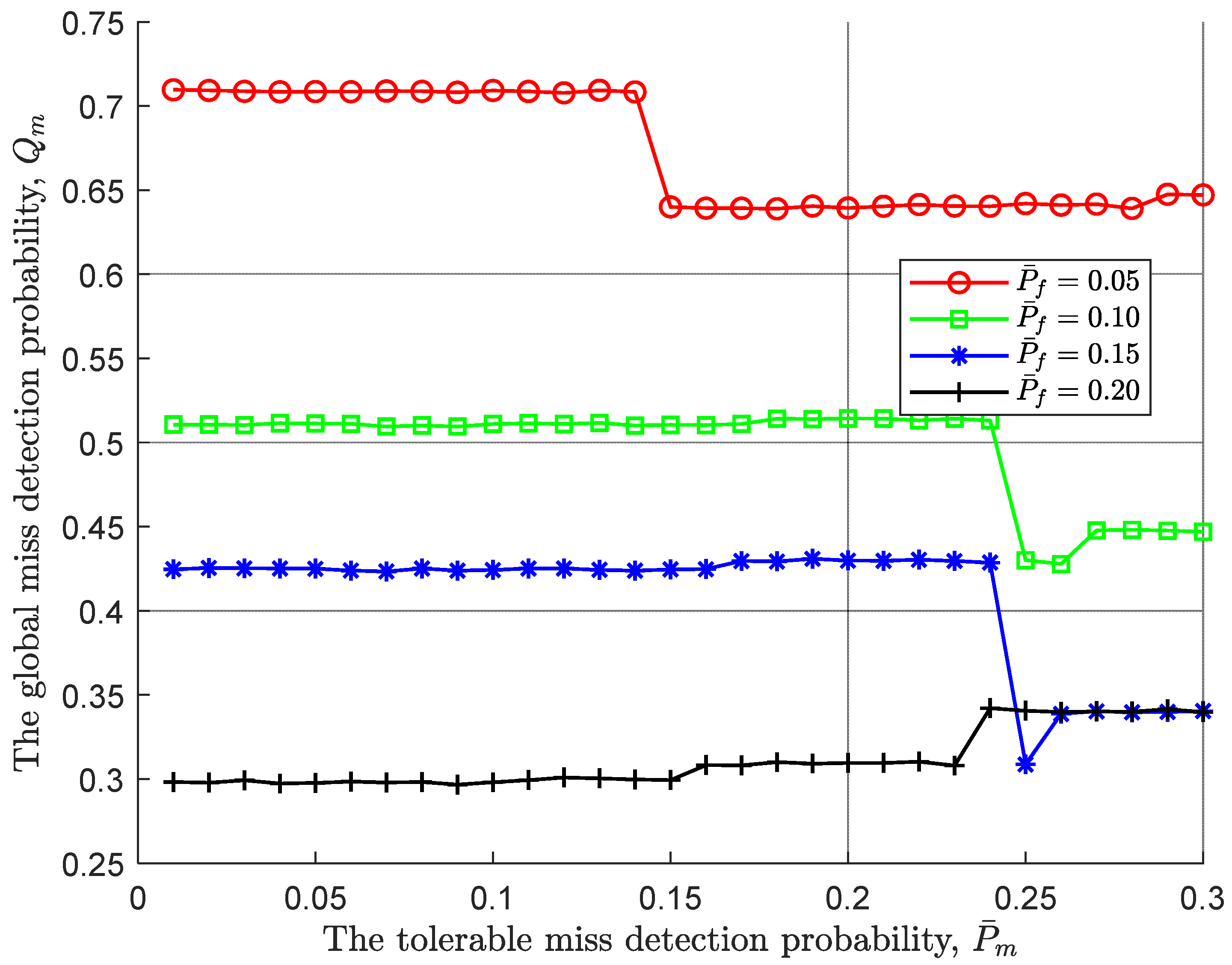
Figure 6. The average cost vs the tolerable false alarm probability under various costs of each observation taken.

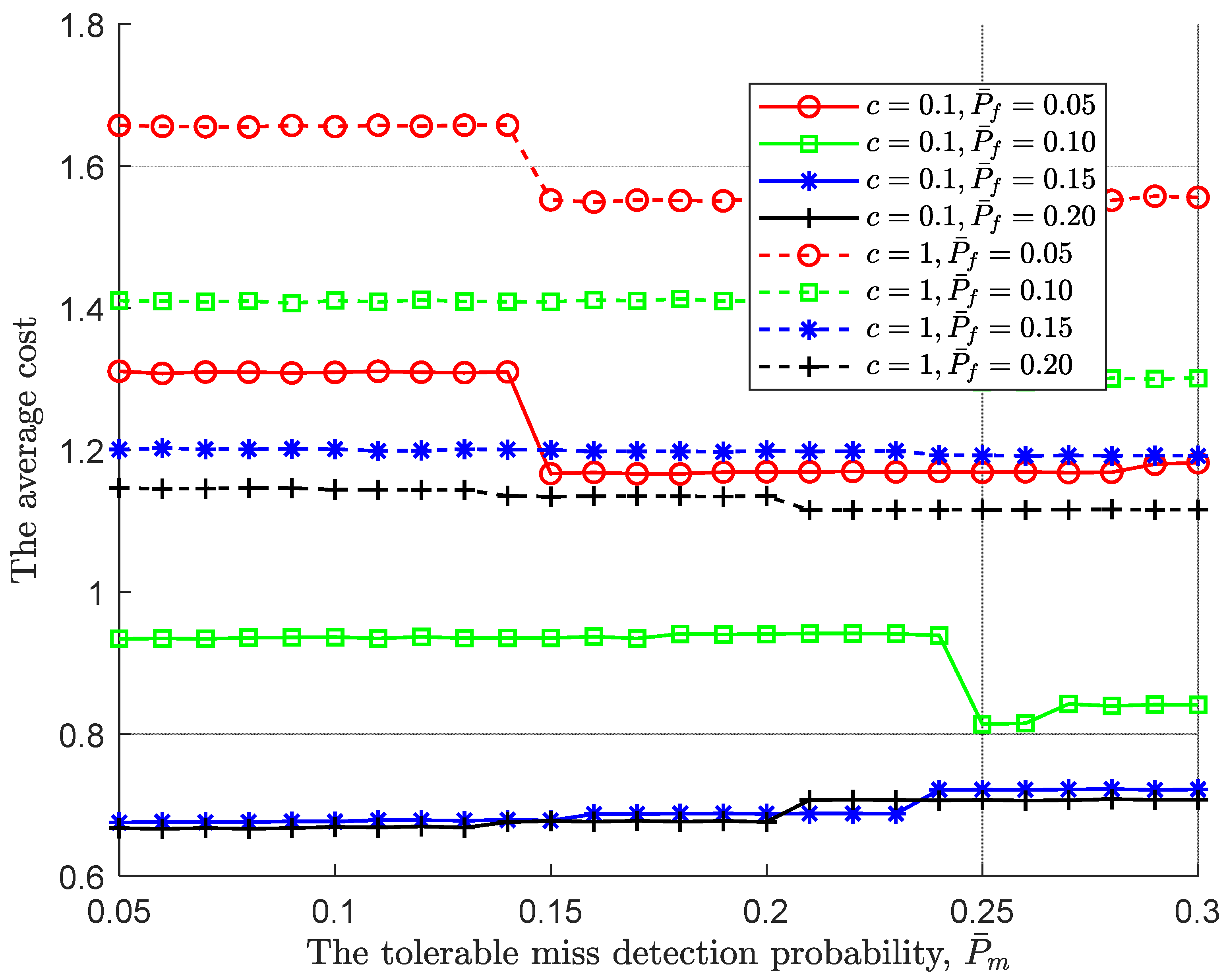
As with Figure 6, the larger cost of each observation taken results in a lager average cost in Figure 7. Following the global miss detection probability in Figure 5, the average cost follows it. The simulation result also confirms once again that the global miss detection dominates the average cost. In summary, following PBPO methodology, the optimal sequential detection rule can be reached as the sensing environments to minimize the cost at a IoT device.

5. Conclusions

In this article, we delved into the distributed sequential detection rule for CSS in a cognitive IoT. Consequently, we first establish a spectrum sensing model in the periodic spectrum sensing frame structure and propose a sequential detection framework. On basis of this, we further define the stopping time and cost function for a IoT device and propose an optimization problem about the average cost. Moreover, PBPO methodology is applied to solve such a finite horizon problem, thereby analysing the stopping time for the optimal sequential detection. Finally, a series of numerical simulation results show that correctness and effectiveness of our proposed sequential detection rule in terms of the stopping time and thresholds.

Author Contributions

Conceptualization, J. W.; methodology, J.W.; software, J.W.; validation, J.W.; formal analysis, J.W.; investigation, J.W.; resources, J.W.; data curation, J.W.; writing—original draft preparation, J.W.; writing—review and editing, J.W. and M. D.; visualization, J.W.; supervision, J.W., Z.Q., M.D., J.B., X.X., and W.C.; project administration, J.W. and J.B.; funding acquisition, J.W. and J. B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China under Grant No. 62201186, Open Fund of Key Laboratory of Flight Techniques and Flight Safety, CAAC (No. FZ2022KF12), Open Research Fund of National Mobile Communications Research Laboratory, Southeast University (No. 2022D16), and National Natural Science Foundation of China under Grant No. U1809201.

Conflicts of Interest

The authors declare no conflict of interest.

References

Nasser, A.; Al Haj Hassan, H.; Abou Chaaya, J.; Mansour, A.; Yao, K.C. Spectrum sensing for cognitive radio: Recent advances and future challenge. Sensors 2021, 21, 2408. [Google Scholar] [CrossRef] [PubMed]
Arjoune, Y.; Kaabouch, N. A comprehensive survey on spectrum sensing in cognitive radio networks: Recent advances, new challenges, and future research directions. Sensors 2019, 19, 126. [Google Scholar] [CrossRef] [PubMed]
Liu, X.; Jia, M.; Zhou, M.; Wang, B.; Durrani, T.S. Integrated cooperative spectrum sensing and access control for cognitive industrial Internet of Things. IEEE Internet of Things Journal 2023, 10, 1887–1896. [Google Scholar] [CrossRef]
Gharib, A.; Ejaz, W.; Ibnkahla, M. Distributed spectrum sensing for iot networks: Architecture, challenges, and learning. IEEE Internet of Things Magazine 2021, 4, 66–73. [Google Scholar] [CrossRef]
Zhu, R.; Zhang, X.; Liu, X.; Shu, W.; Mao, T.; Jalaian, B. ERDT: Energy-efficient reliable decision transmission for intelligent cooperative spectrum sensing in industrial IoT. IEEE Access 2015, 3, 2366–2378. [Google Scholar] [CrossRef]
Ansere, J.A.; Han, G.; Wang, H.; Choi, C.; Wu, C. A reliable energy efficient dynamic spectrum sensing for cognitive radio IoT networks. IEEE Internet of Things Journal 2019, 6, 6748–6759. [Google Scholar] [CrossRef]
Wan, R.; Wu, M.; Hu, L.; Wang, H. Energy-efficient cooperative spectrum sensing scheme based on spatial correlation for cognitive internet of things. IEEE Access 2020, 8, 139501–139511. [Google Scholar] [CrossRef]
Miah, M.S.; Hossain, M.A.; Ahmed, K.M.; Rahman, M.M.; Calhan, A. An energy efficient cooperative spectrum sensing for cognitive radio-internet of things with interference constraints. 10 February 2021, PREPRINT (Version 1) available at Research Square, 10 February. [CrossRef]
Dao, N.N.; Na, W.; Tran, A.T.; Nguyen, D.N.; Cho, S. Energy-efficient spectrum sensing for IoT devices. IEEE Systems Journal 2020, 15, 1077–1085. [Google Scholar] [CrossRef]
Long, Y.; Li, Y.; Ju, H.; He, R.; Fang, X. Throughput optimization in energy harvesting based cognitive iot with cooperative sensing. 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Helsinki, Finland, 2021; pp. 1–5. [Google Scholar] [CrossRef]
Abbas, G.; Abbas, Z.H.; Waqas, M.; Hassan, A.K. Scalable learning-based heterogeneous multi-band multi-user cooperative spectrum sensing for distributed IoT systems. Journal of Network and Computer Applications 2020, 164, 102686. [Google Scholar] [CrossRef]
Gharib, A.; Ejaz, W.; Ibnkahla, M. Integrated cooperative spectrum sensing and access control for cognitive industrial Internet of Things. IEEE Open Journal of the Communications Society 2020, 1, 1066–1083. [Google Scholar] [CrossRef]
Ejaz, W.; Ibnkahla, M. Multiband spectrum sensing and resource allocation for IoT in cognitive 5G networks. IEEE Internet of Things Journal 2017, 5, 150–163. [Google Scholar] [CrossRef]
Zhang, L.; Liang, Y.C. Joint spectrum sensing and packet error rate optimization in cognitive IoT. IEEE Internet of Things Journal 2019, 6, 7816–7827. [Google Scholar] [CrossRef]
Miah, M.S.; Ahmed, K.M.; Islam, M.K.; Mahmud, M.A.R.; Rahman, M.M.; Yu, H. Enhanced sensing and sum-rate analysis in a cognitive radio-based internet of things. Sensors 2020, 20, 2525. [Google Scholar] [CrossRef] [PubMed]
Lu, W.; Hu, S.; Liu, X.; He, C.; Gong, Y. Incentive mechanism based cooperative spectrum sharing for OFDM cognitive IoT network. IEEE Transactions on Network Science and Engineering 2019, 7, 662–672. [Google Scholar] [CrossRef]
Gao, S.; Zhang, N.; Kang, G. Improved cooperative spectrum sensing scheme using truncated SPRT in internet of things. 2019 IEEE 2nd International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, China, 2019; pp. 89–93. [Google Scholar] [CrossRef]
Wu, J.; Li, P.; Zhang, J.; Chen, Z.; Bao, J. SPRT-based cooperative spectrum sensing with performance requirements in cognitive unmanned aerial vehicle networks (CUAVNs). Sequential Analysis 2022, 41, 53–67. [Google Scholar] [CrossRef]
Liang, Y.C.; Zeng, Y.; Peh, E.C.; Hoang, A.T. Sensing-throughput tradeoff for cognitive radio networks. IEEE transactions on Wireless Communications 2008, 7, 1326–1337. [Google Scholar] [CrossRef]
Poor, H.V.; Hadjiliadis, O. Quickest detection; Cambridge University Press: London, UK, 2008. [Google Scholar] [CrossRef]
Varshney, P.K. Distributed detection and data fusion; Springer Science Business Media: New York, USA, 1996. [Google Scholar]

Figure 1. The periodic spectrum sensing frame structure of a cognitive IoT.

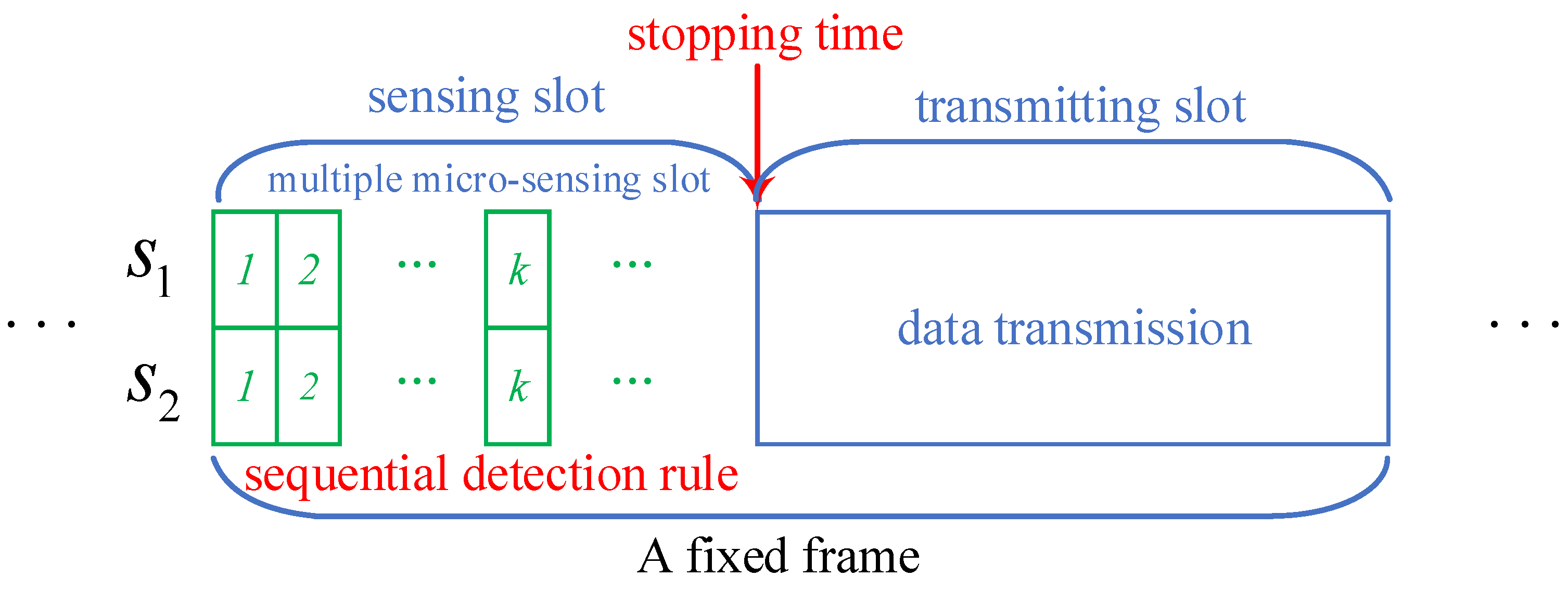
Figure 7. The average cost vs the tolerable miss detection probability under various costs of each observation taken.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Distributed Sequential Detection for Cooperative Spectrum Sensing in Cognitive Internet of Things

Abstract

1. Introduction

2. Materials and Methods

2.1. Spectrum Sensing Model

2.2. Sequential Detection

3. Disributed Sequential Detection

3.1. Problem Formulation

3.2. Preliminary Analysis

3.3. Optimal Stopping Time

3.4. Optimal Decision Rule

4. Simulation results

5. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe