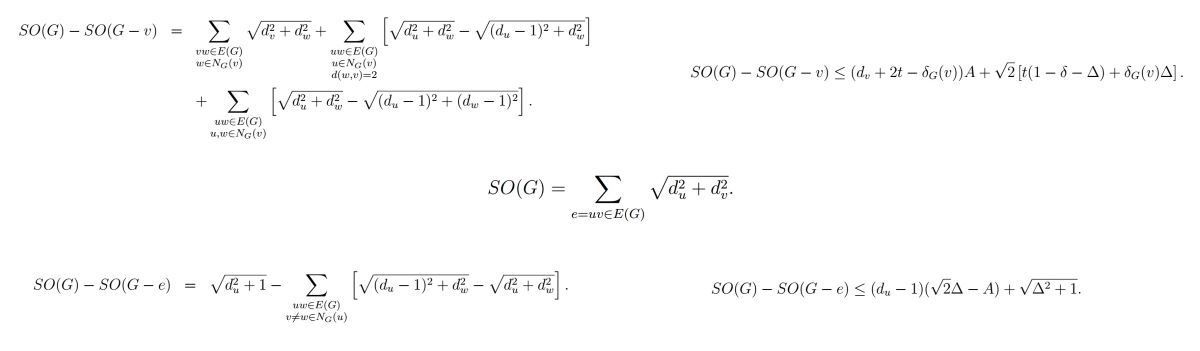Prerpints.org logo
Preprint
Article

The Effect of Vertex and Egde Removal on Sombor Index

Altmetrics

Downloads

127

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 December 2023

Posted:

26 December 2023

You are already at the latest version

Alerts
Abstract
Sombor index was recently defined in 2021 as a new vertex degree based topological index by Gutman and has received great attention of mathematicians and chemists. In this work, we determine how much the Sombor index is effected when we delete a vertex or an edge from a graph. Using the formulae obtained here successively, one can calculate the Sombor indices of large graphs by means of Sombor indices of smaller graphs which are obtained by deletion of vertices or edges.
Keywords: 
Subject: Computer Science and Mathematics  -   Discrete Mathematics and Combinatorics

MSC:  05C07; 05C10; 05C30; 68R10

1. Introduction

Throughout this paper, we let G = ( V , E ) be a simple graph with the vertex set V ( G ) = { v 1 , v 2 , ⋯ , v n } and edge set E ( G ) = { v i v j : v i , v j ∈ V ( G ) } . We call | V ( G ) | = n and | E ( G ) | = m to be the order and the size of G. Sometimes, we use G ( n , m ) in place of G to emphasize the order and size of G. By simpleness, we mean that we do not allow loops or multiple edges. If v i and v j are adjacent vertices of G and if the edge e connects them, this situation will be denoted by e = v i v j . In such a case, the vertices v i and v j are called adjacent vertices and the edge e is said to be incident with v i and v j . Adjacency and incidency play a very important role in the spectral graph theory, a sub-area of graph theory dealing with linear algebraic study of graphs and graph energy. For any vertex v ∈ V ( G ) , we denote the degree of v by d G ( v ) or briefly d v . The smallest and biggest vertex degrees in a graph will be denoted by δ and Δ , respectively. Neighbourhood of a vertex is defined as N G ( u ) = { v ∈ V ( G ) : v is adjacent to u in G } . Neighbourhood degree sum of a vertex u is defined as δ G ( u ) = ∑ v ∈ N G ( u ) d G ( v ) . Let δ G ( v ) be the sum of all vertex degrees in the neighbourhood of v.
Graph theory is becoming increasingly popular due to its possible applications in Chemistry, Pharmacology, Physics, Neuroscience, Network Science and many other areas. Each day, new areas are added to the list. This popularity is due to the fact that a molecule or a social science application can be modeled by a graph. For molecules, one can obtain such a graph by replacing each atom by a vertex and adding an edge between two atoms if there is a chemical bond between those atoms. Graphs obtained in such a way are called chemical (molecular) graphs. Once modeled, we can study this graph by mathematical methods using the existing combinatorial, number theoretical, topological, linear algebraic, etc. methods. At the end of such mathematical calculations, we obtain a number which is characteristic to the graph under consideration. Such numbers are actually invariants and they remain the same under isomorphism. The main step is to establish some exact result, an upper or lower bound, or at least some regression between the obtained mathematical number and same physico-chemical property of the molecule. This step brings together Chemistry and Mathematics. The oldest known example is the Wiener index introduced in 1947 by Chemist Harold Wiener to determine the boiling points of some alkane isomers. Today there are more than 3000 such mathematical formulae to study properties of molecules. Mathematicians call them graph theoretical indices or topological graph indices and Chemists call them molecular descriptors. Today, serious part of research related to graph theory is published on such descriptors and indices.
A recently introduced topological index is the Sombor index. It was defined in [9] by Ivan Gutman in 2021 by the formula
S O ( G ) = ∑ e = u v ∈ E ( G ) d u 2 + d v 2 .
Gutman studied some mathematical and chemical properties of this index in [8,11]. In parallel with these studies, many other researchers also considered various mathematical properties of Sombor index in [4,5,13,15,16,17,19,20,21,23,26]. Chemical applications of the Sombor index have been studied in [1,2,3,6,7,18,22,24] in detail. After defining the Sombor index, its modified version was put forward in [14], and studied in [10,12,25,27].
For an r-regular graph G, Sombor index is equal to S O ( G ) = 2 m r . Also as the sum of the vertex degrees is equal to twice the number of edges, we can restate this as S O ( G ) = 2 2 m 2 / n .
In this paper, we use the ingenious methods which are used in mathematics to calculate large mathematical objects by means of smaller objects which are easier to calculate. These methods are vertex and edge removal. Here we shall determine how much Sombor index changes when a vertex or an edge is deleted from a graph.

2. Effect of vertex removal on Sombor index

In this section, we study how much Sombor index changes when a vertex is deleted from a graph. According to the enumarations we do with different graphs, there are two different cases where the vertex to be deleted is pendant or not. So we shall see those two cases seperately below.
Theorem 1.
Let v ∈ V ( G ) be of degree d v > 1 . Then
S O ( G ) − S O ( G − v ) = ∑ v w ∈ E ( G ) w ∈ N G ( v ) d v 2 + d w 2 + ∑ u w ∈ E ( G ) u ∈ N G ( v ) d ( w , v ) = 2 d u 2 + d w 2 − ( d u − 1 ) 2 + d w 2 + ∑ u w ∈ E ( G ) u , w ∈ N G ( v ) d u 2 + d w 2 − ( d u − 1 ) 2 + ( d w − 1 ) 2 .
Proof. 
From the definition of Sombor index, we can partition the edges of the graph G into four families: i) u w ∈ E ( G ) such that v ≠ u , w ∉ N G ( v ) , ii) u w ∈ E ( G ) such that u ∈ N G ( v ) , d ( w , v ) = 2 , iii) u w ∈ E ( G ) such that u , w ∈ N G ( v ) , and iv) v w ∈ E ( G ) such that w ∈ N G ( v ) . According to this edge partition, we can alternatively restate the Sombor index of graph G as
S O ( G ) = ∑ u w ∈ E ( G ) v ≠ u , w ∉ N G ( v ) d u 2 + d w 2 + ∑ u w ∈ E ( G ) u ∈ N G ( v ) d ( w , v ) = 2 d u 2 + d w 2 + ∑ u w ∈ E ( G ) u , w ∈ N G ( v ) d u 2 + d w 2 + ∑ v w ∈ E ( G ) w ∈ N G ( v ) d v 2 + d w 2
as conveniently. If we remove a non-pendant vertex v from the graph G, then the edge partition of G − v would be i) u w ∈ E ( G ) such that v ≠ u , w ∉ N G ( v ) , ii) u w ∈ E ( G ) such that u ∈ N G ( v ) , d ( w , v ) = 2 , and iii) u w ∈ E ( G ) such that u , w ∈ N G ( v ) . That is, only the edges of type iv) will disappear. Hence the Sombor index of the remaining graph G − v is
S O ( G − v ) = ∑ u w ∈ E ( G ) v ≠ u , w ∉ N G ( v ) d u 2 + d w 2 + ∑ u w ∈ E ( G ) u ∈ N G ( v ) d ( w , v ) = 2 ( d u − 1 ) 2 + d w 2 + ∑ u w ∈ E ( G ) u , w ∈ N G ( v ) ( d u − 1 ) 2 + ( d w − 1 ) 2 .
Hence the desired result follows. □
Using this theorem, we can directly deduce an upper bound for the change in Sombor index when a non-pendant vertex is deleted from a graph:
Corollary 1.
Let v ∈ V ( G ) be of degree d v > 1 . Let δ G ( v ) be as above. Let A = 2 δ 2 − 2 δ + 1 . If there are t pairs of vertices in the neighbourhood of v forming an edge of G, then
S O ( G ) − S O ( G − v ) ≤ ( d v + 2 t − δ G ( v ) ) A + 2 t ( 1 − δ − Δ ) + δ G ( v ) Δ .
Proof. 
From Theorem 1
S O ( G ) − S O ( G − v ) ≤ ∑ v w ∈ E ( G ) w ∈ N G ( v ) 2 Δ + ∑ u w ∈ E ( G ) u ∈ N G ( v ) d ( w , v ) = 2 2 Δ − ( δ − 1 ) 2 + δ 2 + ∑ u w ∈ E ( G ) u , w ∈ N G ( v ) 2 Δ − 2 ( δ − 1 ) = d v 2 Δ + δ G ( v ) − d v − 2 t 2 Δ − 2 δ 2 − 2 δ + 1 + t 2 ( Δ − δ + 1 ) = d v 2 Δ + δ G ( v ) 2 Δ − δ G ( v ) 2 δ 2 − 2 δ + 1 − d v 2 Δ + d v 2 δ 2 − 2 δ + 1 − 2 2 t Δ + 2 t 2 δ 2 − 2 δ + 1 + t 2 Δ − t δ 2 + t 2 .
Since A = 2 δ 2 − 2 δ + 1 , we have
S O ( G ) − S O ( G − v ) ≤ A ( d v + 2 t − δ G ( v ) ) + 2 ( t ( 1 − δ − Δ ) + δ G ( v ) Δ ) .
□
Corollary 2.
Let G be a tree and let v ∈ V ( G ) be of degree d v > 1 . Let δ G ( v ) be as above. If there are t pairs of vertices in the neighbourhood of v forming an edge of G, then
S O ( G ) − S O ( G − v ) ≤ d v + 2 t − δ G ( v ) + 2 Δ ( δ G ( v ) − t ) .
The proof depends on the fact that in a tree, δ = 1 and hence A = 1 . Note that Corollary 2 is also valid when the graph has at least one pendant vertex but is not a tree.
Now, we give results for deleting a pendant vertex from a graph:
Theorem 2.
If v ∈ V ( G ) is a pendant vertex, then
S O ( G ) − S O ( G − v ) = 1 + d w 2 + ∑ u w ∈ E ( G ) u ∈ N G ( v ) d ( w , v ) = 2 d u 2 + d w 2 − ( d u − 1 ) 2 + d w 2 .
That is, the formula in Theorem 1 simplifies.
Corollary 3.
If v ∈ V ( G ) is a pendant vertex and u is its support vertex, then
S O ( G ) − S O ( G − v ) ≤ 2 Δ d u − ( d u − 1 ) A
where A is given in Corollary 1.
Proof. 
Using Theorem 2, as A = 2 δ 2 − 2 δ + 1 , we have
S O ( G ) − S O ( G − v ) = 1 + d w 2 + ∑ u w ∈ E ( G ) u ∈ N G ( v ) d ( w , v ) = 2 d u 2 + d w 2 − ( d u − 1 ) 2 + d w 2 ≤ ∑ u w ∈ E ( G ) w ∈ N G ( v ) 2 Δ + ∑ u w ∈ E ( G ) u ∈ N G ( v ) d ( w , v ) = 2 2 Δ − ( δ − 1 ) 2 + δ 2 ≤ 2 Δ d v + ( d u − 1 ) 2 Δ − A .
Hence the result follows. □

3. Effect of edge removal on Sombor index

In this section, we will determine the change on Sombor index when we remove an edge from graph G. First we check the effect of deleting a pendant edge.
Theorem 3.
If e = u v ∈ E ( G ) be a pendant edge with pendant vertex v, then
S O ( G ) − S O ( G − e ) = d u 2 + 1 − ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) ( d u − 1 ) 2 + d w 2 − d u 2 + d w 2 .
Proof. 
From the definition of Sombor index, we can reorganize the Sombor index of the graph G as
S O ( G ) = ∑ r s ∈ E ( G ) u ≠ r , s ∉ N G ( u ) d r 2 + d s 2 + ∑ u w ∈ E ( G ) w ∈ N G ( u ) d u 2 + d w 2 = ∑ r s ∈ E ( G ) u ≠ r , s ∉ N G ( u ) d r 2 + d s 2 + ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) d u 2 + d w 2 + d u 2 + 1 .
If we remove a pendant edge e = u v with pendant vertex v, then we get
S O ( G − e ) = ∑ r s ∈ E ( G ) u ≠ r , s ∉ N G ( u ) d r 2 + d s 2 + ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) ( d u − 1 ) 2 + d w 2 .
Hence the result follows. □
Theorem 3 implies that it is possible to obtain the maximum value of the decrease in the Sombor index when a pendant edge is deleted from the graph:
Corollary 4.
For a graph G and a pendant edge e = u v with pendant vertex v, we have
S O ( G ) − S O ( G − e ) ≤ ( d u − 1 ) ( 2 Δ − A ) + Δ 2 + 1 .
Proof. 
By Theorem 3, we have
S O ( G ) − S O ( G − e ) = ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) d u 2 + d w 2 − ( d u − 1 ) 2 + d w 2 + d u 2 + 1 ≤ ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) ( 2 Δ − A ) + Δ 2 + 1 .
Since there are d u − 1 edges in the neighbourhood of the vertex u, the result follows. □
Next result gives a similar formula for the amount of change in the Sombor index of a graph when a non-pendant edge is deleted:
Theorem 4.
Let e = u v ∈ E ( G ) be a non-pendant edge. Then
S O ( G ) − S O ( G − e ) = d u 2 + d v 2 − ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) ( d u − 1 ) 2 + d w 2 − d u 2 + d w 2 − ∑ v w ∈ E ( G ) u ≠ w ∈ N G ( v ) ( d v − 1 ) 2 + d w 2 − d v 2 + d w 2 .
Proof. 
By the definition of Sombor index, we can group the edges in G as follows:
S O ( G ) = ∑ r s ∈ E ( G ) u ≠ r ∉ N G ( u ) v ≠ s ∉ N G ( v ) d r 2 + d s 2 + ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) d u 2 + d w 2 + ∑ v w ∈ E ( G ) u ≠ w ∈ N G ( v ) d v 2 + d w 2 + d u 2 + d v 2 .
If we remove a non-pendant edge e from the graph G, Sombor index of graph G − e becomes
S O ( G − e ) = ∑ r s ∈ E ( G ) u ≠ r ∉ N G ( u ) v ≠ s ∉ N G ( v ) d r 2 + d s 2 + ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) ( d u − 1 ) 2 + d w 2 + ∑ v w ∈ E ( G ) u ≠ w ∈ N G ( v ) ( d v − 1 ) 2 + d w 2 .
Hence the result is obtained. □
The following result giving the maximum amount of change in the Sombor index of a graph in terms of the size of the graph when a non-pendant edge is deleted from the graph can be deduced from the above results:
Corollary 5.
Let e be a non-pendant edge in G. Then
S O ( G ) − S O ( G − e ) ≤ 2 m Δ − ( m − 1 ) A .
Proof. 
We have
S O ( G ) − S O ( G − e ) = ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) d u 2 + d w 2 − ( d u − 1 ) 2 + d w 2 + ∑ v w ∈ E ( G ) u ≠ w ∈ N G ( v ) d v 2 + d w 2 − ( d v − 1 ) 2 + d w 2 + d u 2 + d v 2 ≤ ∑ u w ∈ E ( G ) v ≠ w ∈ N G ( u ) 2 Δ − A + ∑ v w ∈ E ( G ) u ≠ w ∈ N G ( v ) 2 Δ − A + 2 Δ = ( m − 1 ) 2 Δ − A + 2 Δ
giving the required result. □
In many calculations with graphs, cut vertices and bridges help us to do the calculations much easier as they partition the graph into blocks which are much smaller than the given graph. In the following result, we use this method to calculate Sombor index of some large graphs in terms of Sombor indices of the blocks of the given graphs.
Theorem 5.
Let G be a graph and let e = u v be a bridge in G. Let d G u = k + 1 and d G v = t + 1 . Then
S O ( G ) − S O ( G − e ) = ( k + 1 ) 2 + ( t + 1 ) 2 + ∑ i = 1 k ( k + 1 ) 2 + d u i 2 − k 2 + d u i 2 + ∑ j = 1 t ( t + 1 ) 2 + d v j 2 − t 2 + d v j 2 .
Proof. 
Let the two blocks of G connected with the bridge e be G 1 and G 2 . Let the neighbours of u apart from v be u 1 , u 2 , ⋯ , u k and let the neighbours of v apart from u be v 1 , v 2 , ⋯ , v t . Let A = { x y | x , y ∈ V ( G 1 ) , x , y ≠ u } and B = { x y | x , y ∈ V ( G 1 ) , x , y ≠ v } . We can organize S O ( G ) as follows:
S O ( G ) = d u 2 + d v 2 + ∑ i = 1 k d u 2 + d u i 2 + ∑ j = 1 t d v 2 + d v j 2 + ∑ x y ∈ A ∪ B d x 2 + d y 2 .
Similarly
S O ( G − e ) = ∑ i = 1 k ( d u − 1 ) 2 + d u i 2 + ∑ j = 1 t ( d v − 1 ) 2 + d v j 2 + ∑ x y ∈ A ∪ B d x 2 + d y 2 .
Hence the required result is obtained easily after some calculations. □
Theorem 5 can be generalized to some number of bridges seperating some number of blocks.
The difference in Theorem 5 can also be stated in terms of the Sombor indices of the two blocks G 1 and G 2 as follows. The proof is omitted as it is similar to the previous ones:
Corollary 6.
Let G be a graph and let e = u v be a bridge in G as in Theorem 5. Let d G u = k + 1 and d G v = t + 1 . Then
S O ( G ) − S O ( G − e ) = ( k + 1 ) 2 + ( t + 1 ) 2 + ∑ i = 1 k ( k + 1 ) 2 + d u i 2 + ∑ j = 1 t ( t + 1 ) 2 + d v j 2 + ∑ x y ∈ A ∪ B d x 2 + d y 2 − S O ( G 1 ) − S O ( G 2 ) .
In the following result, we delete a path bridge between two blocks of a graph instead of deleting a bridge:
Theorem 6.
Let G be a graph and let e = u v be a path bridge of length r. That is, between u and v, there are r vertices w 1 , w 2 , ⋯ , w r all having degree 2 in G. Let C = { w 1 , w 2 , ⋯ , w r } , d G u = k + 1 and d G v = t + 1 . Then the change in the Sombor index of G when the set C is deleted from G is
S O ( G ) − S O ( G − C ) = ( k + 1 ) 2 + 4 + ( t + 1 ) 2 + 4 + 2 ( r − 1 ) 2 + ∑ i = 1 k ( k + 1 ) 2 + d u i 2 − k 2 + d u i 2 + ∑ j = 1 t ( t + 1 ) 2 + d v j 2 − t 2 + d v j 2 .
Proof. 
The edges in G can be partitioned as A and B as in the proof of Theorem 5, { u w 1 , w 1 w 2 , w 2 w 3 , ⋯ , w r − 1 w r , w r v } , { u u 1 , u u 2 , u u 3 , ⋯ , u u k } , { v v 1 , v v 2 , v v 3 , ⋯ , v v t } . Then the partitioning of G − C would be A and B, { u u 1 , u u 2 , u u 3 , ⋯ , u u k } , { v v 1 , v v 2 , v v 3 , ⋯ , v v t } . Considering the fact that the degrees of the end vertices u and v will decrease by one in G − C , the proof follows. □
Our next result is about deleting a pendant path from a graph. Let u v 1 v 2 v 3 ⋯ v r be a pendant path in a graph G such that d u = k + 1 , d v 1 = d v 2 = d v r − 1 = d v r + 1 = 2 . Let us denote the set { v 1 , v 2 , ⋯ , v r − 1 , v r } by T. Then we have the following result:
Theorem 7.
Let G be a graph and let T = { v 1 , v 2 , ⋯ , v r − 1 , v r } be a pendant path of length r as above. Then the change in the Sombor index of G when the set T is deleted from G is
S O ( G ) − S O ( G − T ) = ∑ i = 1 k ( k + 1 ) 2 + d v i 2 − k 2 + d v i 2 + ( k + 1 ) 2 + 4 + 2 ( r − 2 ) 2 + 5 .
Proof. 
The edges in G can be partitioned as { u v 1 , v 1 v 2 , v 2 v 3 , ⋯ , v r − 1 v r } , { u u 1 , u u 2 , u u 3 , ⋯ , u u k } and A = { x y ∈ E ( G − T ) | x , y ≠ u } . Similarly, the edges in G − T can be partitioned as { u u 1 , u u 2 , u u 3 , ⋯ , u u k } and A. Considering the vertex degrees in G and G − T , the result follows. □
As an application of this result, we calculate the Sombor index of a tadpole graph:
Example 1.
Let G = T r , s in Theorem 7. Let T be the pendant path P s of G so that G − T = C r . Here k = 2 . Hence by Theorem 7, we get
S O ( G ) = S O ( T r , s ) = S O ( C r ) + 9 + 4 + 9 + 4 − 4 + 4 − 4 + 4 + 9 + 4 + 2 ( s − 2 ) 2 + 5 = 2 2 ( r + s ) + 3 13 + 5 − 8 2 .

4. Nordhaus-Gaddum type result for Sombor index

Let G be a graph and let G ¯ be its complement. For a vertex v in V ( G ) , d G v + d G ¯ v = n − 1 . Also for any tree T and for a vertex v in V ( T ) , d T v + d T ¯ v = m . It is an obvious fact that if G is r-regular, then G ¯ is r ′ = ( n − 1 − r ) -regular. Also for an r-regular graph G, we have r = 2 m / n . If the end vertices of an edge e are x and y, then this edge is said to be of type { x , y } . Hence an r-regular graph has n r / 2 edges of type { r , r } . Therefore we the following result:
Theorem 8.
If G is an r-regular graph, then its Sombor index is
S O ( G ) = n r 2 2 2 .
Theorem 8 is enough to show the following Nordhaus-Gaddum type result on Sombor index:
Theorem 9.
If G is an r-regular graph, then the following relation is satisfied:
S O ( G ) + S O ( G ¯ ) = n 2 2 r 2 + ( n − 1 − r ) 2 .
Proof. 
Note that the size of the complement graph G ¯ is
m ( G ¯ ) = n ( n − 1 ) 2 − n r 2 = n 2 ( n − 1 − r )
and hence we obtain the required relation using the regularity of the complement graph G ¯ :
S O ( G ¯ ) = n ( n − 1 − r ) 2 ( n − 1 − r ) 2 = n 2 2 ( n − 1 − r ) 2 .
This proves our required relation. □
The following example gives a nice application of Theorem 8 to calculate the Sombor index of the complement of a cycle graph.
Example 2.
By Theorem 8, we can write
S O ( C n ) + S O ( C n ¯ ) = n 2 2 n 2 − 4 n + 7 .
As C n has n edges of type { 2 , 2 } , S O ( C n ) = 2 n 2 . Therefore by subtracting this S O ( C n ) from Eqn. (2), we can deduce the Sombor index of the complement of the cycle graph. As C n ¯ has n ( n − 1 ) / 2 edges of type { n − 3 , n − 3 } , S O ( C n ¯ ) = n 3 − 4 n 2 + 3 n 2 / 2 which gives us the same result.

5. Conclusions

The effects of vertex and edge removal from a graph are useful in calculating some property of large graphs in terms of the same property of a smaller graph. Sometimes, using iteratively, one can manage to obtain a property of a really large graph in terms of the same property of many other smaller graphs. Here, the calculations are made for a pendant and non-pendant vertex, a pendant and non-pendant edge, a pendant path, a bridge, a bridge path. Using these results, Sombor index of cyclic graphs and tadpole graphs are obtained. Finally, some Nordhaus-Gaddum type results are obtained for Sombor index.

Conflicts of Interest

The authors acknowledges that there is no potential conflict of interest. No part of it has been published or simultaneously submitted to any other journals.

References

  1. Alikhani, S., Ghanbari, N. Sombor index of polymers. MATCH Communications in Mathematical and in Computer Chemistry, 86, 2021, 715–728.
  2. Asif, F., Zahid, Z., Husin, M. N., Cancan, M., Tas, Z., Alaeiyan, M., Farahani, M. R. On Sombor indices of line graph of silicate carbide Si2C3-I[p,q]. Journal of Discrete Mathematical Sciences and Cryptography, 25, 2022, 301–310.
  3. Das, K. C., Cevik, A. S., Cangul, I. N., Shang, Y. On Sombor Index. Symmetry-Basel, 13 (1):140, 2021.
  4. Deng, H., Tang, Z., Wu, R. Molecular trees with extremal values of Sombor indices. International Journal of Quantum Chemistry, 121 (11), 2021, Article, e26622.
  5. Devaragudi, V., Chaluvaraju, B. Block Sombor index of a graph and its matrix representation. Open Journal of Discrete Applied Mathematics, 6, 2023, 1-11.
  6. Divyashree, B. K., Jagadeesh, R., Siddabasappa. Sombor indices of TUAC6 and TUZC6 nanotubes. Journal of Applied Chemical Science International, 13 (4), 2022, 70–79.
  7. Fang, X., You, L., Liu, H. The expected values of Sombor indices in random hexagonal chains, phenylene chains and Sombor indices of some chemical graphs. International Journal of Quantum Chemistry, 121 (17), 2021, Article, e26740.
  8. Gutman, I. Some basic properties of Sombor indices. Open Journal of Discrete Applied Mathematics, 4 (1), 2021, 1-3.
  9. Gutman, I. Sombor indices-back to geometry. Open Journal of Discrete Applied Mathematics, 5 (2), 2022, 1-5.
  10. Gutman, I., Redˇzepovi´c, I., Furtula, B. On the product of Sombor and modified Sombor indices, Open Journal of Discrete Applied Mathematics, 6, 2023, 1–6.
  11. Gutman, I. Geometric approach to degree-based topological indices: Sombor indices. MATCH Communications in Mathematical and in Computer Chemistry, 86 (1), 2021, 11-16.
  12. Huang, Y., Liu, H. Bounds of modified Sombor index, spectral radius and energy. AIMS Mathematics, 6 (10), 2021, 11263–11274.
  13. Horoldagva, B., Xu, C. On Sombor index of graphs. MATCH Communications in Mathematical and in Computer Chemistry, 86, 2021, 793–713.
  14. Hunag, Y., Liu, H. On the modified Sombor indices of some aromatic compounds. Journal of South China Normal University (Natural Science Edition, 53 (4), 2021, 91–99 (in Chinese).
  15. Kulli, V. R., Gutman, I. Computation of Sombor indices of certain networks, SSRG Int. J. Appl. Chem. 8, 2021, 1–5.
  16. Liu, H., Gutman, I., You, L., Huang, Y. Sombor index: review of extremal results and bounds. Journal of Mathematical Chemistry, 60 (5), 2022, 771-798.
  17. Liu, H., You, L., Huang, Y. Sombor index of c-cyclic chemical graphs. MATCH Communications in Mathematical and in Computer Chemistry, 90, 2023, 495-504.
  18. Liu, H., Chen, H., Xiao, Q., Fang, X., Tang, Z. More on Sombor indices of chemical graphs and their applications to the boiling point of benzenoid hydrocarbons, International Journal of Quantum Chemistry. 2021; 121, e26689.
  19. Oboudi, M. R. Mean value of the Sombor index of graphs. MATCH Communications in Mathematical and in Computer Chemistry, 89, 2023, 733–740.
  20. Oboudi, M. R. On graphs with integer Sombor index. Journal of Applied Mathematics and Computing, 69, 2023, 941–952.
  21. Rada, J., Rodríguez, J. M., Sigarreta, J. M. General properties on Sombor indices. Discrete Applied Mathematics, 299, 2021, 87–97.
  22. Redžepovic, I. Chemical applicability of Sombor indices. Journal of the Serbian Chemical Society, 86, 2021, 445–457.
  23. Reja, S., Nayeem, A. On Sombor index and graph energy. MATCH Communications in Mathematical and in Computer Chemistry, 89, 2023, 451–465.
  24. Shashidhara, A. A., Ahmed, H., Nandappa, D. S., Cancan, M. Domination version: Sombor index of graphsand its significance in predicting phsicochemical properties of butane derivatives, Eurasian Chemical Communications, 5, 2023, 91-102.
  25. Shooshtari, H., Sheikholeslami, S. M., Amjadi, J. Modified Sombor index of unicyclic graphs with a given diameter, Asian-European Journal of Mathematics, 2023. [CrossRef]
  26. Unal, S. O. Sombor index over the tensor and Cartesian product of monogenic semigroup graphs. Symmetry, 14 (5), 2022, Article, 1071.
  27. Zuo, X., Rather, B. A., Imran, M., Ali, A. On some topological indices defined via the modified Sombor matrix. Molecules, 27, 2022, Article, 6776.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated