Students-Centered Assessment Research on Holographic Learning Paradigm Based on Intelligent Analytic Hierarchy Process in Teaching of Bridge Engineering Course

Preprint

Article

Students-Centered Assessment Research on Holographic Learning Paradigm Based on Intelligent Analytic Hierarchy Process in Teaching of Bridge Engineering Course

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

23 December 2023

Posted:

26 December 2023

You are already at the latest version

Alerts

Abstract

The key to building a strong bridge country lies in talent, and the foundation lies in education. The cultivation of bridge engineering talents is related to the future and destiny of building a strong bridge country. This course adopts the educational philosophy of "holographic teaching method" centered on the comprehensive development of students, cultivating "engineering thinking" guided by engineering education certification, enhancing "abilities and qualities" through professional knowledge, reconstructing the course knowledge content system through engineering philosophy thinking, and implementing the ideological and political construction of the course in a multi-level unified manner of "explicit + implicit". Based on restructuring the course content system, we will strengthen the construction of diversified course resources, integrate theory with practice throughout the entire process of the course, practice the concept of "bridge architects + bridge engineers" parallel development, and cultivate cross-border and compound talents with comprehensive qualities of "engineering + art + humanities".

Keywords:

Subject: Social Sciences - Education

1. Introduction

As a compulsory course in civil engineering, the teaching objectives of bridge engineering include but are not limited to cultivating students' basic understanding of the stress characteristics of various bridge types and components, mastering the structural principles of large-span, medium and small bridges, and new bridge structures, and becoming familiar with the design characteristics and application scope of common construction methods. As the core course of transportation characteristic universities under the background of large-scale infrastructure and intelligent transportation, its classroom teaching effect has a profound impact on the cultivation of students' engineering and technical abilities [1,2,3]. However, considering the teaching characteristics of this type of course, such as wide application scope, complex and variable bridge types, cumbersome design specifications, and high difficulty in calculation content, traditional teaching methods only focus on explaining theoretical knowledge, often neglecting the integration of software technology and engineering project practice related to bridge disciplines, resulting in a decrease in students' classroom enthusiasm and participation, and a significant reduction in teaching efficiency. Therefore, exploring and adapting research methods for bridge teaching is particularly important.

With the development of the times, there has been a diverse demand for theoretical, practical, complex, and landscape oriented teaching in bridge engineering [4,5,6,7]. Practical teaching plays an important role in the training system of undergraduate engineering talents, and is an important teaching method that connects theoretical classrooms with engineering practice. However, the practical teaching mode in engineering has problems such as low efficiency, poor effectiveness, and students being prone to "hasty observation", making it difficult to achieve the expected results, and even less able to fully reflect the teaching philosophy of "student-centered development". The theoretical characteristic of bridge engineering is that the knowledge content is a summary of engineering experience, the knowledge system is complex, and the logical line is not particularly clear. Without practical experience accumulation, students find it difficult to deeply understand the scientific principles of bridge engineering knowledge. The complexity of bridge engineering is reflected in the diverse structural systems, lengthy calculation principles, and the difficulty for students to quickly and effectively understand the force transmission mechanism of the structure in the mechanical calculation process. Therefore, the construction of complex and diverse bridge structural systems is extremely difficult. With the gradual transformation of concepts in recent years, the demand for bridge aesthetics in society has gradually increased. However, there is currently a shortage of talents with relevant knowledge in the engineering design industry, especially bridge engineers who understand structural aesthetics. This has led to a one-sided pursuit of "novelty, uniqueness, and uniqueness" in design, which in turn has led to a deviation in bridge aesthetics. It is imperative to improve the professional aesthetic literacy of bridge engineering professionals, which puts high demands on our higher education, especially engineering education [8,9,10].

"Putting students at the center" is the core foothold of humanistic education theory [11]. The goal of education should be to promote the development of students, making them "free" individuals who can adapt to change and know how to learn. Advocating meaningful learning, he believes that learning is the realization of the learner's inner potential, a meaningful psychological process, and characterized by individual active learning. Teaching evaluation is an important measure for monitoring teaching quality. How to objectively evaluate teaching not only affects the fair operation of university teaching, but also seriously affects the exploration and cultivation of innovative talents [12,13]. The traditional teaching evaluation system focuses on the aspect of teachers' teaching, such as teaching attitude, teaching content, teaching methods, teaching effectiveness, and student evaluation. It is obvious that this system is a "teacher centered" teaching evaluation, which mainly evaluates teachers and cannot fully reflect the actual results achieved by students. It is easy to generalize and cannot truly reflect the quality of teaching [14].

We are in an era full of expectations and tolerance for innovation, conceptualization, and breakthrough, and the transformation of education and teaching is imperative. Under such an impact, it is necessary and worth pondering how to implement the student-centered teaching philosophy and how to formulate evaluation standards for the teaching ability of university teachers. Bridge Engineering is an important core compulsory course in civil engineering. Through long-term teaching practice and evaluation statistics, student feedback, and survey questionnaires, the team has found that the course has a deep theoretical foundation but is disconnected from practice, the textbook is rigorous but not flexible enough, and the objective learning situation of students who are eager for knowledge but mechanically memorize and calculate can bring the following pain points:(1) The problem of insufficient analytical ability in practical bridge engineering is mainly reflected in the lack of spontaneous cognitive construction knowledge system ability, weak modeling ability in real-world bridge engineering, and lack of independent analysis and judgment ability in software calculation, resulting in students lacking analytical ability in practical engineering.(2) The problem of weak thinking in bridge design due to integration and transfer is mainly reflected in unclear logical thinking in bridge structural component design, chaotic composition of bridge structural system design framework, and weak global perspective in bridge engineering conceptual design, resulting in students staying in a stage of confusion with knowledge.(3) The lack of flexible and innovative bridge aesthetic literacy is mainly reflected in the lack of emphasis on shape selection in the structural analysis process, inadequate analysis of variability in the structural calculation process, and lack of active landscape awareness in the conceptual design process, leading to students' lazy habit of valuing force calculation and neglecting aesthetic shape.

In order to address the significant issues of teacher and student role positioning, teacher teaching design, and student learning ability in the traditional bridge engineering teaching process, the course team proposed a teaching model based on the holographic concept on the basis of teaching practice, and evaluated the teaching effect using the intelligent Analytic Hierarchy Process (AHP) evaluation method [15,16,17,18]. We have constructed and implemented a holographic learning paradigm centered on the comprehensive development of students. This concept, based on the characteristics of broad course information, deep organizational content, and a pattern of comprehensive education, takes the "basic idea of combining strength and form" as the core implementation path, practices the concept of integrated development of "bridge engineers + bridge architects", guides students to establish a scientific and rational view of bridge engineering, and cultivates cross-border innovative talents with comprehensive qualities of "engineering + art".

2. Teaching philosophy model

2.1 Philosophy

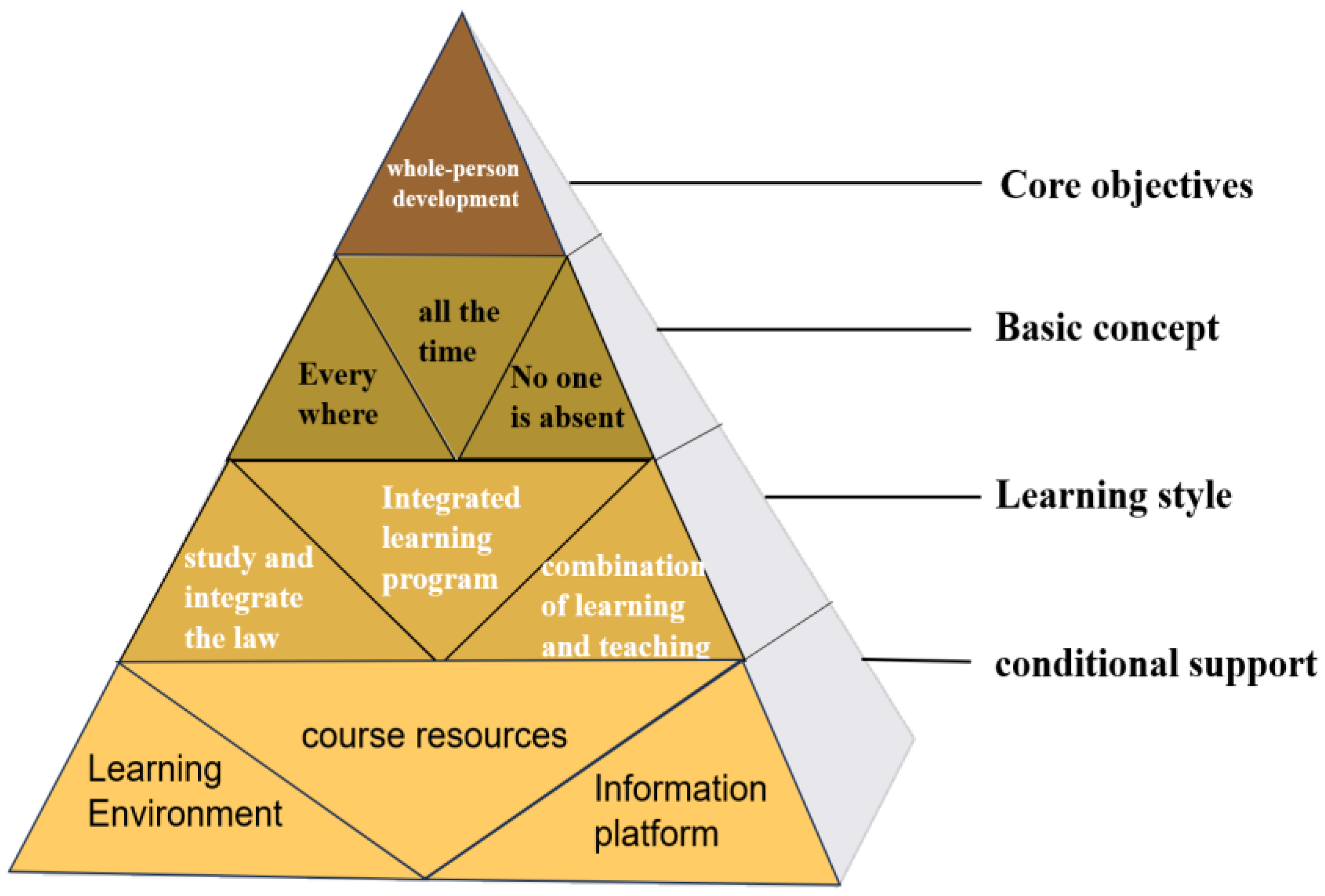
Holistic learning refers to a paradigm that advocates for the comprehensive development of individuals and an enhanced approach to learning. Aligned with the principles of talent cultivation and the demands of future advancement, it aims to nurture students' capacity to adapt to societal transformations and spearhead epochal shifts. The core goal of holistic learning entails fostering the all-encompassing growth of individuals, with its cornerstone concept residing in the ubiquitous, perpetual, and ubiquitous nature of learning. Engaging in a pedagogical approach characterized by fusion, continuity, and integration, its underlying pillars rest upon the scaffolding provided by the learning environment, curriculum resources, and information platforms.

The essence of holistic learning bears semblance to the "pyramid" model (Figure 1), an architectural structure that ensures the scientific essence, integrated nature, and developmental trajectory of holistic learning. Among these interrelated components, the fundamental concepts, learning methodologies, and contextual support converge to serve the attainment of the core aspirations underlying "holistic development." The basic concepts form the lynchpin of a humanistic interpretation of these aspirations, whereas the learning methodologies embody the diverse practical manifestations of these grounding principles. Finally, the contextual support serves as the foundational bedrock that underpins the efficacy and sustainability of the learning methodologies.

2.2 Train of thought

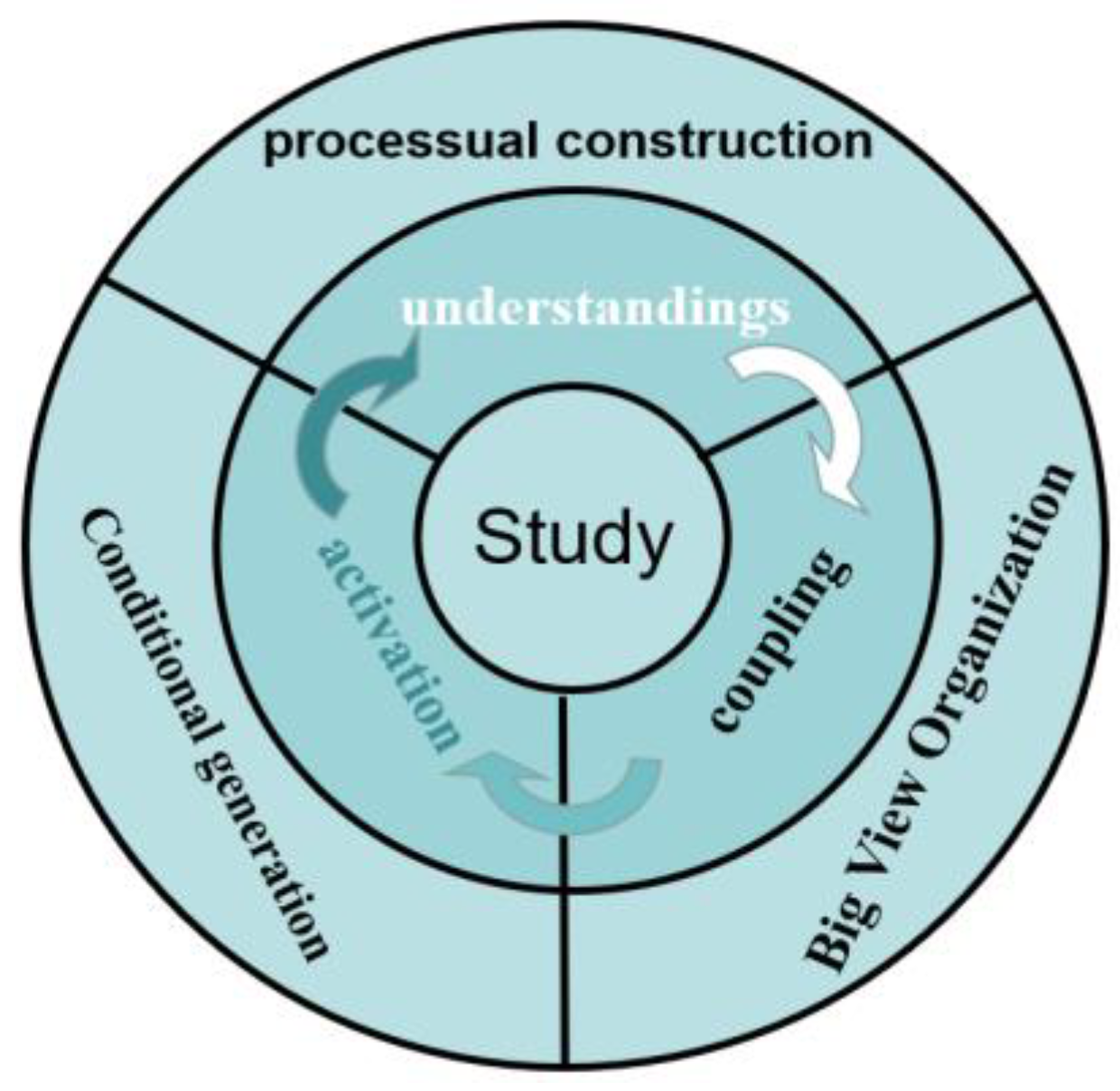
In the holistic learning mode, the knowledge acquired by students is not fragmented or isolated, but structured and conducive to knowledge growth, transformation, and transfer. Process-based construction is employed to facilitate an understanding of knowledge, while a big-picture perspective is used to promote knowledge connections. Conditioned generation is employed to promote knowledge activation, thus creating a "comprehend-connect-activate" holistic learning model (Figure 2).

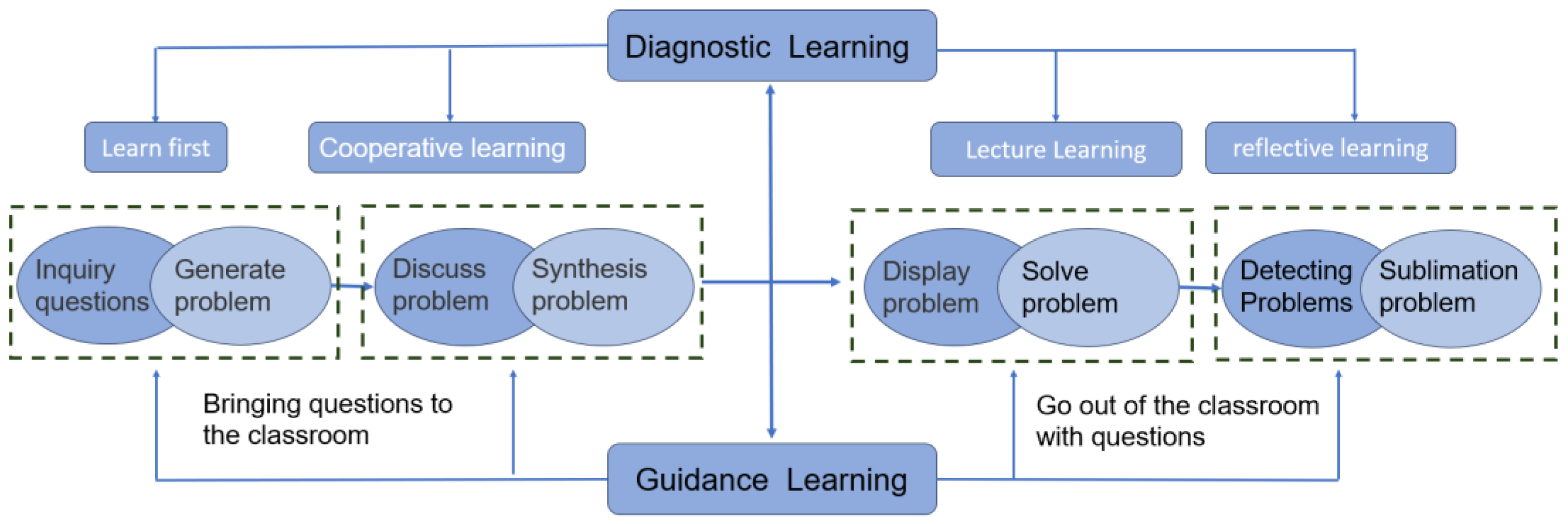
Under the guidance of the holistic concept, learning is regarded as the process of "doing scholarship." Learning takes place through questioning, and questioning leads to learning. Learning occurs through action, and action leads to learning. An inquiry-based and student-centered holistic learning model is constructed, known as the "question-based" learning model (Figure 3). The holistic teaching concept emphasizes starting with "discovering problems" and going through the process of "interest exploration" to upgrade "transfer and innovation" abilities, culminating in the construction of the "holistic information" knowledge system, resulting in a "one for all" learning effect. In teaching practice, students are empowered to become the masters of their learning, participating in a vibrant and diverse classroom environment where they openly express their viewpoints. Teachers and students are closely connected, with teachers effectively grasping the pulse of the classroom and playing their role as "guides," while students act as "explorers."

3. Analytical Hierarchy Process

Analytic Hierarchy Process (AHP) is a multi-objective decision-making method that combines qualitative and quantitative methods. The basic idea of this method for risk identification is to decompose complex risk problems into various constituent factors, group these factors according to dominant relationships to form an ordered hierarchical structure, determine the relative importance of each factor in each level relative to the overall goal of the previous or highest level through pairwise comparison and judgment, and sort them to determine the main risk modes and risk factors of the system. AHP reflects the basic characteristics of people's decision-making thinking, namely decomposition, judgment, and synthesis.

The Analytic Hierarchy Process mainly includes three parts: constructing a hierarchical structure model; Establish a judgment matrix group; Hierarchical sorting and consistency testing. These three parts will be briefly introduced below.

3.1. Building a hierarchical model

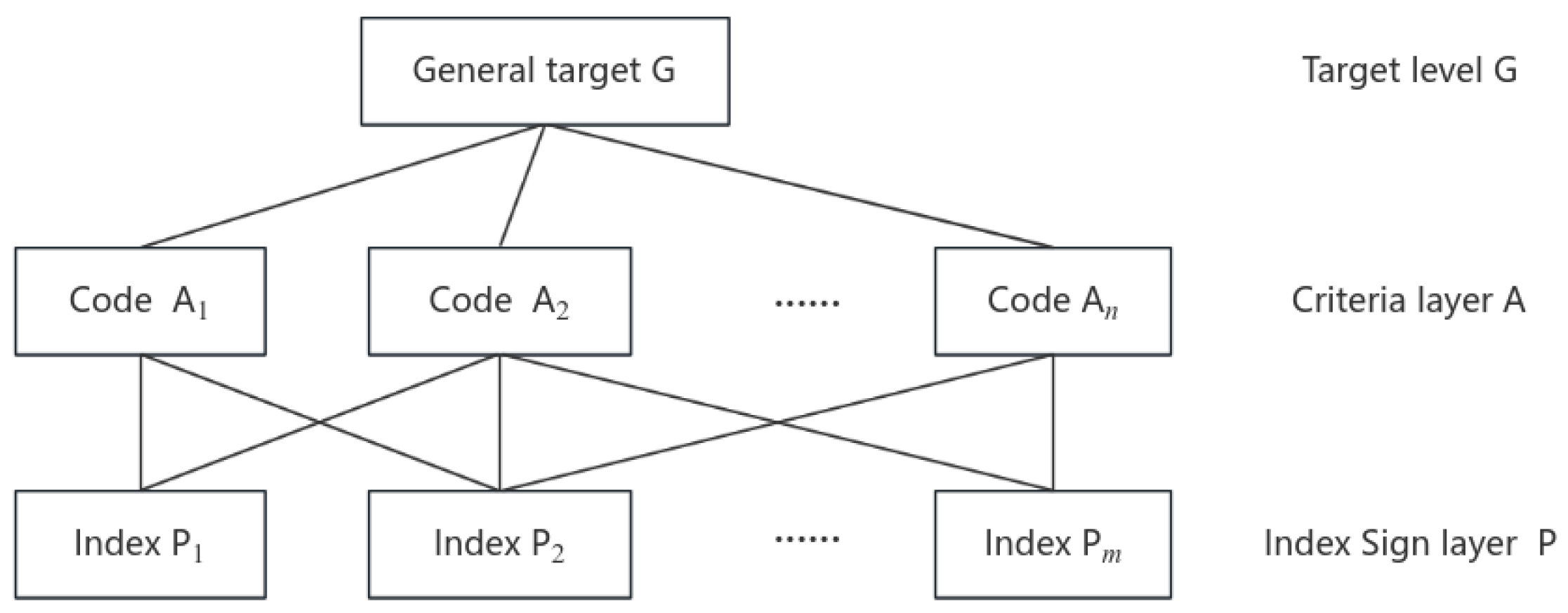
Analyze the interrelationships and subordinate relationships among all factors that affect the teaching effectiveness of bridge engineering courses, organize and level risk issues, and establish a systematic hierarchical structure model. Merge elements with common attributes into a group as a hierarchy in the structural model; Elements at the same level have a constraining effect on the elements at the next level, while also being constrained by the elements at the previous level. The entire hierarchical model consists of three levels from top to bottom (as shown in Figure 4):

(1) Target layer G: contains only one element, representing the overall goal of teaching effectiveness evaluation, that is, the learning effectiveness of bridge engineering courses;

(2) Criterion layer A: represents the various sub objectives involved in achieving the overall goal, namely the potential factors that affect the teaching effectiveness of bridge engineering. Taking knowledge learning as an example, these potential factors include the knowledge system of bridge engineering, mechanical principles, engineering experience, etc;

(3) Indicator layer P: represents the various sub factors that cause various influencing factors in the criterion layer, such as educational background, learning habits, expression ability, thinking mode, etc.

3.2. Constructing a judgment matrix group

The purpose of establishing a judgment matrix is to measure the relative importance of each element in each level to a neighboring element in the previous level. The specific process is to use a certain element in the adjacent upper layer as a criterion, compare and judge the elements in that layer pairwise, quantify the comparison results according to specific scoring rules, and form a judgment matrix.

Taking criterion layer A as an example, the judgment matrix formed by pairwise comparison results is:

A = {(a_{i j})}_{n \times n}, (i, j = 1, 2, \dots, n)

, where The relative importance of element i to element j is considered from the G layer, and this value is determined using a 1-9 scoring rule. According to the definition of

a_{i j}

, it can be inferred that:

a_{i j}

> 0,

a_{i i}

= 1,

a_{i j}

= 1/

a_{j i}

3.3. Hierarchical sorting and consistency testing

The problem of ranking the importance of hierarchical elements is to sort them based on their relative importance to the higher-level elements or the overall goal of the highest level, in order to achieve the goal of risk identification. The sorting problem is divided into hierarchical single sorting and hierarchical total sorting.

By calculating the maximum eigenvalue and corresponding eigenvector of the judgment matrix, the relative importance weight of a certain layer element relative to the relevant elements of the previous layer is calculated. This sorting is called hierarchical single sorting; After calculating the single ranking value of each element in a certain level relative to the previous level, the relative importance weight of a certain level element relative to the entire level can be calculated by weighting and synthesizing the weights of the previous level elements themselves. This ranking is called hierarchical total ranking. By sorting the importance of hierarchical elements in a single order and a total order, the relative importance of each element in the criterion layer and each element in the indicator layer can be obtained, thereby determining the main influencing factors on the teaching effectiveness of bridge engineering.

Due to the complexity of the system, the diversity of personnel understanding, and the subjective one sidedness and instability, achieving complete consistency is very difficult. Therefore, in order to ensure consistency in hierarchical sorting, it is necessary to perform consistency checks on the given judgment matrix. Taking hierarchical single sorting as an example, consistency testing usually uses consistency ratio as the testing standard, which is defined as:

C R = \frac{C I}{R I}

(1)

Where, the calculation formula for consistency indicators is:

C I = \frac{λ_{\max} - n}{n - 1}

λ_{\max}

was determining the maximum eigenvalue of matrix A,

R I

is an indicator of average random consistency, which is related to the order of the judgment matrix n and can be found in Table 1.

4. Particle Swarm Optimization

4.1. Basic concepts

The process of parameter optimization adopts a dynamic optimization method, which originates from the foraging thinking of birds in nature. It compares particles to birds and treats them as a basic individual. The speed, position and fitness represent the group characteristics of each basic individual. In the extreme value optimization problem, the speed and position of each particle are constantly and dynamically adjusted according to its own moving experience of other particles, so as to achieve the purpose of approaching the extreme value faster.

It is described mathematically as follows: in a D-dimensional search space composed of functional solutions containing d independent variables, randomly distributed n particles that can move freely, including particle position is

X_{i} = (x_{i 1}, x_{i 2}, \dots, x_{i d})

and velocity is

V_{i} = (v_{i 1}, v_{i 2}, \dots, v_{i d})

,the dynamic adjustment equation is as follows：

v_{i, j} (t + 1) = w v_{i, j} (t) + c_{1} r_{1} [p_{i, j} - x_{i, j} (t)] + c_{2} r_{2} [p_{g, j} - x_{i, j} (t)]

(2)

x_{i, j} (t + 1) = x_{i, j} (t) + v_{i, j} (t + 1)

(3)

In formula:

i

——number of particles

j

——dimensions of particles

w

——inertial weight

t

——the current number of iterations

c_{1}, c_{2}

——acceleration factor, whose value is not negative

r_{1}, r_{2}

——random factors, whose values are located at [0,1]

p_{i, j}

——the position corresponding to individual optimal value of

i

particle

p_{g, j}

——the position corresponding to optimal value of entire particle population

In order to prevent the blind search of particles in the search space and the detachment boundary of particle position velocity, the optimization efficiency is further improved, to impose certain constraints on the position and velocity of free particles. Generally, the position of particle is confined to the interval

[- X_{\max}, X_{\max}]

, and the particle velocity is limited to the interval

[- V_{\max}, V_{\max}]

4.2. Algorithm optimization

Although PSO algorithm has strong versatility and fast convergence, there are still problems of local optimal results and low efficiency of late iteration. Therefore, this paper optimizes PSO algorithm from these two aspects.

Causes for the precocious occurrence of PSO algorithm: as the iteration process goes on, the particle swarm search space continuously shrinks to a certain limited local range due to the initialization value of the variable, so only the optimal result in the local range, rather than the optimal result in the whole search space. In order to improve this defect, we refer to the mutation principle in the genetic algorithm during the iterative calculation process, so that some variables are no longer limited to an initial value, and can have a certain opportunity to reinitialize and increase the particle population diversity. The variant operation substantially broadens the population search space during computation, raising the possibility of finding the optimal solution by the particle swarm algorithm while maintaining the original population diversity.

For the problem of low late iteration efficiency of PSO algorithm, this paper improves the iteration efficiency by optimizing the inertial weight

w

based on the basic algorithm. Inertial weights characterize the level of particle inheritance to the previous velocity, which largely determines the rate of particle evolution (i.e., iterative efficiency). Studies have shown that a large inertial weight is favorable for the global search, while a smaller inertial weight is favorable for the local search. To achieve full potential of global search and local search, linear decreasing inertial weights are introduced, i.e.:

w (k) = w_{s t a r t} - \frac{(w_{s t a r t} - w_{e n d}) \times k}{T_{\max}}

(4)

In formula:

w_{s t a r t}

——initial inertia weight

w_{e n d}

——inertial weight at iteration to maximum number

k

——number of current iterations

T_{\max}

——maximum iterative algebra

4.3. Algorithm process

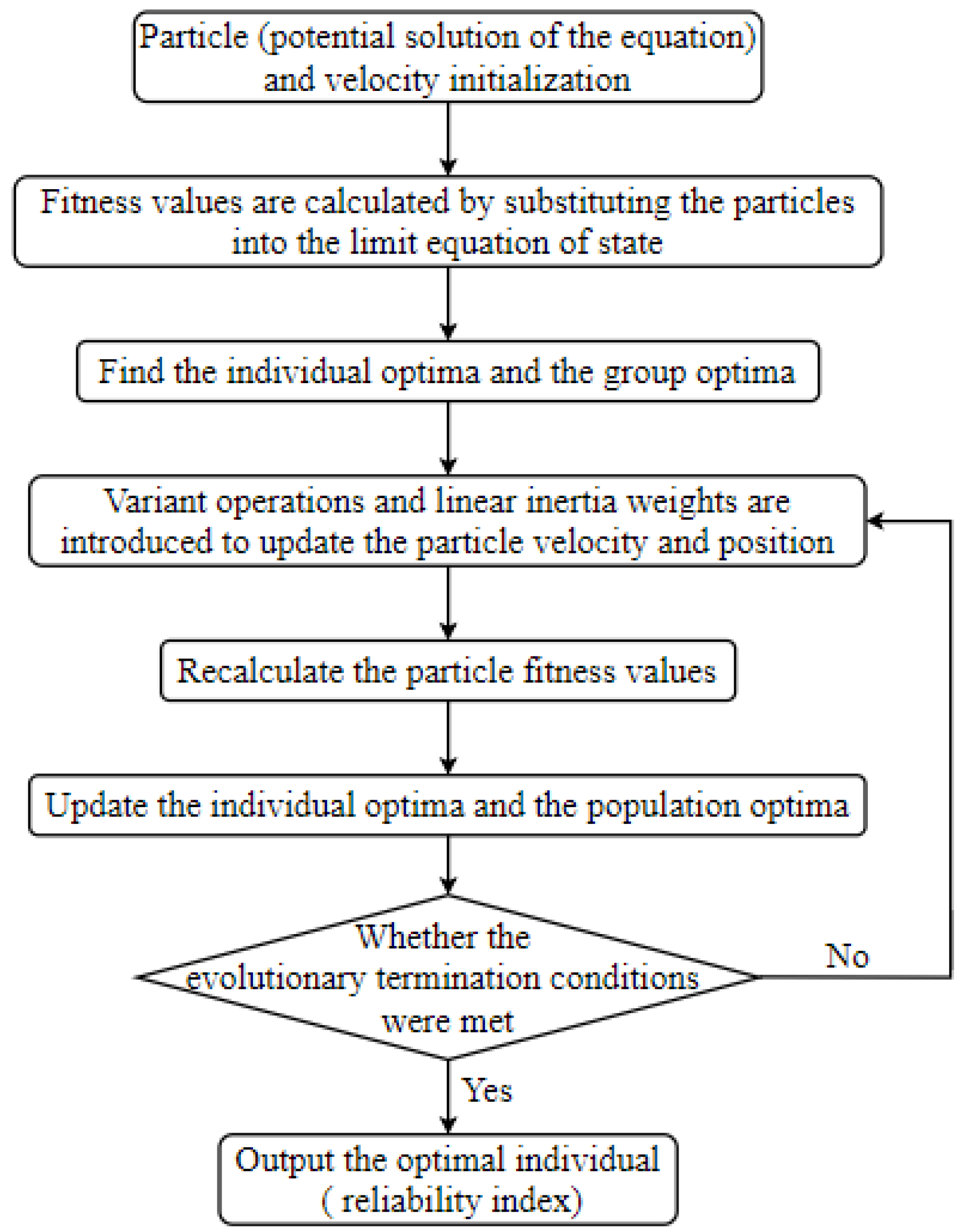
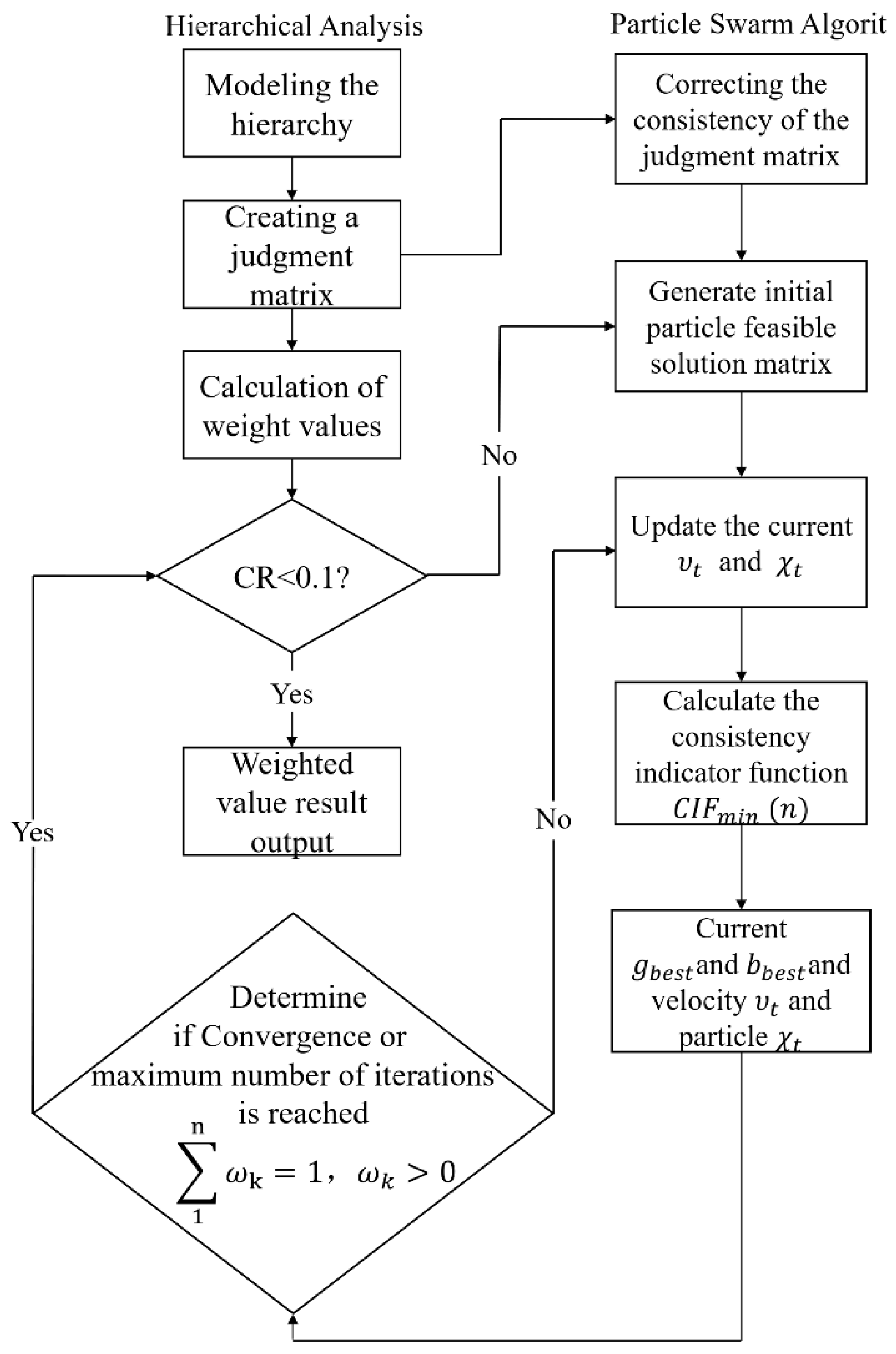
After obtaining the mathematical model of the structure reliability index, it is solved by PSO algorithm. The solution process is shown in Figure 5.

5. Teaching design scheme of Bridge Engineering Course

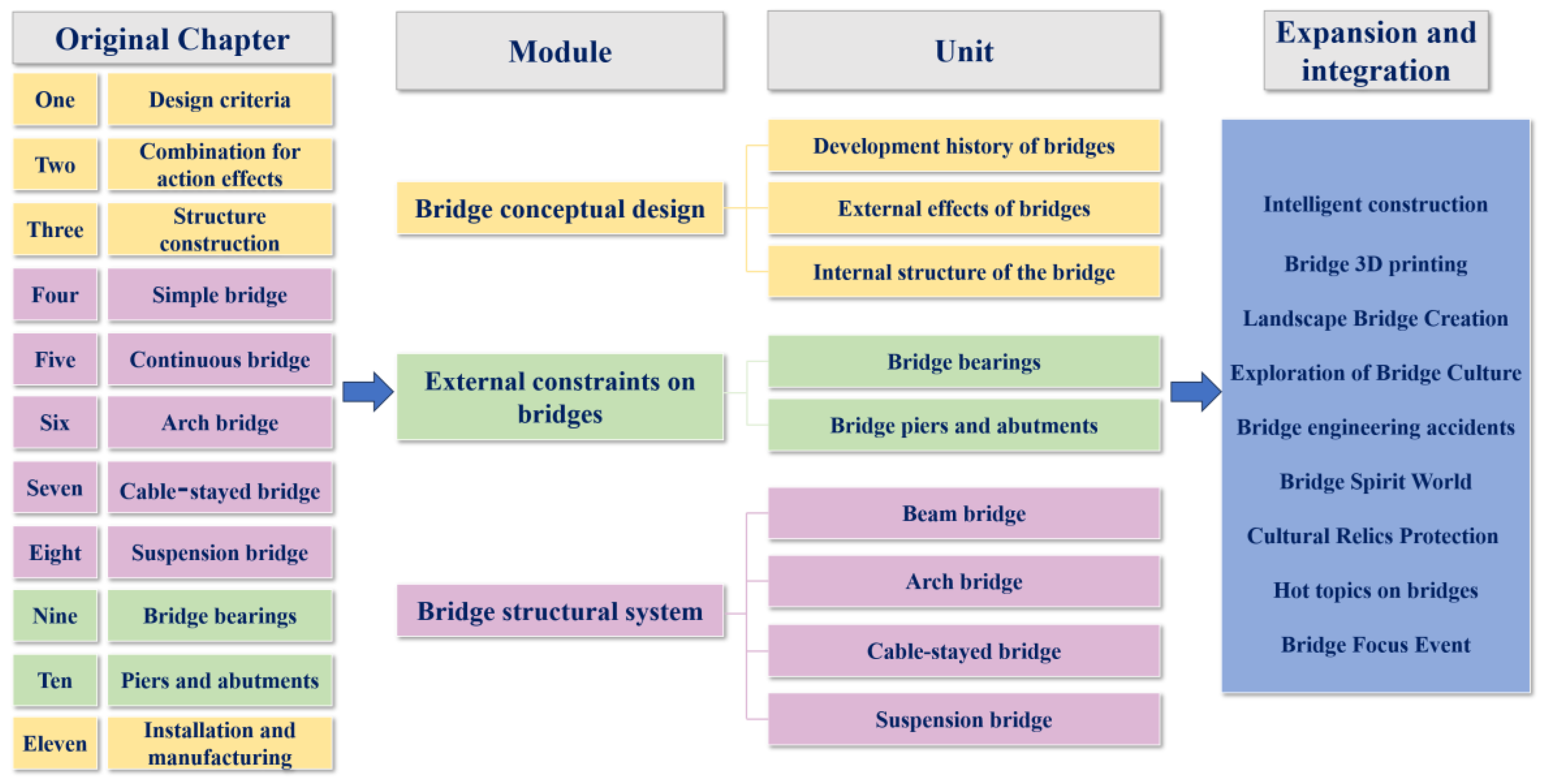
5.1. Restructuring the curriculum content system

With the cultivation of students' logical thinking as the main line, the curriculum system will be reconstructed, and the original chapters will be condensed and reconstructed into three modules and nine units. Starting from the conceptual design of bridges, establish a holistic understanding of bridges from a macro level; Clarify the external constraints of the bridge and establish a solid foundation for the bridge with underlying logic; Build a bridge structural system and design different bridge types at the top level. At the same time, in response to the problem of the lack of cutting-edge content in the era, we will expand multi-directional content, integrate diverse scenarios, and focus on aspects such as "intelligent construction of bridges, landscape bridge creation, hot topics on bridges, and key events on bridges". We will focus on the depth and breadth of the content, broaden the horizons of students, cultivate disciplinary thinking, and clarify the internal connections and logic of bridge engineering. Establish a network framework (seen Figure 2) between knowledge using a conceptual approach.

Figure 6. Reconstruction and Expansion of the Content System of Bridge Engineering.

5.2. Multidimensional guided teaching methods

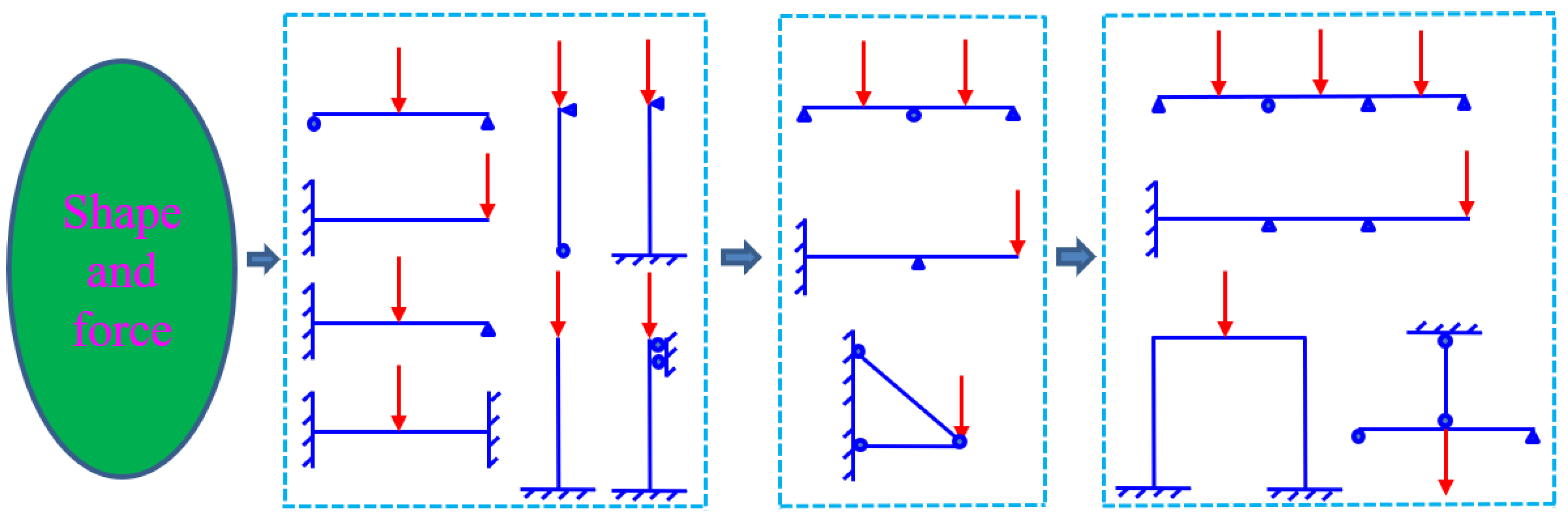
In the teaching process, emphasis is placed on combining qualitative analysis with quantitative calculation, combining micro analysis with macro analysis, and combining scientific reasoning with philosophical speculation. Guided by "engineering philosophy" and using the basic principle of "force form combination" as the core means, establish a teaching model that integrates "conceptual design, qualitative analysis, and quantitative calculation", practice the concept of comprehensive development of "bridge engineers" and "bridge architects", establish a scientific and rational "bridge engineering worldview", and cultivate students' broad mindedness and grand pattern.

Figure 7. Basic principle of force shape combination.

5.3. Integrating course resources through multiple channels

The learning environment is an important factor that affects learning. In today's highly developed internet technology, students are constantly immersed in the encirclement of information. Based on the concept of holographic learning, establish a learner centered environment and strengthen the integration of physical, digital, and cultural environments (see Table 2). The teaching team has built online and offline, material humanities, virtual reality and other multi-channel resources, such as the MOOC online open class of Bridge Engineering, the teaching material of Bridge Engineering, the WeChat official account "Poetic and Picturesque Talk about Bridges", the "Collection of Bridge Poetry", and the bridge physical model.

5.4. Multidisciplinary intersection and integration of "engineering + art"

By analyzing the stress characteristics and aesthetic design of bridge structures in a targeted manner, and discussing the application of aesthetic knowledge through case studies, students can deepen their understanding of bridge aesthetics. By combining mechanical analysis with bridge aesthetics as a teaching method, enriching classroom teaching content, and further mobilizing students' enthusiasm for classroom learning, bridge engineers and bridge architects cross integrate and develop, cultivating interdisciplinary talents with comprehensive qualities of "science + art + humanities".

5.5. Evaluation of teaching effectiveness

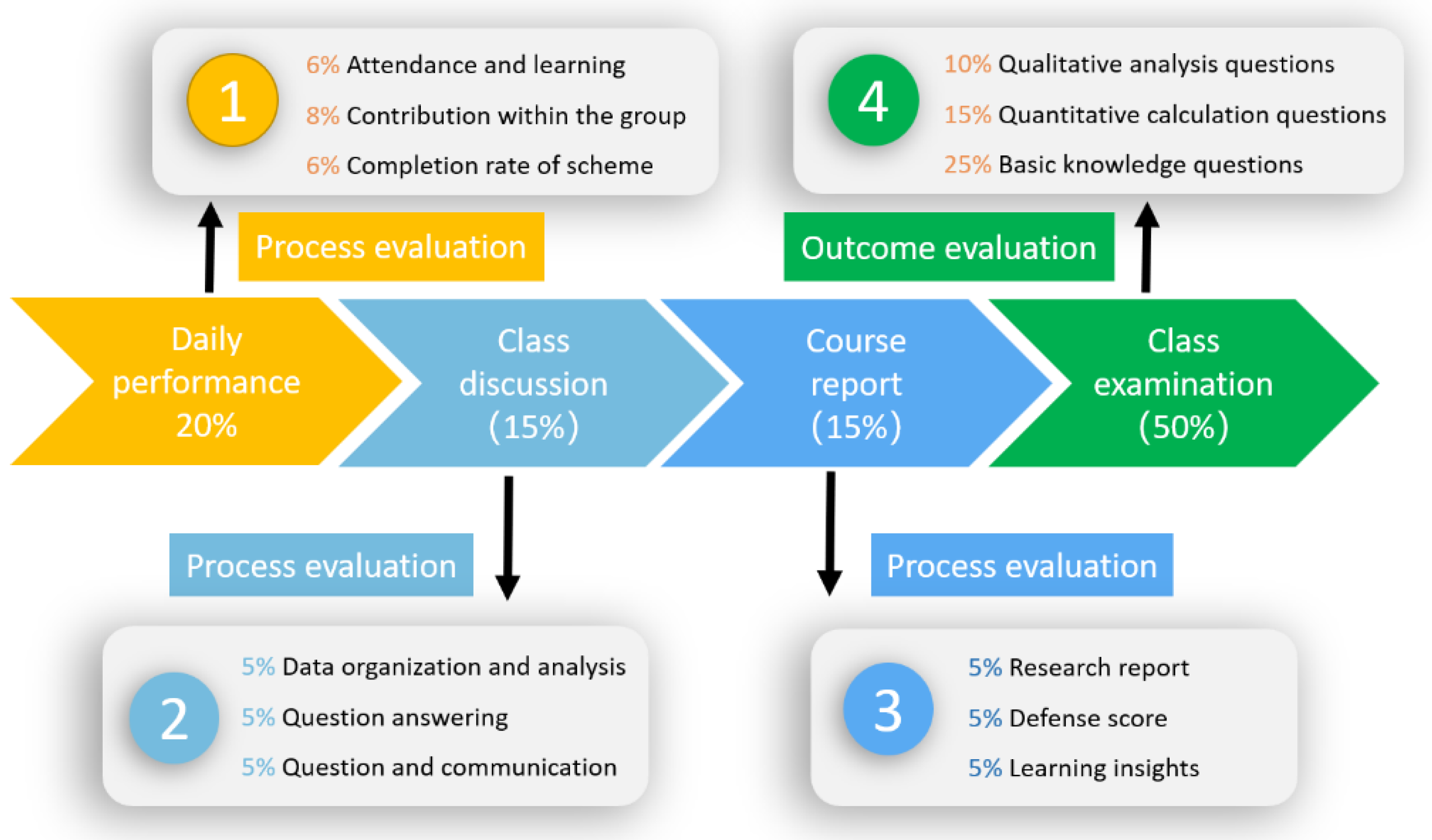
The course grade evaluation consists of four parts (see Figure 8): regular performance (20%), discussion classes (15%), course projects (15%), and final exams (50%). Each discussion class and course project has designed qualitative evaluation indicators such as humanistic literacy, team collaboration, and information technology capabilities to evaluate students' comprehensive literacy. The concept of "diversified and comprehensive" assessment reflects the process and results, quantitative and qualitative, individual and team, science and humanities, ability and literacy.

6. Application

Teaching activities are led by teachers, with students as the core members of learning. Therefore, as a group, teachers and students have a more intuitive understanding of classroom teaching and the most voice. Therefore, conducting interviews with teacher and student groups on the evaluation indicators of bridge engineering teaching can fully grasp the actual situation of evaluating bridge engineering teaching in the course, which is of great significance and can ensure the rationality and operability of the evaluation indicator system.

6.1. Selecting interviewees

After recommendation, a total of 40 teachers were selected as interviewees, all of whom are full-time teachers in the field of civil engineering and have more than 3 years of experience in teaching courses related to civil engineering. Teachers are familiar with the training work of bridge engineering courses in classroom teaching, and have their own opinions on course evaluation, which can ensure the reliability and effectiveness of interview results.

6.2. Develop interview outline

To truly achieve the development and implementation of student-centered teaching evaluation standards, the core needs to rely on a set of scientific and student-oriented evaluation indicators, and adhere to the indicator system that focuses on evaluating teaching quality based on student learning outcomes rather than teacher teaching effectiveness. To achieve student-centered evaluation indicators, it is necessary to closely evaluate students' teaching feedback and feelings in teaching philosophy, teaching content, teaching process, and teaching effectiveness, as shown in Table 3.

6.3. Implementation of interviews

The interview was conducted using a survey questionnaire combined with video and phone calls. Firstly, record teaching videos and send them online to the interviewing teachers. Then arrange a quiet interview environment. At the beginning of the interview, introduce the purpose of the interview, and then follow the interview outline. The interview time should be controlled at around 10 minutes.

6.4. Analytic Hierarchy Process Statistical Results

Using Analytic Hierarchy Process to determine the weight of indicators, collecting data from questionnaire surveys, investigating the importance of each indicator, and finally using SPSS software to determine the weight of indicators, in order to construct an evaluation index system for bridge engineering course teaching. Among them, SPSS is an auxiliary software for statistical analysis of data. This study mainly uses SPSS to provide assistance in model construction, calculation process, and result analysis for the decision-making process of Analytic Hierarchy Process.

Based on the above principles and formulas, the ranking weights of the A level indicators in the teaching evaluation indicators of bridge engineering courses are obtained using SPSS software, as shown in the Table 3. According to the SPSS software, the consistency test CR for A-level indicators is 0.0412 and CR<0.1, so it is considered to meet the consistency test requirements with the maximum eigenvalue λ_max is 3.1102.

Table 3. Factor weights of index layer A.

Index A	A1	A2	A3	A4	Wi
A1	1	0.25	0.5	0.3	0.2136
A2	4	1	2	2	0.2578
A3	2	0.5	1	0.3	0.3847
A4	3	0.5	3	1	0.1439

Using SPSS software, obtain the ranking weights of P1 level indicators in the teaching evaluation indicators of bridge engineering courses, as shown in Table 4. According to the SPSS software, the consistency test CR for P1 level indicators is 0.0442, and CR<0.1, so it is considered to meet the consistency test requirements, with the maximum eigenvalue λ_max is 4.1516.

Using SPSS software, obtain the ranking weights of P2 level indicators in the teaching evaluation indicators of bridge engineering courses, as shown in Table 5. According to SPSS software, the consistency test CR for P2 level indicators is 0.0382, and CR<0.1, so it is considered to meet the consistency test requirements, with the maximum eigenvalue λ_max is 2.9918.

Using SPSS software, obtain the ranking weights of P3 level indicators in the teaching evaluation indicators of bridge engineering courses, as shown in Table 6. According to the SPSS software, the consistency test CR for P3 level indicators is 0.0625 and CR<0.1, so it is considered to meet the consistency test requirements with the maximum eigenvalue λ_max is 4.1182.

Using SPSS software, obtain the ranking weights of P4 level indicators in the teaching evaluation indicators of bridge engineering courses, as shown in Table 7. According to the SPSS software, the consistency test CR for P4 level indicators is 0.0343, and CR<0.1, so it is considered to meet the consistency test requirements with the maximum eigenvalue λ_max is 3.1167.

6.5. Optimization of evaluation system based on particle swarm optimization algorithm

The consistency index function solution mentioned in the above Analytic Hierarchy Process is a conventional method, but the solution process is difficult to handle and is a classic nonlinear optimization problem. Therefore, in the case where the judgment matrix has been determined, it is proposed to use Particle Swarm Optimization (PSO) to encode particles, construct fitness functions, and optimize nonlinear programming problems, so that the optimal weight value solution can be obtained when the consistency index function is minimized.

Compare the optimal fitness value obtained from the first generation with the historical optimal particle swarm fitness value, and update the historical optimal fitness value. Perform n cycles to find the optimal fitness value (i.e. CR<0.1). If the constraint conditions are met, jump out. Otherwise, continue with the cycle iteration, which can be seen Figure 9.

Write the particle swarm optimization algorithm as a module of Matlab mathematical software program, and the system can effectively execute the algorithm and gradually execute iterative commands. As the algorithm iterates, the system gradually optimizes to obtain a judgment matrix that meets the consistency requirements, and recalculates the corresponding weight allocation.

Original matrix of level A was as follows,

A = [\begin{matrix} 1 & \frac{1}{4} & \frac{1}{2} & \frac{1}{3} \\ 4 & 1 & 2 & 2 \\ 2 & \frac{1}{2} & 1 & \frac{1}{3} \\ 3 & \frac{1}{2} & 3 & 1 \end{matrix}]

Optimization matrix of level A was as follows,

\bar{A} = [\begin{matrix} 1 & 0.2736 & 0.4694 & 0.3461 \\ 3.6556 & 1 & 2.1192 & 1.9508 \\ 2.1304 & 0.4547 & 1 & 0.3722 \\ 2.8891 & 0.5126 & 2.6869 & 1 \end{matrix}]

Original matrix of level A1 was as follows,

A_{1} = [\begin{matrix} 1 & \frac{1}{3} \\ 3 & 1 \end{matrix}]

Optimization matrix of level A1 was as follows,

\bar{A_{1}} = [\begin{matrix} 1 & 0.3108 \\ 3.2173 & 1 \end{matrix}]

Original matrix of level A2 was as follows,

A_{2} = [\begin{matrix} 1 & \frac{1}{3} & \frac{1}{4} \\ 3 & 1 & 2 \\ 4 & \frac{1}{2} & 1 \end{matrix}]

Optimization matrix of level A2 was as follows,

\bar{A_{2}} = [\begin{matrix} 1 & 0.3605 & 0.2204 \\ 2.7738 & 1 & 1.8567 \\ 4.5365 & 0.5386 & 1 \end{matrix}]

Original matrix of level A3 was as follows,

A_{3} = [\begin{array}{l} \begin{matrix} 1 & \frac{1}{4} & \frac{1}{5} & \frac{1}{3} & \frac{1}{2} \\ 4 & 1 & 2 & 2 & \frac{1}{3} \\ 5 & \frac{1}{2} & 1 & \frac{1}{3} & \frac{1}{3} \\ 3 & \frac{1}{2} & 3 & 1 & \frac{1}{2} \\ 2 & 3 & 3 & 2 & 1 \end{matrix} \end{array}]

Optimization matrix of level A3 was as follows,

\bar{A_{3}} = [\begin{array}{l} \begin{matrix} 1 & 0.2359 & 0.2048 & 0.3525 & 0.4737 \\ 4.2391 & 1 & 2.3657 & 2.1675 & 0.2913 \\ 4.8829 & 0.4227 & 1 & 0.3204 & 0.3039 \\ 2.8368 & 0.4613 & 3.1208 & 1 & 0.4458 \\ 2.1109 & 3.4325 & 3.2896 & 2.2432 & 1 \end{matrix} \end{array}]

Original matrix of level A4 was as follows,

A_{4} = [\begin{matrix} 1 & 2 & \frac{1}{3} \\ \frac{1}{2} & 1 & 3 \\ 3 & \frac{1}{3} & 1 \end{matrix}]

Optimization matrix of level A4 was as follows,

\bar{A_{4}} = [\begin{matrix} 1 & 1.8795 & 0.2952 \\ 0.5320 & 1 & 2.8794 \\ 3.3872 & 0.3473 & 1 \end{matrix}]

The above matrices all meet CR<0.1 after correction, indicating that the initial matrix meets the requirements of consistency testing after being corrected by the intelligent particle swarm optimization algorithm.

6.6. Overall evaluation of bridge engineering course teaching

Provide a set of evaluation levels V= (v1, v2, v3, v4), where v1 represents poor evaluation results, v2 represents moderate evaluation results, v3 represents good evaluation results, and v4 represents excellent evaluation results

According to the evaluation of the teaching level of 40 selected teachers, the single factor evaluation results of bridge engineering course teaching were analyzed, as shown in Table 8.

Table 4. Single factor evaluation results.

Evaluation factors A	Evaluation factors P	Evaluation level
Evaluation factors A	Evaluation factors P	v1	v2	v3	v4
A1	P11	0	5	15	20
A1	P12	0	3	11	26
A2	P21	0	3	13	24
	P22	0	2	17	21
	P23	0	4	15	21
A3	P31	0	3	13	24
	P32	0	5	18	17
	P33	0	1	14	25
	P34	0	2	15	23
	P35	0	1	12	27
A4	P41	0	1	14	25
A4	P42	0	3	13	24

According to the formula of fuzzy evaluation set, we can obtain V= (0, 0.1102, 0.2317, 0.6581). According to the principle of maximum membership degree, the fourth indicator value of bridge engineering teaching is the highest, so the teacher's comprehensive evaluation score for this course is "excellent".

7. Conclusion

Starting from the practical needs of bridge engineering course education, this study constructs a holographic concept bridge engineering course teaching evaluation system based on the intelligent analytic hierarchy process. This system can evaluate the current implementation of student-centered curriculum teaching in schools. The comprehensive evaluation of scientific and effective bridge engineering course teaching has important theoretical and practical significance, providing guidance for the future development of bridge engineering education. The research conclusion of this article is as follows:

(1) In response to the contradiction between the theoretical and practical aspects of bridge engineering teaching content, traditional teaching content has been restructured to form a clear knowledge logic system from the perspectives of structural concept design, external constraints, and internal construction.

(2) A bridge landscape knowledge system that comprehensively considers engineering and art has been proposed to meet the practical needs of bridge aesthetic literacy in the current urban construction process, guiding students to develop towards innovative talents with comprehensive qualities of bridge engineers and architects.

(3) A holographic learning environment based on the integration of physical, digital, and humanistic environments has been constructed in the teaching context, guiding students to learn everywhere, all the time, and all the media they can access.

(4) A student-centered teaching evaluation system for bridge engineering courses has been proposed, which establishes a hierarchical model from the perspectives of teaching philosophy, teaching objectives, teaching process, and teaching effectiveness to scientifically and effectively evaluate learning outcomes.

(5) The use of particle swarm analytic hierarchy process can intelligently search and identify the factor weight matrix in the analytic hierarchy process, providing a convenient means for scientifically and effectively evaluating the teaching achievements of bridge engineering courses.

Author Contributions

Investigation, D.M. and W.J.; Methodology, D.F. and Z.Z.; Writing—Original draft, D.F.; Writing—Review and editing, D.F and W. J.. All authors have read and agreed to the published version of the manuscript.

Funding

The Natural Science Foundation of Jiangsu Province (Grant No. BK20200793).

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The authors wish to express their sincere to the Natural Science Foundation of Jiangsu Province (Grant No. BK20200793).

Conflicts of Interest

The authors declare no conflict of interest.

References

Sacks, R. , and R. Barak. Teaching Building Information Modeling as an Integral Part of Freshman Year Civil Engineering Education [J]. Journal of Professional Issues in Engineering Education & Practice 136.1(2010):30-38. [CrossRef]
Zhou Y. Optimization of Civil Engineering Materials Experiment Teaching Design [J]. International Conference on Education, Management, Computer and Society 2016. [CrossRef]
Kobayashi M , Kitabatake M , Noda K ,et al. Computer-aided Design teaching in the Civil Engineering Course- As an Introductory education -[J].Japanese Colleges of Technology Education Journal, 2013:309-313.
Zhang X J and Peng W B. Exploration and practice of teaching reform in bridge engineering courses [J]. Higher Architecture Education, 17.6(2008):4.
Wu M and Xiong G J. The Inspiration of CDIO Outline on Innovative Teaching of Bridge Engineering [J]. Higher Architecture Education, 16.5(2007):102-106.
Wu M and Xiong G J. Exploration and Practice of Bridge Engineering Teaching Reform Based on Engineering Ability Cultivation [J]. Journal of Changsha Railway University (Social Science Edition),11.1(2010):5.
Zeng Y, Xu X. The Construction and Optimization of an AI Education Evaluation Indicator Based on Intelligent Algorithms[J].International Journal of Cognitive Informatics and Natural Intelligence,2022,16(1):1-22. [CrossRef]
Ran G Q. Cultivating top-notch innovative talents in basic disciplines with student-centered approach [J]. Research on the Development of Higher Education, 2016(2):3.
Dang M, Zhang C W, Yang Z, et al. Exploration and Innovation of a Student Centered Integrated Teaching Model for Vehicle Engineering Majors through Competition and Education [J]. Era Automotive, 2023(21):44-46.
Yang L and Lin W Q. Reflection on the Construction System Architecture of Engineering Disciplines in Ordinary Universities [J]. Educational Research, 7(2019): 49-50.
Chun L. Students-centered" Classroom Teaching Design in Higher Vocational Colleges[J]. Journal of Xiangyang Vocational and Technical College, 2015.
Lin Y .Student-Centered Teaching Design and Practice of Database Course[J]. 2020. [CrossRef]
Davies J , Welch C , Hargis J .The Bridge Course Design: Formative Assessment and Student-Centered Learning in Cross-Course Classrooms[J].International Journal for the Scholarship of Teaching & Learning, 2008, 2(2). [CrossRef]
Hong Z , Xiao-Bing N , Jing-Wei Z ,et al.Design and Practice of Student-centered Teaching Mode of Electrical Engineering and Automation Courses[J].Education Teaching Forum, 2019.
Simon D. Evolutionary optimization algorithms[M].John Wiley &Sons,2013.
Cuevas E, Cienfuegos M,Zaldívar D,et al.A swarm optimization algorithm inspired in the behavior of the social-spider[J].Expert Systems with Applications,2013,40(16): 6374-6384. [CrossRef]
Ayyarao T S L V, Ramakrishna N S S, Elavarasan R M, et al. War strategy optimization algorithm:a new effective metaheuristic algorithm for global optimization[J].IEEE Access,2022,10:25073-25105. [CrossRef]
Javanbarg M B, Scawthorn C,Kiyono J,et al. Fuzzy AHP-based multicriteria decision making systems using particle swarm optimization[J].Expert systems with applications, 2012,39(1):960-966. [CrossRef]

Figure 1. Holographic Learning "Pyramid" Model.

Figure 2. Learning model of the holographic concept.

Figure 3. Holographic conceptual learning paradigm of "problem-oriented and learning-centered".

Figure 4. Hierarchical structure.

Figure 5. Solution process of reliability index based on PSO algorithm.

Figure 8. Teaching effectiveness evaluation system.

Figure 9. Particle Swarm Optimization Process of Analytic Hierarchy Process.

Table 1. Average Random Consistency Index Values.

Order $n$	1	2	3	4	5	6	7	8	9	10	11	12
$R I$	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49	1.52	1.54

Table 2. The construction of learning environment under the holographic concept.

Type	Construction	Action
Physical environment	Holographic Learning Classroom	Support centralized learning, group learning, and personalized learning
	Network classroom
	Laboratory
	Prop	Bridge physical model, playing cards, teaching baton, tape measure, LEGO
	Textbook	Learning physical materials
	Etc.	Project site, campus bridges, bridges in daily life
Digital environment	Online courses	Autonomous learning, testing, tracking and evaluation
	Virtual simulation experiment	Immersive experience
	Rain Classroom	Roll call and collective interaction
	Wechat and QQ groups	Q&A, personalized interaction
	Ipad	Problem solving and drawing
	Bridge game	Virtual environment participation in bridge construction
	Tiktok	Bridge Micro Video Collection
	Wechat official account	Learning and sharing experiences
	VR	Mmersive experience
	Mechanics Master Software	Rapid modeling and analysis
Cultural environment	Enterprise personnel	Joint guidance, integrating theory with practice
	Movies	Movies related to bridges, Spring Festival Gala programs related to bridges, and variety shows related to bridges
	Poetry	Bridge Culture Cultivation
	Story	Bridge emotional resonance
	Etc.	Bridge cuisine, bridge wine, bridge paintings, etc

Table 3. Teaching evaluation standards.

Evaluation dimension	Evaluation points
A1:Teaching philosophy	P11:The teaching philosophy embodies the student-centered education philosophy, embodies the idea of cultivating morality and talents, and is in line with the characteristics of the subject and the requirements of the curriculum.
A1:Teaching philosophy	P12:Guided by the construction of new engineering disciplines, we will promote education and teaching reform and improve talent cultivation capabilities.
A2:Teaching content	P21:The teaching content has depth and breadth, reflecting high-level, innovative, and challenging aspects.
	P22:Reflecting the forefront of the discipline, infiltrating professional ideas, and utilizing high-quality teaching resources.
	P23:The teaching content meets the needs of the industry and society, handles the teaching emphasis and difficulties appropriately, focuses on the existing knowledge and experience of students, and has scientific content.
A3:Teaching process	P31:Emphasize student-centered innovative teaching, reflecting teacher led and student-centered approaches.
	P32:The teaching objectives are scientific and accurate, in line with the requirements of the syllabus, subject characteristics, and student reality, reflecting the requirements for knowledge, abilities, and thinking.
	P33:Orderly teaching organization and reasonable arrangement of teaching process; Innovative teaching methods and strategies, emphasizing teaching interaction, inspiring students to think and solve problems.
	P34:Creating a teaching environment with information technology to support teaching innovation.
	P35:Innovate the content and methods of assessment and evaluation, emphasizing the solution and application of formative evaluation and generative problems.
A4:Teaching effectiveness	P41:Classroom teaching is attractive, the classroom atmosphere is harmonious, students have active thinking, and participate deeply in the classroom.
	P42:Students develop their knowledge, abilities, and thinking to achieve teaching objectives.
	P43:Forming a teaching model that is suitable for the characteristics of the subject and students has significant reference and promotion value.

Table 4. Factor weight of indicator P1 under indicator A1.

Index P1	P11	P12	Wi
P11	1	0.3	0.35
P12	3	1	0.65

Table 5. Factor weights of indicator P2 under indicator A2.

Index P2	P21	P22	P22	Wi
P21	1	0.3	0.25	0.4135
P22	3	1	2	0.3171
P23	4	0.5	1	0.2694

Table 6. Factor weight of indicator P3 under indicator A3.

Index P3	P31	P32	P33	P34	P35	Wi
P31	1	0.25	0.2	0.3	0.5	0.1798
P32	4	1	2	2	0.3	0.1827
P33	5	0.5	1	0.3	2	0.2637
P34	3	0.5	3	1	0.5	0.1726
P35	2	3	0.5	2	1	0.2012

Table 7. Factor weights of indicator P4 under indicator A4.

Index P4	P41	P42	P43	Wi
P41	1	2	0.3	0.3124
P42	0.5	1	3	0.2138
P43	3	0.3	1	0.4738

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Students-Centered Assessment Research on Holographic Learning Paradigm Based on Intelligent Analytic Hierarchy Process in Teaching of Bridge Engineering Course

Abstract

1. Introduction

2. Teaching philosophy model

2.1 Philosophy

2.2 Train of thought

3. Analytical Hierarchy Process

3.1. Building a hierarchical model

3.2. Constructing a judgment matrix group

3.3. Hierarchical sorting and consistency testing

4. Particle Swarm Optimization

4.1. Basic concepts

4.2. Algorithm optimization

4.3. Algorithm process

5. Teaching design scheme of Bridge Engineering Course

5.1. Restructuring the curriculum content system

5.2. Multidimensional guided teaching methods

5.3. Integrating course resources through multiple channels

5.4. Multidisciplinary intersection and integration of "engineering + art"

5.5. Evaluation of teaching effectiveness

6. Application

6.1. Selecting interviewees

6.2. Develop interview outline

6.3. Implementation of interviews

6.4. Analytic Hierarchy Process Statistical Results

6.5. Optimization of evaluation system based on particle swarm optimization algorithm

6.6. Overall evaluation of bridge engineering course teaching

7. Conclusion

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe