Prerpints.org logo
Preprint
Article

Investigating the Terrain of Class-incremental Continual Learning: A Brief Survey

Altmetrics

Downloads

300

Views

179

Comments

0

This version is not peer-reviewed

Submitted:

24 December 2023

Posted:

27 December 2023

You are already at the latest version

Alerts
Abstract
Continual learning, a crucial facet of machine learning, involves the perpetual acquisition of valuable insights from incoming data, sans the necessity for full dataset access. Esteemed as a fundamental goal in artificial intelligence, continual learning grapples with an enduring challenge—catastrophic forgetting. A proficient model must exhibit adaptability for new data assimilation and robustness to retain existing knowledge. Class-incremental learning (CIL) aids the gradual integration of knowledge from newly introduced classes, forming a universal classifier. However, directly training the model with fresh class instances triggers a problem—forgetting distinguishing features of prior classes, causing a performance decline. Addressing such issues in machine learning, this survey aims to delineate significant challenges, outcomes, and recent advancements, including our contributions to CIL techniques, especially in image classification.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Continuous learning (CL) refers to a framework for acquiring new information from streaming data while maintaining a considerable amount of previously acquired knowledge. Imitation learning is a type of machine learning (ML) that is particularly effective at handling tasks which are closely aligned with human behaviour and cognitive processes. Considering that new information and previously acquired knowledge do not consistently adhere to a symmetrical distribution of data, continuous learning must be more rigorous in nature. The conventional ML model is trained using static, well-labeled, and uniformly distributed training data [1]. While the tangible world is constantly evolving, intelligent agents are required to possess the ability to learn and retain information continuously. The use of a continual learning model facilitates the assimilation of new information while concurrently safeguarding previously acquired knowledge over an extended duration. The notable resemblance in operational characteristics between the operation of this system and the cognitive mechanisms of a biological organism’s brain makes it a major focus point in the advancement of artificial intelligence systems. In recent times, there has been a growing acknowledgment of the significance of its involvement in several domains including intelligent robotics, autonomous driving, and unmanned aerial vehicles (UAVs) [2,3].
During the process of acquiring new information, the backpropagation method is used to modify the parameter weights based on the loss seen in the sequential data that is accessible. Consequently, the model’s ability to retain previously acquired information will be adversely affected by the aforementioned phenomenon. Catastrophic forgetting (CF) is a well-recognized phenomenon in the field of continual learning. To address the challenges associated with CF, a model needs to possess both plasticity, enabling it to learn new information, and stability, facilitating the consolidation of current knowledge.
Besides the backpropagation algorithm, there exists an alternative approach for model creation that is rooted in non-iterative training. The learning process described by Zhang et. al. [4] is characterized by a combination of both global order and local randomness, resulting in a high level of efficiency.
People have a remarkable aptitude for learning in dynamic circumstances. The brain has the capacity to gradually learn and retain information throughout consecutive tasks, owing to its extensive neuro-physiological development through evolution. Hence, the examination of the brain’s knowledge-processing ideas via physiological techniques serves as a source of inspiration for the advancement of algorithmic methodologies. There are mechanisms in place that govern the equilibrium amongst the degree of stability and adaptability of brain regions and cognitive processes, which are created in response to external stimuli [5,6]. The concept of Hebbian Plasticity has been used to elucidate the mechanisms by which neurons react to external inputs [7]. It is postulated that in instances whenever a single neuron influences the behavior of another, there is an expectation that the synaptic connection between them would undergo a process of reinforcement. The enhancement of Hebbian plasticity may be achieved by the implementation of synaptic restrictions and the incorporation of feedback signals [8,9]. The notion of a parallel training system was first introduced in a seminal paper by authors cited as [10]. The findings indicate that the area of the hippocampus exhibits quick learning capabilities and short-term flexibility, whereas the cerebral cortex, on the other hand, demonstrates slower learning processes and the formation of long-term memories. Numerous studies have been conducted in response to the aforementioned notion. Goodfellow et. al. led a research on the impact of catastrophic forgetting (CF) on deep neural networks (DNNs), whereby they advocated the use of the dropout strategy [11,12,13]. In their study, Kirkpatrick et. al. conducted an evaluation of the significance of parameter weight and put forward the notion that model stability may be effectively maintained by the use of weight regularization [14]. The process of distillation was used as a means of amalgamating novel and preexisting information [15]. The retention of outdated data was observed, and the incorporation of playback was implemented when needed [16]. A group of researchers performed questionnaires pertaining to continual learning approaches. In the cited references [17,18], several methodologies are presented that are predicated upon distinct structural frameworks, with a primary emphasis on the explication of the model. Nevertheless, the current body of research is fairly outdated and lacks comprehensive analysis, particularly in regard to methods that address the challenges associated with CF.
The subsequent sections of this research are organized in the following manner. Section 2 explains, in brief, the problem definition for class-incremental (CI) learning more precisely. Section 3 presents the general setup of prevalent CL systems. Section 4 provides an overview of the relevant literature pertaining to class-incremental learning. Section 5 discusses some of our previous research pertaining to CL systems. In Section 6 we examine possible future work and we conclude in Section 7.

2. Problem formulation

The configuration may be articulated as follows. A class-incremental learning (CIL) system takes data in the form of a stream ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , where y i denotes the given class label for the data point x i . Data is divided into multiple tasks, in theory, maintaining an ongoing flow. Within a CI environment that adheres to an incremental approach, task identification is fundamentally lacking throughout the inference process. Nevertheless, this phenomenon may occur throughout the training process; nevertheless, it is not practical to presume the presence of task ID for such occurrences. Our technique determines the demarcation of task boundaries by aggregating data into batches. More precisely, each set of data functions as the fundamental entity for a certain undertaking. Within the specified constraints, the model undergoes retraining and selects exemplars for future use. While the possibility of implicitly preserving a task ID is available, it is not used in our present technique.
In a disjoint class-incremental arrangement, the classes encountered in each task demonstrate a state of being isolated or different from one another. The frequency of classes in each new task stays consistent. It is worth mentioning that there might be discrepancies in the number of data points in each class, often known as data imbalance. Therefore, the total number of data points may vary across various activities.
In blurry B CIL configuration, in which B represents a percentage, often a small value, it is postulated that each task is characterized by a certain number of novel classes that serve as the defining elements of the task. However, it is also acknowledged that the task may include information from distinct classes, as well as a proportion of B % of classes that pertain to different tasks. In this particular circumstance, it is apparent that there is an undersupply of lucidity about the classification of tasks and their respective defining classes. Consequently, the borders of tasks are seen as indistinct or ambiguous. The CIL setups that are disjoint or blurry may be expressed as:
Class - incremental learning ( disjoint ) ⇒ ⋂ t = 0 T = Φ , Class - incremental learning ( blurryB ) ⇒ ⋂ t = 0 T ≠ Φ
T represents a total amount of tasks, while t represents a specific task.
CF is significantly more difficult to solve because previously encountered classes are never revealed in the next tasks when using the disjoint CIL setup. Conversely, blurryB CIL lacks clarity regarding the separation across tasks, resulting in B% of the information gathered from other (secondary classes) appearing in each task and (100-B)% of the information originating from primary classes. This is a broader concept than disjoint CIL, which is equivalent to blurry0 CIL.

3. General architecture of class-incremental learning setups

The fundamental elements of a generic class-incremental learning system for rehearsal-based, regularization-based, and architecture-based are delineated.

3.1. Regularization-based CIL

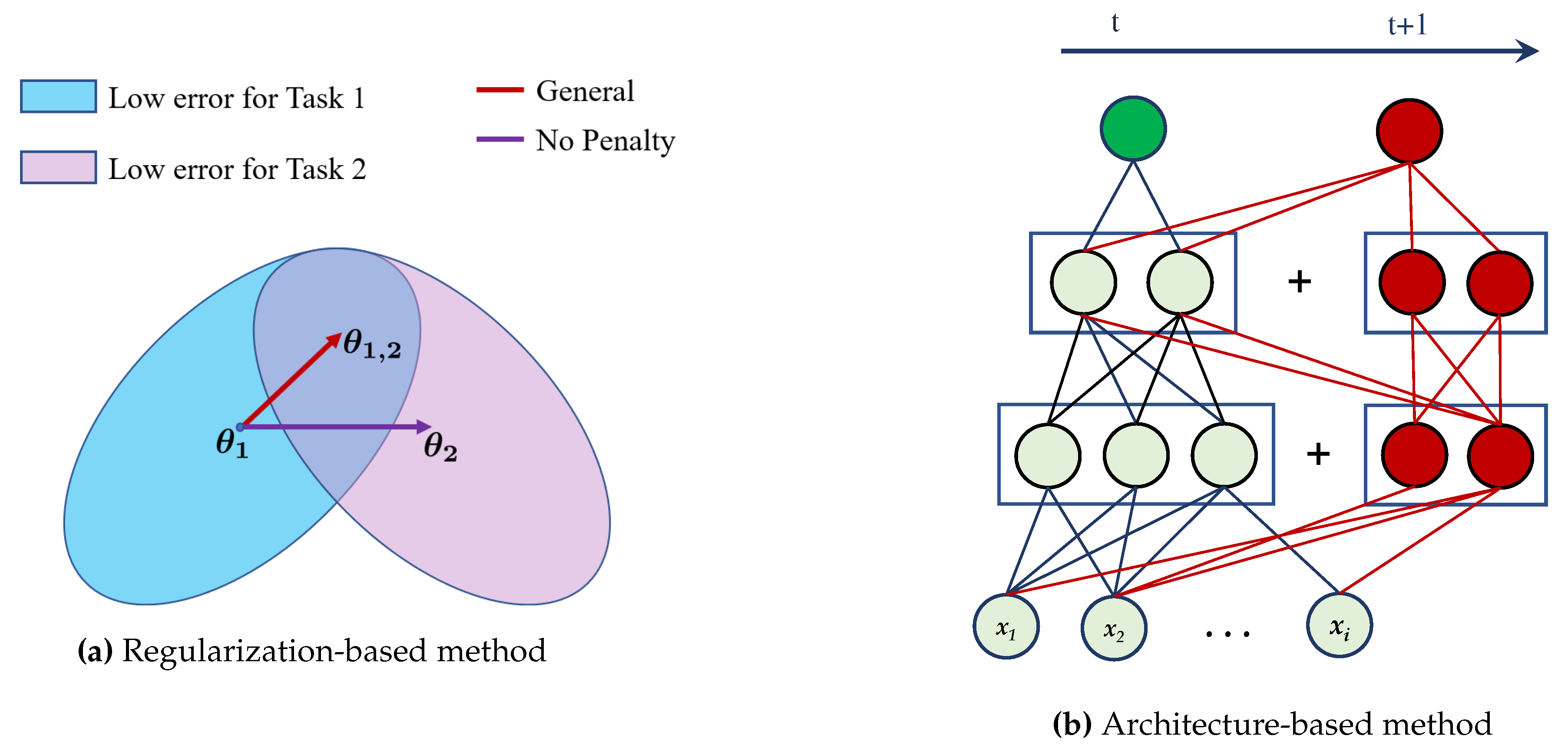
The use of regularization-based methodologies may potentially mitigate the occurrence of forgetting since these techniques aim to prevent substantial changes in network parameters upon the introduction of a new task. Bayesian, distillation, and optimization trajectory-based methods are significant subcategories within the realm of these kinds of methods. In this particular case, the loss function is subject to regularization using importance-based methods in order to mitigate fluctuations in the values of the parameters that have significant value in previous tasks. A general illustration showing the working of this approach is depicted in Figure 1a.
Distillation-based approaches include the transfer of acquired knowledge from a previously trained model to a fresh model. In contrast, optimization trajectory-based methods use the geometric attributes of local minima to address the issue of CF. The solutions outlined in the preceding statement are susceptible to task-to-task domain shift, as noted by Aljundi et al. (2017). The setting of the demonstration of regularization-based continual learning techniques is shown in Figure 1a.

3.2. Architecture-based CIL

The underlying justification for employing architecture-based techniques is in the recognition that different tasks necessitate separate sets of separate parameters. Consequently, these parameter sets can be fixed or augmented. The aforementioned strategies demonstrate efficacy in mitigating the phenomenon of CF on a global scale. However, it is imperative to note that their successful implementation necessitates the presence of a resilient foundational network. Furthermore, it is important to acknowledge that these techniques are applicable only within a restricted range of tasks. A schematic representation illustrating the functioning of this technique is presented in Figure 1b.

3.3. Rehearsal-based CIL

Rehearsal-based methodologies involve the maintenance of a memory that serves as the basis for a limited number of samples derived from earlier acquired tasks. Simultaneous learning of a novel task while having accessibility to samples from already learned tasks facilitates the incorporation of high-level information to the task at hand. Figure 2 depicts a schematic representation that illustrates the operational principles of this technique.

4. Literature review

4.1. Approaches in rehearsal-based CIL

It is a typically used technique in which a limited number of previous training data points are stored in a tiny memory buffer. The primary obstacles arise from the very constrained storage capacity, necessitating careful consideration of both the construction and use of the memory buffer. In terms of construction, it is important to exercise caution while selecting, compressing, augmenting, and updating the saved previous training data points. This process is essential in order to effectively and flexibly retrieve the previous knowledge. Previous research has used predetermined criteria for the selection of exemplars. An approach known as Reservoir Sampling [19,20,21] is used to randomly retain a certain number of previous training samples acquired from each training batch. The use of a Ring Buffer [22] serves to guarantee an equitable distribution of previous training exemplars across all classes. The Mean-of-Feature [16] algorithm is designed to pick a balanced number of training samples from each class whose values fall nearest to the average of the features. There exist numerous additional algorithms such as k-means [19], plane distance [20], and entropy [20], nevertheless, their performance is shown to be suboptimal [19,20]. Advanced strategies in optimization often involve gradient-based approaches that can be optimized.

4.2. Approaches in regularization-based CIL

Many studies have focused on enhancing the optimization process via the lens of loss landscapes. For instance, instead of using a specific method, Stable-SGD [23] allows for the discovery of a flat local minimum by the adjustment of several elements in the training process, like dropout, rate of learning decay, and the size of the batch. The research investigation conducted by MC-SGD [24] provides evidence that the local minima achieved by multi-task learning, which involves training all successive tasks jointly, as well as continuing learning, may be linked along a linear trajectory characterized by low error. Additionally, MC-SGD employs experience replay to identify an improved solution along this trajectory. The Linear Connector [25] utilizes the Adam-NSCL [26] algorithm and feature distillation technique to derive solutions for both the previous and current tasks that are linked by a linear pathway with minimal error. This is then followed by a linear averaging process. From an empirical standpoint, it can be observed that both phenomena can be ascribed to the acquisition of a more resilient representation, characterized by qualities such as orthogonality, sparsity, and uniform scattering.

4.3. Approaches in architecture-based CIL

Several network architectures, including Piggyback [27], WSN [28], and H2 [29], have been developed to optimize a binary mask inside a fixed network architecture. These architectures aim to pick specific neurons or parameters for each task while keeping the masked portions of the old tasks (nearly) frozen to avoid CF. PackNet [30], UCL [31], CLNP [32], AGS-CL [33], and NISPA [34] employs explicit identification of crucial neurons or parameters for the present task. Subsequently, they discard the less significant components for subsequent tasks. This process is accomplished through iterative pruning [30], activation value [32,33,34], uncertainty estimation [31], and other relevant techniques. Due to the restricted capacity of the network, the “free” parameters have a tendency to reach saturation when more incremental tasks are added. Hence, these approaches often need the imposition of sparsity limitations on parameter use and the selective reutilization of previously frozen parameters, potentially impacting the learning process of each individual job. In order to address this predicament, the network design has the potential to be flexibly enlarged in the event that its capacity proves inadequate for effectively learning a new job. This may be achieved via the use of several techniques such as DEN [35], CPG [36], and DGMa/DGMw [37].

5. Our works and methodologies

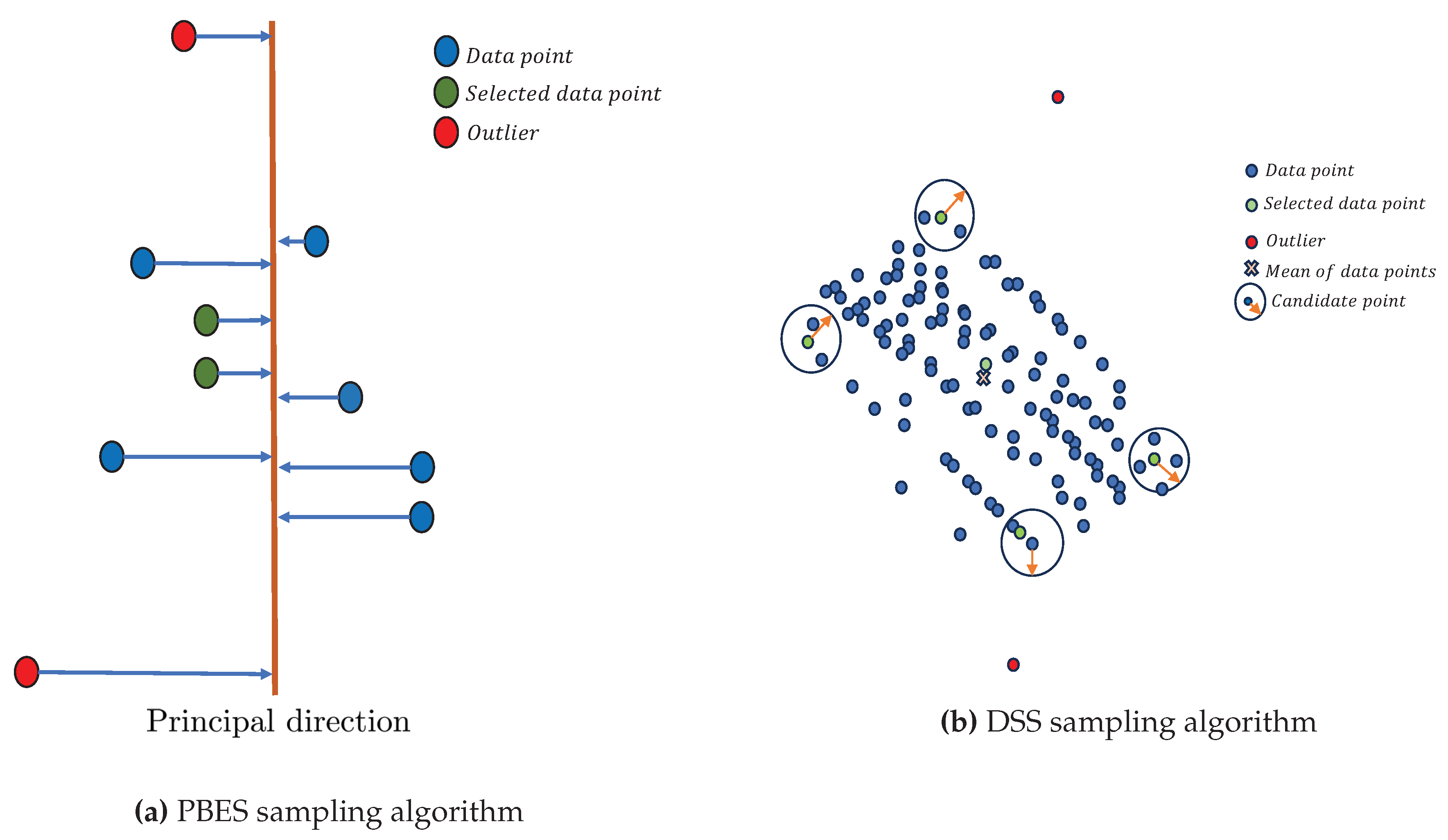
The research [38] presents an innovative sampling technique that effectively identifies representative data from inbound data used for training, hence mitigating the issue of CF. To collect the exemplars, the initial step involves projecting the incoming data points onto principal directions using the PCA algorithm. Subsequently, two median points are selected from each principal direction until the desired number of exemplars is reached. Another addition to the work is the implementation of a learning regime utilizing KeepAugmentation [39] in order to generate a well-balanced training dataset based on an initially unbalanced dataset. Figure 3a, illustrates the working of the “PBES” algorithm. This work has achieved 6.13% better accuracy on the CIFAR100, 8% on Sports100, 21.28% on Sports73, and 1.23% on Tiny-ImageNet datasets compared to other SOTA techniques.
In our study [40], we introduce a cutting-edge sampling technique called “DSS” that utilizes K-center clustering. This technique is characterized by its simplicity, implementation efficiency, ability to maintain diversity among stored exemplars, and resilience to data outliers. We evaluate its performance in offline class-incremental learning scenarios, considering both blurry and disjoint task boundaries. In order to obtain a representative subset of exemplars, the method initially decreases the dimensions of the incoming data stream, hence enhancing its efficiency in processing. Initially, a point that is closest to the mean is chosen and thereafter placed in the rehearsal memory, represented as P. Following this, an additional exemplar, denoted as e, is selected. This exemplar is picked based on its maximum distance from the current set of exemplars, denoted as P. Furthermore, e must satisfy the condition of having at least n nearby data points within a specified distance r. It is important to note that the values of n and r are provided as hyper-parameters. The process is repeated until the required m points have been selected. Further information can be found in [40], and the operational process of the “DSS” algorithm is shown in Figure 3b. The results show that the “DSS” outperforms other cutting-edge methods such as BiC and GDumb, consistently by at least 10% in accuracy.
In our paper [41], we propose the utilization of Natural Gradient within the regularization-based CIL framework as a strategy to improve the efficacy of neural network training, while simultaneously preserving the accuracy of inference results. The methodology we present has the potential to optimize the training process, leading to a reduction in time required to reach a similar grade of accuracy by 7.71%. For further information, please see the reference provided [41].

5.1. Experimental work

In the experiments carried out a comparative analysis was first performed among our proposed technique and established SOTA methodologies, namely GDUMB [42], Rainbow Memory [43], BiC [44], and iCaRL [16]. Additionally, we conduct a comparative analysis of our methodology in relation to two other methods, namely upper-bound and fine-tuning. In the fine-tuning technique, the training process only incorporates the new class images while disregarding the stored exemplars.
The application of cross-entropy loss is limited to the novel class images, while the investigation of distillation loss is omitted. Therefore, the quantity of exemplars is equal to zero. The fine-tuning strategy is considered a conservative estimate for our situation with regard to performance. In the context of the lower limit, the exemplars are not retained in rehearsal memory, and the training process for all tasks is conducted without taking into account any stored exemplars. The upper-bound technique incorporates all previously seen data points in each task and imposes the loss of cross-entropy. In summary, the quantity of exemplars assigned to each class corresponds to the total number of images associated with that specific class.

5.2. Datasets and Metrics used

Our research has conducted experiments using widely recognized image datasets, including CIFAR100, iFood251, Sports73, and Sports100.
In order to assess the effectiveness of our research, we have employed well-established performance indicators, namely Average accuracy, Last accuracy, and per-task accuracy.

6. Future directions

The examination of biologically inspired methodologies, such as neuroplasticity and synaptic consolidation, has the potential to facilitate the development of CL systems that are more efficient and adaptable. Moreover, it is essential to do research on domain-agnostic techniques that facilitate the transfer of knowledge across a wide range of tasks and datasets, hence improving the generalization capabilities of models. An additional area that has yet to be thoroughly investigated is the use of meta-learning methodologies in order to construct models that possess the ability to swiftly adapt to novel classes. The research on the intersection of interpretability, fairness, online, and class-incremental learning has received little attention and is in need of more investigation. In general, these unexplored pathways have the potential to provide more comprehensive, adaptable, and accountable class-based learning methods.

7. Conclusion

This review paper has presented a concise examination of class-incremental learning, elucidating its fundamental principles, obstacles, and current
approaches. The significance of ongoing adaptation in response to constantly changing streams of data and the need to address the issue of catastrophic forgetting (CF) have been thoroughly examined. The literature review emphasizes the continued effort to design class-incremental learning algorithms that are efficient, effective, and adaptable, emphasizing the urgent need for more research and development. The expansion of the area is apparent; yet, there exists a significant amount of unexplored possibilities, notably in the domains of interpretability, cross-domain transfer, and biologically inspired models. As the pursuit of more adaptable and inclusive artificial intelligence (AI) systems progresses, the exploration of class-incremental learning remains a vital area of focus within the field of machine learning.

References

  1. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778. [CrossRef]
  2. Feng, F.; Chan, R.H.; Shi, X.; Zhang, Y.; She, Q. Challenges in task incremental learning for assistive robotics. IEEE Access 2019, 8, 3434–3441. [Google Scholar] [CrossRef]
  3. Mozaffari, A.; Vajedi, M.; Azad, N.L. A robust safety-oriented autonomous cruise control scheme for electric vehicles based on model predictive control and online sequential extreme learning machine with a hyper-level fault tolerance-based supervisor. Neurocomputing 2015, 151, 845–856. [Google Scholar] [CrossRef]
  4. Zhang, J.; Li, Y.; Xiao, W.; Zhang, Z. Non-iterative and fast deep learning: Multilayer extreme learning machines. Journal of the Franklin Institute 2020, 357, 8925–8955. [Google Scholar] [CrossRef]
  5. Power, J.D.; Schlaggar, B.L. Neural plasticity across the lifespan. Wiley Interdisciplinary Reviews: Developmental Biology 2017, 6, e216. [Google Scholar] [CrossRef] [PubMed]
  6. Zenke, F.; Gerstner, W.; Ganguli, S. The temporal paradox of Hebbian learning and homeostatic plasticity. Current opinion in neurobiology 2017, 43, 166–176. [Google Scholar] [CrossRef] [PubMed]
  7. Morris, R.G. Do hebb: The organization of behavior, wiley: New york; 1949. Brain research bulletin 1999, 50, 437. [Google Scholar] [CrossRef] [PubMed]
  8. Abbott, L.F.; Nelson, S.B. Synaptic plasticity: taming the beast. Nature neuroscience 2000, 3, 1178–1183. [Google Scholar] [CrossRef] [PubMed]
  9. Song, S.; Miller, K.D.; Abbott, L.F. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nature neuroscience 2000, 3, 919–926. [Google Scholar] [CrossRef] [PubMed]
  10. McClelland, J.L.; McNaughton, B.L.; O’Reilly, R.C. Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connectionist models of learning and memory. Psychological review 1995, 102, 419. [Google Scholar] [CrossRef] [PubMed]
  11. Goodfellow, I.J.; Mirza, M.; Xiao, D.; Courville, A.; Bengio, Y. An empirical investigation of catastrophic forgetting in gradient-based neural networks. arXiv preprint arXiv:1312.6211 2013. [CrossRef]
  12. Nokhwal, S.; Pahune, S.; Chaudhary, A. EmbAu: A Novel Technique to Embed Audio Data using Shuffled Frog Leaping Algorithm. Proceedings of the 2023 7th International Conference on Intelligent Systems, Metaheuristics & Swarm Intelligence, 2023, pp. 79–86. [CrossRef]
  13. Tanwer, A.; Reel, P.S.; Reel, S.; Nokhwal, S.; Nokhwal, S.; Hussain, M.; Bist, A.S. System and method for camera based cloth fitting and recommendation, 2020. US Patent App. 16/448,094.
  14. Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; others. Overcoming catastrophic forgetting in neural networks. Proceedings of the national academy of sciences 2017, 114, 3521–3526. [Google Scholar] [CrossRef] [PubMed]
  15. Li, Z.; Hoiem, D. Learning without forgetting. IEEE transactions on pattern analysis and machine intelligence 2017, 40, 2935–2947. [Google Scholar] [CrossRef] [PubMed]
  16. Rebuffi, S.A.; Kolesnikov, A.; Sperl, G.; Lampert, C.H. icarl: Incremental classifier and representation learning. Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, 2017, pp. 2001–2010. [CrossRef]
  17. Losing, V.; Hammer, B.; Wersing, H. Incremental on-line learning: A review and comparison of state of the art algorithms. Neurocomputing 2018, 275, 1261–1274. [Google Scholar] [CrossRef]
  18. Chefrour, A. Incremental supervised learning: algorithms and applications in pattern recognition. Evolutionary Intelligence 2019, 12, 97–112. [Google Scholar] [CrossRef]
  19. Chaudhry, A.; Rohrbach, M.; Elhoseiny, M.; Ajanthan, T.; Dokania, P.K.; Torr, P.H.; Ranzato, M. On tiny episodic memories in continual learning. arXiv preprint arXiv:1902.10486 2019. [CrossRef]
  20. Riemer, M.; Cases, I.; Ajemian, R.; Liu, M.; Rish, I.; Tu, Y.; Tesauro, G. Learning to learn without forgetting by maximizing transfer and minimizing interference. arXiv preprint arXiv:1810.11910 2018. [CrossRef]
  21. Vitter, J.S. Random sampling with a reservoir. ACM Transactions on Mathematical Software (TOMS) 1985, 11, 37–57. [Google Scholar] [CrossRef]
  22. Lopez-Paz, D.; Ranzato, M. Gradient episodic memory for continual learning. Advances in neural information processing systems 2017, 30. [Google Scholar]
  23. Mirzadeh, S.I.; Farajtabar, M.; Pascanu, R.; Ghasemzadeh, H. Understanding the role of training regimes in continual learning. Advances in Neural Information Processing Systems 2020, 33, 7308–7320. [Google Scholar]
  24. Mirzadeh, S.I.; Farajtabar, M.; Gorur, D.; Pascanu, R.; Ghasemzadeh, H. Linear mode connectivity in multitask and continual learning. arXiv preprint arXiv:2010.04495 2020. [CrossRef]
  25. Lin, G.; Chu, H.; Lai, H. Towards better plasticity-stability trade-off in incremental learning: A simple linear connector. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 89–98. [CrossRef]
  26. Wang, S.; Li, X.; Sun, J.; Xu, Z. Training networks in null space of feature covariance for continual learning. Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition, 2021, pp. 184–193. [CrossRef]
  27. Mallya, A.; Davis, D.; Lazebnik, S. Piggyback: Adapting a single network to multiple tasks by learning to mask weights. Proceedings of the European conference on computer vision (ECCV), 2018, pp. 67–82. [CrossRef]
  28. Kang, H.; Mina, R.J.L.; Madjid, S.R.H.; Yoon, J.; Hasegawa-Johnson, M.; Hwang, S.J.; Yoo, C.D. Forget-free continual learning with winning subnetworks. International Conference on Machine Learning. PMLR, 2022, pp. 10734–10750.
  29. Jin, H.; Kim, E. Helpful or Harmful: Inter-task Association in Continual Learning. European Conference on Computer Vision. Springer, 2022, pp. 519–535. [CrossRef]
  30. Mallya, A.; Lazebnik, S. Packnet: Adding multiple tasks to a single network by iterative pruning. Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, 2018, pp. 7765–7773. [CrossRef]
  31. Ahn, H.; Cha, S.; Lee, D.; Moon, T. Uncertainty-based continual learning with adaptive regularization. Advances in neural information processing systems 2019, 32. [Google Scholar]
  32. Golkar, S.; Kagan, M.; Cho, K. Continual learning via neural pruning. arXiv preprint arXiv:1903.04476 2019. [CrossRef]
  33. Jung, S.; Ahn, H.; Cha, S.; Moon, T. Continual learning with node-importance based adaptive group sparse regularization. Advances in neural information processing systems 2020, 33, 3647–3658. [Google Scholar]
  34. Gurbuz, M.B.; Dovrolis, C. Nispa: Neuro-inspired stability-plasticity adaptation for continual learning in sparse networks. arXiv preprint arXiv:2206.09117 2022. [CrossRef]
  35. Yoon, J.; Yang, E.; Lee, J.; Hwang, S.J. Lifelong learning with dynamically expandable networks. arXiv preprint arXiv:1708.01547 2017. [CrossRef]
  36. Hung, C.Y.; Tu, C.H.; Wu, C.E.; Chen, C.H.; Chan, Y.M.; Chen, C.S. Compacting, picking and growing for unforgetting continual learning. Advances in Neural Information Processing Systems 2019, 32. [Google Scholar]
  37. Ostapenko, O.; Puscas, M.; Klein, T.; Jahnichen, P.; Nabi, M. Learning to remember: A synaptic plasticity driven framework for continual learning. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 11321–11329. [CrossRef]
  38. Nokhwal, S.; Kumar, N. PBES: PCA Based Exemplar Sampling Algorithm for Continual Learning. 2023 2nd International Conference on Informatics (ICI). IEEE, 2023. [CrossRef]
  39. Gong, C.; Wang, D.; Li, M.; Chandra, V.; Liu, Q. Keepaugment: A simple information-preserving data augmentation approach. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021, pp. 1055–1064. [CrossRef]
  40. Nokhwal, S.; Kumar, N. DSS: A Diverse Sample Selection Method to Preserve Knowledge in Class-Incremental Learning. 2023 10th International Conference on Soft Computing & Machine Intelligence (ISCMI). IEEE, 2023. [CrossRef]
  41. Nokhwal, S.; Kumar, N. RTRA: Rapid Training of Regularization-based Approaches in Continual Learning. 2023 10th International Conference on Soft Computing & Machine Intelligence (ISCMI). IEEE, 2023. [CrossRef]
  42. Prabhu, A.; Torr, P.H.; Dokania, P.K. Gdumb: A simple approach that questions our progress in continual learning. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part II 16. Springer, 2020, pp. 524–540.
  43. Bang, J.; Kim, H.; Yoo, Y.; Ha, J.W.; Choi, J. Rainbow memory: Continual learning with a memory of diverse samples. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021, pp. 8218–8227. [CrossRef]
  44. Wu, Y.; Chen, Y.; Wang, L.; Ye, Y.; Liu, Z.; Guo, Y.; Fu, Y. Large scale incremental learning. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 374–382. [CrossRef]
Preprints 94317 g001
Figure 1. Illustration of Regularization- and Architecture-based methods
Figure 1. Illustration of Regularization- and Architecture-based methods
Preprints 94317 g001
Preprints 94317 g002
Figure 2. Typical illustration of rehearsal-based method
Figure 2. Typical illustration of rehearsal-based method
Preprints 94317 g002
Preprints 94317 g003
Figure 3. Illustration of our sampling algorithms
Figure 3. Illustration of our sampling algorithms
Preprints 94317 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated