Preprint
Article
The N-Oscillator Born-Kuhn Model: An In-depth Analysis of Chiro-optical Properties in Complex Chiral Systems
Altmetrics
Downloads
85
Views
40
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
26 December 2023
Posted:
27 December 2023
You are already at the latest version
Alerts
Abstract
A comprehensive theory is developed for the chiral optical response of two configurations of the N-oscillator Born-Kuhn model (NOBK): the helically stacked and the corner stacked models. In the helical NOBK model, there is always a chiral response regardless of the value of N, whereas in the corner NOBK, only configurations with even N demonstrate a chiral response. Generally, the magnitudes of optical rotatory dispersion (ORD) and circular dichroism (CD) increase with N when the parameters of each oscillator are fixed. In cases of weak coupling, the spectral shapes of ORD and CD remain invariant, while strong coupling significantly alters the spectral shapes. For large damping, the spectral amplitude becomes smaller, and the spectral features become broader. In the presence of small damping, strong coupling introduces degeneracy in the coupled oscillator system, leading to multiple spectral features in both ORD and CD across the entire spectral region. This simple model not only can help in the design of tunable chiral metamaterials but also enhance our understanding of chiro-optical responses in structures with different configurations.
Keywords:
Subject: Physical Sciences - Optics and Photonics
1. Introduction
Chiral metamaterials – the artificially created structures that use subwavelength building blocks to break the reflection symmetry – exhibit strong optical activity and possess chiral optical properties. The importance of chiral metamaterials lies in their ability to manipulate the polarization state of light and enable new functionalities that are not readily available in naturally occurring materials. By designing chiral metamaterials with tailored optical responses, researchers can develop novel devices such as circular polarizers,[1] chiral lenses,[2] chiral absorbers,[3] etc., for applications in various fields, including optics, telecommunications, sensing[4], and imaging[5]. Understanding the chiral optical properties of these metamaterials is essential for harnessing their potential in practical applications. Chiral optical properties arise from the difference in the interaction of left-handed circularly polarized light (LCP) and right-handed circularly polarized light (RCP) with the metamaterial structures. When illuminated with circularly polarized light, chiral metamaterials induce a phase or absorption difference between LCP and RCP components, leading to a net optical activity characterized by optical rotatory dispersion (ORD) and circular dichroism (CD).
Numerical calculations are essential for understanding complex chiral structures and predicting their optical responses. Various methods, such as finite-difference time-domain (FDTD) calculation,[6] finite element method (FM),[7] discrete dipole approximation (DDA),[8,9] and rigorous coupled-wave analysis (RCWA),[10] are commonly employed for such simulations. Numerical modeling allows researchers to optimize the design of chiral metamaterial structures for specific applications. However, interpreting the results and establishing a clear physical picture linking the calculated outcomes to the intricate structures can be challenging due to the complexity of the systems and numerical algorithms.
Recently, the Born-Kuhn (BK) model has emerged as a promising approach to address this challenge.[11,12] The BK model considers spatially stacked coupled oscillators with different orientations, providing a classic framework to predict the optical activity of chiral molecules. This model treats electrons in a molecule as damped Lorentzian oscillators subjected to an external electromagnetic wave, and it has been successfully applied to explain the chiral response of two perpendicular corner-stacked nanorods.[13] A generalized version of the BK model was later presented for stacked plasmonic nanorods with arbitrary azimuthal angles or polarization directions, enabling accurate predictions of optical and non-optical activity for various two-nanorod systems.[14] The BK model has also been extended to study chiroptical properties in systems with non-linear coupling, incorporating perturbative terms for each oscillator.[15] In a recent work, a systematic comparison between the BK model and the FDTD results has been conducted, demonstrating that these methods can successfully predict the chiro-optical properties of corner-stacked plasmonic nanorods. [16]
However, in more complicated experimental scenarios, a greater number of oscillators has to be considered. For instance, Larsen et al. fabricated a triply stacked Ag oligomer with dielectric spacer layers in-between each of the Ag layers.[17] According to the correspondence principle from the BK model to plasmonic structures, each Ag layer can be treated as a damped harmonic oscillator, leading to a 3-oscillator BK model for the entire oligomer structure. In more complex scenarios, the number of plasmonic layers can be further increased, giving rise to an N-oscillator BK model. For example, in the Au-nanoparticle decorated DNA structures, a chain of Au nanoparticles was arranged in a chiral manner around a central axis.[18,19] In this case, each Au nanoparticle acts as a damped harmonic oscillator, and the entire Au-nanoparticle decorated DNA structure can be represented by an N-oscillator BK model. Moreover, Song et al. experimentally realized Au-nanoparticle decorated double helical DNA structures,[20] introducing additional complexity in configuration to the analogous BK model. Thus, it becomes important to theoretically extend the previously discussed 2-oscillator BK model to an N-oscillator BK model and investigate how the number of oscillators and the coupling among them influence the chiro-optical property. Experimental observations also indicate that the N-oscillator BK model may exhibit different oscillator configurations, which can significantly impact the resulting chiro-optical response. Therefore, it is expected that a systematic theoretical exploration of N-oscillator BK model holds great promise in providing valuable insights into the behavior of chiral structures with multiple oscillators and offers opportunities to elucidate the intricate mechanisms underlying their chiro-optical properties.
Here we present a general theory for N-Oscillator Born-Kuhn (NOBK) models with two different configurations: the helically stacked and vertically stacked models. The exact analytic experissions for ORD and CD responses of these model are derived and their chiro-optical spectral features have been investigated systematically for different damping and coupling situations.
2. N-Oscillator Born-Kuhn models
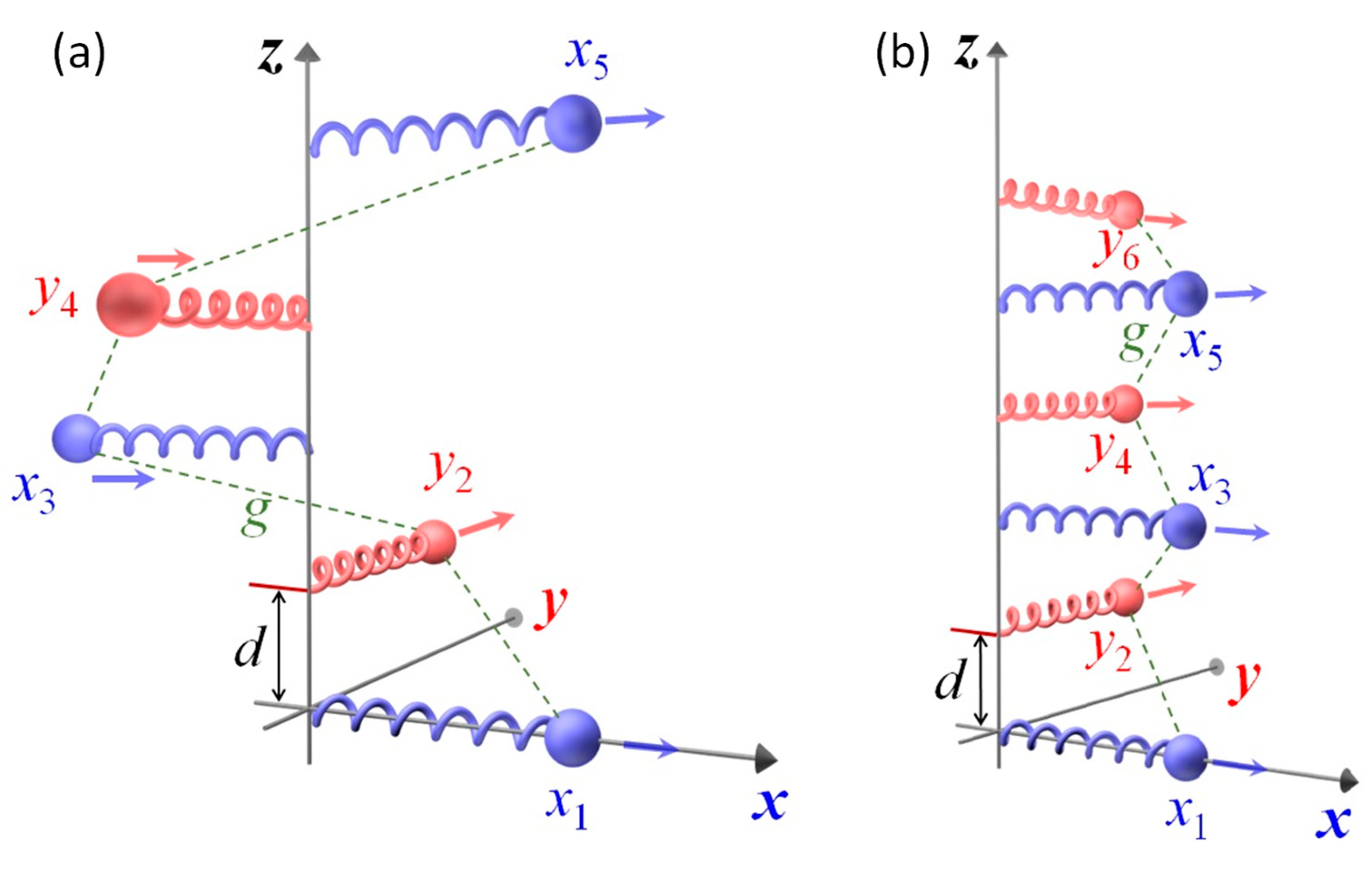
We consider two kinds of N-Oscillator Born-Kuhn (NOBK) models, the helically stacked and vertically stacked NOBK models as shown in Figure 1. Using the convention in which positive displacement always corresponds to particle’s motion in the positive direction of either - or -axis, and restricting consideration to identical damping coefficients , identical resontant frequencies , as well as identical nearest-neighbors coupling constants , the equations of motion for the oscillators in the helical NOBK model (Figure 1A) are,
 where the alternating on the left hand side are due to simple physical considerations, and there are N equations corresponding to N oscillators in the system. Since our primary interest is in system’s gyrotropic response, we assume harmonic drive in the form of a plane electromagnetic wave of frequency and wave number propagating in the positive -direction,
where and are the effective charge and mass parameters characterizing the oscillating charge distributions. Applying the steady state solutions,
where the alternating on the left hand side are due to simple physical considerations, and there are N equations corresponding to N oscillators in the system. Since our primary interest is in system’s gyrotropic response, we assume harmonic drive in the form of a plane electromagnetic wave of frequency and wave number propagating in the positive -direction,
where and are the effective charge and mass parameters characterizing the oscillating charge distributions. Applying the steady state solutions,
Figure 1.
N-Oscillator Born-Khon models: (a) the helically stacked and (b) the corner stacked.

Equation 1 can be cast in a matrix form,
with
where
For the corner NOBK model (Figure 1B), the equations of motion can be written as
The steady state solutions for Equation 6 can also be written as a matrix form of Equation 4, with
The general solution for Equation 4 can be written as,
According to Appendix A, if is the element of the inverse matrix , then
where the symbol or means taking an integer less or equal to the term in [], , and .
For both the helical and corner NOBK models, the induced polarization can then be found as,[21,22]
where , is the bulk concentration of NOBK molecules. The “” sign is for the helical NOBK model, and the “” sign is for the corner NOBK model. Insert Equation 9 into Equations 10 and 11, one has,
with
The exact expressions for polarization as a function of become rather cumbersome and not very illuminating for , which motivates us to use the quasi-static (long-wavelength) approximation, , and keep only linear terms in ,
Since for both helical and corner NOBK models, according to Equation 15, and can be written as, [16,21,22]
with
where is the gyration, representing chiral induced polarization. If we only consider chiral effect, after averaging in three-dimensional space, we get
The chiral optical response of a chiral medium is defined by three optical parameters: the index of refraction, ORD, and CD. The index of refraction for RCP, denoted as and LCP, denoted as are distinct and can be represented as, [16,23] with being the average index of refraction. In the limit of , , which is determined by . The ORD and CD can be calculated as follows,
where is optical rotation angle, is the change in the absorbance of the spectra due to the LCP and RCP incidence, is the normalized speed of light in vacuum, where v is the speed of light in vacuum, and x is the path length of the medium.
In the following section, we will discuss in detail how different NOBK models, the number of oscillators, and oscillator parameters affect the ORD and CD responses, i.e., and .
2.1. Helical NOBK model
Let’s look at N = 2 case, l = 1 and j =2, so, . Table 1 shows the calculated , , and for N = 2l (even numbers ofoscillators) and N = 2l + 1 (odd number odcillators), with . It is noticed that when N = 2l, the expressions for , , and become more complecated, while for N = 2l + 1 they are much simpler.
Below we will give an extensive discussion on how both ORD and CD change with N under different damping and coupling consitions. To make all the quantaties comparible, we set , , and , thus .
- (1)
- Large damping
In cases where b is large and c is very small, corresponding to weak coupling (, the expressions in Table 1 yield
Table 1.
The resulted , , and expression for helical NOBK models
| N | |||
| 3 | |||
| 7 | |||
| 9 |
Table 2.
The resulted , , and expression for corner NOBK models
| N | |||
i.e., according to Equations 20 and 21, the functional shapes of both ORD and CD with respect to x remain unchanged. Only the magnitude of ORD and CD experiences a linear increase with N. Figure 2a,b show the plots of and versus x for and at N = 2 to 9. As expected, the overall amplitudes of and increase with N. exhibits a primary peak around , precisely at , where attains its maximum value. At , reaches zero. Beyond these two x values, is negative. Thus, for a fixed c with the increase of N, this peak becomes sharper. On the contrary, exhibits a bisinuate line shape. At , . This observation is consistent across all values of N, b, or c, since at , and according to the expressions for in Table 1, the value is real. At , reaches a negative dip; while at , achieve a positive peak. Due to strong damping, both and curves are not symmetric about , and the overall magnitudes of and are smaller than 0.04.
In addition, and are both influenced by the coupling strength c. Figure 2c,d present two-dimensional (2D) map plots of and with varying c from 0.01 to 0.6 for N = 6. Several features can be seen: (1) The peak intensity of consistently increases with c, as indicated by Equation 24, . (2) The peak exhibits increased broadening with higher c values. (3) The separation of the negative dip location and positive peak location for increases with c. In more detail, Figure 3a shows plots of and versus x for & at N = 2 to 9. While most plots display a prominent peak, those for N = 2, 3, and 5 exhibit a notably broad peak. Also, the plots for different N show varying zero-crossing locations, as evident in Figure 2a. Although the maximum continues to monotonically increase with c, the location undergoes slight shifts. For N = 2, 4, 6, and 8, ; whereas for N = 5, 7, and 9, varies from 0.93, to 0.96, then to 0.97. In the case of N = 3, the broad peak prevents a clear definition of a maximum. Additionally, for , the spectral shape of becomes more complicated.
For odd N, the still maintains the bisinuate line-shape, but both and vary with N. Specifically, the (, ) values are (0.48, 1.31), (0.66, 1.23), (0.73, 1.19), and (0.77, 1.17) for N = 3, 5, 7, and 9, respectively. This implies that the seprataion between and decreases with N. For even N (except for N = 2), the shape of becomes more complicated at : For N = 4 and 6, distinct double dips emerge, while for N = 8, a notably broad dip appears.
As the coupling strength c increases to 0.6, indicating a scenario of strong damping and strong coupling, both and relationships for N = 2 to 9 closely resemble those at c = 0.2, with distinct , , and for a fixed N, as shown in Figure 3b. For N = 2, 4, 6, and 8, ; while for N = 5, 7, and 9, varies from 0.93, to 0.94, then to 0.95. The values of (, ) are (0.31, 1.35), (0.58, 1.26), (0.69, 1.22), and (0.73, 1.19) for N = 3, 5, 7, and 9, respectively.
Figure 4.
The plots of and at N = 2 to 9 for and (a) , and (c) .
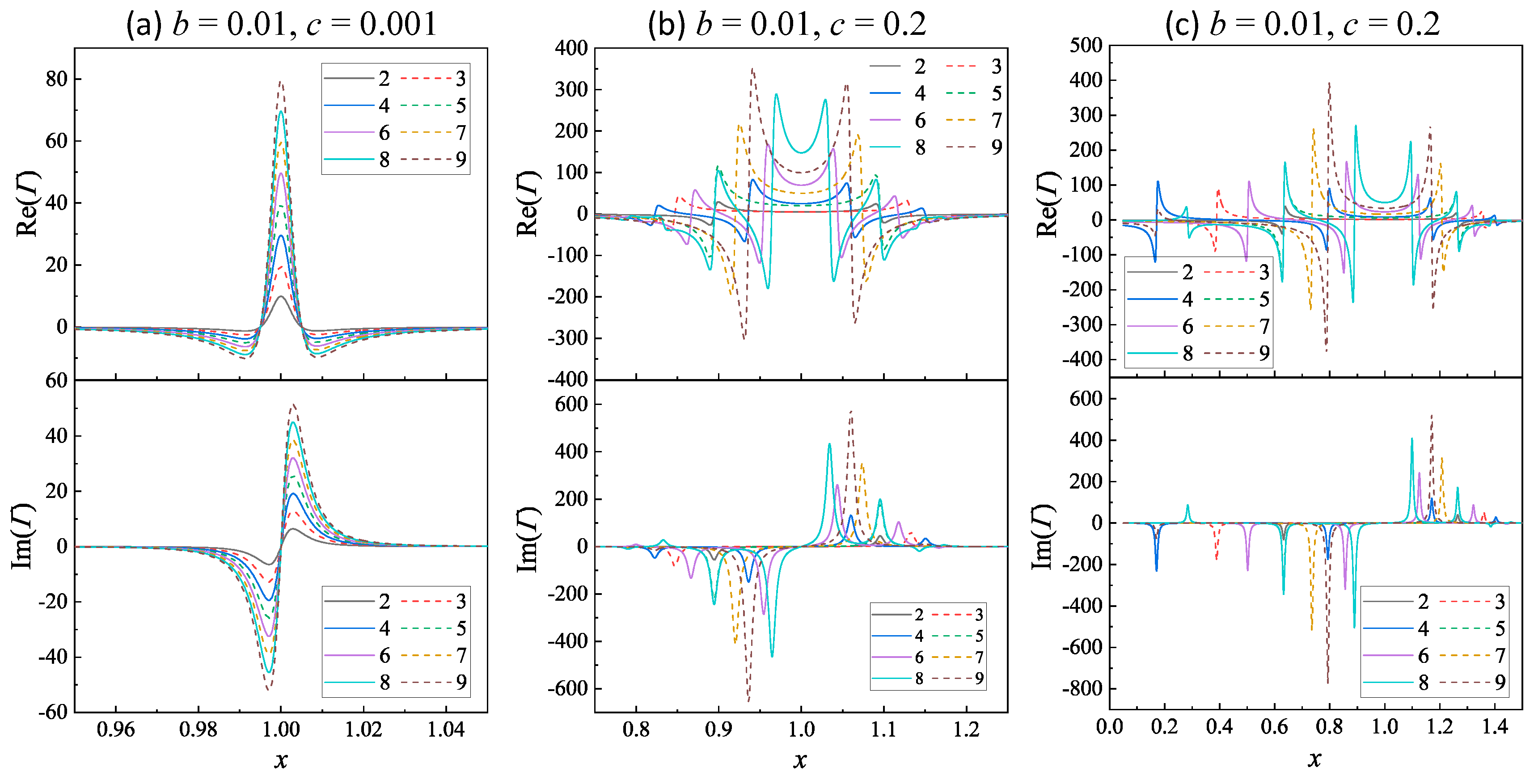
- (1)
- Small damping
Figure 4 plots the selected and relationships for N = 2 to 9 at b = 0.01 and c = 0.001, 0.2, and 0.6. In the scenario where , corresponding to large damping and weak coupling, both and have the same spectral shape as shown in Figure 4a. They are symmetric about , with for all N. There are two zero-crossings for , located at 0.995 and 1.005, respectively. Thus, the spectra are notably sharper than those in Figure 2a and the corresponding maximum values are on the order of 10 – 80, significantly larger than those in situations with larger damping. For relationship, both and are at 0.997 and 1.003, resulting in a small spectral span but much greater magnitudes compared to Figure 2b. Clearly, the magnitude of both and increases monotonically with N.
When c increases to 0.2, both and relationships become more complicated as shown in Figure 4b. For N = 3, 5,7, and 9, the spectra share a similar shape, featuring a positive curved band centered around and two large negative dips near each zero-crossing location, with the width of the central band decreasing with N. For N = 2, 4, 6, and 8, the central bands are relatively narrower than their N + 1 counterparts. While the spectrum is slightly off symmetry about , there are N/2 zero crossings in and regions, respectively. Near each zero crossing, there is either a negative dip or a positive peak. Similar features are observed for the relationship: For N = 3, 5, 7, and 9, there is only a negative dip at and a positive peak at , with specific (, ) being (0.85, 1.13), (0.89, 1.095), (0.92, 1.07), and (0.94, 1.06), respectively. For N = 2, 4, 6, and 8, N/2 positive peaks and N/2 negative dips are evident in the spectra. Specifically, for N = 2, and appear at 0.89 and 1.09; for N = 4, two negative dips occur at 0.94 and 0.82, and two positive peaks at 1.06 and 1.15; for N = 6, the negative dips are at 0.95, 0.87, 1.17, and postive peaks locate at 1.04, 1.12, 0.80; for N = 8, dips are at 0.96, 0.89, 0.79, and 1.14, peaks at 1.03, 1.1, 1.17, and 0.83. Clearly the number of peaks/dips in the plots corresponds to the number of zero crossings in the plots.
As c increases to 0.6, signifying a strong coupling case, the and relationships become even more complicated as shown in Figure 4c. All the and spectra become markedly asymmetric, with espectral features stretched in region. For N = 2, 3, 4, 5, 6, 7, and 8, both the and spectra closely resemble those at c = 0.2, yet with increased asymmetry and expanded separations of relative peaks or dips. However, for N = 9, two zero-crossing locations emerge for at and for , negative dips appear at 0.79 and 0.17, accompanied by two positive peaks at 1.17 and 1.4.
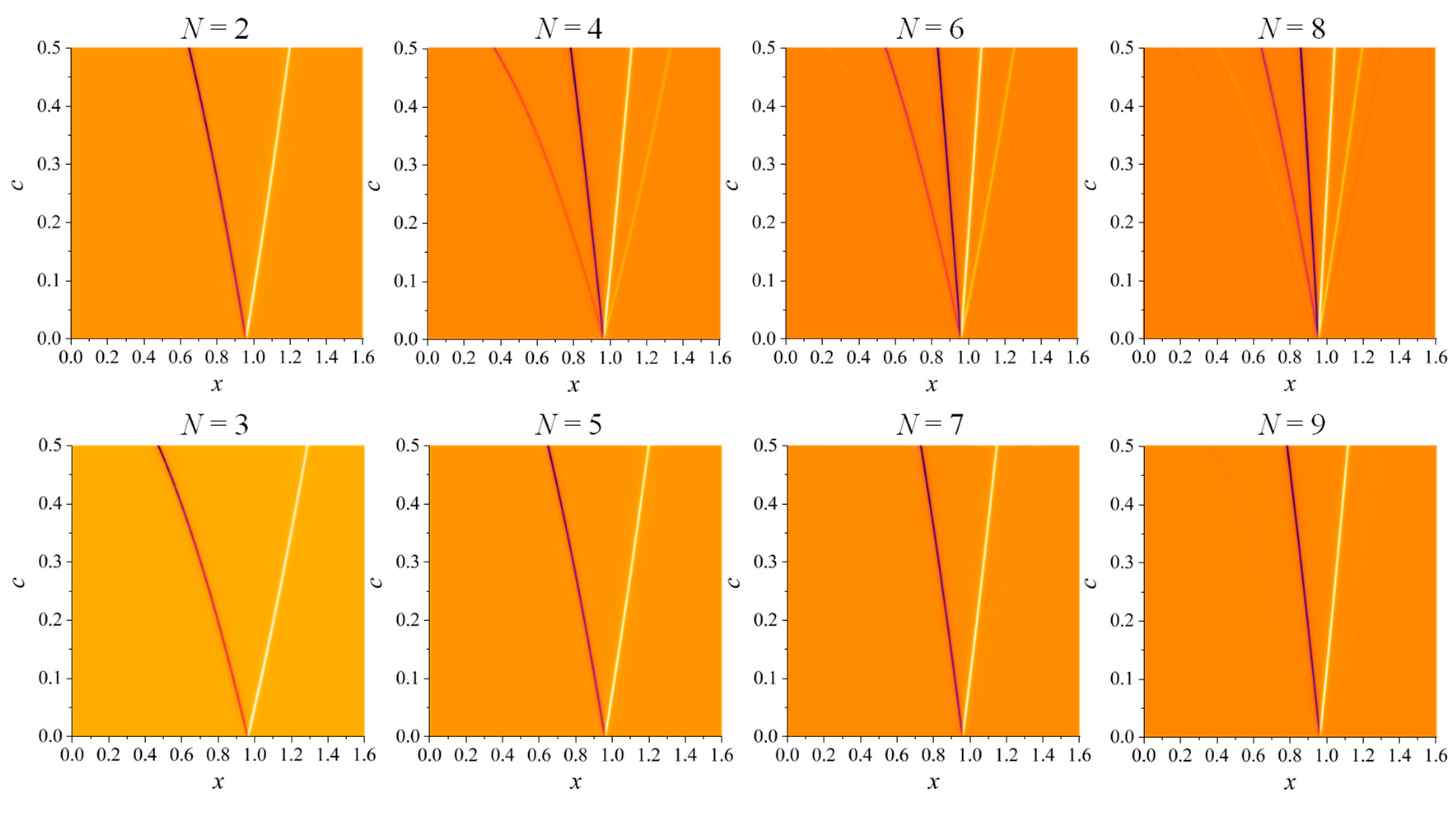
To better understand the observed splitting behaviors for different values of c, Figure 5 presents the 2D maps of as c varies from 0.001 to 0.6. The darker line-like fetures in the plots represent sharp dips while the bright curves represents sharp peaks. Initially, all maps exhibit one dip and one peak at very small c, and depending on N and c, these dip and peak split into multiple dip and peak lines. For N = 2, 3, 5, and 7, the dominate features in the maps consist of one dip line and one peak line at and , respectively. With the incease of c, the separation between and increases monotonically. However, for the same c, the and seperations become smaller with increased N. In contrast, for even N (> 2), multiple dips and peaks emerge. For example, for N = 4, two distinct dip lines appear at and two peak lines occur at . These four lines remain in both N = 6 and N = 8 maps. But in the N = 6 map, a faint peak line emerges to the left of the second dip line, and a very weak dip line appears to the right of the second peak line. For N = 8, compared to N = 6, a very weak dip line is added on the far left, while a weak peak line is introduced on the far right.
The splitting of the peaks/dips for large c arises from the degeneracy of the coupled oscillators in a weak damping case. When c is very small, the dominant oscillation modes in the NOBK system are the bonding and anti-bonding modes. As discussed in Ref.[16], the and correspond to bonding and anti-bonding modes of the system for N = 2. In fact, as c increases, the stronger coupling between two adjacent oscillators leads to the degeneration of oscillation modes. Since b is very small, the NOBK system can be treated as N-coupled harmonic oscillators with an intrinsic frequency of . Due to the coupling, the new collective oscillation mode becomes,[24]
By numerically examining the negative dip and positive peak locations of , we find that these locations are exactly corresponding to all the collected modes for N = 2l and some selected modes for N = 2l + 1. In fact, an equation can be used to fit all these x locations. For N = 2l, according to Equation 25, there are a total of 2l resonant modes emerging, which correspond to the l dips and l peaks shown in the top row of Figure 5. By fitting these locations, we find that . Thus, each of the collective modes of the N = 2l BK oscillators can exhibit a chiral response. For N = 2l + 1, when k = l + 1, , meaning that each oscillator in the NOBK model vibrates with its own intrinsic frequency, results in the absence of chiral response. Therefore, for N = 3, only two chiral modes with (which correspond to and , or ) are present. For N = 5, except for the , only when the modes of and demonstrate chiral response, and these two modes give , which is consistent with the case for N = 2. For N = 7, we found two a values, and , which correspond to and , and modes. For N = 9, also two a values are valide, and , due to and , and modes. Thus, for N = 2l + 1, all modes with do not exhibit chiral response. Such a result is due to the intrinsic mirror semmetry of the collective osscilation of these modes. Let’s take N = 5 for example, the eigen vectors for are , , , , and , respectively. The clearly eigen vector for shows non-zero x-component oscillators, and they are on the same plane; while the eigen vectors for and are mirror vectors about x-z plane: the amplitudes for the first y-oscillator and second y-oscillator are interchangible. Therefore, these two modes do not show chiral response. Similar features are observed for the eigen vectors for and of N = 7 case, and eigen vectors for & , & for N = 9 case.
2.2. Corner NOBK model
For corner NOBK model, according to Appendix A, the element of the inverse matrix can be written as,
Thus,
Due to structure symmetry, for N = 2l + 1, . Therefore, only when N = 2l, the corner NOBK model has a non-vanished The resulting expressions of , , and for N = 2l are summaried in Table 2.
Figure 6.
The plots of and of the corner NOBK models at N = 2, 4, 6, and 8 for (a) and ; (c) and and (d) and .
Figure 6.
The plots of and of the corner NOBK models at N = 2, 4, 6, and 8 for (a) and ; (c) and and (d) and .

When , and , i.e., the chiral response for N = 2 and N = 4 are the same, same for N = 6 and N = 8. Figure 6a,c show the and spectra for & and & . For both cases, due to the generancy, only two cureves exist. However, compared to case, the responses of case are much narrow but with a much higher magnitude in both and . However, when c increases, all spectra start to degenerate. For example, as shown in Figure 6b, for & , four different spectra emerge for both and . Similar trend is observed for & as shown in Figure 6d. The spectra behaviors at high damping constnat (say ) are very similar to those discussed in chiral NOBK model. But for small damping situation, the behaviors look very different. The functional format of looks like multiple band structure. For N = 2, there is a postive band between and 1.1. For N = 4, two postive bands appear, one is between and 0.94, the other between and 1.16. For N = 6, three bands are shown, to 0.87, to 1.04, and to 1.17. In between these positive bands, there are two negative bands. For , there are multiple peaks and dips quite symmetrically distributed around x = 1, each spectrum has N/2 numbers of peaks and equal number of dips. Compare to the weak coupling case, the magnitudes of both and are about one order of magnitude larger.
3. Conclusion
In conclusion, our work presents a comprehensive theory elucidating the chiral optical response of two distinct N-oscillator Born-Kohn models: the helically stacked and the corner stacked configurations. Each model comprises N identical damped oscillators with uniform coupling strength between adjacent oscillators. Our findings reveal that in the helical NOBK model, a chiral response is consistently observed irrespective of the value of N, which is due to the intrinsic mirror symmetry-breaking arrangement. However, the corner NOBK model exhibits chiral response only in configurations with even N, as odd N oscillators possess mirror symmetry and do not exhibit chiral response. Furthermore, our study demonstrates that the magnitudes of ORD and CD monotonically increase with N when the parameters of each oscillator are held constant. Specifically, we consider two scenarios: large damping and small damping. In instances of weak coupling, the spectral shapes of ORD and CD remain unchanged, whereas strong coupling induces significant alterations in their spectral shapes. For large damping, both ORD and CD exhibit small spectral amplitudes, with relatively simple and broad spectral features. In contrast, for small damping, strong coupling introduces degeneracy in the coupled oscillator system, resulting in multiple zero crossings in the ORD spectrum and multiple peaks/dips in the CD spectrum. The number of zero-crossings for ORD and peaks/dips for CD is directly related to N. Especially for CD, the collective eigen vibrations of the N = 2l helical oscillators correspond to the dips and peaks observed; while for N = 2l +1 helical oscillators, only those collective modes with no mirror symmetry eigen vector pairs can demonstrate chiral response. This comprehensive theoretical framework not only can help in the design of chiral metamaterials but also enhances our understanding of chiro-optical responses in structures with similar configurations. For example, for chiral plasmonic materials, experimentally the damping parameter b is determined by the quality of the deposited plasmonic materials and the instrinsic material properties. If the quality of the deposited material is poor, the damping b will be large, one can observe broad and simple chiral response like those shown in Figure 2, regardless of the coupling strength c. However, if high quality material is used and deposited, resulting in a small b, then the chiral optical response of the system can be tuned by the coupling strengths as well as the number of the plasmonic layers.
Author Contributions
Y.Z.: Conceptualization, Data analysis, Writing – original draft, Writing – review & editing. A.G.: Mathematica programing, Data analysis, Writing – review & editing. J. T.: General matrix theory development, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Declaration of generative AI and AI-assisted technologies in the writing process
During the preparation of this work the authors used ChatGPT in order to proof-write the manuscript, i.e., to get rid of possible grammar errors and change the sentence structures. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.
Data Availability Statement
All data are presented in the manuscript.
Acknowledgments
The authors thank Yanjun Yang for helping with Figure 1 and Nima Karimitari for useful discussions.
Appendix A
Appendix A. Inverse of the tridiagonal matrix
We consider the inverse of the general tridiagonal matrix
The inverse of this matrix can be computed using co-factor matrices. The main result is the following. First we define the second order linear recurrences
Then the inverse matrix () can be expressed as
This result is taken from Ref. [25].
A.1 Inverse of matrix of helical NOBK model
Let be the matrix of the helical NOBK model. To simplify the notation, let , then the matrix becomes,
The matrix is symmetric, tri-diagonal, with the diagonal and the other two diagonals , where . We first define the second order linear recurrences
with and ; and
Next we compute and . They are satisfying the same linear recurrence equations and initial (terminal) conditions but reversing the order. Hence we have for . We just need to compute the s.
We have essentially computed in the beginning.
Then we note that has the exactly same recursive formula as but reversing the order by starting from and . Hence we have for , i.e.,
To simplify the notation, let , since , recall that , the denominator is calculated as
Then
Note that , , and , we can simplify the denominator to be,
This implies that
and for
and .
A.2. Inverse of matrix of corner NOBK model
The matrix for the corner NOBK model can be written as,
Here and . The inverse of is given by
where the is with and and satisfies the recurrence relation
and the satisfies the recurrence relation
Then we note that has the exactly same recursive formula as but reversing the order by starting from and . Hence we have for , i.e.,
To simplify the notation, we let and
Hence for ,
and when ,
References
- Kaschke, J.; Wegener, M. Optical and Infrared Helical Metamaterials. 2016, 5, 510–523. [Google Scholar] [CrossRef]
- Li, J.; Yang, G.; Yuan, Y.; Wu, Q.; Zhang, K. Ultra-Thin Chiral Metasurface-Based Superoscillatory Lens. Frontiers in Materials 2022, 8. [Google Scholar] [CrossRef]
- Ashalley, E.; Ma, C.-P.; Zhu, Y.-S.; Xu, H.-X.; Yu, P.; Wang, Z.-M. Recent progress in chiral absorptive metamaterials. Journal of Electronic Science and Technology 2021, 19, 100098. [Google Scholar] [CrossRef]
- Yoo, S.; Park, Q.H. Metamaterials and chiral sensing: a review of fundamentals and applications. Nanophotonics 2019, 8, 249–261. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Zhu, A.Y.; Oh, J.; Devlin, R.C.; Rousso, D.; Capasso, F. Multispectral Chiral Imaging with a Metalens. Nano Letters 2016, 16, 4595–4600. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Tasco, V.; Cuscunà, M.; Todisco, F.; Benedetti, A.; Tarantini, I.; Giorgi, M.D.; Sanvitto, D.; Passaseo, A. Nanoscale 3D Chiral Plasmonic Helices with Circular Dichroism at Visible Frequencies. ACS Photonics 2015, 2, 105–114. [Google Scholar] [CrossRef]
- Lee, S.; Kang, J.-H.; Yoo, S.; Park, Q.H. Robust numerical evaluation of circular dichroism from chiral medium/nanostructure coupled systems using the finite-element method. Scientific Reports 2018, 8, 8406. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Y.; Zhao, Y.P. Optical properties of helical Ag nanostructures calculated by discrete dipole approximation method. Applied Physics Letters 2007, 90, 221501. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Zhao, Y.P. The visible extinction peaks of Ag nanohelixes: A periodic effective dipole model. Applied Physics Letters 2011, 98, 083102. [Google Scholar] [CrossRef]
- Tao, Z.; Zhang, J.; You, J.; Hao, H.; Ouyang, H.; Yan, Q.; Du, S.; Zhao, Z.; Yang, Q.; Zheng, X.; et al. Exploiting deep learning network in optical chirality tuning and manipulation of diffractive chiral metamaterials. 2020; 9, 2945–2956. [Google Scholar] [CrossRef]
- Kuhn, W. The physical significance of optical rotatory power. Transactions of the Faraday Society 1930, 26, 293–308. [Google Scholar] [CrossRef]
- Born. On the Theory of Optical Activity. The Royal Society Publishing 1935, 150, 84–105.
- Yin, X.; Schaferling, M.; Metzger, B.; Giessen, H. Interpreting chiral nanophotonic spectra: the plasmonic Born-Kuhn model. Nano Lett 2013, 13, 6238–6243. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.S.; Zhu, W.; Lee, J.K.; Lezec, H.J.; Agrawal, A. Microscopic origin of the chiroptical response of optical media. Sci Adv 2019, 5, eaav8262. [Google Scholar] [CrossRef] [PubMed]
- Gui, L.; Hentschel, M.; Defrance, J.; Krauth, J.; Weiss, T.; Giessen, H. Nonlinear Born-Kuhn Analog for Chiral Plasmonics. ACS Photonics 2019, 6, 3306–3314. [Google Scholar] [CrossRef]
- Karimitari, N.; Ai, B.; Zhao, Y. A comparison study of the born-kuhn model and the finite-difference-time-domain calculations on stacked plasmonic nanorods. Journal of Physics D: Applied Physics 2022, 55, 325104. [Google Scholar] [CrossRef]
- Larsen, G.K.; He, Y.; Ingram, W.; LaPaquette, E.T.; Wang, J.; Zhao, Y. The fabrication of three-dimensional plasmonic chiral structures by dynamic shadowing growth. Nanoscale 2014, 6, 9467–9476. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Song, C.; Wang, J.; Shi, D.; Wang, Z.; Liu, N.; Ding, B. Rolling Up Gold Nanoparticle-Dressed DNA Origami into Three-Dimensional Plasmonic Chiral Nanostructures. Journal of the American Chemical Society 2012, 134, 146–149. [Google Scholar] [CrossRef] [PubMed]
- Kuzyk, A.; Schreiber, R.; Fan, Z.; Pardatscher, G.; Roller, E.-M.; Högele, A.; Simmel, F.C.; Govorov, A.O.; Liedl, T. DNA-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature 2012, 483, 311–314. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Blaber, M.G.; Zhao, G.; Zhang, P.; Fry, H.C.; Schatz, G.C.; Rosi, N.L. Tailorable Plasmonic Circular Dichroism Properties of Helical Nanoparticle Superstructures. Nano Letters 2013, 13, 3256–3261. [Google Scholar] [CrossRef] [PubMed]
- Svirko, Y.P.; Zheludev, N.I. Polarization of light in nonlinear optics; Wiley, 2000. [Google Scholar]
- Schäferling, M. Chiral Nanophotonics; Springer International Publishing, 2017. [Google Scholar]
- Amnon Yariv, P.Y. Optical Waves in Crystals: Propagation and Control of Laser Radiation; Wiley, 2002. [Google Scholar]
- Pain, H.J. The Physics of Vibrations and Waves, 4th ed.; Wiley, 1993. [Google Scholar]
- Huang, Y.; McColl, W.F. Analytical inversion of general tridiagonal matrices. Journal of Physics A: Mathematical and General 1997, 30, 7919. [Google Scholar] [CrossRef]
Figure 2.
The plots of (a) and (b) for and at N = 2 to 9. The 2D maps of (c) and (d) with for N = 6.
Figure 2.
The plots of (a) and (b) for and at N = 2 to 9. The 2D maps of (c) and (d) with for N = 6.
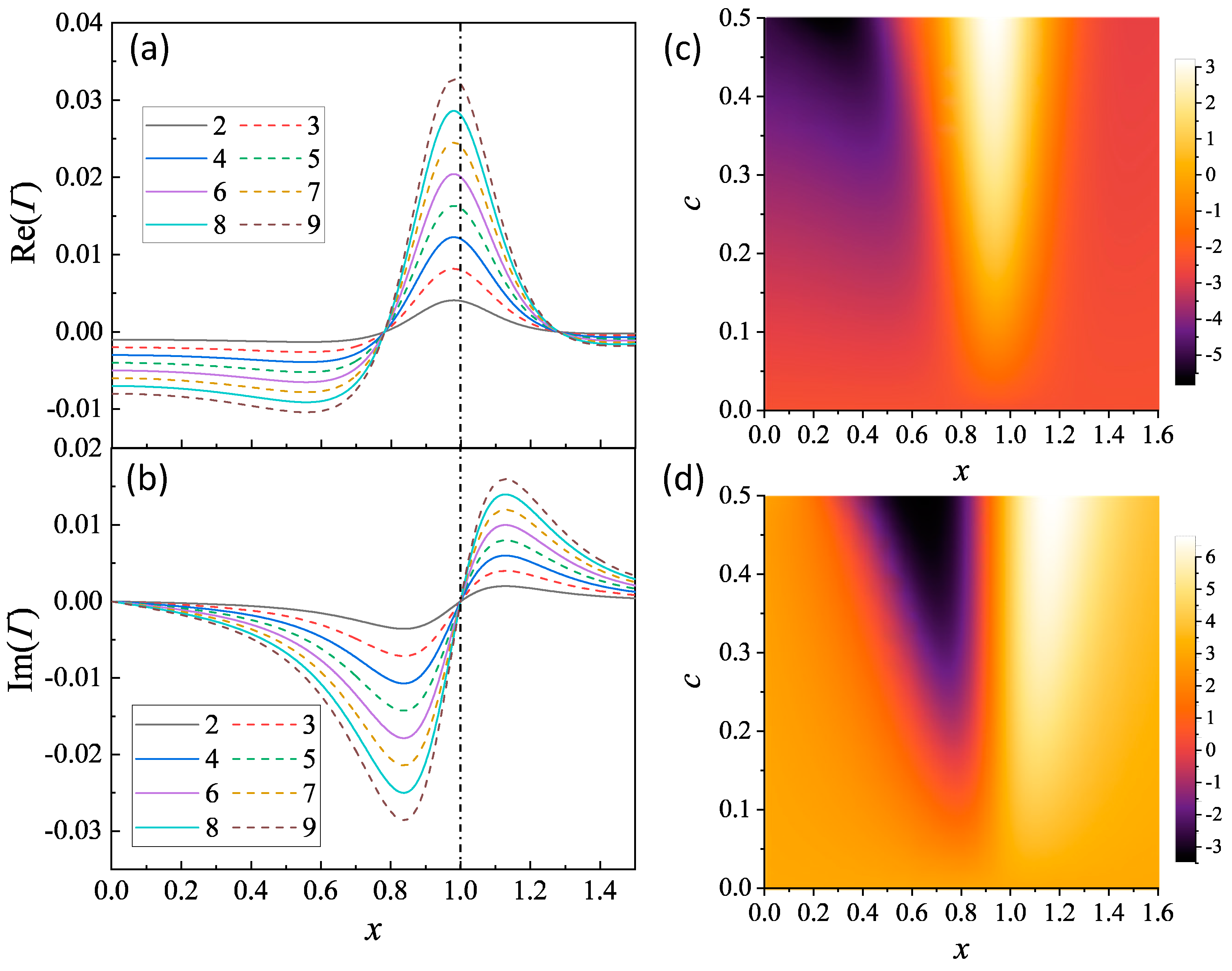
Figure 3.
The plots of and at N = 2 to 9 for and (a) and (b) .
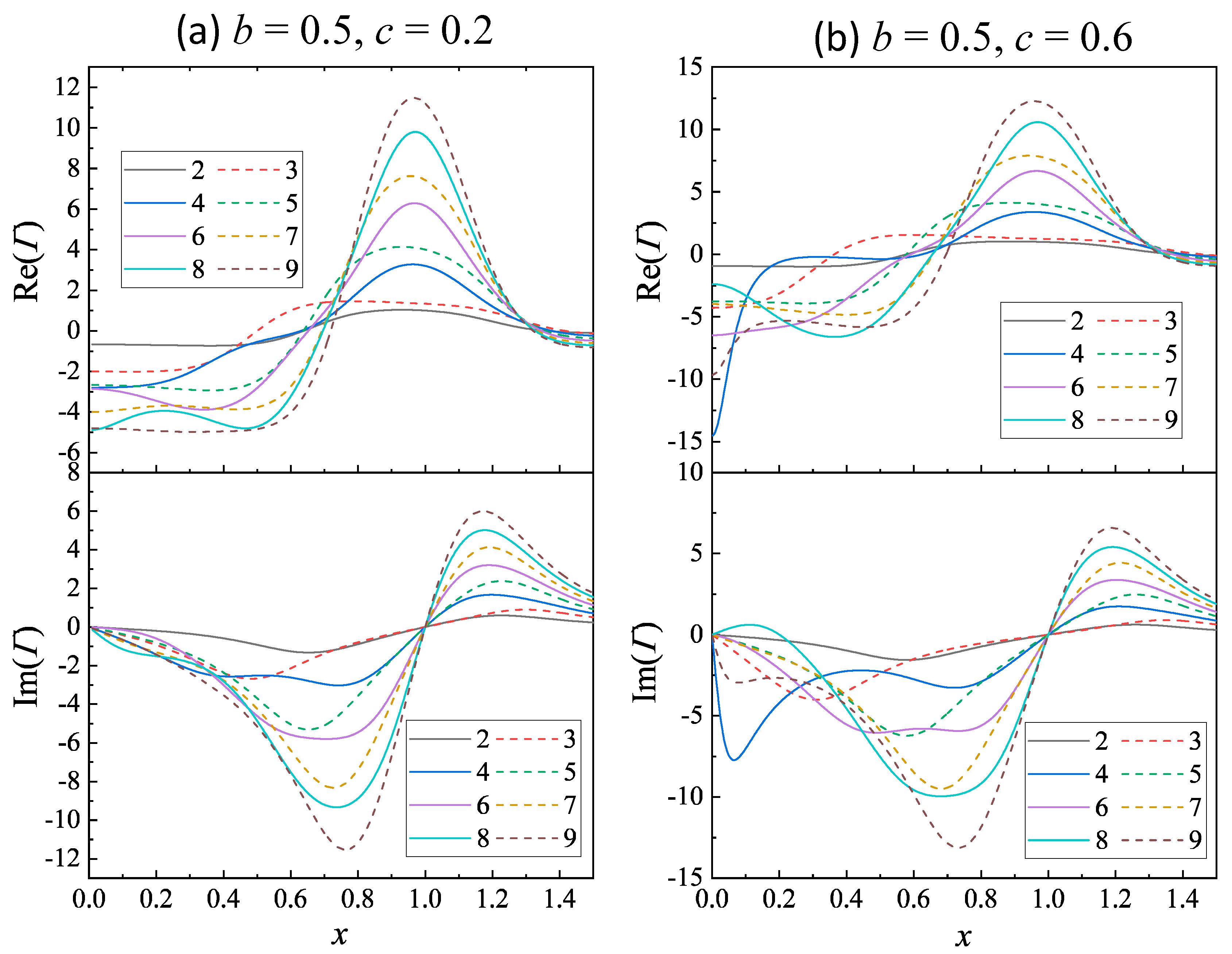
Figure 5.
The 2D maps of for at different N.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








