Preprint
Article
Existence of a Hölder Continuous extension on embedded balls of the 3-Torus for the Periodic Navier Stokes Equations
Altmetrics
Downloads
74
Views
27
Comments
0
This version is not peer-reviewed
Submitted:
26 December 2023
Posted:
27 December 2023
You are already at the latest version
Alerts
Abstract
\abstract{The existence of vorticies is well known in fluid mechanics and particularly in turbulence theory. In the context of the millennium problem of the Clay Institute on the existence (or not) of Global solutions in time of the Periodic Navier Stokes equations (PNS) results are now proposed to confirm that Global solutions do not exist in the general case of PNS defined on $\mathbb{T}^3$. This corresponds to part ($D$) proposition in the Navier Stokes problem as posted by C.Fefferman. Recent work has shown that for the Euler equations defined on the 3-Torus there exists a H\"older continuous solution for the third component of velocity $v_3$ at the center of each cell or cube of the 3-Torus Lattice. It has also been determined that as the kinematic viscosity changes from the corresponding value at $\nu=0$ to the fully viscous case for the Periodic Navier Stokes equations (PNS) at the value $\nu=1$ the solution reaches a peak ($\frac{\partial v_3}{\partial y_3} = 0$ ) in $y_3$. (third component of $\vec{r}=(y_1,y_2,y_3)$ in Cartesian co-ordinates) Here in the viscous case there exists a dipole which is not centered at the center of the cell of the Lattice. This immediately implies that since the dipole by definition has an equal in magnitude positive and negative peak in the third component of velocity, then the dipole Riemann cut-off surface is covered by a closed surface which is the sphere $\|\vec{r}\|=1$ and where a given cell of dimensions $[-1,1]^3$ is circumscribed on a sphere of radius $1$. For such a closed surface containing a dipole it necessarily follows that the flux at the surface of the sphere of $v_3$ wrt to surface normal $\vec{n}$ is zero including at $y_i, i=1\dots 3$ is zero at the points where the surface of sphere touches the cube walls. At the finite time singularity on the sphere a rotation boundary condition is deduced. Here $\frac{\partial v_3}{\partial \vec{n}}= \vec{n}\cdot \nabla v_3$. Also a boundary condition on the sphere shows rotation of sphere. Finally as a result, on the sphere a solution for $v_3$ is obtained which is proven to be H\"older continuous and it is proven that it is possible to extend H\"older continuity on the sphere uniquely to all of the interior of the ball.}
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
1. Introduction
In physics the dimensions of a massive object can be ignored and can be treated as a pointlike object, i.e. a point particle. In electrostatic theory, point particles with electric charge are referred to as point charges. Two point charges, one with charge and the other one with charge separated by a distance d, constitute an electric dipole. An object with an electric dipole moment p is subject to a torque when placed in an external electric field E. In the context of viscous fluid dynamics and at the very heart of turbulent fluid flows are many interacting vortices that produce a chaotic and seemingly unpredictable velocity field. Gaining new insight into the complex motion of vortices and how they can lead to topological changes of flows is of fundamental importance in our strive to understand turbulence. One aim is to form an understanding of vortex interactions by investigating the dynamics of point vortex dipoles interacting with a hierarchy of vortex structures using idealized point vortex models [1]. The existence of dipoles describes vortex motion and can possibly lead to a better understanding of the turbulence problem. A fully lagrangian numerical method for simulation of 3D nonstationary flow of viscous and ideal incompressible fluid is developed in [2]. This method is based on the representation of a vortex field as a set of dipole particles. An introduced vector-function D describes density of dipole momentum. The equation for this function is in accordance with Navier-Stokes equations. The vorticity is equal to curl of dipole momentum density. Thus vortex field is always solenoidal. The dipole particles are generated at a body surface and are moving and interacting. The region where function D is essentially non-zero approximately coincides with the vortex region. Each dipole particle induces the velocity field which is equal to field of a point dipole at large distance from the particle. But near a particle the induced velocity field takes into account the particle volume and viscosity of the liquid. The method can be applied for simulation of ideal and viscous flows. The dynamics of a dipole without external strain using a long simulation time and a large box size has been studied in [3]. There numerical results are provided for a viscous dipole. In [3] from a practical point of view, the dipole field turns out to be generated from an impulse jet flow and, more generally, when an external forcing characterized by a net linear momentum, is present. Dipoles can originate from jets generated at a strait, or from the coupling between topography and the oscillating tide motion. Dipolar vortices are also self-propagating, which implies some consequences on the transport of mass and heat. For instance, a dipole can trap passive scalars such as phytoplankton [4] within its core, and thereafter transport it. Contrary to the single monopole which is known mathematically to converge towards a Lamb-Oseen vortex by viscous diffusion, this problem seems not to be settled in the case of the dipole. Numerical solutions have been computed by [5] starting with various initial conditions: an initial Lamb dipole, two Rankine vortices or elliptic Kirchhoff vortices, all giving at the end of the simulation a Lamb-like dipole. Finally the presence of a tail behind the dipole and the cause of its formation have been studied as a viscous symmetry breaking. This has been particularly put into evidence theoretically [6] or experimentally [7] in the presence of an external strain. Wang et al. [8] have examined globally dynamical stabilizing effects of the geometry of the domain at which the flow locates and of the geometry structure of the solutions with the finite energy to the three-dimensional 3D incompressible Navier Stokes and Euler systems. The global well-posedness for large amplitude smooth solutions to the Cauchy problem for 3D incompressible NS and Euler equations based on a class of variant spherical coordinates has been obtained, where smooth initial data is not axi-symmetric with respect to any coordinate axis in Cartesian coordinate system. In their work [8] they have considered such variant spherical coordinates with Dirichlet type boundary conditions and have proven existence, uniqueness and exponentially decay rate in time of the global strong solution to the initial boundary value problem for 3D incompressible NS equations for a class of the smooth large initial data and a class of the special bounded domain described by variant spherical coordinates. In the present work it has been determined that as the kinematic viscosity changes from the corresponding value at to the fully viscous case for the Periodic Navier Stokes equations (PNS) at the value the solution reaches a peak ( ) in . (third component of in Cartesian co-ordinates) Here in the viscous case there exists a dipole which is not centered at the center of the cell of the Lattice. This immediately implies that since the dipole by definition has an equal in magnitude positive and negative peak in the third component of velocity, then the dipole Riemann cut-off surface is covered by a closed surface which is the sphere and where a given cell of dimensions is circumscribed on a sphere of radius 1. For such a closed surface containing a dipole it necessarily follows that the flux at the surface of the sphere of wrt to surface normal is zero. In terms of mathematical analysis of the NS equations in a thin spherical shell, the convergence of the longitudinal velocity averaged in the radial direction across the shell to the strong solution to the two-dimensional NS equations on a sphere as the thickness of the shell converges to zero has been rigorously proved by Temam and Ziane. However a Dirichlet type impenetrability condition is used there with all three components of velocity(no gradients at the wall). In the present work a Neumann impenetrability condition is used with the gradient of the third component of velocity. Here at the six points where the sphere touches the cube walls, it has been determined that the velocities satisfy PNS and the function is Hölder continuous there . By using the spherical co-ordinate system in terms of Cartesian co-ordinates and using the chain rule the solution can be extended to all of the sphere. This is the first extension. In terms of pure rotation which signifies rotation of the sphere. Finally as a result in the present work, on the sphere with a Neumann boundary condition, (Here ) a non smooth solution [9] for exists which is Hölder continuous and it is proven that it is possible to extend Hölder continuity on the sphere uniquely to all of the interior of the Ball of radius one. Although non-uniqueness is proposed to occur for solutions in the interior of the ball for PNS equations there exists at least one solution there that is Hölder continuous.
2. Materials and Methods
Consider the incompressible 3D Navier-Stokes equations defined on the 3-Torus . The PNS system is,
where is velocity, is pressure and is the forcing function. Here , where , , and denote respectively the x, y and z components of velocity. Introducing Poisson’s equation (see [10–12]), the second derivative is set equal to the second derivative obtained in the expression further below, as part of , and
where the last three terms on rhs of Equation (2) can be shown to be equal to [13]. Along with equations below, the continuity equation in Cartesian co-ordinates is . The one parameter group of transformations on a critical space of PNS is,
Next the right hand side of the group of transformations Equation (3)are mapped to variable terms. Here and are in the interval ∈,
The double transformation here is used for notational clarity. Note that the original Navier-Stokes equations are preserved and rearranged in the following form,
where are given in [14,15] and it has been shown there that this decomposition is valid and that on a volume of an arbitrarily small sphere embedded in each cell of the lattice centered at the central point of each cell of the 3-torus, is negligible for the case of no viscosity(Euler equation) and for viscosity the existence of a dipole occurs with the centre of the dipole occurring shifted away from the centre of the given cell. From this equation we can solve for algebraically and differentiating wrt to and using Poisson’s equation by setting the representation of each of the two partial derivatives wrt to equal to each other we can obtain,
which is exactly the following equation,
where is the external forcing vector and is the velocity in each cell of the 3-Torus.
For the three forcing terms, set them equal to products of reciprocals of degenerate WeierstrassP functions shifted in spatial co-ordinates from the center
The is the center of each cell of the lattice in . Upon substituting the WeierstrassP functions and their reciprocals into Equation (7) together with the forcing terms given by (in Eq. (8)), it has been determined that in the equation terms in it are multiplied by reciprocal P functions that touch the centers of the cells of the lattice thus simplifying Eq(7). The initial condition in at is instead of a product of reciprocal degenerate P function for forcing, is a sum of these functions. The parameter m in the P function if chosen to be small gives a ball,
In the case when fluid region has a connected boundary and certain smoothness conditions are fulfilled, Leray proved the solvability of the Navier Stokes equations in his famous paper [16]. The same result holds when the flux of the velocity vector (all 3 components of velocity) across each connected component of the boundary vanishes. This condition means that the flow region contains neither sources nor sinks.
Now continuing the analysis, the function associated with in [14,15] can be calculated as follows,
where are pressure gradient derivative terms wrt to and z as functions of t.
Solutions of Equation (7) exist in the form where the function can be explicitly written as
where is the corresponding eigenvalue associated with the solution of Eqs.(7-8). Setting the two functional forms for equal to each other and solving the ordinary differential equation for [see [14,15] , a LambertW function solution exists for and the form of solution is a W function multiplied by a JacobiSN complex valued function in . [see [15]-chapter8]
It has recently been shown in [14] that the following PDE results on a suitable subspace of the solution space for which holds on an epsilon ball about the center of each cell of the lattice and existing (to be shown) dipole center of a given cell of ,
3. Results
The solution in [14] occurs for large and time t. The solution was rescaled in . (In the form , where is a large complex valued shift.) In [14] this was valid for that is the Euler equations. In this paper the same shift occurs but as approaches unity and given the reduced PNS equations the relationship in terms of the definition of the LambertW function as shown in Equation (14) exists. The variable is complexified. As a result the first derivative wrt to can be written using the chain rule as,
Here it is assumed that , where is arbitrary large complex valued data in the complex norm in the complex space . (The test value of the form of this function turns out to be where B is precisely determined to produce the Riemann surface further obtained and , where central point occurs for and is the dipole off center point for high viscosity. There are two balls, one about the origin with associated low viscosity and one about the shifted away from origin dipole center associated with high viscosity). Also the variable is the complexification of the -component of velocity given by PNS equations on . (recall one can use either or or or with a factor of introduced. It can be shown that as gets large . Also note for the viscous case)
The argument of the shifted Riemann surface obtained is derived from the definition of the LambertW function. The argument of the W function which is a function of , say is set equal to . It is precisely as follows,
When the logarithm terms are subtracted the other terms are put to the right hand side of the equation. Taking the exponential of both sides cancels the logarithm and leaves us with an exponential of a binomial in . Linearizing the exponential gives the dipoles in Figure 2a,b. The "plot3d" command is used where four functions are plotted together, that is, , , u and v, where . Here w is the complex LambertW function associated with the viscous solution. One solves for in terms of .
Figure 1.
A Dipole pair associated with a contour plot of -component velocity .
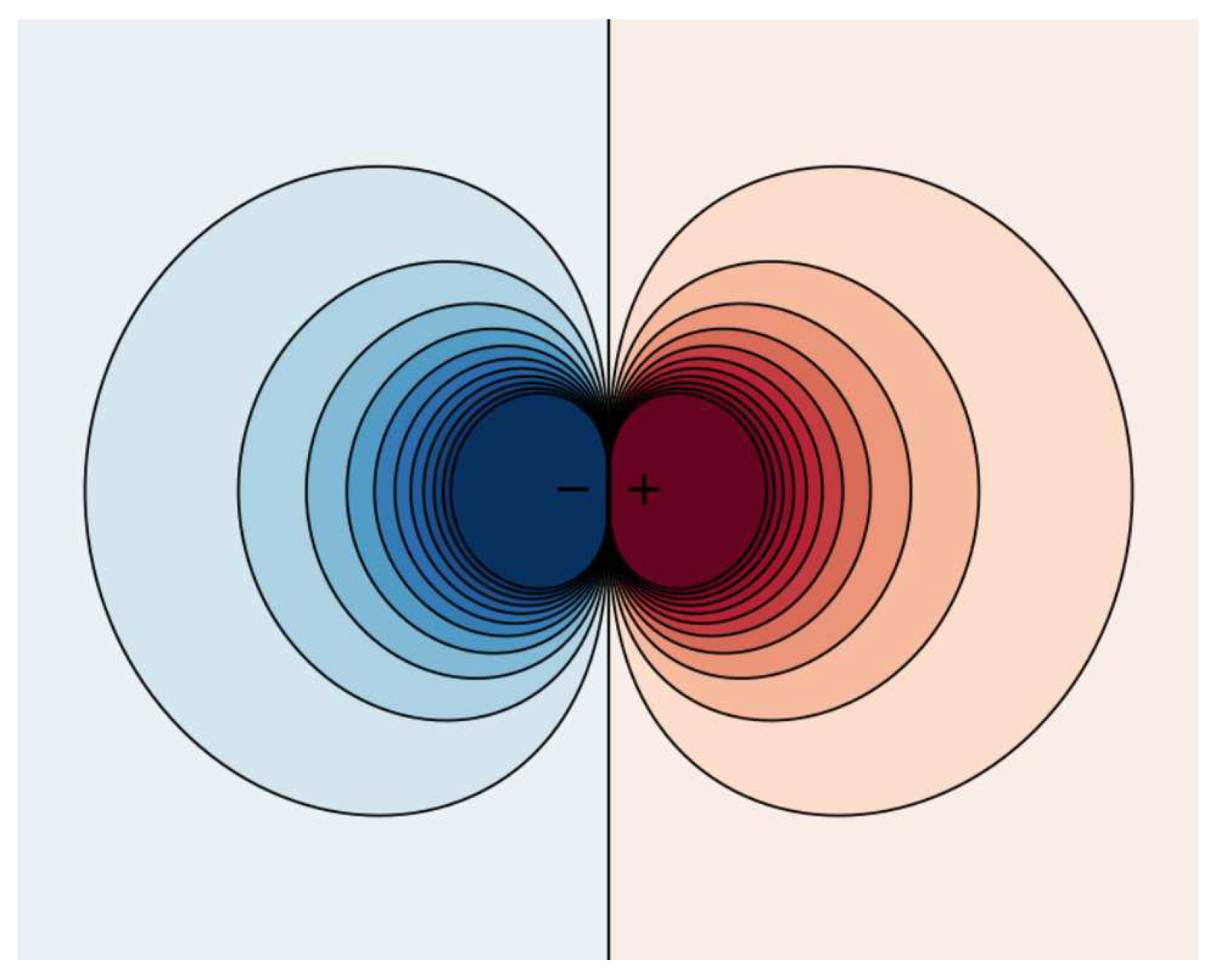
The command lines in Maple are:
Note that we use the following: Given a constant c we can solve simply by solving which says , W is the LambertW function. The values are large in for viscous flows but become physical when we divide by . In Figure 3 the quantity is scaled down by dividing by an appropriate large . Here the Riemann surface is centralized for small time s and very small viscosity in comparison to the viscosity shown in Figure 2a,b where an offset center exists of a dipole. For the (arbitrary) small viscosity this occurs near the center of the sphere. For low viscosity compared to the higher viscosity case, a finite time singularity occurs well before the higher viscous case. In the first command line of the previous program, taking the negative of both sides and then operating by the exponential function gives on the left side the argument of the LambertW function solution to the viscous problem.
The vanishing of the derivative of wrt to is connected to Rummer and Fet’s theory [17] of expressing the volume integral of the Laplacian on an epsilon ball, where in Eq(14) the following reduced PDE occurs when viscosity is included in the PNS equations and thus the reduced form obtained,
Here the viscosity term is not taken to be zero but the gradient of omitted term in the derivative of wrt to vanishes itself. This is due to the chain rule and the large shift in the initial condition in . As a result dividing by viscosity , the following equation is introduced,
Now it has been pointed out in chapter 8 of reference [14,15] that since approaching 1 from the right of 1 provides us with a blowup at minus infinity from the right side of some with linear graphs intersecting arbitrarily large values at , that it remains to show that the simplified equation, Equation (15), with introduced in place of the derivative term squared has a solution which is Hölder continuous and whose solution has a first derivative blowup from the left at blowup point . This has already been shown in [14]. Taking , we have full viscosity in the PNS problem as expected. In [14] the solution was in terms of a LambertW function and for zero viscosity. Here it is seen that as goes from 0 to 1 that the the solution has a derivative in which approaches zero. In Figure 1 and Figure 2a,b the Riemann surfaces are obtained using Maple for the complexification of the solution in terms of the initial condition and large t determined. [also see [18] on how to obtain the Maple plots of general Riemann surfaces using the "charisma function" Note that Figure 1 is a contour plot of the Riemann surface of .]
In the foregoing analyses a matching of two solutions for and hence has been carried out. One solution is the extended solution in [14] in which a LambertW solution is obtained as a function of a linear combination of spatial and time variables respectively and particularly for the shifted large data problem. The second solution is determined to be as in [15] which is the product of a JacobiSN function and a different form of a time dependent function. This is denoted as . Equating the two forms of the functions’ LambertW arguments obtained yields,
The incomplete elliptic integral EllipticE is defined as,
Differentiating twice and solving for gives,
Here the constant R and is such that,
In particular R is chosen to be extremely small and is very large and as a benchmark test the values considered are,
where these values are substituted in the left side of Eq.(20). (C=1 is set in Equation (10) for the function ) This temporal solution for the function can be identified as a Hölder continuous function as shown in Figure 4.
In the viscous case there exists a dipole which is not centered at the center of the cell of the Lattice. This immediately implies that since the dipole by definition has an equal in magnitude positive and negative peak in the third component of velocity, then the dipole Riemann cut-off surface is covered by a closed surface which is the sphere and where a given cell of dimensions is circumscribed on a sphere of radius 1. See Figure 5. For such a closed surface containing a dipole it necessarily follows that the flux at the surface of the sphere of wrt to is zero. Finally as a result on the sphere a solution for is obtained which is proven to be Hölder continuous and it is proven that it is possible to extend Hölder continuity on the sphere to all of the interior of the sphere.
Recalling the WeierstrassP function (P) based , and solutions in , and co-ordinates,
The governing PDE at the boundary of of the sphere is directly determined from Eqs.(7-8) and the zero flux condition since the sphere contains a dipole, where all the derivatives , are taken to be zero. The resulting PDE in Cartesian co-ordinates is,
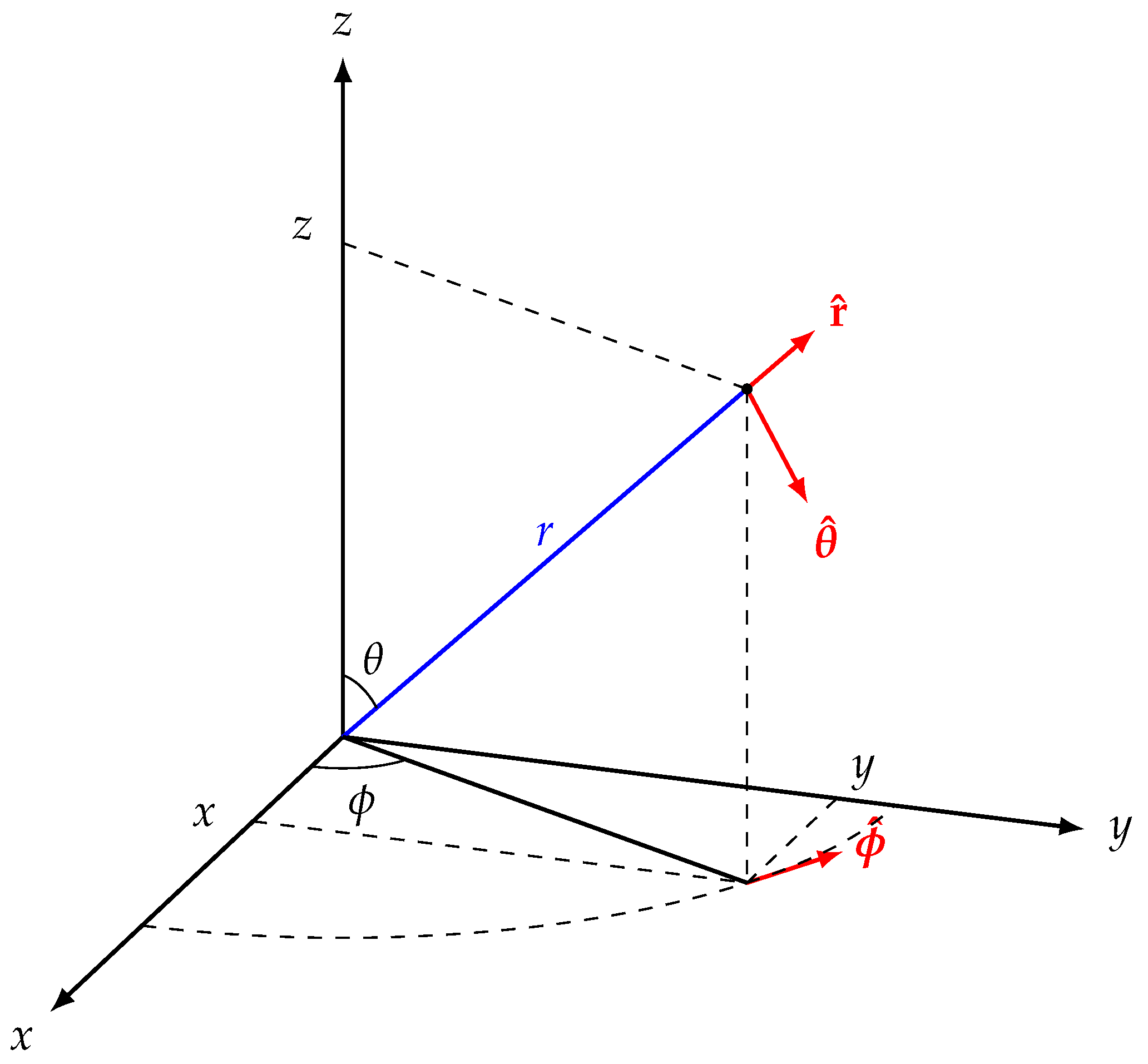
Factoring out the derivative of wrt to s and taking the other factor to be zero, upon substituting , and into Equation (31) gives a solvable PDE. The corresponding equation has as inputs the functions , and again respectively. Taking each of these functions to be Hölder continuous in s results in a PDE that has no s derivatives in it. Hence it can be easily shown that the resulting PDE has as solution a Hölder continuous function in at six points where the surface of the sphere coincides with the boundary of a given open cube. This must be the solution on the sphere boundary which is therefore Hölder continuous. This follows since we have the following co-ordinate transformations between Cartesian and spherical co-ordinates,(see Figure 6)
It is relatively straightforward to show by using the chain rule and the above transformations on the surface of the sphere that the new function in terms of is separable on the surface of the sphere and thus is in the same Hölder continuous form as the six points mentioned earlier that are known to be Hölder continuous in s there.
4. Main Theorem
Finally using the result, that on the sphere a solution for is obtained which is proven to be Hölder continuous it is next proven that it is possible to extend Hölder continuity on the sphere uniquely to all of the interior of the ball,
Theorem 1.
Let be a smooth domain and suppose , where . Then there exists a function so that
Proof of Theorem 1.
The following fact is used
Let and let be such that . for all . Define:
If , then setting one gets that . To prove that is finite for every , we fix . If then:
where we have used the fact that if and then .
and so
Note that if , then we can choose in previous inequality to obtain . Thus . Thus h extends f. Next it is proven that
, for all , .
Given , by the definition of h there exists such that,
SInce , we get
Letting gives
Finally interchanging the roles of and proves that h is Hölder continuous. □
Finally there is a theorem in ([20] Problem 13 Sec.18) that proves the unique determination for the extension of into the closure of A. The statement of the theorem without proof is given here,
Theorem 2.
Let . Let be continuous. Let Y be a Hausdorff space. Then f can be extended to a continuous function and g is uniquely determined by f.
It was proven above that there is an extension to the interior of the boundary where the PNS equations hold. So working backwards there exists an extension for the function defined on the interior of the sphere to the closure of the interior of the sphere thereby extending to the ball of radius 1.
5. Discussion
The fundamental idea of the present work is that of how external forces can lead to order in turbulent flow and in particular for the 3D Periodic Navier Stokes equations. The Turbulence problem is an open and important current problem. What is turbulence? Turbulence is disorder and fluctuation. The nonlinear 3D Navier Stokes equations have been solved in this paper through a sequence of earlier works by the corresponding author of the present paper. There has been a great search by many researchers for order in turbulent flow. When turbulence arises, even if we could see these flows, it is difficult to discern any order in the whirling currents and eddies they contain. Michael Schatz at the Georgia Institute of Technology in Atlanta has recently shown with experiments and simulations that flow patterns with a surprising amount of order can underlie turbulent flow. Prediction of turbulence is very difficult to do, however they showed that there are ordered structures when conducting experiments in the lab. [19] Although many feel that it is hopeless to predict the complex spatio-temporal dynamics of turbulence there is now some hope that this view can be relaxed somehow and in fact to a satisfying degree. The existence of a sphere centered at each point of each cell of the lattice with a Neumann zero flux condition as proven in this paper shows that there is order in turbulent flow. We know this since for the flux of , 3’rd component of velocity, it is zero and on the sphere at the singular point in time. Note that on the surface of the sphere, in 2D which signifies rotation of the sphere (Taylor Green Vortex solves this for example) together with the flux of third component of velocity, at the north and south pole of the sphere. As an analogy, if we consider the dynamics of rotating (about planet’s axes) planetary motion and keep in mind that the spherical shapes of the planets in our solar system and beyond obey this law shown in this work, namely that gases and liquids are more or less restrained from flowing outwards of the surface of a given planet(such as earth for example) as space is a near perfect vacuum surrounding the planets it makes physical sense that this is true. Why? Because of universal gravitation which acts as an external force to the flow of gases and liquids within the planets and keeps an atmospheric circulation zone in tact and attached to the surface of the sphere of a given planet. The 3-Torus is the easiest 3-manifold to understand. In 1984, Alexei Starobinsky and Yakov Zeldovich at the Landau Institute in Moscow proposed a cosmological model where the shape of the universe is a 3-torus. To visualize the three-torus, we can obtain it by gluing just like the two-Torus: We start with a cube, and glue each face of the cube to the parallel face, by parallel translation. [See Thurston [21] on how to visulaize a three-Torus] In this cosmological structure that is being proposed again it is true that there is definitive order in turbulent flow in that little or no significantly viscous fluid crosses the boundary of a sphere. So we partition the flow dynamics in two areas of such cubes of the 3-Torus, namely inside and outside the sphere. The Hölder continuous function for on the ball of radius 1 proves that acceleration can be arbitrarily large on the ball. Existence of non Hölder solutions on the ball is reserved for future work. For Dirichlet boundary conditions on the sphere existence and uniqueness of solutions may be possible. [8] The no-flux condition proves that there is an equilibrium condition that turbulence adjusts or sets to. Observing inside the spherical windows we see that there may exist infinitely many eddies and whirls. Now what can be said about the exterior of the sphere for all spheres in the lattice? Here one has to solve numerically for the flow problem of PNS in the corners of the cubes where there exist 8 vertices each with a cone surface for each cube in the lattice. It seems that there would be some flow interaction between all corners of the cubes and outside the spheres. So there can be trajectories confined within the sphere and outside of the sphere chaotic trajectories interacting with a multitude of corners in the lattice. Spatially and temporally we have partitioned the flow problem associated with PNS equations.
6. Conclusions
In this paper it has been determined that as the kinematic viscosity changes from the corresponding value at to the fully viscous case for the Periodic Navier Stokes equations (PNS) at the value the solution reaches a peak ( ) in . (third component of in Cartesian co-ordinates) Here in the viscous case there exists a dipole which is not centered at the center of the cell of the Lattice. This immediately implies that since the dipole by definition has an equal in magnitude positive and negative peak in the third component of velocity, then the dipole Riemann cut-off surface is covered by a closed surface which is the sphere and where a given cell of dimensions is circumscribed on a sphere of radius 1. For such a closed surface containing a dipole it necessarily follows that the flux at the surface of the sphere of wrt to surface normal is zero. In terms of mathematical analysis of the NS equations in a thin spherical shell, the convergence of the longitudinal velocity averaged in the radial direction across the shell to the strong solution to the two-dimensional NS equations on a sphere as the thickness of the shell converges to zero has been rigorously proved by Temam and Ziane. However a Dirichlet type impenetrability condition is used there with all three components of velocity(no gradients at the wall). In the present work a Neumann impenetrability condition is used with the gradient of the third component of velocity. Here at the six points where the sphere touches the cube walls, it has been determined that the velocities satisfy PNS and the function is Hölder continuous there . By using the spherical co-ordinate system in terms of Cartesian co-ordinates and using the chain rule the solution can be extended to all of the sphere. This is the first extension. Finally as a result in the present work, on the sphere with a Neumann boundary condition, (Here ) a non smooth solution [9] for exists which is Hölder continuous and it is proven that it is possible to extend Hölder continuity on the sphere uniquely to all of the interior of the Ball of radius one. Although non-uniqueness is proposed to occur for solutions in the interior of the ball for PNS equations there exists at least one solution there that is Hölder continuous. In the present study a point vortex at the center of the cells exists with a finite time singularity for Euler’s equation for derivatives of the velocities and as the kinematic viscosity changes from zero to one(maximum) then there is a surface vortex first derivative singularity along an atmospheric circulation layer. The inner part of this layer touching the surface of a planet is the sphere.The fluid below this sphere of atmosphere is viscous fluid. This is evident by looking at Figure 1 and Figure 2a,b. There the dipole centre is not touching this sphere layer. The model proven in this paper has cosmological applications which are justified by PNS equations.
Funding
This research received no external funding.
Data Availability Statement
Other parties’ data were not created nor analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
Technical Maple software support was beneficial for the research carried out in this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- K. Lydon, S.V. Nazarenko, and J. Laurie Dipole, Dynamics in the point vortex model. J. Phys. A: Math. Theor. 2022, 55, 1–30. [Google Scholar]
- D.A. Syrovatskii, G. YA. Dynnikova, Sergei V. Guvernyuk and G. Arutunyan. Using the dipole particles for simulation of 3D vortex flow of a viscous incompressible flow, In Proceedings of the IV International Conference on Particle-based Methods - Fundamentals and Applications,PARTICLES2015, 1-10.
- I. Delbende and M. Rossi. The dynamics of a viscous vortex dipole. Physics of Fluids 2009, 1–24. [Google Scholar] [CrossRef]
- A. Provenzale, Transport by coherent barotropic vortices, Annu. Rev. Fluid Mech 1999 31, 55?93.
- J.H.G.M. van Geffen, and G.J.F van Heijst. Viscous Evolution of 2D dipolar vortices. Fluid Dyn. Res 1998, 22, 191–213. [Google Scholar] [CrossRef]
- S. Kida, M. Takaoka, and F. Hussain. Formation of head-tail structure in a two-dimensional uniform straining flow. Phys. Fluids A 1991, 3(11), 2688–2697. [Google Scholar] [CrossRef]
- R.R. Trieling, J.M.A. van Wesenbeeck, and G.J.F. van Heijst. Dipolar vortices in a strain flow. Phys. Fluids 1998, 10(1), 144–159. [Google Scholar] [CrossRef]
- Shu Wang and Yongxin Wang. The Global Well-Posedness for Large Amplitude Smooth Solutions for 3D Incompressible Navier-Stokes and Euler Equations Based on a Class of Variant Spherical Coordinates. Mathematics 2020, 8, 1195, 1–19. [Google Scholar] [CrossRef]
- C.L. Fefferman. Existence and Smoothness of the Navier Stokes Equation. Millennium Prize Problems. Clay. Math. Inst. Camb. (MA) 2006, 57, 1–6. [Google Scholar]
- T. E. Moschandreou and K. C. Afas. Existence of incompressible vortex-class phenomena and variational formulation of Rayleigh Plesset cavitation dynamics. Applied Mechanics 2021, 2(3), 613–629. [Google Scholar] [CrossRef]
- T. E. Moschandreou. No Finite Time Blowup for 3D Incompressible Navier Stokes Equations via Scaling Invariance. Mathematics and Statistics 2021, 9(3), 386–393. [Google Scholar] [CrossRef]
- T. E. Moschandreou and K. Afas, Periodic Navier Stokes Equations for a 3D Incompressible Fluid with Liutex Vortex Identification Method, Intech Open, 2023, 1-22. [CrossRef]
- R, Poisson Equation for Pressure. www.thevisualroom.com/poisson for pressure.html poisson-equation-for- pressure.
- T.E. Moschandreou. Exploring Finite-Time Singularities and Onsager’s Conjecture with Endpoint Regularity in the Periodic Navier Stokes Equations. Global Journal of Researches in Engineering: I Numerical Methods 2023, Volume 23 Issue 1 Version 1.0, 45–59. [Google Scholar]
- T.E. Moschandreou, K.Afas and K. Nguyen. Theoretical and Computational Fluid Mechanics: Existence, Blow-up, and Discrete Exterior Calculus Algorithms, 1st ed.; Chapman and Hall/CRC: Boca Raton, USA, 2024; pp. 1–338. [Google Scholar]
- J. Leray. Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math. 1934, 63, 193–248. [Google Scholar] [CrossRef]
- Yu B, Rumer, A I Fet, Theory of Unitary Symmetry (In Russian-Published in Moscow), 1970-01-01.
- D. Jeffrey, Branch cuts and Riemann surfaces,arXiv:2302.13188 [math.CV] 2023 1-7. [CrossRef]
- B.Suri, J.Tithof, R.O.Grigoriev, and M.F.Schatz, Forecasting Fluid Flows Using the Geometry of Turbulence, Phys.Rev.Lett. 118,11 4501 2017. [CrossRef]
- J.R. Munkres, Topology, Pearson 2’nd edition 2017.
- W.P. Thurston, Three dimensional Geometry and Topology, Volume 1, Princeton University Press,1997, page 31.
Figure 2.
Riemann surface plots near boundary of sphere and cube wall. One positive and one negative Riemann surface is shown. Here the kinematic viscosity is equal to one.
Figure 2.
Riemann surface plots near boundary of sphere and cube wall. One positive and one negative Riemann surface is shown. Here the kinematic viscosity is equal to one.
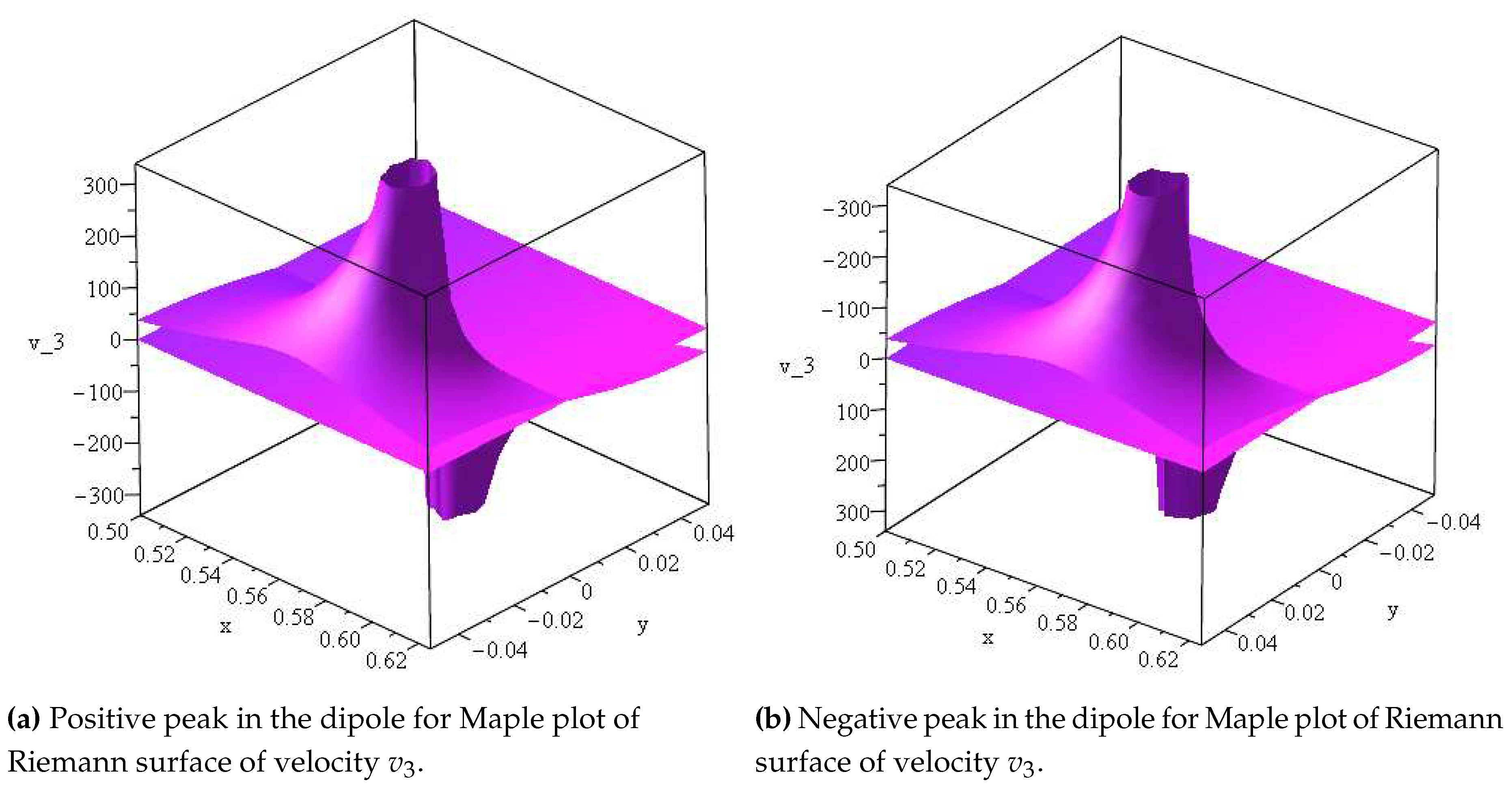
Figure 3.
Pair of equal and opposite dipoles at central location for and . Here the Dipole center is near the origin of sphere circumscribed in cube of dimensions . Shown is the Maple plot of Riemann surface of velocity . Here as shown in [14], the result shows a singularity near the origin for the first derivative in time s. The singularity for small kinematic viscosity occurs at s much sooner than in Figure 2a,b for the offset high viscosity centre case.
Figure 3.
Pair of equal and opposite dipoles at central location for and . Here the Dipole center is near the origin of sphere circumscribed in cube of dimensions . Shown is the Maple plot of Riemann surface of velocity . Here as shown in [14], the result shows a singularity near the origin for the first derivative in time s. The singularity for small kinematic viscosity occurs at s much sooner than in Figure 2a,b for the offset high viscosity centre case.
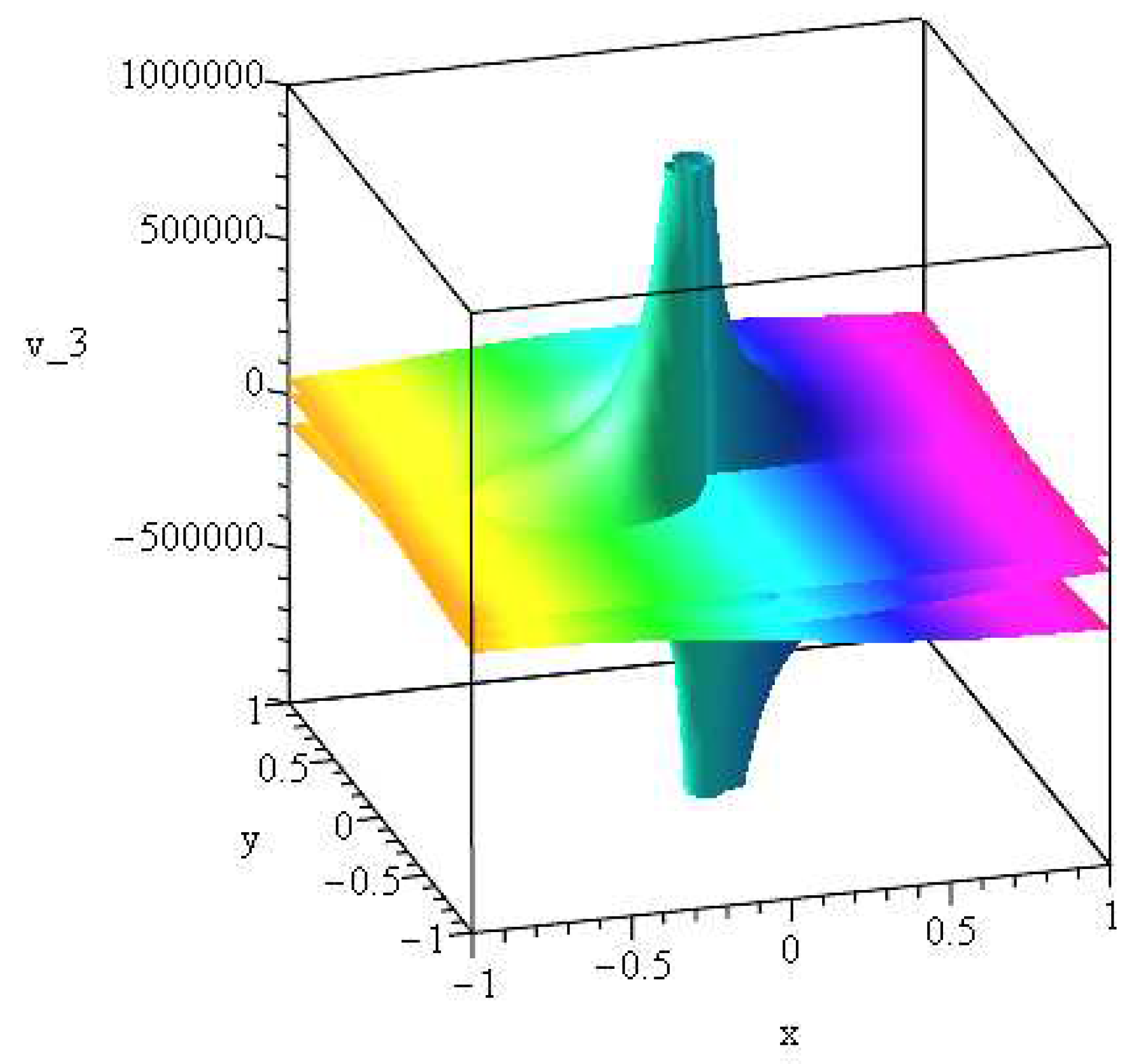
Figure 4.
Plot of Hölder continuous function via matching.
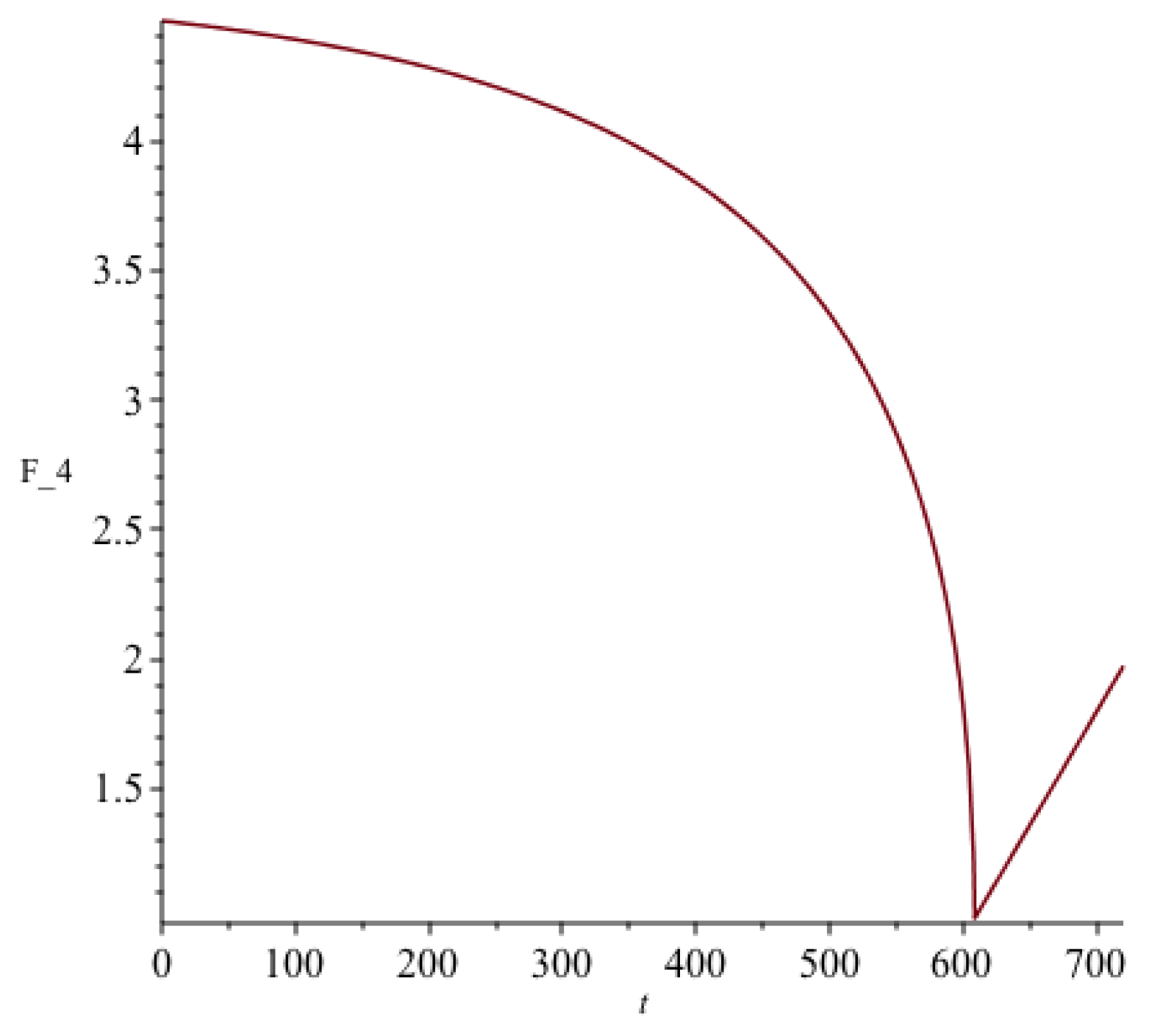
Figure 5.
A cube cell circumscribed on a sphere of radius 1.
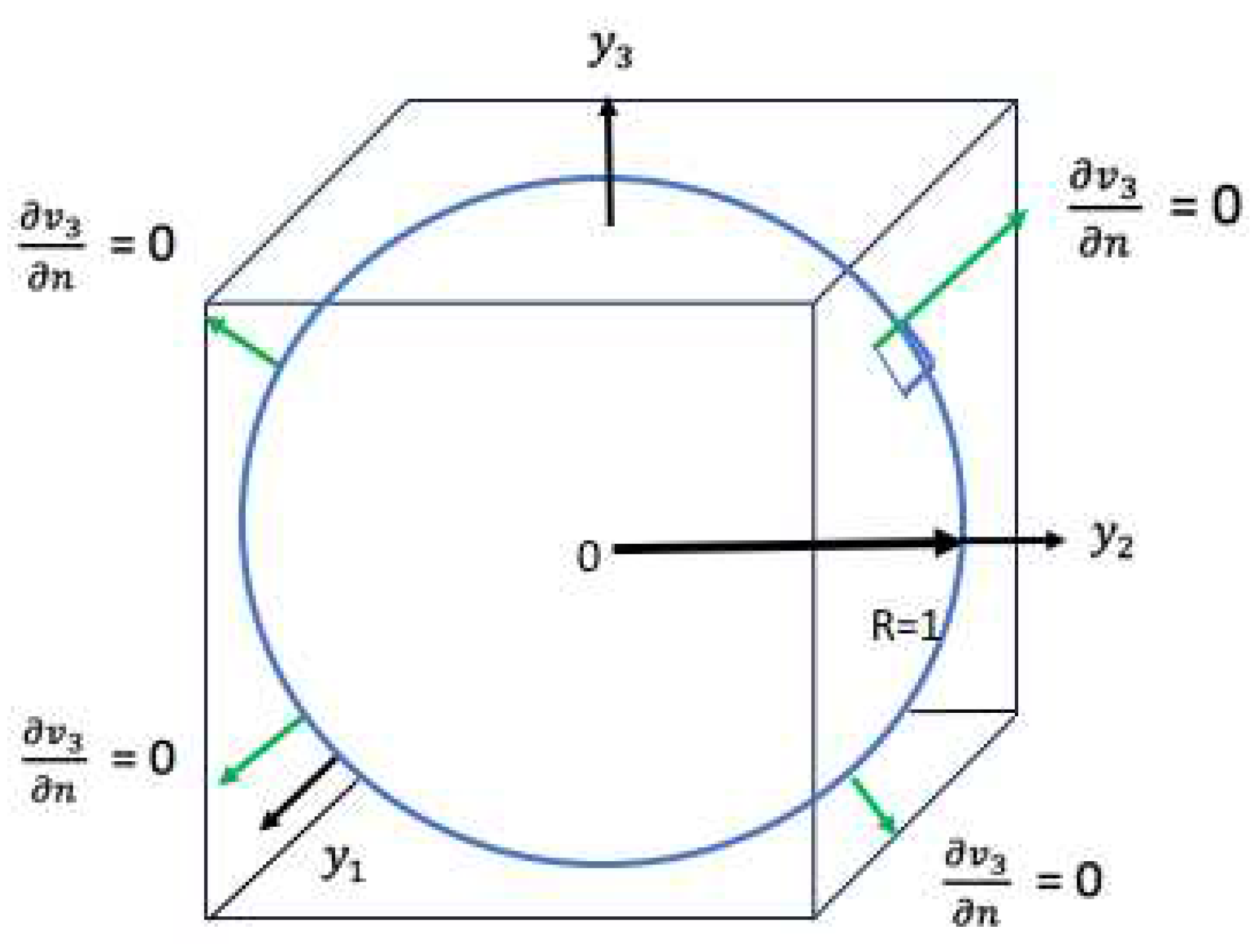
Figure 6.
Spherical co-ordinate system associated with transformations to prove that Hölder continuity holds on sphere.(TikZ.net[A.Tsagkaropoulos]).
Figure 6.
Spherical co-ordinate system associated with transformations to prove that Hölder continuity holds on sphere.(TikZ.net[A.Tsagkaropoulos]).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




