Intrusion detection is generally carried out by matching network traffic patterns with known attack patterns or by identifying abnormal network traffic patterns. One statistical methodological approach used in intrusion detection is Statistical Process Control (SPC) by constructing a control chart. Hotelling’s T2 control chart is a multivariate control chart commonly used to monitor the mean process. The performance of the T2 chart in monitoring mean shifts can be increased if a robust estimator is utilized. Based on previous research, T2 based on the Fast-MCD estimator has good performance in monitoring low to medium outlier contaminated data. Therefore, the MRCD estimator can be used to detect intrusion. On the other hand, this research focuses on developing a bootstrap-based robust Hotelling’s T2 charts with Fast-MCD and MRCD estimators for evaluating performance in detecting intrusion on intrusion detection datasets. Based application of UNSW-NB15, the proposed chart has better performance than the conventional T2 and Fast-MCD-based T2 despite the longer execution time.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction

Intrusion detection is a process of monitoring events occurring within a computer system or network, followed by analyzing the monitoring data to identify indications of intrusion attempts. Intrusion refers to attempts to gain unauthorized access to a computer system or network, potentially threatening the availability, integrity, and confidentiality of a computer network system. The system used to perform intrusion detection is known as an Intrusion Detection System (IDS) [1]. Intrusion detection is generally carried out by matching network traffic patterns with known attack patterns or by identifying abnormal network traffic patterns [2]. In general, anomaly-based network intrusion detection systems are categorized into three categories: knowledge-based systems, computational approaches, and statistical approaches [3]. One statistical methodological approach used in intrusion detection is Statistical Process Control (SPC), widely applied across various sectors including industries and services. Besides detecting changes in manufacturing and service processes, SPC can also be applied in IDS. Research has explored the application of SPC in the context of intrusion detection [4].

Statistical Process Control (SPC) has played a major role in product quality control since Shewhart [5] introduced the control chart techniques by applying statistical methods to monitor the industrial processes. One of the multivariate control charts which is commonly used to monitor the process mean is Hotelling’s T² control chart [6], which can be used to monitor either individual or subgroup observations. In SPC concepts, an outlier can be defined as an observation that significantly deviates from other observations, which indicates that the observation is observed by a different process [7]. The Hotelling’s T² chart is not suitable to detect the presence of multiple outlier [8], due to the masking and swamping effect [9], especially for highly outlier contaminated data. The statistic of T², which is based on the classical estimator, is easily affected and decreased by the presence of outliers [10,11]. Moreover, the performance of control charts will decrease if the variables monitored increase [12].

To overcome those problems, several methods have been proposed to minimize the effects of outliers by changing the classical estimator with a robust estimator, especially for the covariance matrix estimator. The performance of the T² control chart in monitoring mean shifts will increase if a robust estimator is utilized [13]. Many robust methods have been adopted to develop a T² control chart to minimize the effect of outliers. These methods such as Minimum Volume Ellipsoid (MVE) [14], Trimming Method [15,16], Minimum Vector Variance [17,18], Successive Difference Covariance Matrix (SDCM) [10,19], Minimum Covariance Determinant (MCD) [15,20], Reweighted minimum covariance determinant (RMCD) [21], and Fast Minimum Covariance Determinant (Fast-MCD), whose good performance on monitoring small to medium outlier contaminated data with 30% breakdown point [22]. The latest development of robust estimators is the Minimum Regularized Covariance Determinant (MRCD) method [23], which uses the concept of data-driven algorithm and regularization to avoid overfitting problems. The MRCD estimator can be used to detect outliers in high-dimensional data. Besides the robust estimator, the Hotelling’ T² chart can also be developed using a non-parametric approach as a control limit, namely the bootstrap resampling method [24].

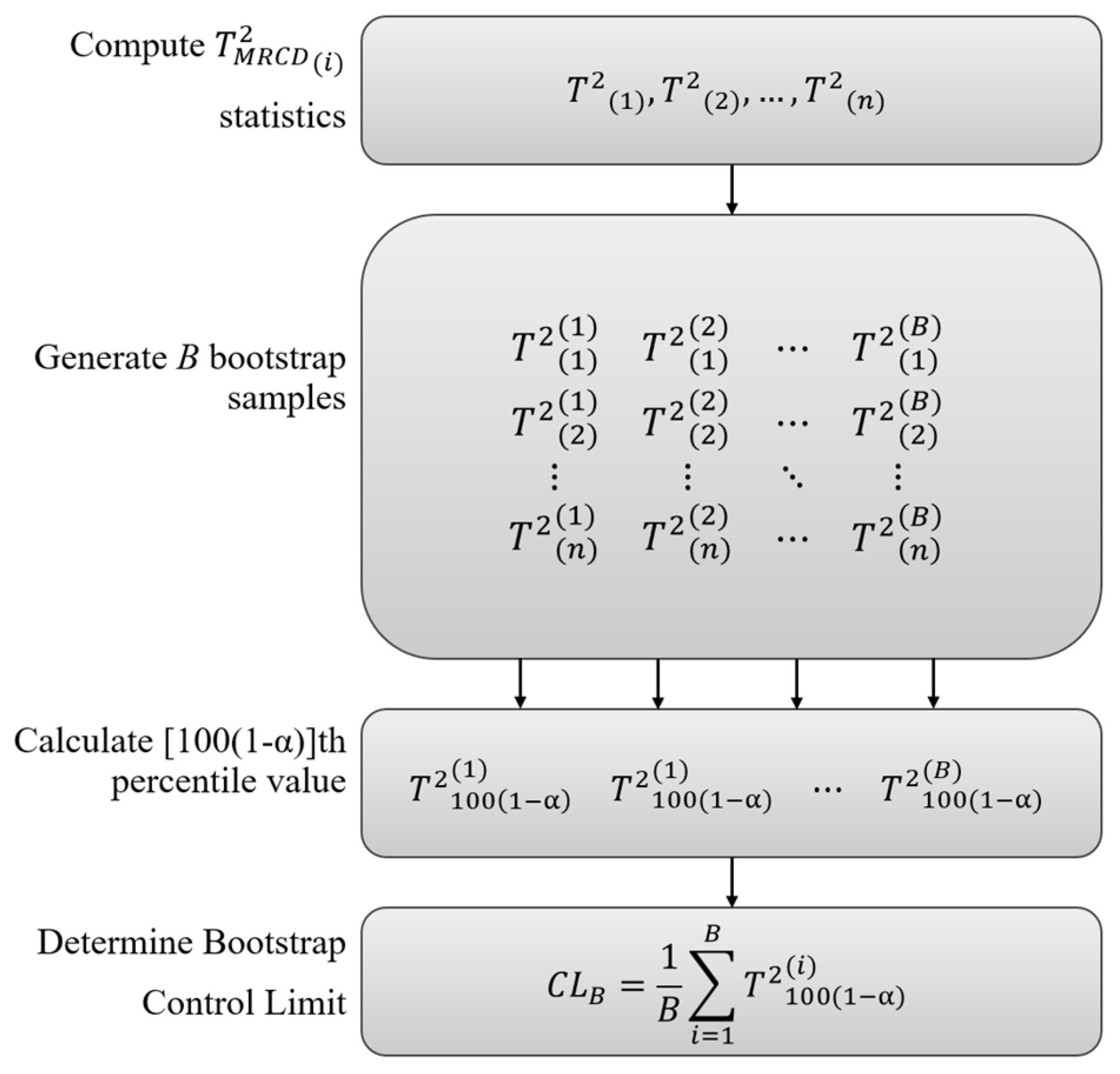
This research focuses on developing bootstrap-based robust T² control charts with MRCD estimators for detecting intrusion. This method will be applied to the UNSW-NB15 dataset. The rest of this paper is organized as follows: Section 2 presents the related work. In Section 3, the explanation of the proposed chart construction is presented. Section 4 provides the methodology and procedure of the proposed chart. Section 5 shows the application results of the proposed chart for the IDS dataset. Finally, Section 6 is allocated for the conclusion and future research.

2. Related Works

The SPC method commonly used in intrusion detection is a multivariate control chart. Ye et al. [25] initiated the use of Markov Chain techniques, T² Hotelling, and chi-square multivariate tests for intrusion detection. Then Ye et al. [26] proposed a technique based on Hotelling's T² that can detect both counter relationships and mean-shift anomalies. Qu, Hariri, and Yousif [27] use the T² Hotelling diagram to detect intrusions on a network called real-time Multivariate Analysis for the Network Attack detection algorithm (MANA) by updating control limits at certain time intervals. Zhang, Zhu, and Jin [28] developed a Support Vector Clustering (SVC) based control diagram with performance results similar to the T² diagram for detecting anomalies in computer networks. Tavallaee et al. [29] apply Covariance Matrix Sign (CMS) to detect Denial of Service (DoS) attacks. Sivasamy and Sundan [30] compared the performance of the T² Hotelling control chart with the SVM and TANN methods and found that Hotelling’s T² accuracy level was high for all types of attack classes.

In addition to Hotelling's T², Rastogi et al. [31] stated that in theory MEWMA and MCUSUM can be used in intrusion detection, however, intrusion detection data involves many quality characteristics so MEWMA and MCUSUM are not suitable for use. Camacho et al [32] use PCA based on Multivariate Statistical Process Control (MSPC) to monitor intrusions. Ahsan et al. [33] use PCA-based Hotelling’s T² which produces more efficient computational time. The use of non-parametric control limits improves performance on the T² control diagram with a Successful Difference Covariance Matrix (SDCM) in the form of Kernel Density Estimation [34] and Bootstrap Resampling [35]. Then Ahsan et al. [36] developed robust Hotelling’s T² based on Fast-MCD which shows better performance in detecting outliers in intrusion detection systems.

3. Proposed Chart

In this section, the procedures of the proposed chart are explained. The Minimum Regularized Covariance Determinant (MRCD) estimator is employed to enhance the robustness of the mean vector and covariance matrix on the chart’s performance for intrusion detection.

3.1. Multivariate Hotelling’s T² Control Chart

In this section, a short brief of the conventional Hotelling’s T² control chart is shown. Hotelling’s T² is a multivariate control chart, a generalization of the t-student distribution, that can be used to monitor the process mean. Let

x_{i}

where

i = 1, 2, \dots, n

are identic and independently random vectors which follow the multivariate normal distribution

x_{i} ~ N_{p} (μ, Σ)

. The data structure can be written as

X = [\begin{matrix} \begin{matrix} x_{1}^{T} & x_{2}^{T} \end{matrix} & \begin{matrix} \dots & x_{n}^{T} \end{matrix} \end{matrix}]

with mean vector

\bar{x} = \frac{1}{n} \sum x_{i}

and covariance matrix

S = \frac{1}{n - 1} \sum (x_{i -} \bar{x}) {(x_{i} - \bar{x})}^{T}

. The

T_{i}^{2}

statistics can be calculated as follows [6]:

T_{i}^{2} = (x_{i} - \bar{x})^{'} S^{- 1} (x_{i} - \bar{x})

(1)

Conventional Hotelling’s T² chart follows the assumption of multivariate normal distribution [37], so the control limit can be generated by following F-distribution with the equation:

C L = \frac{p (n + 1) (n - 1)}{n^{2} - n p} F_{α; p; n - p}

(2)

where n is the total number of observations p is the variables quantity with 𝛼 is the false alarm rate. The monitoring process is said in-control if T² statistics are not greater than the control limit.

3.2. Bootstrap Control Limit-Based T² Chart

In some cases, a random variable might not follow any certain distributions. To overcome this problem, the bootstrap method can be applied to estimate the parameter of unknown distribution [38,39]. Despite initially proposed on classic T² statistics [24], this control limit also can be adopted on the proposed chart by putting robust statistics on the first step. The algorithm of bootstrap control limit calculation (see Figure 1 for illustration) is presented as follows:

Algorithm of Bootstrap Control Limit

Step 1.: Compute the statistic T² with n observations
Step 2.: Generate B times bootstrap samples from statistic T² for n observations with replacement (e.g., B=1,000).
Step 3.: Calculate 100(1-α).th percentile for each bootstrap resample for statistic $T^{2 (l)}$ ; $l = 1, 2, \dots, n$
Step 4.: Determine the bootstrap control limit by averaging each replication using

{C L}_{B} = \frac{1}{B} \sum_{i = 1}^{B} {T^{2}}_{100 (1 - α)}^{(l)}

3.2. MRCD Algorithm

The minimum Covariance Determinant (MCD) based method is the most widely used robust estimator of multivariate location and scatters [40]. This method is designed to determine

H_{M C D}

defined as subset with the smallest sample covariance determinant. The MCD estimates for the mean vector and covariance matrix correspond to the mean vector and covariance matrix of

H_{M C D}

. Define h as the subset size where

\frac{n}{2} \leq h < n

, and

h \geq p

must be fulfilled, otherwie the MCD covariance matrix will be singular. The MCD algorithm calculates every subset possible as many as

(\begin{matrix} n \\ h \end{matrix})

possible combinations in order to get

H_{M C D}

. So, this method is time-consuming and not suitable for estimating large datasets.

Minimum Regularized Covariance Determinant (MRCD) estimators are proposed [23] as the extension of MCD. The MRCD is a robust estimator that uses various combinations of target matrix and regularization weight determined through data-driven procedures. The application of the MRCD estimator has good robustness and can be used to deal with outliers in high-dimensional data.

Let

X = {\{x_{1}, x_{2}, \dots, x_{i}, \dots, x_{n}\}}^{'}

where

x_{i} = {\{x_{i 1}, x_{i 2}, \dots, x_{i p}\}}^{'}

from a p-variate observations. First, the data need to be standardized using the Qn estimator [41] and put these values in a diagonal matrix

D_{X}

. The median of each variable also needs to be computed and put in a location vector

v_{X}

. The stardardized obesvations are then stated on U that constructed under a set of

u_{i}

as follows:

u_{i} = D_{X}^{- 1} (x_{i} - v_{X})

(3)

The next step is defining the Target Matrix (T) and scalar regularization parameter

(ρ)

. T is a

p \times p

diagonal matrix that consists of estimated univariate scales, while

ρ

is a weighted parameter that can be obtained by the data-driven approach which satisfies

0 \leq ρ \leq 1

. Then define

h \times p

covariance matrix

K (H)

of h-subset of H on the standardized data U as follows:

K (H) = ρ T + (1 - ρ) c_{γ} S_{U} (H)

(4)

where

S_{U} (H)

is the covariance matrix of the h-subset for U and

c_{γ}

is the consistency factor [42]

Mathematical operation (7) can be done with a spectral decomposition

T = Q λ Q^{'}

where

λ

is the diagonal matrix containing the eigenvalues of T, while Q is the orthogonal matrix containing the corresponding eigenvectors. The previous equation can be rewritten as follows

K (H) = Q λ^{1 / 2} [ρ I + (1 - ρ) c_{α} S_{W} (H)] λ^{1 / 2} Q^{'}

(5)

where W, containing the transformation of standardized observations

w_{i} = λ^{1 / 2} Q^{'} u_{i}

. Consequently, it follows

S_{W} (H) = λ^{- 1 / 2} Q^{'} S_{U} (H) Q λ^{- 1 / 2}

The subset MRCD

H_{M C D}

obtained by minimizing the determinant of the regularized covariance matrix K(H) as:

H_{M R C D} = \underset{H \in Ω}{argmin} (d e t (K (H))) H_{M R C D} = \underset{H \in Ω}{a r g m i n} (\det (ρ I + (1 - ρ) c_{α} S_{W} (H)))

(6)

Once the

H_{M R C D}

is determined, then the location and scatters of the MRCD estimator can be defined as.

\overset{`}{{\bar{x}}_{M R C D}} = v_{X} + D_{X} {\bar{H}}_{M R C D}

(7)

S_{M R C D} = D_{X} Q λ^{1 / 2} [ρ I + (1 - ρ) c_{α} S_{W} (H_{M R C D})] λ^{1 / 2} Q^{'} D_{X}

(8)

3.3. MRCD-Based T² Chart

In order to develop the robust Hotelling’s T² control chart, this study changes the classic estimators of mean vectors

\bar{x}

and covariance matrix

S

from equation (1) with the estimated value of mean vector and covariance matrix from robust estimators. Robust T² statistic based on MRCD was constructed as follows

T_{M R C D; i}^{2} = (x_{i} - {\bar{x}}_{M R C D})^{'} S_{M R C D}^{- 1} (x_{i} - {\bar{x}}_{M R C D})

(9)

Due to the unknown distribution of the proposed chart, its control limit for both charts are estimated using the bootstrap resampling method to develop an adaptive control chart. The detailed procedure for the control limit is presented in the previous subsection.

4. Methodology

In developing the proposed robust T² chart based on the MRCD estimator, there are two phases required to be undertaken. Phase I is building a normal profile from the in-control or the normal profile, while Phase II is detecting the intrusion using the calculated statistics and control limit from Phase II. Phase I needs to calculate the mean vector, covariance matrix, and bootstrap control limit. The procedure of Phase I is shown as following these steps:

Phase I: Building Normal Profile

Step 1.: Form the in-control or normal data matrix $X_{n o r m a l}$
Step 2.: Calculate ${\bar{x}}_{M R C D}$ and $S_{M R C D}$ , which are the robust estimated values of normal data $X_{n o r m a l}$ using the MRCD algorithm in equation (11) and (12)
Step 3.: Calculate $T_{M R C D; i}^{2}$ using equation (14) from normal data $X_{n o r m a l}$
Step 4.: Determine $α$ and compute the bootstrap control limit ${C L}_{B; M R C D}$

Then the estimated normal profile and control limit from Phase I are utilized in the detection process in Phase II. The procedure of Phase II is shown as follows:

Phase II: Detection

Step 1.: Form the new data matrix $X_{t e s t}$
Step 2.: Calculate $T_{M R C D; i}^{2}$ from new data $X_{n o r m a l}$ as follows:

$T_{M R C D; i}^{2} {= (x_{t e s t; i} - {\bar{x}}_{M R C D})}^{T} S_{M R C D}^{- 1} (x_{t e s t; i} - {\bar{x}}_{M R C D})$

where ${\bar{x}}_{M R C D}$ and $S_{M R C D}$ are taken from Phase I
Step 3.: Detect if $T_{M R C D; i}^{2} > {C L}_{B; M R C D}$ then the observation is labeled as an intrusion and if $T_{M R C D; i}^{2} \leq {C L}_{B; M R C D}$ then the observation is labeled as normal

Moreover, the performance of the proposed can be assessed and evaluated by the confusion matrix table shown in Table 1. The classification goodness method could be measured by the degree of goodness and degree of error. The goodness in intrusion detection can be divided into two types:

True Positives (TP) are intrusion records that are successfully detected as intrusion.
True Negatives (TN) are normal records that are correctly stated as normal.

The errors in detecting intrusion also can be divided into two types:

False Positives (FP) are normal records that are incorrectly detected as intrusions.
False Negatives (FN) is an intrusion records that unsuccessfully detected as normal records.

FP leads to a false alarm while FN results in an undetected intrusion on the chart. Those types of error can be used to calculate the degree of error namely FP Rate and FN Rate [43]. While the level of goodness can be measured using the Area Under Curves (AUC) as follows [44]:

A U C = \frac{1}{2} (\frac{T P}{T P + F N} + \frac{T N}{T N + F P})

(10)

F P R a t e = \frac{F P}{T N + F P}

(11)

F N R a t e = \frac{F N}{T P + F N}

(12)

5. Results and Discussions

The UNSW-NB15 dataset was built using the IXIA PerfectStorm tool at the Australian Centre for Cyber Security (ACCS) by generating a combination of normal activities and realistic, modern artificial attacks for research purposes related to Network Intrusion Detection Systems (NIDS) [45]. Compared to other NIDS datasets, UNSW-NB15 excels in complexity, referring to patterns of modern network traffic attacks, making it suitable for evaluating intrusion detection systems [46]. The training set of UNSW-NB15 consists of 175,341 records with 38 metric features and record labels which are normal labels and several types of intrusion labels that are presented in Table 2.

The data application is conducted through three methods: conventional Hotelling’s T², robust T² based on Fast-MCD, and the proposed diagram, which is the robust T² based on MRCD. The construction of the control chart is divided into two phases: Phase I for establishing control limits and Phase II for the detection process and calculating the performance of the control chart. 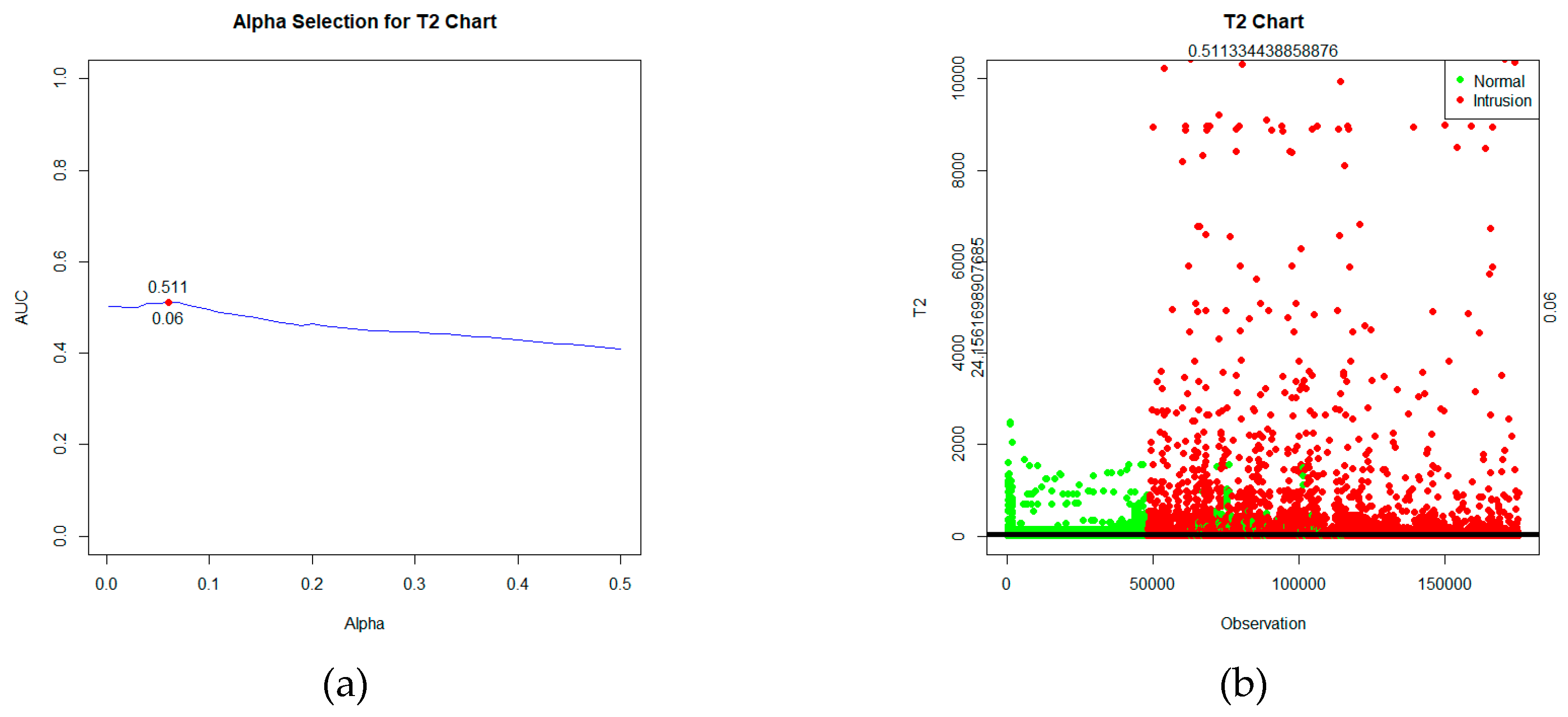In the conventional Hotelling’s T² control chart, the T² statistic is calculated using equation (2.29), with control limits determined based on the significance level using the criteria of the highest AUC value, which is α=6%, as depicted in Figure 2(a). After computing the statistics and establishing control limits, the control chart can be visualized, as shown in Figure 2(b).

Based on Figure 2, the statistical plot depicts two types of data labels: green for normal data and red for intrusion data. These statistics will be tested against the control limits. If the value of the statistic T² >

{C L}_{B}

, the observation is detected as an intrusion. While if the statistic T² ≤

{C L}_{B}

, the observation is detected as normal. Based on the labels and the detection outcomes obtained, a confusion matrix table can be formed in Table 3.

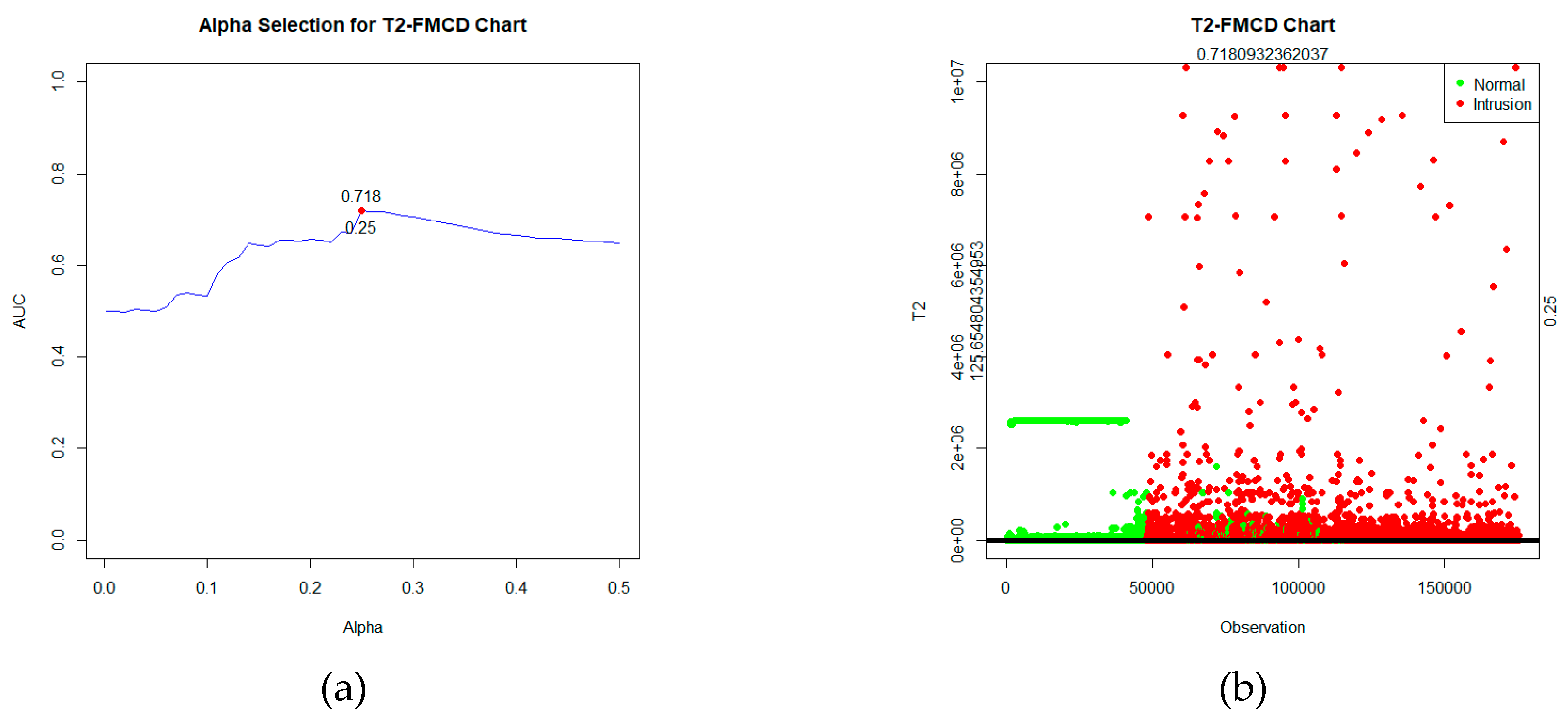
Next, in the construction of a control chart for Robust T² based on Fast-MCD, the T² statistic is calculated, and the control limits are determined based on the significance level using the criteria of the highest AUC value, which is α=25%, as depicted in Figure 3(a). After computing the statistics and establishing the control limits, the control chart can be visualized, as seen in Figure 3(b).

Based on the figure, the statistical plot depicts two types of data labels: green for normal data and red for intrusion data. These statistics will be tested against the control limits. If the value of the statistic T²_FMCD >

{C L}_{B}

, the observation is detected as an intrusion. While if the statistic T²_FMCD ≤

{C L}_{B}

, the observation is detected as normal. Based on the labels and the detection outcomes obtained, a confusion matrix table can be formed and evaluated as Table 4.

Based on Table 4, it can be known that the performance of Robust T² based on Fast-MCD on the UNSW-NB15 data is quite good, with an AUC value of 0.718. Additionally, with an FP Rate of 0.25, there's a relatively low FN rate of 0.314.

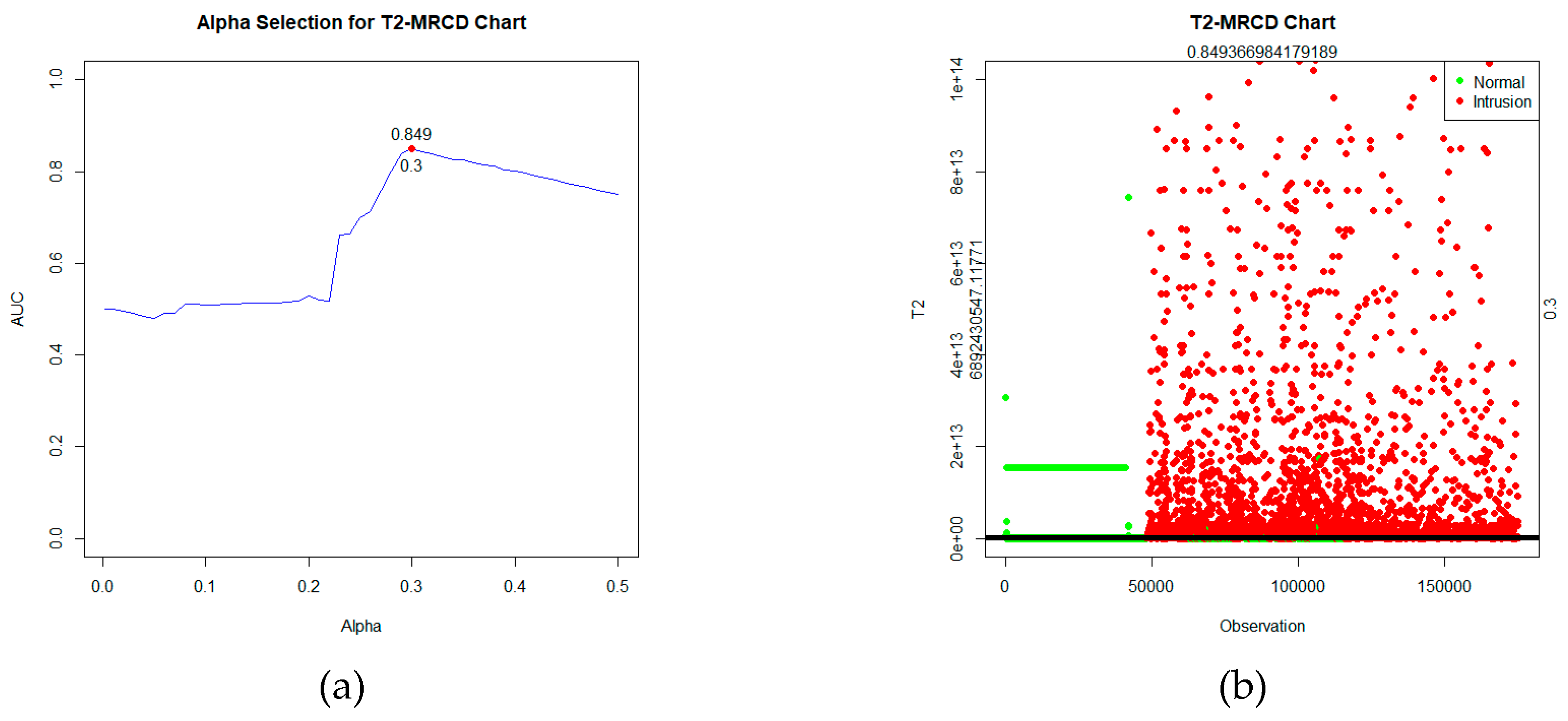
For constructing the proposed chart of Robust T² based on MRCD, the T² statistic is calculated using, and the control limits are determined based on the significance level using the criteria of the highest AUC value, which is α=30%, as depicted in Figure 4(a). After computing the statistics and establishing control limits, the control chart can be visualized, as shown in Figure 4(b).

Based on Figure 4, the statistical plot depicts two types of data labels: green for normal data and red for intrusion data. These statistics will be tested against the control limits. If the value of the statistic T² _MRCD >

{C L}_{B}

, the observation is detected as an intrusion. While if the statistic T²_MRCD ≤

{C L}_{B}

, the observation is detected as normal. Based on the labels and the detection outcomes obtained, a confusion matrix table can be formed and evaluated in Table 5.

Based on Table 5, it's apparent that the performance of Robust T² based on MRCD on the UNSW-NB15 data is excellent, with an AUC value of 0.849. Additionally, with an FP Rate of 0.298, there's an exceptionally low FN rate of only 0.004.

After applying the UNSW-NB15 data using these three methods, the performance of each chart can be compared and evaluated based on several goodness and error criteria, as presented in Table 6.

Table 6 displays the Accuracy, AUC, FP Rate, FN Rate, and execution time of the three methods used in this study. The conventional T² method, with its straightforward steps, took only 286 seconds. The Fast-MCD-based T² method, known for its efficiency, required 1,470 seconds. Meanwhile, the MRCD-based T², featuring a complex algorithm, took a longer time of 8,108 seconds.

The duration of execution time correlates with the quality of the chart's performance in detecting intrusions. Based on the AUC values, the conventional T² Hotelling chart showed poor performance in intrusion detection, achieving an AUC of only 0.511. Both robust T² charts demonstrated better performance than the conventional T². The Fast-MCD-based T² had a relatively good AUC value of 0.718. On the other hand, the proposed MRCD-based T² had the best performance with the highest AUC value of 0.849 and an exceptionally low FN Rate of 0.004, indicating a very low chance of undetected intrusions.

6. Conclusion and Future Research

The application of the UNSW-NB15 data revealed that the MRCD-based T² Hotelling exhibited better performance in detecting intrusion, with a 0.902 Accuracy and 0.848 AUC value. This proposed chart successfully outperformed the conventional T² Hotelling and the Fast-MCD-based T² Hotelling, which had AUC values of 0.511 and 0.718, respectively despite the longer execution time. For further research, this proposed chart still can be modified by applying another non-parametric approach as the control limit. Applying an MRCD estimator for monitoring processes for variance shifts or simultaneous shifts in mean and variance also can be constructed. The latest robust estimator, Cellwise MCD [47], known for its efficiency can be considered to be implemented to overcome the MRCD’s problem in terms of long duration of execution time.

Author Contributions

I.K.P.: writing original draft and data analysis. M.A.: Conceptual methodology, Supervising and validating the results. M.M.: Performed analysis and data visualization. M.H.L.: Validating the results.

Acknowledgments

The authors gratefully acknowledge financial support from the Institut Teknologi Sepuluh Nopember for this work, under the project scheme of the Publication Writing and IPR Incentive Program (PPHKI) 2022

Conflicts of Interest

The authors declare no conflict of interest.

References

Bace, R.; Mell, P. NIST special publication on intrusion detection systems. Nist Special Publication, 2001.
Lee, W.; Stolfo, S.J. A framework for constructing features and models for intrusion detection systems. ACM Transactions on Information and System Security; 2000; Volume 3.
Wu, G.; Huang, Y. Design of a New Intrusion Detection System Based on Database. 2009 International Conference on Signal Processing Systems; 2009; pp. 814–817.
Park, Y. A Statistical Process Control Approach for Network Intrusion Detection, Georgia Insitute of Technology, 2005.
Shewhart, W.A. Some applications of statistical methods to the analysis of physical and engineering data. Bell System Technical Journal 1924, 3, 43–87. [Google Scholar] [CrossRef]
Hotteling, H. Multivariate Quality Control. In Techiques of Statistical Analysis; McGraw-Hill: New York, NY, USA, 1947. [Google Scholar]
Hawkins, D.M. Identification of Outliers; Springer: Berlin, Germany, 1980; Volume 11. [Google Scholar]
Chenouri, S.; Steiner, S.H.; Variyath, A.M. A multivariate robust control chart for individual observations. Journal of Quality Technology 2009, 41, 259–271. [Google Scholar] [CrossRef]
Rousseeuw, P.J.; Van Zomeren, B.C. Unmasking multivariate outliers and leverage point. Journal of the American Statistical Association 1990, 85, 633–639. [Google Scholar] [CrossRef]
Sullivan, J.H.; Woodall, W.H. A comparison of multivariate control charts for individual observations. Journal of Quality Technology 1996, 28, 398–408. [Google Scholar] [CrossRef]
Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons, 2005; Volume 589. [Google Scholar]
Ahsan, M.; Khusna, H. Evaluasi Diagram Kontrol Multivariat berbasis Independen Principal Component Analysis (PCA). INFERENSI 2018, 1, 89–92. [Google Scholar] [CrossRef]
Williems, G.; Pison, G.; Rousseeuw, P.J.; Van Aelst, S. A Robust Hotelling Test. Metrika 2002, 125–138. [Google Scholar] [CrossRef]
Vargas, N.J. Robust estimation in multivariate control charts for individual observations. Journal of Quality Technology 2003, 35, 367–376. [Google Scholar] [CrossRef]
Alfaro, J.L.; Ortega, J.F. A comparison of robust alternatives to hotelling’s T2 control chart. Journal of Applied Statistics 2009, 36, 1385–1396. [Google Scholar] [CrossRef]
Abu-Shawiesh, M.O.A.; Kibria, B.M.G.; George, F. A robust bivariate control chart alternative to the hotelling’s T2 control chart. Quality and Reliability Engineering International 2014, 30, 25–35. [Google Scholar] [CrossRef]
Yahaya, S.S.S.; Ali, H.; Omar, Z. An alternative hotelling T 2 control chart based on minimum vector variance (MVV). Modern Applied Science 2011, 5, 132. [Google Scholar] [CrossRef]
Herwindiati, D.E.; Djauhari, M.A.; Mashuri, M. Robust multivariate outlier labeling. Communications in Statistics Simulation and Computation 2007, 36, 1287–1294. [Google Scholar] [CrossRef]
Williams, J.D.; Woodall, W.H.; Birch, J.B.; Sullivan, J.O.E.H. On the distribution of hotelling’s T2 statistic based on the successive differences covariance matrix estimator. Journal of Quality Technology 2006, 38, 217–229. [Google Scholar] [CrossRef]
Jensen, W.A.; Birch, J.B.; Woodall, W.H. High breakdown estimation methods for phase I multivariate control charts. Quality and Reliability Engineering International 2007, 23, 615–629. [Google Scholar] [CrossRef]
Utami, A.N.F.; Suwanda. Penggunaan Estimator Robust Reweighted Minimum Covariance Determinant pada Diagram Kontrol T2 Hotelling untuk Monitoring Penyebaran Covid-19 di Korea Selatan. Jurnal Riset Statistika 2021, 63–72. [Google Scholar] [CrossRef]
Ahsan, M.; Mashuri, M.; Lee, M.H.; Kuswanto, H.; Prastyo, D.D. Robust Adaptive Multivariate Hotelling T2 Control Chart Based on Kernel Density Estimation for Intrusion Detection System. Expert Systems with Applications 2020, 145, 113105. [Google Scholar] [CrossRef]
Boudt, K.; Rousseeuw, P.J.; Vanduffel, S.; Verdonck, T. The minimum regularized covariance determinant estimator. Statistics and Computing 2020, 30, 113–128. [Google Scholar] [CrossRef]
Phaladiganon, P.; Seoung, S.B.; Chen, V.C.P.; Baek, J.G.; Pa, S.K. Bootstrap-Based T2 Multivariate Control Charts. Communications in Statistics - Simulation and Computation 2011, 40, 645–662. [Google Scholar] [CrossRef]
Ye, N.; Li, X.; Chen, Q.; Emran, S.M.; Xu, M. Probabilistic techniques for intrusion detection based on computer audit data. IEEE Trans. Syst. Man, Cybern. Part ASystems Humans 2001, 31, 266–274. [Google Scholar] [CrossRef]
Ye, N.; Emran, S.M.; Chen, Q.; Vilbert, S. Multivariate statistical analysis of audit trails for host-based intrusion detection. IEEE Transactions on Computers 2002, 51, 810–820. [Google Scholar] [CrossRef]
Qu, G.; Hariri, S.; Yousif, M. Multivariate Statistical Analysis for Network Attacks Detection. The 3rd ACS/IEEE International Conference onComputer Systems and Applications, 2005; 2005–14. [Google Scholar]
Zhang, Z.; Zhu, X.; Jin, J. SVC-Based Multivariate Control Charts for Automatic Anomaly Detection in Computer Networks. IEEE, 2007. [Google Scholar]
Tavallaee, M.; Lu, W.; Iqbal, S.A.; Ghorbani, A. A Novel Covariance Matrix based Approach for Detecting Network Anomalies. Sixth Annual Conference on Communication Networks and Services Research, 2008. [Google Scholar]
Sivasamy, A.; Sundan, B. A Dynamic Intrusion Detection System Based on Multivariate Hotelling’s T2 Statistics Approach for Network Environments. The Scientific World Journal.
Rastogi, R.; Khan, Z.; Khan, M.H. Network Anomalies Detection Using Statistical Technique : A Chi- Square approach. International Journal of Computer Science Issues 2012, 9, 515–522. [Google Scholar]
Camacho, J.; Pérez-Villegas, A.; García-Teodoro, P.; Maciá-Fernández, G. PCA-based multivariate statistical network monitoring for anomaly detection. Computers & Security 2016, 59, 118–137. [Google Scholar] [CrossRef]
Ahsan, M.; Mashuri, M.; Kuswanto, H.; Prastyo, D. Intrusion detection system using multivariate control chart Hotelling's T2 based on PCA. International Journal on Advanced Science, Engineering and Information Technology 2018, 8, 1905–1911. [Google Scholar] [CrossRef]
Ahsan, M.; Mashuri, M.; Kuswanto, H.; Prastyo, D.D.; Khusna, H. T2 control chart based on successive difference covariance matrix for intrusion detection system. Journal of Physics: Conference Series 2018, 1028. [Google Scholar] [CrossRef]
Ahsan, M.; Mashuri, M.; Khusna, H. INTRUSION DETECTION SYSTEM USING BOOTSTRAP RESAMPLING APPROACH OF T² CONTROL CHART BASED ON SUCCESSIVE DIFFERENCE COVARIANCE MATRIX. Journal of Theoretical & Applied Information Technology 2018, 96, 8. [Google Scholar]
Ahsan, M.; Mashuri, M.; Lee, M.H.; Kuswanto, H. Robust Adaptive Multivariate Hotelling T2 Control Chart Based on Kernel Density Estimation for Intrusion Detection System. Expert Systems with Applications 2020, 145, 113105. [Google Scholar] [CrossRef]
Montgomery, D.C. Introduction to Statistical Quality Control, 7th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2013. [Google Scholar]
Efron, B. Bootstrap Methods: Another Look at the Jacknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
Efron, B.; Tibshirani, R. An introduction to the bootstrap; CRC Press, 1994. [Google Scholar]
Rousseeuw, P.J. Multivariate estimation with high breakdown point. Mathematical Statistics and Applications 1985, 8, 283–297. [Google Scholar]
Rousseeuw, P.; Croux, C. Alternatives to the median absolute deviation. J. Am. Stat. Assoc. 1993, 88, 1273–1283. [Google Scholar] [CrossRef]
Croux, C.; Haesbroeck, G. Influence function and efficiency of the minimum covariance determinant scatter matrix estimator. Journal of Multivariate Analysis 1999, 71, 161–190. [Google Scholar] [CrossRef]
Han, J.; Kamber, M.; Pei, J. Data Mining Concepts and Techniques; Morgan Kaufmann: USA, 2012. [Google Scholar]
Bekkar, M.; Djemaa, H.; Alitouch, T. Evaluation Measure for Models Assesment Over Imbalanced Data Sets. Journal of Information Engineering and Aplications 2013, 27–38. [Google Scholar]
Moustafa, N.; Slay, J. UNSW-NB15: A comprehensive data set for network intrusion detection. In Proceedings of the 2015 Military Communications and Information Systems Conference. Canberra, 2015, Australia: MilCIS 2015-IEEE Stream; pp. 1–6. [Google Scholar]
Moustafa, N.; Slay, J. The evaluation of Network Anomaly Detection Systems: Statistical analysis of the UNSW-NB15 data set and the comparison with the KDD99 data set. Information Security Journal: A Global Perspective 2016, 25, 18–31. [Google Scholar] [CrossRef]
Raymaekers, J.; Rousseeuw, P.J. The Cellwise Minimum Covariance Determinant Estimator. Journal of the American Statistical Association 2023. [CrossRef]

Figure 1. Bootstrap Control Limit Algorithm.

Figure 2. T² Chart of (a) Control Limit Selection and (b) Statistic Plot.

Figure 3. Fast-MCD-based T² Chart of (a) Control Limit Selection and (b) Statistic Plot.

Figure 4. MRCD-based T² Chart of (a) Control Limit Selection and (b) Statistic Plot.

Table 1. Confusion Matrix Table.

Actual	Detection
Actual	Intrusion	Normal
Intrusion	True Positives (TP)	False Negatives (FN)
Intrusion	False Positives (FP)	True Negatives (TN)

Table 2. Characteristics of UNSW-NB15 Dataset.

Label	Number of Records	Percentage
Normal	56.000	31,94
Intrusion	119.341	68,06
-Analysis	2.000	1,14
-Backdoor	1.746	1,00
-DoS	12.264	6,99
-Exploits	33.393	19,04
-Fuzzers	18.184	10,37
-Generic	40.000	22,81
-Reconnaissance	10.491	5,98
-Shellcode	1.133	0,65
-Worms	130	0,07
Total	175.341	100,00

Table 3. Confusion Matrix and Performance Evaluation for Conventional Hotelling’s T² Chart

Actual	Detection		Accuracy	AUC	FP Rate	FN Rate
Actual	Intrusion	Normal	Accuracy	AUC	FP Rate	FN Rate
Intrusion	9,853	109,488	0.376	0.511	0.060	0.917
Normal	3,354	52,646

Table 4. Confusion Matrix and Performance Evaluation for Fast-MCD-based T² Chart

Actual	Detection		Accuracy	AUC	FP Rate	FN Rate
Actual	Intrusion	Normal	Accuracy	AUC	FP Rate	FN Rate
Intrusion	81,871	37,470	0.711	0.718	0.250	0.314
Normal	13,991	42,009

Table 5. Confusion Matrix and Performance Evaluation for MRCD-based T² Chart

Actual	Detection		Accuracy	AUC	FP Rate	FN Rate
Actual	Intrusion	Normal	Accuracy	AUC	FP Rate	FN Rate
Intrusion	118,915	426	0.902	0.849	0.298	0.004
Normal	16,671	39,329

Table 6. Confusion Matrix and Performance Evaluation for MRCD-based T² Chart

Control Chart	Accuracy	AUC	FP Rate	FN Rate	Execution Time (s)
Conventional T²	0.376	0.511	0.060	0.917	286
T² Fast-MCD	0.711	0.718	0.250	0.314	1,470
T² MRCD	0.902	0.849	0.298	0.004	8,108

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Multivariate Robust MRCD Based Hotelling’s T2 Control Chart with Bootstrap Control Limit for Intrusion Detection

Abstract

1. Introduction

2. Related Works

3. Proposed Chart

3.1. Multivariate Hotelling’s T2 Control Chart

3.2. Bootstrap Control Limit-Based T2 Chart

3.2. MRCD Algorithm

3.3. MRCD-Based T2 Chart

4. Methodology

5. Results and Discussions

6. Conclusion and Future Research

Author Contributions

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.1. Multivariate Hotelling’s T² Control Chart

3.2. Bootstrap Control Limit-Based T² Chart

3.3. MRCD-Based T² Chart