Preprint
Article
Designing Advanced Drug Delivery Systems: Core-Shell Alginate Particles through Electro-Fluid Dynamic Atomization
Altmetrics
Downloads
103
Views
38
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
27 December 2023
Posted:
28 December 2023
You are already at the latest version
Alerts
Abstract
Innovations in drug delivery systems are crucial for enhancing therapeutic efficiency. Our research presents a novel approach based on Electro-fluid dynamic atomization (EFDA) to fabricate core-shell monophasic particles (CSMp) from sodium alginate blends of varying molecular weights. This study explores the morphological characteristics of these particles in relation to material properties and process conditions, highlighting their potential in drug delivery applications. A key aspect of our work is the development of a mathematical model that simulates the release kinetics of small molecules, specifically sodium diclofenac. By assessing the diffusion properties of different molecules and gel formulations through transport and rheological models, we have created a predictive tool for evaluating the efficiency of these particles in drug delivery. Our findings underscore two critical independent parameters for optimizing drug release: the external shell thickness and the diffusivity ratios within the dual layers. This allows for precise control over the timing and intensity of the release profile. The study advances our understanding of EFDA in the fabrication of CSMp and offers promising avenues for enhancing drug delivery systems by tailoring release profiles through particle characteristic manipulation.
Keywords:
Subject: Chemistry and Materials Science - Materials Science and Technology
1. Introduction
In the last few years, due to the rapid growth and the development in the pharmaceutical area, new drug delivery systems based on liposomes, micelles, and polymeric micro- or nanoparticles are emerging to improve the therapeutic activity [1,2,3,4]. Polysaccharides, the most widely used biopolymer class, contain repeating mono- or disaccharide units linked by glycosidic bonds that confer the ability to encapsulate drug molecules in their interstitial spaces and provide controlled release of cargo drug molecules [5,6]. Among them, sodium alginates are mainly considered due to several advantages, including their cheapness, availability in nature, chemical tenability, ease of preparation, biocompatibility, biodegradability, low immunogenicity, and moderate gelation process, that address their use for many applications in the pharmaceutical industry as a drug- and protein-delivery systems [7,8]. As a polysaccharide, alginate is one of the most used materials in applications such as the encapsulation of drugs, proteins, insulin, and cells in particles. Alginate particles undergo a crosslinking by either external or internal gelation and become a spherical porous hydrogel network when reacting with certain divalent cations such as Ca2+ [9,10]. Their water solubility, combined with the chemical affinity with divalent ions, offers the chance to process them by sustainable and reliable processing routes such as electrospraying, which can assure accurate control and variability of the chemical-physical properties of the 3D network [11,12]. Furthermore, the hydrophilic nature of sodium alginate, due to the presence of carboxyl and hydroxyl groups along its molecular backbone, significantly contributes to the successful encapsulation of hydrophilic drugs [13]. Otherwise, this makes them poorly compatible with hydrophobic drug molecules –i.e., anti-inflammatory drugs such as ibuprofen [14] or antibiotics such as ciprofloxacin [15] In this view, the presence of carboxyl and hydroxyl groups recently enabled to investigate different routes based on chemical grafting with hydrophobic side groups to modify the hydrophilic character of the polymer carrier, with relevant improvements in terms of drug loading via self-assembly [16]. Likewise, the peculiar transport properties —associated with highly controllable swelling properties of the polymer network under different pH — can help to regulate the diffusion of fluids and/or other kinds of macromolecules oriented to both drug and cell strategies— in the presence of external stimuli exerted by the local microenvironment (i.e., chemical, mechanical) [17]. They have been widely investigated for drug delivery routes such as oral, parenteral, pulmonary, and transdermal as alone or combined with other polymers in order to efficiently encapsulate cells or a broad set of molecular drugs [18,19].
In the last years, several techniques, including batch emulsification solvent evaporation, coacervation method, microfluidic technology, spray drying, and high-voltage electrospray have been explored to prepare drug-loaded delivery systems [20,21]. However, most of the polymer-based methods have some drawbacks, such as low encapsulation efficiency, wide particle size distribution, and high initial burst release, in addition to the use of toxic solvents used to form solid polymer particles that continue to be a concern for their pharmaceutical applications [22,23]. In this view, Electro fluid dynamic technology (EFDA) is a low-cost technique based on the application of a high voltage to form particles in the micrometric range, suitable to design highly customized drug loaded devices [24]. EFDA is a non-continuous dropping mode, strongly influenced by the local polymer density and molecular weight, and, consequently, by the electrical forces required to overcome the surface tension of the drop at the tip of needle [25]. The formed droplets are collected into a crosslinking bath (i.e., CaCl2), to allow their ionic gelation to finally obtain spherical beads with homogeneous size prior to reach the excess of charge on the droplet surface [26,27]. The processing of ionotropic polymers as alginates allows for the entrapment of cells, active molecules and/or pharmaceutical species to form chemically functionalized carriers suitable to differently address the biological response [27,28]. Morphology and particle sizes can be highly adjusted by accurately setting process parameters (i.e., polymer concentration, voltage applied, needle diameter, working distance) [29,30]. The implementation/modification of the experimental setup, also offers the opportunity to increase the structural complexity of the devices (i.e., core shell, Janus, etc) to more efficiently encapsulate and release active molecules [31,32]. For instance, a recent study has proposed the use of EFDA particles with monophasic composition and core shell architecture for the encapsulation of lysin salt ketoprofen [33], also preserving their functionality, due to the use of mild solvents [34].
For a robust design and process parameters optimization, the use of mathematical models is extremely important to provide a predictive screening of diffusion phenomena involved in drug delivery systems [35]. For this purpose, in this work, Core-shell monophasic particles (CSMp), from sodium alginates with different viscosities were fabricated in order to design a transport model suitable to describe the diffusion of small molecules through their architecture.
2. Results and Discussion
The viscosity (η, Pa∙s) and viscoelastic properties play a crucial role in the EFDA to process the polymer solutions, affecting the morphology of microparticles [36]. For instance, the higher viscosity of solutions generates larger and spherical microparticles, while lowers viscosities generate smaller particles [37]. Detailed rheological characterization was conducted to better understand how these properties contribute to the process. Figure 1A presents the flow behavior of Hv (red box) and Lv (green cross) alginate. Both samples exhibit a Newtonian behavior, with average viscosity (η) values of and Pa∙s for alginate Hv and Lv, respectively. To further investigate the differences between the two samples, a master curve was constructed by normalizing the viscosity values with respect to the mean value (referred to as η0) [38,39]. The data points show perfect overlap, as depicted in Figure 1B.
It has been observed that solution properties can impact the physical characteristics of microgels, including diffusion, which is linked to viscosity by the Stokes-Einstein equation [40]. When lower viscosities are employed, the polymeric matrix dissolves rapidly within the first few minutes of contact with water [29]. However, although this problem is solved by using high viscosity polymer, they can represent a limitation for the drug diffusion [41]. Furthermore, with high-viscosity polymers, it becomes impractical to conduct shear characterization tests. To address this, frequency sweep tests were performed. Figure 1C illustrates the typical trend of polymer solutions, with G’’ (loss modulus) predominating on G’ (storage modulus) within the frequency range studied. These rheological findings provide valuable insights into the flow and viscoelastic properties of the alginate samples, shedding light on their behavior during the spraying process.
The size of particles and core-shell structure are crucial indications of product quality since they influence the release profile of encapsulated molecules and preserving particle form and composition through production is critical for fabrication of microparticles [42]. Besides, shell properties, such as shell material and shell thickness, allow its adaptability to control the release kinetics of the core-shell microspheres [43]. This work aimed to design core-shell monophasic microparticles (CSMp) of alginate by using two solutions with different viscosities (i.e, Lv- and Hv) for core and shell compartments, respectively for drug delivery applications. The scheme of EFDA technology is represented in Figure 2A.
The morphology of CSMp was investigated by optical imaging. It was observed that microparticles have regular morphology, smooth surface, a mean diameter of 865.7 ± 28.13 µm, and do not tend to agglomerate (Figure 2B). FTIC-Albumin was qualitatively used to label the core (Lv) alginate to evidence the core-shell architecture of the microparticles (Figure 2C,D).
The use of staining agents was an important tool to collect quantitative information of the particle architecture (i.e., core diameter, shell thickness), to be used as input for the transport model. However, the use of fluorescent labels was not fully satisfying to measure these characteristic sizes, due to the presence of a strong background noise of the images (Figure 2C) that affected data reproducibility. In this view, further investigations were performed via image analysis, recording an average core diameter equal to 457.1 ± 63.07 µm and a shell thickness of 254.7 ± 14.25 µm.
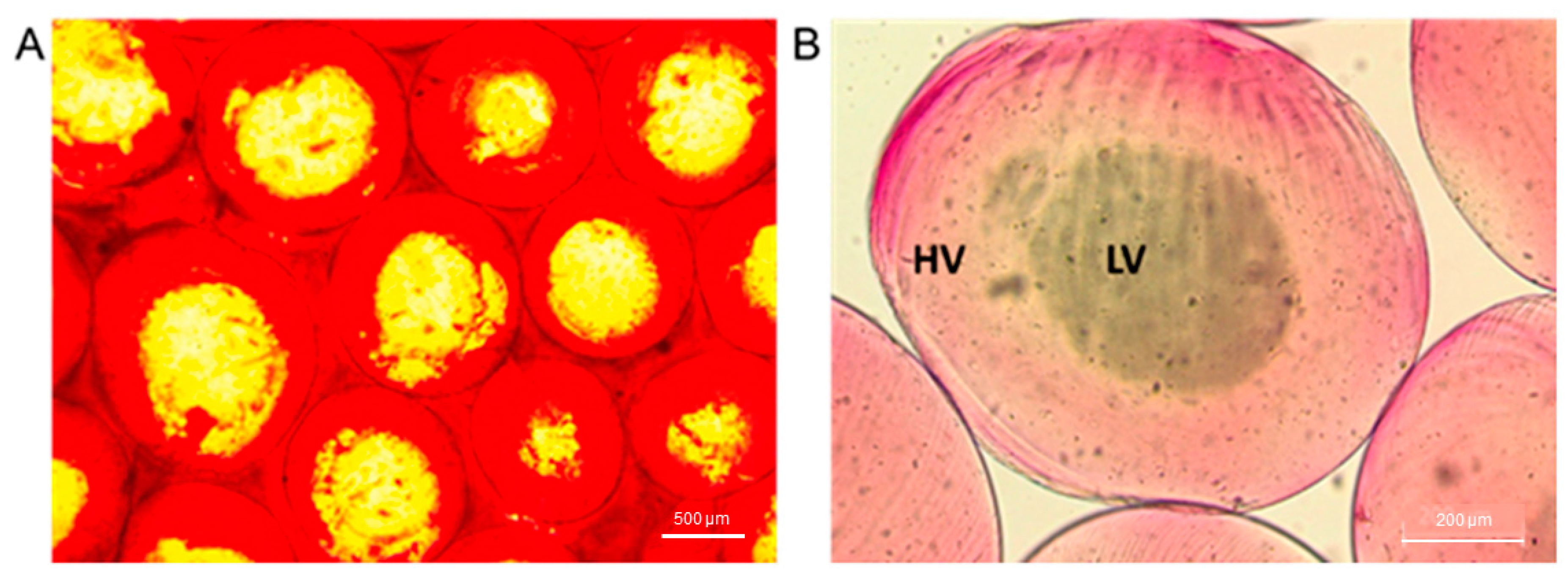
Considering previous studies focused on the alginate gel adsorption of staining agents in aqueous solutions [40,41], Alizarin Red was used to qualitatively remark Hv and Lv phases into CSMps (Figure 3A). Alizarin Red is usually used in in vitro studies to stain calcium deposits; Accordingly, in the case of alginate-based materials, it tends to interact with CaCl2 salts that work as crosslinking agent [42]. Therefore, dark red regions reported in Figure 3A can be related to Ca rich phases of alginates mainly present into the shell of alginate particles, where the crosslinking mechanism is more efficient, while slight red stained areas can be detected into the inner regions of the particle where the access of calcium ions is partially inhibited. After washing the samples (Figure 3b), this effect was confirmed, despite the staining is strongly mitigated by the water molecule diffusion.
Besides, alginate beads were variously proposed as templates to support cell interactions, due to their biocompatibility, also in the absence of bioactive signals [31]. For instance, a recent study proved the ability of alginate microgels - fabricated via EFDAs - to support in vitro viability of mesenchymal stem cells, by an accurate balance of process/solution parameters, particles morphological features and cell/surface interaction [29]. In this context, the further addition of bioactive signals or molecular drugs into alginate microparticles can play a relevant role on the biological response, as a function of the release mechanisms, determined by the synergic contribution of chemical composition and structural properties [44].
In this view, it is becoming stringent an accurate design of mathematical models able to predict in feasible way all the mechanisms related to these phenomena in vivo under different external conditions. Accordingly, herein a mathematical model was developed to simulate the release of a probe molecule – i.e., sodium diclofenac - through a double-layered alginate hydrogel system. In the past similar models were used to predict diffusion of several solute in gel or hydrogels showing the potential of such approach for fine-tune the transport properties [45,46,47,48,49,50]. The present model was based on the premise that diffusion is isotropic in space. This assumption involves the entire system can be described mathematically according to a radial symmetry, that allowed to simplify the model by reducing the variables and analyzing the problem as a function of time and radial coordinates only. Figure 4A provides a schematic representation of the system, which is divided into three distinct zones. The innermost zone, ranging from to , corresponds to the inner alginate core. In this region, the initial concentration of diclofenac is assumed to be and the diffusion process is characterized by a diffusivity, .
The second zone extends from to , representing a shell created with a different molecular weight alginate. It possesses an initial concentration, , and a diffusivity, . Finally, the outermost zone spans from to . Here, the drug diffuses into an outer volume with an initial concentration, , and a diffusivity, . In this model, we assumed purely diffusive transport with no convective motions, even in the external domain . The size of the outer volume is chosen to be . This decision ensures that our model aligns with the typical physiological condition, where the external volume greatly surpasses the particle volume.
To accurately model the multi-layer structure of the system, we considered discontinuous initial conditions and diffusivity values. This is because the core and shell of the particle have different concentrations and diffusivities. Additionally, diffusivity was treated as a spatial function within the model. To maintain the radial symmetry assumption, null flux conditions were applied at the boundaries. The primary driving force of the process under investigation is mass diffusion. This phenomenon is governed by concentration gradients and the surface area where diffusion occurs. It is essential to note that in spherical coordinates, the surface area increases as we move along the radius. Considering our earlier assertion that diffusion only happens along the radial coordinate, we derive equation 1. On the left side of this equation, we have the accumulation term, while the diffusion term is on the right. Equation 2 makes explicit the variation in diffusivity across the three zones described previously. Notably, diffusivity exhibits discontinuities at the points along the radius where there is a transition from one material to another. Analogously, equation 3 and equation 2, identify the discontinuities in initial conditions as we move from one zone to another. In its general form, the model proposed considers three different values of initial concentration. Lastly, equation 4 provides the boundary conditions. Null flux must be enforced in both instances to preserve the symmetry of the problem.
Part of the simulation parameters, such as core and shell diameters, were chosen to be in the same range as the simulated system. On the other hand, diffusivity values were estimated using existing models to understand how design parameters could be used to fine-tune the latter. From the values that can be found in the literature [51,52,53,54], it can be derived that the diffusivity of small molecules in alginate hydrogel does not vary significantly as a function of alginate concentration. For molecules having a molecular weight comparable with the one of Diclofenac the value found in literature is in the order of magnitude of [55]. To estimate the diffusivity of a molecule, it is possible to use the Stokes-Einstein equation [40], which links a diffusivity of the molecule to the viscosity of the medium in which it diffuses. In Eq. 5 is the diffusivity in homogeneous medium, the Boltzmann constant, the temperature in kelvin, the viscosity of the medium and the characteristic size of the diffusing particle.
Then, to calculate the effective diffusivity value in the hydrogel, eq. 6 from Lustig-Peppa model can be used [56]. In this model, the effective diffusivity is calculated from a corrective factor with respect to the diffusivity in the medium. In this model is the characteristic mesh size of the hydrogel, is its volume fraction and is again characteristic size of the diffusing particle.
In this model, a small mesh size or high-volume fraction contributes to reduce the diffusivity from the value . While the volume fraction of the hydrogel can be easily determined, the mesh size can be harder to measure. There are several empirical correlations that allow an estimation of the mesh size [56,57,58,59]. These measurements suggest an estimated mesh size between and [56]. To the purpose of simulate a conservative scenario we will consider an average value of . From the crystallographic structure of Diclofenac we obtained a value of 10.10 Å for the hydrodynamic radius of the molecule [60]. Using equation 5, it was possible to estimate the diffusivity value in water to be . The diffusivity in the hydrogel was then calculated using equation 6, this calculation however returned a value of that has a negligible difference with the value in water. This result agrees with several previous experimental studies [51,52,53,54] and demonstrate how the small characteristic size of Diclofenac allows it to diffuse between the alginate mesh without significant restrictions. At the same time, this also suggests that the multiple layer system can be used to control transport of larger molecules. A list of the parameter used together with boundary conditions is provided in Table 1.
Table 1.
The table contains the value used during numerical simulations. When multiple simulations were conducted, we indicate the range of values assumed by the parameters.
Table 1.
The table contains the value used during numerical simulations. When multiple simulations were conducted, we indicate the range of values assumed by the parameters.
| Parameter | Value | Units |
|---|---|---|
With these numerical simulations, we want to investigate how process parameters can be used to create controlled drug release systems. Figure 4B,C show the results of the numerical simulations, on the right of the figures the parameters used are reported. For the initial conditions we used a unit concentration in the core zone, and for the shell and outer zone a zero concentration. Similarly, the diffusivity for each zone was set to different values, depending on the simulation. The radius of the inner core was fixed at . In Figure 4B, the simulation was carried out using the diffusivity parameters estimated earlier and by varying the thickness of the outer shell. The outer radius was gradually increased from up to while still leaving the core size fixed at . This choice was made to assess the ability of the gap to retard the outward flow of Diclofenac. What emerges from this first simulation is that it is possible to influence the maximum value and time of mass flux through an appropriate choice of shell thickness. Specifically, in the simulation for an value of there is a , for of there is a , and for of there is a . At the same time, it is possible to observe that the peak decreases and the diffusion curve decays more slowly, the latter observation is indicative of increased transport resistance that is added by the thicker layer in which Diclofenac must diffuse. In Figure 4C, the simulation was carried out using a shell thickness fixed with and varying the ratio of diffusion coefficients. The diffusion coefficient of the outer zone was fixed at while that of the inner zone was varied between to . This choice was made to simulate various diffusivity ratios and to estimate how the diffusivity of the core in which Diclofenac is present may affect mass transport. The simulations show that the diffusivity of the core affects the peak height and shape of the diffusion curve while leaving the characteristic time of the maximum unchanged. When the core diffusivity exceeds that of the outer shell, the curve decays more slowly respect to other cases, and the peak height is reduced significantly. The latter phenomenon can be interpreted as turning the core into a reservoir whose contents slowly diffuse due to precise calibration of the diffusivity ratio.
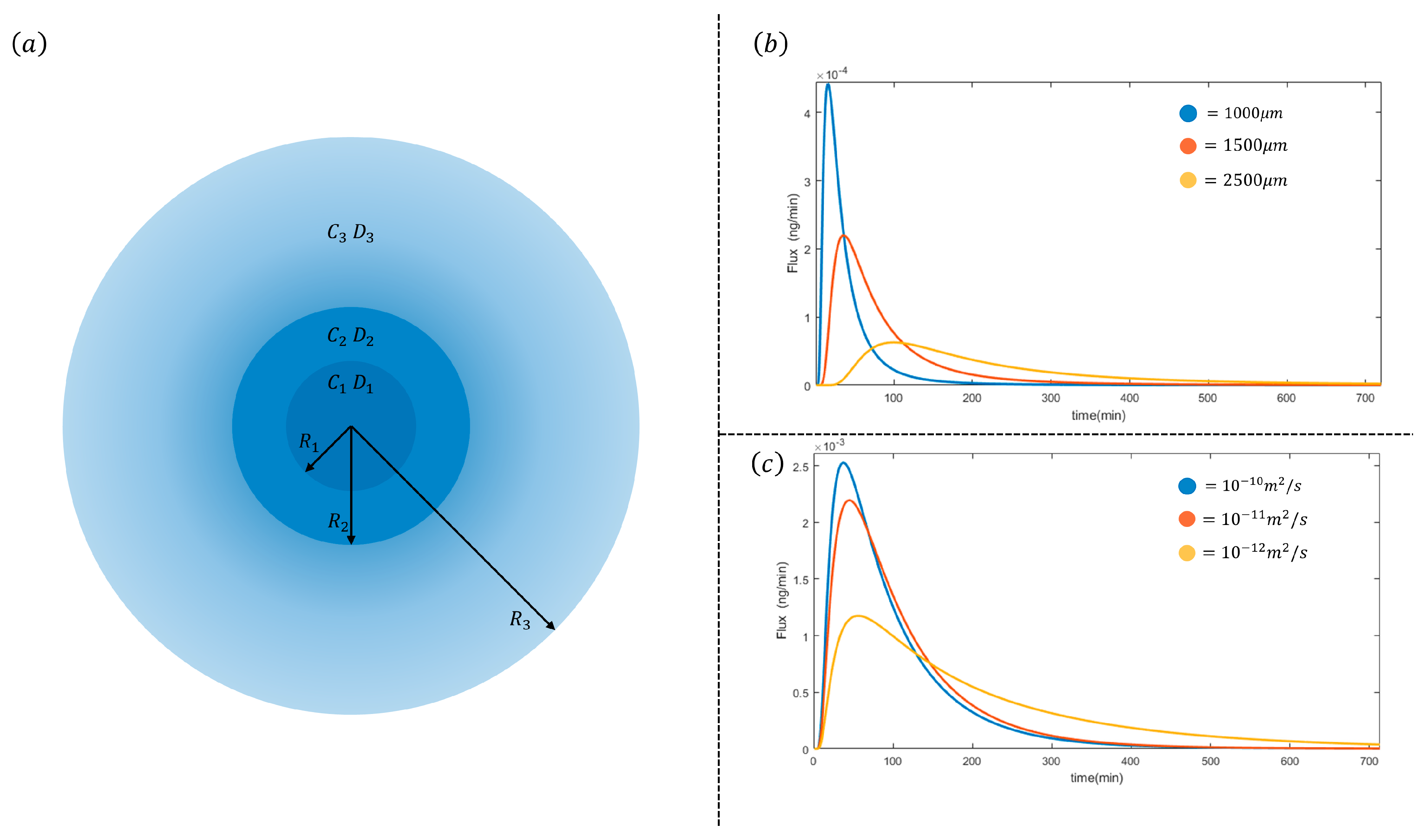
Figure 4.
Schematized model and simulation results. A) Schematization of the domain of interest. The central core ranging from to is the first alginate zone, while the second zone goes from to . The flux is evaluated at , on the boundary between alginate bead and outer zone. Radius represents the entire volume of our simulation. Please notice that our assumption of would make it hard to represent the figure in a precise scale without confusion. Therefore, the figure must be considered qualitative, and we suggest to read Table 1 for details on the modeling parameters. Figures B) and C) show numerical experiments of possible combinations involving hydrogel core/shell ratio and diffusivity ratio. In Figure B the shell thickness is gradually increased showing a time shift of the peak to the right as well as its lowering. In figure C) the ratio of diffusivity coefficients changed progressively, in this second case it is possible to influence the peak height and release time while leaving the characteristic peak time unchanged.
Figure 4.
Schematized model and simulation results. A) Schematization of the domain of interest. The central core ranging from to is the first alginate zone, while the second zone goes from to . The flux is evaluated at , on the boundary between alginate bead and outer zone. Radius represents the entire volume of our simulation. Please notice that our assumption of would make it hard to represent the figure in a precise scale without confusion. Therefore, the figure must be considered qualitative, and we suggest to read Table 1 for details on the modeling parameters. Figures B) and C) show numerical experiments of possible combinations involving hydrogel core/shell ratio and diffusivity ratio. In Figure B the shell thickness is gradually increased showing a time shift of the peak to the right as well as its lowering. In figure C) the ratio of diffusivity coefficients changed progressively, in this second case it is possible to influence the peak height and release time while leaving the characteristic peak time unchanged.

With these simulations, it has been demonstrated how, using two experimentally independent parameters, a tailored release curve can be obtained. This result, combined with the technological ability to create hydrogels having specific characteristics, demonstrates how alginate can be used as a carrier for drug delivery.
Noteworthy, the proposed modeling approach is not limited to the use of Sodium Diclofenac - as probe in this work - but may be extended/adapted to other types of molecules, as a function of the application target in the biomedical field. In the last years, core shell particles made of alginates were preferentially addressed to load hydrophilic molecules like protein suitable for oral delivery administration. Indeed, the peculiar ability of alginate to form gel-like structures in the presence of acid conditions, can be successfully used to prevent a massive release of drug into the stomach, thus promoting a gradual release in the first intestinal tract [61]. However, the high versatility of alginates to create molecular complexes by different interactions (i.e., electrostatic, chemical, physical) with other biopolymers, can be addressed to the design of a wide range of hybrid carriers suitable for the fabrication of customized drug delivery systems for targeting applications (i.e., colon) [62,63].
4. Materials and Methods
2.1. Preparation of Alginate Microparticles
Low viscosity (LV, 250 cPs) and high viscosity (HV, 20,000-40,000 cPs) sodium alginates (SA) from brown algae and anhydrous calcium chloride (CaCl2) were purchased by Sigma Aldrich, Milan, Italy. Deionized water was used for the preparation of the solutions. Sodium alginate (SA) aqueous solutions were prepared at 2% w/v for the HV-SA and 0.5% w/v for the LV-SA sodium alginate. For the fabrication of microgels, a commercial machine (NF500 MECC, Fukuoka, Japan) was used, equipped with a tailor-made magnetic stirrer working as a collector in agreement with previous studies [25]. The EFDA parameters were optimized to control the size and shape of microgels. Briefly, the solutions were placed in two different 5 mL syringes, connected each one to a syringe pump with an imposed feed rate equal to 0.5 and 2.0 mL/h, respectively. The applied voltage was set at 25 kV, while the tip-to-collector distance was set at 150 mm. Droplets were collected into a CaCl2 solution at a concentration of 1.1% under magnetic stirring to trigger the ionotropic interaction in the aqueous solution.
2.2. Microparticles characterization
In order to characterize and evaluate the morphology of core-shell particles, optical microscopy (DM750, Leica, Germany) was used. For the characteristic size and thicknesses 10 optical images were used to measure 7-10 microgels by the use of ImageJ software (Version 1.52s, National Institute of Health, USA). The architecture CSMp was further investigated by confocal microscopy. Briefly, 1 mg/mL of albumin–fluorescein isothiocyanate conjugate (FITC-albumin, Sigma Aldrich, Milan, Italy) was added to the LV-SA solution before the EFD process, then, core-shell particles were fabricated with the set parameters. After collecting particles, they were observed by confocal microscope.
To distinguish between the core and the shell structures and obtain more clear observation, an alizarin red solution was used. CSMp were put in contact with alizarin red dye (1% in dH2O). Then, microgels were washed until the excess of dye was removed. Optical images were taken after each of the mentioned steps.
2.3. Rheological setup
Rheological measurements for both alginate samples (Hv and Lv) were conducted at room temperature (25°C) using a stress-controlled rheometer (Anton Paar Physica MCR 301 Instruments) equipped with a double gap measuring geometry (DG26.7/TI-SN9317). Temperature control was achieved using a Peltier cooler/heater connected to an external circulating water bath (Lauda) [64]. Prior to the measurements, the samples underwent a pre-shear process at a shear rate of 200 1/s for 1 minute to eliminate any potential loading effects. Flow curves were obtained by varying the shear rate ( ̇) in the range 0.01–200 1/s under steady shear flow conditions. To confirm linear viscoelasticity, strain sweep tests were performed at a fixed angular frequency (ω = 1 rad/s), with the amplitude ranging from 0.01 to 200 %. Oscillatory flow tests were conducted within the linear viscoelastic regime. Frequency sweep tests were carried out by varying the frequency in the range of 0.1-100 rad/s. These tests provide insights into the frequency-dependent behavior of the alginate samples.
2.4. Modelling
A mathematical model of drug diffusion was developed to simulate different core-shell combinations and predict how the system will release the contained drug. The model is based on a standard 1D mass balance in radial coordinates where two different zones are considered (core and shell) with two different diffusivities. Details on the model are reported in the result session The simulations were performed using the MATLAB 2021b environment with the “pdepe” initial-boundary problem solver. In each simulation, we estimated the released flux for a total time of 12 hours.
5. Conclusions
The fabrication of microparticles via EFDA technology has demonstrated the potential for developing drug delivery systems, particularly core-shell particles. Here, we have shown that monophasic alginate particles with different viscosities can be designed with monodisperse size and suitable core-shell architecture. Microparticles were successfully produced and characterized experimentally, providing further empirical evidence to substantiate the reliability of the dual-layer hydrogel system. Their size characterization highlighted a good control and repeatability of the production process, which are crucial for the potential scalability of this drug delivery platforms towards the realization of personalized devices for precision medicine. The use of solutions with different viscosities provides a robust method to design core shell platform with improved interface for a more efficient transport and controlled release of drugs. Rheological characterization of the system validated the mechanical characteristics. The mathematical model has emerged as a critical tool for interpreting the intricate interactions governing the kinetics of drug release. It has enabled a detailed quantitative analysis of how various hydrogel parameters influence drug release rates, offering substantial predictive capability for refining drug delivery system designs. Additionally, the model’s broad applicability spans a wide spectrum of molecules based on their size, opening opportunities to experiment and fine-tune the core-shell hydrogel methodology for diverse therapeutic uses.
These results not only represent an important advancement in the design of hydrogel-based drug delivery systems but also underline the potential of these systems in improving the efficacy and safety of therapeutic drug administration. Future work will focus on the application of this technology to specific drugs and medical conditions, to further explore specific benefits for in vitro application. However, this should require more accurate investigations to focus on the long-term stability of hydrogel and microparticles, the influence of different environmental factors on the drug release kinetics, and the biological safety, in the perspective to also evaluate in vivo response.
Author Contributions
Conceptualization, V.G. S.C.; methodology I.C-M, C.S.; investigation, I.C-M, C.S, R.F., Z.R.; resources, V.G., S.C.; data curation, Z.R., R.F.; writing—original draft preparation, I.C-M, C.S.; ; writing—review and editing, I.C-M, C.S, R.F., Z.R., S.C., V.G.; supervision, V.G., S.C.; funding acquisition, V.G. All authors have read and agreed to the published version of the manuscript.
Funding
AFOSR 3DNEUROGLIA (FA9550-18-1-0255), MSCA-ITN-2020-ASTROTECH (GA956325).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Faheem, A.M.; Abdelkader, D.H. Novel Drug Delivery Systems. In Engineering Drug Delivery Systems; Seyfoddin, A., Dezfooli, S.M., Greene, C.A., Eds.; Elsevier, 2020; pp. 1–16.
- Romana, B.; Hassan, Md.M.; Sonvico, F.; Garrastazu Pereira, G.; Mason, A.F.; Thordarson, P.; Bremmell, K.E.; Barnes, T.J.; Prestidge, C.A. A Liposome-Micelle-Hybrid (LMH) Oral Delivery System for Poorly Water-Soluble Drugs: Enhancing Solubilisation and Intestinal Transport. European Journal of Pharmaceutics and Biopharmaceutics 2020, 154, 338–347. [Google Scholar] [CrossRef]
- Sultana, A.; Zare, M.; Thomas, V.; Kumar, T.S.S.; Ramakrishna, S. Nano-Based Drug Delivery Systems: Conventional Drug Delivery Routes, Recent Developments and Future Prospects. Med Drug Discov 2022, 15, 100134. [Google Scholar] [CrossRef]
- Liu, R.; Luo, C.; Pang, Z.; Zhang, J.; Ruan, S.; Wu, M.; Wang, L.; Sun, T.; Li, N.; Han, L.; et al. Advances of Nanoparticles as Drug Delivery Systems for Disease Diagnosis and Treatment. Chinese Chemical Letters 2023, 34, 107518. [Google Scholar] [CrossRef]
- Ahmad, A.; Mubarak, N.M.; Jannat, F.T.; Ashfaq, T.; Santulli, C.; Rizwan, M.; Najda, A.; Bin-Jumah, M.; Abdel-Daim, M.M.; Hussain, S.; et al. A Critical Review on the Synthesis of Natural Sodium Alginate Based Composite Materials: An Innovative Biological Polymer for Biomedical Delivery Applications. Processes 2021, 9. [Google Scholar] [CrossRef]
- Prasher, P.; Sharma, M.; Mehta, M.; Satija, S.; Aljabali, A.A.; Tambuwala, M.M.; Anand, K.; Sharma, N.; Dureja, H.; Jha, N.K.; et al. Current-Status and Applications of Polysaccharides in Drug Delivery Systems. Colloid Interface Sci Commun 2021, 42, 100418. [Google Scholar] [CrossRef]
- Agüero, L.; Zaldivar-Silva, D.; Peña, L.; Dias, M.L. Alginate Microparticles as Oral Colon Drug Delivery Device: A Review. Carbohydr Polym 2017, 168, 32–43. [Google Scholar] [CrossRef]
- Hariyadi, D.M.; Islam, N. Current Status of Alginate in Drug Delivery. Adv Pharmacol Pharm Sci 2020, 2020, 8886095. [Google Scholar] [CrossRef] [PubMed]
- Jeyhani, M.; Mak, S.Y.; Sammut, S.; Shum, H.C.; Hwang, D.K.; Tsai, S.S.H. Controlled Electrospray Generation of Nonspherical Alginate Microparticles. ChemPhysChem 2018, 19, 2113–2118. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wei, W.; Ni, B.-J. Chapter 3 - Algae-Based Alginate Biomaterial: Production and Applications. In Biomass, Biofuels, and Biochemicals; Ngo, H., Guo, W., Pandey, A., Chang, J.-S., Lee, D.-J., Eds.; Elsevier, 2022; pp. 37–66 ISBN 978-0-323-96142-4.
- Altobelli, R.; Guarino, V.; Ambrosio, L. Micro- and Nanocarriers by Electrofludodynamic Technologies for Cell and Molecular Therapies. Process Biochemistry 2016, 51, 2143–2154. [Google Scholar] [CrossRef]
- Guarino, V.; Khodir, W.K.W.A.; Ambrosio, L. Biodegradable Microparticles and Nanoparticles by Electrospraying Techniques. J Appl Biomater Funct Mater 2012, 10, 191–196. [Google Scholar] [CrossRef]
- Yang, J.-S.; Xie, Y.-J.; He, W. Research Progress on Chemical Modification of Alginate: A Review. Carbohydr Polym 2011, 84, 33–39. [Google Scholar] [CrossRef]
- Irvine, J.; Afrose, A.; Islam, N. Formulation and Delivery Strategies of Ibuprofen: Challenges and Opportunities. Drug Dev Ind Pharm 2018, 44, 173–183. [Google Scholar] [CrossRef] [PubMed]
- Yayehrad, A.T.; Wondie, G.B.; Marew, T. Different Nanotechnology Approaches for Ciprofloxacin Delivery Against Multidrug-Resistant Microbes. Infect Drug Resist 2022, 15, 413–426. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhu, Q.; Li, Z.; Yan, H.; Lin, Q. The Molecular Structure and Self-Assembly Behavior of Reductive Amination of Oxidized Alginate Derivative for Hydrophobic Drug Delivery. Molecules 2021, 26. [Google Scholar] [CrossRef] [PubMed]
- Zou, Z.; Zhang, B.; Nie, X.; Cheng, Y.; Hu, Z.; Liao, M.; Li, S. A Sodium Alginate-Based Sustained-Release IPN Hydrogel and Its Applications. RSC Adv 2020, 10, 39722–39730. [Google Scholar] [CrossRef] [PubMed]
- Hariyadi, D.M.; Islam, N. Current Status of Alginate in Drug Delivery. Adv Pharmacol Pharm Sci 2020, 2020, 8886095. [Google Scholar] [CrossRef]
- Abourehab, M.A.S.; Rajendran, R.R.; Singh, A.; Pramanik, S.; Shrivastav, P.; Ansari, M.J.; Manne, R.; Amaral, L.S.; Deepak, A. Alginate as a Promising Biopolymer in Drug Delivery and Wound Healing: A Review of the State-of-the-Art. Int J Mol Sci 2022, 23. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Zuo, X.; Zhou, Z.; Gu, Y.; Zheng, H.; Wang, X.; Wang, G.; Xu, C.; Wang, F. PLGA-Based Micro/Nanoparticles: An Overview of Their Applications in Respiratory Diseases. Int J Mol Sci 2023, 24. [Google Scholar] [CrossRef] [PubMed]
- Pushpamalar, J.; Sathasivam, T.; Gugler, M.C. Hydrogel BeadsBeads of Natural PolymersPolymers as a Potential Vehicle for Colon-Targeted Drug DeliveryDrug Delivery BT - Bio-Carrier Vectors: Methods and Protocols; Narayanan, K., Ed.; Springer US: New York, NY, USA, 2021; pp. 171–182. ISBN 978-1-0716-0943-9. [Google Scholar]
- Gali, L.; Pirozzi, A.; Donsì, F. Biopolymer- and Lipid-Based Carriers for the Delivery of Plant-Based Ingredients. Pharmaceutics 2023, 15. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Zhang, B.; Sun, R.; Liu, W.; Zhu, Q.; Zhang, X.; Wang, R.; Chen, C. PLGA-Based Biodegradable Microspheres in Drug Delivery: Recent Advances in Research and Application. Drug Deliv 2021, 28, 1397–1418. [Google Scholar] [CrossRef]
- Jaworek, A. 1 - Electrohydrodynamic Microencapsulation Technology. In Encapsulations; Grumezescu, A.M., Ed.; Academic Press, 2016; pp. 1–45 ISBN 978-0-12-804307-3.
- Guarino, V.; Ambrosio, L.; Bellini, D. Process for the Preparation of Microspheres Comprising Semisynthetic Polymers 2009.
- Zhao, S.; Huang, C.; Yue, X.; Li, X.; Zhou, P.; Wu, A.; Chen, C.; Qu, Y.; Zhang, C. Application Advance of Electrosprayed Micro/Nanoparticles Based on Natural or Synthetic Polymers for Drug Delivery System. Mater Des 2022, 220, 110850. [Google Scholar] [CrossRef]
- Cruz-Maya, I.; Guarino, V. 3D Scaffolds Fabrication via Bicomponent Microgels Assembly: Process Optimization and In Vitro Characterization. Micromachines (Basel) 2022, 13, 1726. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Maya, I.; Altobelli, R.; Alvarez-Perez, M.A.; Guarino, V. Mineralized Microgels via Electrohydrodynamic Atomization: Optimization and In Vitro Model for Dentin–Pulp Complex. Gels 2023, 9. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Maya, I.; Altobelli, R.; Marrese, M.; Guarino, V. Design of Alginate Based Micro-gels via Electro Fluid Dynamics to Construct Microphysiological Cell Culture Systems. Polym Adv Technol 2021, 32, 2981–2989. [Google Scholar] [CrossRef]
- Rentería-Ortega, M.; Salgado-Cruz, M.D.L.P.; Morales-Sánchez, E.; Alamilla-Beltrán, L.; Farrera-Rebollo, R.R.; Valdespino León, M.; Calderón-Domínguez, G. Effect of Electrohydrodynamic Atomization Conditions on Morphometric Characteristics and Mechanical Resistance of Chia Mucilage-Alginate Particles. CyTA - Journal of Food 2020, 18, 461–471. [Google Scholar] [CrossRef]
- Guarino, V.; Caputo, T.; Calcagnile, P.; Altobelli, R.; Demitri, C.; Ambrosio, L. proce Cellulose-Based Microspheres for Oral Administration of Ketoprofen Lysinate. J Biomed Mater Res B Appl Biomater 2018, 106, 2636–2644. [Google Scholar] [CrossRef]
- Zhang, X.; Qu, Q.; Zhou, A.; Wang, Y.; Zhang, J.; Xiong, R.; Lenders, V.; Manshian, B.B.; Hua, D.; Soenen, S.J.; et al. Core-Shell Microparticles: From Rational Engineering to Diverse Applications. Adv Colloid Interface Sci 2022, 299, 102568. [Google Scholar] [CrossRef] [PubMed]
- Guarino, V.; Altobelli, R.; Caputo, T.; Ambrosio, L.; Caserta, S.; Calcagnile, P.; Demitri, C. Mono- and Bi-Phasic Cellulose Acetate Micro-Vectors for Anti-Inflammatory Drug Delivery. Pharmaceutics 2019, 11. [Google Scholar] [CrossRef] [PubMed]
- Enayati, M.; Ahmad, Z.; Stride, E.; Edirisinghe, M. One-Step Electrohydrodynamic Production of Drug-Loaded Micro- and Nanoparticles. J R Soc Interface 2009, 7, 667–675. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Mathematical Modeling of Drug Delivery. Int J Pharm 2008, 364, 328–343. [Google Scholar] [CrossRef]
- Kim, M.K.; Lee, J.Y.; Oh, H.; Song, D.W.; Kwak, H.W.; Yun, H.; Um, I.C.; Park, Y.H.; Lee, K.H. Effect of Shear Viscosity on the Preparation of Sphere-like Silk Fibroin Microparticles by Electrospraying. Int J Biol Macromol 2015, 79, 988–995. [Google Scholar] [CrossRef]
- Rutkowski, S.; Si, T.; Gai, M.; Frueh, J.; He, Q. Hydrodynamic Electrospray Ionization Jetting of Calcium Alginate Particles: Effect of Spray-Mode, Spraying Distance and Concentration. RSC Adv 2018, 8, 24243–24249. [Google Scholar] [CrossRef]
- Dodero, A.; Vicini, S.; Alloisio, M.; Castellano, M. Rheological Properties of Sodium Alginate Solutions in the Presence of Added Salt: An Application of Kulicke Equation. [CrossRef]
- Dodero, A.; Vicini, S.; Alloisio, M.; Castellano, M. Sodium Alginate Solutions: Correlation between Rheological Properties and Spinnability. J Mater Sci 2019, 54, 8034–8046. [Google Scholar] [CrossRef]
- Miller, C.C.; Walker, J. The Stokes-Einstein Law for Diffusion in Solution. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 1997, 106, 724–749. [Google Scholar] [CrossRef]
- Lokhande, A.B.; Mishra, S.; Kulkarni, R.D.; Naik, J.B. Influence of Different Viscosity Grade Ethylcellulose Polymers on Encapsulation and in Vitro Release Study of Drug Loaded Nanoparticles. J Pharm Res 2013, 7, 414–420. [Google Scholar] [CrossRef]
- Yan, W.-C.; Tong, Y.W.; Wang, C.-H. Coaxial Electrohydrodynamic Atomization toward Large Scale Production of Core-Shell Structured Microparticles. AIChE Journal 2017, 63, 5303–5319. [Google Scholar] [CrossRef]
- van der Kooij, R.S.; Steendam, R.; Frijlink, H.W.; Hinrichs, W.L.J. An Overview of the Production Methods for Core–Shell Microspheres for Parenteral Controlled Drug Delivery. European Journal of Pharmaceutics and Biopharmaceutics 2022, 170, 24–42. [Google Scholar] [CrossRef]
- Eleftheriadou, D.; Evans, R.E.; Atkinson, E.; Abdalla, A.; Gavins, F.K.H.; Boyd, A.S.; Williams, G.R.; Knowles, J.C.; Roberton, V.H.; Phillips, J.B. An Alginate-Based Encapsulation System for Delivery of Therapeutic Cells to the CNS. RSC Adv 2022, 12, 4005–4015. [Google Scholar] [CrossRef] [PubMed]
- Cu, Y.; Saltzman, W.M. Mathematical Modeling of Molecular Diffusion through Mucus. Adv Drug Deliv Rev 2009, 61, 101–114. [Google Scholar] [CrossRef] [PubMed]
- Thu, B.; Gåserød, O.; Paus, D.; Mikkelsen, A.; Skjåk-Bræk, G.; Toffanin, R.; Vittur, F.; Rizzo, R. Inhomogeneous Alginate Gel Spheres: An Assessment of the Polymer Gradients by Synchrotron Radiation-Induced x-Ray Emission, Magnetic Resonance Microimaging, and Mathematical Modeling. Biopolymers 2000, 53, 60–71. [Google Scholar] [CrossRef]
- Sheth, S.; Barnard, E.; Hyatt, B.; Rathinam, M.; Zustiak, S.P. Predicting Drug Release From Degradable Hydrogels Using Fluorescence Correlation Spectroscopy and Mathematical Modeling. Front Bioeng Biotechnol 2019, 7. [Google Scholar] [CrossRef] [PubMed]
- Axpe, E.; Chan, D.; Offeddu, G.S.; Chang, Y.; Merida, D.; Hernandez, H.L.; Appel, E.A. A Multiscale Model for Solute Diffusion in Hydrogels. Macromolecules 2019, 52, 6889–6897. [Google Scholar] [CrossRef] [PubMed]
- Caccavo, D. An Overview on the Mathematical Modeling of Hydrogels’ Behavior for Drug Delivery Systems. Int J Pharm 2019, 560, 175–190. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Lumpkin, J.A.; Rosenblatt, J. Mathematical Modeling of Drug Release from Hydrogel Matrices via a Diffusion Coupled with Desorption Mechanism. Journal of Controlled Release 1994, 32, 17–25. [Google Scholar] [CrossRef]
- Dembczynski, R.; Jankowski, T. Characterisation of Small Molecules Diffusion in Hydrogel-Membrane Liquid-Core Capsules. Biochem Eng J 2000, 6, 41–44. [Google Scholar] [CrossRef] [PubMed]
- Gabardo, S.; Rech, R.; Ayub, M.A.Z. Determination of Lactose and Ethanol Diffusion Coefficients in Calcium Alginate Gel Spheres: Predicting Values To Be Used in Immobilized Bioreactors. J Chem Eng Data 2011, 56, 2305–2309. [Google Scholar] [CrossRef]
- Puguan, J.M.C.; Yu, X.; Kim, H. Diffusion Characteristics of Different Molecular Weight Solutes in Ca–Alginate Gel Beads. Colloids Surf A Physicochem Eng Asp 2015, 469, 158–165. [Google Scholar] [CrossRef]
- Øyaas, J.; Storrø, I.; Svendsen, H.; Levine, D.W. The Effective Diffusion Coefficient and the Distribution Constant for Small Molecules in Calcium-Alginate Gel Beads. Biotechnol Bioeng 1995, 47, 492–500. [Google Scholar] [CrossRef] [PubMed]
- Miyamoto, S.; Shimono, K. Molecular Modeling to Estimate the Diffusion Coefficients of Drugs and Other Small Molecules. Molecules 2020, 25. [Google Scholar] [CrossRef]
- Abrami, M.; Marizza, P.; Zecchin, F.; Bertoncin, P.; Marson, D.; Lapasin, R.; de Riso, F.; Posocco, P.; Grassi, G.; Grassi, M. Theoretical Importance of PVP-Alginate Hydrogels Structure on Drug Release Kinetics. Gels 2019, 5. [Google Scholar] [CrossRef]
- Turco, G.; Donati, I.; Grassi, M.; Marchioli, G.; Lapasin, R.; Paoletti, S. Mechanical Spectroscopy and Relaxometry on Alginate Hydrogels: A Comparative Analysis for Structural Characterization and Network Mesh Size Determination. Biomacromolecules 2011, 12, 1272–1282. [Google Scholar] [CrossRef]
- Offeddu, G.S.; Axpe, E.; Harley, B.A.C.; Oyen, M.L. Relationship between Permeability and Diffusivity in Polyethylene Glycol Hydrogels. AIP Adv 2018, 8, 105006. [Google Scholar] [CrossRef]
- Rehmann, M.S.; Skeens, K.M.; Kharkar, P.M.; Ford, E.M.; Maverakis, E.; Lee, K.H.; Kloxin, A.M. Tuning and Predicting Mesh Size and Protein Release from Step Growth Hydrogels. Biomacromolecules 2017, 18, 3131–3142. [Google Scholar] [CrossRef]
- Diclofenac. Available online: https://go.drugbank.com/drugs/DB00586.
- Gombotz, W.R.; Wee, S.F. Protein Release from Alginate Matrices. Adv Drug Deliv Rev 2012, 64, 194–205. [Google Scholar] [CrossRef]
- Oshi, M.A.; Lee, J.; Kim, J.; Hasan, N.; Im, E.; Jung, Y.; Yoo, J.-W. PH-Responsive Alginate-Based Microparticles for Colon-Targeted Delivery of Pure Cyclosporine A Crystals to Treat Ulcerative Colitis. Pharmaceutics 2021, 13. [Google Scholar] [CrossRef]
- Agarwal, T.; Narayana, S.N.G.H.; Pal, K.; Pramanik, K.; Giri, S.; Banerjee, I. Calcium Alginate-Carboxymethyl Cellulose Beads for Colon-Targeted Drug Delivery. Int J Biol Macromol 2015, 75, 409–417. [Google Scholar] [CrossRef]
- Ferraro, R.; Caserta, S. SLE3S-Water System: A Linear Rheological Characterisation. Rheol Acta 2023, 62, 365–375. [Google Scholar] [CrossRef]
Figure 1.
Rheological properties of Sodium Alginate solutions with low (Lv) (≈ 250 cPs) and high viscosity (Hv) (20,000-40,000 cPs). A) Viscosity curve versus shear rate B) Viscosity normalized respect to the plateau value and C) oscillatory measurements to evaluate G’ and G’’ values.
Figure 1.
Rheological properties of Sodium Alginate solutions with low (Lv) (≈ 250 cPs) and high viscosity (Hv) (20,000-40,000 cPs). A) Viscosity curve versus shear rate B) Viscosity normalized respect to the plateau value and C) oscillatory measurements to evaluate G’ and G’’ values.
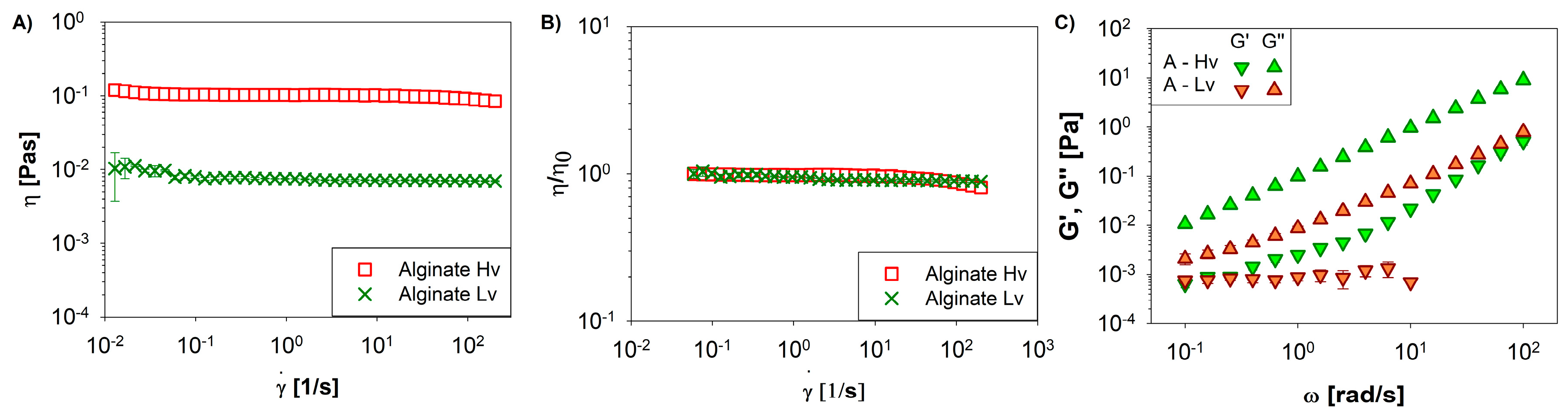
Figure 2.
Sodium Alginate microgels with core-shell architecture. A) Scheme of Electro Fluid Dynamic Atomization process: the use of coaxial needles enabled to process low viscosity (LV) alginate (≈ 250 cPs) solution for the core, and high viscosity (HV) alginate (20,000-40,000 cPs) (blue) for the shell; B) Morphological aspect of microgels via optical microscopy (scale bar: 500 µm); C-D) Fluorescence images of microgels with FTIC-Albumin labeled inner phase before C) and after D) image elaboration to remove the background (scale bar: 200 µm)..
Figure 2.
Sodium Alginate microgels with core-shell architecture. A) Scheme of Electro Fluid Dynamic Atomization process: the use of coaxial needles enabled to process low viscosity (LV) alginate (≈ 250 cPs) solution for the core, and high viscosity (HV) alginate (20,000-40,000 cPs) (blue) for the shell; B) Morphological aspect of microgels via optical microscopy (scale bar: 500 µm); C-D) Fluorescence images of microgels with FTIC-Albumin labeled inner phase before C) and after D) image elaboration to remove the background (scale bar: 200 µm)..
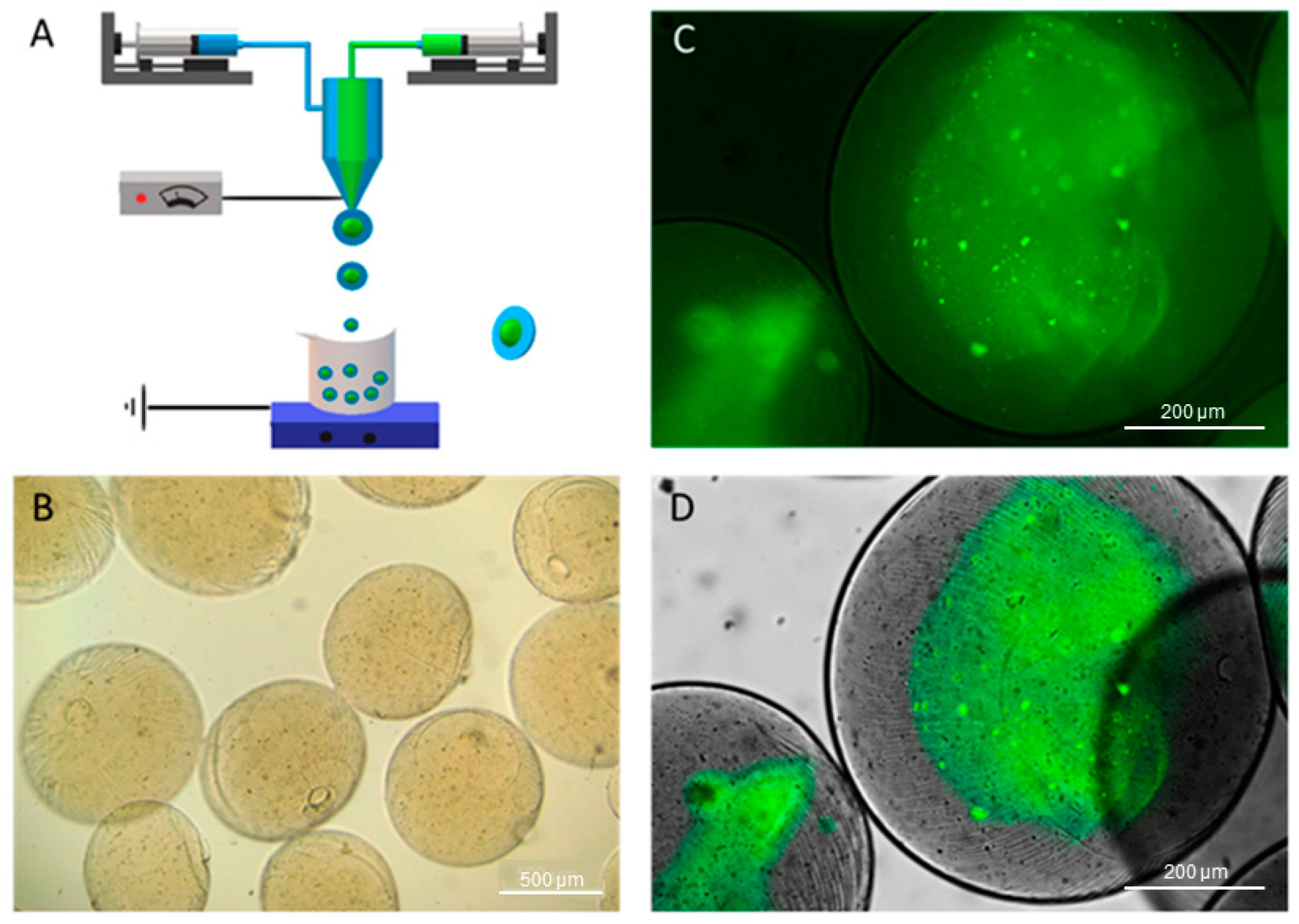
Figure 3.
Dye adsorption: A) alginate microgels in contact with Alizarin red dye (1% in dH2O) (scale bar: 500 µm). B) Details of core-shell microgels after washing to remove the dye in excess (scale bar: 200 µm).
Figure 3.
Dye adsorption: A) alginate microgels in contact with Alizarin red dye (1% in dH2O) (scale bar: 500 µm). B) Details of core-shell microgels after washing to remove the dye in excess (scale bar: 200 µm).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









