Numerical Study of the Impacts of Stochastic Forcing on the Vortex in Fluid Flow

Preprint

Article

Numerical Study of the Impacts of Stochastic Forcing on the Vortex in Fluid Flow

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Jingyun Lv^*,Xin Hou,Jingli Chen

This version is not peer-reviewed

Submitted:

28 December 2023

Posted:

28 December 2023

You are already at the latest version

Alerts

Abstract

This paper provides the numerical investigation of two-dimensional stochastic Navier-Stokes equation driven by additive white noises. The vorticity-stream function method is presented to calculate the incompressible fluid flow. In order to solve the formulation of steam function equation, we propose a Crank-Nicolson Fourier pseudo-spectral method. Numerical results obviously show that the presence of stochastic forcing can have an impact upon the shapes of vortex in fluid flow. To a certain extent, the phenomenon of eddy shedding and the formation of some new vortex in a random medium can be observed, which make it possible for us to conduct optimal control experiments in the development of vortex structures.

Keywords:

Subject: Computer Science and Mathematics - Computational Mathematics

1. Introduction

Stochastic Navier-Stokes equation (SNSE) has aroused wide concern mainly because of their potential applications in fluid mechanics, which can be quite useful for modelling the random flow motions of Newtonian incompressible fluids and explaining the mechanisms of turbulence phenomenon (see [6,10,11,13] and references therein). Unlike deterministic Navier-Stokes equation, solutions of SNSE are random fields with some statistical characteristics, complex dynamics and interesting properties ([8,10]). Since the seminal work of Bensoussan and Temam [7], the theoretical analysis of SNSE has been intensively investigated in the literatures (see above referred works). However, rather little has been done in numerical technique for SNSE.

In this study, we focus on the numerical investigation of time-dependent incompressible SNSE with the additive spatial white noise as follows:

\begin{matrix} \frac{\partial u}{\partial t} + u \cdot \nabla u - \frac{1}{R e} Δ u + \nabla p = \dot{W} (x), x \in Ω, 0 < t \leq T, \end{matrix}

(1.1)

with the incompressibility constraint:

\begin{matrix} div u = 0, x \in Ω, 0 < t \leq T, \end{matrix}

(1.2)

subject to the homogeneous Dirichlet boundary conditions:

\begin{matrix} u (x, t) = 0, x \in \partial Ω, 0 < t \leq T, \end{matrix}

(1.3)

and the problem is supplemented by the initial condition:

\begin{matrix} u (x, 0) = u_{0} (x), x \in Ω, \end{matrix}

(1.4)

in which

Ω \subset R^{2}

is a bounded domain with regular boundary

\partial Ω

;

u = u (x, t) = (u (x, t), v (x, t))

is the Eulerian velocity field;

R e

is the Reynolds number;

p = p (x, t)

is the associated pressure field;

W = (W_{1}, W_{2})

stands for the stochastic external forcing, where

W_{1}

and

W_{2}

are independent components, considered as the space-dependent white noise.

Currently, Wiener Chaos expansion for SNSE is considered in [9], this algorithm can only work on relatively short-time intervals. The implicit and semi-discrete Euler method and finite element discretizations are studied in [2,4], the strong convergence is proved in the mean-square sense, but the numerical simulations are not presented in their works. In [5], the author proposes the semi-group and cubature techniques for SNSE, a weak convergence is proved for the method proposed above. Breit et al. [3] studied convergence rates for a finite element based on space-time approximation in terms of convergence in probability. Wu et al. [12] established numerical ergodicity of two dimensional stochastic Navier-Stokes equations. However, as we know, the numerical investigation of impacts of noises on the vortex in fluid flow has not been addressed yet, which is indeed a fascinating problem. This paper aims to develop the vorticity-stream function combined with the Fourier pseudo-spectral method for solving the SNSE. Typically, making use of the stochastic solution to observe the effects of random forcing on the vortex in fluid flow.

The paper is organized as follows: In Section 2, we describe the vorticity-stream function method to deal with the SNSE and propose the Fourier pseudo-spectral method to solve the stream-function equation. The results of numerical experiments on the two test models are offered in Section 3. The conclusions are provided in the final section.

2. Numerical algorithms

In this section, the vorticity-stream function method [7] combined with the Fourier pseudo-spectral method are proposed for the numerical investigation of two-dimensional time-dependent incompressible SNSE. To begin with, we give the derivation of the vorticity-stream function formulation for the incompressible flows. The basic idea of this method is to replace the vorticity in the vorticity-stream function formulation by the Poisson equation for the stream-function. Secondly, a Crank-Nicolson Fourier pseudo-spectral method is used to solve the derived vorticity-stream function equation.

2.1. The vorticity-stream function method

The incompressibility constraint (1.2) entails the existence of a suitable stream-function

ψ (x, y, t)

such that, for any fixed

t \geq 0

\begin{matrix} u (x, t) = curl ψ = (- \frac{\partial ψ}{\partial y}, \frac{\partial ψ}{\partial x}) . \end{matrix}

(2.1)

We introduce the evolution of the vorticity

ω

u

\begin{matrix} ω = curl u = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}, \end{matrix}

(2.2)

which, substituted into the curl condition (2.1), yields the Poisson equation for the stream function

\begin{matrix} ω = curl curl ψ = Δ ψ = \frac{\partial^{2} ψ}{\partial x^{2}} + \frac{\partial^{2} ψ}{\partial y^{2}} . \end{matrix}

To eliminate the pressure, we take the curl to both sides of (1.1):

\begin{matrix} \frac{\partial ω}{\partial t} - \frac{1}{R e} Δ ω + \frac{\partial ψ}{\partial x} \frac{\partial ω}{\partial y} - \frac{\partial ψ}{\partial y} \frac{\partial ω}{\partial x} = curl \dot{W} . \end{matrix}

(2.3)

Therefore, based on (2.1)-(2.3), the momentum equation (1.1) can be reformulated as the vorticity transport equation:

\begin{matrix} \frac{\partial ω}{\partial t} - \frac{1}{R e} Δ ω + \nabla^{⊥} ψ \cdot \nabla ω = \tilde{W}, \end{matrix}

(2.4)

where

\begin{matrix} \tilde{W} = \frac{\partial^{2} W_{2}}{\partial x \partial y} - \frac{\partial^{2} W_{1}}{\partial y \partial x}, u = \nabla^{⊥} ψ = (- \frac{\partial ψ}{\partial y}, \frac{\partial ψ}{\partial x}) . \end{matrix}

Here, the space-dependent white noise

W_{l} (l = 1, 2)

can be numerically approximated using the Fourier modes as

\begin{matrix} \frac{\partial^{2} W_{1}}{\partial x \partial y} = \sum_{k = 1}^{\infty} σ_{k} η_{1 k} ϕ_{k} (x, y), \frac{\partial^{2} W_{2}}{\partial y \partial x} = \sum_{k = 1}^{\infty} σ_{k} η_{2 k} ϕ_{k} (x, y) \end{matrix}

with the mutual independence random variables

η_{1 k}, η_{2 k} \sim N (0, 1)

σ_{k}

is a decay coefficient and

ϕ_{k}

is Fourier modes truncated with

ϕ_{k} (x, y) = \sqrt{2} sin (k π x) sin (k π y)

Noticing that the velocity field

u

is divergence-free due to (2.1). Furthermore, the Dirichlet boundary condition (1.3) now read

\begin{matrix} \nabla ψ (x, y, t) = 0, for (x, y) \in \partial Ω, t \geq 0 . \end{matrix}

(2.5)

We can simply rewrite the boundary condition (2.5) as

\begin{matrix} ψ (x, y, t) = \frac{\partial ψ}{\partial n} (x, y, t) = 0, (x, y) \in \partial Ω, t \geq 0, \end{matrix}

(2.6)

where

\frac{\partial ψ}{\partial n}

denotes the outward normal derivative.

Finally, the initial condition (1.4) can be rewritten in terms of

ψ

\begin{matrix} ψ (x, y, 0) = ψ_{0} (x, y), (x, y) \in Ω . \end{matrix}

(2.7)

2.2. Crank-Nicolson Fourier pseudo-spectral method

Denote by

t_{n} = n Δ t, n = 0, 1, \dots N

the time mesh point with a uniform time step

Δ t > 0

, which satisfy

0 \leq t_{n} \leq T

and

Δ t = T / N

. Let

ω^{n}

and

ψ^{n}

denote as the approximation of

ω

and

ψ

at time

t^{n}

. Now, we approximate the Eq.(2.4) by the second-order Crank-Nicolson scheme in time

\begin{matrix} \frac{ω^{n + 1} - ω^{n}}{Δ t} + \frac{1}{2} {(\nabla^{⊥} ψ \cdot \nabla ω - \frac{1}{R e} Δ ω)}^{n + 1} = - \frac{1}{2} {(\nabla^{⊥} ψ \cdot \nabla ω - \frac{1}{R e} Δ ω)}^{n} + \tilde{W} . \end{matrix}

(2.8)

Using the operator notation, the above equations look like the following

\begin{matrix} [1 + \frac{Δ t}{2} (\nabla^{⊥} ψ^{n + 1} \cdot \nabla - \frac{1}{R e} Δ)] ω^{n + 1} = [1 - \frac{Δ t}{2} (\nabla^{⊥} ψ^{n} \cdot \nabla - \frac{1}{R e} Δ)] ω^{n} + Δ t \tilde{W} . \end{matrix}

(2.9)

For the spatial discretization, we use a classical Fourier pseudo-spectral method on a periodic domain

Ω

. Firstly, the vorticity field is represented as Fourier series

\begin{matrix} ω (x, t) = \sum_{k \in Z^{2}} \hat{ω} (k, t) e^{i k \cdot x}, \end{matrix}

where

i^{2} = - 1

and the Fourier transform of

ω

is defined as

\begin{matrix} \hat{ω} (k, t) = \frac{1}{4 π^{2}} \int_{Ω} ω (x, t) e^{- i k \cdot x} d Ω, \end{matrix}

with

k = (k_{x}, k_{y})

and

x = (x, y) \in [0, L_{x}] \times [0, L_{y}]

. The uniform Fourier discretization is adapted in space and is truncated at

k_{x} = - N_{x} / 2

and

k_{x} = N_{x} / 2 + 1

k_{y} = - N_{y} / 2

and

k_{y} = N_{y} / 2 + 1

, where

N_{x}

and

N_{y}

are the number of grids in x and y directions, respectively.

Using the Fourier transform of both sides of the Eq.(2.9), we obtain

\begin{matrix} (1 + \frac{Δ t}{2} \cdot (i k) \cdot \nabla^{⊥} ψ^{n + 1} + \frac{{| k |}^{2}}{R e}) {\hat{ω}}^{n + 1} = (1 - \frac{Δ t}{2} \cdot (i k) \cdot \nabla^{⊥} ψ^{n} - \frac{{| k |}^{2}}{R e}) {\hat{ω}}^{n} + Δ t \tilde{W}, \end{matrix}

(2.10)

in which the term

\nabla^{⊥} ψ^{m} (m = n + 1 or n)

also can be transformed by

\begin{matrix} \nabla^{⊥} ψ^{m} = \sum_{k \in Z^{2}} (i k^{⊥}) {\hat{ψ}}^{m} (k) e^{i k \cdot x}, \end{matrix}

(2.11)

where

k^{⊥} = (- k_{y}, k_{x})

. Therefore, the approximation of velocity

u^{n}

can be computed from the vorticity be means of Biot-Savart’s law in Fourier formulation

\begin{matrix} u^{n} (x) = \sum_{k \in Z^{2}} \frac{i k^{⊥}}{{| k |}^{2}} {\hat{ω}}^{n} (k) e^{i k \cdot x} . \end{matrix}

(2.12)

It should be noted that the Fast Fourier transform (FFT) is used for the transformation between physical and Fourier space.

3. Numerical experiments

In this section, we apply the Fourier pseudo-spectral schemes to solve the two-dimensional SNSE. To help us better understand the effects of the random forcing on the vortex in fluid dynamics, we can first solve the deterministic Navier-Stokes equation (without stochastic forcing), and then calculate the stochastic moments from (2.10) and (2.12) by numerical integrations. Under this framework, the stochastic solution and deterministic solution of the corresponding unforced problem can be compared in our numerical experiments.

3.1. Numerical example 1

In this numerical experiment, the computational domain is taken as

Ω = [0, 2 π] \times [0, 2 π]

. We consider the following initial condition for vorticity

ω = v_{x} - u_{y}

\begin{matrix} ω (x, y, 0) & = exp ({(x - π)}^{2} + 5 {(y - 3 π / 4)}^{2}) - 0.1 \times sech ({(x - 3 π / 4)}^{2} + 5 {(y - 3 π / 4)}^{2}) \\ - 0.2 \times exp ({(x - 5 π / 4)}^{2} + 5 {(y - 5 π / 4)}^{2}), \end{matrix}

where the initial velocity field components

u = - \frac{1}{2} \int_{0}^{y} ω (x, s, 0) d s

and

v = \frac{1}{2} \int_{0}^{x} ω (s, y, 0) d s

We choose the time step

Δ t = 0.001

and the number of grids

N_{x} = N_{y} = 128

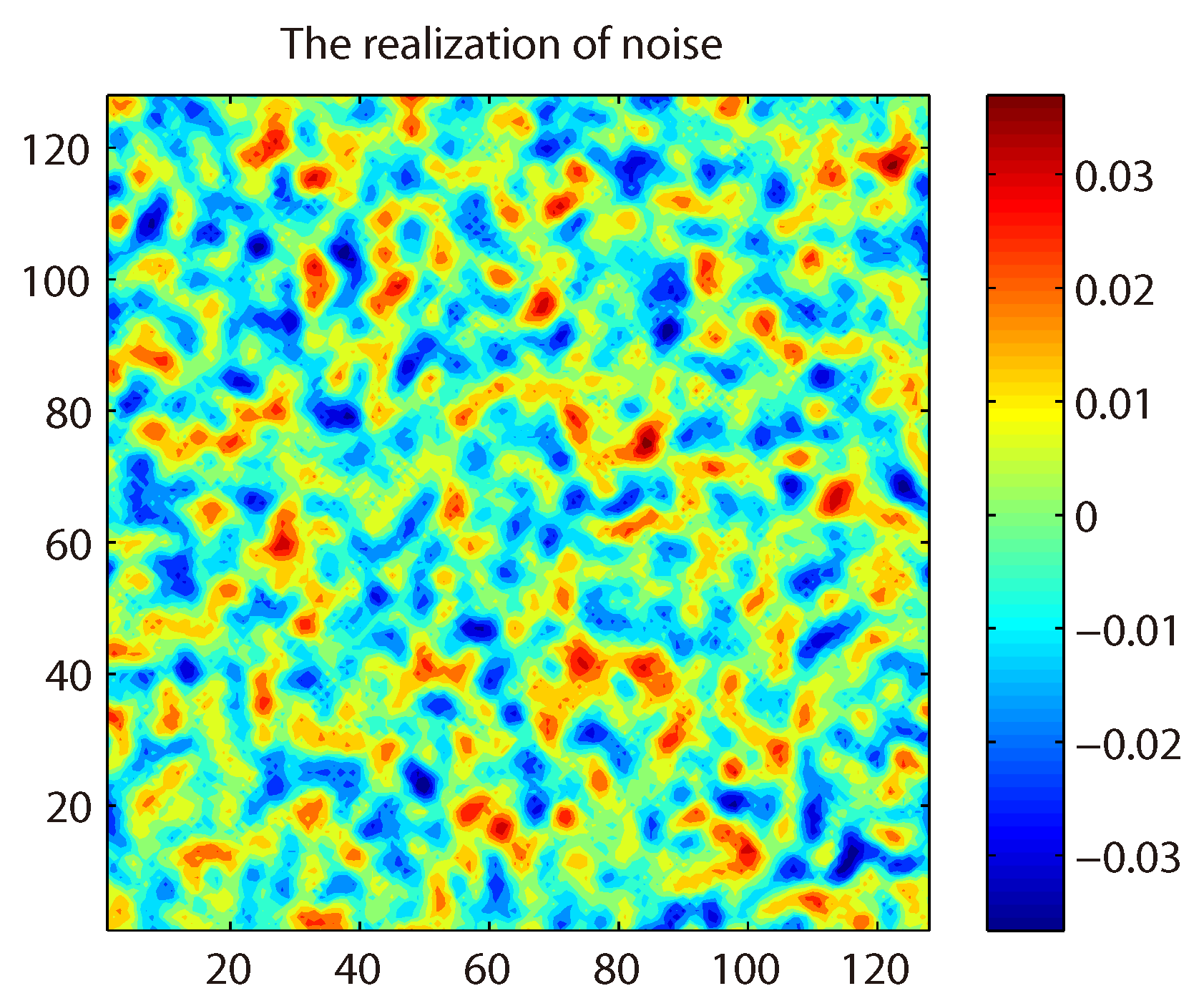
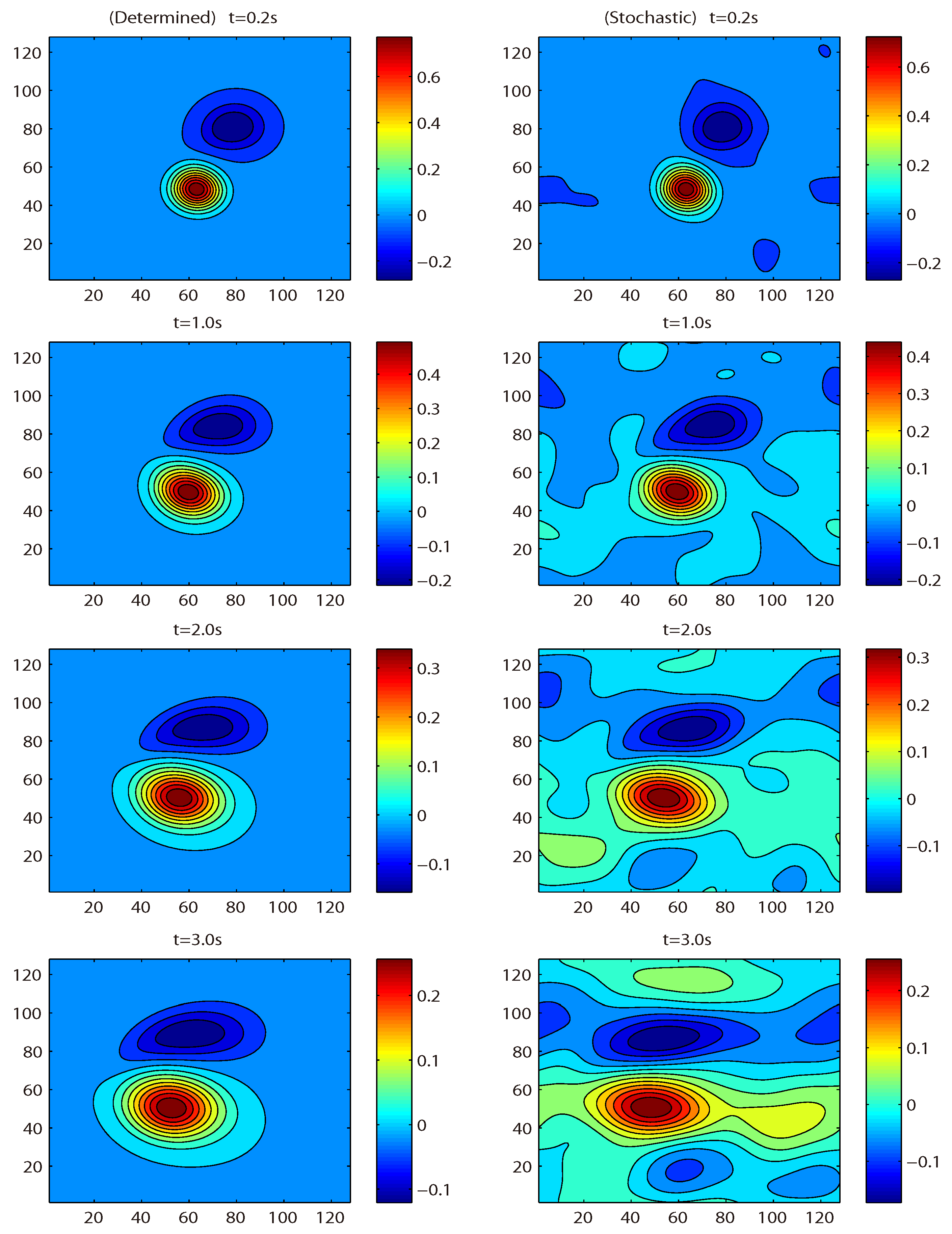
. Before solving the flow problem for the stochastic case, we present some random vorticity field with white noise in Figure 1, where the random noise is generated by Monte-Carlo sampling. We give the numerical contour plots for the vorticity of deterministic and stochastic problems at time

t = 0.2, 1.0, 2.0, 3.0

for the Reynolds number

R e = 100

in Figure 2. Clearly, the presence of stochastic noise can change the structures of vortex in fluid flow. Furthermore, when the time

t = 3.0

, we can observe that the eddies are shedding from the double vortexes and some new vortexes are formatting in the random medium.

3.2. Numerical example 2

We consider the solutions of the vorticity

ω

subject to the following initial condition:

\begin{matrix} ω (x, y, 0) & = exp ({(x - π)}^{2} + 5 {(y - 3 π / 4)}^{2}) + exp ({(x - π)}^{2} + 5 {(y - 5 π / 4)}^{2}) \\ - 0.5 \times exp ({(x - 5 π / 4)}^{2} + 2.5 {(y - 5 π / 4)}^{2}), (x, y) \in Ω, \end{matrix}

where the domain

Ω = [0, 2 π] \times [0, 2 π]

The Reynolds number is chosen as

R e = 10

. We also set the time step

Δ t = 0.001

and the number of grids

N_{x} = N_{y} = 128

. The stochastic and deterministic Navier-Stokes equation are solved at time

t = 0.2, 1.0, 2.0, 3.0

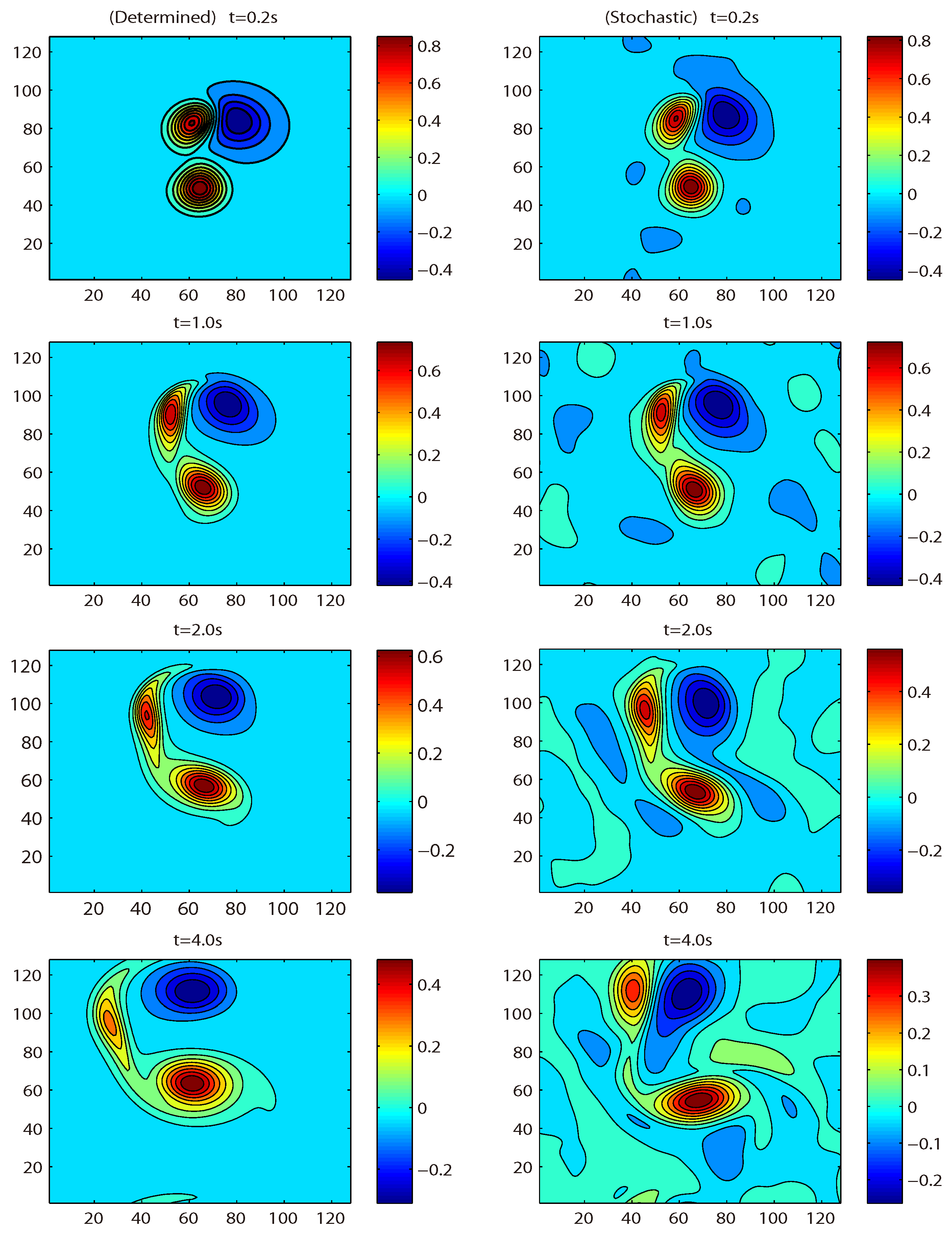
, respectively. In Figure 3, it is clearly exhibited that the patterns of vortexes are changed with the evolution of random forcing. Moreover, at time

t = 3.0

, we can see that the presence of stochastic forcing can accelerate the eddy separation from the warm vortex. The generation of turbulence flow with a random noise forcing can be commonly observed in the fluid flow.

4. Conclusions

In this paper, we propose the vorticity-stream function method combined with the Fourier pseudo-spectral method to simulate the two-dimensional incompressible SNSE. Numerical results demonstrate that the proposed method can be quite useful for modelling the random flow motions of incompressible fluids. Furthermore, the proposed method in this paper can be better used to study the effects of the random forcing on the vortex in fluid dynamics. However, there is a number of unresolved issues. In particular, further work on this subject is required on:

1. Numerical analysis. This study is concerned with the numerical simulations of the impacts of random forcing on the vorticity in fluid dynamics. It appears that the error analysis and convergence order of the proposed method is beyond the scope of this paper.

2. Random forcing. This paper is limited to the case of the additive random forcing dependent of spatial variables. The sources of randomness might not describe the actual physical behavior in fluid flow. The SNSE driven by multiplicative space-time white noise is being addressed in our ongoing research.

Acknowledgments

This work is supported by R&D Program of Beijing Municipal Education Commission (KM202310853001), Youth Foundation of Beijing Polytechnic College (BGY2021KY-05QT), Research Project of Beijing Polytechnic College (BGY2023KY-53) and Beijing Natural Science Foundation(No. 1224036).

References

A. Bensoussan, R. Temam. Equations stochastiques du type Navier-Stokes. J. Funct. Anal. 1973, 13, 195–222. [Google Scholar] [CrossRef]
Z. Brzeźniak, E. Carelli, A. Prohl. Finite element based discretizations of the incompressible Navier-Stokes equations with multiplicative random forcing. IMA J. Numer. Anal. 2014, 34, 502–549. [Google Scholar]
D. Breit, A. Dodgson. Convergence rates for the numerical approximation of the 2D stochastic Navier-Stokes equations. Numer. Math. 2021, 147, 553–578. [Google Scholar] [CrossRef]
E. Carelli, A. Prohl. Rates of convergence for discretizations of the stochastic incompressible Navier-Stokes equations. SIAM J. Numer. Anal. 2012, 50, 2467–2496. [Google Scholar] [CrossRef]
P. Dörsek. Semigroup splitting and cubature approximations for the stochastic Navier-Stokes equations. SIAM J. Numer. Anal. 2012, 50, 729–746. [Google Scholar] [CrossRef]
F. Flandoli, D. Gatarek. Martingale and stationary solutions for the stochastic Navier-Stokes equation. Probab. Theory Related Fields 1995, 102, 367–391. [Google Scholar] [CrossRef]
M.M. Gupta, J.C. Kalita. A new paradigm for solving Navier-Stokes equations: streamfunction-velocity formulation. J. Comput. Phys. 2005, 207, 52–68. [Google Scholar] [CrossRef]
M. Hairer, J.C. Mattingly. Ergodicity of the 2D Navier-Stokes equations with degenerate stochastic forcing. Ann. Math. 2006, 164, 993–1032. [Google Scholar] [CrossRef]
T.Y. Hou, W. Luo, B. Rozovskii, H.-M. Zhou. Wiener Chaos expansions and numerical solutions of randomly forced equations of fluid mechanics. J. Comput. Phys. 2006, 216, 687–706. [Google Scholar] [CrossRef]
J.C. Mattingly, E. Pardoux. Malliavin calculus and the randomly forced Navier-Stokes equation. Comm. Pure Appl. Math. 2006, 59, 1742–1790. [Google Scholar] [CrossRef]
R. Mikulevicius, B. Rozovskii. Stochastic Navier-Stokes equations for turbulent flows. SIAM J. Math. Anal. 2004, 35, 1250–1310. [Google Scholar] [CrossRef]
S. Wu, X. Wang, J.H. Huang. Numerical ergodicity of two dimensional stochastic Navier-Stokes equations with Gaussian noise. Comput. Math. Appl. 2023, 141, 15–32. [Google Scholar] [CrossRef]
G. Zou, G. Lv, J. Wu. Stochastic Navier-Stokes equations with Caputo derivative driven by fractional noises. J. Math. Anal. Appl. 2018, 461, 595–609. [Google Scholar] [CrossRef]

Figure 1. The realization of random vorticity field with white noise.

Figure 2. Numerical results for the velocity field of solutions to SNSE (right) and its corresponding deterministic problem (left).

Figure 3. Numerical results for the velocity field of solutions to SNSE (right) and its corresponding deterministic problem (left).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Numerical Study of the Impacts of Stochastic Forcing on the Vortex in Fluid Flow

Abstract

1. Introduction

2. Numerical algorithms

2.1. The vorticity-stream function method

2.2. Crank-Nicolson Fourier pseudo-spectral method

3. Numerical experiments

3.1. Numerical example 1

3.2. Numerical example 2

4. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe