Prerpints.org logo
Preprint
Article

Radargrammetric 3D Imaging through Composite Registration Method Using Multi-Aspect SAR Imagery

Altmetrics

Downloads

125

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 December 2023

Posted:

28 December 2023

You are already at the latest version

Alerts
Abstract
Interferometric synthetic aperture radar (InSAR) and tomographic SAR measurement techniques are commonly used for the three-dimensional (3D) reconstruction of complex areas, while the effectiveness of these methods relies on the interferometric coherence among SAR images with minimal angular disparities. Radargrammetry exploits stereo image matching to determine the spatial coordinates of corresponding points in two SAR images, and acquire their 3D properties. The performance of the image matching process directly impacts the quality of the resulting digital surface model (DSM). However, the presence of speckle noise, along with dissimilar geometric and radiometric distortions, poses considerable challenges to achieve accurate stereo SAR image matching. To address the aforementioned challenges, this paper proposes a radargrammetric method based on composite registration of multi-aspect SAR images. The proposed method combines coarse registration using scale invariant feature transform (SIFT) with precise registration using normalized cross-correlation (NCC) to achieve accurate registration between multi-aspect SAR images with large disparities. Furthermore, the multi-aspect 3D point clouds are merged by the proposed radargrammetric 3D imaging method, resulting in 3D imaging of target scenes based on multi-aspect SAR images. For validation purpose, this paper presents a comprehensive 3D reconstruction of the Five-hundred-meter Aperture Spherical radio Telescope (FAST) by using Ka-band airborne SAR images. It does not necessitate prior knowledge of the target and is applicable to the detailed 3D imaging of large-scale areas with complex structures. In comparison to other SAR 3D imaging techniques, it reduces the requirements for orbit control and radar system parameters. To sum up, the proposed 3D imaging method with composite registration guarantees imaging efficiency while enhances the imaging accuracy of crucial areas with limited data.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Synthetic Aperture Radar (SAR) is an active microwave radar imaging system that offers advantages over optical or optoelectronic sensors in terms of all-weather, all-day, and high-resolution imaging capabilities (SAR plays a crucial role in remote sensing applications over long distances) [1,2]. The utilization of SAR imaging technology enables the acquisition of high-quality three-dimensional (3D) scene models, bearing significant implications in academic, military, commercial, and disaster management domains. With the rapid advancements in SAR theories and technologies, various SAR imaging techniques have emerged to gather 3D information of observed scenes, including interferometric SAR (InSAR) [3–5], tomographic SAR (TomoSAR) [6–8], and radargrammetry [9–11]. Among these techniques, radargrammetry uses images with parallax to calculate terrain elevation information by substituting image information of corresponding pixels into 3D imaging model's equation system. Compared to the InSAR and TomoSAR techniques, radargrammetry enables the use of images acquired at different times and locations, thereby imposing fewer restrictions on platforms and images. As a result, radargrammetry alongside optical photogrammetry, has achieved numerous accomplishments in digital photogrammetry and surface elevation inversion [12,13].
The process of acquiring high-quality 3D imaging through radargrammetry involves two main steps: corresponding point measurement and analytical stereo positioning. Initially, corresponding points are derived by registering multi-aspect SAR images. These corresponding points are subsequently utilized in the radargrammetric equations to calculate the 3D model of the target scene. The conventional methods for corresponding point measurement in SAR images comprise statistical detection techniques and feature-based matching algorithms [14]. Additionally, leveraging prior information such as Digital Elevation Models (DEM) and ground control points enables achieving high-precision image matching, although its applicability is limited [15,16]. Statistical detection methods typically rely on grayscale or gradient information in the images and employ matching methods (e.g., correlation and mutual information methods) to align image windows. On the other hand, feature-based matching algorithms extract features that are less affected by grayscale variations among different sources. However, due to the presence of noise and complex distortions in SAR images, the accuracy and efficiency of feature extraction for complex scenes at a single scale are suboptimal. Furthermore, various geometric models for SAR image reconstruction have been proposed, including F. Leberl's Range-Doppler (RD) equations (model) [17], G. Konecny's geocentric range projection model [18] and the Range-Coplanarity model [19], etc. Studies have compared the applicability and accuracy of these different mathematical models, revealing that the F. Leberl model requires fewer parameters and exhibits a broader range of applications [20,21].
However, the quality of SAR images directly impacts the matching of corresponding points, with noise and ghosting being potential issues that can adversely affect the quality of 3D imaging results. Furthermore, the accuracy of multi-aspect SAR image registration and airborne platform parameters serves as input parameters in the imaging equations, directly influencing the final calculation results. During the process of 2D SAR imaging, calibrating the platform parameters is also necessary. The distortion caused by parallax in multi-aspect SAR images can disrupt the measurement of corresponding points. Traditional registration methods suffer from low accuracy and efficiency, making the resolution of the parallax-registration contradiction a challenge in radargrammetry [15]. Additionally, the accuracy of 3D imaging depends on the resolution and quantity of SAR images. However, the practical constraints of efficiency pose a realistic challenge in achieving high-precision 3D imaging in radargrammetry.
To address the aforementioned issues, this paper proposes a multi-aspect SAR radargrammetric method with composite registration. It utilizes composite registration methods combining multi-scale scale invariant feature transform (SIFT) and normalized cross-correlation (NCC) for detecting corresponding points in multi-aspect SAR image pairs. After segmenting the large-scale SAR image based on the coarse registration results from SIFT, each region is subjected to NCC precise registration following resampling, enabling efficient and rapid extraction of matching points. Then, the platform parameters are calibrated according to the imaging mode of SAR images, allowing for high-precision stereo imaging of the target region using the F. Leberl imaging equations. Finally, a multi-aspect point cloud fusion algorithm based on DEM is utilized to obtain the high-precision reconstruction result of the target scene.
To eliminate the errors caused by SAR image quality and platform parameters, we first calibrate the platform coordinate and other parameters of the motion compensation in the SAR imaging process. Then, high-precision multi-aspect SAR images are acquired. Specifically, this paper adopts the registration of SAR images using stereo image groups, thereby mitigating the difficulty of registration caused by large disparities. This method enhances registration efficiency and accuracy, simultaneously increasing the disparity threshold for image pairs and improving the accuracy of 3D imaging. Moreover, this paper proposes a composite registration method that enables automatic and robust registration. The proposed method initially applies feature-based coarse registration and window-based precise registration. Subsequently, 3D reconstruction is performed based on feature extraction, thereby enhancing the registration accuracy and efficiency for crucial targets.
For validation purpose, this paper presents a comprehensive 3D reconstruction of the Five-hundred-meter Aperture Spherical radio Telescope (FAST) through the proposed method. The method effectively utilizes the benefits of multi-aspect SAR images to remove overlaps and eliminate shadow areas. It validates the accuracy and effectiveness of the theories and methods introduced in this paper. The rest of the paper is organized as follows. Section 2 outlines the proposed methods for SAR image registration and 3D imaging. The experimental results of these methods are presented in Section 3, with a detailed analysis of the registration and 3D imaging results found in Section 4. Finally, Section 5 provides a summary of this paper.

2. Methods

Radargrammetry applies radar imaging principles to calculate the 3D coordinates of a target. The 3D coordinates are obtained by using the construction equations (i.e., equations for 3D reconstruction based on geometric models), which are based on the observational information of the corresponding point from different aspect angles. Figure 1 illustrates that multi-aspect SAR images have the capability to achieve 3D imaging when satisfying the requirements of the construction equations.
The construction equations necessitate the information of corresponding point in SAR images from different aspect angles, making image registration a crucial step in determining these corresponding points. Therefore, this paper proposed a composite registration method that combines SIFT coarse registration with NCC precise registration to address the disparity and registration contradictions. Subsequently, we interpret principles and fundamental procedures of these registration algorithms, the process of achieving high-precision 3D imaging for complex structured targets is described in detail, illustrated in Figure 2. The SAR imaging algorithm (BP algorithms) stated in Step 1 [22] will not be introduced in this paper. The subsequent sections will focus on Steps 2 to Steps 4.
Step 1: By selecting (filtering) the original data and imaging results according to the platform trajectory and image disparity, we can acquire a multi-aspect SAR image sequence composed of multiple groups of image pairs. The utilization of stereo image groups can increase the disparity threshold in image pair registration, effectively mitigating the disparity-registration contradiction.
Step 2: Implementing coarse registration and segmentation using multi-scale SIFT for two SAR images requiring registration. Subsequently, resampling each region and achieve precise image registration using the NCC algorithm. The utilization of composite registration in sub-regions mitigates the impact of challenges such as layover and perspective contraction on the registration of multi-aspect SAR images.
Step 3: Based on the registration information of each pixel in the primary image, which is obtained from the image pairs, the 3D coordinates of corresponding points are computed using the RD equations. This process generates a main point cloud for image pair and multiple regional point clouds for sub-regions. To enhance the accuracy of the imaging equations' solution, a weighted cross-correlation coefficient based method is adopted for the registration results of corresponding points in the stereo image group. Furthermore, motion compensation is applied on the trajectory data to reduce the impact of platform parameter errors on the results.
Step 4: Performing point cloud fusion based on DEM. In this process, the point clouds in selected regions are filtered based on the cross-correlation coefficient, enabling the fusion of high-density point clouds and obtaining the final point clouds of the scene.

2.1. Generation and Selection of Multi-aspect SAR Images

This paper divides circular SAR data into multiple sub-apertures, and utilizes strip fitting imaging method [22] as depicted in Figure 3, resulting in sub-aperture images. Subsequently, all SAR images are selected and arranged based on their aspect angles. As a result, the raw SAR image sequence and corresponding platform information of the circular SAR are obtained. The fitting method compensates for coordinate data during imaging, enabling strip-mode imaging of circular SAR sub-aperture data. Theoretically, there is no difference between circular SAR and strip SAR data. Therefore, both multiple strip SAR images and circular SAR sub-aperture images can be obtained. Generally, circular SAR data can obtain more image pairs, but with a narrower swath width, facilitating high-precision reconstruction in small areas.
By integrating image sequences from multiple trajectories, the original multi-aspect image database is obtained and primarily classified based on aspect angles and trajectories. Within this database, any image can be designated as the primary image. The secondary images are selected from the same or different trajectories with a certain disparity threshold. These secondary images, in conjunction with the primary image, form independent stereo image group, respectively. The images in the database are further categorized to generate a multi-aspect SAR image sequence composed of multiple stereo image groups.

2.2. Multi-aspect SAR Image Registration

To address the discrepancy between disparity and registration in SAR image pairs, this paper proposes a composite registration method that combines SIFT for coarse registration and NCC for precise registration. First, the secondary images are resampled based on the results of segmentation and the affine matrices of each region obtained through coarse registration. Subsequently, precise registration is performed on each sub-region to obtain the final registration results for the image pair.
Increasing the number of image pairs can augment the input parameters of the RD equations, thereby enhancing the positional accuracy, while increasing the computational complexity. The number of secondary images is constrained by the available data and the disparity threshold in coarse registration. To improve the efficiency and increase the disparity threshold, this paper registers the stereo image group and establishes a connection between the two image pairs by transferring parameters obtained from coarse registration. As illustrated in Figure 4, the disparity threshold is increased by transferring parameters through a secondary image, and the overall computational complexity is primarily determined by the number of precisely registered image pairs.
Although in theory, the composite registration method can achieve registration for images with large disparities, practical considerations restrict the improvement in registration accuracy and efficiency, such as the anisotropy of target scattering coefficient and shadowing caused by disparity. Consequently, the disparity threshold for direct registration generally does not exceed 5°, and the maximum disparity between the primary and secondary images within the same stereo image group does not exceed 15°.

2.2.1. Coarse Registration Using the SIFT Algorithm

Coarse registration first obtains feature descriptors for each image from image pairs at different scales, and then performs feature matching. For each stereo image group, separate image scale spaces are established for the primary and secondary images [23]. The Gaussian difference scale space is utilized for detecting keypoints, computing the main orientation and feature descriptor of them. The SIFT registration results for the image pair are obtained by calculating the Euclidean distance between the feature descriptors of each keypoint [24].
Despite undergoing several preliminary screenings, such as the elimination of edge points and points with low contrast, there are still incorrect matching points. To address this problem, the random sample consensus (RANSAC) method is employed to filter the matching points [25], facilitating the estimation of the affine matrix through the least squares (LS) method. Specifically, k random matching points are selected, and the unknown affine matrix R j i is obtained by solving the LS problem, which is represented by:
min R j i ∑ m = 1 k [ n m i − R j i n m j ] T [ n m i − R j i n m j ]
where, n m i = ( x m i , y m i , 1 ) T and n m j = ( x m j , y m j , 1 ) T represent the homogeneous coordinates of the matching point m in the image i and image j, respectively. The remaining matching points are filtered using the estimated affine matrix. The matching points that meet the error requirement are then included in the affine matrix estimation, resulting in the filtered coarse registration points and the overall affine matrix estimation. Subsequently, image is divided into different sub-regions through clustering based on the distribution of the filtered feature points, and coarse registration is conducted for each sub-region of the image pair using the same method. This process yields resampling parameters, including regional affine matrices and predefined regional sampling rates.

2.2.2. Precise Registration Using NCC Matching

Due to the limited quantity and accuracy of corresponding points obtained solely through SIFT feature matching in coarse registration, it is necessary to perform precise registration to achieve sub-pixel level alignment. In this paper, resampling parameters obtained from the coarse registration are utilized to resample secondary images. The resampled secondary images are then subject to precise registration with the primary image. The NCC method is employed to match images from two different azimuth aspect angles. After the affine transformation of sub-region, the rotational and scaling discrepancies of the target are greatly reduced. The NCC method is employed to identify corresponding points in the images and calculate their correlation coefficients and offsets. The expression for extending NCC to 2D images is provided in:
ρ = ∑ ω = 1 2 n + 1 ∑ υ = 1 2 n + 1 ( I 1 ( x 1 + ω , y 1 + υ ) − I 1 ¯ ( x 1 , y 1 ) ) ( I 2 ( x 2 + ω , y 2 + υ ) − I 2 ¯ ( x 2 , y 2 ) ) ∑ ω = 1 2 n + 1 ∑ υ = 1 2 n + 1 ( I 1 ( x 1 + ω , y 1 + υ ) − I 1 ¯ ( x 1 , y 1 ) ) 2 ∑ ω = 1 2 n + 1 ∑ υ = 1 2 n + 1 ( I 2 ( x 2 + ω , y 2 + υ ) − I 2 ¯ ( x 2 , y 2 ) ) 2
where, I ¯ ( x , y ) is:
I ¯ ( x , y ) = ∑ ω = 1 2 n + 1 ∑ υ = 1 2 n + 1 I ( x + ω , y + υ ) ( 2 n + 1 ) ⋅ ( 2 n + 1 )
where, I ( x , y ) represents the amplitude value at the corresponding coordinate in the image, which is used to compute the similarity between the reference image I1 and the matching image I2. The NCC algorithm involves sliding windows of size (2n+1)×(2n+1), centered at selected point in the reference image I1 and the matching window of same size (2n+1)×(2n+1) in image I2. The similarity between the windows is computed by calculating the cross-correlation coefficient. The window in image I2 is continuously moved, and the point with the maximum cross-correlation coefficient is selected as the corresponding point for the selected point in I1. By iterating through all the points in I1 and repeating the aforementioned steps, the precise registration result is obtained. To enhance imaging efficiency and accuracy, the registration results are filtered based on the final cross-correlation coefficients and the grayscale values of window's center pixel.

2.3. Three-Dimensional Coordinates Calculation Based on Radargrammetry

After completing the registration of a stereo image group, the corresponding pixel coordinates of the primary image in different image pairs are obtained. Then the 3D coordinates of corresponding points can be calculated using the RD equation system. These equations reflect the relationship between the objects on the ground and the corresponding pixels in the image, as shown in Figure 1. RD equation system consists of two components: the range sphere equation (4) and the Doppler cone equation (5). These equations relate the position vector of a target R = ( X , Y , Z ) T with its image coordinate ( x S , y S ) within the image. Furthermore, the equation system incorporates the platform coordinate vector R S = ( X S , Y S , Z S ) T , velocity vector R ˙ S = ( X ˙ S , Y ˙ S , Z ˙ S ) T and additional imaging parameters correspond to the azimuth coordinate x s , namely the pixel spacing in the range direction m y , the scanning delay D s , and the squint angle of the radar signal θ.
The range sphere equation:
| R − R S | = ( X − X s ) 2 + ( Y − Y s ) 2 + ( Z − Z s ) 2 = y s m y + D s
The Doppler cone equation:
R ˙ S T ( R − R S ) = | R ˙ S | | R − R S | sin θ
In the case of zero-Doppler processed SAR data, the right-hand side of Equation (5) is set to zero, given by:
X ˙ S ( X − X S ) + Y ˙ S ( Y − Y S ) + Z ˙ S ( Z − Z S ) = 0
Each pixel corresponds to two equations, which is underdetermined. However, by performing registration, the coordinates of identical points in different images are obtained, simultaneously satisfying the RD equation system of those respective images. For a pixel ( x S 0 , y S 0 ) in the primary image S0, a set of RD equation system exists for each corresponding point ( x S i , y S i ) , i = 1, 2,..., n, in the secondary images Si. Consequently, this yields a total of 2n+2 equations for the point, resulting in an overdetermined equation system, which is employed to calculate the 3D coordinates of each point.
In addition to improving SAR image quality and accuracy and enhancing registration precision through composite registration, calibration of platform coordinates and velocity parameters is necessary. To convert data from inertial measurement unit (IMU) to a unified coordinate system, this paper adopts a fusion method that combines platform IMU data PI with GPS data PG, as expressed in Equation (7). The LS method is applied to derive the coordinate transformation parameters T and P, enabling transformation from the platform coordinate system to the imaging coordinate system. The transformed IMU data is then compensated using linear fitting, resulting in platform parameters that exhibit higher accuracy compared to GPS data, as depicted in Figure 5. Based on the compensated coordinate in the geodetic coordinate system, the corrected velocity and other parameters can be obtained.
min T , P ∑ | T P I + P − P G |
For a pixel of the primary image, there can be a maximum of 2(n+1) equations from n image pairs. Initially, the image pair with the highest correlation coefficient in the registration result is selected, resulting in four equations and an optimal solution R1. Subsequently, equation system for the remaining image pairs are computed by utilizing R1 as the initial value, which generates additional results Ri, i = 2, ..., n. The combination of these results, along with the equation system result R0 composed of all equations, constitute the final result Ri, i = 0, 1,..., n, for this point within the stereo image group set. Finally, employing the cross-correlation coefficient ki, i = 0, 1, ..., n, from image pairs’ registration as the weight, where k0 = 1, the LS method is utilized to obtain the optimal estimation of the coordinates R, as demonstrated below:
min R ∑ i = 0 n k i | R − R i |
High-precision 3D reconstruction is achieved for a stereo image group, resulting in a main point cloud corresponding to the stereo image group. Additionally, independent 3D imaging is performed on the prominent regions of each image, result in multiple 3D point cloud results within individual image pairs. Therefore, the point cloud of each stereo image group comprises the main point cloud and multiple regional point clouds. Ultimately, a collection of 3D point clouds is obtained from the entire SAR image sequence, where each point includes relevant information such as its corresponding pixels in the image pairs.

2.4. Point cloud fusion

The point clouds obtained from different image pairs may have positioning errors ranging from several meters to tens of meters, originated from inaccuracies in SAR images and platform parameters, while each point cloud may contain erroneous data. In this paper, a point clouds fusion method based on digital elevation model (DEM) is used to fuse point cloud sequence while removing incorrectly positioned results, resulting in the final 3D cloud of the target scene.
Fusion of two point clouds with correspondence points can be easily achieved. The correspondence points p m i and p m j , m = 1, 2,…, k, between the two point clouds, are correspond to identical image pixels ( x m , y m ) . The transformation matrix R j i from point group p m j to point group p m i can be calculated as depicted by Equation (9), where R j i typically approximates a translation matrix.
min R j i ∑ m = 1 k | p m i − R j i p m j |
For fusion of two point clouds without correspondence points, the first step is to calculate the corresponding DEM for each point cloud. This paper adopts the elevation fitting to extract DEM from point clouds. Specifically, it starts with density-based clustering within a small range around each pixel, and then performs kriging interpolation to obtain the elevation for that pixel. This process obtains the corresponding DEM for each point cloud, while removing erroneously positioned results with low connectivity from the main body of the point cloud.
The main point cloud of an image pair is selected as the reference point cloud. The affine matrix R between a specific point cloud’s DEM ( p m ) and the reference point cloud’s DEM ( p m 0 ) is obtained by utilizing the LS method. This transformation minimizes the elevation differences between the transformed DEM ( R ⋅ p m ) and the point cloud ( p m 0 ) in the same area, resulting in the transformation coordinates of the point cloud relative to the reference point cloud and completing the fusion of the two point clouds. After the fusion of all point clouds in the point cloud sequence is complete, the 3D imaging results of the target scene are obtained.

3. Materials

3.1. Study Area

The FAST located in the Dawodang depression, Guizhou Province, China, is selected as the study target. FAST comprises various components such as a 500m diameter spherical reflector, six feed source support towers, and 50 reflector support columns. As shown in Figure 6, the complex structure of FAST, including the feed source support towers and reflector support columns, brings significant issues of perspective shrinkage and layover in the multi-aspect SAR images. Furthermore, the complex scattering characteristics of the FAST spherical reflector structure hinder effective two-dimensional SAR imaging and 3D imaging. Limited by the radar observation geometry and data availability, the major problems of the sub-aperture SAR images are shadows, layover, and perspective shrinkage. As a result, certain target structures are not visible in the multi-aspect SAR images, directly impeding the process of 3D imaging.

3.2. Data Source

The Ka-band SAR data is acquired by the airborne SAR system of Aerospace Information Research Institute, Chinese Academy of Sciences (AIRCAS). Table 1 illustrates the parameters of the SAR images, and Figure 6 showcases the optical image, the stripmap SAR image of FAST and the flight track of SAR platform. Two flights were conducted to acquire the multi-aspect SAR data. The center of the circular SAR flight path is approximately 200 m in proximity to the central point of the FAST, with flight radius of approximately 6000 m. The multi-aspect SAR images with sub-aperture angles of 3° were utilized in this paper. Each image covered an area range of 400 m×3000 m (azimuth × range) with the range resolution and azimuth resolution of approximately 0.2 m.
In this study, we selected 16 multi-aspect SAR image pairs obtained from two flights, which were categorized into six stereo image groups based on the flight track and similarity, as shown in Figure 6. Table 2 presents the composition of each stereo image group. Some images in the group are not utilized for 3D imaging and acquiring the ultimate point cloud. Instead, they serve as auxiliary images for parameter transmission within the stereo image group. Usually, these images have high similarity to other images and the corresponding flight tracks of these images are very close.

4. Results

To demonstrated the feasibility of the proposed 3D imaging method, we performed 3D imaging of FAST using multi-aspect SAR images obtained from an airborne Ka-band SAR system. These sub-aperture SAR images derived from circular SAR data collected along two different paths.

4.1. Composite Registration Results.

Composite registration was used to obtain the information of corresponding points in multi-aspect SAR images. Firstly, the SIFT-based coarse registration and segmentation were performed on acquired multi-angle SAR stereo image groups. The process of coarse registration and segmentation for an image pair is presented Figure 7. Figure 7a illustrates the segmentation and resampling fusion results of the image pair after coarse registration, while Figure 7b shows the enlarged results of specific regions in Figure 7a,c,d show the fusion result of the image pair before and after sub-regional coarse registration, respectively. Figure 7e presents the fusion result of another image pair after sub-regional coarse registration, and it is evident that the two images have a significant disparity. The fusion results display the two images after coarse registration in the same figure, represented by red and green colors, respectively. The overlap between the primary structures in two colors indicates the effectiveness of registration, while consistent colors in the same region indicate higher similarity.
The fusion results of sub-regions in different image pairs before and after segmentation and resampling are compared in Figure 8. The first and second columns show three sub-regions in the image pairs, respectively. Distinct differences in geometric distortion between the left and right images can be observed. The third column is the resampled right image (in red) generated before sub-regional coarse registration overlaid on the left image (in green). The fourth column is the fusion results of resampled right image (in red) and the left image (in green). In the third and the fourth columns, the red and green color represent the disparity between the left image and the resampled right image. When the structures corresponding to the two colors are closely aligned, it means there is no disparity between the homologous points, and the corresponding image matching algorithm is effective. It is evident that coarse registration and segmentation resampling effectively mitigate the impact of overlapping and perspective contraction issues on the registration of multi-aspect SAR images.
Precise registration is then performed on the resampled image pair. Figure 9 shows the cross-correlation coefficient result images for precise registration of an image pair. Typically, higher cross-correlation coefficient in distinct areas of SAR images signify improved registration results and enhanced 3D imaging accuracy of the corresponding target objects. The cross-correlation coefficient of the pixel is utilized for 3D imaging and point cloud fusion.
The registration results of the primary images in each image pairs are acquired after coarse and precise registration, which include the pixel coordinates and segmentation results of corresponding points in different image pairs, along with the cross-correlation coefficients. By combining the registration results of different image pairs, the registration results of each pixel in the primary images among different image pairs are obtained. This information encompasses multi-aspect details of the target points, which will improve the accuracy of the reconstruction equations and be used in point cloud fusion.

4.2. 3D Imaging Results

After registration of each stereo image group, 3D point cloud sequence was obtained based on radargrammetry. Figure 10 shows both the sub-region point clouds obtained from partial image pairs and the fusion results of partial point clouds. Obtaining high-precision 3D point clouds for certain areas becomes difficult when employing images with substantial disparity for 3D imaging without composite registration. The displayed sub-region point clouds originates from sub-regions of various image pairs, exhibiting the structure on the side of the target building in the airborne sub-aperture SAR image. The partial fusion result combines the main point clouds with the sub-regional point clouds from three stereo image groups, achieving multi-aspect point clouds fusion of the target region. After initial filtering and clustering, these partial point clouds still contain erroneous results, which require elimination through a point cloud fusion process based on DEM. The final result is obtained in the local Cartesian coordinates coordinate system, which is the reference coordinate system with the x-axis directed towards the East. Some of the point clouds shown in Figure 10 are not transformed into the reference coordinate system, while all the results presented in this paper are shown in reference coordinate system or in platform coordinate system, with units in meters.
The final reconstruction result is obtained by merging the sequences of point clouds. Figure 11 shows the multi-aspect 3D imaging results of FAST, from six distinct perspectives. Figure 11s shows the overall reconstruction results from a specific viewpoint, Figure 11b–g present the exhibiting 3D image from six different aspect angles. The downward perspective of the display is set at approximately 35 degrees, with a viewing angle difference of approximately 90 degrees between Figure 11b–e, while the viewing angle of Figure 11f,g falls between these four images.
This paper successfully obtains the 3D point cloud of the target scene by the radargrammetric method with composite registration, which is depicted in Figure 11. The reconstruction process successfully reconstructed the intricate facility of the FAST, including its main structure and most regions within the mountainous surroundings. However, due to layover problems, the available data in this paper is insufficient to obtain the complete point cloud data of certain structures, including surrounding mountainous areas and specific towers.
Figure 12 shows the top view of the final result, and compares the 3D image with the optical image in the corresponding regions. Figure 12d presents the height profile along the red line in Figure 12c, which corresponds to the 5-meter wide slice region. The curve fitting from the point cloud represent DEM profile. Figure 12d demonstrates that the point clouds obtained in this study accurately represents the DEM profiles of the relevant areas. The interpolated DEM is employed to filter the point cloud, removing the majority of isolated point clouds above the curve while retaining structures below the curve.

5. Discussion

5.1. The 3D Imaging Analysis of FAST

The results show that the proposed composite registration method in this study can achieve high-precision registration of multi-aspect SAR images. Coarse registration based on SIFT, which is commonly used for optical image matching and can also be applied to SAR images, effectively eliminates the differences between image pairs. Although the SIFT feature extraction and matching accuracy is limited, the algorithm's robustness can be enhanced through the transfer of resampling parameters during stereo image group. Subsequently, NCC fine registration is performed on the resampled image pairs, resulting in higher accuracy and density of registration results for 3D imaging.
The coverage range of stereo image groups can provide a preliminary determination of the overall 3D imaging area. As shown in Figure 10 and Figure 11, while partial point clouds represent the intersection of the coverage areas between image pairs from different path, the final 3D imaging result is the intersection of two circular SAR scans areas. Deviation of the center of certain SAR images from the center of the FAST leads to a loss of point cloud data for structures around FAST. Although the actual SAR images exhibit a wide range resolution, certain mountainous regions were excluded from the imaging results in this paper to reduce computational complexity. Figure 11's final point cloud retains part of independent mountain structures.
Through point cloud fusion, the complete target structure can be obtained using multi-aspect point clouds. Figure 10 illustrates that the reconstruction result from a single image pair only provides a partial view due to layover. While Figure 11 demonstrates a comprehensive 3D image of the target scene through the fusion of multi-aspect point clouds, the reconstruction of some regions remains incomplete due to issues such as insufficient data and layover. As shown in Figure 12, there are many gaps in the DEM profile. At the same time, there are errors in the 3D imaging results of the individual image pairs showcased in Figure 10, as well as in the regional point cloud. While pixel selection was conducted during the registration process based on pixel grayscale values and cross-correlation coefficients, clustering is still necessary during point cloud fusion to eliminate isolated points and retain partially connected point clouds. However, this method does not effectively eliminate erroneous point clouds underneath the DEM model, as shown in Figure 12, thereby directly impacting the imaging results of specific structures like the interior of the feed sources support tower and the surrounding support columns. Moreover, it may undiscriminatingly exclude certain isolated and sparse point clouds, including the point clouds of fine structures like the ropes connecting feed source.

5.2. The Complex Structures Constructed by the 3D Imaging Method

The 3D imaging method proposed in this paper can achieve precise reconstruction of partial structures. In Figure 10 and Figure 11, the 3D structure of FAST is clearly depicted, allowing for the observation of the suspended feed sources above the spherical reflector and a portion of the connecting ropes. However, due to the elongated shape and the limited imaging capability of SAR images regarding small objects such as ropes and feed sources, as well as the challenge in distinguishing them from the background, ensuring the points corresponding to these structures appearing in the 3D point cloud results of each image pair becomes difficult. The point clouds of these specific structure results in low density and continuity, they were excluded as erroneous results during the final point cloud fusion process. Nonetheless, manual selection or the utilization of optical flow methods, object recognition, and tracking algorithms can effectively separate such structures separately, providing a convenient solution.
The height of the feed sources support towers in 3D imaging results was measured to be approximately 170 m, which aligns with the actual situation. These towers can be used as reference point cloud in the process of multi-aspect point cloud fusion, facilitating scene calibration. As an important sub-region with multi-aspect point clouds, they can generate high-density partial 3D point clouds in the final point cloud results. Due to the complexity of scattering characteristics, repetitive structures, and significant multipath effects on the reflector surface, the imaging and registration of multi-aspect SAR images result in less satisfactory. As shown in Figure 7, the reflective surface in the SAR images are not complete, accompanied by the presence of noise in certain areas. Consequently, the 3D imaging of the reflector surface, was not achieved, as depicted in Figure 11, where there are nearly no valid 3D point cloud results in the FAST reflector surface. Furthermore, the NCC-based precise registration exhibits poorer performance in registering areas with periodic structures.
The proposed method could be applied in complex and unknown scenes, which require observing the research object from various aspect angles. The special phenomena of shadow region, overlays or reflectors in high-resolution SAR images pose difficulties in registering and 3D imaging. The characteristics of specific structures in SAR make image registration particularly challenging, while these phenomena can also impact the results of partial structures in complex buildings. Especially for SAR images obtained from different perspectives, the differences in backscattering characteristics of the same object can vary significantly, posing further challenges for object recognition in multi-aspect images. Moreover, multi-aspect point clouds of the same structure can also have significant differences, making point cloud fusion. Therefore, it is essential to consider diverse methods for target recognition and point cloud fusion. The generated 3D point clouds produced by this method are well-suited for multi-aspect imaging mode, enhancing the quality of multi-aspect SAR images.

6. Conclusions

This paper proposed a method for multi-aspect SAR 3D imaging using composite registration based on radargrammetry. By employing the composite registration of stereo image groups, it enables the registration of multi-aspect SAR images, facilitating high-precision 3D imaging in complex scenes without requiring prior knowledge of the target area. This method has the capability to acquire 3D imaging data from various perspectives, utilizing multi-aspect SAR images acquired at different times and trajectories, result in a comprehensive 3D representation of the unknown scene. It signifies an important advancement in the practical application of radargrammetry for 3D imaging.
The 3D imaging method proposed in this study is based on SAR image data, which is susceptible to the issue in SAR images such as layover. Consequently, the registration methods and point cloud fusion utilized in 3D imaging exhibit certain limitations, and delicate structures like ropes and support columns cannot be entirely reconstructed. We will further consider more feature extraction and matching methods for registration and segmentation processes, achieving automatic identification, extraction, and high-density imaging of key targets.
Furthermore, insufficient data in the experiments results in incomplete reconstruction of specific scenes, such as mountainous regions and buildings. Although this paper only uses multi-aspect SAR images from two circular SAR, multi-source SAR images acquired through SAR imaging algorithms that comply with the geometric model can be used for 3D imaging, including satellite SAR images with special compensation. While the imaging area in this paper may not be extensive, the computational complexity resulting from an expanded coverage area should also be considered. To address these challenges, we will concentrate on the 3D scattering characteristics of the target scene, explore novel and efficient data acquisition methods and processing methods, and advance the practical application of detailed multi-dimensional information acquisition in complex scenes.

Author Contributions

Conceptualization, Y.L., Y.D. and W.X.; methodology, Y.L. and H.Z.; validation, Y.L. and W.X.; formal analysis, Y.D.; investigation, Y.L. and C.Y.; resources, C.Y. and H.Z.; data curation, L.W.; writing—original draft preparation, Y.L. and W.X.; writing—review and editing, Y.L. and W.X.; visualization, Y.L.; supervision, W.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was jointly funded by the National Natural Science Foundation of China (Grant No. 62301535, 62001451, 62201548).

Acknowledgments

The authors would like to thank the anonymous reviewers for their valuable comments in improving this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Perry, R.P.; Dipietro, R.C.; Fante, R.L. SAR imaging of moving targets. IEEE Transactions on Aerospace and Electronic Systems. 1999, 35, 188–200. [Google Scholar] [CrossRef]
  2. Raney, R. K.; Runge, H.; Bamler, R.; Cumming, I. G.; Wong, F. H. Precision SAR processing using chirp scaling. IEEE Transactions on Geoscience and Remote Sensing. 1994, 32, 786–799. [Google Scholar] [CrossRef]
  3. Gatelli, F.; Monti Guamieri, A.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing. 1994, 32, 855–865. [Google Scholar] [CrossRef]
  4. Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Problems. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
  5. Rosen, P. A.; Hensley, S.; Joughin, I. R.; Li, F. K.; Madsen, S. N.; Rodriguez, E.; Goldstein, R. M. Synthetic aperture radar interferometry. Proceedings of the IEEE. 2000, 88, 333–382. [Google Scholar] [CrossRef]
  6. Lu, H.L.; Zhang, H.; Deng, Y.K.; Wang, J.L.; Yu, W.D. Building 3-D reconstruction with a small data stack using SAR Tomography. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing. 2020, 13, 2461–2474. [Google Scholar] [CrossRef]
  7. Reigber, A.; Moreira, A. First demonstration of airborne SAR tomography using multibaseline L band data. IEEE Transactions on Geoscience and Remote Sensing. 2000, 38, 2142–2152. [Google Scholar] [CrossRef]
  8. Fornaro, G.; Serafino, F.; Soldovieri, F. Three dimensional focusing with multipass SAR data. IEEE Transactions on Geoscience and Remote Sensing. 2003, 41, 507–517. [Google Scholar] [CrossRef]
  9. Méric, S.; Fayard, F.; Pottier, É. Radargrammetric SAR image processing. In Geoscience and Remote Sensing; IntechOpen: London, UK, 2009; pp. 421–454. [Google Scholar]
  10. Kirk, R.L.; Howington-Kraus, E. Radargrammetry on three planets. The international archives of the photogrammetry. Remote Sensing and Spatial Information Sciences, 2010; 37, 973–980. [Google Scholar]
  11. Balz, T.; Zhang, L.; Liao, M. Direct stereo radargrammetric processing using massively parallel processing. ISPRS J. Photogramm. Remote Sens. 2013, 79, 137–146. [Google Scholar] [CrossRef]
  12. Palm, S.; Oriot, H.; Cantalloube, H. Radargrammetric DEM extraction over urban area using circular SAR imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4720–4725. [Google Scholar] [CrossRef]
  13. Di Rita, M.; Nascetti, A.; Fratarcangeli, F.; Crespi, M. Upgrade of FOSS DATE Plug-In: Implementation of a new radargrammetric DSM generation capability. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2016, XLI-B7, 821–825. [Google Scholar] [CrossRef]
  14. Brown, L.G. A survey of image registration technology. ACM Computing Surveys. 1992, 24, 325–376. [Google Scholar] [CrossRef]
  15. Hao, X.G.; Zhang, H.; Wang, Y.J.; Wang, J.L. A framework for high-precision DEM reconstruction based on the radargrammetry technique. Remote Sens. Lett. 2019, 10, 1123–1131. [Google Scholar] [CrossRef]
  16. Dong, Y.; Zhang, L.; Balz, T.; Luo, H.; Liao, M. Radargrammetric DSM generation in mountainous areas through adaptive-window least squares matching constrained by enhanced epipolar geometry. ISPRS Journal of Photogrammetry and Remote Sensing. 2018, 137, 61–72. [Google Scholar] [CrossRef]
  17. Leberl, F.; Raggam, J.; Kobrick, M. On stereo viewing of SAR images. IEEE Transactions on Geoscience and Remote Sensing, 1985; GE-23, 110–117. [Google Scholar] [CrossRef]
  18. Konecny, G.; Schuhr, W. Reliability of radar image data. International Archives of Photogrammetry and Remote Sensing. 1988, 27, 456–469. [Google Scholar]
  19. Cheng, C. Q.; Zhang, J. X.; Huang, G. M.; Luo, C. F. Spaceborne SAR imagery stereo positioning based on Range-Coplanarity equation. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012; 39, 431–436. [Google Scholar] [CrossRef]
  20. Capaldo, P.; Nascetti, A.; Porfiri, M.; Pieralice, F.; Fratarcangeli, F.; Crespi, M.; Toutin, T. Evaluation and comparison of different radargrammetric methods for Digital Surface Models generation from COSMO-SkyMed, TerraSAR-X, RADARSAT-2 imagery: Analysis of Beauport (Canada) test site. ISPRS J. Photogramm. Remote Sens. 2015, 100, 60–70. [Google Scholar] [CrossRef]
  21. Guimarães, U.S.; Narvaes, I.D.S.; Galo, M.D.L.B.T.; da Silva, A.D.Q.; Camargo, P.D.O. Radargrammetric methods to the flat relief of the amazon coast using COSMO-SkyMed and TerraSAR-X datasets. ISPRS J. Photogramm. Remote Sens. 2018, 145, 284–296. [Google Scholar] [CrossRef]
  22. Chen, Z.; Zhang, Z.; Zhou, Y.; Wang, P.; Qiu, J. A novel motion compensation scheme for airborne very high resolution SAR. Remote Sens. 2021, 13, 2729. [Google Scholar] [CrossRef]
  23. Lindeberg, T. Scale-space theory: A basic tool for analysing structures at different scales. Journal of Applied Statistics. 1994, 21, 224–270. [Google Scholar] [CrossRef]
  24. Lowe, D. G. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision. 2004, 60, 91–110. [Google Scholar] [CrossRef]
  25. Nistér, D. Preemptive RANSAC for live structure and motion estimation. Machine Vision and Applications. 2005, 16, 321–329. [Google Scholar] [CrossRef]
  26. Baselice, F.; Budillon, A.; Ferraioli, G.; Pascazio, V. Layover solution in SAR imaging: A statistical method. IEEE Geosci. Remote Sens. Lett. 2009, 6, 577–581. [Google Scholar] [CrossRef]
Preprints 94760 g001
Figure 1. (a) Imaging geometry of one certain aspect angle; (b) Geometric relation of multi-aspect airborne observation geometry.
Figure 1. (a) Imaging geometry of one certain aspect angle; (b) Geometric relation of multi-aspect airborne observation geometry.
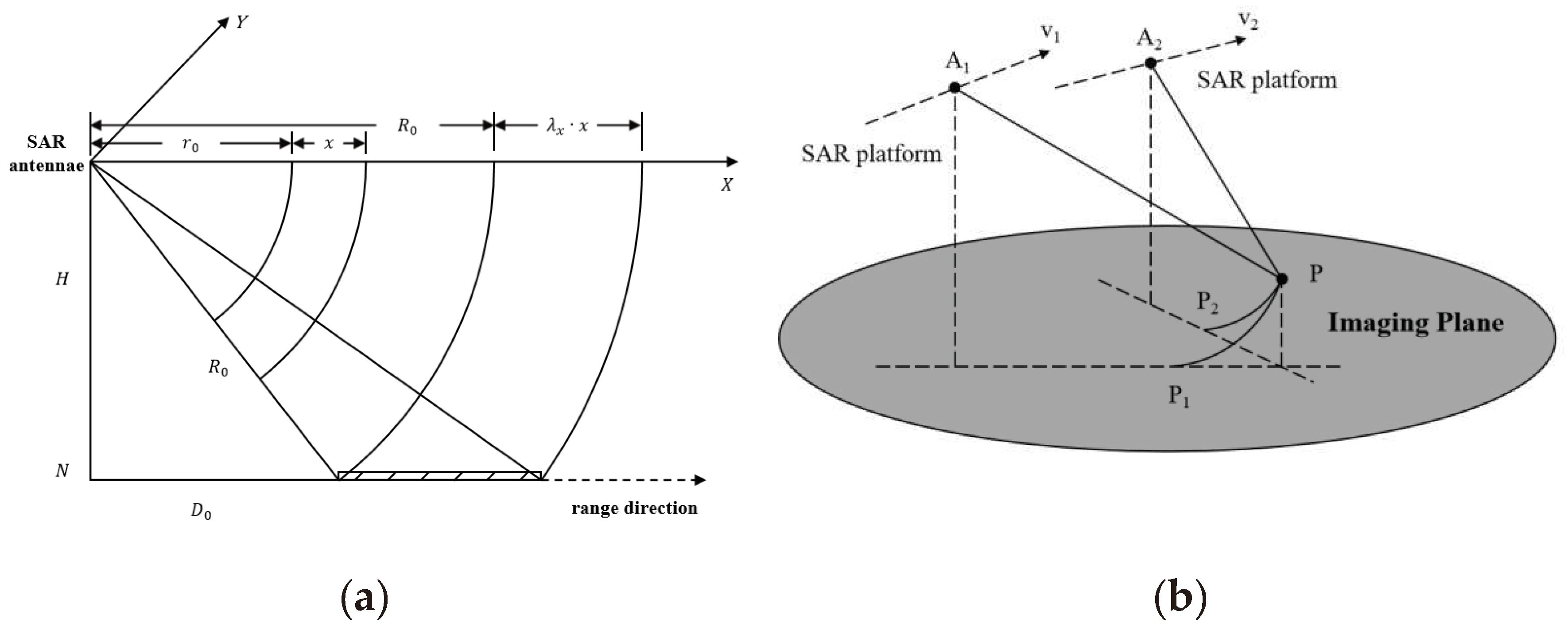
Preprints 94760 g001
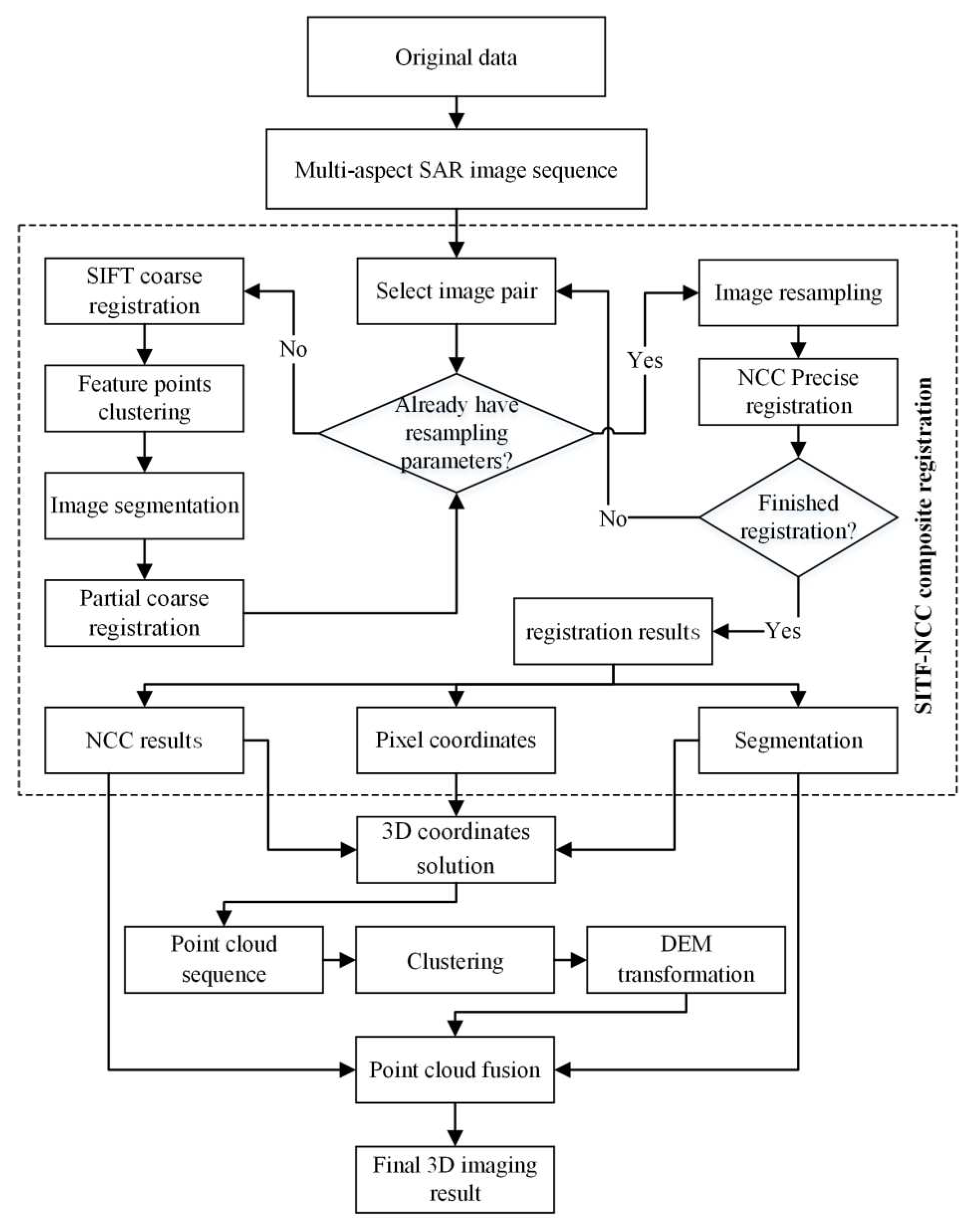
Preprints 94760 g002
Figure 2. Flowchart of 3D imaging in radargrammetry based on composite registration.
Figure 2. Flowchart of 3D imaging in radargrammetry based on composite registration.
Preprints 94760 g002
Preprints 94760 g003
Figure 3. Aperture-dependent motion error and compensation.
Figure 3. Aperture-dependent motion error and compensation.
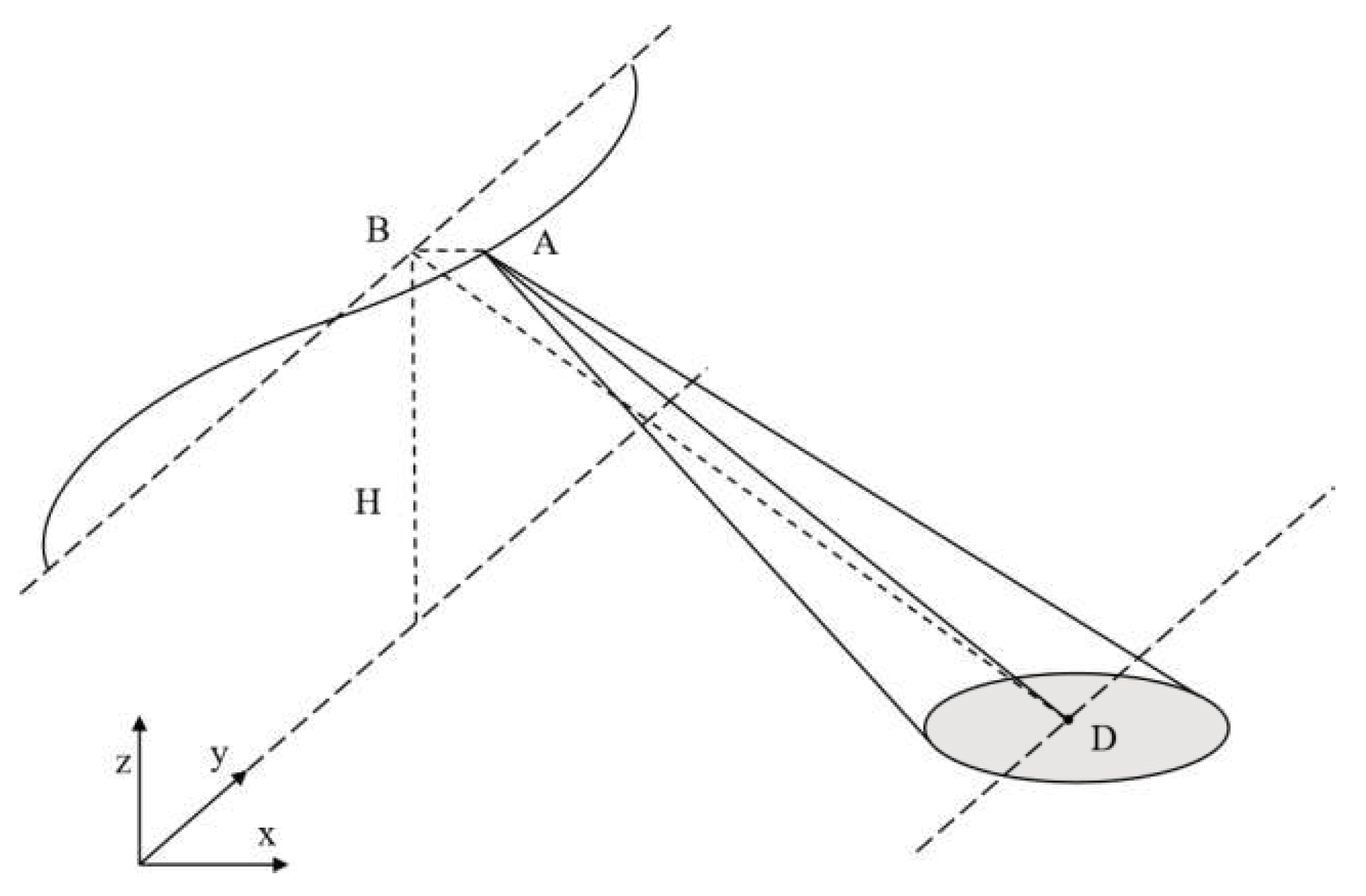
Preprints 94760 g003
Preprints 94760 g004
Figure 4. Illustration of composite registration for stereo image group.
Figure 4. Illustration of composite registration for stereo image group.
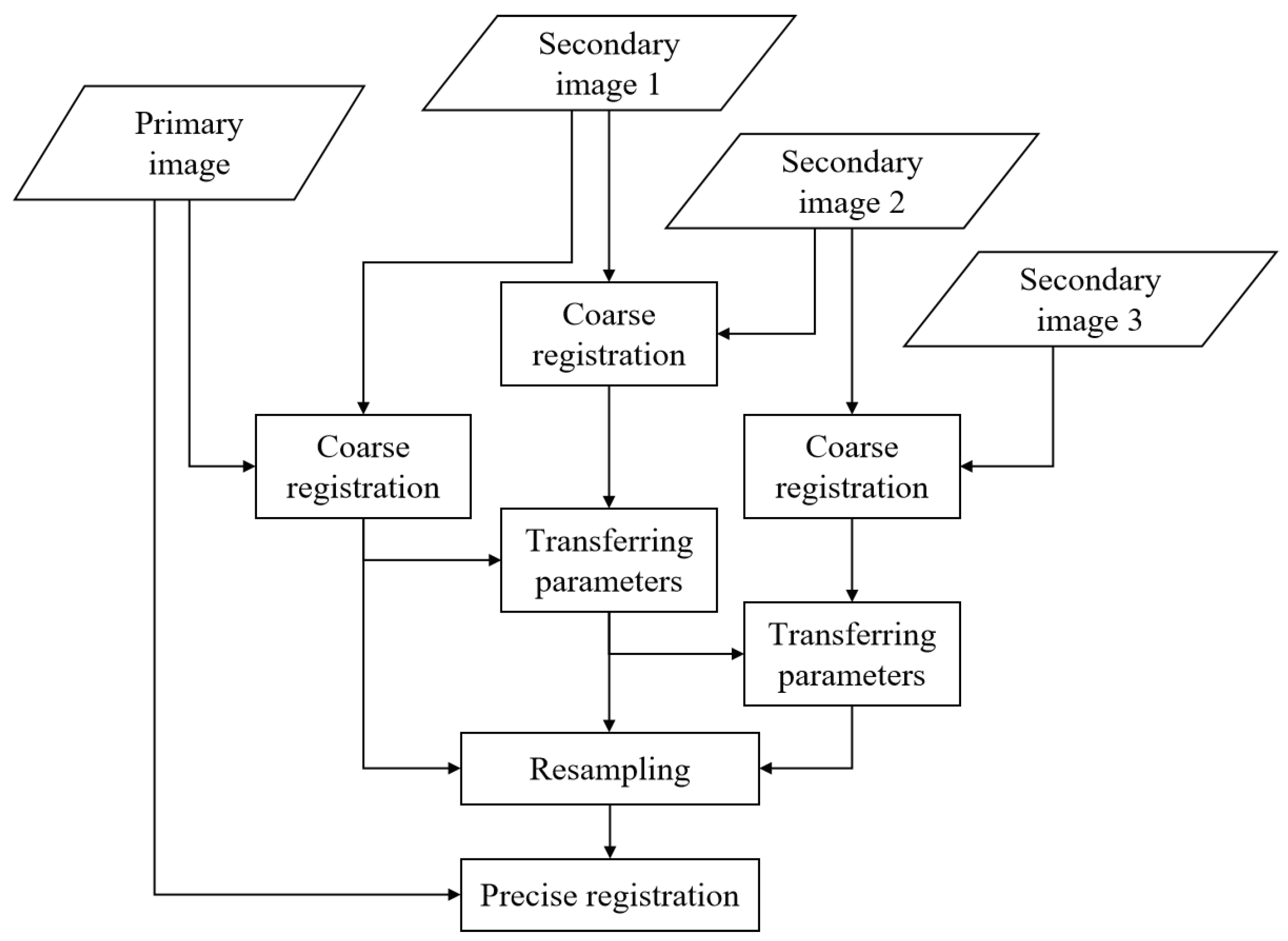
Preprints 94760 g004
Preprints 94760 g005
Figure 5. Fusion of GPS data, IMU data, and motion-compensated trajectory.
Figure 5. Fusion of GPS data, IMU data, and motion-compensated trajectory.
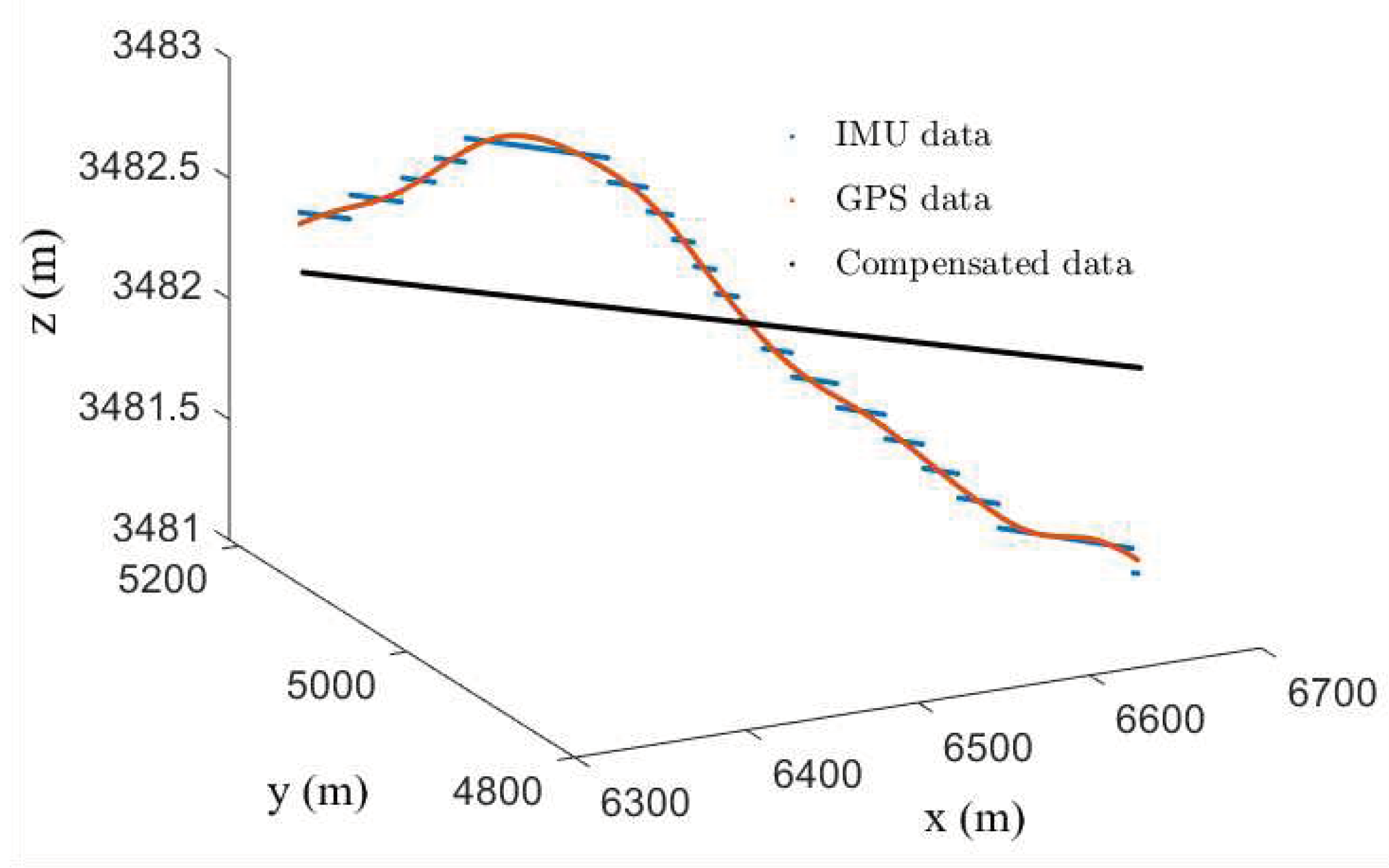
Preprints 94760 g005
Preprints 94760 g006
Figure 6. (a) The optical image of FAST; (b) The stripmap SAR image of the FAST; (c) Flight tracks of SAR platform and the range of corresponding tracks for the stereo image groups.
Figure 6. (a) The optical image of FAST; (b) The stripmap SAR image of the FAST; (c) Flight tracks of SAR platform and the range of corresponding tracks for the stereo image groups.
Preprints 94760 g006
Preprints 94760 g007
Figure 7. (a) Coarse registration result for a sub-aperture SAR image pair; (b) An enlarged image showcases the coarse registration and segmentation results in the central region of the image pair; (c) Fusion result obtained through the coarse registration without sub-regional resampling for the image pair; (d) Fusion result obtained through the sub-regional coarse registration and resampling of the image pair. (e) Final fusion result of another image pair.
Figure 7. (a) Coarse registration result for a sub-aperture SAR image pair; (b) An enlarged image showcases the coarse registration and segmentation results in the central region of the image pair; (c) Fusion result obtained through the coarse registration without sub-regional resampling for the image pair; (d) Fusion result obtained through the sub-regional coarse registration and resampling of the image pair. (e) Final fusion result of another image pair.
Preprints 94760 g007
Preprints 94760 g008
Figure 8. Details of sub-regional coarse registration. The registration results of three sub-region are listed in three rows separately. The 1st and 2nd columns represent the left and right image for registration; The 3rd column is the fusion results of resampled right image (in red) and the left image (in green) without segmentation. The 4th column is the fusion results of resampled right image (in red) and the left image (in green) following the sub-region registration.
Figure 8. Details of sub-regional coarse registration. The registration results of three sub-region are listed in three rows separately. The 1st and 2nd columns represent the left and right image for registration; The 3rd column is the fusion results of resampled right image (in red) and the left image (in green) without segmentation. The 4th column is the fusion results of resampled right image (in red) and the left image (in green) following the sub-region registration.
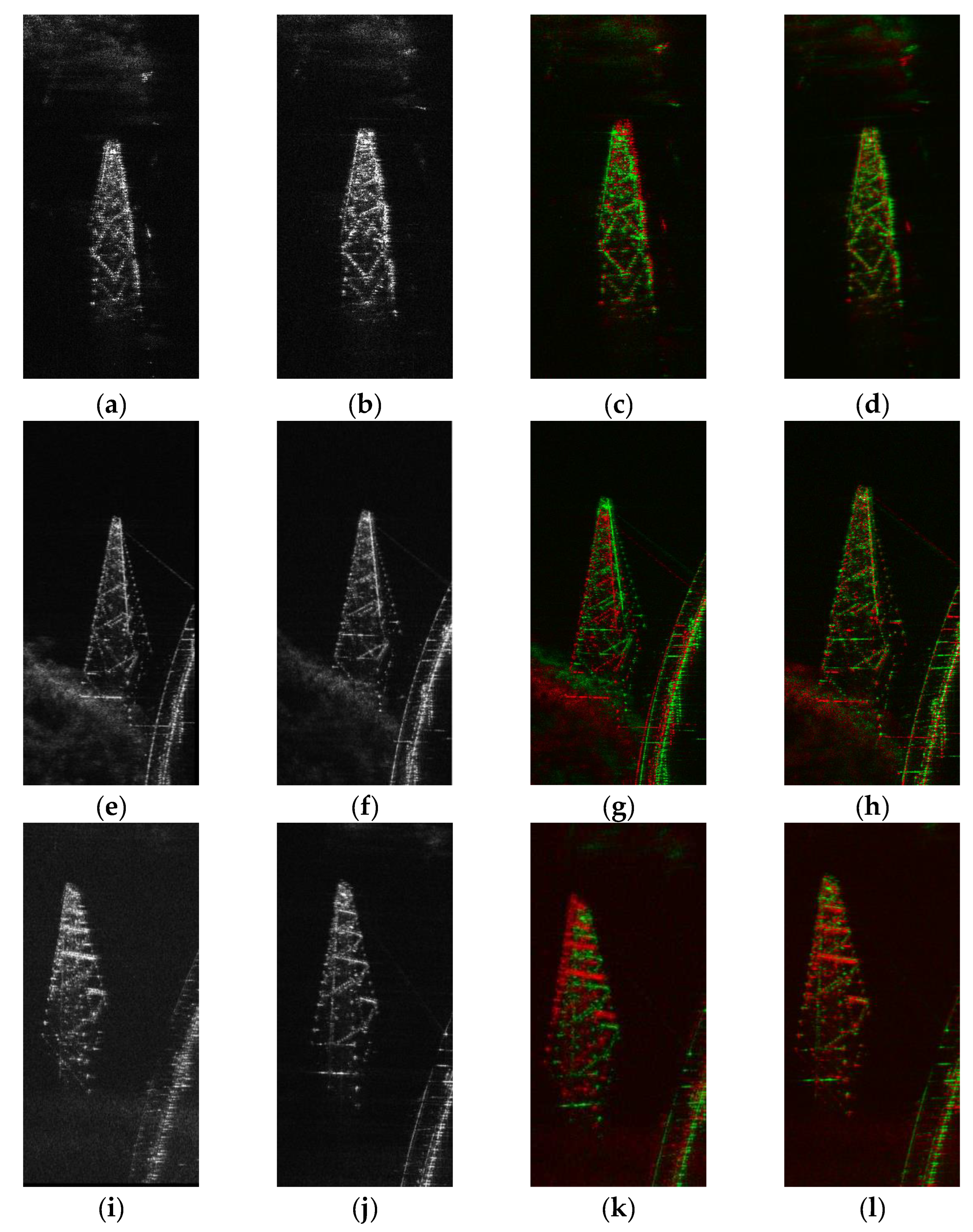
Preprints 94760 g008
Preprints 94760 g009
Figure 9. The cross-correlation coefficient image after precise registration of an image pair.
Figure 9. The cross-correlation coefficient image after precise registration of an image pair.
Preprints 94760 g009
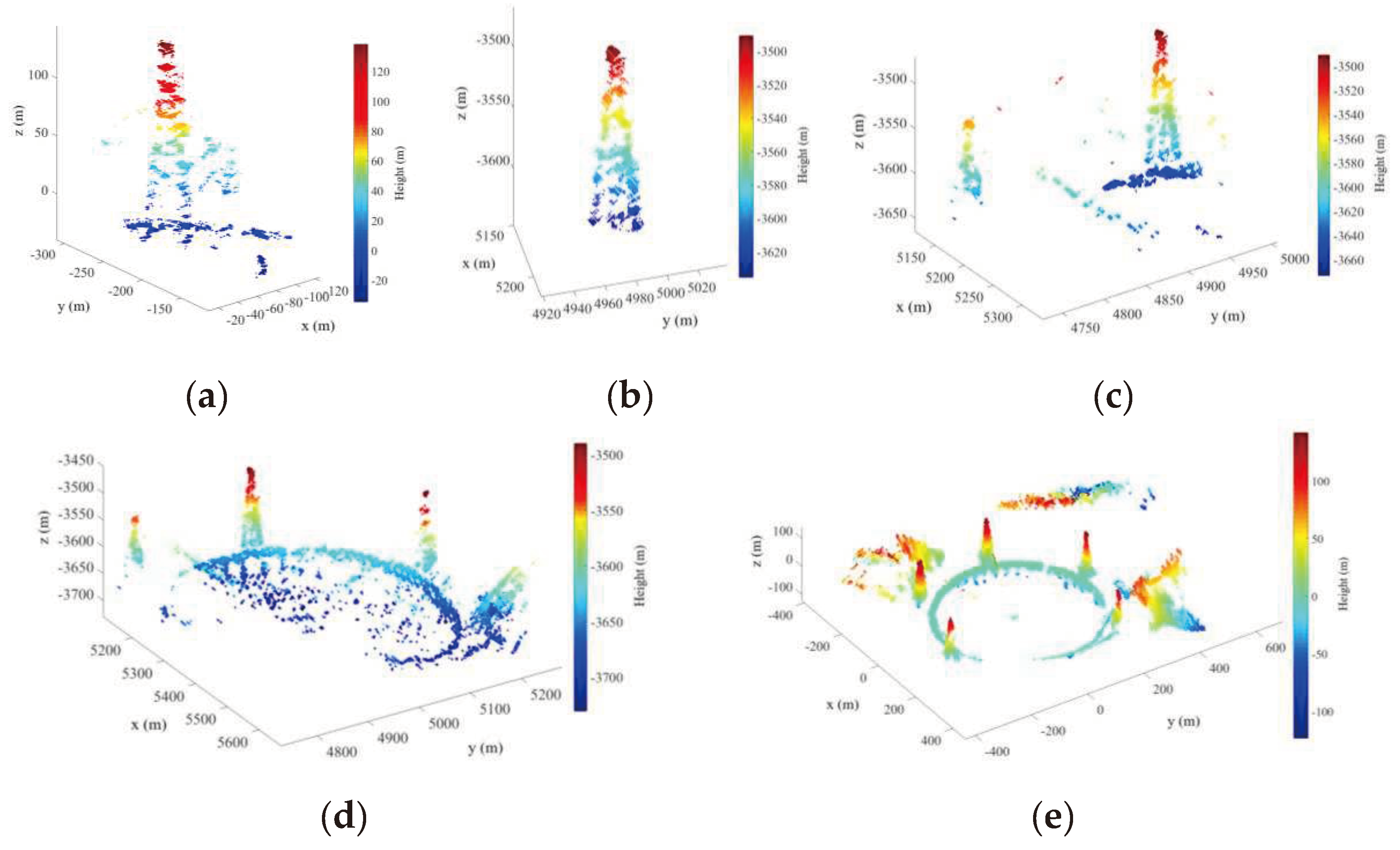
Preprints 94760 g010
Figure 10. (a-c) Sub-region point clouds from different image pairs, which are 3D imaging results of the sub-region containing power transmission towers; (d) Point cloud results for a single image pair; (e) The fusion results of partial sub-region point clouds.
Figure 10. (a-c) Sub-region point clouds from different image pairs, which are 3D imaging results of the sub-region containing power transmission towers; (d) Point cloud results for a single image pair; (e) The fusion results of partial sub-region point clouds.
Preprints 94760 g010
Preprints 94760 g011
Figure 11. FAST multi-aspect 3D imaging results. (a) The overall reconstruction results; (b-e) The reconstruction results presented from different aspect angles with a viewing angle difference of approximately 90 degrees; (f) The reconstruction results presented from the aspect angle between (d,e); (f) The reconstruction results presented from the aspect angle between (b,c).
Figure 11. FAST multi-aspect 3D imaging results. (a) The overall reconstruction results; (b-e) The reconstruction results presented from different aspect angles with a viewing angle difference of approximately 90 degrees; (f) The reconstruction results presented from the aspect angle between (d,e); (f) The reconstruction results presented from the aspect angle between (b,c).
Preprints 94760 g011
Preprints 94760 g012
Figure 12. (a) The aerial view of the reconstruction results; (b) Optical image of the corresponding area in (a); (c) Zoomed aerial view of the reconstruction results after rotation. The red line represent the test sites for DEM quality evaluation; (d) Profile of the reconstruction results and DEM fitting curve corresponding to the red line in (c).
Figure 12. (a) The aerial view of the reconstruction results; (b) Optical image of the corresponding area in (a); (c) Zoomed aerial view of the reconstruction results after rotation. The red line represent the test sites for DEM quality evaluation; (d) Profile of the reconstruction results and DEM fitting curve corresponding to the red line in (c).
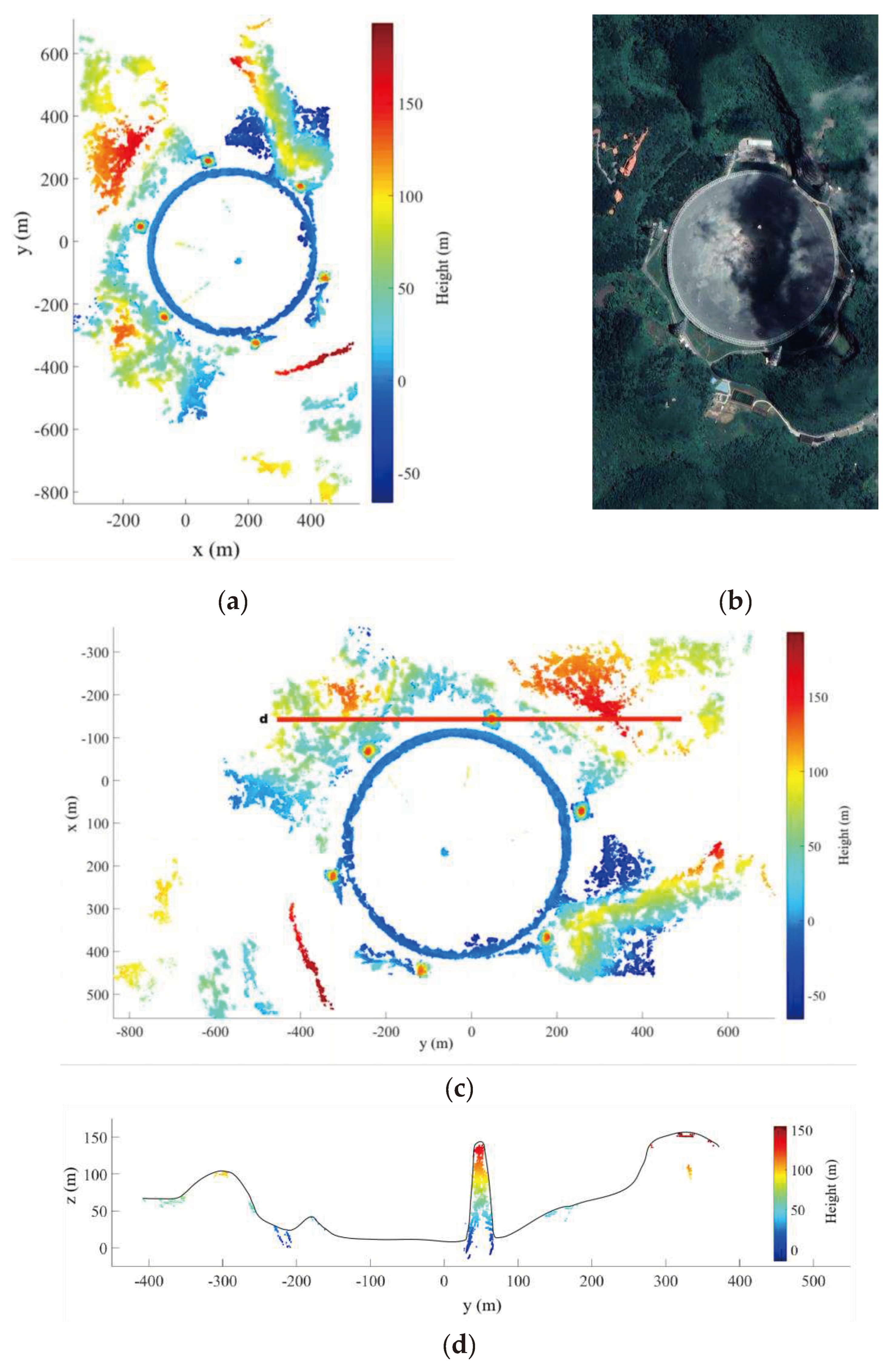
Preprints 94760 g012
Table 1. Parameters of the airborne Ka-band SAR.
Table 1. Parameters of the airborne Ka-band SAR.
Parameter Value
bandwidth 3600 MHz
baseline length 0.60 m
incident angle 50°
flight radius 6000 m
flight altitude 3000 m
ground elevation 900 m
Table 2. The number of images included in each stereo image group.
Table 2. The number of images included in each stereo image group.
Name Number of image pairs Number of images
Group 1 3 5
Group 2 2 4
Group 3 2 3
Group 4 4 6
Group 5 2 4
Group 6 3 4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated