Fast Analytic‐Numerical Algorithms for Calculating Self and Mutual Inductances of Air Coils

Preprint

Article

Fast Analytic‐Numerical Algorithms for Calculating Self and Mutual Inductances of Air Coils

Altmetrics

Downloads

107

Views

Comments

A peer-reviewed article of this preprint also exists.

Ryszard Palka^*

This version is not peer-reviewed

Submitted:

28 December 2023

Posted:

28 December 2023

You are already at the latest version

Alerts

Abstract

This paper deals with a method of calculating the self and mutual inductances of various air coils located arbitrarily in space. Known elementary solutions (the Biot-Savart formulas) were used to determine the magnetic field of infinitely thin current loops and infinitely thin wires of finite length linking magnetically other coils. Unlike commonly used algorithms, these elementary solutions were not extensively transformed analytically but were used to perform calculations by direct numerical integration. This enabled very quick and accurate obtaining of the self-inductance values as well as determining the dependence of mutual inductances on the position of both coils. This method allows analysis of different coil configurations (misaligned coils, inclined to each other, etc.) that other methods do not cover. It also enables the determination of the forces acting on the coils, as well as the calculation of the magnetic field distribution from any coil configuration. The obtained results were compared with those presented by other authors.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Nowadays, contactless energy transfer (CET) offers great opportunities to power various types of mobile devices. Typical inductive CET system consists of a primary side DC/AC resonant converter, a transformer and an AC/DC secondary system that converts the high-frequency AC energy to meet the requirements specified by the load parameters. The secondary side is not connected electrically to the primary side, which has many obvious advantages. High-power CET systems are used in the automotive and transportation industries, among others, as battery chargers [1,2,3].

Many CET devices use magnetically coupled air coils. These include wireless energy transfer, various types of accelerators, electronic systems, biomedical [4] and robotics applications, etc. Some applications use a coreless transformer based on printed circuit board winding layout without a ferrite core [5]. The advantages of coreless coils are their lower weight and increased mechanical durability. Moreover, designing the shape is simpler and gives much more opportunities to adapt it to the rest of the system. The problems of designing coreless systems are discussed, for example, in articles [6,7,8].

Converting energy in the primary and secondary circuits of CET systems is a standard and well-recognized task for designers of power electronic systems. Calculating the magnetic coupling of air coils is also a well-developed scientific topic, however, due to the variety of newly designed coils (their shapes and tasks), as well as the possibility of their arbitrary mutual position in space, it is necessary to develop fast and accurate algorithms for calculating their self and mutual inductances.

2. Principles for calculating the self- and mutual inductances of air coils

Methods for calculating the self and mutual inductances of different air coils have been presented in many articles [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23].

First, it is worth mentioning the fundamental paper by F.W. Grover [9], who presented a method for calculating mutual inductance of circular filaments in any positions. He used equations describing the magnetic field of elementary current loops to determine their mutual inductances for various mutual positions. A similar methodology was also used in this paper.

The article [10] by J.T. Conway shows the use of Bessel Functions to calculate the inductance of different non-coaxial coils. A continuation of this article is paper [11], in which elliptic integrals were used to calculate inductances. In [12] the inductance calculations for coils of parallel axes using Bessel and Struve functions are shown.

The articles by Babic and his various co-authors [13,14,15,16,17,18,19,20] also solve many basic problems of calculating the self- and mutual inductances of different coils in any mutual position.

It is also worth mentioning the article [21], in which the authors developed a fast and effective algorithm for calculating the inductance of coaxial coils by integrating appropriate elementary solutions. The authors of [22] also described a method for calculating mutual inductances for coils with misalignment by integrating elementary field solutions.

Reference to above articles is provided later in this paper. There are, of course, many other important articles on the above topic and it is impossible to list them here.

Much simpler algorithms were proposed in this paper, primarily involving the calculation of the flux linkage for various coil configurations. Analytical solutions for simple coil configurations and numerical integration of elementary solutions were used to create a computational tool that allows quick and accurate calculations of the self- and mutual inductances of various air coils for any of their mutual positions. The obtained results were compared with those presented by other authors.

2.1. Basics of magnetic field theory used for inductance calculations

The magnetic energy

W_{m}

of a system carrying a current

I

(with the uniform current density

J

) can be calculated as a volume integral over the magnetic energy density. For arrangements with

μ = μ_{0}

in the entire space with volume

V

it reads:

W_{m} = \frac{1}{2} \int_{V} B H d V,

(1)

where

B

and

H

are the magnetic induction and magnetic field strength vectors, respectively.

Using the definition of vector potential

A

B = rot A, div A = 0

(2)

and Maxwell's first equation

rot H = J

(3)

the following form of equation (1), very useful for calculating the magnetic field energy, is obtained:

W_{m} = \frac{1}{2} \int_{V} A J d V .

(4)

Formula (4), unlike formula (1), requires integration only in areas where the electric current density is different from zero, which greatly speeds up calculations. Finally, the inductance of the wire carrying the current

I

can be calculated from the formula:

L = 2 W_{m} / I^{2} .

(5)

In the case of two independent electrical circuits leading currents

I_{1}

and

I_{2}

(with the current densities

J_{1}

and

J_{2}

), respectively, the formula for magnetic energy can be written as follows:

\begin{matrix} W_{m} & = \frac{1}{2} \int_{V} B H d V = \frac{1}{2} \int_{V} (B_{1} + B_{2}) (H_{1} + H_{2}) d V = \frac{1}{2} \int_{V} (B_{1} H_{1} + B_{2} H_{2} + B_{1} H_{2} + B_{2} H_{1}) d V = \\ = \frac{1}{2} L_{1} {I_{1}}^{2} + \frac{1}{2} L_{2} {I_{2}}^{2} + \frac{1}{2} M_{1, 2} I_{1} I_{2} + \frac{1}{2} M_{1, 2} I_{1} I_{2} . \end{matrix}

(6)

The integral

\int_{V} B_{1} H_{2} d V

in formula (6) can be written according to equation (4) as:

\int_{V} B_{1} H_{2} d V = \int_{V} A_{1} J_{2} d V .

(7)

Formula (7) makes it possible to calculate the mutual inductance of two magnetically coupled circuits as:

M_{1, 2} = \frac{1}{I_{1} I_{2}} \int_{V} A_{1} J_{2} d V .

(8)

Integration in the formula (8) should also be carried out only in areas where the current density

J_{2}

is different from zero.

Formulas (5) and (8) enable easy calculation of self and mutual inductances in systems where the vector potential has only one component. It can be given analytically or calculated numerically.

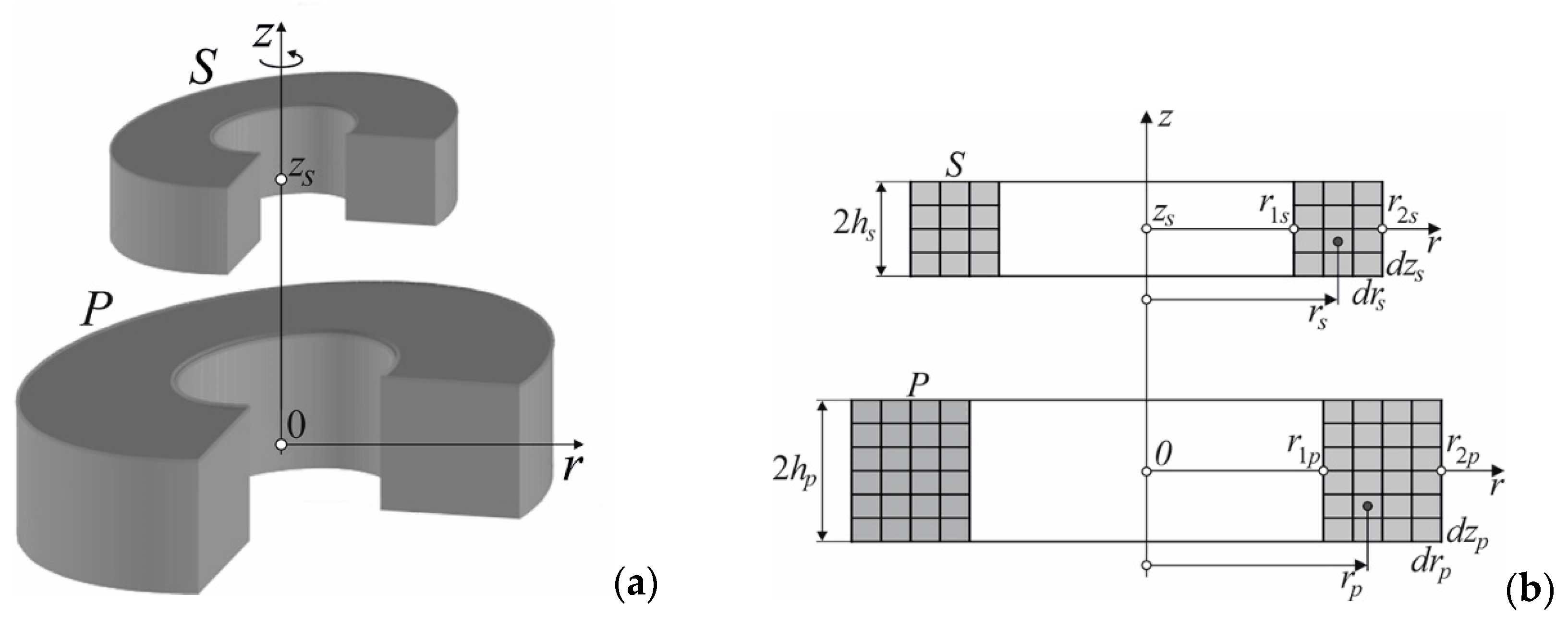
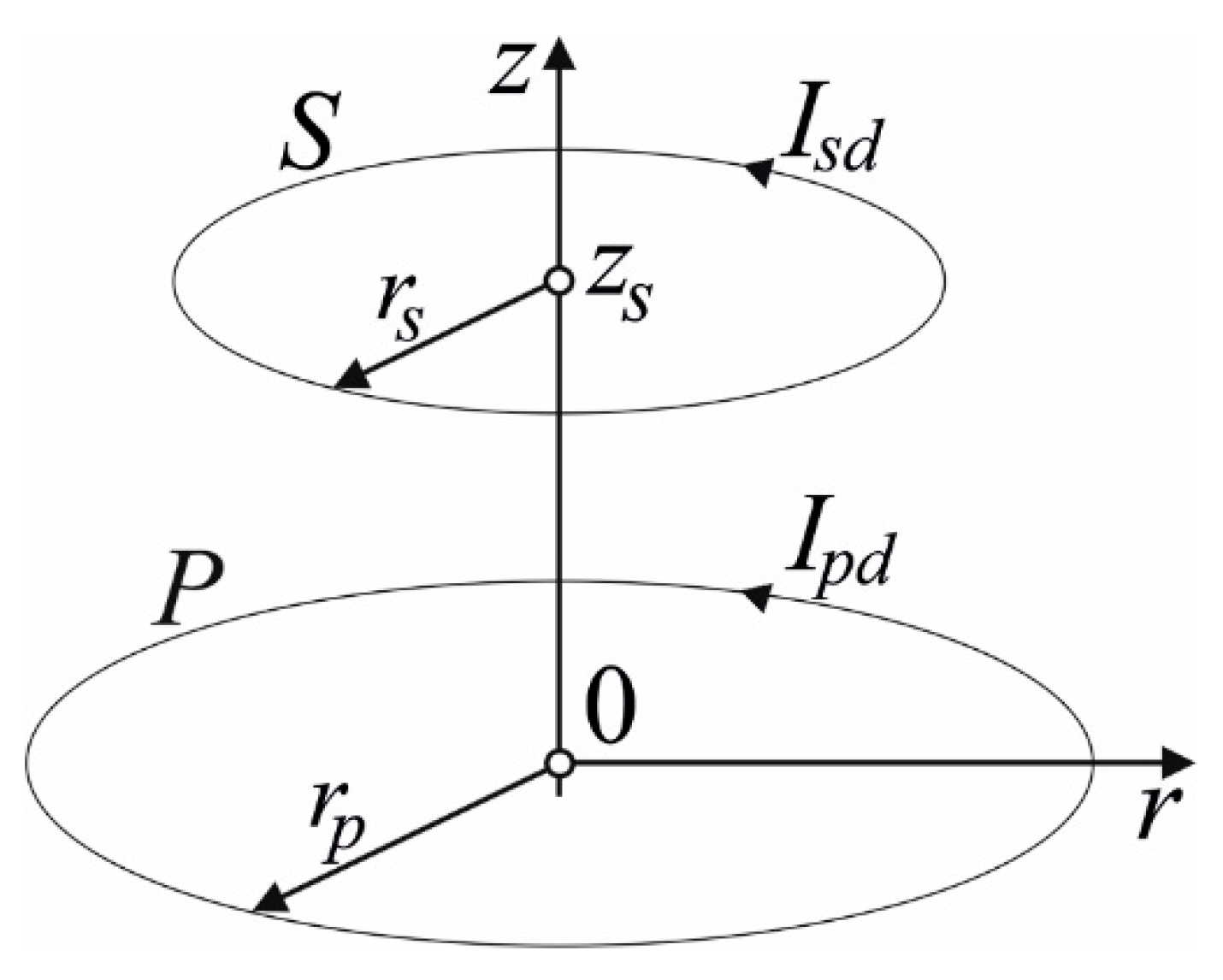
3. Cylindrical air coils

This chapter presents equations and numerical algorithms enabling the calculation of the self- and mutual inductances of various configurations of cylindrical air coils with a rectangular cross-section.

3.1. Magnetic field of cylindrical coils

Figure 1a shows a system of two coaxial cylindrical coils (with rectangular cross-section) marked with the letters P (primary) and S (secondary). To calculate the magnetic field of this coils system, the cross-section of each coil is divided into cylindrical coils with a rectangular cross-section. The problem of determining self- and mutual inductances, as well as the field distribution of such coils, is thus reduced to determining the interactions between elementary thin coaxial coils. A similar approach to this issue was also discussed in articles [23,24].

Figure 1b illustrates the dimensions and discretization of both coils. The inner radii of the coils are denoted by

r_{1 p}

and

r_{1 s}

, the outer radii by

r_{2 p}

and

r_{2 s}

, and their heights by

2 h_{p}

and

2 h_{s}

, respectively. The currents flowing in the coils are marked by

I_{p}

and

I_{s}

, respectively. The value of the current flowing in each elementary loop

I_{p d}

and

I_{s d}

results from the discretization of the coils. In all considerations of this paper, the center of the primary coil is always located in the center of the coordinate system.

The proper selection of the values of the discretization parameters

d r_{p}, d z_{p}, d r_{s}, d z_{s}

is a key issue determining the accuracy of this algorithm. In each of the presented solutions, the obtained results were tested depending on the type of discretization. Due to the very high speed of the algorithm, it was possible to achieve very fine discretization of all areas. In some cases, this discretization should correspond to the actual arrangement of turns in the coils.

Figure 2 shows two infinitesimally thin coaxial current loops of radii

r_{p}

and

r_{s}

, respectively. The center of the primary loop is located in the center of the coordinate system and the center of secondary loop is located at

(0, z_{s})

To calculate the magnetic field of the primary coil, the formulas for the vector potential of infinitely thin current loops from [25, p. 260] were used. The formulas in [25] also take into account the singularity in the potential formula for

r = 0

. The elementary vector potential of the partial current loop with the current

I_{p d}

of the primary coil with the radius

r_{p}

can be written as follows [25]:

{d A}_{p} = \frac{μ_{0} I_{p d}}{2 π} \sqrt{\frac{r_{p}}{r}} [K (u) \cdot (\frac{2}{u} - u) - E (u) \cdot \frac{2}{u}] d r_{p} d z_{p},

(9)

where:

u = \sqrt{\frac{4 r r_{p}}{{(r + r_{p})}^{2} + z^{2}}}, I_{p d} = \frac{I_{p}}{2 h_{p} (r_{2 p} - r_{1 p})}

(10)

and

K (u)

and

E (u)

are elliptic integrals of the first and second kind, respectively.

The total vector potential of the primary coil can be calculated as the integral:

A_{p} = \int_{r 1 p}^{r 2 p} \int_{- h p}^{h p} {d A}_{p} .

(11)

For the magnetic energy we get:

W_{m} = \frac{1}{2} \int_{V} A_{p} I_{p d} d V = \int_{r 1 p}^{r 2 p} \int_{- h p}^{h p} A_{p} I_{p d} π d r d z = \int_{r 1 p}^{r 2 p} \int_{- h p}^{h p} \int_{r 1 p}^{r 2 p} \int_{- h p}^{h p} d A_{p} I_{p d} π r d r d z .

(12)

Finally, the self-inductance of the primary coil can be calculated as in Eq. (5). The self-inductance of the secondary coil is calculated in the same way (after moving it to the center of the coordinate system). The mutual inductance between both coils is obtained using formula (8), whereby the energy is calculated using formula (12) (after changing one of the integration surfaces to the secondary coil area).

The number of turns of the primary winding

N_{p}

and secondary winding

N_{s}

should also be considered in the calculations of inductances – it is necessary to multiply the obtained results by the square of the number of turns for self-inductances and by the product of the number of turns of the primary and secondary windings for mutual inductances. Determining the fourfold integral (12) when calculating inductance is the main problem of the method. To shorten the calculation time, various approximations of the elliptic integrals

K (u)

and

E (u)

were tested. Finally, the formulas given in [26] (pages 591 and 592) were used:

K (u) = a_{0} + a_{1} w + a_{2} w^{2} + a_{3} w^{3} + a_{4} w^{4} + (b_{0} + b_{1} w + b_{2} w^{2} + b_{3} w^{3} + b_{4} w^{4}) \ln (1 / w),

(13)

E (u) = c_{0} + c_{1} w + c_{2} w^{2} + c_{3} w^{3} + c_{4} w^{4} + (d_{0} + d_{1} w + d_{2} w^{2} + d_{3} w^{3} + d_{4} w^{4}) \ln (1 / w) .

(14)

The coefficient values

a_{0} - a_{4}, b_{0} - b_{4}, c_{0} - c_{4}, d_{0} - d_{4}

are given in [26] and

w = 1 - u^{2}

. The error of this approximation is less than 2x10^-8.

3.2. Comparison with results obtained by other authors and the finite element method

The method was verified by comparing the results obtained by other authors, as well as by calculations using the finite element method (FEM). Article [21] shows a method for precise calculating of the mutual inductances of different cylindrical coaxial coils. This article compares its own results with nine results obtained by other authors, so it provides a good summary of the topic. Here, a comparison for two selected configurations will be shown. For example, in [21], the mutual inductance was calculated for coils with the following dimensions:

r_{1 p} = 0, 3 m,

r_{2 p} = 0, 4 m,

r_{1 s} = 0, 1 m,

r_{2 s} = 0, 2 m,

h_{p} = 0, 05 m,

h_{s} = 0, 05 m,

z_{s} = 0, 2 m,

N_{p} = 100,

N_{s} = 100

Article [21] gives a result of the mutual inductance

M = 0.845 445 761 529 6840 mH

(page 4901309, Table II, Case 1). An identical value (16 significant places) was obtained in paper [12] (page 81, Table VI, Case 1). In article [14] 8 significant places in the mutual inductance value are identical (page 1664), but the result is incorrect because it gives the value of the mutual inductance in

μ H

and not in

mH

. It also seems that providing so many significant places in the result does probably not make much sense due to limited calculation accuracy – the accuracy of 7-9 places appears to be entirely adequate. The method proposed here gives a result of

M = 0.845 445 78 mH

All configurations of cylindrical coaxial coils can be additionally quickly analyzed using the two-dimensional FEM to verify different analytical-numerical methods proposed by various authors. The magnetic field distribution in the configuration analyzed above is shown in Figure 3a (both coils are powered by the current having the same value and direction), while the field distributions when powering single coils are shown in Figure 3b,c, respectively. The values of self-inductances calculated using the FEM from formula (5) is equal to

L_{p} = 9.541 0842 mH

and

L_{s} = 2.581 5732 mH

, respectively, and the mutual inductance calculated according to Eq. (8) is

M = 0.845 467 88 mH

Figure 4 shows the dependence of

M

and its derivative

d M / d z

versus the axial displacement of the secondary coil calculated by the proposed method and the FEM (both methods give identical results). The beginning of the trajectory is marked by the point with coordinates

(r = 0 m, z_{s} = 0.2 m)

, and its end by the point with coordinates

(r = 0 m, z_{s} = 0.4 m)

. The derivative of mutual inductance provides information about the forces acting on the coils depending on their relative position (see Section 6).

The papers [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] discuss, among other things, many configurations of cylindrical coaxial coils and determine their mutual inductances. These results were also confirmed using the computational algorithm described herein. This algorithm also enables quick and accurate determination of the mutual inductances during the movement of the secondary coil, as well as the self-inductances of both coils.

The scope of applications of the method presented above is very limited to very basic configurations (cylindrical coaxial coils), but at the same time this method provides additional opportunities to compare and check the results with 2D-FEM.

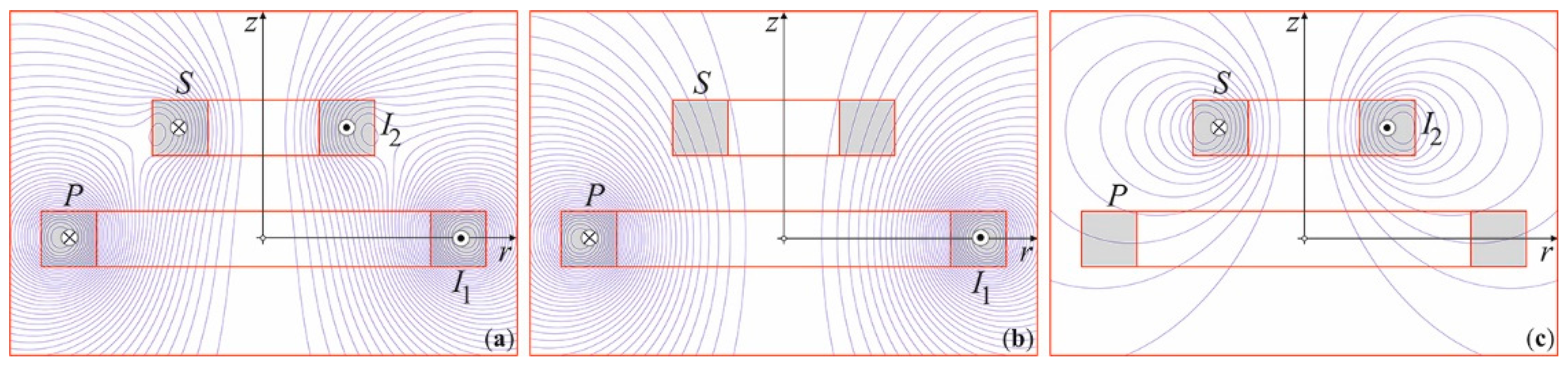
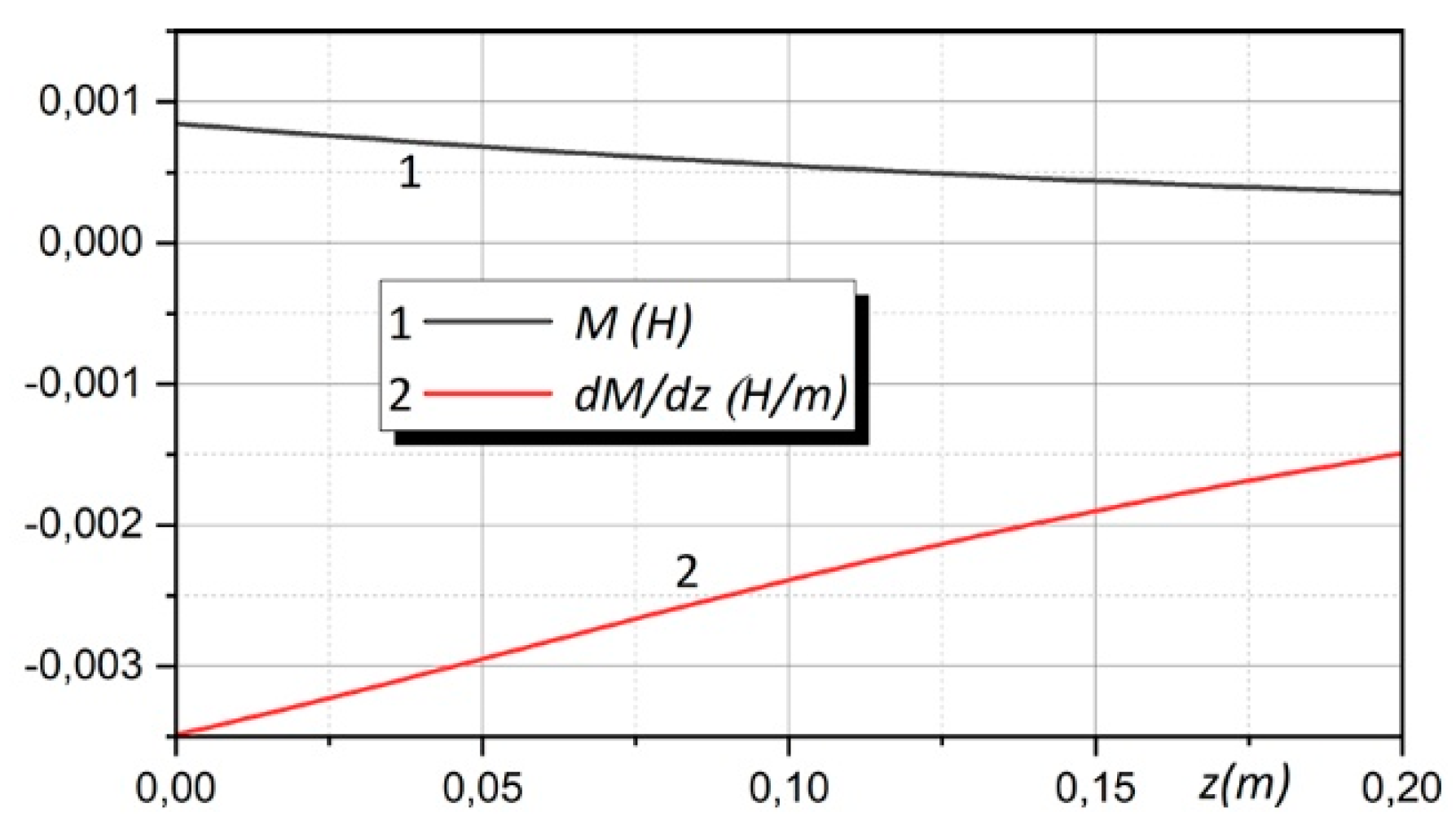
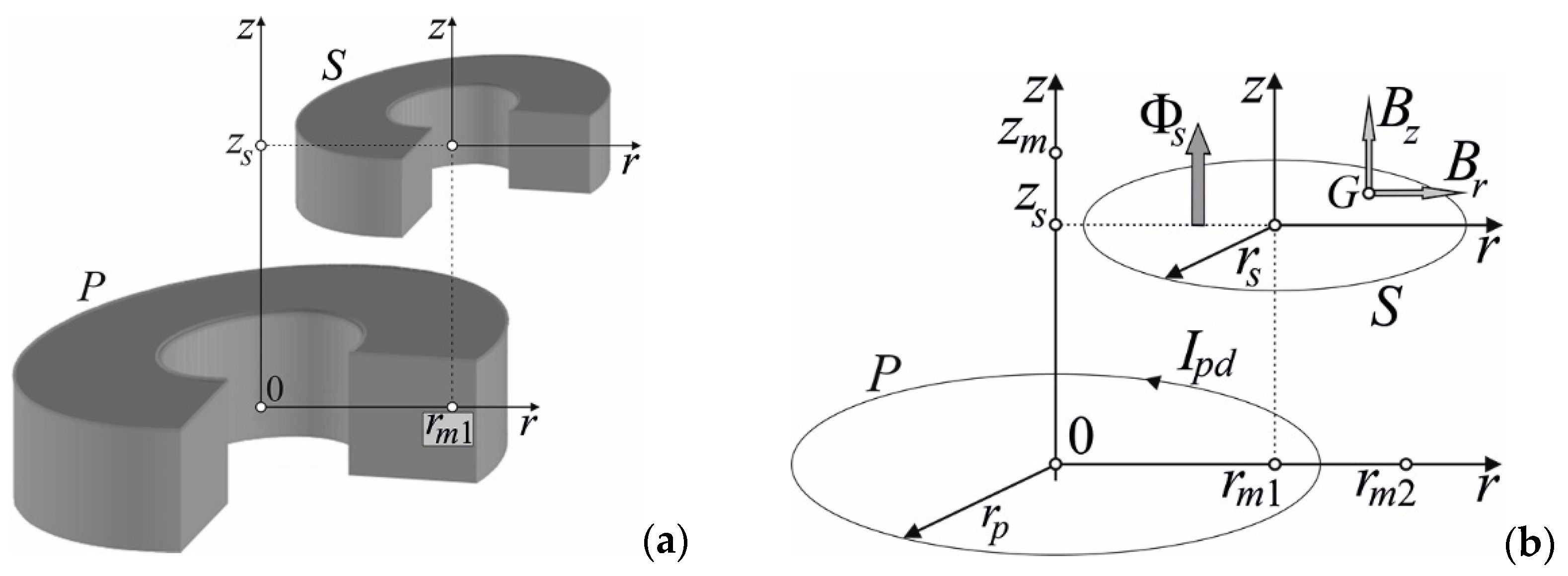
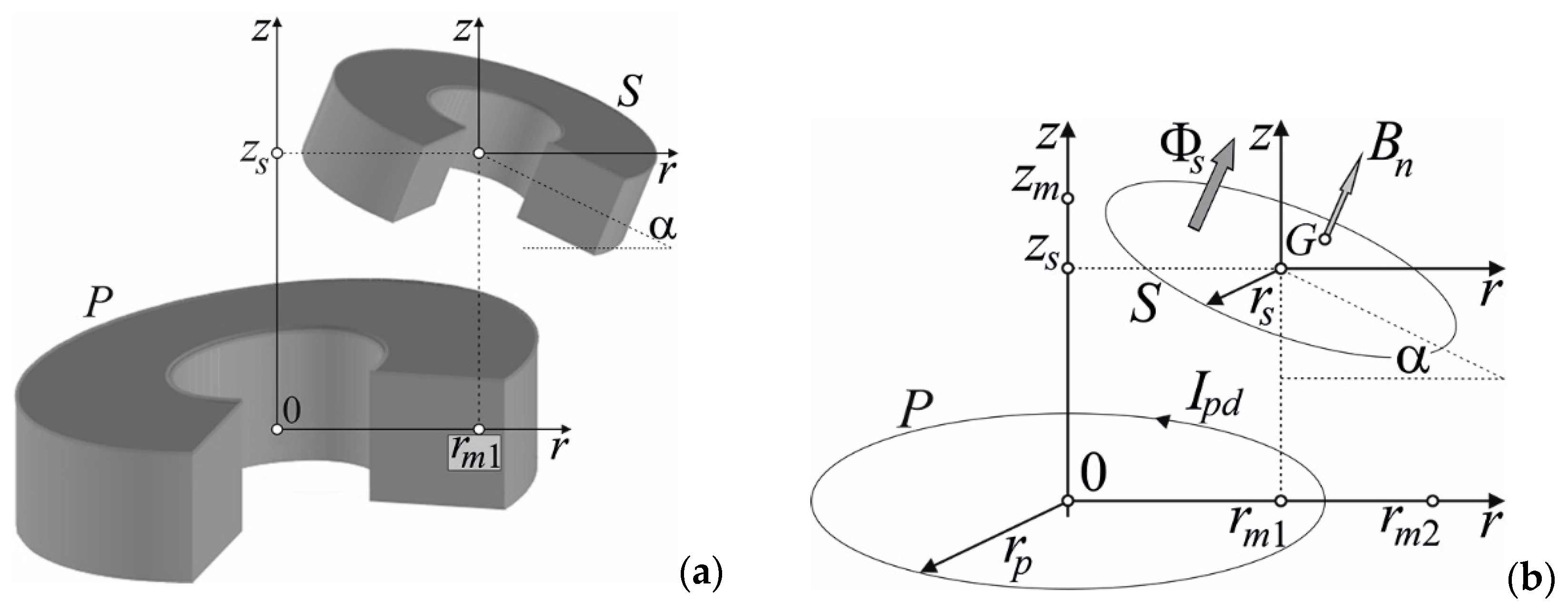
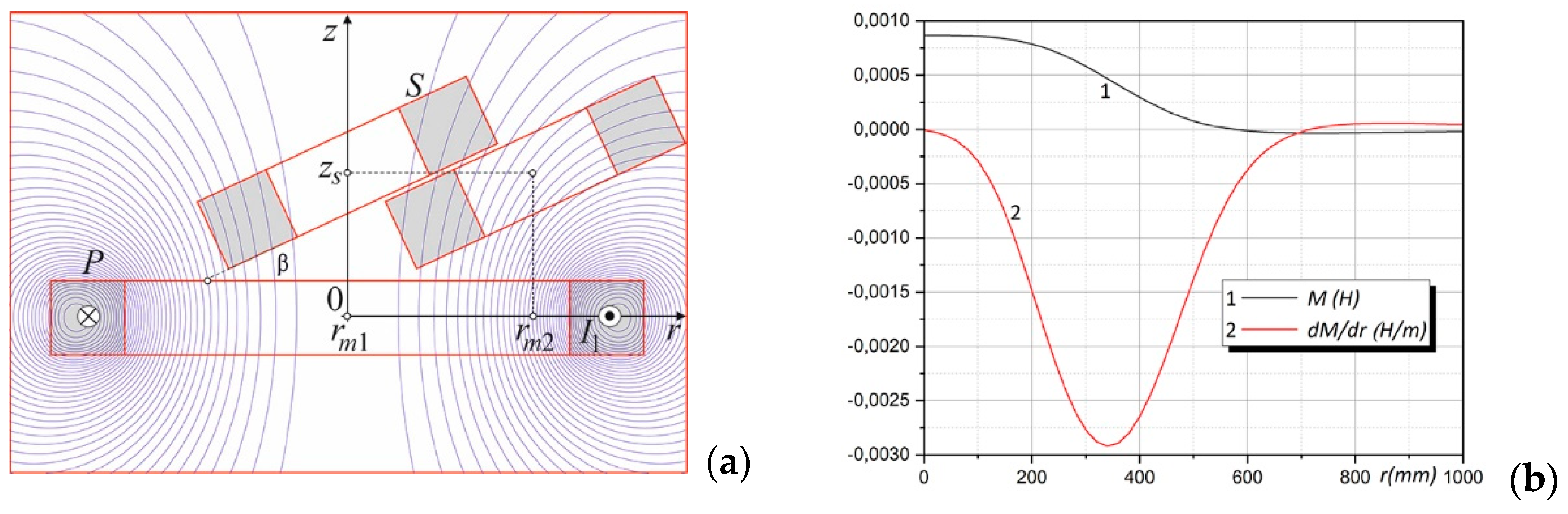
3.3. Non-coaxial cylindrical coils

In the case of non-coaxial cylindrical coils, or otherwise arbitrarily located in space, to determine the mutual inductance, the magnetic flux linking the secondary coil when powering the primary coil must be calculated. Figure 5 shows an arrangement of misaligned parallel cylindrical coils. The center of the secondary coil lies at the point with coordinates

(r_{m 1}, z_{s})

The magnetic field components generated by the primary coil on the surface defined by the elementary loop of the secondary coil (point G) can be determined from the relationship

B = rot A

B_{r} = - \frac{\partial A_{p}}{\partial z}; B_{z} = \frac{1}{r} \frac{\partial (r A_{p})}{\partial r} .

(15)

Using dependencies:

\frac{\partial K (u)}{\partial u} = \frac{E (u)}{u (1 - u^{2})} - \frac{K (u)}{u}; \frac{\partial E (u)}{\partial u} = \frac{E (u) - K (u)}{u},

(16)

these components can be expressed as:

B_{r} = \frac{μ_{0} I_{p d} z u}{4 π r \sqrt{r_{p} r}} [E (u) \frac{r_{p}^{2} + r^{2} + z^{2}}{{(r_{p} - r)}^{2} + z^{2}} - K (u)],

(17)

B_{z} = \frac{μ_{0} I_{p d} u}{4 π \sqrt{r_{p} r}} [E (u) \frac{r_{p}^{2} - r^{2} - z^{2}}{{(r_{p} - r)}^{2} + z^{2}} + K (u)] .

(18)

The magnetic flux penetrating the surface of the elementary loop of the secondary coil can be calculated as the surface integral of the induction vector perpendicular to this surface:

Φ_{s} = \int_{S} B_{z} d S .

(19)

The mutual inductance between both coils can finally be written as:

M = Φ_{s} / I_{p} .

(20)

The value of the total magnetic flux linking the secondary coil is calculated by determining the flux generated by each elementary loop of the primary coil in a single loop of the secondary coil. This procedure is repeated for all secondary coil loops and the results are averaged.

Formulas (19-20) can be used to calculate the mutual inductance for any position of the secondary coil relative to the primary coil. The method was verified by comparing the results obtained by other authors. For example, in article [12], the mutual inductance was calculated for coils with the following dimensions:

r_{1 p} = 7.1247 cm,

r_{2 p} = 8.5217 cm,

r_{1 s} = 9.69645 cm,

r_{2 s} = 13.84935 cm,

h_{p} = 7.1374 cm,

h_{s} = 1.2065 cm,

z_{s} = 7 . 366 cm,

r_{m 1} = 30 . 988 cm,

N_{p} = 1142,

N_{s} = 516

Article [12] gives a result of

M = - 1.422 560 384 213 514 mH

(page 79), and the method described here gives a result of

M = - 1.422 5607 mH

. The same example was solved in [19], but the result given there

M = - 1 . 422 583 607 μ H

(page 95) is incorrect due to wrong units (

μ H

instead of

mH

). The self-inductances of both coils (not calculated in above papers) are equal to

L_{p} = 0 . 141 662 41 H

and

L_{s} = 0.086 260 334 H

, respectively.

The method shown here allows for easy calculation of mutual inductance values for any secondary coil movement trajectory. The beginning of the trajectory is marked by the point with coordinates

(r_{m 1}, z_{s})

, and its end by the point with coordinates

(r_{m 2}, z_{m})

(see Figure 5).

In [10] (page 1027, Table II), the mutual inductances of two identical coplanar current loops of radius 1 m lying on top of each other, for the secondary coil moving in the r-direction were calculated. In this case, there is no need to discretize the coil area – the considerations are then carried out automatically for the current loops. Calculations were performed (according to [10]) for the following data:

r_{2 p} = 1 m,

r_{1 p} \to r_{2 p},

r_{2 s} = 1 m,

r_{1 s} \to r_{2 s},

h_{p}, h_{s} \to 0,

z_{s}, z_{m} \to 0,

r_{m 1} = 0 m,

r_{m 2} = 20 m,

N_{p} = 1,

N_{s} = 1

. Using the method presented here, the same values were obtained with an accuracy of 7-9 significant places and these results will not be presented. Instead, the results of mutual inductance calculations are shown when the secondary coil moves obliquely from the point with coordinates

(r_{m 1} = 0 m, z_{s} = 0.002 m)

to the point C with coordinates

(r_{m 2} = \sqrt{3} m, z_{m} = 1.002 m)

, to the point D with coordinates

(r_{m 2} = 1 m, z_{m} = (\sqrt{3} + 0.002) m)

and axially to the point E with coordinates

(r_{m 2} = 0 m, z_{m} = 2.002 m)

. In each of these cases, the offset was defined so that the final distance from the center of the secondary coil to the center of the primary coil was the same (2 m). Figure 6a shows final positions of the secondary coil (points C, D and E). The proposed method gives the same results by moving the secondary coil axially as the method discussed in Section 3.2 (point E). The results for point D lie between the curves for points C and E and are not shown here. Figure 6b gives the values of the mutual inductance of the coils as a function of displacement in generalized coordinates (depending on the direction of movement). This figure also shows the derivative of the mutual inductance in the movement direction, which will be used to calculate the forces between both coils (see Section 6). The mutual inductance of the coils decreases significantly when the secondary coil is moved by a distance greater than the radius of the primary coil, and then becomes negative due to the change in the direction of the magnetic flux in the secondary coil.

The above method can also be used to calculate the mutual inductance of coils arranged arbitrarily in space. Figure 7a shows a system of two such cylindrical coils – the surface of the secondary coil can be inclined to the surface of the primary coil in any way. The center of the secondary coil lies at the point with coordinates

(r_{m 1}, z_{s})

, and its plane is shifted by angle

α

in relation to the r-axis. Figure 7b illustrates the system of two elementary current loops of the primary and secondary coils and shows how to calculate the magnetic flux in the secondary coil loop generated by the primary coil loop. To determine this flux, the normal components of the induction vector on the surface of the secondary coil loop must be calculated and integrated over this surface.

Using this algorithm, the mutual inductance of cylindrical coils can be easily determined for the secondary coil placed in any position, which allows for the determination of characteristics like those shown in Figure 6b. Figure 8a shows an arrangement of coils lying diagonally to each other. The final position of the secondary coil is also marked here. Calculations were made for coils with dimensions from Section 3.2. The inclination angle was

β = 15 \deg,

the coordinates of the starting point were

(r_{m 1} = 0 m, z_{s} = 0, 2 m)

and the end point coordinates were

(r_{m 2} = 1 m, z_{s} = 0, 2 m)

. Since the distance between the centers of the coils in the analyzed case is small, it was possible to take into account only a small angle

β

due to the possibility of contact between both coils for its larger values. The results are shown in Figure 8b.

For the oblique relative position of the coils, the mutual inductances are slightly larger for small displacements than in the case of parallel arrangement, then they decrease significantly and for larger displacements they become negative values due to the change in the direction of the magnetic flux in the secondary coil.

As has already been said, the efficiency and accuracy of the algorithm depend greatly on the accuracy of the discretization of the primary and secondary coil regions. They also depend strongly on the discretization of the elementary surfaces of the secondary coil current loops (the number of points at which the values of the magnetic field components and the flux orthogonal to this surface are calculated). These are typical problems of all numerical calculations in which numerical integration is performed.

Using formulas (17) and (18), it is also possible to determine the distribution of magnetic field generated by systems of any number of cylindrical coils arranged arbitrarily in space (see Section 5).

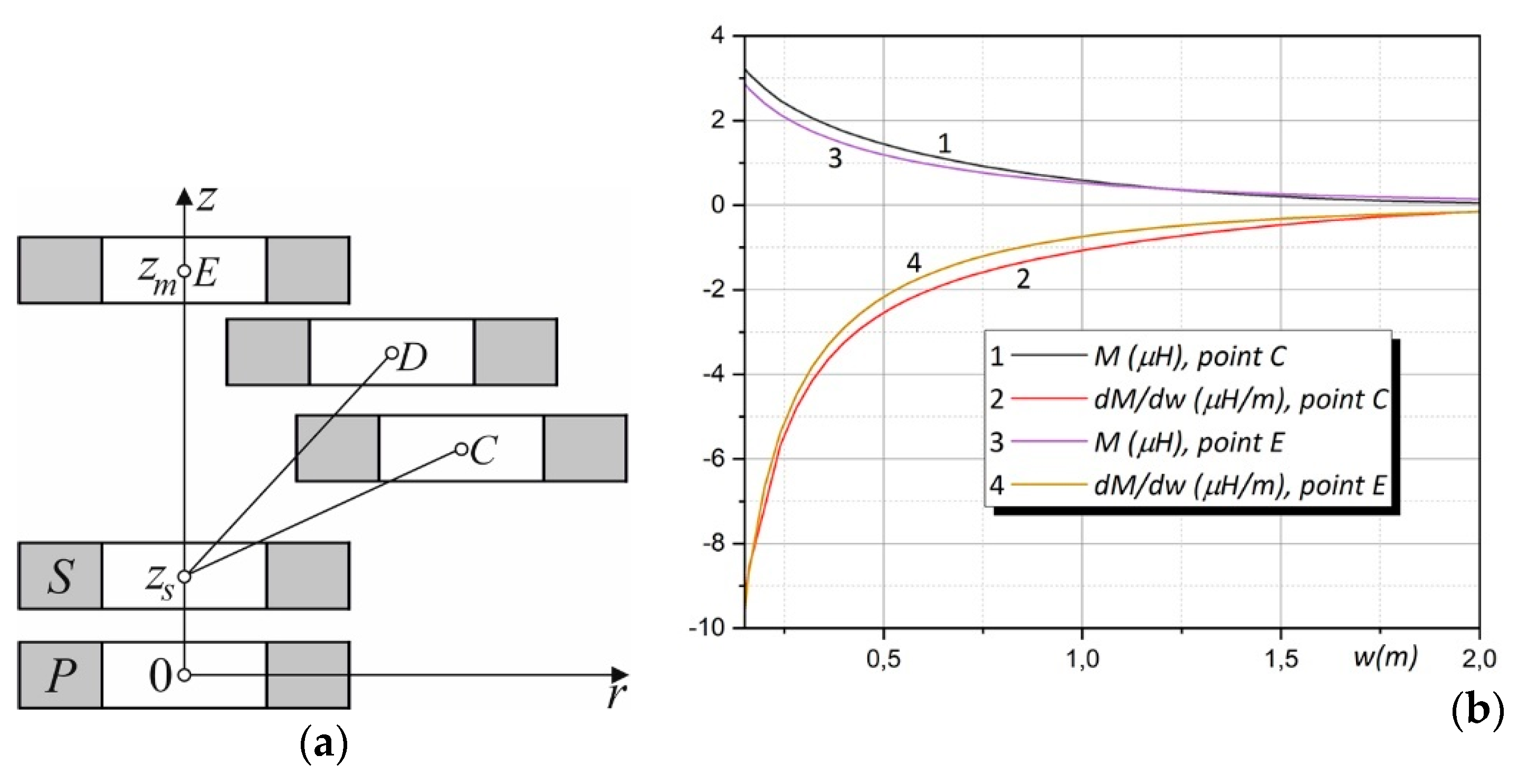
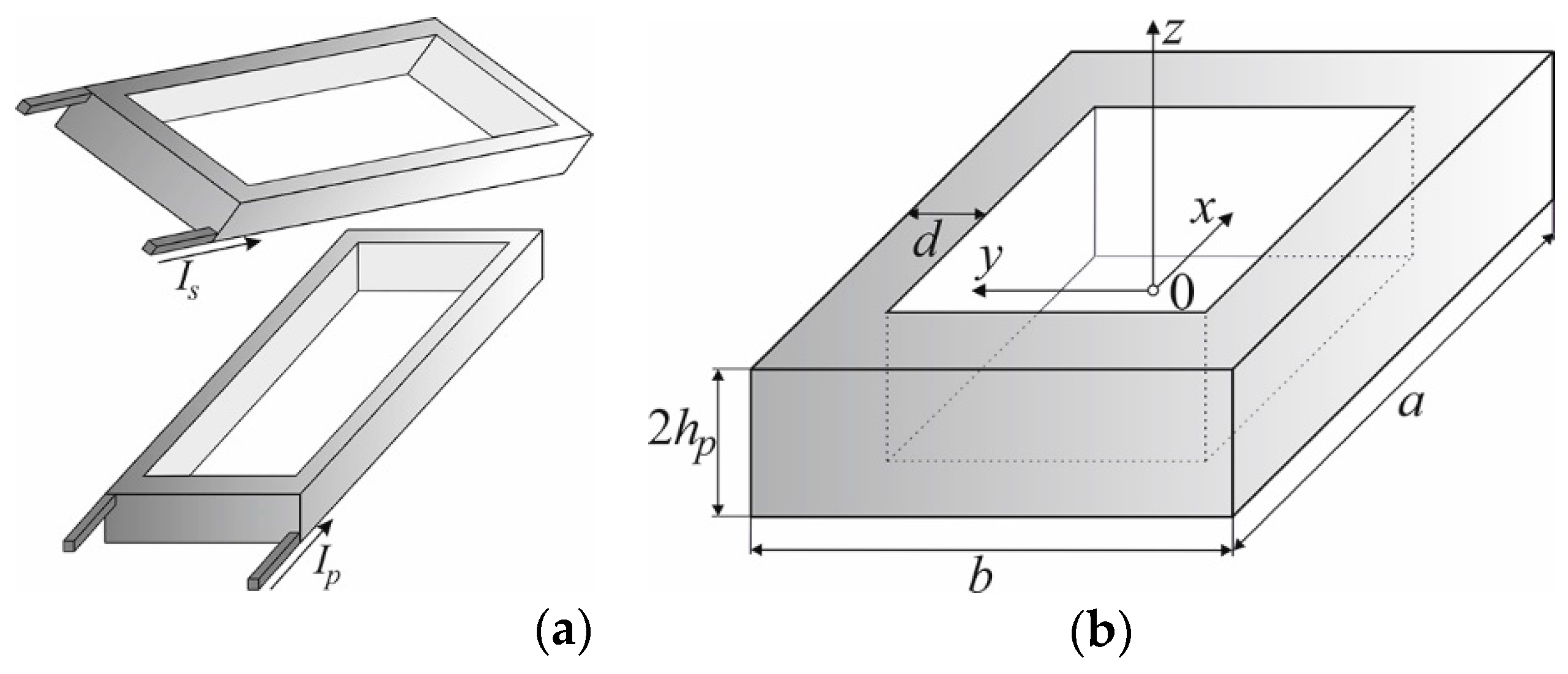
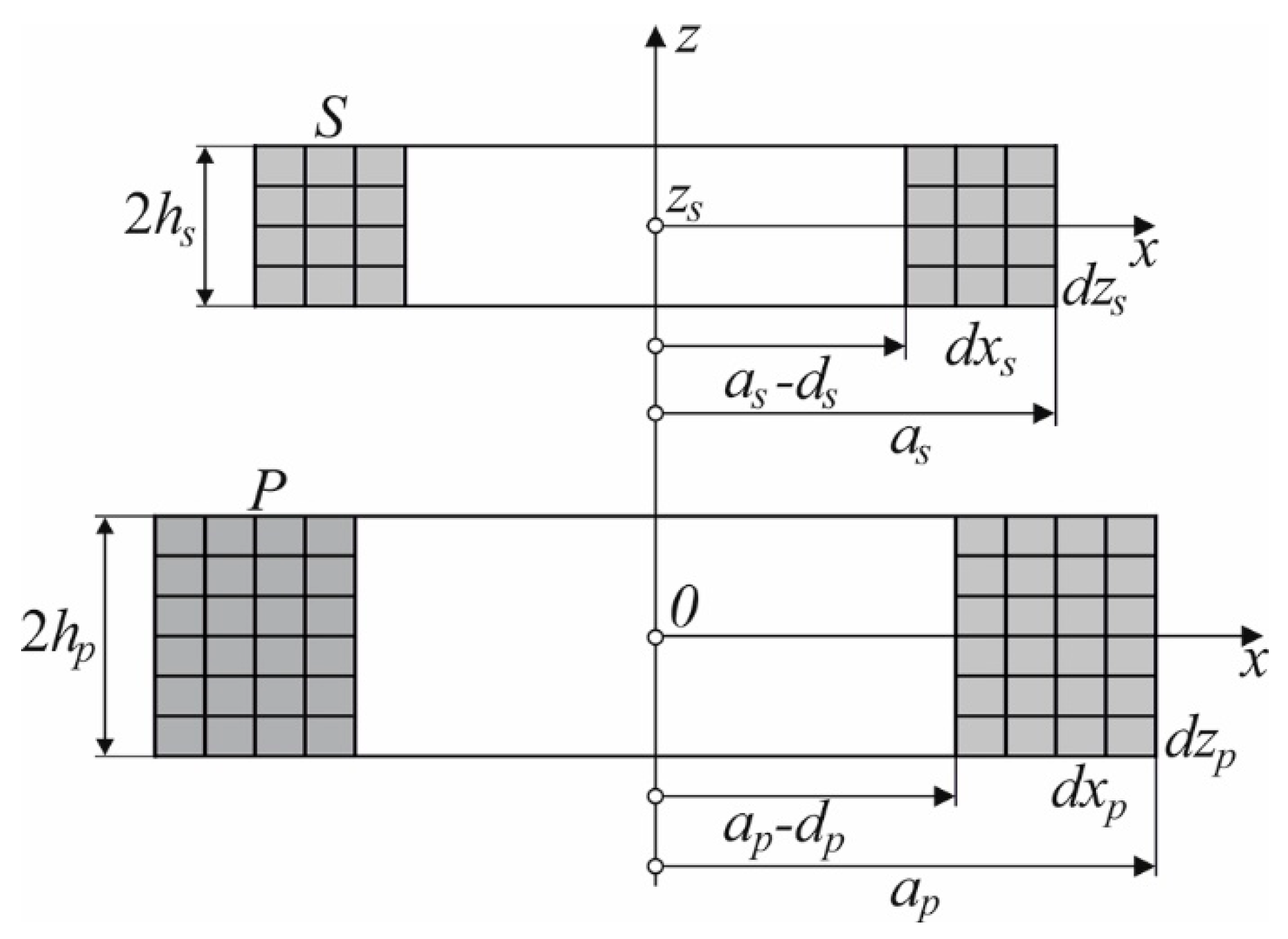
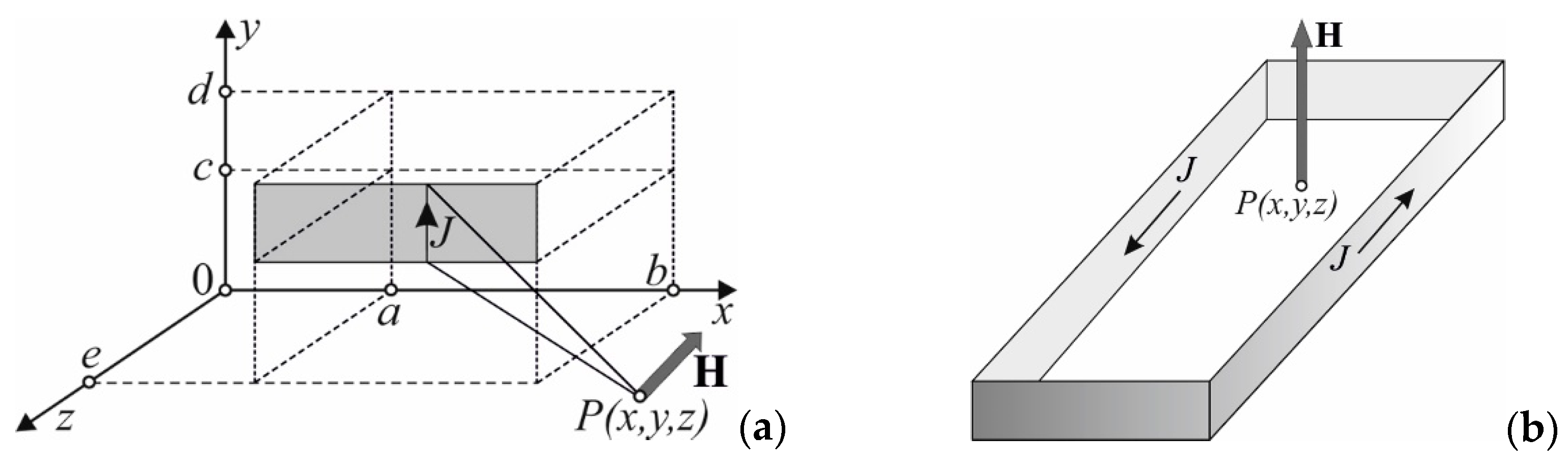
4. Rectangular air coils

This section deals with the calculation of self- and mutual inductances of rectangular coils in any mutual position, as well as the distribution of magnetic fields of such coil systems. Figure 9a shows a system of rectangular coils, in which the secondary coil is in any position in relation to the primary coil. Figure 9b gives the dimensions of the primary coil.

The use of formulas (5-8) to calculate self- and mutual inductances in this case is impossible and the magnetic flux linkage method described in section 3.4 was used for calculations. Figure 9b and Figure 10 illustrate the dimensions and discretization of both coils. The center of the primary coil is located in the center of the coordinate system and the center of the initial position of the secondary coil for coaxial coils is located at

(0, z_{s})

To calculate the magnetic field of elementary current loops created by discretization of the primary coil from Figure 10, the Biot-Savart formula defining the magnetic field of an infinitely thin conductor of finite length carrying a current of density

J

was used (Figure 11a). This made it possible (by integrating the Biot-Savart formula) to determine the values of the magnetic field intensity at any point in space

P (x, y, z)

generated by an infinitely thin band conductor.

The components of the magnetic field

H_{z}

and

H_{x}

at point

P (x, y, z)

are written as follows:

H_{z} = \frac{J}{4 π} [\ln \frac{y - d + \sqrt{{(x - b)}^{2} + {(y - d)}^{2} + {(z - e)}^{2}}}{y - c + \sqrt{{(x - b)}^{2} + {(y - c)}^{2} + {(z - e)}^{2}}} + \ln \frac{y - d + \sqrt{{(x - a)}^{2} + {(y - d)}^{2} + {(z - e)}^{2}}}{y - c + \sqrt{{(x - a)}^{2} + {(y - c)}^{2} + {(z - e)}^{2}}}],

(21)

\begin{matrix} H_{x} = \frac{J}{4 π} [\arctan \frac{(x - b) (y - d)}{(z - e) \sqrt{{(x - b)}^{2} + {(y - d)}^{2} + {(z - e)}^{2}}} + \\ - \arctan \frac{(x - b) (y - c)}{(z - e) \sqrt{{(x - b)}^{2} + {(y - c)}^{2} + {(z - e)}^{2}}} + \\ - \arctan \frac{(x - a) (y - d)}{(z - e) \sqrt{{(x - a)}^{2} + {(y - d)}^{2} + {(z - e)}^{2}}} + \\ + \arctan \frac{(x - a) (y - c)}{(z - e) \sqrt{{(x - a)}^{2} + {(y - c)}^{2} + {(z - e)}^{2}}}] \end{matrix}

(22)

By changing the variables

(x, y, z)

appropriately, the above equations make it possible to calculate the components of the magnetic field of any surface with the current parallel to a coordinate surface, and finally, the magnetic field of the infinitely thin rectangular current loop from Figure 11b. Thus, the primary coil can be approximated by infinitely thin rectangular band coils or, as in the case of cylindrical coils, by thin rectangular current loops whose geometry and position are determined by the centers of gravity of the discretization elements. The magnetic flux penetrating the surface of the elementary loop of the secondary coil can be calculated as the integral according to Eq. (19) for the normal component of the induction vector. This procedure is repeated for all secondary coil loops and the results are averaged. The mutual inductance between both coils can finally be calculated as in Eq. (20). Similar methods, using the magnetic flux linking other rectangular coils were used, among others, in [23,24].

The method presented in the previous Section was used to calculate self- and mutual inductances for rectangular coils in any of their mutual positions. Formulas (21) and (22) were used to calculate the magnetic flux linking the secondary coil.

The effectiveness of the method was illustrated by calculations of self and mutual inductances of two coaxial rectangular coils with identical cross-section dimensions as in Section 3.2 (Figure 3a). The dimensions of the coils were as follows:

a_{p} = b_{p} = 0, 3 m,

a_{s} = b_{s} = 0, 1 m,

d_{s} = 0, 1 m,

h_{p} = 0, 05 m,

h_{s} = 0, 05 m,

N_{p} = 100,

N_{s} = 100.

The center of the primary coil was located in the center of the coordinate system and the center of the secondary coil was located in the initial position at

(x_{s}, z_{s})

. The coordinates of the starting point for the secondary coil were

x_{s} = 0 m, z_{s} = 0, 2 m

and the end point coordinates were

x_{s} = 1 m, z_{s} = 0, 2 m

. Calculations were made for two cases: for parallel coils and for coils arranged obliquely to each other as in Figure 8a for cylindrical coils (the inclination angle

β = 15 \deg

). The self-inductances of both coils are equal to

L_{p} = 11.477932 mH

and

L_{s} = 3.1543544 mH

, respectively. These inductances are slightly larger than the inductances of cylindrical coils with the same cross-section because cylindrical coils obviously have a smaller surface area. The results of the mutual inductance calculations are shown in Figure 12.

As can be seen from Figure 12, the relationship between mutual inductances and displacement for parallel and oblique coils is very similar. Mutual inductances for an oblique coil have slightly higher values for displacements in the range of 180 mm-650 mm than for parallel coils. The derivative of mutual inductance has a strongly exposed maximum (for a displacement of approx. 330 mm-420 mm), which means that for these displacements the forces acting on the coils are significantly increased (see Section 6).

The described method also gives very accurate results when calculating self- and mutual inductances, as well as field distributions for spiral coils, helical coils, very thin coils [24,27], and coils with nonuniform current density distributions [20]. This requires the proper selection of discretization parameters of the coil areas and the magnetic flux integration areas, as well as the selection of equivalent radii when modeling spiral or Archimedean coils [28,29], e.g.

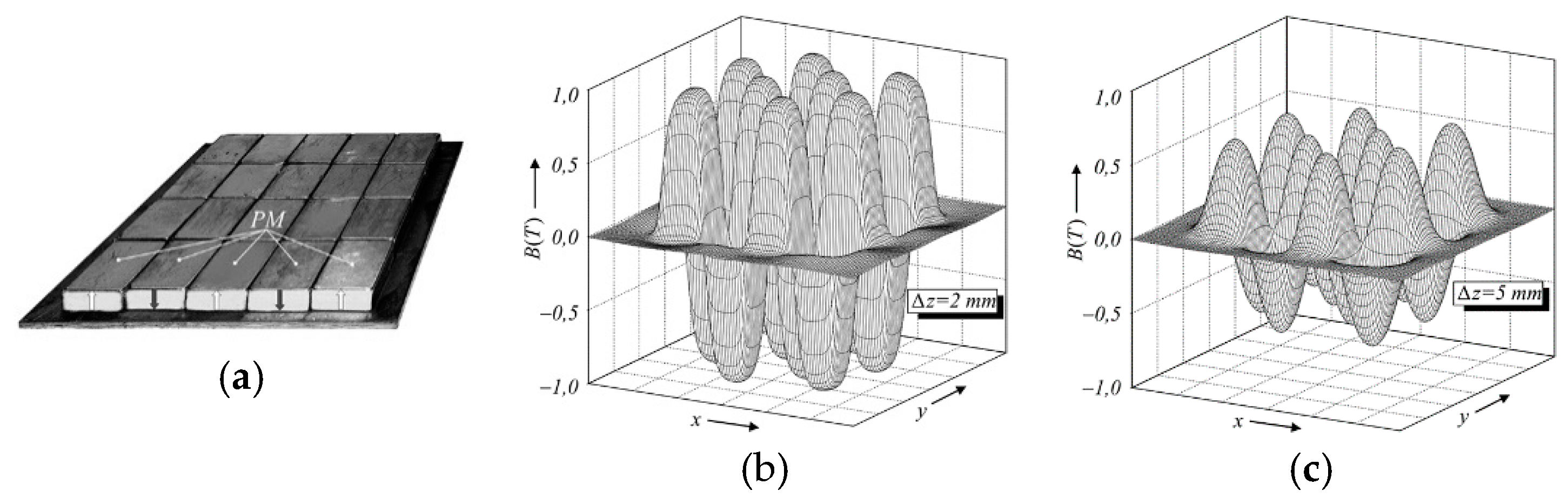
5. Magnetic field of current coils, permanent magnets and high temperature superconductors

Using formulas (17), (18), (21) and (22), it is also possible to determine the distribution of magnetic field generated by systems of any number of cylindrical or rectangular coils arranged arbitrarily in space. Figure 13 shows, for example, the distribution of the magnetic field (normal component of the magnetic induction vector) over a circular and a rectangular coil depending on the thickness of the electrically conductive area.

The field distributions in Figure 13 are identical to the field distributions of high-temperature bulk superconductors in various saturation states (also in the Meissner state) [21,30,31], as well as the fields of permanent magnets (Figure 13 (a) and (b)) – the computational model in Figure 11b corresponds directly to the computational model of a permanent magnet. The results shown in Figure 13 are very important in the design of various actuators, levitating systems, as well as in the generation of forces in electric machines with permanent magnets. From them it can be concluded that fully saturated configurations (Figure 13 (e) and (f)) are worse for the generation of large forces due to the shape of the magnetic field having one maximum. Distributions from Figure 13 (a) and (b) are much more favorable due to the large gradient of the field distribution and its large values in the entire range [30].

The described method was also used, for example, to calculate the magnetic field of a system of coils or permanent magnets. Figure 14 shows the magnetic field above the permanent magnet configuration used in superconducting levitation systems without degrees of freedom [31].

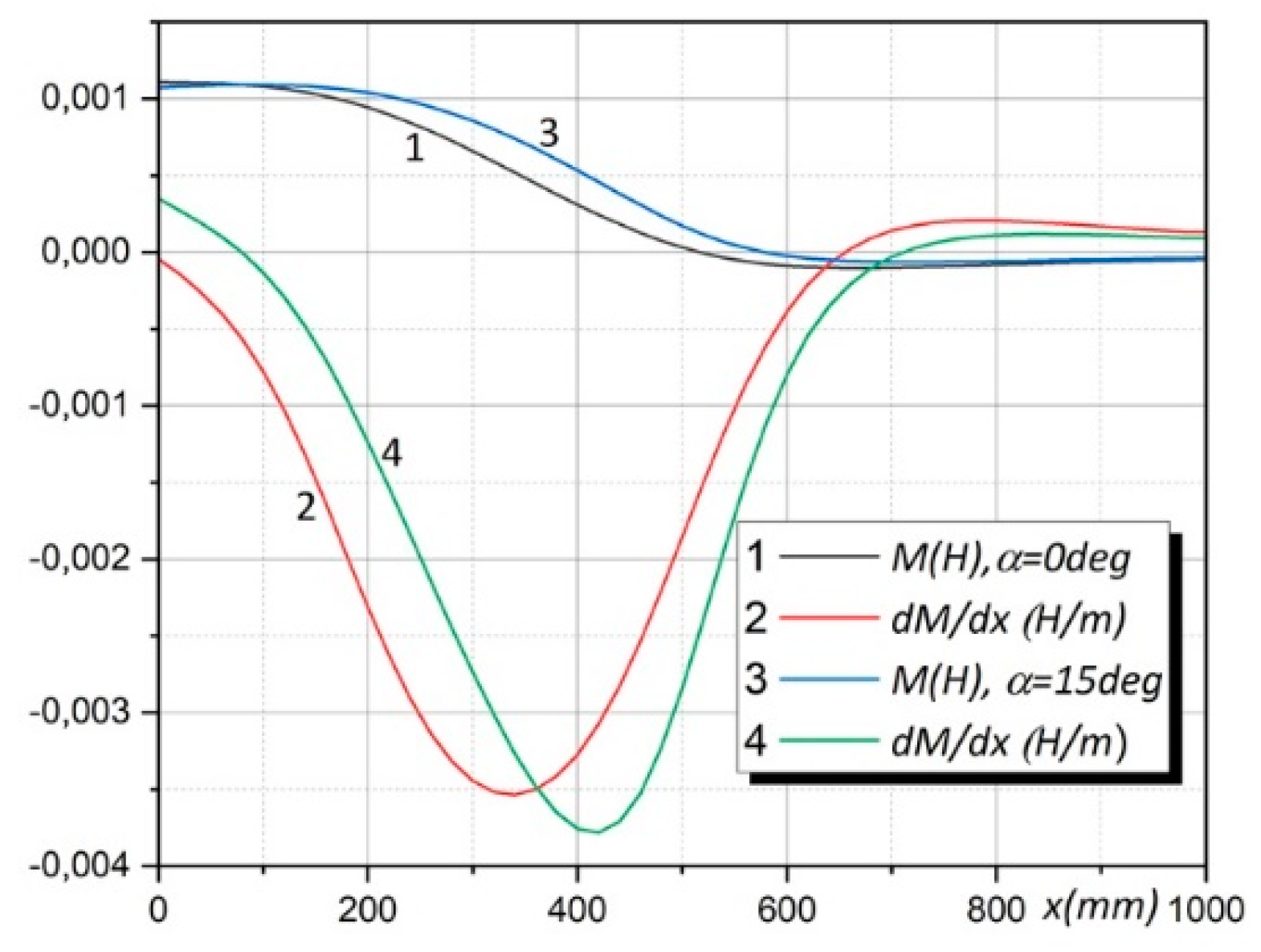
6. Moving coils: induced voltages and forces

Knowledge of the self- and mutual inductance values makes it possible to calculate the forces acting on the secondary coil and define equations of its motion. Figure 15 shows a linear accelerator system with three primary coils arranged along the x-axis (in the Cartesian coordinate system). The resistances of the coils have the values

R_{p}

and

R_{s}

, the voltages at their terminals are

u_{p}

and

u_{s}

, and the currents are

i_{p}

and

i_{s}

respectively. The secondary coil is short-circuited and moves in x-direction due to the forces coming from the primary coils powered by an external voltage source.

The voltage equation (for constant self-inductance values of both coils) for the first primary coil can be written as follows [32]:

u_{p} = R_{p} i_{p} + L_{p} \frac{{d i}_{p}}{d t} + M \frac{{d i}_{s}}{d t} + i_{s} \frac{\partial M}{\partial x} \frac{d x}{d t} .

(23)

The voltage equations for the subsequent primary coils are identical to that for the first coil. For the secondary coil we have:

u_{s} = R_{s} i_{s} + L_{s} \frac{{d i}_{s}}{d t} + M \frac{{d i}_{p}}{d t} + i_{p} \frac{\partial M}{\partial x} \frac{d x}{d t} .

(24)

Due to the constant self-inductance value, the force

F_{x}

caused by the primary coil interacting with the secondary coil can be calculated as the derivative of magnetic energy with respect to displacement [15,17,32]:

F_{x} = - \frac{\partial M}{\partial x} i_{p} i_{s} .

(25)

From Equation (25) it can be concluded that the switching of subsequent accelerator coils should take place during large changes in the mutual inductance of the coils. By appropriately turning on and off the voltage in subsequent primary coils, a sufficiently high thrust force can be achieved in the entire system. The dynamics of the secondary coil motion can be easily described by solving a system of differential equations (23-25). This coil system can also be analyzed from the point of view of powering a vehicle moving above the primary coil system.

Modeling of magnetic field distributions leading to desired distributions, and thus ultimately ensuring appropriate values of self and mutual inductances, was dealt with, among others, in articles [32,33,34].

7. Conclusions

The energy calculation method and the magnetic flux linkage method have proven to be extremely effective in calculating the self and mutual inductances of various air coil configurations, both cylindrical and rectangular. Simplifying the computational algorithm by replacing very complicated analytical calculations with numerical integration made it possible to obtain a numerical algorithm with very high speed and accuracy. The proposed algorithm has become therefore a very practical tool enabling the calculation of the inductances and magnetic field distributions of any air coil configurations. By appropriate mirror reflections it is also possible to take into account the position of the coils above a semi-infinite ferromagnetic plate or between two such plates, which greatly expands the scope of the proposed method.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

Triviño, A.; González, J.M.; Aguado, J.A. Wireless Power Transfer Technologies Applied to Electric Vehicles: A Review. Energies 2021, 14, 1547. [Google Scholar] [CrossRef]
Razu, M.R.R.; et al. Wireless Charging of Electric Vehicle While Driving. IEEE Access 2021. [Google Scholar] [CrossRef]
Carvalho, N.B.; et al. Wireless Power Transmission: R&D Activities Within Europe. IEEE Transactions on Microwave Theory and Techniques 2014, 62(4), 1031–1043. [Google Scholar] [CrossRef]
Schormans, M.; Valente, V.; Demosthenous, A. Practical Inductive Link Design for Biomedical Wireless Power Transfer: A Tutorial. IEEE Transactions on Biomedical Circuits and Systems 2018, 12, 1112–1130. [Google Scholar] [CrossRef]
Wardach, M.; et al. Hybrid Excited Synchronous Machine with Wireless Supply Control System. Energies 2019, 12, 3153. [Google Scholar] [CrossRef]
Kalisiak, S.; et al. Contactless power supply system with resonant circuit parameter change compensation. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, United Kingdom, 30 August – 01 September 2011. [Google Scholar]
Marcinek, M.; et al. Resonant frequency stabilization technique in series-series contactless energy transfer systems. Archives of Electrical Engineering 2017, 66(3), 547–558. [Google Scholar] [CrossRef]
Panchal, C.; Stegen, S.; Lu, J. Review of static and dynamic wireless electric vehicle charging system. Engineering Science and Technology, an International Journal 2018, 21, 922–937. [Google Scholar] [CrossRef]
Grover, F.W. The Calculation of the Mutual Inductance of Circular Filaments in Any Desired Positions. Proceedings of the I.R.E. October 1944, 620–629. [Google Scholar] [CrossRef]
Conway, J.T. Inductance Calculations for Noncoaxial Coils Using Bessel Functions. IEEE Trans. Magn. 2007, 43, 1023–1034. [Google Scholar] [CrossRef]
Conway, J.T. Noncoaxial Inductance Calculations Without the Vector Potential for Axisymmetric Coils and Planar Coils. IEEE Trans. Magn. 2008, 44, 453–462. [Google Scholar] [CrossRef]
Conway, J.T. Inductance Calculations for Circular Coils of Rectangular Cross Section and Parallel Axes Using Bessel and Struve Functions. IEEE Trans. Magn. 2010, 46, 75–81. [Google Scholar] [CrossRef]
Babic, S.; Salon, S.; Akyel, C. The Mutual Inductance of Two Thin Coaxial Disk Coils in Air. IEEE Trans. Magn. 2004, 40, 822–825. [Google Scholar] [CrossRef]
Babic, S.; Akyel, C. New analytic-numerical solutions for the mutual inductance of two coaxial circular coils with rectangular cross section in air. IEEE Trans. Magn. 2006, 42, 1661–1669. [Google Scholar] [CrossRef]
Babic, S.; Akyel, C. Magnetic Force Calculation Between Thin Coaxial Circular Coils in Air. IEEE Trans. Magn. 2008, 44, 445–452. [Google Scholar] [CrossRef]
Babic, S.; et al. Mutual Inductance Calculation Between Circular Filaments Arbitrarily Positioned in Space: Alternative to Grover’s Formula. IEEE Trans. Magn. 2010, 46, 3591–3600. [Google Scholar] [CrossRef]
Babic, S.; et al. New Formulas for Mutual Inductance and Axial Magnetic Force Between a Thin Wall Solenoid and a Thick Circular Coil of Rectangular Cross-Section. IEEE Trans. Magn. 2011, 47, 2034–2044. [Google Scholar] [CrossRef]
Babic, S.; Akyel, C. New Formulas for Mutual Inductance and Axial Magnetic Force Between Magnetically Coupled Coils: Thick Circular Coil of the Rectangular Cross-Section-Thin Disk Coil (Pancake). IEEE Trans. Magn. 2013, 49, 860–868. [Google Scholar] [CrossRef]
Babic, S.; et al. Mutual Inductance Calculation between Misalignment Coils for Wireless Power Transfer of Energy. Progress In Electromagnetics Research M. 2014, 38, 91–102. [Google Scholar] [CrossRef]
Babic, S.; et al. The Analytical Formula for Calculating the Self-Inductance for the Circular Coil of the Rectangular Cross-Section with a Nonuniform Current Density. Progress In Electromagnetics Research M. 2021, 103, 15–23. [Google Scholar] [CrossRef]
Župan, T.; Štih, Ž.; Trkulja, B. Fast and Precise Method for Inductance Calculation of Coaxial Circular Coils with Rectangular Cross Section Using the One-Dimensional Integration of Elementary Functions Applicable to Superconducting Magnets. IEEE Transactions on Applied Superconductivity 2014, 24, 4901309. [Google Scholar] [CrossRef]
Zhang, X.; Meng, H.; Wie, B.; Wang, S.; Yang, Q. Mutual inductance calculation for coils with misalignment in wireless power transfer. J. Eng. 2019, 16, 1041–1044. [Google Scholar] [CrossRef]
Alkasir, A. Analytical Modeling of Self- and Mutual Inductances of DD Coils in Wireless Power Transfer Applications. Journal of Electromagnetic Engineering and Science 2022, 22, 162–170. [Google Scholar] [CrossRef]
Cheng, Y.; Shu, Y. A New Analytical Calculation of the Mutual Inductance of the Coaxial Spiral Rectangular Coils. IEEE Trans. Magn. 2014, 50, 7026806. [Google Scholar] [CrossRef]
Ollendorff, F. Berechnung magnetischer Felder; Softcover reprint of the original 1st ed. 1952; Springer: Vienna, Austria, 2012; ISBN 9783709130254. [Google Scholar]
Abramowitz, M.; Stegun, I. A. Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables. Dover Books on Mathematics, 0009-Revised Edition, June 1, 1965. ISBN-13 978-0486612720.
Mohan, S.S.; et al. Simple accurate expressions for planar spiral inductances. IEEE J. Solid-State Circuits 1999, 34, 1419–1424. [Google Scholar] [CrossRef]
Hussain, I.; Woo, D.-K. Self-Inductance Calculation of the Archimedean Spiral Coil. Energies 2022, 15, 253. [Google Scholar] [CrossRef]
Aditya, K. Analytical design of Archimedean spiral coils used in inductive power transfer for electric vehicles application. Electrical Engineering 2018. [Google Scholar] [CrossRef]
May, H.; et al. Evaluation of the magnetic field – high temperature superconductor interactions. COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering 2004, 23, 286–304. [Google Scholar] [CrossRef]
Patel, A.; et al. The Use of an MgB₂ Hollow Cylinder and Pulse Magnetized (RE)BCO Bulk for Magnetic Levitation Applications. IEEE Transactions on Applied Superconductivity 2013, 23, 3. [Google Scholar] [CrossRef]
Palka, R. Synthesis of Application-Optimized Air Gap Field Distributions in Synchronous Machines. Energies 2022, 15, 2322. [Google Scholar] [CrossRef]
Sikora, R.; Palka, R. Synthesis of Magnetic-Fields. IEEE Trans. Magn. 1982, 18, 385–390. [Google Scholar] [CrossRef]
Palka, R. Synthesis of magnetic fields by optimization of the shape of areas and source distributions. Electr. Eng. 1991, 75, 1–7. [Google Scholar] [CrossRef]

Figure 1. Two coaxial cylindrical coils: General view (a); Dimensions and discretization of the primary and secondary coil (b).

Figure 2. Two infinitesimally thin coaxial current loops.

Figure 3. Magnetic field of two coaxial cylindrical coils. Both coils powered (a); Only primary coil powered (b); Only secondary coil powered (c).

Figure 4. Mutual inductance of two-coaxial cylindrical coils and its derivative as a function of z-displacement.

Figure 5. Non-coaxial cylindrical coils: General view (a); Model for calculating the magnetic flux linking the secondary coil (b).

Figure 6. The initial position of the secondary coil and its three final positions (a); Mutual inductance and its derivative of non-coaxial cylindrical coils as a function of displacement in generalized coordinates (b).

Figure 7. Cylindrical coils in any mutual position: General view (a); Model for the magnetic flux linkage calculations (b).

Figure 8. Cylindrical coils in any mutual position (two positions of the secondary coil are marked) (a); Mutual inductance and its derivative as a function of displacement in r-direction (b).

Figure 9. Two rectangular coils in any position (a); Dimensions of the primary coil (b).

Figure 10. Dimensions and discretization of the rectangular primary and secondary coils.

Figure 11. Computational model of an infinitely thin band conductor with the current sheet J (a); The elementary rectangular current loop of the primary coil from Figure 10 generating a magnetic field of value H at a point P(x,y,z) (b).

Figure 12. Mutual inductance of rectangular coils and its derivative as a function of x-displacement for parallel and inclined coils.

Figure 13. Distribution of the normal component of the magnetic induction vector (normalized values) over a circular and a rectangular coil. For current sheet (a) and (b); For coils of finite thickness (c) and (d); For coils carrying electric current throughout the entire volume (e) and (f).

Figure 14. System of permanent magnets exciting a magnetic field in a superconducting levitation system without degrees of freedom (a); Normal component of the magnetic induction vector at a distance of 2 mm from the surface of the magnets (b); at a distance of 5 mm (c).

Figure 15. A linear actuator system consisting of three primary coils and one secondary coil moving at speed v due to forces acting between the coils.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Fast Analytic‐Numerical Algorithms for Calculating Self and Mutual Inductances of Air Coils

Abstract

1. Introduction

2. Principles for calculating the self- and mutual inductances of air coils

2.1. Basics of magnetic field theory used for inductance calculations

3. Cylindrical air coils

3.1. Magnetic field of cylindrical coils

3.2. Comparison with results obtained by other authors and the finite element method

3.3. Non-coaxial cylindrical coils

4. Rectangular air coils

5. Magnetic field of current coils, permanent magnets and high temperature superconductors

6. Moving coils: induced voltages and forces

7. Conclusions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe