Probability of Ship Collision during the Fully Submerged Towing Process of Floating Offshore Wind Turbines

1. Introduction

As energy consumption continues to rise, conventional non-renewable energy resources are increasingly depleted[1]. The global climate crisis is accelerating, posing threats to human health and safety[2]. The overuse of fossil fuels is a major contributor to the crisis[3]. Efficient utilization of renewable clean energy and reduction of greenhouse gas emissions are the keys to achieving low-carbon sustainable development and addressing global challenges[4]. Wind power technology, with its minimal space requirements, low costs, high energy capture efficiency, and mature technical development, has become a global focus for new energy technology development[5]. However, due to limitations in land area and the completion of nearshore development, focusing on deepwater Floating Offshore Wind Turbines(FOWTs) has become the consensus in the industrial and scientific research communities[6]. Major industrialized countries around the world are actively developing offshore wind power, with the global installed capacity of offshore wind power setting new records repeatedly[7].

Currently, extensive research on FOWTs has been conducted by numerous scholars, yielding distinguished outcomes. As Table 1 shows, these studies not only encompass the responses of wind, wave, and current loads on the mooring system, floating foundations, tower, and blades of FOWTs of various sizes, but also includes reliability analyses of the internal gearbox and electrical systems, providing ample research materials and data for industrial practice. However, these studies predominantly focus on the operational phase of FOWTs, with only a few scholars[8,9] investigating the external risks encountered during the transportation of FOWTs to the designated site.

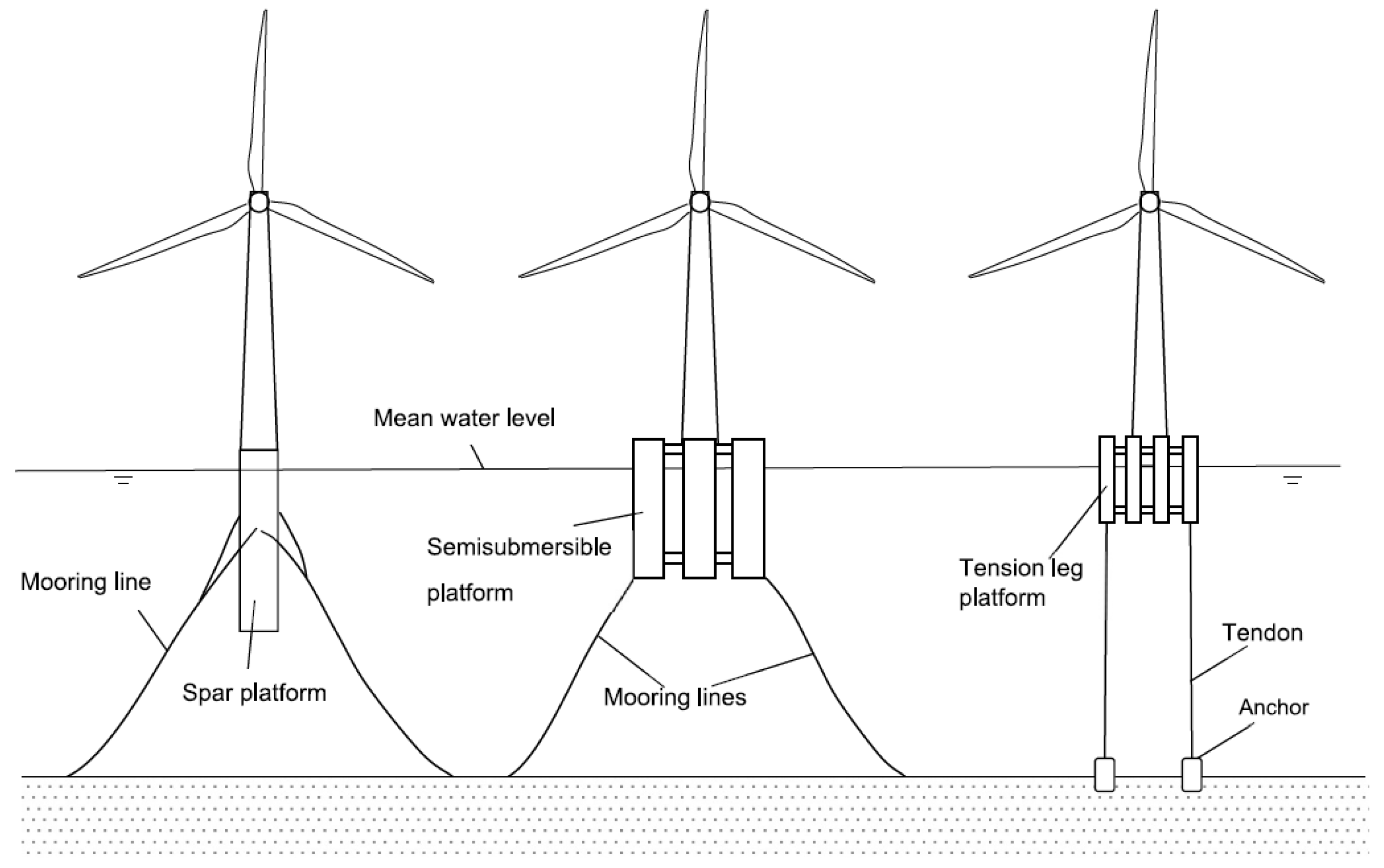
However, relevant studies on the subject do exist and can be referenced. To investigate the potential risks associated with the transportation process of Floating Offshore Wind Turbines (FOWTs), it is essential to have a comprehensive understanding of the types of FOWTs and the transportation processes involved. 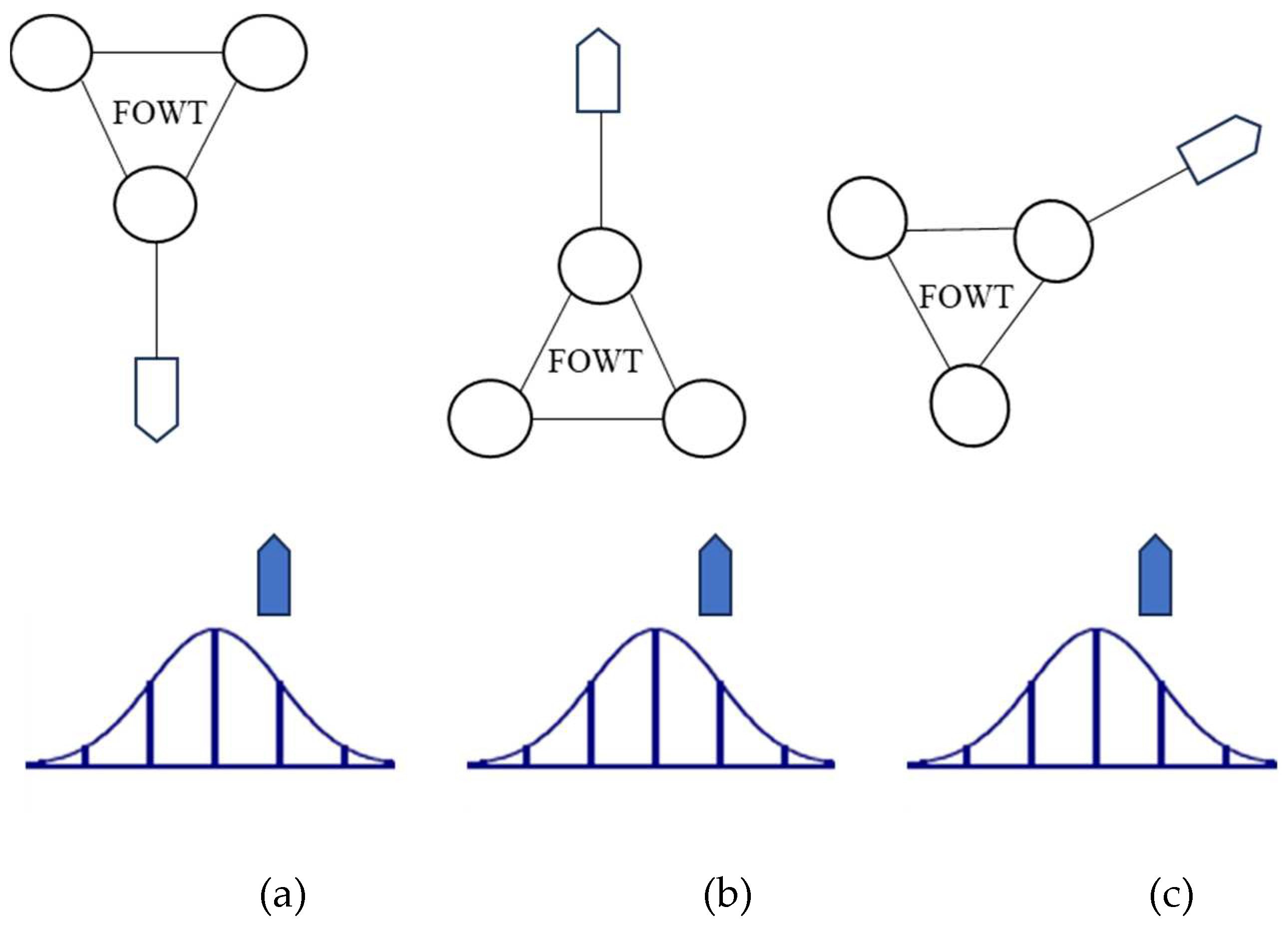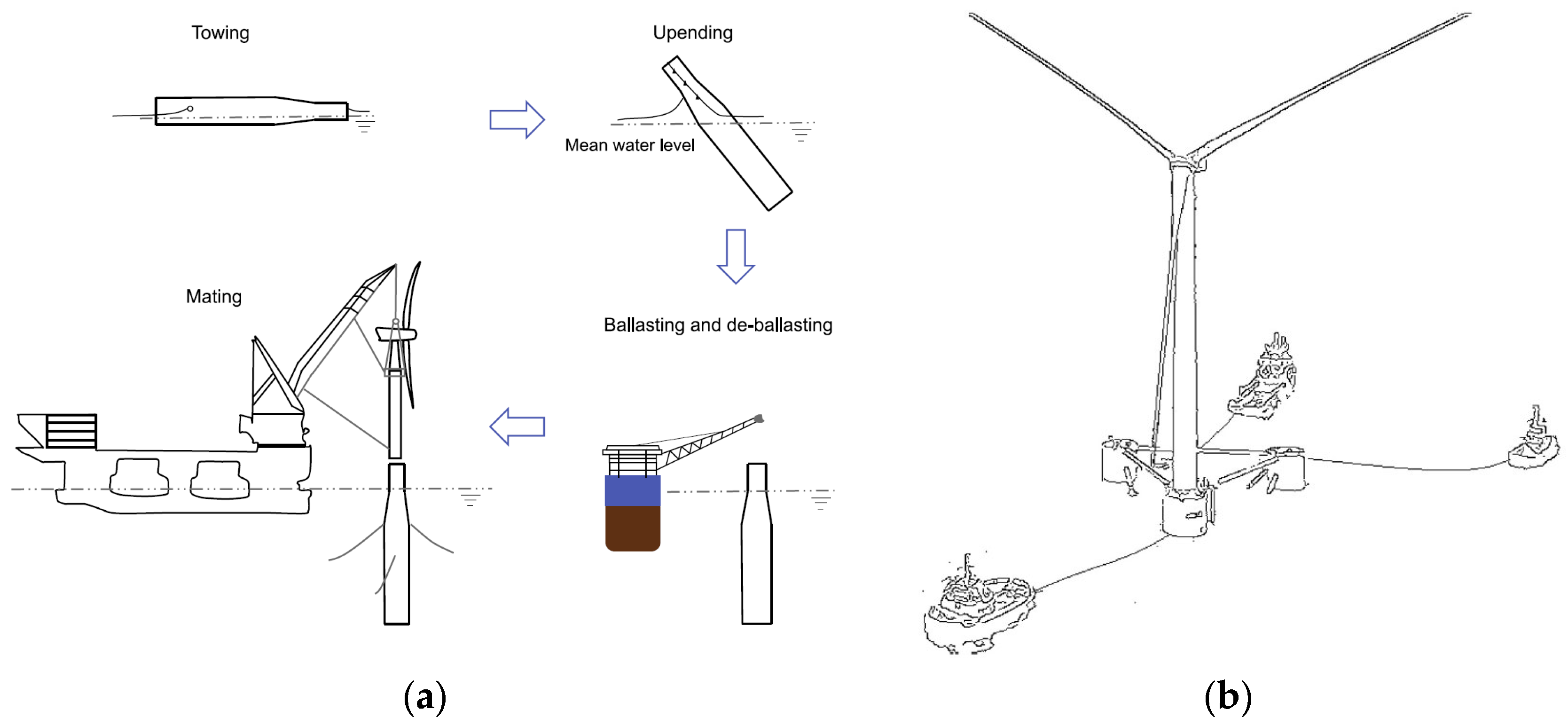Firstly, with regard to the types of FOWTs, according to articles by Soares [20], Anders[21], and others, FOWTs are primarily categorized into three major types: Spar-type, Semi-Submersible-type, and Tension Leg Platform (TLP), as illustrated in Figure 1. Each of these three types of FOWTs possesses distinct characteristics, leading to variations in the methods employed for their transportation to predetermined sites. Spar-type FOWTs typically employ a modular transportation approach, where the floating structure is first towed to the designated site and positioned, followed by the assembly of blades, generator units, and towers at the dock. These components are then transported to the site and assembled through docking installation, shown as Figure 2a. Semi-Submersible-type FOWTs are usually directly towed to the predetermined site by tugboats and positioned upon arrival, shown as Figure 2b. TLP-type FOWTs can be transported either on a barge or suspended beneath a vessel, transported to the designated site, and subsequently positioned and installed, shown as Figure 3. Depending on the chosen engineering and transportation methods, the types of vessels used may include, but are not limited to, tugboats, crane barges, heavy lift cargo vessels, jack-up barges, purpose-built jack-up vessels, semi-submersible crane vessels, among others. Notably, methods such as the twin-hull floating and lifting technique, which are still under validation, are not included in the aforementioned vessel types[22,23]. It is these differences that contribute to substantial variations in the risks associated with the transportation process of FOWTs.

According to Xue[8] and Zhang’s[9] papers, these differences are primarily manifested in various aspects as follows:

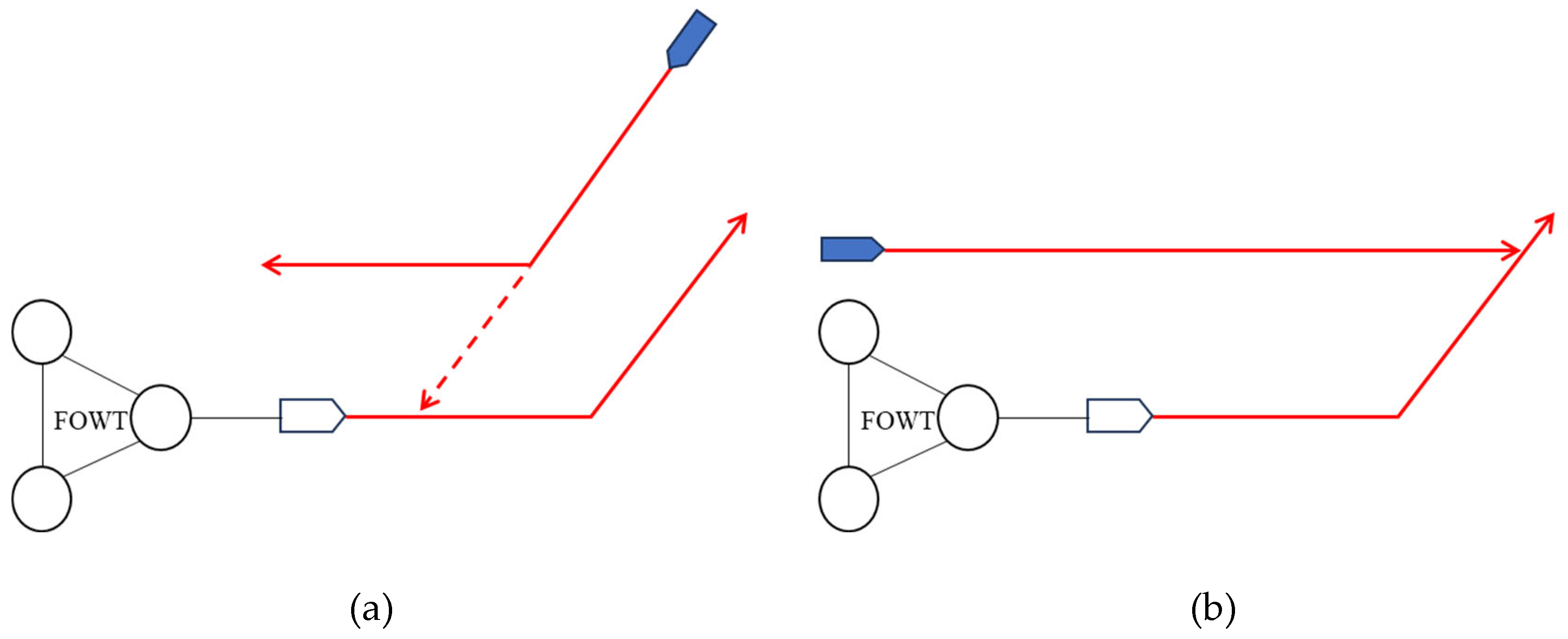
• The towing process establishes a flexible connection between FOWTs and tugboats, implying that the relevant operations of the towing vessel cannot rigidly transmit to the FOWTs. Consequently, the motion of FOWTs is uncontrolled, primarily governed by inertia and resistance. In contrast, the transportation form carried by engineering vessels does not encounter such concerns, as all components are on the engineering vessels and can be considered integral to the hull.
• Spar-type floating structures exhibit less conspicuous visual targets during the towing transport process, thereby increasing the likelihood of collisions with other vessels.
• Due to the higher centre of gravity during the transportation procedure, semi-submersible and TLP-type FOWTs experience larger wave loads during the towing process, and these effects are more pronounced. This implies that these two types of FOWTs are less suitable for transportation via towing methods in regions with adverse sea conditions.

After gaining an understanding of the transportation processes associated with Floating Offshore Wind Turbines (FOWTs), the exploration of relevant and analogous studies by other scholars becomes highly valuable. Presencia and Shafiee[26] conducted an analysis of engineering vessels during construction and their collisions with wind turbines, summarizing numerous historical studies in the process. Their work reveals a shift in research focus towards maritime vessel and structure collisions with wind turbines since 2005, with increasing diversity in considered vessel types and collision scenarios, accompanied by the development of increasingly intricate mathematical models. Commonly employed approaches involve statistical distribution and frequency calculations to determine collision probabilities. LS-DYNA or other finite element simulation software is often utilized to simulate accident consequences. Furthermore, they provided a methodology for calculating the probability of collisions between engineering vessels and fixed offshore wind turbines, combining probability distributions with qualitative analysis to estimate the likelihood of different wind turbine components being struck by vessels.

Dai et al. [27]delved into the collision analysis of wind farm service vessels and fixed offshore wind turbines. Their research employed a standard Quantitative Risk Assessment (QRA) process, categorizing vessel types and collision modes, constructing event trees and accident trees, and adapting them to Bayesian network algorithms utilizing directed acyclic networks. The consequence aspect of their study utilized numerical simulation to obtain local and global yield limit energy for various collision scenarios. Additionally, comprehensive research on ship-to-ship collisions has been well-established, as demonstrated by Zhang's[28] thorough analysis and summary in his paper, encompassing both analytical methods and numerical simulations. The findings of these scholars provide a foundational basis and a conceptual framework for the present study.

This study focuses on employing an analytical approach to investigate the probability and consequences of vessel collisions during the transportation process of FOWTs, using the planned construction of a floating wind farm in the Wanning Sea area of China as the research subject. Mathematical models are developed to encompass various collision scenarios, collision intensities, and the post-collision motion of objects. The study's findings can assist engineers in selecting more suitable transportation methods based on the size and type of wind turbines, thereby enhancing construction safety.

2. Materials and Methods

2.1. Case & Site Introduction

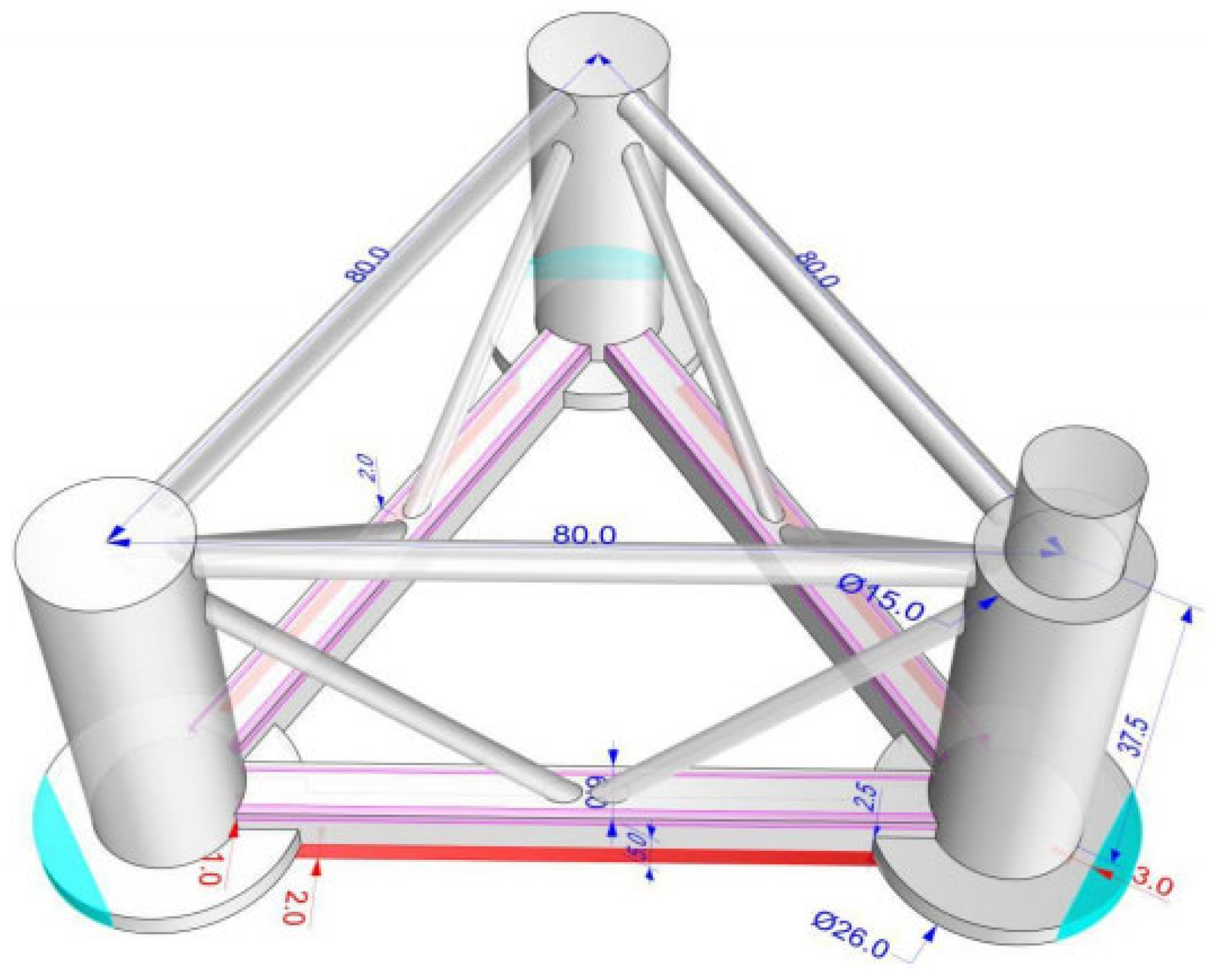
This study selects the area under development for a Floating Offshore Wind Farm (FOWF) in the eastern waters of Wanning City, Hainan Province, China, as the research site. The study focuses on the 16~18 megawatt Floating Offshore Wind Turbines (FOWTs) deployed at this location, and all pertinent data can be found in Table 2 and Figure 4. Due to the absence of freight ports in the vicinity of the Floating Offshore Wind Farm (FOWF) region, as indicated by statistical data from the China Maritime Safety Administration's Automatic Identification System (AIS)[29], and in accordance with research findings by Wang[30,31], Wan[32] and Guan et al.[33], it has been observed that within a 50-kilometer radius around the FOWF, there is a lack of major shipping channels. The predominant vessels navigating in this proximity are several cargo vessels and most of them are small and middle size fishing boats, as evidenced by the results presented in Table 3.

Unfortunately, due to confidentiality concerns and the progression status of the project, a substantial amount of detailed parameters is currently unavailable. Therefore, some of the data utilized in this study is derived from research conducted by other scholars in the relevant region or is sourced from data publicly disclosed on government websites during the composition of scholarly papers.

2.2. Presupposition

In initiating this study, it is crucial to establish a set of hypothetical conditions pertinent to the transportation process of floating offshore wind turbines (FOWT). The primary objectives of these hypotheses are as follows:

• Alignment with Engineering Reality: The foremost objective is to ensure the alignment of the assessment scenario with engineering reality. While the assessment of extreme scenarios may yield dramatic results, it lacks practical engineering significance. Accidents caused by the subjective intentions of personnel are not within the scope of normal construction conditions. Therefore, it is imperative to utilize assumptions that resonate with engineering reality, filtering out scenarios that may not have practical engineering implications.
• Reduction of Data Requirements: Another crucial objective is to minimize the amount of required data. Certain assumptions can significantly reduce the collection of raw data, including wind and wave conditions and ship types. This reduction in data requirements serves to streamline model calculations, simplifying the computational complexity of the model and making the assessment process more efficient.
• Specification of Usage Scenarios and Conditions: The third objective is to specify usage scenarios and conditions. Different scenarios and conditions may necessitate variations in assessment methods and equations, requiring the use of alternative algorithms for evaluation. To avoid confusion in application, this study limits the scenarios and conditions, providing clarity for ship collision assessment.

In summary, this research integrates the regulations of the International Maritime Organization (IMO), the China Classification Society, and Rijkswaterstraat to propose the following hypotheses through the analysis of case studies and sites:

• All ship operators will refrain from actively causing accidents.
• All ship operators will adhere to relevant laws and regulations.
• No ship will experience equipment damage at the time of departure from the port.
• FOWT transportation will not take place during adverse sea conditions or within the next 24 hours when adverse sea conditions are expected.
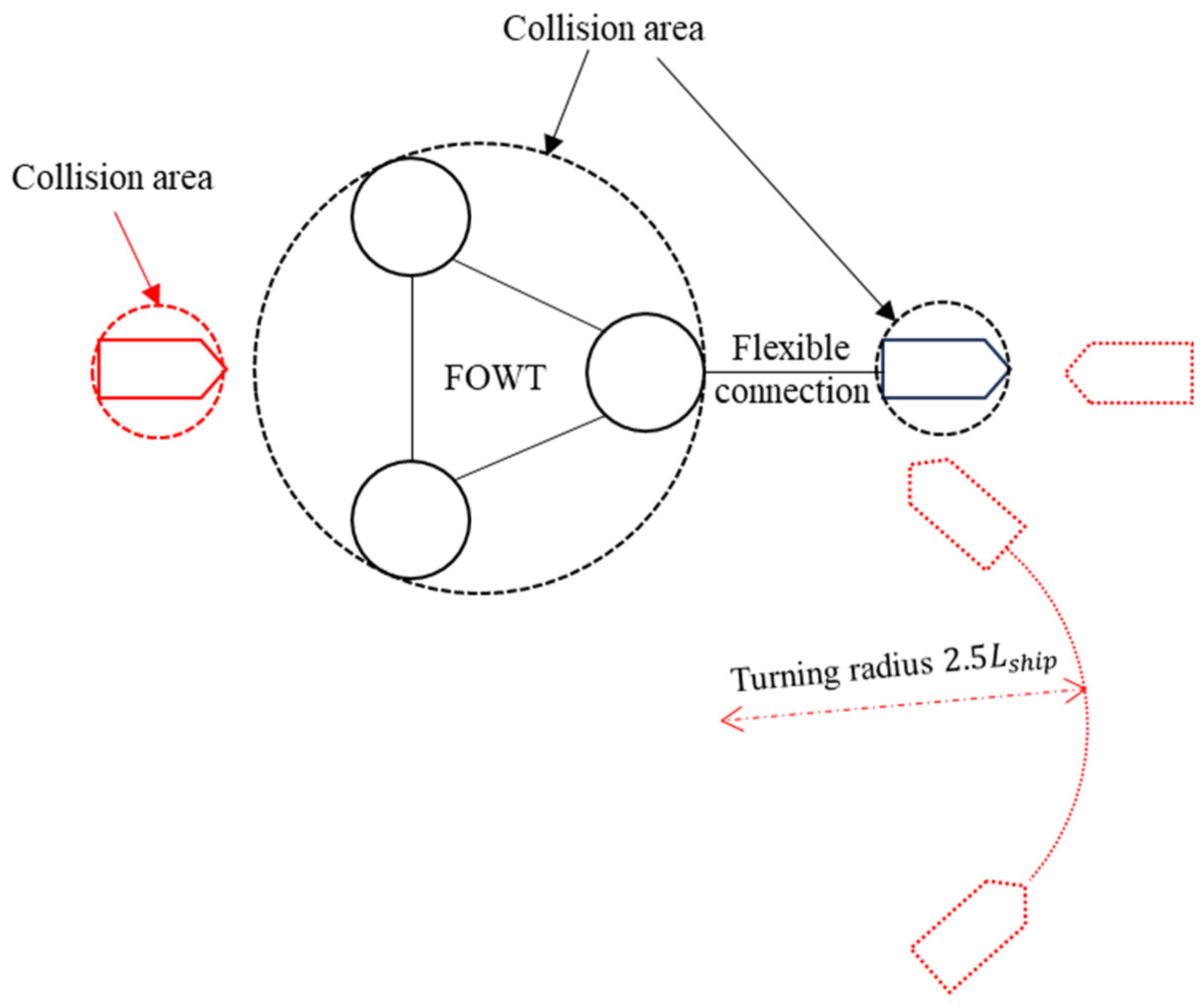
• The circle formed by the length and width of the target object will be considered as the collision area. Collision is deemed to have occurred if the circles of two target objects are tangent.
• The root cause of all accidents is attributed to mechanical equipment and environmental factors.
• The possibility of collisions due to objects falling from the target object and floating on the sea is not currently considered.

These hypotheses effectively confine collisions to daylight hours with favorable sea conditions and good visibility within a specific time frame, excluding accidents caused by human subjective intentions or errors. This deliberate scope allows for a focused analysis of collision risk assessment results, emphasizing spontaneous and unpredictable causes.

2.3. Ship Collision Analytical Model

To investigate the potentiality of collisions involving historical vessels and towed transport fleets using a deductive approach, it is imperative to initially comprehend the various scenarios in which collisions occur. Subsequent to this understanding, an analysis of these collision scenarios is conducted to discern the fundamental causes underlying these accident scenarios. This analysis further facilitates the delineation of the constituents of accident scenarios, culminating in the establishment of a mathematical model. As depicted in Figure 5, collisions between vessels and towed transport formations primarily manifest in two distinct categories: vessel-to-vessel collisions and vessel-to-FOWT collisions. Notably, these two collision categories correspond to two distinct collision modes: bow impact and impact during evasive manoeuvres. Therefore, this segment will be subdivided into two sections for investigation. The first involves the deductive analysis and model development of vessel-to-vessel collision scenarios. In this section, consideration will also be given to whether the motion of the FOWT connected by a flexible coupling can lead to secondary incidents. The second part entails the deductive analysis and model development of vessel-to-FOWT collision scenarios.

Nevertheless, it is imperative to preface with some general settings. As mentioned in the assumptions section, collision occurrence is considered once the circles of the target objects are tangent. Equation (1) to (2) provide the methodology for calculating the collision area diameters for both vessels and Floating Offshore Wind Turbines (FOWTs). It is noteworthy that, while the Pedersen algorithm is currently well-established for calculating the probability of vessel-to-vessel collisions based on AIS data in commercial waterways, it is specifically developed for ship collisions occurring in navigational channels. Given the absence of commercial shipping lanes in the vicinity of the study area and the prevalence of fishing vessels, the navigation patterns applicable to the Pedersen algorithm may not be suitable. Consequently, the use of a normal distribution to assess the position and trajectory of vessel navigation is not applicable in this context.

$$W_S=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.\left(L_S+B_S\right)$$

(1)

$$W_T=\raisebox{1ex}{$4\sqrt{3}$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\left(\raisebox{1ex}{$D_f$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+R_f\right)$$

(2)

Where ${\mathit{W}}_{\mathit{S}}$ is the equivalent width of the ship; ${\mathit{L}}_{\mathit{S}}$ is the length of the ship; ${\mathit{B}}_{\mathit{S}}$ is the breadth of the ship; ${\mathit{W}}_{\mathit{T}}$ is the equivalent width of the FOWT; ${\mathit{D}}_{\mathit{f}}$ is the distance between the center of floaters; ${\mathit{R}}_{\mathit{f}}$ is the radius of floaters;

Lastly, consideration is given to the methodology employed for probability calculations. To analyze the reasons behind collisions between two vessels, it is essential to investigate the fundamental causes of collision incidents. Table 4 presents a series of fundamental reasons for vessel collisions, along with the corresponding symbols used in this study, the respective values employed, and the origins of these numerical values.

$$P_r\left(t_e\right)=\raisebox{1ex}{$0.5$}\!\left/ \!\raisebox{-1ex}{$0.605$}\right.{\left(\raisebox{1ex}{$t_e$}\!\left/ \!\raisebox{-1ex}{$0.605$}\right.\right)}^{0.4}{e}^{-{\left(\raisebox{1ex}{$t_e$}\!\left/ \!\raisebox{-1ex}{$0.605$}\right.\right)}^{0.5}}$$

(3)

$$t_e=\raisebox{1ex}{$D_E$}\!\left/ \!\raisebox{-1ex}{$V_{ij}$}\right.$$

(4)

Where ${\mathit{V}}_{\mathit{i}\mathit{j}}$ is the relative speed of ship i and j; ${\mathit{t}}_{\mathit{e}}$ is the evasive duration; ${\mathit{D}}_{\mathit{E}}$ is the evasive distance, set as 2.5km. These two equations are used to calculate the time may take for ships to make evasive reactions when they have vision with each other. If there is no evasive reaction on both sides, a collision accident may happen highly likely.

Having acquired the necessary foundations and general research methods, the discussion now turns to the consideration of whether the transportation route intersects with navigational channels. If the transportation route traverses or partially intersects with a navigational channel, the vessel behavior in the channel needs to be taken into account during transportation, and collision probabilities are computed based on this information. Conversely, if the transportation route does not intersect with or closely approach navigational channels, the behavioral patterns of fishing vessels and other ships in the target area need to be considered. Given the distinct calculation methods required for these two scenarios, they warrant separate discussions.

2.3.1. Channel Area Collision Analytical Model

As delineated earlier, if there is an overlap between the transportation route and the primary navigational channels, it necessitates the consideration of potential collisions occurring separately for vessels in the navigational channels and the transportation fleet. In such instances, adhering to the Pedersen method, it is posited that the navigational behavior of vessels in the channel follows a normal distribution. Conversely, the towed transport fleet is conceptualized as an obstacle possessing a certain level of active avoidance capability—a circumstance not addressed in the Pedersen method, which assumes static obstacles without evasion functionalities along the route. According to the description in Figure 6, this situation gives rise to four major collision categories: encounter, overtaking, crossing, and bend collision. The bend collision category can be further subdivided into the opposite direction and same direction scenarios. Consequently, the ensuing deductive analysis will commence by examining and modeling these scenarios individually.

Figure 6. Three collision scenarios: (a) encounter collision; (b) overtaking collision; (c) crossing collision.

Figure 6. Three collision scenarios: (a) encounter collision; (b) overtaking collision; (c) crossing collision.

Figure 7. Two bend collision types: (a) opposite direction; (b) same direction.

Figure 7. Two bend collision types: (a) opposite direction; (b) same direction.

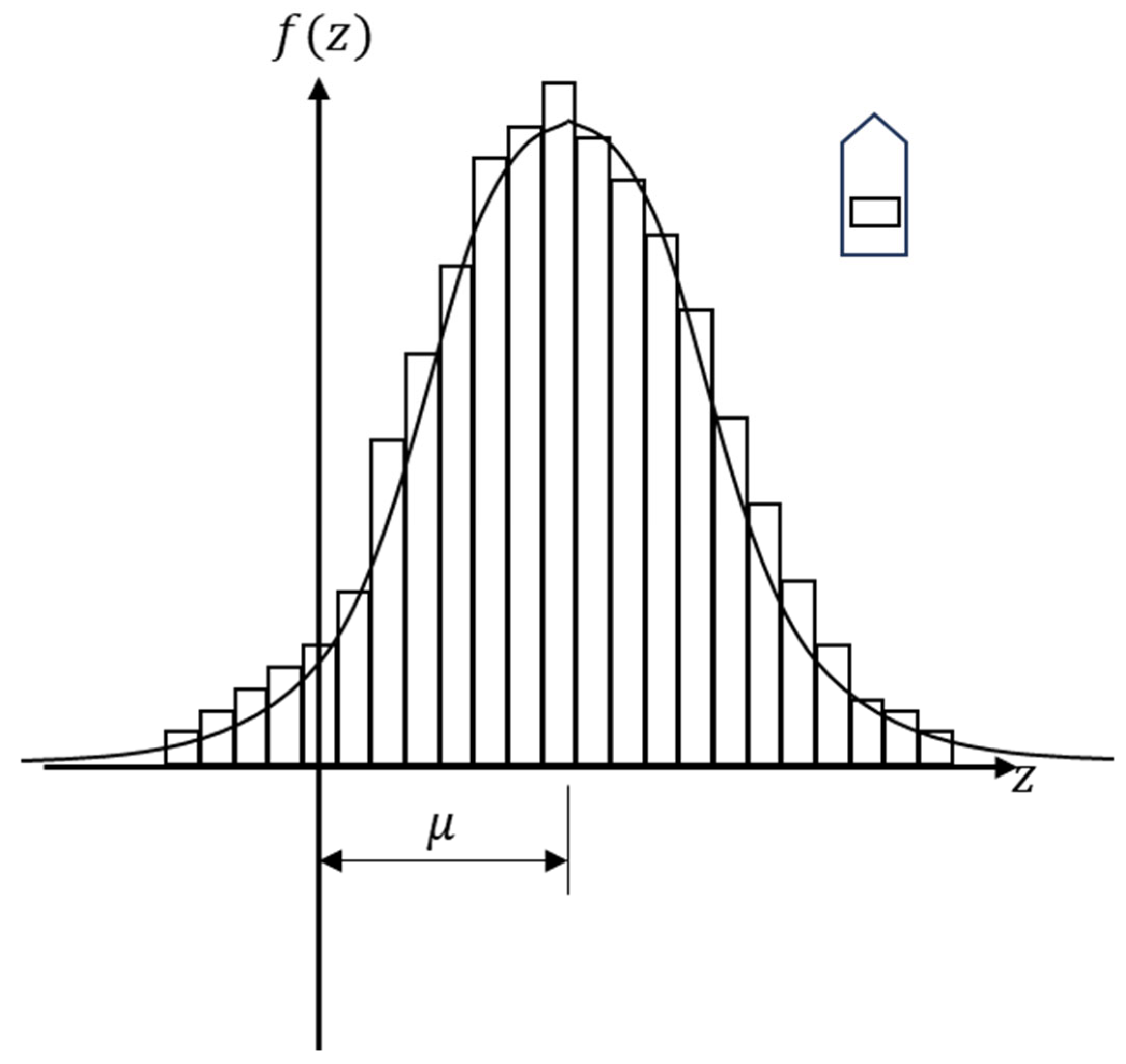
Firstly, analyze the three scenarios depicted in Figure 6. For vessels navigating in the channel, their navigational behavior typically conforms to a normal distribution, as illustrated in Formula (5), with Figure 8 providing supplementary clarification of this normal distribution. In the event of contact between two vessels or a vessel and FOWT, it can be assumed that the geometric collision circles of vessel-to-vessel or vessel-to-FOWT are tangent. The length of this segment is defined as the geometric collision diameter. Formula (6) represents the geometric diameter for vessel-to-vessel collisions, and Formula (7) represents the geometric diameter for vessel-to-FOWT collisions. Thus, the time elapsed before an incident occurs, after a vessel in channel i detects the towed transport fleet, is determined by the reaction distance between the two vessels, relative velocity, and geometric collision diameter. The expression (8) provides the function for the number of collisions between vessels on channel i and the fleet within a unit of time. By substituting Equation (5), (6), and (7) into (8), the total number of vessels colliding with the fleet on channel i within time t can be obtained, as expressed in Formula (9). It is noteworthy that, when investigating encounters and overtaking collisions, the sequence of vessel collisions needs to be considered. Therefore, appropriate modifications to the term $\left({\mathit{D}}_{\mathit{S}-\mathit{S}}+{\mathit{D}}_{\mathit{S}-\mathit{T}}\right)$ in the equation are required, reflecting that vessels in the channel cease to collide with the fleet after encountering the first object in the towed transport fleet.

$$f\left(z\right)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2\pi }\sigma $}\right.exp\frac{-{\left(z-\mu \right)}^2}{2{\sigma }^2}$$

(5)

$$D_{S-S}=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.\left(L_{S1+S2}+B_{S1+S2}\right)$$

(6)

$$D_{S-T}=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.\left(L_S+B_S\right)+\raisebox{1ex}{$4\sqrt{3}$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\left(\raisebox{1ex}{$D_f$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+R_f\right)$$

(7)

$$N_i=\raisebox{1ex}{$Q_i$}\!\left/ \!\raisebox{-1ex}{$V_i$}\right.f_i\left(z_i\right)\left(D_{S-S}+D_{S-T}\right)V_{ij}d{z}_{i}dt$$

(8)

$$N_t=\sum _i\underset{0}{\overset{t}{\int }}\underset{z_i}{\int }\raisebox{1ex}{$Q_i$}\!\left/ \!\raisebox{-1ex}{$V_i$}\right.\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2\pi }\sigma $}\right.exp\frac{-{\left(z_i-\mu \right)}^2}{2{\sigma }^2}\left(D_{S-S}+D_{S-T}\right)V_{ij}d{z}_{i}dt$$

(9)

Where $\mathit{z}$ is the distance from the centerline of navigation route; $\mathit{\mu }$ is the mean value of the spatial distribution; and $\mathit{\sigma }$ is the standard deviation; ${\mathit{D}}_{\mathit{S}-\mathit{S}}$ is the geometrical collision diameter between ships; ${\mathit{D}}_{\mathit{S}-\mathit{T}}$ is the geometrical collision diameter between ship and FOWT; ${\mathit{L}}_{\mathit{S}\mathbf{1}+\mathit{S}\mathbf{2}}$ is the total overall length of ships; ${\mathit{B}}_{\mathit{S}\mathbf{1}+\mathit{S}\mathbf{2}}$ is the total breadth of ships; ${\mathit{N}}_{\mathit{i}}$ is the collision candidate in shipping route $\mathit{i}$ during unit period; ${\mathit{Q}}_{\mathit{i}}$ is the quantity of ships in shipping lane; ${\mathit{V}}_{\mathit{i}}$ is the velocities of ships in shipping lane; ${\mathit{N}}_{\mathit{t}}$ is the total number of collision candidate in shipping lane during the transportation fleet pass the shipping lane; $t$ is the duration of transportation fleet pass the shipping lane.

Once the total number of vessels potentially involved in collisions within the route is determined, the collision frequency can be calculated by combining the probabilities corresponding to various collision forms. Equation (10) represents the calculation method for the frequencies of three common collision forms, where the value of ${\mathit{P}}_{\mathit{c}}$ can be referenced from Table 5.

$$F_{collison}=N_t·P_c$$

(10)

The intricacies of bends collision scenarios, as illustrated in Figure 7, introduce a level of complexity. Traditionally, the establishment of a reliable analytical model necessitates considerations such as the operational status and inspection frequency of the Vessel Traffic System (VTS), as well as factors including the reaction distance between vessels. The integration of these diverse factors makes it challenging to formulate a robust analytical model. Consequently, when scrutinizing this particular issue, it is plausible to posit that the occurrence of such accidents is rooted in anomalies with vessels navigating the channel itself. Within the temporal window subsequent to detecting the towed transport fleet, these vessels fail to execute appropriate course adjustments, and the fleet is unable to evade successfully. This leads to the formulation of equations (11) and (12). Additionally, given the inherent absence of evasion capabilities in Floating Offshore Wind Turbines (FOWTs), the analysis of collisions between navigating vessels and FOWTs obviates the need to consider fleet evasion scenarios.

$$F_{collision}=N_t·P_{Human}·\left(1-P_{ca}\right) \text{for} \text{opposite} \text{direction} \text{bend} \text{collision}$$

(11)

$$F_{collision}=N_t·P_{Human}·{\left(1-P_{ca}\right)}^2 \text{for} \text{same} \text{direction} \text{bend} \text{collision}$$

(12)

The aforementioned model employs a deductive approach to analyze and construct a frequency estimation model for collisions between FOWTs transport fleets and vessels in navigational channels. The analytical process reveals the multitude of factors that must be considered when assessing vessel collisions. In practical engineering applications with similar requirements, it is advisable to deploy safety vessels on the periphery of the fleet to alert passing vessels to alter their course, thereby mitigating the risk of accidents.

2.3.2. Non-Channel Area Collision Analytical Model

For towed projects not situated near navigational channels, the methods mentioned earlier cannot be applied to estimate collision frequencies. The navigational behavior of fishing vessels often involves repetitive movements within a specific region, while engineering vessels navigate linearly between operation sites and docks, avoiding impassable areas. Both behaviors are challenging to statistically analyze and predict due to their unique characteristics. Consequently, a reanalysis of collision scenarios between these two types of vessels is necessary, and the specific analytical approach is illustrated in Figure 9.

Firstly, an estimation of the total number of vessels that could potentially collide in a given maritime area needs to be conducted. This estimation should be based on monthly statistics, taking into account the differences in fish species present in the sea during different months, as well as restrictions imposed by fishing bans in the vessels' respective countries. These factors can lead to significant variations in the number of fishing vessels, vessel types, and concentrated distribution areas in a particular maritime region. In this study, an assumption of uniform vessel density in a given maritime area is employed.

Next, the calculation involves determining all vessels that could potentially navigate into the path of the transport fleet during transportation. Essentially, this entails two-dimensional quantification of the overtaking problem: calculating the range within which all nearby vessels, traveling at speeds ranging from $-{\mathit{v}}_{\mathbf{2}}$ to ${\mathit{v}}_{\mathbf{2}}$ (where ${\mathit{v}}_{\mathbf{2}}>{\mathit{v}}_{\mathbf{1}}$, the speed of the transport fleet), would converge towards the transport fleet from various directions during the transportation process at the speed of ${\mathit{v}}_{\mathbf{1}}$.

Finally, when a navigating vessel visually detects or radar scans the towed transport fleet on its predetermined course, an avoidance response should be initiated. In the event of a collision, it indicates a malfunction in the propulsion and/or steering systems of the navigating vessel. Therefore, the probability of such occurrences should be factored into the analysis.

In summary, equations (13) to (16) provide the mathematical analytical model for collisions of this nature.

$${\rho }_{pmi}={\displaystyle \sum }_m{\displaystyle \sum }_i\raisebox{1ex}{$N_{mi}$}\!\left/ \!\raisebox{-1ex}{$A_p$}\right.$$

(13)

$$A_{candidates}=\underset{\left(v_2-v_1\right)t}{\overset{\left(v_2+v_1\right)t}{{\displaystyle \int }}}\underset{-v_{2}t}{\overset{v_{2}t}{{\displaystyle \int }}}\sqrt{x^2+y^2-2xycos\left[\theta \left(t\right)\right]}dxdy$$

(14)

$$\theta \left(t\right)=\underset{0^{°}}{\overset{{360}^{°}}{{\displaystyle \int }}}co{s}^{-1}\raisebox{1ex}{$v_1\left(1-t^2\right)$}\!\left/ \!\raisebox{-1ex}{$v_2$}\right. dt$$

(15)

$$F_{collision}={\rho }_p·A_{candidates}·\left\{P_c+P_{pf}\left[1-P_r\left(t_e\right)\right]+P_{sf}\left[1-P_r\left(t_e\right)\right]\right\}$$

(16)

Where ${\mathit{\rho }}_{\mathit{p}\mathit{m}\mathit{i}}$ is the i type ship density in m month in the project area; ${\mathit{N}}_{\mathit{m}\mathit{i}}$ is the number of i type of ship in m month; ${\mathit{A}}_{\mathit{p}}$ is the project area; ${\mathit{A}}_{\mathit{c}\mathit{a}\mathit{n}\mathit{d}\mathit{i}\mathit{d}\mathit{a}\mathit{t}\mathit{e}\mathit{s}}$ is the ship location area which may collision with transport fleet when ships in velocity ${\mathit{v}}_{\mathbf{2}}$; ${\mathit{v}}_{\mathbf{1}}$ is the fleet velocity; $\mathit{x}$ is the horizontal displacement of ships; $\mathit{y}$ is the vertical displacement of ships; $\mathit{t}$ is the duration of the fleet from port to the wind farm; ${\mathit{F}}_{\mathit{c}\mathit{o}\mathit{l}\mathit{l}\mathit{i}\mathit{s}\mathit{i}\mathit{o}\mathit{n}}$ is the frequency of collision. 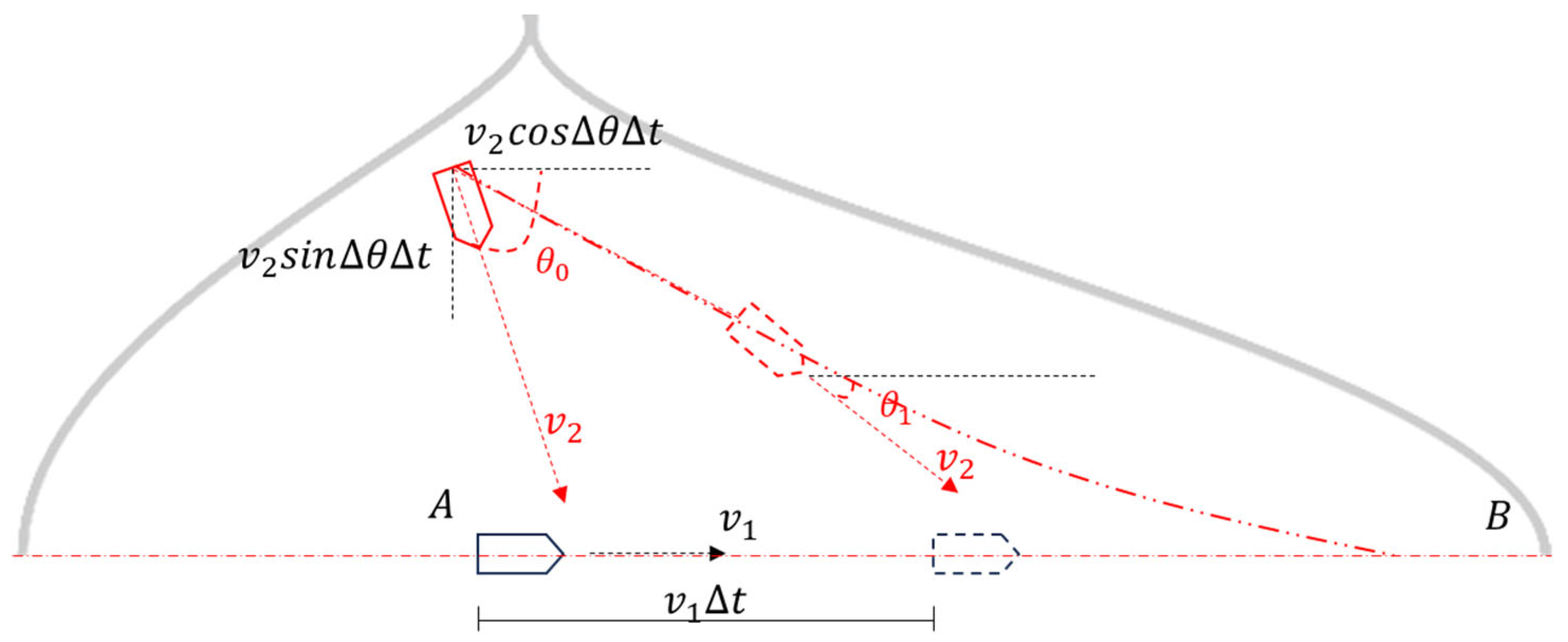Figure 10 helps to understand the process of building the analytic model. Assuming that during the process of a fleet moving from point A to point B at a velocity ${\mathit{v}}_{\mathbf{1}}$, there is a ship approaching the fleet at a velocity ranging from 0 to ${\mathit{v}}_{\mathbf{2}}$ at each $\Delta \mathit{t}$ moment. Then, within the total duration t from point A to point B, the cumulative area of all the positions where ships could potentially collide with the fleet is as depicted in the figure. In this process, the direction angle of the domain vessel ${\mathit{v}}_{\mathbf{2}}$ varies with time, and the relative position between the two ships also diminishes as time elapses. The analysis process did not take into account the collision geometry between the ship hull and the FOWT, as the collision geometry of ships and FOWTs is negligible at the scale of the sea area, rendering it insignificant for computational purposes.

According to the above analytic formula, the collision frequency between the transport fleet and the ships in a non-channel area can be roughly calculated.

In summary, the analytical scale and methods applied by the fleet in navigating through and avoiding channel routes exhibit significant differences. The fundamental cause of these differences lies in the distinct characteristics of the navigation channels and the traffic volume: the navigational behavior and traffic volume of vessels in primary channels are more predictable compared to those in fishing zones, with a considerable amount of research having utilized various methods to analyze them; hence, collision probability calculations can be conducted on a smaller scale using relatively mature distribution methods. In contrast, the behavior of vessels in non-channel areas, particularly fishing boats, is more challenging to statistically analyze and predict, necessitating the estimation of collision probabilities on a larger scale through geometric analysis techniques.

3. Results

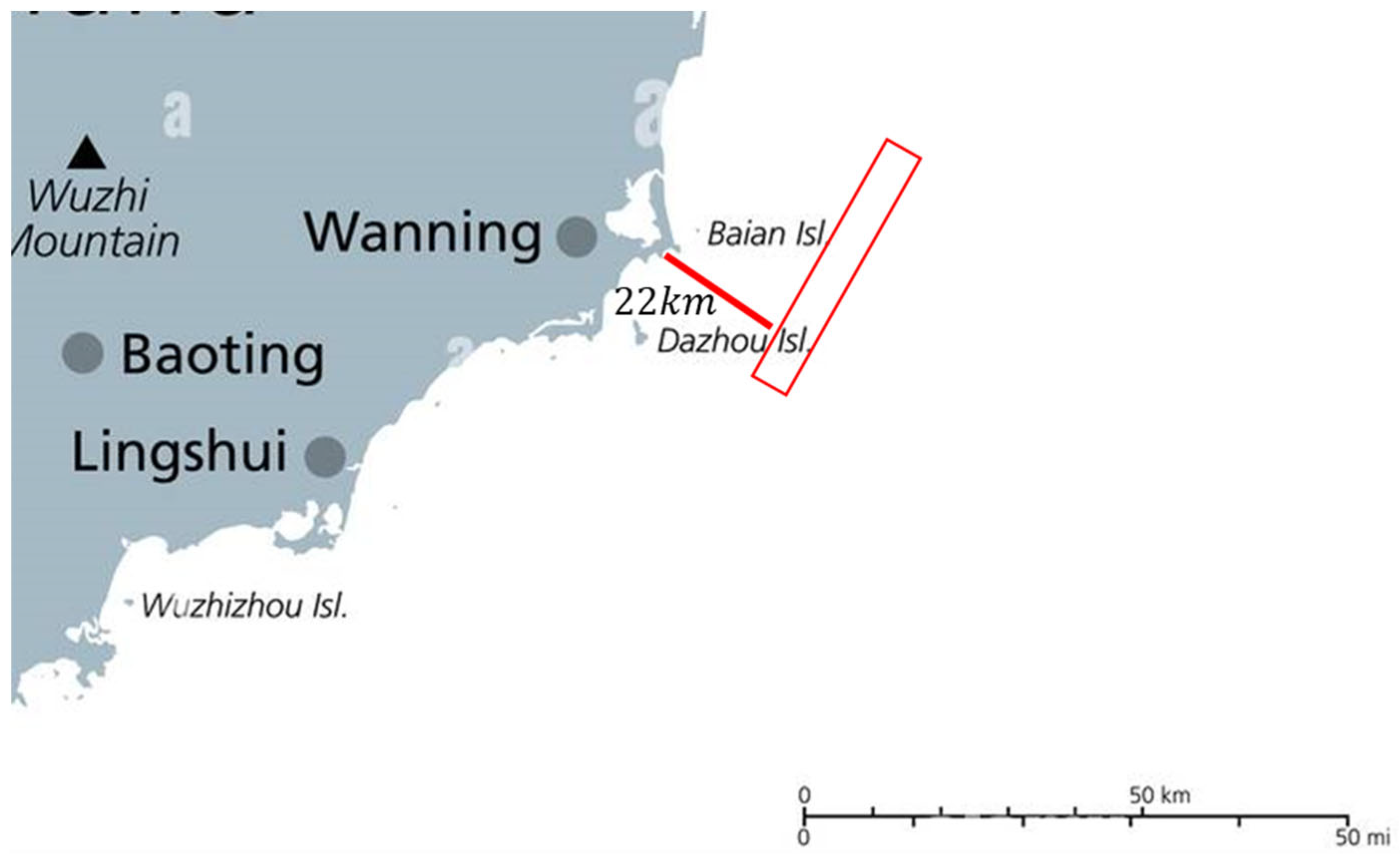
The floating offshore wind farm under study is located 22km to the southeast of Wanning City, Hainan Province, China, as depicted in Figure 11. Although the route from the turbine loading pier to the wind farm site does not traverse any navigational lanes, the surrounding area is within the fishing grounds of offshore fishing vessels.

Due to the lack of publicly available monthly statistics on the number of fishing vessels in various sea areas by Chinese official sources, this paper utilizes the data for the months of April, June, and September published by Guan et al. [33] in their research. The relevant sea areas are shown in Figure 12, with detailed data presented in Table 6. According to the data, the target sea area encompasses approximately 945,000 square kilometres. Considering that most vessels operate in nearshore regions, the actual fishing vessel distribution area is delimited to a 150-kilometer offshore radius, resulting in a target sea area of approximately 350,000 square kilometres.

In this study, the speed of the towed transport fleet is set at 4 knots (7.4 km/h), and the cruising speed of fishing vessels is set at 9-12 knots (18-22 km/h). After calculation, the collision number during transportation in three months is presented in Table 7, Table 8 and Table 9.

The results indicate that the analytical model employed in this study effectively calculates the estimated number of collisions involving vessels of various speeds within the target area, approaching from multiple directions and encountering fleets during the towing process. This suggests that the equations constructed in this research possess practical utility. Subsequent sections will provide a detailed discussion of the numerical content of the outcomes.

4. Discussion

Due to the fact that the case corresponding to this paper is located in waters near non-navigation channels, it is not possible to validate some parts of the analytical model. However, since the collision model for crossing navigation channels is further developed from the Pedersen model, its reliability has been widely recognized by the industry. In the future, validation work will be carried out when relevant data is sufficient.

Through the analysis of the analytical model and the results data, it is not difficult to identify the following five phenomena that require special attention:

• The longer the towing process, the higher the probability of ship collisions.
• The earlier the ships in the domain detect the transport fleet, the more likely they are to avoid collision accidents.
• The slower the towing speed, the more prone to ship collisions.
• The faster the ships in the domain are sailing, the more likely they are to have collisions.
• In terms of collision forms, crossing>overtaking>encounter.

Furthermore, through the analysis of the evaluation data, this paper proposes some disaster prevention and mitigation suggestions corresponding to the case:

• Conduct transport operations during good visibility conditions as much as possible.
• The fleet should have conspicuous markers to warn nearby ships to give way.
• If possible, arrange for peripheral patrol ships for the fleet as a warning.
• The speed during the transportation process should not be too low.
• The transport route design should be as short as possible, and try to avoid the channel as much as possible.
• Collision buffer devices should be installed on the side of the ship and the FOWT to minimize the impact force of the collision.
• Conducting transportation during the closed season is safer than transporting during the fishing season.

5. Conclusions

In summary, this paper has constructed a mathematical model for the analysis of ship collisions during the FOWT towing process by using analytical methods and combining the research results of predecessors. This model repeatedly considers the waters that the FOWT towing process may pass through, the possible collision scenarios, and takes into account the possibility of collisions between ship and FOWT transport fleets of different months and speeds. From the results, it can be inferred that June may be the best time for the FOWTs to enter the Wanning FOWF project. Relevant practitioners need to pay special attention to enhancing the target visibility of the fleet during the transportation process and avoid excessively slow transportation speeds.

In the future, more data on the FOWT transportation process and related accident reports will be collected to further optimize this model.