Numerical Modelling of the Thermoforming Behavior of Thermoplastic Honeycomb Composite Sandwich Laminates

Preprint

Article

Numerical Modelling of the Thermoforming Behavior of Thermoplastic Honeycomb Composite Sandwich Laminates

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Varun Kumar Minupala^*,

Matthias Zscheyge,Thomas Glaesser,Maik Feldmann,

Holm Altenbach

Varun Kumar Minupala^*,

Matthias Zscheyge,Thomas Glaesser,Maik Feldmann,

Holm Altenbach

This version is not peer-reviewed

Submitted:

28 December 2023

Posted:

29 December 2023

You are already at the latest version

Alerts

Abstract

Lightweight component design is effectively achievable through the sandwich structures, many past research studies in the aerospace and racing sectors (since 1920s) has proven it. To extend their application into automotive and other transport industries, the manufacturing cycle times must be reduced. This can be achieved by thermoplastic sandwich materials of continuous fibre-reinforced thermoplastic (CFRTP) cover layers and thermoplastic honeycomb cores. To widespread the application of flat thermoplastic-based sandwich panels into complex parts, a novel forming technology was developed by the Fraunhofer Institute of Microstructure of Materials and Systems (IMWS). For an increase in reproducibility of the sandwich component production and a decrease in manufacturing defects, numerical modelling methods and experimental validation are needed. The finite element (FE) modelling of this thermoforming process is a thermo-mechanical assignment with all three: material, geometry, and boundary non-linearities. In the scope of this work, the material behavior of different sandwich components (cover layers, honeycomb core, interface) under thermo-mechanical loads is characterized in detail, and a complex numerical model is developed to describe the thermoforming process of thermoplastic-based sandwich laminate. The critical forming condition like wrinkling that occurs due to friction in a sandwich or poor intra-ply shear in cross-ply studied, validated, and optimized. A thermoplastic sandwich made of polypropylene (PP) honeycomb core and polypropylene glass fibre (PP/GF) cross-ply as cover layers was used for this study, and numerical modelling was executed in LS-DYNA software.

Keywords:

Subject: Engineering - Industrial and Manufacturing Engineering

1. Introduction

Thermoplastic composite sandwich structure made of honeycomb core and laminated with UD-tape cross-ply cover layers on the top and bottom sides offers reduced mass and high bending stiffness. The honeycomb structure comprises an array of thin-walled hollow hexagonal cells arranged together, resulting in minimal material per unit area. In addition to that, the honeycomb structure provides relatively high out-of-plane compression and out-of-plane shear properties. Meanwhile, cross-ply as cover layers offer a high tensile strength in the fibre direction, resulting in-plane orthotropic properties.

The production of hexagonal honeycombs at an industrial scale is carried out through tube extrusion, expansion, and corrugated processes [1,2,3]. These processes are operated at multiple stages and require long production times, which in total results in high production costs and therefore, limits them to a low volume production [4]. To solve this, ThermHex Waben GmbH has introduced a continuous production process, where a thin thermoplastic polymer film is extruded (1^st Step) and vacuum formed to form a half hexagon (2^nd Step), followed by folding to form a honeycomb (3^rd Step), at the end lamination with cover layers (4^th Step) resulting in composite sandwich structure as shown in Figure 1 (a). The so-produced semi-finished laminate is called as Organosandwich, which is aimed for mass production with maximum production speeds of up to 20 m/min with a panel width of 1.2 m [5].

With the added advantage of thermoplastic material behavior and the suitability for high volume production, the flat semi-finished panels can be further processed into complex shapes using the thermoforming technique so that they can be used in different applications, especially in automotive sector. To form and include functionalizing elements into sandwich components, a multi-stage thermoforming technique known as thermoplastic Sandwich Molding (TSM) is developed at Fraunhofer IMWS, with manufacturing cycle time of 4 s [6]. Simultaneously, with the process technique approach, Fraunhofer IMWS develops the numerical models and perform simulations to adapt the novel technology to the digital process chain.

2. Thermoplastic Sandwich Forming

The TSM technology allows processing of semi-finished thermoplastic sandwich panels into ready-to-use lightweight parts. Focus of this research is to develop a manufacturing process that allows the honeycomb core sandwich laminate to confront the mold shape without wrinkling and core collapsing or buckling. The novel TS-molding manufacturing process of FRTP sandwich components comprises of three main process steps as shown the Figure 1 (b), starting by IR-heating of the semi-finished sandwich laminate, followed by forming of the sandwich laminate into pre-defined shape and then injection molding around the edges [6].

Figure 1. Organosandwich (a) continuous production of honeycomb core and in-line lamination of coverlayers, (b) schematic illustration of the novel manufacturing process of TS-Molding [3,4,23,24].

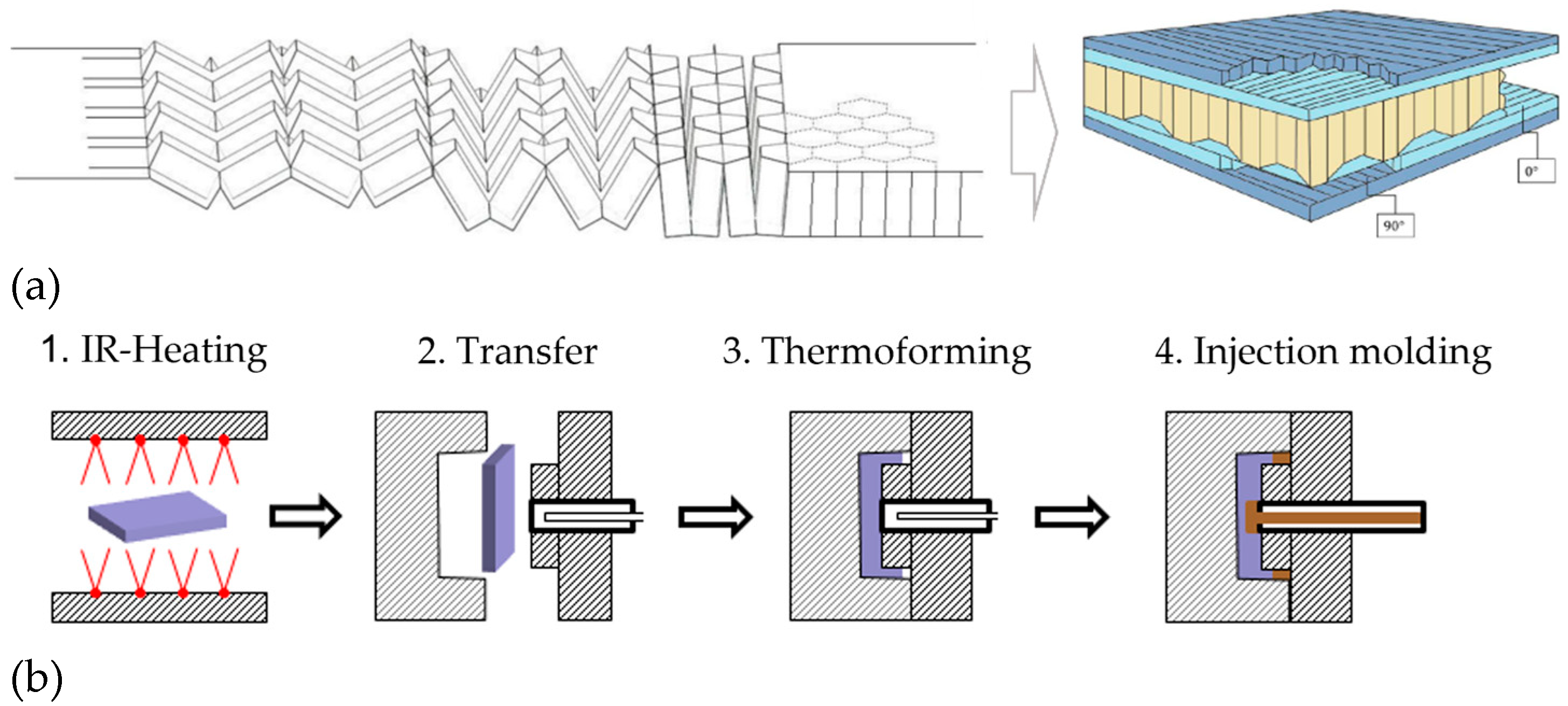
Specifically, thermoforming is carried out through a press by closing the two-sided tool in three successive sub-process steps. In the first step of the closing movement, the sandwich structure is formed in areas of the later part in which the core must remain intact. After this forming step, the press stops the closing movement for a short time allowing cooling by tool contact and thereby solidification of the face sheet matrix. After this short break, the tool moves further and fully closes by pressing the sandwich edges into a compact laminate. Pressing is particularly important at the component edge for sealing of the sandwich to protect the core and later for integration of functional elements. The pressed edge also acts as a transition zone between the formed sandwich structure and over-molded edges [4].

3. Materials and Finite Element Modelling

Using mathematical models, physics laws, and computer science, it is essential to reduce the physical work and save the extensive time that is required to conduct numerous experiments through a trial-and-error approach. The finite element analysis (FEA) approach starts with material description and material characterization, followed by FE-modelling with necessary boundary conditions and loading cases. Simulation results are used to identify undesirable deformations in part at the early stages of thermoforming process development, as shown in Figure 2.

3.1. Sandwich Material Description

The Organosandwich used for this study comprised a PP honeycomb core and PP/GF UD-Tape-based Cross-Ply cover layers. During the production of such laminates, a thin PP film is formed to a honeycomb core and laminated with the PP/GF cross-ply using heating and double band press. This lamination allows a strong weld joint between the core and cover layers as they share the same thermoplastic material. There is no requirement for additional adhesive layers, unlike in Nomex or another type of sandwich laminate, making the production more sustainable and economical.

Table 1. Sandwich material description of the used configuration 12THPP120CP820.

Sandwich Entity	Dimension
Sandwich thickness	12 mm
Cover layer thickness	0.5 mm
Honeycomb core thickness	11 mm
Cell size	5 mm
Standard panel dimension	1200 mm x 2500 mm (L x W)
Weight per unit density	3120 – 3240 g/m²

ThermHex Waben GmbH [23].

Table 2. Mechanical properties at room temperature of the PP core and PP/GF UD-Tape.

Material	Density (kg/m³)	Young’s Modulus (GPa)	Yield stress (GPa)	Poisson’s Ratio	Specific heat capacity (J/kg K)	Thermal Conductivity (W/m K)
PP	980	1.55	0.2	0.41	1794	0.161
PP/GF 60	1540	29.39	0.4	0.40	1160	0.308

3.2. Coverlayers Wrinkle Analysis

The thermal and mechanical loads on sandwich components result in different deformation modes, on the one hand, cover layers exhibit following behavior,

ply-elongation
inter-ply slip
ply shear and
wrinkle or in-plane buckling [7,8].

On the other hand, the core component exhibits in-plane tension and compression, and out-of-plane buckling due to compression [2]. In thermoforming process development, the focus is to produce a part without any defects. Sometimes, CFRTPs such as woven laminate or non-woven laminate (cross-ply) during thermoforming show surface defects, which usually develop due to buckling or wrinkling. The wrinkle formation in cover layers in non-homogeneous sandwich materials is treated as a local phenomenon. This kind of deformation can be initially estimated through a model of axial loaded flat sandwich structure (see Figure 3), the prediction of onset wrinkle in cover layers is done with calculation of the maximum compressive stresses in the cover layer.

There exist different mathematic models to estimate the maximum compressive stress for initiation of wrinkle formation in the cover layers, based on the homogeneous and non-homogeneous core materials. For non-homogeneous core, isotropic cover layers, and where height of the core is relatively high compared to that of thickness of face sheet (see Figure 1 (a)), Williams [9] made a suitable analysis. This analysis is based on the initial assumption that the axial stress in the direction of load on the core is zero, known as anti-plane stress assumption [8]. The core here is infinitely thick therefore, wrinkles are exponentially decayed on the cover layers away from the core axis. The mathematical expression of wrinkle formation stress for cover layers is derived as,

σ_{w r} = [\frac{0.825}{{(1 - {ν_{c l}}^{2})}^{1 / 3}}] {(E_{c l} E_{c} G_{c})}^{1 / 3},

(1)

where

σ_{w r}

is the maximum compressive stress for wrinkle formation,

ν_{c l}

is the Poisson’s ration of the cover layer,

E_{c l}

E_{c}

are the Young’s modulus of cover layer and core respectively,

G_{c}

is the in plane shear modulus of the core. An additional assumption is made in the current study, based on the thermoplastic sandwich lamination, where additional molten polymer is deposited in the core and cover layer bonding regions. Therefore, orthotropic cover layers are considered as locally isotropic in the contact region between core and cover layer, calculating the Equation 1 for Organosandwich at processing temperature, the maximum in-plane compressive stress which result in wrinkle formation is estimated as below,

σ_{w r} = [\frac{0.825}{{(1 - {0.4}^{2})}^{1 / 3}}] {(16.27 * 130 * 0.09)}^{1 / 3} = 5.03 N / m m ² .

(2)

3.3. Spatial Discretization of Organosandwich

TS-molding is a combined process of thermoforming and over-molding, however only thermoforming is discussed in this paper. The demonstrator part used for this study comprises different zones like forming and pressing regions. Therefore, the sandwich is divided into three parts: a honeycomb core, top and bottom face sheets, where each part is sub-modelled using shell element theory. The honeycomb structure is generally modelled using three methods: (1) meso model, (2) volume model, and (3) shell model. Bounding to the manufacturing process, where the honeycomb structure significantly influences the forming locally and globally, the meso model approach is chosen in this study. Using mesh discretization, a complex geometry is divided into smaller entities and simpler subdomains. Then, their respective partial differential equations are solved by applying the principles of boundary value problem. During the selection of element types and their related interpolation functions of the physical quantity for e.g., displacement, temperature, etc., is considered.

In finite element method approach the strong form of the initial boundary value problem for small displacements is written as follows,

\nabla \cdot σ + b = ρ \ddot{u} in Ω,

(3)

where

ρ

is the density,

\ddot{u}

is the time derivative of displacement, with the auxiliary conditions like, essential boundary conditions

u_{i} = {\bar{u}}_{i} o n Γ_{u_{i}}

and natural boundary conditions

σ_{i j} n_{j} = {\bar{t}}_{i} o n Γ_{f_{i}}

. The weak form is then written as

\int_{Ω}^{} ρ δ u \cdot \ddot{u} d Ω + \int_{Ω}^{} δ ε ∶ σ d Ω = \sum_{i = 1}^{n} \int_{Γ_{f}}^{} {δ u}_{i} {\bar{f}}_{i} d Γ + \int_{Ω}^{} {δ u}_{} \cdot b d Ω,

(4)

which is used to develop the discrete equations in the Galerkin procedure. The displacement approximation of standard FEM method is defined through shape functions, for a displacement

u_{i}

of an isoparametric element, the interpolation function is (Hughes 1987),

𝑢𝑖ℎX,t=𝐼=1𝑛𝑛𝑒𝑁𝐼𝜉𝑋𝑢𝑖𝑗𝑡, X∈Ω,

(5)

where

n_{e}

is the number of nodes of elements, for a standard four node element the shape functions

N_{I}

are written as,

N_{I} (ξ) = \frac{1}{4} (1 + ξ_{I} ξ) (1 + η_{I} η),

(6)

here

ξ (X)

η (X)

are the expressions of mapping of physical domain to its parent domain. [10]

3.4. Thermo-Mechanical Modelling

Thermoforming is a combined problem of mechanical analysis and thermal analysis, where stresses generation due to mechanical deformation as well as temperature variation are vital. In thermo-mechanical coupled finite element model, accurate evaluation of mechanical stresses and thermal stresses at each point of the physical subdomain must be done under the influence temperature. The heat conduction in the structure is governed by Fourier’s law of conduction [18], straining in the structure generates heat in transient and dynamic processes [11]. Thermo-mechanical material model assumed here a three-dimensional non-linear, transient heat conduction problem for a domain

Ω

bounded by

Γ

, the governing differential equation written as,

\frac{\partial}{\partial x} (k_{x} \frac{\partial T}{\partial x}) + \frac{\partial}{\partial y} (k_{y} \frac{\partial T}{\partial y}) + \frac{\partial}{\partial z} (k_{z} \frac{\partial T}{\partial z}) + Q (x, y, z, t) = ρ c \frac{\partial T (x, y, z, t)}{\partial t},

(7)

where

T (x, y, z)

is the temperature at point and for time

t

Q (x, y, z, t)

is the internal strength of heat source,

ρ

is the density,

c

is the specific heat and

k_{x}, k_{y}, k_{z}

are thermal conductivities in the

x, y, z

directions respectively, at initial conditions

t = 0

, temperature is

T_{0}

[12].

Standard mesh FE model has an inherent, overly stiff phenomenon that causes poor accuracy in solving complex problems, to address this Liu [19] applied the smoothing gradient technique and established the smoothed Galerkin weak form. Further, a node based smoothing finite element method was introduced to construct the smoothing domain of transient thermal mechanical analysis to obtain better results than standard FEM [12]. The balance equations for the coupled problem are composed of force field and thermal field balance equation [13]. By substituting the thermal shape functions of element nodes in the Galerkin weak form for transient heat conduction, the discretized system of equilibrium equations is expressed as following matrix form,

N_{T} \{\frac{\partial T}{\partial t}\} + [K_{T} + K_{T}^{h}] \{T\} = \{P\},

(8)

where

N_{T}

is the thermal capacitance matrix,

K_{T}

is the conduction matrix,

P

is the thermal load vector of the predefined thermal shape functions. After defining the initial temperature field, the respective values at an arbitrary time

t

can be approximated by applying the backward difference technique to the Equation 8.

The governing equations for thermo-mechanical problem over the specific domain

Ω

bounded by

Γ

are written as,

Equilibrium equation : σ_{i j, j} + b_{i} = 0,

(9)

Displacement boundary : u_{i} = u_{Γ} on Γ_{u},

(10)

Stress boundary : σ_{i j} n_{i} = f_{Γ} on Γ_{f},

(11)

Strain displacement relations : ε_{i j} = \frac{1}{2} (u_{i, j} + u_{j, i}),

(12)

where

σ_{}

ε

and

u

are the stress, strain, and displacement,

b

is the body force,

u_{Γ}

and

f_{Γ}

are the displacement and traction on the essential and natural boundaries. The above stress and strain are an expression of thermal expansion coefficient,

σ_{i j} = δ_{i j} λ ε_{k k} + 2 μ ε_{i j} - δ_{i j} (3 λ + 2 μ) α ∆ T (t),

(13)

in the above equation

λ

and

μ

are Lame’s constants, they can be derived from the Poisson’s ratio and Young’s modulus,

δ_{i j}

is the Kronecker delta,

α

is the thermal expansion coefficient, and

∆ T (t)

is the change in temperature with the time

t

. In the Equation 10,

ε_{i j}

is the total strain, which is sum of elastic, plastic, and thermal strain,

ε_{i j} = ε_{i j}^{e} + ε_{i j}^{p} + ε_{i j}^{T} .

(14)

With the temperature field obtained, the thermal stress and strain analysis can be performed using the standard Galerkin weak form,

\int_{Ω}^{} {\{δ ε (u)\}}^{T} \{σ\} d Ω - \int_{Ω}^{} {\{δ u\}}^{T} \{b\}_{} d Ω - \int_{Γ_{f}}^{} {\{δ u\}}^{T} \{f_{Γ}\} d Γ = 0,

(15)

where

u

is the displacement field, which is interpolated using linear shape functions as below,

u = \sum_{i = 1}^{n} Φ_{i} d_{i},

(16)

d_{i}

is the nodal displacement of the node

i

, and

Φ_{i}

is the linear shape function. By solving the Equation 15 using Equation 16, the discretized system of equations for a thermo-mechanical problem can be expressed in the form of matrix as follow,

K_{d} \{d\} = \{F\},

(17)

where

K_{d}

is the stiffness matrix comprised of product of elastic coefficient matrix and strain displacement matrix,

F

is the load vector. For time-dependent non-linearity of materials the Equation 11 is solved by using Newton-Raphson iteration method at each time step.

3.5. Thermoforming Model Development

The thermoforming model developed here is aimed to describe all three, geometric, material, and boundary non-linearities of thermoforming process of sandwich laminate. For this a simplified geometry model is developed considering the actual geometry. A unit cell representation of the sandwich and honeycomb core is shown in the Figure 5 (a). thereby, L is the length orientation, W is the width orientation, and H is the sandwich thickness and out-of-plane direction. The shell element formulation for cell walls as well as face sheet is done using Reissner-Mindlin kinematic assumption. The thermo-mechanical properties like temperature dependent E-modulus from DMA tests and temperature dependent Stress-Strain behavior from tensile tests (DIN EN ISO 527-1) are presented in Figure 4 (a) and (b) respectively. The thermo-physical properties like temperature specific heat capacitance and thermal conductivity are obtained through respective testing methods. Further, validated test results are presented by Minupala [4]. These temperature dependent material properties are taken as the input for the respective material models.

As there exists two different materials, face sheet is modelled using MAT_Reinforced_Thermoplastic, and core is modelled using MAT_Elastic-Viscoplastic_Thermal, both the materials are combined with the MAT_Thermal_Isotropic to form a thermoforming model in LS-DYNA interface.

Figure 5. (a) Representative idealized sandwich honeycomb cell (b) Initial thermal state of the sandwich after heating step in thermoforming process.

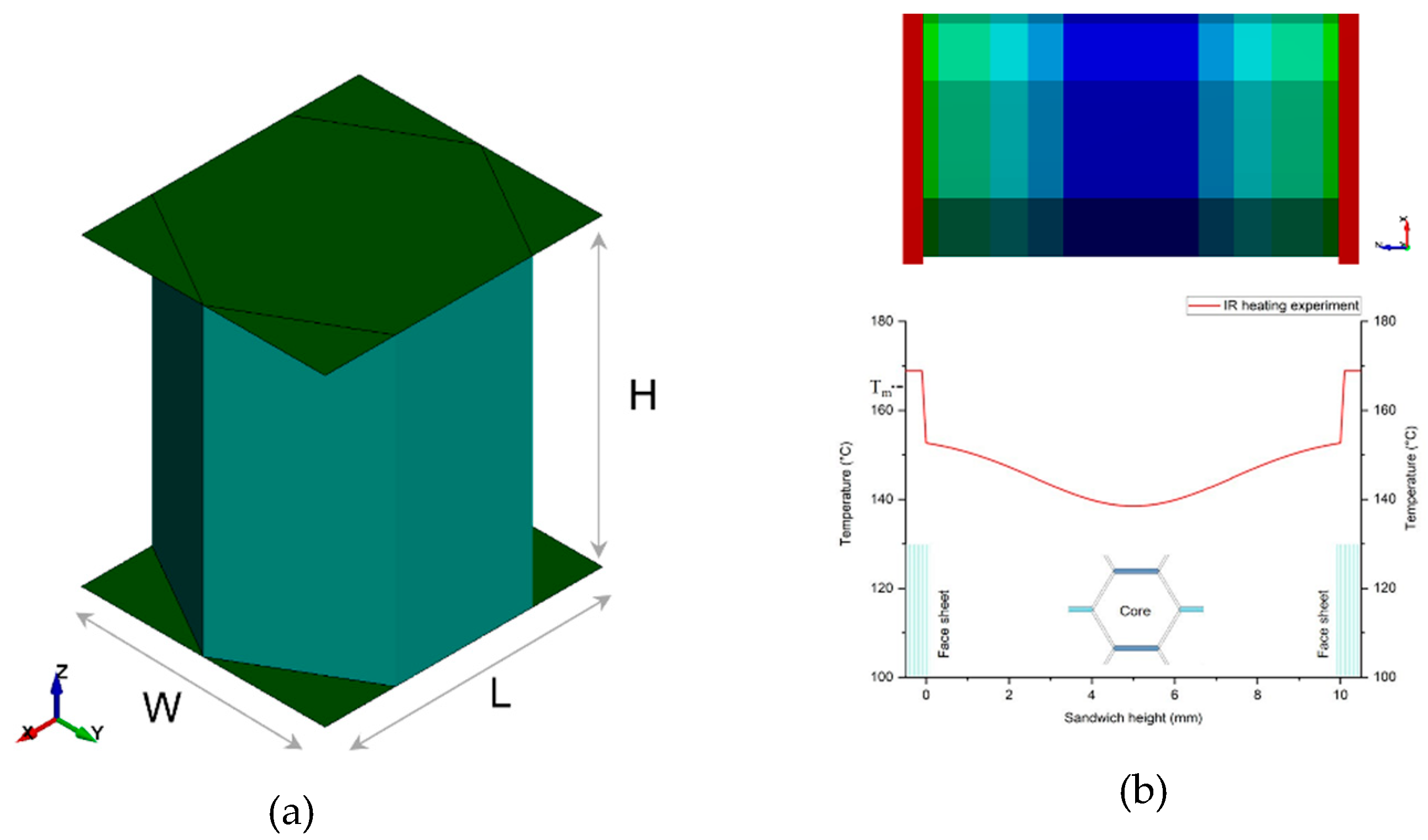
The thermal state of the sandwich laminate is achieved through IR-heating process, where the sandwich laminate is heated from top and bottom sides so there is a symmetrical thermal state through the thickness. Numerous experiments were conducted by controlling intensity of the heat and heating time, Glaesser explained this technique in detail in his thesis work [6]. The finalized temperature profile of the sandwich, where face sheet is brought to matrix melt temperature T_m and core is at varying temperatures from T_g and below as shown in Figure 5 (b).

4. Results and Discussion

4.1. Thermoforming

Thermoforming results of the PP and PP/GF based Organosandwich components are shown in the Figure 6 (a), which is a simplified sandwich model formed between positive and negative tool forms. The form structure is a demonstrator part, which is developed to analyze different forming mechanisms and forming parameters.

Here, we show the optimized thermoforming results with controlled laminate temperature and forming velocity. Owing to sandwich bending principle, the top face sheet experiences in-plane tension, on the other side bottom face sheet experiences in-plane compression [8]. With tension and compression on top and bottom sides, the core exhibits pure out-of-plane shear deformation under bending [14]. The cross-ply as face sheet which has fiber orientations in 0° and 90°, in Y and X directions respectively, show in-plane shear stresses in 3D forming area as shown in Figure 6 (b). In the 3D forming region as shown in Figure 6 (b), it is observed that shear stresses are highly concentrated and larger in magnitude compared to 2D forming region. The in-plane shear stresses will develop axial compression in the transition between shear compression and shear tension. Therefore, unwanted deformations like wrinkle formation as in Figure 7 occur only in distinctive areas of the cross-ply laminate depending on the fiber orientation [7].

4.2. Critical Stress Analysis

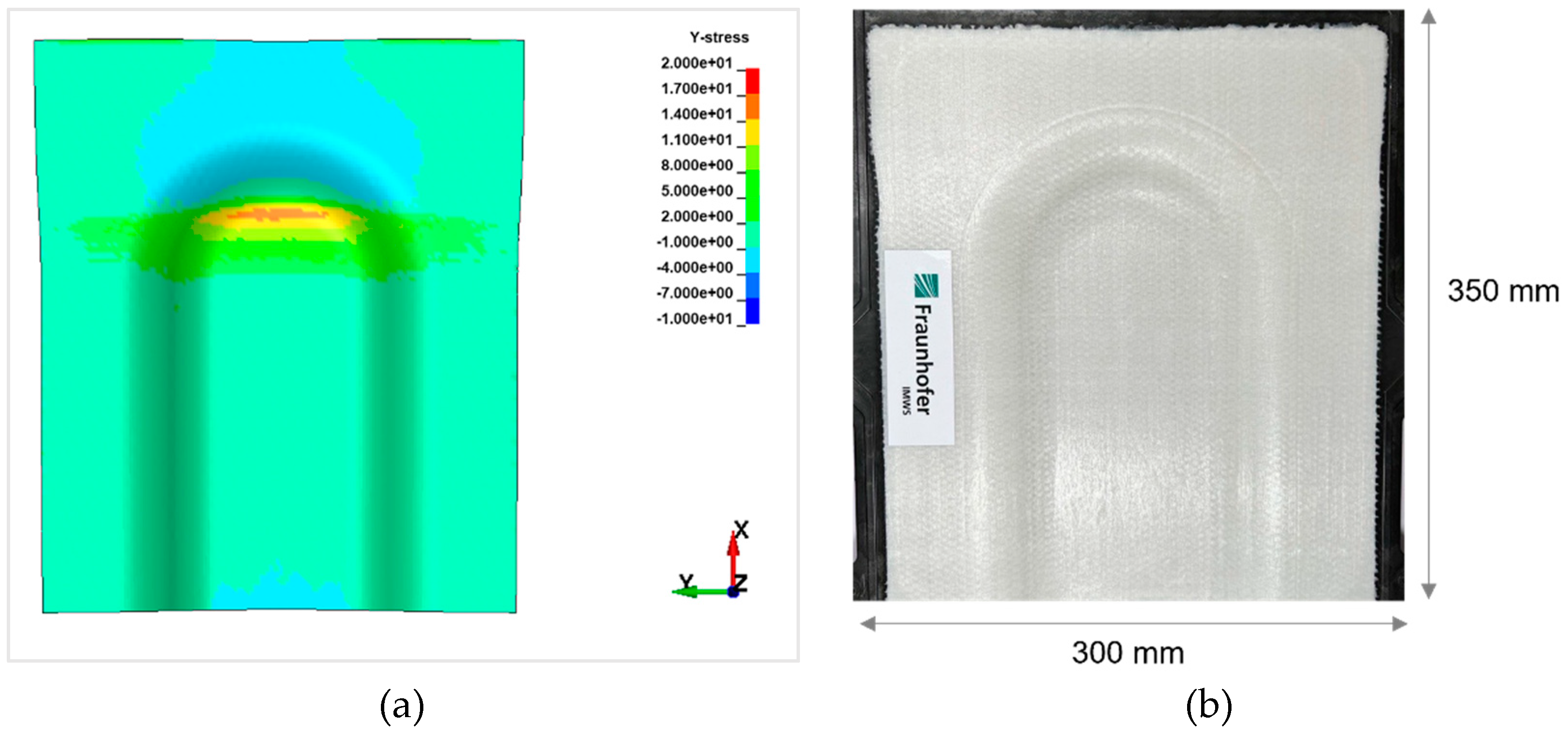
Sandwich bending for a global tension on the top side exerts global compression on the bottom side. Examining a cross-ply under forming or draping, whilst fibres in the principal axis are subjected to tension, the transverse fibres show compression behavior. Combining these two effects, the in-plane instabilities likely to happen on the bottom face sheet are wrinkling or buckling. For a chosen sandwich construction and selected 3D part geometry, the thermoforming results show a surface waviness on the bottom cover layer in 3D forming region as shown in Figure 7. With the detailed study of the results and stress plots in the specific region, the outer ply oriented at 90° on the bottom face sheet is subjected to local tension in X-direction, and the inner ply oriented at 0° on the bottom face sheet is subjected to local compression in Y-direction.

In Figure 8, the inner UD-ply oriented in 0° to Y-axis shows maximum tensile stress 17 MPa and maximum compressive stress 5.2 MPa. The axial compressive stresses in the respective ply are above the maximum critical compressive stress for wrinkle formation, as mentioned in the Equation 2,

σ_{w r}

is 5.03 MPa. As the maximum compressive stresses in the ply exceeds the limit the wrinkle formation on the coverlayer is inevitable. The prediction of mathematical model and simulation results show critical regions in the thermoforming of Organosandwich, which can be used for the design or process optimization.

4.3. Considerations and Product Optimization

From thermoforming simulations, the identified critical regions can be rectified with different approaches like optimization of process parameters, boundary conditions and design modification. Although process parameters like laminate temperature and tool velocity influence both in-plane and out-of-plane buckling, the wrinkle effect in Figure 7 is not their influence. From numerous experiments, the thermal state of the laminate and velocity ramp of the tool are optimally finalized; further modifications in these parameters lead to adverse effects like buckling. The second approach is modification of boundary conditions, which means the holding position of the laminate inside tool with grippers and clamps. There exists already a clamping system in the tool around U-profile (acts like clamping ring in classical forming technologies [15]), which minimizes the bending stresses, its influence was discussed in the previous work [16]. In composite laminate forming, this type of wrinkles are rectified by using a spring-loaded frame gripper system; the springs act as tensioners and generate in-plane tension during forming in the respective direction [17]. The pre-consolidated laminate is placed inside a frame with specific springs and transported to the heating station and forming machine, this kind of gripper system inside the process slows down the manufacturing cycle as hitching and removing the laminate will add additional steps. With time constraints, the idea of including additional steps to the process is not taken into consideration. The existing vacuum gripper system inside the tool middle of the form cavity stays as the standard.

The direct basis of optimization is to get rid of critical axial compressive stresses, when existing process parameters does not allow further modifications, the remaining option is designing modification. To make any changes to the existing part design, one needs to investigate the forming mechanisms at first and their influence on the structural performance subsequently. As the stress concentration is limited to 3D region, a minor change is made to the existing shell structure as shown in Figure 9.

The existing design as shown Figure 9 (a) of uniform thickness through the structure is modified to a reduced thickness of approximately 10% in the three-dimensional bending region, as shown in Figure 9 (b). This reduced thickness generates out-of-plane compression inside the sandwich, and as a reaction, an in-plane local tension is developed, which counters the previously existing critical wrinkle stress. The results of the modified part design are shown in Figure 10. The maximum compressive stresses in Y-direction for UD-ply orientation in 0° are 3.5 MPa, whereas average maximum compressive stresses are around 1 MPa, see Figure 10 (a), which are way below the limit of

σ_{w r}

5.20 MPa. With this design modification, there is a drop in maximum axial compressive stresses by 33% during forming.

Cross-ply of 0°/90° orientation is good at tensile loads on the sandwich structure. Therefore, the top cover layer on the demonstrator part shows no defects in both designs. Thermoforming trials, with the Figure 9 (a) design, have always resulted in wrinkles on the bottom cover layer, with the modified design as Figure 9 (b) does not show any wrinkles, see Figure 10 (b).

5. Conclusions

The PP-based sandwich laminates tested for thermoforming bahavior under different conditions described in this paper. All the thermoforming parameters tested through numerical modelling validated with experimentally produced results. At the end, thermoplastic honeycomb sandwich laminate’s limitations for thermoformability are described. A brief introduction to the thermoforming of thermoplastic sandwich structure was given. With advanced numerical tools, a finite element model is developed to describe the complex thermoform process, making the TSM technology suitable for industrial applications. As the novel thermoforming process is aimed for a high-volume production process like automotive applications, critical deformations can be analyzed with this numerical method at early stages of part design and optimizations are provided by an economical way. Because the wrinkle deformations in the CFRTP could influence the structural properties of a part and decrease the tensile and compressive strength up to 20 – 30 % [25]. Therefore, it is necessary to identify the critical regions in the part through its manufacturing process and eradicate them with optimal solutions. This research work provides the analysis of such deformations in the sandwich structure and helps in optimizing the thermoforming process and further contributes to structural performance of a sandwich component.

Author Contributions

Conceptualization, Minupala, V.K. and Glaeser, T.; methodology, and software, Minupala, V.K.; validation, Minupala, V.K. and Glaeser, T.; formal analysis, Minupala, V.K.; investigation, Glaeser, T.; resources, Zscheyge, M.; writing—original draft preparation, Minupala, V.K.; writing—review and editing, Zscheyge, M.; visualization, Minupala, V.K.; supervision, Feldmann, M.; Altenbach, H.; project administration, Glaeser, T.; funding acquisition, Zscheyge, M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Federal Ministry of Education and Research (BMBF), under the following projects, HyWaSand and HybridLFTSandwich.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Feldmann and approved by the Institutional Review Board (or Ethics Committee) of Fraunhofer IMWS (date of approval 01.12.2023).

Acknowledgments

I hereby, thank our technical engineer Peter Stache and our lab assistant Lars Brink for technical support the manufacturing trials.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Fan, X. Investigation on processing and mechanical properties of the continuously produced thermoplastic honeycomb. Ph.D. Thesis; Katholieke Universiteit Leuven, Leuven, 2006.
Gibson, L.J.; Ashby, M.F. Cellular solids: Structure and properties, 2nd ed.; Cambridge University Press: Cambridge, 1997, ISBN 0-521-49911-9.
Pflug, J.; Bart, V.; Ignaas, V.; Philipp, B.; Dirk, V. CONTINUOUSLY PRODUCED HONEYCOMB CORES. Honeycomb Core Materials 2003.
Minupala, V. K.; Glaesser, T.; Zscheyge, M. Simulation of thermoforming process of thermoplastic based sandwich laminates made of cross-ply and honeycomb core; Ed., 5th. Internationa Conference & Exhibition on Thermoplastic Composites, Bremen, 13 - 15 October 2020.
Pflug, J.; Zerling, F.; Schlimper, R.; Minupala, V.K.; Glaesser, T. Eds. Continuous Production of Thermoplastic Honeycomb Sandwich Panels for Thermoformed and Functionalized Automotive Parts; International Conference on Sandwich Structures (ICSS-13), Knoxville, TN, USA, 23-26 October 2022, 2022.
Gläßer, T. Beitrag zur großserientauglichen Fertigung von thermoplastischen endlosfaserverstärkten Sandwichbauteilen. Ph.D. Thesis; Otto-von-Guericke-University Magdeburg, Germany, 2022.
Bhattacharyya, D., Ed. Composite sheet forming; Elsevier: Amsterdam, Oxford, 1997, ISBN 0-444-82641-6.
Robert, P. L.; Weichuan, L.; Uy, M. Facesheet Wrinkling in Sandwich Structures. NASA/CR-1999-208994 1999.
William, D. Sandwich Contruction: A practical approach for the use of designers, 1947.
Belytschko, T.; Organ, D.; Krongauz, Y. A coupled finite element-element-free Galerkin method. Computational Mechanics 1995, 17, 186–195. [CrossRef]
Li, G.; Cinefra, M.; Carrera, E. Coupled thermo-mechanical finite element models with node-dependent kinematics for multi-layered shell structures. International Journal of Mechanical Sciences 2020, 171, 105379. [CrossRef]
Zhang, S.; Cai, Y.; Wang, H.; Li, E.; Li, G.; Wu, Y. A fast reanalysis solver for 3D transient thermo-mechanical problems with temperature-dependent materials. Computers & Structures 2020, 238, 106298. [CrossRef]
Liu, Y.; Long, H.; Zhang, S.; Song, J.; Zhou, Q.; Wei, Y. Coupling effect of strain gradient strengthening and thermal softening on the microscale plastic behavior of metallic materials. European Journal of Mechanics - A/Solids 2023, 102, 105117. [CrossRef]
Heimbs, S. Sandwichstrukturen mit Wabenkern: Experimentelle und numerische Analyse des Schädigungsverhaltens unter statischer und kurzzeitdynamischer Belastung. Doctoral Thesis; University of Kaiserslautern, 2008.
Advani, S.G.; Hsiao, K.-T. Manufacturing techniques for polymer matrix composites (PMCs); Woodhead: Cambridge, 2012, ISBN 978-0-85709-625-8.
Minupala, V.K. Numerical analysis of thermoforming behavior of sandwich components with continuous fiber reinforced thermoplastic face sheets and honeycomb core. Master thesis; University Duisburg-Essen, Essen, 03.12.20.
Haanappel, S. Forming of UD fibre reinforced thermoplastics: a critical evaluation of intra-ply shear: A critical evaluation of intra-ply shear; University of Twente, Enschede, 2013.
Fourier, J. Theorie analytique de la chaleur, par m. fourier. Chez Firmin Didot, père et fils; 1822.
Liu, GR. A generalized gradient smoothing technique and the smoothed bilinear form for Galerkin formulation of a wide class of computational methods. Int J Computational Methods 2008;5(02):199–236.
Minupala, V. K.; Vynhal, M.; John, M.; Zscheyge, M. Simulation of process techniques involved in advanced manufacturing of CFRTP composite parts. 6th. International Conference & Exhibition on Thermoplastic Composites, Bremen, 12 - 13 October 2022.
Fraunhofer Piolt Plant Center for Polymer Synthesis and Processing PAZ. Fraunhofer PAZ (polymer-pilotanlagen.de) (accessed on 15.12.2023).
HyWaSand Effiziente Sandwich-Leichtbaustrukturen mit hoher Oberflächengute. Hybride Materialien | HyWaSand (werkstoffplattform-hymat.de) (accessed on 15.12.2023).
ThermHex Waben GmbH: Thermoplastic polypropylene honeycomb cores for lightweight sandwich panles and composites. ThermHex - Honeycomb cores for lightweight sandwich panels (accessed on 15.12.2023).
Glaesser, T.; Stache, P.; Zscheyge, M.; Koelzig, K. International patent on Method for producing a sandwichcomposite component with pressed two- or three-dimensional shape and such a sandwich component; WO 2020/200796 A2; Fraunhofer-Gesellschaft zur Förderung der Angewandten Forscgung E. V.
Nartey, M.; Zhang, T.; Gong, B.; Wang, J.; Peng, S.; Wang, H.; Peng, H.-X. Understanding the impact of fibre wrinkle architectures on composite laminates through tailored gaps and overlaps. Composites Part B: Engineering 2020, 196. [CrossRef]
Glaesser, T.; Stache, P.; Zscheyge, M. TS-Moulding Fertigungstechnologie zur großserientauglichen Herstellung endlosfaserverstärkter Thermoplastsandwichstrukturen: Fachaufsatz Werkstoffe, 2022.

Figure 2. FEA workflow of process simulation of thermoforming and part design.

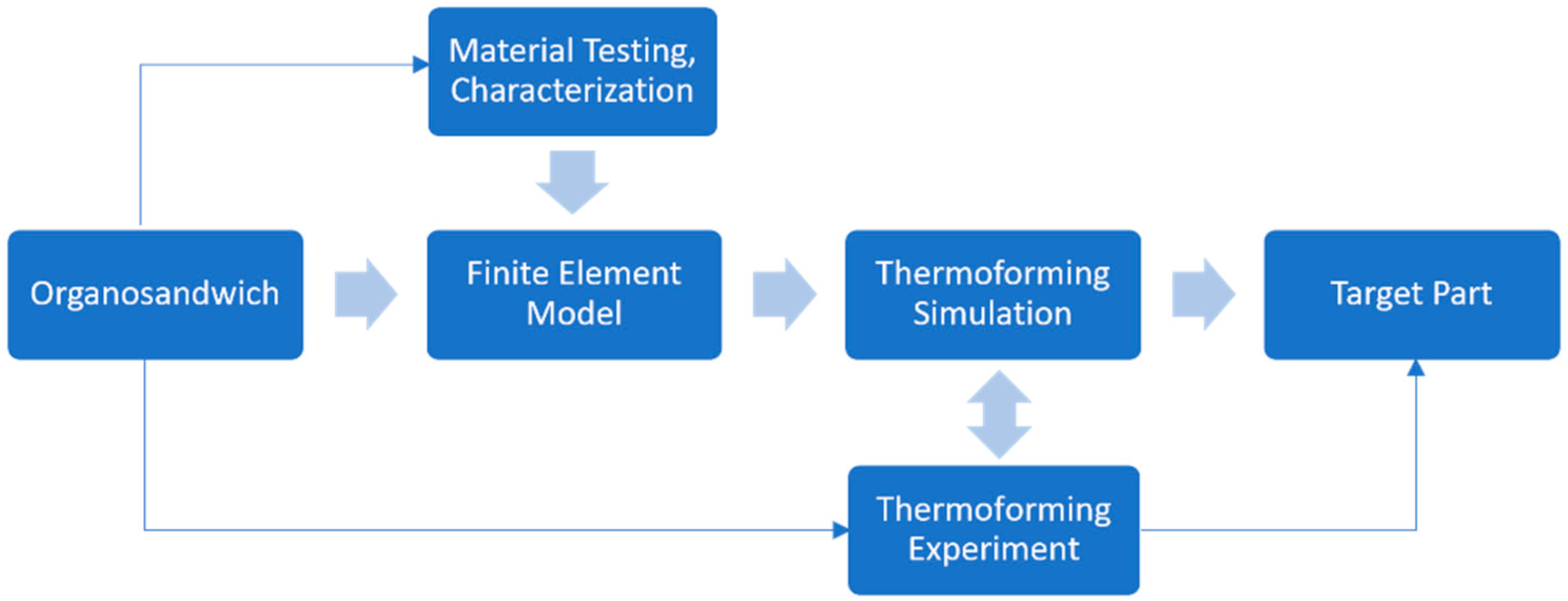
Figure 3. Localized non-harmonic wrinkle mode of sandwich cover layers [8].

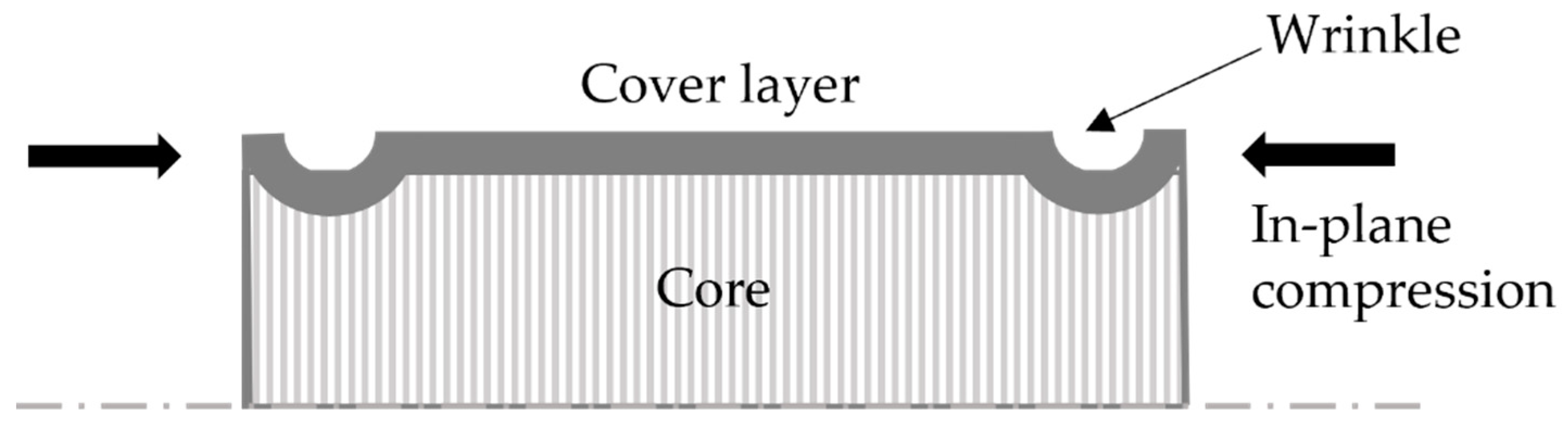
Figure 4. Thermo-mechanical material properties (a) temperature dependent E-modulus, (b) temperature dependent Stress-Strain curves.

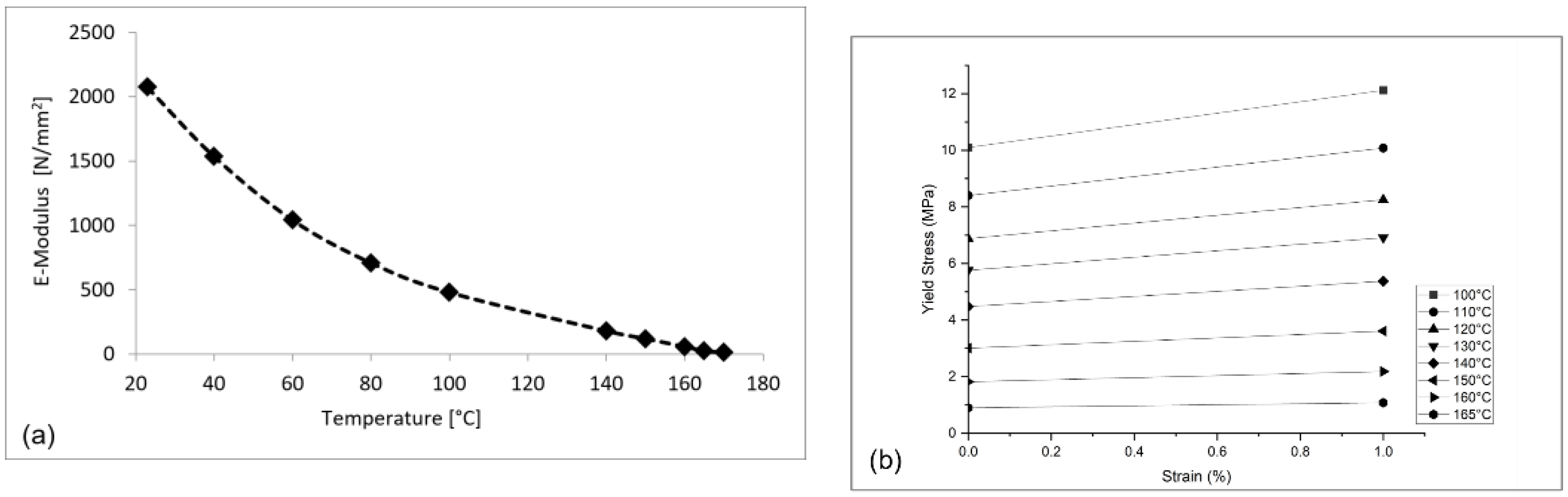
Figure 6. Simulation showing (a) Thermoformed Organosandwich 3D-shell demonstrator, (b) shear stresses in the bottom cover layer.

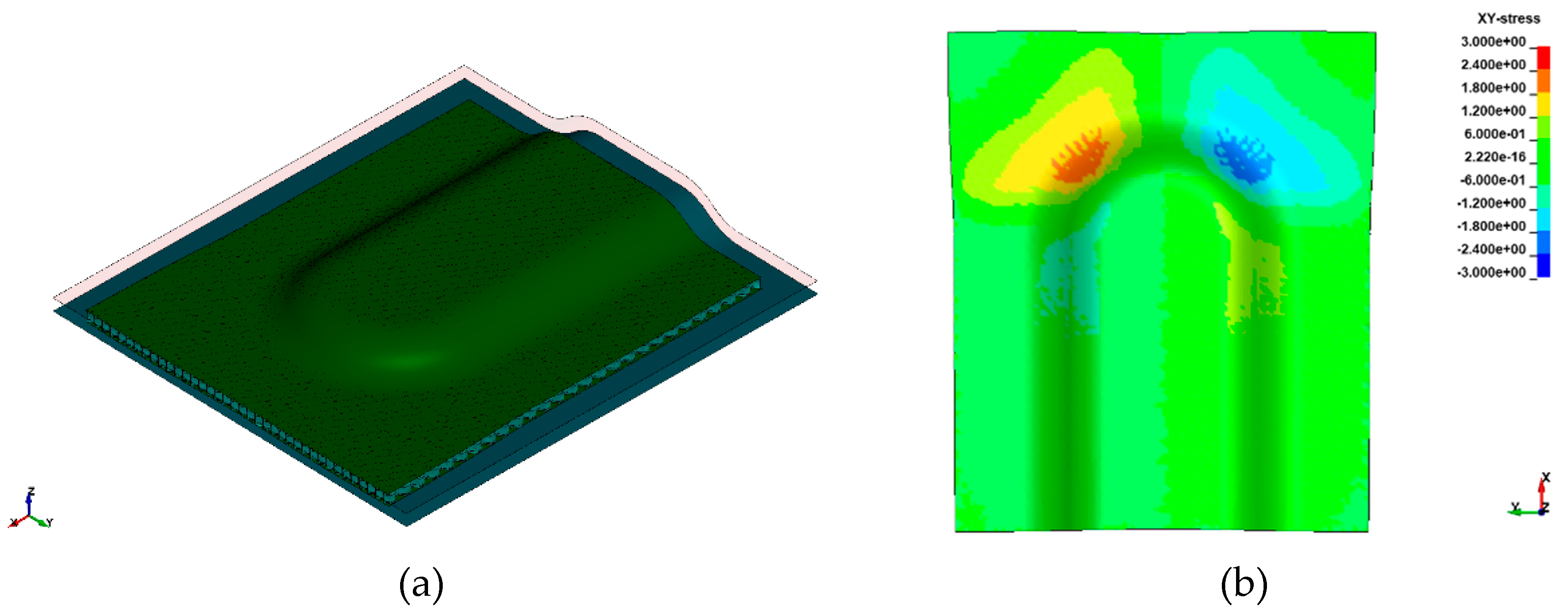
Figure 7. Thermoformed Organosandwich 3D-shell demonstrator part showing wrinkles on bottom cover layer.

Figure 8. Compressive stresses inside the inner ply of bottom layer, indicating wrinkles [in MPa].

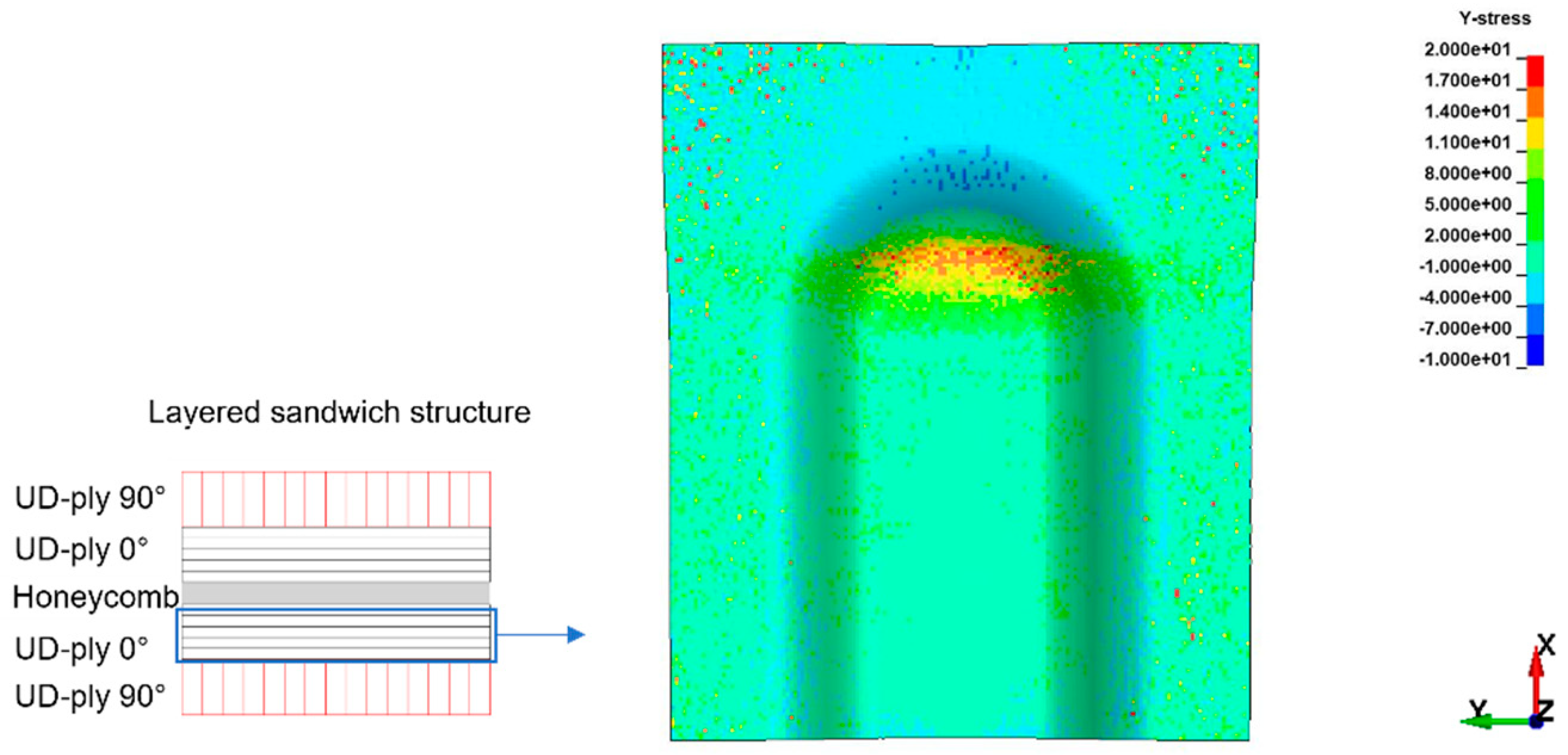
Figure 9. 3D-shell demonstrator, (a) original design with uniform thickness, (b) modified design with reduced thickness [6].

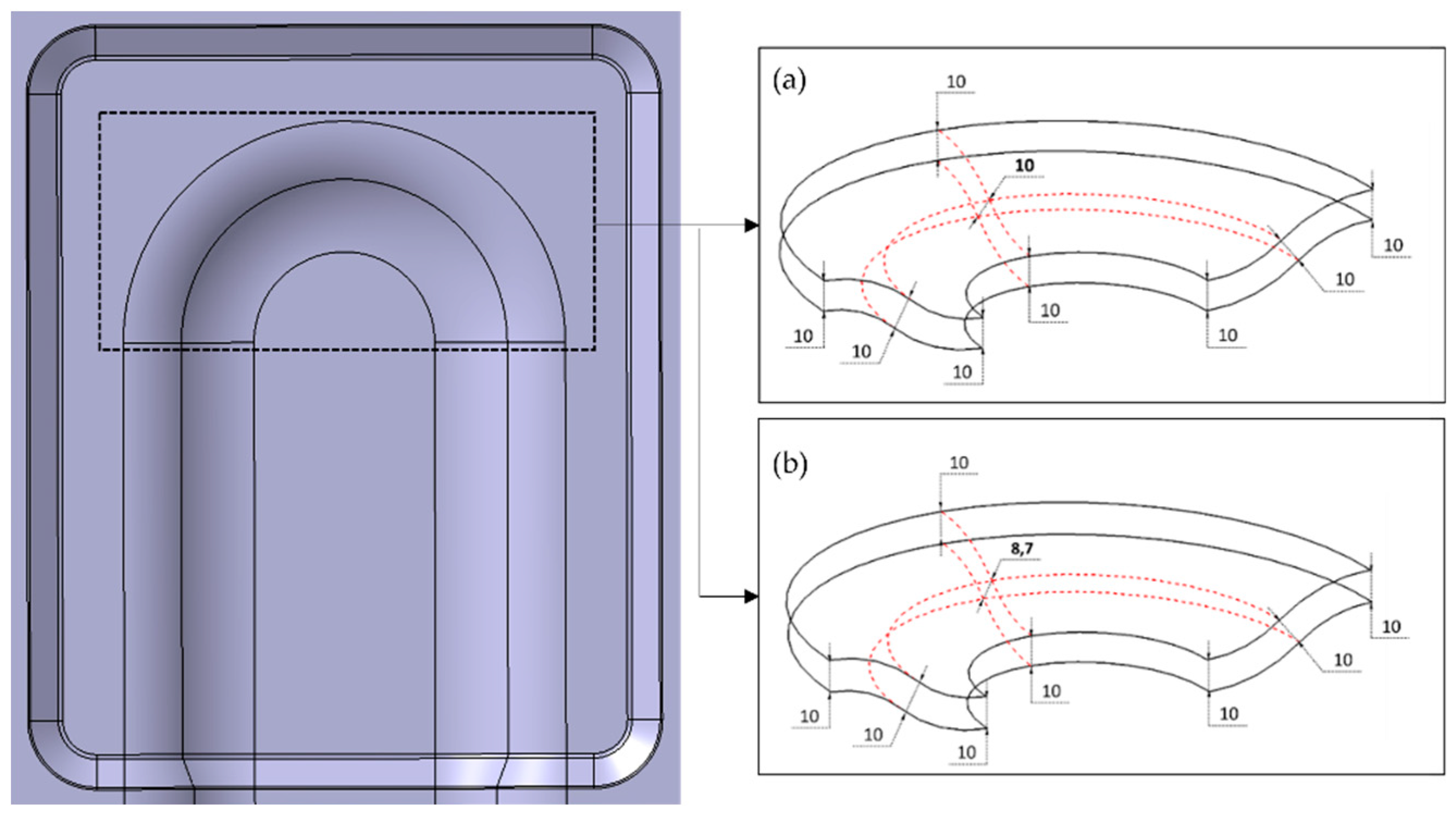
Figure 10. Modified design results (a) compressive stresses in the UD-ply of bottom cover layer, (b) thermoformed part of modified design.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Numerical Modelling of the Thermoforming Behavior of Thermoplastic Honeycomb Composite Sandwich Laminates

Abstract

1. Introduction

2. Thermoplastic Sandwich Forming

3. Materials and Finite Element Modelling

3.1. Sandwich Material Description

3.2. Coverlayers Wrinkle Analysis

3.3. Spatial Discretization of Organosandwich

3.4. Thermo-Mechanical Modelling

3.5. Thermoforming Model Development

4. Results and Discussion

4.1. Thermoforming

4.2. Critical Stress Analysis

4.3. Considerations and Product Optimization

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe