Robust Method for Unsupervised Scoring of Inmunohistoquemical Staining

Immunohistochemistry is a powerful technique, widely used in biomedical research and clinics, that allows to determine the expression levels of some proteins of interest in tissue samples by means of the intensity of color due to the expression of biomarkers using specific antibodies. As such, immunohistochemical images are complex and problematic to be quantified. Recently we proposed a novel method including a first separation stage based on nonnegative matrix factorization (NMF) that achieved good results. However, that method was highly dependent on sparseness and non-negativity parameter choice and on algorithm initialization. Furthermore, the previously proposed method needed a reference image as starting point for the NMF algorithm. In the present work, we propose a new, simpler and robust method for the automated unsupervised scoring of immunohistochemical images based on bright field. Our work is focused on images from tumor tissues marked with blue (nuclei) and brown (protein of interest). The new proposed method represents a simpler approach that, in one side, avoids the use of NMF for the separation stage, and in the other side, circumvents the need for a control image. This new approach determines the subspace spanned by the two colors of interest by means of principal component analysis (PCA) with dimension reduction. This subspace is a two-dimensional space, allowing the finding of color vectors by considering the peaks of density of points. The method also develops a new scoring stage by avoiding, again, reference images, making the procedure more robust and less dependent on the parameters. Experiments for the semi-quantitative scoring of images in five categories exhibit promising and consistent results when compared to manual scoring carried out by experts.

Keywords:

Subject: Engineering - Telecommunications

1. Introduction

Detection of biomarker expression in tissue images is a common technique both in research laboratories and in the clinic. This detection is carried out through the use of chromogens of different colors that bind to the antigens of interest using an antibody-antigen detection system, a technique known as Immunohistochemistry (IHC) [1]. This allows the presence of the chromogen and the protein to which it binds by observing the tissue using bright field microscopy. Capturing images of the tissue allows the subsequent preservation and analysis of the tissue expression pattern of analyzed proteins. Usually, the quantification of the presence, concentration and distribution of the chromogen is carried out manually by viewing and comparing the images by experts.

Two widely used chromogens are 3,3’-Diaminobenzidine (DAB) and Hematoxylin (H) [2,3,4,5,6]. While the presence of DAB is detected as a brown stain, H appears as a blue one. When combined, H stain marks cells nuclei, whereas DAB reveals the greater or lesser presence of the protein of interest. The IHC image evaluation and quantification procedure lacks objectivity, as it is a subjective method done by experts, exposed to observer variations. Indeed, even the same observer can make different evaluations of the same image at different times [7]. Furthermore, manual scoring is affected by visual distortion due to the perception of colors and their intensity depending on the surrounding colors [8]. This is particularly important in protocols that use two dyes. Finally, IHC visual scoring it is a time-consuming procedure for experts. For this reason, demand for automated scoring procedures is increasing in laboratories and in the clinic [9]. This type of protocols must include a stage for separating both stains to perform the scoring with greater reliability.

Scoring systems can be classified on those based on the perceived intensity of staining, and those based on the percentages of stained cells, while some others mix both criteria. Regarding the most used categories, they range from the simplest systems that divide tissue samples into positive or negative, depending on whether or not the observed staining exceeds certain thresholds; to those that use a set of scoring levels depending on the greater or lesser presence of stain, the so-called semi-quantitative scoring systems [8]. Although some platforms and applications for semiquantitative scoring of IHC images already exist, they require the intervention of researchers as well as reference images. Examples of these systems are QuPath [10], IHC Profiler [11] or DAB-quant [12].

The stage of stain separation is necessary in automated scoring systems, since it allows the obtention of image features based on each stain. The separation stage cannot be performed in the RGB color space, because the concentration of the light-absorbing material follows the Beer-Lambert law (although not exactly, due to some degree of dispersion). For this reason, a transform based on this law is applied to the RGB image, obtaining the coordinates of each pixel in a new space: the optical density (OD). Within this space, the intensity of each coordinate can be considered as a linear combination of the intensities due to each staining [13].

Separation methods in the literature can be classified into two categories: supervised and unsupervised (or blind) methods [14,15]. In the first case, the coordinates of each used stain are known in the OD space; otherwise, they require the intervention of the observer or the use of reference images to complete their calculation. In the second case, unsupervised methods use techniques like independent component analysis (ICA) [16,17], non-negative matrix factorization (NMF) [13,18] or non-negative least squares (NNLS). These techniques suffer from a strong dependence on initialization. Thus, these methods need a previous estimation of the stain vectors coordinates to achieve a correct separation, guiding the search towards the correct solution. Some approaches which are based on deep learning [4,19] need a large number of training images, so they cannot be considered as unsupervised techniques.

Some approaches have exploited singular value decomposition (SVD) in order to calculate the subspace where the OD data lie [20,21] in the context of supervised methods. Principal component analysis (PCA) works in the same direction as SVD, searching for the principal direction of the data: those that preserve the greatest quantity of variance or power (when uncentred PCA is performed) [22].

In this work, we propose an unsupervised method for comparative biomarker quantification that improves the method presented in our previous work [14]. Accordingly, this new methodology represents a simpler and more robust method for color separation, with very low dependence on the selected parameters, and a more accurate quantification without the need for reference or control images.

We circumvent the use of NMF for the stain separation stage, whose results are very dependent on the starting point. Instead, the proposed method exploits the concentration of DAB (brown) and H (blue) to estimate the vectors associated to the color of both stains. This stage has been provided with robustness, in order to achieve consistent results for the estimation of the stain vectors with no prior information, even avoiding the use of reference images that the method in [14] needs.

For the scoring stage, features whose values mostly increase with the concentration of the stains helped us to develop a procedure for the initialization of the clustering algorithm (k-means). While in our previous work a set of three parameters, together with the use of two reference images were needed, in the present work the initialization procedure provides excellent results for common values of the two parameters that we use and, again, avoiding the use of reference images. This makes totally unnecessary any intervention of the observer and allows a totally automated procedure.

2. Methods

We developed an automated and unsupervised procedure for the scoring of IHC images with two stains: Hematoxylin and DAB. The quantification of the set of images is done in three steps: stain separation, feature extraction and, finally, clustering and scoring. A semi-quantitative scoring system clusters the images in five groups and assigns scores from “1+” to “5+” for each image, being “1+” the lowest level of DAB expression.

2.1. Stain separation

The stain separation step is carried out within the color space given by the transform provided by the Beer-Lambert Law. Let

I_{m} \in R^{3 \times N}

be the matrix of RGB intensities of the mth analyzed image, where N is the total number of pixels of each color plane. Then the relative optical density matrix for this image,

X_{m}

, is obtained as

X_{m} = - log (\frac{I_{m}}{I_{o}}),

(1)

where

I_{o}

is the maximum level of intensity at each pixel (255 for 8 bit images) and the function

log (I_{m})

is applied to each entry of the matrix

I_{m}

. This provides a representation of each pixel in a

R^{3}

space where each color corresponds to a direction, being a higher darkness of the color represented by a higher norm of the vector. So, each color (including its darkness) can be represented by the coordinates of its corresponding vector within this space. Since the image was obtained by means of an IHC procedure, the color vector of each pixel lies, mainly, within the subspace generated by the color vectors associated to both stains: that due to H (blue) and that due to DAB (brown). This allows to estimate the matrix

X_{m}

as [13]

{\hat{X}}_{m} = W_{m} H_{m},

(2)

where

{\hat{X}}_{m}

is the matrix that estimates

X_{m}

W_{m}

is a

3 \times 2

matrix whose columns are the color vectors associated to both stains for mth image and

H_{m}

is a

2 \times N

matrix whose rows are the intensities or activations of each column of

W_{m}

at each pixel of the mth image.

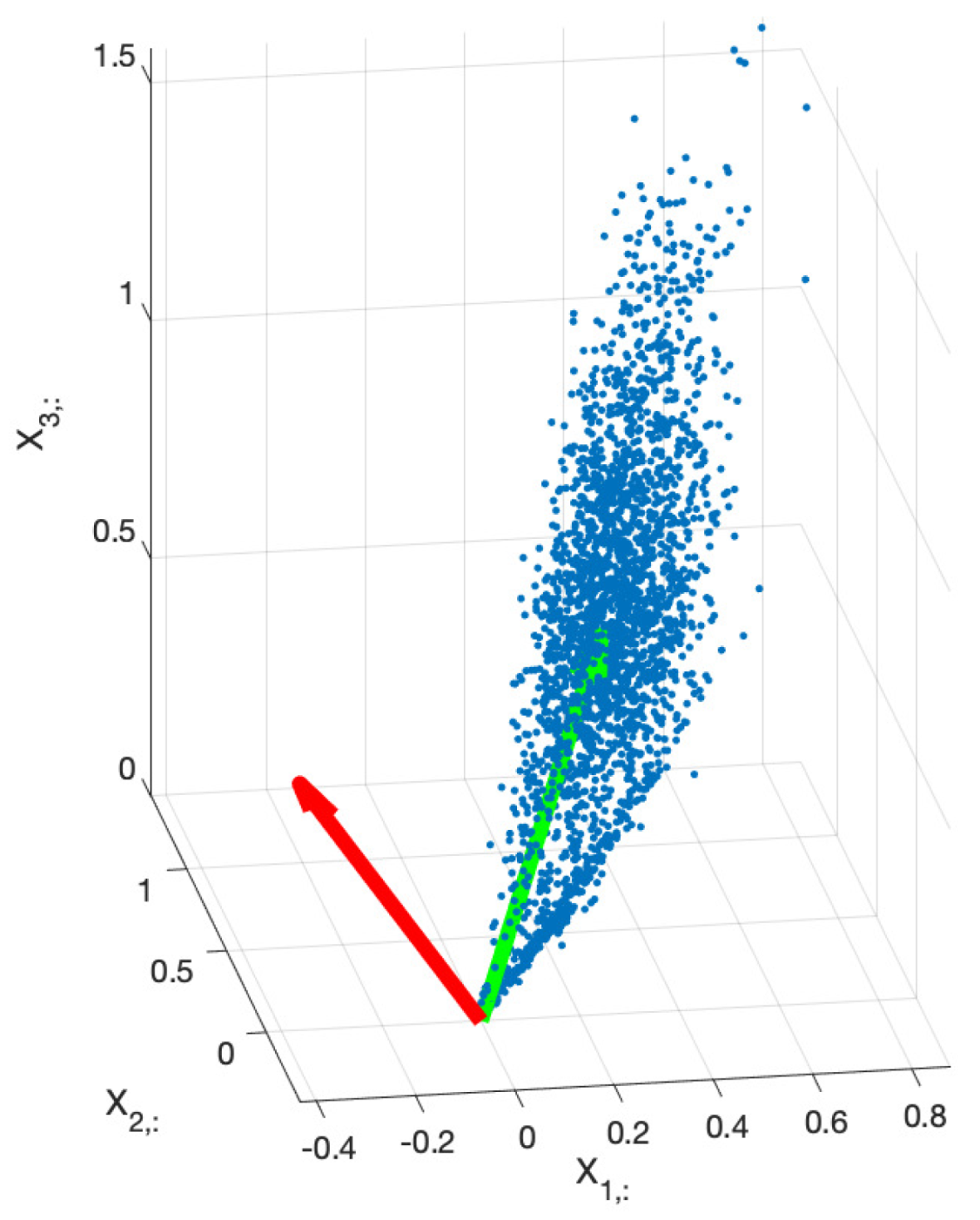
We exploit this fact in order to simplify the problem by means of dimension reduction. The subspace generated by the columns of

W_{m}

is found by means of the application of uncentred Principal Component Analysis (PCA) to the matrix

X_{m}

. This provides the principal directions of the data, that lie within the above mentioned subspace (although the principal directions do not have to coincide with the columns of

W_{m}

) as can be seen in Figure 1.

Let

Q_{m} = [\begin{matrix} {q_{m}}_{1} & {q_{m}}_{2} & {q_{m}}_{3} \end{matrix}]

(3)

be the unitary matrix whose columns are the eigenvectors of

R_{m} = X_{m} X_{m}^{T} / N

and

L_{m} = diag {{L_{m}}_{1}, {L_{m}}_{2}, {L_{m}}_{3}}

(4)

be the diagonal matrix whose nonzero entries are the eigenvalues of

R_{m}

. The superscript T stands for transpose. Both the eigenvectors and the eigenvalues are in descending order. Since

X_{m} \approx {\hat{X}}_{m}

, the principal subspace is given by the two first columns of

Q_{m}

, as the third eigenvalue,

{L_{m}}_{3}

, is very small compared to

{L_{m}}_{1}

and

{L_{m}}_{2}

. The columns of

X_{m}

are projected onto the principal subspace (the plain defined by the first two principal direction), thus obtaining the

2 \times N

matrix of principal components

Z_{m} = [\begin{matrix} \sqrt{{L_{m}}_{1}^{- 1}} \cdot {q_{m}^{T}}_{1} \\ \sqrt{{L_{m}}_{2}^{- 1}} \cdot {q_{m}^{T}}_{2} \end{matrix}] \cdot X_{m} .

(5)

Since all columns of

X_{m}

lie at the first octant, the color vectors are relatively close at

R^{3}

Euclidean space. A simple projection onto the

R^{2}

subspace defined by

{q_{m}}_{1}

and

{q_{m}}_{2}

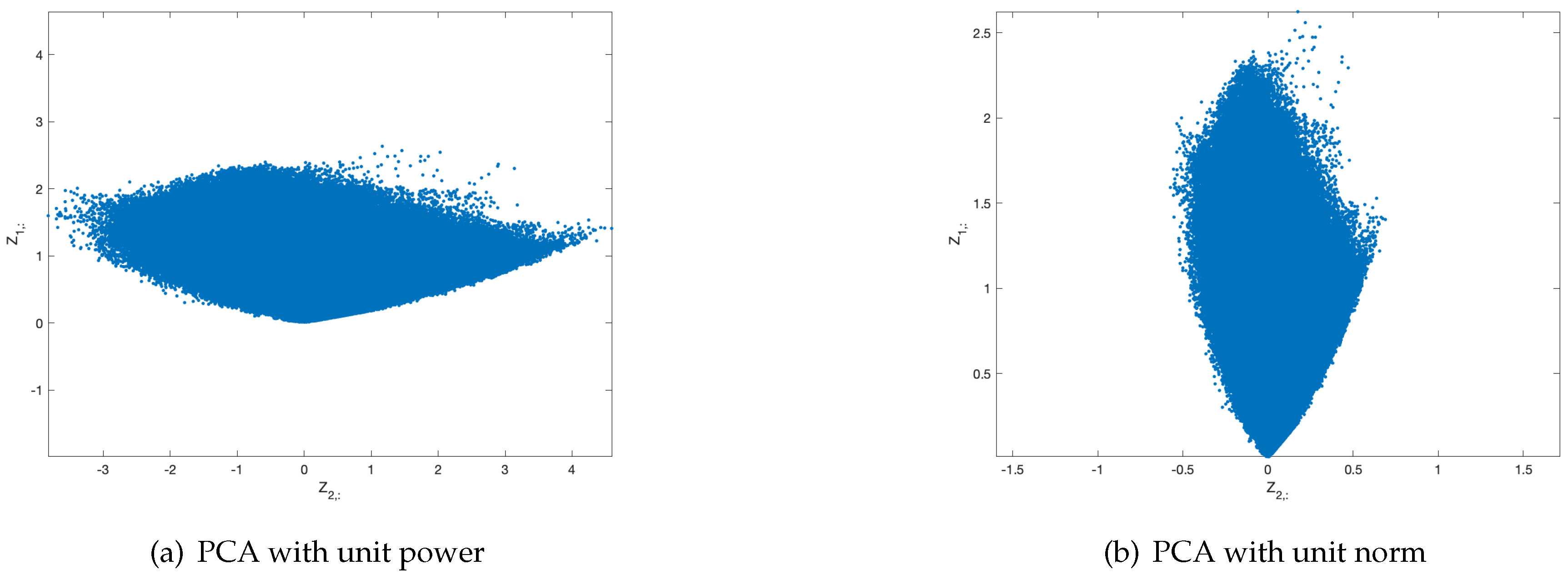
, keeping the scales of the principal components would lead to a 2D scattering where it would be difficult to precisely distinguish the color vectors associated to each stain. This is the reason why the columns of

X_{m}

are projected onto the subspace defined by

{q_{m}}_{1} \sqrt{{L_{m}}_{1}}

and

{q_{m}}_{2} \sqrt{{L_{m}}_{2}}

, i.e., PCA with unit-power principal components is performed [22]. This expands the scattering on the second principal component direction, as we show in Figure 2, and allows to recover the stain color vectors more accurately.

2.1.1. Stain color basis estimation

The next step of the procedure consists in the estimation of the two basis vectors for the stain colors, i.e., the columns of the matrix

W_{m}

. Due to the projection in (5) the columns of this matrix are projected into the same subspace defined by the principal directions

B_{m} = [\begin{matrix} \sqrt{{L_{m}}_{1}^{- 1}} \cdot {q_{m}^{T}}_{1} \\ \sqrt{{L_{m}}_{2}^{- 1}} \cdot {q_{m}^{T}}_{2} \end{matrix}] \cdot W_{m} .

(6)

Let

θ_{m} (n)

and

r_{m} (n)

be the angle and norm of the nth column of

Z_{m}

. Since, in many pixels, only one stain is dominant, the values of

r_{m} (n)

are higher around the basis vectors. So the columns of

B_{m}

are estimated by means of the angles where large concentrations of high levels of

r_{m} (n)

are found. The range of values of

θ_{m} (n)

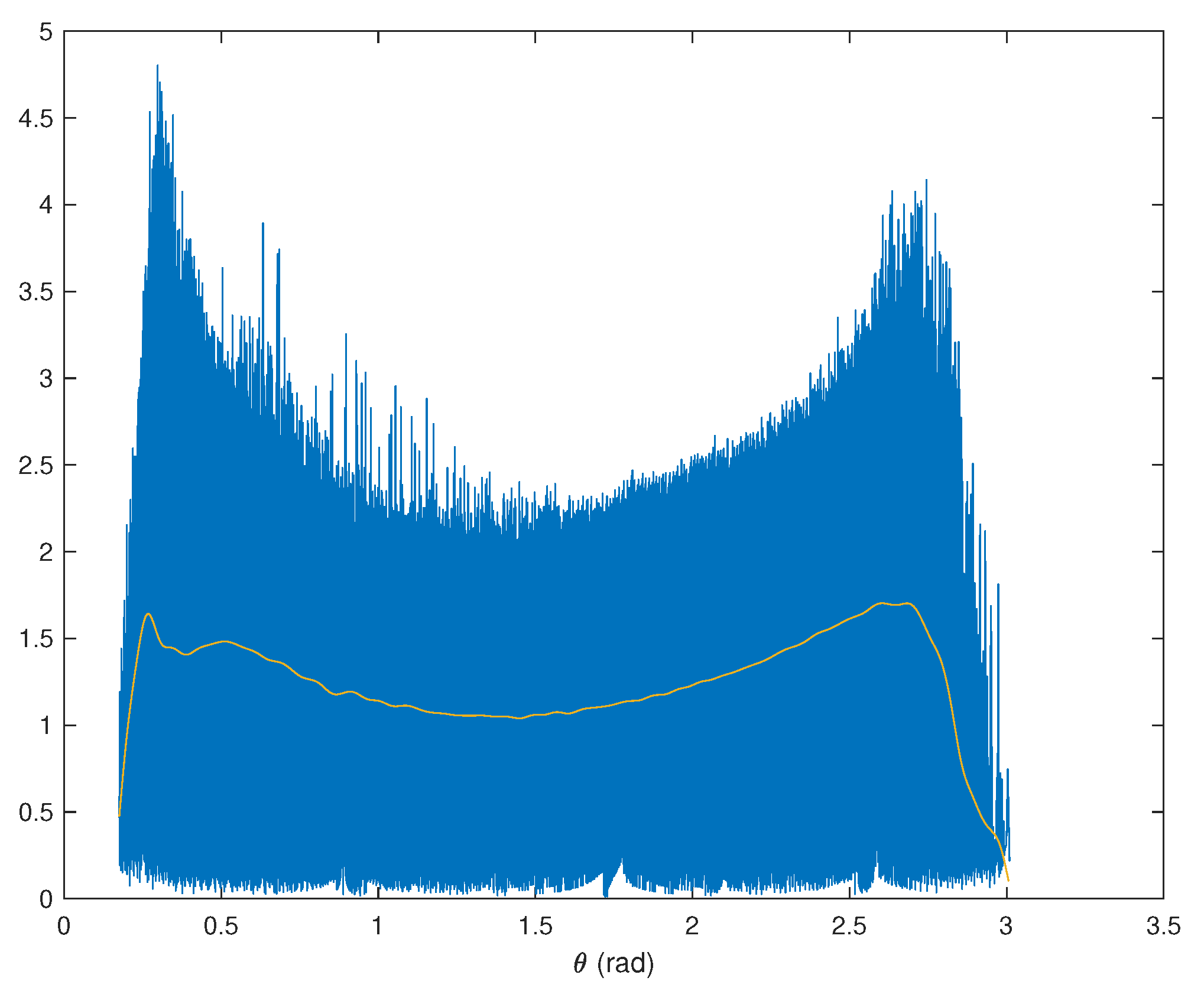
is divided into 1000 bins for a sufficient angle resolution. For the kth bin, whose center is given by

ϕ_{m} (k)

, the mean of the values of

r_{m} (n)

such that

θ_{m} (n)

lies within the bin is computed. Then, this function is smoothed by a lowpass eighth-order Butterworth filter with digital cutoff frequency equal to

0.035

to get the function

v_{m} (k)

, as illustrated in Figure 3.

Therefore,

B_{m}

is estimated by means of

{\hat{B}}_{m}

, defined as

{\hat{B}}_{m} = [\begin{matrix} cos ({ϕ_{m}}_{1}) & cos ({ϕ_{m}}_{2}) \\ sin ({ϕ_{m}}_{1}) & sin ({ϕ_{m}}_{2}) \end{matrix}]

(7)

where

{ϕ_{m}}_{1}

and

{ϕ_{m}}_{2}

are the main peaks in the filtered version of

r_{m} (n)

. Since it is possible the existence of more than two peaks, in order to avoid a bad selection of the true angles of both basis vectors, a procedure was implemented. Due to the nature of the data, the basis vectors are always near the extrema of

ϕ_{m} (n)

(in an ideal case, the points of the scattering are a linear combination of the basis vectors with nonnegative coefficients). So, the maximum of

v_{m} (k)

is selected as the position for one the basis vectors. The other peak is selected from the angle bins that lies within the opposite half of the total range of

ϕ_{m} (k)

. This ensures that the selected angles correspond to a good estimate of the basis vectors.

It is easy to see that the estimate of

W_{m}

corresponding to

{\hat{B}}_{m}

is given by the representation of the columns of this matrix in the whole 3D space as

{\hat{W}}_{m} = [\begin{matrix} {q_{m}}_{1} \sqrt{{L_{m}}_{1}} & {q_{m}}_{2} \sqrt{{L_{m}}_{2}} \end{matrix}] \cdot {\hat{B}}_{m} .

(8)

2.1.2. Color deconvolution

From (2) we can write the decomposition of

X_{m}

in terms of

{\hat{W}}_{m}

and

H_{m}

X_{m} = {\hat{W}}_{m} \cdot H_{m} .

(9)

This describes, for each column of

H_{m}

, an overdetermined system of equations as

W_{m}

and

X_{m}

are known. Therefore, the stain concentration matrix for the mth is estimated by means of a linear least squares problem as

{\hat{H}}_{m} = {\hat{W}}_{m}^{+} X_{m}

(10)

where

{\hat{W}}_{m}^{+} = {({\hat{W}}_{m}^{T} {\hat{W}}_{m})}^{- 1} \cdot {\hat{W}}_{m}

is the Moore-Penrose pseudoinverse of the full-rank matrix

{\hat{W}}_{m}

[23]. This procedure is known as color deconvolution [24]. Since the concentration of each stain at every pixel must be nonnegative, the values

{[{\hat{H}}_{m}]}_{i j} < 0

are set to 0.

The estimate is improved by means of the following procedure. The values

{[{\hat{H}}_{m}]}_{i j}

for columns of

{\hat{H}}_{m}

that have only one nonzero entry are recalculated by using the corresponding column of

{\hat{W}}_{m}

. After this, a new estimate of the basis vectors is computed as the mean of the columns of

Z_{m}

for which one stain is dominant, i.e., when the value for a concentration is, at least, 10 times that for the other. A new estimate of

{\hat{H}}_{m}

is computed following the procedure described from equation (10).

2.1.3. Average basis vectors

Once the previous procedure is carried out, the average of the matrices

{\hat{W}}_{m}

is computed

\bar{W} = {〈{\hat{W}}_{m}〉}_{m} .

(11)

Then the concentration matrix is estimated for each image as

{\bar{H}}_{m} = {\bar{W}}^{+} X_{m}

. Again, the values

{[{\bar{H}}_{m}]}_{i j} < 0

are set to 0 and then the values

{[{\bar{H}}_{m}]}_{i j}

for columns of

{\bar{H}}_{m}

that have only one nonzero entry are recalculated.

2.2. Feature extraction

A set of four features is computed for each image. Since the columns of

{\hat{W}}_{m}

and

\bar{W}

were not normalized, we take into account them together with

{\hat{H}}_{m}

and

{\bar{H}}_{m}

. The jth column of

{\hat{W}}_{m}

(resp.

\bar{W}

) is denoted as

{\hat{W}}_{m_{:, j}}

(resp.

{\bar{W}}_{:, j}

) and the ith row of

{\hat{H}}_{m}

(resp.

{\bar{H}}_{m}

) is denoted as

{\hat{H}}_{m_{i, :}}

(resp.

{\bar{H}}_{m_{i, :}}

). Let

M_{1} (m)

be the mean of the the intensity average of all the pixels of DAB stain for the mth image according to the results for the average basis vectors

M_{1} (m) = \frac{1}{3 N} {∥{\bar{W}}_{:, 2} \cdot {\bar{H}}_{m_{2, :}}∥}_{1} = \frac{1}{3 N} {∥{\bar{W}}_{:, 2}∥}_{1} \cdot {∥{\bar{H}}_{m_{2, :}}∥}_{1} = \frac{1}{3 N} \sum_{i = 1}^{3} {[\bar{W}]}_{i 2} \sum_{j = 1}^{N} {[{\bar{H}}_{m}]}_{2 j}

(12)

where the 1-norm of the matrix is computed entry-wise, i.e., it is the sum of the entries of the matrix (they are all nonnegative). For row vectors we computed the norm as for column vectors. Then the first feature for the mth image is defined as the average of the DAB intensity in this image, normalized by the maximum value that this quantity reaches among the entire set of images

f_{1} (m) = \frac{M_{1} (m)}{max_{m} {M_{1} (m)}} .

(13)

The second feature is based on the relation between the robust maxima (99th percentile) of both stains: H and DAB. Let

R_{1} (m)

(resp.

R_{2} (m)

) be the robust maximum of the intensities matrix for H stain (resp. DAB stain), according to the results for the average basis vectors, i.e., the robust maximum of the matrix

{\bar{W}}_{:, 1} \cdot {\bar{H}}_{m_{1, :}}

(resp.

{\bar{W}}_{:, 2} \cdot {\bar{H}}_{m_{2, :}}

). Then, we define

{\bar{R}}_{2} (m) = \frac{R_{2} (m)}{max_{m} R_{2} (m)}

(14)

and

{\bar{R}}_{1} (m) = \frac{R_{1} (m)}{R_{1} (m = arg {max}_{m} R_{2} (m))} .

(15)

The second feature is then defined as

f_{2} (m) = \frac{{\bar{R}}_{2} (m)}{{\bar{R}}_{1} (m)} .

(16)

The third feature is analogue to the first one, but using 2-norm, i.e., based on the average power of the intensity. Let

M_{2} (m)

\begin{matrix} M_{3} (m) = \frac{1}{\sqrt{3 N}} {∥{\bar{W}}_{:, 2} \cdot {\bar{H}}_{m_{2, :}}∥}_{F} = \frac{1}{\sqrt{3 N}} {∥{\bar{W}}_{:, 2}∥}_{2} \cdot {∥{\bar{H}}_{m_{2, :}}∥}_{2} \\ = \frac{1}{\sqrt{3 N}} \sqrt{\sum_{i = 1}^{3} {[\bar{W}]}_{i 2}^{2}} \sqrt{\sum_{j = 1}^{N} {[{\bar{H}}_{m}]}_{2 j}^{2}} \end{matrix}

(17)

where

{∥\cdot∥}_{F}

is Frobenius norm of the matrix. Then we define the third feature,

f_{3} (m)

f_{3} (m) = \frac{M_{3} (m)}{max_{m} {M_{3} (m)}} .

(18)

Although very goods results are achieved when using the above defined features, the inclusion of a fourth one improves the behavior of the clustering procedure. The feature

f_{4} (m)

is defined as the square root of the average power of the intensity of the DAB stain at every pixel according to the results for the basis vectors estimated for each image,

f_{4} (m) = \frac{1}{\sqrt{3 N}} {∥{\hat{W}}_{m_{:, 2}} \cdot {\hat{H}}_{m_{2, :}}∥}_{F} = \frac{1}{\sqrt{3 N}} {∥{\hat{W}}_{m_{:, 2}}∥}_{2} \cdot {∥{\hat{H}}_{m_{2, :}}∥}_{2}

(19)

2.3. Clustering and scoring

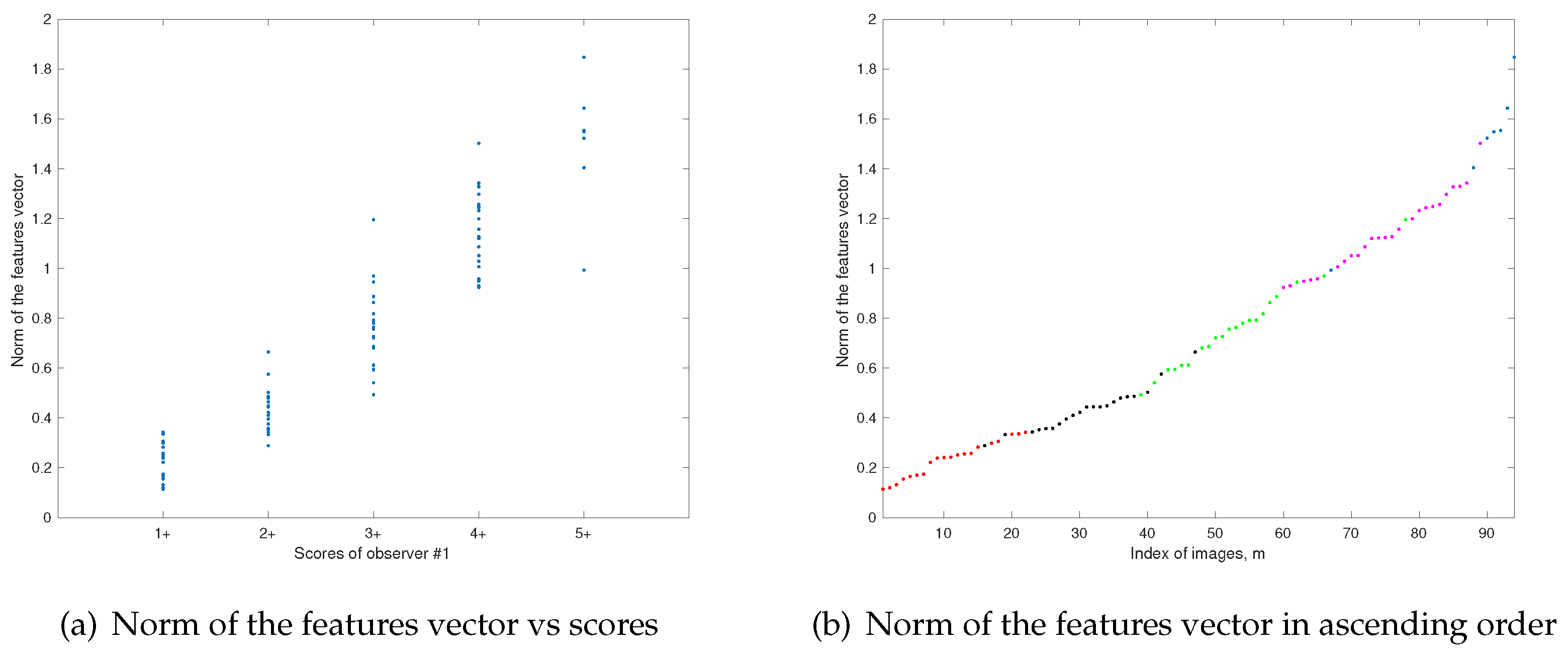
As a general behavior the values of the four defined features increase when the concentration of DAB stain increases. Consequently, a simple, automated an efficient procedure was used to initialize the algorithm k-means for clustering. Also, this property allows us to assign the scores in a increasing order of the centroids norms. Let

f (m)

be the vector of features whose ith entry is

f_{i} (m)

. In order to initialize the clustering algorithm we computed the p-norm of the vector

{∥f (m)∥}_{p} = {(\sum_{i = 1}^{T} {|f_{i} (m)|}^{p})}^{1 / p}

(20)

where T is the length of the vector of features

f (m)

. A certain range of values can lead to good initialization and results for the clustering algorithm. In Section 3 we discuss about these values.

When the values of

{∥f (m)∥}_{p}

are sorted in ascending order the result is not a linear function of m, but rather a power function. For an automated initialization of the clustering algorithm, the range of values of

{∥f (m)∥}_{p}^{q}

are divided into 5 intervals with the same length, which provides a good starting point. Therefore, the kth interval is

I_{k} = [E_{k}^{(i)}, E_{k}^{(s)}]

where

\begin{matrix} E_{k}^{(i)} & = & \frac{k - 1}{5} (max {∥f (m)∥}_{p}^{q} - min {∥f (m)∥}_{p}^{q}) + min {∥f (m)∥}_{p}^{q} \end{matrix}

(21)

\begin{matrix} E_{k}^{(s)} & = & \frac{k}{5} (max {∥f (m)∥}_{p}^{q} - min {∥f (m)∥}_{p}^{q}) + min {∥f (m)∥}_{p}^{q} . \end{matrix}

(22)

Although the value of q could change for different sets of features, square root is a good selection for the four proposed. We followed the criterion of fitting the first and second half of the sorted values of

{∥f (m)∥}_{p}

to a power function and set q as the average of both resulting powers. For the selected 4 features, the value is close to 2. In Section 3 we discuss about the possible values of this parameter. The initial clusters are assigned based on the norm of the features vector; if this norm lies in the kth interval, then the corresponding vector belongs to the kth cluster. So the initial kth cluster,

Ω_{k}^{(0)}

, is set as

Ω_{k}^{(0)} = \{m : {∥f (m)∥}_{p}^{q} \in I_{k}\} \forall k = 1, \dots, 5 .

(23)

The initial kth centroid is set as the mean of the features vectors that belong to the kth cluster

c_{k} = \sum_{m \in Ω_{k}} f (m) \forall k = 1, \dots, 5 .

(24)

These initial centroids were used for k-means algorithm equiped with a measure of distance based on p-norm. Only 3 iterations of the algorithm are needed to achieve the scores of the images.

3. Results and discussion

Our dataset was the same as in [14] and consisted of 94 images taken from stained xenograph tumors, using HCT116 cells implanted in mice treated with either vehicle or with a cell-permeable

α

-ketoglutarate derivative, dimethyl

α

-KG (DMKG), followed by treatment with the mTORC1 inhibitor temsirolimus (TEM) or with metformin (MET). Samples were processed as described in [25]. All procedures were approved by the corresponding institutional organizations (APAFIS# 10090 2017052409402562 v2). Omission of the primary antibody in the immunostaining procedure was used as a negative control. Images were acquired in TIFF format with a Leica DM6000B microscope using

\times 20

\times 40

objective lenses and a Leica DFC500 digital camera. All images were independently scored from “1+” to “5+” by four expert observers. The agreement among observers measured as the percentage of images that have been annotated with the same score by all experts is

70.21 %

. This makes that the maximum mean agreement of a scoring with all observers be

90.96 %

3.1. Results for stain separation step

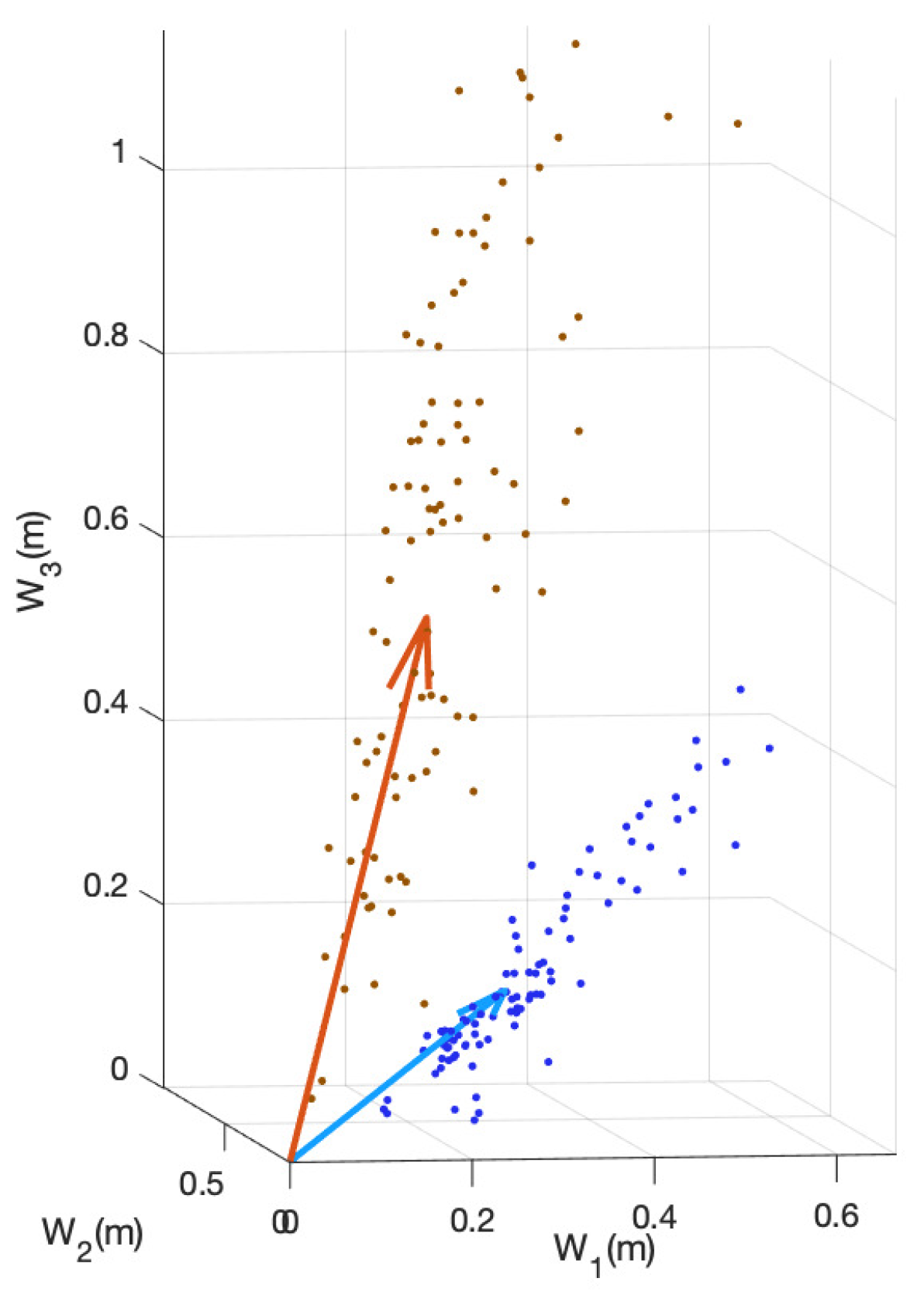
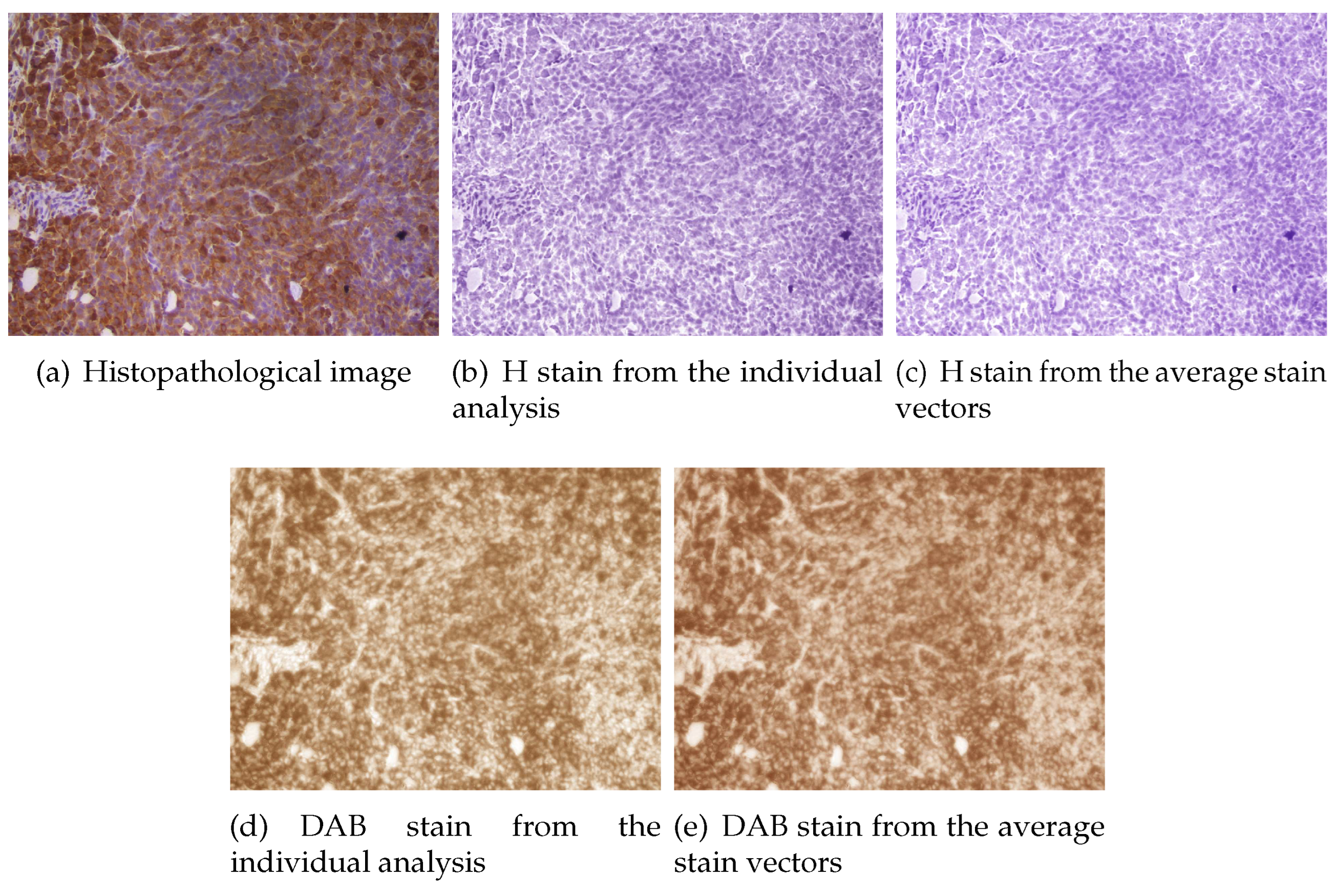
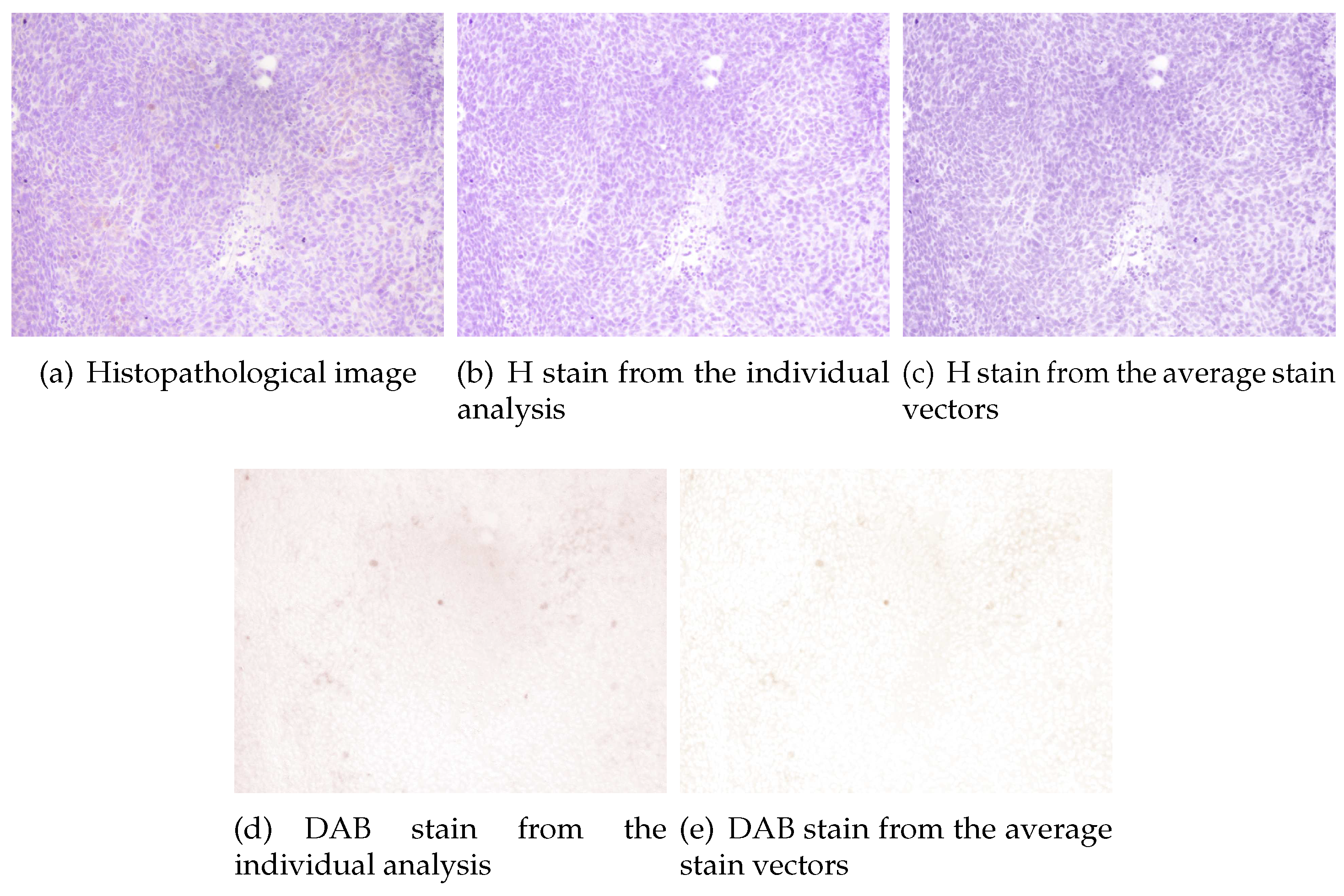
The stain separation procedure achieves satisfactory results, providing a good decomposition of DAB and H planes, showing consistent solutions along the whole set of images. In Figure 4 the estimated color stain vectors for each image, together with the mean of these color vectors, are depicted. Note that the direction of the vectors is very similar for all the images. In Figure 5 and Figure 6 the results for the separation procedure are show for two example images from the set. In the first case the processed image has a high concentration of both (DAB and H) stains, whereas the second image has a very low concentration of DAB satin. In both figures two results are shown: that for individual analysis without considering the rest of images, based on the estimate from (8); and the estimation of stain concentrations from the average stain vectors estimated in (11). In all cases the color of H stain is correctly estimated. Furthermore, even if the color of DAB stain for the second image is not very accurate at the first analysis, the calculated concentrations of this stain are similar to that obtained from the average stain vectors.

3.2. Performance of the scores prediction

In [14] we showed that 1-norm of the DAB concentration stain correlates better than average threshold method (ATM) score and pixel-wise H-score to the scorings of the observers. There we used two other features (related to that denoted as

f_{3} (m)

in the present work, but not the same) that improved the correlation. Here we show how the correlation for 1-norm increases when we add the features

f_{2} (m)

f_{3} (m)

and

f_{4} (m)

. All the features that we propose increase (in general) when the score increases, which allows us to use the norm of the feature vector for an automated initialization of the clustering algorithm, due to the high correlation between this norm and the score of each image, as it can be seen in Figure 7.

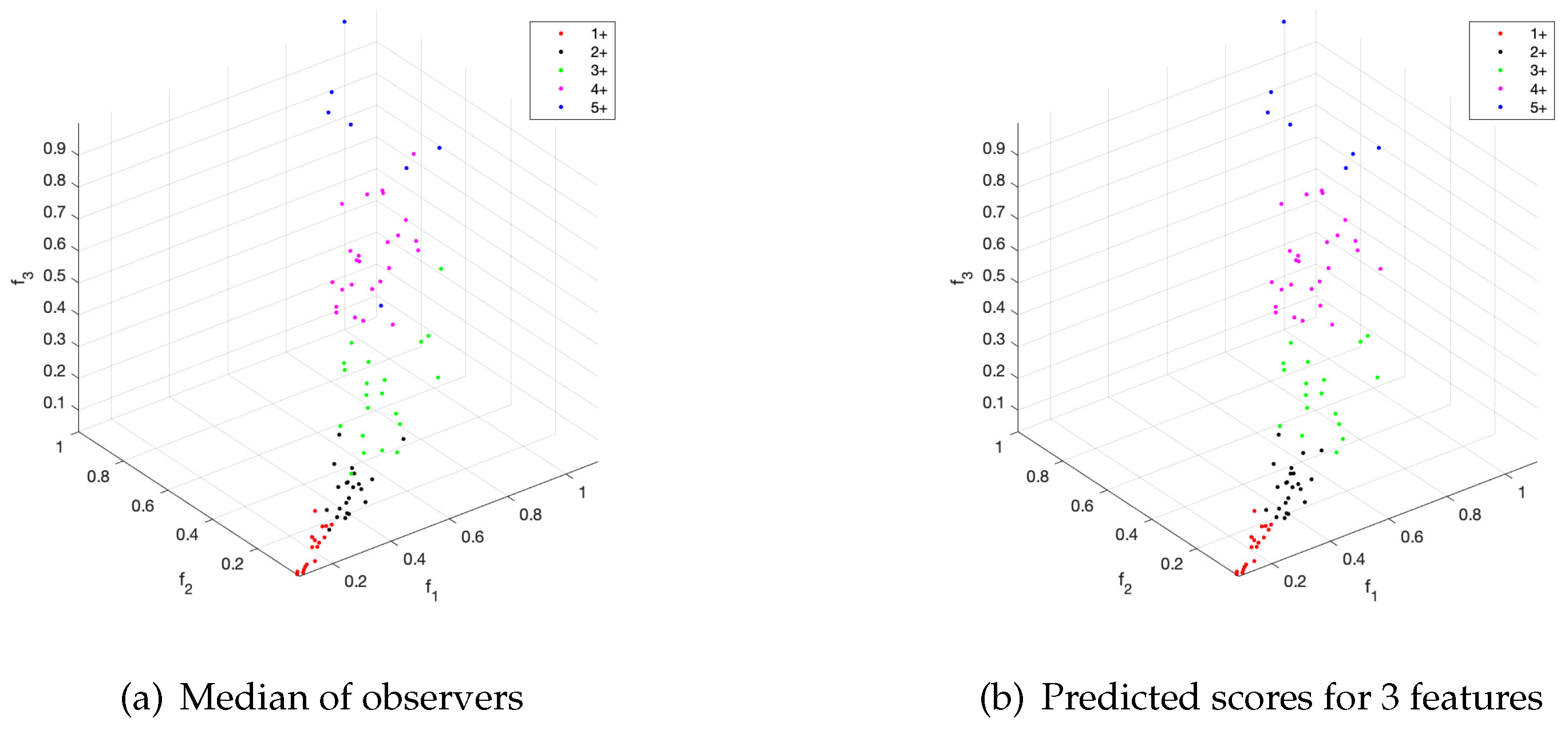
Furthermore, the use of only the first three features allows to achieve excellent results by using the above mentioned automated procedure for the initialization. Figure 8 shows a comparison of the prediction scores and the median of the observers’ scores for each triple of feature values. Despite small differences the automated scoring achieves a high level of similarity with the reference truth.

Although the procedure was conceived to use four features, we also tested its behavior when only two or three features are exploited. Table 1 shows the main results for 2, 3 and 4 features in terms of percentage of coincidences with each observer and with the median of the observers’ scores. Features

f_{1}

and

f_{2}

were the couple used for testing our method with 2 features. After, we added

f_{3}

and, finally,

f_{4}

. A high level of coincidence is achieved for 3 and 4 features, whereas the level of coincidences for two features was acceptable.

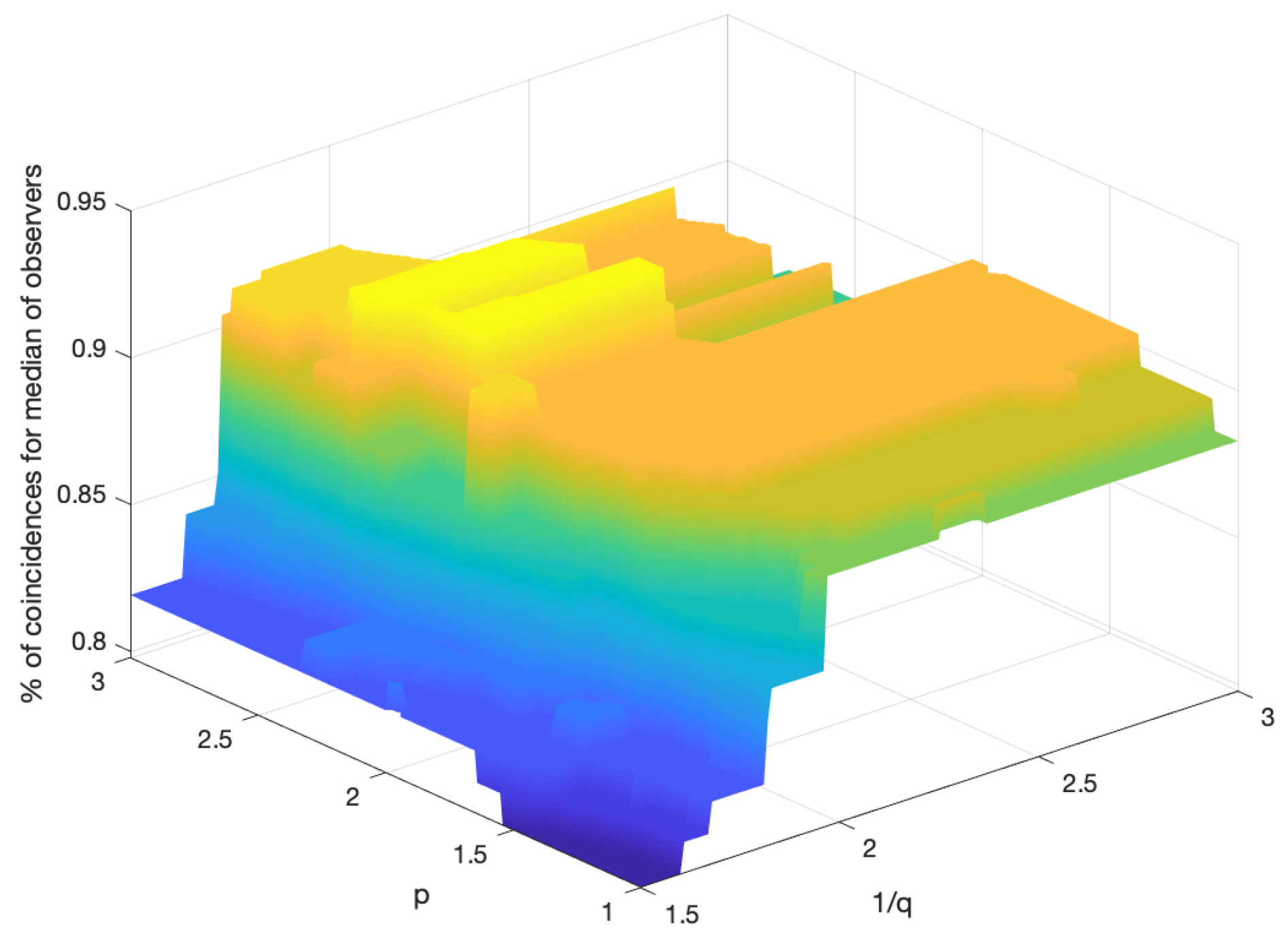
A wide range of values are suitable for the parameters p (p-norm for initialization and distance in clustering algorithm) and q (the power for reshaping the curve of values of the norm of the features vector). Figure 9 shows the percentage of coincidences of the scoring assigned by the proposed algorithm with the median of the scores assigned by the observers. For values of more than

90 %

low correlation between p and q can be observed. This leads to consider the proposed method quite robust, in terms of the selection of the parameters, which enables an automated procedure for the scoring of the IHC images.

4. Conclusions

In recent years, automated scoring methods have been developed for the evaluation of IHC images. However, these methods suffer from problems related to the need for researchers to intervene at a certain point in the process, the use of control or training images or the dependence of the results on the choice of certain parameters.

In the present work we have proposed a completely unsupervised method that allows scoring IHC images without the need for reference images and without dependence on the set up of several parameters. The procedure consists of a first stage of separation of the DAB and H stains. In this stage, PCA allows working in a lower dimensional space (a plane), which allows finding the vectors associated with both stains in a simple and efficient way. Once these vectors and the matrix of intensities of both stains are obtained, four characteristics are used to cluster the images, although it has been proven that the use of three of them provides very good results and, even, the use of only two achieves acceptable results. The clustering method used (k-means) is based on automated initialization, without the need for reference images or parameter setup, making it a robust unsupervised method.

The proposed method has been tested with a database of 94 images and the reference truth was taken from four expert observers. The scoring was made up of five categories and the algorithm reached a mean percentage of correct predictions of 87.23% for a maximum of 90.96% (due to the experts’ opinion percentage of coincidences, which limited the average maximum percentage of correct predictions). Adapting the method to a different number of categories would be immediate, as in our previous work.

As a future line of work, we consider it interesting to find simple, fast and effective methods to locate nuclei and to develop new features related to the DAB stain of nuclei, since this could help to improve the results.

Author Contributions

Conceptualization, I.D.-D., A.S., and I.F.; methodology, I.D.-D. A.S., and I.F.; data curation, I.D.-D., A.S., I.F., M.T., C.B. and R.V.D.; formal analysis, I.D.-D., A.S., I.F., M.T., C.B. and R.V.D.; writing-original draft preparation, I.D.-D., A.S. and I.F.; writing-review and editing, I.D.-D., A.S., I.F., M.T. and R.V.D.; funding acquisition, A.S., I.D.-D., I.F. and R.V.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by grant PID2021-123090NB-I00 funded by MCIN/AEI/10.13039/501100011033 by “ERDF A way of making Europe”, by grant PID2021-124251OB-I00 MCIN/AEI/ 10.13039/501100011033 by “ERDF A way of making Europe”, and by FEDER/Junta de Andalucía-Consejería de Economía y Conocimiento grant number US-1264994.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data that support this study are available from the author R.V.D., upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

IHC	Immunohistochemistry
RGB	Red-Green-Blue
DAB	3,3’-Diaminobenzidine
H	Hematoxylin
CD	Color Deconvolution
NMF	Non-Negative Matrix Factorization
OD	Optical Density
PCA	Principal Component Analysis

References

Miettinen, M. Immunohistochemistry of soft tissue tumours - review with emphasis on 10 markers. Histopathology 2014, 64, 101–118. [CrossRef]
Filliol, A.; Saito, Y.; Nair, A.; Dapito, D.H.; Yu, L.X.; Ravichandra, A.; Bhattacharjee, S.; Affo, S.; Fujiwara, N.; Su, H.; Sun, Q.; Savage, T.M.; Wilson-Kanamori, J.R.; Caviglia, J.M.; Chin, L.; Chen, D.; Wang, X.; Caruso, S.; Kang, J.K.; Amin, A.D.; Wallace, S.; Dobie, R.; Yin, D.; Rodriguez-Fiallos, O.M.; Yin, C.; Mehal, A.; Izar, B.; Friedman, R.A.; Wells, R.G.; Pajvani, U.B.; Hoshida, Y.; Remotti, H.E.; Arpaia, N.; Zucman-Rossi, J.; Karin, M.; Henderson, N.C.; Tabas, I.; Schwabe, R.F. Opposing roles of hepatic stellate cell subpopulations in hepatocarcinogenesis. Nature 2022, 610, 356–365. [CrossRef]
Grosset, A.A.; Loayza-Vega, K.; Adam-Granger, É.; Birlea, M.; Gilks, B.; Nguyen, B.; Soucy, G.; Tran-Thanh, D.; Albadine, R.; Trudel, D. Hematoxylin and Eosin Counterstaining Protocol for Immunohistochemistry Interpretation and Diagnosis. Applied Immunohistochemistry & Molecular Morphology 2019, 27.
Nielsen, P.S.; Georgsen, J.B.; Vinding, M.S.; Østergaard, L.R.; Steiniche, T. Computer-Assisted Annotation of Digital H&E/SOX10 Dual Stains Generates High-Performing Convolutional Neural Network for Calculating Tumor Burden in H&E-Stained Cutaneous Melanoma. International Journal of Environmental Research and Public Health 2022, 19. [CrossRef]
Konukiewitz, B.; Schmitt, M.; Silva, M.; Pohl, J.; Lang, C.; Steiger, K.; Halfter, K.; Engel, J.; Schlitter, A.M.; Boxberg, M.; Pfarr, N.; Wilhelm, D.; Foersch, S.; Tschurtschenthaler, M.; Weichert, W.; Jesinghaus, M. Loss of CDX2 in colorectal cancer is associated with histopathologic subtypes and microsatellite instability but is prognostically inferior to hematoxylin-eosin-based morphologic parameters from the WHO classification. Br J Cancer 2021, 125, 1632–1646. [CrossRef]
van der Loos, C.M. Multiple immunoenzyme staining: methods and visualizations for the observation with spectral imaging. The journal of histochemistry and cytochemistry : official journal of the Histochemistry Society 2008, 56, 313–328. [CrossRef]
Kitaya, K.; Yasuo, T. Inter-observer and intra-observer variability in immunohistochemical detection of endometrial stromal plasmacytes in chronic endometritis. Exp Ther Med 2013, 5, 485–488. [CrossRef]
Aeffner, F.; Wilson, K.; Martin, N.T.; Black, J.C.; Hendriks, C.L.L.; Bolon, B.; Rudmann, D.G.; Gianani, R.; Koegler, S.R.; Krueger, J.; Young, G.D. The Gold Standard Paradox in Digital Image Analysis: Manual Versus Automated Scoring as Ground Truth. Archives of Pathology and Laboratory Medicine 2017, 141, 1267–1275, [https://meridian.allenpress.com/aplm/article-pdf/141/9/1267/1449767/arpa_2016-0386-ra.pdf]. [CrossRef]
David K Meyerholz, A.P.B. Fundamental Concepts for Semiquantitative Tissue Scoring in Translational Research. ILAR Journal 2018, 59, 13–17. [CrossRef]
Bankhead, P.; Fernández, J.; McArt, D.G.; Boyle, D.P.; Li, G.; Loughrey, M.B.; Irwin, G.W.; Harkin, D.P.; James, J.A.; McQuaid, S.; Salto-Tellez, M.; Hamilton, P.W. Integrated tumor identification and automated scoring minimizes pathologist involvement and provides new insights to key biomarkers in breast cancer. Laboratory Investigation 2018, 98, 15–26. [CrossRef]
Varghese, F.; Bukhari, A.B.; Malhotra, R.; De, A. IHC Profiler: an open source plugin for the quantitative evaluation and automated scoring of immunohistochemistry images of human tissue samples. PLoS One 2014, 9, e96801. [CrossRef]
Patel S, Fridovich-Keil S, R.S.F.K.J. DAB-quant: An open-source digital system for quantifying immunohistochemical staining with 3,3?-diaminobenzidine (DAB). PLoS ONE 2022, 17. [CrossRef]
Vahadane, A.; Peng, T.; Sethi, A.; Albarqouni, S.; Wang, L.; Baust, M.; Steiger, K.; Schlitter, A.M.; Esposito, I.; Navab, N. Structure-Preserving Color Normalization and Sparse Stain Separation for Histological Images. IEEE Transactions on Medical Imaging 2016, 35, 1962–1971.
Sarmiento, A.; Durán-Díaz, I.; Fondón, I.; Tomé, M.; Bodineau, C.; Durán, R.V. A Method for Unsupervised Semi-Quantification of Inmunohistochemical Staining with Beta Divergences. Entropy 2022, 24. [CrossRef]
Roy, S.; kumar Jain, A.; Lal, S.; Kini, J. A study about color normalization methods for histopathology images. Micron 2018, 114, 42–61. [CrossRef]
Trahearn, N.; Snead, D.; Cree, I.; Rajpoot, N. Multi-class stain separation using independent component analysis. Medical Imaging 2015: Digital Pathology; Gurcan, M.N.; Madabhushi, A., Eds. International Society for Optics and Photonics, SPIE, 2015, Vol. 9420, pp. 113 – 123. [CrossRef]
Alsubaie, N.; Trahearn, N.; Raza, S.; Snead, D.; Rajpoot, N. Stain Deconvolution Using Statistical Analysis of Multi-Resolution Stain Colour Representation. PLoS ONE 2017, 12(1). [CrossRef]
Li, X.; Plataniotis, K.N. A Complete Color Normalization Approach to Histopathology Images Using Color Cues Computed From Saturation-Weighted Statistics. IEEE Transactions on Biomedical Engineering 2015, 62, 1862–1873. [CrossRef]
Bencze, J.; Szarka, M.; Kóti, B.; Seo, W.; Hortobágyi, T.G.; Bencs, V.; Módis, L.V.; Hortobágyi, T. Comparison of Semi-Quantitative Scoring and Artificial Intelligence Aided Digital Image Analysis of Chromogenic Immunohistochemistry. Biomolecules 2022, 12. [CrossRef]
Macenko, M.; Niethammer, M.; Marron, J.S.; Borland, D.; Woosley, J.T.; Guan, X.; Schmitt, C.; Thomas, N.E. A method for normalizing histology slides for quantitative analysis. 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, 2009, pp. 1107–1110. [CrossRef]
Salvi, M.; Michielli, N.; Molinari, F. Stain Color Adaptive Normalization (SCAN) algorithm: Separation and standardization of histological stains in digital pathology. Computer Methods and Programs in Biomedicine 2020, 193, 105506. [CrossRef]
Jolliffe, I.; Springer-Verlag. Principal Component Analysis; Springer Series in Statistics, Springer, 2002.
Golub, G.H.; van Loan, C.F. Matrix Computations, fourth ed.; JHU Press, 2013.
Ruifrok, A.C.; Johnston, D.A. Quantification of histochemical staining by color deconvolution. Anal Quant Cytol Histol 2001, 23, 291–299.
Bodineau, C.; Tomé, M.; Courtois, S.; Costa, A.S.H.; Sciacovelli, M.; Rousseau, B.; Richard, E.; Vacher, P.; Parejo-Pérez, C.; Bessede, E.; Varon, C.; Soubeyran, P.; Frezza, C.; Murdoch, P.d.S.; Villar, V.H.; Durán, R.V. Two parallel pathways connect glutamine metabolism and mTORC1 activity to regulate glutamoptosis. Nature Communications 2021, 12, 4814. [CrossRef]

Figure 1. Scatter plot (blue) of the columns of matrix

X_{m}

for one example image with DAB and H stains. For a better visualization a sampling of the entries was made before to depict the scatter plot. As can be seen, the points lies mainly at the plain defined by the stain vectors. The principal directions (green and red), along the two first principal components are depicted. These orthogonal directions lie at the same plain defined by the color stain vectors, although they do not coincide. The principal components allow us to simplify the problem of searching the stain vectors to a 2D problem.

Figure 1. Scatter plot (blue) of the columns of matrix

X_{m}

Figure 2. Scatter plot of the principal components for an example image when a) PCA with unit power principal components or b) PCA with unit norm loading vectors are performed. Normalization of the principal components power allows to spread the angle of the scattering, so the angle between the stain vectors is greater, improving the accuracy of the estimate. In the other hand, normalization of the norm of loading vectors keep the distance between the stain vectors, which reduces the accuracy. The second principal component was depicted along horizontal axis for visual convenience.

Figure 3. Norm

r_{m} (n)

(blue) of the columns of

Z_{m}

for an example image versus the angle of the columns together with the smoothed mean of concentration,

v_{m} (k)

(yellow). Searching for the peaks of this last function leads to the angles corresponding to the stain vectors within the subspace of principal components.

Figure 3. Norm

r_{m} (n)

(blue) of the columns of

Z_{m}

for an example image versus the angle of the columns together with the smoothed mean of concentration,

v_{m} (k)

(yellow). Searching for the peaks of this last function leads to the angles corresponding to the stain vectors within the subspace of principal components.

Figure 4. Scatter plot of the estimates

{\hat{W}}_{m}

for the whole set of analyzed images and for both H (blue) and DAB (brown) stain colors, together with the columns of the mean

\bar{W}

also for both colors. The consistency of the results for nearly all images can be noted.

Figure 4. Scatter plot of the estimates

{\hat{W}}_{m}

for the whole set of analyzed images and for both H (blue) and DAB (brown) stain colors, together with the columns of the mean

\bar{W}

also for both colors. The consistency of the results for nearly all images can be noted.

Figure 5. Example of stain separation of an IHC image form the set: a) Original image, b) H stain from the exclusive analysis of this image, c) H stain from the average stain vectors computed in (11), d) DAB stain from the analysis of this image and e) DAB stain from the average stain vectors. This is an example where the analysis of the image basically coincides with the average, since the intensities of both stains are high.

Figure 6. Example of stain separation of another IHC image form the set: a) Original image, b) H stain from the exclusive analysis of this image, c) H stain from the average stain vectors computed in (11), d) DAB stain from the analysis of this image and e) DAB stain from the average stain vectors. This is an example where the exclusive analysis of the image does not provides a good estimate of the DAB stain vector, due to the very low concentration of this stain, although the intensity of the separated DAB stain is very similar to that obtained for the average DAB vector.

Figure 7. Correlation between the norm of the features vector and the scores of the observer #1 shown as a plot of a) the norm versus the scores and b) the sorted norm versus the indices of the images. In this last figure the scores are shown in different colors in ascending order. In both cases the high correlation between the norm and the scores can be observed. This is used for the automated initialization of the clustering algorithm.

Figure 8. Scatter plot of the fisrt 3 features together with: a) median of the scores assigned by observers and b) predicted scores for these features after clustering algorithm.

Figure 9. Percentage of coincidences of the scoring procedure with the median of the observers for the use of four features versus parameters p (norm) and

1 / q

(root applied to the norm of the features vector for the initialization).

Figure 9. Percentage of coincidences of the scoring procedure with the median of the observers for the use of four features versus parameters p (norm) and

1 / q

(root applied to the norm of the features vector for the initialization).

Table 1. Accuracy achieved by the proposed algorithm (% of coincidences with observers). The use of two, three or four features was compared.

Reference		$f_{1}$ , $f_{2}$ ¹	$f_{1}$ , $f_{2}$ , $f_{3}$ ²	$f_{1}$ , $f_{2}$ , $f_{3}$ , $f_{4}$ ³
Observer 1		86.17	89.36	90.43
Observer 2		78.72	79.79	78.72
Observer 3		85.11	88.30	89.36
Observer 4		86.17	89.36	90.43
	Mean of results⁴	84.04	86.70	87.23
Observer’s median⁵		88.30	91.49	92.55

p = 1.5, q = 1 / 1.8, 1

iteration. ²

p = 1.9, q = 1 / 1.75 2

iterations. ³

p = 2.5, q = 2 3

iterations. ⁴ Mean of above results ⁵ Comparison to the median of the observers’ scores.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Robust Method for Unsupervised Scoring of Inmunohistoquemical Staining

Abstract

1. Introduction

2. Methods

2.1. Stain separation

2.1.1. Stain color basis estimation

2.1.2. Color deconvolution

2.1.3. Average basis vectors

2.2. Feature extraction

2.3. Clustering and scoring

3. Results and discussion

3.1. Results for stain separation step

3.2. Performance of the scores prediction

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe