Prerpints.org logo
Preprint
Article

Parameter optimization of Friction Pendulum Bearings Based on the Adaptive Genetic Algorithm Considering the Overall Evolutionary Status

Altmetrics

Downloads

58

Views

15

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 December 2023

Posted:

29 December 2023

You are already at the latest version

Alerts
Abstract
Improper design of friction pendulum bearings can lead to poor seismic reduction performance and may result in the failure of local vulnerable components. And the parameter design of friction pendulum bearings mainly relies on experience and verification calculations at present. This paper proposes an adaptive genetic algorithm considering the overall evolution state of the population, adjusting crossover and mutation probabilities adaptively based on individual fitness and population diversity. Compared to traditional algorithms, it exhibits better global search capabilities and convergence efficiency. Combining the improved genetic algorithm with finite element models, a parameter optimization method is proposed. The parameters of friction pendulum bearings are optimized, providing reference for the design of seismic isolation devices.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

After the COVID-19 pandemic, the growth of the global urban population is re-turning to a positive trajectory, with an estimated addition of 2.2 billion urban resi-dents by 2050. Mega-cities such as Tokyo, Shanghai, and Mexico City, with populations exceeding ten million, are facing challenges like land resource constraints and traffic congestion [1,2]. Global urban development experiences indicate that scientific development and utilization of urban underground space are essential pathways to improve living spaces in cities and transform urban development patterns [3,4]. However, in some countries, the development and utilization of underground space face the threat of seismic disasters. Taking China as an example, it is located between the Pacific seismic zone and the Eurasian seismic zone, making it the world's largest region with intense seismic activity originating from shallow sources. The frequency, intensity, and widespread distribution of seismic activity in this region are high. In recent years, the concept of seismic reduction has gradually been applied in underground structures. By reducing the seismic response of underground structures, their seismic resistance can be effectively improved. The common method for seismic reduction in underground structures is to install seismic isolation devices at vulnerable components in the structure. These seismic isolation devices concentrate seismic damage, protecting critical components from damage during earthquakes and preventing overall instability and failure of underground structures. Commonly used seismic isolation devices for underground structures include shear panel dampers [5], lead-core rubber bearings [6], friction pendulum bearings [7], and column-end sliding bearings [8].
When enhancing the seismic resistance of underground structures using seismic isolation devices, improper design of these devices may reduce the seismic reduction effectiveness and could potentially lead to the damage of local vulnerable components [9]. At present, the parameter design of these seismic isolation devices mainly relies on experience and verification calculations. In the optimization design of seismic isolation devices, qualitative analysis methods are predominantly employed, resulting in low optimization precision [10]. With the development of computer technology, various intelligent algorithms to optimize complex nonlinear problems have been introduced. Researchers have gradually applied these algorithms in the field of engineering. Di Trapani et al. implemented the calculation of section forces for a three-dimensional reinforced concrete frame structure within OpenSees. They utilized a genetic algorithm to optimize the location and quantity of steel jacketing, effectively enhancing the seismic resistance and deformability of reinforced concrete structures under earthquake effects [11]. Bekdas et al. proposed a method utilizing the bat algorithm to optimize parameters of tuned mass dampers. This approach was applied to optimize design variables such as mass, period, and damping ratio of tuned mass dampers [12].
Genetic algorithms treat each feasible solution as an individual in the population. By simulating the biological evolution process in nature, genetic operations such as crossover, recombination, and mutation are applied to individuals. This process retains superior individuals while eliminating inferior ones, gradually guiding the population toward the global optimum, ultimately obtaining the global optimal solution [13]. The genetic algorithm exhibits weak correlation with the initial population settings. It possesses strong robustness, and can find the global optimal solution for optimization problems. This paper proposes an improvement to the traditional genetic algorithm and combines the enhanced algorithm with the finite element calculation method to introduce a parameter optimization method. Taking the friction pendulum bearing as an example, the paper optimizes the parameters of seismic isolation devices.

2. Influence of Cross Probability and Mutation Probability on Genetic Algorithm

Genetic algorithms require repeated crossover and mutation operations on individual genes during the optimization process. The algorithm controls these operations through the crossover probability (Pc) and mutation probability (Pm). Pc and Pm are key parameters in genetic algorithms. In traditional genetic algorithms, the values of Pc and Pm are fixed. To investigate the specific impact of Pc and Pm on the optimization process of genetic algorithms, the Rastrigin function was chosen to test the optimization efficiency and global search capability under different parameter settings. Rastrigin function is a highly multimodal function [14], and its expression is:
R a s x , y = 20 + x 2 + y 2 − 10 c o s 2 π x + cos ⁡ 2 π y
The diagram of the Rastrigin function is shown in Figure 1. The function has a minimum value of 0 when x=0 and y=0. As seen in the figure, the function has numerous local optima to challenge the global optimization capability of the algorithm.
The initial population size for the genetic algorithm is set to 50, the chromosome length is 24, the number of generations is 1000, the Pc varies from 0.6 to 1.0, and the Pm ranges from 0 to 0.4. When the Pm is 0.2, the optimization process of the genetic algorithm with different Pc is illustrated in Figure 2.
It can be observed from the figure that when Pc is low, the genetic algorithm converges quickly, and the search process is stable, but it is prone to local optimum, known as premature convergence. However, when Pc is high, the stability of the genetic algorithm decreases, leading to a reduction in search efficiency.
When the Pm is 0.8, the optimization process of the genetic algorithm with different Pm is illustrated in Figure 3.
It can be observed from the figure that as the Pm increases, the global search capability of the genetic algorithm enhances, making it easier to escape the local optimum traps of the Rastrigin function. However, with the increase in the Pm, the search becomes unstable, evolving towards deteriorating individuals from the global optimum.
The orthogonal analysis of the genetic algorithm's Pc and Pm is conducted. The errors in the optimal values for x and y after optimization are illustrated in Figure 4 and Figure 5 respectively.
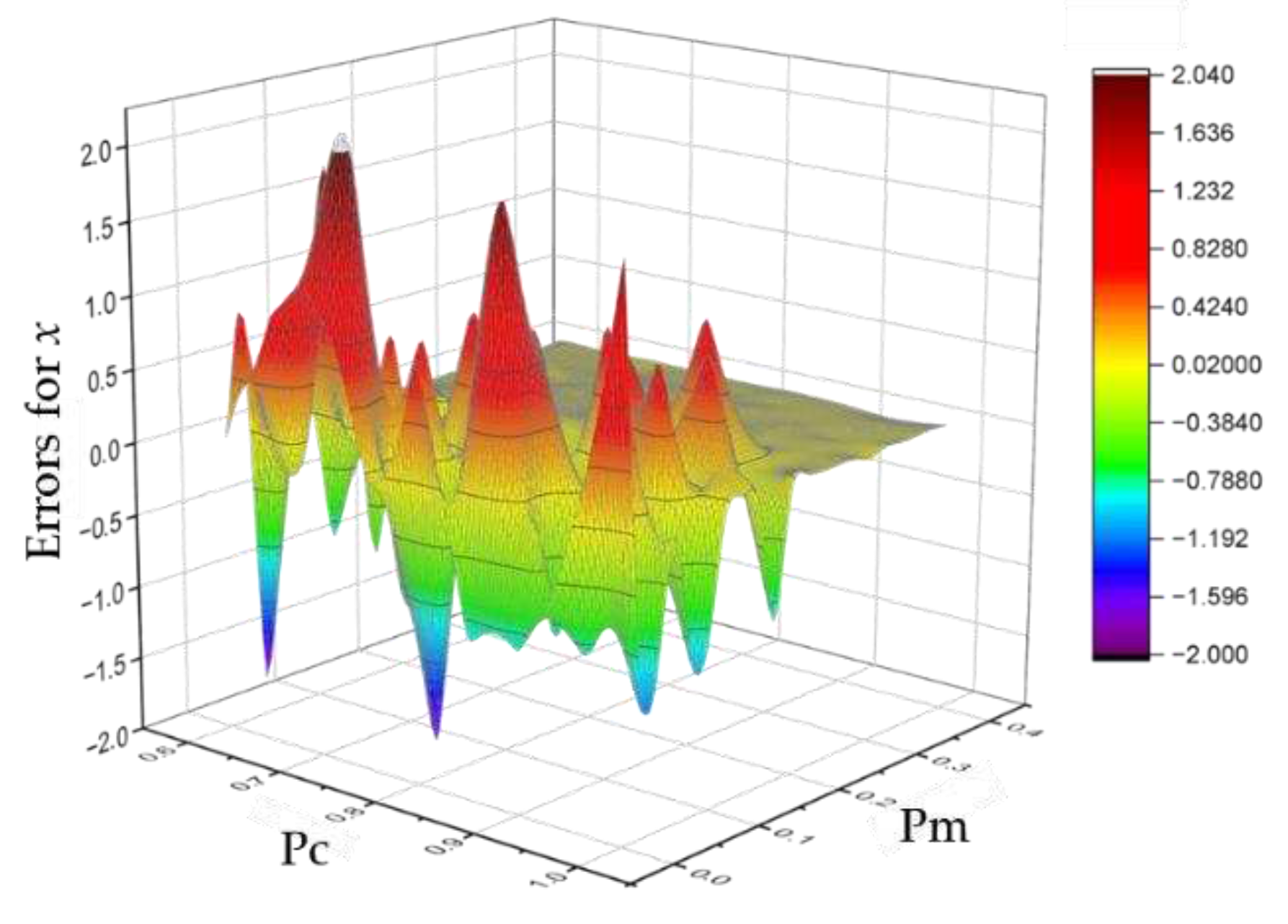
Preprints 94902 g004
Figure 4. Errors for x of different combinations Pc and Pm.
Figure 4. Errors for x of different combinations Pc and Pm.
Preprints 94902 g004
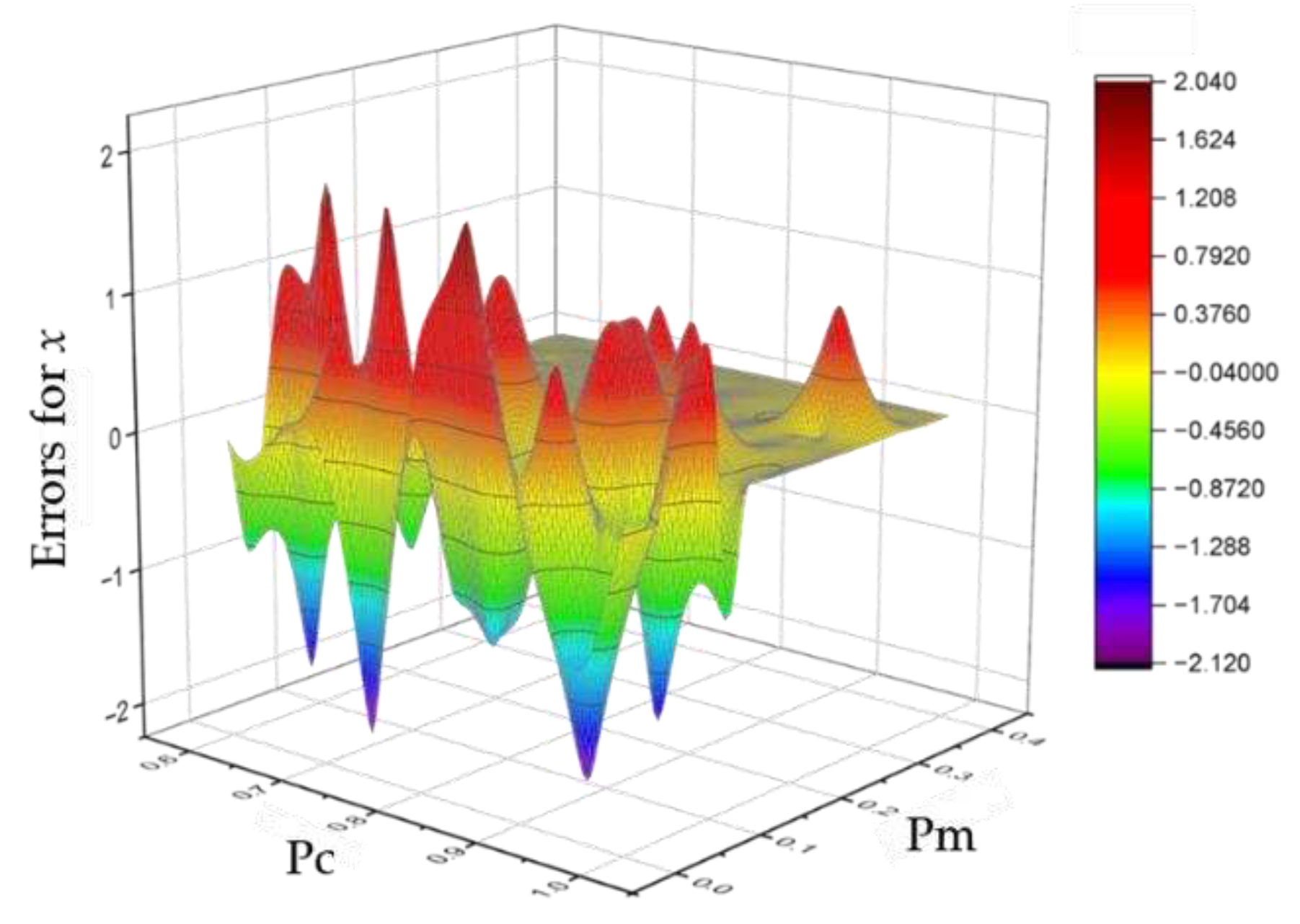
Preprints 94902 g005
Figure 4. Errors for y of different combinations Pc and Pm.
Figure 4. Errors for y of different combinations Pc and Pm.
Preprints 94902 g005
According to the optimization results of the genetic algorithm, it can be observed that when the Pc and Pm are too small, the optimization tends to converge to a local optimum. However, when the Pc and Pm are too large, the population may evolve in a direction far from the optimal solution, making it difficult to converge. The value of Pc and Pm is crucial for the optimization process of the genetic algorithm.

3. Adaptive Genetic Algorithm Considering the Overall Evolutionary Status

3.1. Adaptive Genetic Algorithm

In traditional genetic algorithms, the values of crossover probability and mutation probability are fixed. Recognizing that fixed Pc and Pm values may not meet the requirements of complex optimization problems, Srinivas et al. introduced an adaptive genetic algorithm where Pc and Pm are dynamically adjusted during the algorithm's execution. The algorithm's Pc and Pm are automatically adjusted based on the fitness of the population individuals [15]. When an individual has good fitness, the adaptive genetic algorithm lowers the individual's Pc and Pm to prevent disruption of excellent genes. Conversely, for individuals with poor fitness, larger Pc and Pm are used to enhance the algorithm's global search capabilities. Building upon this concept, various adaptive genetic algorithms have been developed [16,17,18,19]. Yan et al. proposed a bilinear adjustment model for crossover and mutation probabilities [18]. And Wang introduced a nonlinear adaptive model [19]. These adaptive genetic algorithms primarily use individual fitness as the basis for adjusting Pc and Pm, overlooking the impact of population evolutionary status on algorithm efficiency.

3.2. Genetic algorithm considering population diversity

Population diversity refers to the distribution state of individuals in the feasible space. When the population diversity is high, individuals are dispersed in space. When the population diversity is low, individuals in the population are similar, and the search is concentrated in a small area. As genetic optimization progresses, the number of similar individuals increases. Population diversity gradually decreases, and global search capability weakens accordingly. Population diversity can reflect the evolutionary status of a genetic algorithm. Increasing the Pc and Pm when diversity decreases can effectively enhance the algorithm's global search capability.
Population diversity has been assessed using various metrics. Currently, commonly used indicators include population fitness standard deviation, individual Hamming distance, and population entropy. Hamming distance is typically applicable only to genes encoded in binary, limiting its use. Population entropy requires clustering analysis and may not accurately represent population diversity in a timely manner. Population fitness standard deviation has become a widely adopted and effective evaluation metric. A larger fitness standard deviation indicates higher dispersion of the population in the feasible space, reflecting greater population diversity.
Proposed an adaptive genetic algorithm that simultaneously considers individual fitness and population diversity. The Pc and Pm for inferior individuals should be increased when the population diversity is low to enhance the search capability. Conversely, when the population diversity is high, the Pc and Pm for superior individuals should be decreased to ensure the preservation of their excellent genetic. The formulas for calculating the Pc and Pm are as follows:
P c = P c 1 + ( P c 2 − P c 1 ) e x p ⁡ [ − 10 f ' − f ¯ f m a x − f ¯ ] ， f ' ≥ f ¯ P c 2 + ( P c 1 − P c 2 ) f ' − f ¯ f m i n − f ¯ ， f ' < f ¯ ， S i ≥ S 0 2 P c 2 + ( P c 0 − P c 2 ) f ' − f ¯ f m i n − f ¯ ， f ' < f ¯ ， S i < S 0 2
P m = P m 1 + ( P m 2 − P m 1 ) e x p ⁡ [ − 10 f ' − f ¯ f m a x − f ¯ ] ， f ' ≥ f ¯ P m 2 + ( P m 1 − P m 2 ) f ' − f ¯ f m i n − f ¯ ， f ' < f ¯ ， S i ≥ S 0 2 P m 2 + ( P m 0 − P m 2 ) f ' − f ¯ f m i n − f ¯ ， f ' < f ¯ ， S i < S 0 2
where, f m a x is the maximum fitness of individuals in the population, f ¯ is the average fitness of individuals in the population, f ' is the fitness of the individual with higher fitness in the parent individuals, f is the fitness of the individual entering the mutation operator, S i is the fitness standard deviation of the current population, S 0 is the initial fitness standard deviation, P c 0 > P c 1 > P c 2 > P c 3 , and P m 0 > P m 1 > P m 2 > P m 3 , with all values in the range [0, 1]. The adaptive genetic algorithm considering population diversity is illustrated in Figure 5.

3.3. Validation of the efficiency of the improved genetic algorithm

The traditional genetic algorithm is denoted as GA, the basic adaptive genetic algorithm as AGA-1, the bilinear adaptive genetic algorithm as AGA-2, the nonlinear adaptive genetic algorithm as AGA-3, and the adaptive genetic algorithm considering the overall evolutionary status of the population as AGACO. The optimization capabilities of these five adaptive genetic algorithms are compared using the minimum value problem of the Rastrigin function. Here, P c 0 = 0.7 , P c 1 = 0.6 , P c 2 = 0.4 , P c 3 = 0.2 , P m 0 = 0.3 , P m 1 = 0.2 , P m 2 = 0.1 , P m 3 = 0.02 。The population size is set to 100, the chromosome length is 24, and the number of generations is 500. The process of finding the minimum value of the function using different genetic algorithms is shown in Figure 6.
It can be observed from the figure that GA, AGA-1, and AGA-2 converge to local optimal solutions without finding the global optimum. AGA-3 and AGACO find the global optimum. AGACO converges earlier than AGA-3, and AGA-3 has a final error of 0.02419, while AGACO has a final error of 0.00342. By comparing the five genetic algorithms, it can be concluded that the traditional genetic algorithm, due to fixed Pc and Pm, are prone to premature convergence or the destruction of excellent genotypes in complex optimization problems. And adaptive genetic algorithms can reduce the destruction of excellent genotypes while enhancing global search efficiency. However, if only the individual fitness is considered and the overall evolutionary status is ignored, there is still a risk of getting stuck in local optima when population diversity decreases. The genetic algorithm that simultaneously considers the population diversity and individual fitness can effectively improve convergence efficiency and avoid premature convergence.

4. Finite Element Numerical Simulation

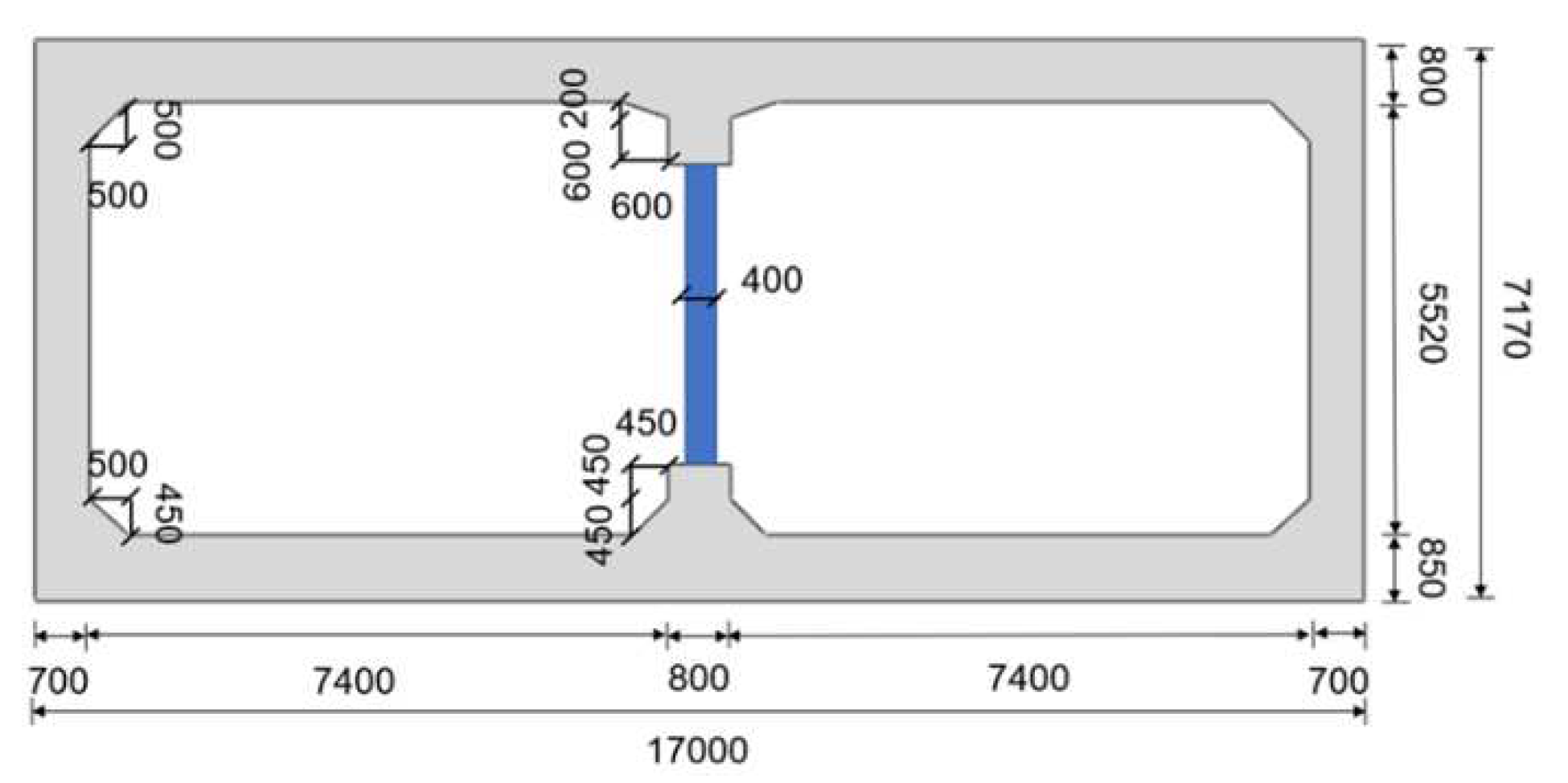
Daikai Station is chosen as the underground structure for the application of friction pendulum bearings. The cross-section of the station is illustrated in Figure 8, representing a two-span station on one level. The station has a width of 17m, a height of 7.17m, a central pillar width of 0.4m, side wall thickness of 0.7m, top plate thickness of 0.8m, and bottom plate thickness of 0.85m. The spacing of the central pillars along the tunnel alignment is 3.5m. To simplify the analysis, the station materials were considered equivalent to homogeneous materials, using an elastic constitutive model. The material has a density of 2500kg/m3, a Poisson's ratio of 0.2, and an elastic modulus of 31.5Gpa.
Preprints 94902 g008
Figure 7. Cross-section of Daikai station.
Figure 7. Cross-section of Daikai station.
Preprints 94902 g008
Based on historical seismic damage records [20,21], the burial depth of the station is 4.8m, and the soil layers at the site can be roughly divided into six layers, each with specific soil properties as indicated in Table 1. Rayleigh damping is employed for the soil layers. Using Abaqus modal analysis functionality, the first and second mode frequencies of the site were determined to be 1.8Hz and 4.2Hz respectively. Calculating with Formula (4), the Rayleigh damping coefficients for the soil layers were obtained as α=0.799 and β=0.00264.
ξ = α 2 × 1 ω 1 + β 2 × ω 2
The friction pendulum bearing has a height of 110mm and a width of 400mm. The beam elements are used to simulate the friction pendulum bearing, and the finite element model is shown in the Figure 8. A linear elastic constitutive model was selected to simulate the material properties. The material of the friction pendulum bearing is steel, with a density of 7850kg/m3, elastic modulus of 206GPa, and Poisson's ratio of 0.3.
Preprints 94902 g009
Figure 8. Finite element model of the friction pendulum bearing.
Figure 8. Finite element model of the friction pendulum bearing.
Preprints 94902 g009
The friction pendulum bearing is placed at the top of the column in the station, and the overall finite element model is shown in the Figure 9.

5. Parameter optimization of friction pendulum bearings

5.1. Key parameters of friction pendulum bearings

During the seismic process, the slider of the friction pendulum bearing is mainly subjected to the vertical pressure W, the normal force on the sliding surface N, frictional force f, and the horizontal restoring force F transmitted by the structure. Assuming the friction coefficient of the sliding surface is μ, the equivalent radius of sliding surface is R, the angle of rotation is θ and the horizontal sliding distance of the slider is D, the following calculation formula can be obtained based on the moment balance condition:
W   =   N · c o s θ
f   =   μ W · sgn ⁡ ( θ . )
F ⋅ R cos ⁡ θ   =   W ⋅ D + f ⋅ R
When θ is relatively small, formula (7) can be simplified to formula (8):
F   =   W D R + f = W D R + μ W sgn ⁡ ( θ . )
The force-displacement curves of friction pendulum bearings with different equivalent radius and friction coefficients under the same vertical pressure are shown in Figure 10.
When simulating friction pendulum bearings, the focus is on modeling the mechanical characteristics, particularly the force-displacement curve. The mechanical performance of friction pendulum bearings is mainly influenced by the friction coefficient and the equivalent radius, which are the key parameters of friction pendulum bearings.

5.2. Key parameters of friction pendulum bearings

Kobe seismic wave is selected as the input wave, and Dakai station is selected as the underground structure. The optimization variables include the friction coefficient and equivalent radius of the friction pendulum bearing, with the friction coefficient values ranging from 0.01 to 0.10 and the equivalent radius values from 1m to 10m. The parameters are encoded using Gray code, with each parameter represented by a code of 6 units in length. The optimization objective is to maximize the friction pendulum bearing's seismic reduction effectiveness. The calculation formula for seismic reduction effectiveness is as follows:
γ = R 0 − R f R 0
where, R f is the dynamic response of the central column with the seismic isolation device installed, and R 0 is the dynamic response without the seismic isolation device.
The optimization of friction pendulum bearing parameters can be viewed as a mathematical problem of finding the maximum value of a function. Design parameters serve as independent variables, while seismic reduction effectiveness represents the dependent variable. Utilizing the finite element model as a function solver, the model parameters are adjusted based on design parameters, and the seismic reduction effectiveness is computed.
Set the crossover probabilities for the adaptive genetic algorithm as P c 0 = 0.7 , P c 1 = 0.6 , P c 2 = 0.4 , P c 3 = 0.2 , and mutation probabilities as P m 0 = 0.3 , P m 1 = 0.2 , P m 2 = 0.1 , P m 3 = 0.02 . The population size is set to 30, and the total number of generations is set to 100. The formula for calculating individual fitness is:
f k = γ k − γ m i n γ m a x − γ m i n + 1 e − 3
where, f k is the fitness of the k-th individual in the population, γ m a x is the fitness of the individual with the highest fitness and γ m i n is the fitness of the individual with the lowest fitness. To avoid hiding individuals with zero fitness, a small constant value is added after the calculation. The optimization process for the friction pendulum bearing parameters is shown in Figure 11.
It can be observed from the figure that, due to the utilization of an adaptive genetic algorithm considering overall evolutionary status, even in the later stages of evolution, some individuals continue to perform random searches in the space attempting to find the other optimum. Eventually, the friction coefficient of the friction pendulum bearing converges to 0.01, and the equivalent radius converges to 3.30m. When the friction pendulum bearing is set to these parameter values, the seismic reduction effectiveness is maximized.

3. Conclusion

This paper analyzes the impact of Pc and Pm on the optimization process of genetic algorithms. A genetic algorithm considering the overall evolutionary status is proposed. Utilizing the improved genetic algorithm and finite element calculation method, the parameters of friction pendulum bearings are optimized, leading to the following conclusions:
1) When the Pc and Pm of the genetic algorithm are small, the algorithm converges quickly, and the optimization process is stable, but it is prone to converge to local optimal solution rather than global optimal solution. When the Pc and Pm are large, the randomness of spatial search is high, and the genes of excellent individuals are easily disrupted, making convergence difficult. Choosing appropriate values of Pc and Pm is crucial for the optimization ability of genetic algorithms.
2) Using the population diversity as an evaluation metric, an adaptive genetic algorithm considering the overall evolutionary status is proposed. The algorithm dynamically adjusts the Pc and Pm based on the fitness of individuals and the diversity of the population. Comparing AGACO with other genetic algorithms validates that AGACO has better global search capability and convergence efficiency.
3) Combining the improved genetic algorithm with the finite element model, the parameters of friction pendulum bearings are optimized. The optimization results provide reference suggestions for the design of friction pendulum bearings in future.

Author Contributions

Conceptualization, G.Y. and M.M.; methodology, P.J.; software, P.J. and X.M.; validation, P.J., G.Y. and X.M.; formal analysis, P.J.; investigation, X.M.; resources, G.Y. and M.M.; data curation, P.J.; writing—original draft preparation, P.J.; visualization, P.J.; super-vision, G.Y.; project administration, X.M.; funding acquisition, G.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zheng, Z.J., Wang, Z.L., Liu, S., Ma, W. Exploring the spatial effects on the level of congestion caused by traffic accidents in urban road networks: A case study of Beijing. Travel Behav. Soc. 2024, 35, 100728. [CrossRef]
  2. Chen, X.S., Xu, Y.J., Bai, X., Chu, K.F. Exploration on the Comprehensive Planning Mode of Underground Space in High-density Urban Residential Areas. Chinese Journal of Underground Space and Engineering 2022, 18(01), 1-11. [CrossRef]
  3. Broere, W. Urban underground space: Solving the problems of today's cities. Tunn. Undergr. Space Technol. 2016, 55, 245-248. [CrossRef]
  4. Qiao, Y.K., Peng, F.L., Sabri, S., Rajabifard, A. Low carbon effects of urban underground space. Sustain. Cities. Soc. 2019, 45: 451-459. [CrossRef]
  5. Chen, Z.Y., Fan, H., Bian, G.Q. Parameter Analysis of Shear Panel Dampers Under High Axial Compression. Adv. Steel Constr. 2015, 11(01): 1-14. [CrossRef]
  6. Liu, Z.Q., Chen, Z.Y., Liang, S.B., Li, C.X. Isolation mechanism of a subway station structure with flexible devices at column ends obtained in shaking-table tests. Tunn. Undergr. Space Technol. 2020, 98, 103328. [CrossRef]
  7. Chen, Z.Y., Jia, P. Seismic response of underground stations with friction pendulum bearings under horizontal and vertical ground motions. Soil Dyn. Earthq. Eng. 2021, 151,106984. [CrossRef]
  8. Zhuang, H.Y., Zhao, C., Chen, S., Fu, J.S., Zhao, K., Chen, G.X. Seismic performance of underground subway station with sliding between column and longitudinal beam. Tunn. Undergr. Space Technol. 2020, 102, 103439. [CrossRef]
  9. Chen, Z.Y., Jia, P., Liu, Z.Q. Parameter analysis of friction pendulum bearings in underground stations during the earthquake. China Civil Engineering Journal 2022, 55(04), 12-22. [CrossRef]
  10. Zhou, Y. Resilience-based seismic mitigation measure and optimal layout for subway stations. Master thesis, Tongji University, Shanghai, China, 2020.
  11. Di Trapani, F., Malavisi, M., Marano, G.C, Sberna, A.P., Greco, R. Optimal seismic retrofitting of reinforced concrete buildings by steel-jacketing using a genetic algorithm-based framework. Eng. Struct. 2020, 219, 110864. [CrossRef]
  12. Bekdaş, G., Nigdeli, S.M., Yang, X.S. A novel bat algorithm based optimum tuning of mass dampers for improving the seismic safety of structures. Eng. Struct. 2018, 159, 89-98. [CrossRef]
  13. Bagley, J.D. The behavior of adaptive systems which employ genetic and correlation algorithms. Doctor thesis, University of Michigan, Michigan, 1967.
  14. Rastrigin, L.A. Random Search in Problems of Optimization, Identification and Training of Control Systems. J. Cybern. 1974, 3, 93–103. [Google Scholar] [CrossRef]
  15. Srinivas, M., Patnaik, L.M. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man Cybern. 1994, 24(4), 656-667. [CrossRef]
  16. Sung, W., Hsiao, C. IHPG algorithm for efficient information fusion in multi-sensor network via smoothing parameter optimization. Informatica 2013, 24(2), 291-313. [CrossRef]
  17. Song, J., Hou, C., Xue, G., Ma, M. Study of Constellation Design of Pseudolites Based on Improved Adaptive Genetic Algorithm. J. Commun. 2016, 11(9), 879-885. [CrossRef]
  18. Yan, M., Hu, H., Otake, Y., Taketani, A., Wakabayashi, Y., Yanagimachi, S., Wang, S., Pan, Z., Hu, G. Improved adaptive genetic algorithm with sparsity constraint applied to thermal neutron CT reconstruction of two-phase flow. Meas. Sci. Technol. 2018, 29(5), 055404. [CrossRef]
  19. Wang, L.L. Research on emergency management capability evaluation of hazardous chemical supply chain. Chem. Eng. Trans. 2017, 62, 1369–1374. [Google Scholar] [CrossRef]
  20. Hiroomi, I., Toshio, H., Nozomu, Y., Masahiko I. Damage to Daikai Subway Station. Soils Found. 1996, 36, 283-300. [CrossRef]
  21. Nguyen, V.Q., Nizamani, Z.A., Park, D., Kwon, O.S. Numerical simulation of damage evolution of Daikai station during the 1995 Kobe earthquake. Eng. Struct. 2020, 206, 283-300. [CrossRef]
  22. Yamamoto, S., Kikuchi, M., Ueda, M., Aiken, I. A mechanical model for elastomeric seismic isolation bearings including the influence of axial load. Earthq. Eng. Struct. Dyn. 2009, 38, 157-180. [CrossRef]
Preprints 94902 g001
Figure 1. Rastigin function diagram.
Figure 1. Rastigin function diagram.
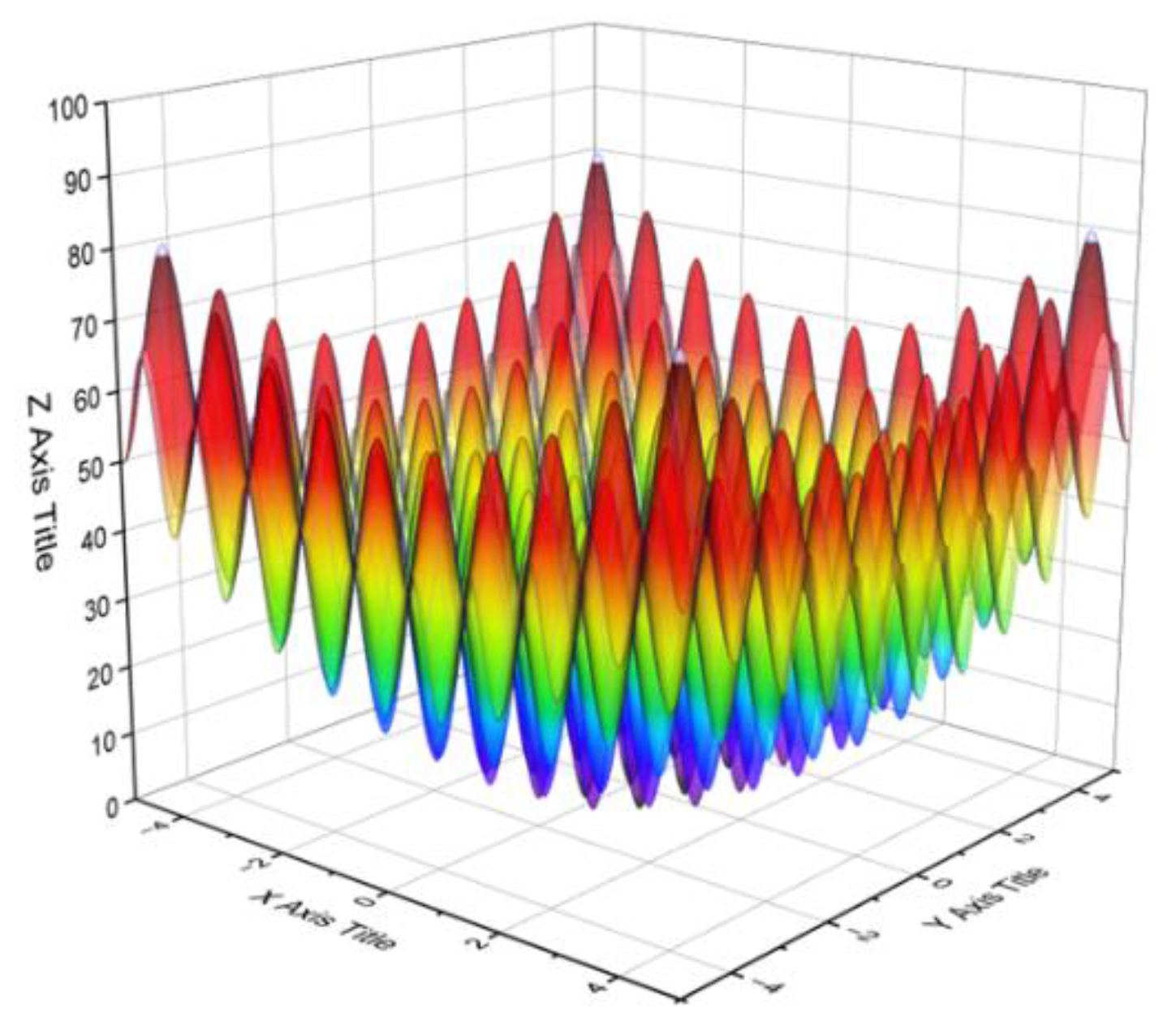
Preprints 94902 g001
Preprints 94902 g002
Figure 2. Optimization process with different Pc.
Figure 2. Optimization process with different Pc.
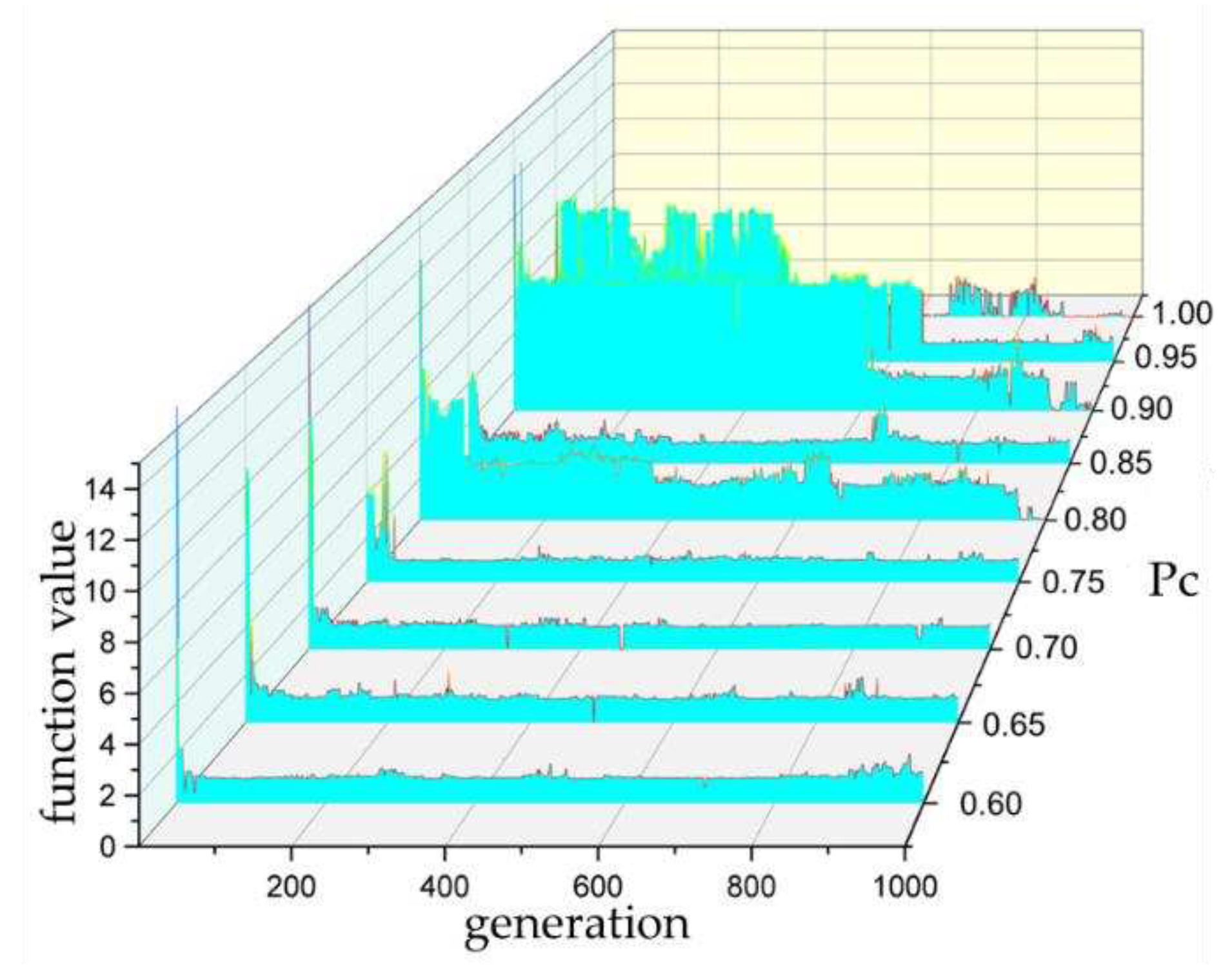
Preprints 94902 g002
Preprints 94902 g003
Figure 3. Optimization process with different Pm.
Figure 3. Optimization process with different Pm.
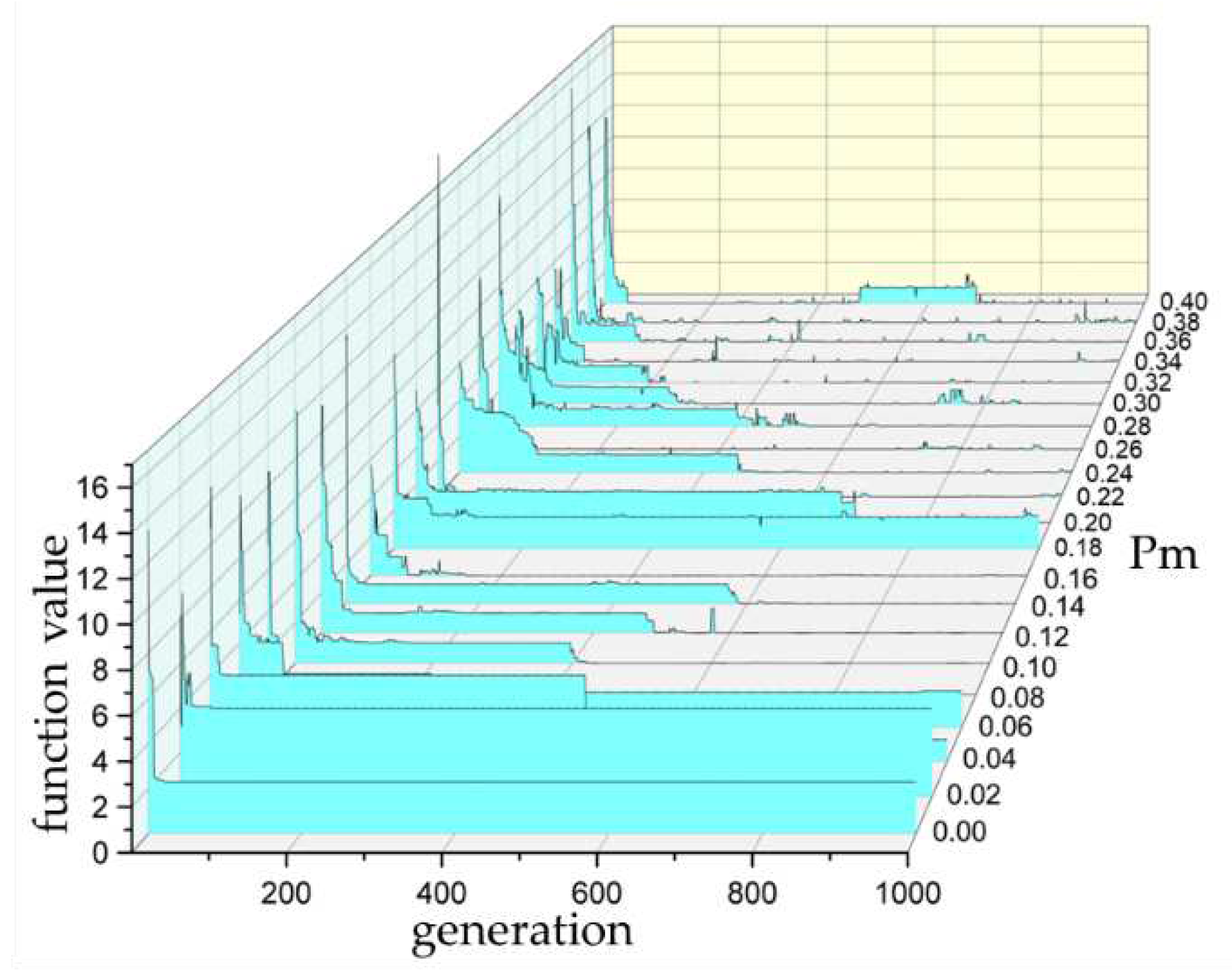
Preprints 94902 g003
Preprints 94902 g006
Figure 5. Improved adaptive genetic algorithm flowchart.
Figure 5. Improved adaptive genetic algorithm flowchart.
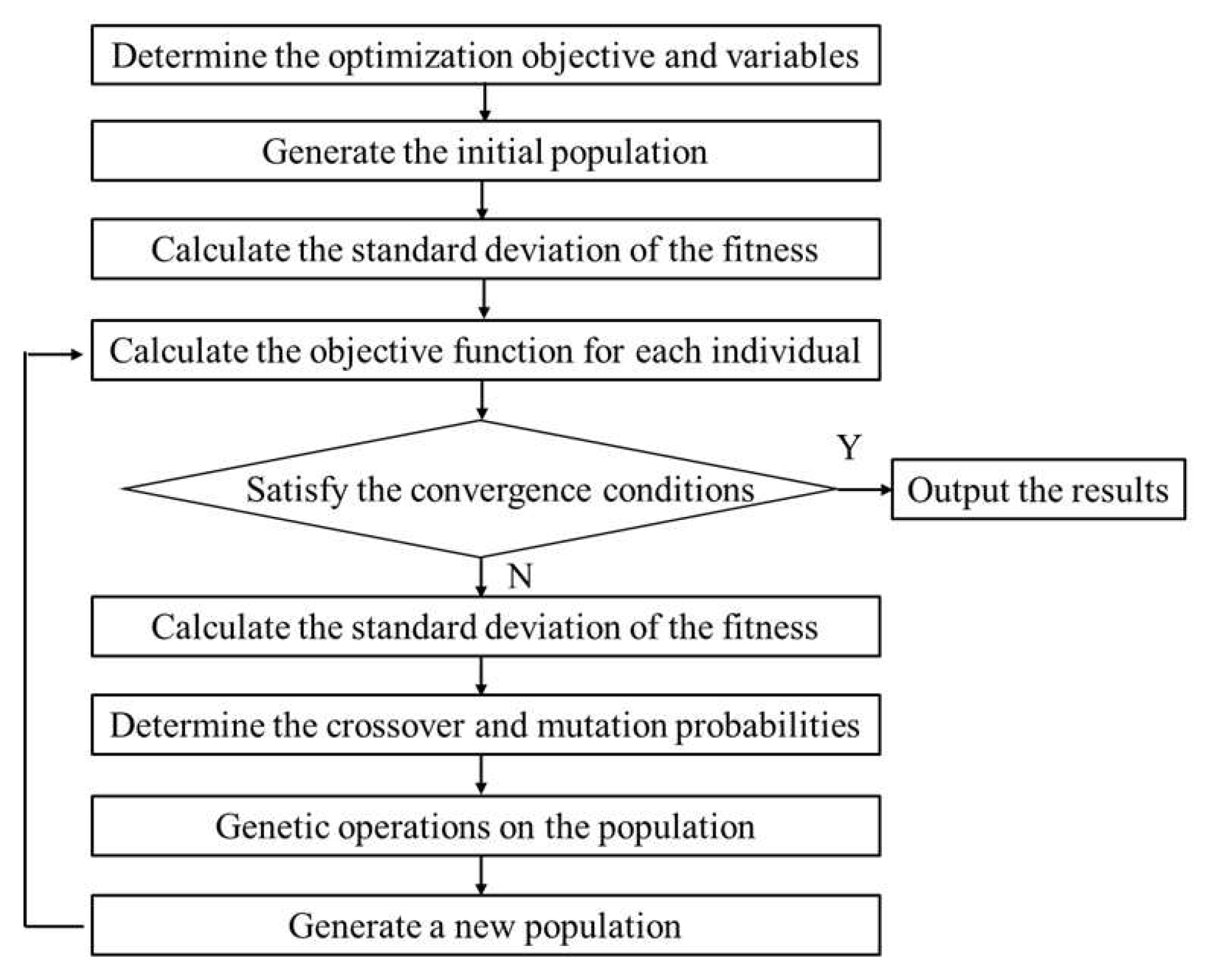
Preprints 94902 g006
Preprints 94902 g007
Figure 6. Optimization processes of different genetic algorithms.
Figure 6. Optimization processes of different genetic algorithms.
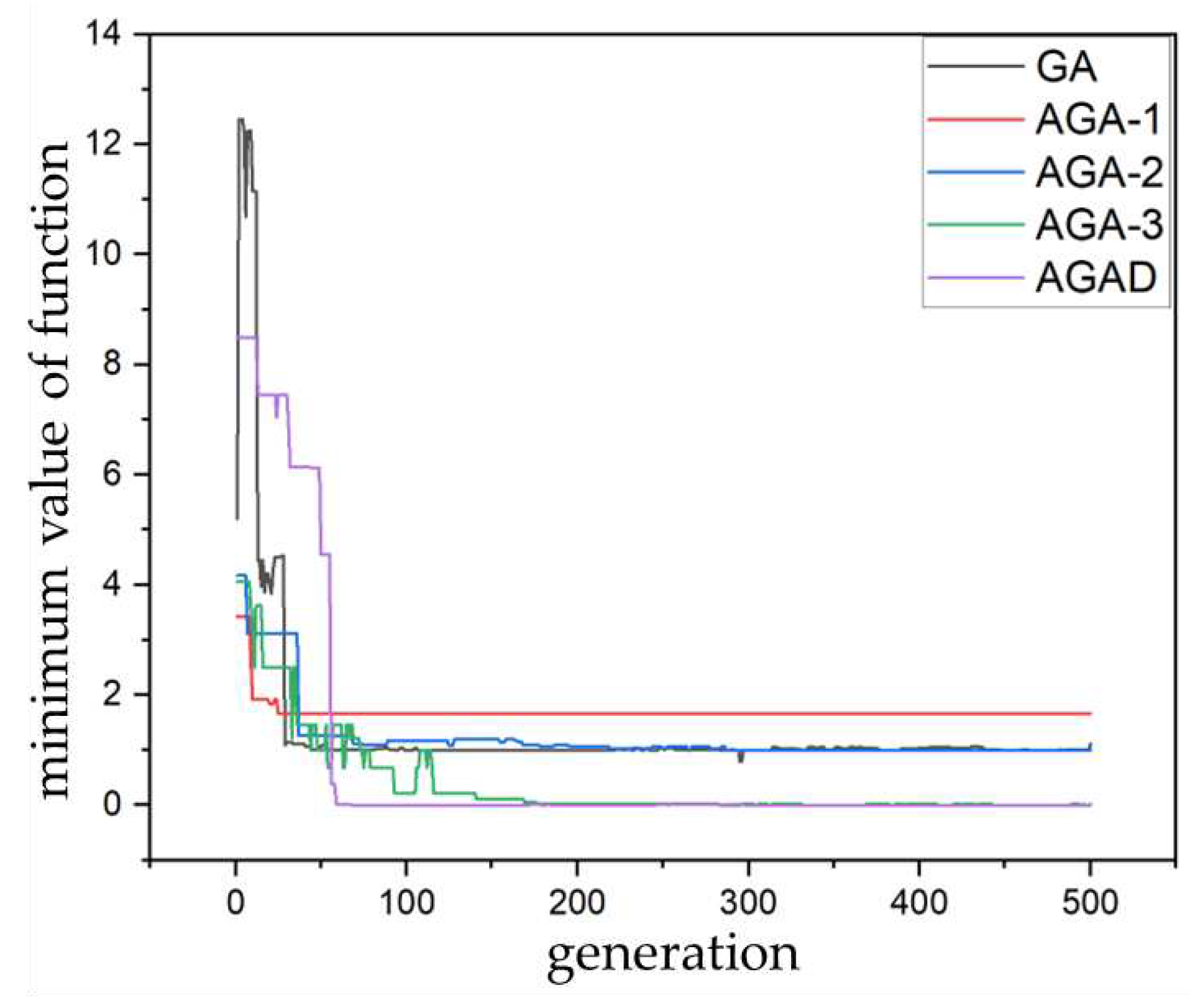
Preprints 94902 g007
Preprints 94902 g010
Figure 9. Overall finite element model.
Figure 9. Overall finite element model.
Preprints 94902 g010
Preprints 94902 g011
Figure 10. Force-displacement curve with different equivalent radius and friction coefficients.
Figure 10. Force-displacement curve with different equivalent radius and friction coefficients.
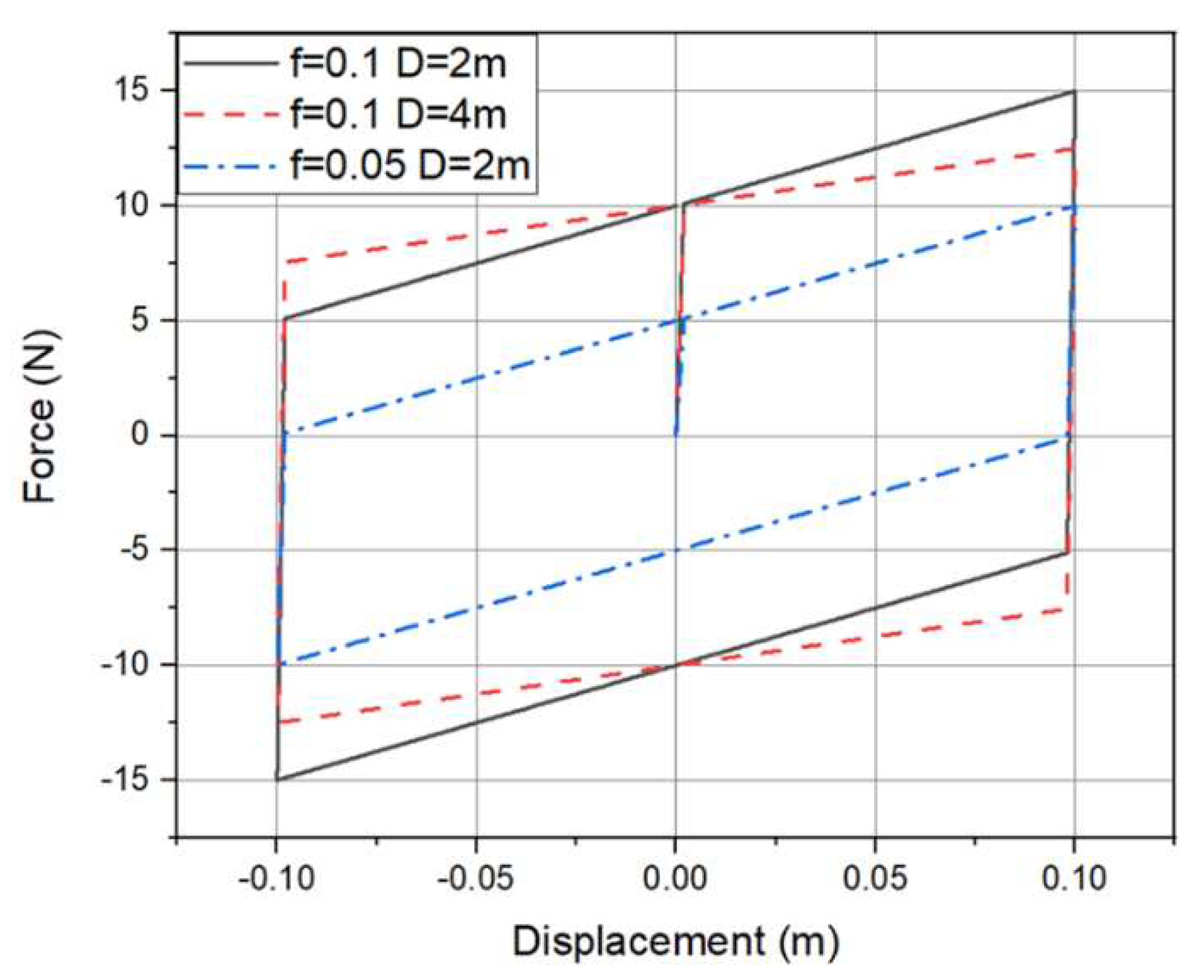
Preprints 94902 g011
Preprints 94902 g012
Figure 11. Evolution process of two key parameters: (a) Evolution process of friction coefficients; (b) Evolution process of equivalent radius.
Figure 11. Evolution process of two key parameters: (a) Evolution process of friction coefficients; (b) Evolution process of equivalent radius.
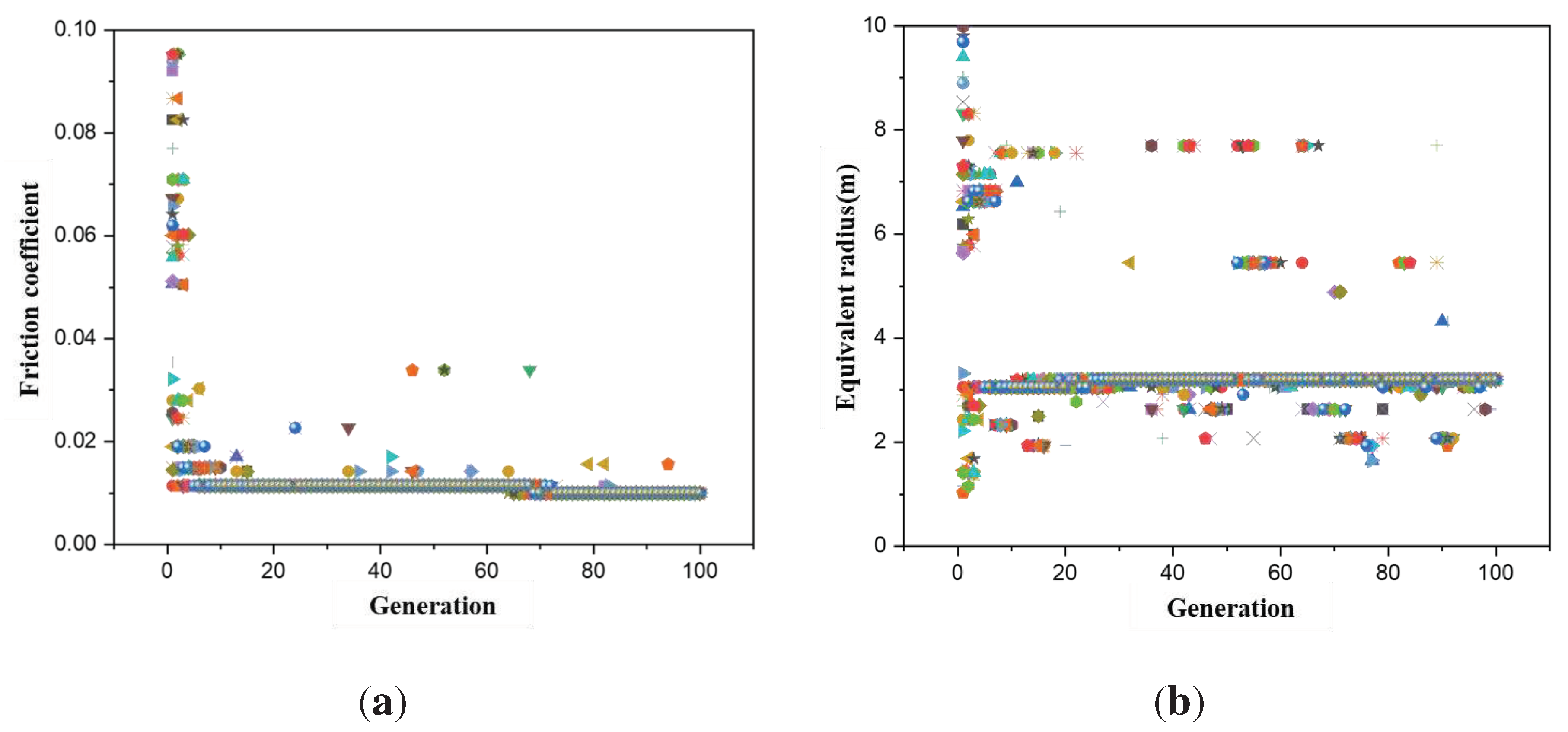
Preprints 94902 g012
Table 1. Material properties of each soil layer.
Table 1. Material properties of each soil layer.
Soil type Thickness (m) Density
(kN/m3)		 Shear wave velocity (m/s) Poisson's ratio Dynamic modulus of elasticity (Mpa)
Clay 1 19 140 0.333 99.3
Sand 4.1 19 140 0.488 111
Sand 3.2 19 170 0.493 164
Clay 3.1 19 190 0.494 205
Clay 5.8 19 240 0.49 326
Sand 22 20 330 0.487 648
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated