Preprint
Article
Galactic Spiral from ROTASE Model with Large Enough ρ Is Equivalent to Archimedean Spiral
Altmetrics
Downloads
103
Views
106
Comments
1
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
02 January 2024
Posted:
04 January 2024
You are already at the latest version
Alerts
Abstract
This paper serves as a seamless continuation of the previous work titled "Special Spirals are Produced by the ROTASE Galactic Spiral Equations with the Sequential Prime Numbers." Upon revisiting the data, a noteworthy observation emerged: the special spirals can be meticulously aligned with the prime spiral on a point-by-point basis through careful scaling and rotation for the parameter ρ remaining a constant greater than one. As ρ increases, both the scaling factor and rotation angle exhibit a corresponding augmentation, albeit with an intriguing caveat—the rotation angle asymptotically approaches its limit of 90°. Notably, the galactic spiral can be perceived as a remarkably close approximation of the Archimedean spiral, with the degree of proximity increasing as ρ grows larger. Furthermore, an intriguing correspondence arises when ρ takes on a value of 1; at this value, the galactic spiral bears a striking resemblance to the Fermat spiral, the space between two consecutive spiral loops undergoes a continuous reduction as the loop's radius expands, yet it never diminishes to zero; simultaneously, the area between two successive loops experiences an augmentation with the value of ρ.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
In 2022, I authored a paper titled “Special Spirals are Produced by the ROTASE Galactic Spiral Equations with the Sequential Prime Numbers” [1]. This work stemmed from a spontaneous exploration, driven by curiosity, wherein prime numbers were employed as variables for the galactic spiral equations derived from the ROTASE model. The ROTASE model, an acronym for “ROtating Two Arm Sprinkler Emission,” was proposed to elucidate the potential mechanism behind the formation of spiral arms in disc galaxies. The resulting galactic spiral equations offer compelling depictions of the spiral patterns observed in most, if not all, spiral galaxies [2].
The spirals generated by the galactic spiral equations, with prime numbers as variables, bear a striking resemblance to the well-known prime spiral (PS). The latter is constructed with a prime number as the spiral winding angle in radians, with the same prime number determining the distance of the spiral point from the center. For simplicity, the spirals produced by the galactic spiral equations with prime numbers are henceforth referred to as Galactic Prime Spirals (GPS) in this paper.
Despite the visual similarity between GPS and the prime spiral, their construction mechanisms are fundamentally incompatible. The angle employed as the calculation variable in the galactic spiral equations signifies the “time” of spiral arm development, not the spiral winding angle. The calculation process involves three intricate steps, and the distances of corresponding spiral points, calculated with ρ = 2.5 and R = 1, are notably larger than those of prime spiral points. Moreover, the galactic spiral initiates at the Y-axis, further distinguishing it from the prime spiral, which starts at the X-axis.
Initially, I did not perceive any connection between the galactic prime spirals and prime spirals with those original data. Placing them on the same plot seemed unfeasible, given their entirely distinct construction methods. However, a persistent curiosity led me to revisit the data and make a surprising discovery. Upon a meticulous comparison of the galactic prime spirals with prime spirals, I found a mysterious connection—the former can be regarded as scaled prime spirals. Each data point aligns remarkably well with proper scaling and rotation, as elucidated in detail in this paper. Thus, this work serves as a continuation of my earlier paper, driven entirely by curiosity.
2. The Difference of the Spiral Calculation between the Prime Spiral and the Galactic Spiral
The galactic spiral equations, serving as the foundation for our exploration, originate from the ROTASE model, a conceptual framework proposed as an alternative mechanism to elucidate the enigmatic formation of spiral arms in disc galaxies [2]. At the core of this model lies a pivotal concept—the existence of a mysterious entity referred to as X-matter. Analogous to the water emitted by a two-arm sprinkler irrigating lawns, X-matter is emitted from opposing sides of the galaxy’s center. Intriguingly, the term “X” denotes its unknown nature, akin to the naming convention of “X-ray,” a label given by Wilhelm Röntgen upon its discovery in 1895.
X-matter plays a pivotal role in the ROTASE model, enhancing the rate of new star formation within the galaxy. The precise characterization of X-matter remains an open question, prompting speculation about whether it manifests as a particle, an unidentified physical field, or another elusive entity yet to be defined and subject to speculation.
For readers unfamiliar with the intricacies of the galactic spiral equations, gaining insight into the mechanics of spiral formation in the ROTASE model proves beneficial. This understanding allows one to discern the distinctions in the spiral-forming processes between the galactic spirals discussed in this study and the more conventional prime spirals.
2.1. The Formation of Prime Spiral
First, let’s delve into the formation of the prime spiral. It’s essential to note the existence of another prime spiral variant known as the Ulam spiral [3]. The Ulam spiral is generated by arranging positive integers in a square spiral, and when marking the prime numbers within this arrangement, significant concentrations of primes become evident along diagonal, horizontal, and vertical lines. However, our focus here is on a distinct type of prime spiral.
The mathematical expression for the prime spiral is represented by the formula:
Here, rPS is the distance of the prime spiral point from the center, θ signifies the spiral winding angle counterclockwise, measured in radians rather than degrees. Equation (1) describes a standard Archimedean spiral [4], as depicted in Figure 1.
Figure 1A visually presents the initial four points of the prime spiral, providing a glimpse into its construction process. The first point (2,2) exhibits a distance of 2 units from the center and a winding angle of 2 radians, equivalent to 114.59°. Similarly, the fourth spiral point (7,7) features a distance of 7 units from the center and a winding angle of 7 radians, corresponding to 401.7°. This pattern continues, illustrating the sequential formation of prime spiral points.
In Figure 1B, the first 100 prime spiral points are displayed. While most data points may appear scattered without a discernible spiral feature, the central area exhibits subtle spiral characteristics. However, the intriguing spiral pattern becomes more evident in Figure 1C, where the first 1000 data points reveal a structured arrangement. This configuration consists of a total of 20 spirals, organized into two distinct groups and separated by symmetrically located spiral gaps on both sides.
The simplicity of the prime spiral’s formation is noteworthy. For a detailed explanation of why special spirals are formed by prime numbers, a valuable resource is the YouTube video titled “Why do prime numbers make these spirals?” [5], accessible as of the date of this writing.
2.2. The Formation of the Galactic Spiral
In contrast to the straightforward formation of the prime spiral, the genesis of the galactic spiral within the ROTASE model is notably intricate. The underlying galactic spiral equations trace their origins to the motion of X-matter, a substance emitted from the galactic center and dragged by the galactic matter with a flat rotation.
Figure 2 provides a visual representation of the intricate process involved in the formation and calculation of spiral arms within the ROTASE model. Interested readers can delve into the details of the ROTASE model and the derivation of galactic spiral equations in the references [2,6]. For an alternative conceptualization, readers may also refer to a similar model where boats initially anchor at a central round island, sequentially navigating across a circular river, employing the same mathematical mechanism to derive galactic spiral equations [7].
Assuming the galactic bar is aligned along the Y-axis and rotates clockwise, the emission of X-matter originates from the galactic center, traverses the galactic bar, and exits at point A (12 o’clock position). Subsequently, the X-matter moves freely, dragged by the rotational dynamics of galactic matter, tracing the trajectory outlined by the white dashed curve and arriving at point B. At any given point B(x, y), when the X-matter undergoes a minimal displacement “ds” over an infinitesimally short time “dt,” the corresponding travel distances in the X-axis direction (“dx”) and the Y-axis direction (“dy”) can be calculated through the following differential equations:
where, Vr is the galactic matter rotation velocity; Ve is the X-matter emission velocity; α denotes the angle of the distance r of the X-matter at the point B(x, y) with respect to the Y-axis.
And
The initial values of x and y are set as:
where R is the rotation radius of the bar, or the half length of the galactic bar. The angular rotation velocity of the galactic bar is given by:
The rotation angle θ of the bar is:
Equation (6) allows us to substitute “dt” in Equation (2) with “dθ”:
In other words, the galactic bar rotation angle θ serves as a time reference, akin to an old mechanical clock where 90 degrees of minute hand rotation equals 15 minutes. Equation (2) can thus be rewritten as:
where,
The differential Equation (8) can be solved within the polar coordinate system, yielding four solutions across three distinct cases, as detailed in the references [2]. To compute the trajectory of X-matter movement along the white dashed line in Figure 2, from point A(0, R) to point B(x, y), the Equation (8) can be effortlessly implemented in a simple computer program.
However, the formation of the spiral arms, induced by the X-matter, is a progressive physical event that evolves over time. To establish a temporal reference, we adopt the current galactic bar as the “zero” time in the ROTASE model, signifying the present. Consequently, all spiral arms are considered to have formed in the past.
Referring to Figure 2, when the galactic bar was positioned at point C in the past at an angle θ relative to the current bar along the Y-axis, X-matter emitted at C will travel to position D(x’, y’). This movement follows the black dashed curve at time “t,” during which the bar rotates by an angle θ relative to its current position along the Y-axis. The coordinates of D(x’, y’) represent a mathematical backward rotation by θ from the position B(x, y).
The mathematical expressions for this backward rotation are given by:
Plotting (x’, y’) generates one spiral arm of the galaxy. However, since spiral galaxies typically exhibit two spiral arms with perfect central symmetry, the other arm can be generated by considering symmetry (-x’, -y’).
Upon careful consideration of the above analysis, it becomes evident that the angle θ in the differential galactic spiral Equation (8) represents “time,” not the spiral winding angle. The actual winding angle is denoted as β and defined by:
Here, θ serves as an independent variable, while α depends on the time “θ” and the velocity of X-matter emission, Ve. This distinction is crucial, leading to the conclusion that the galactic prime spirals, generated by prime numbers as input variables, are not inherently related to the prime spiral.
Returning to the discussion of the galactic prime spiral and the prime spiral, for the previously calculated galactic prime spiral with ρ = 2.5 and R = 1.
Figure 3A presents the first 1000 points (red dots) of the galactic prime spiral and the first 1000 points (black dots) of the prime spiral, plotted on the same scale. The noticeable size difference—2.29 times for the galactic prime spiral compared to the prime spiral—initially provides no apparent indication of a potential match. However, Figure 3B scales down the galactic prime spiral by 0.4363 to precisely match the size of the prime spiral, achieving equality in distance at the 1000th point:
Figure 3B clearly shows that the galactic prime spirals have the same curvature as the prime spiral after scaling, but the data points are not matched with each other, mismatch is more clearly shown in the zoomed-in central area by Figure 3C, a visual inspection in Figure 3C reveals all data points are mismatched within the central first 100 points. Despite this initial disparity, Figures 3B and 3C strongly hint that the two unrelated spiral curves could be possibly matched through rotation, albeit with no guarantee of precise point-to-point correspondence due to the distinct mathematical mechanisms governing each spiral.
The magic unfolds when the galactic prime spiral undergoes a proper clockwise rotation, resulting in an unexpected match with the prime spiral. The rotation angle is meticulously chosen to synchronize the coordinates of the 1000th point of the galactic prime spiral with those of the 1000th point of the prime spiral:
Figure 4 displays the outcome of the 66.423° clockwise rotation of the galactic prime spiral and the prime spiral. Figure 4A showcases the rotated galactic prime spiral (red “X”) with 1000 points and the prime spiral (black dots), and Figure 4B provides a close-up of the central area. Surprisingly, both figures distinctly reveal that the galactic prime spiral seamlessly matches the prime spiral, point by point.
Figure 5A displays the galactic prime spiral, calculated with 50,000 prime numbers using ρ = 2.5 and R = 1. It has been scaled down by 0.4363 and rotated by 66.423°. Figure 5B is the prime spiral, also calculated with 50,000 prime numbers. Figure 5C combines both spirals. Remarkably, despite being computed through entirely different methods, the two spirals appear visually identical, point by point.
Upon close inspection and a meticulous one-to-one comparison, there exists a minuscule difference between the data points of the two spirals in the central starting area. However, this small discrepancy is imperceptible to the naked eye, and such difference quickly diminishes with increasing values of ρ. Consequently, the galactic spiral Equation (8) with ρ > 1 can be considered a remarkably close approximation of the Archimedean spiral equation. The higher the value of ρ, the closer the galactic spiral aligns with the Archimedean spiral.
Figure 6 illustrates the linear variation in the size of the galactic prime spiral concerning the parameter ρ, referenced to the size of the prime spiral. The scaling factor is determined as the ratio of the distance of the 1000th point of the galactic prime spiral to the distance of the 1000th point of the prime spiral. The orange line is the fitting line with the ρ in 6 to 15 range, this figure shows that the scaling factor linearly increases with the ρ when the ρ is large enough (ρ > 4) and basically equals ρ with R =1. The parameter R is also a scaling factor, which directly amplifies the size of the galactic spiral, but will not change the galactic spiral patterns, the galactic spiral pattern is only decided by the behavior of the ρ as seen later.
In Figure 7, the rotation angle (in degrees) undergoes a change corresponding to the parameter ρ, representing the angle required for the galactic prime spiral to align with the prime spiral. The orange curve in the figure represents the fitted line based on the equation:
As observed, the rotation angle increases with the parameter ρ, gradually approaching its asymptotic limit of 90 degrees. It’s important to note that the prime spiral initiates from the X-axis, while the galactic spiral begins at the Y-axis. Both spirals wind counterclockwise, resulting in a natural 90° difference at their starting points. Consequently, it would be expected that all galactic prime spirals, calculated with different ρ values, need to rotate 90° clockwise to precisely match the prime spiral. However, the unexpected results depicted in Figure 7 introduce a puzzling aspect, and the underlying reason for this deviation remains unclear.
Based on the Figure 4, Figure 5, Figure 6 and Figure 7, we can conclude that when the parameter ρ is large enough, the galactic spiral with a constant ρ is equivalent to the Archimedean spiral. This is a totally unexpected result beyond the scope of the initial derivation of the galactic spiral equations from the ROTASE model.
2.3. Galactic Prime Spiral with ρ < 1
A crucial solution to the differential Equation (8) is expressed as:
Equation (14) holds paramount significance as it distinctly determines the evolution of the spiral pattern in the galactic spiral with ρ variation, showcasing dramatic changes correlated with different values of ρ, as vividly illustrated in Figure 8.
For ρ < 1, where the maximum value of sin(α) is 1, and the distance r must be greater than 0, therefore, the distance r of the spiral points from the center is constrained by:
This restriction results in a spiral-ring pattern with the ring’s radius defined by Equation (15), as depicted in Figure 8A–C, which are not plotted in the same scale, each with a ring radius of 1.25, 2.5, and 10, respectively.
For ρ = 1, the radius of the ring is infinite, implying infinite spiral loops with no distinct ring, and the space between consecutive loops gradually decreasing with the radius of the loop, but never reaching zero, resembling the characteristics of a Fermat spiral [8]. However, unlike the Fermat spiral, in the galactic spiral with ρ = 1, the area between two consecutive loops increases with the radius of the loop.
The spiral-ring pattern of the galactic spiral finds application in describing ring galaxies and various natural species on Earth, such as Aloe polyphylla, Camellia Flower, and Pinecone [2,7].
For ρ > 1, the galactic spiral transitions into an Archimedean spiral, exemplified in Figure 7E. Notably, the galaxy J101652.52-004630.0 exhibits an Archimedean spiral pattern fitting perfectly with the galactic spiral equation (8) and ρ = 2.5.
Figure 8 showcases galactic spirals with various constant ρ values. However, in the ROTASE model, the parameter ρ can change with time (θ or t) in any format and at any time. This time dependence introduces infinite possible spiral patterns, exemplified in Figure 9. Figure 9A,B are called 8-shaped double ring patterns, because their outer profiles look like 8-shaped patterns; the Figure 9C can be named as double-8-shaped double ring pattern, because the outer profile has vertical 8-shaped double ring pattern and the middle profile has the horizontal 8-shaped double ring pattern. The 8-shaped double ring patterns are so elegant and special, readers may wonder that those striking patterns can only theoretically exist by mathematical illustration. However, they do popularly exist in the nature. The galaxies UGC 12646 and NGC 7098 have the 8-shaped double ring pattern of Figure 9A; the galaxy SDSS J015701.50-001644.4 has the 8-shaped double ring pattern of Figure 9B; and the galaxies NGC 1079, NGC 3018 and ESO 507-16 have the double-8-shaped double ring pattern of the Figure 9C [2]. How did the nature make such beautiful and highly symmetric patterns with precision engineering in such cosmological scale? We can only admire nature’s super magic power which can create everything including ourselves.
Figure 9D illustrates spiral patterns with ρ increasing with time “θ” following an exponential function, closely resembling a Logarithmic spiral. This pattern finds resonance in the cross section of the Nautilus shell, fitting neatly with galactic spiral equations with ρ changing over time according to an exponential function [7].
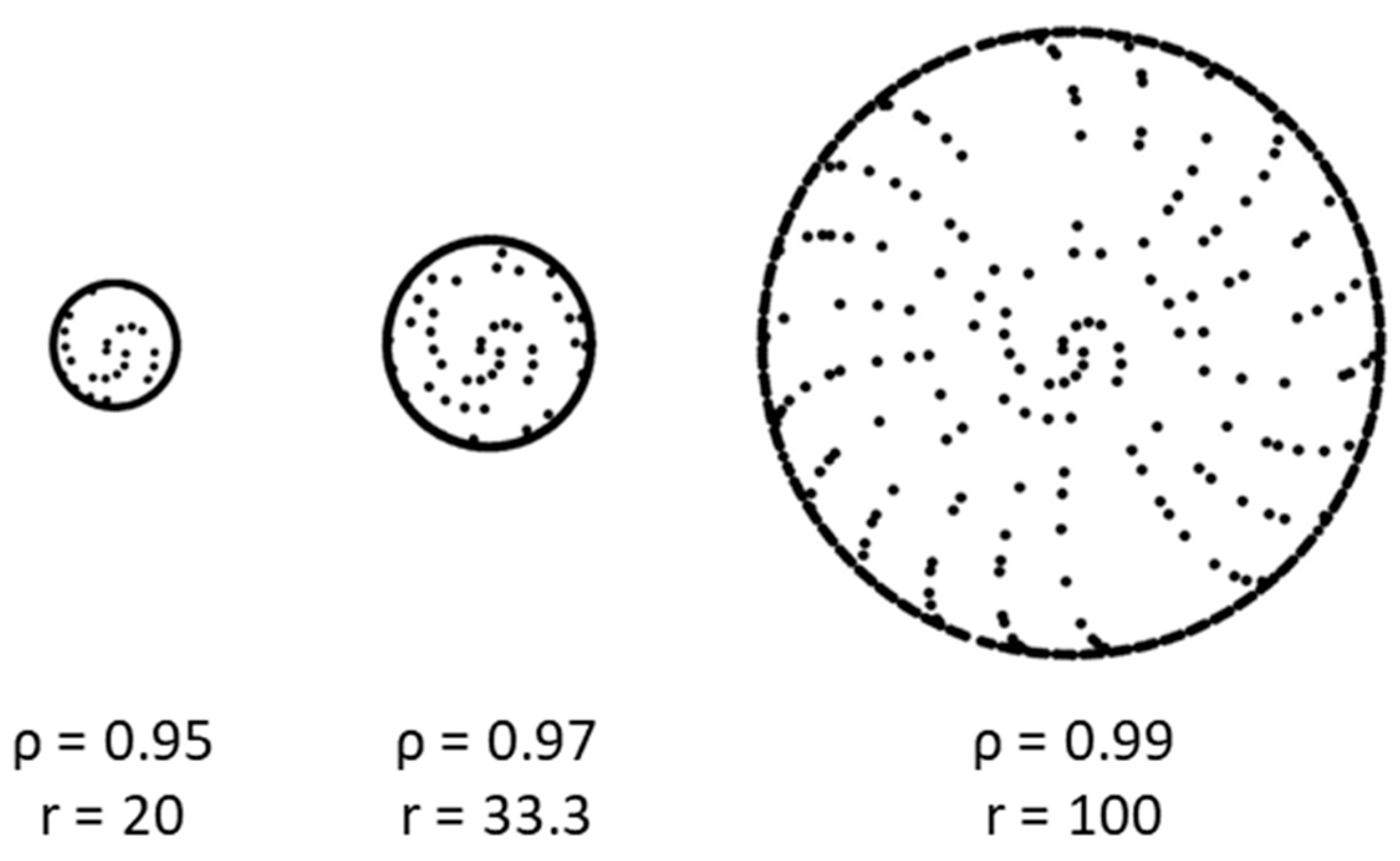
Figure 10 presents three galactic prime spirals with ρ values of 0.95, 0.97, and 0.99, respectively, all plotted on the same scale. Each exhibits a distinct spiral-ring pattern with the radius of the ring defined by Equation (15). While the central areas of these patterns resemble the prime spiral, it’s noteworthy that none of the data points can be reasonably matched to those of the prime spiral through scaling and rotation.
3. Summary
The prime spiral can be replicated by the galactic spiral equations with prime numbers as variables through appropriate scaling and rotation. The galactic spiral serves as a very close approximation to the Archimedean spiral when the parameter ρ exceeds 1. As ρ increases, the galactic spiral approaches the Archimedean spiral more closely. The scaling factor and rotation angle increase with the parameter ρ, with the rotation angle gradually approaching the limit of 90°. For ρ = 1, the galactic spiral pattern resembles the Fermat spiral, featuring a decreasing space between consecutive loops as the loop radius increases, yet never reaching zero; additionally, the area between two consecutive loops increases with the radius of the loop.
Funding
This research received no funding.
Data Availability Statement
No additional data are needed.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pan, H. Special Spirals are Produced by the ROTASE Galactic Spiral Equations with the Sequential Prime Numbers. AJAMS 2022, 8, 69–77. [Google Scholar] [CrossRef]
- Pan, H. Spirals and rings in barred galaxies by the ROTASE model. IJP 2021, 9, 286–307. [Google Scholar] [CrossRef]
- Stein, M.L.; Ulam, S.M.; Wells, M.B. A Visual Display of Some Properties of the Distribution of Primes. American Mathematical Monthly 1964, 71, 516–520. [Google Scholar] [CrossRef]
- Lockwood, E.H. A Book of Curves; Cambridge University Press: Cambridge, UK, 1967; pp. 173–164. [Google Scholar]
- https://www.youtube.com/watch?v=EK32jo7i5LQ.
- Pan, H. New formulas and mechanism for the spiral arm formation of Galaxies. IJP 2019, 7, 73–85. [Google Scholar] [CrossRef]
- Pan, H. Introduction of New Spiral Formulas from ROTASE Model and Application to Natural Spiral Objects. AJAMS 2021, 7, 66–76. [Google Scholar] [CrossRef]
- Dixon, R. Mathographics. New York: Dover, 1991; p. 121.
Figure 1.
the prime spirals with 3 different spiral points.
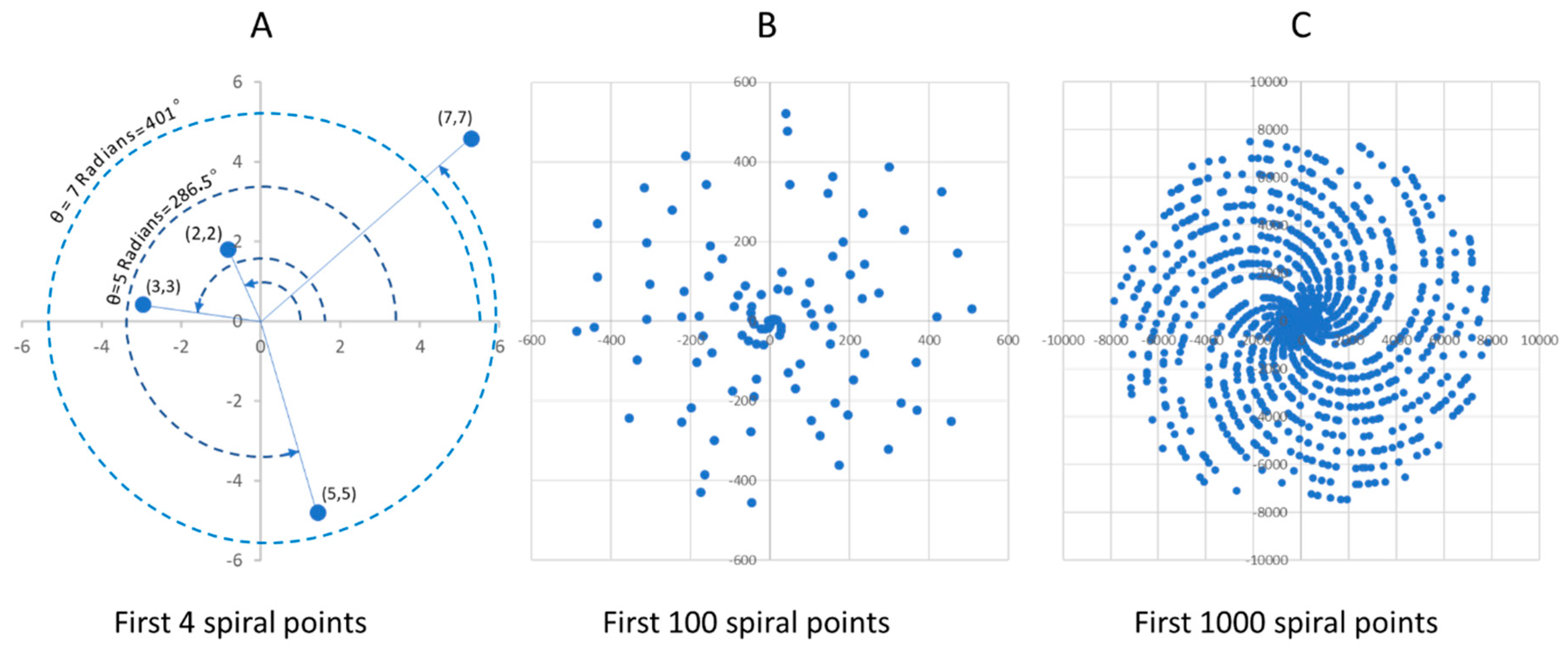
Figure 2.
illustration of the formation and calculation of the galactic spiral.
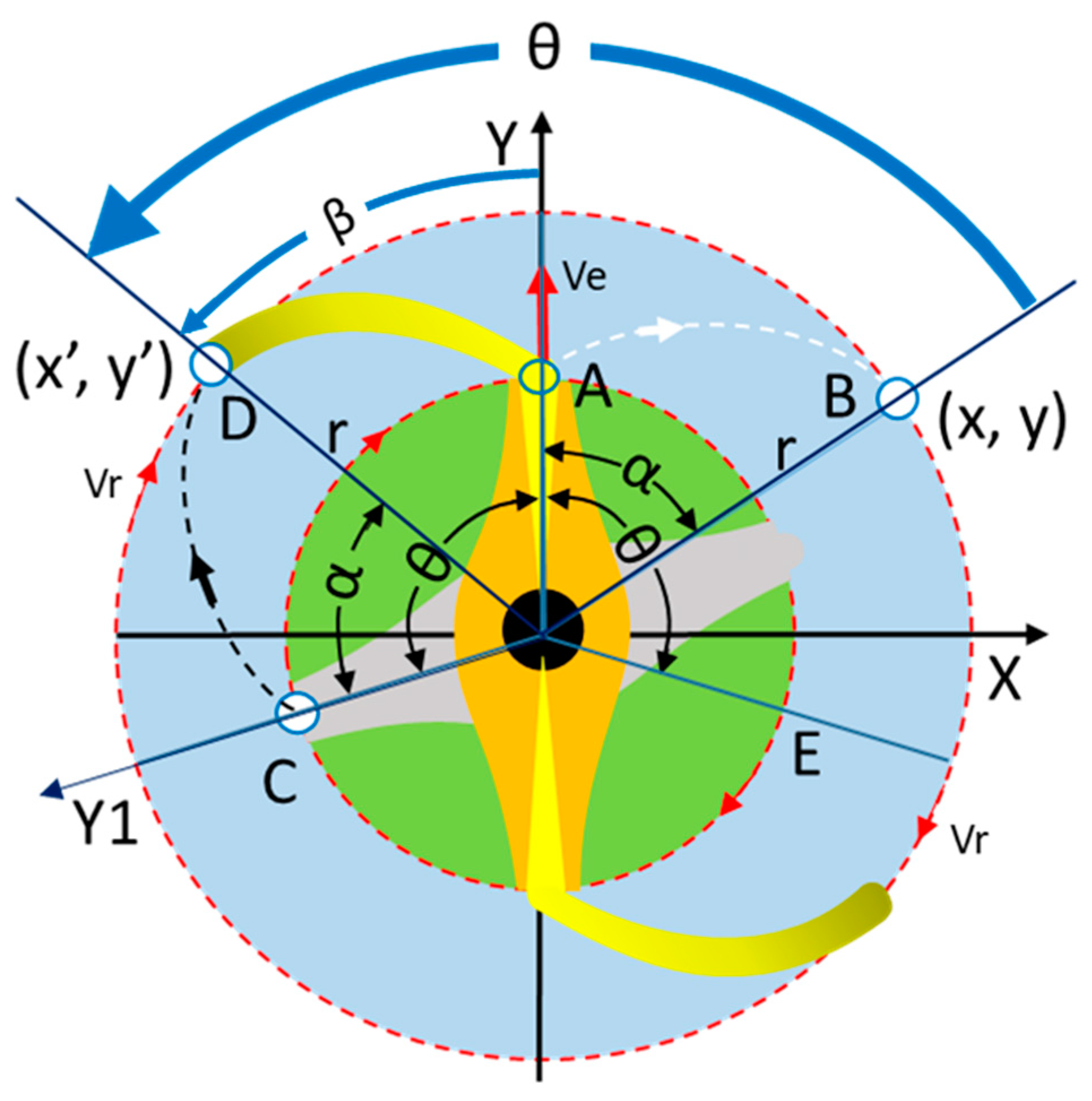
Figure 3.
A: red dots are the original galactic prime spiral of the first 1000 points along with the black dots of the first 1000 points of the prime spiral. B: the galactic prime spiral of the first 1000 points is scaled down by 0.4363 along with the first 1000 points of the prime spiral. C: the zoom-in area of central first 100 points of Figure 3B.
Figure 3.
A: red dots are the original galactic prime spiral of the first 1000 points along with the black dots of the first 1000 points of the prime spiral. B: the galactic prime spiral of the first 1000 points is scaled down by 0.4363 along with the first 1000 points of the prime spiral. C: the zoom-in area of central first 100 points of Figure 3B.
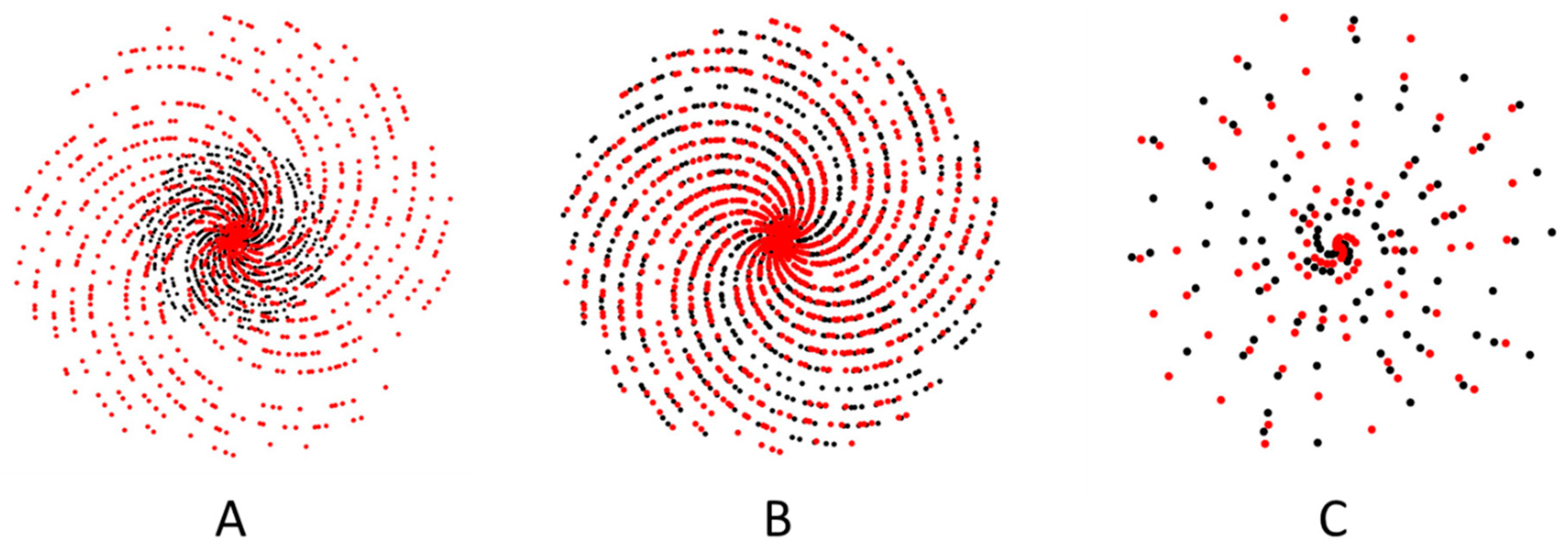
Figure 4.
scaled down by 0.4363 and rotated by 66.423°, the galactic prime spiral (red “X”) matches the prime spiral (black dots). A: First 1000 points of the galactic prime spiral along with the first 1000 points of the prime spiral. B: Zoom-in the central first 100 points of Figure 4A.
Figure 4.
scaled down by 0.4363 and rotated by 66.423°, the galactic prime spiral (red “X”) matches the prime spiral (black dots). A: First 1000 points of the galactic prime spiral along with the first 1000 points of the prime spiral. B: Zoom-in the central first 100 points of Figure 4A.

Figure 5.
left is the galactic prime spiral calculated with first 50000 prime numbers scaled down by 0.4363 and rotated clockwise by 66.423°; middle is the prime spiral at the right with 50000 prime numbers; right is the combined the galactic prime spiral (red) and the prime spirals (black, hidden under the red dots), the two spirals are visually identical.
Figure 5.
left is the galactic prime spiral calculated with first 50000 prime numbers scaled down by 0.4363 and rotated clockwise by 66.423°; middle is the prime spiral at the right with 50000 prime numbers; right is the combined the galactic prime spiral (red) and the prime spirals (black, hidden under the red dots), the two spirals are visually identical.
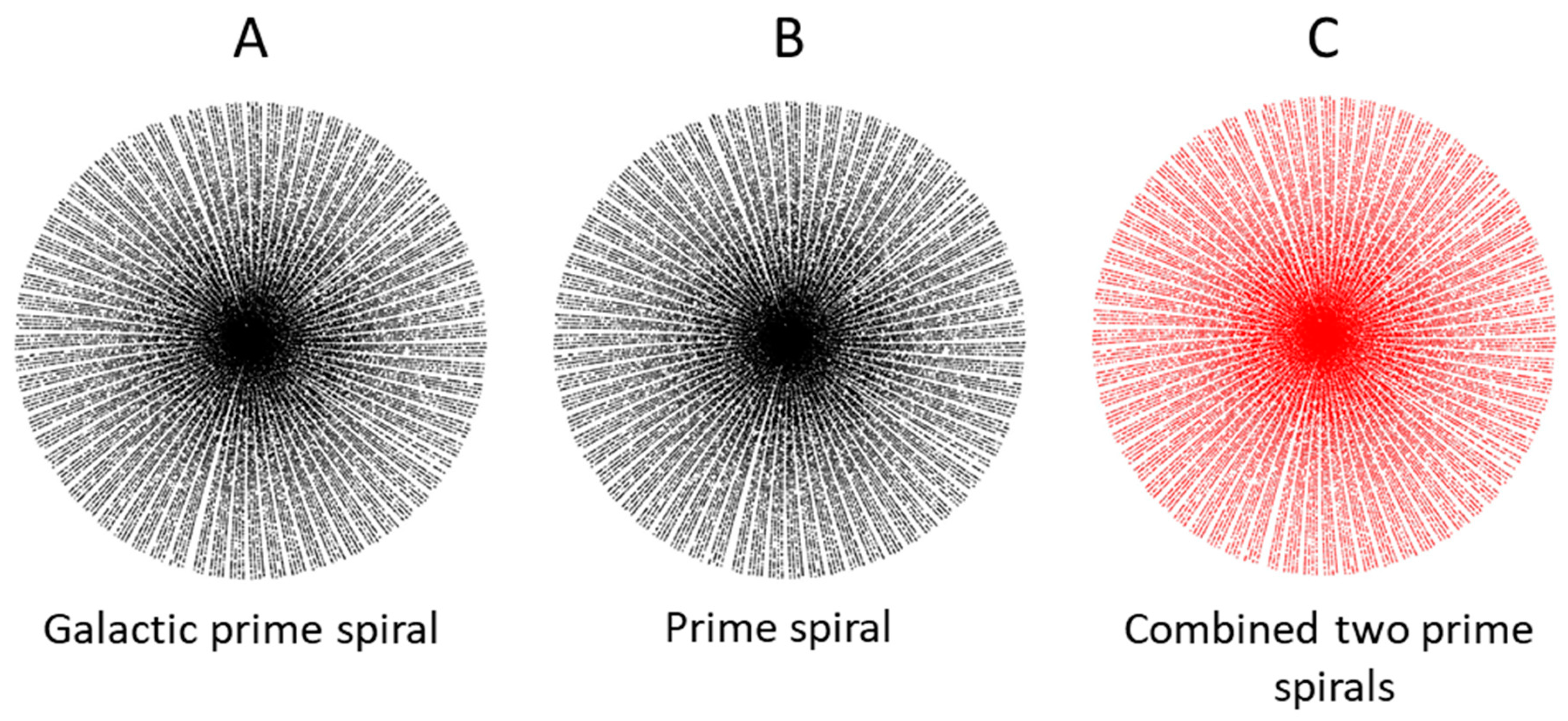
Figure 6.
the change of the size of the galactic prime spiral with the parameter ρ (R =1).
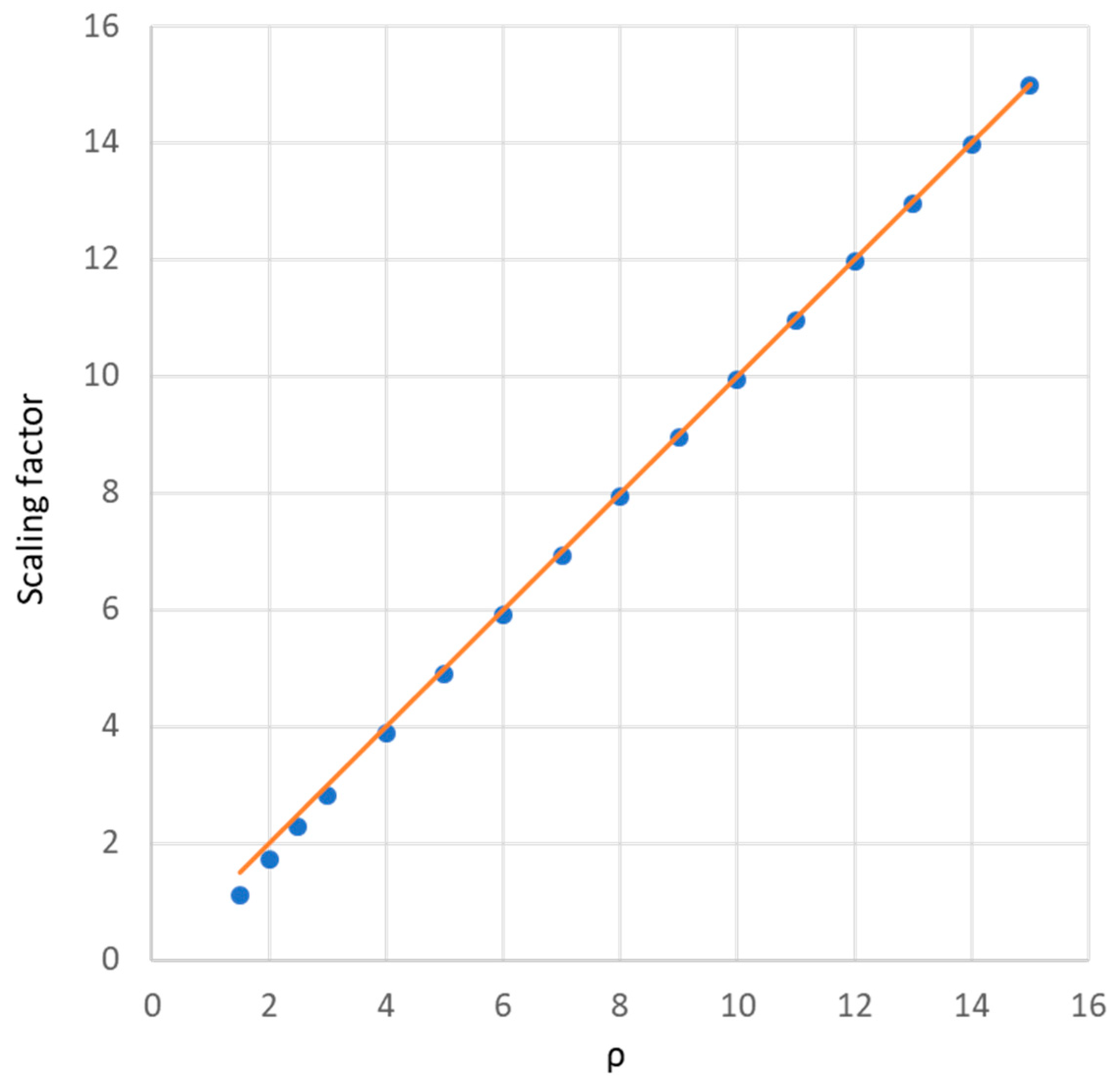
Figure 7.
the rotation angle of the galactic prime spiral to match the prime spiral. The blue dots are the rotation angle in degree and the orange line is the fitting curve by the equation listed in the Figure.
Figure 7.
the rotation angle of the galactic prime spiral to match the prime spiral. The blue dots are the rotation angle in degree and the orange line is the fitting curve by the equation listed in the Figure.
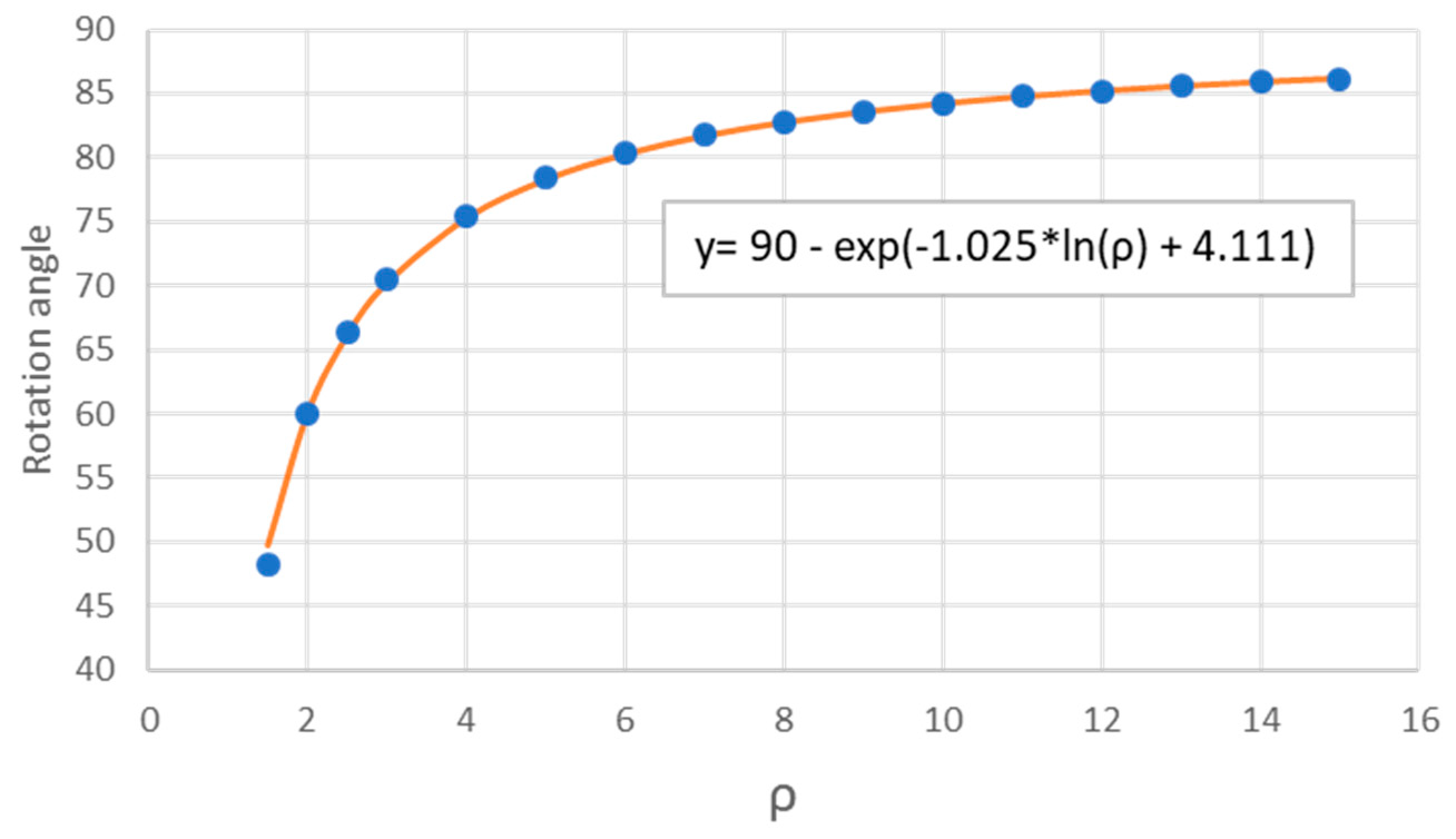
Figure 8.
Galactic spiral changes with the parameter ρ, not plotted in the same scale. The top row is the single spiral patterns; the second row is the two-spiral patterns with central symmetry.
Figure 8.
Galactic spiral changes with the parameter ρ, not plotted in the same scale. The top row is the single spiral patterns; the second row is the two-spiral patterns with central symmetry.
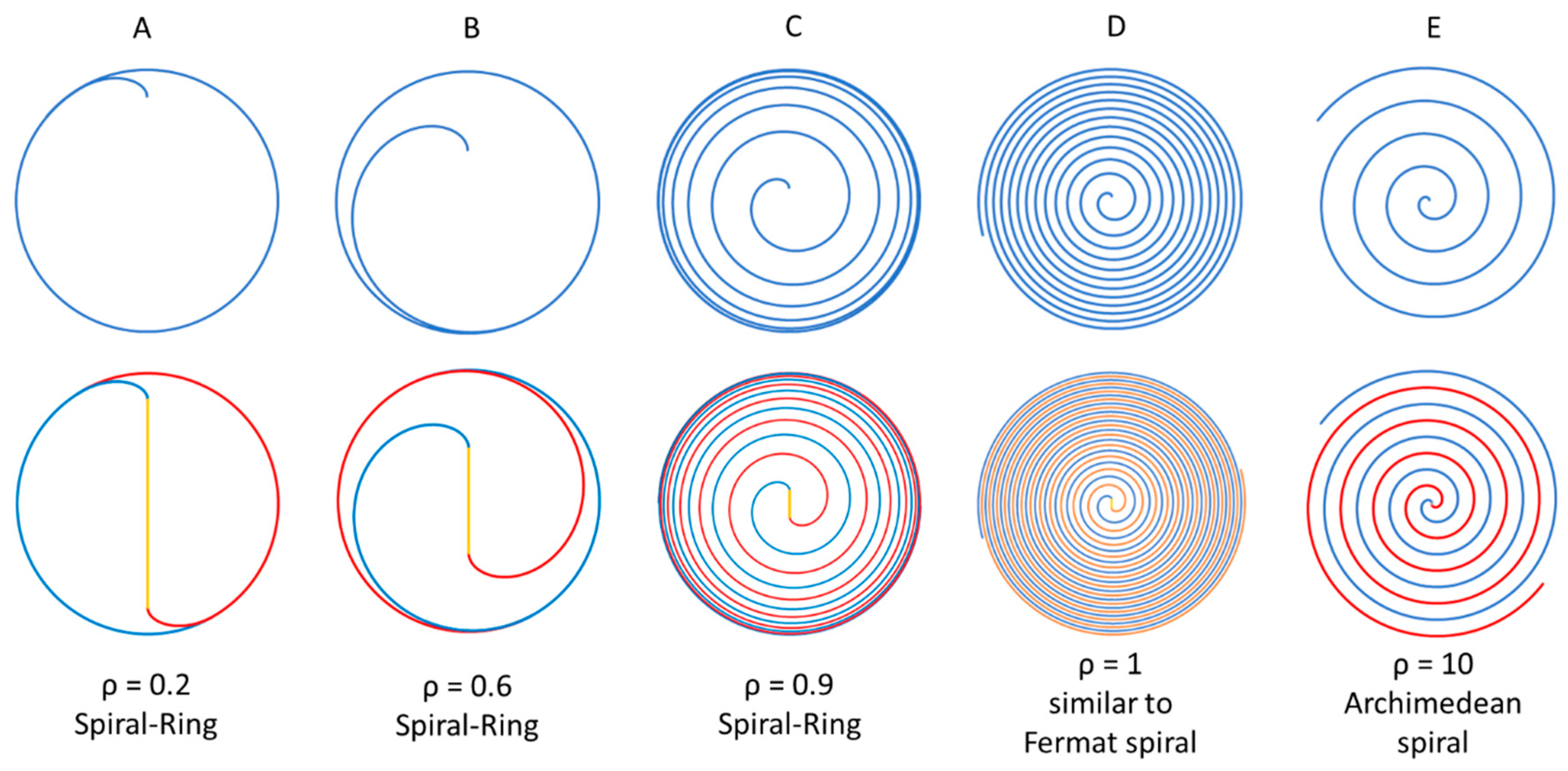
Figure 9.
Galactic spirals with parameter ρ change with time “θ”.
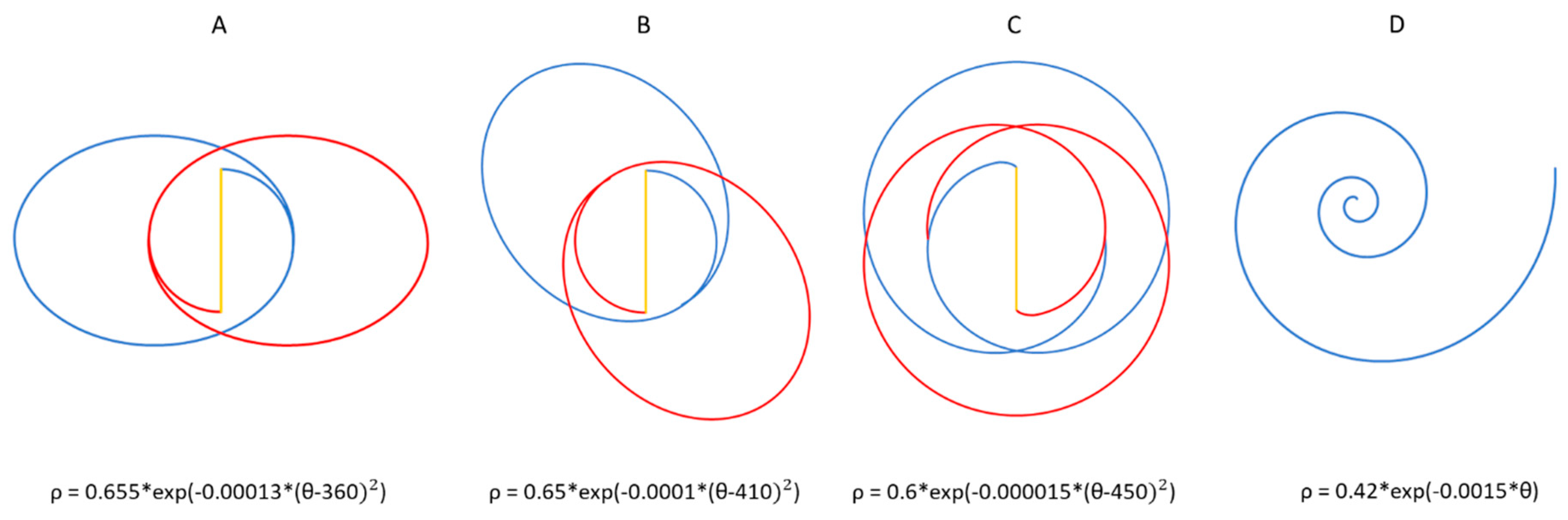
Figure 10.
galactic prime spirals with ρ = 0.95, 0.97 and 0.99, respectively, plotted on the same scale.
Figure 10.
galactic prime spirals with ρ = 0.95, 0.97 and 0.99, respectively, plotted on the same scale.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





