Preprint
Article
A Performance Simulation Methodology of Whole Turboshaft Engine Based on ThroughFlow Modelling
Altmetrics
Downloads
122
Views
22
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
28 December 2023
Posted:
03 January 2024
You are already at the latest version
Alerts
Abstract
To accurately predict the matching relationships between the various components and the engine performance in the whole aero-engine environment, this study introduces a two-dimensional throughflow simulation method for the whole aero-engine. This method is based on individual throughflow solvers for the turbo-machinery and the combustor. It establishes a throughflow simulation model for the whole engine by integrating with the compressor-turbine co-operating equations and boundary conditions. The turbo-machinery throughflow solver employs a circumferentially averaged form of the time-dependent Navier-Stokes equations (N-S) as the governing equation. The combustor solver uses the Reynolds Average Navier-Stokes (RANS) method to solve flow and chemical reaction processes by constructing turbulence, combustion, and radiation models. The accuracy of the component solver is validated using Pratt & Whitney’s three-stage axial compressor (P&W3S1) and General Electric’s high-pressure turbine (GE-EEE HPT), and the predicted results are consistent with the experimental data. Finally, the developed throughflow method is applied to simulate the throttling characteristics of the WZ-X turboshaft engine. The results predicted by the throughflow program are consistent with the GasTurb calculations, including the trends of shaft power delivered, specific fuel consumption (SFC), inlet airflow, and total pressure ratio of the compressor. The developed method to perform throughflow simulation of the whole aero-engine eliminates the dependence on a general component map. It can quickly obtain the meridian flow field parameters and overall engine characteristics, which is expected to guide the design and modification of the engine in the future.
Keywords:
Subject: Engineering - Aerospace Engineering
1. Introduction
The traditional aero-engine development mode usually relies on physical experiments and a serial development model of ‘design-test validation-modify design-retest’ to expose design problems, which leads to the problems of long development cycles, high costs, and elevated risks. The limitations of this traditional development model have become obvious in meeting the ever-increasing performance requirements and complexities of aircraft engines, while numerical simulation has emerged as a crucial tool driving the transformation of aircraft engine development models. Throughout the pre-research plans published by developed countries and the current research and development systems [1,2,3], the transformation from the ‘traditional design’ by means of a large number of experiments to the ‘predictive design’ based on numerical simulation has been basically completed, which greatly reduces the development cycle and test cost of the engine [4].
Numerical simulation of aero-engine aerodynamic performance can include component levels and whole engine levels. The numerical simulation method has been dramatically developed for compressor and turbine components. From the one-dimensional average diameter calculation and the through-flow calculation of the S1 stream surface and S2 stream surface to the three-dimensional flow theory [5], and then to the full three-dimensional viscous calculation based on the Navier-Stokes equations, the mature multi-level analysis and design system have been initially formed. However, at the whole engine level, the performance evaluation of aero engines is mainly based on zero-dimensional (0D) thermodynamic cycle parameter calculations [6]. Due to the simplification of models, the accuracy of 0D depends on a large number of components and whole engine test data and cannot reflect the flow field of the engine. There have been a few reports on three-dimensional whole-engine calculations in recent years. Teixeira and colleagues from Numeca[7,8] conducted steady-state and unsteady-state three-dimensional numerical simulations of the micro turbojet engine KJ66. The total number of grids is approximately 19.2 million, of which the computational domain includes one blade passage for every turbomachinery blade row, a 60° sector for the combustion chamber, and a half exhaust hood. The steady calculation of the whole engine uses 288 cores and takes about 52 hours to reach the convergence state. The fuel flow and speed are given as input parameters according to the experimental data. Certainly, the computational cost of three-dimensional whole-engine simulations is still high, and it does not provide practical solutions for analyzing whole-engine performance in the preliminary design stage. Therefore, through-flow calculations remain crucial in the aero engine design process. The two-dimensional numerical simulation of the whole aero-engine can provide a large amount of meridional plane information while possessing advantages such as low computational cost and ease of implementation, making them highly promising for further development.
Whole-engine two-dimensional throughflow simulation has been reported in previous literature. Nigmatullin and Ivanov [9] solved the unsteady Euler equations based on the axisymmetric assumption using the high-order accuracy finite difference Godunov scheme on the S2 stream surface. They used the body force model to simulate the blade row's viscous loss and flow deflection effects. The concept of a digital test bench at the throughflow simulation level has been realized to a certain extent. Stewart [10] adopted a method to solve the axisymmetric Euler equations for integrated throughflow simulation of the E3 engine and nacelle. Petrovic et al. [11,12] employed the finite element method to solve the throughflow governing equations based on the stream function approach. They combined a series of empirical models to construct the whole engine throughflow simulation model. The combustion chamber simulation used a simplified zero-dimensional model, that is, the matching between the compressor and the turbine components adopted numerical zooming technology. When Yang et al. [13,14] conducted a throughflow simulation of the KJ66 engine, employing artificially distributed fuel source terms for the combustion process in the combustion chamber without considering the true distribution of the temperature field within the combustion chamber. Liu et al. [15] conducted throughflow simulations for a turbojet engine at design and off-design operating points, but the calculation results showed oscillatory convergence.
Inspired by the discussions in the previous sections, this paper introduces a novel approach for steady-state two-dimensional throughflow simulation of the whole aero engines. The approach is based on individual throughflow solvers for turbo-machinery components and the combustion chamber, and establishes the whole aero-engine throughflow simulation platform with co-operating equations and boundary conditions as constraints for the iterative simulation of the characteristics of the full engine and components. The present study assesses publicly available compressor and turbine test cases to verify the accuracy of the throughflow solver. Subsequently, a turboshaft engine is used as a case to test the overall performance of the engine and the simulation capacity of the meridian flow field by the whole engine simulation platform. The throughflow results are compared with zero-dimensional thermodynamic cycle analysis results demonstrating consistency in the predicted outcomes of both approaches.
2. Throughflow Simulation Methods
2.1. Throughflow Methods for Components
The whole engine throughflow simulation platform developed in this study includes a turbo-machinery throughflow solver and a combustor throughflow solver. The turbo-machinery throughflow solver is developed based on the time-marching Navier-Stokes throughflow modeling proposed by Dawes[16] and Simon[17]. However, it includes many new details and extensions [18], which can be used for axial compressors, centrifugal compressors, and axial turbines. The combustor throughflow solver solves the two-dimensional N-S equations on the center plane of the swirler, as well as combustion chemical reactions and thermal radiation effects, which can be used for straight-flow combustors and reverse-flow combustors [19].
2.1.1. Turbo-machinery Modeling
The governing equations for the through-flow modeling of the turbomachinery are strictly derived from the three-dimensional Navier-Stokes equations in the cylindrical coordinate system by the circumferentially averaged method, which can be written as Eq.(1).
where
and
The closure of the viscous blade force term and the inviscid blade force term in the governing equation is very important. The Sb2 and Sbv on the right side of Eq.(1) cannot be directly solved and require modeling. The modeling of Sb2 is based on the assumption of an average flow surface and is solved using an implicit computational method [20]. The average flow surface is determined by summing up the deflecting angles along the blade camber, where the deflecting angles at the inlet of the blade are equal to the incidence (i), and the deviation (δ) is taken at the exit of the blade. The blade region is distributed in the form of a Bézier curve between the two. The viscous blade force Sbv is modeled using the distributed loss model proposed by Horlock [21] to establish the relationship between the loss coefficient and entropy increase, where the loss coefficient is given by experimental data or empirical models [22,23,24,25,26].
The numerical solution of the governing equations is performed using a finite volume method based on the grid center. The Roe scheme is employed for convection flux calculation, and the TVD scheme is applied for flux correction based on MUSCL interpolation. The viscous flux is calculated using a second-order central difference, and a multi-step Runge-Kutta method is utilized for time-marching solution [27]. Additionally, the Baldwin-Lomax model solves the turbulent eddy viscosity coefficient. The time-marching flow method can automatically capture specific forms of shock waves without adding a shock wave model.
2.1.2. Combustor Modeling
When simulating the two-dimensional combustor, it is necessary to simplify the three-dimensional combustor into a two-dimensional structure based on the following considerations:
- Retain the main structural characteristics of the flame tube and the main flow features in the flame tube, including swirler jets, primary hole jets, mixing hole jets, etc.;
- Maintain the flow distribution in the combustion zone and mixing zone;
- Neglect detailed processes such as fuel atomization and evaporation.
The simplified geometric model of the combustion chamber is illustrated in Figure 1, where the air intakes structures such as swirler, primary holes, and mixing holes are simplified into annular slots. Only the flow inside the flame tube is simulated to maintain the flow distribution in the combustor. Based on the combustion organization within the combustor, the flow inside the flame tube is divided into the combustion zone and the mixing zone. The air in the combustion zone enters through the head swirler, the cooling gas in the middle zone that does not participate in the combustion process enters through the main combustion hole. The air in the mixing zone enters through the mixing hole. The fuel is simplified as a gaseous fuel, which enters the combustion zone through the inlet of the swirler. It mixes with the air in the combustion zone and reacts chemically.
The total air flow in the combustion zone, , includes the air flow entering from the head swirler, , the cooling air flow at the head, , the cooling air flow in front of the primary hole cross section, , the air flow entering from the primary hole, , and the portion of the cooling air in the intermediate zone that participates in the combustion process, (usually taken as 50%).
The total airflow in the mixing zone includes the amount of air entering from the mixing hole,, and the amount of cooling air, ,
The simplified two-dimensional combustor in this study is an axisymmetric structure, and its grid is generated in the body-fitted coordinate system. The general governing equations for the two-dimensional combustor in cylindrical coordinates can be expressed as Eq.(5),
Depending on the value of ϕ, this equation represents the continuity, momentum, turbulence kinetic energy, turbulence kinetic energy dissipation rate, enthalpy, species mass fractions, and radiation flux. The k-ε two-equation model is used for the turbulence model. The EBU-Arrhenius model is used for the combustion model, and the four-flux radiation model is used to consider the radiation effect.
According to the compressor outlet parameters and the flow distribution law of the combustion chamber, the boundary conditions for the inlet of the two-dimensional combustion chamber are generated. On the solid wall, the non-slip wall condition is used for the momentum equation, and the zero-gradient boundary condition is used for other scalar equations. The pressure-velocity coupling algorithm is solved using the SIMPLE algorithm. The governing equations are discretized using a hybrid difference scheme, and the discretized linear equations are solved using the TDMA algorithm, with under-relaxation applied to enhance the stability of the solution.
2.2. Whole engine simulation platform
The turboshaft engine simulation platform is based on the individual turbo-machinery solver for the compressor/turbine and the combustor solver developed by the authors mentioned above. Taking a single-shaft turboshaft engine with a power turbine as an example, the overall engine can be divided into six major components: the inlet, compressor, combustion chamber, gas turbine, power turbine, and exhaust nozzle. The station divisions for each component are shown in Figure 2, where 0-0 represents the engine inlet section; 3-3 is the compressor outlet section; 41-41 is the exit section of the gas turbine inlet guide vane; 5-5 is the exit section of the gas turbine; 6-6 is the exit section of the power turbine, and 9-9 is the exit section of the nozzle.
Figure 3 shows the input and output boundary conditions at the component level for the throughflow simulation platform, in which the variables listed within each component represent the input values, and the variables outside each component represent the output values. The arrows indicate the direction of information transmission between components. Due to the different physical characteristics of the compressor, turbine, and combustor, different boundary conditions are applied for solving. The boundary condition of the turbomachinery solver is that at a certain speed, the inlet total pressure, total temperature, airflow angle, and outlet backpressure are specified. The boundary conditions of the combustor solver are given total pressure, total temperature, static pressure, static temperature, inlet flow rate, and fuel-air ratio at the inlet, and the outlet is a zero gradient condition.
Taking Figure 3 as an example, the engine operating speed is Nc, and the inlet total temperature Tt1 and total pressure Pt1 are converted according to the atmospheric environment and flight conditions. Simultaneously, the compressor outlet static pressure P3 is specified to complete the calculation for the intake-compressor component combination. The compressor outlet parameters, including total temperature Tt3, total pressure Pt3, static temperature T3, static pressure P3, and outlet flow W3, are assigned to the combustor inlet, and the fuel-air ratio φ is given to calculate the combustor of the combustion chamber. Subsequently, the total temperature Tt4, total pressure Pt4, and flow angle of the combustion chamber outlet are assigned to the gas turbine inlet, and atmospheric pressure P0 is specified at the nozzle outlet to complete the turbine-nozzle component calculation. For steady-state simulation of a single-shaft turboshaft engine, the cooperative operation of the compressor and turbine must satisfy mass flow continuity and power balance conditions, that is, the combustion chamber outlet flow W4 and the turbine inlet flow W41, the gas turbine power Lgas and the compressor power Lcom need to meet the constraints in Eq.(6),
where Lex is power offtake and ηmech is spool mechanical efficiency.
For a certain operating speed of the engine, based on the co-operating equations of the engine and the parameter values of the critical section, the steady-state operating point of the whole engine can be solved using the Newton-Raphson iteration method. Therefore, for a certain compressor speed Nc, the power turbine speed Np is a fixed value, and the compressor backpressure P3 and the fuel-air ratio ϕ are taken as the independent variables. Combined with Eq. (6), the residual equation zi (i=1,2) is obtained,
Define as the residual matrix, and as the trial value vector, then the residual value vector Z is a function of the trial value vector X, i.e. . Determining the co-operating point is finding the trial value X that makes Z tend to 0. The Newton-Raphson method is used to solve this system of nonlinear equations. Assume that the trial value vector and residual vector of the nth step have been calculated, then the trial value vector of the (n+1)th step is , where J is the Jacobian matrix. The equation can be expanded as:
where the calculation formula of partial derivative is
where is the perturbation value of the trial value. The new trial value is recalculated until the residual meets , which can be considered to complete the flow calculation of the engine cooperating point. Each solver is connected to each other and controlled by the external system of Fortran program so as to transmit data between codes and establish the engine simulation platform, as shown in Figure 4.
3. Component Validations Cases
3.1. P&W3S1 axial compressor
The P&W3S1 three-stage axial compressor is an experimental unit designed by Pratt & Whitney Company in the late 1970s to study the aerodynamic performance of the rear stage of a high-load axial compressor. The model has inlet guide vanes, and its rotor and stator blade profiles are non-standard, featuring a circular arc for the mean camber line. Additionally, the thickness distribution follows the NACA 65 series. According to the references [28,29], the design parameters of P&W3S1 are a speed of 5455 r/min, a pressure ratio of 1.357, and a flow rate of 4.30 kg/s. The flow calculation grid is shown in Figure 5, and the entire mesh has 450 × 80 points. The cell clustering is applied to the leading and trailing edges of the blades to better capture changes in blade forces, and it is also performed near the hub and shroud to calculate shear stress near the endwalls.
Due to limited experimental data in the references, this study also employed Numeca software for three-dimensional viscous simulations with a mesh of 4.46 million nodes in order to verify the prediction accuracy of the meridional flow field by the throughflow method. A comparison of the computed and experimental results for the design speed condition is presented in Table 1. The throughflow results show a computational error of less than 1% compared to Numeca simulation results. Compared with experimental results, the efficiency and the mass flow rate are higher by approximately 1.4% and 0.6% respectively, and the pressure ratio is higher by 0.1%. The results show that the throughflow results is consistent with the experimental results and the 3D calculation results under the design conditions.
The predicted relative Mach number distributions obtained from the throughflow calculations and the circumferentially averaged results from the three-dimensional simulations are presented at the design point condition in Figure 6. It can be observed that the trend of relative Mach number distribution from throughflow calculations is similar to that from three-dimensional computations. The maximum relative Mach number in the passage occurs near the leading edge of the first-stage rotor, reaching approximately 0.52. It indicates that the internal flow within the compressor is predominantly subsonic.
Figure 7 presents the radial profiles of total pressure and temperature at the P&W3S1 outlet under the design condition, compared with the experimental data [29] and Numeca results. It can be seen that the throughflow results are consistent with the overall distribution trend of the experimental values and the Numeca results. The total temperature distribution obtained by the throughflow calculation is steeper in the endwall region, slightly higher in the tip region, and slightly lower. However, the maximum temperature difference is within 0.5K compared with the experimental data. It shows that the throughflow model developed in our study can simulate the radial mixing phenomenon more accurately.
In order to evaluate the capacity of the solver to predict the off-design point performance of the compressor, the performance of P&W3S1 at 85%, 100%, and 105% design speed is simulated, respectively. The obtained compressor speed characteristics are shown in Figure 8. Comparing the total pressure ratio obtained by the throughflow calculation and the experiment, the two results are consistent at 100% design speed, and the maximum relative error under off-design speed conditions does not exceed 2%. Additionally, comparing the efficiency characteristics, the relative error between the flow results and the test results is about 2% at the design speed, and the relative error between the non-design speed and the test value is about 3%. One possible reason is that the rotor tip clearance correction is not considered in this paper, and the loss estimation needs to be revised, which leads to slightly higher efficiency for most working conditions of the compressor. Another reason may be that the off-design speed exceeds the estimated range of the empirical correlations. The throughflow solver developed in this paper can naturally predict the mass flow rate under chock conditions. However, the predicted near-stall flow rate is slightly higher than the experimental value.
3.2. GE-EEE high-pressure turbine
The GE-EEE high-pressure turbine is one of the research results of NASA’s Energy Efficient Engine program. In this study, this turbine component is chosen as the simulation object to validate the predictive capability of the throughflow solver for turbine characteristics. The computational grid is shown in Figure 9, where the black and red regions represent bladeless zones, and the green region is the blade zone. The cell clustering is applied near the hub and shroud, and the leading and trailing edges of the blades. The total number of cells is 240×120.
The NASA report [30] provides lots of detailed experimental data. The researchers complete a characteristic line calculation by fixing the ratio of inlet total pressure to outlet static pressure πTS and adjusting the physical rotational speed, and the inlet total pressure and total temperature are fixed values. Figure 10 shows the total-to-total pressure ratio in function of the corrected speed for a varying downstream static pressure. Under a wide range of rotational speeds, the expansion ratio predicted by the throughflow model is quite Consistent with the test results, and the two are almost completely coincident at low speeds. As the corrected speed increases, the calculated value is slightly lower than the test value, and the maximum error is still within 2%, indicating that the throughflow model is more accurate for turbine performance prediction.
In order to verify the prediction accuracy of the throughflow model to the radial distribution of parameters, the Numeca software is used for three-dimensional viscosity numerical simulation. We select an operating point in References [30] to calculate. The boundary conditions are set the inlet total pressure of 345.951kPa, the inlet total temperature is 711.5K, the backpressure is 61.941kPa, and rotational speed is 8279.5 rpm. Table 2 shows the comparison of the performance parameters obtained by throughflow and Numeca calculations. Under this condition, the flow rate and expansion ratio obtained by the throughflow and three-dimensional calculation are basically consistent, and the isentropic efficiency is 1.16 % higher.
Figure 11 shows the radial distribution of the exhaust flow angle and Mach number of each blade obtained from the throughflow solver (TF) and Numeca. The absolute value is taken in the stator, and the relative value is taken in the rotor. The solid line is the calculation result of the throughflow model, and the dotted line is the Numeca result. The calculation results of the inlet and outlet flow angles of each row of blades in the main flow area are basically consistent with the three-dimensional calculation values, and the maximum error is within 3 °. The difference near the endwall area is slightly larger, especially at the rotor tip. The main reason is that the three-dimensional flow characteristics of the area near the endwall are obvious, and the current empirical model system is deficient. From Figure 11c,d, it can be seen that the trend of the inlet and outlet Mach number of each blade row calculated by the TF is basically consistent with the three-dimensional calculation circumferential average result. The TF results are generally high, especially the Mach number at the outlet of the inlet guide vane, which is 0.1 higher than that of the three-dimensional results, and the Mach number at the inlet of the first-stage rotor is also correspondingly high during the downstream value transfer process.
Figure 12 shows the radial distribution of the total pressure ratio and the total temperature ratio at the outlet of the GE-EEE high-pressure turbine. The total pressure ratio obtained by the throughflow and the three-dimensional calculation is basically consistent with the test results, and it is only slightly higher than the experimental value above 60% of the blade height. The total temperature ratios predicted by the two calculation methods are higher than the experimental results. The main reason is that the throughflow calculation and the three-dimensional calculation do not consider the influence of film cooling.
The above comparisons preliminarily indicate that the throughflow solver developed in this study can accurately predict components' design and off-design characteristics. It has captured the main flow features and demonstrates reasonable consistency compared with experimental results and three-dimensional simulations. Next, we apply the throughflow model to the simulation of the whole engine.
4. Whole Engine Validations Case
4.1. Case Background
In this study, a single-shaft turboshaft engine, WZ-X, was selected as a case of the whole aero-engine throughflow simulation. Its main components include an axial-radial combined compressor, a combustion chamber, a two-stage uncooled gas turbine, and a two-stage power turbine. Due to the lack of a geometric model of the prototype engine combustion chamber and the combustor solver only simulates the flow in the flame tube, this study uses a straight flow combustor instead of the prototype combustor to provide a reasonable inlet parameter distribution for the gas turbine.
When generating the whole aero-engine throughflow calculation grid, the engine model is divided into three grid sub-areas: axial-radial combined compressor, combustor, and turbine component combination. The throughflow calculation grids of each sub-region are generated respectively. Table 3 gives an overview of the cell count of each part of the mesh, and the computational domain of throughflow simulations is shown in Figure 13. The turboshaft engine is a single-shaft and geometrically fixed structure, and there is no need to change its mesh when calculating different working states.
The throttling characteristics of the maximum emergency, maximum power rating, intermediate emergency, and maximum continuous condition of the engine are calculated. Table 4 shows the corrected speed of the gas generator corresponding to each working state of the engine, in which the maximum power rating is at the WZ-X design condition. The engine inlet and outlet boundaries are given according to the sea level standard atmospheric environment. The initial compressor backpressure and fuel-air ratio are given according to the design value, and the off-design condition calculations take the design operating condition result as the initial field to reduce the iteration loop. In order to ensure the convergence of each component solution, the power matching between the compressor and the gas turbine and the mass flow continuity between the combustor and the turbine are adjusted by means of iterations of two parameters: the compressor output static pressure and the fuel-air ratio.
4.2. Results and Analysis
Figure 14 shows the convergence history of the whole turboshaft engine simulation at the maximum power rating. As shown in Figure 14a, after four times iterations of the whole engine simulations, the relative error between the combustor outlet flow and the turbine inlet flow (Z1) and the relative error between the compressor power and turbine power (Z2) are less than 1 %. At the same time, it can be seen from Figure 14b that the mass flow rate of each component has reached complete convergence in the last time iteration loop of the whole engine simulation. It indicates that the throughflow calculation of the turboshaft engine meets the co-working conditions.
The aerodynamic parameter distribution calculated by the simulation of the whole engine can better describe the flow field details of each component. Figure 15 shows the meridional plane distributions of the dimensionless static temperature, static pressure, and relative Mach number of the WZ-X turboshaft engine under the maximum power rating. After the air enters the compressor, it gradually decelerates and diffuses, and shock waves appear in the axial flow rotor and the centrifugal impeller channel, respectively. After the shock waves, the static pressure further rises and reaches the maximum static pressure at the axial diffuser outlet. The Mach number changes drastically within a small range at the radial diffuser inlet, and there are obvious low-speed areas and separation areas in the axial diffuser. The combustion process in the combustor mainly occurs at the head of the swirler. Under the influence of the adverse pressure gradient, multiple backflow zones are formed behind the swirler, filled with high-temperature gas. On one hand, it contributes to the evaporation of fuel, on the other hand, can provide a stable ignition source. The temperature of hot gas decreases gradually through mixing with the downstream cold air and the radiation heat transfer and convective heat transfer effect of the high-temperature zone on the surrounding gas. Finally, the air injected from the mixing hole and the film hole on the wall adjusts the temperature distribution at the combustor outlet to a reasonable range. Although the combustor exit temperature exhibits significant variations, the velocity changes are relatively small. High-temperature and high-pressure gas expands in the turbine to do work, and the relative Mach numbers in the turbine are both less than 1, which indicates that both the gas turbine and the power turbine operate in a subcritical state.
Due to the lack of experimental data in the WZ-X engine model, this section also uses the traditional zero-dimensional engine overall performance calculation software Gasturb to calculate the engine thermodynamic cycle. The component characteristic diagram (compressor, gas turbine, and power turbine) adopts the test characteristics of prototype engine components, and the corresponding aerodynamic parameter design values of the WZ-X engine compressor, combustion chamber, gas turbine, and power turbine need to be used as input conditions for the zero-dimensional overall performance calculation. The input conditions of the throughflow simulation platform only require the engine inlet and outlet conditions and engine speed, as described above.
Figure 16 shows the variation of shaft power delivered, SFC, inlet air mass flow, and compressor pressure ratio of the WZ-X engine with different speed. In all operating conditions, the inlet air flow, compressor pressure ratio, and engine shaft power increase monotonously of the increase in gas generator speed, which is consistent with the trend of the 0D calculation results. The SFC decreases nonlinearly with the increase of the gas generator speed, and the downward trend gradually slows down at high speeds. In summary, the throughflow simulation platform has the potential to simulate the whole turboshaft engine along the matching line, which can be used to guide the design and modification of the turboshaft engine.
5. Conclusions
This article developed and evaluated a method for a two-dimensional throughflow simulation method of the whole turboshaft engine. The approach is based on component flow-through models and utilizes Newton-Raphson method to calculate iteratively the compressor backpressure and fuel-air ratio required for the turboshaft engine matching operation, so as to build the whole engine throughflow calculation platform and realize the serial iterative simulation of engine components. Through the research in this article, the following conclusions can be drawn:
1) The throughflow solver developed in this article can be applied to both the design point and off-design point characteristics of the compressor and turbine, as well as meridional flow field prediction. The calculation error is less than 2 % compared with the experimental results, and it can automatically predict component blockage conditions;
2) Compared with the traditional 0D overall performance simulation method, the throughflow simulation platform no longer requires a common characteristic diagram and can be used as an independent analysis and calculation tool;
3) The throttling characteristics obtained by the throughflow simulation of the WZ-X turboshaft engine are consistent with the results of the zero-dimensional thermodynamic cycle, which can truly and accurately reflect the flow details on the meridional plane of the engine.
The key to this calculation method is to maintain the accuracy of component flow in the two-dimensional simulation of the full engine while ensuring the effectiveness of the whole aero-engine balance algorithm. The introduction of this method provides a more accurate and comprehensive analysis method for whole-engine simulation and is expected to have a positive impact on aero-engine design and performance evaluation.
Author Contributions
Conceptualization, S.Z. and X.H.; methodology, S.Z., X.H. and T.Z.; software, S.Z., A.M. and T.Z.; formal analysis, S.Z. and A.M.; investigation, S.Z.; writing—original draft preparation, S.Z.; writing—review and editing, N.G.; project administration, N.G.; funding acquisition, N.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Nanjing University of Aeronautics and Astronautics (KFA18626).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest. to publish the results”.
References
- Nichols L.D., Chamis C.C. Numerical Propulsion System Simulation: An Interdisciplinary Approach. AIAA/NASA/OAI Conference on Advanced SEI Technologies, Cleveland, USA, 4 - 6 September 1991. [CrossRef]
- Homsi P., Tobias L. VIVACE-Value Improvement through a Virtual Aeronautical Collaborative Enterprise. Technical Leaflet Final, 2007. [CrossRef]
- Alexiou A., Tsalavoutas T. Introduction to Gas Turbine Modelling with PROOSIS, 1st ed, Madrid: Empresarios Agrupados Internacional (EAI), U.K, 2011.
- Cao J.G. Status, Challenges and Perspectives of Aero-Engine Simulation Technology. J. Propul. Techno. 2018, 39, 961-970. (In Chinese). [CrossRef]
- Wu C.H. A General Theory of Three-Dimensional Flow in Subsonic and Supersonic Turbomachines of Axial-, Radial-, and Mixed-Flow Type. Technical Note, Washington, USA, January 1952. [CrossRef]
- Hosseinimaab S.M., Tousi A.M. A New Approach to Off-Design Performance Analysis of Gas Turbine Engines and Its Application. Energy Conv. Manag. 2021, 243, 1-17. [CrossRef]
- Teixeira M., Romagnosi L., Mezine M., Yannick B., Anker J., Claramunt K., Hirsch C. A Methodology for Fully-Coupled CFD Engine Simulations, Applied to a Micro Gas Turbine Engine. In Proceedings of ASME Turbo Expo 2018 Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11-15 June 2018. [CrossRef]
- Romagnosi L., Li Y.C., Mezine M., Teixeira M., Vilmin S., Anker J.E., Claramunt K., Baux Y., Hirsch C. A Methodology for Steady and Unsteady Full-Engine Simulations. In Proceedings of ASME Turbo Expo 2019 Turbomachinery Technical Conference and Exposition, Phoenix, Arizona, UAS, 17-21 June 2019. [CrossRef]
- Nigmatullin R.Z., Ivanov M.J. The Mathematical Models of Flow Passage for Gas Turbine Engines and Their Components. AGARD Lecture Series, Paris, France, 15-16 December 1994.
- Stewart E.M. Axisymmetric Aerodynamic Numerical Analysis of a Turbofan Engine. In Proceedings of the ASME 1995 International Gas Turbine and Aeroengine Congress and Exposition, Houston, Texas, USA, 5–8 June 1995. [CrossRef]
- Petrovic M.V., Ahmed A-R., Wiedermann A. A Quick Method for Full Flange-to-Flange Industrial Gas Turbine Analysis Based on Through-Flow Modelling. J. Gas. Propuls. Power 2015, 8, 9-18. [CrossRef]
- Wiedermann A., Petrovic M.V. Through-Flow Modeling of Single- and Two-Shaft Gas Turbines at Wide Operating Range. In Proceedings of ASME Turbo Expo 2018 Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11-15 June 2018. [CrossRef]
- Yang C., Wu H., Du J., Zhang H.W., Yang J.G. Full-Engine Simulation of Micro Gas Turbine Based on Time-Marching Throughflow Method. Appl. Therm. Eng. 2022, 217, 1-13. [CrossRef]
- Yang C., Wu H., Du J., Zhang H.W., Yang J.G. Numerical Study on Throughflow Simulation of Components and Full Engine of Aero-Engine. J. Eng. Thermophys. 2023, 44, 894-902. (In Chinese).
- Liu X.H., Zhou C.H., Song M.X., Jin D.H., Gui X.M. Overall Simulation of a Turbojet Engine Based on Throughflow Modeling. Acta Aeronaut. Astronaut. Sin, 2020, 41, 123199-123199. (In Chinese).
- Dawes W.N. Toward Improved Throughflow Capability: The Use of Three-Dimensional Viscous Flow Solvers in a Multistage Environment. J. Turbomach. - Trans. ASME, 1992, 114, 8-17. [CrossRef]
- Simon J. F. Contribution to Throughflow Modelling for Axial Flow Turbomachines. Doctor, University of Liege, Liege, 2007.
- Yang X.F. Analysis and Design of Combined Compressor with Throughflow Model. Master, Nanjing University of Aeronautics and Astronautics, Nanjing, 2016. (In Chinese).
- Hou K.X. Research on Numerical Simulation of Reactive Flow in Combustor with Detailed Chemical Kinetic. Master, Nanjing University of Aeronautics and Astronautics, Nanjing, 2007. (In Chinese).
- Jin H.L., Jin D.H., Li X.J., Gui X.M. A Time-Marching Throughflow Model and its Application in Transonic Axial Compressor. J. Therm. Sci, 2010, 19, 519-525. [CrossRef]
- Horlock J.H. On Entropy Production in Adiabatic Flow in Turbomachines. J. Basic Eng. 1971, 93, 587-593. [CrossRef]
- Wright P.I., Miller D.C. An Improved Compressor Performance Prediction Model. Rolls-Royce Report, 1991.
- Dunham J. Compressor Off-Design Performance Prediction Using an Endwall Model. In Proceedings of the ASME 1996 International Gas Turbine and Aeroengine Congress and Exhibition. Birmingham, UK, 10-13 June 1996. [CrossRef]
- Wiesner F.J. A Review of Slip Factors for Centrifugal Impellers. J. Eng. Power 1967, 89, 558-566. [CrossRef]
- Zhu J.Q., Sjolander S.A. Improved Profile Loss and Deviation Correlations for Axial-turbine Blade Rows. In Proceedings of GT2005 ASME Turbo Expo 2005: Power for Land, Sea and Air, Reno-Tahoe, Nevada, USA, 6-9 June 2005. [CrossRef]
- Kacker S.C., Okapuu U. A Mean Line Prediction Method for Axial Flow Turbine Efficiency. J. Eng. Power, 1982, 104, 111-119. [CrossRef]
- Blazek J. Computational Fluid Dynamics: Principles and Applications, 3rd ed. Hayton J.: Butterworth-Heinemann, UK, 2015. [CrossRef]
- Burdsall E.A., Jr. Canal E., Lyons K.A. Core Compressor Exit Stage Study-Ⅰ Aerodynamic and Mechanical Design. Pratt & Whitney Aircraft Group, 1979.
- Behlke R.F., Burdsall E.A., Jr. Canal E., Korn N.D. Core Compressor Exit Stage Study-Ⅱ Final Report. Pratt & Whitney Aircraft Group, 1979.
- Timko L.P. Energy Efficient Engine High Pressure Turbine Component Test Performance Report. Cleveland: NASA Lewis Research Center, 1990.
Figure 1.
Flow distribution model of the two-dimensional combustor.
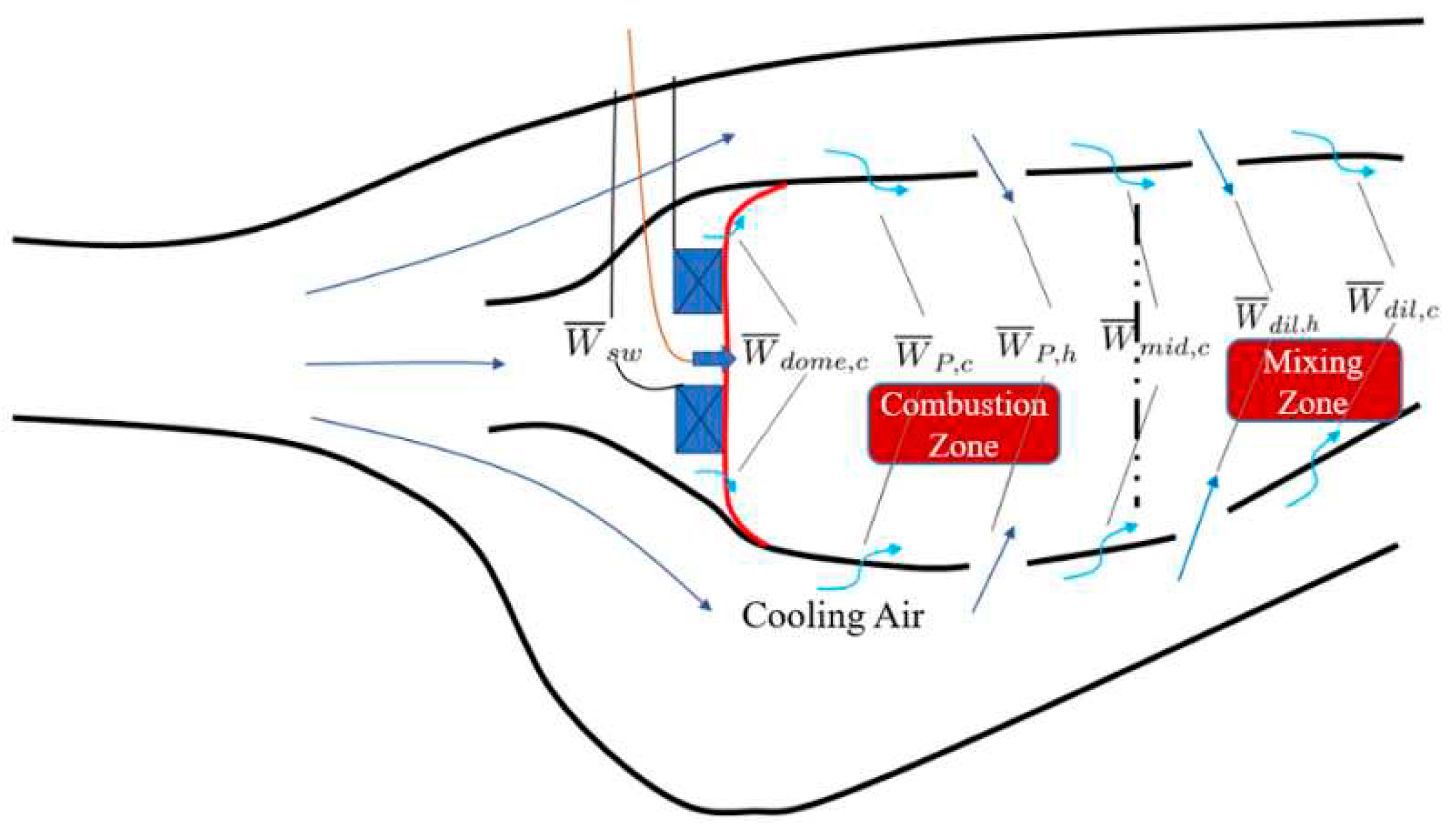
Figure 2.
Cross section of a single-shaft turboshaft engine.

Figure 3.
Illustrates the computational methodology.

Figure 4.
Flow chart of whole aero engine calculation.
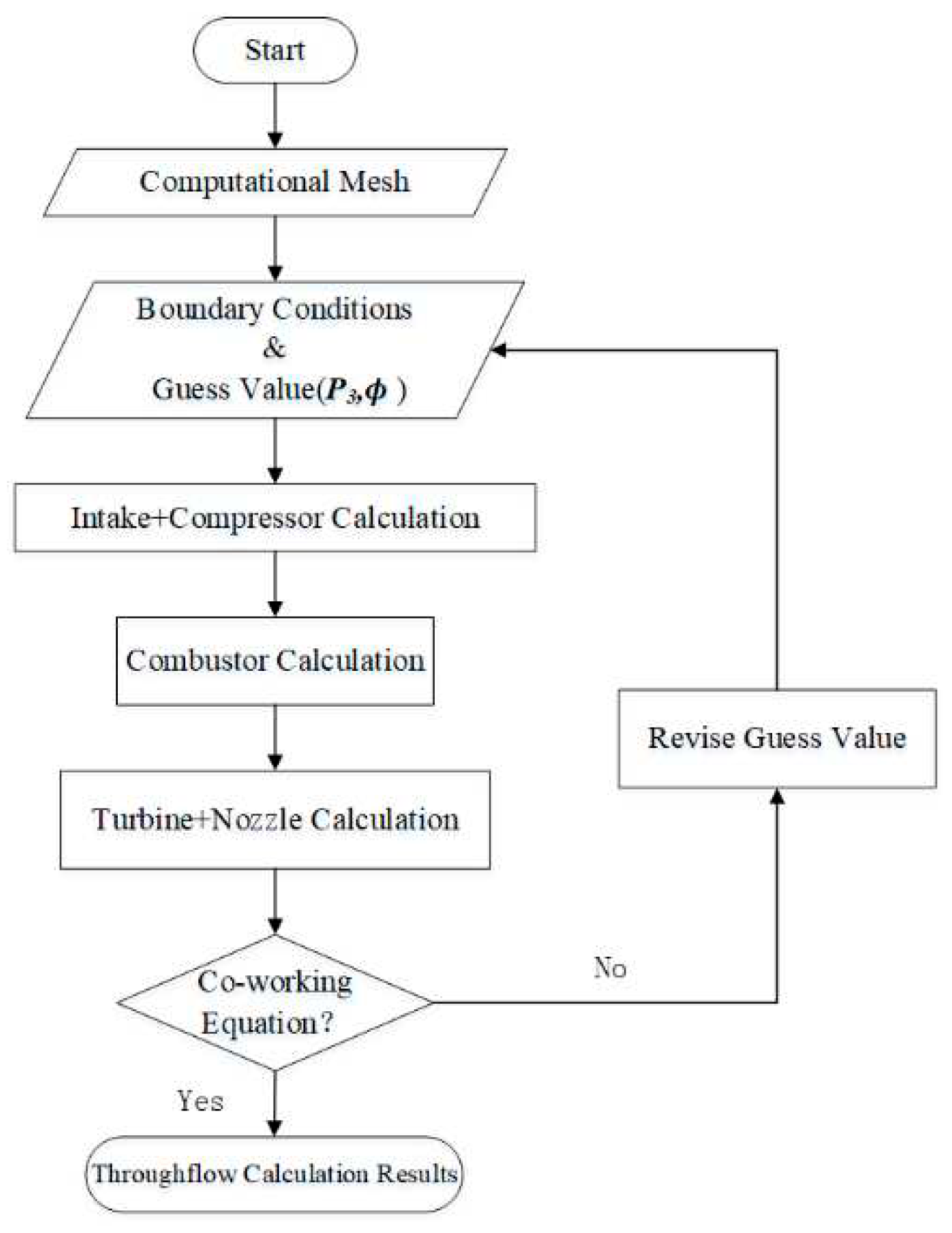
Figure 5.
Throughflow computational mesh of P&W 3S1.
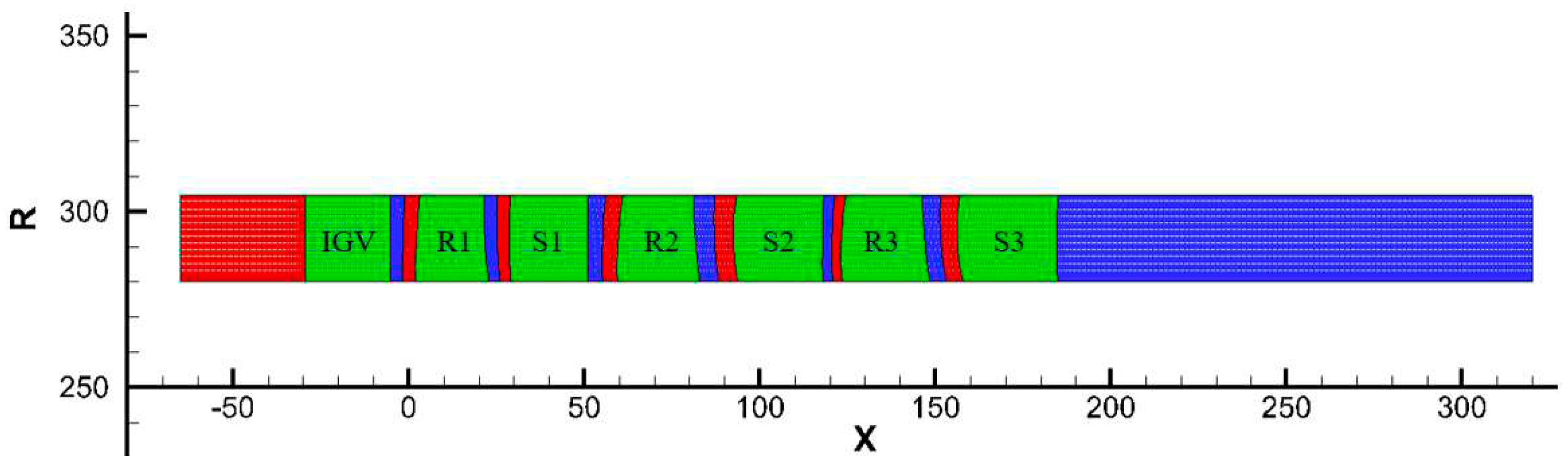
Figure 6.
Relative Mach number contours in the P&W3S1. (a) Throughflow; (b)Nmueca.
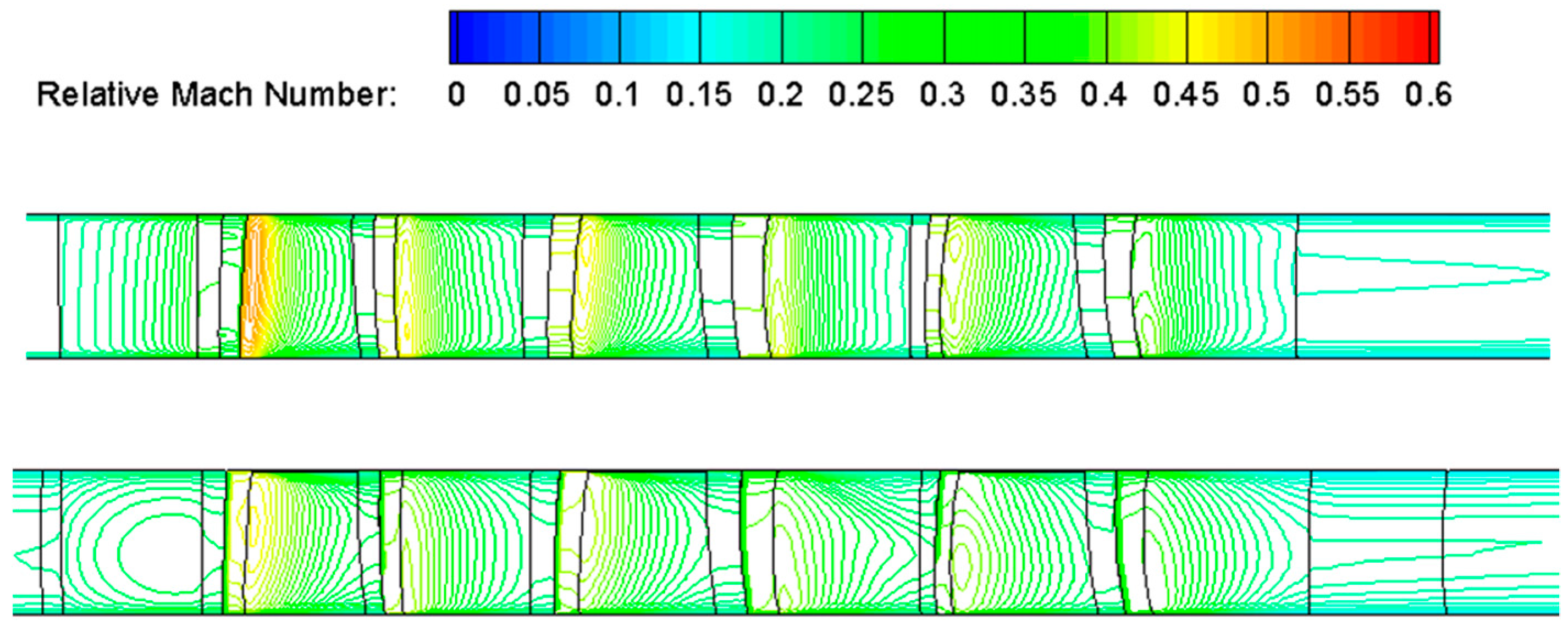
Figure 7.
Radial distributions of (a) outlet total temperature and (b) outlet total pressure under design conditions.
Figure 7.
Radial distributions of (a) outlet total temperature and (b) outlet total pressure under design conditions.
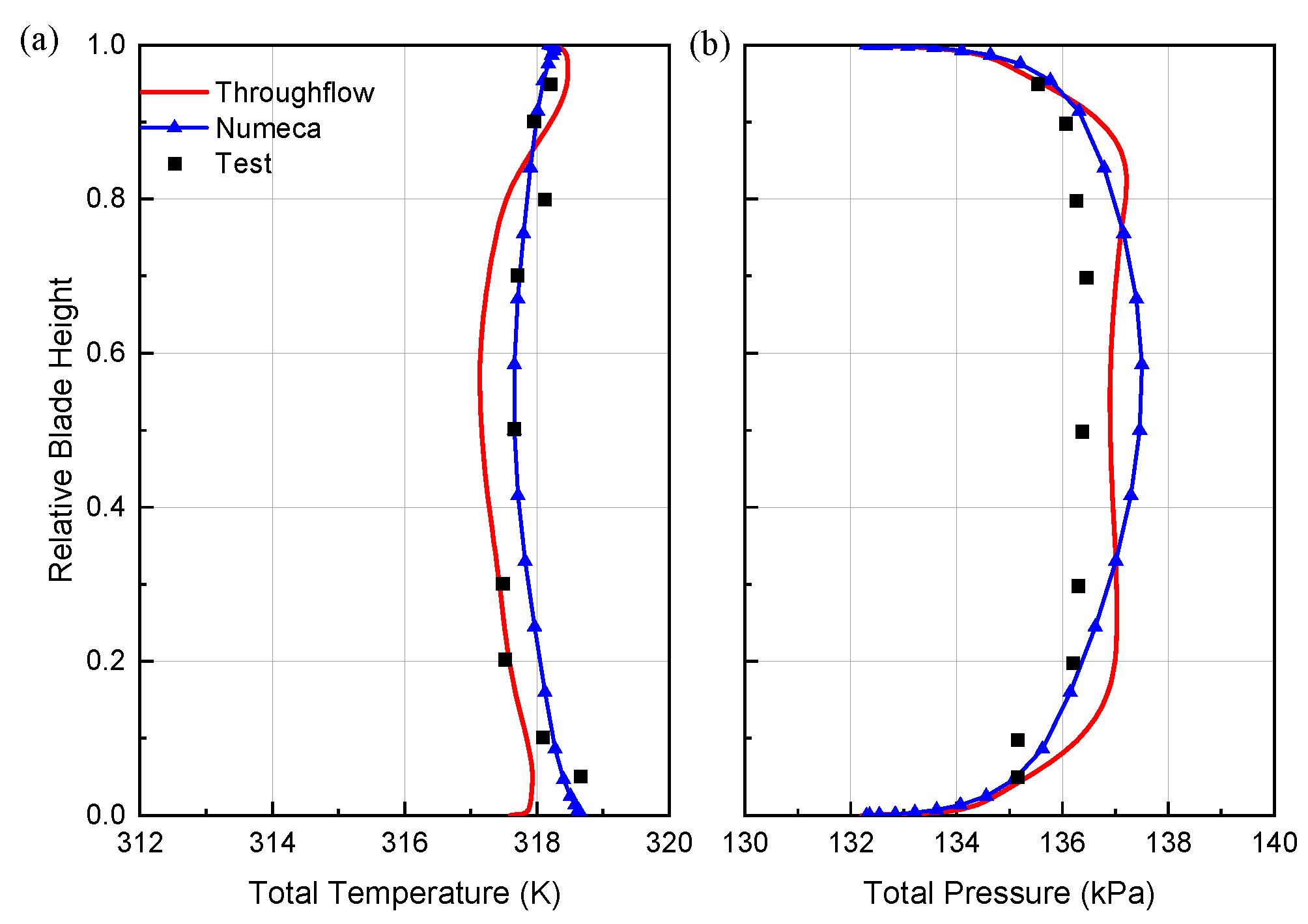
Figure 8.
Performance characteristics of P&W3S1 at different speeds. (a) Total pressure ratio; (b) Isentropic efficiency.
Figure 8.
Performance characteristics of P&W3S1 at different speeds. (a) Total pressure ratio; (b) Isentropic efficiency.
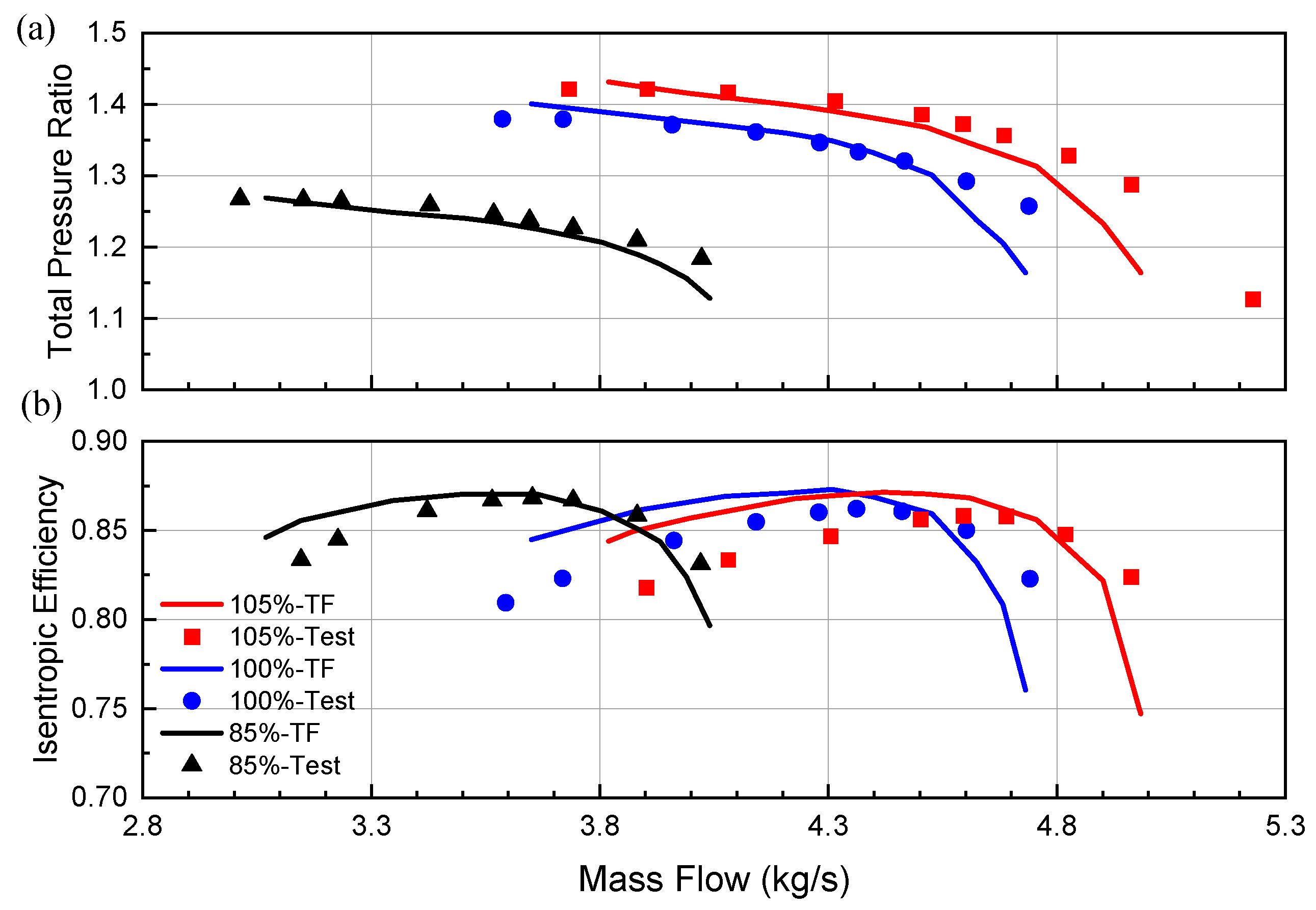
Figure 9.
Computational mesh of GE EEE high-pressure turbine.

Figure 10.
Expansion ratio varies with the corrected speed.
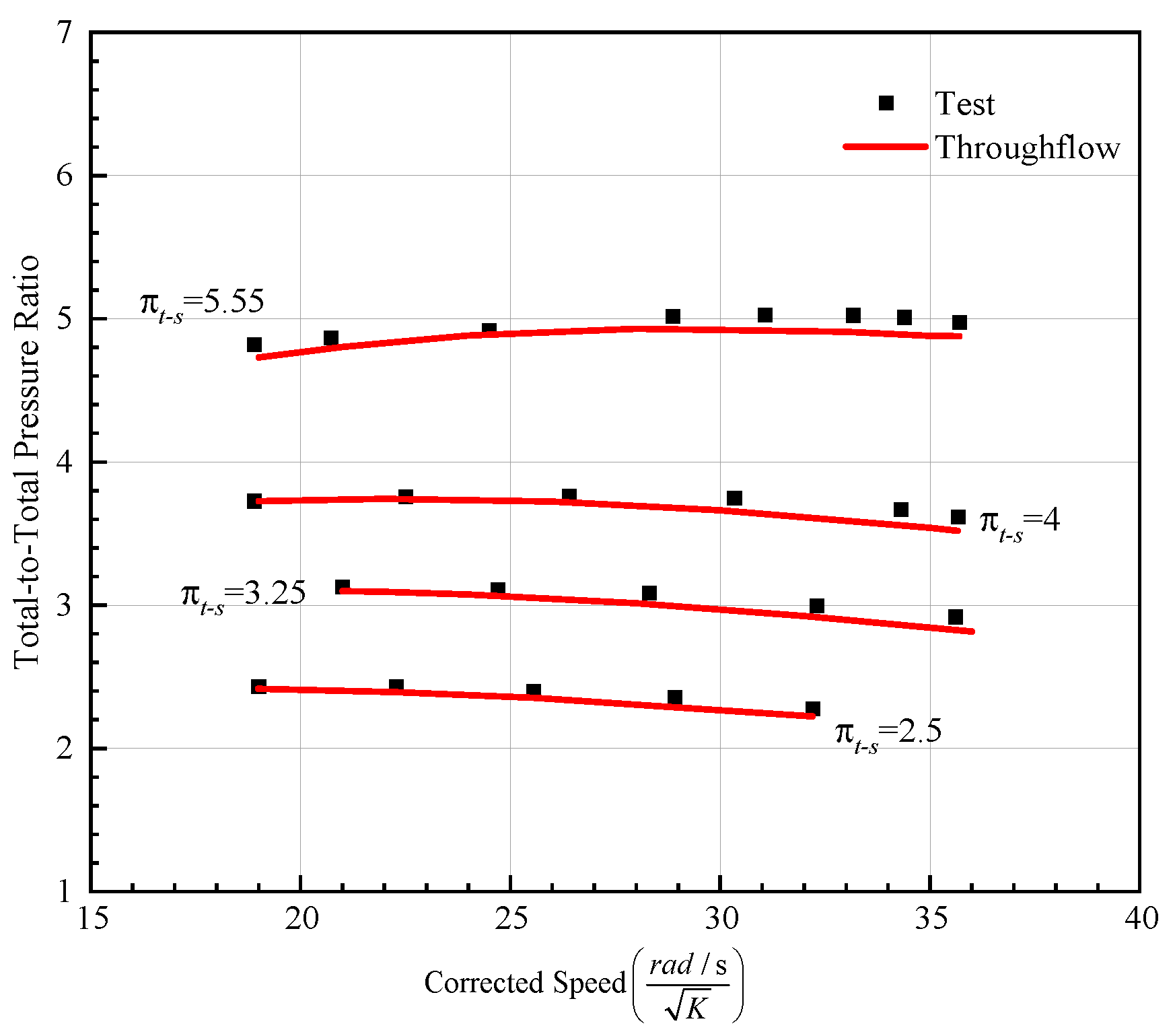
Figure 11.
Comparison of the radial profiles calculated by throughflow and Numeca. (a) Inlet flow angle; (b) Outlet flow angle; (c) Inlet Mach number and (d) Outlet Mach number.
Figure 11.
Comparison of the radial profiles calculated by throughflow and Numeca. (a) Inlet flow angle; (b) Outlet flow angle; (c) Inlet Mach number and (d) Outlet Mach number.
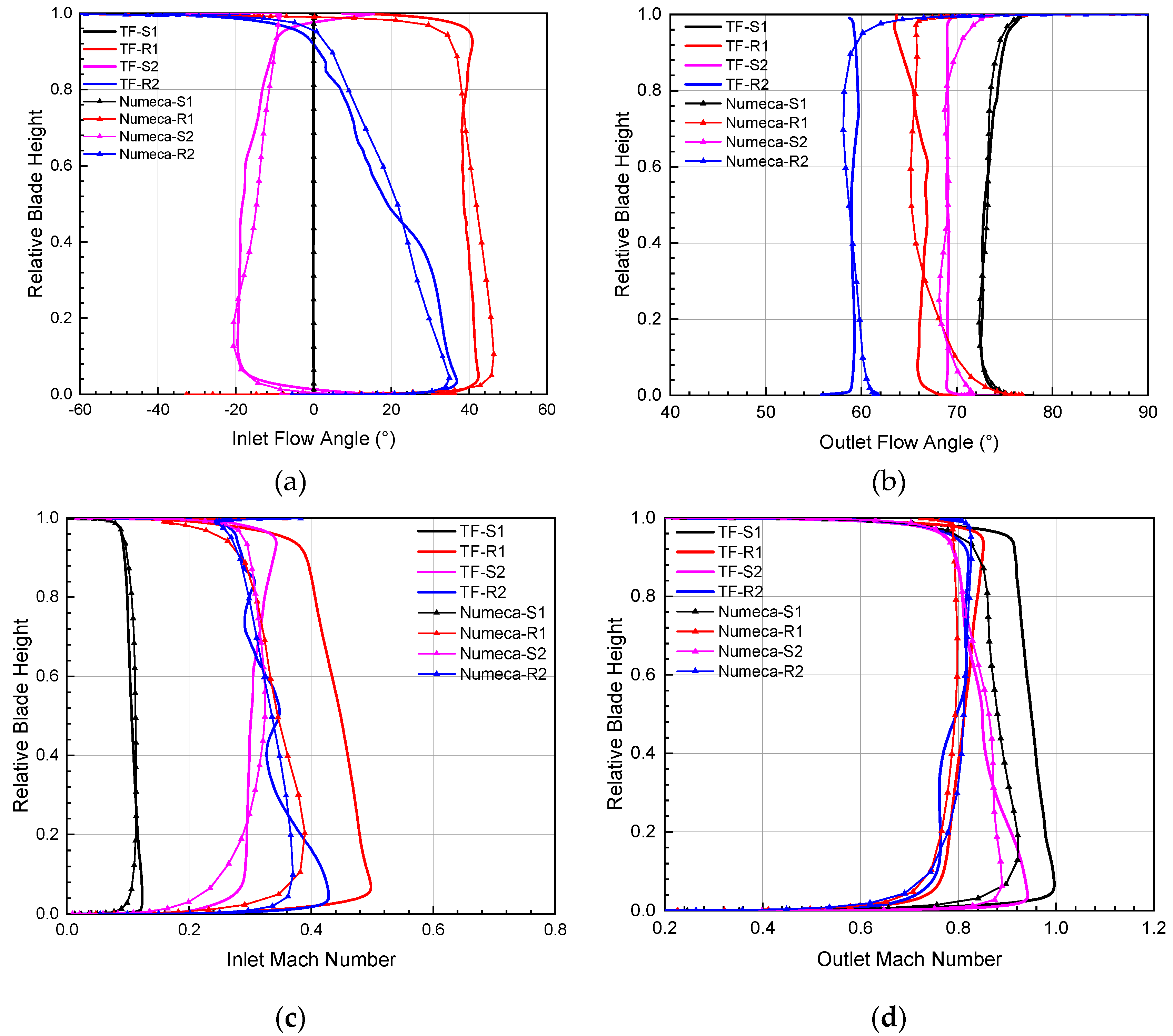
Figure 12.
Radial distribution of (a) total pressure ratio and (b) total temperature ratio at the turbine exit plane.
Figure 12.
Radial distribution of (a) total pressure ratio and (b) total temperature ratio at the turbine exit plane.
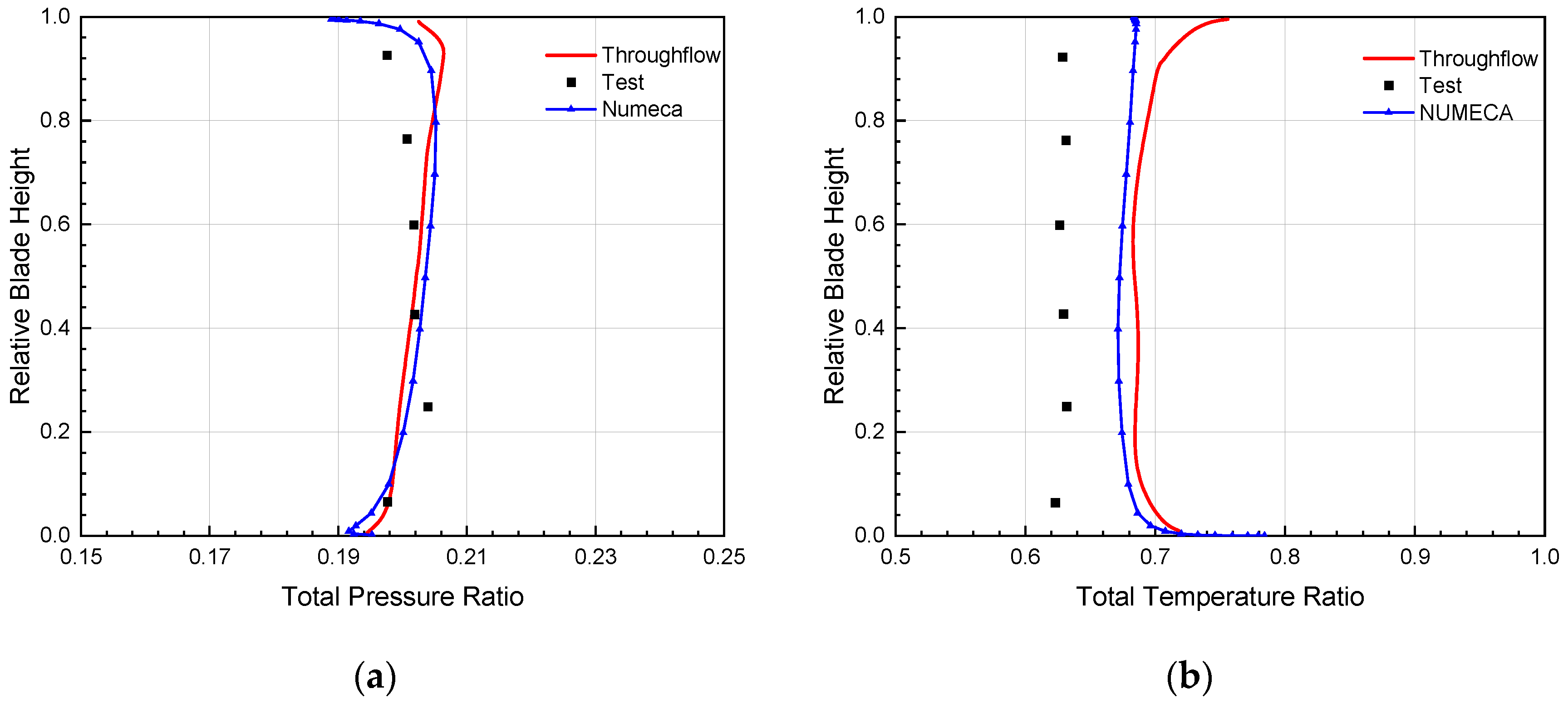
Figure 13.
Computational mesh of the WZ-X engine.
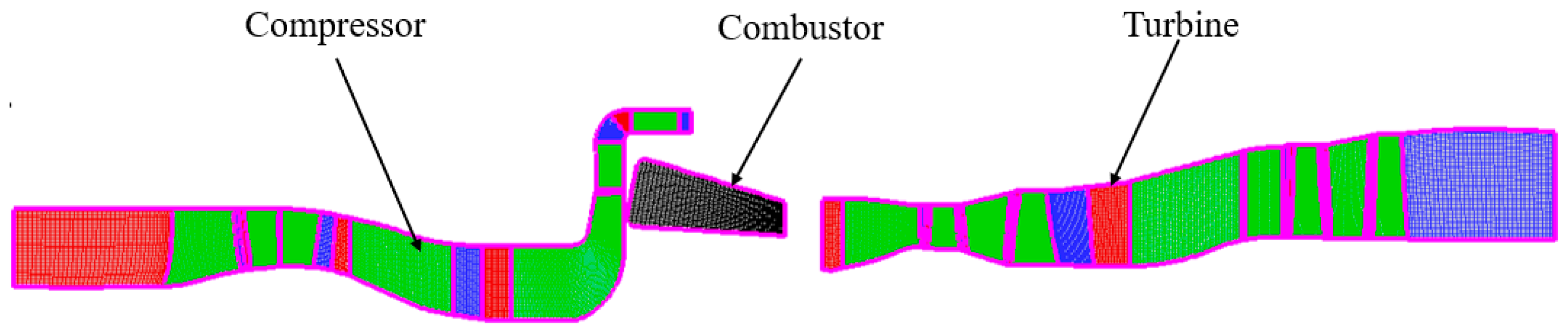
Figure 14.
Convergence history of the whole turboshaft engine simulation for under the maximum power rating. (a) The variation of Z1 and Z2 with iteration times of the whole engine calculation platform; (b) Mass flow of each component in the last time iteration loop.
Figure 14.
Convergence history of the whole turboshaft engine simulation for under the maximum power rating. (a) The variation of Z1 and Z2 with iteration times of the whole engine calculation platform; (b) Mass flow of each component in the last time iteration loop.
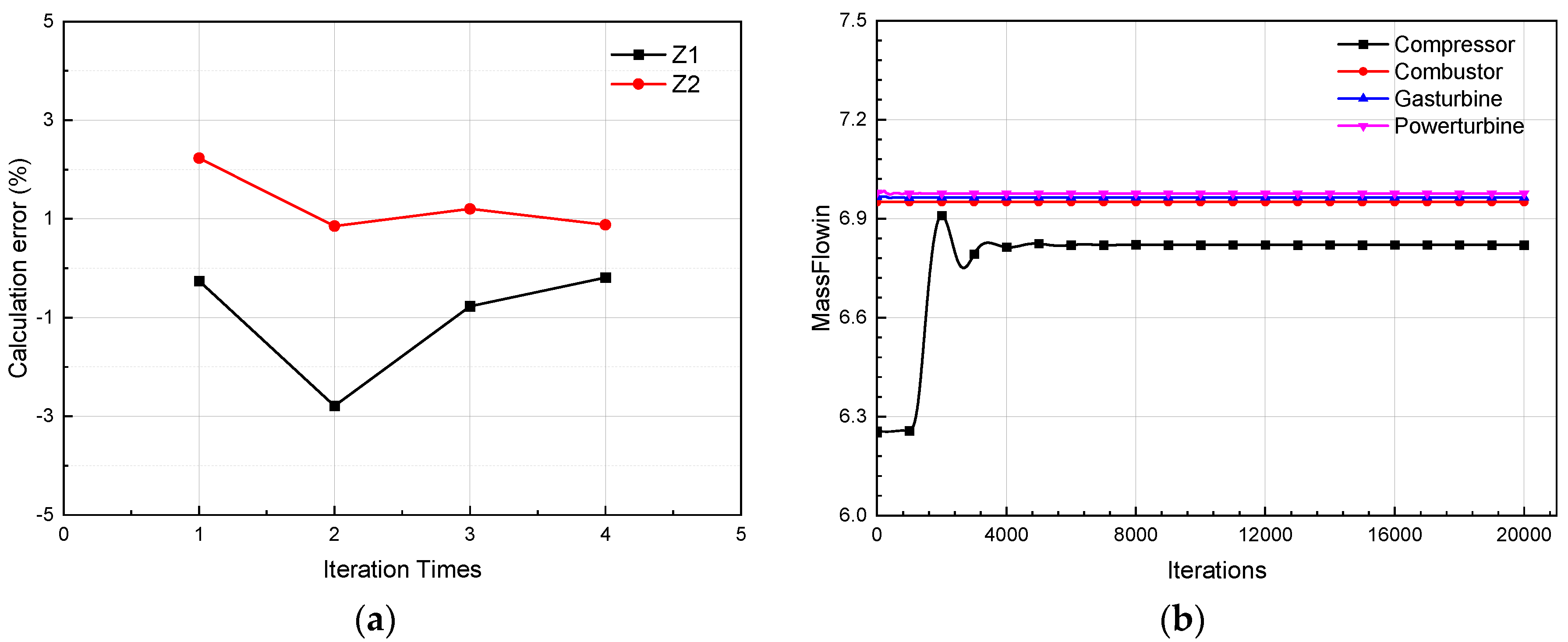
Figure 15.
Meridional flow field contours of the WZ-X engine under the maximum power rating. (a) Dimensionless static temperature; (b) Dimensionless static temperature; (c) Relative Mach number.
Figure 15.
Meridional flow field contours of the WZ-X engine under the maximum power rating. (a) Dimensionless static temperature; (b) Dimensionless static temperature; (c) Relative Mach number.
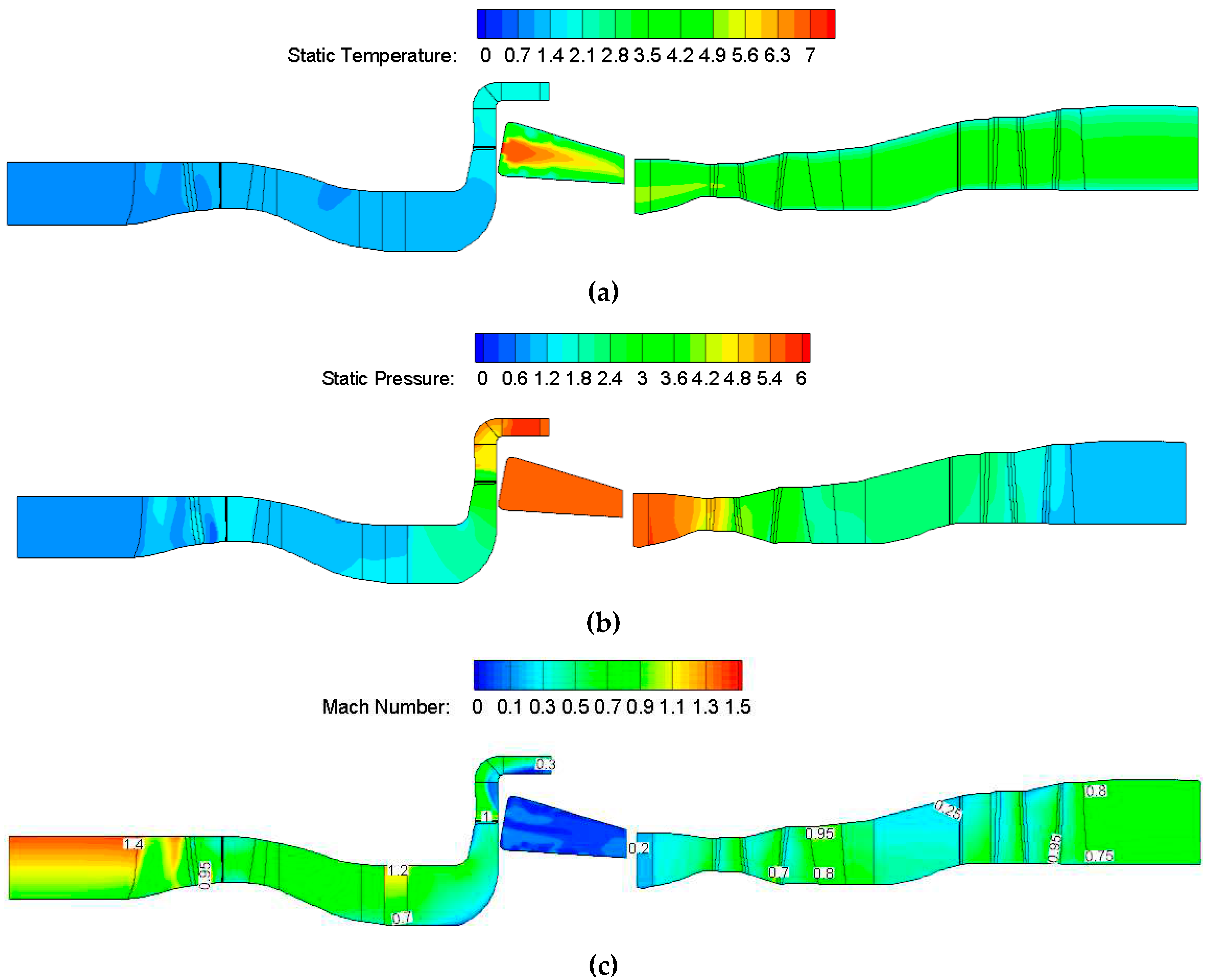
Figure 16.
Comparison of partial throttling characteristics of the WZ-X turboshaft engine. (a) Shaft power delivered; (b) SFC; (c) Air mass flow and (d) Compressor total pressure ratio.
Figure 16.
Comparison of partial throttling characteristics of the WZ-X turboshaft engine. (a) Shaft power delivered; (b) SFC; (c) Air mass flow and (d) Compressor total pressure ratio.
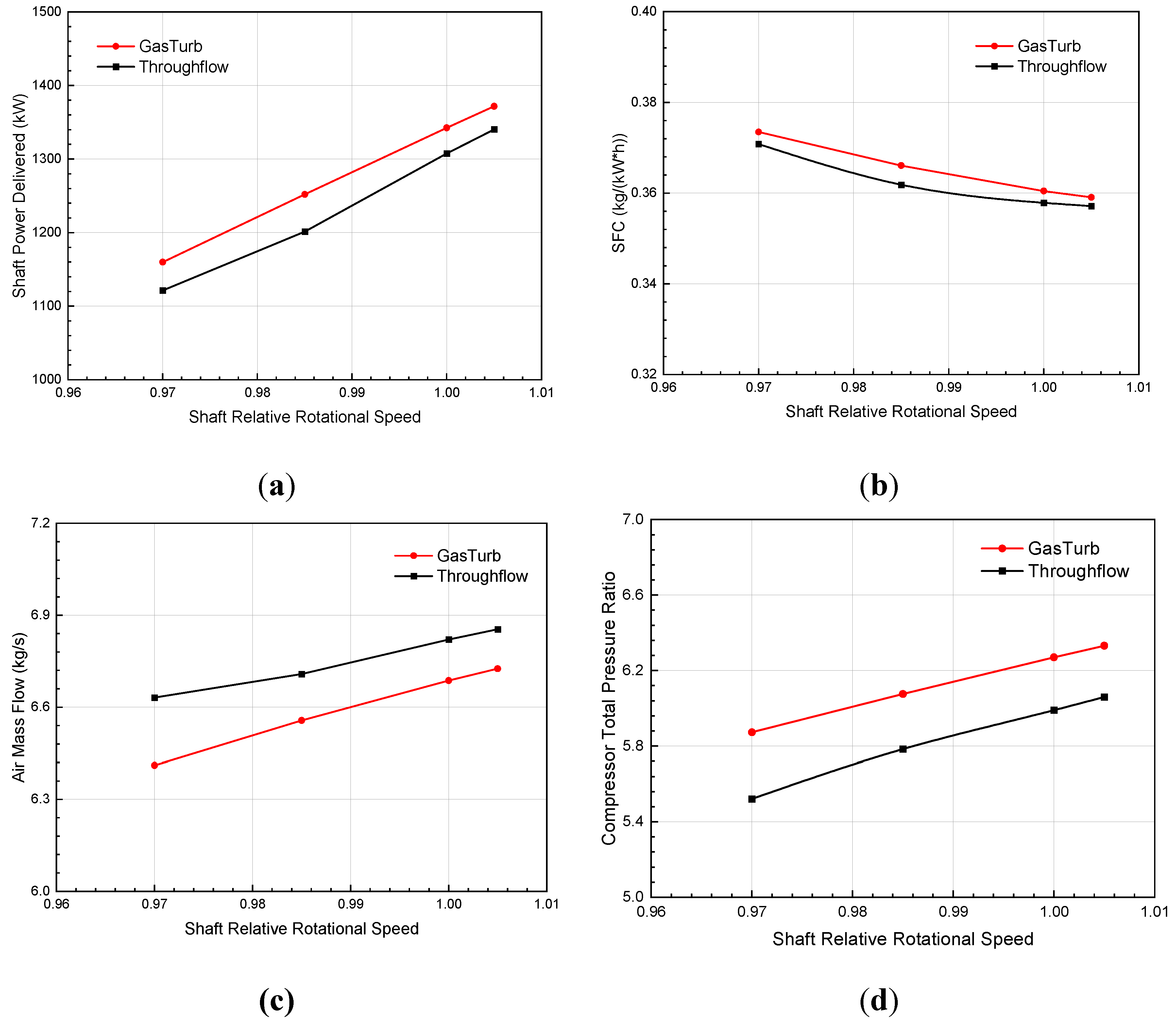
Table 1.
Comparison of calculated and tested results at the design condition.
| Parameter | Experiment[29] | Throughflow | Numeca |
|---|---|---|---|
| Mass flow (kg/s) | 4.28 | 4.308 | 4.307 |
| Total pressure ratio | 1.346 | 1.349 | 1.347 |
| Isentropic efficiency | 0.861 | 0.873 | 0.8572 |
| Total temperature ratio | / | 1.102 | 1.1036 |
Table 2.
Comparison of the throughflow and Numeca results.
| Mass Flow (kg/s) | Expansion Ratio | Isentropic Efficiency | |
|---|---|---|---|
| Throughflow | 11.91 | 4.944 | 0.9317 |
| Numeca | 12.01 | 4.938 | 0.9213 |
| Error(%) | 0.8 | 0.2 | 1.16 |
Table 3.
Cell count of WZ-X engine.
| Zone | Cell count |
|---|---|
| Compressor | 507×41 |
| Combustion chamber | 525×41 |
| Turbine | 41×41 |
Table 4.
Partial throttling characteristic speed setting.
| Working condition | Engine speed |
|---|---|
| Maximum emergency | 1.005 |
| Maximum power rating | 1.0 |
| Intermediate emergency | 0.985 |
| Maximum continuous condition | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






