Prerpints.org logo
Preprint
Article

Investigation into Seismic Behavior of Reinforced Concrete Frames with Subsequently Added Floors and Modeling of Connecting Joints

Altmetrics

Downloads

89

Views

57

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 December 2023

Posted:

03 January 2024

You are already at the latest version

Alerts
Abstract
The size of the population and the need for residential spaces are increasing. One possible solution is to add new floors to existing buildings. The positive aspects of such a solution with respect to its socio-economic impact and impact on the environment is that large amounts of carbon dioxide release will be avoided, waste and its treatment will be reduced, and agricultural land and green spaces will be preserved. However, adding floors to existing structures might be structurally challenging, especially in terms of the behavior under seismic actions. This paper presents a numerical study of a reinforced concrete frame in an old building to which new floors are subsequently added. The analysis shows that the frame does not behave as a whole with the old part of the structure, nor does it behave the same as if it were made with rigid joints compared to additional ones connected using hinge joints. The change from the corner (knee) joint to the external joint has its own effect on the distribution of internal forces in the structure as a whole and in the joint in particular.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The purpose of this study is to investigate the seismic behavior of reinforced concrete frame structures that have been extended vertically with additional floors at some point during their service life, specifically focusing on the joints by which the extension is connected to the existing structure and how to appropriately model the joints when checking the load-carrying capacity and serviceability of the entire extended structure.
The motivation for this study arose from observing construction trends in the Republic of Kosovo. Economic developments and population growth have resulted in an increase in the need for residential space [1]. In some cases, this is achieved by adding new floors on top of existing structures. Several cases of this practice are illustrated in Figure 1. Such vertical or upward extensions need to be carefully planned, designed, and checked to ensure a safe structure. The problem is further compounded as there are illegal buildings with no building permits issued (https://2012-2017.usaid.gov/results-data/success-stories/laying-foundations-ownership-rights-and-vibrant-property-market-through) and the region is highly seismically active [2]. Cases in which vertical extensions are made on top of old buildings that were not designed according to the principles and rules of modern (seismic) codes or to sustain the loads prescribed in these modern codes, and that also may have deteriorated over their service life, may be dangerous and require careful examination [3].
At the same time, there are many benefits to the vertical extension of buildings and there seems to be an ongoing trend calling for an increase in this approach (https://urbanflows.ac.uk/vertical-extension-sustainable-future/ and https://urbanistarchitecture.co.uk/upward-extension/). The major advantage is related to the potential for attaining more sustainable solutions, not only for single buildings, but on a city scale. Vertical extension avoids the consumption of new land and city sprawl, thus preserving natural habitats, green areas, and agricultural land. An alternative to vertical extension is to demolish the existing building and build a new, taller structure. Building demolition is associated with financial cost, environmental pollution in terms of the emission of carbon dioxide, and the creation of waste, which requires extra management and brings additional costs. It also creates problems for the residents who live there in terms of moving out and paying rent for some other residence until the new building is constructed in place of the old one. Improving existing structures also consumes fewer resources than tearing down and rebuilding, making it more environmentally friendly [4].
These are all great advantages and arguments for vertical extensions, but at the same time, it is essential to secure the structural safety of these extensions. This study focuses on structural behavior under seismic action, investigating how to appropriately design and model joints between new floors and the existing building. If a vertical extension is not designed and executed properly, the vulnerability and seismic risk increases as the danger of the building collapsing increases. Often, the connection between an existing reinforced structure and the vertical extension is considered rigid in structural analyses, just as if the building had been erected in its entirety at the beginning. In practice, these joints may not behave as such. Figure 2 shows a case of building on an additional floor of a building in Albania, and what happened during an earthquake in 2019. How to appropriately design and execute joints (nodes) between the existing structure and new columns is another part of this study. The connection between the elements of the floor or additional floors and the base building cannot be achieved completely using monolithic, i.e., rigid, elements. These connections depend on many factors, such as the difference in material between the old building and the new additional part of the construction.
There might also be other issues that negatively impact the connection between the old building and the added floors, such as the impact of dirt accumulated throughout the years or the inadequate opening of the newly made holes that cannot be cleaned effectively and the cleaning of the hole cannot be monitored. All of these elements lead to a connection with defects, and it cannot be treated as a full monolithic or rigid connection. Similar connection details may be found in prefabricated structures, but the connections made there are safer because the anchorage location is detailed at an appropriate time and the holes are opened while the structural element is being cast. Figure 3 illustrates some details that have been used in vertical extensions and prefabricated construction.
The connection of the new and old columns or the column–beam node will also present a problem in terms of the changes in its state. These changes occur when changing from knee nodes to external nodes. If the connection is not rigid and it does not interact equally with the other part, the first plastic hinge is located in the connection between the new column and the old one. Also, the action of the outer forces on the nodes changes based on the level of its stiffness or rigidity. Figure 4 shows how the joint and acting forces change.
It is known that within the architectural frame, specifically at the terminal node of the structure, the reinforcement bars end at the ultimate knee node. The addition of a new floor is a problem that requires the defining of the level of stiffness to be used in the design of these new additions, especially in seismic locations.
The added construction does not react in the same way as the old (base) building under the action of a dynamic impact. The tendency of the building’s movement under the action of an earthquake is always to act in the opposite direction to the seismic wave. Therefore, if the additional floors are not connected to the existing building by rigid or stiff joints, they will have a tendency to act in the opposite direction from the base building and in the direction of the seismic wave. This is illustrated in Figure 5.
The case of the slipping of the additional floor is also seen in Figure 2. In the studied building, there was a tendency for the additional floor to move in the opposite direction to the movement of the base of the building in the earthquake in Albania in 2019.
When this is known at the design stage, the design must be based on the principle of strong columns–weak beams. This principle means that in the case of a collapse, only the beam, floor, or story will collapse, and not the column, which presents a loss in the stability of the building. Therefore, in the case of adding a new floor, this phenomenon will show whether or not the column is rigid enough. There are two plastic hinges in the connecting joint: one in the tied new column and the other in the old beam. This phenomenon is illustrated in Figure 6.
There are also differences in the vibration modes of the building, depending on whether the added floor is joined by a hinged or stiff connection. The largest changes are observed in the second and third vibrations (Figure 7 and Figure 8) and higher.
The issues described are generally not included in codes. To date, a consensus has not been reached on a single-joint modeling technique either in the scientific literature or in the codes, in spite of the fact that many research groups worldwide, during the last three decades, have performed a wide range of experimental and theoretical studies on this topic to evaluate the cyclic behavior of beam–column joints [7]. The analogy can be also used in the case of the additional floor’s joint. Therefore, there is a need for intervention in old buildings where much of the existing building stock exhibits a number of deficiencies, rendering them susceptible to damage from future earthquakes [8]. The only viable solution is retrofitting, despite the difficulties that may arise from socio-economic constraints and the lack of an established code framework [8]. This motivates researchers to contribute to and develop this area of study further in the future in order to ensure the safety of both old structures and those with vertical extensions.

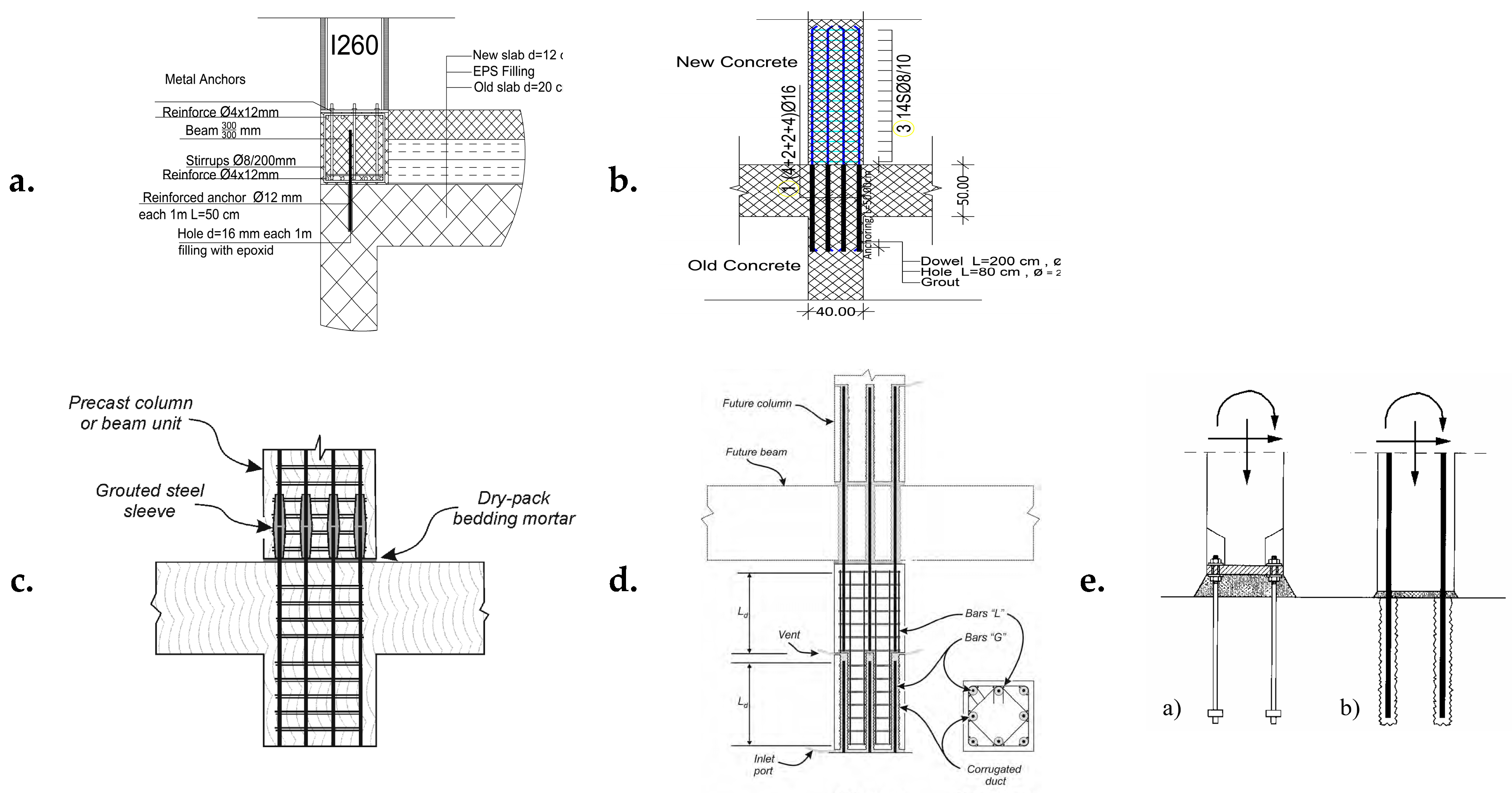
2. Literature Review

Even though the motivation for the study comes from the cases noted in Kosovo, there are many examples of research related to vertical extensions around the world. The following summary provides the details and conclusions of published studies.
Bahrami et al. [1] explored sustainable population growth and the need for research on expanding the capacities of old buildings. This growth also determines the changes in future constructions. The authors examined the impact of renovations and the construction of additional floors on people’s lives, both financially and environmentally. The analysis of old buildings was performed using software apps and utilizing finite element methods such as StruSoft FEM-Design. The analyzed building was assessed based on on-site data and using norms and coefficients from Eurocodes. The analysis focused on the changes in the expansion of the building in height, intervening at key points of the old structure. Finally, the authors analyzed the effects and capacity of the building elements under the new conditions after the construction of the new floor, comparing the load-bearing capacity before and after reinforcement.
Kyakula et al. [3] dealt with how existing buildings, constructed according to outdated codes, can be analyzed and the reserve capacity they possess as old structures. The analysis was based on the ULS design analysis according to Eurocode and British standards for cases involving the construction of additional floors. A comparison was made between the ultimate limit state and the expressions used in the design according to linear analysis, and the percentage of reserve capacity in the elements of the old building was determined. The analysis also included an assessment of additional services in new buildings compared to old ones. Evaluations of the foundations, the stress on old buildings, studies of the soil, and the impact on it due to existing construction were conducted. The loads used in the old building were assessed, and the analysis was performed according to the current codes. The possibilities for modifications in vertical elements such as walls and columns and their impact on the building’s foundations were also examined. In conclusion, before proceeding with the construction of additional floors, an investigation into the structural integrity of the building should be conducted. Its capacity should be assessed, and the reserve capacity of the existing elements should be analyzed, which ranges from 9% to 42% depending on the construction elements and load cases.
The focus of the study by Johansson et al. [4] was the demand for additional floors in existing buildings. This study explored the methods of constructing additional floors in several public buildings and hotels in Sweden. The authors addressed the increasing demand for open spaces and the associated costs, financial impact, and societal implications. The authors also discussed the environmental impacts and examined the methods used in strengthening buildings after the addition of new floors. The load-bearing capacities of elements, bonding and materials used, and models to ensure stability were analyzed. Fire safety was also addressed. The advantages and disadvantages of constructing additional floors considering previous experiences were taken into account. The study also featured the conditions for constructing additional floors, following technical and urban requirements. A guide was also provided for use in cases of adding extra floors. Static calculations and an inspection of elements that had been stressed and were subject to additional loads from the added floors were conducted accordingly. The building was not subjected to seismic influences. The authors concluded that different results are obtained depending on the project and approach. Finally, recommendations were imparted.
Zhulidova M. [9] dealt with the behavior of an old building and its load-bearing capacity, as well as the materials used. They took into account the geometric aspect of the elements and the foundation conditions for the possibility of constructing an additional floor. Examples of constructing additional floors using steel structures and their connection to the existing structure were examined. Various cases of adding extra floors in Europe and Russia were considered, and several cases analyzed the advantages and disadvantages of adding floors to these buildings. It assayed the case of adding a metal-structured story utilizing the perimeter of the existing building. The columns were founded on the ground and anchored to the external perimeter walls. This type of addition was implemented to avoid putting any additional load on the old building. The intermediate construction was made of steel without any reliance on the old building. Lightweight materials such as steel, wood, and lightweight concrete reinforced with composite structures were used in the walls and floors. Lastly, as a conclusion, the author claimed to have found the best vertical construction method, followed by an analysis of clients’ requirements and financial costs. It was identified that there is a lack of experience in such constructions. However, even in this study case, there was no approach to address the impact on joints from horizontal and seismic loads, only from vertical gravity loads.
The study of Soikkeli A. [10] focused on a global issue. With the increasing population in urban areas and the need for new construction, there is a risk of diminishing green spaces and agricultural lands. Hence, there arises a need to address the addition of new floors to existing buildings. The author analyzed the use of lightweight materials in constructing these additional floors, as well as the issue of the appearance and impact of old buildings and extra floors on neighboring structures, as well as the social, economic, and esthetic aspects of buildings. The work was fully based on the building regulations in Finland as revised in April 2011 (Chapter E1). The author also discussed fire protection and other installation systems, and the possibility of using prefabricated elements, or even containers. However, in this work, there was no treatment of the behavior of buildings regarding seismic influences.
The focus of Sundling R. [11] was a study review aiming to obtain a better understanding of the reasons and the needs for constructing additional floors. The analysis covered financial and social aspects, environmental impacts, barriers and legislative changes, and the legal permitting process for adding floors to buildings. The methodology of various studies and comparisons between different cases were also discussed, along with analogies and the differences between them. The time of construction, the age of the buildings, and the codes under which they were built, as well as their compliance with current codes, were analyzed. Four cases were examined, and their findings were discussed. Lessons were drawn on how to approach planning and permit acquisition and the assessment of existing structures, reinforcement, and intervention with additional floors. The treatment of connections between the old building and the new floor was also discussed. The materials used in the construction of old buildings were discussed, along with the possibilities of implementation and a strategy consisting of seven phases or stages. The conclusion of this study was to encourage investors and property owners to add floors to their buildings. The knowledge gained from these four case studies should be disseminated, and lessons should be drawn on how to vertically expand buildings by adding new floors to existing ones.
In the study of Shihoara H. [12], the joint connecting the beam and column was analyzed. It was found that the joint is the key element in the survival of the building and its response to seismic influences. It was observed that the joint can collapse due to seismic actions from shear force, highlighting the importance of proper design. The analysis focused on the equilibrium of external and internal forces and avoiding exceeding the permissible strains in joints. Diagonal cracks in the joint indicate the direction of internal forces. Shihoara analyzed the joint using two methods, known as joint mode equilibrium and beam mode equilibrium. The study concluded that in the cases of external, internal, and corner joints (knee joints), the distribution of strain follows only one rational path. The ratio of joint reinforcement to tangential forces plays a significant role in external joints, whereas it does not have the same impact on internal joints. The capacity of the joint is increased by the adhesion between reinforcement and concrete, which is a key factor in joints.
In Structural connections for precast concrete buildings—Guide to good practice, prepared by Task Group 6.2 [6], the group of authors of this guide examined the connecting joints of prefabricated elements. They assessed various connections, such as column–column, beam–column, and foundation-to-vertical element connections. The research also examined the other connections used with prefabricated elements. Anchorages were discussed, as well as the influence of tangential forces on anchorage and the connections between elements. The seismic aspect of the connection of prefabricated elements was also addressed in this study. The structural integrity of the building as a whole and its connections was also considered, as well as the behavior of the construction and its connections under horizontal forces and their effects on the structure.
In Eurocode 2: Design of concrete structures—Part 1-1: General rules and rules for buildings [13], the European design standard Eurocode 2 has addressed reinforced concrete structures as well as the connections between beams and columns. The study of this connection was carried out for monolithic cases and corner (knee) joints with open and closed moments. Section 6.5.4 of the code covers the general conditions and equilibrium conditions of the joint(node), outlining the types of joints and their treatment. Section 10 provides a superficial treatment of prefabricated elements, and Section 10.9.4 addresses the connections and supports of prefabricated elements. Section 10 talks about rules, conditions, and forms of connections. The design, execution, and maintenance conditions of the joints are also discussed, along with the materials used and the possibilities of anchoring. Half-joint connections, the treatment of transverse forces, and when to consider them as a basis or not are also covered. Annex J2 provides the methods for treating corner (knee) joints with open and closed moments and the reinforcement patterns for absorbing moments and shear forces in joints. There are several cases of corner joints, such as joints with columns and beams with equal geometric characteristics. In joints with strong columns and weak beams, the dimensions of the columns dominate compared to the beams, and in joints with weak columns and strong beams, the dimensions of the beams dominate compared to the columns. This code does not address the connection between column and column or column and beam for superstructures or additional stories.
In Eurocode 8: Design of structures for earthquake resistance—Part 1: General rules, seismic actions and rules for buildings [14], the beam–column joint is addressed under Section 5.4.3.3, which outlines the minimum conditions for the connection of the column on a beam and the amount of reinforcement required. Section 5.11 of the code covers prefabricated elements and their connections. Specifically, the connection between the column and beam is addressed under Section 5.11.2, which provides the conditions for the connection. The distance of the connection from critical parts of the joint, the design forms, and the dissipation of accumulated energy is discussed. It is mentioned that the joint should have at least 50% of the moment capacity for it to be treated rigidly. Section 5.11.2.2 presents an evaluation of joint resistance, but if any of the methods in EC2 and EC8 do not cover a particular case, experimental studies relating to that problem should be applied. This opens up the path for us to treat our specific case, which is the connection and behavior of additional floor columns in existing buildings. The behavior of additional stories in a typical frame has not been addressed in any case.
The American code for the design of joint connectors for prefabricated elements [15] describes three types of connections: strong, ductile, and deformable connections. It addresses the conditions and behavior of connections based on the building soil sites and seismic zone conditions. It also covers the use of materials and the anchoring of vertical and horizontal elements. It addresses the minimum concrete class and anchoring lengths. Vertical connections in cases of adding floors to a building or existing frame are not specifically addressed. However, the connection can be used as an analogy, utilizing the requirements that need to be fulfilled. Every connection used in structural elements must meet the criteria of transferring vertical and horizontal loads, including those from wind and seismic forces, down to the foundation.
In ACI 318-11: Building Code Requirements for Structural Concrete and Commentary [16] the method of connection and the role of the connection beam–column, and vice versa, is addressed. In this code, connections are addressed in Chapter 7, particularly under subchapter 7.9. The commentary on the connection emphasizes that it should function to continuously ensure a future without damage or failure. Chapter 11 addresses transversal forces and reinforcement methods for joints used in monolithic concrete and minimum reinforcement. Subchapter 11.11.7 elaborates on the moment transfer from slab to column and the method of reinforcement. It covers the moment transfer caused by all types of forces. Chapter 12 addresses different types of anchorage and anchorage lengths in columns from the slab or beam, as well as the effect of shear forces in the critical zone. Chapter 16, starting from page 275, treats prefabricated elements, whereas Commentary R16.2.2 clarifies that the behavior of prefabricated elements is different from monolithic structures, and the connections of elements need to be treated specifically, particularly considering seismic loads. The transfer of forces in beam elements is also addressed, taking into account shrinkage, temperature, and laboratory results of joints. Connections of elements should also address proper stability and adequate ductility. This has to be applied when the designers use different materials for the connections of elements. Chapter 21 addresses the aspect of joint behavior in a monolithic concrete frame. This chapter deals with the seismic aspect of the frame and joint, and technical conditions of element embedment such as columns, beams, and reinforcement bars to withstand external forces such as moment, shear force, or axial force.
In ACI 550.1R-01: Emulating Cast-in-Place Detailing in Precast Concrete Structures [17], this code addresses all possible joints and connections between the beam and the column, and the column and other elements. It also covers the determination of plastic hinge behavior. The joints are cast in place, specifically, on site. This code also covers the aspect of seismic impacts by enhancing the stability of the structure and the connection itself. It discusses the optimal points for implementing the connection, preferably at locations with the lowest external force effects. Various methods of connection are addressed, such as strong connections, ductile connections, and deformable connections. This is all carried out considering the stability and functionality of the joints in high seismicity zones.
Lazarević et al. [18] presents the method of adding floors to an existing building. The authors evaluated an old building and analyzed its dynamic and static behavior. The obtained results led the authors to decide to reinforce and renovate the existing building and add five new floors. The additional floors were constructed using a steel structure and external supporting columns. The columns were connected to the building, and the construction of the new floors was also supported by an elevator shaft. The joints and strains at critical points, both in the old and renovated parts of the building, were analyzed thoroughly. The authors analyzed the dynamic behavior according to the conditions of Eurocode 8 and the seismic conditions of Croatia. The construction methods were presented and the completion of the building was achieved. However, no section provides an analysis of the joints or their behavior in seismic conditions in relation to the old building.

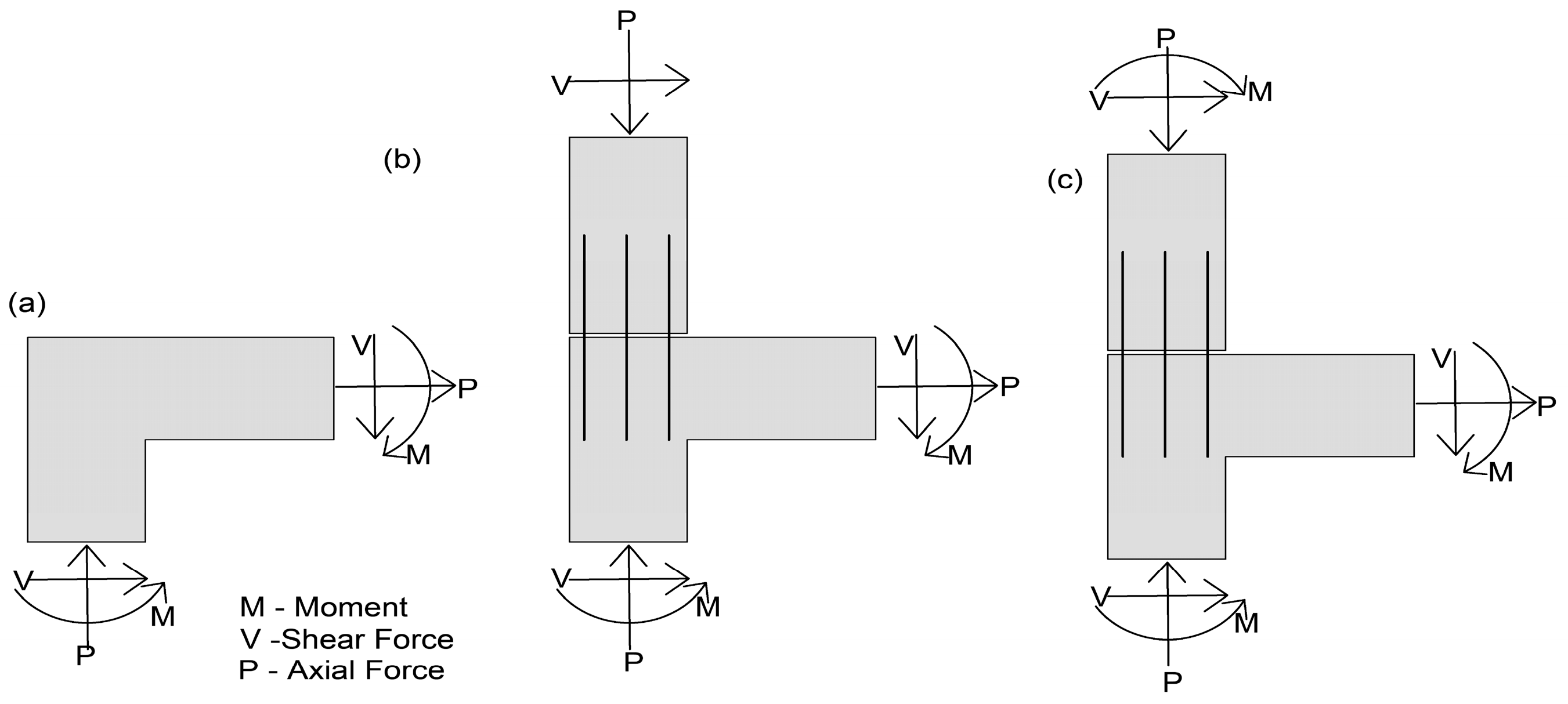
3. Numerical Study

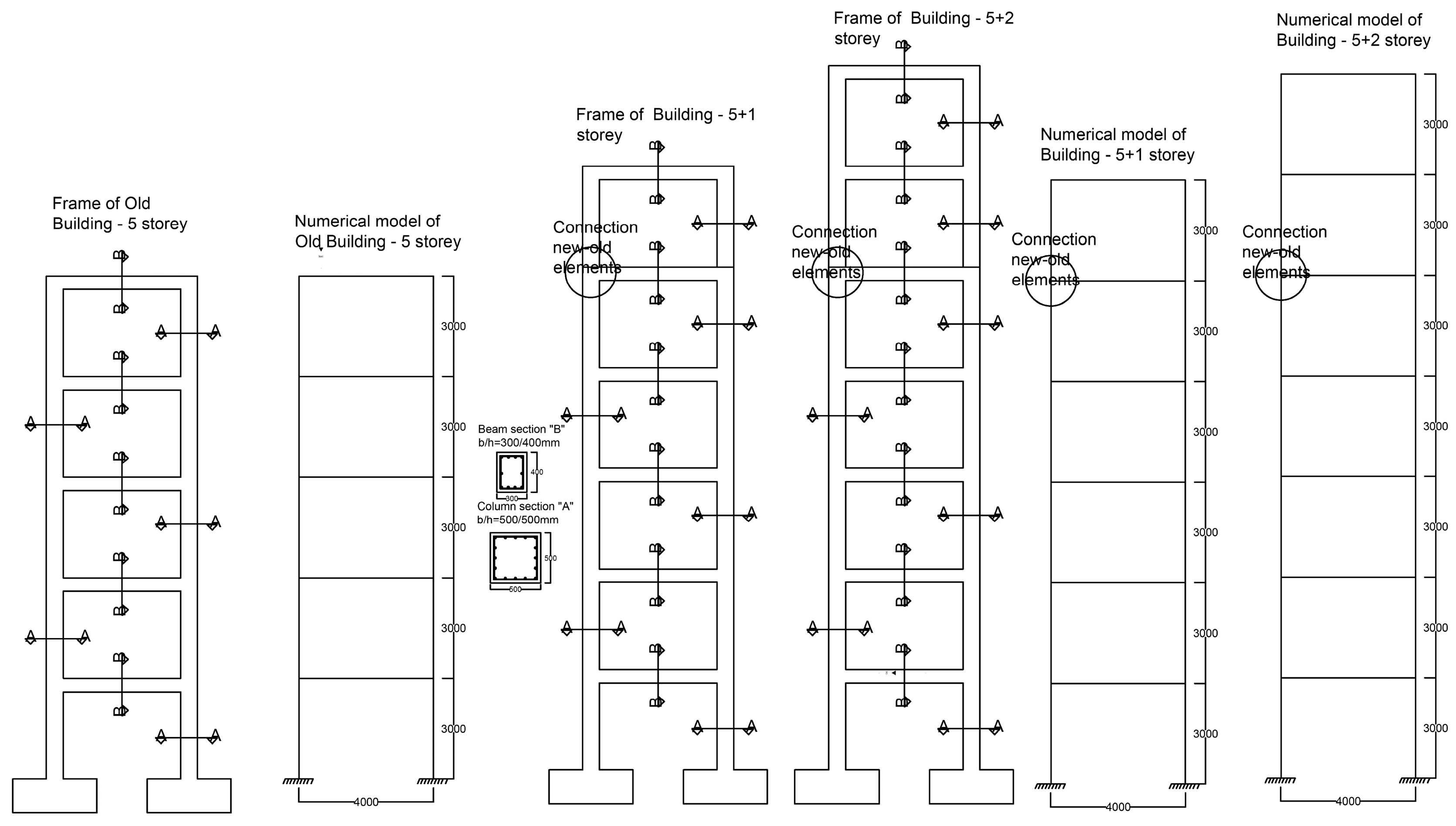
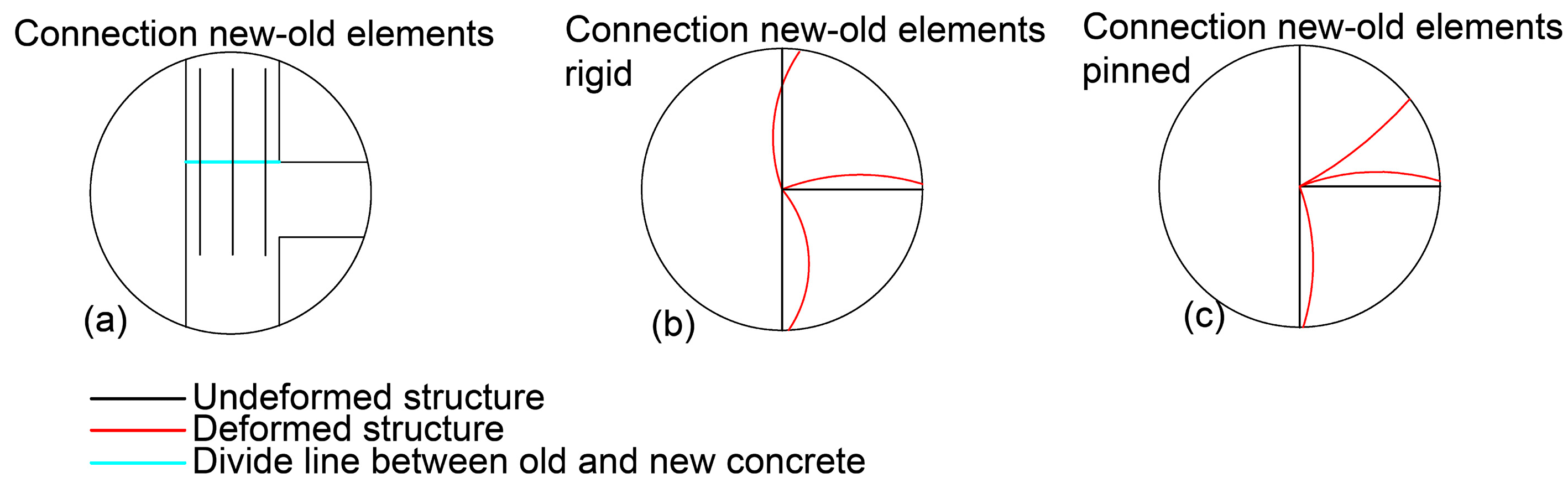
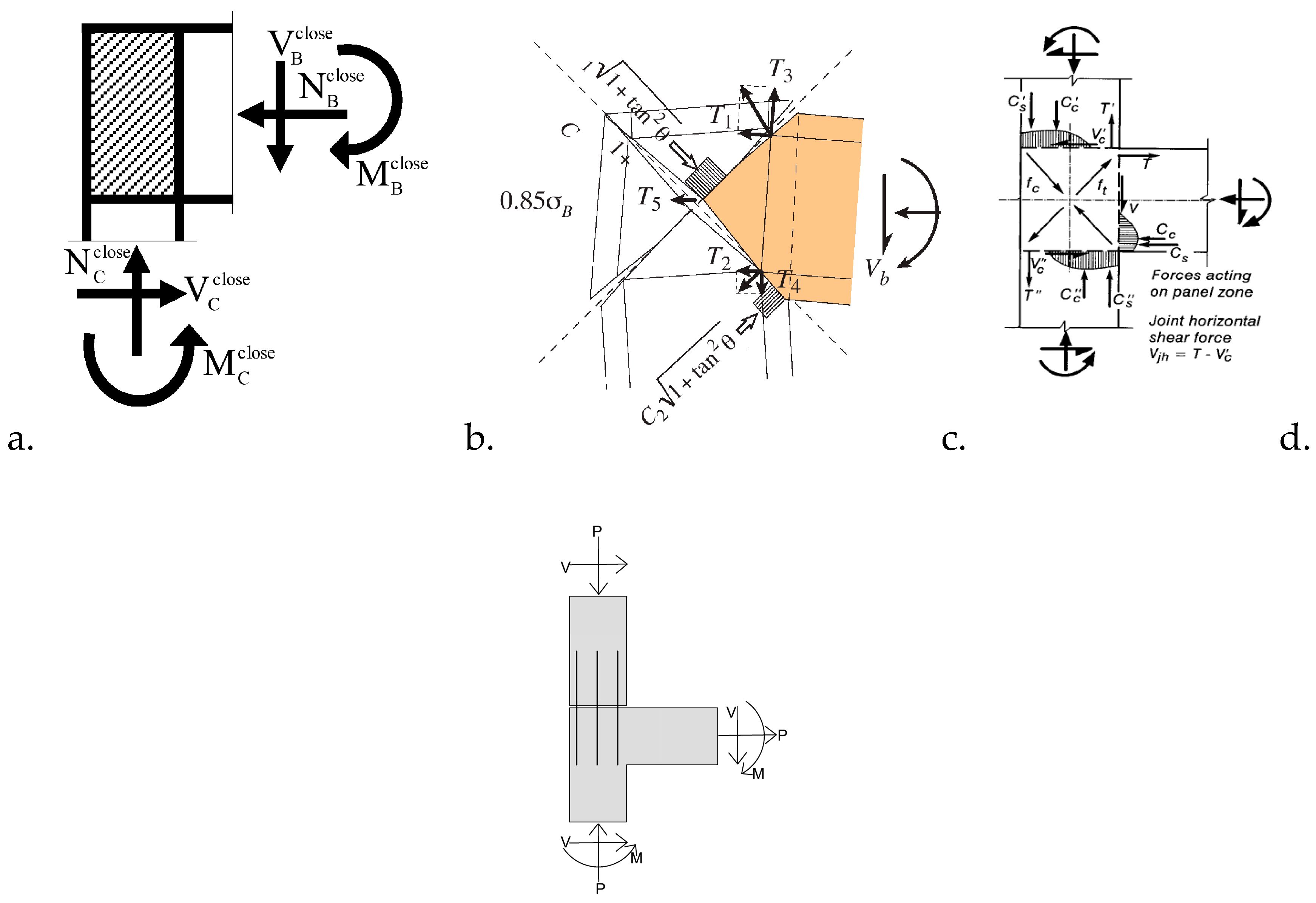
3.1. Model Description

A numerical study is conducted using a model of a frame reinforced concrete building to which a floor is subsequently added. The old frame structure, in some cases, might possess cultural value from the structural engineering perspective, as such structures represent the construction practices of reinforced concrete (RC) buildings during the 1960s and 1970s in the country [19]. They were designed and constructed primarily to withstand vertical loads, following the seismic codes for construction at that time [19]. An investigation and analysis of a frame model needs to be carried out to review the ongoing interventions.

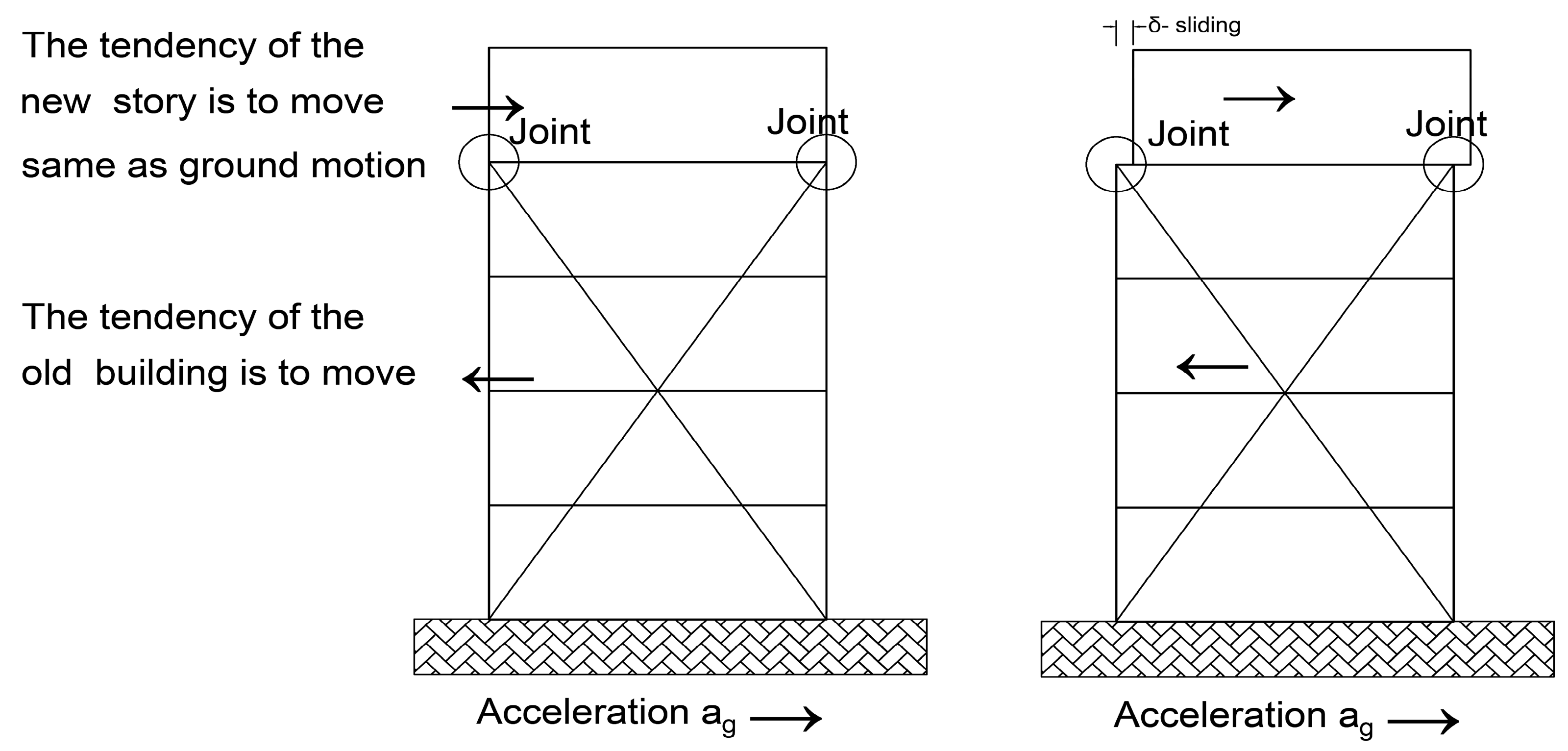
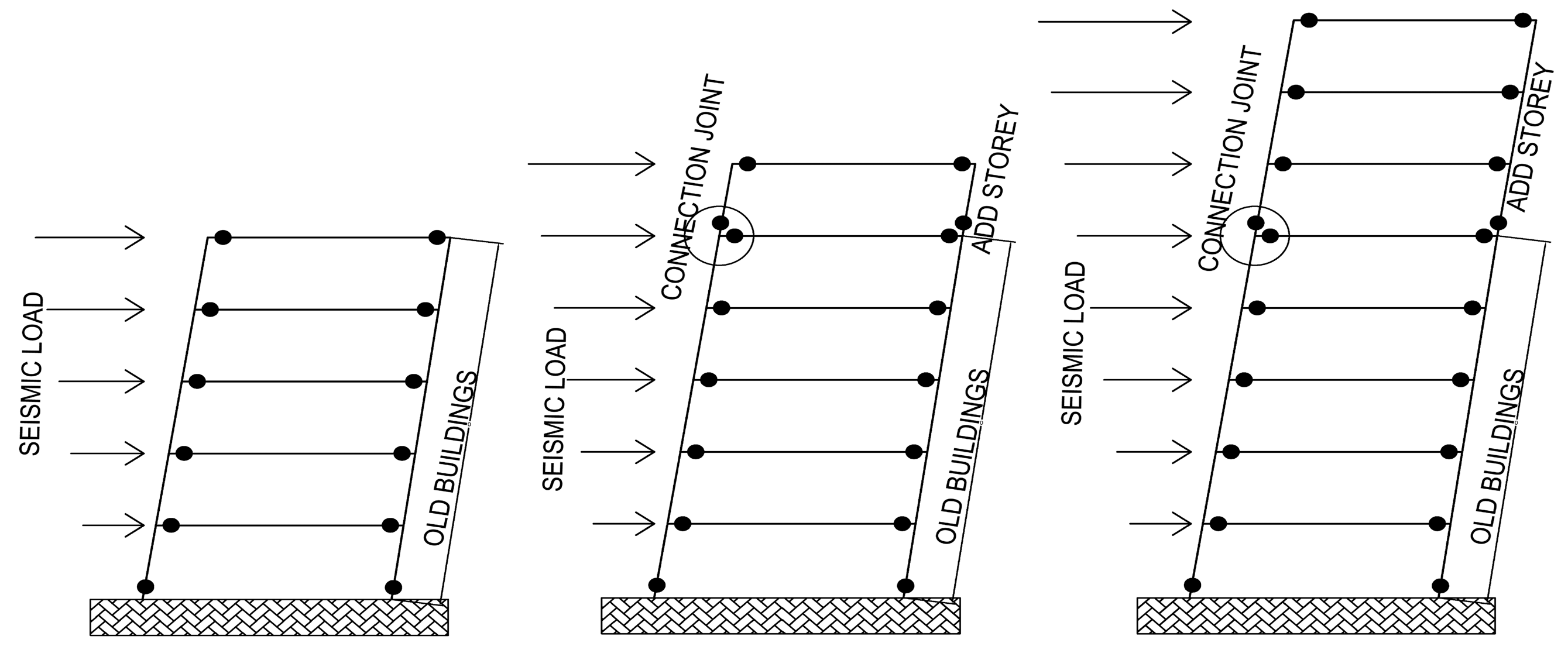
3.2. Old Frame Structure

The old frame structure, which is the starting point for the analysis of the response to seismic effects, consists of columns and beams, and is fully fixed. The technical specifications of the materials are as follows: columns b/h = 500/500 mm; beams b/h = 300/400 mm; (where b-the width, h-the depth), concrete class adopted for the old frame C 25/30; adopted reinforcement S-400/500; columns symmetrically reinforced by 16 Ø16 mm bars, and stirrups Ø8/150 mm. The old structure has a length (L) of 4000 mm and height (H) of 3000 mm. The frame undergoes a linear load of g = 15 kN/m in the beams, and the applied load will be q = 12 kN/m; the snow load is considered as s = 7.50 kN/m. The frame is calculated for a seismic zone with an acceleration of ag = 0.25 g, soil category C, all according to the provisions of EC8. The behavior factor is q = 2.0, and the spectrum is type 1. Figure 9 presents the base of the old frame and the frames with additional floors at specified geometric characteristics and numerical models. Figure 9 also shows the connections, indicated by a circle that determines the connection points. The classical connection (like in Figure 3a,b) is commonly used in the site and is determined by the developers who design the buildings and additional floors according to the investors’ requirements.

3.3. Frame Structures with Additional Floors

New floors are added to the existing old frame. The new floors have the same geometric characteristics as the old ones, but different material characteristics, such as concrete class C 30/37 and reinforcement S500. The columns are symmetrically reinforced, similar to the old columns, while the height of the added floors is H = 3000 mm. The permanent and other applied loads remain the same as in the old model. The characteristics of the soil and seismic acceleration remain unchanged, whereas the connection between the old and new frames is hinged and rigid.
The design takes into account the fact that for the design of structures that are stable and resistant to external actions, including seismic forces, it is essential to adhere to the principle of strong column–weak beam, which is a crucial parameter controlling the performance of structures [20,21,22,23]. During the design process, it is necessary to focus on ensuring that the RC frame joints possess sufficient ductility and a high load-carrying capacity [24]. Therefore, the requirement for reinforcements and special treatment of columns is always justified because, in all cases, a column functions as a compression member [25].

3.4. Numerical Calculations

The results from the static and dynamic calculations of the adapted models are presented. The satisfactory performance of RC frames depends on the proper design and detailing of their components, including beams, columns, and joints. Joints need to be well designed and detailed to meet both strength and ductility requirements [26]. To fulfill these conditions, it is necessary to perform a thorough analysis and numerical calculations for specific cases. Therefore, for accurate assessment and analysis, it is necessary to consider the dynamic characteristics of the system. The calculations adopted the seismic action using horizontal spectrum 1 according to EC8. Structure loads with additional floors and other static external loads were considered according to EC1 and EC2 [27]. The results of the numerical and mathematical calculations depend on the applied loads and determine the low load-bearing capacity of vertical supporting structures, which is a decisive factor in choosing a method for constructing additional floors [28]. The calculations were conducted using SAP2000 and ETABS, both of which operate with finite elements based on the analysis of the model and the linear, planar, and solid material properties. The designing of elements is achieved by employing points and lines as fundamental components for drawing the desired models, subsequently transformed into linear, planar, solid, and spatial elements. According to the software manuals, these are comprehensive computer programs with integrated systems for modeling, analysis, designing, and optimizing various civil and engineering structures. They perform static and dynamic analyses, linear and nonlinear analyses, seismic analyses, pushover analyses, and many other analyses, making these programs the state of the art in structural analysis. Their work is characterized by relying on vectors created for each type of material used and performing mathematical operations to provide a more realistic and reliable analysis. Deformations within the structure are governed by the displacements of nodal points of the finite elements. All formulas are based on matrices of mass, stiffness, damping, forces, and displacements. The equations used in the model, as outlined in the manuals, for example, in the modal analysis are useful to understand the behavior of the structure and base in Eigenvector analysis, Ritz-Vector analysis, etc.. Figure 10 presents three vibration modes for the adapted frame models and the base model. The same figure also depicts un-deformed frame models, with the labeling of joints that serve to provide the displacement results. Table 1 presents the basic dynamic characteristics of the frames, including the period and frequency results. (T) represents the period expressed in seconds and varies for each frame in the seismic analysis, indicating the behavior of the frame under dynamic or seismic actions. Similarly, (f) frequency varies as a function of the period, and the values change depending on the type of frame under consideration, expressed in hertz (Hz). In the third column, we have the mass participation for each mode of vibration, satisfying the conditions specified by EC8, where the values exceed 90% of the mass participation in the frame behavior, expressed as a percentage (Rxm). In the last column, the amplitude of the frame is presented for each period, expressed in meters (Ux). These characteristics help us better understand the behavior of each frame, which will be further discussed in the next chapter. Table 2 shows the displacement results for joint 6 in all models (a, b, c), joint 13 in models with additional floors (b, c), and joint 15 of Frame c. These results comply with frames that use stiff connections or hinged connections between the base frame a and frames b and c, which include the additional floors. In Table 2, (ux) denotes the horizontal displacement of each analyzed node under dynamic loading for each mode, while (uz) signifies the vertical displacement of the node occurring after the deformation of the frame and displacement along the x-axis. All values are expressed in meters (m) with precision to four decimal places, elucidating nuanced variations for each specific case and individual node.
The calculations of the different frame models show that the acceleration at the joints varies depending on the height and stiffness of the structure. Table 3 presents the accelerations at the connection joint and the new additional joints. The base acceleration for seismic calculations is taken as ag = 0.25 g. The acceleration data are derived from the results obtained through computer calculations based on the fundamental formula F=ma, where acceleration at nodes is presented in meters per second squared (m/s^2). The data is provided specifically for nodes 6, 13, and 15, as the analysis focuses on capturing variations at these nodes, which represent the end nodes of the respective frames and an additional node relative to the base 5-story frame.
Table 4 presents the forces and moments at the connection joints and the joints above the connections. These effects derive from the external forces, indicating how they behave within the structural system. These data depict the maximum and minimum values of seismic response derived from both diagrams and the results table, as presented by the program's analysis data.

4. Discussion of the Results

The dynamic characteristics of structures are of particular importance, especially in seismic zones. Figure 10 presents the vibration modes of three different height frames and the un-deformed models of the reinforced concrete frame. The footings are considered as fully restrained joints, not taking into account structure–foundation interactions [29]. The first three vibration modes tell us that as the height increases, the first period of the frame or structure also increases. The base frame is represented in Figure 10a and has a regular form of periods. Figure 10b,c present the frame with an additional floor. The characteristic of this frame is the connection with the existing ones, executed in two ways: rigid or hinged. The periods differ in shape and behavior compared to the periods of the base frame. Not only between the additional floor frames, but also within the frames, as shown in Figure 10b,c, there is a difference in behavior depending on the implemented connection. The stiffness is different, which affects the quality of the additional frame connection. Figure 10d,e also depict that there is a loss in stiffness in areas where we have a higher value of periods, depending on the connection. With the increase in the number of floors, the possibility of dynamic value changes in the structure also increases. In this case, there is also a change in the direction of the base periods. This implies that the behavior of an exterior beam–column connection is very complex, since the failure modes of the RC joint not only depend on the joint, but also depend on the connecting elements [30]. Here, we observe the tendency of the detachment of the additional frame at the connection, trying to move in the opposite direction to the inertia of the frame, which occurs in the case of ground motion. In other words, the additional frames tend to move in the same direction as the ground motion. The generally used design of the connection does not behave as an integral part of the old structure, as evidenced by the periods presented in Figure 10. Table 1 presents the numerical values of the periods and frequencies for the cases shown in Figure 10. It is clear that the difference in periods between the same model varies depending on the type of connection adopted. The participation of mass in the modal analysis is satisfactory in terms of the EC8 criteria (90% of mass activated in the first three modes) and is shown in Table 1 for the first three periods. Table 1 also presents the maximum displacement of the models according to the first three periods under the seismic action, ag = 0.25 g. It is clearly observed that the addition of floors not only changes the behavior and direction of the vibration, as seen in mode shapes, but also affects the displacement due to seismic action, depending on the connection between the additional floor and the existing frame. This difference is more pronounced in the second and third periods, indicating the phenomenon of the counter-directional action of the additional floors compared to the existing structure. Therefore, we posit that beam–column joints have a significant role in shaping RC frame building resistance to different loading conditions [31]. The proper treatment of the connection between the new structure and the existing one and its adequate solution is crucial. This is especially important for buildings with great cultural and historical value and for buildings [32] intended to have extra floors. Table 2 shows the displacements of joints 6, 13, and 15. These joints were selected based on the fact that joint 6 is being connected to the new frame, while joints 13 and 15 are the joints of the new frames. The obtained results derive from the displacement in the x- and z-axes and are expressed in meters. These results also demonstrate that the more floors that are added, the more diverse the behavior of the floor towards a structure without additions or constructed with rigid, semi-rigid, or hinged connections. The comparison of displacements is always carried out between the old frames and new frames with an additional connection on the old structure at the same points. Table 3 presents the acceleration results at the respective joints, which are the focus of the analysis. The acceleration in the vertical direction of the building changes relative to the base acceleration presented. The seismic acceleration ag = 0.25 g was considered, while at the joints, it was increased depending on the height and stiffness of the joint, considering the connection between the existing frame and the new one. Herein, from these results, it can be seen that the acceleration in the frame is higher in cases where there are no rigid connections between the new and old frames. Therefore, it is crucial to determine the correct stiffness of the joint in cases such as additional construction or additional floors in seismic zones. For non-seismically designed (NSD) structures, it is very important to model the nonlinearities in the beam–column joints in order to capture realistic seismic behavior [33]. Table 4 presents the effects on joints 6, 13, and 15 from the external forces. This table shows the changes regarding joint 6 in cases where there is no addition and in cases where the additional floors are part of the existing frame. Figure 11 schematically shows the connection that is commonly realized and the deformation of joint 6 depending on the stiffness of the connection between the old and new frames.
In cases of stiff connection, the deformation will be similar to the one shown in Figure 11b. If there is a pinned connection, then the deformation will be as shown in Figure 11c. Implementing the connection as shown in Figure 11a does not guarantee that the connection is rigid, or at least indicate a sufficient level of stiffness that would classify its behavior as rigid. Therefore, additional research is needed to understand how this joint behaves. Depending on the impacts on the joints presented in Table 4, the joint will change behavior, as shown in Figure 4. The change will not only be evident in the external form, but also in the internal forces, which will undergo a behavior change. This change occurs because the shape of the joint changes from a joint with two elements to a joint with three elements, and for different connections.
The outcome results in Table 4 indicate that the case shown in Figure 12c needs to be addressed in order to determine the distribution of internal forces within the joint. Consequently, tests should be conducted to verify the value of stiffness in the connection between the new and existing elements. Repaired structures, structural members, and connections must be designed to have design strengths at all sections that are at least equal to the required strengths calculated for factored loads and forces in the combinations specified in ACI 562M-13 [34]. The examination of this joint will be decisive for the future reconstruction and repair of old buildings for safer utilization.

5. Conclusions

A frame with added floors behaves differently compared to one without extra floors, even when rigid connections are used. In the case of frames with added floors, there is a tendency for the floor to shift in the opposite direction to the base structure under seismic action. This proclivity induces a displacement or a partial detachment of the flooring from the existing old structure, attributable to the seismic vibrations generated by earthquake waves. In light of this, we concluded that designs that consider the joint to be rigid are inadequate because the structure does not behave in such a way. The node, which was initially central up to the addition of the new floors, now changes the behavior of internal forces depending on the achieved stiffness of the node explored in additional research. For the structural behavior, both individually and with the additional floors, a new form of the node's connection must be selected. Accordingly, further studies will be conducted focusing on the following cases:
  • Conducting experimental studies to determine the stiffness coefficient of the connecting joint.
  • Conducting studies to determine the behavior of the structure as a whole under seismic loads.
  • Conducting surveys on the behavior of internal forces in joints when the function changes from a cornered or knee joint to an exterior joint.

Author Contributions

A.SH. and J.B.; methodology, A.SH.; software, A.SH.; validation, J.B; formal analysis, A.SH.; investigation, A.SH.; resources, A.SH.&J.B; data curation, A.SH.; writing—original draft preparation, A.SH.; writing—review and editing, J.B.; visualization, A.SH.; supervision, J.B.; project administration, A.SH.; funding acquisition, A.SH.; J.B. and A.A.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data are contained within the article.

Acknowledgments

We appreciate the Alb-Architect company for the support and financial assistance for the realization of this study.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bahrami, A.; Deniz, S.; Moalin, H. Vertical Extension of a Multi-Storey Reinforced Concrete Building. Int. J. App. Mech. Eng. 2022, 27, 1–20. [Google Scholar] [CrossRef]
  2. Ross S. Stein and Volkan Sevilgen (2019), Albania earthquake strikes highest-hazard zone in the Balkans, devastating nearby towns, Temblor, http://doi.org/10.32858/temblor.057. [CrossRef]
  3. Kyakula, M.; Kapasa, S.; Opus, A.E. Considerations in Vertical Extension of Reinforced Concrete Structures. In Proceedings from the International Conference on Advances in Engineering and Technology 2006; Elsevier: Amsterdam, The Netherlands, pp. 109–116; https://doi.org/10.1016/B978-008045312-5/50013-3. [CrossRef]
  4. Johansson, B.; Thyman, M. Strengthening of Buildings for Storey Extension. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, 2013; p. 113. [Google Scholar]
  5. Task Group 7.3. Seismic Design of Precast Concrete Building Structures—State of Art Report; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2003; ISSN 1562-3610. ISBN 2-88394-067-3. [Google Scholar]
  6. Task Group 6.2. Structural Connections for Precast Concrete Buildings—Guide to Good Practice; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2008; ISBN 978-2-88394-083-3. [Google Scholar]
  7. Masi, A.; Santarsiero, G.; Verderame, G.; Russo, G.; Martinelli, E.; Pauletta, M.; Cortesia, A. Capacity Models of Beam-Column Joints: Provisions of European and Italian Seismic Codes and Possible Improvements. In Eurocode 8 Perspectives from the Italian Standpoint Workshop; Reluis Italian National Research Project; Doppiavoce: Napoli, Italy, 2009; ISBN 9788889972168. Available online: http://hdl.handle.net/11390/863397 (accessed on).
  8. Thermou, G.E.; Pantazopoulou, S.J.; Elnashai, A.S. Retrofit Design Methodology for Response Modification of Substandard RC Buildings. In Proceedings of the 2nd fib Congress, Naples, Italy, 5–8 June 2006; Paper No. 950. [Google Scholar]
  9. Zhulidova, M. Reconstruction of an Existing Building with One Additional Storey. Bachelor’s Thesis, Saimaa University of Applied Sciences Technology, Lappeenranta, Finland, 2019. [Google Scholar]
  10. Soikkeli, A. Additional floors in old apartment blocks. Energy Procedia 2016, 96, 815–823. [Google Scholar] [CrossRef]
  11. Sundling, R. A development process for extending buildings vertically–based on a case study of four extended buildings. Constr. Innov. 2019, 19, 367–385. [Google Scholar] [CrossRef]
  12. Shihoara, H. Quadruple Flexural Resistance in R/C Beam-Column Joints. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; Paper No. 491. [Google Scholar]
  13. EN 1992-1-1:2004; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
  14. EN 1998-1:2004; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
  15. ACI 550.2R-13; Design Guide for Connections in Precast Jointed Systems: Reported by Joint ACI-ASCE Committee 550. American Concrete Institute: Farmington Hills, MI, USA, 2013; ISBN-13:978-0-87031-812-2, ISBN:0-87031-812-8.
  16. ACI 318-11; Building Code Requirements for Structural Concrete and Commentary: Reported by ACI Committee 318. American Concrete Institute: Farmington Hills, MI, USA, 2011; Structural Building Codes; ISBN:978-0-87031-744-6.
  17. ACI 550.1R-01; Emulating Cast in Place Detailing in Precast Concrete Structures: Reported by Joint ACI-ASCE Committee 550. American Concrete Institute: Farmington Hills, MI, USA, 2001.
  18. Lazarević, D.; Anđelić, M.; Atalić, J. Structural addition design for the Euroherc Building in Zagreb. Građevinar 2011, 63, 1021–1032. [Google Scholar]
  19. Mazzolani, F.; della Corte, G.; Faggiano, B. Seismic Upgrading of R/C Buildings by means of advanced techniques: The ILVA-IDEM Project. In Proceedings of the 3rd World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; Paper No. 2703. [Google Scholar]
  20. Abdelwahed, B. A review on reinforced concrete beam column joint: Codes, experimental studies, and modeling. J. Eng. Res. 2020, 8, 63–79. [Google Scholar] [CrossRef]
  21. Shiohara, H. New Model for Joint Shear Failure of R/C Exterior Beam-Column Joints. In Proceedings of the 4th US–Japan Workshop on Performance Based Earthquake Resistant Engineering for RC Structures, Toba, Japan, 22–24 October 2002. [Google Scholar]
  22. Shiohara, H.; Shin, Y.W. Analysis of Reinforced Concrete Knee Joints Based on Quadruple Flexural Resistance. In Proceedings of the 8th US National Conference on Earthquake Engineering, San Francisco, CA, USA, 18–22 April 2006; Paper No. 1173. [Google Scholar]
  23. Abdelwahed, B. Numerical analysis of progressive collapse for reinforced concrete frames. Appl. Comput. Mech. 2019, 13, 85–98. [Google Scholar] [CrossRef]
  24. Abdelwahed, B. Beam-Column Joints Reinforcement Detailing Adequacy in Case of a Corner Column Loss-Numerical Analysis. Lat. Am. J. Solids Struct. 2019, 16, e216. [Google Scholar] [CrossRef]
  25. Nagaraju, D.; Sai, G.; Akhil, K.; Srikanth, S.; Prasad, T.; Rama, K.; Rao, K. Evaluation of Existing Building for Performance Check if another Floor Is Proposed for Construction. Int. Res. J. Eng. Technol. 2018, 5, 2799–2808. [Google Scholar]
  26. El-Naqeeb, M.H.; El-Metwally, S.E.; Abdelwahed, B.S. Performance of Exterior Beam-Column Joints with U-Shaped Bars for Different Stirrups Detailing: Numerical Study. Eng. Res. J. 2021, 172, C1–C19. [Google Scholar] [CrossRef]
  27. Shala, A.; Bleiziffer, J. Analysis of existing reinforced concrete buildings and buildings with additional floors under seismic load. In Proceedings of the Simpozij Doktorskog Studija Građevinarstva, Zagreb, Croatia, 9–10 September 2019. [Google Scholar] [CrossRef]
  28. Pakhomova, L.; Zhadanovskii, B.; Chernyshov, A.; Iumasheva, A.; Pankova, E. Effectiveness of reconstruction with additional floors for buildings of different construction periods. E3S Web Conf. 2019, 110, 01084. [Google Scholar] [CrossRef]
  29. De Luca, F.; Verderame, G.M.; Manfredi, G. Eurocode-based seismic assessment of modern heritage RC structures: the case of the Tower of the Nations in Naples (Italy). Eng. Struct. 2014, 74, 96–110. [Google Scholar] [CrossRef]
  30. Naderpour, H.; Nagai, K. Shear strength estimation of reinforced concrete beam–column sub-assemblages using multiple soft computing techniques. Struct. Des. Tall Spec. Build. 2020, 29, e1730. [Google Scholar] [CrossRef]
  31. Abdelwahed, B.S.; Kaloop, M.R.; El-Demerdash, W.E. Nonlinear Numerical Assessment of Exterior Beam-Column Connections with Low-Strength Concrete. Buildings 2021, 11, 562. [Google Scholar] [CrossRef]
  32. Shala, A.; Bleiziffer, J. Assessment, repair, rehabilitation and strengthening of earthquake-damaged buildings. In Proceedings of the 1st Croatian Conference on Earthquake Engineering (1CroCEE), Zagreb, Croatia, 22–24 March 2021; pp. 1685–1690, ISBN 978-953-8168-47-5. [Google Scholar] [CrossRef]
  33. Sharma, A.; Eligehausen, R.; Hofmann, J. Influence of Joint Modeling on Seismic Evaluation of Non seismically Designed RC Frame Structures. In Proceedings of the 2nd European Conference on Earthquake Engineering and Seismology, Istanbul, Turkey, 25–29 August 2014. [Google Scholar] [CrossRef]
  34. ACI 562M-13; Code Requirements for Evaluation, Repair, and Rehabilitation of Concrete Buildings (ACI 562M-13) and Commentary, Reported by ACI Committee 562. American Concrete Institute: Farmington Hills, MI, USA, 2013; ISBN-13: 978-0-87031-813-9, ISBN: 0-87031-813-6.
  35. Sagbas, G. Nonlinear Finite Element Analysis of Beam-Column Subassamblies. Master’s Thesis, Department of Civil Engineering, University of Toronto, Toronto, ON, Canada, 2007. ISBN:9780494400968 049440096X. Available online: https://hdl.handle.net/1807/119245 (accessed on).
  36. Bayhan, B. Numerical simulation of shaking table tests on 3D reinforced concrete structures. Struct. Eng. Mech. 2013, 48, 151–171. [Google Scholar] [CrossRef]
Preprints 95016 g001
Figure 1. Buildings in Kosovo: Hani Elezit, Suhareka and Prizren, Prishtina.
Figure 1. Buildings in Kosovo: Hani Elezit, Suhareka and Prizren, Prishtina.
Preprints 95016 g001
Preprints 95016 g002
Figure 2. Building hit by an earthquake in Shijak, Albania, in 2019.
Figure 2. Building hit by an earthquake in Shijak, Albania, in 2019.
Preprints 95016 g002
Preprints 95016 g003
Figure 3. Several examples of connections executed in practice and from the literature(a) & (b) executed in Kosovo, ((c) [5], (d) [5], (e) [6]) for the addition of floors and prefabricated elements.
Figure 3. Several examples of connections executed in practice and from the literature(a) & (b) executed in Kosovo, ((c) [5], (d) [5], (e) [6]) for the addition of floors and prefabricated elements.
Preprints 95016 g003
Preprints 95016 g004
Figure 4. Column knee joint: (a) existing joint, (b) pinned connection, (c) rigid connection.
Figure 4. Column knee joint: (a) existing joint, (b) pinned connection, (c) rigid connection.
Preprints 95016 g004
Preprints 95016 g005
Figure 5. Tendency of the displacement of the added floor on the old building.
Figure 5. Tendency of the displacement of the added floor on the old building.
Preprints 95016 g005
Preprints 95016 g006
Figure 6. Display of the plastic cracks on the old building and the building with added floors.
Figure 6. Display of the plastic cracks on the old building and the building with added floors.
Preprints 95016 g006
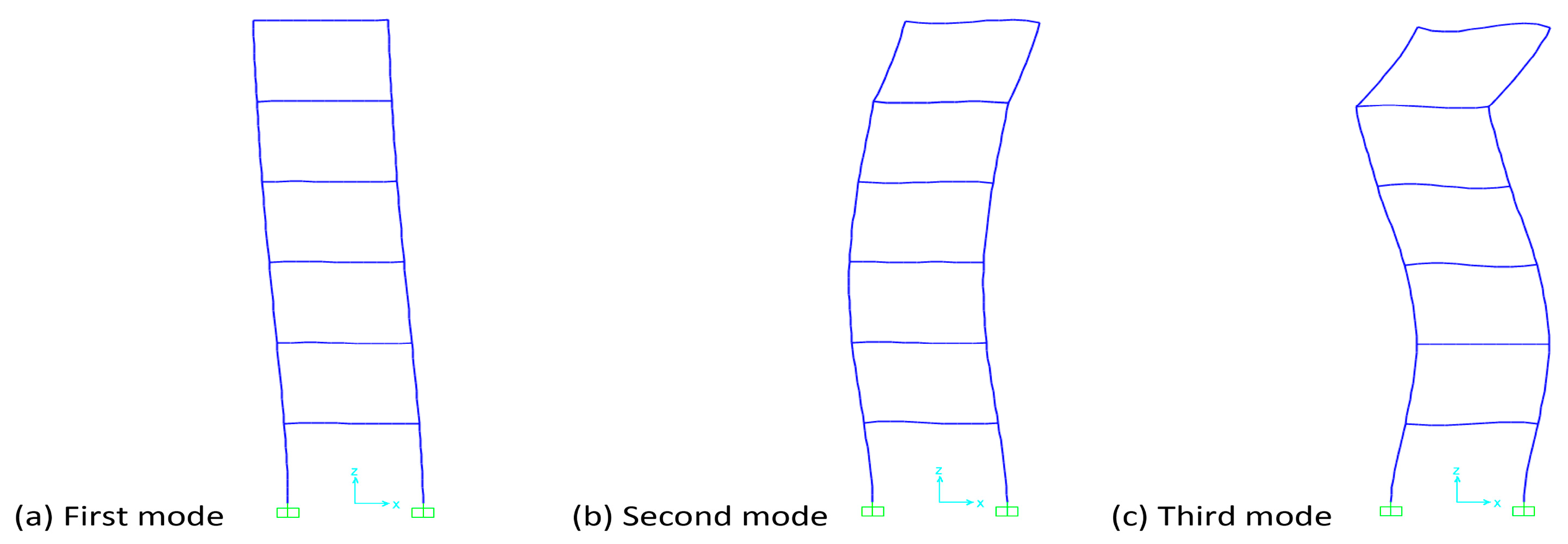
Preprints 95016 g007
Figure 7. Modes when the joint of the added floor is hinged.
Figure 7. Modes when the joint of the added floor is hinged.
Preprints 95016 g007
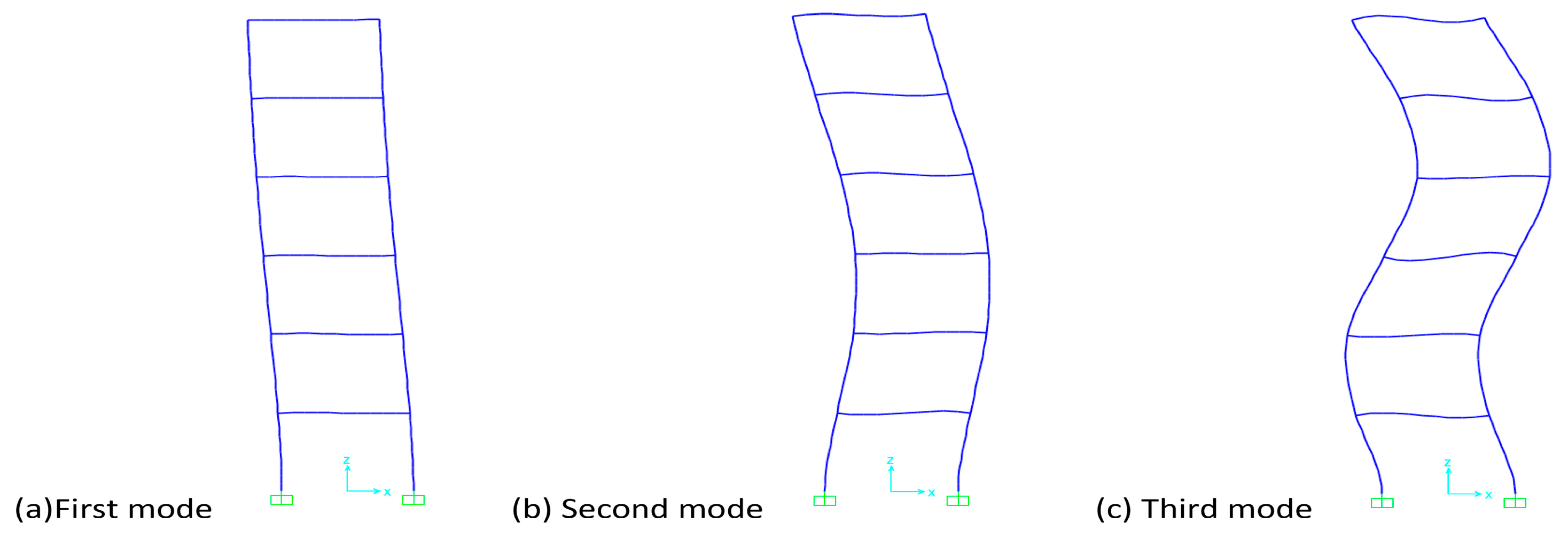
Preprints 95016 g008
Figure 8. Modes when the joint of the added floor is rigid.
Figure 8. Modes when the joint of the added floor is rigid.
Preprints 95016 g008
Preprints 95016 g009
Figure 9. Numerical model and column and beam cross-sections of the old frame and the frames with additional floors.
Figure 9. Numerical model and column and beam cross-sections of the old frame and the frames with additional floors.
Preprints 95016 g009
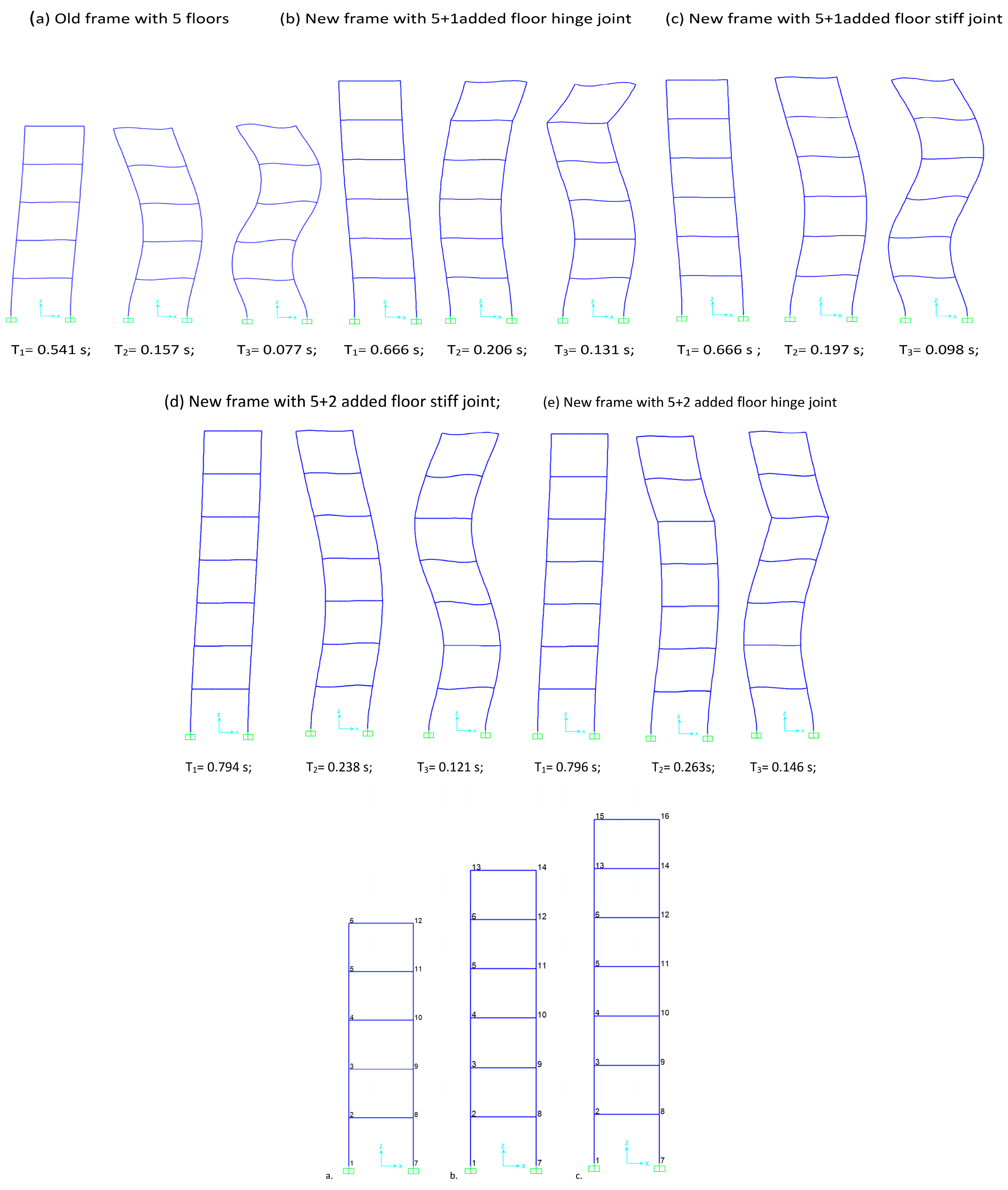
Preprints 95016 g010
Figure 10. Periods and modes for the three models of base frames and frames with additional floors, as well as the un-deformed models.
Figure 10. Periods and modes for the three models of base frames and frames with additional floors, as well as the un-deformed models.
Preprints 95016 g010
Preprints 95016 g011
Figure 11. Connection at joint 6 and its deformation on rigid and hinged connections.
Figure 11. Connection at joint 6 and its deformation on rigid and hinged connections.
Preprints 95016 g011
Preprints 95016 g012
Figure 12. Cases of joints: (a) knee [36], (b) knee with internal forces [12], (c) external treated by internal forces [35], (d) untreated hinge connection.
Figure 12. Cases of joints: (a) knee [36], (b) knee with internal forces [12], (c) external treated by internal forces [35], (d) untreated hinge connection.
Preprints 95016 g012
Table 1. Dynamic characteristics of the models.
Table 1. Dynamic characteristics of the models.
Model No. Period, T (s) Frequency, f (Hz) Mass of Part. Rxm Mod. Ampl Ux (m) Case Earthq.
Old frame 1 0.541 1.848 0.788 −0.183
2 0.157 6.379 0.912 −0.0055
3 0.077 13.061 0.965 0.0007
Old frame plus 1 new floor, rigid connection 1 0.666 1.501 0.785 −0.2796
2 0.197 5.08 0.904 −0.0102
3 0.0098 10.161 0.954 0.0013
Old frame plus 1 new floor, hinge connection 1 0.666 1.501 0.785 0.2796
2 0.206 4.861 0.885 0.0103
3 0.131 7.661 0.93 −0.023
Old frame plus 2 new floors, rigid connection 1 0.794 1.259 0.783 −0.3575
2 0.238 4.207 0.899 −0.0161
3 0.121 8.25 0.946 −0.022
Old frame plus 2 new floors, hinge connection 1 0.796 1.256 0.779 −0.3573
2 0.263 3.806 0.876 −0.0179
3 0.146 6.827 0.937 0.0039
Table 2. Displacement results of sample research study expressed in m.
Table 2. Displacement results of sample research study expressed in m.
Model Period Node 6—ux (m) Node 6—uz (m) Node 13—ux (m) Node 13—uz (m) Node 15—ux (m) Node 15—uz (m)
Old frame T1 0.1878 0.002
T2 −0.169 0.0059
T3 −0.124 0.0053
Old frame plus 1 new floor, rigid connection T1 −0.1538 0.002 −0.1716 0.002
T2 −0.0481 0.0058 −0.1608 0.0061
T3 0.0753 0.0049 −0.1317 0.0057
Old frame plus 1 new floor, hinge connection T1 −0.1536 0.002 −0.1718 0.002
T2 −0.842 −0.0045 0.1934 −0.0061
T3 −0.1775 −0.0003 0.1354 −0.0013
Old frame plus 2 new floors, rigid connection T1 0.1277 −0.0019 0.1462 −0.002 0.1589 −0.002
T2 0.0303 0.0054 −0.0697 −0.006 −0.1523 0.0063
T3 −0.1395 −0.0003 −0.322 −0.0053 0.1338 −0.0059
Old frame plus 2 new floors, hinge connection T1 0.1251 −0.0019 0.1473 −0.002 0.1615 −0.0021
T2 0.0804 0.0043 −0.0697 0.006 −0.17 0.0051
T3 0.175 −0.008 0.0219 0.0001 −0.0902 0.0005
Table 3. Acceleration at the connection joint and additional joints.
Table 3. Acceleration at the connection joint and additional joints.
Model ag, Node 6 (m/s2) ag, Node 13 (m/s2) ag, Node 15 (m/s2)
Old frame 0.499
Old frame plus 1 new floor, rigid connection 0.399 0.473
Old frame plus 1 new floor, hinge connection 0.405 0.479
Old frame plus 2 new floors, rigid connection 0.308 0.34 0.41
Old frame plus 2 new floors, hinge connection 0.325 0.344 0.411
Table 4. Effects of shear forces and moments on analyzed nodes.
Table 4. Effects of shear forces and moments on analyzed nodes.
Model Forces Node 6 over Column Node 6 under Column Node 6 Beam Node 13 over Column Node 13 under Column Node 13 Beam Node 15 under Column Node 15 Beam
Old frame M (kN/m) + 120.05 30.67
M (kN/m) − 30.67 120.05
V (kN) + 5.219 −112.678
V (kN) − 51.755 37.318
Old frame plus 1 new floor, rigid connection M (kN/m) + −13.302 126.055 77.378 120.319 30.925
M (kN/m) − 37.286 98.621 155.62 30.925 120.319
V (kN) + 3.648 39.995 −1.639 3.648 −37.187
V (kN) − 50.309 61.334 118.246 50.309 112.809
Old frame plus 1 new floor, hinge connection M (kN/m) + 0 149.92 77.9 125.249 38.863
M (kN/m) − 0 77.899 149.92 38.863 125.249
V (kN) + 12.954 30.598 −3.043 12.954 −33.97
V (kN) − 41.75 70.106 116.953 41.75 116.026
Old frame plus 2 new floors, rigid connection M (kN/m) + 14.766 140.781 109.175 -13.635 116.917 96.929 109.626 20.253
M (kN/m) − 51.838 101.228 185.801 36.458 88.588 145.351 20.253 109.626
V (kN) + 33.118 47.756 13.746 0.209 33.118 −6.928 0.209 −42.528
V (kN) − 54.919 73.806 133.742 46.698 54.919 −113.068 46.698 107.468
Old frame plus 2 new floors, hinge connection M (kN/m) + 0 164.431 92.517 −21.26 142.378 89.252 119.299 29.543
M (kN/m) − 0 92.517 164.431 36.079 122.492 166.477 29.543 119.299
V (kN) + 40.831 40.537 4.239 −1.037 40.831 3.934 −1.037 −37.788
V (kN) − 47.459 79.886 124.235 47.995 47.459 123.93 47.995 112.209
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated