Preprint
Article
A Natural Origin of the Beautiful Gamma Function from the WJ Distribution
Altmetrics
Downloads
99
Views
19
Comments
0
This version is not peer-reviewed
Submitted:
30 December 2023
Posted:
03 January 2024
You are already at the latest version
Alerts
Abstract
We show succinctly a natural origin of the beautiful Gamma function in light of the WJ distribution, linking to quite distinct fields.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
Introduction
The Gamma function, as initiated for factorial problems, is ingeniously set forth by the infinite integral function (IF) in single exponent (SE) of
for ( in the case that is a complex number) [1,2,3,4,5]. This integral function is the most applied form of the factorial function though other extensions exist and extends to the entire complex plane via analytic continuation except non-positive integers which just result in simple poles.
In a variety of fields such as probability and statistics, quantum physics, string theory, artificial intelligence, and machine learning, this beautiful Gamma function finds a broad range of applications exemplar in the appearance of gamma distribution, beta function, Dirichlet’s distribution, Stirling’s asymptotic expansion, the zeta function and Riemann’s hypothesis.
In contrast, the WJ distribution is a double exponential (or bi-exponent (BE)) probability distribution function [6], described by the following formula
or in equivalence
with ( is the digamma function), defined over the domain of (−, +). According to Equations (2) or (3), the WJ distribution function has three different free parameters , and : The parameter shifts the location of the curve but does not exert effect on the shape of the distribution. The parameters and taking positive values jointly govern the shape of the curve and make a contribution of to the horizontal setting of the curve.
The WJ distribution function, unifying a series of classical distributions, affords effectively a universal mechanism to tackle extreme events and critical phenomena, ranging from extraordinary occurrences to critical properties, enormously diverse in types and disparate in properties [6,7,8,9]. Still, the WJ distribution function has been corroborated to be an appropriate procedure in analyzing the Kohlrausch-Williams-Watts (KWW) relaxation [10] and well representing the Gaussian function with a specific set of the parameters (, , ) [11], along with potential application in information theory [12].
Results
In this work, we shall establish a close linkage between the Gamma function and the WJ distribution. We define a bi-exponent integral function (BEIF), , in the vein of the WJ distribution
Alternatively, the same definition applies to ,
which will be incurred in the process of deduction later.
By rearranging the terms in Equation (4), we obtain
Conducting the partial integration, Equation (6) turns out to be
which leads to the expression as follows
Considering the fact that the argument has the same outcome as that of for the infinite integral, thus Equation (8) adopts the formulation
The part in the great bracket is analogous to Equation (2) with the variable set () being changed to (), that is, the corresponding integral function assumes the form
Evidently, we get a recurrence relation for the bi-exponent integral function
It is perceived that Equation (11) is the same form as the recurrence relation of the Gamma function in disguise
In point of fact, Equation (4) is reducible to the following single-exponent infinite integral (SEIF)
which yields in essence the same expression as Equation (1) for the Gamma function with , after we carry out the exchange of the variables
Moreover, it is recognized that is scalable to , viz.,
Nonetheless, the association of the Gamma function with the WJ distribution may be instructively scrutinized from the embedding of the former in the formula of the latter (cf. Equations (2) & (3)). Since the WJ distribution is a probability distribution function and has intrinsically the unitary property of the total integration
we may directly acquire the Gamma function given in the argument of by inserting the explicit formula of in Equation (2) and rearranging
which is identical to Equation (4). Consequently, we have demonstrated that the Gamma function may be naturally inferred from the WJ distribution , or in other words, the bi-exponent integral function is equivalent to the Gamma function. Conclusively, it is appreciated that the BEIF of Equation (4) is correspondent to the Gamma function of Equation (1), which is particularly transparent in its reduced form of Equation (13). Figure 1 presents the amplitude of the Gamma function or equivalently in complex plane in 3D created with Matlab & Origin.
Concerning the probability distribution function for the Gamma function, we come to two representations, one of which is designated by the original WJ distribution of Equation (2) (or equivalent of Equation (3)) and the other is, based on Equation (13), the classic form of the Gamma distribution specified by
Their first and second statistical quantities, the expectation and the square deviation , respectively, read
and
for the original WJ distribution, as well as
and
for the classical expression of the Gamma distribution derivable from the original WJ distribution.
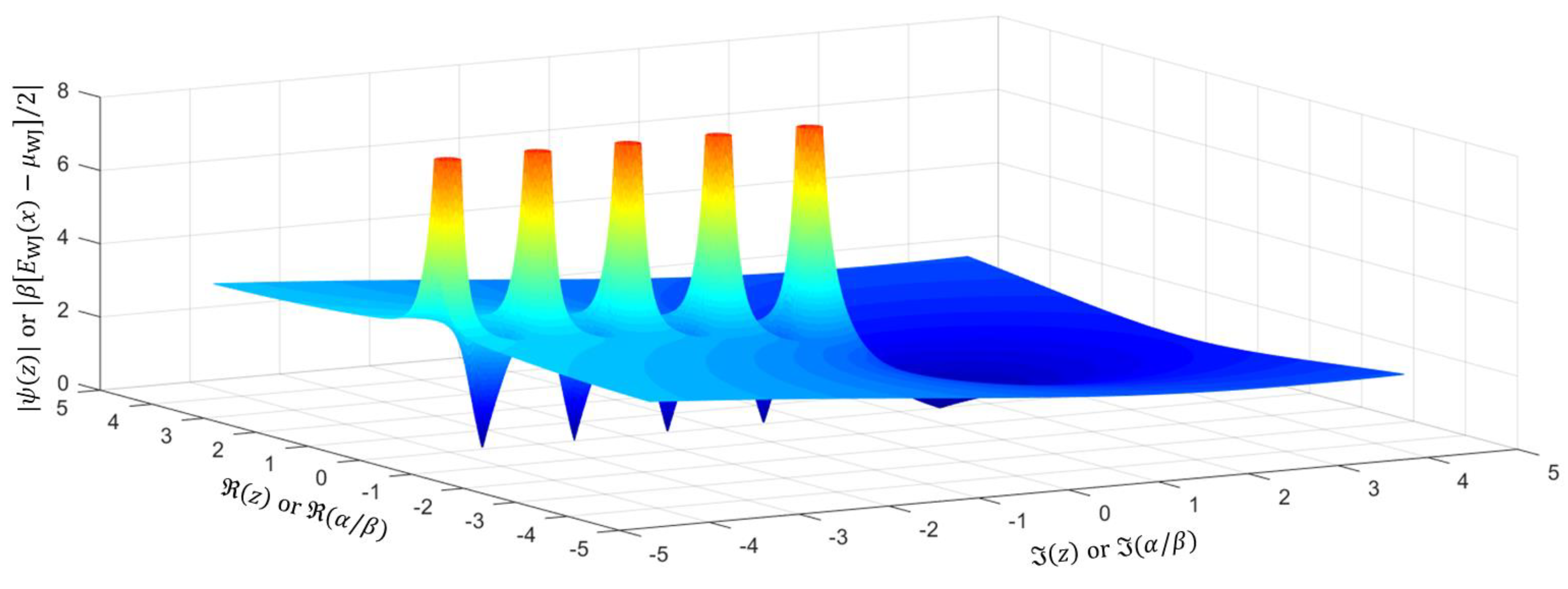
It is immediately noticed that the two kinds of the Gamma distribution, essentially resulting from the WJ distribution, have quite distinctive characteristics, as partially reflected in their statistical quantities as above-elucidated. Relating to the expectation of the original WJ distribution (cf. Equation (19)), Figure 2 plots the amplitude of the digamma function or equivalently in complex plane in 3D created with Matlab & Origin for direct visualization.
In addition, we can conduct Fourier or Laplace transformation on these two different representations, separately. As the WJ distribution is defined over the whole domain (, ), a Fourier transform is pertinent
By replacing the expression of Equation (2), we have the explicit formulation of
for the transform. Correspondingly, a Laplace transform can be performed on the classical form of the Gamma distribution in the form of Equation (18)
or explicitly
Conclusion
We have shown that the WJ distribution may offer a concise definition of the beautiful Gamma function, prospectively casting a deeper insight into the natural origin of the latter.
Acknowledgement
We express our gratitude to Dr. J.W. Wu for generous support.
Author Contributions
J.H.W., G.Y.L. and Q.J. conceived the idea; J.H.W., G.Y.L. and Q.J. performed the analytical derivations; G.Y.L. and Q.J. conducted the numerical analyses; J.H.W., G.Y.L. and Q.J. contributed to the preparation of the manuscript.
Competing financial interests
The authors declare no competing financial interests.
References
- Davis, P.J. Leonhard Euler's Integral: A Historical Profile of the Gamma Function. The American Mathematical Monthly 1959, 66, 849–869. [Google Scholar] [CrossRef]
- Borwein, J.M.; Corless, R.M. Gamma and Factorial in the Monthly. The American Mathematical Monthly 2018, 125, 400–424. [Google Scholar] [CrossRef]
- Whittaker, E.T.; Watson, G.N.; Moll, V.H. A course of modern analysis, 5th ed.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Oldham, K.B.; Myland, J.C.; Spanier, J. An Atlas of Functions, 2nd ed.; Springer-Verlag: New York, NY, USA, 2009. [Google Scholar]
- Havil, J. Gamma: Exploring Euler's Constant; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Wu, J.H.; Jia, Q. A universal mechanism of extreme events and critical phenomena. Sci. Rep. 2016, 6, 21612. [Google Scholar] [CrossRef] [PubMed]
- Bramwell, S.T.; Holdsworth, P.C.W.; Pinton, J.F. Universality of rare fluctuations in turbulence and critical phenomena. Nature 1998, 396, 552–554. [Google Scholar] [CrossRef]
- Bramwell, S.T. The distribution of spatially averaged critical properties. Nat. Phys. 2009, 5, 443–447. [Google Scholar] [CrossRef]
- Albeverio, S.; Jentsch, V.; Kantz, H. (Eds.) Extreme Events in Nature and Society; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Wu, J.H.; Jia, Q. The heterogeneous energy landscape expression of KWW relaxation. Sci. Rep. 2016, 6, 20506. [Google Scholar] [CrossRef]
- Ge, S.R.; Wu, J.H. The Analysis of WJ Distribution as an Extended Gaussian Function: Case Study. Appl. Sci. 2022, 12, 7773. [Google Scholar] [CrossRef]
- Liang, G.Y.; Xue, H.; Jia, Q.; Wu, J.H. Some Properties of the WJ Distribution and Implication in Information Theory. J. Phys. Conf. Ser. 2019, 1237, 022081. [Google Scholar] [CrossRef]
Figure 1.
Plotting the absolute value of Gamma function or equivalently in complex plane in 3D created with Matlab & Origin.
Figure 1.
Plotting the absolute value of Gamma function or equivalently in complex plane in 3D created with Matlab & Origin.
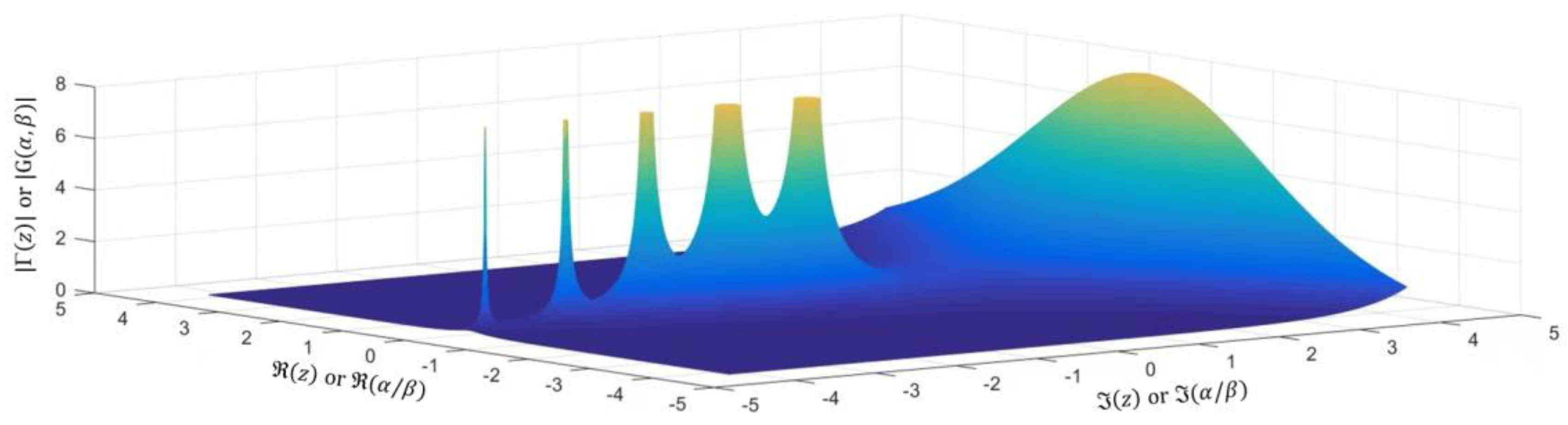
Figure 2.
Plotting the absolute value of the digamma function or equivalently in complex plane in 3D created with Matlab & Origin.
Figure 2.
Plotting the absolute value of the digamma function or equivalently in complex plane in 3D created with Matlab & Origin.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





