Prerpints.org logo
Preprint
Article

Optimization of Greedy Randomized Adaptive Search Procedure

Altmetrics

Downloads

106

Views

58

Comments

0

This version is not peer-reviewed

Submitted:

31 December 2023

Posted:

02 January 2024

You are already at the latest version

Alerts
Abstract
Although the behavioral mechanism studying is a difficult and complex task, it can produce an important systems optimization impact. In this work, we use, in this paper, inference system approach to represent reasoning mechanism and the operations of dynamic systems to extract mental representations from traveling salesman and convert them into cognitive structures. For this we develop an extraction automatic method to create knowledge bases and, later, data are stocked into structure based on transition maps and the performances of these created maps get improved through combining the reinforcement learning thus augment traveller's deciding capacity from historical data. These transition maps help to find best actions for obtaining useful new policies. Generated intermediate transition maps are gathered to give a global map called main map whose advantage is to improve the learning process. The main idea of this approach is to improve learning capability by using a reinforcement learning technique as exploration and exploitation strategy of the metaheuristique GRASP method and the use of the fuzze logical rules mechanism allowing concepts model to have more variability of states. The results obtained after simulation as presented in this paper are very encouraging.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In the litterature, the traveling salesman problem (TSP) is the more intensively studied optimization problem. TSP requires a large computational capacity which gives it properties similar to NP-hard combinatorial problems which require the use of heuristic techniques when looking for solutions. TSP, is described as follows: A tour is formed by n cities, each city is visited once and return to the starting one. The complete tour is must be combined by all cities and objective is to minimizing/maximizing costs of the deplacement. Mathematically, TSP is well defined and understood but there are no exact methods to solve it and heuristic methods are the only way currently to work with (Donald, 2010; Chaudhuri, Kajal, 2010). The cognitive approach (Tolman, 1948) is concerned when knowledge acquisition situations in which the learner must assume complex reasoning activities tending towards an explicit goal. So, knowledge modélisation with rules of inference and concept networks is researchers prefered formalization in computer studies. inference systems are a powerful tool that responds favorably to the needs of researchers in this area. In this work, the reasoning task realised by the traveler to deel with the best minimum/maximum cost tour is recognised as a cognitive task. Starting from this remark, we present, in this paper, a new approach vision for optimizing TSP decision making in reasoning task based on cognitive formalism augmented by reinforcement machine learning RL (Maikel, Maria, Garcia, Koen, 2004; Elpiniki, Peter, 2008).
A special case of inference system is the one proposed by Kosko in 1986 (Kosko, 1986) called causal graph diagram which are wholly established techniques based on Axelrod’s cognitive maps (CM) (Axelrod, 1976) here the values ​​of the weights are in the ’intercale [−1, 1] or [0, 1] which now imply fuzzy causal relationships between the concepts of the system (Donald, 2010; Jacek, 1996; Zhong, 2008). Figure 1 shows an inference system where Each vertex represents a concept (property of the system to be studied) whose state represents the degree of its membership function and having a numerical value in the interval [0, 1].

2. Research Method

2.1. Theoretical approach Basis

The operation of inference systems consists in evaluating the outputs by incorporating into the system a set of rules natural language based. For there to be compatibility between the sensor data, these rules and the output parameters, a fuzzy system must be broken down into three parts.
The fuzzification process is to translate digital data from a sensor concepts into a linguistic variable. The designer formulated membership function of the fuzzy system extract linguistic variables from quantitative sensor data (for example, data coming from a sensor could be distance = 25.03 meters. After fuzzification, we would have so distance = 30% near, 50% medium, 20% far). The inference mechanism then applies each of the inference rules during this second step. These rules of inference represent the knowledge that we have about the system formulated by the experts of the studied domain. The defuzzification process, which constitutes the last step, consists in merging the different commands generated by the inference mechanism and transforming this output linguistic variable into numerical data. Thus, three principal elements are necessary to define fuzzy system:
  • Input/Output Fuzzy variables,
  • A fuzzy rules set, and
  • A mechanism Fuzzy inference.
The causal relations between concepts are represented by directed edges with signed numbers, called links or a weight, that indicant’s the degrees of the concepts relationship. The weights link values between concepts are depicted as matrixes as show on Figure 1. The vector A1=(0.3, 0.1, 0.1) is a system state vector shown by Figure 1 and the inference process is defined by an iterative matrix calculation process. Suppose Vn be the state vector after the nth iterative calculation process starting from initial state vector V0, and W be the causal weight values matrix, the inference process is assumed as a repeating process of Equation 1 calculating until the system convergence to stable state, otherwise the system diverge.
V n + 1 = f ( v n × W + V n )
Where ƒ is habitually defined as:
f x = 1   x ≄ 1 x   ( 1 > x > − 1 ) − 1   − 1 ≀ x
The final steady state (output vector after convergence systems) is a system feedback to the making environment changes. Throughout inference process, state transitions are invisible to users.

2.2. Reinforcement Machine Learning Processes

The decision is made through a process of trial/error process where, in each state s of the state space S, the experimenter selects randomly an action a from possible actions set A because reinforcement machine learning (Ottoni et al., 2022) is based on the interaction in an unknown environment. The choice of action is guided by defined policy π such that a = π(s). In response, the system receives a reward r = R(s, a) and moves to the next state s’ = T(s, a). The interactions < s, a, r, s’ > between the entity and the environment continue until the system reaches a terminal state leading to the end of the steps. The Markov Decision Process (MDP) framework is the formal description of reinforcement machine learning and is defined by:
  • States set s Є S,
  • Actions set a Є A(s),
  • Reward function r(s, a) Є R, and
  • Transition probability between states ℩(s ’| s, a) = ℩a(s, s’).
Beginning with any initial state, the objective is to find the best action policy strategy that achieves maximizing rewards in all steps where the traveler action choice is according to these outputs. So, the environment either sends award or penalty defined by r k = h ( s k ,   a k ,   s k + 1 ) . The ψ value of a state s∈S subordinated to an action a is defined as the return reward that traveller can expect to obtain by selecting this action in a state s by following policy π.
ψ * ( s ,   a ) = m a x   ψ π ( s ,   a )
The optimal policy π * ( s ) = a r g   m a x a ψ * ( s ,   a ) is defined by the optimal ψ-function action ψ * ( s ,   a ) = m a x π ψ π ( s ,   a ) which makes it possible to determine the optimal state-action with the following policy π* if ψ * ( s ,   a ) = m a x ψ π ( s ,   a ) allows to define the optimal policy where ψπ(s, a) = E ÎŁÎłri and ψ*(s, a) is the optimal state-action with following policy and if we reach the ψ*(si, ai) for each pair (s, a) then we say that the goal can be reached starting from any initial state, in this case the update equation of the learning parameter is:
ψ t ( s ,   a ) = ( 1 − α ) ψ t ( s ,   a ) + α r + Îł m a x ψ t ( s ’ ,   a )

2.3. Greedy Randomized Adaptive Search Procedure

The Greedy Randomize Adaptive Search Procedure (GRASP) method (Kitjacharoenchai, et al, 2019) is a metqheuristic iterative process, where two phases are necessary at each iteration phase. The first phase is constructive builds a realizable solutions and the second phase is the local search phase. During the Local Search Phase LSP investigations are for searching the best neighbourhood solution and the constructive phase continues until a local minimum be found and the best solution is kept as a final solution. In this manner, the LSP phase consists in improving solution obtained during the constructive phase. The probabilistic aspect of GRASP method is given by the randomly action choice among the possible actions of actions set A, not necessarily the best. The selection criterion, in this case, is reduced to the greedy criterion. For more understand, the LSP phase consists of successively replacing the current solution with a better one from its neighbourhood, so it works iteratively and the search algorithm success depends on the neighbourhood choice.
Here, TSP is studied in order to show how learning capability is improved and a data acquisition issue of the model has been addressed in the rationale of the proposed framework. In complex adaptive system the capacity to memorize most previously encountered states, enables it to mount a more effective reaction in any future encounters of the same state. However, these explain the mathematical adjustment basis of mathematical of the Q-learning algorithm in the sense of instructing the system to consider optimally its history, i.e. the learning parameter value ψ aim to memorize the state visited.
For all and each interaction with the environment, the dynamic systems are distinguished by their dynamic improvements in current policy . So this is a local improvement that does not require an assessment of the overall strategy. This observation exiges that the value of the ψ-function in step (i+1) must be equal to 0. mathematically, it is traslated by: ψn(si+1, a) = 0 and therefore equation (3) of the function ψ becomes as follows:
ψτ+1(si, ai) = ψτ(si, ai) + α [ri – ψτ(si, ai)]
The ψ-function value enables system to apply a more effective action in any state previously visited. So, the ψ-function value is here to instruct to optimally consideration the historical past. If the agent is in a one state that is already visited with a ψ value it will be directly exploited to move to the next state, otherwise he will explore the possible actions in this state according to their respective probabilities. ψ-function value update is achieved using following two equation described below:
ψ t + 1 ( s i , a i ) = ψ t ( s i , a i ) + α ( 1 − ψ t ( s i , a i ) )   / / i f r = 1
ψ t + 1 ( s i , a i ) = ( 1 − α ) ψ t ( s i , a i )   / / i f r = 0
The all states of the system are defined after fuzzyfication stage by the input sensory concepts type. The output vector is represented by, after one step, the output concepts type concepts that represent the realised actions after defuzzyfication operation. the decision-making mechanism is represented by the motor concepts. The explorations task of the actions implys’ a linear update scheme of probabilities ℩ (Ramos, et al., 2003).
℩Îș+1 (si, ai) = ℩Îș(si, ai) + ÎČ(1 - ℩Îș(si, ai)) // If r = 1
℩Îș+1 (si, ai) = (1-ÎČ)℩Îș (si, ai) // If r = 0

2.4. The Proposed approach to Improve Making Decision

All dynamic system requires a balance between exploitation process and exploration process in the optimal actions search where an imbalance situation can generate either a premature convergence, to a chaotic state, or a divergence to deadlock situation. This equilibrium is achieved through combination of the reinforcement learning paradigm implemented by Q-Learning algorithm and GRASP metaheuristic based method in performing actions. The actions selecting method is achieved by fuzzy rules based system formed by a set of if-then linguistic rules where inputs/outputs are fuzzy statements as bellows:
if a set of conditions are satisfied then a set of results can be inferred
The proposed technic that using theoretical aspects described above is summarized by pseudo code of equations (9) and (10). Updating values of the learning function
ψ t ( s i , a ) = ( 1 − α )   ψ t ( s i , a ) + α ( r + Îł m a x ψ t ( s t , a i ) )
s the current state, a the action executed in the state s, r the reward,, s’ the new state, ÎČ is a discount parameter (0≀ÎČ≀1), learning factor α(0 ≀α≀1). The updating values of ℩ij, probability is given the equation 10:
Ω k + 1 (   a i ) = Ω k (   a i ) + ÎČ [ 1 - Ω k (   a i ) ]

2.5. Treating TSP as a Sequential Decision Process

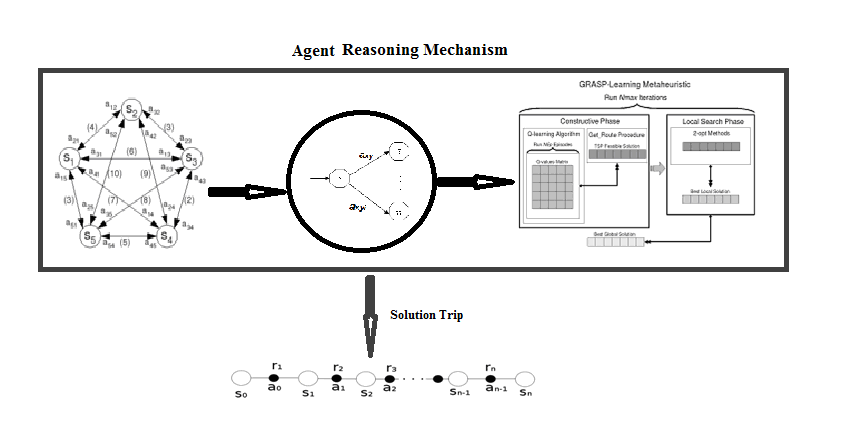
One of the alternatives to treat TSP as a sequential decision problem (Donald, 2010; Feo, Resende, 1995) is to consider the states set S formed by all cities to solve it where the states set cardinality is equal to the problem instance size. These reduce the risk that S suffers the curse of dimensionality. In our case study, TSP is treated as same as a sequential decision problem based on this alternative. To better explain our proposed approach, let we consider a five cities TSP instances as shown in the M(N, A, W) map Figure 5. N is the set of nodes, A the set of arcs between nodes and W is the weight of arcs. a12 corresponds to visit city s2 from city s1.
Consider the map M(N,A,W), the quintuplet D = {T, S, A, ℩, ψ, W} is the representation as a sequential decision process and is defined for TSP as follows:
  • Iteration set T: defined by T = {1,
, N}, everywhere the number N of cities which form a TSP route is a cardinality of T.
  • States set S: represented by S = {s1,
, sN}, that all state si, i=1,...,N corresponds to a one city.
  • Possible actions set A: denoted by:
  • Ap ={âˆȘAp (si), i=1...N ) = {a12 , a13 ,
 , aN,N-1}
  • →Ap = {a12,..., a1N}âˆȘ....âˆȘ{aN1,...,aN(N-1)}
  • →Ap = {a12,
 ,aN(N-1)}
4.
Transition probability ℩: probability function of states s∈S were ℩ij(sj|si, aij) are the probabilities to found state sj from state si selecting action aij.
5.
ψ-learning parameter: the values of each pair of state/action designed the quality function denoted ψ(si,ai).
6.
Weight matrix W: involve weight between two concepts and it is a function of S X S in ℜ assigning a weight Wij to each pair (si,sj). The way to initialize weights is that Wij is taken inversely proportional to the distance between states cities Wij = 1/di.
According to the proposed approach described above, Figure 3 represents the solution process with reinforcement machine learning technique.
Note that some actions cannot be available when building a solution. To elucidate this constraint, consider the following partial solution: Solutionp : s1→s2 →s3
Solutionp designate, in step 3 and in state s3 , the available possible actions are A(s3)= {a34, a35}, since the "cities" s1 and s2 (action a31 and a32) are not allowed to avoid repetitions in itinerary.
In conclusion, the main traveling salesman objective is to find shortest path of visiting n cities exactly one and only once before to return to initial city (Leon et al, 2013) where dij represents distance between cities i and j; In the permutation matrix, decision variable xij = 1 income that the path is from city i to city j; xij = 0 be a sign of the route which isn’t chosen by the salesman. Equation (8) represents the objective function, and equations (12) (13) designate constraints that each city will be visited only one. One solution to the problem, can be encoded as a permutation matrix, i.e. a binary square matrix containing exactly one ’1’ per column and row. In this matrix, a line represents a city and a column indicates the order of visiting this city’s during a tour. For Figure 4, one possible tour denoted by CEBADC (S3S5S2S1S4S3) in graph of Figure 4 is shown in Table 1.

2.6. Inference Model for Solving TSP

The inference mechanism, by if-then rules of the fuzzy logic, start after fuzzyfication process of the input data’s in the value interval [0, 1] is accomplished. At each iteration or episode in the search for the acceptable solution, the modelled system is in a state which is represented by concepts of an inference system constructed at this stage called transition card. The traveler of commerce arrived at this stage is always seeking to transit to a future city (state), among the possible cities (possible states) by optimizing the reward of the environment and respecting the constraints imposed, a city is visited once and only once, by adapting his behaviour by removing actions that are not permitted at this stage.
x new state, axy
.axyi possible actions at step k and y
.yi are possible cities to visits. The behaviour is also guided at each step by using the λ parameter transition between state si, this parameter is equal to 0 if the state is not visited and equal to 1 if the state is already visited.
λ = 1   city is visited 0   state not visited
For TSP the fuzzy rules can be designated as:
Rulek : IF x1 is s1 and x2 is s2
and xk is sk THEN yk is Ok
Where x1,x2,
,xk are the input at step k. s1,s2,
sk the membership function of the fuzzy rules represents states and yk the rule Rulek output designated by the membership function Ok. This fuzzy rule is also known as Mamdani fuzzy type model or linguistic fuzzy model. In our example TSP case study, the fuzzy rule associated for the transition card at step k can became as:
If x1 is C and x2 is E and x3 is B and x4 is A then y is D
If x1 is C and x2 is B and x3 is A and x4 is D then y is E
In the example above we described the traveler behaviour at a step in final decision in order to help the reader better understand the mechanism of reasoning implemented in this work. The next following example describes an intermediate situation at step 3. The traveler has to choose between two actions that lead to two different states. In step 3 the salesman person is in the city D where initial starting state is A and was the city he passed is the city C, the next possible cities are city B or city E; therefore the traveler must choose the city be visited in next step. Because balanced between exploration and exploitation must be assured based on the data of the table of the parameter function ψ values and on the possible action probability at each step the traveler has visited the cities A, C and transition D and now have to choose the next city to visit. Here there are two options either to go to the city B or city E. based on the constructed map Figure 6 , the choice is guided by the probabilities of possible actions at this level and the value of the function ψ if it has already taken this path. Output vectors as a solution step are:
Solstep1(1 0 1 0 0), Solstep2(1 0 1 1 0 ), Solstep3(1 1 1 1 0), Solstep4(1 1 1 1 1 )
As we have indicated bellow there is two possible actions namely aDB and aDE and their corresponding ψ-values and probabilities are as depicted in Table 2. The ψ-function values of (state, action) initially receives a null value for all items, i.e. ψ(si,aij) = 0, and a table of action probabilities initially receives a 1/n value for everyone actions at each associated state and n is the number of actions at this stage. At all iteration, the ψ-value and probability actions updated are made with applying pseudo code described in section 2.4. The ψ value is smoothed to 1 for the success concept, which income that this concept is active, after the environment’s response on the action that give the best result.

3. Results and Discussions

The objective in this paper is not the search for the optimal solution of TSP because there are several methods that have given good results. The targeted objective here is behavioral adaptation (Holland, 2006; Elpiniki, Peter, 2004; Web TSP page, 2010) in decision making during an autonomous entity reasoning mechanism, combining recurrent neural networks with fuzzy logic. Tests were carried out using four instances of the TSPLIB library from TSP web page: Burma14, ulysse16, gr17 and bays29. These fore instances are useful small test data sets for TSP algorithms. For the information about instances used in the experiment is presented in Table 3:
All statistics generated after 250 runs on each city set are shown in Table 4 below:
Reinforcement learning GRASP method used here to improve conventional Kosko’s inference system shows that inference system have learn from experiences capability and an historical past optimal way use to model and simulate dynamic cognitive mechanism (Stylios, Peter 2004). Therefore, at each stage, only one concept is supposed active, i.e. its value is equal to 1, and the rest transitional card concepts are taken o value. The modeled system evolution is realized by the reasoning mechanism implemented using the inference process explained by the pseudo code of section 2.4.

4. Conclusion and Future Work

In knowledge acquisition situations in which the learner must assume complex reasoning activities tending towards an explicit goal the cognitive approach is concerned. So, knowledge representation with rules of inference and concept networks is researchers prefered formalization in computer modeling are a powerful tool that responds favorably to the needs of researchers in this area. In computer science and other related science th Studys of TSP behaviour are mainly consumption time and related cost important optimization traveler. In the last years, a lot of technics have been made to give best solution using heuristic methods. The proposed method for TSP improving decision making and dicussed in this paper is based on cognitive aspects engendred by traveler behavior witch is enhanced by introducing reinforcement learning GRASP method. An heuristic way, based on the agregation fusion of an intermidiate transition maps, of updating concepts output value is presented and the whole inference system parameters were obtained and which led to more best results. Many studies in this field have shown that the behavioral mechanism is par excellence a cognitive task that consists to deal with environment changes. In this work we have focused on the reasoning mechanism of TSP applying new machine learning approach that based on fuzzy logic, recurrent neural network and reinforcement learning GRASP method. From a mathematical point of view, in future work, we aim to test our approach on several problems that implies mechanism of reasoning as a cognitive task in order to to improve mathematical model proposed in this paper.

Acknowldgements

This work is one of the lot results of a research project method of Optimization for adaptive complex dynamic systems supported by the MISC laboratory of Constantine 2 University, Algeria.

References

  1. Devendra D. ’Traveling Salesman Problem, theory and applications’. Intech Janeza publisher, 2010, 51000 Rijeka, Croatia, ©.
  2. Chaudhuri A., Kajal D. ‘A study of TSP using fuzzy self organizing map’, TSP Theory and Applications, Prof. Donald Davendra (Ed.), 2010, ISBN: 978-953-307-426-9, Intech Books.
  3. Tolmam E. ’Cognitive maps in rats and men’. Review vol 55, 1948. [CrossRef]
  4. Maikel L., Ciro R., Maria M., Garcia R. B., Koen V., ‘fcm for modeling complex systems’. 2004, Springer.
  5. Elpiniki P., Peter G. ‘A weight adaptation method for fcm to a process control problem’. 2008, Springer.
  6. Kosko B. ’ Fuzzy cognitive maps’, JJMM Studies, 65-75, 1986. [CrossRef]
  7. Axelrod R., ’Structure of decision: The Cognitive Maps of Political Elites’, Princeton N.J, Princeton University Press, 1976.
  8. Jacek M. ‘Solving the Travelling Salesman Problem with a Hopfield type NN’. Warsaw University, Poland. 1996, Published in Demonstration Mathematica, pp 219-231.
  9. Zhong H. "Temporal fuzzy cognitive maps", IEEE international conference on fuzzy systems, 2008. [CrossRef]
  10. Ottoni A.L.C., Oliveira M.S.D., et al." Reinforcement learning for the travelling salesman problemwith refueling". Complex Intell Syst., (2022),Springer.
  11. Sutton R. S., Barto A. G. ‘Reinforcement Learning: An Introduction’. Book. 2005, The MIT Press, London, England.
  12. Kitjacharoenchai P., et al." Multiple TSP with drones: Mathematical model and heuristic approach", Volume 129, March 2019, page 14-30, Elsevier.
  13. Jeremiah I, et al. "Integrating Local Search Methods in Metaheuristic Algorithms for Combinatorial Optimization: The Traveling Salesman Problem and its Variants," 2022 IEEE Nigeria (NIGERCON), 2022. [CrossRef]
  14. Ramos I. C. O., Goldbarg M. C., Goldbarg E. F. G., Doriq A. D., Farias J. P. F., ’ProtoG Algorithm applied to TSP’ In XXIII International Conference of the Chilean Computer Science Society; IEEE; pages 23-30; Los Alamitos, 2003.
  15. Feo T., Resende M. ’Greedy randomized adaptive search procedures’; Journal of global optimisation; Vol 06; March 1995; pages numbers 109-133; ISBN 0925-5001.
  16. 16. Leon ?.; Napoles G.; Bello R.; ?krtchian I.; Depaire B.; Van hoof K.; ’Tackling Travel Behavior M An approach based on fcm’; International Journal of Computation Intelligence Systems; Vol 6; 2013.
  17. Holland J. H.. ’Studying complex adaptive systems’. 2006. [CrossRef]
  18. Elpiniki P., Peter G. ‘A Weight Adaptation Method for fc to a process control problem’; 2004; Springer.
  19. 19. Web TSP page ”http;//comopt.ifi.uni-heidelberg.d/software/tsplib/index.html/.
  20. Buche C.; et al. ‘fcm for the Simulation of Individual Adaptive Behaviors’; 2010; Wiley&Sun.
  21. Stylios C. D.; Peter P. G.; ‘Modeling complex systems using fcm’ IEEE; 2004.
Preprints 95070 g001
Figure 1. Example of an inference system.
Figure 1. Example of an inference system.
Preprints 95070 g001
Preprints 95070 g002
Figure 2. Framework of the reinforcement GRASP-Learning Method (Jeremiah, et al., 2022).
Figure 2. Framework of the reinforcement GRASP-Learning Method (Jeremiah, et al., 2022).
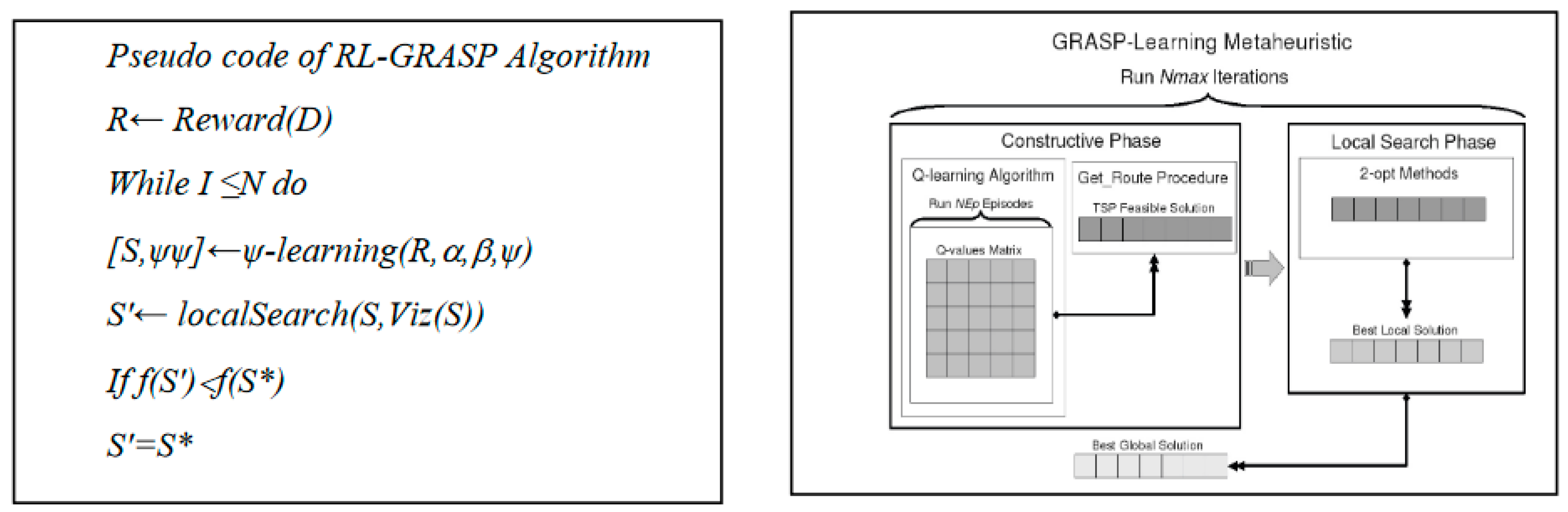
Preprints 95070 g002
Preprints 95070 g003
Figure 3. Solution of TSP represented as a reinforcement learning Problem.
Figure 3. Solution of TSP represented as a reinforcement learning Problem.
Preprints 95070 g003
Preprints 95070 g004
Figure 4. TSP Graph with 5 cities.
Figure 4. TSP Graph with 5 cities.
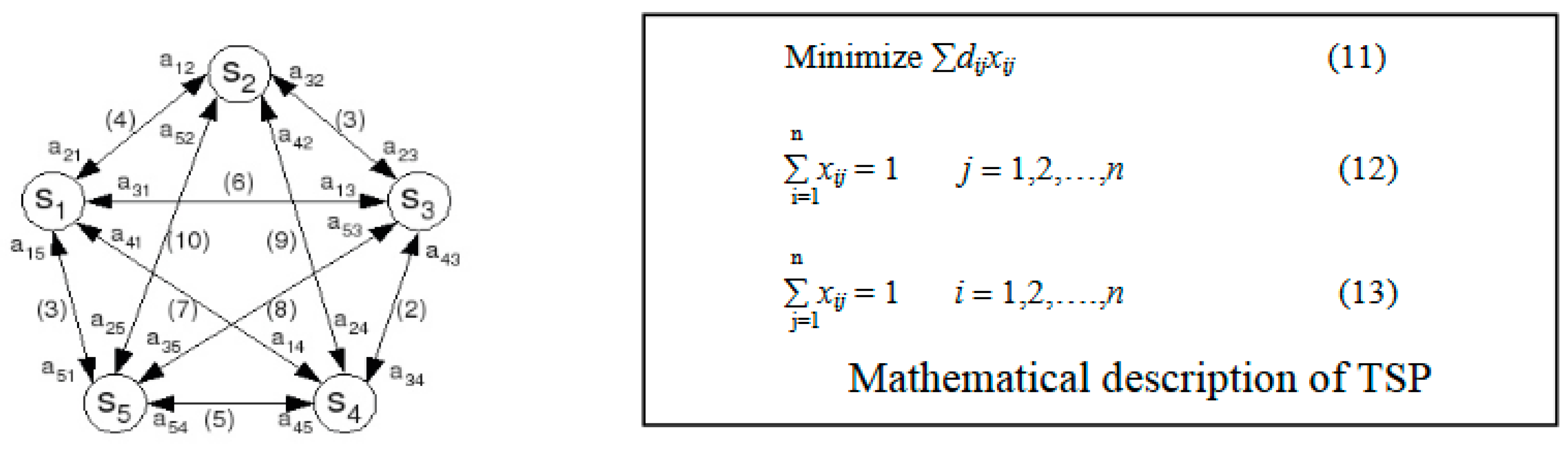
Preprints 95070 g004
Preprints 95070 g005
Figure 5. of Transition map.
Figure 5. of Transition map.
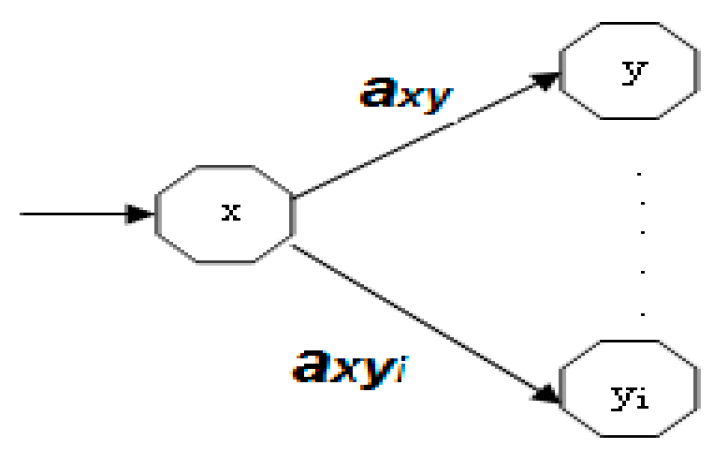
Preprints 95070 g005
Preprints 95070 g006
Figure 6. Transition map at step 3.
Figure 6. Transition map at step 3.
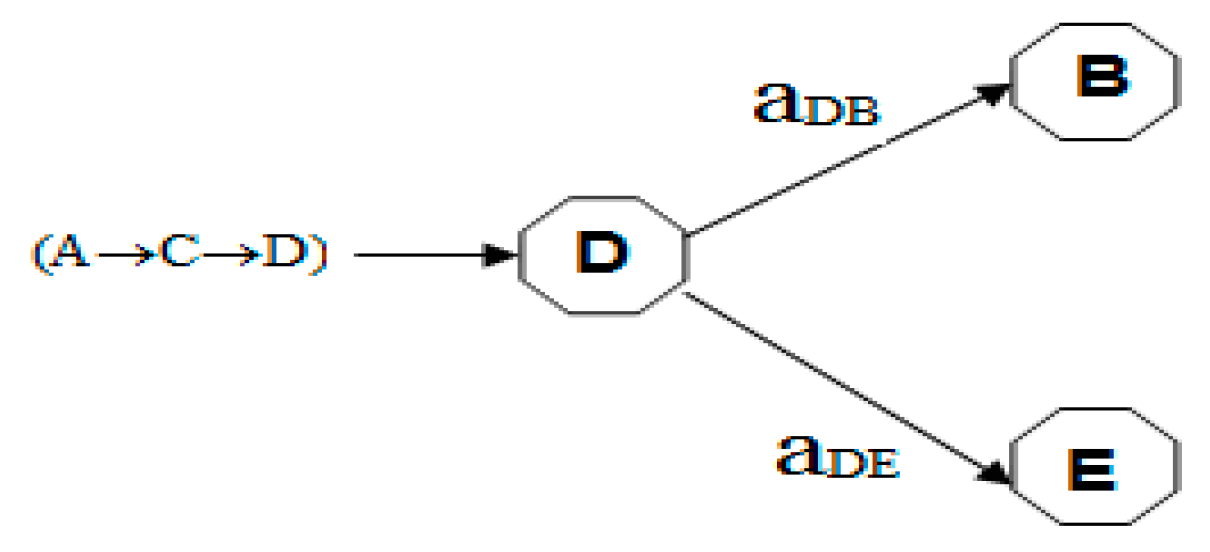
Preprints 95070 g006
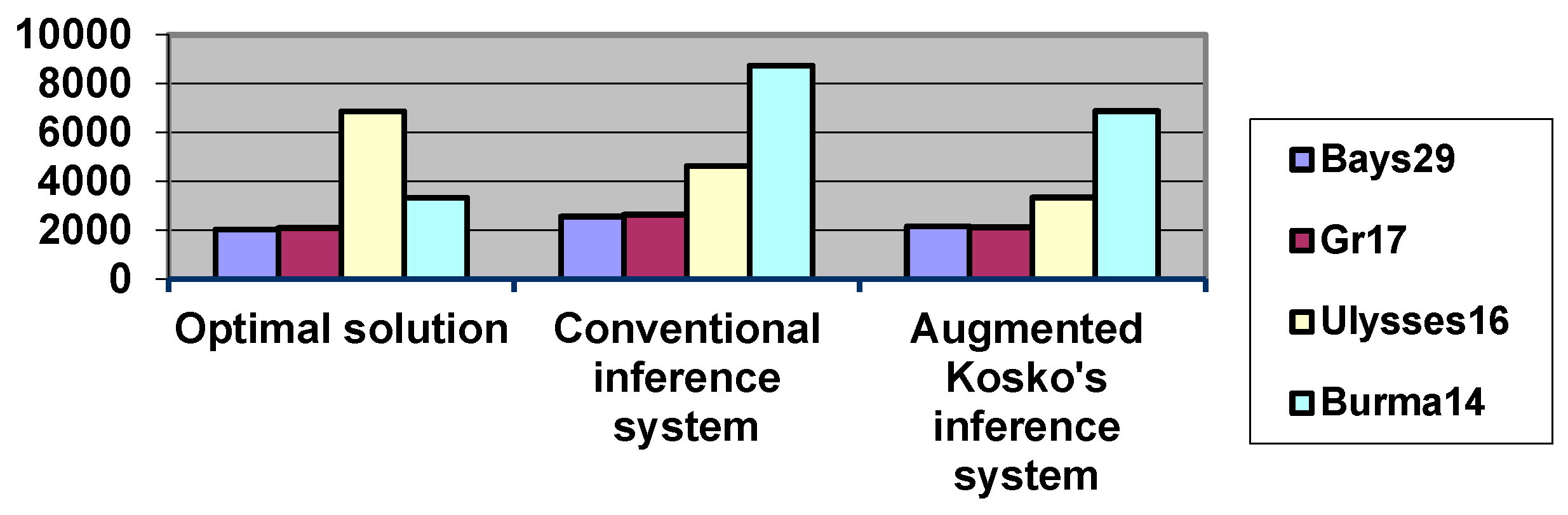
Preprints 95070 g007
Figure 7. Solution comparison of the conventional and augmented inference system.
Figure 7. Solution comparison of the conventional and augmented inference system.
Preprints 95070 g007
Table 1. Matrix of TSP with 5-cities.
Table 1. Matrix of TSP with 5-cities.
S1 S2 S3 S4 S5
S1 0 0 0 1 0
S2 0 0 1 0 0
S3 1 0 0 0 0
S4 0 0 0 0 1
S5 0 1 0 0 0
Table 2. Probability of actions and ψ-learning function Parameters.
Table 2. Probability of actions and ψ-learning function Parameters.
Actioni ℩(ai) ψLearning(si, ai)
ActionDB ℩db Value (B adb)
Value
ActionDE ℩de Value (E ade)
Value
Table 3. Information TSP instances.
Table 3. Information TSP instances.
TSP Lib instance Number of cities Optimal solution
bays29 29 2020
gr17 17 2085
Ulysses16 16 6859
Burma14 14 3323
Table 4. Statistics Comparison.
Table 4. Statistics Comparison.
Instances
 Number of iteration Conventional
Inference System		 Deviation Conventional
Inference System		 Augmented Inference System
Reinf. GRASP method		 Deviation
augmented Inference System Reinf. GRASP method
bays29 250 2560 26.03% 2155 0.29%
gr17 250 2630 23,31% 2109 0,17%
Burma14 250 4624 34.15% 3334 0,33%
Ulysses16 250 8726 27,21% 6873 0,20%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated