Prerpints.org logo
Preprint
Article

Analyzing Extreme Winds over Turkey and Their Relationships with Synoptic Patterns Using Cluster Analysis

Altmetrics

Downloads

140

Views

62

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 December 2023

Posted:

03 January 2024

You are already at the latest version

Alerts
Abstract
Climate research shows that extreme weather events and their effects are increasing in frequency, severity, and impact. Extreme wind events can cause massive societal and economic damage. High wind occurrences and their causes must be identified because they are hard to define and understand. Extreme wind modeling affects wind power plant planning, installation, and building modeling. This applies to city, vegetation, and vegetational area modeling. The scientific literature utilizes statistical, dynamic (Weather Research and Forecasting-WRF), and machine learning methods to identify extreme wind speeds. This study explores the relationship between lower-level extreme wind speeds and upper-level parameters like Z500, and T850 based on cluster analysis. The aim is to explore the correlation between upper-level atmospheric dynamics and lower-level wind behavior. K-Means cluster analysis method was employed to classify Turkish regions with similar severe wind episodes. WRF model simulation findings from NEWA (New European Wind Atlas) project (2019) were used for that purpose. The NEWA project's wind speed data at 100m a.g.l. was used for cluster analysis. We simplify the process by grid point reduction and applying the top 2% percentile as threshold value. Self-Organized Maps (SOM) clustering was also applied using the upper-level variables.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

The assets that modern societies have developed are severely threatened by the strong winds and violent storms of today [1]. Studies on climatology and mid-latitude cyclones have grown in recent years to evaluate severe storms and strong winds. In order to represent this link, global or regional climate models are used. These models attempt to capture the relationship between the frequency and intensity of cyclones and extreme winds. According to research [1,2], severe winds are occurring more frequently in Europe now than they did at the end of the twenty-first century.
Numerous studies have been carried out in the existing body of literature to develop models for climatological variables, including temperature, precipitation, and strong or extreme wind patterns. Most of the scholarly work in the field of study employs statistical methodologies, including but not limited to Extreme Value Theory, Generalized Pareto Distribution (GDP), Annual Maxima, and Peak Over Threshold. In addition, statistical decomposition techniques, such as Principal Component Analysis (PCA) and Empirical Orthogonal Function (EOF), are frequently employed in climatological analyses. Furthermore, in the field of meteorological analysis, clustering methods like Ward's and k-Means, as well as artificial network approaches like Self-Organized Maps are also commonly utilized machine learning methods.
The main objective of all these techniques is to classify data (observations or variables) into defined subgroups with similar attributes. Using meteorological stations or gridded data and considering characteristics like temperature, wind and precipitation, this division can yield equally distributed observations. This aids climate regionalization and understanding regional climate trends. Categorizing data by time intervals, such as hours, days, or months, and numerous elements can also reveal synoptic patterns. This allows weather phenomena and dynamics to be studied. However, an accurate evaluation requires precise data aggregation. So that the aggregation of ensemble members helps assess uncertainty and model performance. As a prerequisite for statistical models to give accurate results, long-term data helps classical statistical models to yields better results. Extreme Value Theory and GPD analysis are proven statistical models utilized in climatological studies [3,4,5,6,7].
Advanced statistical approaches, such as cluster analysis, Principal Components Analysis (PCA), and Empirical Orthogonal Function analysis (EOF), are employed for the purposes of exploring data and reducing dimensionality. Their primary focus lies on comprehending the structure and patterns within large quantities of data, often employed for analyzing severe phenomena such as wind events. Empirical Orthogonal Function analysis (EOF) [8] is an additional statistical approach employed in climate studies. It aims to identify structures within a two-dimensional dataset that account for the greatest amount of variation, like Principal Component Analysis (PCA) [9]. It is also employed to decrease the size of a dataset containing multiple variables into a smaller dataset with fewer variables, hence lowering variance. One dimension reflects the structure to be discovered, whereas the other does not represent its realization size. For instance, when studying spatial structures that vary over time, time is the structure size and space is the sample dimension. EOFs are first-dimensional structures from the analysis. The variability of wind direction statistics for both average and extreme wind occurrences [10], as well as surface wind patterns [11,12], has been evaluated by the application of EOF analysis in several research.
Aside from traditional statistical techniques, clustering method K-means, as well as artificial network approaches like Self-Organized Maps, are commonly employed in the study of meteorological data. Cluster analysis utilizes a similarity matrix to group climatic time-series datasets that have similar characteristics. These categories can be further analyzed in detail to get insight from the shared properties of the datasets in each climatic sub-region group. Cluster analysis in climatology or meteorology aims to establish distinct categories of synoptic types or climate regimes, as well as to identify climatic subregions by grouping stations and/or grid points [13]. The examination of clustering methods is typically categorized into two groups: hierarchical and non-hierarchical procedures.
As a non-hierarchical clustering method, the k-means algorithm is widely acknowledged as a prominent clustering approach and is extensively employed in academic research. Several extensions of the k-means algorithm have been presented in academic literature. The k-means clustering algorithm, developed by Wong and Hartigan in 1979 [14] is a method of vector quantization that facilitates the partitioning of data into a predefined number of clusters. The k-means approach and its extensions, commonly used in unsupervised learning for clustering in pattern recognition and machine learning, are consistently impacted by the initializations of clusters that are predetermined. According to Sinaga and Yang [15], it may be inferred that the k-means algorithm does not fall under the category of unsupervised clustering methodologies. The implementation of the k-means approach is quite straightforward, and it is capable of handling large-scale data collections. The proposed algorithm ensures convergence and exhibits generalizability to clusters of varying forms and sizes, including elliptical clusters.
There exist numerous studies that employ the k-means clustering on wind event analysis due to its simplicity and linear nature. The study conducted by Pena and colleagues examines the correlation between strong wind events and atmospheric circulation patterns in Catalonia through the utilization of k-means clustering [16]. The subject of Bernardino and his friends' discussion was the categorization of synoptic and local-scale wind patterns in a coastal area of the Tyrrhenian Sea (Italy) using the k-means clustering method [17]. Another study implemented the k-means algorithm to cluster the multivariate wind speed data from the 75 Turkish provinces. The clustering was based on monthly mean wind speed data sets [18]. Burlando utilized k-means cluster analysis to evaluate the synoptic-scale surface wind climate patterns in the Mediterranean Sea [19]. The study employed k-means and EOF analysis to evaluate the occurrence of severe windstorms over Europe in both current and future climate conditions [20].
On the other hand, the self-organizing map (SOM) [21] is a categorization technique commonly employed in climate research. Unlike K-means clustering, SOMs can effectively reveal complex and non-linear relationships within high-dimensional data spaces. It utilizes a neural network algorithm and an unsupervised learning approach to discern patterns within datasets. The method generates a two-dimensional array of categories that represent the probability density function of the input data. The array contains a greater number of categories in regions where the data density is higher. The ultimate allocation organizes comparable attributes in proximity, disparate ones at a further distance, and gradual transitional categories in the intervening space [22].
Cavazos employed the SOM technique to uncover significant intra-seasonal changes in the North American monsoon. This is achieved by analyzing various atmospheric variables daily, including 850hPa meridional winds, 700hPa specific humidity, 500hPa geopotential heights, and 850-500hPa thickness [23]. The Self-Organizing Map is employed for the purpose of categorizing the variables of the mid-troposphere, namely the air temperature, geopotential height, and specific humidity at the 700hPa level. This classification is conducted to identify generalized atmospheric patterns. Additionally, the SOM is utilized to recreate the synoptic patterns of climate in the Antarctic region, based on data obtained from ice cores [24]. The classification of meteorological station data using the SOM technique is discussed in another study to evaluate many factors, including temperature, humidity, wind, daylight hours, and solar radiation, among others [25]. In their study, Khedairia and Khadir conducted a classification analysis on meteorological data from the Annaba region, located in the North-East of Algeria. They employed self-organizing map (SOM) and k-means clustering methods for their research [26]. The origin of wind gusts in Australia was investigated using the SOM approach by Spassiani and colleagues, focusing on meteorological factors [27]. In another study, Zhao and colleagues utilized SOM to identify the specific characteristics of large-scale atmospheric circulation patterns that contribute to extreme wind events in Beijing, China during the spring and winter seasons [28]. In a study conducted by Kim et al., the researchers examined the categorization of strong wind events and gusty winds in Korea. They utilized the Self-Organizing Map technique to identify and classify locations with similar wind characteristics [29].
This study aims to present the initial efforts to analyze extreme winds over Turkey using k-means clustering on ground-level and SOM clustering on upper-level, respectively. Accordingly, the study analyzed the association between the clustering results at the lower and upper levels and investigated the impact of upper-level patterns on extreme wind speeds at the lower level. The paper is organized into three main sections, excluding this introductory section. In Section 2, the two data sets are introduced: 100m above ground level for wind speed cluster analysis and a set parameter for upper-level clustering. The data selection criteria are also explained. Valuable insights regarding the wind speed data are given before proceeding to the clustering process. Next, the clustering process at 100m above ground level and synoptic level are described in detail, and cluster validation metrics are discussed. In Section 3, both k-means and SOM clustering results are evaluated in synoptic terms. In Section 4, we conclude with the findings of the study.

2. Materials and Methods

2.1. Data

In this study, two sets of data are utilized to apply the methodology described in the context of this paper: (i) time-series of wind speed at 100m above ground level from 1989 to 2018; (ii) time-series of upper-level variables between 1989 to 2018. Both data sets are employed in cluster analysis purposes at ground-level and upper-level respectively.

2.1.1. Wind Speed Data

The wind speed data is the simulation results obtained from the New European Wind Atlas (NEWA) project. NEWA is a European project aiming to develop a standard for wind energy site assessment. It uses mesoscale simulations and field measurements to estimate extreme winds, crucial for wind turbine design. The atlas focuses on the 10-minute-average wind speed at hub height, known as the 50-year wind, following IEC-61400-1:2005 standards [30]. The objectives of the New European Wind Atlas (NEWA) project are to undertake air flow tests in difficult terrain, establish a model chain for the atlas, and produce a freely accessible wind atlas covering Europe and Turkey. Extreme winds, turbulence, shear, and wind turbine siting characteristics are the key areas of study. Additionally, the research combines large-eddy modeling and computational fluid dynamics (CFD) to better understand flow over complex terrain and aid in the creation of simpler, more effective models [31].
The NEWA project uses WRF model simulations with 3km horizontal resolution, 396x612 grids per 3km, 250m terrain, and 1km altitude data, with 48 daily data for 7 levels which are 50, 75, 100, 150, 200, 250 and 500m. a.g.l. respectively [32]. The dataset, also referred to as NEWA, contains a total of 396x612 grid points as latitudes and longitudes pairs. Every grid point within the dataset contains distinct data variables, such as wind speed, wind direction, temperature, etc., with 30 minutes measurement frequency (total of 48 observations per calendar day). In order to simplify the clustering process, the grid point reduction method was applied to the original data set. The grid point reduction (Figure 1) was conducted in a systematic manner based on the selection criteria as follow:
i , j ⟺ i m o d 6 = 0 ∧ j m o d 6 = 0
For the initial trial, a single grid out of every six was selected, with the beginning point located at coordinates (0,0). A total of 6732 grid points (66x102) were selected and evaluated (Figure 1).
In this study, the extreme wind statistics were defined using the 98th percentile of the data for each grid, considered as the representative percentile for extreme winds. Bierstedt's study [10] investigated the link between average seasonal winds and severe winds in the Baltic Sea region. The climate gridded data sets, coastDat2 and HiResAFF, were employed for the time periods of 1948-2009 and 1850-2009, respectively. Seasonal wind roses are utilized to analyze the dispersion of average and exceptional winds in relation to wind direction. The 98th percentile is chosen to represent the extreme wind speeds in the data sets. It has been shown as the average speed of the data set, both to show the level of representation of the selected data subset and to give general information about wind data at 100m a.g.l. (Figure 2).
The coastal elevation of Turkey, encompassed by seas on three sides, gradually increases to 2,500m as it progresses inland, transforming into valleys, plateaus, and even mountain ranges. The topography of Turkey indicates that wind intensity levels are likely to be higher, particularly in coastal and mountainous regions. The Aegean Sea exhibits more wind intensity compared to adjacent regions. The Aegean Sea is influenced by winter frontal systems originating from the Mediterranean region. The North and South Aegean regions are respectively influenced by the Etesian winds from the northeast and northwest during the summer periods. The average wind speed overview depicted in Figure 2 is in line with the described expected wind flow through Turkey.

2.1.2. Upper-Level Data

The present study, in specifically, makes use of three essential atmospheric variables: geopotential at 500hPa (Z500), temperature at 850hPa (T850), and mean sea level pressure (MSLP), all extracted from daily pressure level records spanning three decades, from 1989 to 2018. These variables have been selected owing to their significance in meteorological and climatological research. In the study of large-scale weather patterns and atmospheric circulation dynamics, geopotential height at 500hPa is a significant marker [16,35]. It provides important insights into mid-tropospheric flow patterns, aiding weather forecasting and understanding climatic anomalies [36]. Temperature at 850hPa, located in the lower troposphere, is a further significant metric that accurately represents the atmosphere's thermal structure. It is instrumental in studying thermal advection, stability, and the evolution of weather systems [37]. MSLP is a key meteorological parameter, providing insight into surface weather patterns and aiding in the prediction of cyclone paths and strength [16].
As a result of the research, the association between lower and upper-level clustering findings was evaluated, as well as the effect of upper-level synoptic patterns on severe wind speeds at lower level (100m a.g.l). The geographical scope of the dataset focuses on a region defined by 5°W to 55°E longitude and 55°N to 25°S latitude, a zone that includes a diverse range of climatic regimes, from the Mediterranean climates in the north to the tropical and equatorial climates towards the south. This choice of region allows for a detailed exploration of atmospheric dynamics across different climatic zones, enhancing the applicability and relevance of the study's findings. The data's spatial resolution is set at 0.25 degrees, balancing between computational feasibility and the required details to capture meteorological features [38]. The ERA5 dataset provides a more precise representation of the atmosphere compared to previous datasets due to its high spatial resolution and extensive temporal coverage. As a result, it serves as a more dependable and accurate foundation for climatic and atmospheric research. [39]. To concentrate on synoptic-scale processes, which are primarily responsible for influencing weather and climate variability, a daily observational frequency of one is selected. [40]. The use of daily data allows for detailed observation and analysis of the changes in large-scale atmospheric variables over time, while keeping the data quantities at a tolerable level for efficient processing and analysis using clustering techniques.

2.2. Cluster Analysis

2.2.1. Clustering Extreme Wind Regimes

K-means clustering is a frequently used unsupervised machine learning approach that aims to partition a dataset into a predefined number of clusters (k) by iteratively minimizing the variation within each cluster [41]. K-means clustering is a simple and efficient method for identifying patterns in large data sets. Furthermore, it is versatile, enabling its use with various data formats. Conversely, the process initiates by randomly choosing a collection of k cluster centroids from the data. In each iteration, the algorithm assigns each data point to the cluster centroid that is closest to it, adopting a distance metric, typically the Euclidean distance. Afterwards, the cluster centroids are adjusted to represent the mean of the data points allocated to each cluster. This process iterates until convergence, at which stage the cluster assignments and centroids no longer experience significant alterations. The k-means algorithm can be briefly described by the following steps:
  • The process of initializing centroids involves selecting k initial centroids from the data, which can be done randomly or by utilizing a more sophisticated initialization technique like k-means++. K-means++ is an enhanced initialization approach for k-means clustering [42] that aims to select more representative beginning cluster centroids, leading to faster convergence and improved clustering outcomes. The method sequentially determines the next centroid by selecting the data point that has the highest distance from the current centroids. By adopting this approach, the initial centroids are dispersed, thereby decreasing the probability of getting caught in local optima.
  • For each data point, calculate its distance to all centroids, and assign the data points to the nearest centroid,
a p = a r g m i n k = 1 , . . , K x p − c k 2
where a p is the cluster assignment for data point x p , c k is the centroid of cluster k , and   . 2 is the squared Euclidian distance.
  • Recompute the centroid of each cluster as the mean of the data points assigned to that cluster,
c k = 1 S k ∑ p ϵ S k x p
where c k is the updated centroid of cluster k , X p is the set of data points assigned to cluster k , and S k is the number of data points in cluster k .
  • Repeat steps 2 and 3 until the centroids converge, so that positions do not change significantly between iterations. The K-means algorithm seeks to minimize the objective function, which is the sum of squared distances between each data point and its nearest centroid. The goal of the algorithm is to minimize the within-cluster sum of squares (WCSS),
W C C S = ∑ i = 1 k ∑ x ∈ C i x − μ i
where k is the number of clusters and μ i is the mean for cluster C i .
The k-means clustering approach was used for cluster analysis of wind speed data at a height of 100m above ground level. The first stage of the cluster analysis involves a thorough data transformation process. The data was arranged in a grid pattern of 66x102, with 10531 observations at each grid point. Each grid point was determined by latitude and longitude pairs. The data captures the highest 2% (98th percentile) of wind speed data at each location. Therefore, due to the absence of temporal alignment across grids, the dataset structure emphasizes spatial characteristics rather than temporal dynamics. The transformation procedure involves transforming the high-dimensional data into a two-dimensional matrix. In this matrix, each row represents a grid point, and each column corresponds to one of the 10531 wind speed observations at that place. Highlighted throughout studies on the analysis of high-dimensional spatial data [43], this stage is essential for the successful implementation of the k-means method. Before applying the K-means algorithm, it is crucial to normalize the dataset. Since K-means clustering is affected by the magnitude of the data, normalization ensures that the algorithm performs at its optimal level by assigning equal importance to all characteristics. This is accomplished using conventional techniques such as Min-Max scaling [44]. The significance of this stage is emphasized in clustering research, where the magnitude of characteristics greatly influences the clustering result [45].
Determining the optimal number of clusters is a critical step in clustering approaches. In order to achieve this goal, we employ the Elbow test to determine the optimal number of clusters. The Elbow approach entails assessing the number of clusters (K) within the range of 1 to 10. WCSS, also known as Within-Cluster Sum of Squares, represents the cumulative sum of the squared distances between every site and the centroid of the cluster. The Within-Cluster Sum of Squares (WCSS) plot exhibits a form that resembles an elbow when plotted against the K value. As the number of clusters rises, the WCSS value drops. To analyze the wind data, two metrics were computer: the overall variance explained by the number of clusters (Figure 3a) and the within-cluster sum of squares (WCSS) by the number of clusters (Figure 3b). Moreover, several clustering experiments were conducted by utilizing different numbers of optimum clusters. While the difference between 6 and 7 clusters was not significant in terms of their values, it may be argued that the clustering analysis with 6 clusters provides a more accurate representation when considering the synoptic domain.
A set of different centroid initialization techniques has been applied in the scope of this study such as changing initial seed, random centroid initialization, and k-means++ initialization method. The empirical results have showed that the k-means clustering with k-means++initialization method yield the better clustering results when it is compared to the Turkey’s wind regime.

2.2.2. Upper-Level Clustering

Self-organizing maps (SOMs) have been widely discussed and utilized in several synoptic climatology studies. Self-Organizing Maps (SOMs), developed by Teuvo Kohonen in the 1980s, are an unsupervised learning approach utilized for clustering, visualization, and reducing dimensionality. A self-organizing map (SOM) primarily functions by transforming input data with several dimensions into a lower-dimensional representation, usually two-dimensional, while maintaining the topological characteristics of the original input space [46]. This approach involves the organization of a network of neurons, where each neuron is connected to a weight vector that has the same dimensions as the input data. During the training process, the algorithm consistently modifies these weights to precisely reflect the fundamental patterns in the data. In the self-organizing map (SOM), the preprocessing phase is crucial for optimizing clustering efficiency and often involves normalizing or standardizing input features. This ensures that attributes with larger numerical ranges do not significantly influence the generation of the map [47]. Furthermore, by reducing the number of dimensions in the input data, principal component analysis (PCA) can be used to increase the computing efficiency of the self-organizing map (SOM) algorithm [48].
Another component of SOM clustering involves defining the dimension of the SOM. A larger self-organizing map (SOM) with more neurons offers an improved resolution, allowing for the identification of a greater number of distinctions within the data. Consequently, the utilization of complex patterns and connections within the data becomes possible, which is particularly advantageous when dealing with vast datasets characterized by intricate structures. However, bigger maps require more processing resources and longer training time. Furthermore, overfitting can occur when the dimensions of the map are exceedingly large when compared to the complexity and scale of the information. Conversely, a compact self-organizing map (SOM) provides a broader viewpoint of the data, condensing comprehensive patterns and correlations. While this strategy may be computationally efficient and offer useful insights into the data, it may fail to consider complex aspects and subtle differences included in the information.
During the training phase, each input vector is compared to all neuron weights, and the neuron with the weight vector that is most similar to the input (referred to as the Best Matching Unit, BMU) is identified. The weights of the Best Matching Unit (BMU) and its neighboring neurons are subsequently adjusted to better match the input vector. The correction is performed using a learning rate and a neighborhood function, often following a Gaussian distribution. This technique is iterated multiple times. The weight adjustment can be mathematically expressed using the equation:
w v t + 1 = w v t + θ u , v , t · α t · x t − w v t
where w v t is the weight vector of neuron v at time t , θ u , v , t is the neighborhood function centered around the BMU u , α t is the learning rate, and x t is the input vector. A self-organizing map describes this cyclical process. The SOM nodes' output weight vectors are transformed back into their original data patterns.
The dimensions of the SOM are a critical factor in its design and have a direct influence on its ability to effectively represent the incoming data. The size and configuration of a self-organizing map (SOM) determine the level of granularity at which the input data is organized and presented. The optimal size of a self-organizing map (SOM) is often determined by empirical analysis, considering the requirements of the application and the properties of the data. Heuristic approaches, cross-validation, and the use of topography and quantization error-based criteria are among the strategies employed to determine the size. [49].
A four-phased approach has been followed for upper level cluster analysis with SOM: (i) revealing the seasons with most occurrence of extreme wind events at the ground level data set (NEWA); (ii) filtering out the seasons from upper level dataset where the vast majority of the extreme wind events occurred and form a reduced dataset for it; (iii) running EOF and PCA analysis for all three variables independently prior to SOM clustering; (iv) executing SOM cluster analysis using the extracted PCs.
First, to calculate the events within each month, the 98th percentile data was sorted by month. These results were presented as percentages (Figure 4). With a percentage of 40.5 throughout the entire data set, the winter season was found to be the windiest season in this dataset based on the findings of these counts. In the data set, the second windiest season was spring (30.25%), followed by autumn (15.7%) and summer (13.3%).
The winter subtropical high-pressure systems in the Northern Hemisphere are centered over the oceans because of the spatial expansion and strengthening of the thermic high-pressures in Siberia and North America (Canadian/Greenland). These high-pressure systems exhibit a regional weakening because of strong cooling in large continental areas in the north. However, dynamic semicontinuous and cold low-pressure systems about 60 degrees north latitude in the North Atlantic (Iceland) and North Pacific (Aleutian) successfully extend their influence on general flows over ocean between the southern 30–35 degrees north latitudes. These systems are located on the North Pacific and North Atlantic. Because of this, there is a high likelihood of intense precipitation and storms occurring over regions where these pressure systems are effective [50].
The upper-level variables were filtered so that the winter days for 30-years period were included in the final data set. The final dimensions for the reduced data set for each variable is 2707x121x201, where 2707 is the number of days within the selected period, and 121x201 is the total number of grid points for the selected region. The final data set has temporal alignment, so that each row corresponds to a row (2707 samples) and each column (grid point) corresponds to a feature (24321 features). Unit transformations has been also applied to obtain the actual values for each variable. Data normalization or standardization is a common preprocessing step for SOM that guarantees scale homogeneity [51]. Methods such as Z-score normalization or Min-Max scaling can be incorporated into this procedure. In order to normalize the input, Min-Max scaling has been applied to the reshaped dataset. Prior to SOM clustering, the EOF analysis was applied to the mix-max normalized datasets separately for dimensional reduction purposes. As EOF per variable is applied independently, the aim is to avoid the potential issue of one variable's magnitude dominating the combined EOF analysis due to differences in units or variability. The threshold for cumulative variance for the mean sea-level pressure, geopotential height, and temperature is set to 90%, 90% and 85% respectively. Based on the EOF analysis 8, 8, and 9 PCs have been determined as the optimal number of PCs that explained the desired level of cumulative variance as 91.19%, 91.54%, and 86% per upper-level variable, mean sea-level pressure, geopotential height, and temperature respectively (Figure 5).
Next, the SOM cluster analysis method was used for our upper-level clustering experiments. For clustering, the PCs from each dataset were extracted and a reduced data containing PCs from each dataset were built. The final upper-level dataset has time-series dimensions of 121 (number of latitude points), 201 (number of longitude points), and 25 PCs. Data reorganization and normalization process was applied to all three PC datasets. Since SOM clustering requires two-dimensional input, so that the data was reorganized into two-dimensional array of 2707x25, where each row represents the grid points for the selected region, and columns represents the data time-series for that specific grid point.
In terms of SOM structure, determining the optimal dimensions of a Self-Organizing Map (SOM) is of utmost importance for achieving optimal performance and comprehensibility. An excessively large map can result in overfitting, whereas an excessively small map may overlook crucial data structures [49]. An often-used method for determining the size is the heuristic formula M = N 5 , where M is the number of neurons and N represents the length of data time-series per grid point. Alternative approaches include employing cross-validation techniques or utilizing rule-of-thumb principles dependent on the complexity of the dataset [51]. However, at this stage of the study, the SOM dimensions were determined empirically and the SOM structures in different dimensions were examined. Experimental results showed that a SOM structure of 3x3 was more representative. The following parameters were set for clustering for each data set: learning rate as 0.5, the neighborhood function as Gaussian, the radius of the neighborhood function as 0.5, and the activation distance as Euclidian distance. The training process was performed using random vector selection, instead of sequential pick-up strategy.
Consequently, the SOM algorithm mapped the high-dimensional upper-level data into a 3x3 grid structure, so called SOM nodes. Each some node was associated with separate set of days which represented a distinct atmospheric condition. As a subsequent analysis, the set of days for each SOM node was identified and the frequency of extreme wind events were calculated on the NEWA dataset for the given days for each NEWA grid point. The frequency analysis was also examined to reveal the correlation between the atmospheric conditions represented by each SOM node and the occurrence of extreme wind events. This correlation was depicted through a contour graph, illustrating the distribution and frequency of these events along with each cluster. The aim was to extract and to highlight the upper atmospheric patterns that are likely to lead to extreme wind conditions.

3. Results

3.1. Extreme Wind Regimes over Turkey

Turkey features a coastal region with an elevation of 0 meters, encompassed by seas to the north, west, and south. However, its inland areas are characterized by plateaus, which exhibit altitudes of 1000 meters and higher. The mountain ranges in Turkey, specifically the Northern Anatolian Mountains in the north and the Taurus Mountains in the south, extend in a west-to-east direction. These mountainous regions have elevations ranging from 2000m to 2500m. The mountain ranges situated in the western region of the area extend in a northwest to southeast direction. Additionally, the elevations of the mountains and plateaus located in the eastern part of the region exceed 2500 meters. The presence of rows of bays and coves along the Aegean coast results in a channeling effect that influences the intensity of wind. This impact causes strong wind flow to spread towards the inner Aegean region along these bays. When analyzing wind intensity in Turkey, it is seen that elevated wind intensity levels are anticipated, particularly in coastal areas and mountainous regions, according to the country's topographical characteristics. The wind intensity in the Aegean Sea is notably higher in comparison to its neighboring areas. During the winter season, the frontal systems associated with the low-pressure system located in the vicinity of the Mediterranean region exert an influence on the Aegean Sea. The North Aegean region is influenced by the northeastern Etesian winds throughout the summer season, whereas the South Aegean region is affected by the northwest Etesian winds [52].
The k-means clustering successfully characterized the wind dispersion patterns in the Aegean Region, considering the influence of the terrain. Nevertheless, the impact of the Black Sea and Mediterranean Region Mountain ranges on Central Anatolia was adequately represented by the k-means clustering algorithm with 6-cluster test (Figure 6a). Also, the average values of all clusters were illustrated in Figure 6b. The resulting graph was used to highlight the cluster grid points in terms of contour plots.
The experiments conducted for upper-level cluster analysis were examined with a different approach. EOF results are used to identify the primary patterns of variability in upper-level data, especially in the identification of synoptic patterns. Geopotential height, a measure of the actual height of a pressure level in the atmosphere, is essential for comprehending synoptic weather patterns. An EOF examination of GPH (Geopotential Height) at 500hPa level may identify prevailing wave patterns, such as ridges and troughs, which govern the movement of weather systems [53]. Following EOFs modes could show secondary patterns, such as localized weather occurrences or smaller-scale characteristics. Less dominant but still significant patterns, such as a cutoff low, which can be associated with strong winds and stormy conditions can be detected via third EOF mode. Furthermore, mean sea level pressure (MSLP), a crucial factor in surface meteorological conditions, displays influence over wind patterns, storm courses, and frontal systems [54]. The first Empirical EOF mode often aligns with the principal synoptic pattern, including factors such as the location and intensity of high and low-pressure systems. Successive EOF modes might potentially detect additional characteristics, such as frontal systems, pressure gradients, or localized pressure anomalies. More localized pressure anomalies that drive mesoscale wind events, which can be particularly extreme, can be captured by third EOF mode. In addition, EOF analysis can detect significant temperature anomaly patterns linked to occurrences like heatwaves, cold spells, or the location of air masses in the temperature study [55]. The initial EOF mode can uncover large-scale temperature variations, such as the distribution of warm and cold air masses or the existence of temperature anomalies. Sequential EOF modes have the potential to capture smaller-scale temperature fluctuations, such as boundaries between air masses or differences in temperature inside specific areas.
The negative phase of an EOF pattern refers to a period during which the spatial pattern is in opposition to the average or mean state of the dataset. This indicates the presence of a negative anomaly or a spatial structure that deviates from the usual pattern. This phase is linked to a distinct spatial structure or characteristic that diverges from the typical pattern. In contrast, the positive phase occurs when the spatial pattern closely resembles or is enhanced compared to the average or mean condition, indicating a positive anomaly or a more prominent spatial structure. This aids in comprehending the temporal and spatial characteristics of distinct patterns and their influence on the overall variability of the dataset. EOF patterns' negative and positive phases are frequently utilized for the analysis of climate or meteorological phenomena's temporal progression.
The first EOFs of each synoptic variable explain the largest fraction of the variance in the dataset. The three leading EOFs of the data, as shown in Figure 7, account for 70.5%, 63.95%, and 58.94% of the total variance for the MSLP, Z500, and T850 variables, respectively. In Figure 7, the initial empirical orthogonal functions (EOFs) of GPH and T, which collectively account for 27% of the variance, along with the first EOF of MSLP, which accounts for 35% of the variance, are likely the most significant synoptic-scale patterns for the region. The majority of the EOF1 MSLP visuals exhibit negative anomalies, which are consistently observed across the whole region encompassing Turkey, the Mediterranean, and western Italy. Positive anomalies can also be seen in the basin of the Caspian Sea to the north and in the Gulf of Basra to the encompassing Turkey, the Mediterranean, and western Italy. The EOF1 GPH exhibits a pronounced gradient in Turkey, which arises from a positive anomaly in the East Anatolia region and negative anomalies in southern Europe and northern Africa. This scenario depicts strong winds, particularly in the western areas. In Turkey, the EOF1 T exhibits a prominent positive anomaly at its center, whereas a negative anomaly is detected in West Africa and northern Russia.
The second EOFs, which consist of 24% GPH, 19% MSLP, and 21% T, represent secondary yet significant patterns. The EOF2 MSLP exhibits pronounced gradients in Turkey, with a negative anomaly in northern and northwestern Europe and a positive
anomaly in Arabia. In the EOF2 GPH, Italy and Greece exhibit a negative anomaly center, while northeastern Europe shows a positive anomaly. Turkey is located within a pronounced gradient that originates from the west. A significant temperature gradient is developing over Turkey in EOF2 T as a result of the favorable impact of the positive anomaly in Russia, coupled with negative anomalies in the central Mediterranean and northern Africa. These variations may be attributed to the irregularities in the placement of the ridges and troughs (GPH), the distinct pressure centers (MSLP), and the related thermal gradients (T). The interaction of these patterns can result in fluctuations in both the speed and direction of wind, which can give rise to rare cases of extreme wind events.
The third Empirical Orthogonal Functions (EOFs), which consist of geopotential height (GPH) with a weight of 12%, mean sea level pressure (MSLP) with a weight of 17%, and temperature (T) with a weight of 11%, are most likely to represent the less persistent, more localized, or transitional characteristics of the atmospheric state. These could suggest brief yet powerful weather phenomena, such as low-level lows (GPH), temporary pressure anomalies (MSLP), and localized temperature fluctuations (T), which can cause catastrophic wind events. These characteristics are especially important for the occurrence of localized extreme wind occurrences, which could be linked to certain atmospheric disturbances. The EOF3 MSLP is seen to have a strong gradient in Turkey, which has been caused by a negative anomaly in Eastern Europe and Russia and a positive anomaly effect in Africa. Similarly, there seems to be a pronounced gradient in EOF3 GPH along the west-east axis across Turkey.
In synoptic climatology, EOFs decompose a dataset into orthogonal (independent) modes of variability, which helps in understanding the spatial patterns and their temporal evolution. However, SOMs are considered as a complementary tool to classify large-scale atmospheric patterns, like those represented by the selected PCs from EOF analysis. The self-organizing map (SOM) arranges many synoptic scenarios into a grid, such as a 3x3 grid in our empirical setup. Each node in the grid indicates either a typical pattern or a group of similar patterns. The utilization of this grid arrangement enables a straightforward and precise representation and examination of intricate atmospheric dynamics. EOFs/PCs and SOMs together offer a potent toolkit for recognizing, categorizing, and displaying atmospheric patterns in synoptic climatology. EOFs provide a linear and orthogonal breakdown of the data, but SOMs offer a non-linear and more adaptable approach to classify and analyze the data. Self-organizing maps (SOMs) can capture intricate and nuanced correlations in the data, beyond the limitations of empirical orthogonal functions (EOFs) which impose orthogonality constraints on the patterns. The Principal Components (PCs) generated from the EOF analysis are used as input for the Self-Organizing Map (SOM). This ensures that the SOM training is concentrated on the most important patterns of variability discovered by the EOF analysis. So that SOM helps in interpreting large-scale drivers of local climate variability and is a part of statistical downscaling methodologies [56].
Once the SOM cluster analysis was completed, the days that belong to each SOM node, referred as SOM neurons, were extracted. Each SOM node was visualized based on the mean geopotential height and mean sea-level pressure as contour plots together (Figure 8). A comprehensive analysis was conducted to see how these nodes may accurately represent the cumulative variability observed in the EOFs. This section primarily examines how the SOM nodes can exhibit different synoptic-scale characteristics that may impact extreme surface winds.
  • SOM Node (C1): SOM node C1 (Figure 8a) indicates the low-pressure area in southern part of Italy and northern Africa. This low-pressure area is affecting the western region of Turkey, while a thermal-forming high-pressure system above central Georgia, such as the Siberian Highland, is affecting the northern region of Turkey, particularly inner Anatolia, the central and eastern Black Sea region, and the Eastern Anatolian region. These areas experience intense gradients, leading to strong winds. The Low-Pressure Area over the Mediterranean generates powerful winds to the west of Turkey, with the central region of high pressure originating from colder air masses. The combination of these systems results in strong winds on some days.
  • SOM Node (C2): Similar to the C1 pattern, Africa experiences a region of low atmospheric pressure, whereas the northeast of Turkey has an area of high atmospheric pressure. Furthermore, an area of high atmospheric pressure is detected in the eastern region of the Caspian Sea, while a region of low atmospheric pressure is discovered in the northwest. Additionally, there is another high-pressure area in northern Central Europe. As a result of the impact of these pressure fields, Turkey experiences a significant pressure gradient effect. When examining the broader GPH area, there is a more pronounced variation in the southern parts. The presence of steep gradients contributes significantly to the occurrence of frequent and intense windy conditions in the western parts of Turkey, spanning from the northwest to the southwest. No direct effect can be identified for isotherm areas (Figure 8b).
  • SOM Node (C3): This pattern mainly focuses on the northeastern region of Europe, where a cyclone is impacting the Black Sea and extending its influence across Turkey. Additionally, an anti-cyclone is exerting its impacts on Greece and the Mediterranean. The occurrence of winds on the Thrace can be attributed to the presence of pressure gradient zones. When looking at the geopotential height values, the effects of the ridge area of large-scale waves can be observed. Although these patterns and the periods when extremely windy days occur can be explained for the Thrace region, they cannot be fully explained for the whole of Turkey. It is thought that it can be explained by more local scale events. (Figure 8c).
  • SOM Node (C4): During the period when this pattern is effective, there is a low-pressure center located over the Black Sea, and it is observed that the high-pressure center shifts towards the west of North Africa. Additionally, there is a high-pressure area in the East. A pattern that is effective all over Turkey is observed with the influence of strong temperature gradients. This pattern, depending on the frontal activity, has an increasing effect on days with strong winds throughout Turkey. The geopotential height field does not seem to have much effect on this pattern because it represents a large-scale pattern. It can be seen here that during the winter months when high winds occur on Turkey, events on a synoptic scale rather than a broad scale have a greater impact. Strong gradients are seen in this pattern. (Figure 9a).
  • SOM Node (C5): In this pattern, the southwestern parts of Turkey, Central Anatolia and the western Black Sea region are under the general influence of the anticyclone (Azores Anticyclone) over central Italy and northern Africa. The northeastern parts are under the general influence of a cyclonic area. Accordingly, a strong gradient area has been detected in both the Black Sea and Southeastern Anatolia regions, which explains the strong winds. It has been observed that events on a synoptic scale have a greater impact. In addition, it has been determined that the cyclones formed over the Black Sea and the frontal patterns that develop regarding it increase the days of strong winds in this region. (Figure 9b).
  • SOM Node (C6): A pattern is observed in which the Azores high pressure area expands over the Mediterranean and reaches over Turkey. In northeastern Asia, there is a strong gradient area where a low-pressure pattern is formed. These patterns may explain the high wind days in the northeast and west. However, the high wind days in the south cannot be explained by this pattern. (Figure 9c).
  • SOM Node (C7): Due to the interaction of short and long waves on the wave pattern at the upper levels of the atmosphere, it is seen that, unlike other patterns, a short-wave trough is formed at the upper level. This trough affects the western regions through Greece. Turkey is generally under the influence of high pressure and the number of strong windy days is not high. Extremely windy days occurred off the coast of Cyprus due to the high-pressure gradient. The wave interaction that occurred over Syria at ground level appears to be more effective in this pattern. (Figure 10a).
  • SOM Node (C8): In this pattern, the general effect of a high-pressure area is seen, which is effective over all of Turkey, except the Mediterranean, and whose center extends to the north-east of Central Anatolia. The temperature field created a strong gradient only over the Black Sea. There is a low-pressure area over the northeast. In this pattern, Turkey is under the influence of a low-pressure area whose center is over northeastern Europe and expanding over the Black Sea, and a high-pressure area
whose center originates from the Atlantic Ocean but also forms a center over Turkey. This caused the strong gradient and high wind days to occur only over the central and eastern Black Sea. There is also a pressure gradient from the Eastern Anatolia region. (Figure 10b).
  • SOM Node (C9): In this pattern, there is a low-pressure area centered on the western and central Mediterranean and affecting the western and southwestern regions of Turkey, and a low-pressure area in the northeast that originates over Siberia and the Caspian Sea and extends its effect to the northeastern part of Turkey. In addition to the strong gradients formed in the low-pressure area, strong gradients also formed in the isotherm areas. However, strong gradients are also observed in the geopotential height field. In this pattern, strong isobar, isotherm, and geopotential high gradients are seen together over Turkey. Thus, it characterizes very well the days with the strongest winds in Turkey. (Figure 10c).
The significant pressure differentials appear to create regions of strong winds throughout Turkey. The occurrence of low-pressure and high-pressure areas, namely in the Mediterranean and the Black Sea, coupled with the corresponding frontal systems, greatly impact the frequency of days marked by extreme winds. Furthermore, the Low-Pressure Centre, primarily located over the Black Sea, exerts a significant impact on wind intensification due to its frontal effect in the area. Lastly, the Azores and Siberia, places known for their high-pressure systems, play a significant role in creating substantial gradients over Turkey. These gradients are essential for the development of extreme winds. To summarize, it has been observed that most of the SOM nodes were representative enough to identify the common pressure systems which are effective throughout the Turkey during the winter period. Moreover, the vast majority of the extreme wind events were explained by the SOM nodes.
Another key point of this work is to figure out the correlation between SOM nodes and the clustering outcomes at the lower-level, which is crucial in describing extreme wind events at lower-level. Within this framework, a basic set of statistical data that includes the event days for each SOM node and the outcomes of clustering at a lower level was extracted. For this analysis, the k-means cluster with the highest mean speed was chosen. The rationale behind this decision assumed that the cluster exhibiting the highest average speed (lying within the range of strong storms according to the Beaufort wind scale) would have the highest correlation with SOM patterns. Based on the k-means clustering results, the mean wind speed of the grid points within the cluster aligns with this definition (mean wind speed > 22). The grid locations and extreme wind days are derived from data collected at 100m a.g.l. The chosen grid points are mostly located in elevated regions of Turkey and the Crete Island region (Figure 11).
In the next step, the total event-day count data of each SOM node and the lower-level cluster grid points data corresponding to these days were extracted. At this stage, two different statistical data were obtained: lower-level days count per grid point matching the node days for all SOM nodes, and the average wind speed per grid point for the matching per SOM node days. To extract the correlation between the days in the SOM nodes and event-days in lower-level cluster, the mean of event-days for all grid points was calculated and the calculated mean value is divided by the total event-day count per SOM node to extract the coverage in terms of percentage (Mean Event-Day Percentage). Lastly, Mean Wind Speed was calculated for all grid points for the matching SOM node days. Statistical data (Table 1) reveals the fact that the SOM node patterns extracted using wintertime period has shown similarities with the all-time k-means clustering results.

4. Conclusions

In this study, the relationship between the ground level wind speeds and the upper-level parameters were investigated. The main objective was to accurately characterize the extreme wind conditions in Turkey and examine their correlation with synoptic patterns. Cluster analysis techniques were employed to identify the correlation between them.
Two distinct atmospheric levels—the upper level and the ground level—were considered during the calculations. The lower-level data used in the first section of the analysis was taken from the NEWA data set, which includes 48 samples daily at 6732 grid points over a 30-year period at 100m. The 98th percentile of the data was obtained for each grid point, and these extracted values were considered as the extreme values for that each grid point. The k-means clustering algorithm was utilized to classify the given data sets. After doing a k-means clustering analysis, 6-clusters were identified. It was discovered that the clustering results matches the widespread presence of high or strong winds throughout Turkey. Moreover, the analysis of the data set revealed that the winter season in the study area exhibits the most frequent occurrences of windy conditions characterized by high wind velocities.
The second phase of the study consisted of using upper-level data sets to investigate synoptic patterns. The analysis was performed using the mean sea level pressure, geopotential at 500hPa, and temperature at 850hPa data sets. The data source for this analysis was the ERA5 Reanalysis data, covering DJF of a 30-year period. The EOF technique was individually applied to the data sets to reduce their dimensionality while preserving the variance. The Self-Organizing Map (SOM) technique was implemented on the MSLP, T850, and Z500 datasets, which were obtained from the EOF results. A total of nine self-organizing map (SOM) nodes were generated, following a structured grid arrangement with dimensions of 3x3. Each node is assigned a unique set of days for a given atmospheric state. As a follow-up study, the days for each SOM node are identified, and the NEWA dataset is used to calculate extreme wind event frequency for each NEWA grid point. Frequency analysis reveals the association between SOM node climate conditions and extreme wind events. It has been found that some SOM clusters effectively represent the known patterns of the research region. However, several clusters within the SOM did not accurately depict the expected trends during the DJF period.
In addition, significant pressure differentials seem to produce extreme wind zones across Turkey during the DJF period. The presence of low-pressure and high-pressure zones, namely in the Mediterranean and the Black Sea, along with the associated frontal systems, significantly influences the frequency of days characterized by extreme winds. Moreover, the Low-Pressure Center, predominantly situated above the Black Sea, exerts a substantial influence on the strengthening of winds as a result of its frontal effect in the region. Finally, the Azores and Siberia, renowned for their high-pressure systems, have a considerable impact on the formation of huge gradients over Turkey. These gradients are crucial for the formation of extreme winds over Turkey.
In conclusion, this study also examined the correlation between the k-means and SOM clustering results. In the scope of this analysis, the relevant statistics were extracted using both clustering outcomes in terms of event-day counts at both levels and mean wind speed at lower-levels. Even SOM clustering efforts were focused on the winter period, the SOM results show similarities with the all-time k-means clustering results in terms of lower-level extreme wind events.

Author Contributions

Conceptualization, U.G.B.G. and Ş.S.M..; methodology, U.G.B.G.; software, U.G.B.G..; writing—original draft preparation, U.G.B.G.; writing—review and editing, Ş.S.M; visualization, U.G.B.G.; All authors have read and agreed to the published version of the manuscript.”

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data used for upper-level cluster analysis is provided by the ERA-5 reanalysis dataset with 0.25° from https://cds.climate.copernicus.eu/ (accessed on 26 November 2023).

Acknowledgments

Data pre-processing and analysis in this study are performed on the workstation with the four processors of Intel Xeon E5-4620 v2 2.6 GHz in the faculty of Aeronautics and Astronautics at Istanbul Technical University. Hersbach, H. et al., (2023) was downloaded from the Copernicus Climate Change Service (C3S) (2023). The results contain modified Copernicus Climate Change Service information 2020. Neither the European Commission nor ECMWF is responsible for any use that may be made of the Copernicus information or data it contains. Acknowledgment is due to Onur Görgün, Ph.D. for his support throughout this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kunz, M.; Mohr, S.; Rauthe, M.; Lux, R.; Kottmeier, C. Assessment of extreme wind speeds from regional climate models – Part 1: Estimation of return values and their evaluation. Nat. Hazards Earth Syst. Sci. 2010, 10, 907–922. [Google Scholar] [CrossRef]
  2. Ulbrich, U.; Leckebusch, G.C.; Pinto, J.G. Extra-tropical cyclones in the present and future climate: A review. Theor. Appl. Climatol. 2009, 96, 117–131. [Google Scholar] [CrossRef]
  3. Palutikof, J.P.; Brabson, B.B.; Lister, D.H.; Adcock, S.T. A review of methods to calculate extreme wind speeds. Meteorol. Appl. 1999, 6, 119–132. [Google Scholar] [CrossRef]
  4. Gong, X.; Richman, M.B. On the application of cluster analysis to growing season precipitation data in North America East of the Rockies. J. Climate 1995, 8, 897–931. [Google Scholar] [CrossRef]
  5. Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 4th ed.; Elsevier: Amsterdam, Netherlands, 2019. [Google Scholar] [CrossRef]
  6. Zhang, Z.; Li, J. Big Data Mining for Climate Change. Elsevier, Amsterdam, Netherlands, 2020. [CrossRef]
  7. Pampuch, L. A.; Negri, R. G.; Loikith, P. C.; Bortolozo, C. A. A review on clustering methods for climatology analysis and its application over South America. Int. J. Geosci. 2023, 14, 877–894. [Google Scholar] [CrossRef]
  8. Lorenz, E. N. Empirical orthogonal functions and statistical weather prediction. Scientific Rep. 1, Statistical Forecasting Project, Massachusetts Institute of Technology Defense Document Center, 1956.
  9. Ünal, Y.S.; Tan, E.; Menteş, Ş.S. Summer heat waves over western Turkey between 1965 and 2006. Theor. Appl. Climatol. 2012, 112, 339–350. [Google Scholar] [CrossRef]
  10. Bierstedt, S.E.; Hünicke, B.; Zorita, E. Variability of wind direction statistics of mean and extreme wind events over the Baltic Sea region. Tellus A: Tellus A Dyn. Meteorol. Oceanogr. 2015, 67, 29073. [Google Scholar] [CrossRef]
  11. Ludwig, F.L.; Horel, J.; Whiteman, C.D. Using EOF Analysis to Identify Important Surface Wind Patterns in Mountain Valleys. Journal of Applied Meteorology 2004, 43, 969–983. [Google Scholar] [CrossRef]
  12. Farjami, H.; Hesari, A. R. E. Assessment of sea surface wind field pattern over the Caspian Sea using eof analysis. Reg. Stud. Mar. Sci. 2020, 35, 101254. [Google Scholar] [CrossRef]
  13. Türkeş, M.; Tatlı, H. Use of the spectral clustering to determine coherent precipitation regions in Turkey for the period 1929–2007. Int. J. Climatol. 2010, 31, 2055–2067. [Google Scholar] [CrossRef]
  14. Hartigan, J.A.; Wong, M.A. A k-means clustering algorithm. Journal of the Royal Statistical Society 1979, 100–108. [Google Scholar] [CrossRef]
  15. Sinaga, K.P.; Yang, M.-S. Unsupervised k-means clustering algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
  16. Peña, J. C.; Aran, M.; Cunillera, J.; Amaro, J. Atmospheric circulation patterns associated with strong wind events in Catalonia. Nat. Hazards Earth Syst. Sci. 2011, 11, 145–155. [Google Scholar] [CrossRef]
  17. Di Bernardino, A.; Iannarelli, A. M.; Casadio, S.; Pisacane, G.; Mevi, G.; Cacciani, M. Classification of synoptic and local-scale wind patterns using k-means clustering in a Tyrrhenian coastal area (Italy). Meteorol. Atmos. Phys. 2022, 134. [Google Scholar] [CrossRef]
  18. Yeşilbudak, M. Clustering analysis of multidimensional wind speed data using k-means approach. In Proceedings of the 5th International Conference on Renewable Energy and Applications, Birmingham, UK, 20-23 Nov 2016; pp. 961–965. [Google Scholar] [CrossRef]
  19. Burlando, M. The synoptic-scale surface wind climate regimes of the Mediterranean Sea according to the cluster Analysis of ERA-40 wind fields. Theor. Appl. Climatol. 2008, 96, 69–83. [Google Scholar] [CrossRef]
  20. Leckebusch, G. C.; Weimer, A.; Pinto, J. G.; Reyers, M.; Speth, P. Extreme wind storms over Europe in present and future climate: A cluster analysis approach. Meteorol. Z. 2008, 17, 67–82. [Google Scholar] [CrossRef]
  21. Kohonen, T. Self-Organizing Maps; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar] [CrossRef]
  22. Cassano, E.; Lynch, A.; Cassano, J.; Koslow, M. Classification of synoptic patterns in the western Arctic associated with extreme events at Barrow, Alaska, USA. Clim. Res. 2006, 30, 83–97. [Google Scholar] [CrossRef]
  23. Cavazos, T.; Comrie, A.C.; Liverman, D.M. Intraseasonal variability associated with wet monsoons in southeast Arizona. J. Climate 2002, 15, 2477–2490. [Google Scholar] [CrossRef]
  24. Reusch, D.B.; Alley, R.B.; Hewitson, B.C. Relative performance of self-organizing maps and principal component analysis in pattern extraction from synthetic climatological data. Polar Geogr. 2005, 29, 188–212. [Google Scholar] [CrossRef]
  25. Srinivasa Raju, K.; Nagesh Kumar, D. Classification of Indian meteorological stations using cluster and fuzzy cluster analysis, and Kohonen artificial neural networks. Hydrol. Res. 2007, 38, 303–314. [Google Scholar] [CrossRef]
  26. Khedairia, S.; Khadir, M.T. Self-organizing map and k-means for meteorological day type identification for the region of Annaba-Algeria. In Proceedings of the 7th Computer Information Systems and Industrial Management Applications, Ostrava, Czech Republic, 26-28 June 2008; pp. 91–96. [Google Scholar] [CrossRef]
  27. Spassiani, A. C.; Mason, M. S. Application of self-organizing maps to classify the meteorological origin of wind gusts in Australia. J. Wind Eng. Ind. Aerodyn. 2021, 210, 104529. [Google Scholar] [CrossRef]
  28. Zhao, W.; Hao, C.; Cao, J.; Lan, X.; Huang, Y. Characteristics of large-scale atmospheric circulation patterns conducive to severe spring and winter wind events over Beijing in China based on a machine learning categorizing method. Front. Earth Sci. 2022, 10. [Google Scholar] [CrossRef]
  29. Kim, H.; Kim, B.-J.; Nam, H.-G.; Jeong, J.; Shim, J.-K.; Kim, K. R.; Kim, S. Classification of homogeneous regions of Strong wind and gust wind in Korea. SOLA 2020, 16, 140–144. [Google Scholar] [CrossRef]
  30. Bastine, D.; Larsén, X.; Witha, B.; Dörenkämper, M.; Gottschall, J. Extreme winds in the new European wind atlas. J. Phys.: Conf. Ser. 2018, 1102, 012006. [Google Scholar] [CrossRef]
  31. Mann, J.; Angelou, N.; Arnqvist, J.; Callies, D.; Cantero, E.; Arroyo, R.C.; Courtney, M.; Cuxart, J.; Dellwik, E.; Gottschall, J.; et al. Complex terrain experiments in the new European wind atlas. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160101. [Google Scholar] [CrossRef]
  32. Menteş, Ş.; Ünal, Y.; Ezber, Y.; Barutçu, B.; Aslan, Z.; Kirkil, G.; Topçu, S.; Erten, E.; İncecil, S.; Önol, B. Yeni Avrupa Rüzgar Atlası (NEWA) Projesi Kapsamında Türkiye Üzerine Rüzgar Enerji Kaynağının Modellenmesi. 2019 (No: 215M386) TÜBİTAK.
  33. Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on pressure levels from 1940 to present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS), (Accessed on 26-11-2023). [CrossRef]
  34. Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1940 to present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS), (Accessed on 26-11-2023). [CrossRef]
  35. Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
  36. Holton, J.R.; Hakim, G.J. An Introduction to Dynamic Meteorology; Academic Press, 2013. [CrossRef]
  37. Wallace, J.M.; Hobbs, P.V. Atmospheric Science; Elsevier, 2006.
  38. Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
  39. Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
  40. Peixoto, J.P.; Oort, A.H. Physics of climate; American Institute of Physics: Melville, NY, 1992. [Google Scholar] [CrossRef]
  41. MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, 21 Jun 1967, 1(14); pp. 281–297.
  42. Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, Louisiana, USA, 7-9 Jan 2007; pp. 1027–1035. [Google Scholar]
  43. Wu, K.-L.; Yang, M.-S. Alternative C-Means Clustering Algorithms. Pattern Recognition 2002, 35, 2267–2278. [Google Scholar] [CrossRef]
  44. Milligan, G.W.; Cooper, M.C. A study of standardization of variables in cluster analysis. J. Classif. 5 1988, 181–204. [Google Scholar] [CrossRef]
  45. Jain, A.K.; Murty, M.N.; Flynn., P.J. 1999. Data clustering: a review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
  46. Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
  47. Kaski, S.; Kohonen, T. Exploratory data analysis by the self-organizing map: Structures of welfare and poverty in the world. In Proceedings of the Third International Conference on Neural Networks in the Capital Markets; 1996; pp. 498–507. [Google Scholar]
  48. Jolliffe, I.T. Principal Component Analysis; Springer Science & Business Media, 2013.
  49. Vesanto, J.; Himberg, J.; Alhoniemi, E.; Parhankangas, J. SOM Toolbox for Matlab 5, Helsinki University of Technology, Helsinki, Finland, Rep. A57. Helsinki University of Technology, Neural Networks Research Centre, Espoo, Finland 2000, No. April.
  50. Tatli, H.; Menteş, Ş.S. Detrended cross-correlation patterns between North Atlantic oscillation and precipitation. Theor. Appl. Climatol. 2019, 138, 387–397. [Google Scholar] [CrossRef]
  51. Kaski, S. Data exploration using self-organizing maps. Ph.D. Thesis, Finnish Academy of Technology, Finland, 1997. [Google Scholar]
  52. Tatli, H.; Dalfes, H.N.; Menteş, Ş.S. A statistical downscaling method for monthly total precipitation over Turkey. Int. J. Climatol. 2004, 24, 161–180. [Google Scholar] [CrossRef]
  53. Qiao, S.; Zou, M.; Cheung, H.N.; Zhou, W.; Li, Q.; Feng, G.; Dong, W. Predictability of the wintertime 500 hpa geopotential height over Ural-Siberia in the NCEP climate forecast system. Clim. Dyn. 2019, 54, 1591–1606. [Google Scholar] [CrossRef]
  54. Thornton, H.E.; Smith, D.M.; Scaife, A.A.; Dunstone, N.J. Seasonal predictability of the East Atlantic pattern in late autumn and early winter. Geophys. Res. Lett. 2023, 50. [Google Scholar] [CrossRef]
  55. Martinez, Y.; Yu, W.; Lin, H. A new statistical–dynamical downscaling procedure based on eof analysis for regional time series generation. J. Appl. Meteorol. Climatol. 2013, 52, 935–952. [Google Scholar] [CrossRef]
  56. Wolski, P.; Jack, C.; Tadross, M.; van Aardenne, L.; Lennard, C. Interannual rainfall variability and som-based circulation classification. Clim. Dyn. 2018, 50, 479–492. [Google Scholar] [CrossRef]
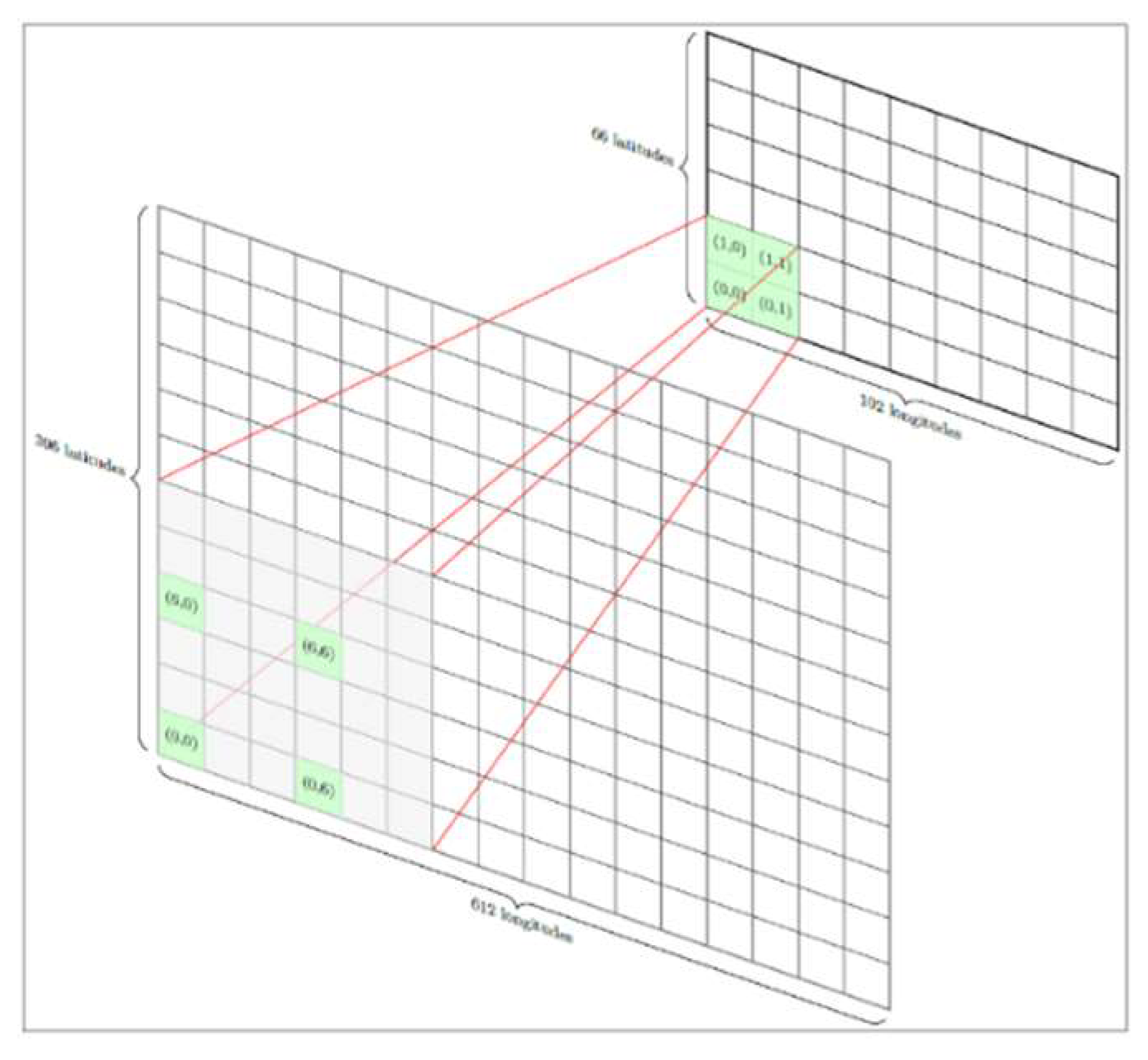
Preprints 95088 g001
Figure 1. Application of grid point reduction to NEWA above ground level data (100m a.g.l.).
Figure 1. Application of grid point reduction to NEWA above ground level data (100m a.g.l.).
Preprints 95088 g001
Preprints 95088 g002
Figure 2. The 98th percentile of wind speed(ms-1) at the selected grid points at 100m a.g.l.
Figure 2. The 98th percentile of wind speed(ms-1) at the selected grid points at 100m a.g.l.
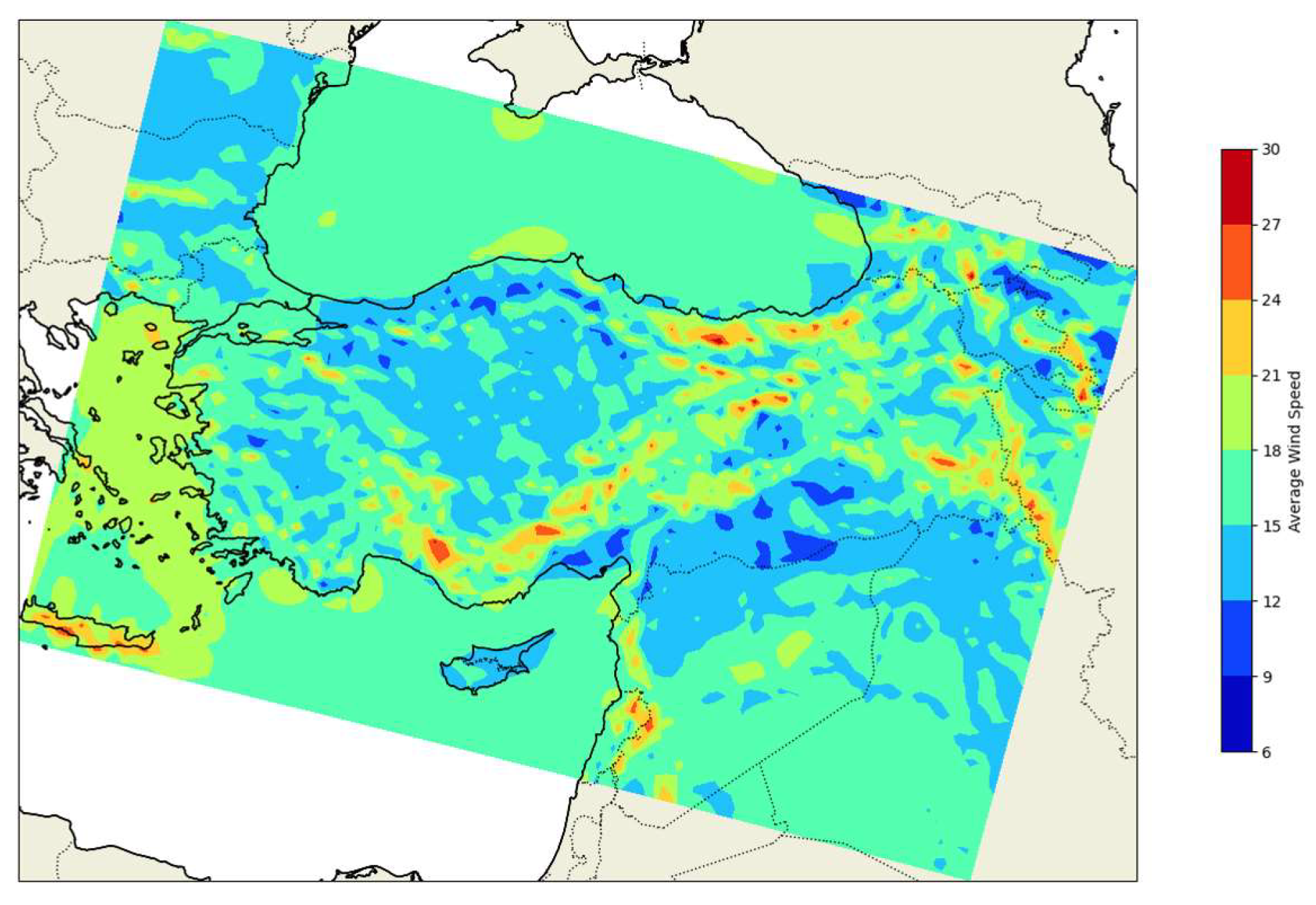
Preprints 95088 g002
Preprints 95088 g003
Figure 3. Elbow method result to determine optimum number of clusters for k-means: (a) total variance explained by the number of clusters; (b) Within-Cluster Sum of Squares (WCSS) by the number of clusters.
Figure 3. Elbow method result to determine optimum number of clusters for k-means: (a) total variance explained by the number of clusters; (b) Within-Cluster Sum of Squares (WCSS) by the number of clusters.
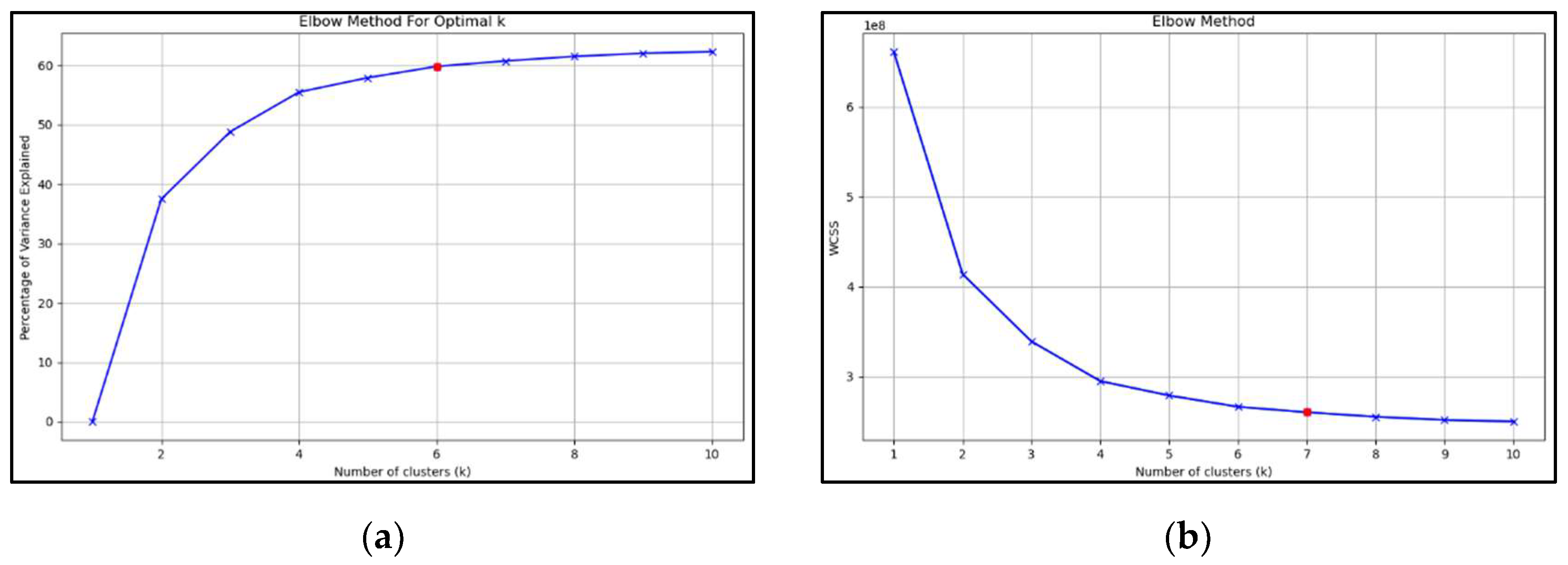
Preprints 95088 g003
Preprints 95088 g004
Figure 4. The percentage of monthly events of 98th percentile data during the 30-years period.
Figure 4. The percentage of monthly events of 98th percentile data during the 30-years period.
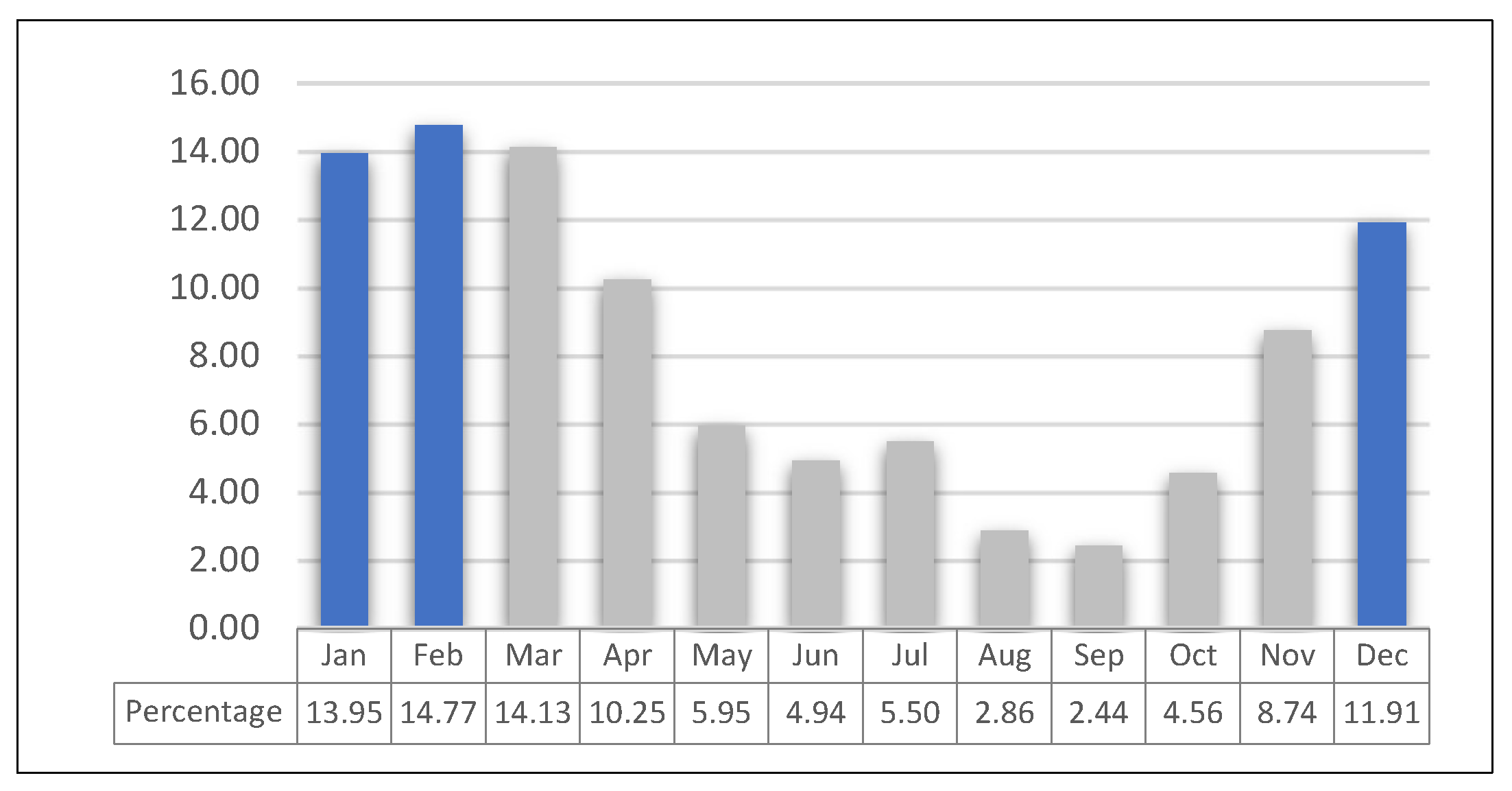
Preprints 95088 g004
Preprints 95088 g005
Figure 5. Scree tests bases on the variance fractions per EOF: (a) geopotential height at 500hPa; (b) mean SLP; (c) temperature at 850hPa.
Figure 5. Scree tests bases on the variance fractions per EOF: (a) geopotential height at 500hPa; (b) mean SLP; (c) temperature at 850hPa.
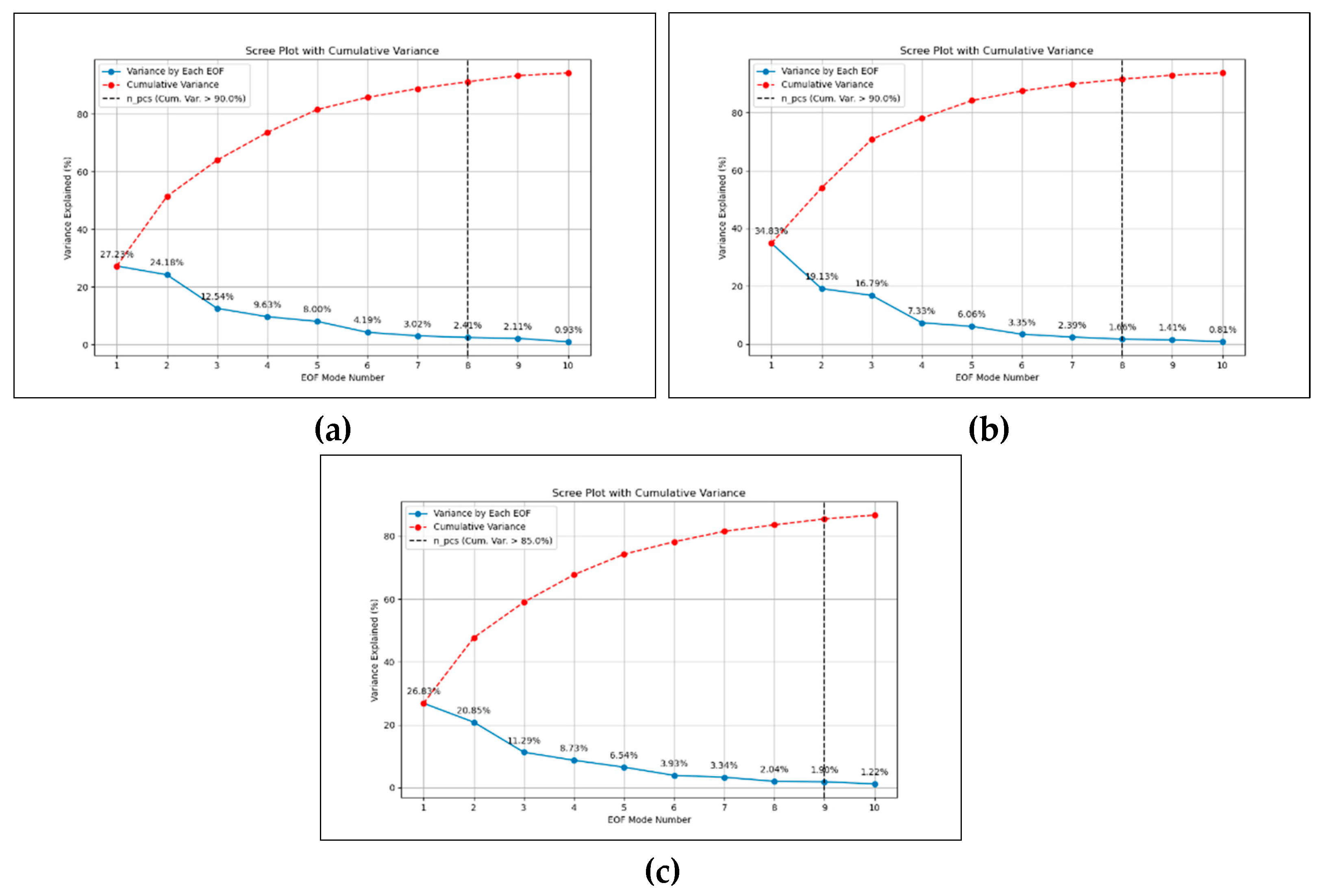
Preprints 95088 g005
Preprints 95088 g006
Figure 6. (a) represent the k-means clustering results at 100m. 6-clusters. Averaged k-means results of every cluster are shown in (b) for 6-clusters.
Figure 6. (a) represent the k-means clustering results at 100m. 6-clusters. Averaged k-means results of every cluster are shown in (b) for 6-clusters.
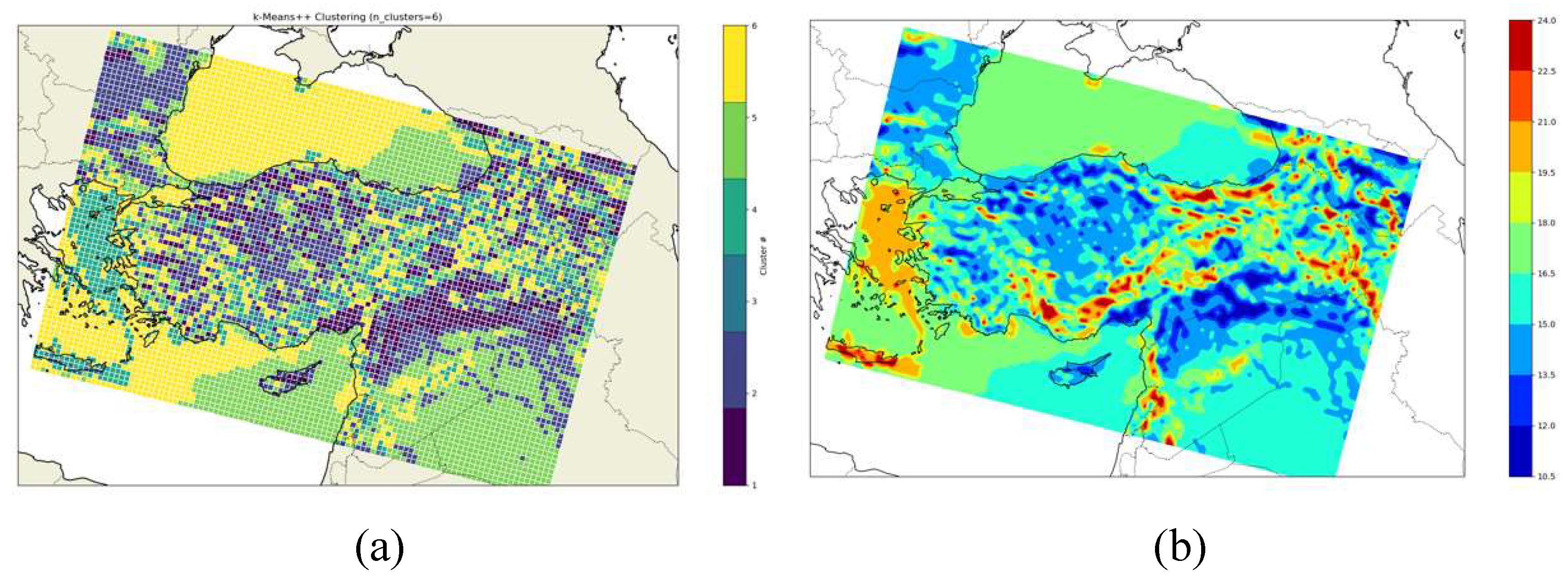
Preprints 95088 g006
Preprints 95088 g007
Figure 7. The first three Empirical Orthogonal Functions (EOFs) during DJF period of 30 years data: (a) MSLP; (b) 500hPa geopotential height; (c) 850hPa temperature.
Figure 7. The first three Empirical Orthogonal Functions (EOFs) during DJF period of 30 years data: (a) MSLP; (b) 500hPa geopotential height; (c) 850hPa temperature.
Preprints 95088 g007
Preprints 95088 g008
Figure 8. Illustration of SOM (3x3) results on DJF period; MSLP as black contour lines, T850 as colored contour line, Z500 as purple contours (gradients): (a) SOM node C1 and days with 98th percentile wind speeds for each grid; (b) SOM node C2 and days with 98th percentile wind speeds for each grid; (c) SOM node C3 and days with 98th percentile wind speeds for each grid.
Figure 8. Illustration of SOM (3x3) results on DJF period; MSLP as black contour lines, T850 as colored contour line, Z500 as purple contours (gradients): (a) SOM node C1 and days with 98th percentile wind speeds for each grid; (b) SOM node C2 and days with 98th percentile wind speeds for each grid; (c) SOM node C3 and days with 98th percentile wind speeds for each grid.
Preprints 95088 g008
Preprints 95088 g009
Figure 9. Illustration of SOM (3x3) results on DJF period; MSLP as black contour lines, T850 as colored contour line, Z500 as purple contours (gradients): (a) SOM node C4 and days with 98th percentile wind speeds for each grid; (b) SOM node C5 and days with 98th percentile wind speeds for each grid; (c) SOM node C6 and days with 98th percentile wind speeds for each grid.
Figure 9. Illustration of SOM (3x3) results on DJF period; MSLP as black contour lines, T850 as colored contour line, Z500 as purple contours (gradients): (a) SOM node C4 and days with 98th percentile wind speeds for each grid; (b) SOM node C5 and days with 98th percentile wind speeds for each grid; (c) SOM node C6 and days with 98th percentile wind speeds for each grid.
Preprints 95088 g009
Preprints 95088 g010
Figure 10. Illustration of SOM (3x3) results on DJF period; MSLP as black contour lines, T850 as colored contour line, Z500 as purple contours (gradients): (a) SOM node C7 and days with 98th percentile wind speeds for each grid; (b) SOM node C8 and days with 98th percentile wind speeds for each grid; (c) SOM node C9 and days with 98th percentile wind speeds for each grid.
Figure 10. Illustration of SOM (3x3) results on DJF period; MSLP as black contour lines, T850 as colored contour line, Z500 as purple contours (gradients): (a) SOM node C7 and days with 98th percentile wind speeds for each grid; (b) SOM node C8 and days with 98th percentile wind speeds for each grid; (c) SOM node C9 and days with 98th percentile wind speeds for each grid.
Preprints 95088 g010
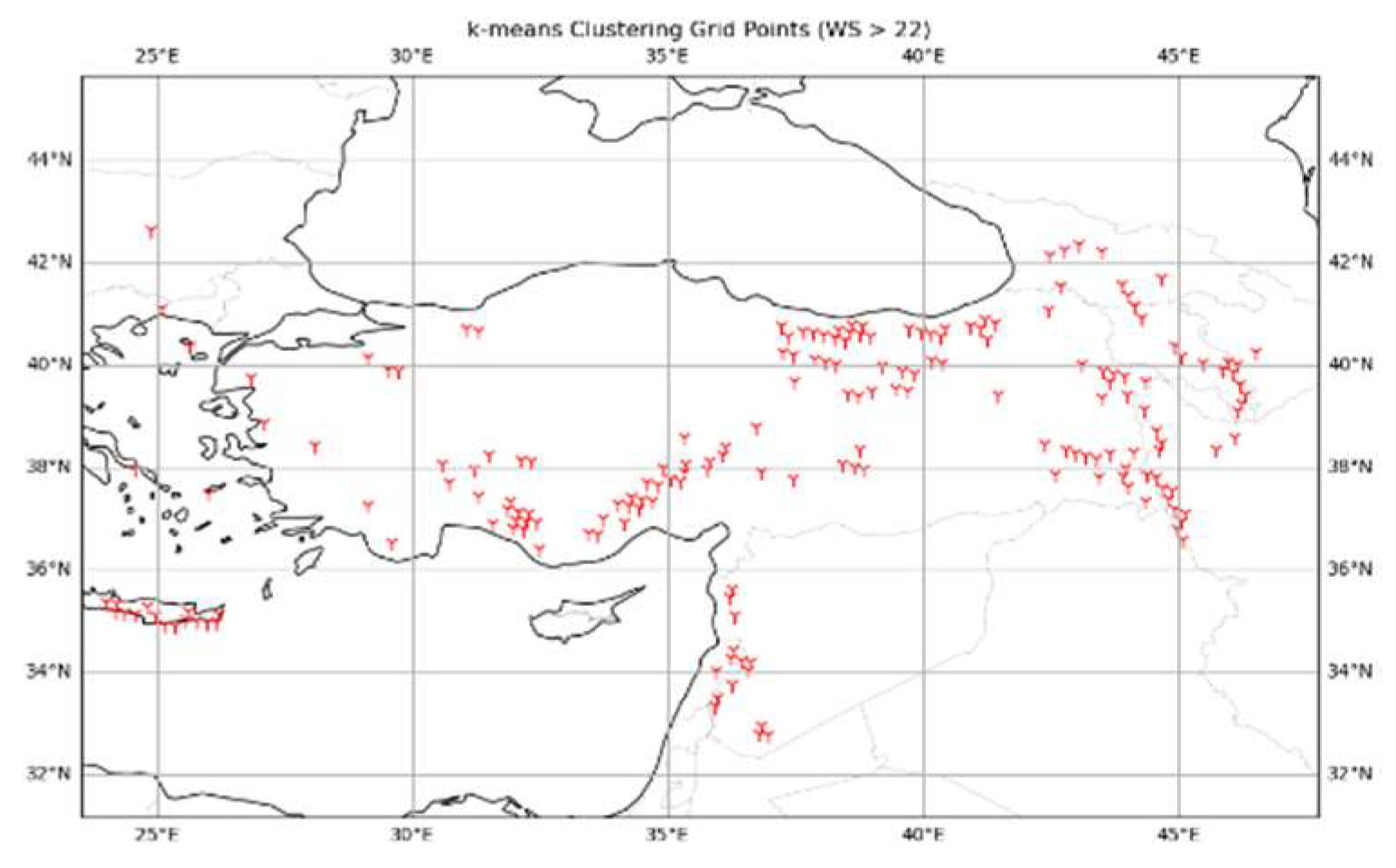
Preprints 95088 g011
Figure 11. Lower-level grid points for cluster (WS > 22) based on k-means clustering results.
Figure 11. Lower-level grid points for cluster (WS > 22) based on k-means clustering results.
Preprints 95088 g011
Table 1. Lower-level k-means clustering grid points where mean wind speed > 22 and upper-level SOM nodes correlation in terms of Total Event-Day Count, Mean Event-Day Percentage, and Mean Wind Speed.
Table 1. Lower-level k-means clustering grid points where mean wind speed > 22 and upper-level SOM nodes correlation in terms of Total Event-Day Count, Mean Event-Day Percentage, and Mean Wind Speed.
C1 C2 C3 C4 C5 C6 C7 C8 C9
Total Event-Day Count 270 311 371 433 290 199 311 224 298
Mean Event-Day Percentage 8.29% 6.76% 4.44% 10.11% 12.37% 10.33% 2.33% 5.41% 15.47%
Mean Wind Speed 22.81 21.82 22.65 22.54 22.53 23.72 22.38 22.64 22.50
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated