Prerpints.org logo
Preprint
Article

Inferencing Space Travel Pricing from Mathematics of General Relativity Theory and Accounting Equation

Altmetrics

Downloads

306

Views

109

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 January 2024

Posted:

03 January 2024

Read the latest preprint version here

Alerts
Abstract
Generalized relativity theory represents the equivalence between the spatial geometric tensor and the energy-momentum tensor, explaining the principles of gravity and the motion of matter in spacetime. In the accounting equation of the supply side, assets equal to liabilities plus owner's equity can be used to explain space travel pricing through mathematical axiomatic set theory. Space travel pricing creates the equity premium effect on value-added assets with a short-term accounting equation inequality, then responds to the supplier’s incremental equity through closing accounts in a fixed financial period. On the demand side, the consumption of space travel can be assumed as a value at risk (VoR) investment to attain the specific spacetime curvature. Spacetime market equilibrium is then achieved to construct the space travel pricing model. The methodology of econophysics and analogy method were applied to infer the space travel pricing between the general relativity theory and the accounting equation. Results show that space travel pricing remains the principle of market equilibrium but needs to be extended to the spacetime scale.
Keywords: 
Subject: Business, Economics and Management  -   Economics

1. Introduction

Space tourism began in 2001 with Dennis Tito’s private trip to the International Space Station, spending 20 million US dollars [1]. With the emergence of private space companies such as SpaceX, Blue Origin, and Virgin Galactic, there has been a growing interest in a market to make space travel more accessible to private individuals [1,2]. Space tourism has many attributes that differ from Earth tourism, like untraditional suppliers, selected tourists, and asymmetric markets [3]. One of the unique attributes of space travel is its ultra-expensive prices. For example, the Virgin Galactic reservation quantity increased from less than 100 in 2006 to over 1,000 in 2023, and the bidding price increased from USD 250,000 to 450,000 [4]. The first research question is, why the space travel is so expensive? This study aims to infer the space travel pricing mechanism by the analogy of general relativity in the physical field and the accounting equation in the economic field.
General relativity theory (GRT), developed by Albert Einstein, discusses gravitation and has been tested as a solid scientific fundamental for physics and cosmology [5]. The theory describes gravity as the spacetime curvature bent by mass and energy. In GRT, mass and energy warp the fabric of space and time, affecting the motion of matter and the passage of spacetime itself [6]. It is worth discussing space travel behavior concerns about GRT because human travel has been flown above the Earth's surface to space, reaching the height from zero to nonzero curvature of spacetime [7]. Space travel pricing can not be derived from the airplane pricing models because the former attains nonzero spacetime curvature behind the Kármán line, and the latter fly flat spacetime curvature below 20 Km height [8]. The second research question is how to derivate the space travel pricing model. This study suggests a perspective from the accounting equation with axiomatic set theory.
The accounting equation, assets equal to the sum of liabilities and equity, forms the basis of accounting principles [9]. Juárez [10] used a mathematical axiomatic set theory indicating the inequality of the accounting equation. The analysis determined that the sets of assets do not equal liabilities plus equity without financial meaning. However, this study infers that inequality happens in a dynamic adjusting period when the expected space travel profit causes equity premium effects; thus, the inequality of the accounting equation only happens in a short period. In accounting, the net income will be brought forward to become incremental equity to balance the accounting equation after the closing account. The space travel pricing model can then be derived during the adjusting period of the supplier’s accounting equation. Moreover, this study explains the pricing model not only from the economic supply side but also from the demand and market equilibrium perspectives.

2. Mathematics of General Relativity Applied in Space Travel

2.1. The Mathematics of General Relativity Applied on Space Travel

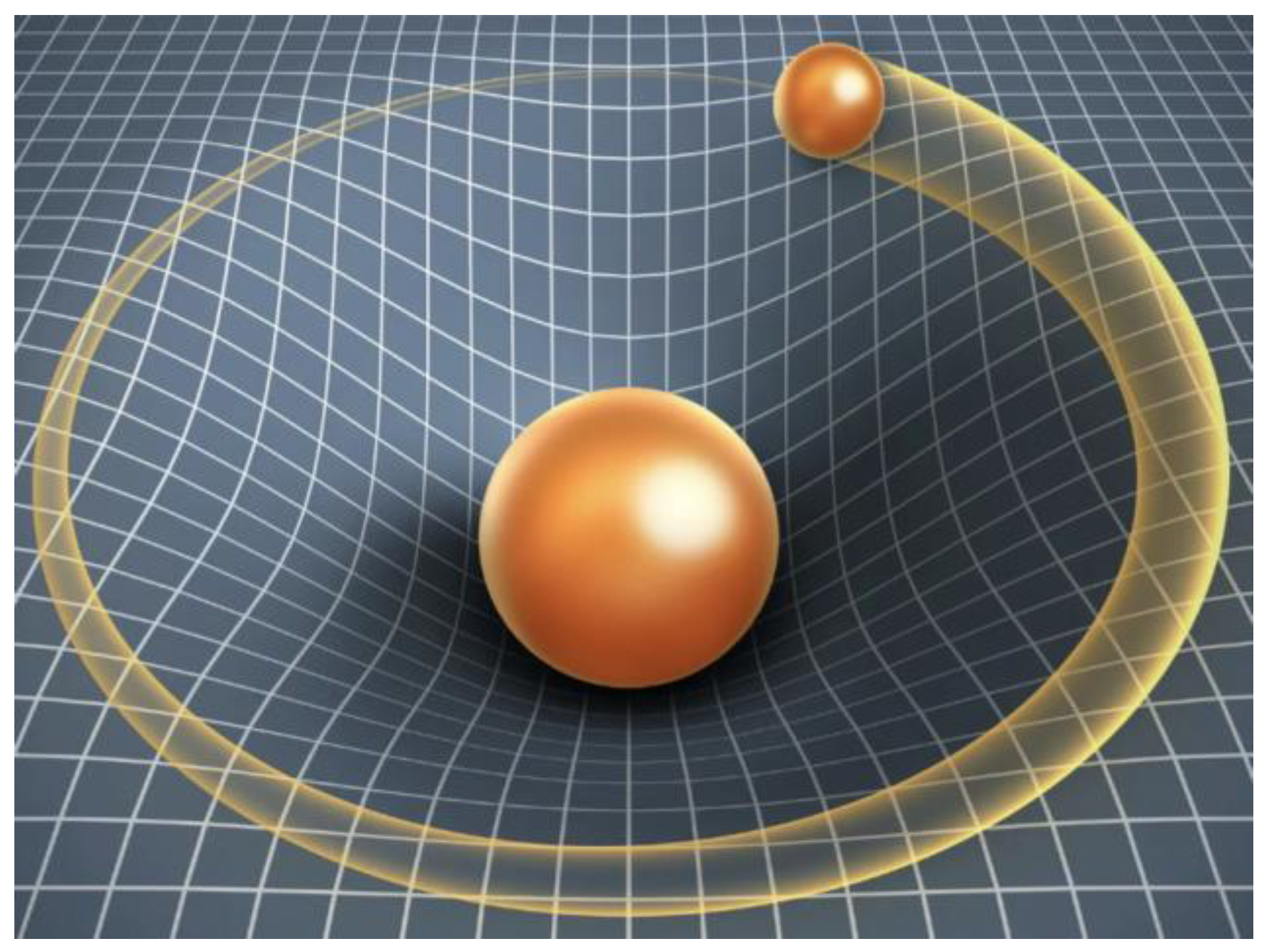
GRT mathematics involves differential geometry and tensor calculus, where concepts like manifolds, tangent spaces, covariant differentiation, and curvature are rigorously defined [11]. At the core of GRT are the Einstein Field Equations, which describe how Einstein tensor equals energy-momentum-tensor [12]. as indicated in Equation (1). GRT presents that matter tells spacetime how to curve, and curved spacetime tells matter how to move [13], as indicated in Figure 1.
R μ v − 1 2 R g μ v = 8 π G C 4 T μ v ,
Where R μ v is the Ricci curvature tensor; R is the Ricci scalar; g μ v is the metric tensor; T μ ν is the energy-momentum tensor; G is the Newtonian constant of gravitation; c is the speed of light, and μ , v are the spacetime coordinates.
Preprints 95143 g001
Figure 1. The spacetime curvature and matter movement.
Figure 1. The spacetime curvature and matter movement.
Preprints 95143 g001
The implication of GRT on space travel is flying to a nonzero curvature, the equivalent of energy-momentum is needed according to the transformation of energy efficiency in space technology [14]. Equation (1) can be realized as the space vehicle flying to the designated orbit with specific spacetime curvature, which needs to reach the required cosmic velocity depending on the energy efficiency [15]. The space technology involved includes mixed-fuel, engine technology, reusable launch vehicles, electromechanical and communication systems, ground control systems, and intelligent manned space vehicles [16]. Therefore, equation (1) represents the energy distribution equation required for traveling to the geometrical space orbit. In other words, a supplier must offer the equivalent energy-momentum at the same level as the orbital energy distribution [17].

2.2. Reasoning Space Travel Pricing through Accounting Equation on Axiomatic Set Theory

The accounting equation has been recognized as the standard system businesses use to record financial transactions. The equation represents the equality relationship between a company’s assets and liabilities plus owner’s equity [18], as shown in equation (2):
Assets = Liabilities + Owner’s Equity
Equation (2) means that the funding sources of assets (An) come from the liabilities (Ln) and owner’s equity (En) [19], where n is the elements in sets. However, Juárez [10] argued the accounting equation’s inequality by applying axiomatic set theory and predicate logic. Using the axiom of union, the set Cn comprises the elements claimed on the subset Ln and the subset En of the capital subsets. By the axiom of extensionality, the sets An and Cn are compared. The axiom of specification allows determining that the capital units of each subset of Cn has similar capital units spread over the subsets of An. Accordingly, the subsets of An are not congruent with the subsets of Cn and, due to this lack of correspondence, An≠Cn , and An≠Ln ⋃ En, and, in general, A≠L ⋃ E. The analysis determined that the sets of assets are not equal to the sets of liabilities and equity, concluding that assets are not equal to liabilities plus equity. This inequality is interpreted within the restrictions of applying the set theory to financial data and algebraic sum without financial meanings [20].
Nevertheless, we found that studies of Juárez [10,20] might have committed Russell's paradox, which can be solved by a Predicativist explanation, the Cantorian solutions, or particular zig-zag solutions [21]. In this study, we apply Ludwig Wittgenstein's Tractatus Logico-Philosophicus to explain that any proposition cannot contain itself, and similarly, a set cannot contain itself [22]. The sets An and Cn fit the logic that the set does not contain itself but can infer that An = Cn , Cn = Ln ⋃ En , An = Ln ⋃ En , in general A = L ⋃ E but Zermelo-Fraenkel set theory is necessary [23]. Given a border field to define sets can solve Russell’s paradox of the inequity of accounting equation. Thus, the spacetime set S is the border field to be introduced to deduct the conditions of accounting equation inequality to be equal, as shown in equation (3):
∀A ∀C (A = C ⇔ ∀S (S ∈ A ⇔ S ∈ C)).
Accounting equation inequality was deduced only by the mathematical set theory without financial meanings originally [10,20]. However, the physical element of spacetime set S can be added to comply with the equality of accounting equation interpreted with financial meanings. The set S implies that space becomes a new production factor for a supplier to offer a space travel product if and only if the accounting equation sustains. The short-term dynamic accounting equation inequality issue of equation (2) is also explained by introducing the spacetime element, which belongs to the two field sets in equation (3). The inequality of accounting equation is a short-term dynamic adjusting process to generate the equity premium when incorporating the spacetime element. When the accounting cycle is complete, the equality of equation (2) is sustained with the spacetime element at the end of an accounting period.

2.3. Space Travel Pricing Process

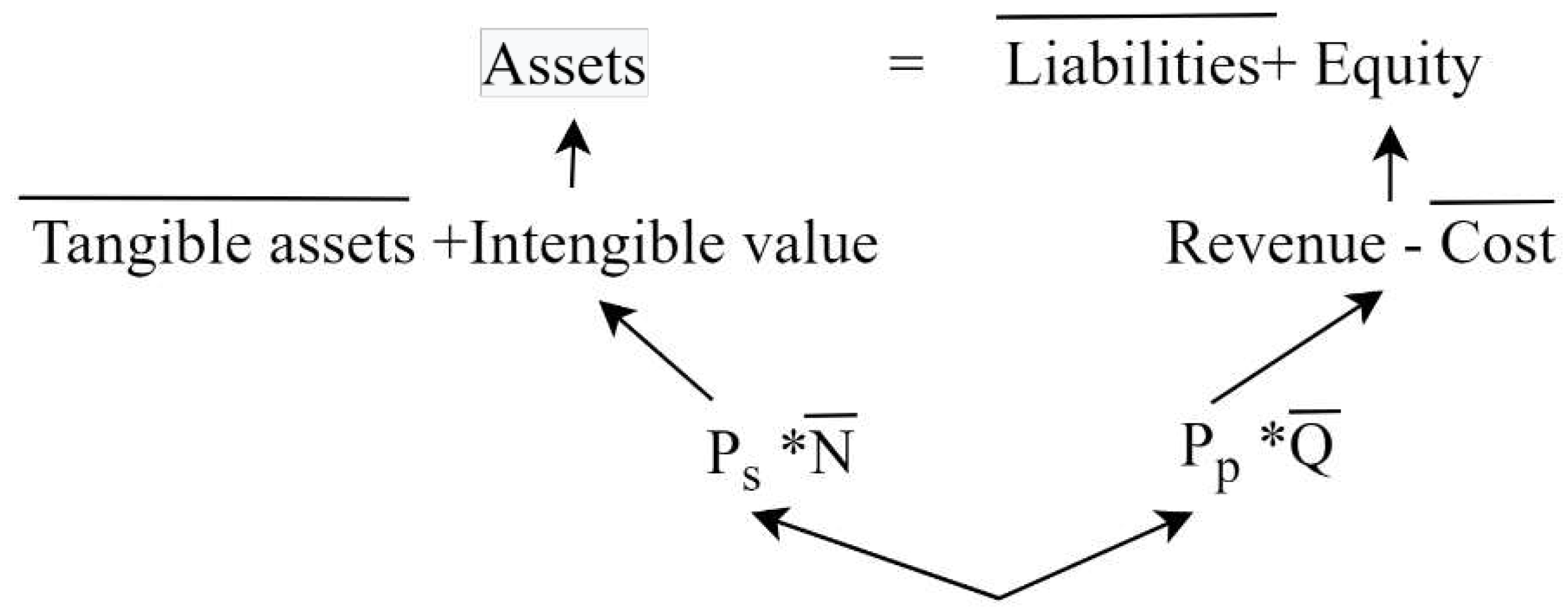
Mapping with equations (1) and (2), a space company uses its assets as resources to reach the geometric coordinate, a specific spacetime curvature of Einstein’s tensor [24]. The funding sources of liabilities and owner’s equity can be analogized to the energy-moment tensor distributed for business operations [25]. To derive the space travel pricing based on the short-term launch and flying operations, the long-term liabilities, operational cost, sales quantities, stock shares, and tangible assets can be assumed ceteris paribus, given all other variables unchanged [26,27], as indicated in Figure 1. The operational net income from space travel will become incremental cash flows and create an equity premium effect to be the primary momentum of driving a company using assets to fly into specific spacetime curvature. In finance, the expected revenue or net income significantly influences the company’s intangible assets, which will reflect its market value, equity premium [28]. The relationship between the space travel pricing and the supplier’s market value is then determined. In summary, the product price Pp has a positive relationship with the stock price Ps [2930] in a space travel company, as indicated in Figure 1.
Preprints 95143 g002
Figure 1. The space travel pricing derivation.
Figure 1. The space travel pricing derivation.
Preprints 95143 g002

3. Methodology

3.1. The Methodology of Econophysics

This study is an interdisciplinary research covering the fields of physics and economics to infer the space travel pricing model on GRT and the accounting equation. The methodology applies econophysics, which was introduced by analogy with similar terms that describe applications of physics to different fields [31]. From the very beginning, Econophysics was the application of the principles of physics to the study of financial markets under the hypothesis that the economic world behaves like a collection of electrons or a group of water molecules that interact with each other [32]. It has always been considered that the econophysicists, with new tools of statistical physics and the recent breakthroughs in understanding chaotic systems [33]. Econophysics has alternative names, such as financial physics, arising initially from its new development of two different disciplines: finance and physics [34].
The methodology has been applied to help finance research with many innovative theories. One of the pricing models is the Black, Scholes, and Merton (BSM) pricing model, which is used for the valuation of stock options by applying the thermodynamic equation to finance [35]. The BSM model involves a principle-theory-type approach as the paradigm of econophysics methodology [36]. Various principles going into the pricing model possess the status of the postulates of empirical generality concerning the behavior of economic agents. 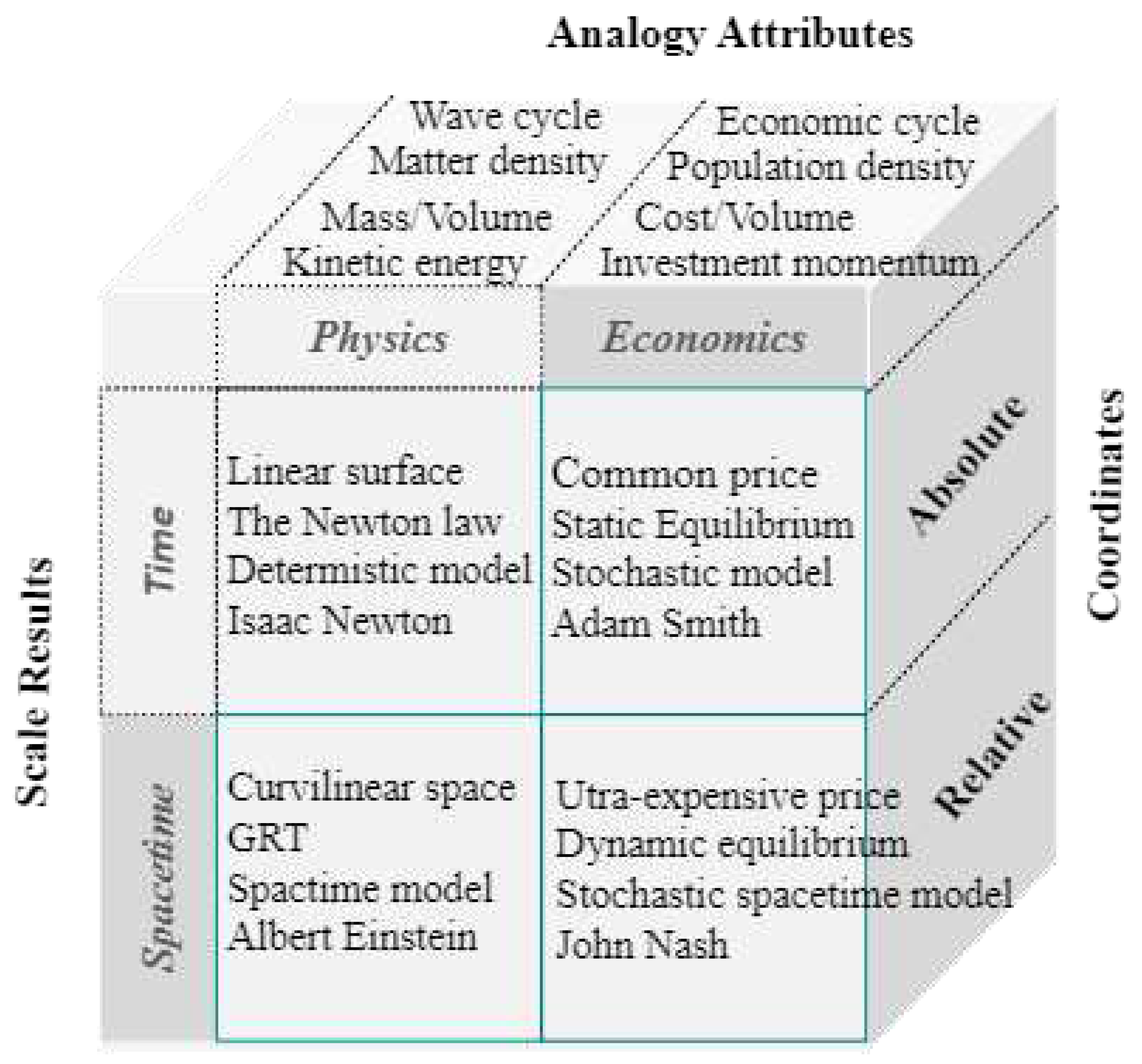Crucially, econophysicists, also using the statistical physics analogy, adopt more of a constructive-theory-type approach [36]. To bridge the gap between physics and economics, this study adopts the analogy method of the econophysics methodology, as indicated in Figure 2, to link the attributes of the two fields for the following inference of space travel pricing [1]. Figure 2 indicates that the analogy attributes of physics and economics are paired with similar meanings. It helps infer the pricing model, no matter whether the scale is the absolute time frame or the relative spacetime tensor.
Preprints 95143 g003
Figure 2. Analogy method.
Figure 2. Analogy method.
Preprints 95143 g003

3.2. Econophyisc Research Propositions

This study follows the methodology of econophysics, applying GRT to infer space travel pricing. Thus, the GR spacetime construct needs to be updated in the pricing model [1]. The assumption of traditional pricing theory is that time and space are independent. The Earth flight pricing model generally takes spatial distance as a primary factor with various pricing strategies for business classes and services [37]. Time is an independent variable in considering price making. The farther the flying distance, the higher the ticket price can be observed in the flight market. Time is only an independent factor that corresponds to the space distance. Temporal span does not necessarily have an equal proportionality with the space transition [38]. For example, the price of a direct flight in a short time is high, which implies that time and space are independent variables of pricing behavior.
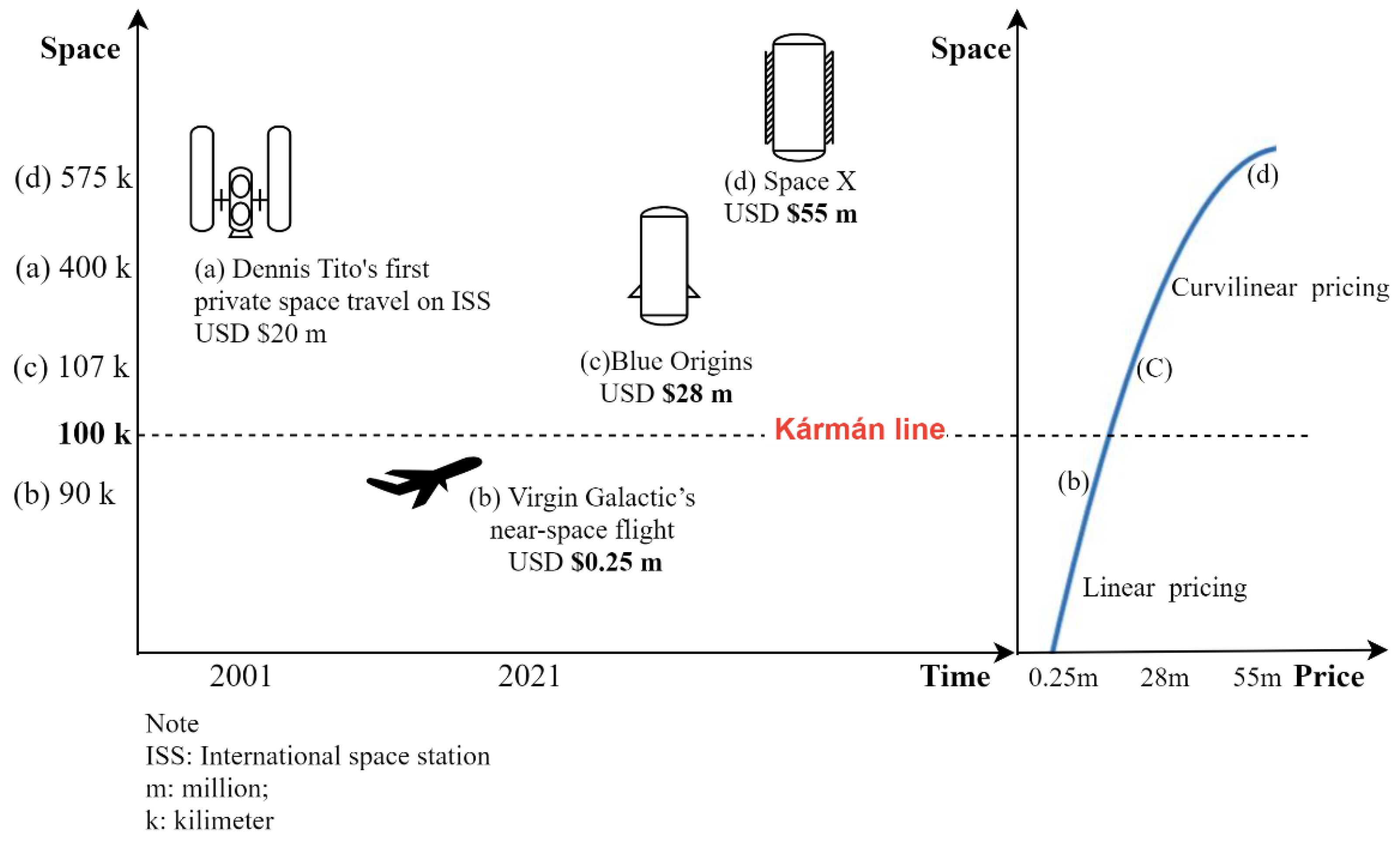
The space pricing model should be updated after applying the spacetime construct. According to the time dilation in GRT spacetime, the pricing model must be interpreted using the Minkowski or Schwarzschild spacetime formula [39]. In the space travel pricing behavior, we observe that Virgin Galactic, Blue Origins, and SpaceX have various pricing, as shown in Figure 2. Blue Origins flies about 107 km above the Earth's surface, which is about 1.2 times higher than Virgin Galactic flies a height of 87 km, but the ticket price is six times the difference. SpaceX's orbital altitude is about 550 kilometers, which is about five times higher than Blue Origins's space altitude with a 20-time difference in price. The relationship between pricing levels and spacetime coordinates is nonlinear [1], as shown in Figure 3.
Preprints 95143 g004
Figure 3. Space travel prices at different altitudes.
Figure 3. Space travel prices at different altitudes.
Preprints 95143 g004
This study argues that space travel pricing concerns the equity premium effect, which depends on the spaceship company’s capability of reaching designed spacetime curvature. The higher the attitude, the higher the equity premium, like SpaceX and Virgin Galactic. We can observe the pricing behaviors involved with the spacetime curvatures of the spacecraft companies in Figure 2. Thus, this study summarizes the proposition 1 as follows:
Proposition 1:
Given the capability of a supplier’s spacetime curvature technology, the pricing of space travel suppliers is positively correlated with the equity premium in the accounting equation.
This study proposes a spacetime pricing model that echoes GRT, which presents the equality relationship between Einstein’s tensor and energy-moment tensor. A space traveler is willing and able to pay to fly to a specific orbital spacetime curvature. The expenditure for achieving the attitude can be referred to the space travel demanding pricing behavior, including a consumer’s motivation, utilities, and elasticity. A space supplier is willing and able to provide its aerospace technology with the equivalent energy-momentum tensor. The Revenue for attaining required spacetime curvature can be referred to the space travel supplying pricing behavior, including production factors, cost, and elasticity. Given the market equilibrium on dealed transactions, the spacetime pricing model reflects not only the supply side but also the demand side.
Proposition 2:
Based on market equilibrium, the spacetime pricing derivations not only apply to the supply side, but also reflect the demand side.

4. Discussions

Equation (1), GRT, is a field theory in physics, equation (2), accounting equation, is a field theory in economics, and equation (3) opens the dialogue between the two field theories by using the spacetime element to link the two sets of physics and economics in the space travel era. The deduction of the space travel pricing model based on the mathematical logic presents the positive correlation between the space travel pricing and the supplier's equity premium. Propositions one and two are

4.1. Supply Side: The Supply Capability of Attaining Space Curvatures

In the beginning of commercial space travel, the pricing strategy is primarily dominated by the suppliers, which means the consumers are price takers due to over-\demanding. Space travel can be dealt with only when the supplier can provide the aerospace technology to achieve a specific space curvature. The space supplier should integrate the resources of the accounting equation (2) to develop its capability to achieve the production factors of space in equation (1). The accounting cycle is as follows: First, the incremental cash flows from the pricing strategy can be regarded as an incremental element of the energy-momentum tensor (Einstein tensor) to attain the incremental spacetime curvature. Second, the successful space launch and travel service will then generate the equity premium because of the event effect. Third, the event effect will raise the supplier's bidding price to increase profit, which will carry forward to the next period when the accounting cycle is completed. Fourth, the incremental equity enlarges the equity premium. The accounting cycle continues to increase the amounts of the accounting equation (2) until the equity premium is offset by the competition of other suppliers. That is, the price of space travel reflects the attainable curvature of the supplier's capacity.

4.2. Demand Side: Space Travel Value-at-Risk Investment

One of the characteristics of space travel is the high-risk attribute, which is similar to adventure tourism with the target market customers, risk lovers, who prefer risky products, such as the extreme sports tourism market. However, risk-lover travelers have different levels of risk tolerance and preference; for example, travelers who prefer to climb the world's highest mountain peak are not the same as those who travel space. No matter what kind of risk lovers, the demand utility can typically be measured by value-at-risk (VaR), which determines the potential or the probability of loss to occur in the assessed entity. VaR can also be written as a distortion risk measure given by the distortion function [40], as shown in the equation (4).
g x = 0         i f   0 ≤ x < 1 − α 1         i f   1 − α ≤ x ≤ 1   The   VaR   at   level   α ∈ 0 , 1
It can be implied that a space traveler is considered an investor who will lose the spending on space travel at the condition of g(x) = 0 in equation (4), which implies a purchase of a space journey is a loss-inducing investment, then the investment can be assessed by the VaR model. The VaR investment from consumers becomes the supplier’s incremental equity, which will cause the equity premium for intangentable asset value-added assets that help the supplier develop its aerospace technology to attain the space curvatures. This is a pricing model where the demand side pays a price to support the supply side in achieving the expected space curvatures.

4.3. Market Equilibrium: Spacetime Equilibrium

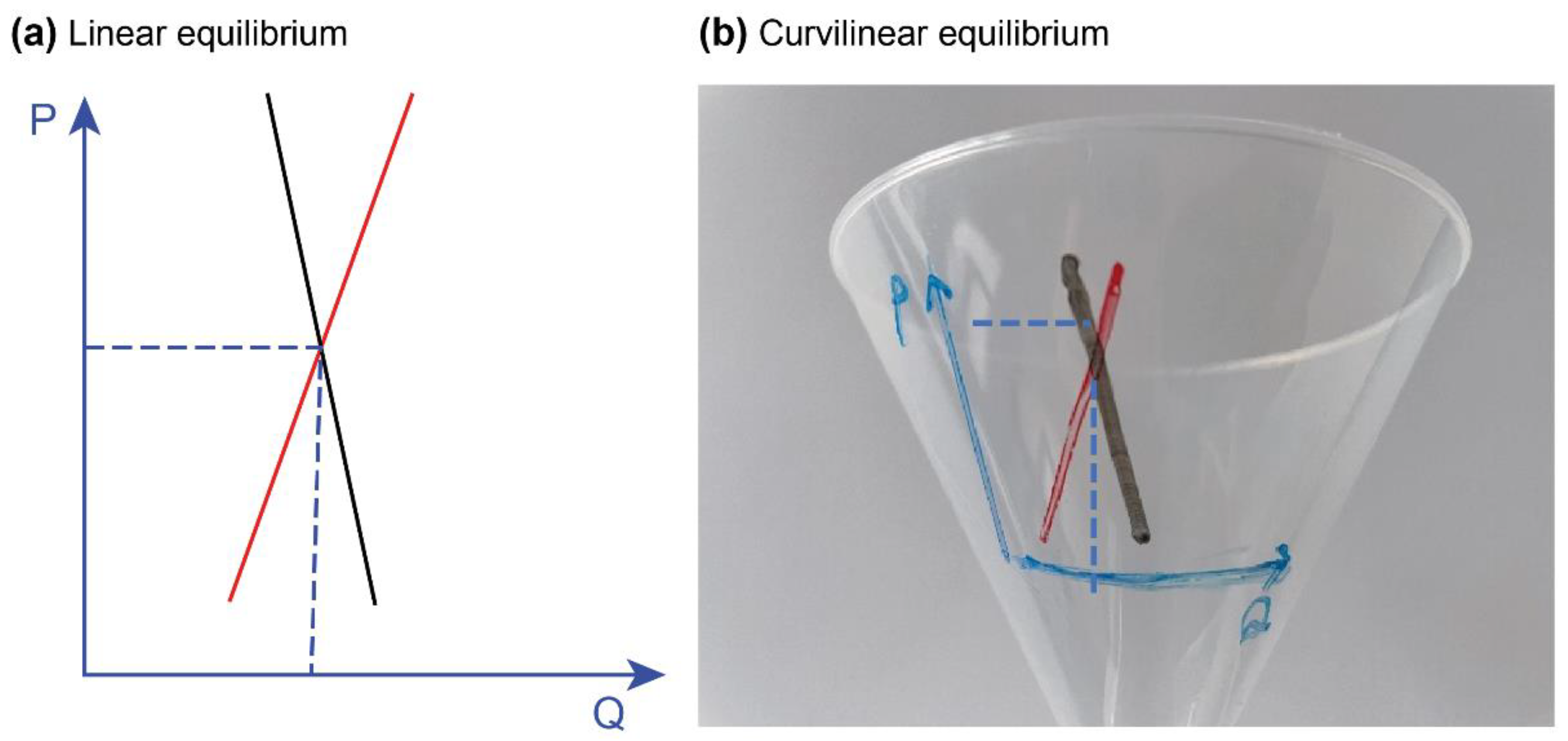
Based on the prerequisites of GR equation (1) and the accounting equation (2), this study infers the space travel pricing model to the economic supply and demand, which is reflected in the economic market equilibrium. The energy-momentum tensor provided by suppliers’ aerospace technology can satisfy the demand of space travelers to reach a specific spacetime curvature. Thus, we can calculate the spacetime curvature matching the energy-moment tensor of the orbital altitude for completing the transaction of the market equilibrium. On the demand side, there is a price that consumers are willing and able to pay for a particular spacetime curvature, and on the supply side, the price implies the suppliers are willing and able to invest to reach the expected spacetime curvature. The market equilibrium is still applied to the pricing model of space tourism. However, we have converted the economic supply and demand from the traditional three-dimensional to the spacetime four-dimensional scale. It is noteworthy that the market equilibria of Earth and space tourism are different. The space travel market equilibrium attains the curvilinear demand and supply intersection, which causes the difference in pricing models between Earth and space travel, as shown in Figure 4.
Preprints 95143 g005
Figure 4. Economic equilibria of time and spacetime references.
Figure 4. Economic equilibria of time and spacetime references.
Preprints 95143 g005

5. Conclusions

5.1. Conclusion

This study applies the mathematical theories of GRT and the accounting equation to deduce the space travel pricing model according to the economic supply, demand, and market equilibrium behaviors. GRT has been generalized by many empirical studies in physics and cosmology. This study applies GRT to infer space travel economic behaviors. The results show that the geometric tensor equals the energy-momentum tensor of GR theory, which can be analogically reasoned to the axiomatic set theory of the accounting equation, assets equal liability plus owner's equity. The space travel pricing reflects the market value of the supplier, as shown in Figure 3. In addition, the demand side’s consumption in space travel can be assumed to be the VaR investment to echo the supplier’s accounting equation sets. In summary, the space travel pricing mechanism is still guided by the invisible hand of market equilibrium following the supply and demand behaviors; however, the spacetime scale must be transformed in the pricing model, which is different from the Earth market equilibrium.
The space travel pricing adjusting process is the inequality of the accounting equation happens because of the equity premium effect on the intangible assets in a short period, but the accounting equation will remain equal after the completion of the accounting cycle due to the incremental cash flows from revenue becoming the incremental equity. In other words, an equity premium caused by pricing behaviors increases a value-added investment in the intangible asset in advance, and then the net income will still be brought forward to be the increment of equity, resulting in a fixed-term equality of the accounting equation. The value-added assets enable the supplier to invest in aerospace technology that transforms the energy-momentum tensor required to achieve a specific curvature of space. On the demand side, space travel pricing assumes that consumer spending on space travel is a VoR investment, and this consumption investment will echo the supply side’s accounting equation sets. Thus, we can conclude that space travel pricing remains the result of an economic market equilibrium between supply and demand based on the transactions that have been dealt.

5.2. Research limitations and Suggestions

Space travel is a nascent industry and is a major tourist attraction. The research limits come from the availability of empirical data because the market is still immature. This study will be more responsive to the actual market behaviors after enough empirical studies. At the same time, spacetime-related theories have to be developed to explain the reality of space economic behaviors. The research directions of innovative fields can be studied from Earth to Space, from independent space and time to integrated spacetime scales, from financial random walk to incremental random walk, and from referential time series to proper time series analyses. The innovative theories will bring a new scientific vision when we conduct studies in the space market. Comparing to the proper time series analysis, the traditional time series would present a higher risk because the fluctuations are actually large. It is one of the market abnormalities that awaits us to explore in space research.
Interdisciplinary theory construction requires cross-domain understanding and interdisciplinary communication between scholars in different fields. However, the academic culture of each field is conservative with its academic terminology and theories. Interdisciplinary cooperation is necessary for innovative theories for science. Moreover, scholars’ in-person cross-domain learning, and research in different fields are more creative and effective in making breakthroughs. This study makes analogical reasoning between the GR theory of physics and the accounting equation set of economics with connections of the two fields through econophysics methodology. However, a deeper exploration into the physical connotation is needed with more mathematical inference.

References

  1. Peng, K.-L., et al., Proposing spacetime scale for space tourism economics. Tourism Economics, 2023. 29(6): p. 1671–1678. [CrossRef]
  2. Lampkin, J. and R. White, The Global Space Industry, in Space Criminology: Analysing Human Relationships with Outer Space. 2023, Springer. p. 25-47.
  3. Olya, H.G.T. and H. Han, Antecedents of space traveller behavioral intentions. Journal of Travel Research, 2020. 59(3): p. 528-544. [CrossRef]
  4. Dileep, M.R. and F. Pagliara, Space Tourism, in Transportation Systems for Tourism. 2023, Springer. p. 269-288.
  5. Wu, E.T., What Are the Truths of Gravity and General Relativity. IOSR Journal of Applied Physics (IOSR-JAP), 2022. 14(01). [CrossRef]
  6. Perlov, D., et al., The Fabric of Space and Time. Cosmology for the Curious, 2017: p. 59-82. [CrossRef]
  7. Penprase, B.E., Spacetime and Curved Space, in Models of Time and Space from Astrophysics and World Cultures. 2023, Springer. p. 129-161.
  8. May, A., The Space Business: From Hotels in Orbit to Mining the Moon–How Private Enterprise is Transforming Space. 2021: Icon Books.
  9. Luo, S. and F. Song, Principles-based versus rules-based: accounting standards precision and financial restatements in China. Asian Review of Accounting, 2022. 30(4): p. 581-615. [CrossRef]
  10. Juárez, F., The accounting equation inequality: A set theory approach. Global Journal of Business Research, 2015. 9(3): p. 97-104.
  11. Dolan, B.P., Einstein's general theory of relativity: A concise introduction. 2023: Cambridge: Cambridge University Press.
  12. Barukčić, I., Unified field theory. Journal of Applied Mathematics and Physics, 2016. 4(08): p. 1379. [CrossRef]
  13. Carroll, S.M., Spacetime and geometry. 2019: Cambridge University Press.
  14. Rodal, J.J., A Machian wave effect in conformal, scalar–tensor gravitational theory. General Relativity and Gravitation, 2019. 51(5): p. 64. [CrossRef]
  15. Wu, J., Y. Xu, and Q. Bai, Introduction to Space Science. 2021: Springer.
  16. Simplício, P., A. Marcos, and S. Bennani, Reusable launchers: development of a coupled flight mechanics, guidance, and control benchmark. Journal of Spacecraft and Rockets, 2020. 57(1): p. 74-89. [CrossRef]
  17. Seo, B.R., Future of space travel. Space Travel for the Masses: History, Current Status, Problems, and Future Directions, Worcester Polytechnic Institute. 2013: Worcester Polytechnic Institute.
  18. Kimmel, P.D., J.J. Weygandt, and D.E. Kieso, Financial accounting: tools for business decision-making. 2020: John Wiley & Sons.
  19. Prasad, S., C.J. Green, and V. Murinde, Company financing, capital structure, and ownership: A survey, and implications for developing economies. 2001: SUERF Studies.
  20. Juárez, F. The foundations of balance sheet and the inequality of the basic accounting equation from the viewpoint of set theory. in Global Conference on Business & Finance Proceedings. 2015. Institute for Business & Finance Research.
  21. Conti, L., Russell’s paradox and free zig zag solutions. Foundations of Science, 2023. 28(1): p. 185-203. [CrossRef]
  22. Ludwig, W., Tractatus logico-philosophicus. 1989: Akadémiai Kiadó.
  23. Makridis, O., Basics of Set Theory, in Symbolic Logic. 2022, Springer. p. 405-458.
  24. Renn, J., The genesis of general relativity: Sources and interpretations. Vol. 250. 2007: Springer Science & Business Media.
  25. Chen, X., Cosmic inquiries. 1999: Columbia University.
  26. Morrell, P.S., Airline finance. 2021: Routledge.
  27. Van Benthem, J., P. Girard, and O. Roy, Everything else being equal: A modal logic for ceteris paribus preferences. Journal of philosophical logic, 2009. 38: p. 83-125. [CrossRef]
  28. Cyril, U.M., O.J. Echobu, and M.C. Chukwuemeka, Evaluation of the Effect of Financial Factors on Shareholders’ Value of Listed Pharmaceutical Firms in Nigeria. International Journal of Finance and Banking Research, 2019. 5(5): p. 114-125. [CrossRef]
  29. Liu, Z., et al., Two-period pricing and strategy choice for a supply chain with dual uncertain information under different profit risk levels. Computers & Industrial Engineering, 2019. 136: p. 173-186. [CrossRef]
  30. Alaagam, A., The relationship between profitability and stock prices: Evidence from the Saudi banking sector. Research Journal of Finance and Accounting, 2019. 10(14). [CrossRef]
  31. Capoani, L., Theory of Commercial Gravitational Fields in Economics: The Case of Europe. Networks and Spatial Economics, 2023: p. 1-40. [CrossRef]
  32. Savoiu, G. and I.I. Siman, History and role of econophysics in scientific research. Econophysics: background and applications in economics, finance, and sociophysics, 2013: p. 3-16.
  33. Săvoiu, G. Statistical thinking and statistical Physics. in Proceedings of International Conference Econophysics, New Economics & Complexity, Hyperion University and Hyperion Research & Development Institute, Victor Publishing House, Bucharest. 2008.
  34. Savoiu, G. and C. Andronache, The potential of econophysics for the study of economic processes. Econophysics background and applications in economics, finance, and sociophysics, 2013: p. 91-133.
  35. Morales-Bañuelos, P., N. Muriel, and G. Fernández-Anaya, A Modified Black-Scholes-Merton Model for Option Pricing. Mathematics, 2022. 10(9): p. 1492. [CrossRef]
  36. Rickles, D., Econophysics and the complexity of financial markets, in Philosophy of complex systems. 2011, Elsevier. p. 531-565.
  37. Phlips, L., The economics of price discrimination. 1983: Cambridge University Press.
  38. Müller, C., et al., Customer-centric dynamic pricing for free-floating vehicle sharing systems. Transportation Science, 2023. 57(6): p. 1406-1432. [CrossRef]
  39. Klainerman, S. and J. Szeftel, Global Nonlinear Stability of Schwarzschild Spacetime under Polarized Perturbations:(AMS-210). Vol. 210. 2020: Princeton University Press.
  40. Sepanski, J.H. and X. Wang, New Classes of Distortion Risk Measures and Their Estimation. Risks, 2023. 11(11): p. 194. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated