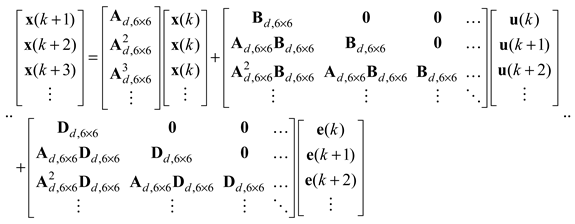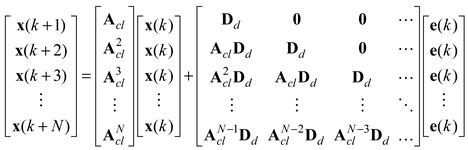Robust EMPC-Based Frequency Adaptive Grid Voltage Sensorless Control for an LCL-Filtered Grid-Connected Inverter

Preprint

Article

Robust EMPC-Based Frequency Adaptive Grid Voltage Sensorless Control for an LCL-Filtered Grid-Connected Inverter

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 January 2024

Posted:

03 January 2024

You are already at the latest version

Alerts

Abstract

A robust explicit model predictive control (EMPC)-based frequency adaptive grid voltage sensorless control is developed for a grid-connected inverter (GCI) via a linear matrix inequality (LMI) approach under the model parameter uncertainties and non-ideal grid environment. The control scheme is achieved by an enhanced prediction model rather than the conventional prediction model provided by fixed parameters to maintain the quality of grid currents injected into the grid when the model parameters are varied. Furthermore, an LMI-based observer is integrated with the disturbance observer to improve the reference tracking performance and reject disturbances. The proposed observer is employed for the grid frequency adaptive control without need of grid voltage sensors. The proposed current controller and observer employ the LMI scheme to maintain a stable and robust operation of the GCI. The discrete-time frequency response and pole-zero map analyses are used to investigate system stability and robustness against parameter uncertainties. Comprehensive simulation, experimental results and analyses clearly demonstrate the robustness of the proposed control scheme under various adverse test conditions with unexpected grid and system uncertainties.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Nowadays, grid-connected inverters (GCIs) are being increasingly developed to facilitate renewable energy generation systems, microgrid or smart grids [1,2]. The GCI systems should operate to effectively transfer the direct current (DC) power from distributed generators to alternative current (AC) power to inject it into the grid even under harsh unexpected grid conditions [3,4]. In particular, reducing the total harmonic distortion (THD) in the GCI output currents is one of the important challenges. In most grid interconnection standard, the harmonic content of the output current should be less than 5% even under non-ideal grid environment [5].

Commonly, to maximize the inverter power transfer efficiency, the pulse width modulation (PWM) inverters are utilized. To reduce the distortion of the injection currents into the utility grid and to meet the power quality standard [6], low pass filters are an essential component between the GCI and the utility grid. Among these filter types, the inductor-capacitor-inductor (LCL) filter offers superior harmonic suppression capability with reduced filter inductor size compared to others. Nevertheless, the stability of the whole system is easily harmed by the resonance peak of LCL filter. Therefore, the current control design should be accomplished not only to produce the high-quality of injected currents under several disturbance sources but also to stabilize the system by damping the resonance phenomenon [7,8].

In addition, the current controller of the GCI system should also consider the disturbance sources which come from both external and internal factors [9]. Particularly, the values of LCL filter components may be drifted from the known nominal values due to the manufacturing tolerance, aging effects, or weak grid conditions, which can be considered as internal uncertainties. The external disturbances primarily arise from the severe distortion or unbalanced behavior of the grid voltages [10,11].

Since power conversion systems should be operated with high efficiency as well as improved flexibility and profitability, many authors have a tendency to focus on robust algorithm, adaptive algorithm or learning algorithm to obtain the system stabilization even in the presence of harsh grid conditions [7,12,13,14,15,16,17]. The linear quadratic regulators (LQR) were proposed as a method to determine the optimal controller gains by means of a cost function minimization [18,19]. Compared to the pole placement method [10], the LQR method offers the advantage of achieving an optimal feedback gain set by choosing appropriate weighting factors. However, the LQR controllers commonly needs the user's experience and knowledge in choosing proper weighting factors. Other approaches in [7,12] present the linear matrix inequality (LMI) to obtain the controller gain optimally, in which the Lyapunov stability condition is employed to guarantee robust stability and good performance despite the model inaccuracy. Even though these studies provide satisfactory performance under parametric uncertainties, several external disturbances such as grid voltage imbalance degrade the current controller operations. Another approach [13] employs H∞ control to deal with the variation of the grid impedance caused by the weak grid. The robust performance of H∞ control is guaranteed even under parametric uncertainties. However, this study did not consider the grid voltage imbalances and frequency fluctuations of the real grid.

As a method to consider the system constraints effectively and to yield a fast output response, model predictive control (MPC) has been studied. If all the parameters in system are well-known, the MPC generally provides an excellent controller performance as well as an accurate output tracking [1,11,14,15,16]. However, the performance of the MPC depends on computationally intensive and accurate system models and parameters. In addition, the system stability of the MPC-based GCI is affected by parametric uncertainties and the weak grid. The LMI-based MPC method was also proposed in [7,17] to solve the problem of the conventional MPC. Although several non-ideal grid conditions were addressed, the control scheme in [7] does not consider a grid voltage sensorless control. Moreover, it does not consider severe parametric uncertainty conditions. In the study [17], the closed-loop analysis was presented to confirm the robust stability. However, severe grid disturbance such as grid harmonics and imbalanced grid voltages was not addressed.

This study investigates a robust explicit MPC (EMPC)-based frequency-adaptive grid voltage sensorless control of a GCI system that achieves robust stability, low computational burden, high efficiency, and good tracking performance despite model inaccuracies as well as external disturbances. Because the proposed control scheme does not require additional sensing devices for realizing the active damping method, integral term, and 2^nd order harmonic compensation term, the computational burden to implement the proposed scheme can be reduced, while maintaining a good tracking performance.

The proposed study is improved in two aspects. First, the LMI-based MPC algorithm is employed by an LQR-based prediction model in order to improve the stability of the GCI system against parametric uncertainties and to reduce the computational burden in comparison to the conventional MPC algorithm in [7]. In the proposed scheme, an LQR-based prediction model is obtained with state and control input at time step k to predict the overall prediction horizon. Second, to realize a current controller without the grid voltage sensors, the proposed controller employs a frequency-adaptive LMI-based resonant extended state observer to guarantee high estimation accuracy for grid voltages and system state variables with various grid conditions. In particular, the proposed LMI-based observer also integrates a disturbance observer to ensure a good performance of the resonant extended state observer by rejecting the influence of disturbances. Comprehensive simulation and experimental results as well as analyses effectively validate the control robustness of the proposed scheme under several adverse conditions such as internal parametric uncertainties as well as unexpected distorted and imbalanced grid.

2. System of a GCI

2.1. Modeling of a GCI with LCL Filter

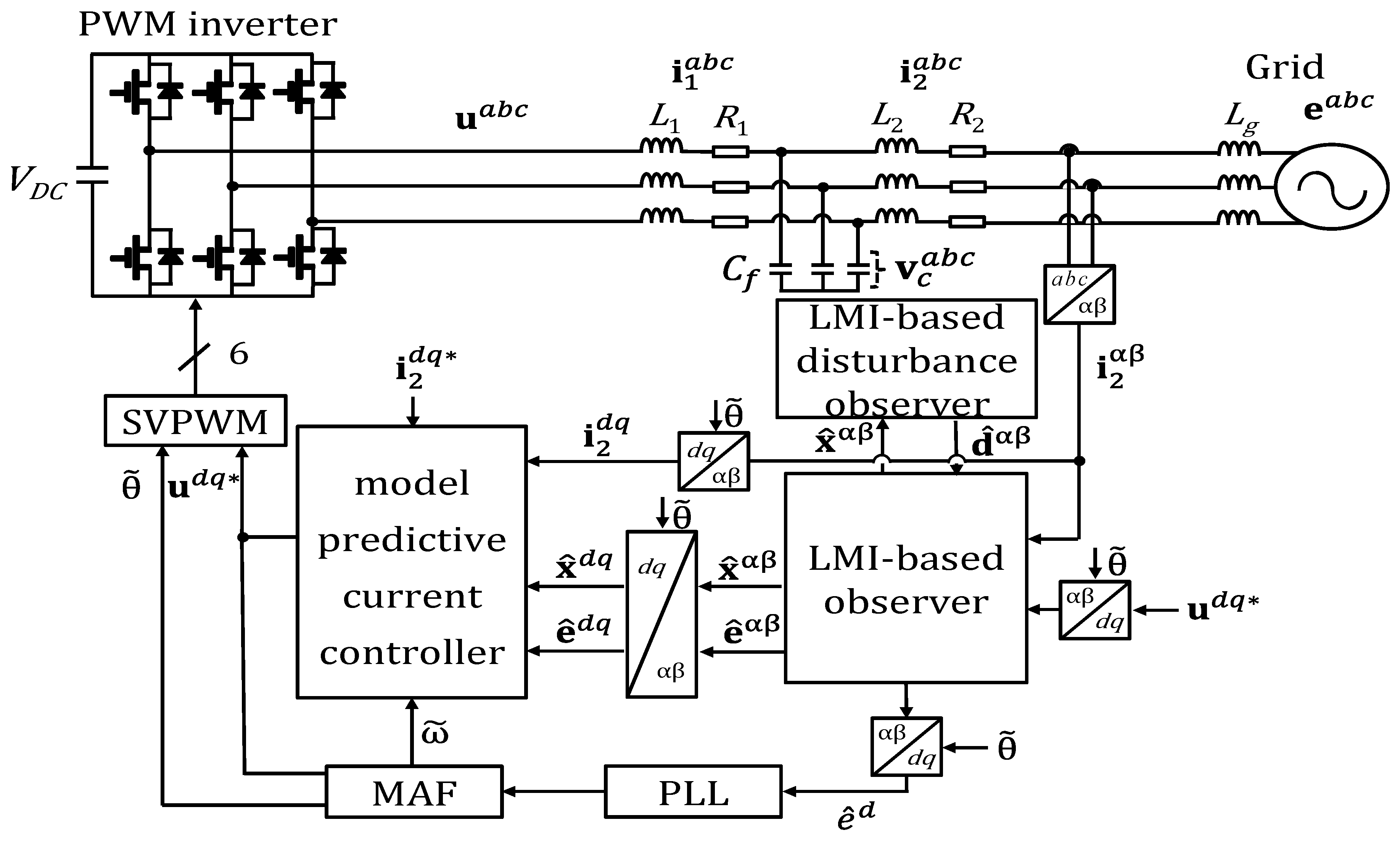
Figure 1 depicts the power circuit of a three-phase LCL-filtered GCI controlled by the proposed scheme which employs only the measurement of dc-link voltage and the grid-side currents. In Figure 1, L₁, R₁, L₂, and R₂ are the inverter-side filter inductance and resistance, and grid-side filter inductance and resistance, respectively, L_g is the grid inductance and C_f is the filter capacitance. In this figure, i₁, i₂, u, and v_c denote the inverter-side currents, the grid-side currents, the inverter output voltages, and the capacitor voltages, respectively, e is the utility grid voltages, d is the disturbance, and the symbol ‘^’ denotes the estimated quantity. Variable

\tilde{ω}

is the angular frequency of the moving average filter (MAF) that is deployed to eliminate frequency fluctuation obtained from the conventional phase lock loop (PLL) under grid voltage distortion. The superscripts ‘qd’ represent the qd-axis variables in the synchronous reference frame (SRF), ‘αβ’ represents the variables in the stationary frame, and ‘abc’ represents the phase variables.

The three-phase variables 'abc' in the natural frame are transformed into the variables ‘dq’ in the SRF by means of the Park’s transformation as:

[\begin{array}{l} f_{q} \\ f_{d} \end{array}] = [\begin{matrix} \cos (θ) & \cos (θ - \frac{2}{3} π) & \cos (θ + \frac{2}{3} π) \\ \sin (θ) & \sin (θ - \frac{2}{3} π) & \sin (θ + \frac{2}{3} π) \end{matrix}] [\begin{matrix} f_{a} \\ f_{b} \\ f_{c} \end{matrix}]

(1)

where f represents the variables and is the phase angle of the SRF.

By applying the Kirchhoff’s law and Park’s transformation, the inverter model is presented in the SRF as follows:

\frac{d}{d t} i_{2}^{q} (t) = - \frac{R_{2}}{L_{2}} i_{2}^{q} (t) - ω i_{2}^{d} + \frac{1}{L_{2}} v_{c}^{q} (t) - \frac{1}{L_{2}} e^{q} (t) + d_{1}

(2)

\frac{d}{d t} i_{2}^{d} (t) = - \frac{R_{2}}{L_{2}} i_{2}^{d} (t) + ω i_{2}^{q} + \frac{1}{L_{2}} v_{c}^{d} (t) - \frac{1}{L_{2}} e^{d} (t) + d_{2}

(3)

\frac{d}{d t} i_{1}^{q} (t) = - \frac{R_{1}}{L_{1}} i_{1}^{q} (t) - ω i_{1}^{d} - \frac{1}{L_{1}} v_{c}^{q} (t) + \frac{1}{L_{1}} v_{i}^{q} (t) + d_{3}

(4)

\frac{d}{d t} i_{1}^{d} (t) = - \frac{R_{1}}{L_{1}} i_{1}^{d} (t) + ω i_{1}^{q} - \frac{1}{L_{1}} v_{c}^{d} (t) + \frac{1}{L_{1}} v_{i}^{d} (t) + d_{4}

(5)

\frac{d}{d t} v_{c}^{q} (t) = - ω v_{c}^{d} - \frac{1}{C_{f}} i_{2}^{q} (t) + \frac{1}{C_{f}} i_{1}^{q} (t) + d_{5}

(6)

\frac{d}{d t} v_{c}^{d} (t) = ω v_{c}^{q} - \frac{1}{C_{f}} i_{2}^{d} (t) + \frac{1}{C_{f}} i_{1}^{d} (t) + d_{6}

(7)

where i₁, i₂, and v_c are the inverter-side current, the grid-side current, and the capacitor voltage, respectively, v_i is the inverter output voltage, e is the grid voltage, d is the disturbances, and ω is the angular frequency of the grid. In a matrix form, the GCI system in (2)-(7) can be presented by the continuous-time state-space model as follows:

\dot{x} (t) = A x (t) + B u (t) + D e (t) + d (t)

(8)

y (t) = C x (t)

(9)

where

x = {[i_{2}^{q}, i_{2}^{d}, i_{1}^{q}, i_{1}^{d}, v_{c}^{q}, v_{c}^{d}]}^{T}

is the state vector,

u = {[v_{i}^{q}, v_{i}^{d}]}^{T}

is the control input vector,

e = {[e^{q}, e^{d}]}^{T}

is the grid voltage vector, and

d = {[d_{1}, d_{2}, d_{3}, d_{4}, d_{5}, d_{6}]}^{T}

is the disturbance vector, and

A = [\begin{matrix} - R_{2} / L_{2} & - ω & 0 & 0 & 1 / L_{2} & 0 \\ ω & - R_{2} / L_{2} & 0 & 0 & 0 & 1 / L_{2} \\ 0 & 0 & - R_{1} / L_{1} & - ω & - 1 / L_{1} & 0 \\ 0 & 0 & ω & - R_{1} / L_{1} & 0 & - 1 / L_{1} \\ - 1 / C_{f} & 0 & 1 / C_{f} & 0 & 0 & - ω \\ 0 & - 1 / C_{f} & 0 & 1 / C_{f} & ω & 0 \end{matrix}]

(10)

B = [\begin{matrix} 0 & 0 \\ 0 & 0 \\ 1 / L_{1} & 0 \\ 0 & 1 / L_{1} \\ 0 & 0 \\ 0 & 0 \end{matrix}], D = [\begin{matrix} - 1 / L_{2} & 0 \\ 0 & - 1 / L_{2} \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{matrix}], C = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \end{matrix}] .

(11)

2.2. System Modeling under Parametric Uncertainties

Because of manufacturing tolerance in real filter parameters, the parameter values are greater than or less than the nominal values. In addition, the weak grid causes the grid impedance value to fluctuate. In this work, the LCL filter parameters are assumed to have uncertainties within certain ranges defined as follows:

L_{2, \min} \leq L_{2} \leq L_{2, \max} = L_{2} / δ_{1} \leq L_{2} \leq L_{2} δ_{1}

(12)

L_{1, \min} \leq L_{1} \leq L_{1, \max} = L_{1} / δ_{2} \leq L_{1} \leq L_{1} δ_{2}

(13)

C_{f, \min} \leq C_{f} \leq C_{f, \max} = C_{f} / δ_{2} \leq C_{f} \leq C_{f} δ_{2}

(14)

where

δ_{1} {and δ}_{2}

are the uncertainty coefficients of the LCL filter

(δ_{1} > 1, δ_{2} > 1) .

Those certain ranges are expressed as a convex combination of vertices

κ = \{\sum_{k = 1}^{2^{3}} ψ_{k} (A_{k}, B_{k}, C_{k}) | \sum_{k = 1}^{2^{3}} ψ_{k} = 1, ψ_{k} \geq 0\} .

(15)

The polytopic uncertainty set 𝜿 contains the uncertain system matrices which are obtained by considering a combination of eight extreme values.

2.3. Model Discretization

To discretize uncertain systems in the continuous-time, the zero-order hold approach is used in the proposed controller with the sampling period T_s for eight vertices of the polytopic model given in (8) and (15) as

x (k + 1) = A_{d i} x (k) + B_{d i} u (k) + D_{d i} e (k) + d_{d}

(16)

y (k) = C_{d i} x (k)

(17)

where

A_{d i} = e^{A_{i} T_{s}} = I + \frac{A_{i} T_{s}}{1!} + \frac{A_{i}^{2} T_{s}^{2}}{2!} + \dots

(18)

B_{d i} = (\int_{0}^{T_{s}} e^{A_{i} T_{s}} d τ) B_{i} = A_{i}^{- 1} (A_{d i} - I) B_{i}

(19)

D_{d i} = (\int_{0}^{T_{s}} e^{A_{i} T_{s}} d τ) D_{i} = A_{i}^{- 1} (A_{d i} - I) D_{i}

(20)

C_{d i} = C

(21)

for i = 1, 2, 3, , 8.

3. Proposed Current Control Design with LMI-based MPC

The MPC is known to be an optimal control strategy that derives control inputs using predicted future states and feedback information. Nevertheless, the optimization procedure must be repeated using new measurement values in each sampling period, so the online implementation causes a heavy computational burden on the digital signal processor (DSP). Moreover, since the performance of the conventional MPC scheme is mainly dependent on the accuracy of the plant model, this scheme is weak under unexpected uncertainties or disturbance [1], [14,15,16] . To address such limitations, the proposed EMPC is combined with LMI tool in this paper to reduce computational burden as well as to ensure satisfied output performance and robustness against both parametric uncertainties and grid disturbances.

3.1. Converional Prediction Model

In the conventional scheme, the inverter model is used to calculate the prediction of future states with the MPC. Using the system state (16), the prediction model from time step (k+1) to (k+N) are given as:

(22)

x_{p} (k + N) = A_{p} x_{p} (k) + B_{p} u_{p} (k + N) + D_{p} e_{p} (k + N)

(23)

u_{p} (k) = - [\begin{matrix} K_{L} & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & K_{L} \end{matrix}] x (k)

(24)

where

x_{p}

is the future prediction states,

u_{p}

is the control inputs,

e_{p}

is the grid voltages, N is the length of prediction horizon, and

K_{L}

is the prediction model gain.

3.2. LQR-based Prediction Model

The conventional prediction model does not take into account the model parameter variations and uncertainties. The performance of the conventional MPC may be rapidly degraded under both internal and external disturbances affecting the system in practical applications. To address these effects, an LQR-based prediction model is presented to reduce the dependence on parameter values of the prediction model. Also, the proposed prediction model has the advantage of requiring only a system state at the current time k.

The LQR-based prediction model provides an optimal prediction model gain

K_{L}

in (24) by means of the minimization of the quadratic cost function as

J_{p} = \sum_{l = 0}^{\infty} x_{p}^{T} (k + l) Q_{p} x_{p} (k + l) + u_{p}^{T} (k + l) R_{p} u_{p} (k + l)

(25)

where

Q_{p}

denotes a positive-definite matrix and

R_{p}

denotes a positive-semidefinite matrix. To generate the optimal

u_{p}

in (24) with closed-loop form, the discrete-time algebraic Riccati equation (ARE) can be determined as follows:

P_{p} = Q_{p} + A_{p}^{T} P_{p} A_{p} - A_{p}^{T} P_{p} B_{p} {(R_{p} + B_{p}^{T} P_{p} B_{p})}^{- 1} B_{p}^{T} P_{p} A_{p}

(26)

where

P_{p}

denotes the solution of the discrete-time Riccati equation. The LQR can easily reach optimal control with minimal control effort. The closed-loop form

A_{c l} = A_{d} - K_{L} B_{d}

can be obtained using the control input (24). The LQR-based prediction model from time step (k+1) to (k+N) which constitutes the enhanced prediction model is determined as

(27)

The LQR-based prediction model generation removes the requirement for future inputs unlike the conventional prediction model (22) and greatly simplifies computational process. The unknown grid voltage in (16) can be considered to be constant as follow [17]:

e (k) = e (k + 1) .

(28)

The proposed LQR-based prediction model is developed to enhance the robustness against the parametric uncertainties without requiring self-tuning processes.

3.3. Explicit Model Predictive Control

By substituting the references of grid-side currents

i_{2}^{q *}

i_{2}^{d *}

and the estimated values of grid voltages

{\hat{e}}^{q}

{\hat{e}}^{d}

in (16), the system reference state and control input are obtained in the steady-state as

v_{c}^{q *} = R_{2} i_{2}^{q *} + L_{2} \tilde{ω} i_{2}^{d *} + {\hat{e}}^{q}

(29)

v_{c}^{d *} = R_{2} i_{2}^{d *} - L_{2} \tilde{ω} i_{2}^{q *} + {\hat{e}}^{d}

(30)

i_{1}^{q *} = i_{2}^{q *} + C_{f} \tilde{ω} v_{c}^{d *}

(31)

i_{1}^{d *} = i_{2}^{d *} - C_{f} \tilde{ω} v_{c}^{q *}

(32)

u^{q *} = R_{1} i_{1}^{q *} + L_{1} \tilde{ω} i_{1}^{d *} + v_{c}^{q *}

(33)

u^{d *} = R_{1} i_{1}^{d *} - L_{1} \tilde{ω} i_{1}^{q *} + v_{c}^{d *}

(34)

where

i_{1}^{q *}

and

i_{1}^{d *}

are the references of inverter-side currents, and

v_{c}^{q *}

and

v_{c}^{d *}

are the references of capacitance voltages.

To design the MPC, a cost function

J_{M P}

is constructed by considering both the difference between the reference and system states, and difference between the reference and control input as follows:

J_{M P} = \sum_{j = 1}^{N} [e_{x} (k + j)]^{T} Q_{M P} [e_{x} (k + j)] + [e_{u} (k + j)]^{T} R_{M P} [e_{u} (k + j)]

(35)

where

e_{x} (k) = \hat{x} (k) - x^{*} (k)

e_{u} (k) = u (k) - u^{*} (k)

x^{*} = {[i_{2}^{q *}, i_{2}^{d *}, i_{1}^{q *}, i_{1}^{d *}, v_{c}^{q *}, v_{c}^{d *}]}^{T}

represents the reference of state vector,

u^{*} = {[u^{q *}, u^{d *}]}^{T}

is the reference of control input vector,

Q_{M P}

is a symmetric positive-definite weighting matrix, and

R_{M P}

is a symmetric positive-semidefinite weighting matrix. To obtain the MPC input

u (k)

, the first derivative of

J_{M P} (k)

with respect to

u (k)

is considered as

\frac{\partial J_{M P} (x (k), u (k))}{\partial u (k)} = 0 .

(36)

Then, the control input of the MPC is derived from (35) as

u (k) = (B_{M}^{T} [\begin{matrix} Q_{M P} & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & Q_{M P} \end{matrix}]) A_{M} {[B_{M}^{T} [\begin{matrix} Q_{M P} & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & Q_{M P} \end{matrix}] B_{M} + R_{M P}]}^{- 1} e_{x} + u^{*} (k)

(37)

u (k) = K_{M P} e_{x} (k) + u^{*} (k)

(38)

where

A_{M} = [\begin{matrix} A_{c l} \\ A_{c l}^{2} \\ A_{c l}^{3} \\ ⋮ \\ A_{c l}^{N} \end{matrix}], B_{M} = [\begin{matrix} D_{d} & 0 & 0 & \dots \\ A_{c l} D_{d} & D_{d} & 0 & \dots \\ A_{c l}^{2} D_{d} & A_{c l} D_{d} & D_{d} & \dots \\ ⋮ & ⋮ & ⋮ & ⋱ \\ A_{c l}^{N - 1} D_{d} & A_{c l}^{N - 2} D_{d} & A_{c l}^{N - 3} D_{d} & \dots \end{matrix}]

At each time step k, the EMPC selects the best MPC input signal to minimize the cost function as in (36). As a result, the errors between system states and references values

e_{x} (k)

are also minimized, and the excellent reference tracking performance is achieved.

3.4. LMI-based Parameter Derivation

To achieve the reference tracking objective of zero steady-state error, the cost function in (35) is minimized. In the conventional full-state feedback controller described in [20], additional integral control terms and resonant control terms tuned at the 2^nd order harmonic are included in the system model to guarantee a good tracking performance even in the presence of the grid voltage imbalances. Obviously, this approach increases the computation burden due to the augmentation of multiple control terms. On the contrary, the proposed method ensures a good performance of reference tracking regardless of balanced or imbalanced grid environment by means of the control input in (37) without using any additional augmentation of control terms.

One of the challenging parts in the MPC design is to determine the proper weighting matrix in the cost function (35) and to stabilize a parametric uncertain system. To address this concern, the LMI method is incorporated into the MPC design, which ensures robustness under parametric uncertainty boundaries. Moreover, it is also easier to systematically find a weighting matrix

Q_{M P}

of the cost function in (35). To design the LMI–based MPC, the Lyapunov function is constructed as

V (k) = e_{x} {(k)}^{T} Q_{M P} e_{x} (k) .

(39)

Minimizing the cost function (35) is difficult when the polytopic uncertainties are included in system model. To overcome this limitation, the LQR-LMI method in [8] is deployed in order to ensure the robust stability of system. Particularly, the LMI approach ensures system stability and robust performance if and only if

V (k + 1) - V (k) \leq - [e_{x} {(k)}^{T} Q_{L} e_{x} (k) + e_{u} {(k)}^{T} R_{L} e_{u} (k)] .

(40)

From (40), the LMI is derived as follows:

{(A_{d i} + B_{d i} Φ)}^{T} Q_{M P} (A_{d i} + B_{d i} Φ) - Q_{M P} < - Q_{L} - Φ^{T} R_{L} Φ .

(41)

where

Q_{L}

and

R_{L}

denote the weighting matrices for the LQR-LMI method,

Φ

is the gain determined in order that the Lyapunov function monotonically decreases. Multiplying the definite matrix

Y (Y = Q_{M P}^{- 1})

on both sides of (41) yields

Y^{T} - Y^{T} Q_{L} Y - {(Φ Y)}^{T} R_{L} Φ Y - {(A_{d i} Y + B_{d i} Φ Y)}^{T} Q_{M P} (A_{d i} Y + B_{d i} Φ Y) \geq 0 .

(42)

Utilizing Schur complement to (42) yields

Z = [\begin{matrix} Y & {(Φ Y)}^{T} & T_{i}^{T} & Y^{T} \\ Φ Y & R_{L}^{- 1} & 0 & 0 \\ 0 & 0 & Y & 0 \\ Y & 0 & 0 & Q_{L}^{- 1} \end{matrix}] \geq 0

(43)

where

Τ_{i} = A_{d i} Y + B_{d i} Φ Y

for i = 1, 2, 3, ⋯, 8. Lastly, the LMI problem in the sense of Lyapunov theory over the infinite horizon is stable if and only if:

\sum_{k = 0}^{\infty} [V (k + 1) - V (k)] = V (\infty) - V (0) \leq \sum_{k = 0}^{\infty} - [e_{x} {(k)}^{T} Q_{L} e_{x} (k) + e_{u} {(k)}^{T} R_{L} e_{u} (k)] .

(44)

As presented in the approach [12],

V (\infty

) is converged to zero in a stable controlled system. Thus, it yields that the cost function of (44) should be less than

V (0)

. If

σ

denotes an upper bound of

V (0),

the LMI holds as

V (0) = e_{x} {(0)}^{T} Q_{M P} e_{x} (0) \leq σ .

(45)

Then, a weighting matrix

Q_{M P}

in (35) can be obtained by solving the optimization problem as

\begin{matrix} M I N σ \\ Y \end{matrix} subject to [\begin{matrix} Z & 0 & 0 \\ 0 & σ & e_{x}^{T} (0) \\ 0 & e_{x} (0) & Y \end{matrix}] \geq 0

(46)

where

Ζ

denotes the matrix in (43). The weighting matrix of the MPC in (35) is obtained as

Q_{M P} = Y^{- 1}

by the LMI optimization method. The main advantage of this approach is that the solution ensures strong robustness and stability under system uncertainties.

3.5. Distorted Harmonic Compensation

To eliminate the negative impacts from the distortion in grid voltages and to ensure high-quality sinusoidal grid currents, the proportional resonance (PR) controllers with grid frequency-adaptive capability are constructed in parallel with the proposed EMPC control scheme. The grid voltage harmonics in the 5^th, 7^th, 11^th, and 13^th orders in ‘abc’ frame are effectively removed only with light computational burden with the PR controllers tuned at 6^th and 12^th orders in SRF. The frequency-adaptive PR controllers are expressed as [21]:

P R_{n} (k) = L_{n P R} \frac{z^{2} + (2 - \frac{{(n \tilde{ω} T_{s})}^{2}}{2} + \frac{{(n \tilde{ω} T_{s})}^{4}}{24}) z + (1 - \frac{{(n \tilde{ω} T_{s})}^{2}}{2} + \frac{{(n \tilde{ω} T_{s})}^{4}}{24})}{z^{2} - 2 \cos (n \tilde{ω} T_{s}) z + 1}

(47)

where n= 6, 12 is the harmonic order,

L_{n P R}

is the PR gain for 6^th and 12^th order. It is worth mentioning that the filtered grid frequency

ω^{˜}

is updated by online for the PR controllers to avoid the degradation of harmonic suppression performance under the grid frequency variation.

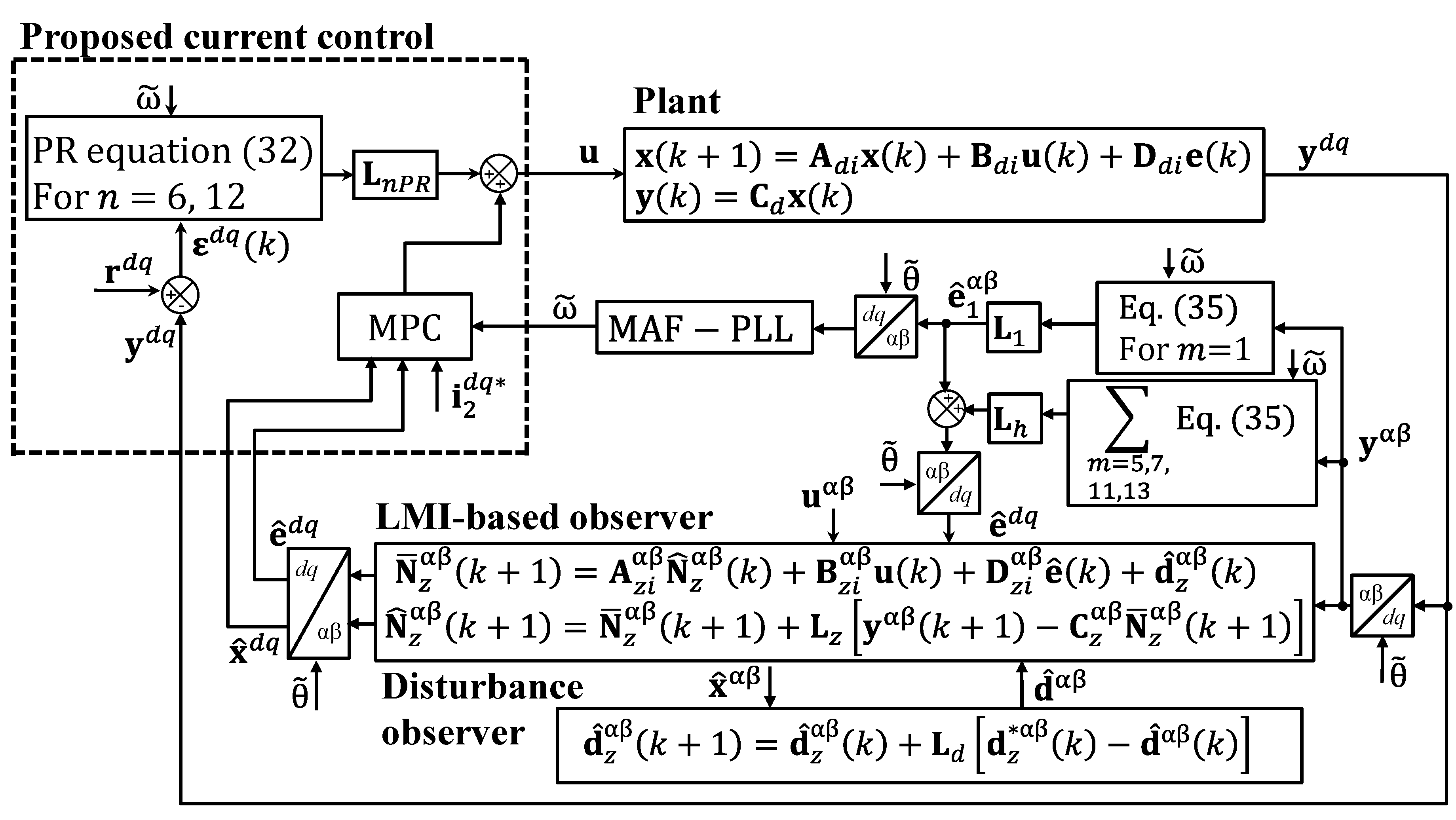
4. Frequency-adaptive Grid Voltage Sensorless Control Scheme

Figure 2 shows the structure of the frequency-adaptive grid voltage sensorless controller, in which

ε^{d q} = r^{d q} - y^{d q}

denotes the grid current error,

r^{d q} = {[i_{2}^{q *}, i_{2}^{d *}]}^{T}

y^{d q} = {[i_{2}^{q}, i_{2}^{d}]}^{T}

, and

L_{1}

and

L_{h}

are the gains of the proposed LMI-based observer.

4.1. LMI-based Observer with Disturbance Observer for Sensorless Control

In this section, an LMI-based observer is deployed to estimate the entire system state variables and grid voltages, which mitigates the influence of the parametric uncertainties. From the grid voltage estimate, the grid phase angle and angular frequency are extracted. Finally, the estimated angular frequency information is used to adjust the LMI-based observer model. In addition, the extracted grid frequency is also updated in the controller and harmonic compensator to prevent performance degradation under frequency fluctuations. Because the proposed LMI-based observer is designed in the stationary reference frame, the system model can be discretized easily irrespective of frequency variation. For the LMI-based observer algorithm, the resonant model is adopted which is expressed as the discrete-time transfer function as [22]

G_{m} = \frac{z^{2} - \cos (m \tilde{ω} T_{s}) z}{z^{2} - 2 \cos (m \tilde{ω} T_{s}) z + 1}

(48)

where m is the harmonic order for m = 1, 5, 7, 11, 13. In state-space, the transfer function in (48) is written as

[\begin{array}{l} {\hat{h}}_{m}^{α} (k + 1) \\ {\hat{h}}_{m}^{β} (k + 1) \end{array}] = [\begin{matrix} 2 \cos (m \tilde{ω} T_{s}) & 1 \\ - 1 & 0 \end{matrix}] [\begin{array}{l} {\hat{h}}_{m}^{α} (k) \\ {\hat{h}}_{m}^{β} (k) \end{array}] + [\begin{array}{l} L_{h}^{α} \cos (m \tilde{ω} T_{s}) \\ - L_{h}^{β} \end{array}] [y^{α β} (k + 1) - C_{d i}^{α β} {\bar{x}}_{d i}^{α β} (k + 1)]

(49)

where

L_{h}

is the resonant observer gain. The grid voltage estimate is constructed by the sum of the fundamental and harmonic components as

{\hat{e}}^{α β} (k) = \sum_{m} {\hat{h}}_{m}^{α β} (k), for m = 1, 5, 7, 11, 13 .

(50)

The proposed LMI-based observer is augmented into the state model in the stationary reference frame as follows:

{\bar{N}}_{z}^{α β} (k + 1) = A_{z i}^{α β} {\hat{N}}_{z}^{α β} (k) + B_{z i}^{α β} u (k) + D_{z i}^{α β} \hat{e} (k) + {\hat{d}}_{z}^{α β} (k) .

(51)

{\hat{N}}_{z}^{α β} (k + 1) = {\bar{N}}_{z}^{α β} (k + 1) + L_{z} [y^{α β} (k + 1) - C_{z}^{α β} {\bar{N}}_{z}^{α β} (k + 1)]

(52)

where

N_{z} = {[x^{α β T}, h_{1}^{α β T}, h_{5}^{α β T}, h_{7}^{α β T}, h_{11}^{α β T}, h_{13}^{α β T}]}^{T}

A_{z i}^{α β} = [\begin{matrix} A_{d i}^{α β} & D_{d i}^{α β} & D_{d i}^{α β} & D_{d i}^{α β} & D_{d i}^{α β} & D_{d i}^{α β} \\ 0 & e_{h 1} & 0 & 0 & 0 & 0 \\ 0 & 0 & e_{h 5} & 0 & 0 & 0 \\ 0 & 0 & 0 & e_{h 7} & 0 & 0 \\ 0 & 0 & 0 & 0 & e_{h 11} & 0 \\ 0 & 0 & 0 & 0 & 0 & e_{h 13} \end{matrix}],

L_{z} = [\begin{matrix} L_{e} \\ L_{1} \\ L_{h} \end{matrix}]

B_{z i}^{α β} = [\begin{matrix} B_{d i}^{α β} \\ 0 \end{matrix}], D_{z i}^{α β} = [\begin{matrix} D_{d i}^{α β} \\ 0 \end{matrix}]

d_{z}^{α β} = [\begin{matrix} d^{α β} \\ 0 \end{matrix}]

C_{z}^{α β} = [\begin{matrix} C_{d}^{α β} & 0 \end{matrix}]

for

i =

1, 2, ⋯, 8,

e_{h m} = [\begin{matrix} 2 \cos (m ω^{˜} T_{s}) & 1 \\ - 1 & 0 \end{matrix}]

L_{z}

denotes the LMI-based observer gain and

L_{e}

denotes state observer gain. The estimated state

{\hat{N}}_{z i}^{α β}

is obtained by the recent measurements of

y^{α β}

and first estimated state

{\bar{N}}_{z i}^{α β}

at time step (k+1)

T_{s}

The disturbance observer is also designed for the purpose of improving the estimation performance of LMI-based observers as follows:

{\hat{d}}_{z}^{α β} (k + 1) = {\hat{d}}_{z}^{α β} (k) + L_{d} [d_{z}^{* α β} (k) - {\hat{d}}_{z}^{α β} (k)] .

(53)

d_{z}^{* α β} (k) = N_{z}^{* α β} (k) - {\hat{N}}_{z}^{α β} (k)

(54)

where

N_{z}^{* α β} = {[x_{d}^{* α β T}, {\hat{h}}_{1}^{α β T}, {\hat{h}}_{5}^{α β T}, {\hat{h}}_{7}^{α β T}, {\hat{h}}_{11}^{α β T}, {\hat{h}}_{13}^{α β T}]}^{T}

and

L_{d}

denotes disturbance observer gain. An error dynamic is derived by subtracting the LMI-based observer in (51)-(52) and a disturbance observer in (53)-(54) from the system model in (16) to yield

[\begin{array}{l} N_{z}^{α β} (k + 1) - {\hat{N}}_{z}^{α β} (k + 1) \\ d_{z}^{α β} (k + 1) - {\hat{d}}_{z}^{α β} (k + 1) \end{array}] = [\begin{matrix} A_{z i}^{α β} - L_{z} C_{z}^{α β} A_{z i}^{α β} & I - L_{z} C_{z}^{α β} \\ - L_{d} & I - L_{d} \end{matrix}] [\begin{array}{l} N_{z}^{α β} (k) - {\hat{N}}_{z}^{α β} (k) \\ d_{z}^{α β} (k) - {\hat{d}}_{z}^{α β} (k) \end{array}]

(55)

z_{e} (k + 1) = η z_{e} (k) .

(56)

The Lyapunov function

ν

(k) is defined to obtain the observer gain set as

υ (k) = z_{e}^{T} (k) W z_{e} (k)

(57)

where

W = [\begin{matrix} W_{1} & 0 \\ 0 & W_{2} \end{matrix}]

is the weighting matrix. To ensure the stable observer, (57) should monotonically decrease, i.e.,

υ (k + 1) < υ (k)

. It leads the LMI as below [17]

η^{T} W η < W < ζ^{2} W = W_{0}

(58)

W_{0} - η^{T} (W W^{- 1}) W η > 0

(59)

where the convergence rate

ζ

(0 <

ζ

< 1) minimizes the Lyapunov function to determine the optimal observer gains. Applying the Schur complement yields

\begin{matrix} M I N ζ \\ W_{0}, W \end{matrix} subject to [\begin{matrix} W_{0} & ɤ^{- 1} \\ ɤ & W \end{matrix}] \geq 0

(60)

where

ɤ = [\begin{matrix} W_{1} A_{z i}^{α β} - Y_{z} C_{z}^{α β} A_{z i}^{α β} & W_{1} - Y_{z} C_{z}^{α β} \\ - Y_{d} & W_{2} - Y_{d} \end{matrix}]

Then, the LMI-based observer gains are obtained as

L_{z} = W_{1}^{- 1} Y_{z}

and the disturbance observer gains are as

L_{d} = W_{2}^{- 1} Y_{d}

. In this paper, the LMI method is solved by using MATLAB toolbox SeDuMi [23] and YALMIP [24]. The proposed LMI-based observer ensures zero estimation error at steady-state even under frequency fluctuation and grid distortion.

4.2. Frequency Estimation

From the grid voltage estimates, the grid phase angle and frequency are directly extracted by using a MAF-PLL [21] to realize the synchronization process without the use of grid voltage sensors. In general, the controller and observer performance is severely influenced by the accuracy of the estimated grid frequency. To prevent the performance degradation caused by the grid frequency variation or fluctuation, the estimated grid frequency is adaptively updated by online. By using the MAF, the filtered grid frequency is represented as follows:

\tilde{ω} (k) = \frac{1}{M} \sum_{i = 0}^{M - 1} \hat{ω} (k - i)

(61)

where

\hat{ω}

is the estimated grid angular frequency from the estimated grid voltages,

\tilde{ω}

is the filtered angular frequency, and

M

is the number of samples in window. Also, the phase delay is compensated by an adaptive delay compensator.

5. Stability Analysis

The stability of the proposed control scheme is investigated under the variation of the grid impedance and parametric uncertainties. The proposed control achieves excellent tracking performance as well as strong robustness under weak grid conditions. The eigenvalue locations and frequency responses of the proposed scheme are presented in the z-domain. Since the grid current controller is designed in ‘dq’ frame while the LMI-based observer is designed in ‘

α β

’ frame in the proposed scheme, the eigenvalues are investigated separately.

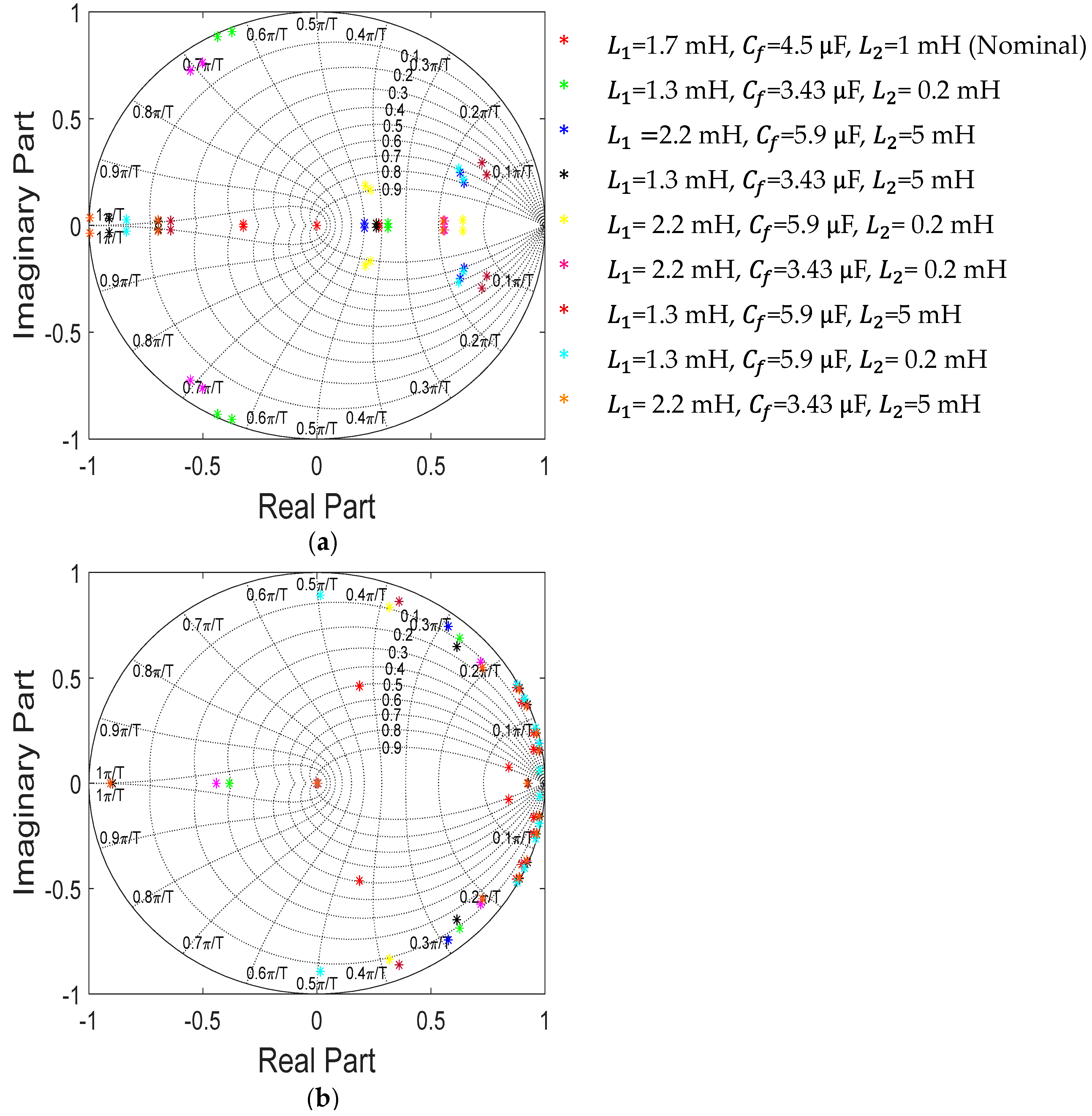
5.1. Eigenvalues of The Proposed Scheme

Figure 3a,b show the eigenvalue plots for the proposed EMPC scheme and the proposed LMI-based observer under the filter parametric uncertainties. It is noted that the grid impedance variation caused by weak grid is included in L₂ variation. It is confirmed from these figures that all eigenvalues maintain inside the stable region of unit circle despite the changes in filter parameters. This effectively proves the robustness of the proposed scheme.

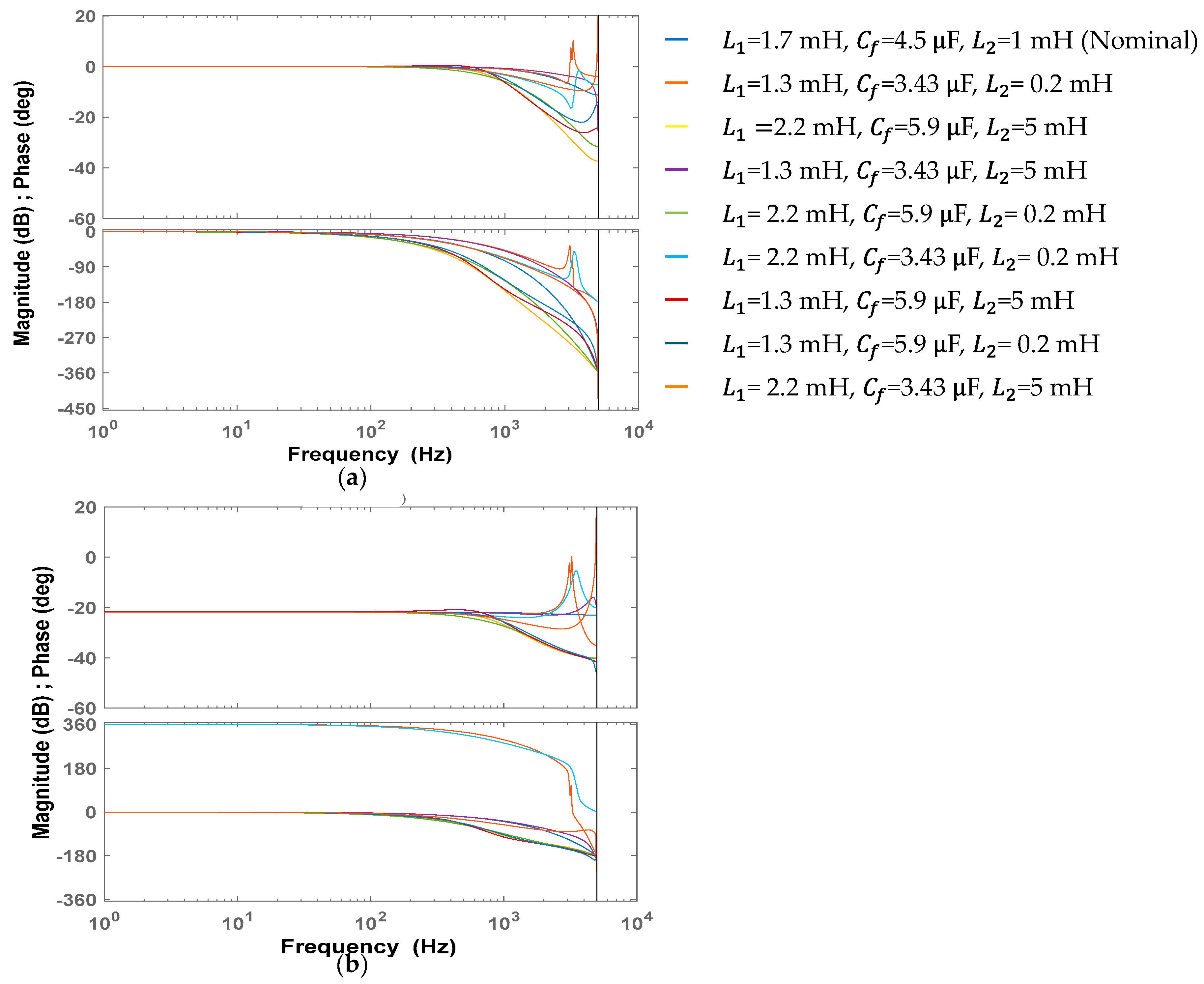
5.2. Frequency Responses of The Proposed EMPC Scheme

Figure 4 shows the frequency responses of the proposed EMPC scheme for the reference tracking performance and disturbance rejection under parametric uncertainties. Frequency responses are obtained for all vertices of the polytopic system model. Similarly, the transfer function is obtained by considering the sum of series L₂ and L_g (L₂ + L_g ). However, the impact of the proposed LMI-based adaptive observer and PR controller are not taken into account. It is clearly confirmed from Figure 4 that the proposed EMPC method provides a superior reference tracking as well as complete disturbance rejection capability.

6. Simulation Validation

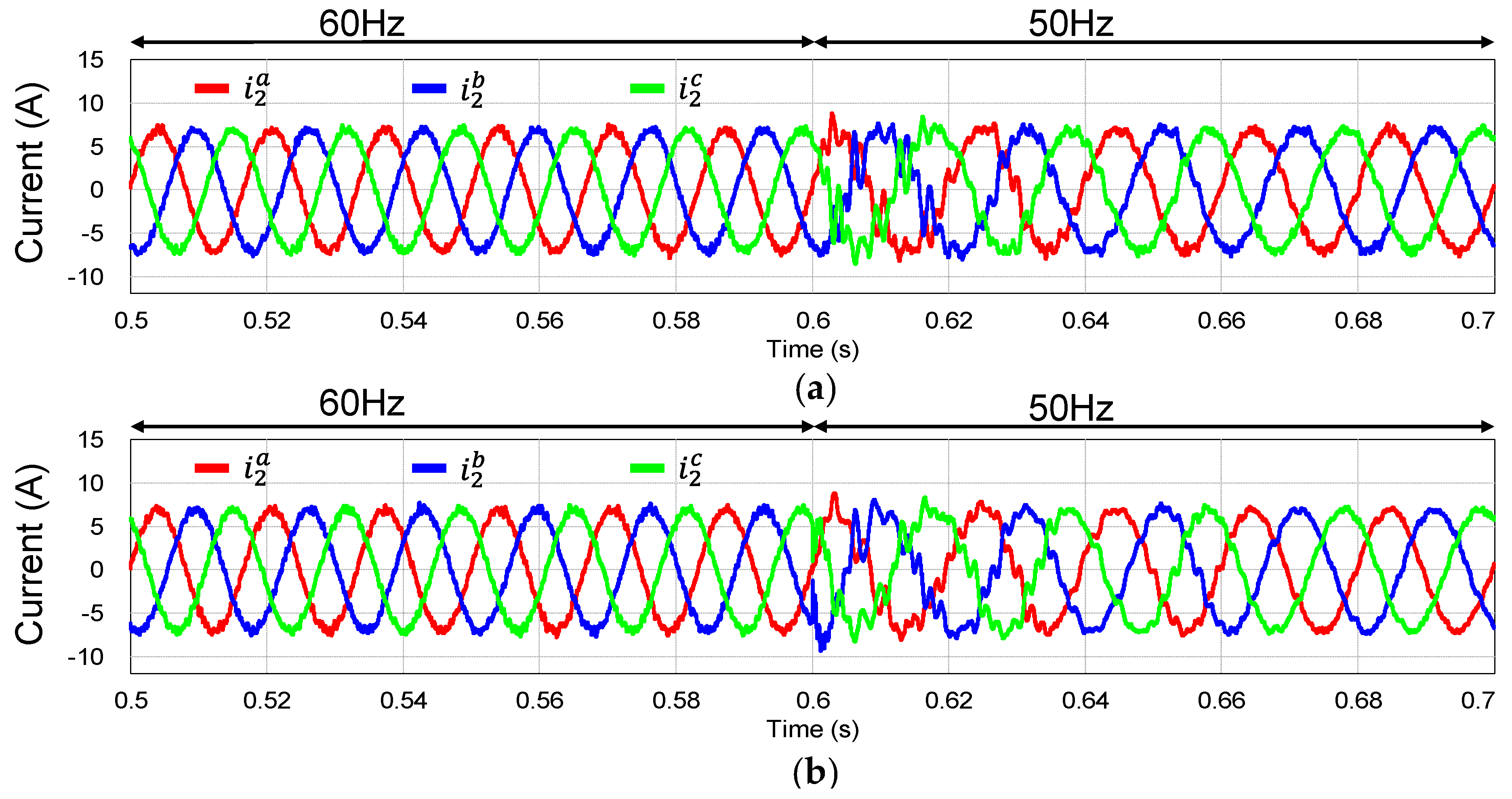
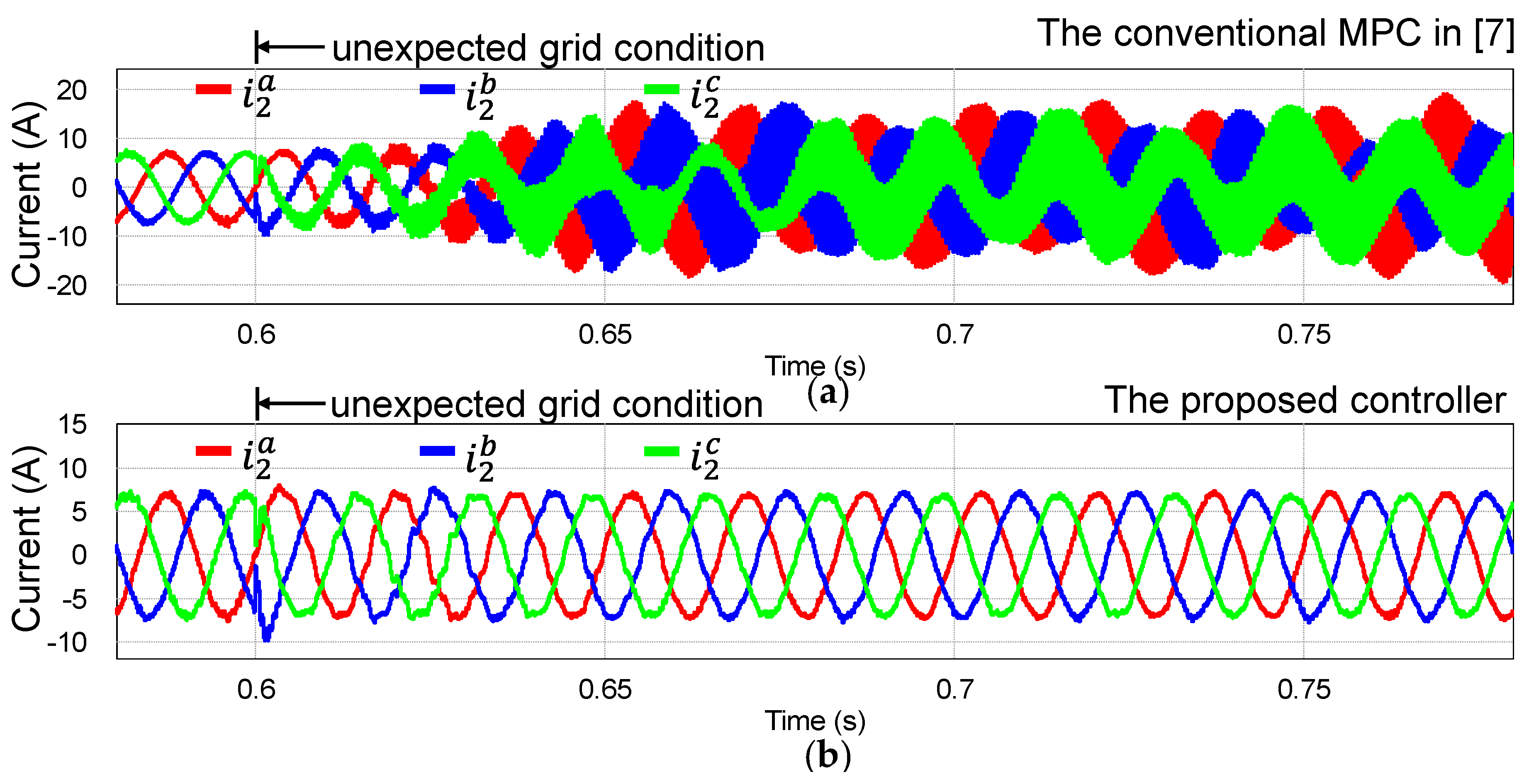
To validate the effectiveness of the proposed scheme, the simulations are conducted using the PSIM software for a three-phase GCI prototype. The GCI system parameters are represented in Table 1. The performance of the proposed control method is evaluated under the 5^th, 7^th, 11^th, and 13^th grid voltage harmonic components with 5% of the fundamental grid voltage magnitude. Figure 5 represents the response of three-phase grid-side currents produced by the proposed control method by the simulation when the grid voltages have distortion and frequency variation from 60 Hz to 50 Hz at 0.6 s. The waveform in Figure 5a shows the high-quality grid currents even under harsh disturbance from grid. Figure 5b shows the current responses when additional grid impedance (

L_{g}

=4 mH) is applied in addition to distorted grid voltages and frequency jump from 60 Hz to 50 Hz at 0.6 s. The results of Figure 5 demonstrate that the proposed current controller ensures strong robustness and good control performance under grid voltage distortion, grid frequency change, and grid impedance uncertainty.

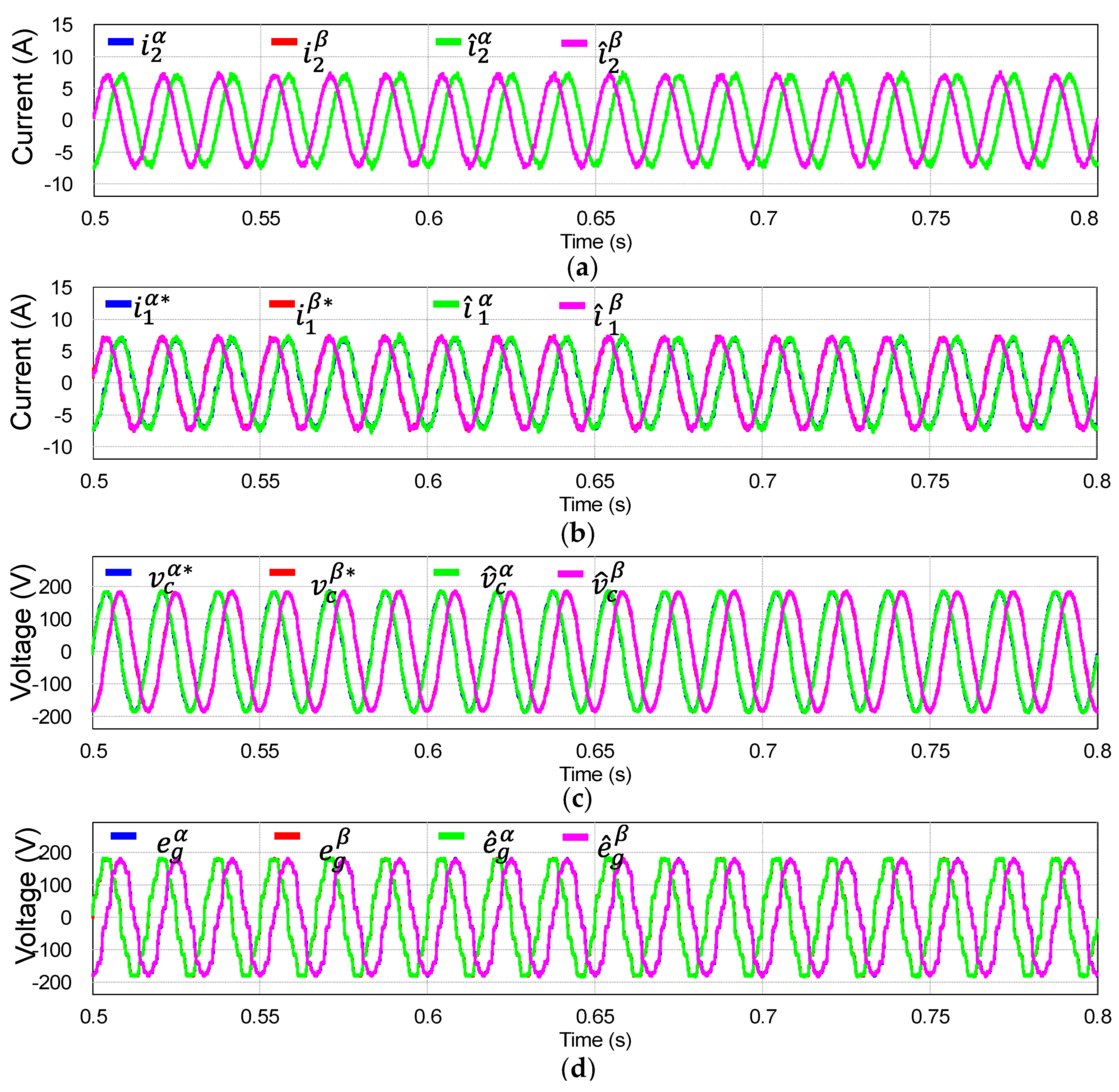
The reliability of a grid voltage sensorless operation are mainly dependent on the estimating performance of the grid voltages. Figure 6 evaluates the estimating performance of the proposed LMI-based observer designed in

α β

frame by simulation results by comparing the estimated states with measured states or references. The estimated and measured states for the grid currents are presented in Figure 6a, the estimated and reference inverter currents in Figure 6b, the estimated and reference capacitor voltages in Figure 6c, and the estimated and measured gird voltages in Figure 6d. It is confirmed that the proposed LMI-based observer ensures stability and estimating capability.

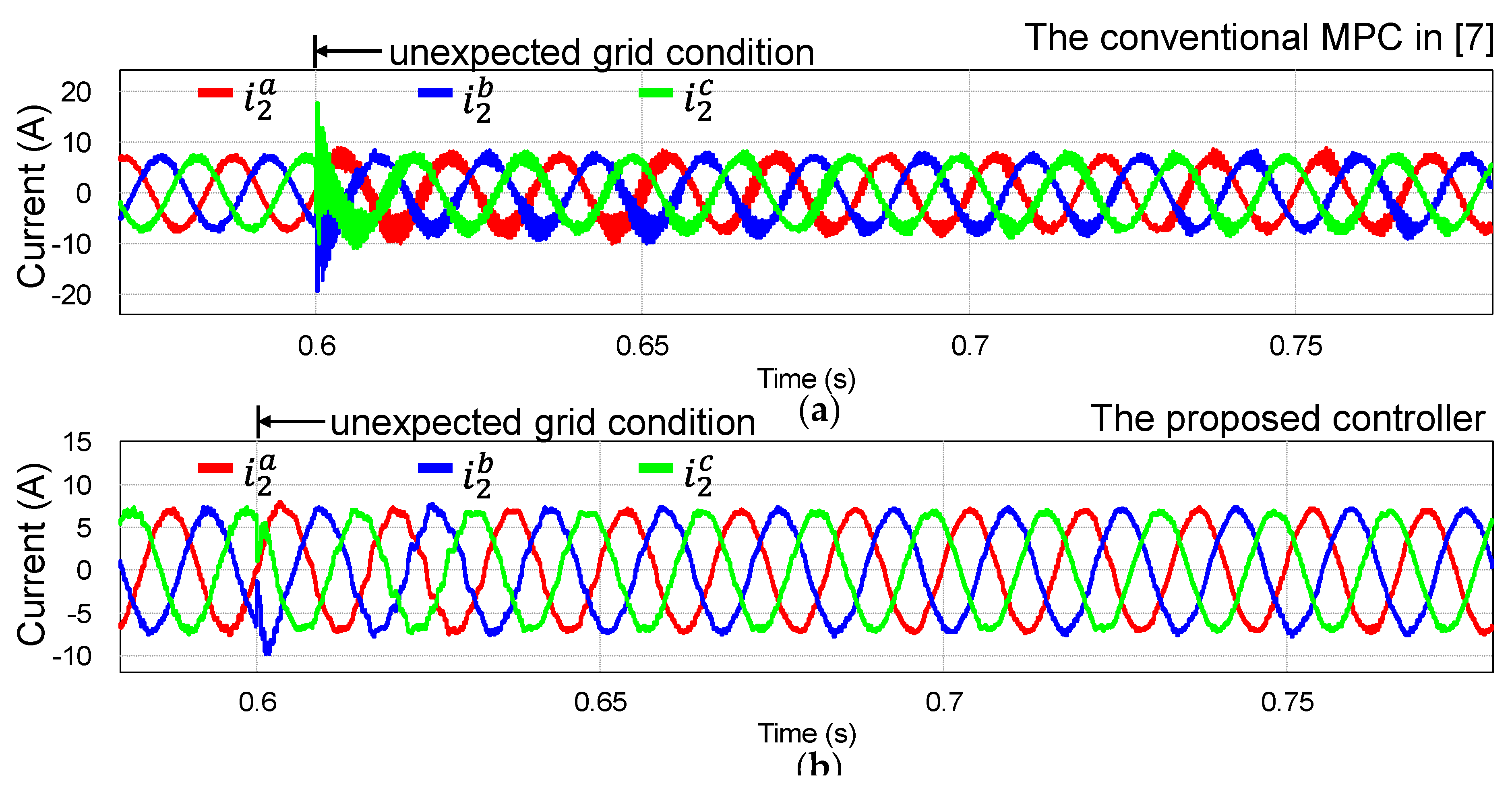
Figure 7 and Figure 8 show the comparative results between the MPC presented in [7] and the proposed controller when the grid condition suddenly changes. For fair comparison of only the controller with the proposed EMPC method, the conventional MPC scheme in [7] is constructed with the same proposed LMI-based observer. Figure 7 shows the grid current responses of two control schemes under the grid voltage distortion and imbalance with uncertain grid impedance. Figure 8 shows the grid current responses controlled by two control schemes under the grid voltage distortion and imbalance as well as filter parametric uncertainty. Two control methods exhibit distinct control performance. As soon as the parametric uncertainty is added to the conventional MPC, the grid-injected current quality is degraded significantly with high oscillation in phase currents as shown in Figure 7a and Figure 8a. On the contrary, the proposed scheme effectively stabilizes the system, yielding sinusoidal currents as in Figure 7b and Figure 8b. After a transient period, the THD values of phase currents in the steady-state are 3.1% and 2.83% in Figure 7b and Figure 8b, respectively, which meets the standard for the quality of the injected output current [6]. The comparison results clearly demonstrate that the proposed scheme ensures strong robustness against unexpected grid conditions.

7. Experimental Validation

The proposed control method is implemented in the lab-based experimental system to validate the control performance and robustness of the presented controller by experiments. Figure 9 depicts the experimental test setup, in which the programmable AC power source is utilized to realize the distorted and imbalanced grid environment. To implement the proposed EMPC-based frequency-adaptive grid voltage sensorless control, the DSP TMS320F28335 is used. To construct the system with the proposed method, only two grid currents and DC-link voltage are measured. The grid voltages are not only contaminated by harmonic distortion, but also imbalanced with

e_{a}

drop to 70.56% from the nominal voltage.

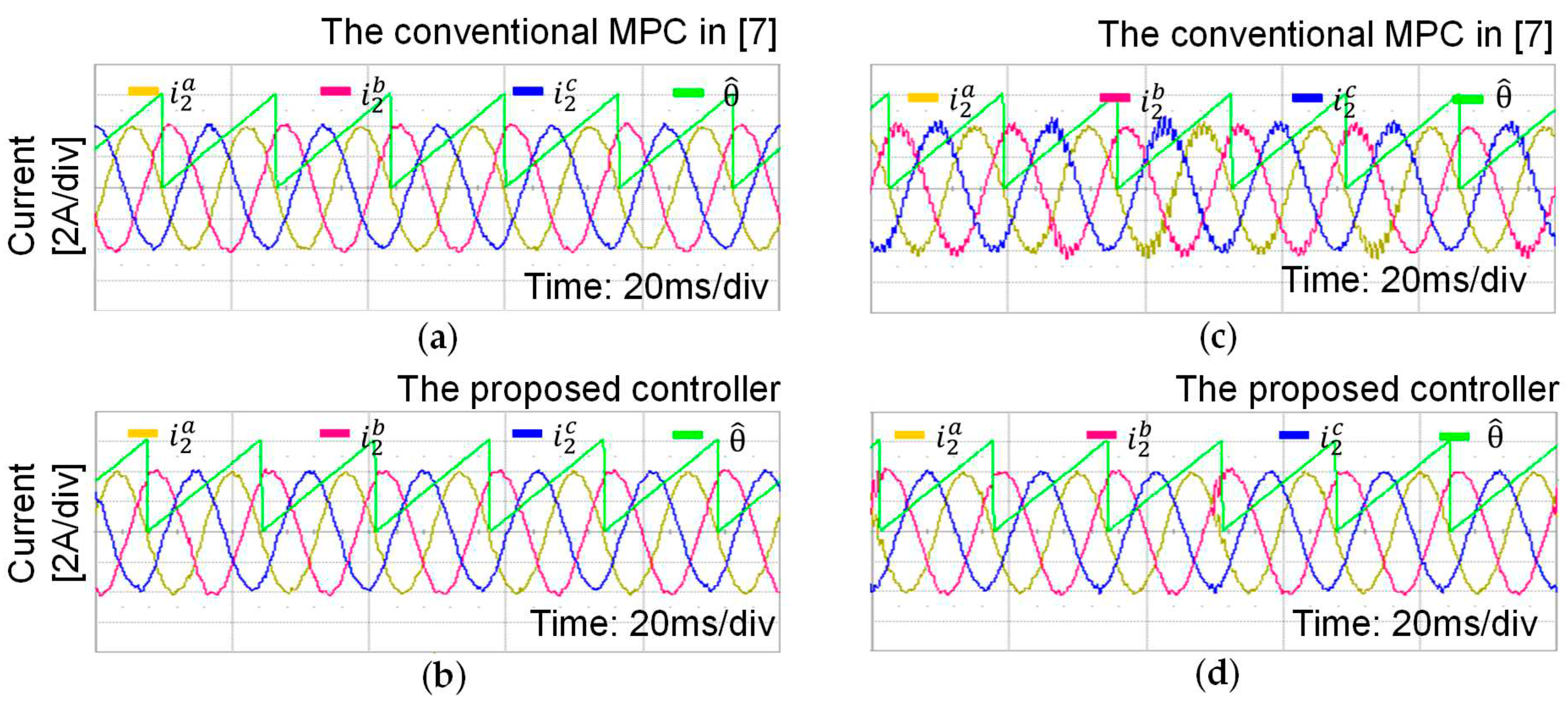
Figure 10 presents the experimental comparison results for steady-state tracking performance between the conventional MPC in [7] and the proposed controller under

C_{f}

uncertainty. In these figures, the grid phase angle estimates are also shown to verify the synchronization performance without grid voltage sensors. The conventional MPC in [7] and the proposed control show similar results with

C_{f} =

1 μF as shown in Figure 10a,b. In contrast, the proposed control exhibits better current quality and less oscillation than the conventional one with

C_{f} =

6 μF as in Figure 10c,d.

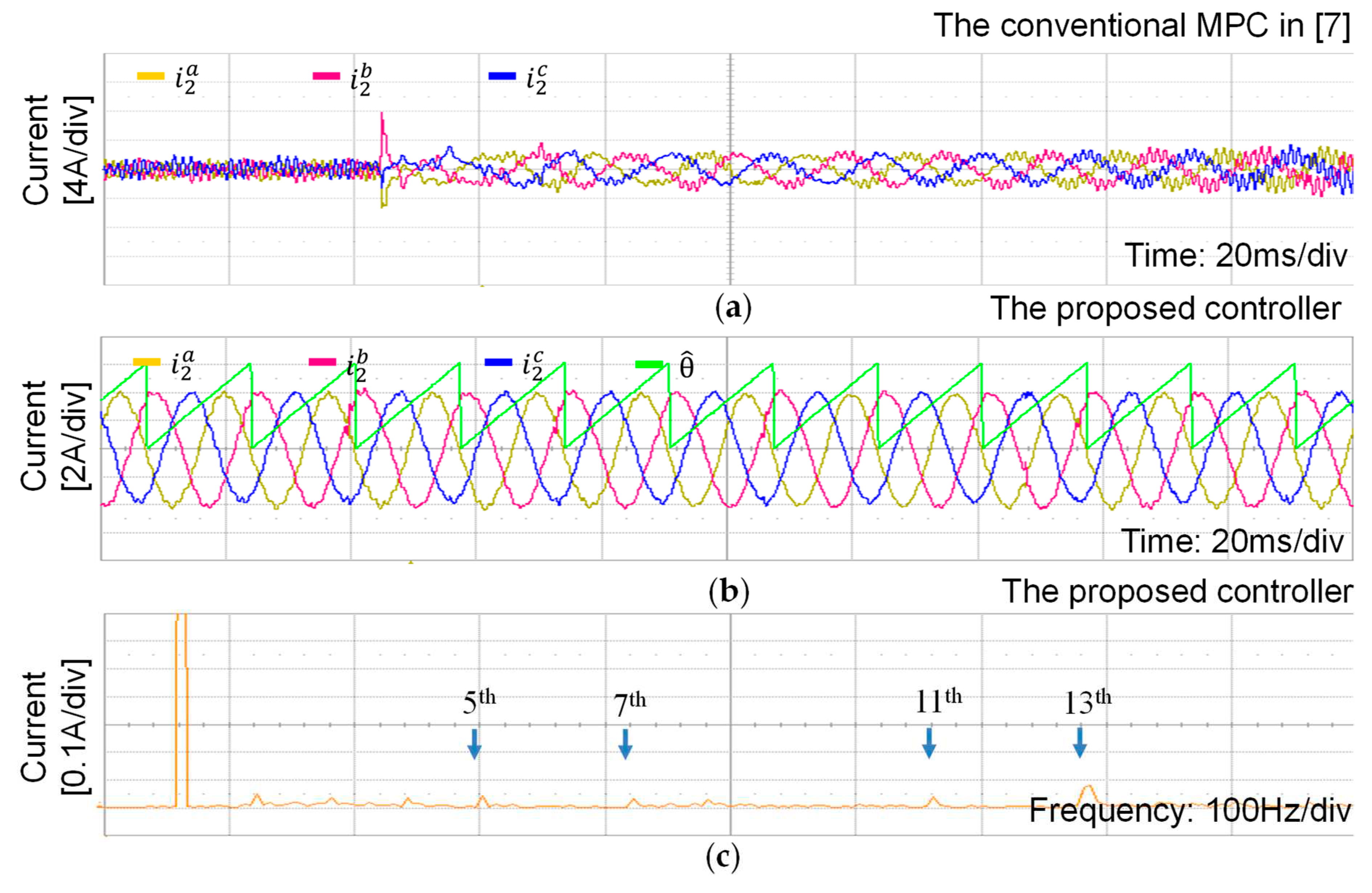
To validate the robustness of the proposed controller under the grid impedance variation caused by weak grid, Figure 11 represents comparative experimental results when the grid impedance (L_g=4 mH) exists under imbalanced and distorted grid voltages. The phase-a current FFT spectrums for the proposed method are also presented in Figure 11c to assess the grid-injected current quality. While the proposed method is quite stable in the presence of such severe grid disturbances, the conventional scheme becomes rapidly unstable with the same conditions before the protection algorithm is finally activated. The experimental results of Figure 10 and Figure 11 match well with the simulation in Figure 7 and Figure 8 in terms of the system stability and grid current quality.

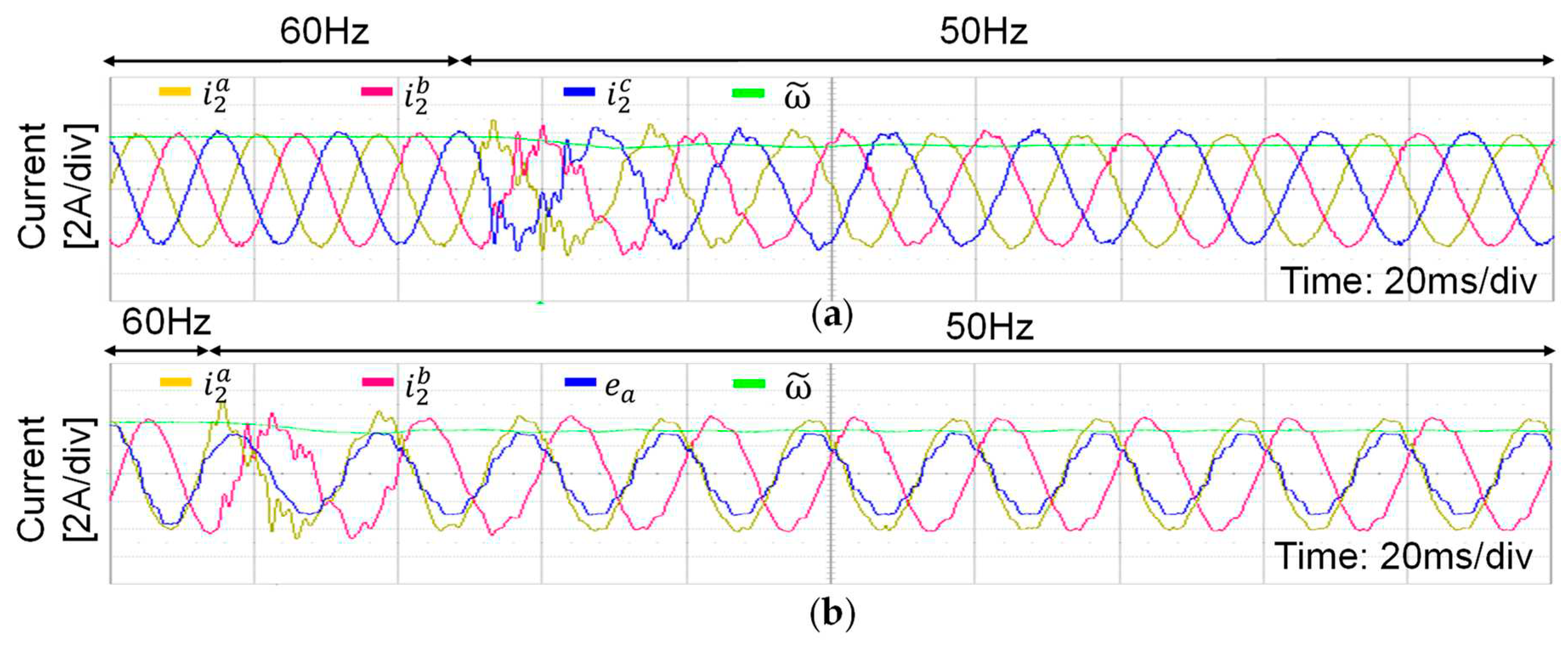
The experimental responses in Figure 12 present the transient performance of the proposed control method under frequency varying from 60 Hz to 50 Hz. As test conditions, while the grid voltage is distorted in Figure 12a, it is distorted as well as imbalanced in Figure 12b. These results demonstrate that the grid currents are quickly restored to the sinusoidal form even under both grid frequency change and harsh grid disturbance such as imbalance and distortion, which well matches the simulation results in Figure 5. Also, the grid frequency estimated by using the MAF-PLL from the estimated grid voltages rapidly tracks new frequency value without a noticeable overshoot. All experimental tests clearly verify the performance and robustness of the proposed method that produces high-quality grid currents even under weak grid conditions and parametric uncertainty without using the measurement of the grid voltages.

8. Conclusions

This paper has presented a robust EMPC-based frequency-adaptive current control combined with LMI approach without using grid voltage sensors for an LCL-filtered GCI in the presence of parametric uncertainties and abnormal grid environment. The proposed control is mainly achieved by an LMI and MPC approaches to ensure the robustness against non-ideal grid and system parameter variations. In addition, the proposed control is also achieved by an LMI-based observer to constitute a frequency-adaptive behavior of grid voltage sensorless algorithm. The LMI-based MPC algorithm is employed with an LQR-based prediction model in order to improve the system stability as well as to reduce the computational burden. A frequency-adaptive grid voltage sensorless control is achieved by an LMI-based resonant extended state observer, which guarantees the high accuracy of estimated grid voltages as well as system state variables under abnormal and unexpected grid conditions. Closed-loop system stability and robustness have been evaluated by the eigenvalue map and frequency responses. Comprehensive simulation and experiments as well as comparison results clearly verify the validity and effectiveness of the presented control method under unexpected adverse test conditions such as parametric uncertainties of system and abnormal grid environment.

Author Contributions

Y.K., T.V.T. and K.-H.K. developed the main idea for the system and control design, and investigated the entire system structure. Y.K. analyzed the system based on the numeric data with the guidance from K.-H.K. T.V.T. conducted the literature survey and simulations. Y.K., T.V.T. and K.-H.K. collaborated to prepare the article.

Acknowledgments

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2019R1A6A1A03032119). This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2022R1F1A1064350).

Conflicts of Interest

The authors declare no conflict of interest.

References

Yang, H.; Zhang, Y.; Liang, J.; Gao, J.; Walker, P.D.; Zhang, N. Sliding-mode observer based voltage-sensorless model predictive power control of PWM rectifier under unbalanced grid conditions. IEEE Trans. Ind. Electron. 2018, 65, 5550–5560. [Google Scholar] [CrossRef]
Carrasco, J.; Franquelo, L.; Bialasiewicz, J.; Galvan, E.; Guisado, R.; Prats, M.; Leon, J.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
De Matos, J.G.; Silva, F.S.; Ribeiro, L.A.D.S. Power control in AC isolated microgrids with renewable energy sources and energy storage systems. IEEE Trans. Ind. Electron. 2014, 62, 3490–3498. [Google Scholar] [CrossRef]
Han, H.; Hou, X.; Yang, J.; Wu, J.; Su, M.; Guerrero, J.M. Review of power sharing control strategies for islanding operation of AC microgrids. IEEE Trans. Smart Grid. 2015, 7, 200–215. [Google Scholar] [CrossRef]
Trinh, Q.-N.; Lee, H.-H. An advanced current control strategy for three-phase shunt active power filters. IEEE Trans. Ind. Electron. 2013, 60, 5400–5410. [Google Scholar] [CrossRef]
IEEE Application Guide for IEEE Std. 1547, IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems; IEEE Std. 1547.2-2008, 2008.
Kim, Y.; Tran, T.V.; Kim, K.-H. LMI-based model predictive current control for an LCL-filtered grid-connected inverter under unexpected grid and system uncertainties. Electronics 2022, 11, 731. [Google Scholar] [CrossRef]
Jalili, K.; Bernet, S. Design of LCL filters of active-front-end two-level voltage-source converters. IEEE Trans. Ind. Electron. 2009, 56, 1674–1689. [Google Scholar] [CrossRef]
Rodriguez-Diaz, E.; Freijedo, F.D.; Vasquez, J.C.; Guerrero, J.M. Analysis and comparison of notch filter and capacitor voltage feedforward active damping techniques for LCL grid-connected converters. IEEE Trans. Power Electron. 2018, 34, 3958–3972. [Google Scholar] [CrossRef]
Yoon, S.J.; Lai, N.B.; Kim, K.-H. A systematic controller design for a grid-connected inverter with LCL filter using a discrete-time integral state feedback control and state observer. Energies 2018, 11, 437. [Google Scholar] [CrossRef]
Jia, Y.; Zhao, J.; Fu, X. Direct grid current control of LCL-filtered grid-connected inverter mitigating grid voltage disturbance. IEEE Trans. Power Electron. 2014, 29, 1532–1541. [Google Scholar]
Bimarta, R.; Kim, K.-H. A robust frequency-adaptive current control of a grid-connected inverter based on LMI-LQR under polytopic uncertainties. IEEE Access 2020, 8, 28756–28773. [Google Scholar] [CrossRef]
Da Ponte Caun, R.; Assuncao, E.; Teixeira, M. C. M. H2/H∞ formulation of LQR controls based on LMI for continuous-time uncertain systems. Int. J. Sys. Sci. 2020, 52, 612–634. [Google Scholar] [CrossRef]
De Matos, J.G.; E Silva, F.S.F; Ribeiro, L.A.D.S. Power control in AC isolated microgrids with renewable energy sources and energy storage systems. IEEE Trans. Ind. Electron. 2015, 62, 3490–3498. [Google Scholar]
Han, H.; Hou, X.; Yang, J.; Wu, J.; Su, M.; Guerrero, J.M. Review of power sharing control strategies for islanding operation of AC microgrids. IEEE Trans. Smart Grid. 2016, 7, 200–215. [Google Scholar] [CrossRef]
Gao, J.; Gong, C.; Li, W.; Liu, J. Novel compensation strategy for calculation delay of finite control set model predictive current control in PMSM. IEEE Trans. Ind. Electron. 2020, 67, 5816–5819. [Google Scholar] [CrossRef]
Nam, N.N.; Nguyen, N.-D.; Yoon, C.; Lee, Y.I. Disturbance observer-based robust model predictive control for a voltage sensorless grid-connected inverter with an LCL filter. IEEE Access 2021, 9, 109793–109805. [Google Scholar] [CrossRef]
Tran, T.V.; Yoon, S.J.; Kim, K.-H. An LQR-based controller design for an LCL-filtered grid-connected inverter in discrete-time state-space under distorted grid environment. Energies 2018, 11, 2062. [Google Scholar] [CrossRef]
Bimarta, R.; Tran, T.V.; Kim, K.-H. Frequency-adaptive current controller design based on LQR state feedback control for a grid-connected inverter under distorted grid. Energies 2018, 11, 2674. [Google Scholar] [CrossRef]
Lai, N.B.; Kim, K.-H. Robust control scheme for three-phase grid-connected inverters with LCL-filter under unbalanced and distorted grid conditions. IEEE Trans. Energy Conver. 2017, 33, 506–515. [Google Scholar] [CrossRef]
Golestan, S.; Ramezani, M.; Guerrero, J.M.; Freijedo, F.D.; Monfared, M. Moving average filter based phase-locked loops: performance analysis and design guidelines. IEEE Trans. Power Electron. 2014, 29, 2750–2763. [Google Scholar] [CrossRef]
Tran, T.V.; Kim, K.-H. Frequency adaptive grid voltage sensorless control of LCL-filtered inverter based on extended model observer. IEEE Trans. Ind. Electron. 2020, 67, 7560–7573. [Google Scholar] [CrossRef]
Sturm, J. F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Method Softw. 1999, 11–12, 625–653. [Google Scholar] [CrossRef]
Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. in Proc. 2004 IEEE Int. Symp. on Comput. Aided Control Syst. Des., Taipei, Taiwan, pp. 284–289, Sep. 2004.

Figure 1. Power circuit of three-phase LCL-filtered GCI controlled by the proposed control scheme.

Figure 2. Structure of a frequency-adaptive grid voltage sensorless controller.

Figure 3. Eigenvalues with LCL parametric uncertainties. (a) The proposed EMPC. (b) The proposed LMI-based observer.

Figure 4. Frequency responses of the proposed EMPC scheme under LCL parametric uncertainties. (a) Reference tracking response. (b) Disturbance rejection response.

Figure 5. Simulation for the proposed control method. (a) Grid currents under grid voltage distortion and frequency change (60 Hz to 50 Hz). (b) Grid currents under grid voltage distortion and frequency change (60 Hz to 50 Hz) when the grid impedance

L_{g}

=4 mH exists.

L_{g}

=4 mH exists.

Figure 6. Simulation for LMI-based observer under grid voltage distortion in

α β

frame. (a) Estimated grid currents and measured grid currents. (b) Estimated inverter currents and reference inverter currents. (c) Estimated capacitor voltages and reference capacitor voltages. (d) Estimated gird voltages and measured gird voltages.

Figure 6. Simulation for LMI-based observer under grid voltage distortion in

α β

Figure 7. Comparison results between the conventional MPC in [7] and the proposed controller under unexpected grid conditions such as grid impedance (

L_{g}

=4 mH) and grid voltage distortion/imbalance (

e_{a}

drops to 70.56% of the nominal value at 0.6 s). (a) Grid currents of the conventional MPC. (b) Grid currents of the proposed controller.

Figure 7. Comparison results between the conventional MPC in [7] and the proposed controller under unexpected grid conditions such as grid impedance (

L_{g}

=4 mH) and grid voltage distortion/imbalance (

e_{a}

drops to 70.56% of the nominal value at 0.6 s). (a) Grid currents of the conventional MPC. (b) Grid currents of the proposed controller.

Figure 8. Comparison results between the conventional MPC in [7] and the proposed controller under system uncertainties (

C_{f}

varies from 4.5 μF to 6 μF) and grid voltage distortion/imbalance (

e_{a}

drops to 70.56% of the nominal value at 0.6 s). (a) Grid currents of the conventional MPC. (b) Grid currents of the proposed controller.

Figure 8. Comparison results between the conventional MPC in [7] and the proposed controller under system uncertainties (

C_{f}

varies from 4.5 μF to 6 μF) and grid voltage distortion/imbalance (

e_{a}

drops to 70.56% of the nominal value at 0.6 s). (a) Grid currents of the conventional MPC. (b) Grid currents of the proposed controller.

Figure 9. Experimental test setup.

Figure 10. Comparative experimental results between the conventional MPC in [7] and the proposed control method under system parametric uncertainties and grid voltage distortion/imbalance. (a) Conventional MPC when

C_{f}

decreases from 4.5 μF to 1 μF. (b) Proposed controller when

C_{f}

decreases from 4.5 μF to 1 μF. (c) Conventional MPC when

C_{f}

increases from 4.5 μF to 6 μF. (d) Proposed controller when

C_{f}

increases from 4.5 μF to 6 μF.

C_{f}

decreases from 4.5 μF to 1 μF. (b) Proposed controller when

C_{f}

decreases from 4.5 μF to 1 μF. (c) Conventional MPC when

C_{f}

increases from 4.5 μF to 6 μF. (d) Proposed controller when

C_{f}

increases from 4.5 μF to 6 μF.

Figure 11. Comparative experimental results between the conventional MPC in [7] and the proposed method under grid voltage distortion/imbalance with grid impedance (

L_{g}

=4 mH). (a) Conventional MPC (b) Proposed controller. (c) FFT result of phase-a current with the proposed controller.

Figure 11. Comparative experimental results between the conventional MPC in [7] and the proposed method under grid voltage distortion/imbalance with grid impedance (

L_{g}

=4 mH). (a) Conventional MPC (b) Proposed controller. (c) FFT result of phase-a current with the proposed controller.

Figure 12. Experimental results of the proposed method. (a) Estimated frequency and grid currents under grid voltage distortion and frequency change. (b) Estimated frequency, measured phase-a grid voltage, and grid currents under grid voltages distortion/imbalance and frequency change.

Table 1. Parameters of GCI system with LCL filter.

Parameters	Value	Units
DC-link voltage	420	V
Filter resistance	0.5	Ω
Filter capacitance	1 / 4.5 / 6	µF
Inverter-side inductance	1.7	mH
Grid-side inductance	1.0	mH
Line-to-line grid voltage in rms	220	V
Grid frequency	50 / 60	Hz
Grid inductance	4.0	mH
Switching frequency	10	kHz

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Robust EMPC-Based Frequency Adaptive Grid Voltage Sensorless Control for an LCL-Filtered Grid-Connected Inverter

Abstract

1. Introduction

2. System of a GCI

2.1. Modeling of a GCI with LCL Filter

2.2. System Modeling under Parametric Uncertainties

2.3. Model Discretization

3. Proposed Current Control Design with LMI-based MPC

3.1. Converional Prediction Model

3.2. LQR-based Prediction Model

3.3. Explicit Model Predictive Control

3.4. LMI-based Parameter Derivation

3.5. Distorted Harmonic Compensation

4. Frequency-adaptive Grid Voltage Sensorless Control Scheme

4.1. LMI-based Observer with Disturbance Observer for Sensorless Control

4.2. Frequency Estimation

5. Stability Analysis

5.1. Eigenvalues of The Proposed Scheme

5.2. Frequency Responses of The Proposed EMPC Scheme

6. Simulation Validation

7. Experimental Validation

8. Conclusions

Author Contributions

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe