Prerpints.org logo
Preprint
Article

The Collapse of a Neutrino Star Singularity: The Mechanism of the Big Bang?

Altmetrics

Downloads

111

Views

59

Comments

0

This version is not peer-reviewed

Submitted:

31 December 2023

Posted:

03 January 2024

You are already at the latest version

Alerts
Abstract
The BKL singularity inside a rotating black hole would be a neutrino star. Once its mass exceeds the limit that neutrino degeneracy pressure could support (larger than 3×1022 M⊙), the neutrino star singularity would collapse, raising the temperature to the maximum and dropping the entropy to the minimum to initiate a Big Bang. From the cosmic microwave background, we find where the Big Bang occurred at about 0.66 times the radius of the surface of last scattering away from us and at Galactic coordinates (l, b) ≃ (286°,-43°). As it expands, the clockwise spinning universe has been veering towards the ellipsoidal. These findings are consistent with independent observations of cosmic inhomogeneities, spatial anisotropies, and time variations.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

Introduction

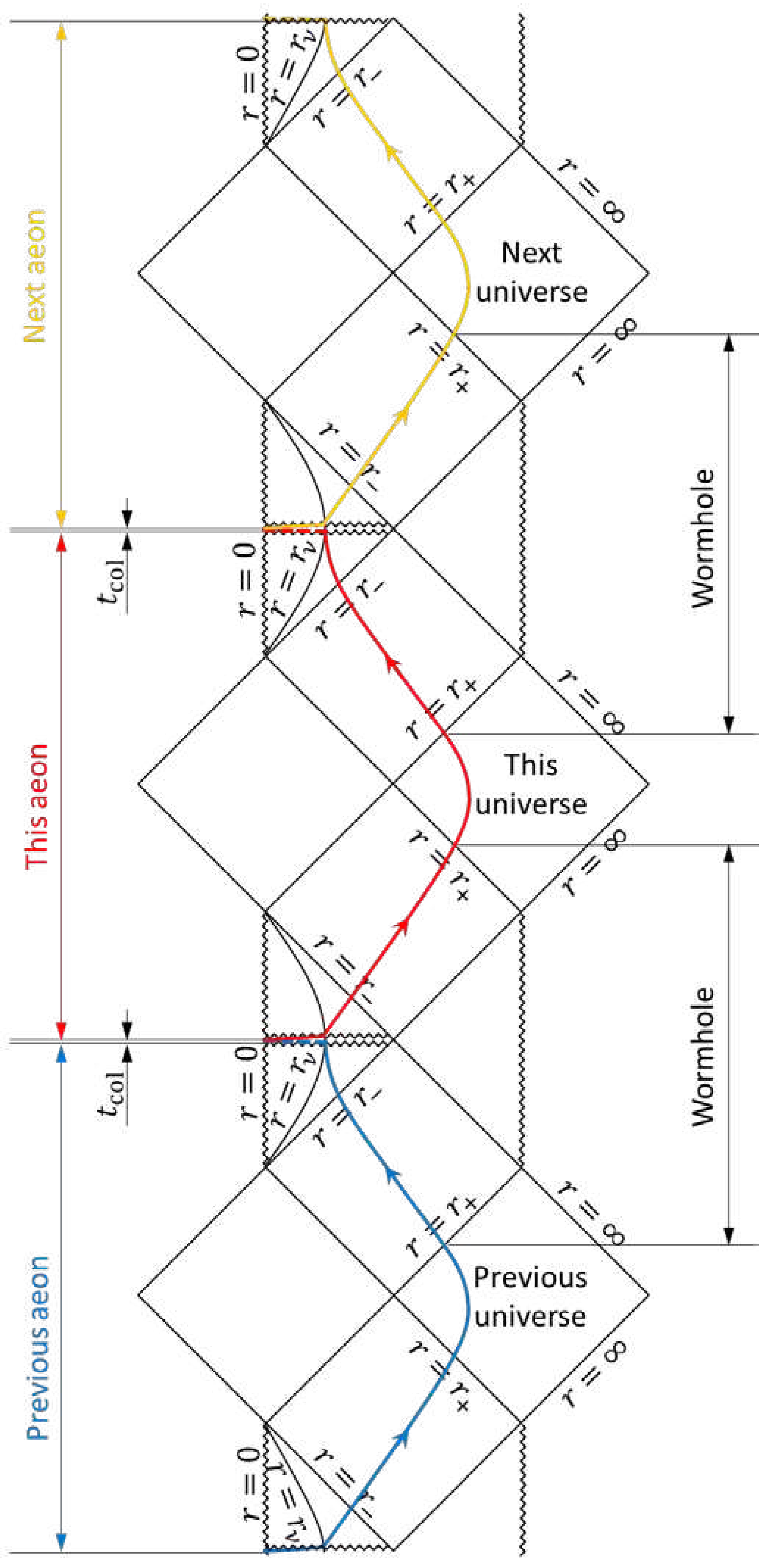
According to the sub-extremal Kerr metric in Boyer–Lindquist coordinates, a rotating black hole has two event horizons. Objects in the exterior universe ( ∆ > 0 ), by crossing the outer horizon r + , can only fall unidirectionally to decrease r-coordinate ( ∆ < 0 ). As the objects enter the inner horizon r − , space and time are inversed back ( ∆ > 0 ). The maximum analytical extension suggests that the objects could exit from the inner horizon, pass through the unidirectional zone, and enter a new universe. This hypothetical path (Figure 1) is a wormhole, but might not be traversable1. Its throat is in the inner horizon with three singularities2, at the center of which is a violet, lethal Belinski–Khalatnikov–Lifshitz (BKL) singularity2-4. The BKL singularity is also a Weyl singularity5, at which the Weyl curvature diverges to infinity: C a b c d = ∞ , corresponding to the maximum entropy (Penrose’s Weyl curvature hypothesis4).
It is believed that the universe started from a pure energy Ricci singularity ( r = 0 ), at which the Weyl curvature vanishes: C a b c d = 0 , equivalent to the minimum entropy4. The mass-energy, including spacetime, of the universe was generated from the Big Bang; the universe was a white hole. This evolution can also be seen in Figure 1.
Now if we divide the whole evolution curve outside the outer horizons, we obtain wormholes. If we divide it inside the inner horizons, we have aeons. Shall we recognize Nature as wormholes or aeons? The latter! As “the endpoint of evolution”6, the BKL singularity is a natural watershed to section the evolution curve. Each aeon starts from a Ricci singularity, then develops, and eventually concludes at (multiple) BKL singularities. The Second Law of thermodynamics is valid for individual aeons.
The critical question left unanswered is about the crossover between aeons. As soon as the Weyl singularities were discovered, King predicted the direction of evolution by stating that “the Weyl singularities are unstable against degenerating into ‘big bang’ singularities: should any matter be projected into them it seems certain that we would get ρ → ∞ ”5. As discussed in Penrose’s work7, Wheeler, Smolin, and others made the same prediction that “new aeons emerge from black-hole singularities.” Penrose also suspected the origination of “[the Big Bang] singularity from [a] wildly chaotic black-hole riddled (BKL?) collapse,” though he opted to the ultimate hypersurface J + for his conformal cyclic cosmology (CCC)7. In this work, we show how the collapse of the BKL singularity initiated the Big Bang.

Collapse of a Neutrino star Singularity

By studying the fundamental particles and reactions of Nature, we find that the BKL singularity would be a neutrino star. While the detail is in our early work8, a brief discussion is provided here. Neutrinos have long been found to be related to vacuum energy9. The neutrino mass would be tied up with the energy density of the vacuum by a reversible reaction:
A + A ¯ ⇌ γ + γ
The fundamental spacetime particles A and A ¯ would annihilate at neutrinos with the release of dark energy into the vacuum, while the energy of the vacuum would recreate the spacetime particles at arbitrary distances (appear as quantum fluctuations). Based on this dynamic equilibrium, estimated from the vacuum energy density9: ε vac ≳ m ν 4 c 5 16 π 2 ℏ 3 , the upper limit of the mass of the lightest neutrino: m ν ≲ 8   m e V .
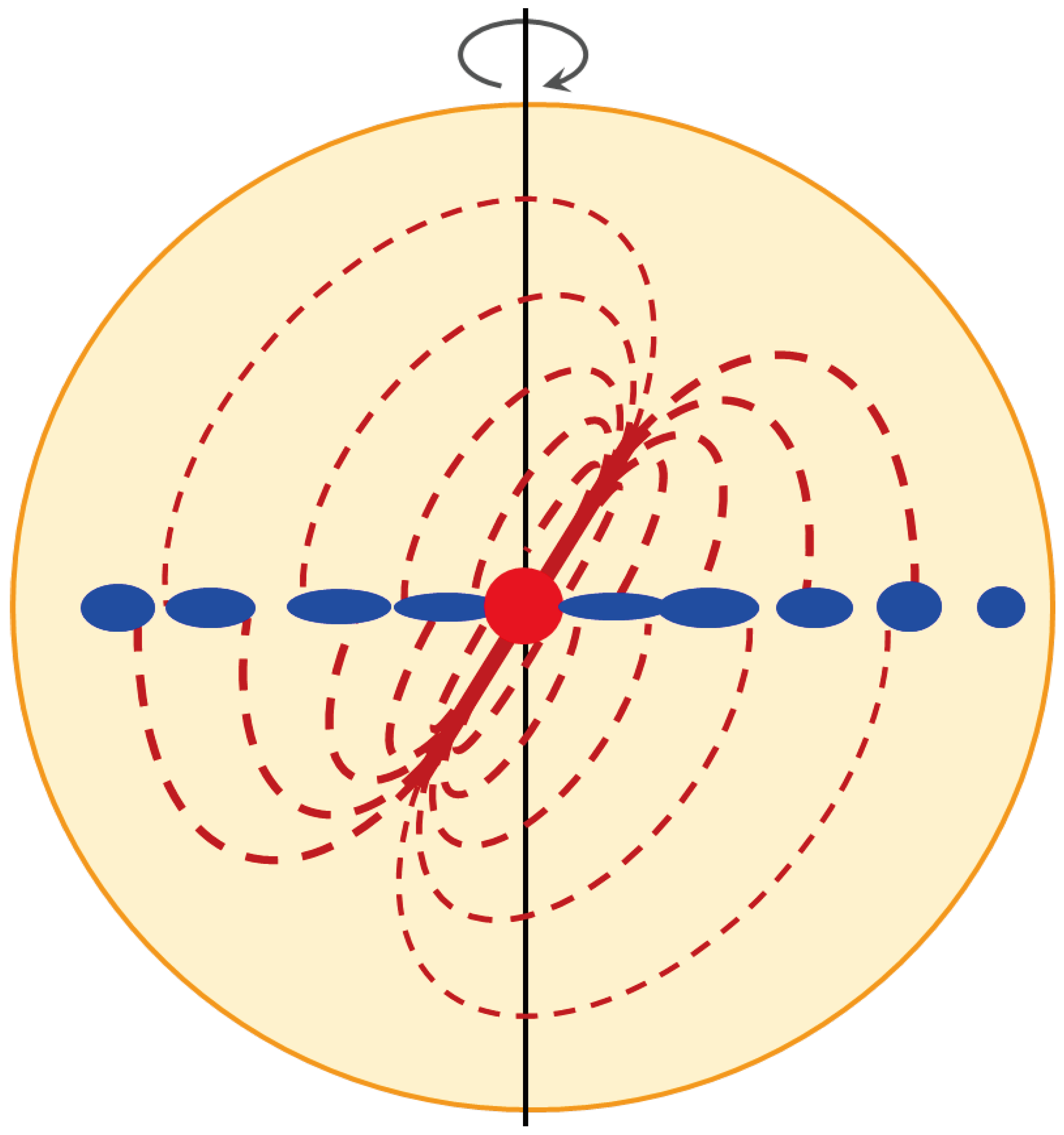
Neutrinos (larger particles such as neutrons have crushed) would accumulate in the inner horizon, forming a neutrino star (its real geometric shape would not be of importance). More importantly, because spacetime annihilates at neutrinos (the forward of reaction 1), the neutrino star, at which geodesics are terminated, would be a spacetime singularity. The annihilation would inevitably accompany with the recreation of spacetime due to high local energy density (the reverse of reaction 1), so the neutrino star singularity would be very chaotic. The recreated spacetime particles and their energy form would not be immobilized (because they are not neutrinos) at the neutrino star, but thrown out as emission beams symmetrically about it (Figure 2). Therefore, spacetime would be stretched along the beams while squashed along the other directions. By approaching the highly compacted, spinning neutrino star, spacetime would become more and more violet and diverge to an infinity curvature. All these characters match those at the BKL singularity2-4. Therefore, unlike any observable astronomical object, a neutrino star would be a singularity hidden within a black hole (Penrose’s weak cosmic censorship hypothesis).
As neutron degeneracy pressure supports neutron stars, neutrino degeneracy pressure would prevent neutrino stars from collapsing. Analogous to the Tolman-Oppenheimer-Volkoff limit for neutron stars, we estimate a mass limit for neutrino stars:
M ν ≈ m n m ν 2 M n ≳ 939.6   MeV 8   meV 2 × 2.2 M ⊙ = 3 × 10 22 M ⊙
where mn, Mn, and M ⊙ are the masses of a neutron, a neutron star, and the sun, respectively. Another method to estimate the mass limit is to calculate the Jeans mass of the neutrino10:
M J , ν = 1.8 M Pl 3 m ν 2 ≳ 1.8 × ( 1.22 × 10 19 GeV ) 3 ( 8   meV ) 2 = 5 × 10 22 M ⊙
where MPl is the Planck mass. Without considering any addition due to the rotation of black holes, both lowermost values estimated from the uppermost neutrino mass are close to the mass of the observable universe, ca. 10 23 M ⊙ . Estimated from the smallest neutrino size (the measured cross section9 is 10-56 cm2, identical to the unification distance in the grand unified theory, 10-28 cm) the volume of a neutrino star with M ν would be as small as 6 m3 (equivalent to r ν = 1   m ).
As King5 foresaw, matter and energy keep falling into a black hole (not an isolated system), so its mass would eventually exceed M ν , resulting in a further collapse. Like any other Oppenheimer-Snyder collapse, it would tremendously raise the temperature (all neutrinos annihilate into pure energy, T > T Pl = 1.4 × 10 32   K ). At such a high temperature, it is natural that the entropy would reach the minimum: S ≡ U − F T < M ν c 2 T Pl = 3 × 10 60   k B , where kB is the Boltzmann constant. In short, as a neutrino star (a future-spacelike singularity, r = 1   m ,    S ≈ 4 π k B G M ν 2 ℏ c = 1 × 10 122 k B ) collapses into a timelike Ricci singularity ( r = 0 ,    S < 3 × 10 60   k B ), a new aeon would start (Figure 1), with expanding spacetime and a new neutrino star (a past-spacelike singularity, r = 1   m ,   S = 3 × 10 60   k B ). This collapse-expansion procedure has been called the Big Bounce; the collapse would be a process opposite to the cosmological inflation11. Thus the evolution curve (Figure 1) would make very small angles with the horizontal right before and after the Big Bang ( dr / dt ≫ c , − 10 − 32 sec ≤ t ≤ 10 − 32 sec ), and have a U-turn at the Big Bang ( t = 0 ). While the collapse at a specific black hole is an ultrashort ( ~   10 − 32   sec ) entropy fluctuation, the Second Law would still be sustained for the entire evolving system (i.e. Nature, a truly isolated system). As Zel’dovich6 pointed out, for “cosmological collapse and black holes,” “the general solution of Einstein’s equations is highly anisotropic near the [BKL] singularity;” for “cosmological expansion and white holes,” “the Kasner solution transform[s] into an isotropic expansion”. By studying the collisions between the anisotropic spacetime from before the Big Bang and the isotropic expansion after the Big Bang, we would find where the Big Bang occurred or the Center of the universe.

The Center and Spin of the Universe

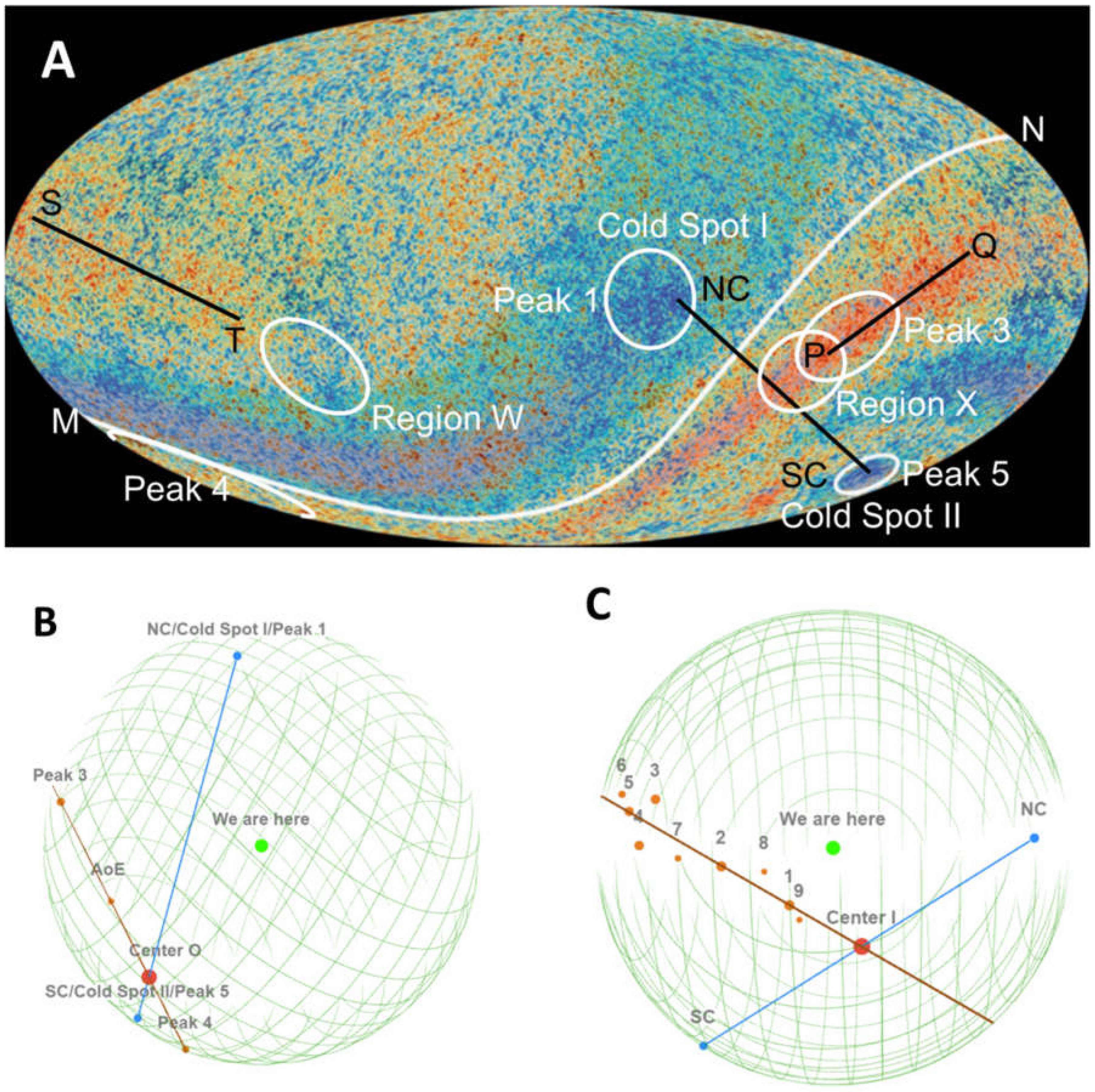
The emission beams Vb (Figure 2) symmetric about the neutrino star, due to weaker collisions with the isotropic Big Bang wave VBB, result in two cold spots in the cosmic microwave background (CMB, Figure 3A): NC, corresponding to Cold Spot I12 and Peak 113,14, at l ,   b = ( 318 ° , − 5 ° ) , and SC, corresponding to Cold Spot II12 and Peak 513,14, at l ,   b = ( 208 ° , − 56 ° ) . The spiral flows Vs falling towards the neutrino star (Figure 2), because of stronger collisions with the VBB, lead to a hot ring. The Center is at the intersection of the Vb line (line NC-SC) and the Vs plane determined by the following methods.
The most noticeable hot region is the large-scale Peak 3 at l ,   b = ( 265 ° , − 20 ° ) (from the figures in ref.14), which, with Peak 4 at l ,   b = ( 173 ° , − 46 ° ) 15, is known as the Axis of Evil16,17 (AoE, Figure 3A), whose vector is in the direction l ,   b = ( 250 ° , 60 ° ) 16. While the AoE offers an interesting starting point, Peak 4 is too close to SC or the Vb (Figure 3B), and hence would not be from the Vs; the calculated intersection (Method O, Table 1) does not seem to match astronomical observations.
By reanalyzing the CMB, we find that arc ST (Figure 3A), similar to Peak 3, shows large-scale high temperatures. Thus arcs PQ and ST are used to determine the Vs plane (Figure 3C):
z = ( − 0.58 ± 0.10 ) x + ( 0.03 ± 0.03 ) y − ( 0.36 ± 0.06 ) r SLS
where r SLS is the radius of the surface of last scattering (SLS). It intersects line NC-SC at l ,   b = ( 286 ° ± 10 ° , − 43 ° − 6 ° + 7 ° ) and at a distance ( 0.66 − 0.01 + 0.03 ) r SLS away from where we are (hereafter represented by the Local Supercluster or LS) (Method I, Table 1). Since r SLS = 14   Gpc 18, the Center is ca. 9.3 Gpc or 30 billion light years away from us. Only half of the hot ring (arcs PQ and ST) is observed, while the other half is hardly visible. This is due to the Doppler effect and the Doppler beaming: the Vs flows were spiraling towards the precursor neutrino star (Figure 2). We therefore find that: i) if we look from the LS to the Center, the universe is rotating or spinning clockwise; ii) the Vs plane is the equatorial plane of the universe; iii) the LS is inside the Northern observable universe; iv) the Northern observable universe is bigger than the Southern; v) the axis of spin of the universe is:
x ,   y , z = 0.13 r SLS , − 0.47 r SLS , − 0.45 r SLS + 0.58 , − 0.03 ,   1.00 t
vi) the spin axis intersects with the SLS at l ,   b = ( 325 ° , 31 ° ) and ( 256 ° , − 62 ° ) ; vii) the angle between the equatorial plane and the Galactic plane is 30 ° ± 5 ° .
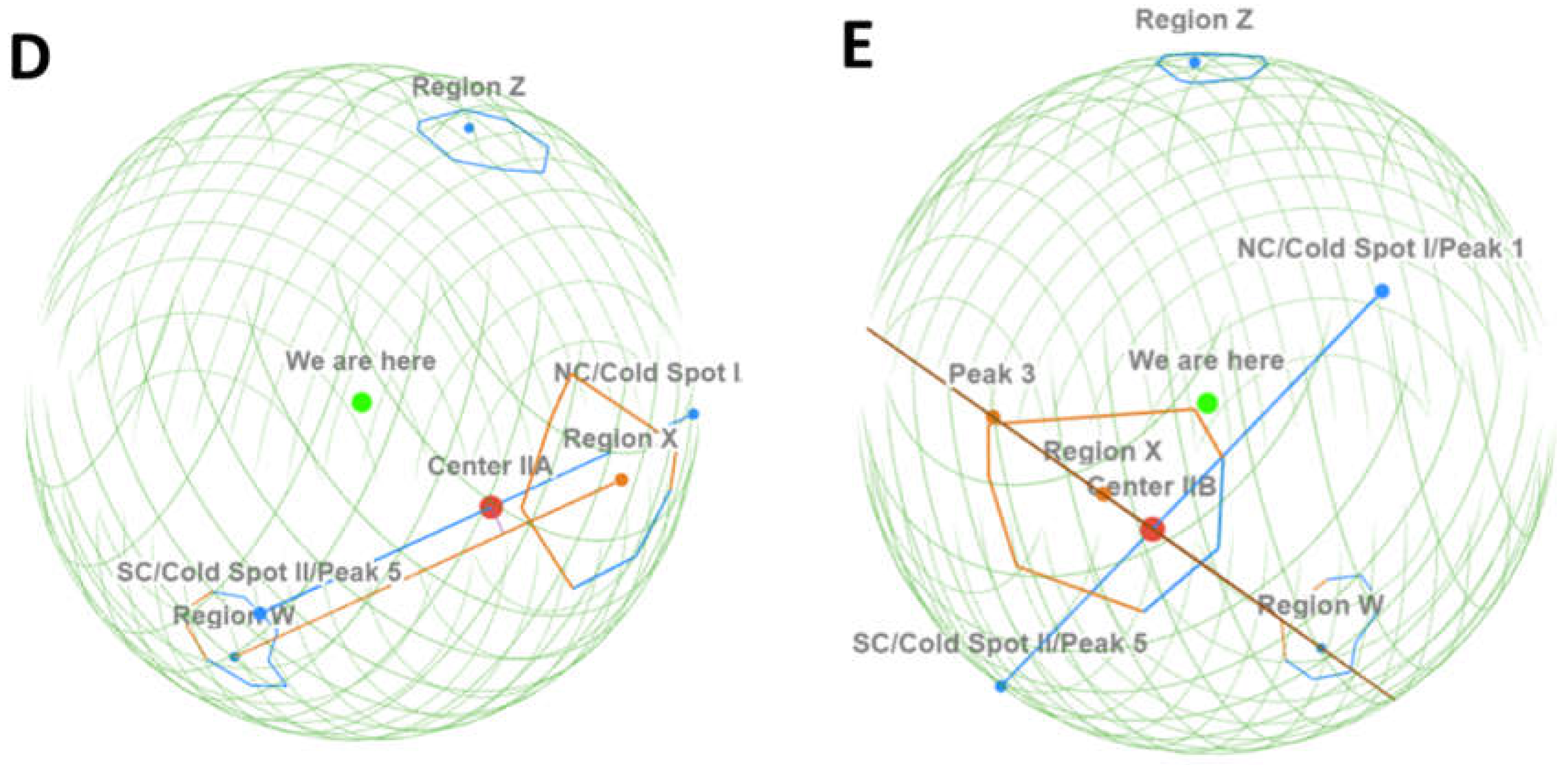
Method II is based on the low-variance circles (LVC) that Gurzadyan and Penrose19,20 found. Regions X and W show characteristic properties of the Vs flows (Figure 3D and Figure 3E), and therefore are employed to define the Vs plane. Based on Bodnia et al.’s coordinates21: Region X at l ,   b = 280.1 ° , − 31.5 ° and Region W at l ,   b = ( 86.1 ° , − 38.2 ° ) , line XW almost intersects line NC-SC (Figure 3D), so the closest point at l ,   b = ( 281 ° , − 46 ° ) and at a distance 0.67 r SLS can be regarded as the Center (Method IIA, Table 1). If the Regions are used to define the Vs plane with Peak 3 (Figure 3E), then the Center is at l ,   b = ( 278 ° , − 48 ° ) and at a distance 0.67 r SLS (Method IIB, Table 1). These results are virtually the same as those from Method I.

Paradox of the Existence of the Center

It is generally believed that the universe has no center, with the reason being that the Big Bang happened everywhere, or that the Hubble flow is observed everywhere. Another would argue that it is nonsense to locate a center within the universe, as space itself was from the Big Bang. Based on our mechanism, the universe is finite and has a center. As in the raisin bread model, the center of the bread is the dough before baking (without gravity), the Center is where the precursor black hole collapsed in the previous aeon and now in the present aeon.
One might also wonder how our mechanism could generate an isotropic and homogeneous universe. It is important to first note that more and more astronomical observations have shown that the universe has small magnitudes of anisotropies and inhomogeneities (details below). Based on our mechanism, any potential massive objects near the precursor neutrino star would have been merged. Without the influence of the surroundings (all the flows discussed above were negligible), the new-born universe was isotropic and homogeneous4,6. During the course of expansion, Hubble’s law is always valid, even for objects with separation greater than the Hubble length22,23. An analysis of the CMB indicates that anisotropic expansion is strongly disfavoured, with odds of 121,000:1 against24. The only deviation away from the cosmological principle is from the centrifugal force that has been deforming the universe. Therefore, while the local universe looks almost isotropic and homogeneous, the original uniformity is maintained for an early image such as the CMB, because the deviation due to the spin is dipolar and overshadowed by the peculiar motion. Unless we were near its edge (we are not), the universe from our mechanism appears very isotropic and homogeneous.

Independent Observational Evidence

While the theoretical analysis indicates that black holes are the embryos of the universes of the next aeons, the match of the results from Methods I and II is a solid piece of direct evidence of our mechanism. Besides them, various independent observational evidence has been reported in the literature. For future convenience, we define a Universal Coordinate System (Figure 4A), in which the LS is set at zero degrees longitude and the r SLS the unit length. The angle between the line from the Center to the LS and the equatorial plane is ca. 28 ° and the distance between the LS and the Center is ca. 0.66 r SLS , so the universal coordinates for the LS are: ( J ,   W , R ) = ( 0 ° , + 28 ° , 0.66 ) .
The first category of evidence is the inhomogeneous compositions of the universe. In the inner horizon of the precursor black hole, the Vb and Vf would sweep in a high angular speed, producing discontinuous clumps of high-density mass-energy across the space (Figure 2). After the Big Bang, these flows, together with the Vs, would collide with the VBB, resulting in overdense clumps and debris as primordial nucleation centers (PNC) for the formation of primordial black holes or primordial galaxies. In addition to the LVC, some PNC would have been observed as the Hawking points25. Compared to structure formation theories in which overdensities are the consequence of minute quantum fluctuations, our mechanism generates the PNC much earlier and more mature, and hence explains multiple extraordinary astronomical facts, such as an unexpectedly large number26 of unexpectedly mature26 and unexpectedly bright27 galaxies observed by the JWST with unexpectedly high mass28,29 formed at an unexpectedly short time26, as well as the extraordinarily large cosmic structures (such as Ho’oleilana30) and black holes (candidates31: Phoenix A and 4C+74.13, etc.). Note that the first galaxies in the early JWST deep fields32, such as SMACS-0723 (close to the Center, W   ~ + 43 ° ), CEERS ( W   ~ + 37 ° ), and GLASS ( W   ~ − 27 ° ), are in the higher-density zones ( W ≤ 58 ° ± 6 ° , the angle between line NC-SC and the Vs plane), so are the large cosmic structures and black holes30,31.
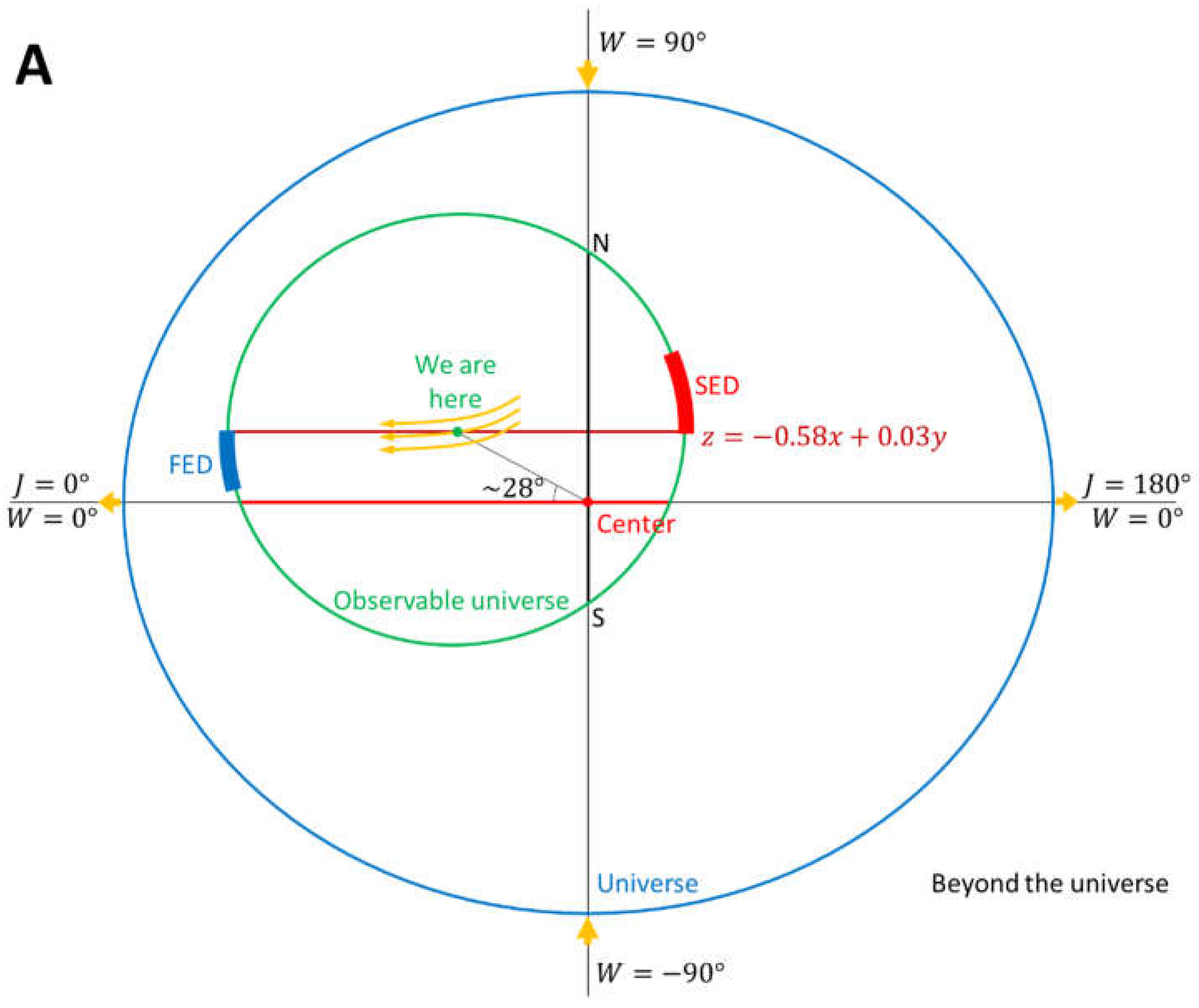
The second category of evidence is cosmic anisotropies. Our mechanism does not provide any massive structures at the Center after the Big Bang (for comparison, before the Big Bang there was a massive neutrino star). With the centripetal force requirement, the spinning universe has been expanding faster along the rotationally radial direction and slower along the axis of spin. Thus the universe has been veering towards the ellipsoidal (Figure 4A). This deformation changes our observable universe accordingly. Campanelli et al. suspected that the SLS was ellipsoidal33. Strictly speaking, the observable universe is not ellipsoidal, because it does not have orthogonal axes as the universe does or, equivalently, the LS is not on the equatorial plane. Therefore, the exact direction of the fastest or slowest expansion is unknown, because it is related to the size of the universe that is unknown (the lowermost would be 3.32 r SLS ). If the dominating Hubble flow were removed, while always in the Northern universe, the LS would move closer to the equatorial plane. Therefore, the fastest expansion direction (FED) of the observable universe shall be close to the outward rotationally radial direction, skewing towards the equatorial plane (Figure 4A). As the expansion is slower along the axis of spin, the slowest expansion direction (SED) shall be close to the inward rotationally radial direction l ,   b = ( 301 ° , − 18 ° ) , skewing away from the equatorial plane (Figure 4A).
This preferred direction is confirmed by multiple independent astronomical observations34-44. Probably because the magnitudes of those anisotropies are very small ( 10 − 5 ~ 10 − 3 ), the observed directions are scattering for different properties, as well as for the same properties (Figure 4B and Figure 4C). With such small anisotropies, the obtained coordinates of the Center (Table 1), though would bias the North, are unnecessary to correct; the SLS can be regarded as a sphere. Other than the fine-structure constant α dipole34,35 that is generally attributed to a different mechanism45,46, slower expansion in the SED appears as lower accelerating expansion (dark energy dipole35), brighter Type Ia supernovae (SNe Ia dipole36), smaller Hubble constant H 0 (galaxy cluster anisotropy37), or mutually approaching flows of galaxies (such as bulk flows38-41). With the understanding that those anisotropies share the same mechanism, we can convert from one to another.
The third category of evidence is time variations. While the LS is moving away from the direction of the slower expansion (Figure 4A), the universe has been expanding in acceleration47,48. While the LS moves away from the direction of the smaller H 0 , the Hubble tension indicates that the H 0 was smaller in the past49. While the LS moves away from the direction of the slower expansion or higher matter density and amplitude of growth of structures, the S8 tension indicates that the S8 value was larger in the past50.

Data Availability Statement

All results in this work are obtained using publicly available data.

Acknowledgments

J.B.B. would like to thank Profs. Z. Shen, K. Yao, X. Jiang, F. Bo, Y. Cheng, S. Han, G. Chen, and Q. Yu at Zhejiang University for their inspiration. N.P.B. would like to dedicate this work to his grandparents in China.

Competing Interests

The authors declare no competing interests.

References

  1. Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for intersteller travel: a tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
  2. Scheel, M.A.; Thorne, K.S. Geometrodynamics: the nonlinear dynamics of curved spacetime. Physics-Uspekhi 2014, 57, 342–351. [Google Scholar] [CrossRef]
  3. Belinskii, V.A.; Khalatnikov, I.M.; Lifshitz, E.M. Oscillatory approach to a singular point in the relativistic cosmology. Adv. Phys. 1970, 19, 525–573. [Google Scholar] [CrossRef]
  4. Penrose, R. Singularities and Time-Asymmetry. In Hawking, S. W. & Israel, W. (eds) General Relativity: An Einstein Centenary Survey (Cambridge University Press, Cambridge, 581-638, 1979).
  5. King, A.R. New types of singularity in general relativity: the general cylindrically symmetric stationary dust solution. Commun. Math. Phys. 1974, 38, 157–171. [Google Scholar] [CrossRef]
  6. Zel’dovich, Ya. B. Creation of particles in cosmology. In Longair, M. S. (ed) Confrontation of cosmological theories with observational data (D. Reidel Pub., Dordrecht, 329-333, 1974).
  7. Penrose, R. Cycles of time: an extraordinary new view of the universe (Bodley Head, London, 2010).
  8. Bao, J.B.; Bao, N.P. On the Fundamental Particles and Reactions of Nature. Preprints 2020, 2020120703. [Google Scholar]
  9. Perkins, D. Particle Astrophysics. 2nd ed. (Oxford Univ. Press, New York, 2003).
  10. Prakash, N. Dark matter, neutrinos, and our solar system (World Sci., Singapore, 2013).
  11. Guth, A.H. Inflationary universe: a possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
  12. Bennett, C.L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: are there cosmic microwave background anomalies? Astrophys. J. Supp. Ser. 2001, 192, 17. [Google Scholar] [CrossRef]
  13. Planck Collaboration: Akrami, Y. et al. Planck 2018 results. VII. Isotropy and Statistics of the CMB. Astron. Astrophys. 2020, 641, A7. [CrossRef]
  14. Caballero, A.M. The Cosmic Microwave Background radiation at large scales and the peak theory. Univ. Cantabria Thesis (2017).
  15. Pietrobon, D.; et al. Needlet detection of features in the WMAP CMB sky and the impact on anisotropies and hemispherical asymmetries. Phys. Rev. D 2008, 78, 103504. [Google Scholar] [CrossRef]
  16. de Oliveira-Costa, A.; et al. Significance of the largest scale CMB fluctuations in WMAP. Phys. Rev. D 2004, 69, 063516. [Google Scholar] [CrossRef]
  17. Wright, A. Across the universe. Nat. Phys. 2013, 9, 264. [Google Scholar] [CrossRef]
  18. Gott III, J.R.; et al. A map of the universe. Astrophys. J. 2005, 624, 463–484. [Google Scholar] [CrossRef]
  19. Gurzadyan, V.G.; Penrose, R. On CCC-predicted concentric low-variance circles in the CMB sky. Eur. Phys. J. Plus. 2013, 128, 22. [Google Scholar] [CrossRef]
  20. Gurzadyan, V.G.; Penrose, R. CCC and the Fermi paradox. Eur. Phys. J. Plus. 2016, 131, 11. [Google Scholar]
  21. Bodnia, E.; et al. Conformal cyclic cosmology signatures and anomalies of the CMB sky. arXiv 2023, arXiv:2208.06021v2. [Google Scholar]
  22. Peebles, P. J. E. Principles of Physical Cosmology (Princeton Univ. Press, Princeton, 1993).
  23. Davis, T.M.; Lineweaver, C.H. Expanding confusion: common misconceptions of cosmological horizons and the superluminal expansion of the universe. Pubs. Astr. Soc. Australia 2004, 21, 97–109. [Google Scholar] [CrossRef]
  24. Saadeh, D.; et al. How isotropic is the universe? Phys. Rev. Lett. 2016, 117, 131302. [Google Scholar] [CrossRef]
  25. An, D.; et al. Apparent evidence for Hawking points in the CMB Sky. Mon. Not. R. Astron. Soc. 2020, 495, 3403–3408. [Google Scholar] [CrossRef]
  26. Witze, A. Four revelations from the Webb telescope about distant galaxies. Nature 2022, 608, 18–19. [Google Scholar] [CrossRef]
  27. Clery, D. Earliest galaxies found by JWST confound theory. Science 2023, 379, 1280–1281. [Google Scholar] [CrossRef]
  28. Labbé, I.; et al. A population of red candidate massive galaxies ~600 Myr after the Big Bang. Nature 2023, 616, 266–269. [Google Scholar] [CrossRef]
  29. Boylan-Kolchin, M. Stress testing ΛCDM with high-redshift galaxy candidates. Nat. Astron. 2023, 7, 731–735. [Google Scholar] [CrossRef]
  30. Tully, R.B.; Howlett, C.; Pomarède, D. Ho’oleilana: An individual baryon acoustic oscillation? Astrophys. J. 2023, 954, 169. [Google Scholar] [CrossRef]
  31. List of most massive black holes. Available online: https://www.wikipedia.org/wiki/List_of_most_massive_black_holes.
  32. Donnan, C.T.; et al. The evolution of the galaxy UV luminosity function at redshifts z ≃ 8 − 15 from deep JWST and ground-based near-infrared imaging. Mon. Not. R. Astron. Soc. 2023, 518, 6011–6040. [Google Scholar] [CrossRef]
  33. Campanelli, L.; Cea, P.; Tedesco, L. Ellipsoidal universe can solve the CMB quadrupole problem. Phys. Rev. Lett. 2006, 97, 131302. [Google Scholar] [CrossRef] [PubMed]
  34. King, J.A.; et al. Spatial variation in the fine-structure constant – new results from VLT/UVES. Mon. Not. R. Astron. Soc. 2012, 422, 3370–3414. [Google Scholar] [CrossRef]
  35. Mariano, A.; Perivolaropoulos, L. Is there correlation between fine structure and dark energy cosmic dipoles? Phys. Rev. D 2012, 86, 083517. [Google Scholar] [CrossRef]
  36. Chang, Z.; Lin, H.-N. Comparison between hemisphere comparison method and dipole-fitting method in tracing the anisotropic expansion of the Universe use the Union2 data set. Mon. Not. R. Astron. Soc. 2015, 446, 2952–2958. [Google Scholar] [CrossRef]
  37. Migkas, K.; et al. Cosmological implications of the anisotropy of ten galaxy cluster scaling relations. Astro. Astrophys. 2021, 649, A151. [Google Scholar] [CrossRef]
  38. Hudson, M.J.; et al. A large-scale bulk flow of galaxy clusters. Astrophys. J. 1999, 512, L79. [Google Scholar] [CrossRef]
  39. Kashlinsky, A.; et al. A measurement of large-scale peculiar velocities of clusters of galaxies: technical details. Astrophys. J. 2009, 691, 1479–1493. [Google Scholar] [CrossRef]
  40. Feldman, H.A.; Watkins, R.; Hudson, M.J. Cosmic flows on 100 h−1 Mpc scales: standardized minimum variance bulk flow, shear and octupole moments. Mon. Not. R. Astron. Soc. 2010, 407, 2328–2338. [Google Scholar] [CrossRef]
  41. Turnbull, S.J.; et al. Cosmic flows in the nearby universe from Type Ia supernovae. Mon. Not. R. Astron. Soc. 2012, 420, 447–454. [Google Scholar] [CrossRef]
  42. Abdalla, E.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar]
  43. Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar]
  44. Aluri, P.K.; et al. Is the Observable Universe Consistent with the Cosmological Principle? Class. Quantum Grav. 2023, 40, 094001. [Google Scholar] [CrossRef]
  45. Davies, P.C.W.; Davis, T.M.; Lineweaver, C.H. Black holes constrain varying constants. Nature 2003, 418, 602–603. [Google Scholar] [CrossRef]
  46. Carlip, S.; Vaidya, S. Do black holes constrain varying constants? Nature 2003, 421, 498. [Google Scholar] [CrossRef] [PubMed]
  47. Perlmutter, S.; et al. Measurement of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
  48. Riess, A.G.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
  49. Riess, A.G.; et al. A comprehensive measurement of the local value of the Hubble constant with 1 km/s/Mpc uncertainty from the Hubble Space Telescope and the SH0ES team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
  50. Battye, R.A.; Charnock, T.; Moss, A. Tension between the power spectrum of density perturbations measured on large and small scales. Phys. Rev. D 2015, 91, 103508. [Google Scholar] [CrossRef]
Preprints 95116 g001
Figure 1. Penrose diagram of the sub-extremal Kerr spacetime. The evolution curve is divided into aeons (blue, red, and orange). Inside inner horizons r − , neutrino stars (future-spacelike BKL singularities) collapse (dash lines, t col   ~   10 − 32   sec ) into timelike Ricci singularities and initiate Big Bangs with spacetimes and neutrino stars (past-spacelike BKL singularities) of new aeons. If the evolution curve is divided outside the outer horizons, hypothetical wormholes are obtained.
Figure 1. Penrose diagram of the sub-extremal Kerr spacetime. The evolution curve is divided into aeons (blue, red, and orange). Inside inner horizons r − , neutrino stars (future-spacelike BKL singularities) collapse (dash lines, t col   ~   10 − 32   sec ) into timelike Ricci singularities and initiate Big Bangs with spacetimes and neutrino stars (past-spacelike BKL singularities) of new aeons. If the evolution curve is divided outside the outer horizons, hypothetical wormholes are obtained.
Preprints 95116 g001
Preprints 95116 g002
Figure 2. A schematic diagram of the inner horizon of a rotating black hole. The eclipse (yellow) is the inner horizon. The eclipse (red) represents a neutrino star. The vertical line (black) is the axis of spin. The horizontal row of clumps (blue) represents the falling spiral flows Vs, going in on the left and coming out on the right. The slashed lines (dark red) are the emission beams Vb, developing symmetrically about the neutrino star. The dashed curves (dark red) represent the back falling flows Vf, either immediately surrounding the Vb or further into the Vs plane.
Figure 2. A schematic diagram of the inner horizon of a rotating black hole. The eclipse (yellow) is the inner horizon. The eclipse (red) represents a neutrino star. The vertical line (black) is the axis of spin. The horizontal row of clumps (blue) represents the falling spiral flows Vs, going in on the left and coming out on the right. The slashed lines (dark red) are the emission beams Vb, developing symmetrically about the neutrino star. The dashed curves (dark red) represent the back falling flows Vf, either immediately surrounding the Vb or further into the Vs plane.
Preprints 95116 g002
Preprints 95116 g003aPreprints 95116 g003b
Figure 3. Methods to determine the Center of the universe. (A) The Planck CMB map is taken from ref.17. All the white symbols and labels are from the literature, and all the blacks from this work. The Center is at the intersection of line NC-SC (the Vb line) and a hot plane (the Vs plane): (B) Center O: determined by Peaks 3 and 4, and the AoE (MN) vector; (C) Center I: determined by arcs PQ (1-2-3&4-5) and ST (6-7-8-9); (D) Center IIA: the closest point on line NC-SC to line XW; (E) Center IIB: determined by Regions X and W, and Peak 3. Region X shows a cold corner (blue); region W shows a hot corner (orange). Other symbols are the LS (green) and 3D globe of the SLS (green).
Figure 3. Methods to determine the Center of the universe. (A) The Planck CMB map is taken from ref.17. All the white symbols and labels are from the literature, and all the blacks from this work. The Center is at the intersection of line NC-SC (the Vb line) and a hot plane (the Vs plane): (B) Center O: determined by Peaks 3 and 4, and the AoE (MN) vector; (C) Center I: determined by arcs PQ (1-2-3&4-5) and ST (6-7-8-9); (D) Center IIA: the closest point on line NC-SC to line XW; (E) Center IIB: determined by Regions X and W, and Peak 3. Region X shows a cold corner (blue); region W shows a hot corner (orange). Other symbols are the LS (green) and 3D globe of the SLS (green).
Preprints 95116 g003aPreprints 95116 g003b
Preprints 95116 g004aPreprints 95116 g004b
Figure 4. Anisotropic universe. (A) A schematic picture for the universe. The universe was born from the Center (red dot) due to the collapse of a neutrino star in Nature. Because the precursor neutrino star span, the universe is ellipsoidal (represented by a blue eclipse), elongated (orange thick horizontal arrow) in the directions parallel to its equator ( W = 0 ° ) and contracted (orange thick vertical arrow) in the direction parallel to its axis of spin ( W = ± 90 ° ). Note that this figure is not to scale, in particular, the size and eccentricity of the universe are unknown. The LS (green dot) is rotating about the axis of spin on the plane (dark red): z = − 0.58 x + 0.03 y , and moving towards the furthest equatorial plane (the direction of orange thin arrows). The faster expansion: FED (blue direction), and the slower expansion: SED (red direction). The observable universe is nearly ellipsoidal (represented by a green eclipse), within which are: the equatorial plane (red line), and the axis of spin (black line, between N and S). (B) Side view, parallel to the equatorial plane; (C) Top view, along the axis of spin. Unit vectors of the observed SED: CMB dipole (red), galaxy cluster anisotropy (blue), bulk flows (grey), Great Attractor (green), SNe Ia dipole (yellow), dark energy dipole (orange), fine-structure constant dipole (violet). The line (dark red) is the rotational plane of the LS (green). All vectors are plotted in length of the radius of SLS; the other symbols are the same as in Figure 3.
Figure 4. Anisotropic universe. (A) A schematic picture for the universe. The universe was born from the Center (red dot) due to the collapse of a neutrino star in Nature. Because the precursor neutrino star span, the universe is ellipsoidal (represented by a blue eclipse), elongated (orange thick horizontal arrow) in the directions parallel to its equator ( W = 0 ° ) and contracted (orange thick vertical arrow) in the direction parallel to its axis of spin ( W = ± 90 ° ). Note that this figure is not to scale, in particular, the size and eccentricity of the universe are unknown. The LS (green dot) is rotating about the axis of spin on the plane (dark red): z = − 0.58 x + 0.03 y , and moving towards the furthest equatorial plane (the direction of orange thin arrows). The faster expansion: FED (blue direction), and the slower expansion: SED (red direction). The observable universe is nearly ellipsoidal (represented by a green eclipse), within which are: the equatorial plane (red line), and the axis of spin (black line, between N and S). (B) Side view, parallel to the equatorial plane; (C) Top view, along the axis of spin. Unit vectors of the observed SED: CMB dipole (red), galaxy cluster anisotropy (blue), bulk flows (grey), Great Attractor (green), SNe Ia dipole (yellow), dark energy dipole (orange), fine-structure constant dipole (violet). The line (dark red) is the rotational plane of the LS (green). All vectors are plotted in length of the radius of SLS; the other symbols are the same as in Figure 3.
Preprints 95116 g004aPreprints 95116 g004b
Table 1. The Center of the universe.
Table 1. The Center of the universe.
Method Primary data Ref Vs plane Center (l, b) d/rSLS S
O Peaks 3, 4 & AoE vector 14-16 z=-1.54x-1.28y-1.67rSLS (222°, -58°)a 0.87 0.12
I Arcs PQ, ST this work z=-0.58x+0.03y-0.36rSLS (286°, -43°) 0.66 0.51
IIA Regions X, W 21 (281°, -46°)b 0.67 0.47
IIB Regions X, W & Peak 3 14, 21 z=-0.74x-0.10y-0.50rSLS (278°, -48°) 0.67 0.45
a) the preliminary trial that did not pass the synchronous test (S is far away from 0.5); b) the point on line NC-SC closest to line XW.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated