1. Introduction
Dew is a ubiquitous phenomenon in nature where it forms during calm and clear nights on vegetation surfaces. Dew is the result of the dropwise condensation of the atmosphere water vapor [
1,
2,
3,
4] when a surface exposed to the nocturnal sky cools enough to reach the dew point temperature. Cooling is due to the negative balance between the radiation emitted by the surface and radiation received by the atmosphere. The corresponding power, on the order of 50 W m
−2 to 100 W m
−2, limits the dew yield to about 1 L.m
-2.d
-1. Practically, dew forms when the difference between the dew point temperature and air temperature is less than a few degrees, corresponding to a relative humidity higher than 70 – 80% [
5]. The maximum measured dew yield is at the moment 0.8 L m
-2 d
-1 [
6].
Dew contribution can be vital for some plants and animals, during drought episodes in humid areas and in semiarid and arid regions [
4,
7,
8,
9,
10]. In certain arid regions, yearly dew is estimated to contribute from 9% to 23% of the total annual rainfall [
8,
11]. In arid regions or during droughts dew gives nightly moisture [
12,
13], which is absorbed by leaves through plant stomata, stem flows [
14] or special physical features as e.g., in aerial vegetation [
2,
15,
16]. Dew could increase leave photosynthesis [
17] and improve the efficiency of water use by plants [
2,
18]. The role of dew in soil biocrust (mainly composed of cyanobacteria, green algae, lichens and mosses) as a water source remains controversial (see e.g. [
19] and Refs. therein). Dew participates in atmospheric chemical processes, such as diurnal and nocturnal cycles of nitrite oxides [
4,
20,
21,
22,
23]. Small animals, such as insects [
24,
25,
26] also rely on dew and non-rainfall water.
In the context of global warming and rarefaction of fresh water, dew can thus be considered as a new source of water in those areas where fresh water, from rain or other sources, is lacking. Dew water can supplement the erratic rain water as it can be collected by population on special collecting devices of planar or hollow shapes [
4]. These devices can also efficiently collect light rain or mist that is normally lost, which increases the water yield [
27]. Water can be used for agriculture [
28] or serve for human consumption once disinfected to ensure safe drinking. The quality of dew water indeed quite generally meets the requirements of the World Health Organization (see e.g., [
4,
20,
26]).
At the global level, Madagascar is ranked 14
th on the lack of access to basic water [
29]. Access to drinking water is a major challenge. In 2022, only 54.4% of the Malagasy population had access to water [
30]. The main factor of this water deficiency is due to the climate change [
31], a decrease in the number of precipitation events causing a reduction in the amount of rainfall, especially in the 2000–2018 period of intensified drying. Extreme drought events magnitude and duration increased from 1950 to 2018, and the recharge of the aquifers is not covering the city's water needs.
It happens that the lack of water is particularly important in the south-western region of Madagascar, whose main city is Toliara, capital of the region. This area is a semi-arid region, with chiefly only two months rain (January and February) in the Madagascar rainy season. This region is thus not spared by water shortage since only 29% of the local population has access to drinking water [
29,
30]. Apart from its aridity, Toliara has the highest temperature in all of Madagascar [
31]. However, the air relative humidity is relatively important, twice as high as that recorded in Sahelian regions [
32]. As a matter of fact, dew data obtained by [
33] for 18 months (Apr. 2013-Sept. 2014) in the same coastal south-western region of Madagascar (Efoetsy) corresponded to near 20% of the yearly rainfall. The main conclusion shows that dewfall in this area can play a non-negligible role in the annual water balance and provides a supplementary source of fresh water during the non-rainy season.
It is worthy to note that, due to the global climate change, dew can exhibit various evolutions in different regions of the world. For instance, dew frequency decreased by 5.2 days per decade from 1961 to 2010 in China due to surface warming and corresponding decrease in relative humidity [
12]. More important, the decrease of dew frequency in arid regions of China (50%) is larger than found in the semi-humid and humid regions (40% and 28%) [
12]. The same trend of decreasing dew frequency is observed in west North Africa between 2005–2020 and predicted for 2020–2100 by using the low and high emissions climatic models [
34]. With the global climate change, the degree of decrease in dew frequency is thus variable in different regions of the world. Dew characteristics are then required to predict the future changes in dew evolution.
It is therefore the object of this paper to precisely quantify the contribution of dew and rain to the annual water balance in the semi-arid region of south-western Madagascar and evaluate its evolution during the measured period 1/1991-7/2023, and by extrapolation from 8/2023 to 7/2033. For that purpose, the dew yield is evaluated from an energy balance model that uses only a few meteorological parameters [
35]; available direct measurements [
36,
37] give elements of comparison between the calculated and measured data. The interpolation in 2023-2033 is made for dew and rain from an artificial neural network approach.
The paper is organized as follows. After having described the methods concerning the calculation of dew yields and the procedures of extrapolation of dew and rain data, one analyzes and discusses the evolution of dew, rain and their relative frequency and contribution in the period 1991-2023, with extrapolation to 2033.
2. Materials and Methods
2.1. Studied Sites
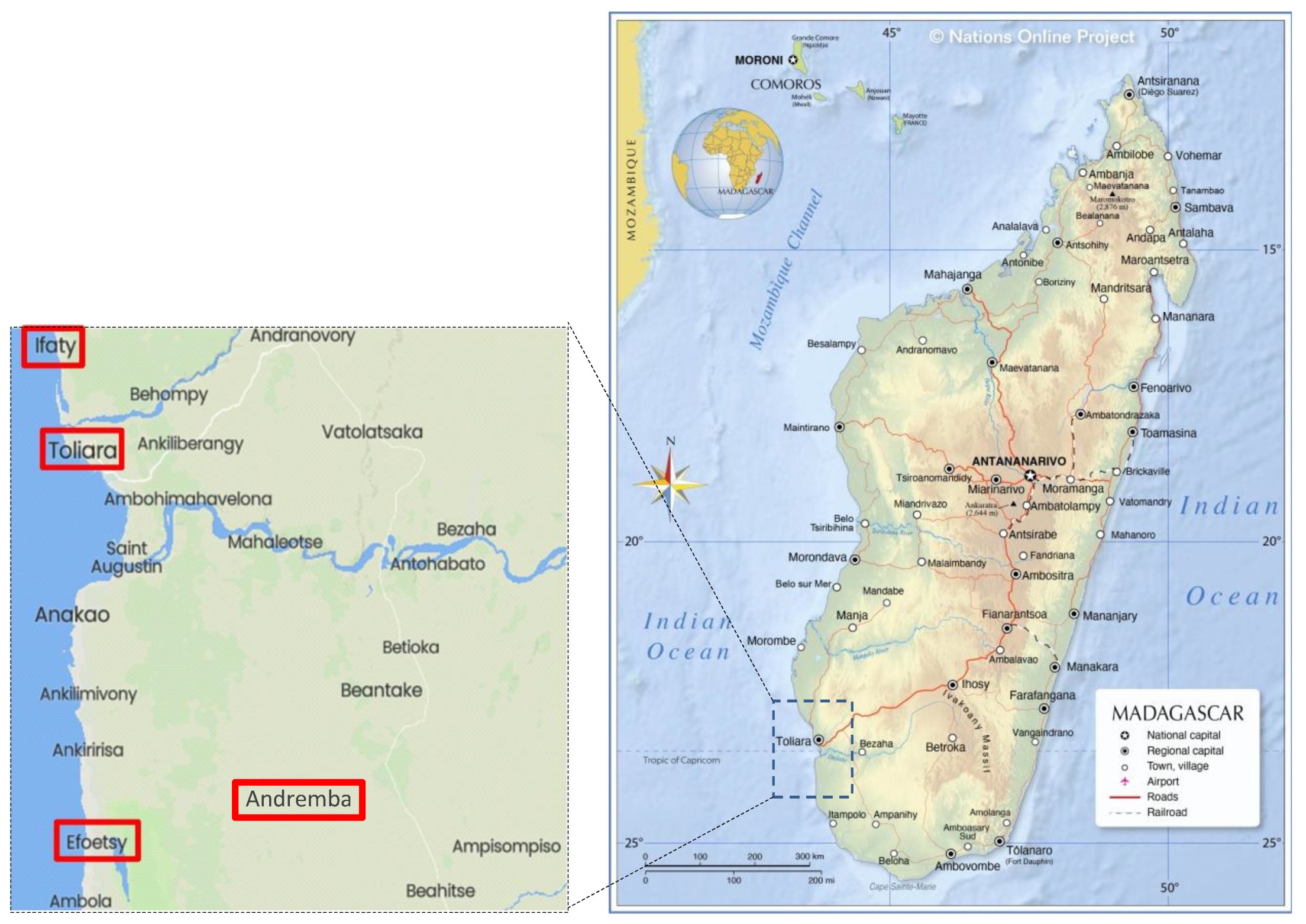
Toliara is located on the south-western coast of Madagascar (23.35° South and 43.67° East, 9 m asl), at the North of the Saint Augustin Bay (
Figure 1). This city is the capital of the Atsimo Andrefana region. The Köppen Geiger climate classification in this area is Bsh (midlatitude steppe and desert climate). The northern boundary of Toliara's urban area is defined by the Fiherenana River, the sole water source for irrigating the downstream plains from the Miary city. Toliara is part of the limestone domain of the southwest of Madagascar. The aspect of the soil is generally dominated by calcareous and sandy soil [
38].
Two other sites, with same climate, are considered. One is close to Toliara, such as the small coastal city of Ifaty (23.14° South and 43.60° East, 80 m asl), 27 kilometers NNW from Toliara. Another site is further from Toliara: Andremba (23.97° South and 44.20° East), more inland (60 km from the sea, 260 m asl, 81 km SSE from Toliara). In addition, calculated data will be compared to dew measurements performed independently [
33] in the nearby coastal village of Efoetsy (2 km from the sea, 10 m asl; 83 km S from Toliara).
Table 1 summarizes these information.
The general information concerning the southern part of Madagascar are summarized in
Table 2. The average annual temperature is 23.9°C. The warmest month is January with a mean temperature of 27.8°C. The coolest month is July, with an average temperature of 20.6°C. The mean annual amount of precipitation in Toliara is 342.9 mm. The month with the most precipitation is January with 73.7 mm of precipitation in average. The month with the least precipitation is July with an average of 5.1 mm [
41]. One of the particularities of the southwestern region of Madagascar is the abundance of humidity in the air. It has been proven that the value of relative air humidity RH in the southwestern part of Madagascar is twice as high than those recorded in the Sahelian zone (mean RH: 77%; min: 12%; max: 100% [
42]). The air relative humidity varies from season to season; it is maximum during the hot and humid months (Nov. – Mar., the rainy season) and minimal during the cool and dry period (Apr. - Oct., the dry season).
2.2. Meteorological Data
The weather data used in this study comes from the ERA5-Land database, which are re-analyzed atmospheric data produced by the ECMWF's Copernicus Climate Change Service. The spatial coverage of these data is 9 km and is in reduced Gaussian grid. The data spans from 1/1991 to 7/2023, with a one-hour time step. The following information are provided: Relative air humidity, air temperature, dew point temperature, cloud cover, and wind speed. As the Toliara’s pluviometer is the only operational pluviometer in the southwestern part of Madagascar, all rain data are derived from the ERA5-Land database [
43]. In this database, when the site does not have direct observations, as e.g. for Andremba, data are the result of extrapolations or interpolations in order to combine them with models outputs. The data of rain used here are all daily-analyzed data. Note that the same rain data are considered for the Ifaty and Toliara sites due to their close vicinity (27 km).
2.3. Dew Evolution
2.3.1. Energy Model
In order to compute the dewfall potential, a physical energy balance model (or “physical model” developed by [
35] is used. The model needs only a few classical meteorological data collected at a given time step ∆
t (here every hour):
Ta (°C), RH (%) or equivalently dew point temperature
Td (°C), cloud cover (
N, oktas), wind speed at 10 m elevation (
V10, m.s
-1). Dew yields in mm per unit of ∆
t, noted
(mm. ∆
t-1), are calculated on the time step ∆
t (expressed in h.) from the following formulation:
The numerical factor ∆
t/12 = 1/12 corresponds here to the data time step ∆
t = 1h. Events with
> 0 correspond to condensation and
< 0 to evaporation. The latter are rejected. The quantity
HL represents the convective heat losses between air and condenser, with a cut-off for wind speed
V >
V0 = 4.4 m.s
-1 where condensation vanishes:
HL = 0 if
V >
V0. When
V ≤
V0,
HL is expressed as:
The quantity
RE in Eq. 1 is the available cooling energy by radiative deficit. Depending on the water content of air (measured by
Td, in °C), the site elevation
H (in km) and the cloud cover
N (in oktas),
RE is evaluated by the following expression:
Daily time series corresponding to > 0 are built after removing all data where rain events are present. The calculated cumulative yields can then be obtained by summing the data e.g on daily, monthly or yearly bases.
2.3.2. Perceptron Analysis for Extrapolation
Concerning the extrapolation of data one considers an approach by Multi-Layer Perceptron Artificial Neural Networks (MLP-ANN). It is a type of artificial neural network inspired by the functioning of the human brain [
44,
45]. Other methods are available such as Long Short-Term Memory (LSTM) Networks [
46,
47] or Spiking Neural Networks with Spike-Timing-Dependent Long Short-Term Memory (SNN-STLSTM) [
48,
49].
Each methods exhibit strengths and weaknesses. The MLP-ANN method is simple to implement and understand, can approximate any continuous function given enough neurons and data and is effective for a large variety of tasks such as classification and regression. However, they are not well-suited for tasks involving temporal sequences or data with time dependencies since they do not have a memory mechanism. They can also easily overfit to the training data if not properly regularized. The LSTM method is capable of learning long-term dependencies, making them worthy for time-series prediction, speech recognition, and natural language processing; it also mitigates the vanishing gradient problem, allowing for better learning over longer sequences. However, it exhibits more complex and computationally intensive work compared to simpler models like MLPs. Training times are longer due to their complexity and the need for sequence processing. The SNN-STLSTM approach can well mimic biological neural processing, which can be more efficient for certain tasks. It can also precisely capture timing information, which is critical for tasks requiring high temporal resolution. It shows a better energy efficiency, especially when implemented on neuromorphic hardware. It is, however, more challenging to implement and train compared to traditional neural network. Training SNNs often requires specialized algorithms and can be less straightforward. In addition, it exhibits some hardware dependency concerning the benefits in energy efficiency.
One here uses the simplest MLP-ANN approach by sake of simplicity and also because such an approach is currently used to predict meteorological variables such as solar radiation prediction [
50], rainfall / evapotranspiration [
51], air quality monitoring [
52] or temperature [
53]. More important, the method was already used to specifically estimate dew [
54]. The multi-layer perceptron is thus a set of interconnected neurons [
55,
56,
57,
58]. Information flows from input to output without backtracking [
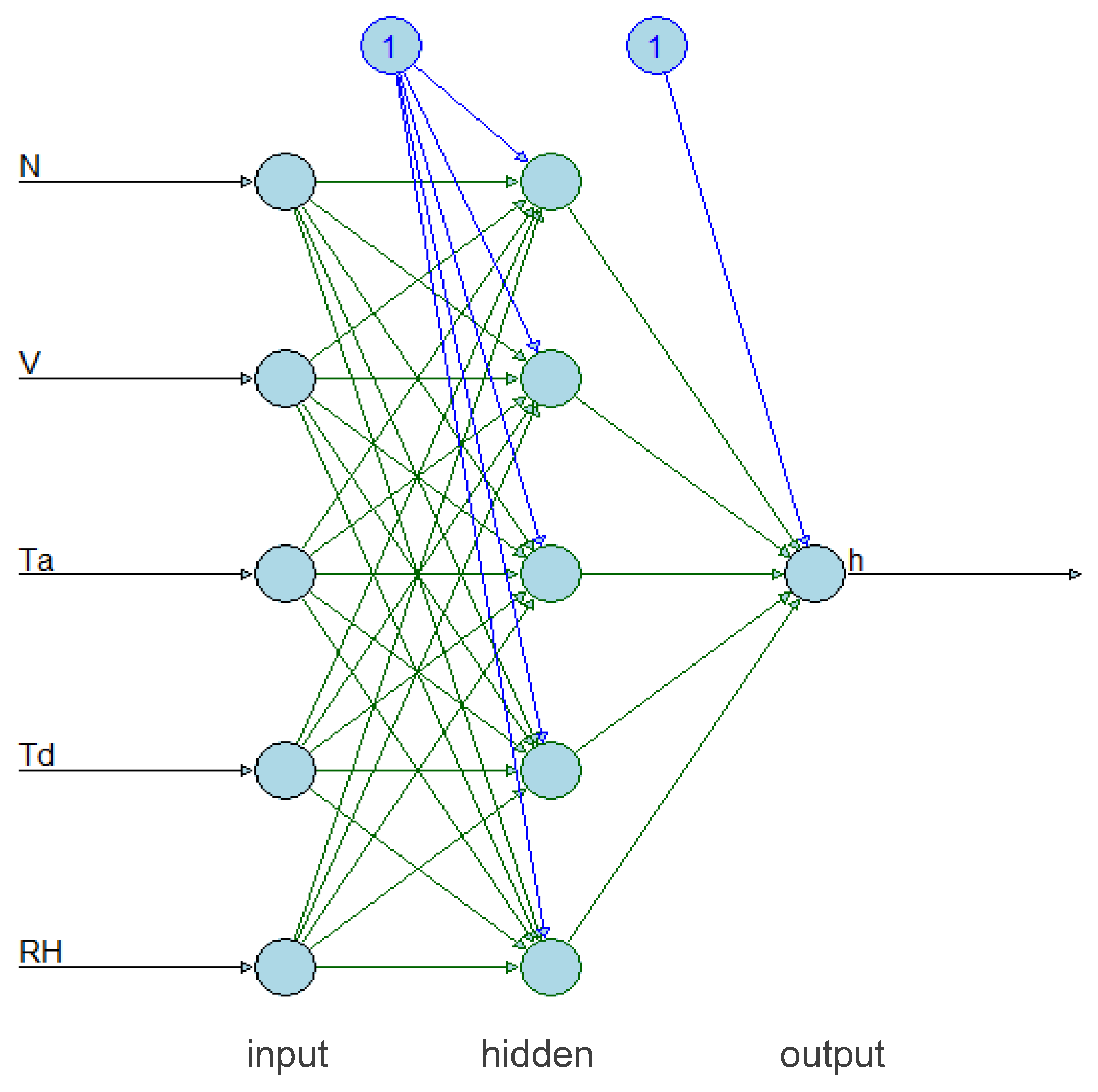
58]. It is composed of three distinct layers (
Figure 2). The first layer or the input layer is formed by the input data on a hourly basis:
Ta (°C),
Td (°C), RH (%),
V (m.s
-1) and
N (oktas). These data, known to correspond to the parameters that determine the dew amount [
4,
35,
54], are introduced in the MLP-ANN on a monthly basis. The use of
Ta, RH and
Td is somewhat redundant as they are related by analytical equations but it increases the accuracy. The second layer is the hidden layer to prepare the data using activation functions in their neuron to present it in the last layer, the output layer, which represents the dew yield
h (mm.mth
-1) output.
For the MLP-ANN network, a back-propagation algorithm is used. The back-propagation algorithm consists in forward-flowing the input data until a network-calculated input is obtained, and then comparing the calculated output to the known actual output. The weights are modified such that at the next iteration the error made between the calculated output is minimized. Taking into consideration the presence of the hidden layers, the error is back propagated backwards to the layer input while changing the weights. The process is repeated on all the data until the output error can be considered as negligible [
59]. The package R interface for 'H2O' [
60] has been used in this study, with the hyperbolic tangent function as an activation function. This function is indeed monotonic and having an identity for 0. It also allows normalization to be applied to the input values. This improves the conditioning of the optimization problem. If some inputs are systematically too large compared to others, they will have a disproportionate contribution to the error gradient, which will prevent the network from using the other variables. In addition, these variables will tend to saturate the hidden units at the start of training, which slows it down. This activation function also allows rapid learning to be performed because it initializes the weights randomly, which makes the model more efficient.
Figure 2.
MLP-ANN configurations for monthly dew yields prediction. When using a MLP-ANN, it is customary to add a value “1” called ‘neuron bias’ to the input of a neuron. The bias is a kind of local weight that is used in several activation functions [
61].
Figure 2.
MLP-ANN configurations for monthly dew yields prediction. When using a MLP-ANN, it is customary to add a value “1” called ‘neuron bias’ to the input of a neuron. The bias is a kind of local weight that is used in several activation functions [
61].
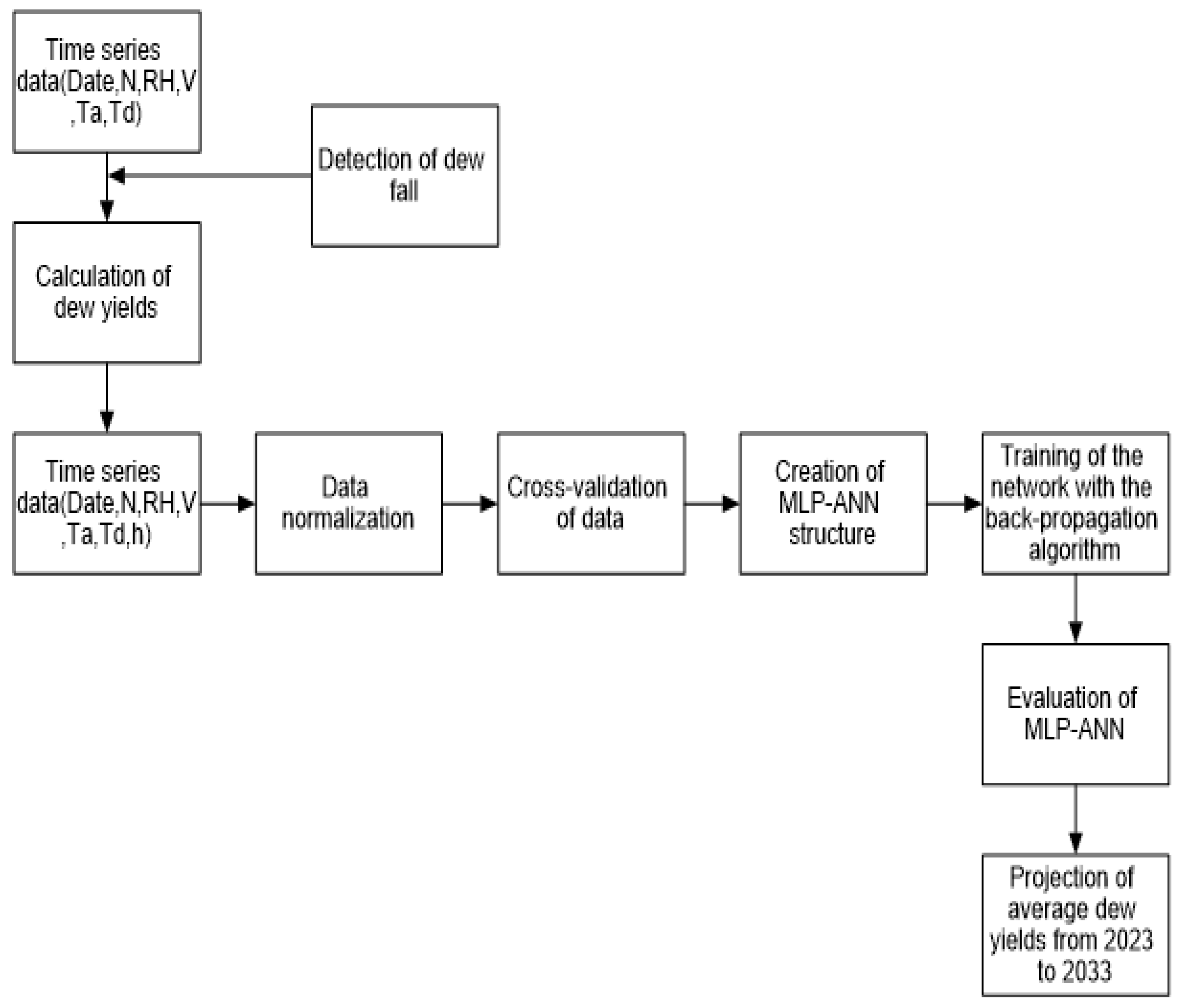
The multi-layer perceptron can give a projection from 2023 to 2033. The corresponding approach is summarized in
Figure 3.
To predict the future value of the rain, we used the package ‘nnfor’ in R software (latest version 0.9.9, published on 2023-11-15). The package is designed for time series and univariate data like rain [
62,
63]. It is an automatic time series modeling, that is it automatically adds an activation function and other neurons to the input layer. With such a package, time series forecasting can be performed with multilayer perceptrons and extreme learning machines. Different model architectures were tried, from no hidden layers to 10 hidden layers. The minimum number of hidden layers to fit data was found to be one.
3. Results
3.1. Comparison with Direct Measurements
In order to determine the level of accuracy of the calculation of dew yields, the calculated data are compared in
Figure 4 with the measurements of Hanisch et al. [
33]. One sees that the few data of measured volumes in Andremba exhibit a larger yield than the calculated values, on order 2.5 times. There are no meteo data available in Efoetsy and the closer site is Toliara. The measured values in Efoetsy are about three times the calculated values in Toliara. Such measured large yields in Andremba and Efoetsy can be understood by the contribution of fog and mist that adds to dew. Such events were indeed observed [
64]. The relative humidity during the night is undeniably quite large in Efoetsy and Andremba (RH = 100%), which favors the formation of radiative fog and the occurrence of mist. As a matter of fact, the typical evolution of dew mass during the night as shown in [
33] exhibits an acceleration after midnight, which is the signature of fog and mist deposing on the dew collector. This behavior is typical in coastal areas and was analyzed in [
65]. Since the calculation from meteo data ignores the fog and mist events that should occur, it gives less condensation volume.
Note that an additional cause of discrepancy between ground measurements and climatic spatial grid values can be attributed to the limitations of input data resolution. As noted in section 2.2, the grid is 9 km in reduced Gaussian grid.
3.2. Dew Evolution
3.2.1. Years 1/1991-7/2023
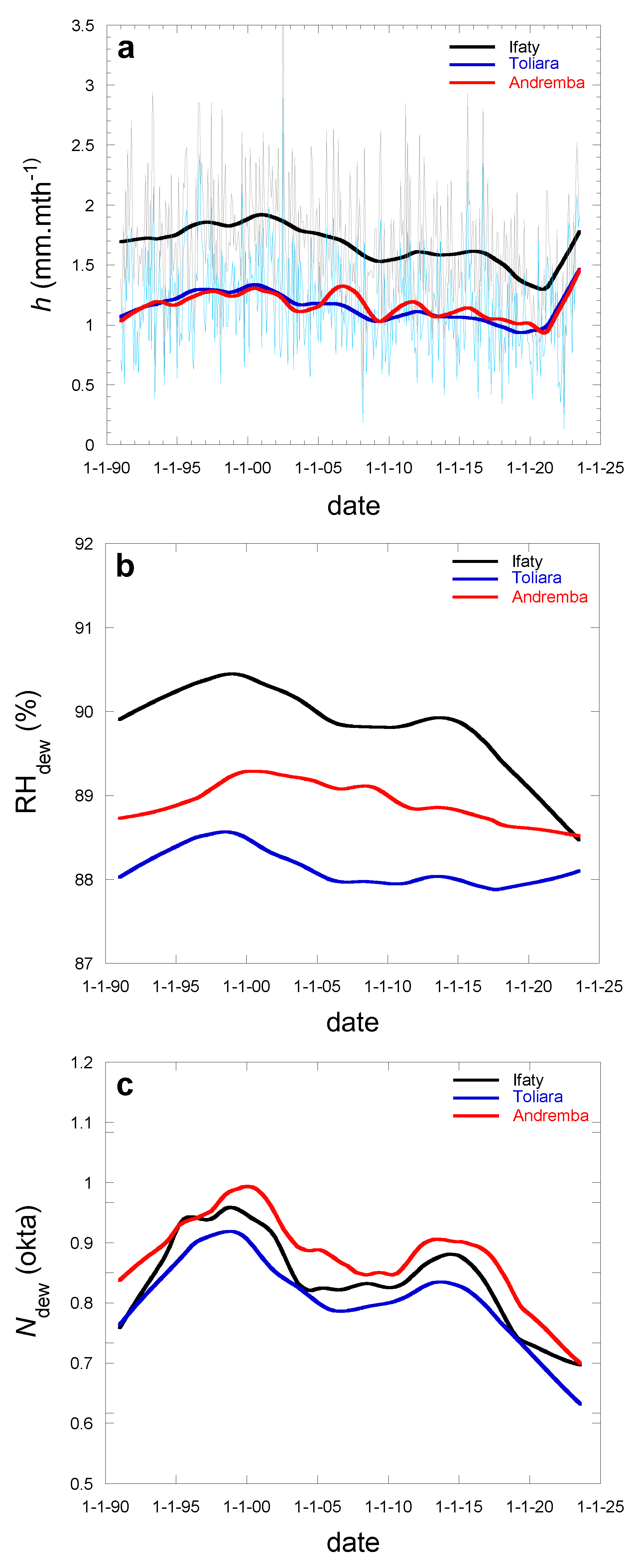
Figure 5a reports the dew yield evolution (in mm.mth
-1) for the three sites as calculated from the model Eq. 1. One first sees that all evolutions are similar, and almost identical for Toliara and Andremba, although Ifaty and Toliara are closer to each other than Toliara and Andremba (see
Figure 1). Toliara and Ifaty displaying similar values of cloud covers (
Figure 5c), the reason can be found in the relative humidities during dew events, smaller in Toliara than in Ifaty (
Figure 5b). The near equal dew values in Toliara and Andremba can be explained by the contributions of lower cloud covers in Toliara that counterbalance smaller RH values (
Figure 5bc).
The evolution exhibits a mean increase of about 22% from 1991 to 2000, a decrease of near 35% from 2000 to 2020 and a subsequent increase from 2020 to 2023 of 20%. The mean dew rate during all the period gives for Ifaty the largest value (1.68 mm.mth
-1) with a standard deviation (SD) of 0.49 mm.mth
-1, for Toliara the mean is 1.16 mm.mth
-1 with SD = 0.40 mm.mth
-1 and for Andremba, the mean is quite close, 1.19 mm.mth
-1 with SD = 0.56 mm.mth
-1. One will see in section 3.3.1 (Figure 10) that the rain behavior is similar. Since rain is a key factor to determines the level of RH in the atmosphere, it is thus natural that dew follows an evolution similar to what is observed with rain.
Table 3 summarizes the main results together with the statistically meaningful trends as discussed just below.
In order to determine the statistical quality of the general trends on the whole measured period one makes use of the Mann-Kendall (MK) and Sen's slope tests. The latter calculates the median of the slopes between all pairs of points in the dataset. It provides a robust estimate of the trend that is less affected by outliers compared to methods like linear regression. The results for the three sites of investigation are listed in
Table 4. One notes that the standard deviation (SD) of the measured data is on the same magnitude for all sites (~ 0.5 mm.mth
-1). Concerning the Mann-Kendall tests of trend statistical significance, the Andremba data do not fulfill the criteria of statistical trend.
Table 3 summarizes these results, which show that all trends are small and negative, meaning that dew yield slowly but surely decreases with time.
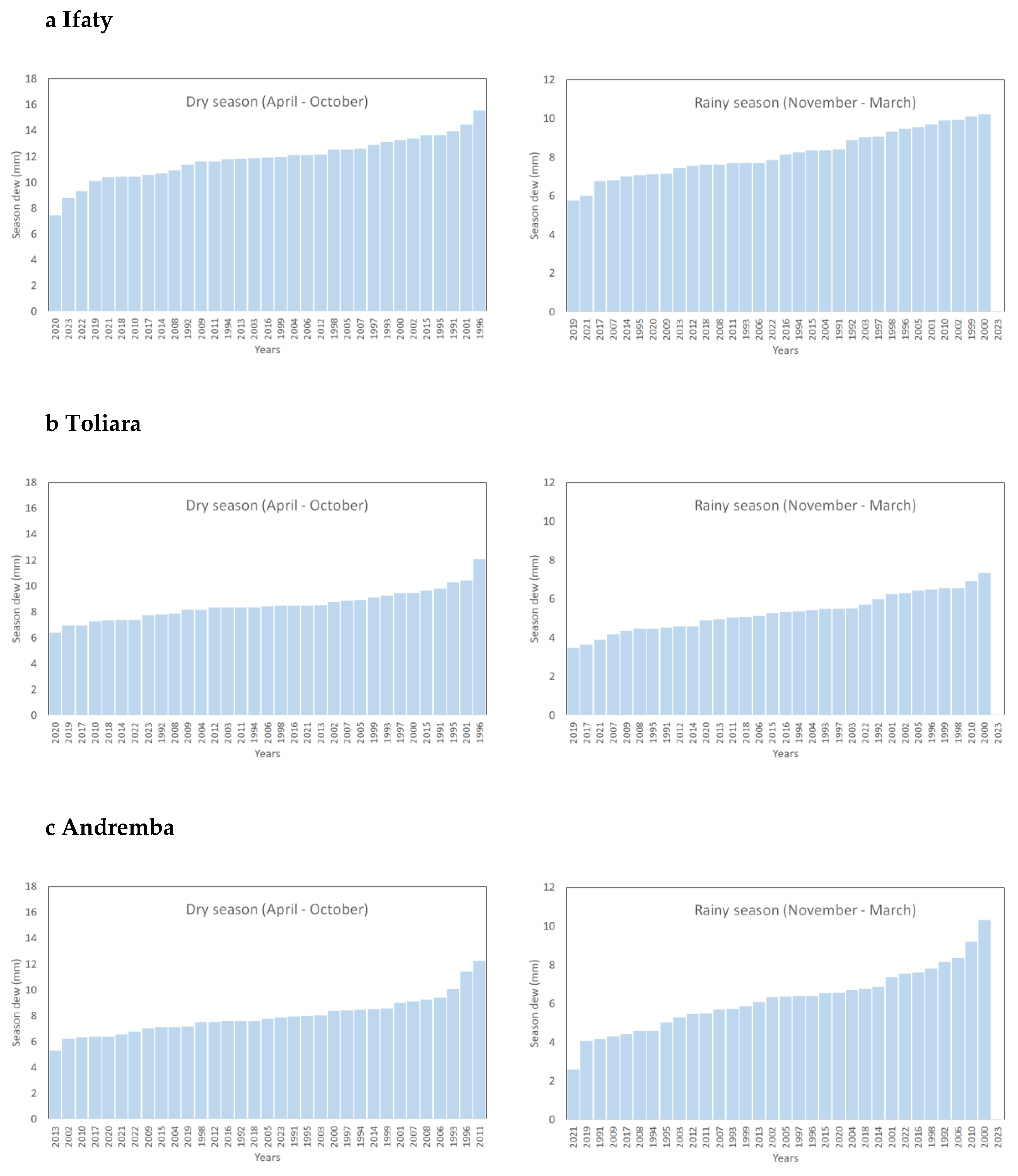
The dates of change of dew trends (2000, 2020) are corroborated in
Figure 6 where are reported the dew yields with respect to the year of calculation in ascending order, for the dry (Apr.-Oct.) and rainy seasons (Nov.-March). For Ifaty the minimum rate is 5.8 mm.season
-1 (rainy season 2019) and the maximum is 16 mm.season
-1 (dry season 1996). For Toliara the results are quite comparable, with a minimum rate is 3.5 mm.season
-1 (rainy season 2019) and the maximum is 12 mm.season
-1 (dry season 1996). Concerning Andremba, the results are also similar, with a minimum rate of 2.5 mm.season
-1 (rainy season 2021) and a maximum of 12 mm.season
-1 (dry season 2011).
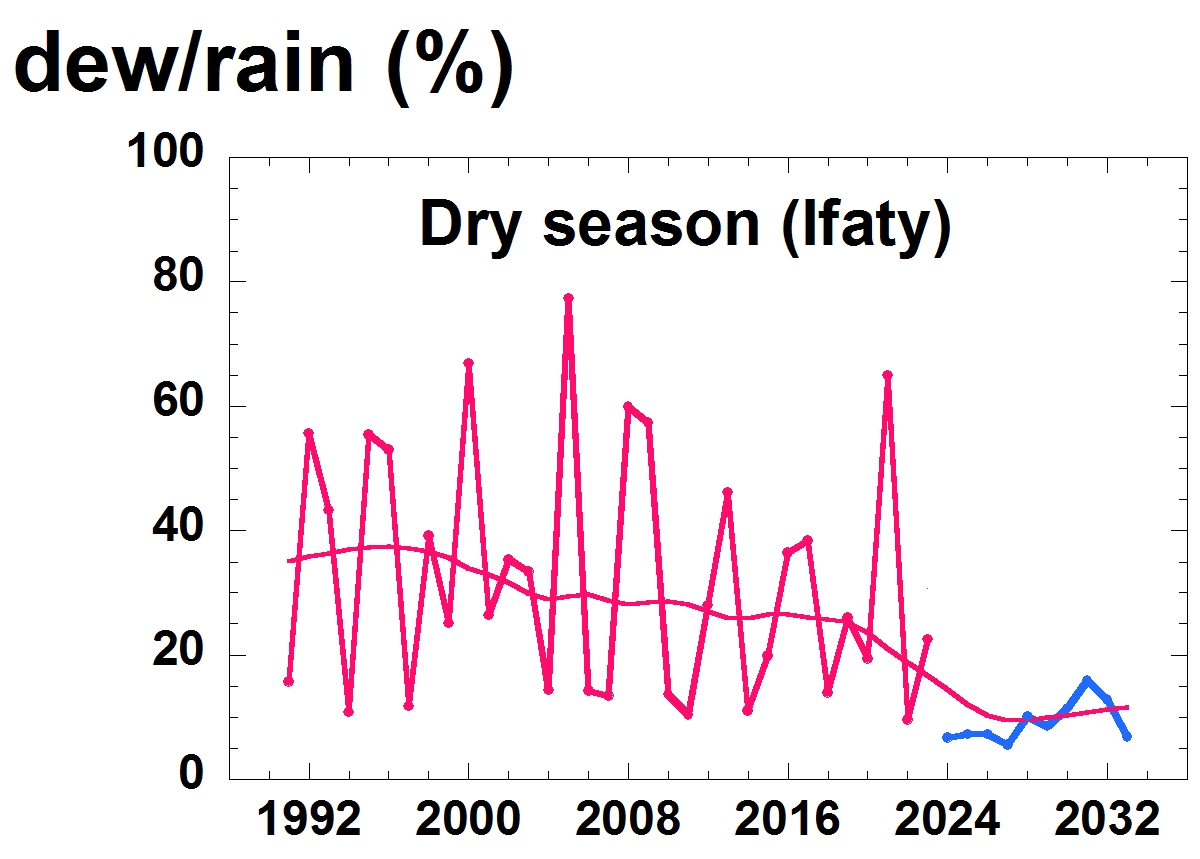
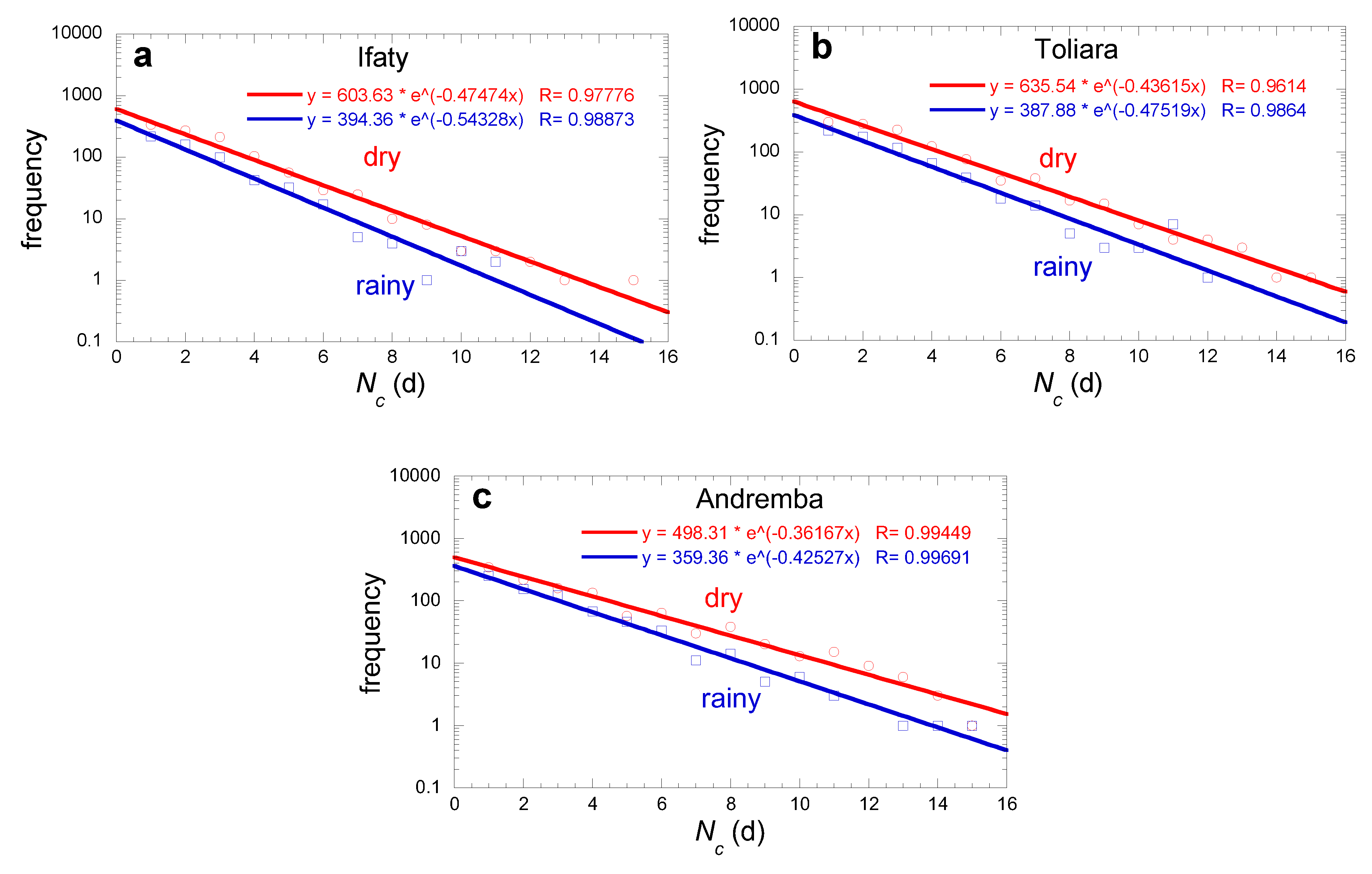
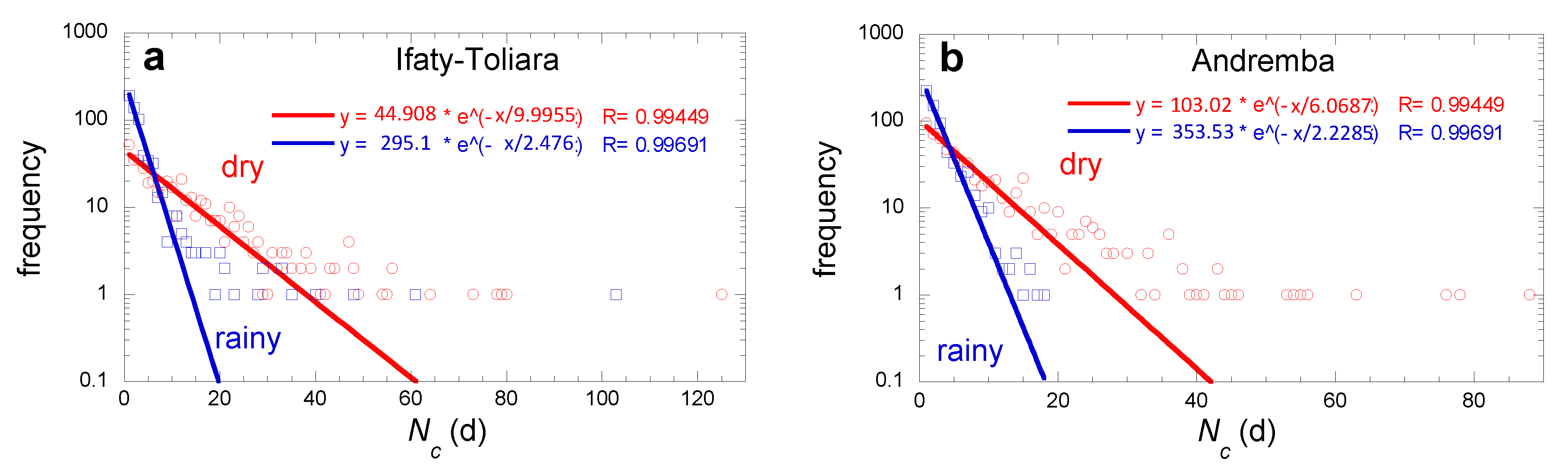
The number of days without dew events is an important parameter as many plants and small animals suffer when no water is available during a long period. Histogram of the data for all the periods are reported in
Figure 7 for both dry and rainy seasons. One sees that dew forms regularly during all seasons, with a frequency larger during the dry seasons for all sites. The ratio of dry/rainy dew frequencies is about 1.5 in Ifaty and Toliara and near 1.3 in Andremba.
The
Figure 7 data can be fitted to an exponential decay where
f is the frequency of events showing the number
Nc of consecutive days without dew:
In this Eq. 4, is a typical number of events and is a typical number of consecutive days without dew. For all sites, is larger in the dry seasons (~ 600) than in the rainy season (~ 400). The number keeps similar values for dry and rainy seasons, on the order of 2 days without dew (minimum 1.84 days during the rainy season in Ifaty, maximum 2.76 days during the dry season in Andremba).
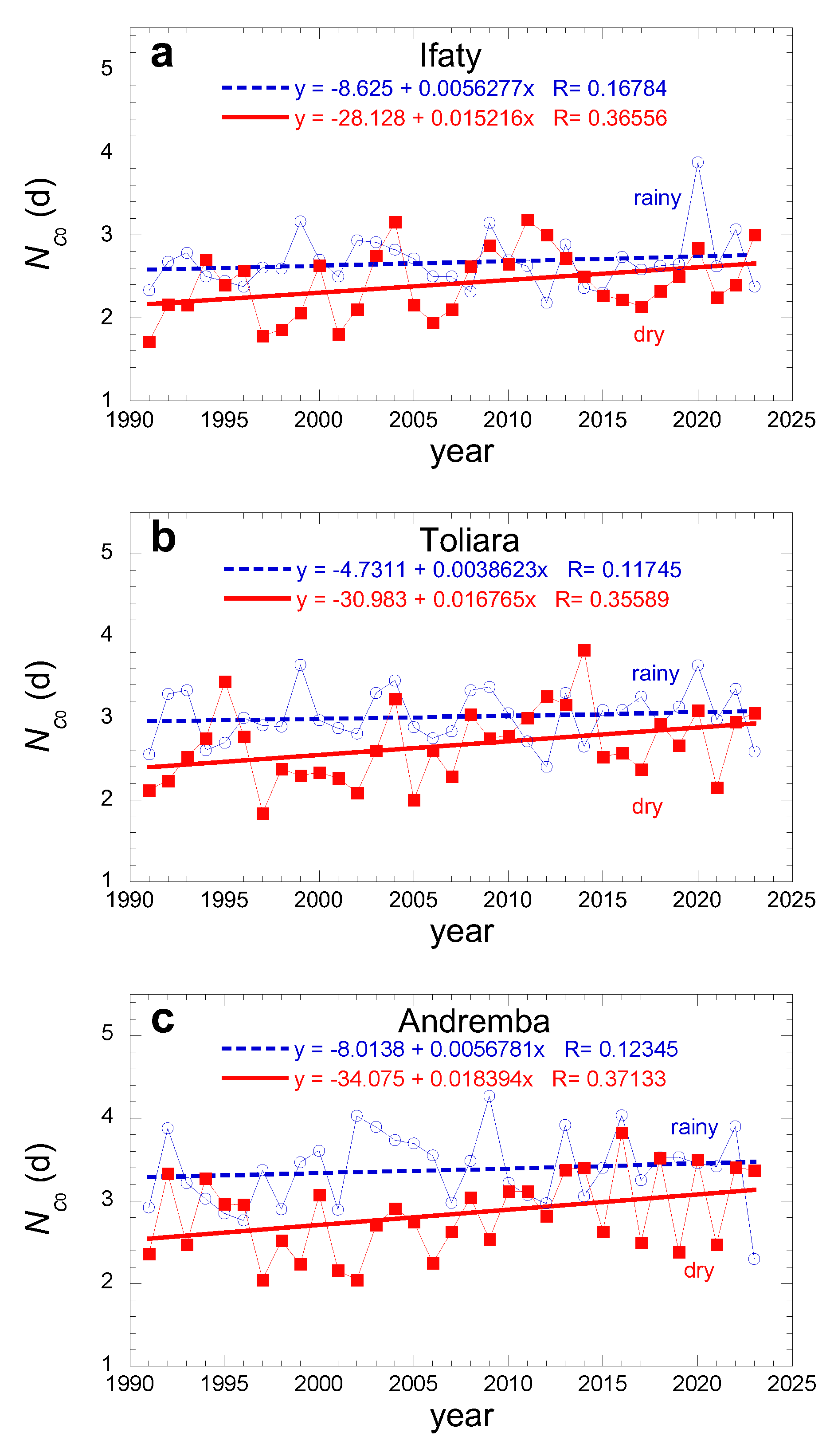
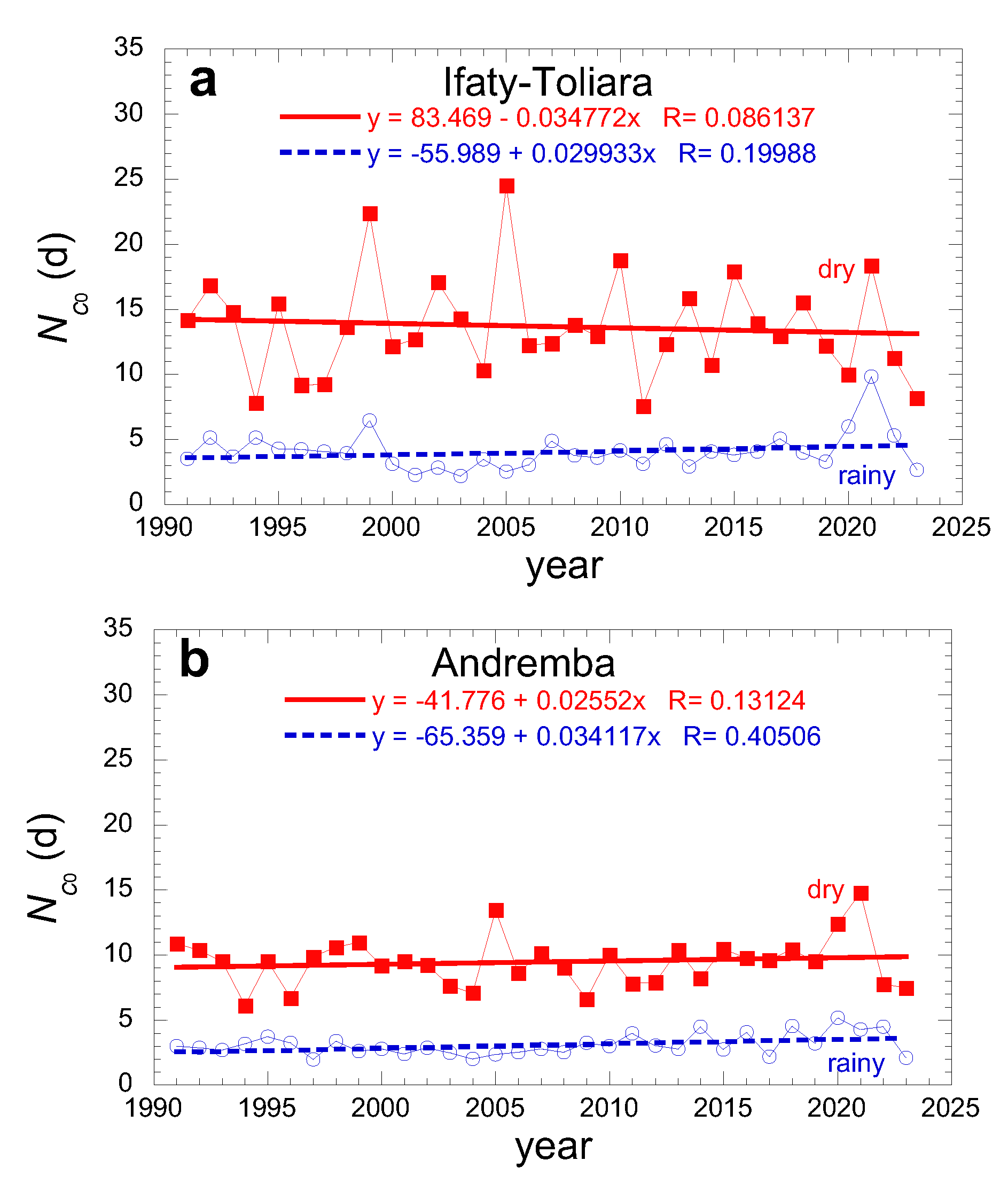
The evolution of the typical number of consecutive days without dew,
Nc0, is reported in
Figure 8 for the dry and rainy seasons in Ifaty, Toliara and Andremba. One observes in all sites that the mean number of consecutive days without dew events is small (~ 2.6 days per year). It is less during the dry season when compared to the rainy season (~3), although the relative humidity is obviously less. This counter-intuitive result is due to the fact that the number of dew events in the rainy season is reduced by more frequent rain occurrences (see Figure 13).
The corresponding statistics is reported in
Table 5, including the Mann-Kendall and the Sen's slope tests to observe a trend. No trends can be defined for the rainy seasons in all sites. A positive trend is well characterized in all sites for the dry season with similar Sen’s slopes, 44×10
-6 mm.yr
-2 (Ifaty), 53×10
-6 mm.yr
-2 (Toliara), and 57×10
-6 mm.yr
-2 (Andremba). A linear fit of the data (
Figure 8) gives similar slopes for all sites, 1.5×10
-2 mm.yr
-2 (Ifaty), 1.7×10
-2 mm.yr
-2 (Toliara), 1.8×10
-2 mm.yr
-2 (Andremba).
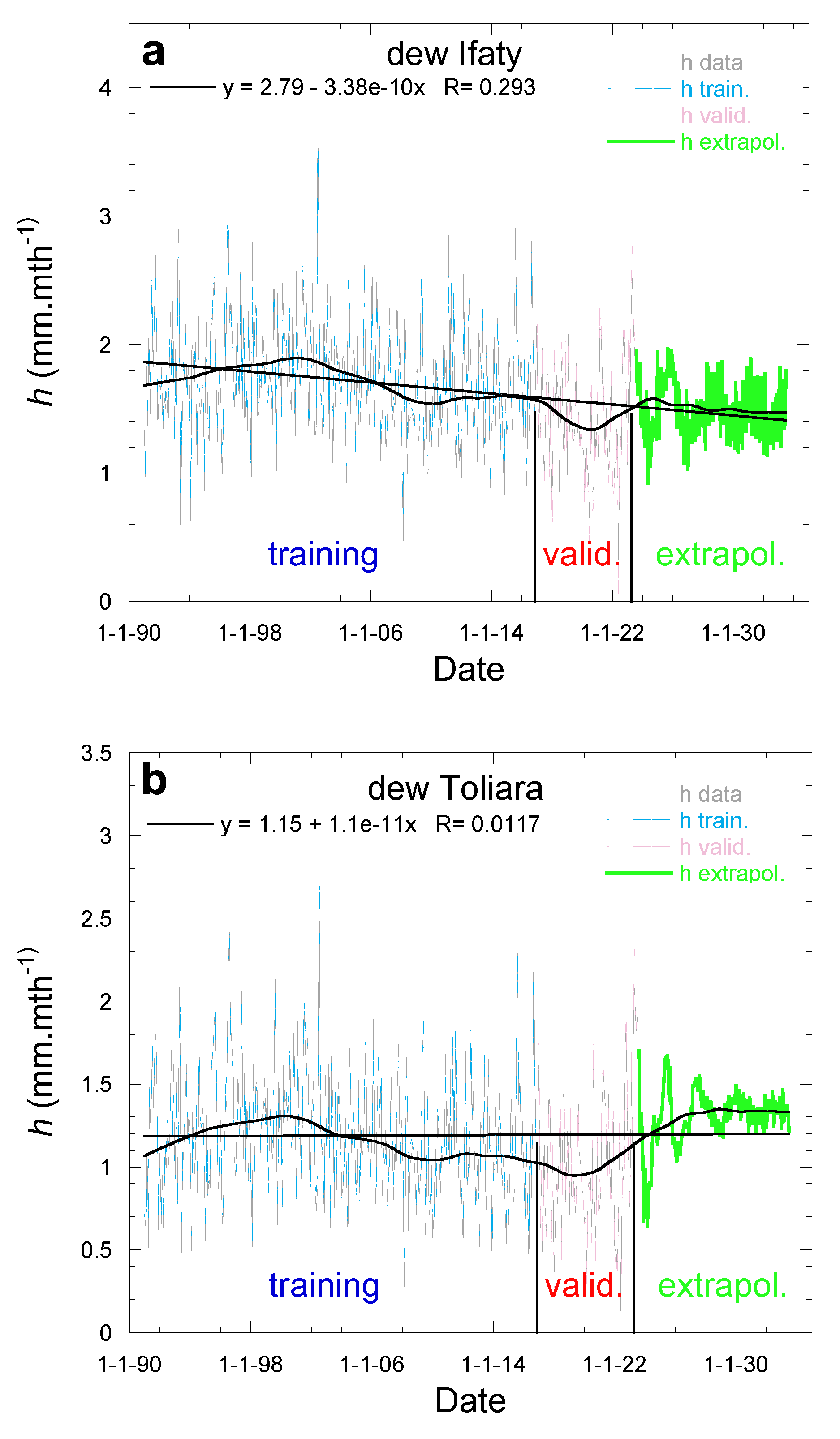
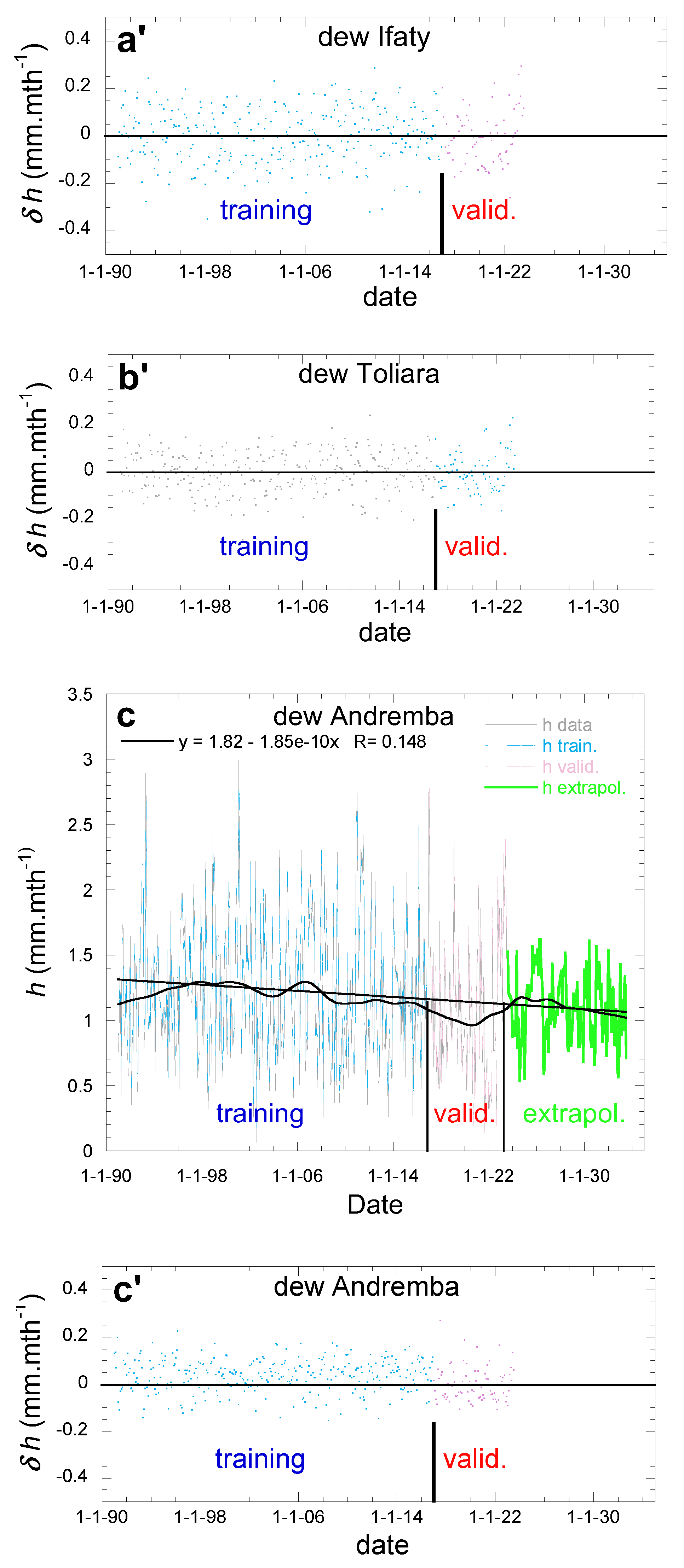
3.2.2. Extrapolation for Years 8/2023-7/2033
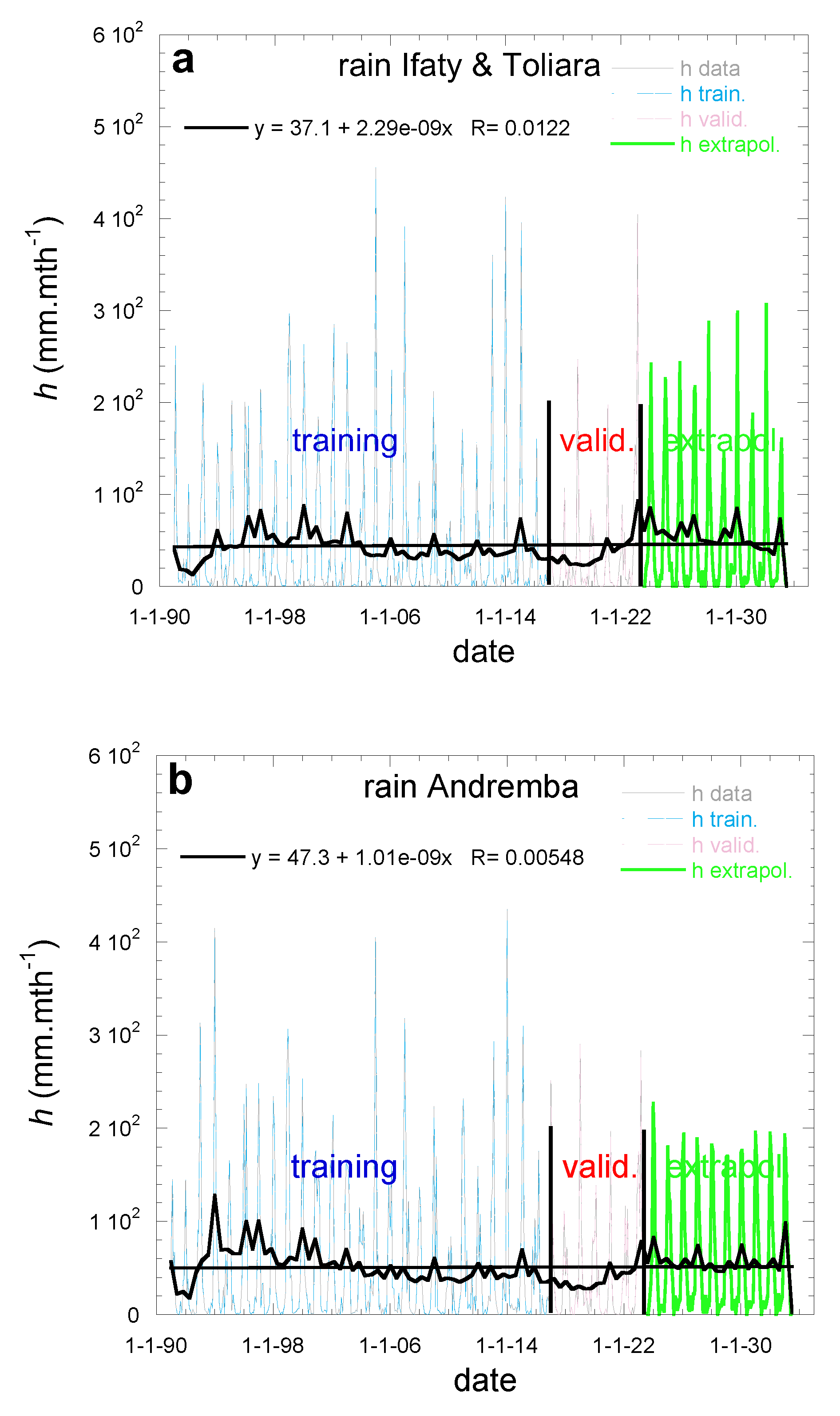
The monthly data from 1/1991 to 7/2023 are extrapolated to the period 8/2023 -7/2033 according to the procedure using MLP-ANN, as described in section 2.3.2. The procedure follows a period of training with 77% of the data (1/1991 – 12/2016) and a period of validation corresponding to 23% of the data (1/2017 – 7/2023). In
Figure 9aa’bb’cc’ the training and validation data are seen to compare well with the dew data as calculated from Eq. 1.
The monthly dew yields are reported in
Figure 9, with smoothening curves for visual aid. In order to determine a trend over the observed period (1/1991-7/2023), the extrapolated period (8/2023-7/2033) and the whole period (1/1991-7/2033), the MK and Sen’s slope statistical methods are applied in
Table 4. Trends are not statistically valid for any periods at Andremba. At Ifaty, the trend is not defined for the extrapolated period while a negative trend is observed for both the observed and the whole periods. At Toliara, a positive trend is seen in the extrapolated period, canceling in the whole period the effect of the negative trend in the observation period. Linear fits of the data (
Figure 9d) on the whole period 1991 – 2033 are in agreement with this analysis, giving the slopes (-3.4 ± 0.5)×10
-4 mm.mth
-1.s
-1 (Ifaty), (-1.1 ± 4)×10
-4 mm.mth
-1.s
-1 (Toliara), (-1.9 ± 0.5)×10
-4 mm.mth
-1.s
-1 (Andremba).
3.3. Rain Evolution
3.3.1. Years 1/1991-7/2023
The rainfall evolution in the period 1/1991-7/2023 is shown in
Figure 10 for Toliara and Ifaty (same data, see section 2.2) and Andremba. Without surprises, the rain amplitudes and evolutions are similar in all sites. One notes obvious differences between the dry and rainy seasons (analyzed below in
Figure 11) and the presence of large peaks related to cyclone events. Between 1991 and 2000 is observed an important rise from ~ 25 to ~ 60 mm.mth
-1, then a long decrease until 2018-2020 with a rise until 2023. As noted in section 3.2.1 (
Figure 5), dew and rain are seen to follow similar evolutions. Rain (together with nearby sea evaporation) indeed provides the atmosphere with large relative humidity needed to condense water vapor [
66].
Figure 10.
Evolution of the monthly rainfalls. (a,b): Training, validation and extrapolation of rain data. The black bold curves are data smoothening and the black lines are linear fits to all data in the period 1/1991-8/2033 (x = date-1/1/1904 in s). (a) Ifaty and Toliara, (b) Andremba. Grey lines: Actual rain data 01/1991 – 07/2023. Blue lines: ANN training period 01/1991 – 12/2016; red lines: ANN validation period 01/2017 – 07/2023; green lines: ANN extrapolation period 08/2023 – 07/2033. (a’, b’): Difference between ANN and actual values data values for (a’) Ifaty and Toliara, (b’) Andremba.
Figure 10.
Evolution of the monthly rainfalls. (a,b): Training, validation and extrapolation of rain data. The black bold curves are data smoothening and the black lines are linear fits to all data in the period 1/1991-8/2033 (x = date-1/1/1904 in s). (a) Ifaty and Toliara, (b) Andremba. Grey lines: Actual rain data 01/1991 – 07/2023. Blue lines: ANN training period 01/1991 – 12/2016; red lines: ANN validation period 01/2017 – 07/2023; green lines: ANN extrapolation period 08/2023 – 07/2033. (a’, b’): Difference between ANN and actual values data values for (a’) Ifaty and Toliara, (b’) Andremba.
Table 6.
Statistical analysis of the rain data according to the Mann-Kendall (MK) and the Sen's slope tests.
Table 6.
Statistical analysis of the rain data according to the Mann-Kendall (MK) and the Sen's slope tests.
| Rain |
Data |
mths. |
Min (mm.mth-1) |
Max (mm.mth-1) |
Mean (mm.mth-1) |
SD (mm.mth-1) |
p-value*
|
MK mea-
ningful trend$
|
Sen’s slope (×10-5 mm.mth-2) |
Sen’s con-
stant |
Ifaty
Toliara |
Meas. |
391 |
0 |
455.6 |
42.343 |
73.426 |
0.244 |
No |
-11.9 |
15.791 |
| Extrap. |
120 |
0 |
307.0 |
53.265 |
71.611 |
0.738 |
No |
0 |
19.793 |
| All |
511 |
0 |
455.6 |
44.907 |
73.081 |
0.496 |
No |
5.1 |
10.790 |
| Andr-emba |
Meas. |
391 |
0 |
435.5 |
48.998 |
74.108 |
0.377 |
No |
-11.8 |
19.225 |
| Extrap. |
120 |
0 |
227.0 |
56.489 |
61.977 |
0.819 |
No |
45.8 |
4.643 |
| All |
511 |
0 |
435.5 |
50.757 |
71.457 |
0.102 |
No |
27.0 |
6.937 |
Figure 11 presents the rainfall yields in the dry season (Apr.-Oct.) and rainy season (Nov.-Mar.). There is obviously a large difference in the volumes of the precipitations, with a ratio ~8 , the mean precipitation rate being in the dry season 61 mm.season
-1 and 485 mm.season
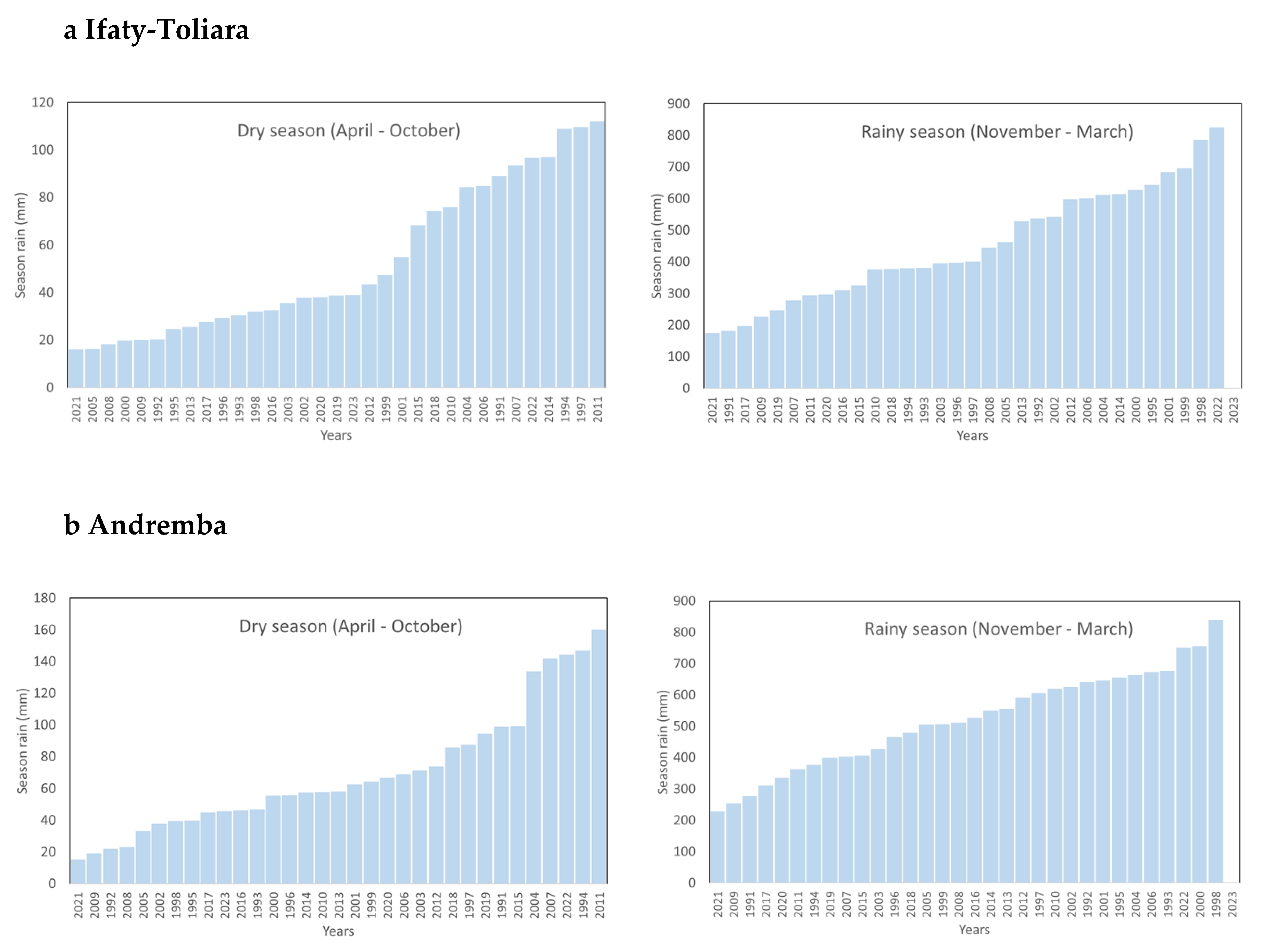
-1 for the rainy season. The minimum rainfall is 18 mm in 2021 (dry season, all sites) and the maximum is 850 mm in 1998 (Andremba) and 2022 (Ifaty-Toliara).
As for dew (see section 3.2.1), the frequency of consecutive rainy days without rain can be well represented by an exponential (Eq. 4;
Figure 12). For all sites, the amplitude
is much larger in the rainy seasons (~ 300-350) than in the dry season (~ 45-100). Unsurprisingly, the average number of days without rain
Nc0 is also much greater in the dry season (6-10 days) than in the rainy seasons (~ 2.45 days).
The evolution of
Nc0, is reported in
Figure 13 for the dry season (Apr. - Oct.) and the rainy season (Nov. - March). One obviously observes a much smaller value (about a factor of 1:3.3) in the rainy season (~ 4 days in Ifaty-Toliara, ~ 3 days in Andremba, see
Table 7) than in the dry season (~ 14 d in Ifaty-Toliara, ~ 9.5 d in Andremba, see
Table 7). The statistical tests (
Table 7) do not allow trends to be detected in the observation period 1/1991-7/2023.
3.3.2. Extrapolation 8/2023-7/2033
The monthly data of the period 1/1991 - 7/2023 are extrapolated to the period 8/2023 -7/2033 according to the procedure using MLP-ANN, as described in section 2.3.2 and more precisely the package ‘nnfor’ in R software. This package was used because it is specially designed for time series and univariate data like rain.
As for dew, the procedure follows a period of training with 77% of the data (1/1991 – 12/2016) and a period of validation corresponding to 23% of the data (1/2017 – 7/2023). In
Figure 10aa’bb’ the training and validation data at Ifaty-Toliara and Andremba compare well with the measured rain data.
The monthly dew yields are reported in
Figure 10, with smoothening curves for visual aid. In order to determine a trend over the observed period (1/1991-7/2023), the extrapolated period (8/2023-7/2033) and the whole period (1/1991-7/2033), the MK and Sen’s slope statistical methods are applied in
Table 7. Trends are found to be not statistically valid for any periods at all sites. Linear fits of the data (
Figure 9d) on the whole period 1991 – 2033 are in agreement with this analysis, giving the slopes with a large SD (2.3 ± 8.5)×10
-9 mm.mth
-1.s
-1 (Ifaty-Toliara ), and (1 ± 8)×10
-9 mm.mth
-1.s
-1 (Andremba). The standard deviations of the values are quite large, which cast some doubts about the actuality of the slopes. As a matter of fact, the statistical quality of this trend is not assessed by the MK and Sen’s slopes methods (
Table 6) in any sites. While the observed positive and negative evolutions during the period are clearly observed (see
Figure 10), they cancel each other when looking to a mean trend.
3.3. Dew-Rain Ratios
In order to determine the contribution of dew in the global water balance, a dew/rain ratio can be defined as:
where
is the volume of rainfall calculated on the same time period as the dew yield
. This factor exhibits quite large variations because in some months
= 0, thus making the contribution of dew the only input in the water balance. In order to average these variations, one will rather consider the yearly mean
or the dry or rainy season means
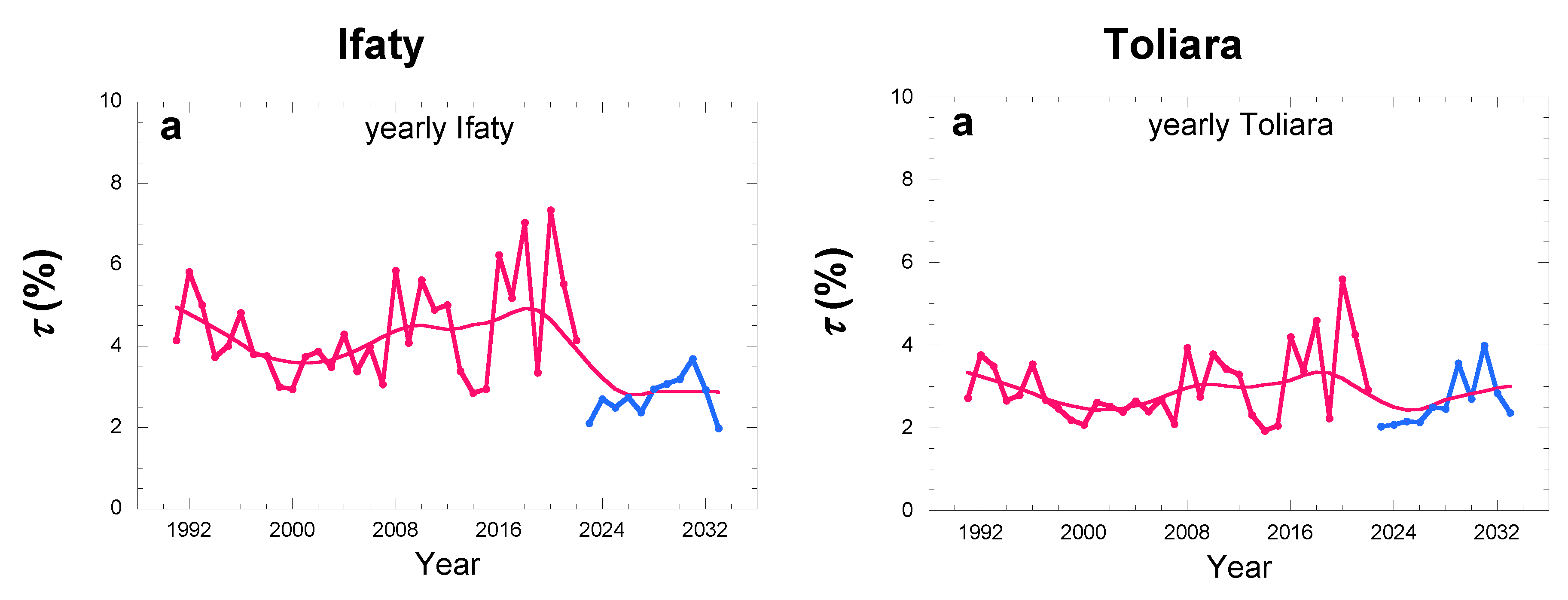
The results are shown in
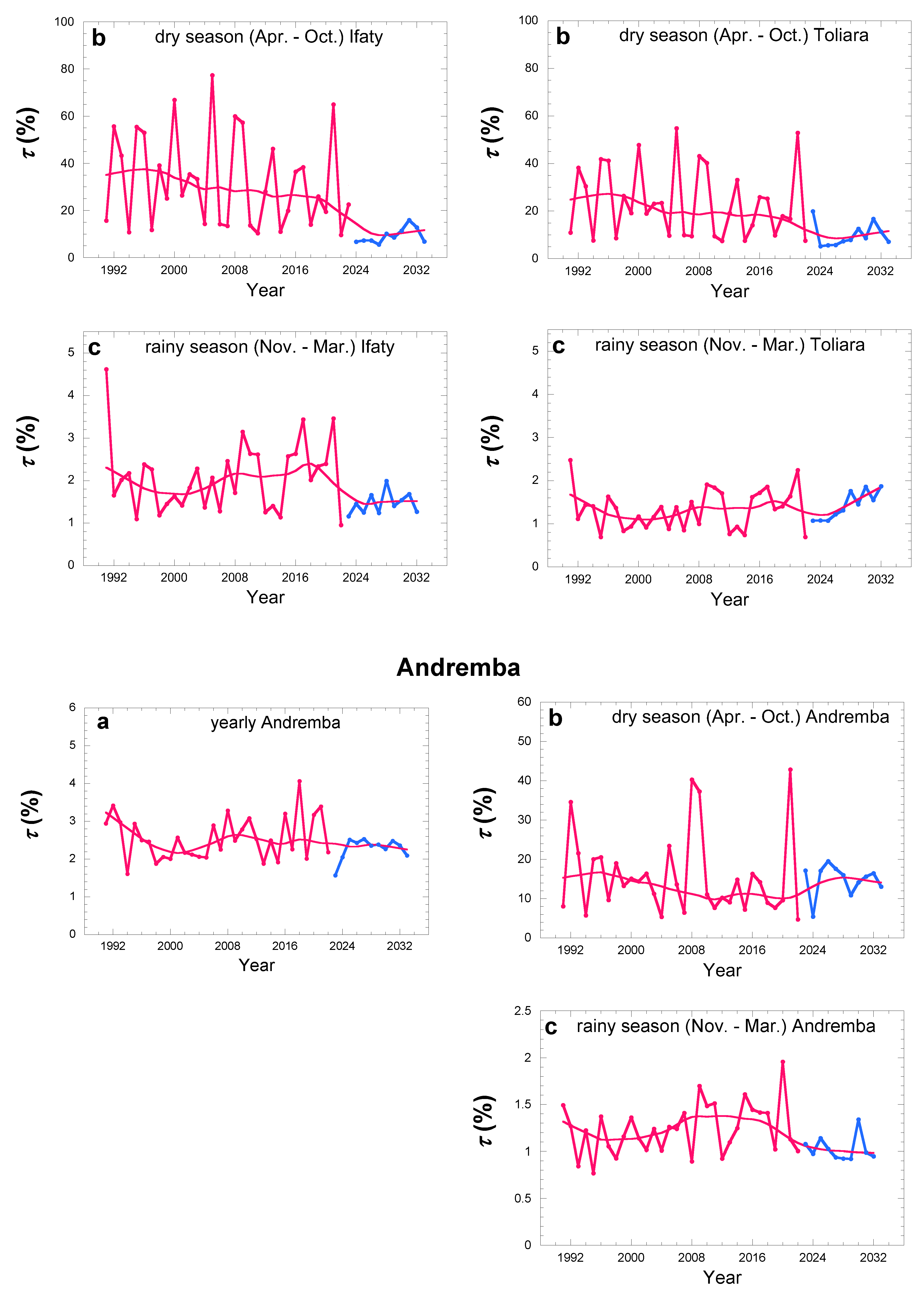
Figure 14 for the three studied sites. Concerning the yearly season, the evolution is the opposite of dew and rain evolutions, with a decrease of ~ 30% from 1991 to 2000, an increase of ~ 30% from 2000 to 2020, a decrease from 2020 to 2023 of 30% and a subsequent weak increase of ~ 10%. The mean values with SD in the period 1991-2033 are (Ifaty) 4.0%
1.3%, (Toliara) 2.9%
0.8% and (Andremba) 2.5%
0.5%. The ratio in the rainy season follows similar behavior but with nearly half mean values: (Ifaty) 1.9%
0.8%, (Toliara) 1.3%
0.4% and (Andremba) 1.2%
0.3%. The evolution behavior in the dry season is less pronounced but compatible with what is observed in the rainy season. The mean values become significantly larger, with larger SD, giving (Ifaty) 27%
20%, (Toliara) 20%
20% and (Andremba) 15%
9%.
In sections 3.2.1 (dew) and 3.3.1 (rain) the similarity of behavior of dew and rain evolution was noted. However, the amplitude of variation of rain being larger than that of dew, the overall behavior of the dew/rain ratio is thus seen to behave inversely to dew and rain evolution, which explains the observation of
Figure 13, particularly clear for the yearly and rainy seasons.
The yearly values are relatively low, but with the contributions of fog and mist in the coastal areas (Efoetsy, Andremba, see section 3.1 and
Figure 4) the non-rainfall contributions can reach three times the dew amount. Contributions up to ~ 10% could therefore be attained, which is a considerable contribution. As a matter of fact, the value τ = 19% was measured in average for a 18-month period at Efoetsy [
33]. Concerning the only dry season, values as large as 27% are observed, which could rise to 80% with the contribution of fog and mist.
Regarding the trends over the different periods, one reports in
Table 8,
Table 9 and
Table 10 the evaluation of the trend statistical quality according to the MK and Sen’s slope tests. It results that no trends are valid for any periods in Andremba. No trends are also valid in any sites and any yearly, dry and rainy seasons for the observation period 1/1991-7/2023. Concerning yearly data, a positive trend is observed for the extrapolation period 8/2023-7/2033 at Toliara and a negative trend for the whole period 1/1991-7/2033 at Ifaty. Concerning the rainy season, the only visible trend is observed at Toliara for the extrapolation period 8/2023-7/2033. It is interesting to note that the dry seasons exhibit only negative trends for the whole period 1/1991-7/2033 at both Ifaty and Toliara.
4. General Discussion
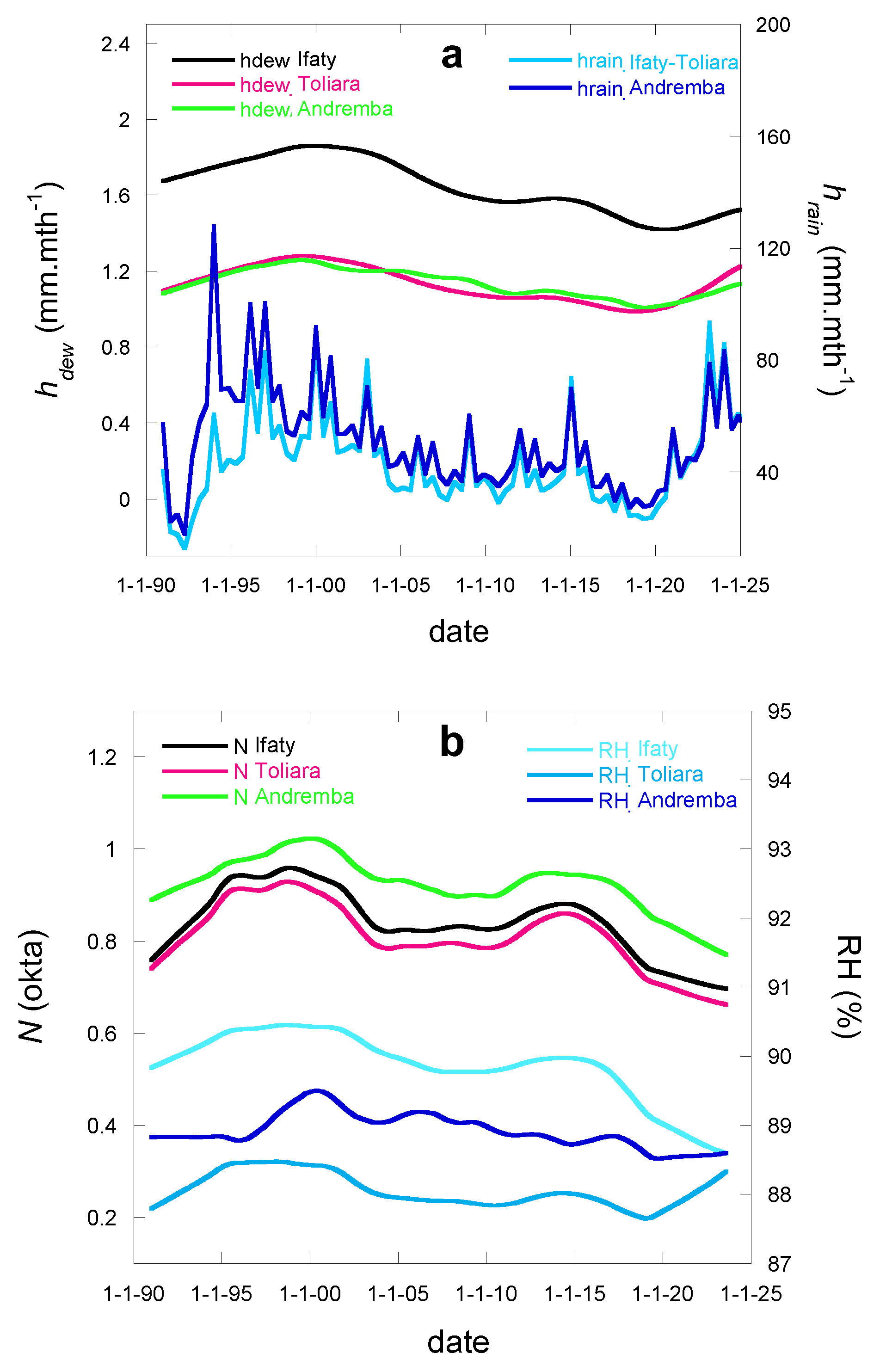
The first result of this study is the recognition that on a rather small area ( ~ 100 × 60 km2) dew can vary much more than rain. For instance, dew varies by 50% between Toliara and Ifaty that are distant of 27 km, and is nearly the same in Toliara and Andremba 81 km distant. In contrast, rain keeps nearly the same values in those three sites. This observation is due to the process of formation of dew, which is a function of quite local values of relative humidity, air flows (wind) and cloud cover. Rain, in contrast, forms in the upper regions of atmosphere and is convected on large distances before falling an a large area.
Another result is the finding that the evolutions of dew and rain are similar (
Figure 15a). The reason can be found in the variation of local relative humidity, which governs the dew yield and increases with increasing rainfall (
Figure 15b). The evolution is non-monotonous, with increase from 1991 to 2000, a decrease up to 2020 and a further increase till 2033. A decrease between 2000 and 2018 was already noted in the study [
37] that ended in 2018 and is a part of a long-lasting trend, at least from the 1950’s. The evolution of cloud cover, which is also an important parameter in dew formation, unsurprisingly follows the same evolution with, however, a very small increase that does not affect the rise of dew yield at large RH.
The evolution of rain is known to follow the ocean surface temperature, which undergoes periodic oscillations known as Indian Ocean Dipole (IOD, see e.g. [
67]). The IOD is negative when the water surface temperature of the Indian Ocean is below normal in the west and above normal in the east. When a negative IOD is observed then in the central-western tropical Indian Ocean the precipitation is below normal while in the eastern tropical Indian Ocean and in the western tropical Pacific Ocean the precipitations are higher than normal. Extreme IOD events (droughts, floods and hurricanes) are likely to increase in the future as a result of the climate change. These events have a tendency to relate with El Niño events, with periods of 5-10 years.
In terms of water content, dew forms much more regularly than rain. The number of consecutive days without dew is the same in the dry and rainy seasons (2-3 days). It is much larger for rain in the dry season (10-15 days) and even in the rainy season (3-5 days). Although the dew yield remains modest (1-2 mm.mth-1) when compared to rain (~ 30 mm.mth-1), corresponding to yearly mean contribution of 3-4%, its contribution during the dry season can be much larger, up to ~ 30% . Its evolution is opposite of rain and dew, due to the larger influence of rain variation in the ratio dew/rain. One notes that the contribution of collected fog and mist can increase by a factor 3 this contribution.
5. Conclusions
Dew yields were calculated in three sites, Ifaty, Toliara and Andremba (Madagascar) between 1991 and 2023 from meteo data thanks to an energy equation. The region has a mid-latitude steppe and desert climate characterized by high humidity, which favors dew formation. When combined with rainfalls, the evolution of dew and rain and their relative importance can be determined in the period. The data are extrapolated from 2023 to 2033 by using artificial neural networks.
The evolution of dew and rain is found similar and in agreement with the variations of the IOD ocean surface temperature. One observes an increase from 1991 to 2000, a decrease up to 2020 and a further increase till 2033. The overall trend in the period 1991-2033 is negative for dew and uncertain for rain.
The contribution of dew with respect to rain is found rather weak when averaged on a year, about 3-4%. However, dew forms very regularly all over the year, which makes its contribution large during the dry season (Apr.-Oct.), up to ~ 30%, due to the conjunction of higher dew yield and lower rainfalls. The values calculated for dew in this work (mean value about 1-2 mm.mth-1) are conservative. The measured non-rainfalls indeed exhibit much larger yields, by a factor on order three. On the Madagascar coast, fog and mist indeed add to dew and considerably increase the contribution of non-rainfall water.
The number of consecutive days without rain or dew is an important factor for the vegetation and in general for animals and human population. The mean number of consecutive days without rain is on order 3-5 days during the rainy season and much larger during the dry season (10-15 days). In contrast, dew is regular all over the year, as shown by a mean number of consecutive days without dew of 2-3 days, making it a reliable source of water for plants, animals and even population if properly stored with rain.
The evolution of the dew and rain water resources is related to the ocean surface temperature governed by the Indian Ocean Dipole. Its variations, alike El Niño, are subjected to the climate change. In particular, extreme events (droughts, floods and hurricanes) are expected to increase in the future.
Author Contributions
Conceptualization, D.B. and M.M.; Formal analysis, M.M. and D.B.; Funding acquisition, A.R. and D.B.; Methodology, A.R., M.M., D.B., Resources, A.R.; Writing— original draft, M.M. and D.B. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data can be given on request at daniel.beysens@espci.fr.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Monteith, J. L., Dew. Q. J. R. Meteorol. Soc., 1957, Volume 83, pp. 322–341.
- Monteith, J. L., Unsworth, M. H. Principles of Environmental Physics. Plants, Animals, and the Atmosphere, 4th Edn, Academic Press, Oxford., 1990.
- Beysens, D. Dew nucleation and growth. C. R. Phys. 2006, 7, 1082. [CrossRef]
- Beysens, D. Dew Water. River Publishers, Gistrup, 2018.
- Dahliou, D., Laarabi, B., Barhdadi, A. Review on dew water effect on soiling of solar panels: Towards its enhancement or mitigation. Sustainable Energy Tech. and Assessments 2022, 49, 101774.
- Kabela, E.D., Hornbuckle, B.K., Cosh, M.H., Anderson, M.C., Gleason, M.L. Dew frequency, duration, amount, and distribution in corn and soybean during SMEX05. Agric. For. Meteorol. 2009, 149, 11-24.
- Jacobs, A. F. G., Heusinkveld, B. G. and Berkowicz, S. M. Dew deposition and drying in a desert system: a simple simulation model. J. Arid Environ. 1999, 42, 211–222.
- Uclés, O., Villagarcia, L., Moro, M. J., Canton, Y. and Domingo, F. Role of dewfall in the water balance of a semiarid coastal steppe ecosystem. Hydrol. Process. 2014, 28, 2271–2280. [CrossRef]
- Wang, L., Kaseke, K. F. and Seely, M. K. Effects of non-rainfall water inputs on ecosystem functions. WIRES Water 2017, 4, e1179. [CrossRef]
- Charnès, A., Cooper, W. W., Rhodes, E. Measuring the efficiency of decision-making units. Eur. J Operational Res. 1978, 2, 429–444. [CrossRef]
- Malek, E., McCurdy, G., Giles, B. Dew contribution to the annual water balances in semi-arid desert valleys. J. Arid Environ. 1999, 42, 71–80.
- Dou, Y., Quan, J., Jia, X., Wang, Q., Liu, Y. Near-Surface Warming Reduces Dew Frequency in China. Geophys. Res. Lett. 2021, 48, e2020GL091923.
- Steinberger, Y., Loboda, I., Garner, W. The Influence of Autumn Dewfall on Spatial and Temporal Distribution of Nematodes in the Desert Ecosystem. J. Arid Environ. 1989, 16, 177–183.
- Shure, D.J., Lewis, A.J. Dew formation and stem flow on common ragweed (Ambrosia artemisiifolia). Ecology 1973, 54, 1152-1155.
- Gerlein-Safdi, C., Koohafkan, M.C., Chung, M., Rockwell, F.E., Thompson, S., Caylor, K.K. Dew deposition suppresses transpiration and carbon uptake in leaves. Agric. Forest Meteorol. 2018, 259, 305-316.
- Berry, Z. C., Emery, N. C., Gotsch, S. G., Goldsmith, G. R. Foliar water uptake: Processes, pathways, and integration into plant water budgets. Plant Cell Environ. 2019, 42, 410–423. [CrossRef]
- Zhuang, Y., Ratcliffe, S. Relationship between dew presence and Bassia dasyphylla plant growth. J. Arid Land 2012, 4, 11–18. [CrossRef]
- Ben-Asher, J., Alpert, P. and Ben-Zyi, A. Dew is a major factor affecting vegetation water use efficiency rather than a source of water in the eastern Mediterranean area. Water Resour. Res. 2010, 46, W10532.
- Kidron, G.J., Kronenfeld, R., Starinsky, A., Xiao, B., Muselli, M. and Beysens, D. Even in a dew desert: Dewfall does not provide sufficient moisture for biocrust growth–Evidence from direct measurements and a meteorological model. J. Hydrol. 2023, 627, 130450.
- Tomaszkiewicz, M., Najm, M. A., Beysens, D., Alameddine, I., El-Fadel, M. Dew as a Sustainable Non-Conventional Water Resource: A Critical Review. Environ. Rev. 2015, 23, 1-18.
- Acker, K., Moeller, D., Auel, R., Wieprecht, W., Kalaß, D. Concentrations of nitrous acid, nitric acid, nitrite and nitrate in the gas and aerosol phase at a site in the emission zone during ESCOMPTE 2001 experiment. Atmos. Res. 2005, 74, 507–524.
- Rubio, M. A., Lissi, E., Villena, G. Nitrite in rain and dew in Santiago City, Chile. Its possible impact on the early morning start of the photochemical smog. Atmos. Environ. 2002, 36, 293–297.
- Rubio, M. A., Lissi, E., Villena, G. Factors determining the concentration of nitrite in dew from Santiago, Chile. Atmos. Environ. 2008, 42, 7651–7656.
- Hamilton, W.J., Seely, M.K. Fog basking by the Namib Desert beetle, Onymacris unguicularis. Nature 1976, 262, 284-285.
- Seely, M., Henschel, J.R., Hamilton III, W.J. Long-term data show behavioural fog collection adaptations determine Namib Desert beetle abundance. South African J. Sci. 2005, 101, 570.
- Kaseke, K.F., Wang, L. Fog and dew as potable water resources: maximizing harvesting potential and water quality concerns. GeoHealth 2018, 2, 327–332.
- Sharan, G., Roy, A.K., Royon, L., Mongruel, A., Beysens, D. Dew plant for bottling water. J. Clean. Prod. 2017, 155, 83-92.
- N'Gobi, G.K., Kounouhéwa, B., Kouchadé, C., Anago, R., Beysens, D. Perception of Dew by Cereal Growers in Semi-Arid Climate (Guéné, North Benin). Int. J. Humanities Social Sciences & Educ. 2018, 5, 25-36.
- Randriatsitohaina, J.B., Raniriketra, C., Mara, T., Champin, L., Taïbi, A.N., Razakamanana, T., Fleurant, C. Vulnérabilité de Toliara face à l’insuffisance en eau, région Sud-Ouest de Madagascar. Madamines 2018, 1, 29-52.
- 5 April.
- Raholijao, N., Arivelo, T.A., Rakotomavo, Z.A.P.H., Voahangin-dRakotoson, D., Srinivasan, G., Shanmugasundaram, J., Dash, I., Qiu, J., 2019. Les tendances climatiques et les futurs changements climatiques à Madagascar-2019. Government of Madagascar, Antananarivo, Madagascar [online] URL: https://www. primature.gov.mg/cpgu/wp-content/uploads/2019/11/Publication_FR_09_Sept_Version_Finale. pdf.
- Grouzis, M., Le Sud-Ouest de Madagascar. Paris, France: Institut de Recherche pour le Développement. Rapport sur le programme de recherché de Gestion des Espaces Ruraux et Environnement à Madagascar (1996-2002), 2004.
- Hanisch, S., Lohrey, C., Buerkert, A. Dewfall and its ecological significance in semi-arid coastal south-western Madagascar. J. Arid Env. 2015, 121, 24-31. [CrossRef]
- Muselli, M., Lekouch, I., Beysens, D. Physical and chemical characteristics of dew and rain in north-west Africa with focus on Morocco: Past and future evolution (2005 – 2100). Atmos. 2022, 13-12. [CrossRef]
- Beysens, D. Estimating dew yield worldwide from a few meteo data. Atm. Res. 2016, 167, 146-155.
- Communiqué de la Présidence de la République de Madagascar sur le projet d’amélioration de l’accès en eau potable, 15 juin 2022. https://www.presidence.gov.mg/actualites/1604-madagascar-220-millions-de-dollars-pour-ameliorer-l-acces-a-l-eau-et-a-l’assainissement-de-base.htmlhttps://www.presidence.gov.mg/actualites/1604-madagascar-220-millions-de-dollars-pour-ameliorer-l-acces-a-l-eau-et-a-l’assainissement-de-base.html.
- Randriamarolaza, L.Y.A., Aguilar, E., Skrynyk, O., Vicente-Serrano, S.M., Domínguez-Castro, F. Indices for daily temperature and precipitation in Madagascar, based on quality-controlled and homogenized data, 1950–2018. Int. J. Clim 2022, 42, 265-288.
- Moriste, D., 2010. Biodiversité des haies vives dans la région de Toliara. Rapport de Licence, Faculté des Sciences, Université de Toliara.
- Nations Online Project, 2022. https://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.nationsonline.org%2Foneworld%2Fmap%2Fmadagascar_map.htm&psig=AOvVaw1MWvWQQTxAm1k8rFdjE65H&ust=1673779532637000&source=images&cd=vfe&ved=0CA8QjRxqFwoTCLi62NjwxvwCFQAAAAAdAAAAABAEhttps://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.nationsonline.org%2Foneworld%2Fmap%2Fmadagascar_map.htm&psig=AOvVaw1MWvWQQTxAm1k8rFdjE65H&ust=1673779532637000&source=images&cd=vfe&ved=0CA8QjRxqFwoTCLi62NjwxvwCFQAAAAAdAAAAABAE, accessed on January 12, 2023.
- Mapcarta. https://mapcarta.com/14494606https://mapcarta.com/14494606, accessed on February 2023.
- Weather Base. https://www.weatherbase.com/weather/weather- summary.php3?s=16176&cityname=Toliara, Madagascar, accessed on February 4, 2022.
- Rasoafaniry, A., 2022. Etude de la contribution de la rosée sur l’adduction en eau dans la commune urbaine de Toliara, Rapport de Master, Ecole Supérieure Polytechnique d’Antananarivo, Madagascar.
- ERA5-Land. https://confluence.ecmwf.int/plugins/servlet/mobile?contentId=140385202#content/view/140385202, accessed on Dec.1, 2023.
- Rumelhart, D. E., Hinton, G. E., Williams, R. J. Learning representations by back-propagating errors. Nature 1986, 323, 533-536.
- Hornik, K., Stinchcombe, M., White, H. Multilayer feedforward networks are universal approximators. Neural Networks 1989, 2, 359-366.
- Hochreiter, S., Schmidhuber, J. Long Short-Term Memory. Neural Computation 1997, 9, 1735-1780.
- Gers, F. A., Schmidhuber, J., Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Computation 2000, 12, 2451-2471.
- Maass, W. Networks of spiking neurons: The third generation of neural network models." Neural Networks 1997, 10, 1659-1671. [CrossRef]
- Zhou, J.L., Guo, Z.M., A hybrid SNN-STLSTM method for human error assessment in the high-speed railway system. Advanced Engineering Informatics 2024, 60, 102408. [CrossRef]
- Alani, A.E., Abraim, M., Ghennioui, H., Ghennioui, A., Ikenbi, I., Dahr, F.E. Short term solar irradiance forecasting using sky images based on a hybrid CNN–MLP model. Energ Reports 2021, 7, 888-900.
- Hunasigi, P., Jedhe, S., Mane, M., Patil-Shinde, V. Multilayer perceptron neural network based models for prediction of the rainfall and reference crop evapotranspiration for sub-humid climate of Dapoli, Ratnagiri District, India. Acta Ecol. Sinica 2023, 43, 154-201.
- Das, B., Dursun, O.O., Toraman, S. Prediction of air pollutants for air quality using deep learning methods in a metropolitan city. Urban climate 2022, 46, 101291.
- Rodriguez, F., Genn, M., Fontan, L., Galarza, A. Very short-term temperature forecaster using MLP and N-nearest stations for calculating key control parameters in solar photovoltaic generation. Sust. Energy Tech. Assessments 2021, 45, 101085.
- Lekouch, I., Lekouch, K., Muselli, M., Mongruel, A., Kabbachi, B., Beysens, D. Rooftop dew, fog and rain collection in southwest Morocco and predictive dew modeling using neural networks. J. Hydrol. 2012, 448, 60-72.
- Lindholm, A., Wahlström, N., Lindsten, F., Schön, T.B. Supervised machine learning. Department of Information Technology, Uppsala University: Uppsala, Sweden, 2019, p.112.
- Kassambara, A., 2018. Machine learning essentials: Practical guide in R. Edition 1.(stdha.com/English).
- Touzet, C. Les réseaux de neurones artificiels, introduction au connexionnisme : Cours, exercices et travaux pratiques. Ec2, 1992, collection de l’EERIE. hal-01338010.
- Abadi, M. Réalisation d’un réseau de neurones ”SOM” sur une architecture matérielle adaptable et extensible à base de réseaux sur puce ”NoC”. Université de Lorraine; Université du Centre (Sousse, Tunisie), 2018. Available online: https://tel.archives-ouvertes.fr/tel-01868313https://tel.archives-ouvertes.fr/tel-01868313.
- Parizeau, M., 2004. Le perceptron multicouche et son algorithme de rétropropagation des erreurs. Département de génie électrique et de génie informatique, Université de Laval.
- https://cran.r-project.org/web/packages/h2o/index.html. Accessed on May, 15 2024.
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. In Proceedings of the national academy of sciences 1982, 79, 2554-2558.
- http://kourentzes.com/forecasting/2019/01/16/tutorial-for-the-nnfor-r-package/ . Accessed on May, 15 2024.
- Kourentzes, N., Barrow, D.K., Crone, S.F. Neural network ensemble operators for time series forecasting. Expert Syst. with Applic. 2014, 41, 4235-4244.
- Buerkert, A. Private communication, 2023.
- Meunier, D., Beysens, D. Dew, fog, drizzle and rain Water in Baku (Azerbaijan). Atmos. Res. 2016, 178, 65-72. [CrossRef]
- Huang, B., Su, T., Zhi, R., Zhang, Z., Shen, H., Wu, Y., Feng, T. Synergistic effect of El Niño Southern oscillation and subtropical Indian Ocean Dipole on Southern China winter precipitation. Atmos. Res. 2023, 293, 106928. [CrossRef]
- IOD, 2023. http://la.climatologie.free.fr/iod/iod.htm. Accessed on Dec. 1, 2023.
Figure 1.
Map of Madagascar with the different sites involved in this study (from [
39]). Inset: Area where dew measurements were calculated and/or collected. Details are highlighted in red boxes (from [
40]).
Figure 1.
Map of Madagascar with the different sites involved in this study (from [
39]). Inset: Area where dew measurements were calculated and/or collected. Details are highlighted in red boxes (from [
40]).
Figure 3.
Algorithm for dew yields prediction. The second block of time series data differs from the first block by the presence of the calculated dew yields.
Figure 3.
Algorithm for dew yields prediction. The second block of time series data differs from the first block by the presence of the calculated dew yields.
Figure 4.
Summed values of dew yield
h (mm) between Apr. 2013 and Sept. 2014. Calculated values (this work) are from meteo data in Ifaty (pink diamonds), Toliara (inverted green triangles) and Amdremba (cyan triangles). Measurement data from [
33] are in Efoetsy (black circles) and in Amdremba (blue squares).
Figure 4.
Summed values of dew yield
h (mm) between Apr. 2013 and Sept. 2014. Calculated values (this work) are from meteo data in Ifaty (pink diamonds), Toliara (inverted green triangles) and Amdremba (cyan triangles). Measurement data from [
33] are in Efoetsy (black circles) and in Amdremba (blue squares).
Figure 5.
Evolution in Ifaty, Toliara and Andremba between 01/1991 and 07/2023 of (a) monthly dew yields h in mm.mth-1 (for clarity reasons only the Andremba data are shown), (b) relative humidity RH (%) and (c) cloud cover N (okta). The bold curves are data smoothening.
Figure 5.
Evolution in Ifaty, Toliara and Andremba between 01/1991 and 07/2023 of (a) monthly dew yields h in mm.mth-1 (for clarity reasons only the Andremba data are shown), (b) relative humidity RH (%) and (c) cloud cover N (okta). The bold curves are data smoothening.
Figure 6.
Dew yield in the dry (Apr. - Oct.) and rainy (Nov. - Mar.) seasons between 1991 and 2023 sorted with respect to years. (a) Ifaty, (b) Toliara and (c) Andremba.
Figure 6.
Dew yield in the dry (Apr. - Oct.) and rainy (Nov. - Mar.) seasons between 1991 and 2023 sorted with respect to years. (a) Ifaty, (b) Toliara and (c) Andremba.
Figure 7.
Frequency of events showing Nc consecutive days without dew in the dry (Apr. - Oct.) and rainy (Nov. - Mar.) seasons for the whole period 1991-2023 (semi-log plot). Red circles and lines: dry season; blue squares and lines: rainy season. (a) Ifaty, (b) Toliara and (c) Andremba.
Figure 7.
Frequency of events showing Nc consecutive days without dew in the dry (Apr. - Oct.) and rainy (Nov. - Mar.) seasons for the whole period 1991-2023 (semi-log plot). Red circles and lines: dry season; blue squares and lines: rainy season. (a) Ifaty, (b) Toliara and (c) Andremba.
Figure 8.
Evolution of the typical number of consecutive days without dew, Nc0, for each dry season (Apr.-Oct., red squares) and each rainy season (Nov.-March, blue circles). The curves are linear fits (dry season: continuous red; rainy season: interrupted blue).
Figure 8.
Evolution of the typical number of consecutive days without dew, Nc0, for each dry season (Apr.-Oct., red squares) and each rainy season (Nov.-March, blue circles). The curves are linear fits (dry season: continuous red; rainy season: interrupted blue).
Figure 9.
(a,b,c): Dew yield training, validation and extrapolation of dew yield. The bold curves are data smoothening. (a) Ifaty, (b) Toliara, (c) Andremba. Grey lines: Calculated from meteo data 01/1991 – 07/2023. Blue lines: ANN training period 01/1991 – 12/2016; red lines: ANN validation period 01/2017 – 07/2023; green lines: ANN extrapolation period 08/2023 – 07/2033. The black lines are linear fits (x = date-reference 1/1/1904 in s). (a’,b’,c’): Deviation between ANN and actual values for (a’) Ifaty, (b’) Toliara, (c’) Andremba.
Figure 9.
(a,b,c): Dew yield training, validation and extrapolation of dew yield. The bold curves are data smoothening. (a) Ifaty, (b) Toliara, (c) Andremba. Grey lines: Calculated from meteo data 01/1991 – 07/2023. Blue lines: ANN training period 01/1991 – 12/2016; red lines: ANN validation period 01/2017 – 07/2023; green lines: ANN extrapolation period 08/2023 – 07/2033. The black lines are linear fits (x = date-reference 1/1/1904 in s). (a’,b’,c’): Deviation between ANN and actual values for (a’) Ifaty, (b’) Toliara, (c’) Andremba.
Figure 11.
Analyses of rainfall for the 1991-2022 period. (a) During the dry season (Apr.-Oct.) presented in ascending order. (b) Same, for the rainy season (Nov.-March). The anomalous large rate corresponds to the Ernest cyclone on Jan. 22, 2005.
Figure 11.
Analyses of rainfall for the 1991-2022 period. (a) During the dry season (Apr.-Oct.) presented in ascending order. (b) Same, for the rainy season (Nov.-March). The anomalous large rate corresponds to the Ernest cyclone on Jan. 22, 2005.
Figure 12.
Frequency of events showing Nc consecutive days without rain in the dry (Apr. - Oct.) and rainy (Nov. -Mar.) seasons for the whole period 1991-2023 (semi-log plot). Red circles and lines: dry season; blue squares and lines: rainy season. (a) Ifaty and Toliara, (b) Andremba.
Figure 12.
Frequency of events showing Nc consecutive days without rain in the dry (Apr. - Oct.) and rainy (Nov. -Mar.) seasons for the whole period 1991-2023 (semi-log plot). Red circles and lines: dry season; blue squares and lines: rainy season. (a) Ifaty and Toliara, (b) Andremba.
Figure 13.
Evolution of the typical number of consecutive days without rain, Nc0, for each dry season (Apr.-Oct., red squares) and each rainy season (Nov.-March, blue circles). The curves are linear fits (dry season: continuous red; rainy season: interrupted blue).
Figure 13.
Evolution of the typical number of consecutive days without rain, Nc0, for each dry season (Apr.-Oct., red squares) and each rainy season (Nov.-March, blue circles). The curves are linear fits (dry season: continuous red; rainy season: interrupted blue).
Figure 14.
Evolution of the dew/rain ratio τ for the three sites Ifaty, Toliara and Andremba. (a) Yearly data, (b) dry season (Apr.-Oct.) and (c) rainy season (Nov. – Mar.) seasons. Red data: 1991-2022; blue data: extrapolation 2023-2033. The red curve is from data smoothening for the full period 2023-2033.
Figure 14.
Evolution of the dew/rain ratio τ for the three sites Ifaty, Toliara and Andremba. (a) Yearly data, (b) dry season (Apr.-Oct.) and (c) rainy season (Nov. – Mar.) seasons. Red data: 1991-2022; blue data: extrapolation 2023-2033. The red curve is from data smoothening for the full period 2023-2033.
Figure 15.
Correlated evolutions of (a) monthly dew and rain events and (b) RH and cloud cover during the measurement period 1/1991 – 7/2023.
Figure 15.
Correlated evolutions of (a) monthly dew and rain events and (b) RH and cloud cover during the measurement period 1/1991 – 7/2023.
Table 1.
Useful information concerning the investigated sites.
Table 1.
Useful information concerning the investigated sites.
| Sites |
Latitude |
Longitude |
Elevation (m) asl |
Distance from the sea (km) |
Köppen Geiger climate |
| Toliara |
23° 4 S |
43° 7 E |
9 |
1 |
Bsh |
| Ifaty |
23° 1 S |
43°6 E |
80 |
1 |
Bsh |
| Andremba |
24°0 S |
44°2 E |
260 |
60 |
Bsh |
| Efoetsy |
24°1 S |
43°7 S |
10 |
2 |
Bsh |
Table 2.
General information.
Table 2.
General information.
| hot & rainy season |
cold & dry season |
mean temp. (°C) |
mean max temp. (Jan.) (°C) |
mean min temp. (Jul.) (°C) |
mean rain (mm.yr-1)*
|
max rain (mm.mth-1)*
|
min rain (mm.mth-1)*
|
mean RH (%)$
|
max RH (%)$
|
min RH (%)$
|
| Nov.-March |
Apr.- Oct. |
23.9 |
27.8 |
20.6 |
342.9 |
73.7 |
5.1 |
77 |
100 |
12 |
Table 3.
Summary of meaningful values during the observed period 1/1991-7/2023 according to
Figure 5 and Figure 9 data and
Table 4.
Table 3.
Summary of meaningful values during the observed period 1/1991-7/2023 according to
Figure 5 and Figure 9 data and
Table 4.
| Sites |
Year of max. yield |
Year of min. yield |
Sen’s slope (×10-5 mm.mth-2) |
| Ifaty |
2000 |
2021 |
-3.8 |
| Toliara |
2000 |
2021 |
-2.4 |
| Andremba |
2000 |
2021 |
- |
Table 4.
Statistical analysis of the dew data according to the Mann-Kendall (MK) and the Sen's slope tests.
Table 4.
Statistical analysis of the dew data according to the Mann-Kendall (MK) and the Sen's slope tests.
| Dew |
Data |
mths. |
Min (mm.mth-1) |
Max (mm.mth-1) |
Mean (mm.mth-1) |
SD (mm.mth-1) |
p-value |
MK mea-
ningful trend$
|
Sen’s slope (×10-5 mm.mth-2) |
Sen’s con-
stant |
| Ifaty |
Meas. |
391 |
0.322 |
3.795 |
1.678 |
0.488 |
<0.0001 |
Yes |
-3.8 |
3.160 |
| Extrap. |
120 |
0.915 |
1.964 |
1.502 |
0.241 |
0.227 |
No |
-2.5 |
2.704 |
| All |
511 |
0.322 |
3.795 |
1.637 |
0.449 |
<0.0001 |
Yes |
-2.6 |
2.712 |
| Toliara |
Meas. |
391 |
0.128 |
2.885 |
1.157 |
0.401 |
<0.0001 |
Yes |
-2.4 |
2.072 |
| Extrap. |
120 |
0.643 |
1.700 |
1.302 |
1.172 |
0.005 |
Yes |
3.7 |
-0.433 |
| All |
511 |
0.128 |
2.885 |
1.191 |
0.366 |
0.165 |
No |
0.5 |
1.008 |
| Andrem-ba |
Meas. |
391 |
0.067 |
3.072 |
1.187 |
0.557 |
0.060 |
No |
-1.5 |
1.720 |
| Extrap. |
120 |
0.534 |
1.622 |
1.096 |
0.270 |
0.234 |
No |
-3.1 |
2.577 |
| All |
511 |
0.067 |
3.072 |
1.165 |
0.506 |
0.055 |
No |
-0.9 |
1.513 |
Table 5.
Statistical analysis of the yearly number of consecutive days without dew events during the period 1/1991-7/2023 according to the Mann-Kendall (MK) and the Sen's slope tests.
Table 5.
Statistical analysis of the yearly number of consecutive days without dew events during the period 1/1991-7/2023 according to the Mann-Kendall (MK) and the Sen's slope tests.
No Dew
Nb. consecu-tive days |
Data |
Min (d) |
Max (d) |
Mean (d) |
SD
(d) |
p-value*
|
MK mea-
ningful trend$
|
Sen’s slope (×10-6 d.yr-1) |
Sen’s con-
stant |
| Ifaty |
Rainy season |
2.179 |
3.875 |
2.67 |
0.324 |
0.721 |
No |
3.9 |
2.643 |
| Dry season |
1.714 |
3.182 |
2.411 |
0.402 |
0.035 |
Yes |
44 |
0.645 |
| Toliara |
Rainy season |
2.405 |
3.645 |
3.021 |
0.318 |
0.457 |
No |
13 |
2.482 |
| Dry season |
1.842 |
3.824 |
2.664 |
0.456 |
0.031 |
Yes |
53 |
0.554 |
| Andrem-ba |
Rainy season |
2.3 |
4.269 |
3.382 |
0.445 |
0.285 |
No |
25 |
2.364 |
| Dry season |
2.048 |
3.824 |
2.841 |
0.479 |
0.035 |
Yes |
57 |
0.546 |
Table 7.
Statistical analysis of the yearly number of consecutive days without rain events during the period 1/1991-7/2023 according to the Mann-Kendall (MK) and the Sen's slope tests.
Table 7.
Statistical analysis of the yearly number of consecutive days without rain events during the period 1/1991-7/2023 according to the Mann-Kendall (MK) and the Sen's slope tests.
No Rain
Nb. consecu-tive days |
Data |
Min (d) |
Max (d) |
Mean (d) |
SD (d) |
p-value*
|
MK mea-
ningful trend$
|
Sen’s slope (×10-6 d. yr-1) |
Sen’s con-
stant |
| Ifaty & Toliara |
Rainy season |
2.174 |
9.833 |
4.086 |
1.448 |
0.653 |
No |
28 |
2.738 |
| Dry season |
7.55 |
24.5 |
13.681 |
3.903 |
0.62 |
No |
112 |
17.657 |
| Andremba |
Rainy season |
1.96 |
5.167 |
3.113 |
0.814 |
0.107 |
No |
79 |
-0.147 |
| Dry season |
6.115 |
14.77 |
9.443 |
1.880 |
0.889 |
No |
10 |
9.174 |
Table 8.
Statistical analysis of the ratio dew/rain averaged over the year during the observation period 1/1991-7/2023, extrapolation period 8/2023-7/2033 and all periods 1/1991-8/2033, with Mann-Kendall (MK) and Sen's slope tests.
Table 8.
Statistical analysis of the ratio dew/rain averaged over the year during the observation period 1/1991-7/2023, extrapolation period 8/2023-7/2033 and all periods 1/1991-8/2033, with Mann-Kendall (MK) and Sen's slope tests.
| Yearly |
Period |
Ratio (%) |
p-value$
|
MK mea-
ningful trend$
|
Sen’s slope
(×10-6 yr-1) |
Sen’s con-stant |
| Min |
Max |
Mean |
SD |
| Ifaty |
1991-2023 |
2.114 |
7.34 |
4.317 |
1.24 |
0.698 |
No |
29 |
2.841 |
| 2023-2033 |
1.986 |
3.687 |
2.75 |
0.49 |
0.161 |
No |
-156 |
-10.358 |
| 1991-2033 |
1.986 |
7.340 |
3.967 |
1.28 |
0.017 |
Yes |
-86 |
7.107 |
| Toliara |
1991-2023 |
1.929 |
5.601 |
2.984 |
0.86 |
0.816 |
No |
14 |
2.152 |
| 2023-2033 |
2.028 |
3.986 |
2.623 |
0.63 |
0.013 |
Yes |
266 |
-9.977 |
| 1991-2033 |
1.929 |
5.601 |
2.914 |
0.81 |
0.818 |
No |
-5.6 |
2.883 |
Andrem-
ba |
1991-2023 |
1.571 |
4.064 |
2.523 |
0.59 |
0.975 |
No |
1.6 |
2.427 |
| 2023-2033 |
1.571 |
2.532 |
2.277 |
0.28 |
1 |
No |
6.7 |
2.037 |
| 1991-2033 |
1.571 |
4.064 |
2.482 |
0.52 |
0.683 |
No |
-6.7 |
2.705 |
Table 9.
Statistical analysis of the ratio dew/rain averaged over the dry seasons during the observation period 1/1991-7/2023, extrapolation period 8/2023-7/2033 and all periods 1/1991-8/2033, with Mann-Kendall (MK) and Sen's slope tests.
Table 9.
Statistical analysis of the ratio dew/rain averaged over the dry seasons during the observation period 1/1991-7/2023, extrapolation period 8/2023-7/2033 and all periods 1/1991-8/2033, with Mann-Kendall (MK) and Sen's slope tests.
| Dry season |
Period |
Ratio (%) |
p-value$
|
MK mea-
ningful trend$
|
Sen’s slope (×10-6 yr-1) |
Sen’s con-stant |
| Min |
Max |
Mean |
SD |
| Ifaty |
1991-2023 |
9.645 |
77.415 |
32.403 |
19.744 |
0.258 |
No |
-905 |
65.033 |
| 2023-2033 |
5.615 |
30.63 |
11.205 |
7.158 |
0.436 |
No |
980 |
-37.535 |
| 1991-2033 |
5.615 |
77.415 |
27.209 |
19.924 |
0.001 |
Yes |
-1858 |
99.681 |
| Toliara |
1991-2023 |
7.453 |
54.779 |
23.390 |
14.473 |
0.345 |
No |
-415 |
36.185 |
| 2023-2033 |
5.191 |
19.856 |
9.829 |
4.824 |
0.213 |
No |
1308 |
-53.281 |
| 1991-2033 |
5.191 |
54.779 |
20.003 |
14.187 |
0.004 |
Yes |
-1069 |
62.949 |
Andrem-
ba |
1991-2023 |
4.689 |
42.802 |
15.662 |
10.054 |
0.209 |
No |
-560 |
35.022 |
| 2023-2033 |
5.379 |
19.477 |
14.785 |
3.907 |
0.35 |
No |
-630 |
45.47 |
| 1991-2033 |
4.689 |
42.802 |
15.403 |
8.985 |
0.601 |
No |
-104 |
18.648 |
Table 10.
Statistical analysis of the ratio dew/rain averaged over the rainy seasons during the observation period 1/1991-7/2023, extrapolation period 8/2023-7/2033 and all periods 1/1991-8/2033, with Mann-Kendall (MK) and Sen's slope tests.
Table 10.
Statistical analysis of the ratio dew/rain averaged over the rainy seasons during the observation period 1/1991-7/2023, extrapolation period 8/2023-7/2033 and all periods 1/1991-8/2033, with Mann-Kendall (MK) and Sen's slope tests.
| Rainy season |
Period |
Ratio (%) |
p-value$
|
MK mea-
ningful trend$
|
Sen’s slope (×10-6 yr-1) |
Sen’s con-stant |
| Min |
Max |
Mean |
SD |
| Ifaty |
1991-2023 |
0.954 |
4.615 |
2.063 |
0.817 |
0.588 |
No |
24 |
1.113 |
| 2023-2033 |
1.165 |
1.991 |
1.465 |
0.257 |
0.283 |
No |
90 |
-2.815 |
| 1991-2033 |
0.954 |
4.615 |
1.942 |
0.767 |
0.386 |
No |
-19 |
2.565 |
| Toliara |
1991-2023 |
0.691 |
2.477 |
1.323 |
0.453 |
0.631 |
No |
13 |
0.813 |
| 2023-2033 |
1.071 |
1.87 |
1.424 |
0.323 |
0.002 |
Yes |
219 |
-8.855 |
| 1991-2033 |
0.691 |
2.477 |
1.353 |
0.428 |
0.153 |
No |
24 |
0.34 |
Andrem-
ba |
1991-2023 |
0.768 |
1.957 |
1.234 |
0.264 |
0.329 |
No |
15 |
0.622 |
| 2023-2033 |
0.921 |
1.339 |
1.028 |
0.13 |
0.371 |
No |
-30 |
2.407 |
| 1991-2033 |
0.768 |
1.957 |
1.189 |
0.256 |
0.298 |
No |
-9.5 |
1.527 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).