Preprint

Article

Adding Shocks to a Prospective Mortality Model

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Guillaume Gautier de la Plaine,

Frédéric Planchet^*

Guillaume Gautier de la Plaine,

Frédéric Planchet^*

This version is not peer-reviewed

Submitted:

03 January 2024

Posted:

04 January 2024

You are already at the latest version

Alerts

Abstract

This work proposes a simple model to take into account the annual volatility of the mortality level observed on the scale of a country like France in the construction of prospective mortality tables. By assigning a fragility factor to a basic hazard function, we generalize the Lee-Carter model. The impact on prospective life expectancies and capital requirements in the context of a life annuity scheme is analyzed in detail.

Keywords:

Subject: Business, Economics and Management - Other

1. Introduction

The construction of life expectancy projections has been the subject of much work since the seminal article by Lee and Carter (Lee and Carter [1992]).

With a view to extrapolating trends observed in the past into the future, most of the approaches proposed are based on a “mortality surface”, measuring mortality forces by age and year at the time, which must then be extrapolated over time.

The models inspired by Lee and Carter start by reducing dimension by performing a PCA and then extrapolating one or two time series associated with the projection on the principal axes.

Bongaarts (Bongaarts [2004]) has proposed a different approach, based on parametric adjustments by year of time and extrapolation of the estimated coefficients each year.

In Bongaarts [2004], however, the author uses a rather frustrating parametric representation (Thatcher’s model) which does not allow all ages to be included. Moreover, he limits his extrapolation to 2 out of 3 parameters, treating them independently, which is a questionable approximation.

Models of this type project regular

t \to μ (x, t)

series. However, when we look at annual variations in the mortality rate in France, for example, we see a fairly high degree of volatility:

Figure 1. Annual variation in mortality rate.

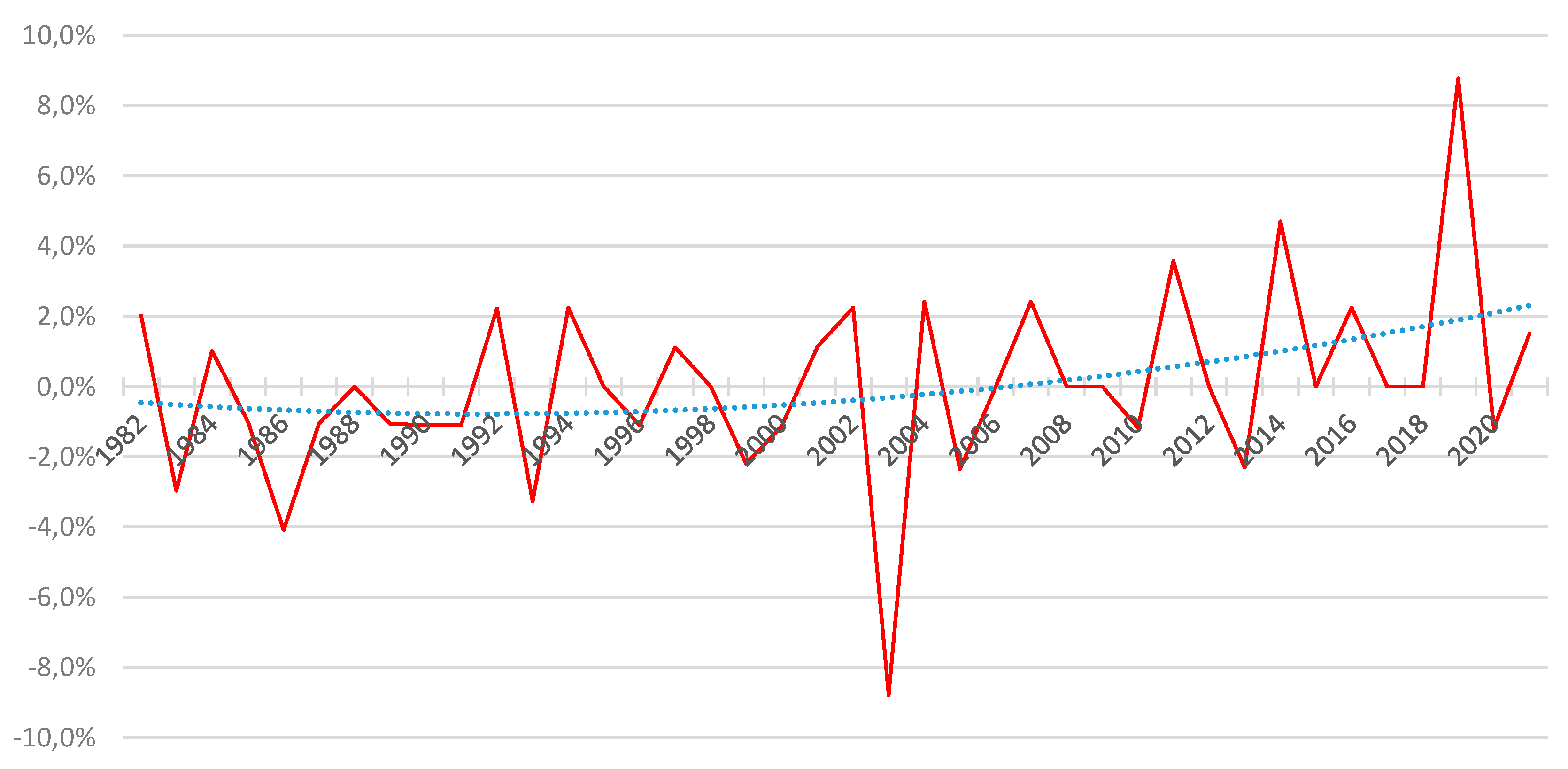
The classic models described above cannot account for these short-term variations. Proposed approaches have been put forward, for example, in Guette [2010] or Currie et al. [2003], but with a slightly different objective, as these works propose to model catastrophes such as wars or epidemics. More recently, an approach using regime-switching models was proposed in Robben and Antonio [2023].

Our aim here is not to model catastrophes, but to incorporate the above volatility into the modeling to provide a more accurate assessment of residual life expectancies when an unbiased estimate of mortality rates is available.

A specific approach is therefore proposed here, with the aim of accounting for this short-term volatility and measuring its impact on the anticipation of prospective residual life expectancies.

2. Proposed Stochastic Mortality Model

We draw inspiration here from the fragility models proposed by Vaupel and his co-authors (Vaupel et al. [1979]), by assigning a regular base hazard function of a shock that depends only on time, under a proportional hazards assumption.

The proposed specification is described below, followed by a method for estimating the parameters within the framework of conditional maximum likelihood.

a. Specification

Consider the following specification of the hazard function for the year of time t:

μ (x, t) = Z_{t} \times μ_{0} (x, t)

with the semi-parametric form of the basic hazard function

\ln μ_{0} (x, t) = α_{x} + β_{x} k_{t}

. The shocks are assumed to be mean-centered, i.e.,

E (Z_{t}) = 1

and the classical identifiability conditions for the basic hazard function are imposed (cf. Brouhns et al. [2002]):

\sum_{x = x_{m}}^{x_{M}} β_{x} = 1 and \sum_{t = t_{m}}^{t_{M}} k_{t} = 0

This involves estimating the parameters of

Z_{t}

and the matrix

(α, β, k)

, then extrapolating the time series

t \to k (t)

b. Log-Likelihood Determination

For maximum likelihood estimation, we know that everything happens as if the number of deaths observed followed a Poisson distribution,

D_{x, t} \sim P (E_{x, t} \times μ (x, t)),

which leads to the following expression for the conditional likelihood for an observation, noting

λ = E_{x, t} \times μ_{0} (x, t)

P (D = d |Z) = e^{- λ Z} \frac{λ^{d}}{d!} Z^{d},

Likelihood is easy to deduce:

P (D = d) = E_{Z} [P (D = d |Z)] = \int e^{- λ z} z^{d} \frac{λ^{d}}{d!} d F_{Z} (z)

We then choose a Gamma distribution of parameters a and b for the distribution of Z, i.e.,

f_{Z} (z) = z^{a - 1} \frac{b^{a} e^{- b \times z}}{Γ (a)}

, which leads to

P (D = d) = \frac{λ^{d}}{d!} \frac{b^{a}}{Γ (a)} \int_{0}^{+ \infty} e^{- (λ + b) z} z^{d + a - 1} d z

. Using the change of variable

u = (λ + b) z

, we obtain the following expression for the likelihood of an observation

P (D = d) = \frac{λ^{d}}{d!} \frac{b^{a}}{Γ (a)} \frac{1}{{(λ + b)}^{d + a}} \int_{0}^{+ \infty} e^{- u} u^{d + a - 1} d z = \frac{λ^{d}}{d!} \frac{b^{a}}{Γ (a)} \frac{1}{{(λ + b)}^{d + a}} Γ (d + a)

which in turn gives log-likelihood

\ln P (D = d) = f (a, b) + d \ln (λ) - (d + a) \ln (λ + b)

with

f (a, b) = \ln (b^{a} \frac{Γ (d + a)}{Γ (d + 1) Γ (a)})

As a function of the parameters

(α, β, k)

and conditional on

(a, b)

, the log-likelihood for an observation is of the form

l (α, β, k) = \ln P (D = d)

with

λ = E_{x, t} \times μ_{0} (x, t) = E_{x, t} \times e^{α_{x} + β_{x} k_{t}}

. Conditional on

(a, b)

, the log-likelihood has the following form (with one additive constant):

\ln L = \sum_{x = x_{m}}^{x_{M}} \sum_{t = t_{m}}^{t_{M}} \ln P (D_{x, t} = d_{x, t} |a, b) = \sum_{x = x_{m}}^{x_{M}} \sum_{t = t_{m}}^{t_{M}} [d_{x, t} \ln (λ_{x, t}) - (d_{x, t} + a) \ln (λ_{x, t} + b)]

It can then be maximized by

(α, β, k)

under the constraint that

\sum_{x = x_{m}}^{x_{M}} β_{x} = 1

and

\sum_{t = t_{m}}^{t_{M}} k_{t} = 0

c. Parameter Estimation

Parameter estimation can be carried out in two stages: in the first stage, the fragility parameter is estimated, then, in the second stage, the above log-likelihood is maximized at

(α, β, k)

The condition

E (Z_{t}) = 1

implies

a = b

. We also have

V (Z_{t}) = \frac{a}{b^{2}} = \frac{1}{a}

, so the disturbance control parameter

Z_{t}

is the inverse of the variance

a = σ_{Z}^{- 2}

. A direct estimate of this parameter can be made as follows, observing that the mean annual output intensities are of the form

\bar{μ} (t) = Z_{t} \times {\bar{μ}}_{0} (t) with {\bar{μ}}_{0} (t) = \frac{\sum_{x = x_{m}}^{x_{M}} E_{x, t} μ_{0} (x, t)}{\sum_{x = x_{m}}^{x_{M}} E_{x, t}}

from which we derive

E (\bar{μ} (t)) = {\bar{μ}}_{0} (t)

V (\bar{μ} (t)) = V (Z_{t}) {\bar{μ}}_{0}^{2} (t)

then

V (Z_{t}) = \frac{V (\bar{μ} (t))}{E {(\bar{μ} (t))}^{2}}

. The variance of

Z_{t}

is therefore equal to the square of the coefficient of variation of

\bar{μ} (t)

σ (Z_{t}) = c v (\bar{μ} (t))

. It is then straightforward to propose as estimator

{\hat{σ}}_{Z}^{2} = \frac{\frac{1}{t_{M} - t_{m} + 1} \sum_{t = t_{m}}^{t_{M}} {(\hat{μ} (t) - \frac{1}{t_{M} - t_{m} + 1} \sum_{t = t_{m}}^{t_{M}} \hat{μ} (t))}^{2}}{{(\frac{1}{t_{M} - t_{m} + 1} \sum_{t = t_{m}}^{t_{M}} \hat{μ} (t))}^{2}}

With

\hat{μ} (t) = \frac{\sum_{x = x_{m}}^{x_{M}} E_{x, t} \hat{μ} (x, t)}{\sum_{x = x_{m}}^{x_{M}} E_{x, t}}

and

\hat{μ} (x, t) = \frac{D_{x, t}}{E_{x, t}}

as estimators, the Hoem estimator of the hazard function.

Once the fragility parameter has been estimated, the aim is to maximize the previously expressed log-likelihood. The partial derivatives of the log-likelihood for an observation are as follows:

\frac{\partial}{\partial p} \ln P (D = d) = d \frac{1}{λ} \frac{\partial λ}{\partial p} - (d + a) \frac{1}{λ + b} \frac{\partial λ}{\partial p} = (\frac{d}{λ} - \frac{d + a}{λ + b}) \frac{\partial λ}{\partial p}

with p one of the parameters

(α, β, k)

. We also have

\frac{\partial λ}{\partial α} = λ

\frac{\partial λ}{\partial β} = k λ

and

\frac{\partial λ}{\partial k} = β λ

Finally, it remains to estimate

(α, β, k)

, which is a solution of the first-order conditions:

\frac{\partial}{\partial α_{x}} \ln L = \sum_{t = t_{m}}^{t_{M}} (\frac{d}{λ_{x, t}} - \frac{d + a}{λ_{x, t} + b}) λ_{x, t} = 0

\frac{\partial}{\partial β_{x}} \ln L = \sum_{t = t_{m}}^{t_{M}} (\frac{d}{λ_{x, t}} - \frac{d + a}{λ_{x, t} + b}) k_{t} λ_{x, t} = 0

\frac{\partial}{\partial k_{t}} \ln L = \sum_{x = x_{m}}^{x_{M}} (\frac{d}{λ_{x, t}} - \frac{d + a}{λ_{x, t} + b}) β_{x} λ_{x, t} = 0

This system is non-linear.

d. Calculating Prospective Residual Life Expectancies

In the proposed model, the calculation of prospective life expectancy

e (x, t) = E (e (x, t |Z)) = \sum_{i \geq 0} \prod_{j = 0}^{i} E [\exp (- μ_{x + j, t + j})]

(1)

takes the form

e (x, t) = \sum_{i \geq 0} \prod_{j = 0}^{i} {(\frac{b}{b + μ_{0} (x + j, t + j)})}^{a}

(2)

because the Laplace transform of a Gamma distribution is

E (e^{- x Z_{t}}) = {(\frac{b}{b + x})}^{a}

. As

E (e^{- μ (x, t)}) = E (e^{- Z_{t} \times μ_{0} (x, t)})

, we deduce that:

E (e^{- μ (x, t)}) = E (e^{- Z_{t} \times μ_{0} (x, t)}) = {(\frac{b}{b + μ_{0} (x, t)})}^{a}

(3)

Note that when

b = a \to + \infty

E (e^{- μ (x, t)}) \to e^{- μ_{0} (x, t)}

and then we find the classic formula

e (x, t) = \sum_{i \geq 0} \prod_{j = 0}^{i} \exp (- μ_{0} (x + j, t + j))

3. Numerical Application

We use data for metropolitan France for the period 2000-2020, for ages 0 to 105 inclusive, from the Agalva and Blanpain study [2021]. All calibration was performed in R.

Prospective analyses are then carried out over the entire age range and for the years from 2021 to 2060.

a. Model Adjustment

All these steps are discussed in turn in the following subsections. Throughout the study, all the results obtained are compared with those given by a Lee-Carter model calibrated on the same data.

Estimation of Gamma Distribution Parameters

The estimation of the pair of parameters

(a, b)

has been made with the raw data and we find

σ_{Z}^{2} = 4, 3 %

, i.e.,

a = b = 550

Estimation of Model Parameters

The calibration of

(α, β, k)

under constraints was then carried out using the Rsolnp package (https://cran.r-project.org/web/packages/Rsolnp/index.html), and more specifically the solnp function (see Ghalanos and Theussl [2015]). In order to carry out this calibration, it was chosen to provide as initial parameters the results of a Lee-Carter model, calibrated using the lca function from the demography package (https://cran.r-project.org/web/packages/demography/index.html) (cf. Hyndman [2023]). All these coefficients are transcribed in the Appendix.

As shown in the following figure, this leads to coefficients

(α, β, k)

very close to those of the reference Lee-Carter model:

Figure 2. Comparison of different coefficients with those of a Lee-Carter model.

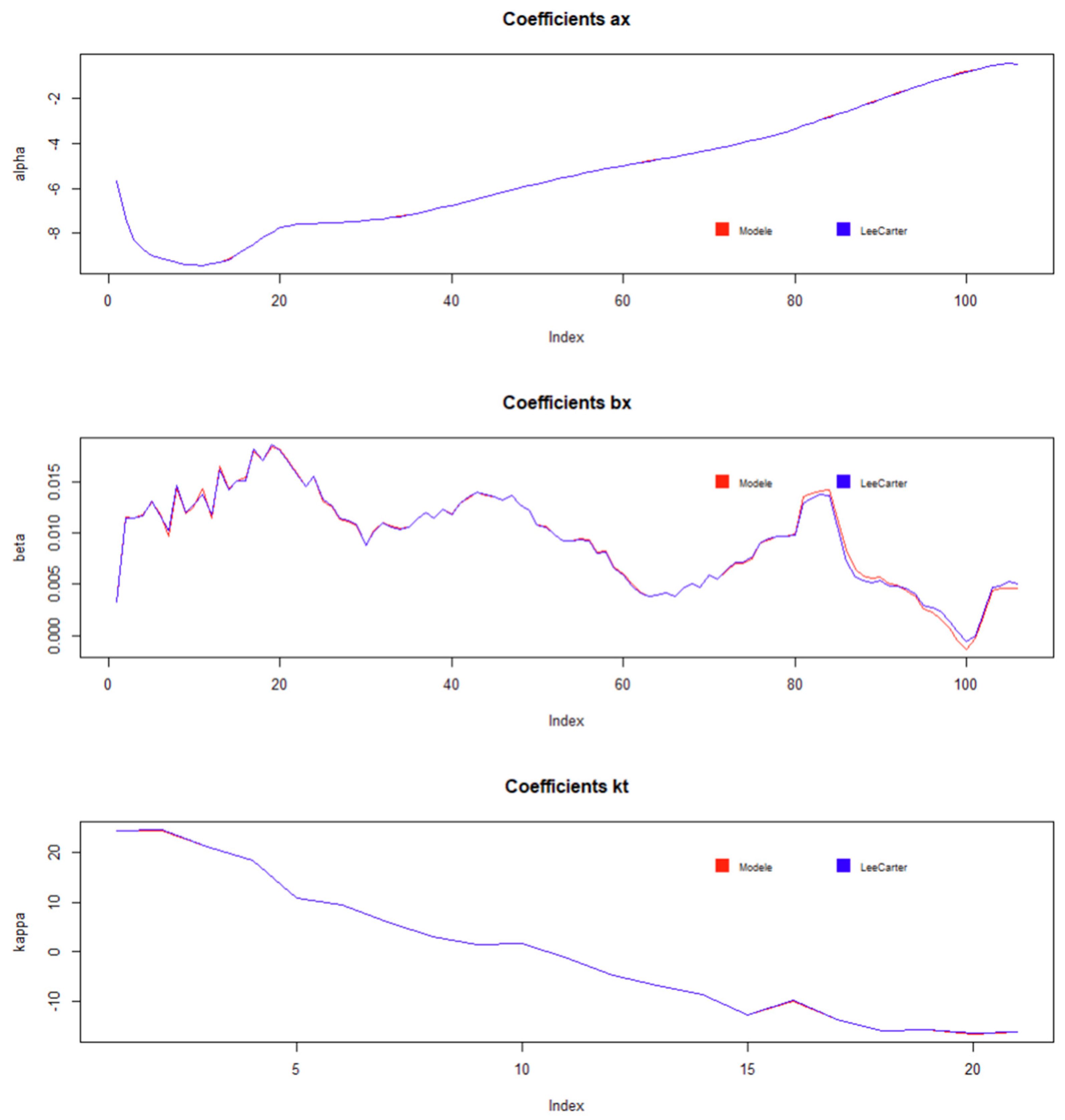
It can be seen that the time parameter shows a slower rate of decline from the 18^ème year of the observation period.

Extrapolation of Time Coefficients

Whether in the model studied here or in the Lee-Carter model used as a reference, the projection of coefficients

{(k_{t})}_{t}

for

t

beyond the calibration range has been done by linear regression, by fitting the following equation to the calibrated parameters:

k_{t} = m \times t + p

In both cases, we find the coefficients shown in the following table:

Table 1. Results of the extension of the time coefficients k.

	m	p
Model studied	-2,19	4401,98
Lee-Carter reference model	-2,19	4402,33

The results are logically very similar in both cases.

b. Projected Mortality Forces

Here, we compare projected mortality forces with and without shocks integrated into the model, as a function of age and year.

First, we look at the evolution of the mortality force as a function of age, for a few fixed years:

Figure 3. Mortality forces by age.

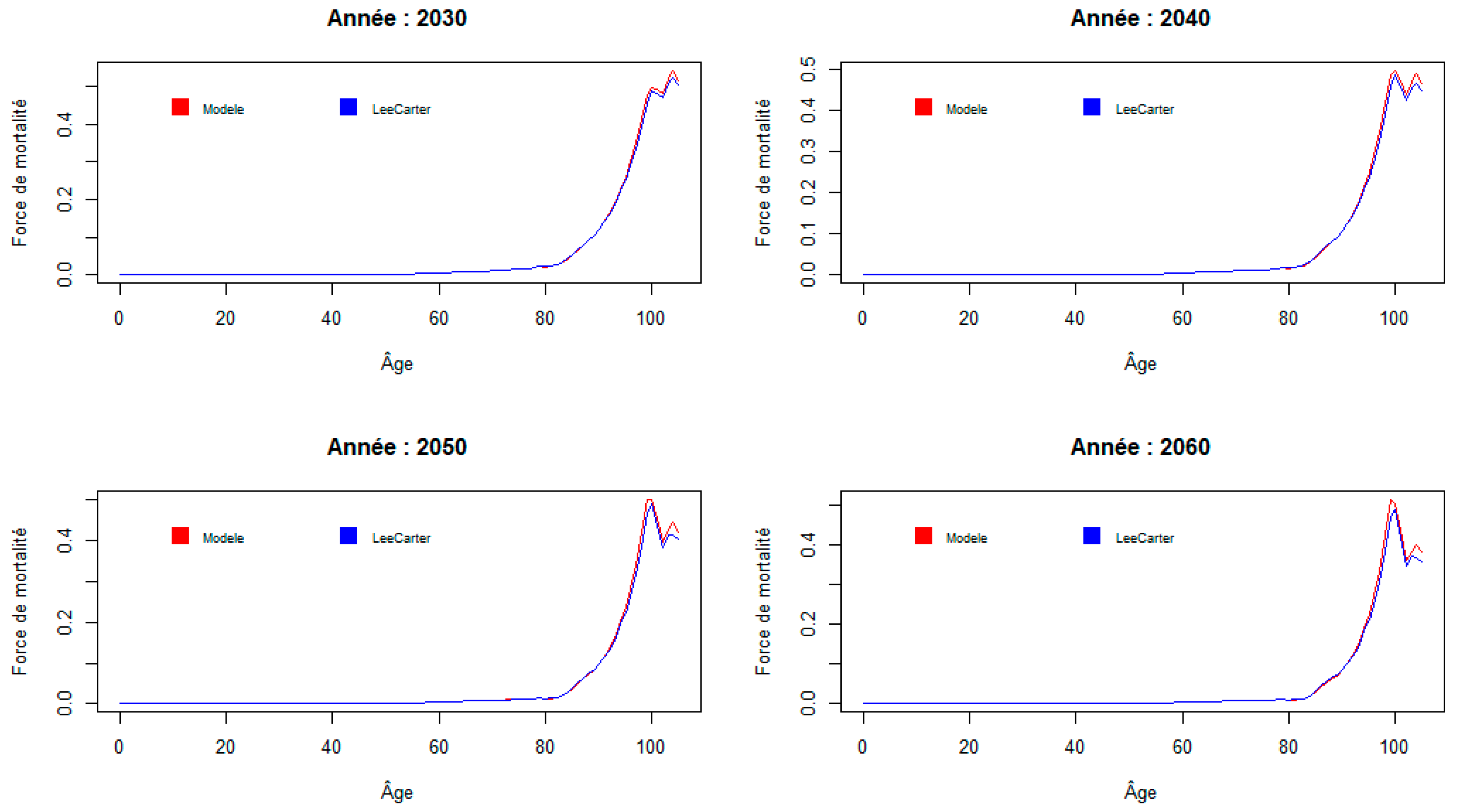
The mortality forces of the two models are very close, except at the highest ages, where the model with shocks tends to predict higher mortality forces. A closer look at the age range [90; 105] reveals the following:

Figure 4. Mortality rates by age from 90 to 105 years.

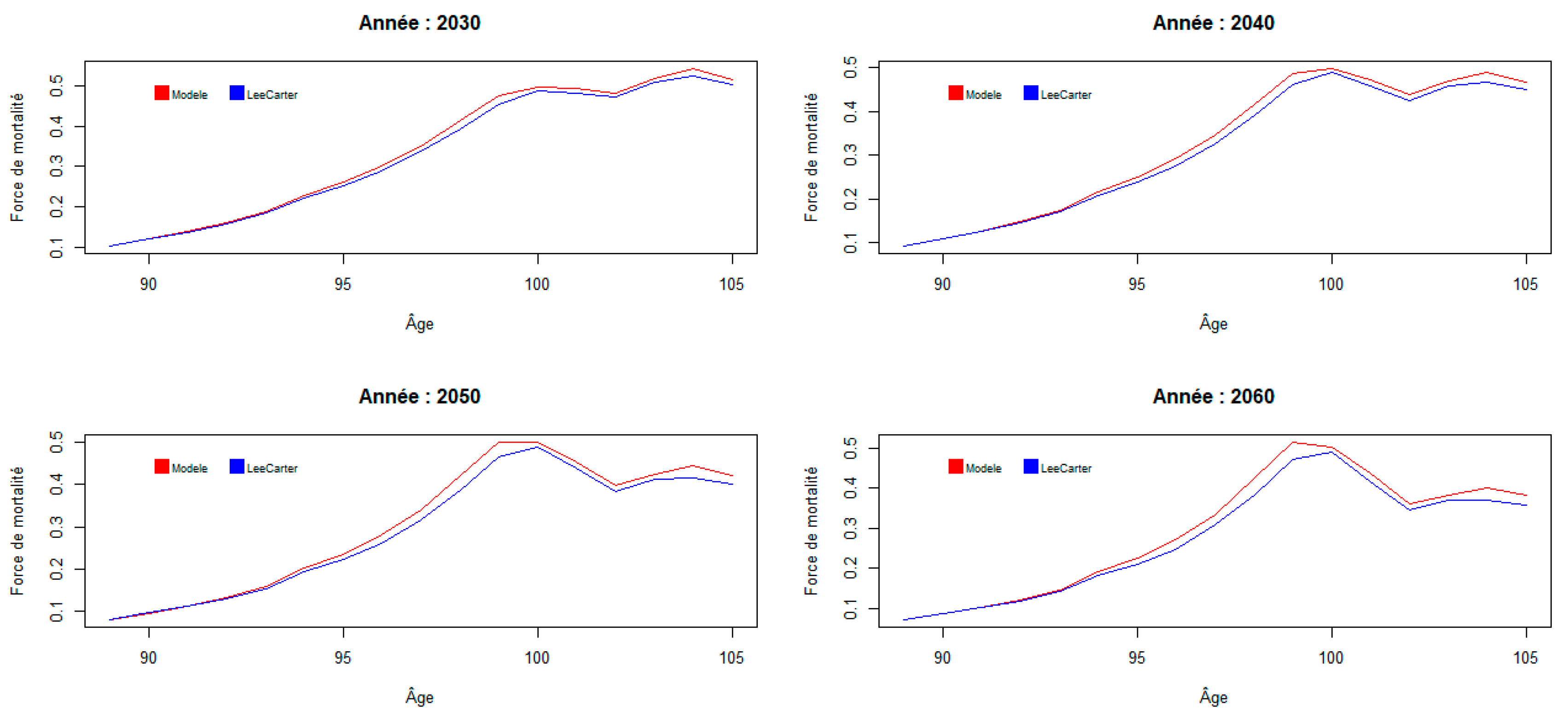
The maximum relative deviation over the entire prospective range is 3.6% at age 80 for the year 2060.

We now compare the mortality forces of the two models over the entire prospective analysis period, for a few selected ages.

Figure 5. Mortality rates by year for selected ages.

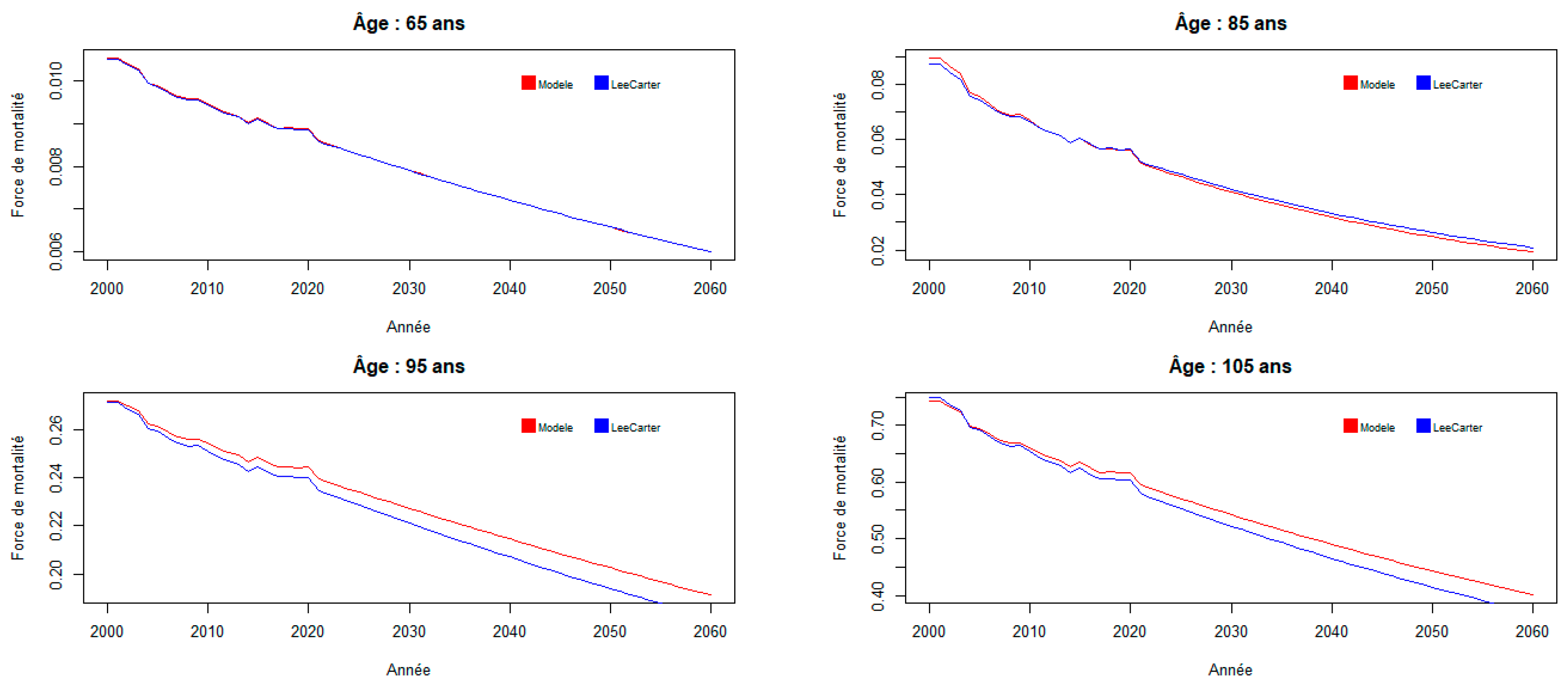
Overall, the mortality model studied tends to predict higher mortality forces than the reference Lee-Carter model at older ages, and the gap increases over time.

Before calculating prospective residual life expectancies, it’s worth looking at the overall impact on mortality forces. To this end, we calculate the following ratio:

r (x, t) = \frac{μ (x, t)}{μ_{L C} (x, t)}

with

μ_{L C} (x, t)

the mortality force derived from the reference Lee-Carter model and

μ (x, t)

model. This ratio is shown in the following figure:

Figure 6. Mortality force ratio over the entire age range and prospective analysis period (2021-2060).

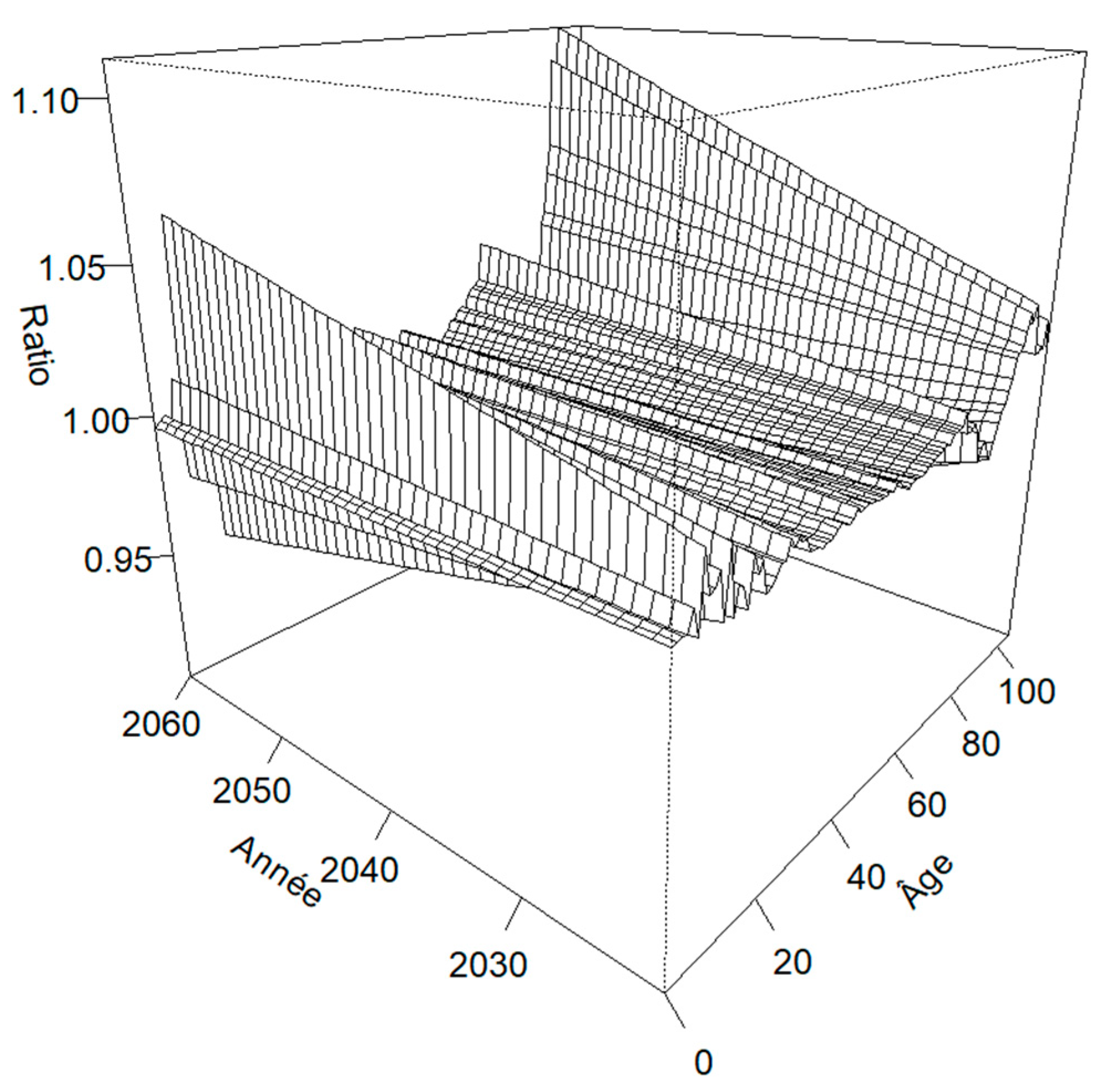
The average value of this ratio for all ages and years combined is 100%, which means that the model studied is equivalent to the Lee-Carter model.

The impact of the introduction of shocks on adjustment is therefore negligible when assessed on a very global basis. However, the difference increases over time, leading the two models to diverge in the medium term and at older ages.

If we restrict ourselves to ages over 65, we obtain a weighted average equal to 99.8%.

In addition, the average mortality rate of the population, calculated on the basis of exposure to risk in 2020, evolves as follows:

Figure 7. Average mortality rate per year, all ages combined, from 2021 to 2060.

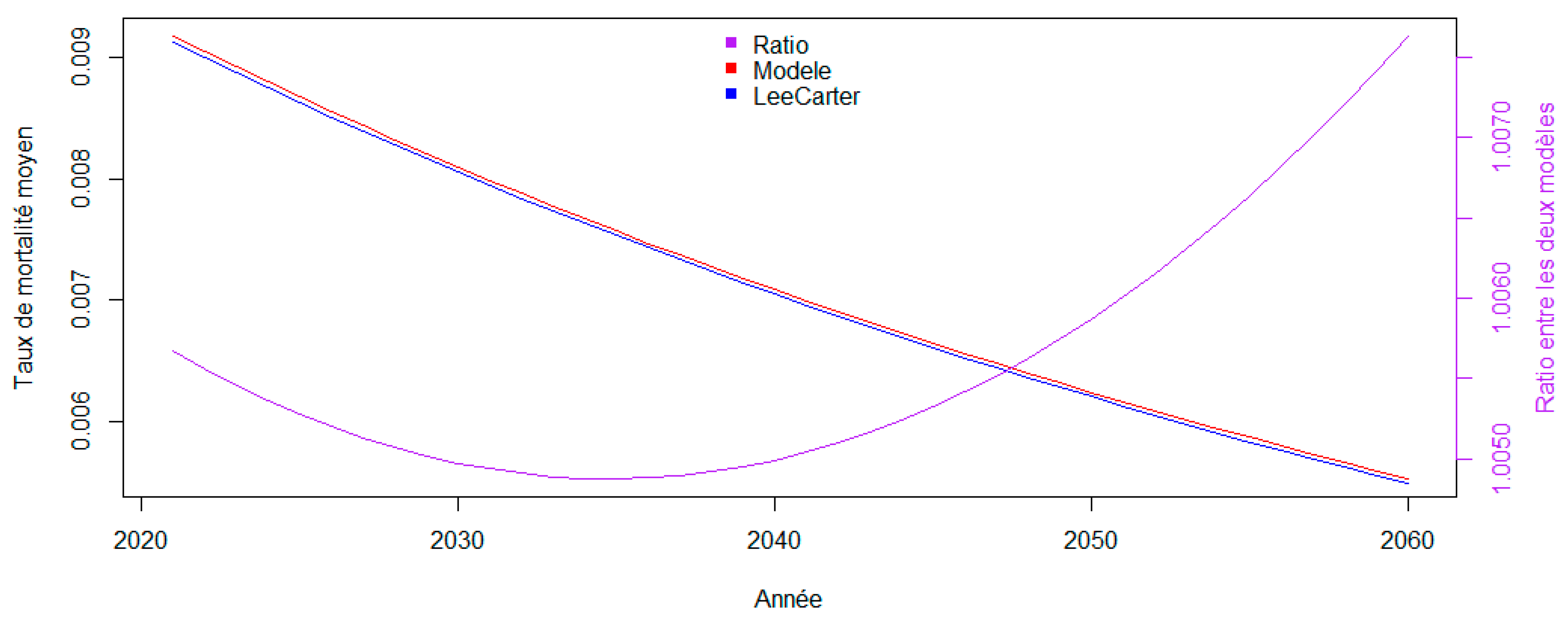
It can be seen that the model studied is on average more pessimistic than the Lee-Carter model on mortality improvement in future mortality.

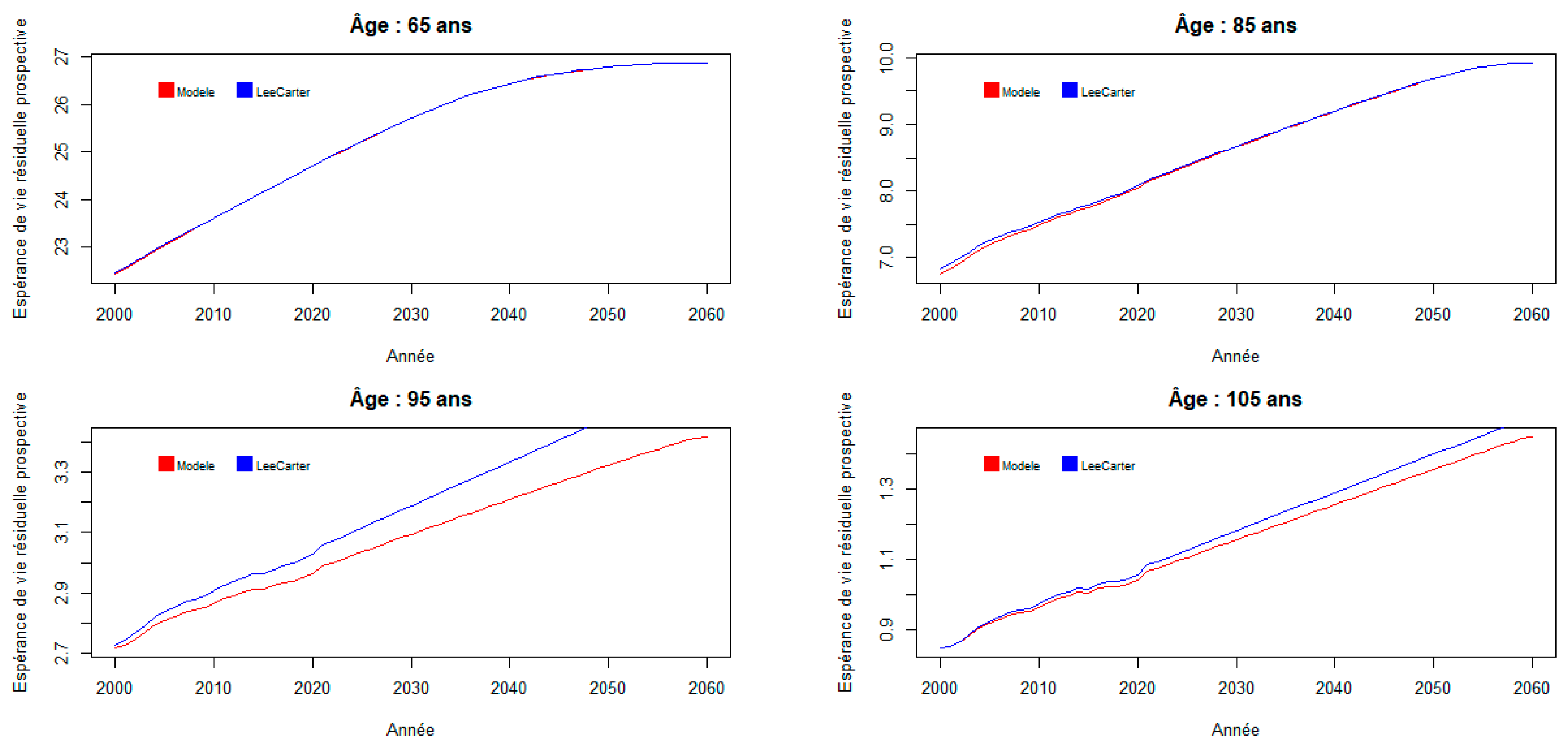
c. Estimating Prospective Residual Life Expectancies

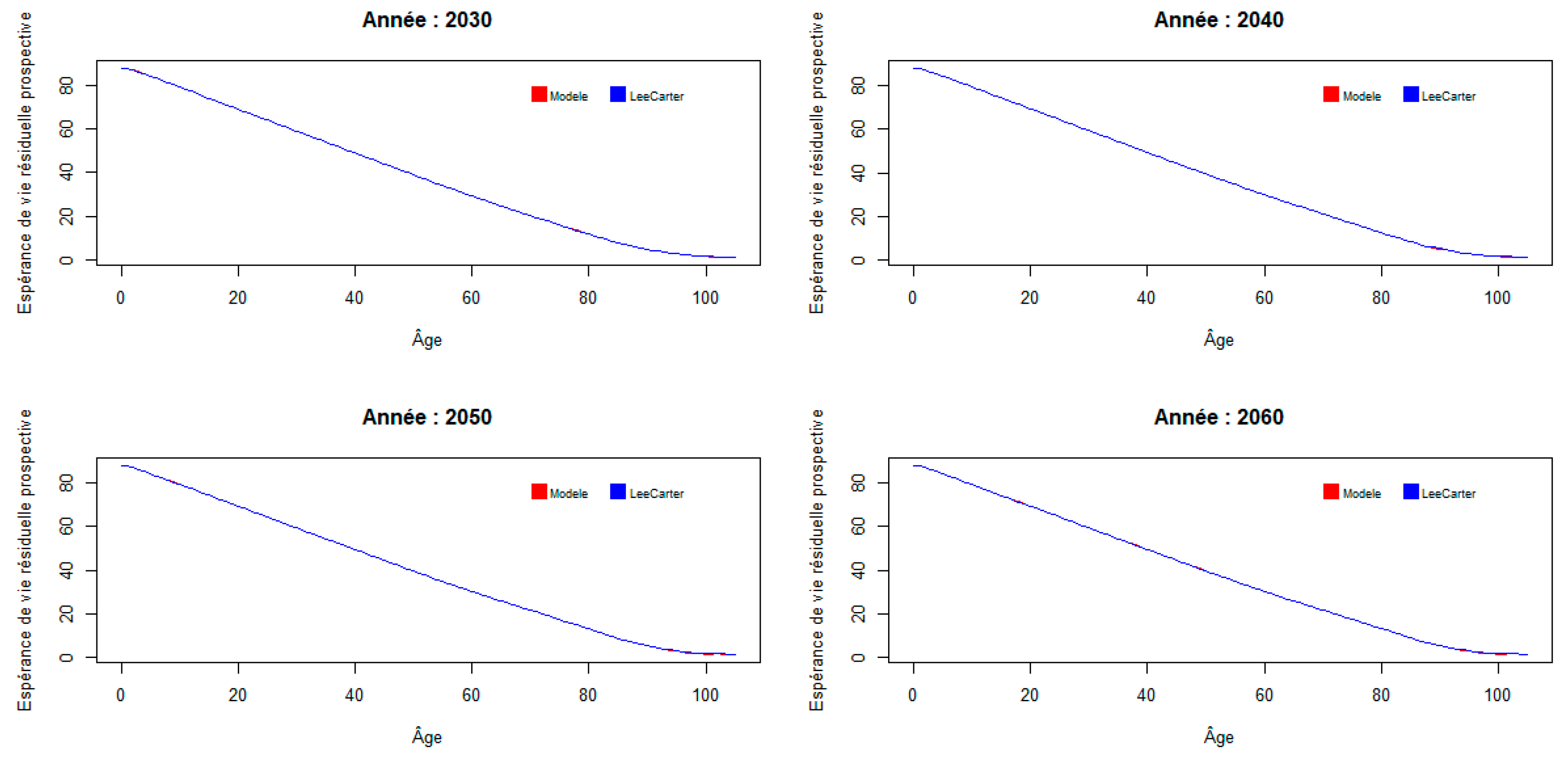
It is then possible to look at the consequences of the mortality model studied on prospective residual life expectancies, first by variable age for a few fixed years, then by variable year for a few fixed ages.

As shown in the following figure, it appears that the mortality model studied does not greatly change prospective residual life expectancies compared to the reference mortality model, except possibly at high ages:

Figure 8. Trends in prospective residual life expectancy by age.

An enlargement of these graphs at older ages is shown below, with the algebraic difference between the two models for each year:

Figure 9. Change in prospective residual life expectancy from age 90 to 105.

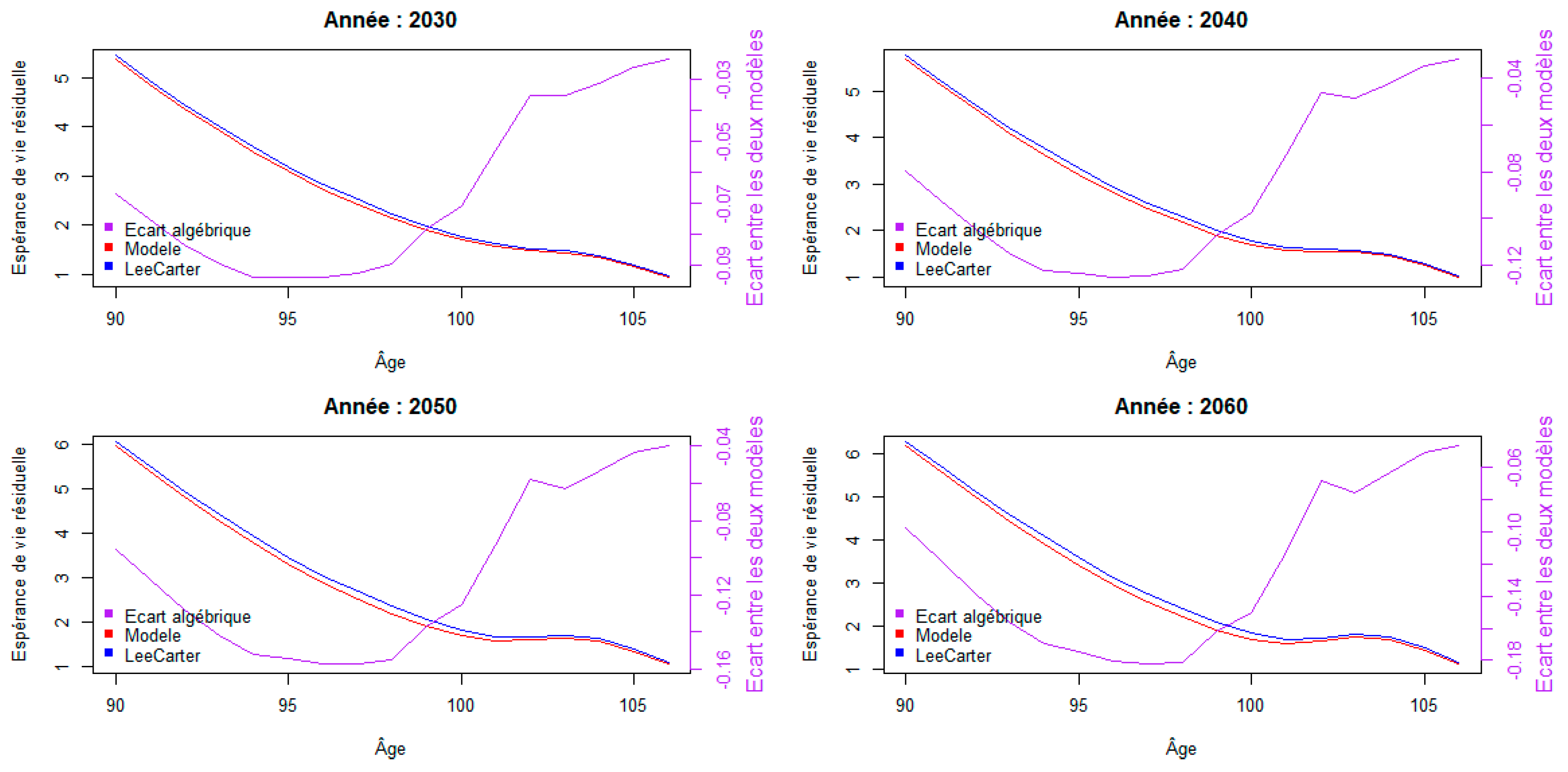
The maximum absolute difference between the two models is found at age 96 for the year 2060, and is worth 0.18, or around 65 days.

In this analysis, we return to the observation made in the previous section: it is at older ages that the difference with the reference Lee-Carter model is most marked.

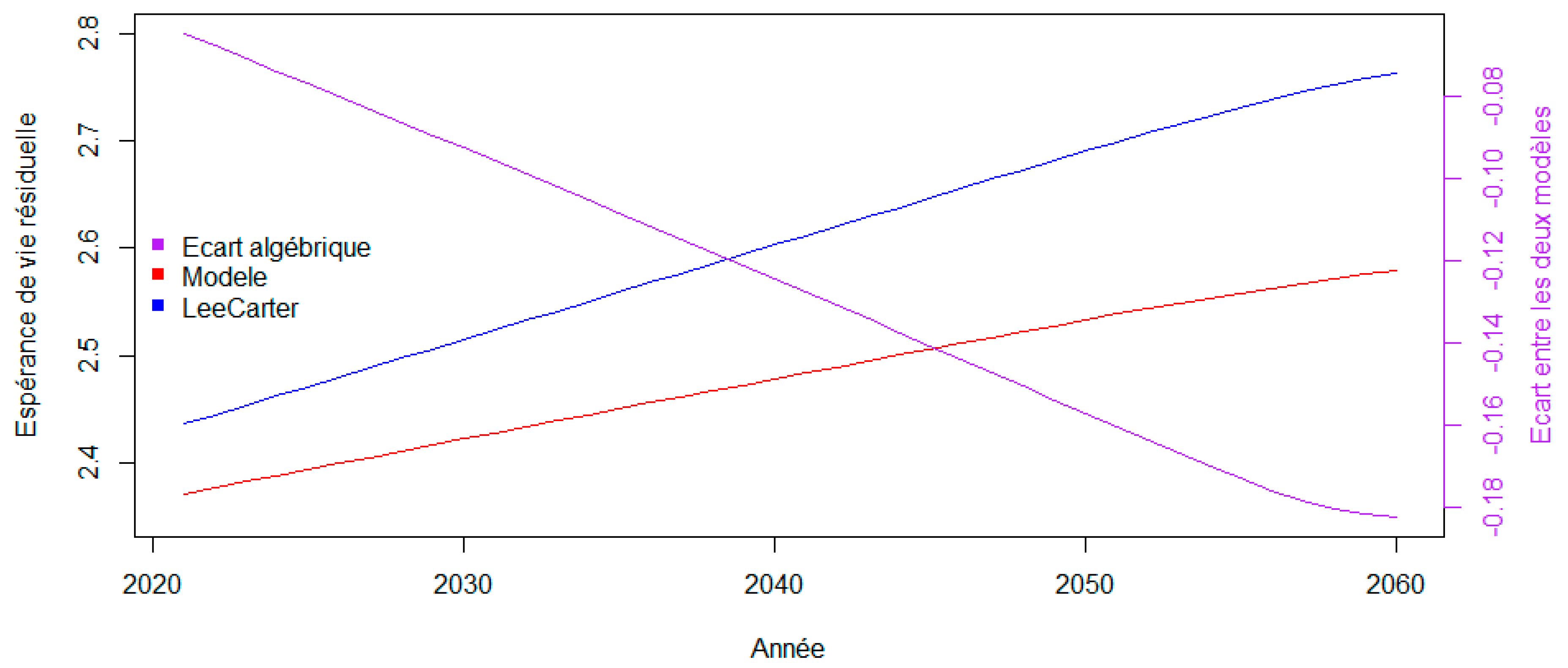
Figure 10. Prospective residual life expectancy by year.

Below is an enlargement for age 96 with the algebraic difference between the two models:

Figure 11. Trend in prospective residual life expectancy by year at age 96.

d. Sensitivity to Fragility Parameter

The volatility of fragility is estimated at 4.3%; however, over a longer period, this parameter can be higher, for example (https://www.ressources-actuarielles.net/C1256F13006585B2/0/39B54166464089AFC12572B0003D88C2/$FILE/20230921_FP.pdf?OpenElement) from 1982 to 2022, it comes out at 5.5%.

With this level of volatility, we note that

P (Z_{t} \geq 1, 09) \approx 5 %

; 9% being the excess mortality rate (https://actudactuaires.typepad.com/laboratoire/2021/03/mortalit%C3%A9-en-france-en-2020-suite.html) for the year 2020, we can deduce that the probability of observing excess mortality at this level is of the order of 5%. Furthermore,

V a R_{99, 5 %} (Z_{t}) \approx 1, 15

, which corresponds to the mortality shock for the “mortality” risk module of the delegated regulation.

On the basis of the central table

μ_{0} (x, t)

adjusted above, the prospective residual life expectancies associated with a volatility coefficient of 5.5% are recalculated using

e (x, t) = \sum_{i \geq 0} \prod_{j = 0}^{i} {(\frac{σ^{- 2}}{σ^{- 2} + μ_{0} (x + j, t + j)})}^{σ^{- 2}}

which leads to the following results:

Figure 12. Evolution of prospective residual life expectancies from age 65 to 105 for selected years, with a new volatility coefficient.

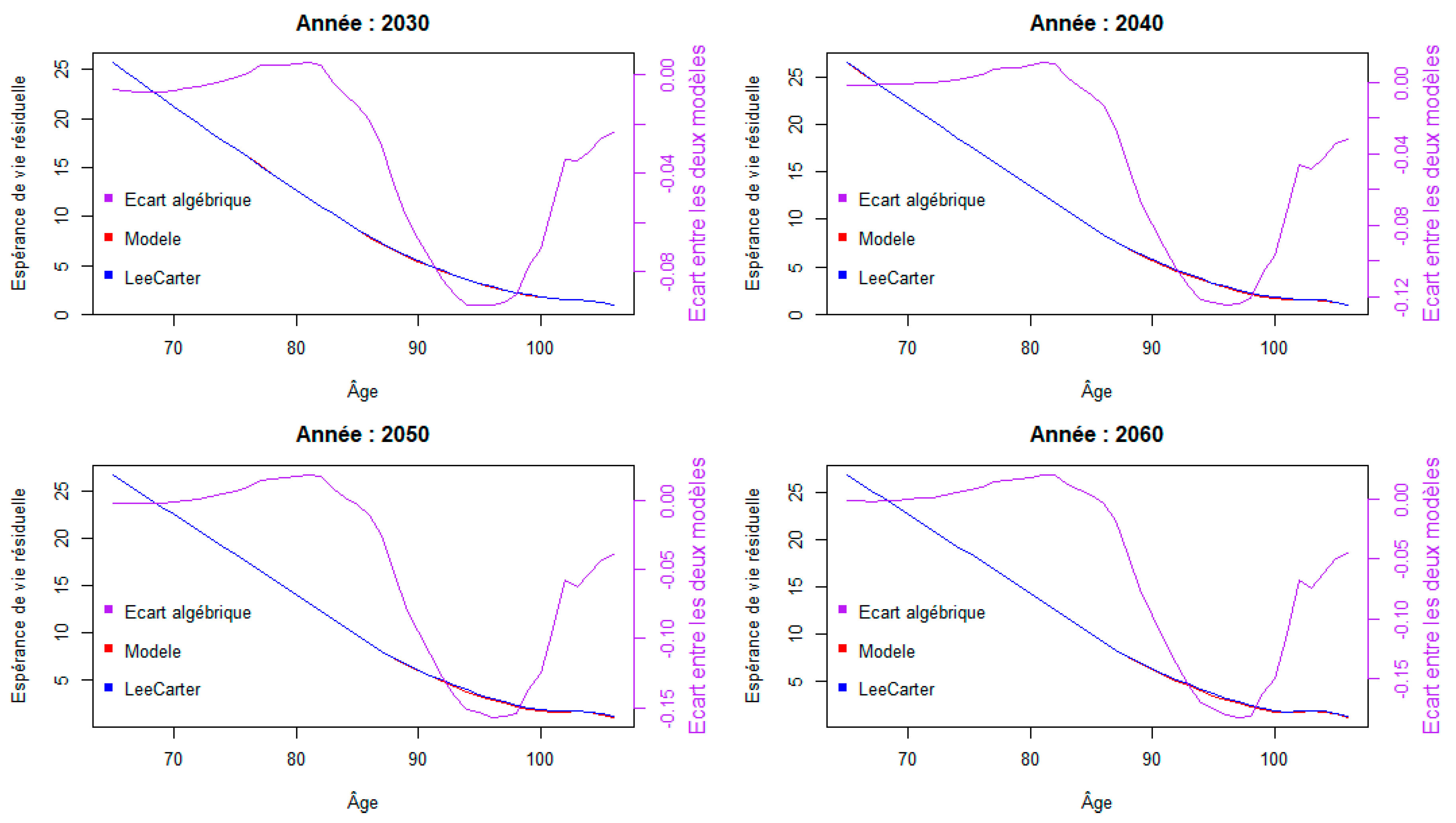
There is no significant difference between the two models with this new volatility setting.

e. Consequences for the Capital Requirement of an Annuity Plan

The presence of the frailty factor therefore has no material impact on central tendency indicators (mortality forces, residual life expectancies, etc.).

However, the random nature of the mortality distribution in a given year has consequences for the assessment of the capital required to protect against adverse deviations in mortality. In the specific context of a life annuity plan, we are therefore led, following a logic analogous to that of the Solvency 2 standard, to consider the 99.5% quantile of the distribution of residual life expectancies induced by frailty. For each age from 60 to 100, we obtain the following results for the ratio between this quantile and the expectation:

Figure 13. Ratio between 99.5% quantile and expectation (SCR).

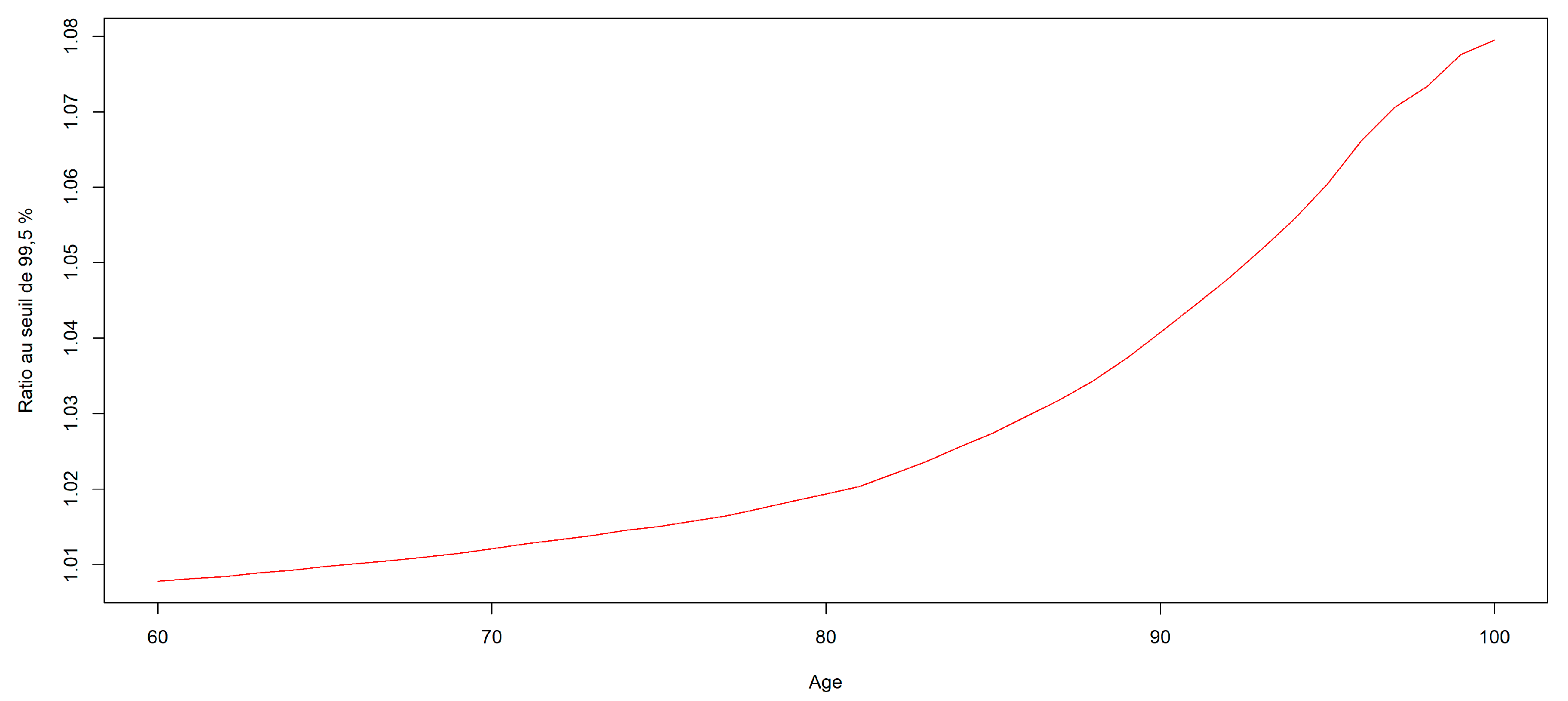
Weighted by the age structure of the French population, the average ratio is around 101.3%.

For its part, the delegated regulation (EU Delegated Regulation n°2015/35: https://eur-lex.europa.eu/legal-content/FR/TXT/?uri=CELEX:32015R0035) imposes a 20% discount on death rates when calculating the SCR associated with longevity risk (cf. art. 138 of delegated regulation EU n°2015/35), which leads to a capital requirement equal to 10% of the expectation.

This means that the volatility observed in annual death rates explains around 12% of the longevity SCR.

4. Conclusions and Discussion

The use of a Gamma frailty model enables us to correctly account for the annual variations in mortality levels observed throughout France.

Incorporating these variations into the fitting of a forward-looking log-Poisson model poses no major difficulty, and a two-stage parameter estimation process enables us to use conventional likelihood maximization algorithms.

The results obtained show that the impact of this additional volatility is negligible on the central tendency indicators.

On the other hand, there is a material impact on the capital requirement associated with longevity risk, with just under 15% of this requirement being induced by the presence of this volatility. The remainder is associated with uncertainty about the trend in death rates.

Thus, while the main hazard associated with the construction of a prospective mortality table remains the uncertainty attached to the determination of the trend (see Juillard et al. [2008] and Juillard and Planchet [2006] for detailed analyses on this point), taking into account these short-term fluctuations in mortality levels provides a better understanding of the determinants of longevity risk.

Appendix A

Table A1. Calibrated model coefficients.

Alpha
Age		Model studied		LC reference model		Age	Model studied	LC reference model	Age	Model studied	LC reference model
0		-5,6542		-5,6553		36	-7,0173	-7,0186	72	-4,0422	-4,0456
1		-7,3447		-7,3457		37	-6,9390	-6,9396	73	-3,9592	-3,9625
2		-8,2790		-8,2804		38	-6,8474	-6,8480	74	-3,8668	-3,8713
3		-8,6679		-8,6695		39	-6,7630	-6,7633	75	-3,7867	-3,7882
4		-8,9672		-8,9721		40	-6,6729	-6,6733	76	-3,6851	-3,6862
5		-9,0765		-9,0803		41	-6,5862	-6,5867	77	-3,5790	-3,5803
6		-9,1958		-9,2028		42	-6,4878	-6,4880	78	-3,4774	-3,4791
7		-9,2892		-9,2924		43	-6,3872	-6,3877	79	-3,3674	-3,3679
8		-9,4087		-9,4124		44	-6,2849	-6,2854	80	-3,2163	-3,2216
9		-9,3935		-9,4009		45	-6,1800	-6,1803	81	-3,0838	-3,0881
10		-9,4223		-9,4329		46	-6,0917	-6,0922	82	-2,9510	-2,9556
11		-9,3577		-9,3662		47	-5,9813	-5,9817	83	-2,8178	-2,8236
12		-9,2768		-9,2809		48	-5,8840	-5,8845	84	-2,6937	-2,7014
13		-9,1674		-9,1742		49	-5,7947	-5,7952	85	-2,5725	-2,5850
14		-8,9411		-8,9443		50	-5,7068	-5,7077	86	-2,4381	-2,4498
15		-8,6907		-8,6949		51	-5,6157	-5,6166	87	-2,3015	-2,3126
16		-8,4690		-8,4721		52	-5,5399	-5,5411	88	-2,1619	-2,1733
17		-8,2022		-8,2047		53	-5,4596	-5,4605	89	-2,0266	-2,0390
18		-7,9805		-7,9814		54	-5,3712	-5,3722	90	-1,8871	-1,9001
19		-7,7424		-7,7441		55	-5,2853	-5,2866	91	-1,7522	-1,7651
20		-7,6642		-7,6654		56	-5,2062	-5,2078	92	-1,6216	-1,6351
21		-7,6042		-7,6051		57	-5,1270	-5,1289	93	-1,4936	-1,5072
22		-7,5935		-7,5952		58	-5,0598	-5,0611	94	-1,3657	-1,3777
23		-7,5824		-7,5837		59	-4,9902	-4,9925	95	-1,2453	-1,2594
24		-7,5520		-7,5540		60	-4,9156	-4,9178	96	-1,1239	-1,1367
25		-7,5513		-7,5531		61	-4,8551	-4,8570	97	-1,0154	-1,0262
26		-7,5195		-7,5211		62	-4,7853	-4,7877	98	-0,9056	-0,9177
27		-7,4982		-7,4995		63	-4,7165	-4,7182	99	-0,8059	-0,8166
28		-7,4795		-7,4816		64	-4,6552	-4,6571	100	-0,7093	-0,7208
29		-7,4393		-7,4409		65	-4,5875	-4,5894	101	-0,6286	-0,6345
30		-7,3880		-7,3899		66	-4,5141	-4,5163	102	-0,5389	-0,5481
31		-7,3594		-7,3607		67	-4,4558	-4,4580	103	-0,4581	-0,4679
32		-7,3008		-7,3012		68	-4,3774	-4,3802	104	-0,4095	-0,4185
33		-7,2536		-7,2544		69	-4,2982	-4,3005	105	-0,4625	-0,4652
34		-7,1764		-7,1771		70	-4,2170	-4,2209
35		-7,1106		-7,1110		71	-4,1381	-4,1415
Beta
Age		Model studied		LC reference model		Age	Model studied	LC reference model	Age	Model studied	LC reference model
0		0,0033		0,0033		36	0,0120	0,0120	72	0,0070	0,0071
1		0,0115		0,0115		37	0,0115	0,0115	73	0,0070	0,0071
2		0,0114		0,0114		38	0,0123	0,0123	74	0,0075	0,0077
3		0,0118		0,0117		39	0,0119	0,0118	75	0,0090	0,0091
4		0,0130		0,0131		40	0,0129	0,0129	76	0,0094	0,0094
5		0,0121		0,0118		41	0,0134	0,0135	77	0,0097	0,0097
6		0,0097		0,0102		42	0,0140	0,0140	78	0,0096	0,0097
7		0,0145		0,0146		43	0,0137	0,0137	79	0,0099	0,0098
8		0,0119		0,0121		44	0,0135	0,0136	80	0,0136	0,0129
9		0,0126		0,0127		45	0,0132	0,0133	81	0,0139	0,0134
10		0,0144		0,0138		46	0,0136	0,0137	82	0,0141	0,0137
11		0,0114		0,0118		47	0,0128	0,0127	83	0,0142	0,0137
12		0,0165		0,0162		48	0,0122	0,0122	84	0,0115	0,0107
13		0,0143		0,0142		49	0,0108	0,0108	85	0,0083	0,0073
14		0,0151		0,0151		50	0,0106	0,0106	86	0,0065	0,0057
15		0,0155		0,0151		51	0,0099	0,0099	87	0,0059	0,0054
16		0,0180		0,0182		52	0,0093	0,0093	88	0,0056	0,0052
17		0,0171		0,0171		53	0,0093	0,0093	89	0,0057	0,0054
18		0,0185		0,0187		54	0,0095	0,0094	90	0,0051	0,0049
19		0,0183		0,0180		55	0,0093	0,0092	91	0,0049	0,0048
20		0,0170		0,0169		56	0,0082	0,0080	92	0,0044	0,0046
21		0,0158		0,0158		57	0,0082	0,0081	93	0,0039	0,0041
22		0,0146		0,0146		58	0,0067	0,0066	94	0,0026	0,0030
23		0,0156		0,0156		59	0,0061	0,0059	95	0,0023	0,0027
24		0,0132		0,0134		60	0,0050	0,0049	96	0,0016	0,0024
25		0,0126		0,0127		61	0,0042	0,0041	97	0,0008	0,0014
26		0,0113		0,0115		62	0,0039	0,0038	98	-0,0005	0,0004
27		0,0111		0,0112		63	0,0040	0,0039	99	-0,0013	-0,0006
28		0,0107		0,0108		64	0,0042	0,0042	100	-0,0002	-0,0001
29		0,0088		0,0088		65	0,0038	0,0038	101	0,0018	0,0022
30		0,0103		0,0102		66	0,0046	0,0046	102	0,0044	0,0047
31		0,0111		0,0110		67	0,0050	0,0051	103	0,0046	0,0048
32		0,0107		0,0106		68	0,0047	0,0047	104	0,0046	0,0053
33		0,0105		0,0104		69	0,0059	0,0059	105	0,0046	0,0051
34		0,0106		0,0105		70	0,0055	0,0055
35		0,0114		0,0113		71	0,0063	0,0064
Kappa
Age	Model studied		LC reference model		Age		Model studied	LC reference model
2000	24,4565		24,4761		2030		-43,8008	-43,8043
2001	24,4627		24,5265		2031		-45,9908	-45,9945
2002	21,2073		21,2070		2032		-48,1809	-48,1847
2003	18,4710		18,4083		2033		-50,3709	-50,3750
2004	10,9651		10,9513		2034		-52,5610	-52,5652
2005	9,4399		9,4231		2035		-54,7510	-54,7554
2006	6,0386		6,0366		2036		-56,9410	-56,9456
2007	3,1599		3,1578		2037		-59,1311	-59,1358
2008	1,4649		1,4631		2038		-61,3211	-61,3260
2009	1,6981		1,6984		2039		-63,5112	-63,5163
2010	-1,1863		-1,1865		2040		-65,7012	-65,7065
2011	-4,7123		-4,7140		2041		-67,8912	-67,8967
2012	-6,6593		-6,6691		2042		-70,0813	-70,0869
2013	-8,5651		-8,5639		2043		-72,2713	-72,2771
2014	-12,6304		-12,6243		2044		-74,4614	-74,4673
2015	-9,8526		-9,8338		2045		-76,6514	-76,6575
2016	-13,5803		-13,5743		2046		-78,8414	-78,8478
2017	-15,8335		-15,8386		2047		-81,0315	-81,0380
2018	-15,6887		-15,6650		2048		-83,2215	-83,2282
2019	-16,4993		-16,4493		2049		-85,4116	-85,4184
2020	-16,1564		-16,2296		2050		-87,6016	-87,6086
2021	-24,0904		-24,0924		2051		-89,7916	-89,7988
2022	-26,2805		-26,2826		2052		-91,9817	-91,9891
2023	-28,4705		-28,4728		2053		-94,1717	-94,1793
2024	-30,6606		-30,6630		2054		-96,3618	-96,3695
2025	-32,8506		-32,8532		2055		-98,5518	-98,5597
2026	-35,0406		-35,0435		2056		-100,7418	-100,7499
2027	-37,2307		-37,2337		2057		-102,9319	-102,9401
2028	-39,4207		-39,4239		2058		-105,1219	-105,1304
2029	-41,6108		-41,6141		2059		-107,3120	-107,3206
					2060		-109,5020	-109,5108

References

Agalva E., Blanpain N. [2021] Projections de population 2021-2070, Insee Résultats.
Bongaarts J. [2004] “Long-range trends in adults mortality: Models and projection methods”, Population Council. [CrossRef]
Brouhns N., Denuit M., Vermunt J.K. [2002] A Poisson log-bilinear regression approach to the construction of projected lifetables, Insurance, Mathematic and Economics, vol. 31. [CrossRef]
Currie I.; Durban M.; Eilers P. [2003] Using P-splines to extrapolate two-dimensional Poisson data, Proceedings of 18th International Workshop on Statistical Modelling, Leuven, Belgium.
Debonneuil E. [2015] Parametric age-dependent mortality model, for applications to retirement portfolios, Actuary’s Thesis, ISFA.
Guilbaud C. [2018] Nouveaux modèles d’analyse et de projection de la mortalité, application a la population française, Mémoire d’actuaire, Dauphine.
Guette V. |2010] La prise en compte des catastrophes dans la modélisation de la mortalité, Actuary thesis, ISFA.
Juillard M., Planchet F., Thérond P.E. [2008] “Perturbations extrêmes sur la dérive de mortalité anticipée”, Assurances et gestion des risques, Vol. 76 (3).
Juillard M., Planchet F. [2006] “Mesure de l’incertitude tendancielle sur la mortalité - application à un régime de rentes”, Assurances et gestion des risques, Vol. 75 (3). [CrossRef]
Lee R. D., Carter L. [1992] “Modeling and forecasting us mortality”, Journal of the American statistical association 87(419), 659{671. [CrossRef]
Planchet F., Thérond P.E. [2011] Modélisation statistique des phénomènes de durée - applications actuarielles, Paris : Economica.
Robben J., Antonio K. [2023] Catastrophe risk in a stochastic multi-population mortality model, Working Paper. 2023; arXiv:2306.15271.
Thatcher A.R. [1999] The Long-term Pattern of Adult Mortality and the Highest Attained Age, Journal of the Royal Statistical Society, 162, Part 1: 5-43. [CrossRef]
Vaupel J. W., Manton K., Stallard E. [1979] “The impact of heterogeneity in individual frailty on the dynamics of mortality”, Demography, 16, pp. 439-454. [CrossRef]
Ghalanos A. Theussl S. [2015] “Rsolnp: General Non-Linear Optimization”, https://cran.r-project.org/package=Rsolnp.
Hyndman R. [2023] “demography: Forecasting Mortality, Fertility, Migration and Population Data”, https://cran.r-project.org/package=demography.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Adding Shocks to a Prospective Mortality Model

Abstract

1. Introduction

2. Proposed Stochastic Mortality Model

a. Specification

b. Log-Likelihood Determination

c. Parameter Estimation

d. Calculating Prospective Residual Life Expectancies

3. Numerical Application

a. Model Adjustment

Estimation of Gamma Distribution Parameters

Estimation of Model Parameters

Extrapolation of Time Coefficients

b. Projected Mortality Forces

c. Estimating Prospective Residual Life Expectancies

d. Sensitivity to Fragility Parameter

e. Consequences for the Capital Requirement of an Annuity Plan

4. Conclusions and Discussion

Appendix A

References

MDPI Initiatives

Important Links

Subscribe