Prerpints.org logo
Preprint
Article

Numerical Study of the Effect of Primary Nozzle Geometry on Supersonic Gas-Solid Jet of Bypass Injected Dry Powder Fire Extinguishing Device

Altmetrics

Downloads

97

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 December 2023

Posted:

04 January 2024

You are already at the latest version

Alerts
Abstract
A two-way coupled model between polydisperse particle phases with compressible gases and a density-based coupling implicit solution method combining the third-order MUSCL with QUICK spatial discretization scheme and the second-order temporal discretization scheme are constructed based on the discrete-phase model (DPM) and the stochastic wander model (DRWM) in the Eu-lerian-Lagrangian framework in conjunction with a unitary particulate source (PSIC) approach and the SST k-ω turbulence model. The accuracy of the numerical prediction method is verified using previous supersonic nozzle gas-solid two-phase flow experiments. Numerical simulation of two-phase jet of dry powder extinguishing agent gas with pilot-type supersonic nozzle was carried out to analyze the influence of geometrical parameters such as length ratio rL and area ratio rA of main nozzle on the two-phase flow field as well as on the jet performance indexes such as particle mean velocity vp,a, velocity inhomogeneity Φvp, particle dispersion Ψp, particle mean acceleration ap,a and so on. By analyzing the parameters, we indicate the requirements for the combination of jet performance metrics for different flame types such as penetrating, spreading, and dispersing.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

According to the publicly available statistics by China National Fire and Rescue Administration, in recent five years (i.e., 2018~2022), an increase in number of variety types of fires caused increasing property losses and heavy casualties (c.f. Figure 1a,b). Therefore, further development of fire-fighting and extinguishing technologies is of great significance for disaster prevention and mitigation. Dry powder fire extinguishing technology is widely used because of its high extinguishing efficiency, wide range of fire types and environmental friendliness. By using a bypass nozzle and an injection type dry powder fire extinguisher, the fire extinguishing agent particles are fully accelerated and necessary dispersed in the gas jet. The supersonic dry powder jet obtained from the nozzle outlet will significantly improve the fire extinguishing efficiency for large-scale fires [1].
Previous extensive research has shown that for the injection type supersonic nozzle jet dry powder fire extinguishing technology, the influence of geometric characteristics is significant and cannot be ignored among the factors that affect the fire extinguishing efficiency, such as the performance of the extinguishing agent, injection conditions, and the geometric structure of the main nozzle or injector.
As a result, there have been many theoretical and experimental studies on the design parameters of gas-solid two-phase nozzles and the performance of gas-solid injectors[2,3]. As the air flows through the orifice plate in the circular duct, a pressure drop effect occurs in the vertical solids injector. By utilizing this pressure drop effect, the jet is able to naturally entrain micron-sized particles[4]. Using experimental and simulation methods, Kim et al. determined the effect of different operating variables and injector geometry on the hydraulic characteristics of rectangular bubble columns of a multiphase injector[5]. Moreover, the physical properties of the working fluid have a significant effect on the performance of such injectors. As the injector inlet pressure or temperature approaches a pseudo-critical state, the mass flow rate of the primary stream shows a nonlinear variation. Transcritical injector systems exhibit higher coefficients of performance than subcritical systems at most primary flow inlet temperatures. Transcritical injectors have better pressure lifting performance, while the subcritical injector only shows a higher entrainment rate at low pressure head ratios[6].
For fluid-particle interactions in the nozzle, the axial characteristic Stokes number is lower than the radial characteristic Stokes number. This is due to the fact that the length scale of the axial motion is significantly larger than the length scale of the radial motion. Which further leads to a preferential response of the particles to axial velocity fluctuations in the gas phase over radial velocity fluctuations. And this in turn leads to a high level of anisotropy in the particle phase velocity fluctuations[7]. The velocity, mass flow rate, and volume fraction of high Stokes number particles injected from the nozzle inlet, as well as the position of the injector, all affect the dynamic range and dispersion of jet particle velocities[8]. Relevant experimental results also show that among the various structural parameters, the length of the nozzle is one of the key indicators affecting the parameters of gas-solid jet flow[9]. Further experimental studies on several different shapes of mixing pipes show that the converging-flat-diffusing shape enhances the ability to transport solid particles[10]. A numerical study of a number of different nozzle shapes Established through experimental data calibration shows that the optimal main nozzle exit position is proportional to the mixing diameter and increases monotonically with increasing gas-phase pressure. At the same time, changes in the angle of convergence of the gas-solid mixing section are quickly reflected in the nozzle performance[11]. Moreover, keeping the injector at the optimal critical pressure ratio, size, and efficiency can provide the highest negative pressure conditions for the mainstream and suction flow[12]. In addition, the double venturi effect of the venturi injector facilitates particle transport[13]. Most of such studies use a single gas-phase bypass nozzle and focus on the effects of its geometry and location. In this study, we simplify the geometric model for computational efficiency. Most of the core components of the flow channel of the dry powder fire extinguishing device have an axisymmetric structure, so we will use the simplified assumption of two-dimensional axisymmetric flow for geometric modeling.
There are two common mathematical description methods for Compressible Gas-Solid Two-Phase Flow: Eulerian-Lagrangian method and Eulerian-Eulerian method. Differences in descriptive methods can also lead to significant differences in computational methods. In order to balance the contradiction between the computational volume and the coupling between phases, this paper adopts the mass-point method in the Eulerian-Lagrangian framework, i.e., the gas phase follows the Eulerian description of the continuous fluid while the discrete phase of the solid particles adopts the Lagrangian description, and the corresponding number of real particles is characterized by the "computational particles" (points with a certain mass). For the scaled nozzle gas-solid two-phase flow, based on the EL framework, the gas-phase SST k-ω turbulence model and the particle random orbit model are used, and the established gas-solid two-phase coupled model has sufficient accuracy in the numerical simulation[14]. In addition, most of the relevant studies dealt only with monodisperse particles, and only a few modeling and simulations considered the polydispersity of the particles. Experimental and computational modeling of particle-containing polydisperse jets with a wide range of Stokes numbers shows that in polydisperse jets, the velocity decay rate grows with decreasing particle size and particle volume fraction, while larger particles have a lower axial velocity decay rate. The axial velocity of monodisperse small particles is close to the single-phase velocity on the centerline, but for polydisperse jets, the axial velocity of the particles is greater than the single-phase velocity for the same Stokes number. This is because the effect of larger particles on the gas phase in turn affects the smaller particles in the polydisperse jet. It is shown that particle polydispersity has a significant effect on particle volume fraction and velocity[15]. The Rosin-Rammler distribution can better model the polydispersity in the droplet diameter distribution of polydisperse droplet systems, and in general, the numerical results are in good agreement with the experimental results. The computational framework of 2D CFD modeling based on this particle size distribution model has become an important tool for predicting flow processes and optimizing injector structures. [16].
Therefore, this paper carries out the design of key geometric parameters such as the length ratio of the main nozzle and the area ratio of the outlet throat based on the induced supersonic nozzle dry powder extinguishing agent gas jet. Based on the gas-phase SST k-ω turbulence model, particle discrete stochastic orbital model, finite volume method, structured combined boundary layer mesh, time-stepping method, and the modified drag model constructed by Zhang et al[1]. were used to analyze the effects of nozzle in-stream and out-of-tube jet parameters. To fully understand the gas-solid two-phase flow behavior inside and outside the powder extinguishing agent transport channel, this paper analyzes the polydisperse two-phase flow field and the influence of main nozzle geometric parameters (length ratio rL, area ratio rA) on jet performance indicators such as particle average velocity vp,a, velocity nonuniformity Φvp, particle dispersion Ψp, and particle average acceleration ap,a. The rest of the paper is organized as follows: the second section describes the interphase coupling model. We then verify the accuracy of the momentum calculation by describing the numerical method and comparing the experimental data in the third section. Finally, the fourth and fifth sections give the analysis of the computational results and the main conclusions of the paper, respectively.

2. Interphase coupled modeling

2.1. Gas-solid two-phase nozzle geometry modeling

In this paper, the numerical simulation is carried out using a scaled axisymmetric main nozzle with a ring bypass injector arranged in the expansion section of the main nozzle as the particle inlet. Figure 1 shows the geometric structure of the nozzle, which is a two-dimensional axisymmetric scaling nozzle consisting of a uniform straight tube section, a tapered convergent section, and a divergent section. The detailed dimensions of this 2D axisymmetric nozzle are given in Table 1, where the length of the straight section ls is 46 mm, the convergent section lc is 69 mm, and the dilatation section ld varies with the length ratio of the main nozzle, and ld is 138 mm when the length ratio rL= 2. The throat radius rt is 8.05 mm, the inlet radius rin is 11.5 mm, and the outlet radius re varies with the area ratio of the nozzle, and re is 16.1 mm when the area ratio rA=4. In addition, the particle injector position linj is taken as 68.3 and width winj is taken as 8.05, and a circular arrangement perpendicular to the outlet section of the main nozzle is used.
Preprints 94973 g002
Figure 2. Main nozzle geometry with annular injector.
Figure 2. Main nozzle geometry with annular injector.
Preprints 94973 g002

2.2. Mathematical model of gas-solid two-phase flow

2.2.1. Continuous phase control equations

The tensor form equation of viscous, compressible and unsteady gas phase flow continuity equation, momentum equation, and energy equation expressed as the summation convention are as follows:
Continuity equation:
∂ ∂ t （ φ g ρ g ） + ∂ ∂ x i ( φ g ρ g v ¯ g , i ) = 0 ,
Momentum equation:
∂ ∂ t ( φ g ρ g v ¯ g , i ) + ∂ ∂ x j ( φ g ρ g v ¯ g , i v ¯ g , j ) = − ∂ p ∂ x i + ∂ ∂ x j ( φ g τ e f f , i j ) − N p V c e l l ∑ n = 0 N F f p , i n ,
Energy equation:
∂ ∂ t ( φ g ρ g e g * ) + ∂ ∂ x i [ ( φ g ρ g e g * + p ) v ¯ g , i ] = ∂ ∂ x i [ φ g ( k e f f ∂ T g ∂ x j + τ e f f , i j v ¯ g , i ) ] − N p V c e l l ∑ n = 0 N ( G f p n + Q f p n ) ,
in which φ g is the gas volume fraction. n is the number of particle packets in the current cell and N is the total number of particle packets in the current cell. And e g * for the specific total energy, k e f f represents the effective thermal conductivity including turbulence effects. G f p n is the power of the work done by the gas on the nth particle packet, with the specific expression G f p n = F f p , i n v g , i . Q f p n is the heat flow rate of heat transfer from the gas to the nth particle packet. Moreover, the effective stress tensor τ e f f , i j = τ m , i j + τ t , i j , where stress tensor τ m , i j and the Reynolds stress tensor τ t , i j , respectively:
τ m , i j = μ （ ∂ v g , i ∂ x j + ∂ v g , i ∂ x i - 2 3 e i j ∂ v g , l ∂ x l ） ,
τ t , i j = μ t （ ∂ v g , i ∂ x j + ∂ v g , i ∂ x i - 2 3 e i j ∂ v g , l ∂ x l ） - 2 3 ρ g k e i j ,
in which μ t and k are the turbulent viscosity and turbulent kinetic energy, respectively. e i j is the identity matrix component.
The SST k-ω turbulence model [17]was used to simplify the turbulence and predict the development of the turbulent flow while closing the set of equations using the ideal gas equation of state. The SST k-ω turbulence model employs a mixing function such that its non-standard ω equations converge to the standard ω equations near the wall and to the standard ε equations away from the wall. Thus, the model retains the advantages of the two standard turbulence models while largely avoiding the disadvantages of both. Given the advantages of relatively low computational cost and acceptable prediction accuracy, it has been widely used in practical engineering calculations. For the SST k-ω turbulence model equations[17], the equations for the turbulent kinetic energy k and the turbulent kinetic energy dissipation rate ω are expressed as:
∂ ( ρ g k ) ∂ t + ∇ ⋅ ( ρ g k v ¯ g ) = τ t : ∇ v ¯ g − ρ g β * k ω + ∇ ⋅ [ ( μ + σ k μ t ) ∇ k ] ,
∂ ( ρ g ω ) ∂ t + ∇ ⋅ ( ρ g ω v ¯ g ) = ρ g v μ t τ t : ∇ v ¯ g − ρ g β ω 2 + ∇ ⋅ [ ( μ + σ ω μ t ) ∇ ω ] + 2 ( 1 − F 1 ) ρ g σ ω 2 1 ω ∇ k ⋅ ∇ ω ,
where μt is denoted as:
μ t = ρ g a 1 k max ( a 1 ω , Ω F 2 ) ,
where β*, σ k ,β, σ ω , σ ω 2 , and a 1 are model constants; F1 and F2 are mixing functions; and Ω is the vorticity.
At the same time, the effect of temperature on the dynamic viscosity and thermal conductivity of the gas cannot be neglected for the high-velocity compressible flow studied in this paper. Therefore, we choose the three-coefficient Sutherland’s law [18] for the description.
2.2.2 Discrete phase control equations
A DPM model is used for the particle phase motion, which is characterized by solving the orbits of the particles by integrating the differential equations of particle motion in the Lagrangian coordinate system. Considering the small size of the studied particles (about 10-100 μm) and the high translational velocities up to hundreds of meters per second, the effect of the rotational motion of the particles was neglected.
In their previous work, Parmar et al.[19] and Ling et al.[20,21] described the aerodynamic composition on computational particles under the plasmonic force model and gave the corresponding analytical expressions:
F f p , i = F q s , i + F a m , i + F p g , i + F S a , i ,
in which F q s , i , F a m , i , F p g , i , and F S a , i denote the quasi-steady state force, added-mass force, pressure gradient force, and Saffman force, respectively. The quasi-steady state force expression is given below:
F q s , i n = π 8 d p 2 ρ g C D ( v g , i − v p , i ) | v g − v p | ,
among them:
v g = v ¯ g + v g ′ ,
v ¯ g is the time-averaged velocity of the gas, v ′ g = ξ 2 k / 3 is the fluctuation velocity of the gas, ξ is a random number with a normal distribution, and k is the turbulent kinetic energy of the gas [22]; v p is the particle velocity; CD and is the drag coefficient.
The expression for the added-mass force is:
F a m , i = C M ρ g V p ( d v g , i d t − d v p , i d t ) ,
in which CM is the added-mass coefficient, which is simplified and set based on spherical particles in this paper, taking CM=0.5, and Vp denotes the computational particle volume.
The expression for the pressure gradient force is:
F p g , i = − V p ∂ p ∂ x i ,
in which p is the pressure of gas.
The expression for the Saffman force is:
F S a = V p 2 K ( ρ g μ ) 1 / 2 d p ( S ⋅ S ) 1 / 4 [ S ⋅ ( v g , i − v p , i ) ] ,
where the constant is taken as K=2.595; S is the deformation tensor[23]. It should be noted that the above Saffman force model is applicable to incompressible flows.
The heat transfer between gas and solid phases can be expressed as:
Q g p = π μ c p g d p ( T g − T p ) N u / P r ,
where c p g is gas specific constant pressure heat capacity; T p is the temperature of the calculated particle; Platt's number P r = 4 γ / ( 9 γ − 5 ) ;Nu is the Nusselt number, and the specific expression adopts the empirical relation proposed by Ranz and Marshall[24].

2.3. Discrete phase physical modeling

2.3.1. Resistance coefficient model

For the supersonic gas-solid two-phase jet studied in this paper, the drag force of the flow on the particles determines the momentum transfer between the phases and hence the velocity field distribution of the particles. Therefore the proper construction of particle drag models is critical. In previous studies, we have found that the rarefaction effect of the gas leads to a reduction in the particle drag coefficient, a reduction in the gas force on the particles, and consequently a reduction in the velocity. However, overcorrection of the rarefaction effect brings about different degrees of overestimation or underestimation of the drag force.
Therefore, in our previous work[1], we integrated the drag coefficient models proposed by Parmar, Henderson and Clift et al. respectively[19,25,26] and proposed the following modified drag coefficient model under the premise of comprehensive consideration of gas compressibility, inertia and rarefaction effects. It is worth noting that since neither the Clift nor the Parmar models take into account gas rarefaction effects, we have made an additional correction for this aspect of rarefaction effects in our existing model:
C D = { f r ( K n p ) C D , C R e p ≤ 1500 f r ( K n p ) C D , P R e p > 1500 ， M p ≤ 1.75 C D , H M p > 1.75 ,
in which CD,C,CD,P and CD,H denote the Clift, Parmar and Henderson drag coefficient models, respectively[19,25,26], with the expressions:
C D , C = { 3 / 16 + 24 / R e p R e p < 0.01 24 / R e p [ 1 + 0.1315 R e p ( 0.82 − 0.05 lg R e p ) ] 0.01 ≤ R e p < 20 24 / R e p [ 1 + 0.1935 R e p 0.6305 ] 20 ≤ R e p < 260 10 [ 1.6435 − 1.1242 lg R e p + 0.1558 ( lg R e p ) 2 ] 260 < R e p ≤ 1500 ,
C D , P = { C D , s t d ( R e p ) + [ C D , M = 0.6 ( R e p ) − C D , s t d ( R e p ) ] M p M p , c r M p ≤ M p , c r C D , M = 0.6 ( R e p ) + [ C D , M = 1 ( R e p ) − C D , M = 0.6 ( R e p ) ] ξ s u b ( M P , R e p ) M p , c r < M p ≤ 1.0 C D , M = 1 ( R e p ) + [ C D , M = 1.75 ( R e p ) − C D , M = 1 ( R e p ) ] ξ sup ( M P , R e p ) 1.0 < M p ≤ 1.75 ,
where CD,std,CD,M=0.6,CD, M=1and CD, M=1.75 specific expressions can be found in the literature[19].
C D , H = 0.9 + 0.34 M p 2 + 1.86 ( M p R e P ) 1 2 [ 2 + 2 s 2 + ( T P T g ) 1.058 s − 1 s 4 ] 1 + 1.86 ( M p R e P ) 1 2 ， M p > 1.75 ,
where s is the molecular speed ratio with the expression:
s = | v g − v p | / ( 2 R g T g ) 1 / 2 ,
where Tg and Tp are the gas and particle temperatures, respectively.

2.3.2. Particle size distribution

This study was carried out with polydisperse particles. For specific particle size distributions, the widely used two-parameter Rosin-Rammler model was used for fitting. We utilize discrete measurements of particle size for smooth Boltzmann function fitting. After obtaining the particle size distribution function, it was discretized using the composite Simpson algorithm. Finally, the Rosin-Rammler fit is used:
Y d = exp [ − ( d p / d p , m ) n s ] ,
in which Yd denotes the mass percentage of particles with diameters greater than dp, dp is the particle size dimension; dp,m is the median diameter, denoted when Yd=1/e≈36.8%;and ns is the size distribution index.
With reference to previous studies, we determined the specific parameters and the number of particle size groupings. For example, for the size measurements of particulate titanium used by Meyer et al[8], the particle distribution parameters were specified as: median diameter dp,m=58.57μm and dispersion coefficient ns=3.709.

3. Numerical Methods and Verification

3.1. Numerical calculation methods

In this paper, ANSYS Fluent is chosen as the solver and the continuous phase calculations are based on the finite volume method. To ensure numerical stability, a density-based coupled implicit solution method is used, while the transient formulation is in second-order implicit format. For the momentum conservation equations, the discretization is performed using the third-order MUSCL schemes, while the QUICK schemes is chosen for the energy conservation equations as well as for the turbulence model equations. The DPM model based on the Lagrangian method is used for the particle phase motion, and the discrete random walk model (DRWM) is combined for unsteady tracking of the particles. Every 20 iterative steps of the continuous-phase flow field, a round of trajectory calculations including one or more steps and source term calculations are performed for each particle, thus advancing the particle along the trajectory round by round, step by step, and sequentially obtaining the particle state (position, velocity, size, temperature, etc.) that has been updated after each step of the calculations.
In order to speed up the convergence of the calculation, we first calculate a steady-state single-phase flow field of the gas based on the mesh and the numerical model until the calculation is converged, this single gas-phase flow field is then used as the initial field for the subsequent gas-solid two-phase calculations. Practical calculations reveal that this method can effectively improve the convergence and thus speed up the calculation.

3.2. Calculation conditions

When high-pressure nitrogen, carbon dioxide, or other flame-retardant gases flow through the scaling nozzle, a supersonic jet is formed. At the same time, due to gas expansion, a relatively low-pressure environment is formed in the expansion section of the main nozzle. Pilot-type supersonic nozzle jet dry powder fire extinguishing technology uses this low pressure environment in the expansion section to attract dry powder extinguishing agent from the bypass injector into the main nozzle. In this way, the particles can be fully accelerated and dispersed in the gas jet, significantly improving the extinguishing performance for different types of flames. The boundary conditions used for the Pilot-type supersonic nozzle studied in this paper are shown in Figure 3.
The main nozzle total pressure ratio and injector total pressure ratio are two key parameters, which are taken as NPR=19.74 and SPR=0.2 respectively. By comprehensive consideration, we selected the particle incident velocity vp,inj=100m/s and mass flow rate qm,p=0.1kg/s as the injection conditions of the particles. Atmospheric pressure atm=101325Pa and constant wall temperature T=300K. Nitrogen was used as the fluid medium for the studied dry powder fire extinguisher, and the extinguishing agent was ammonium dihydrogen phosphate dry powder with a density of ρp=1803 kg-m-3 and a specific heat capacity of Cp=1280 J·kg-1·K-1.

3.2.1. Particle injection

After determining the total mass flow rate qm,p of the injected particles, the particles are injected in a manner that calculates the particles. That is, one particle containing multiple particles is injected at a time, while the entire particle package is tracked as a single computational particle.
The actual number of particles represented by the nth calculated particle N p n can be obtained from the following relation:
N p n m p n N c e l l , i n = q m , p Δ t [ Y d ( d p , min j ( n ) ) − Y d ( d p , max j ( n ) ) ] ,
The two sides of the relation represent the total mass inside the nth particle package calculated in different forms, in which Ncell,in is the total number of grids at the inlet of the injector; Nd is the number of particle size subgroups; time step Δt=10-6 s; d p , min j ( n ) , d p , max j ( n ) , respectively, are the minimum and maximum particle diameters in the package, and the superscript j represents the corresponding particle size interval.

3.2.2. Definition of jet performance indicators

For gas jets, we define key performance metrics including particle mean velocity v p , a N W (or v p , a M W ), velocity inhomogeneity Φ v p M W , and dispersion Ψ p M W to characterize them. It is worth noting that, depending on the range selected, these metrics are subdivided into those counted by actual particle counts and those counted by injected particle packages:
v p , a N W = ∑ n = 1 N c s N p n v p x n / ∑ n = 1 N c s N p n ,
v p , a M W = ∑ n = 1 N c s m p c n v p x n / ∑ n = 1 N c s m p c n ,
Φ v p M W = ∑ n = 1 N c s ( m p c n v p x n − m p c n v p , a N W ) 2 / ( v p , a M W ∑ n = 1 N c s m p c n ) ,
Ψ p M W = ∑ n = 1 N c s ( m p c n ζ p n ) 2 / ( r e ∑ n = 1 N c s m p c n ) ,
There is an optimal range of gas-solid jet extinguishing efficacy for specific types of flames. The above performance indicators characterize the effectiveness of jet fire fighting. vp,a, Φvp, and Ψp, characterize the kinetic energy of the jet, and the inhomogeneity of the particles in the jet in the flow direction and radial direction, respectively. We can divide different flames into three types: spreading flame, penetrating flame, and dispersed flame. Obviously, the optimal fire suppression efficiency areas corresponding to these three types of flames are different [27]. So we carried out the analysis of the jet in the following parametric study using the above mentioned metrics. However, our study does not deal with the range of metrics for optimal fire suppression effectiveness, but rather discusses the effect of nozzle geometry characteristics on these metrics themselves. In the validation of the numerical method, we instead compared the particle mean velocity obtained from the simulation with the experimentally measured particle mean velocity by Meyer et al[8].
Meanwhile, in the subsequent parametric study, we selected two narrow-band regions inside the nozzle to be analyzed. These two areas are located in the area downstream of the injector as well as in the nozzle exit area. In addition to investigating the above performance metrics for representative particles in these two regions, we define the flow and radial mean acceleration of the particles as follows:
a p , a x = ∑ n = 1 N C S m p c n a p x n / ∑ n = 1 N C S m p c n ,
a p , a y = ∑ n = 1 N C S m p c n a p y n / ∑ n = 1 N C S m p c n

3.3. Verification of Grid Independence

We use a locally encrypted quadrilateral structural mesh for meshing the studied supersonic nozzle. The global and local zoom grids used are illustrated in Figure 4. As shown in the figure, encrypted boundary layers were established for the nozzle wall boundary and particle injector wall boundary regions as a way to improve the computational quality of the corresponding regions. At the same time, the grid cell size was controlled in compliance with the limitations of the chosen turbulence model (y+ < 1). Five sets of grids Mesh1-5 with different densities were finally obtained, with grid counts of 3.3w, 6.0w, 8.8w, 13.0w, and 17.4w, which all had masses greater than 0.9.
We performed test calculations for these five different densities of grids and selected two regions located downstream of the injector and at the outlet of the main nozzle, respectively, as representative for monitoring the particle velocity distribution. These two regions are at the same time the monitoring regions where the parameter analysis will be carried out later (Figure 5). The monitoring showed that as the grid was encrypted, the average velocity of the number of particles in the two regions showed an opposite monotonicity, but the difference between the results calculated for the different grids tended to decrease. Especially for Mesh4 and Mesh5, the deviation of the computed results is less than 1% in both regions. For the consideration of balancing the calculation accuracy and calculation time, Mesh4 (13.0w) was finally chosen for subsequent calculations in this paper, and the results were considered reliable. A series of test calculations were carried out for reasons of balancing computational cost and convergence. The results show that the combination of setting the number of particle size groups to 6, the time step Δt= 10-6 s and the Courant number CFL = 1 is cost acceptable and has sufficient accuracy.

3.4. Validation of the modeling approach

In this paper, the supersonic nozzle gas-solid two-phase flow experiments of Meyer et al [8] are utilized to validate the accuracy of the adopted drag coefficient model and numerical methods. Figure 6 shows the core component of the experimental setup from the literature [8]: a rectangular cross-section transparent quartz nozzle. The coordinate origin is located at the nozzle inlet, the x-axis points downstream along the nozzle axis, the y-axis is plumbed upward, and the z-axis forms a right-handed system with the x and y axes.Detailed dimensions of the nozzle are shown in Table 2. The variable calculation parameters in the validation calculations are the granular material (Stellite-21, see Table 3) and the total inlet pressure (5 bar and 9 bar), the other parameters are taken as fixed. Nitrogen gas constant R=296.7J/(kg-K), specific heat ratio γ=1.4, total inlet temperature T0=293K, wall temperature Tw=293K.
We compared two different particle size distributions, monodisperse and polydisperse, using the same particle material (Stellite-21) and the same resistance model (Present resistance model) to show the differences. A comparison between the measured particle mean velocities of particles at the nozzle exit and those obtained from numerical calculations measured by Meyer et al.[8] for different pressure conditions (5 bar and 9 bar) is shown in Figure 7. It can be seen that the calculated values for particle sizes obeying the Rosin-Rammler distribution are closer to the experimental values than those derived for monodisperse particle sizes at different mass loadings, and the calculated values all fall within the error limits. The mean exit velocities at monodisperse particle sizes were significantly higher for both inlet pressures of 5 bar and 9 bar, and the agreement between the data for polydisperse particles and the measured results was clearly superior. Here, based on the work of Meyer et al., the particle size for the monodisperse condition was set to 30 μm, which is clearly lower than the actual average particle size of Stellite-21 particles, which accounts for the overestimation of the exit velocity. From the point of view of the error, the average relative errors are all greater than 5% in the monodisperse case, while the relative errors are about 3% for polydisperse particles at 9 bar operation, and less than 3% at 5 bar operation, which proves the validity of the gas-solid two-phase model and numerical method in this paper.

4. Results and Analysis

4.1. Effect of length ratio rL

In order to study the effect of the length ratio (the ratio of the length ld of the expanding section to the length lc of the converging section) rL, the flow field was simulated for five sets of length ratios with different rL under the condition of area ratio rA=4.
In choosing the scope of the parametric study, the coordinate system used in this paper is a two-dimensional dimensionless coordinate system based on the geometrical model used. The origin of this coordinate system is set at the outlet of the nozzle with the following expressions: X=(x–ls–lc–ld)/de and Y=y/de. In this paper, two cross-sections corresponding to X = 10 (denoted as ζ10) and X = 20 (denoted as ζ20) for the jet initiation and main body segments, respectively, are selected for parametric studies. The jet main section is generally the working range of the fire extinguisher, and in combination with the jet initiation section it provides a more complete picture of the development of the jet.
The analysis reveals that vp,a10 and vp,a20 monotonically increase and Φvp10,Φvp20,Ψp10 and Ψp20 monotonically decrease with increasing rL. Specifically, when rL was increased from 1.5 to 3.5, the performance indexes of the jet were 373.71 to 497.01 m/s for vp,a10, 223.77 to 331.16 m/s for vp,a20, 0.0218 to 0.0037 for Φvp10, 0.0278 to 0.0138 for Φvp20, 0.1191 to 0.0402 for Ψp10, and Ψp20 was 0.2295 to 0.0858. It can be seen that the relative variation of the parameters with rL is very significant, which, from a practical application point of view, implies that it is necessary to choose the nozzle length ratio appropriately in order to balance the fire range and the extinguishing efficiency. Figure 8a–c show the variation of particle mean velocity vp,a, velocity inhomogeneity Φvp and dispersion Ψp with length ratio rL.
These variations arise mainly from the complex changes generated by the gas flow field that follows the variation of the length ratio. Figure 9a–e show a cloud of gas Mach number contours for different length ratios rL. When rL increases, the Mach reflection structure produces a significant change, with the intensity of both the incident oblique shock wave and the central Mach disk decreasing. The intensity of the shock wave of the Mach disk is closer to the positive shock wave in the case of rL=1.5, and the position of the Mach disk is in front of the injector. The center region of the core region of the jet is gradually occupied by a subsonic region, whose radial size increases significantly while its axial size decreases. As X increases, the expansion and oblique shock wave (or compression) waves continue to weaken, and the Ma distribution within the jet sound line at each cross-section becomes more uniform. We analyze the Ma change of the gas flow along the axis for different length ratios rL (Figure 10). It can be found that the difference in Ma variation upstream of the Mach disk is significant, indicating that the upstream expansion of the gas is affected by the increase in the length ratio rL. The increase in rL leads to a decrease in the pre-shock peak and an increase in the post-shock trough of Ma upstream and downstream of the Mach disk, indicating a simultaneous slight decrease in the localized shock wave strength of the Mach disk and the incident oblique shock wave. In addition, each curve of Ma shows asynchronous oscillations in the subsequent part, which explains the fact that the increase of rL affects the axial position of the expansion and oblique shock wave (or compression) waves, and to some extent also their intensity.
Changes in the structure of the Mach disk directly affect the velocity of the particles in it, with particles in different regions obtaining different accelerations. The smaller the particle diameter, the better it follows the gas flow field, and the slightly greater the acceleration. Figure 11a–d show the trajectories of the minimum and maximum mean diameter particles injected from the most upstream and downstream locations of the injector inlet at different length ratios rL. It can be seen that the particle trajectories corresponding to the rL=1.5 case occupy a larger radial position soon after injection. This is due to the fact that, the radial inward velocity component is reduced more significantly than the axial velocity component. None of the smaller mean diameter particles crossed the centerline. As rL increase, particles with larger average diameters or particles ejected from relatively upstream locations of the injector inlet may cross the centerline at more downstream locations, with the one exception being that the particle trajectories corresponding to the rL=1.5 case do not cross the centerline; Particles with smaller average diameters or particles injected from relatively downstream locations are less likely to pass the centerline, and these particles have lower velocities the farther they are from the centerline in their trajectories; On the contrary, a trajectory closer to the centerline is obtained for particles with a larger average diameter or particles ejected from a position relatively upstream of the injector inlet, with similar or even larger velocities.
As rL increases, the confluence moves downstream along the centerline, and the maximum particle velocity, the radial extent of the diameter distribution field, and the particle velocity difference at a given cross-section (e.g., X=10 or 20) decrease. In addition, the largest mean diameter particles move from larger radial locations toward the boundary layer region of the gas jet near the centerline, where gas and particle velocities are significantly lower. Larger and more uniform gas and particle velocities are present near the region close to the centerline(Figure 12). In terms of the behavior of these maximum mean diameter particles, this clearly favors a simultaneous increase in vp,a and a decrease in Φvp and Ψp. In practice, three different scenarios that may have conflicting effects on jet performance metrics when rL is increased must be considered. First, the increase in rL results in a smaller radial position and larger average velocity for all larger particles that can cross the centerline, but the mass fraction of these larger particles decreases; Second, smaller particles that would not otherwise be able to cross the centerline occupy a larger radial position and reach a smaller average velocity, and although it may be randomly affected by uncertainty in the particle trajectories, the mass fraction of these smaller particles should be nearly constant; Finally, some medium-sized particles can cross the centerline before, but not after, and the mass fraction of these particles increases. Thus, vp,a increases monotonically with rL, while Φvp and Ψp decrease monotonically with rL.
Therefore, the performance of nozzle jets with different length ratios has significant differences, and it is necessary to consider choosing different rL for different types of flames. When rL=3.5, the average velocity of particles vp,a reaches the maximum value of 331.16 m/s, and the dispersion Ψp is the minimum value of 0.0858, which gives the nozzle structure a stronger ability to penetrate the target of combustibles, and it is more suitable for penetrating flames; When vp,a is close to 287.05 m/s and Ψp is greater than 0.1487, rL=2.0 is chosen to be more effective for spread flames; At rL=1.5, Ψp reaches a maximum value of 0.2295, and at the same time, the particle velocity inhomogeneity Φvp is 0.0278, at which time this nozzle structure is more effective for dispersive flames.
In addition, we can consider the effect of nozzle geometry features on the working performance of the jet from the perspective of particle mean acceleration pairs. We selected a narrow band region from inside the nozzle directly downstream of the particle injector as well as a narrow band region at the nozzle exit location, denoted as regions X1 and X2, and analyzed a portion of representative particles within these two regions.
In terms of particle acceleration, for the X1 region, the streamwise acceleration increases and then decreases as the length ratio rL increases, peaking at rL=2, while the radial acceleration decreases monotonically. This indicates that the relative velocity along the flow direction tends to increase and then decrease as the length ratio increases, while the relative velocity in the radial direction decreases monotonically. The situation is different at the nozzle exit, where the particle flows are all characterized by first increasing, then decreasing and finally increasing again, and peak at rL=2.5 to rL=2, respectively. This indicates that as the length ratio rL increases, the flow and radial relative velocities between phases first increase, then decrease and then increase again and there is a critical point where they peak respectively.
We can look at all the particles in the entire narrow-band region as a whole, so that the position of this imaginary particle is at the center of mass of this system of masses consisting of all the particles in the region(Figure 13). In the X1 region, where rL is smallest, the virtual particle is in the low velocity region near the high velocity region, when the regional gas velocity is low but there is a large velocity gradient in the radial direction, making the initial difference between ap,ax and ap,ay large, with ap,ax smaller and ap,ay larger. As the flow develops, the virtual particles move slightly toward the center out of the region of large velocity gradient at the same time that the gas velocity at their location increases, so that ap,ax increases while ap,ay begins to decrease. As the flow develops further, the region in which the virtual particles were originally located generates a smaller new high-speed region. But then the virtual particles once again move away from the centerline to the outer low velocity region and hover in this region, with ap,ax and ap,ay leveling off as rL increases.
In the case of length ratio rL=2, the X2 region is exactly at the nozzle exit, but this varies for different length ratios, for minimum RL, the X2 region is located in the outer jet of the nozzle, whereas as rL grows the nozzle grows and the X2 regions are all inside the nozzle. At the same time the growth of rL leads to a nonlinear development of the flow field inside the nozzle in the corresponding region, which results in large fluctuations of ap,ax and ap,ay. Specifically, when rL is smallest, the dummy particles are in the region away from the centerline of the nozzle, where the gas velocity is small and uniform, and this is when both ap,ax and ap,ay are small. As rL increases, the virtual particles migrate substantially near the centerline and approach the relatively low velocity region near the centerline, but the radial velocity gradient in this region is large, so ap,ax grows slightly while ap,ay reaches an extreme value rL increases further, the imaginary particles move away from the centerline in a small way and stay, when the flow field changes causing this region to first enter the high velocity region and approach the low velocity region, which is uniform in the high velocity region and steep in the low velocity region. This explains the diametrically opposed changes in the trends of ap,ax and ap,ay in the final stage.

4.2 Effect of area ratio rA

The simulation of flow field at different area ratios (ratio of main nozzle outlet area to throat area) rA was carried out to investigate the effect of area ratio rA under the length ratio rL=2 condition.
Calculations show that vp,a10 and vp,a20 decrease monotonically with increasing rA, and Φvp10, Φvp20, Ψp10, and Ψp20 first increase and then decrease(Figure 14a–c). Specifically, when rA was increased from 2 to 10, the performance indexes of the jet were 521.65 to 315.23 m/s for vp,a10, 433.30 to 140.68 m/s for vp,a20, 0.0027 to 0.0158 for Φvp10, 0.0076 to 0.0215 for Φvp20, 0.0408 to 0.0856 for Ψp10 and Ψp20 was 0.0624 to 0.0871, in which Φvp10, Φvp20, Ψp10 and Ψp20 all peaked at rA=6, with 0.0178, 0.0236, 0.0977 and 0.1633, respectively. It can be seen that the relative change of each parameter with rA is very obvious. And from the practical application point of view, it is necessary to choose the nozzle area ratio appropriately to balance the fire extinguishing efficiency.
Similarly, the development of the flow can be visualized from the contour cloud plots of the Mach number of the airflow at different area ratios rA (Figure 15a–e). When rA increases, a significant change in the structure of the Mach reflection can be found. The dimensions of both the incident oblique excitation and the central Mach disk increase, and the intensity of the excitation in the Mach disk is closer to that of the positive shock wave. In addition, the position of the Mach disk changes significantly, gradually moving upstream of the nozzle. The center region of the core region of the jet is gradually occupied by the subsonic region, whose radial size increases significantly while the axial size decreases. In the region along the centerline, the increase in rA leads to an upstream migration of the Ma peak located upstream of the Mach disk, with a corresponding decrease in the peak, coinciding with an increase in the Ma valley located downstream of the Mach disk. In addition, the position and intensity of the expansion and oblique shock wave (or compression) waves changed significantly (Figure 16). For example, one peak of Ma reaches a very high value at rA=2. However, in the main body section of the jet, the final difference between all Ma values at different rA is negligible in the final difference.
As can be seen from Figure 17a,c, all trajectories of particles with the smallest diameter cannot pass through the center line; It can also be seen in Figure 17b,d that as rA increases, the trajectories of particles with larger mean diameters are likely to cross the centerline, and for particles that are able to cross the centerline, their subsequent trajectories have intersections further upstream on the centerline and occupy a position farther away from the centerline. The exception to this, as can be seen in Figure 17b, is that the intersection of the particle trajectories corresponding to rA=2 is at a more upstream location than the particle trajectories corresponding to rA=6. In addition, the uncertainty in the particle trajectories increases as rA increases.
It can be observed that the particle velocity decreases and there is no confluence in the particle distribution field for the rA=8 and 10 cases (Figure 18). In the case of rA=2, the particles with larger average diameters move radially inward first and remain axially moving even after crossing the centerline; For rA=4, particles with larger average diameters first move radially inward, and after they cross the centerline, they move outward; For rA=6, the motion trend of particles with larger average diameter possesses the above 2 cases. At the same time, the particle distribution field corresponding to rA=6 is in the most dispersed spatial distribution. Thus, both Ψp10 and Ψp20 first increase and then decrease with rA. In addition, due to the overall decrease in gas velocity, the decrease in particle velocity naturally leads to a monotonic decrease in vp,a10 and vp,a20 with rA. The two particle velocity distributions corresponding to rA=8 and 10 are very homogeneous with only small variations in the cross sections at X=10de and 20de, and the particle diameter distributions of the former have a clearer hierarchical structure than those of the latter. The particle velocity distribution corresponding to rA=6, on the other hand, shows a very clear asymptotic change, i.e., the span of particle velocity becomes smaller with further increase in rA. Therefore, when rA increases, Φvp10 and Φvp20 first increase and then decrease.
Similarly, based on the above analysis, we can list a selection scenario for the area ratio rA for different flame types. At rA=2, the average particle velocity vp,a reaches a maximum value of 433.30 m/s, and the dispersion Ψp is a minimum value of 0.0624, which gives the nozzle structure a stronger ability to penetrate the target of combustibles and is more suitable for penetrating flames; When vp,a is close to 200 m/s and Ψp is greater than 0.0976, choosing rA=8 is more effective for spreading flames; At rA=6, Ψp reaches a maximum value of 0.1633, while the particle velocity inhomogeneity Φvp is 0.236, which is suitable for dispersive flames.
As with the analysis above, we similarly incorporate observations of the flow field development in conjunction with the change in acceleration and hence the development of the flow field (Figure 19). As the area ratio increases, for the X1 region, neither the streamwise accelerations nor the radial accelerations of the particles show a monotonicity, but instead show a complex variation by reaching extreme values at rA=4 and rA=6, respectively. Among them, for the flow acceleration, it is first increasing and then decreasing with the increase of area ratio, while the radial acceleration shows some hysteresis, first decreasing and then increasing and finally decreasing with the increase of area ratio. The X2 region is relatively simple, except that the difference between ap,ax and ap,ay is large when rA is smallest, and as rA grows, ap,ax and ap,ay decrease and then increase almost synchronously. This reflects the situation that the relative velocities of the gas and solid phases grow first and then decrease.
Similarly, we can define a dummy particle to compare the radial position and its corresponding state at different rA. Taking the X1 region as an example, first of all, for the minimum rA, the inside of the nozzle is a more homogeneous low-velocity flow field, and the dummy particles are at a position relatively close to the center of the nozzle. As rA increases, the high-speed zone is developed inside the nozzle, at which time the radial position of the dummy particles also gradually moves outward, and a larger acceleration is obtained. However, when rA increases further, the boundary between the high-speed zone and the low-speed zone inside the nozzle becomes clearer gradually. But at this time, the dummy particles continue to move outward, and gradually pass through the high-speed zone, and then enter into the peripheral low-speed zone again, far away from the centerline, resulting in the velocity dispersion of the particles also increases with the increase in rA and the increases. Thus ap,ax shows a tendency to increase and then decrease.
In contrast, for the case of ap,ay the variation is mainly due to the fact that the flow develops further as the virtual particles move away from the centerline, and the region they pass through produces large fluctuations in the velocity gradient in the radial direction. When rA=6, the internal flow is significantly stratified, which leads to a peak in ap,ay. As rA increases, the flow develops further, the high-speed region expands, the virtual particles move away from the centerline, and the acceleration gradually falls back.
The X2 region is at the exit downstream of the nozzle, and for the smallest rA dummy particles are located almost right near the centerline, and as rA increases, the dummy particles move toward the center region in which the velocity is relatively low. At this point, although the virtual particles are closer to the centerline, the radial velocity gradient increases greatly as the flow develops, which explains the fact that ap,ax decreases to some extent along with it while at the same time ap,ay jumps up substantially. And when the flow develops further, the virtual particles suddenly leap out of the high velocity region and reach the peripheral low velocity gas region away from the centerline, resulting in a further decrease in ap,ax and a concomitant decrease in ap,ay. Only in the final phase does it move back slightly, while the exit high velocity region continues to expand and the gas velocity in this region increases slightly, which results in an increase in ap,ax and ap,ay in the final phase.

5. Conclusion

In this paper, a mathematical model of bidirectional coupling between gas-particle phases is constructed for a two-dimensional axisymmetric supersonic nozzle gas jet containing polydisperse extinguishing agent particles injected from a bypass nozzle. Numerical simulations of gas-solid two-phase flow in a supersonic nozzle were carried out using a modified drag model that simultaneously takes into account gas inertia, compressibility and rarefaction effects. We investigated the effects of the main geometric characteristics of the main nozzle (length ratio rL, area ratio rA) on the defined performance indexes that better reflect the fire extinguishing efficacy of the jet, including the particle flow average velocity vp,a, velocity inhomogeneity Φvp, dispersion Ψp, and particle average acceleration ap.a The main conclusions are summarized as follows.
(1)The prediction accuracy of the Rosin-Rammler polydisperse model based on the particle system for supersonic nozzle gas-solid two-phase flow is better than 3%, while the prediction accuracy of the numerical method based on the monodisperse is about 6%, and the experimental cases under different operating pressures and particle loading ratios fully validate the current modeling framework and numerical method.
(2)Under polydisperse particle conditions, an increase in the area ratio or a decrease in the length ratio usually results in an increase in vp,a and a decrease in the velocities Φvp and Ψp. However, the monotonicity of these parameter variations may not hold under specific conditions, for example, the monotonicity of each performance index of the jet may not be satisfied at larger area ratios.
(3)Under polydisperse particle conditions, length ratios rL≥3.5 and area ratios rA≤2 were chosen for penetrating flames; area ratios rA≈8 and length rL≈2.0 were chosen for spreading flames; and length ratios rL≤1.5 and intermediate area ratios rA≈6 were chosen for dispersing flames.
(4)The changes in the flow field brought about by changes in the area ratio and length ratio are complex. The average particle acceleration does not vary monotonically with the area ratio or length ratio in the selected region. However, the ap,a curve peaks under certain conditions, which may reflect the fact that the corresponding region is a relatively more favorable acceleration domain for particles.

Author Contributions

Conceptualization, L.Z. and H.J.; methodology, L.Z.; software, validation, writing—original draft preparation, Y.F.; investigation, data curation, Y.F. and S.W.; writing—review and editing, L.Z.; funding acquisition, L.Z. and H.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the financial support from the Natural Science Foundation of Zhejiang Province [grant no. LY17E060006.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhang, L.; Sun, M.; Guan, H.; Wu, S.; Jia, H.; Jin, H. Modeling and simulation of supersonic nozzle gas jet laden with polydisperse fire suppressant particles injected from a bypass injector. Chemical Engineering Science 2023, 280. [Google Scholar] [CrossRef]
  2. Chellappan, S.; Ramaiyan, G. Experimental study of design parameters of a gas-solid injector feeder. Powder technology 1986, 48, 141–144. [Google Scholar] [CrossRef]
  3. Kmieć, A.; Leschonski, K. Numerical calculation methods for solids injectors. Powder technology 1998, 95, 75–78. [Google Scholar] [CrossRef]
  4. Xie, Y.; Raghavan, V.; Rangwala, A.S. Naturally entraining solid particle injector. Powder Technology 2011, 213, 199–201. [Google Scholar] [CrossRef]
  5. Kim, M.I.; Sin Kim, O.; Lee, D.H.; Done Kim, S. Numerical and experimental investigations of gas–liquid dispersion in an ejector. Chemical Engineering Science 2007, 62, 7133–7139. [Google Scholar] [CrossRef]
  6. Huang, Y.; Jiang, P.; Zhu, Y. Experimental and modeling studies of thermally-driven subcritical and transcritical ejector refrigeration systems. Energy Conversion and Management 2020, 224. [Google Scholar] [CrossRef]
  7. Lau, T.C.W.; Nathan, G.J. The effect of Stokes number on particle velocity and concentration distributions in a well-characterised, turbulent, co-flowing two-phase jet. Journal of Fluid Mechanics 2016, 809, 72–110. [Google Scholar] [CrossRef]
  8. Meyer, M.; Caruso, F.; Lupoi, R. Particle velocity and dispersion of high Stokes number particles by PTV measurements inside a transparent supersonic Cold Spray nozzle. International Journal of Multiphase Flow 2018, 106, 296–310. [Google Scholar] [CrossRef]
  9. Yang, D.; Xing, B.; Li, J.; Wang, Y.; Gao, K.; Zhou, F.; Xia, Y.; Wang, C. Experimental study on the injection performance of the gas-solid injector for large coal particles. Powder Technology 2020, 364, 879–888. [Google Scholar] [CrossRef]
  10. AbdEl-hamid, A.A.; Mahmoud, N.H.; Hamed, M.H.; Hussien, A.A. Gas-solid flow through the mixing duct and tail section of ejectors: Experimental studies. Powder Technology 2018, 328, 148–155. [Google Scholar] [CrossRef]
  11. Zhu, Y.; Cai, W.; Wen, C.; Li, Y. Numerical investigation of geometry parameters for design of high performance ejectors. Applied Thermal Engineering 2009, 29, 898–905. [Google Scholar] [CrossRef]
  12. Galanis, N.; Sorin, M. Ejector design and performance prediction. International Journal of Thermal Sciences 2016, 104, 315–329. [Google Scholar] [CrossRef]
  13. Xu, J.; Liu, X.; Pang, M. Numerical and experimental studies on transport properties of powder ejector based on double venturi effect. Vacuum 2016, 134, 92–98. [Google Scholar] [CrossRef]
  14. Zhang, L.; Yu, Q.; Liu, T.; Feng, Z.; Sun, M.; Jin, H. Coupled modeling and numerical simulation of gas flows laden with solid particles in de Laval nozzles. Shock Waves 2021, 32, 213–230. [Google Scholar] [CrossRef]
  15. Njue, J.C.W.; Salehi, F.; Lau, T.C.W.; Cleary, M.J.; Nathan, G.J.; Chen, L. Numerical and experimental analysis of poly-dispersion effects on particle-laden jets. International Journal of Heat and Fluid Flow 2021, 91. [Google Scholar] [CrossRef]
  16. Ramesh, S.; Mahajan, C.; Gerdes, S.; Gaikwad, A.; Rao, P.; Cormier, D.R.; Rivero, I.V. Numerical and experimental investigation of aerosol jet printing. Additive Manufacturing 2022, 59. [Google Scholar] [CrossRef]
  17. Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA Journal 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
  18. Sutherland, W. LII. The viscosity of gases and molecular force. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 2009, 36, 507–531. [Google Scholar] [CrossRef]
  19. Parmar, M.; Haselbacher, A.; Balachandar, S. Improved Drag Correlation for Spheres and Application to Shock-Tube Experiments. AIAA Journal 2010, 48, 1273–1276. [Google Scholar] [CrossRef]
  20. Ling, Y.; Haselbacher, A.; Balachandar, S. Importance of unsteady contributions to force and heating for particles in compressible flows. International Journal of Multiphase Flow 2011, 37, 1026–1044. [Google Scholar] [CrossRef]
  21. Ling, Y.; Haselbacher, A.; Balachandar, S. Importance of unsteady contributions to force and heating for particles in compressible flows. Part 2: Application to particle dispersal by blast waves. International Journal of Multiphase Flow 2011, 37, 1013–1025. [Google Scholar] [CrossRef]
  22. Gosman, A.D.; loannides, E. Aspects of Computer Simulation of Liquid-Fueled Combustors. Journal of Energy 1983, 7, 482–490. [Google Scholar] [CrossRef]
  23. Li, A.; Ahmadi, G. Dispersion and Deposition of Spherical Particles from Point Sources in a Turbulent Channel Flow. Aerosol Science and Technology 1992, 16, 209–226. [Google Scholar] [CrossRef]
  24. Ranz, W.E.; Marshall, W.R. Evaporation from drops, part I. Chemical Engineering Progress 1952, 48, 141–146. [Google Scholar]
  25. Henderson, C.B. Drag Coefficients of Spheres in Continuum and Rarefied Flows. AIAA Journal 1976, 14, 707–708. [Google Scholar] [CrossRef]
  26. Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles. 1978. http://refhub.elsevier.com/S0009-2509(23)00539-0/h0015.
  27. Zakhmatov, V.; Tsikanovskii, V.; Kozhemyakin, A. Throwing of fire-extinguishing powder jets from barrels. Combustion, Explosion and Shock Waves 1998, 34, 97–100. [Google Scholar] [CrossRef]
Preprints 94973 g001
Figure 1. Fires caused increasing property losses and heavy casualties(a)Number of fire treatments and property losses in China, (b)Numbers of deaths and injuries caused by fire in China
Figure 1. Fires caused increasing property losses and heavy casualties(a)Number of fire treatments and property losses in China, (b)Numbers of deaths and injuries caused by fire in China
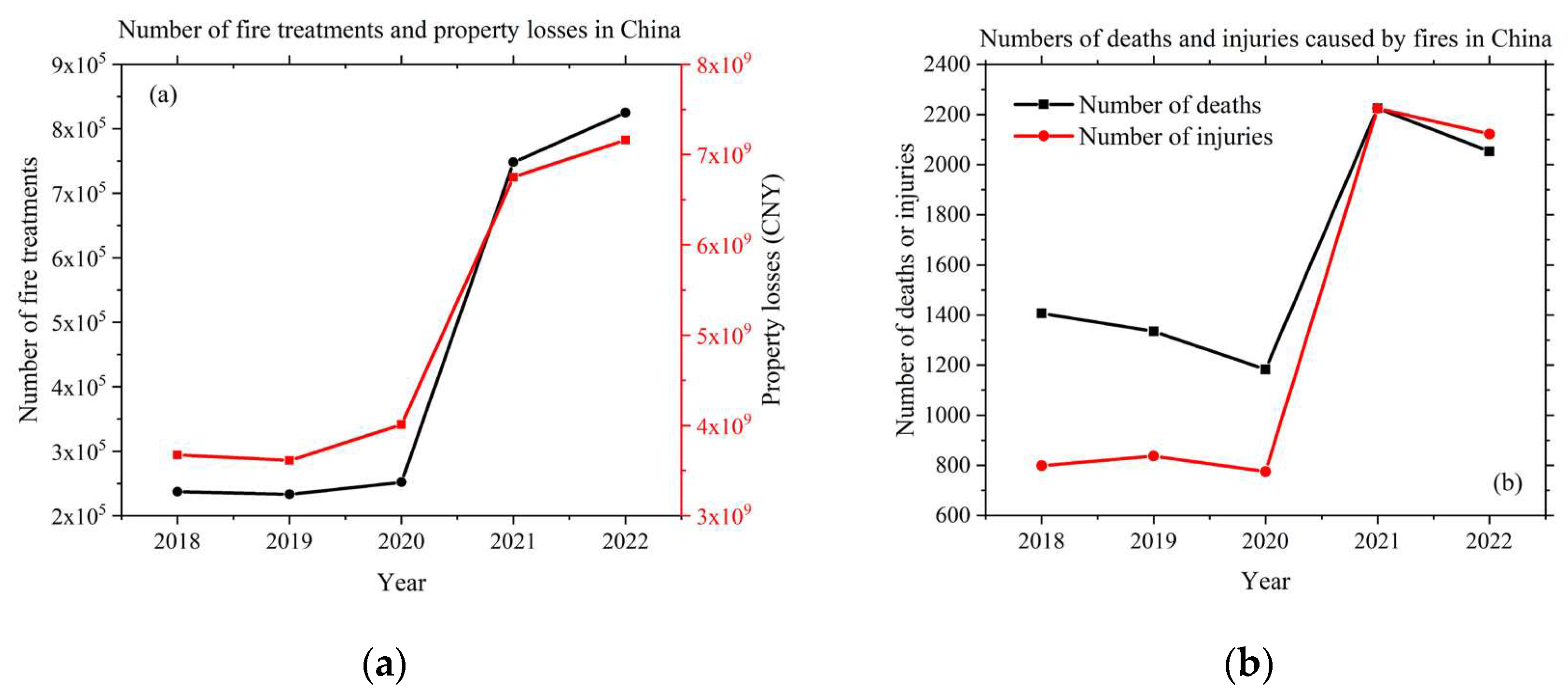
Preprints 94973 g001
Preprints 94973 g003
Figure 3. Axisymmetric 2D main nozzle boundary condition setup.
Figure 3. Axisymmetric 2D main nozzle boundary condition setup.
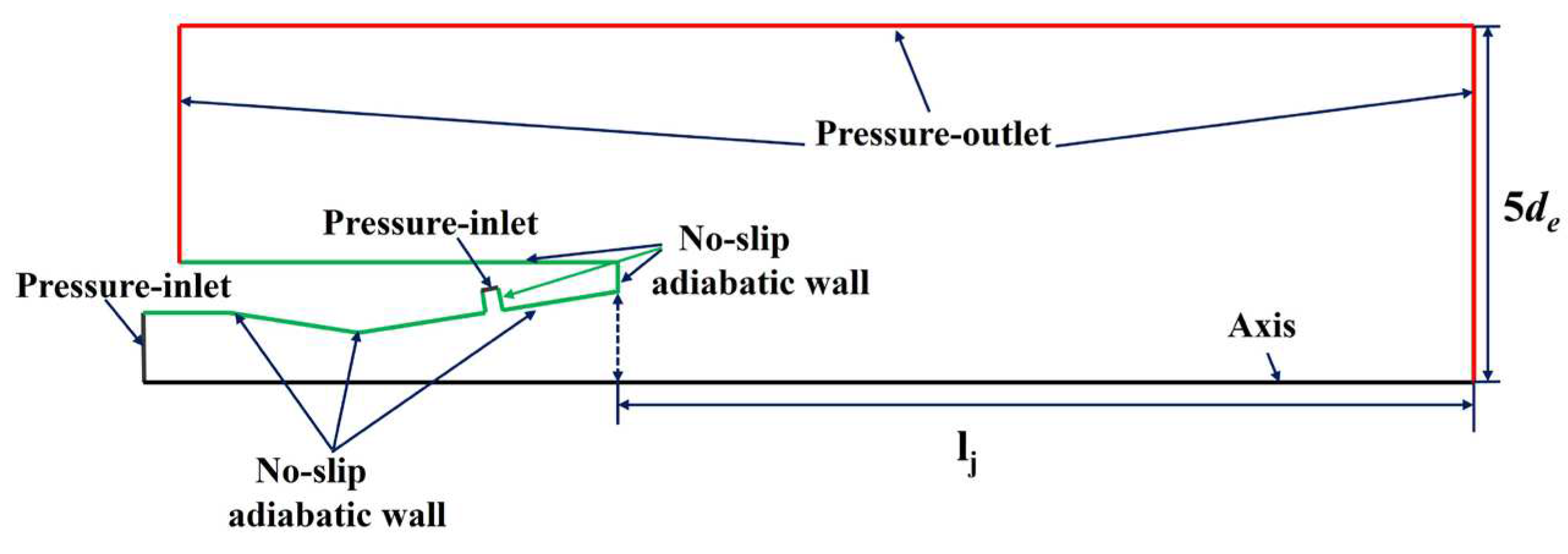
Preprints 94973 g003
Preprints 94973 g004
Figure 4. Computational domain grid.
Figure 4. Computational domain grid.
Preprints 94973 g004
Preprints 94973 g005
Figure 5. Particle number average velocity vp,a in two regions with different density grids.
Figure 5. Particle number average velocity vp,a in two regions with different density grids.
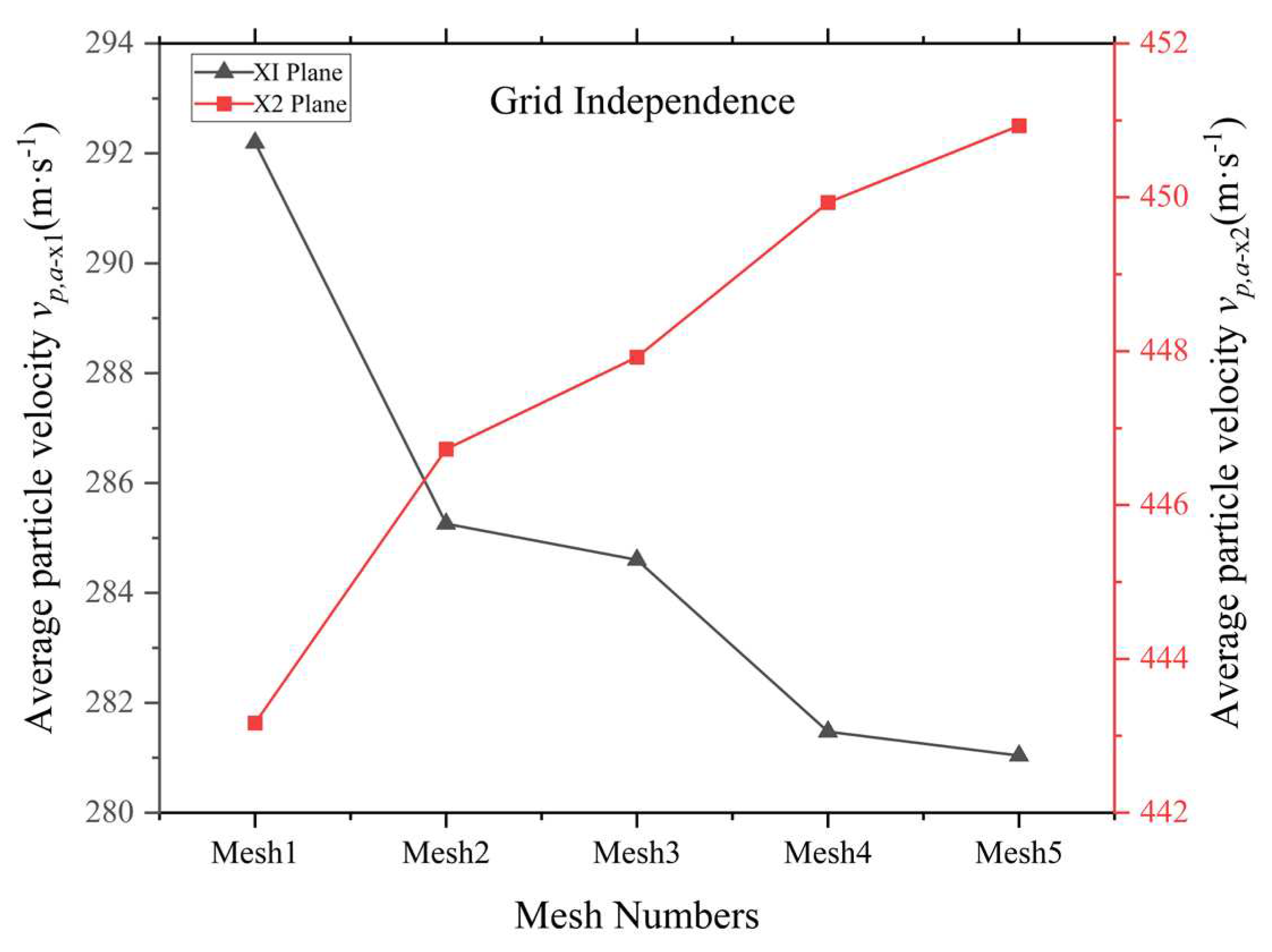
Preprints 94973 g005
Preprints 94973 g006
Figure 6. 3D Square Scaling Nozzle Geometry.
Figure 6. 3D Square Scaling Nozzle Geometry.
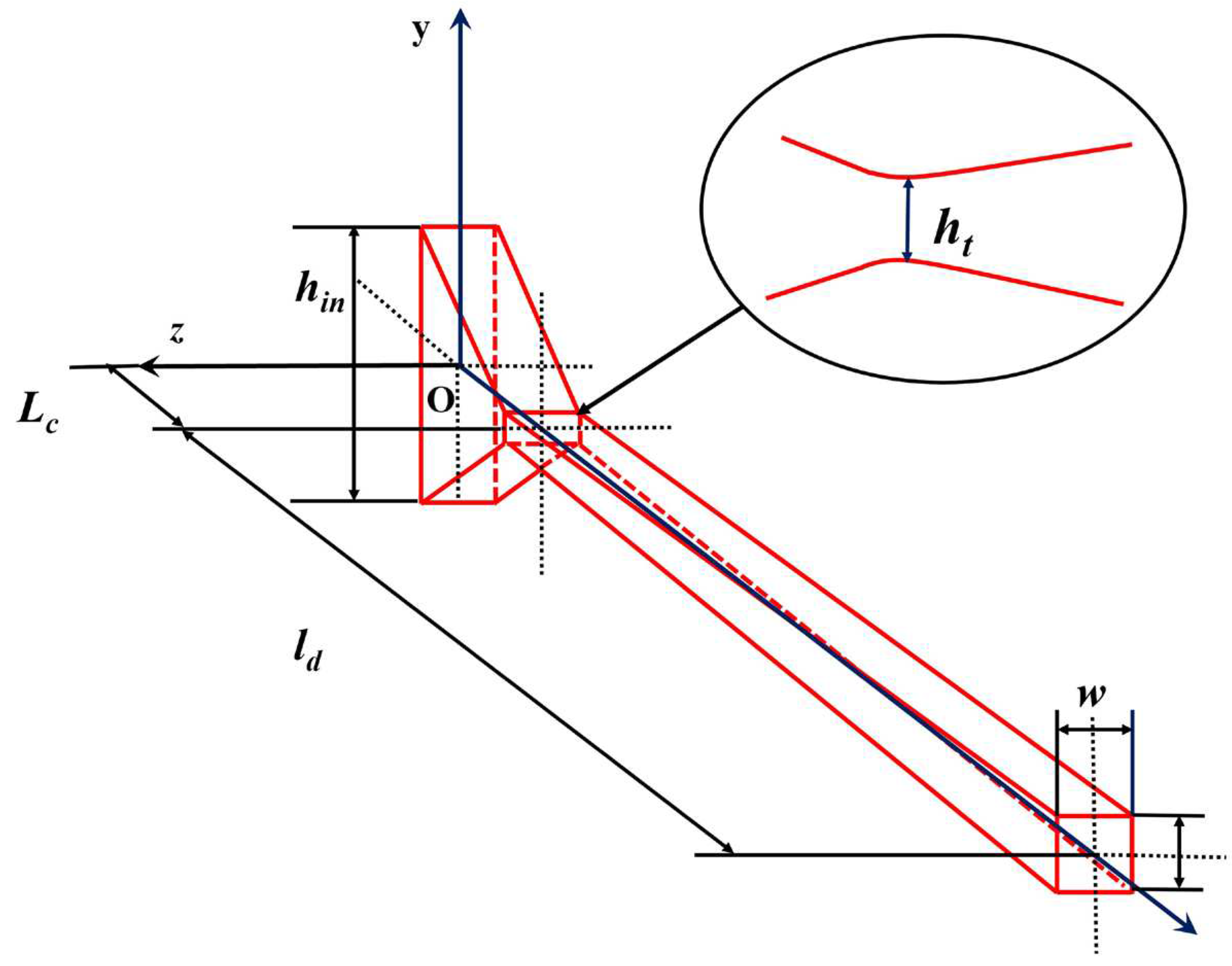
Preprints 94973 g006
Preprints 94973 g007
Figure 7. Weighted average velocity of particle number for different mass loads.
Figure 7. Weighted average velocity of particle number for different mass loads.
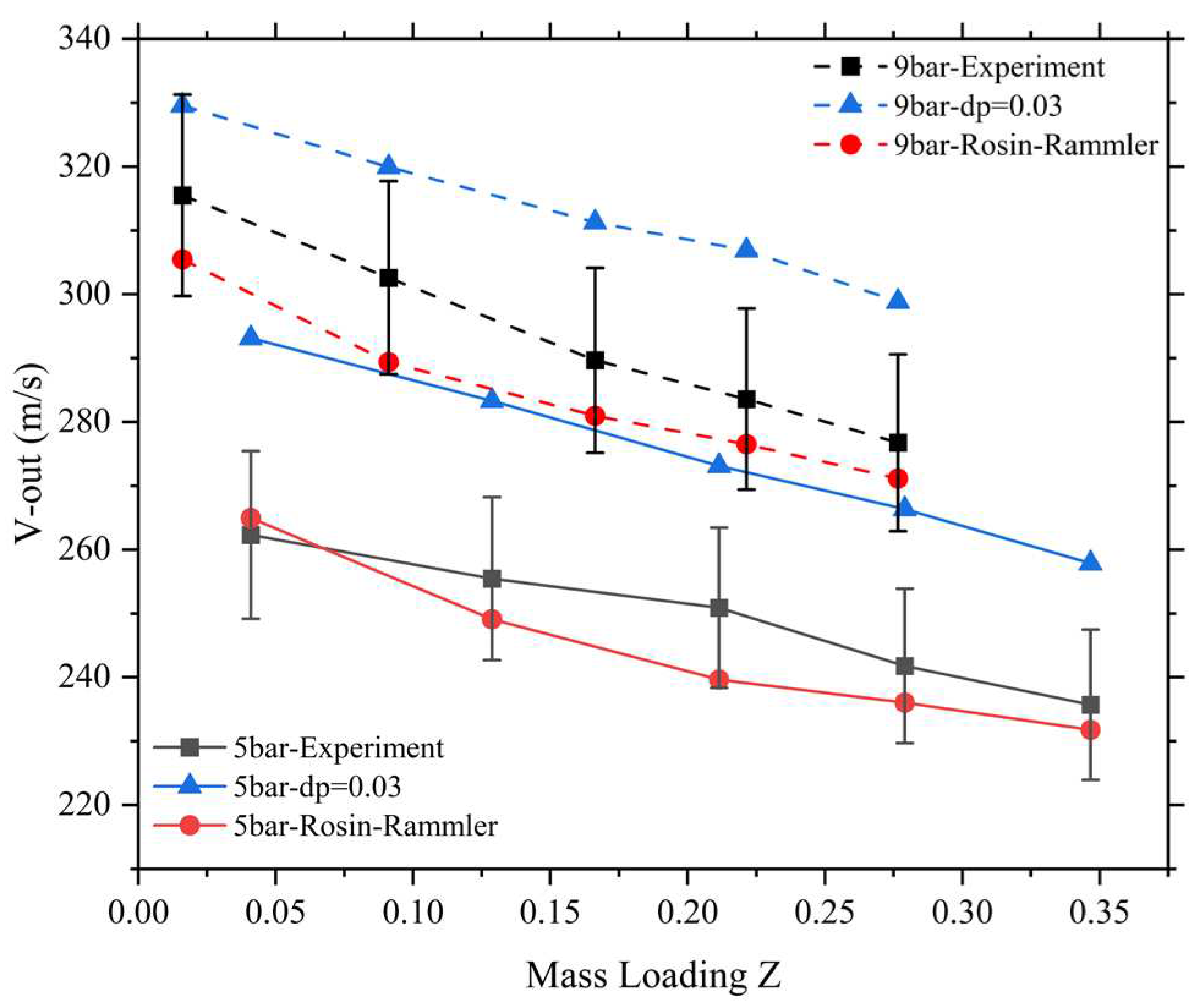
Preprints 94973 g007
Preprints 94973 g008
Figure 8. (a) Average particle velocity, (b)velocity inhomogeneity, and (c)particle dispersion for different length ratios rL
Figure 8. (a) Average particle velocity, (b)velocity inhomogeneity, and (c)particle dispersion for different length ratios rL
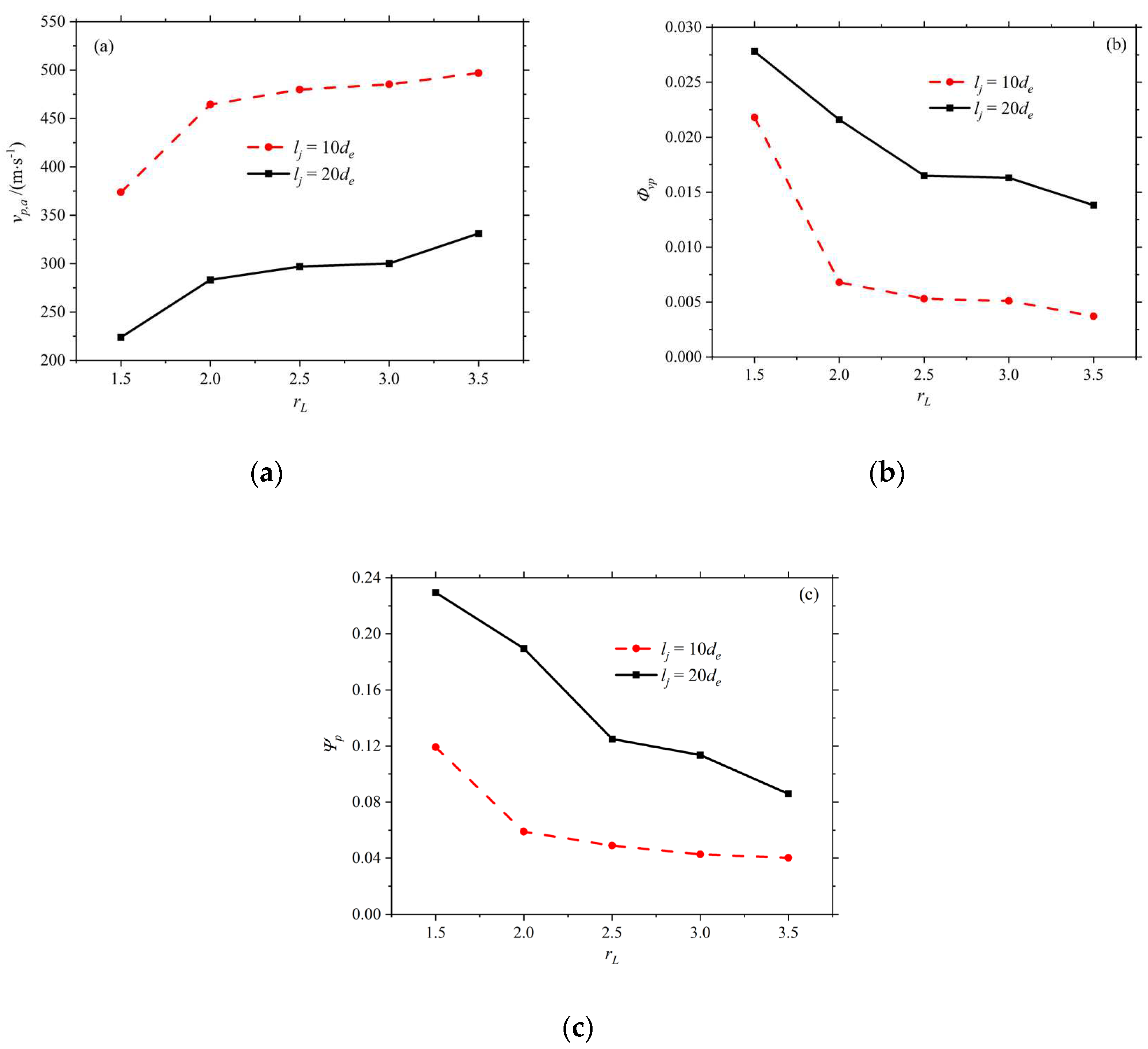
Preprints 94973 g008
Preprints 94973 g009
Figure 9. Contour clouds of airflow Mach number at different length ratios rL: (a)rL=1.5, (b)rL=2.0, (c)rL=2.5, (d)rL=3.0, (e)rL=3.5.
Figure 9. Contour clouds of airflow Mach number at different length ratios rL: (a)rL=1.5, (b)rL=2.0, (c)rL=2.5, (d)rL=3.0, (e)rL=3.5.
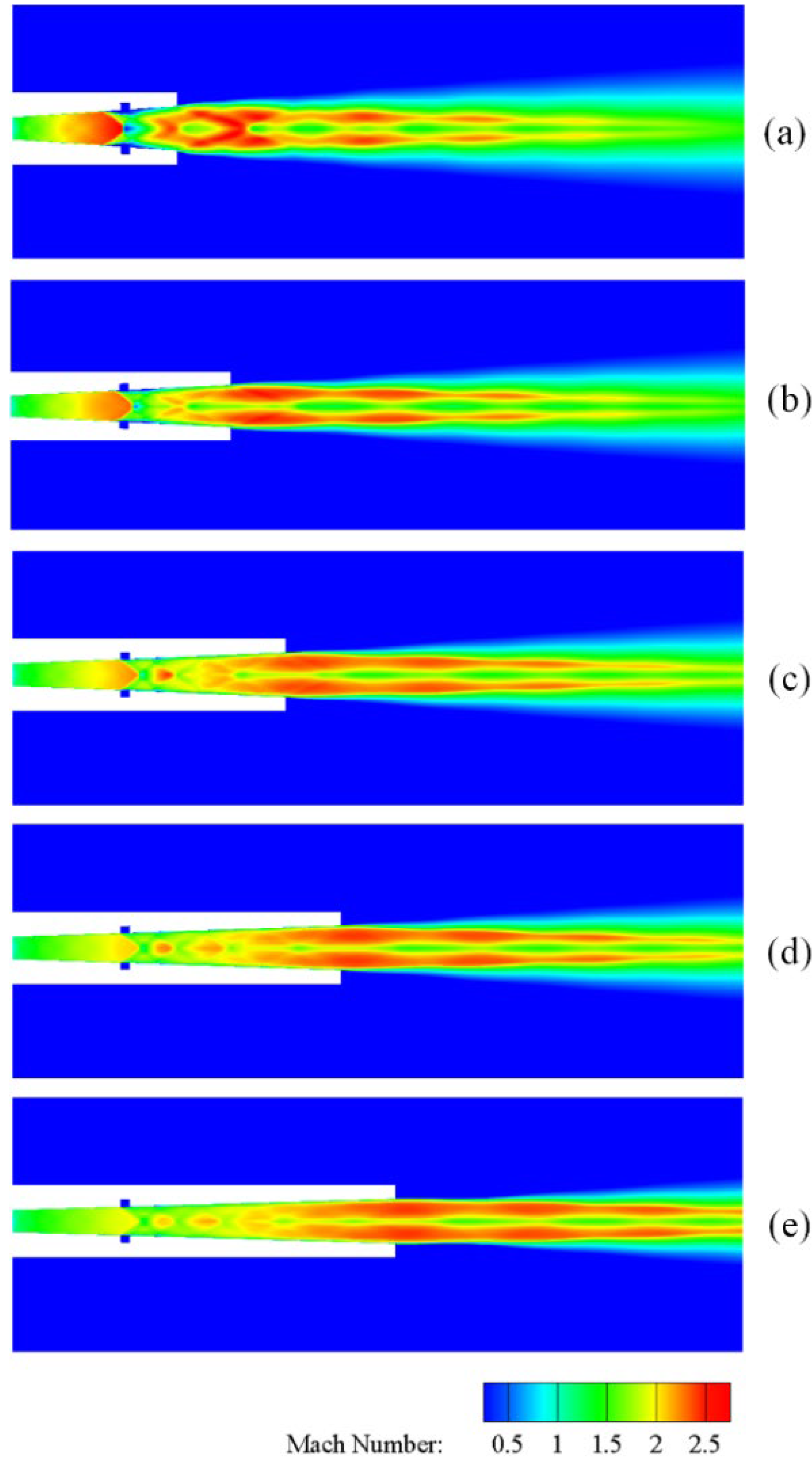
Preprints 94973 g009
Preprints 94973 g010
Figure 10. Mach number of the airflow along the axis for different length ratios rL.
Figure 10. Mach number of the airflow along the axis for different length ratios rL.
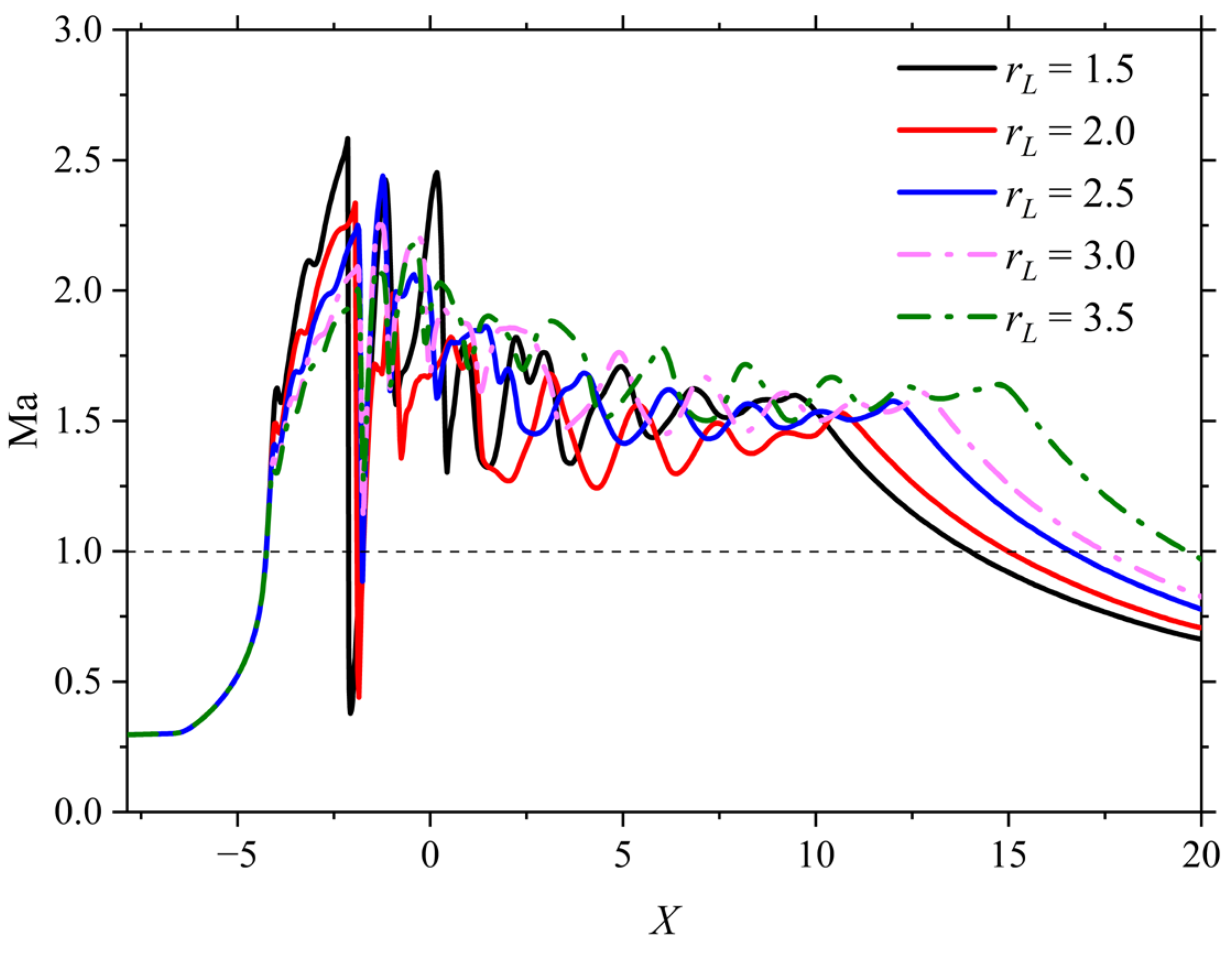
Preprints 94973 g010
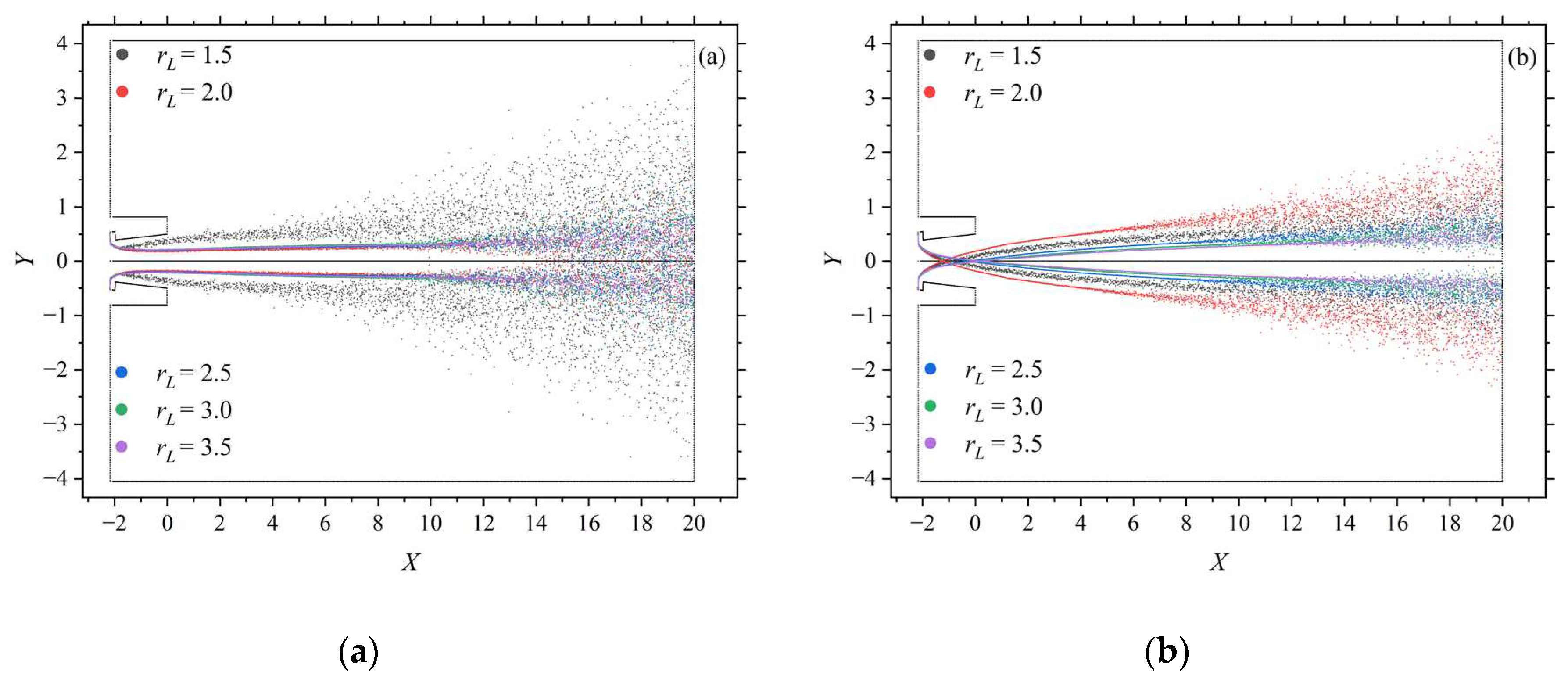
Preprints 94973 g011aPreprints 94973 g011b
Figure 11. Representative particle trajectories for different length ratios rL: (a)minimum average diameter particles sprayed at the upstream-most position of the injection port, (b)maximum average diameter particles, (c)minimum average diameter particles sprayed at the downstream-most position of the injection port, (d)maximum average diameter particles
Figure 11. Representative particle trajectories for different length ratios rL: (a)minimum average diameter particles sprayed at the upstream-most position of the injection port, (b)maximum average diameter particles, (c)minimum average diameter particles sprayed at the downstream-most position of the injection port, (d)maximum average diameter particles
Preprints 94973 g011aPreprints 94973 g011b
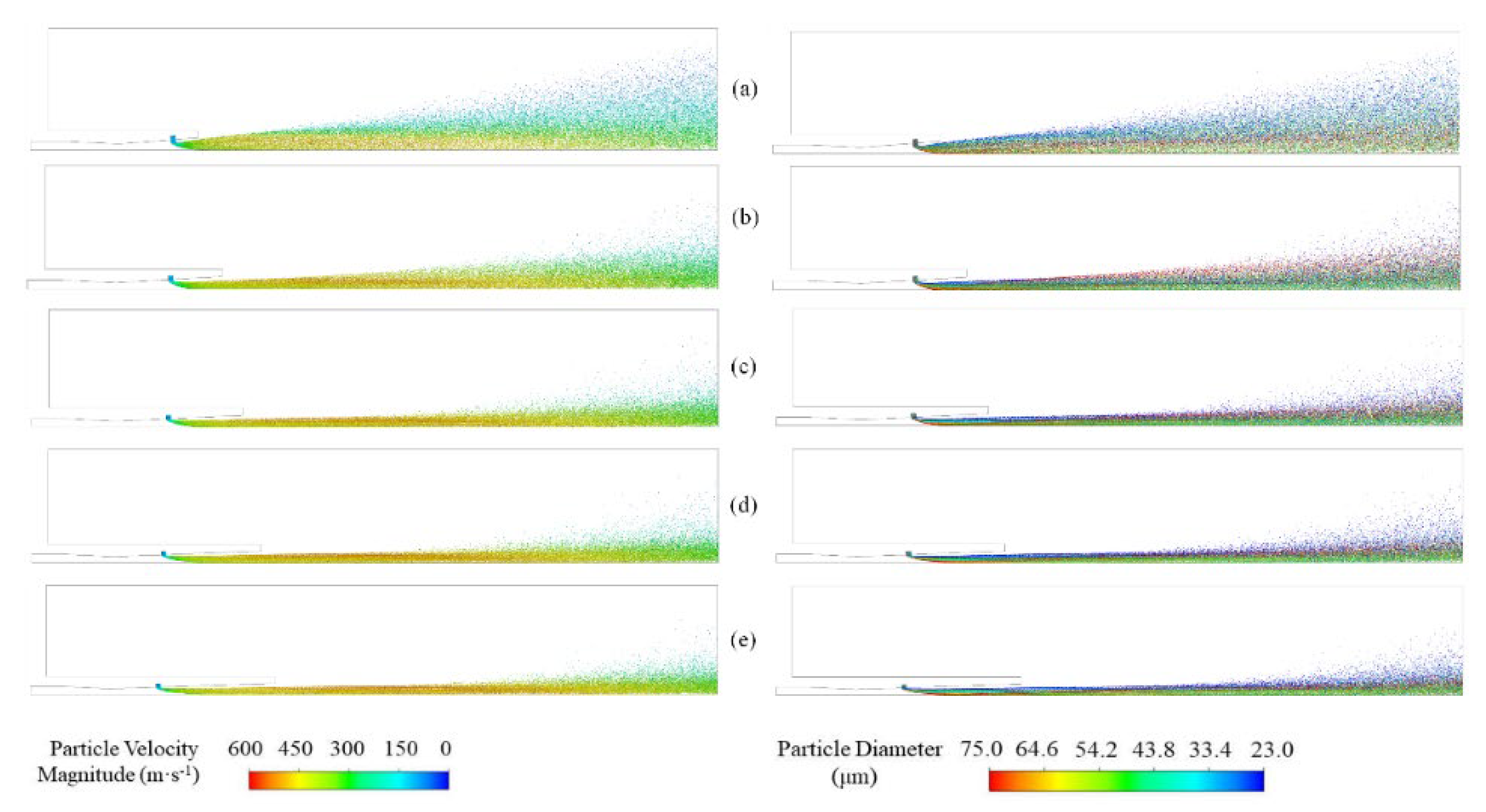
Preprints 94973 g012
Figure 12. Particle velocity magnitude and diameter distribution fields for different length ratios rL: (a)rL=1.5, (b)rL=2.0, (c)rL=2.5, (d)rL=3.0, (e)rL=3.5
Figure 12. Particle velocity magnitude and diameter distribution fields for different length ratios rL: (a)rL=1.5, (b)rL=2.0, (c)rL=2.5, (d)rL=3.0, (e)rL=3.5
Preprints 94973 g012
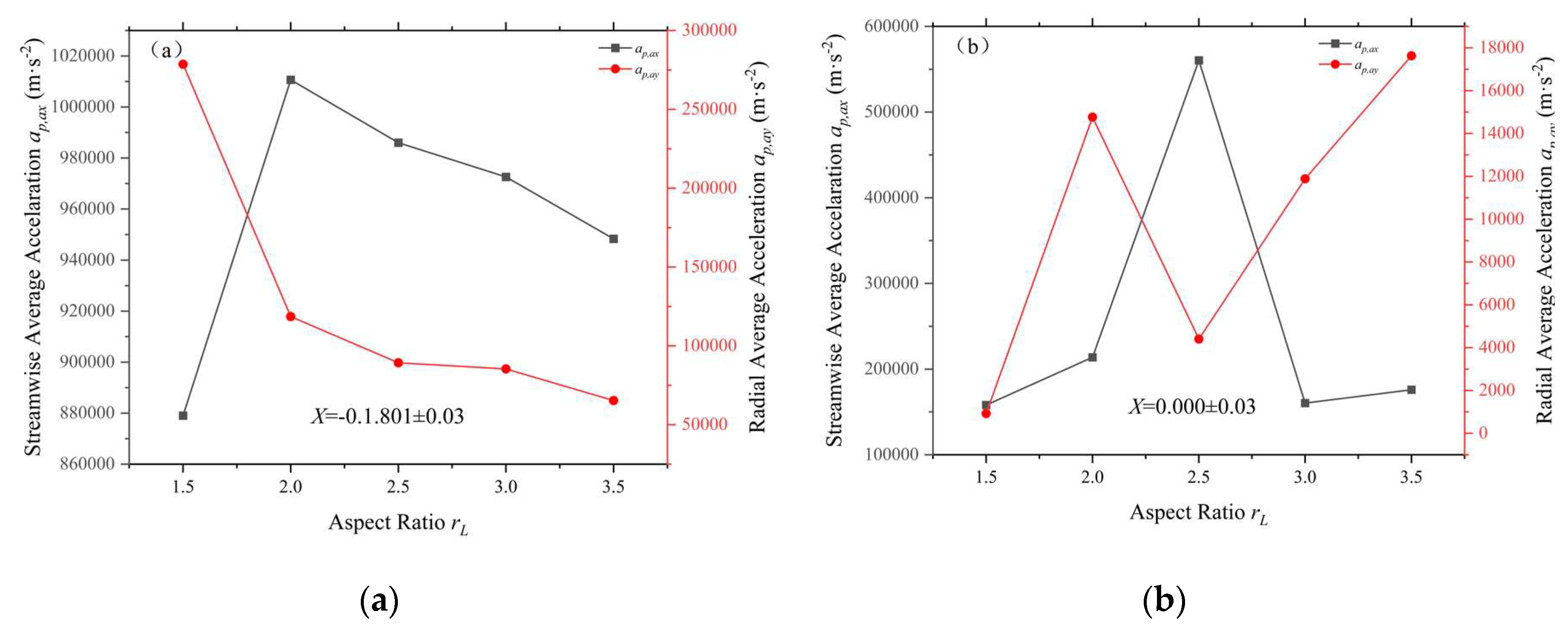
Preprints 94973 g013
Figure 13. Variation of particle flow and radial mean acceleration with length ratio (a)X=-0.1801 (b)X=0.000
Figure 13. Variation of particle flow and radial mean acceleration with length ratio (a)X=-0.1801 (b)X=0.000
Preprints 94973 g013
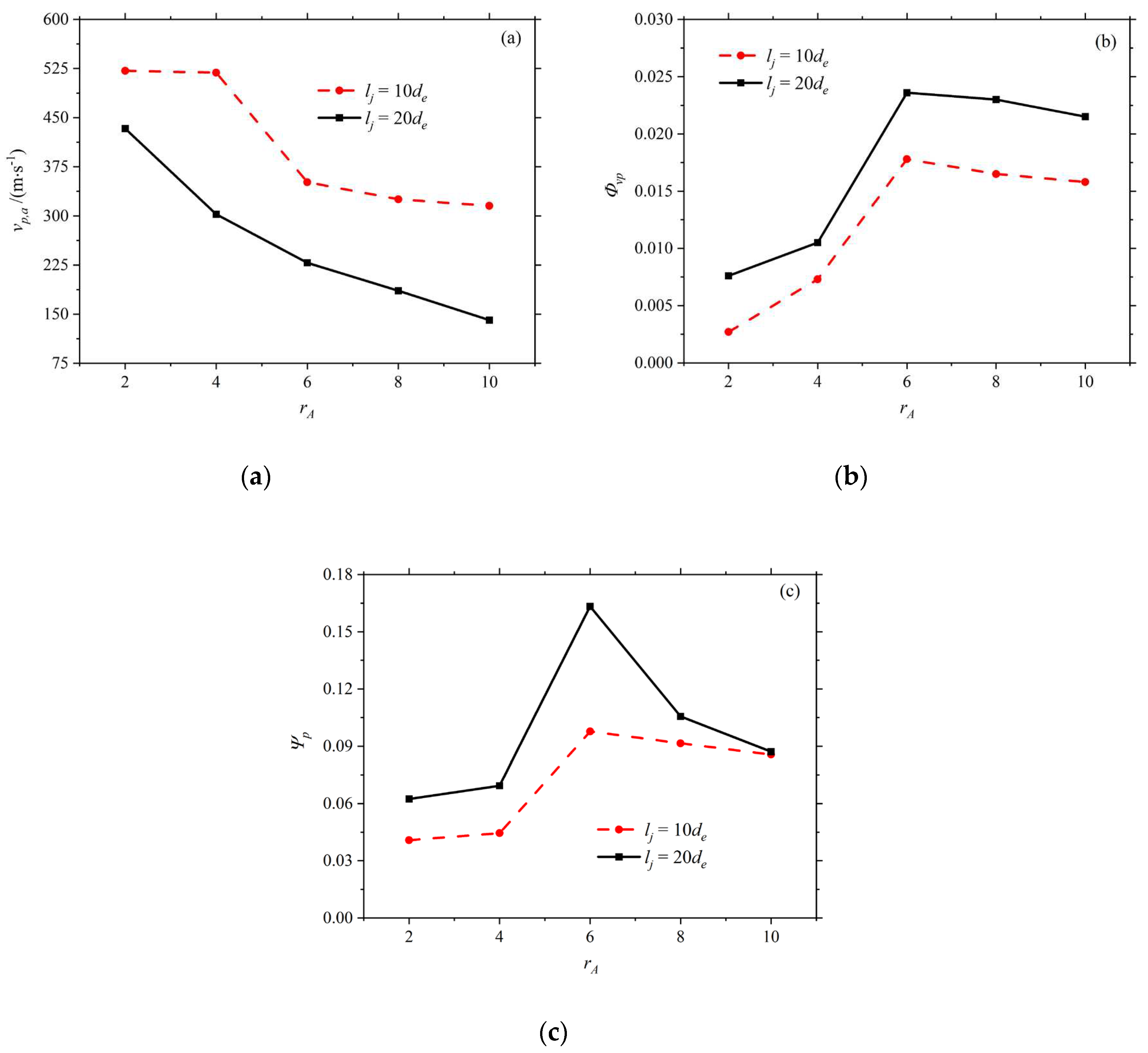
Preprints 94973 g014
Figure 14. (a) Average particle velocity, (b)velocity inhomogeneity, and (c)particle dispersion for different area ratios rA
Figure 14. (a) Average particle velocity, (b)velocity inhomogeneity, and (c)particle dispersion for different area ratios rA
Preprints 94973 g014
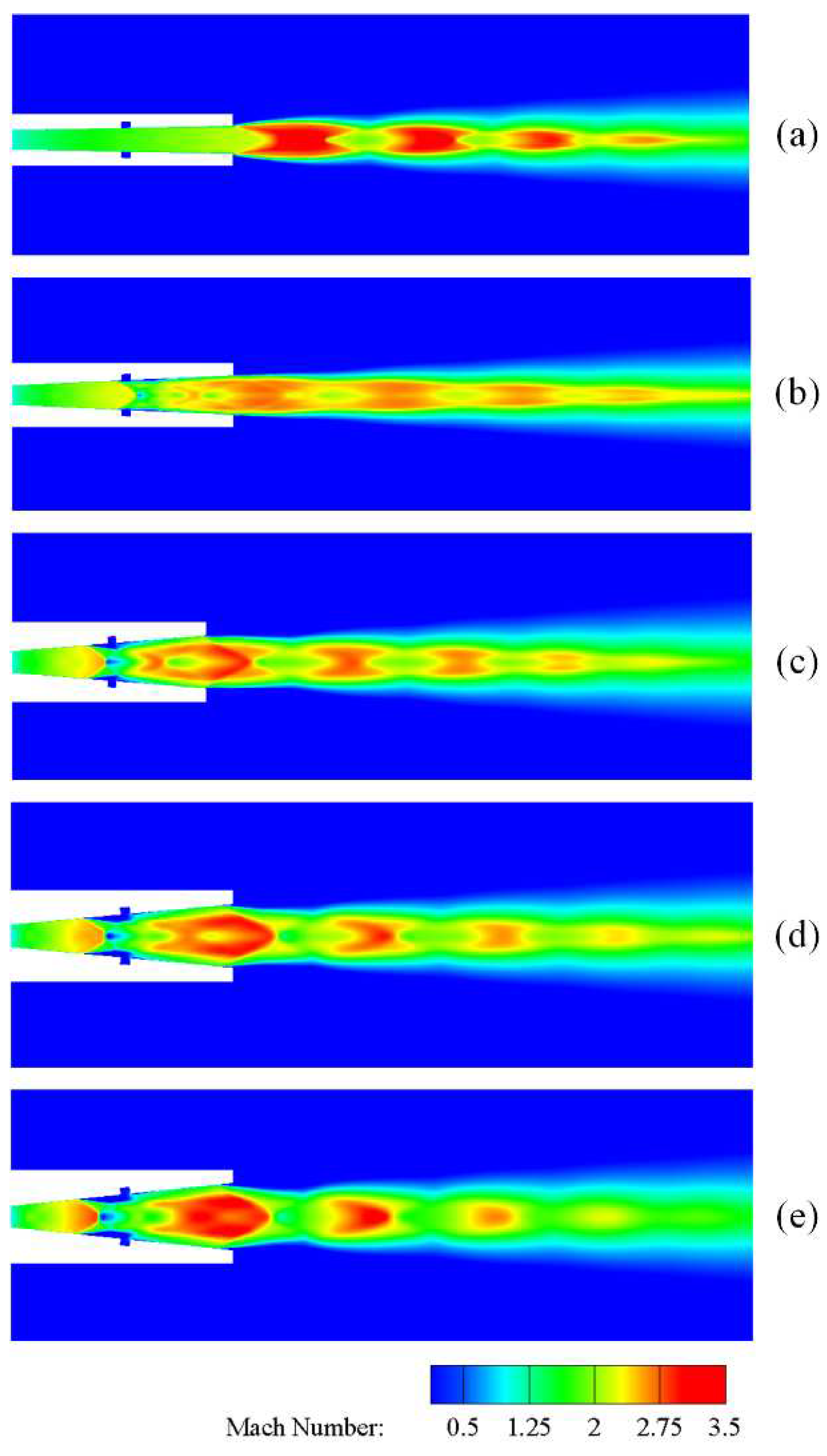
Preprints 94973 g015
Figure 15. Contour clouds of airflow Mach number for different area ratios rA: (a)rA=2, (b)rA=4, (c)rA=6, (d)rA=8, (e)rA=10
Figure 15. Contour clouds of airflow Mach number for different area ratios rA: (a)rA=2, (b)rA=4, (c)rA=6, (d)rA=8, (e)rA=10
Preprints 94973 g015
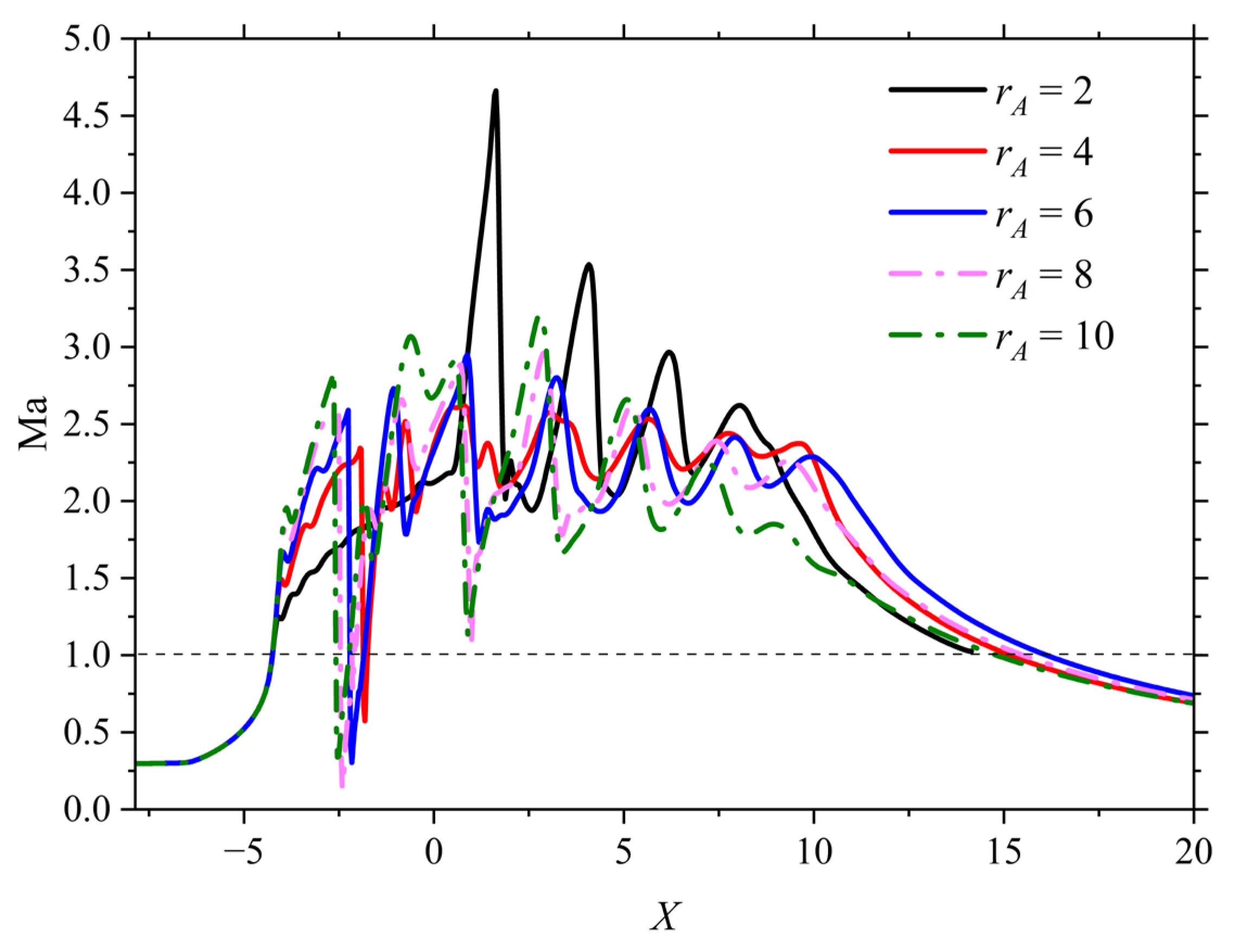
Preprints 94973 g016
Figure 16. Mach number of airflow along the axis for different area ratios rA.
Figure 16. Mach number of airflow along the axis for different area ratios rA.
Preprints 94973 g016
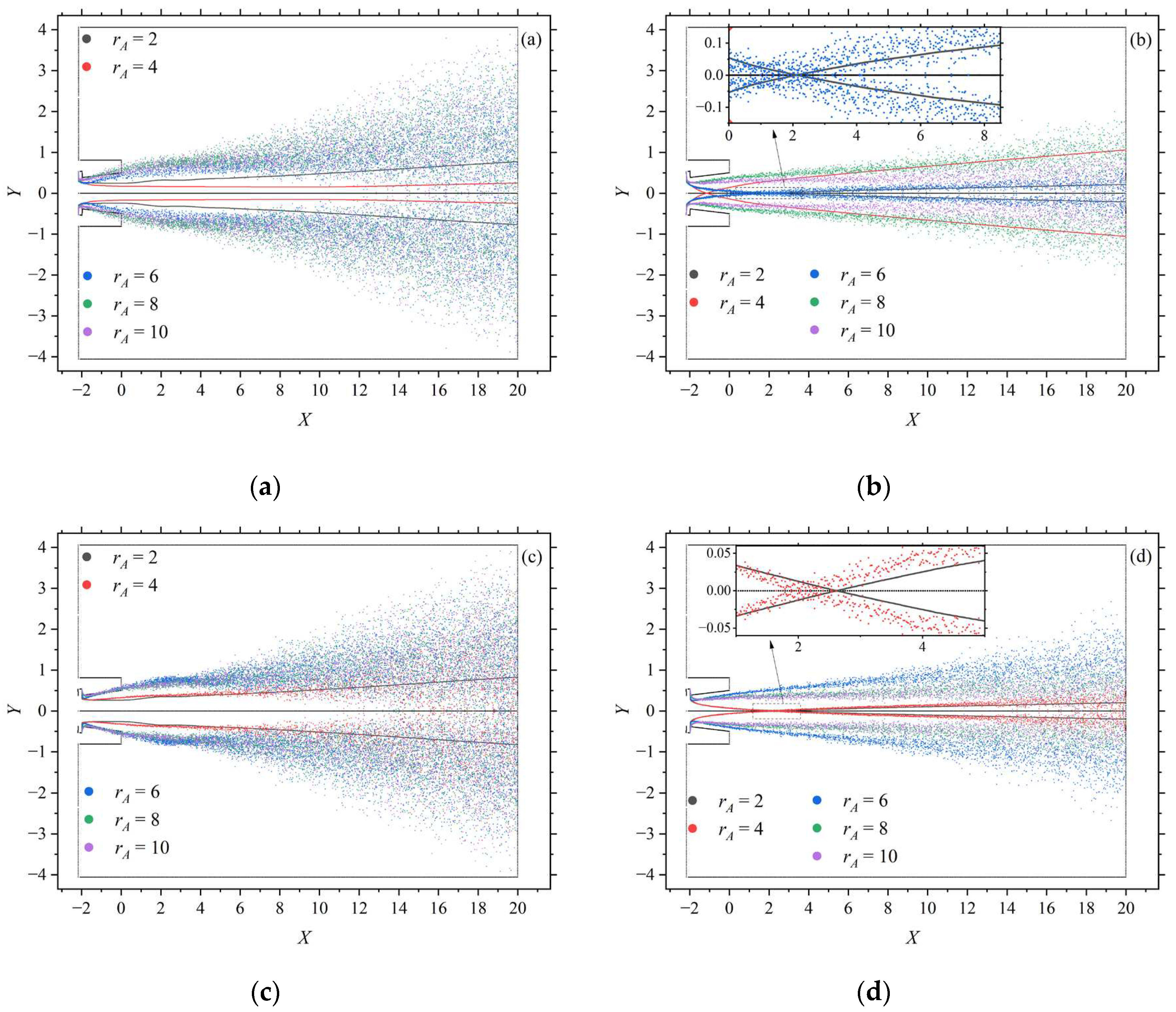
Preprints 94973 g017
Figure 17. Representative particle trajectories for different area ratios rA: (a)minimum average diameter particles sprayed at the upstream-most position of the injection port, (b)maximum average diameter particles, (c)minimum average diameter particles sprayed at the downstream-most position of the injection port, (d)maximum average diameter particles.
Figure 17. Representative particle trajectories for different area ratios rA: (a)minimum average diameter particles sprayed at the upstream-most position of the injection port, (b)maximum average diameter particles, (c)minimum average diameter particles sprayed at the downstream-most position of the injection port, (d)maximum average diameter particles.
Preprints 94973 g017
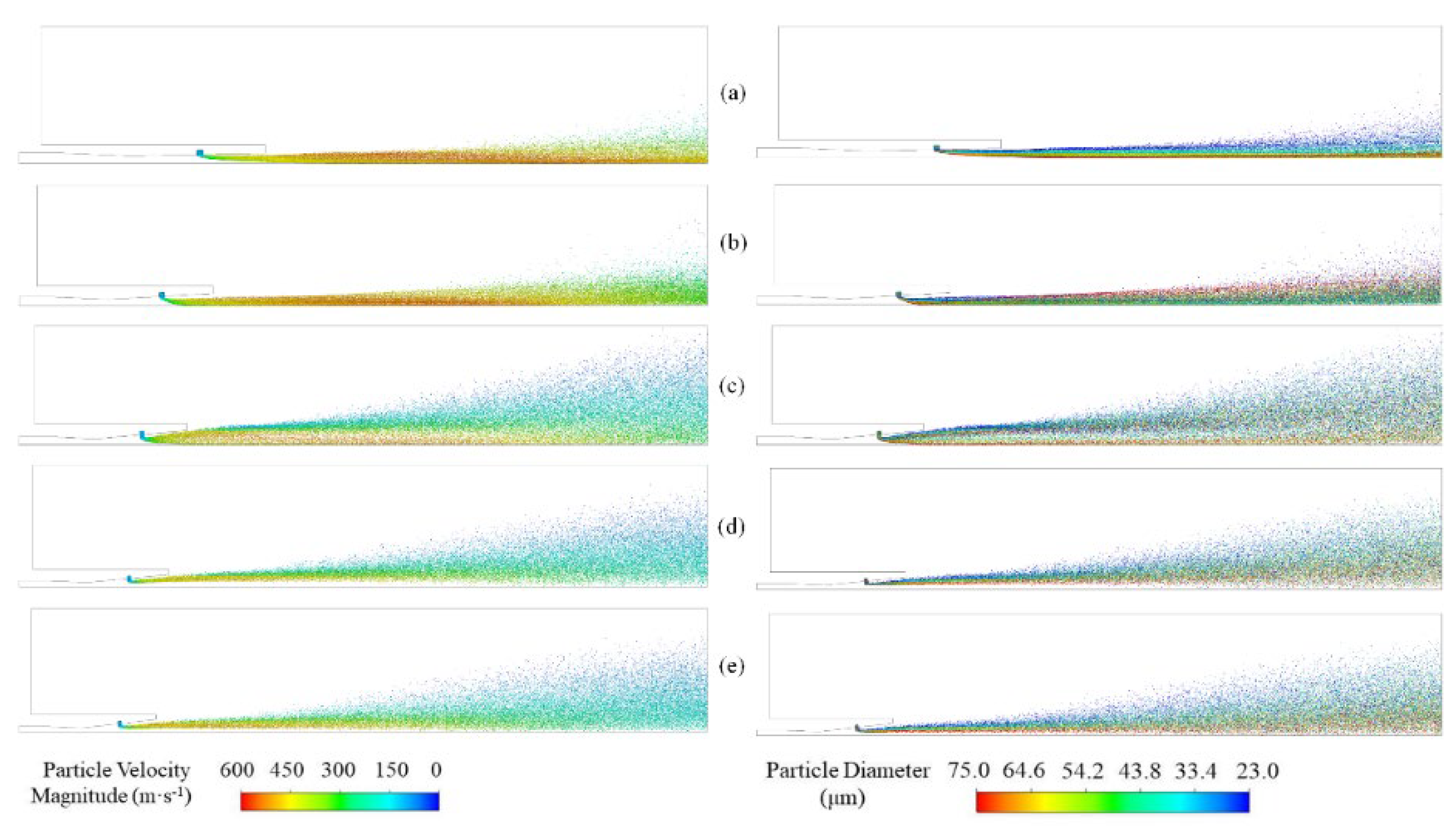
Preprints 94973 g018
Figure 18. Particle velocity size and diameter distribution fields for different area ratios rA: (a)rA=2, (b)rA=4, (c)rA=6, (d)rA=8, (e)rA=10
Figure 18. Particle velocity size and diameter distribution fields for different area ratios rA: (a)rA=2, (b)rA=4, (c)rA=6, (d)rA=8, (e)rA=10
Preprints 94973 g018
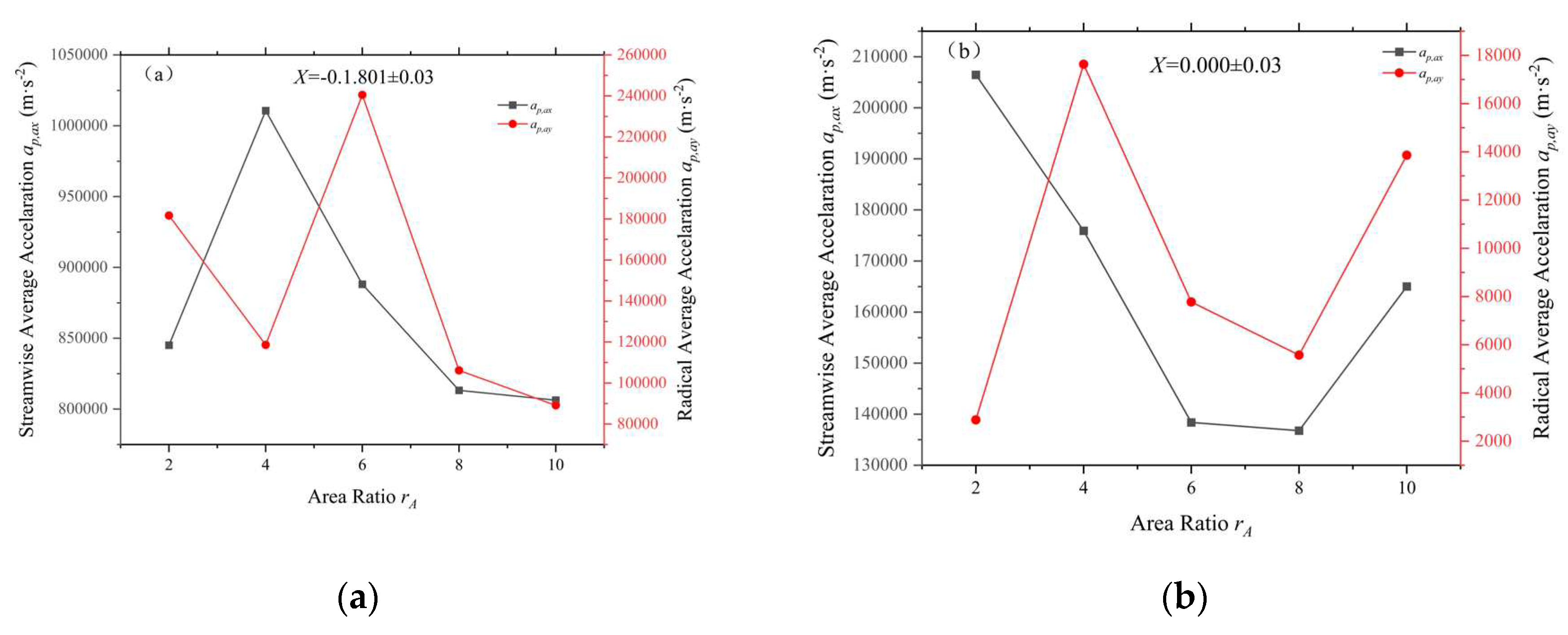
Preprints 94973 g019
Figure 19. Variation of particle flow and radial mean acceleration with area ratio (a)X=-0.1801, (b)X=0.000.
Figure 19. Variation of particle flow and radial mean acceleration with area ratio (a)X=-0.1801, (b)X=0.000.
Preprints 94973 g019
Table 1. Calculated geometric parameters for 2D axisymmetric nozzle
Table 1. Calculated geometric parameters for 2D axisymmetric nozzle
Straight section
ls/(mm)		 Convergent section
lc/(mm)		 Entrance radius
rin/(mm)		 Throat radius
rt/(mm)		 Injector position
linj/(mm)		 Spray width
winj/(mm)
46 69 11.5 8.05 68.3 8.05
Table 2. Nozzle geometry parameters used for validation.
Table 2. Nozzle geometry parameters used for validation.
Convergent section
lc /(mm)		 Convergent section
ld /(mm)		 Entrance height
hin/(mm)		 Entrance height
ht /(mm)		 Outlet height
he /(mm)		 Width
w/(mm)
30 120 17.72 1.02 3.8 3.07
Table 3. Table of parameters for granular materials.
Table 3. Table of parameters for granular materials.
Granular material Particle mass loading Z Specific heat capacity of particles Cp/(J·kg-1·K-1) Particle density
ρp /(kg·m-3)
Stellite-21 0.04-0.35 417 8300
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated