Prerpints.org logo
Preprint
Article

The Effect of Supraharmonic Distortion in MV and LV AC Grids and Derived Limits

Altmetrics

Downloads

145

Views

64

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 December 2023

Posted:

04 January 2024

You are already at the latest version

Alerts
Abstract
Since the integration of electronic devices and intelligent electronic devices into the power grid, power quality (PQ) has consistently remained a significant concern for system operators and experts. Maintaining high standards of power quality is crucial to prevent malfunctions and faults in electric assets and in connected loads. Recently, PQ studies have shifted their focus to a specific frequency range, previously not considered problematic, the supraharmonic 2kHz–150kHz range. This range is not populated by the harmonic components of the 50-60 Hz mains fundamental, but a combination of intentional emissions, switching and non-linearity by-products and various types of resonances. This paper aims to provide a detailed analysis of the impact of SH on power network operation and assets, focusing on the most relevant documented negative effects, namely power loss and heating of grid elements, aging of dielectric materials, failure of medium voltage (MV) cable terminations, and interference to equipment and to power line communication (PLC) technology in particular. Under some shareable assumptions limits are derived and compared to existing ones for harmonic phenomena, providing a clear identification of the primary issues associated with supraharmonics and suggestions for the standardization process. Strictly related is the problem of grid monitoring and assessment of SH distortion, discussing the suitability of normative requirements for instrument transformers (ITs) with specific focus on their accuracy.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Supraharmonic (SH) distortion is intended comprehensively as a set of phenomena of conducted emissions from distorting loads interacting with the feeding network and its elements: other loads, cables, transformers, etc. Such distortion is conventionally located in the 2kHz–150kHz frequency interval, as an extension of the harmonic frequency interval that is limited to 2 kHz for 50 Hz systems.
Supraharmonics are not only to be intended as “faster” harmonics, but their propagation and aggregation characteristics are different, as well as their time behavior (e.g. duration, intermittency, etc.).
This has motivated an intense research effort in the last decade to provide a characterization similar to the one traditionally developed for the harmonics. Depending on the characteristics of the respective sources, such emissions may have a varied and peculiar time-frequency and impedance behavior. Paired to the relative difficulty of carrying out comprehensive tests, authors have concentrated mostly on relevant types of sources, such as wind parks [1,2], photovoltaic (PV) parks [3,4,5], electric vehicle (EV) chargers [6,7,8], and smart lighting (e.g. LED or fluorescent lamps) [9,10], including the various cases of lighting as victims and sources of secondary emissions [11,12].
Studied scenarios have considered mainly Low Voltage (LV) grids for a matter of convenience during test campaigns in terms of safety and availability of accessible sites and variety and number of connected sources. Wind parks indeed, due to the large installed power, are always found connected at the Medium Voltage (MV) level.
Besides the understanding and the characterization of the behavior of SH sources, the most pressing objectives are the definition of suitable limits and the identification at the same time of appropriate quantification methods, as SHs have negative effects on grids and grid components.
The adoption of more or less strict limits of SH distortion depends on the severity of the negative effects that need first to be documented and quantitatively assessed. Such negative effects can be seen as an extension of those attributed to harmonic distortion; they range from stress to dielectrics and insulating materials within cables, transformers and capacitors, including the aging of filter components, to network resonance scenarios, and to various cases of interference, in particular to power line communication (PLC) devices.
In some cases published studies focusing on the harmonic interval may be extended by similarity to the lower portion of the SH interval, such as models for skin effect and proximity effect in conductors [ref], as well as at some extent dielectric losses [ref], as discussed in Section 2.
Phenomena of stress in dielectrics occurring at large electric field intensity within the material [13,14] are of course specific to high nominal voltage values and thus limited to MV gridss. Accelerated partial discharge events are peculiar of AC grids and may occur in principle at both LV and MV levels, although again they are favored by high electric field values. The final consequence of such phenomena is aging of dielectrics [14,15] altra ref su aging of materials with some catastrophic phenomena for example at MV cable terminations with a mix of dielectric stress and local heating as root causes [16,17].
Modern grids see a variety of loads featuring controlled static power converters and interfaced through filters, leading to quite complex scenarios of network resonances [18,19,20]: resonance may occur network wide, e.g. all along one or more branches of a distribution grid up to the point of common coupling (PCC) or intake, or local to a subset of the grid, where some loads (including renewable energy sources) exchange finire finire
The phenomena exemplified above, besides being concerned by the wide frequency span of the SH interval, have also a complex time-frequency pattern: time duration and intermittency of SH emissions may be widely variable and depend not only on the operating conditions of the SH source, but also on the interaction with other connected devices nearby [21,22] and on the quality of the feeding voltage [23,24].
The perspective of this work is on the negative effects rather than the sources and the aggregation or propagation of SH emissions. The objective is to provide an overview of the documented interaction with grid elements and connected devices, where stress, aging, disturbance take place (Section 2). Limits may be then derived under suitable assumptions (e.g. number of concomitant sources, grid impedance, etc.), discussing the relevance of the discussed phenomena (Section 4). To show the representativeness of the discussed literature works and standards, a short bibliographic analysis is reported in Section 3.

2. Negative effects of supraharmonics ????

In the Introduction the negative (or detrimental) effects of supraharmonics have been briefly reviewed and may be synthesized as follows:
  • power losses in conductors, due to frequency dependent phenomena, such as skin effect and proximity effects;
  • aging of insulating materials (mainly in cables and transformers) due to local losses and self heating;
  • aging of capacitors with a combination of effects of dielectric stress (similarly to what occurs to insulating materials) and increased wiring losses (especially for large power capacitors);
  • specific damage to MV cable terminations caused by local heating and electric field gradient;
  • triggering of network resonances (impacting on the resulting voltage or current distortion of primary emissions), including local resonance phenomena between connected loads and apparatuses (favored e.g. by the extensive use of interface and EMC filters) associated to the so called “secondary emissions”;
  • interference to equipment in particular connected at the LV level, consisting of e.g. domestic appliances, information technology (IT), lighting, energy meters, etc.;
  • specific interference to power line communication (PLC) circuits, more and more commonly used at LV, but also at MV, levels, for example to exchange information on energy metering and for control purposes.
Such phenomena are now analyzed more in detail in the following.

2.1. Power losses

The basic rationale for power losses is related to resistive components in conductors, that increase in value roughly proportional to the square root of frequency, as a consequence of the skin effect. If conducting materials are ferromagnetic then the phenomenon is more evident (being the skin depth inversely proportional to the magnetic permeability). In addition, losses may occur also due to the magnetic properties of the material and hysteresis phenomena, as commonplace for transformers. When windings (and tightly packed conductors) are considered, a second effect affects the distribution of the current in the conductors cross section, the proximity effect, also approximately proportional to frequency.
An increase in conductor losses due to frequency is known and stigmatized in the [25] (Figure 14A.4) when testing Instrument Transformers (ITs) for thermal losses at AC (50 or 60 Hz) rather than at DC: for large conductors with diameter D ranging between 40 mm and 100 mm additional losses with respect to an equivalent DC current in terms of rms are about 150% at 50 mm diameter and 270% at 100 mm diameter for Alu conductors, and 180% and 330% for Copper conductors. The estimate is done using the Levasseur formula:
k = 0.25 + 0 . 75 6 + D 4 δ 6 6
with D the conductor diameter and δ the skin depth in the conductor material.
Figure 12 - ref.
A more accurate evaluation of SH effect up to 100 kHz at frequencies higher than those characteristics of the mains and its harmonics [26]. The work takes into account the formulas of the IEC 60287-1-1 standard [27] providing separately the correction factors Y S for skin effect, Y P for proximity effect and Y S C for the screen losses (so well applicable to MV cables).
Y S = X S 4 / ( 192 + 0.8 X S 4 ) 0 < X S ≤ 2.8 − 0.136 − 0.0177 X S + 0.0563 X S 2 2.8 < X S ≤ 3.8 0.354 X S − 0.733 X S > 3.8
with X S containing the frequency dependence.
The IEC 60287-1-1 proposes then two formulations of Y P for the case of two-core cables (or two single-core cables) and three-core cables (or three single-core cables). The two cases are indicated by a subscript “2” and “3”.
Y P , 2 = 2.9 X P 4 192 + 0.8 X P 4 d c s 2
Y P , 3 = X P 4 192 + 0.8 X P 4 d c s 2 0.312 d c s 2 + 1.18 X P 4 192 + 0.8 X P 4 + 0.27
with X P containing the frequency dependence, d c is the conductor diameter and s is the separation of conductor axes (so equal to the sum of the diameter and the gap).
The two “Y” quantities are based on the calculation of the corresponding “X” factors, that in turn contain two “k” coefficients, related to the shape of the conductors: k S is largely equal to unity for round solid and stranded conductors for both copper and aluminum; k P is also unity for solid conductors and takes the value 0.8 for stranded conductors.
Relevant to note, this formula is stated as valid for X P ≤ 2.8 , and, as observed in [26], this does not fit many practical cases, especially for SH frequencies.
A similar, but different, “ Y P ” quantity is thus proposed [26], taken from [28]:
Y P , D = m d c / s 2 G P 2 − 5 d c / s 2 H P / 12
where the two factors G P and H P are again expressed with different approximations at variable X P , as done before for X S , and m is a factor for the cable geometry.
G P = 11 X P 4 / ( 704 + 20 X P 4 ) 0 < X P ≤ 2.8 − 1.04 + 0.72 X P − 0.08 X P 2 2.8 < X P ≤ 3.8 X P / ( 4 2 ) − 0.125 X P > 3.8
H P = 0.333 ( 1 + 0.0283 X P 4 ) / ( 1 + 0.0042 X P 4 ) 0 < X P ≤ 2.8 0.095 + 0.119 X P + 0.0384 X P 2 2.8 < X P ≤ 3.8 ( 2 X P − 4.69 ) / ( X P − 1.16 ) X P > 3.8
For the last quantity, Y S C , that accounts for the effect of the cable screen, the IEC 60287-1-1 proposes a simplified approach, taking the average of the two other factors, Y S and Y P .
To conclude, the three “Y” factors are put together to determine the “new” resistance R ( f ) including dependence on frequency and geometry:
R ( f ) = R D C ( 1 + Y S + Y P + Y S C )
If the simplified expression for Y S C is considered, then (8) can be rewritten as:
R ( f ) = R D C ( 1 + 1.5 ( Y S + Y P ) )
For the accuracy of the published methods to predict additional losses, Topolski et al. [29] provided a comprehensive overview and comparison of various formulas, unfortunately with the frequency interval limited to about 2 kHz. The reference formulation is the one achieved by means of Bessel functions and the selected formulations for the comparison are the Levasseur equation (1) (that the Authors refer to a Schneider Electric application note) and the IEC 60287-1-1 formulation considered above.
The results for a single-strand and multi-strand cable show that the IEC 60287-1-1 formulation for the two skin and proximity effect terms is not so accurate, and underestimates losses for frequencies above about 1 kHz. However, when the terms of skin and proximity effect are taken together (so the sum Y S + Y P is evaluated), the correspondence with the theoretical reference method based on Bessel functions is almost perfect (up to 2.5 kHz. In [26] the comparison was carried out against Finite Element Method (FEM) results, showing a very good correspondence (maximum error of about 6%), if also Y S C is accounted for.
The relevance of supraharmonic components evaluated in [26] over the 2 to 100 kHz interval is confirmed with an increase of total resistance by a factor of 6.5-7, proportional to the square root of the frequency ratio (=100/2=50). The minimum ratio with respect to the fundamental is about 3.5.
Looking for a suitable weight of SH amplitudes with the objective of limiting the losses to the same amount as caused by harmonic components, we observe a factor inversely proportional to the square root of frequency giving the already mentioned factor of 7 between 2 kHz and 100 kHz. Before proceeding the different standpoint of the IEEE Std. C57.110 [30] that defines a quadratic function of the harmonic order as impacting on eddy current losses of transformers, whereas other stray losses have an exponent of 0.8 or less on the harmonic order (that agrees somewhat with the “square root of frequency” behavior). The standard, in its Annex C, reports some considerations on the effect of distortion at higher frequency (such as in the SH interval), observing that skin effect becomes relevant and deviations from the postulated “ h 2 ” behavior are significant. A reduction of 10 % is then estimated already for the first 20 harmonics if skin effect is taken into account. This correction is, however, not sufficient in the SH Interval to match the f behavior.
In general, the total loss increase due to supraharmonics for the observed amplitude values is in the order of 10%-20% of the losses ascribed to harmonics (up to 2 kHz). The present harmonic limits have the objective of limiting losses to a value that requires an over-rating of cables of about 5% [16], considering such amount of harmonic losses acceptable. This ratio is bounded to increase with the extensive use of static power conversion units with increasing switching frequency (renewables, EV chargers, etc.) shifting distortion to higher frequency, namely reducing the harmonic contribution in favor of increased SH components.
Proposing a SH limit curve originating from a 1 / f weight starting from the harmonic limits for residential and industrial environments would imply additional losses equal to those allowed by present limits in the harmonic interval. Going down to a limit value for the single SH component is then more difficult if the number of SH components is not known a priori. A conservative standpoint may be assumed, by adopting a sufficiently large resolution bandwidth (e.g. the frequently adopted 2 kHz), dividing then the SH interval into 74 sub-intervals evenly distributed between 2 and 150 kHz with steps of 2 kHz. The risk is of course an excessive penalization, considering risky and non compliant situations that see an uneven distribution of components, as it is often the case.

2.2. Aging of insulating materials

2.2.1. Partial discharges

In general the effect of supraharmonic distortion on Partial Discharges (PDs) is twofold: premature PD inception and quicker degradation of the material by combining to the ongoing PD events.
One evident parameter is the number of PD events per second n P D and the application of a superimposed supraharmonic component has shown to increase it by about 10%, slightly more at the lowest frequency values (2-5 kHz) than at the highest frequency components (6-9 kHz) tested in [13,14]. The amplitude of the applied SH test signal was 10% of the fundamental.
The conclusion seems that the influence on PD events is limited and reduces with frequency. The applied 10% of SH signal amplitude is already on the safe side for what are the usual amplitudes of SH emissions so that results can be assumed conservative.

2.2.2. Degradation of insulating materials

The tested materials are XLPE and alumina loaded XLPE (with weight % ranging from 1% to 5%). [14] It is interesting to observe that for moderate-to-high stress voltage levels (approximately 55 to 65 kV/mm) the effect of SH components is really minor. Instead when the stress level at the fundamental is set to very high values (about 70 kV/mm) small values of few % make the difference.
It may be concluded that the high voltage stress being one of the necessary ingredients for insulating material degradation by effect of SHs, this scenario occurs only in MV grids, and in particular conditions of high exploitation of the insulating material, such as at cable terminal joints and at very high MV levels (see e.g. Section 2.4).

2.3. Aging of capacitors

There is a number of devices with their dielectric exposed to some kind of SH distortion: such devices encompass first of all capacitors and supercapacitors, then for example batteries, and may be extended to insulating materials in general. Insulating materials (already discussed above) are in reality exposed to SH voltage distortion (i.e. modulation of the electric field within the insulating material), whereas here devices carrying significant SH current are considered (namely for storage and filtering). The focus is on those devices that are connected directly to the AC grid (e.g. for filters and power factor correction), whereas batteries and supercapacitors are connected instead through interface converters and are affected by the local converter ripple rather than by a grid-wide phenomenon. They are instead possibly directly connected when considering DC grids and aging and stress consequential to distortion have been discussed in [15].
In the harmonic interval limits provided by capacitors manufacturers address the overheating caused by dielectric losses and, depending on the application, an oversize of 10% to 20% compared to the dissipation at the fundamental may be sufficient.
Dielectric losses increase as well beyond the harmonic frequency interval, but a second dissipation mechanism take place that is instead usually negligible up to a few kHz. Wiring losses are particularly evident in large capacitors that may be built around smaller modules with a complex internal wiring, including fuses and inductive elements for protection [31]. Wiring losses follow what said in Section 2.1 with a contribution of skin and proximity effects.

2.4. Damage to MV cable terminations

Aging and failure of MV cable terminations is caused by localized heat possibly combined with worsened PD occurrence. Localized heat in particular has been observed in resistive stress-grading elements, where SHs affect the electric field distribution causing hot spots [17]: the large intensity of the flowing current is due to capacitive current proportionally higher for increasing frequency.
A catastrophic failure (that represents a field evidence) occurred at Eagle Pass substation [32] and in successive laboratory tests at ABB, Sweden, also reported in the same reference. The measured on-site voltage distortion was distributed among some characteristic SH components with significantly large amplitude, when compared to the 17.9 kV nominal value. The SH components were: 1.28 kHz with 4.6 kV amplitude, 3.78 kHz (the 3rd harmonic of the switching fundamental) with 1.2 kV amplitude and an atypical value of 12.4 kHz with 3.0 kV amplitude, due to network resonance. Relevant voltage distortion components around the 12.4 kHz resonance are in reality more than one, with the two adjacent to the resonance peak showing amplitude of 2 kV and 1.2 kV, leading to an overall rms value of 3.8 kV.
During lab tests it was determined that using the worst-case observed SH voltage levels, the heat caused at 12.4 kHz was 20 times higher than at 1.28 kHz. This is reasonable as the electric field was approximately 3 times larger (due to a different spatial distribution estimated by finite element method simulations) and the capacitive current approximately 10 times larger (following the frequency ratio).
The mitigation adopted was a different type of cable termination and addition of a filter to reduce the 12.4 kHz component caused by the resonance.
An approach is proposed in [17] starting from the determination of the heat Q dissipated in the stress grading area and in the dielectric of the cable joint. This quantity Q is proportional to the frequency and to the square of the voltage, as it is put in relationship to the electric field intensity. Any temperature increase in the cable joint is shown to be proportional to the excess heat caused by the supraharmonics. For this reason the Q p u quantity is calculated separating and weighting the SH excess heat with that at the nominal frequency. The weighted rms 2 of SHs, each with amplitude V h multiplied by frequency, is divided by the weighted rms 2 of the fundamental (i.e. V 1 2 multiplied by the fundamental frequency f 1 ). It may be said that the weighting with frequency accounts for the capacitive nature of the current, increasing with frequency. For a single SH component of frequency f s h and amplitude V s h the resulting Q value is:
Q p u = f s h V s h 2 f 1 V 1 2
When Q p u approaches the value of 20, failure is very likely, based on the site and lab evidence of [32], but subject to a significant uncertainty as the Eagle Pass cable was a unique case and the cable might have been defective, or particularly susceptible to thermal stress. Some safety margins are then proposed [17] consisting of a multiplying factor m, that takes values of 0.25, 0.5 or 1, identifying a green ( m < 0.25 ), yellow ( 0.25 < m < 0.5 ), orange ( 0.5 < m < 1 ) and red ( m > 1 ) area (the equal signs have been omitted and assigning them to the lower or upper interval does not represent an issue).
A further simplification shown in [17] is to consider supraharmonics below and above 20 kHz, providing two straight limits rather than a more complex curve. Maybe this approach is oversimplifying since the capacitive current is proportional to frequency and between 2 and 20 kHz there is a decade of frequency, as well as 20 kHz and 150 kHz differ by a factor 7.5. In addition, the distribution of the electric field at the termination was quite variable depending on frequency as well. For both factors the variability is much larger than the trimming operated by m, so that a more accurate frequency discrimination seems necessary.
A weighted sum, as commonly done for the weighted total harmonic distortion index, could be adopted to provide an equivalent representation of the heat stress caused by a complex pattern of SH components. In the end what is relevant is the heat stress, that may be assumed proportional to the frequency. Since the SH spectrum may be characterized by a mix of narrowband and broadband components, aggregation with a large resolution bandwidth (e.g. 2 kHz) is more robust and the result less exposed to changes in the lateral bands of switching groups and other modulation byproducts. The examples in [17] indicate a risk of cable termination failure for single SH components in the order of 3 % to 8 %, that means that for a SH spectrum populated by n components of not-too-different frequency the limit must be reduced by n and with different frequencies for the mentioned components, each must receive a limit that is proportional to 1 / f .

2.5. Interference to equipment

This and the next subsection distinguish the two cases of interference to equipment in general and to PLC systems, in particular.
In general, due to the so called “secondary emissions”, amplification of normal emissions is expected, as caused by the presence of other loads connected to the same grid: the reason is that the feeding impedance may be altered by the presence of e.g. input filters and capacitive components, with consequential amplification of current emissions at some frequencies in the SH interval.
This was tested experimentally by combining in pairs an electric vehicle, a LED lamp and a TV set in [33]. The amount of measured emissions from the EV were in the order of 5mA–10mA below 10 kHz and 5 mA located at an isolated component at 55 kHz. Theoretically this was demonstrated in [20,34] considering a grid feeding a set of identical EVs located at different distances from the PCC on the same or two different branches of the LV grid. The EV was modeled with an experimentally determined input impedance, and the mutual effect between EVs caused amplification of current emissions as soon as they were connected to not-to-far feeding points (in the order of 20m–50m.
For comparison the EN 50627 [35] reports various cases of measured emissions from a wide range of sources, including portable tools, electrical appliances, and inverters (such as active infeed inverters, AICs). Low-power devices (such as LED lamps, tools and various power supplies feeding e.g. a fibre switch, a computer, a surveillance camera to cite the most prominent examples) are in any case able to cause emissions in the order of 90dB μ V–100dB μ V in the frequency interval 9kHz–70kHz when measured with a standardized Line Impedance Stabilization Network (LISN): the equivalent current emission level may be obtained considering a LISN impedance variable between 5 Ω and 15 Ω , leading to a range of amplitudes of about 5mA–20mA for the largest emissions. This is in agreement with [33] and provides an indication of worst-case emissions from low-power devices.
Inverters interfacing renewables and energy storage devices are responsible in general for higher emissions, located as narrowband components at the switching frequency harmonics, usually with a fundamental located in the 10kHz–20kHz range (the examples of the EN 50627 [35] report fundamentals of 16 and 18 kHz and the three PV inverters of Figure 20 of the EN 50669 [36] have fundamental of 15, 16 and 20 kHz). Except for dramatic cases, as reported for Belgium in the EN 50627, usual emission levels are about 20 dB higher than the previous ones, thus implying as well ten times higher current emissions and significant chances of interference.
This type of emissions has been observed in normal domestic LV grids, as electrical appliances, EVs and PV inverters are commonplace in the residential grids. The maximum values of emissions were in the order of 0.3V–1V up to 20 kHz, decreasing then gradually by no more than an order of magnitude.
A complex scheme of interference has been observed also for residual current devices (RCDs) [37] with different responses depending on models. Besides undesirable tripping by superposition of SH components, what is most relevant is the possible RCD desensitization tripping then at higher fundamental (50 or 60 Hz) current values than required for electrical safety. Tests performed in [37] at significant, but not unlikely, injected SH current components ( 800 mA between 1 and 5 kHz) confirmed a desensitization of 2–2.5 for two different RCDs, tripping then at residual current values of 58 mA and 76 mA at 50 Hz with significant implications in terms of electrical safety. Such current values under the usual assumption of a 5 Ω grid impedance (the LISN value), correspond to 4 V of SH voltage distortion. By extrapolation of the two SH disturbance levels ( 800 mA and 1300 mA) for the tested RCD model (“A-30”), the minimum SH current causing a deviation above the desired 30 mA tripping threshold is about 600 mA, that corresponds to about 3 V or 130 dB μ V at low frequency (approximately over 2kHz–10kHz). About the assumed 5 Ω value of grid impedance, it represents for sure an overestimation if compared for example with the impedance curves shown in Figure 18 of the IEC 62578 [31], lying in the 0.5 Ω –4 Ω interval. Such an overestimation provides a margin when calculating voltage distortion from an observed current, but not the opposite, and we have seen that current, rather than voltage, disturbance is often relevant.
The EN 61000-4-19 [38] has the objective of establishing relevant and reliable immunity test levels for the differential-mode disturbance in the SH interval. Unfortunately, this standard has not been applied yet, nor enforced by inclusion in any product or generic EMC standard. The first three test profiles (Level 1, Level 2 and Level 3) have amplitude of 0.5 , 3 and 12 V set up to 9 kHz and the decreasing linearly in a log scale by a factor of 5 reaching values of 0.1 , 0.6 and 2.4 V at 95 kHz, where they are then held constant up to 150 kHz.
A straightforward comparison to the emission levels of PLC devices will be done at the end of this section. It is clear that in light of aggregation from different sources, as well as some margin of variability due to e.g. grid resonances and slightly different products characteristics, Level 1 does not provide any confidence that a tested equipment will be immune to SH disturbance. Level 2 provides a safety margin of 10dB–15dB with respect to the observed values, barely sufficient to cover the said aggregation. In fact, 10 sources disturbing the same frequency band within about 50 m would aggregate with a factor of 3.2 minimum, as resulting from a 10 assumption. This was demonstrated for harmonic and SH emissions of EVs in [39]. Level 3 thus seems highly advisable for all grids, noting that there is no big distinction any longer between residential, light industrial and industrial environments for what regards disturbance in the SH interval.
Some cases of highly disturbing inverters should instead be mitigated at the source, providing the necessary decoupling, e.g. by means of series reactors.

2.6. Interference to PLC

Besides some episodes of interference caused by PLC systems (e.g. to lighting, as cited in sec. 5.2.1 of the EN 50627), PLC technology is in general the victim of various forms of emissions. Emissions in the SH frequency interval are not in general disciplined by applicable limits and even for those products with an emission standard (e.g. lighting and electrical appliances with the EN 55014-1 [40]) there are episodes of non complying devices. It is observed that the limits of the EN 55014-1 in the first 9kHz–50kHz range are quite high, allowing 110 dB μ V of quasi-peak amplitude.
Emissions measurements in the SH interval carried out before 2010 seemed to lead to the conclusion that interference to PLC was unlikely, as observed in [41]. However, for the successive years various episodes of interference to PLC devices have been described in the EN 50627 [35], mainly based on documented investigations carried out in Sweden by the local authority. The interfering levels at various frequencies are confirmed of being in excess of 100 dB μ V and interference was suppressed with the application of mitigations (namely EMC filters), bringing emissions to a safe lower level. These two concomitant amplitude values for selected components (with and without interference) for the same system under the same conditions are extremely useful to define a reference line of interference below the lowest of such interfering cases.
A study of the various apparatuses connected to a microgrid (PV inverters, turbine, pump and battery charger) [42] has shown that the PRIME PLC system (an Orthogonal Frequency-Division Multiplexing, OFDM, Narrow-Band device) is significantly disturbed by narrowband components originating from the battery charger and falling into the PLC operating band, between approximately 40 and 80 kHz: the relevant disturbing components are 104 dB μ V at 48 kHz and 81.3 dB μ V at 72 kHz. It is curious that two narrowband components can disturb a system that in principle should be able to hop on different frequencies and tolerate momentary interference on some of them (if not to exclude such frequencies from the list of the OFDM ones).
The various emissions cases discussed so far are collectively represented in Figure 1, showing also the cases of levels with confirmed interference to PLC devices discussed above.

2.7. SH transfer efficiency between MV and LV levels

The negative effects discussed above can be seen as peculiar of the MV or LV level when the involved physical phenomena and devices are considered with a closer look: interference to equipment and to PLC systems is likely to occur at the LV level, whereas cable termination were said characteristic of MV grids, as well as aging of insulating materials especially at a pre-existing high fundamental voltage stress. Conversely dielectric aging may be seen equally occurring at LV and MV levels, as filters are used indistinctly in both cases.
What turns out to be relevant to liaise commented SH distortion levels and to derive comprehensive acceptance limits is the quantification of the transfer between the MV and the LV sides of distribution transformers at the SH frequencies. The SH frequency interval is such that the relevant coupling between the primary and secondary windings is a mix of inductive terms (designed magnetic coupling between windings operating at the fundamental frequency and above it) and capacitive terms (mutual stray capacitance).
A few publications [43,44] provide some measured curves of the transfer ratio between the LV and MV sides and between phases. Usually such transfer ratio is expressed by a multiplication coefficient of the nominal transfer ratio at the fundamental: it is thus expected around unity at low frequency and then decreasing at high frequency, except in the case of resonances.
The behavior of a small 100 kVA, 20/ 0.4 kV (50:1 nominal ratio), delta-wye connected, transformer was studied in [43], by measuring the transfer ratios from LV to MV first (test named “P1”, transfer ratios k 11 , k 12 , k 13 ), with k indicating LV to MV and “11” used for same winding at LV and MV respectively, “12” for finire finire) and then applying the test signal on the MV side, to measure the opposite MV-to-LV transfer capability (test “P2”, transfer ratios h 11 , h 12 , h 13 ), with h indicating MV to LV and the numeric indexes having the same meaning). What may be concluded is:
  • the transfer between LV and MV sides undergoes a significant resonance that is not visible from the MV side; apart from this (where the transfer ratio peaks to almost 10x the 50:1 nominal ratio), the values are low between about 0.2 and 0.01;
  • the usual transfer behavior is that the phase L1 on the LV side influences the corresponding phase L1 on the MV side and similarly the phase L2, but not phase L3; this for a delta-wye transformer as customary used for MV to LV distribution;
  • the transformer has a symmetric behavior for which the self transfer ratios (each LV phase to the corresponding one on the MV side) is the same (Figure 8);
  • the transfer from MV to LV for the same phase is more effective and does not show significant variations vs. frequency, being at around unity (ranging between 0.64 and 2.25 up to 80 kHz).
The more recent study in [44] has tested a 1 MVA, 20/ 0.4 kV, delta-wye connected transformer for both current and voltage transfer characteristics. The frequency interval is unfortunately limited to below 8 kHz, thus limiting the generality of the results that occur around the transformer resonance at some kHz (as identified in [43]) with the risk of being pessimistic. The reported results may be synthesized as:
  • regarding the current LV-to-MV transfer the results for L1 to L1 show an almost unity transfer ratio between 1.6 kHz and 7.6 kHz with a slight amplification (30%) at some components;
  • voltage, instead (always for L1 to L1 from LV to MV) is attenuated by a factor of 3 to 10 in the same frequency range;
  • for the MV to LV transfer the results provided by [43] are not fully confirmed, having found a slightly larger variation (more persistently around a factor of 2 to 3); what is relevant is that in case of an unloaded transformer (not magnetized) the behavior is quite different and variable;
  • last, also the LV-to-LV transfer occurring between the secondary windings of two different transformers through the MV grid was studied and the observed transfer ratio is more than unity (e.g. 2 to 3) at several frequency points, whereas some attenuation should be in general expected; this is a relevant result for what regards the propagation of interference within the same LV grid but on different feeders and parts of the grid.

3. Bibliometric assessment of references and findings

This short section aims at showing the consistency in bibliometric terms of the literature search that has provided the sources on which Section 2 and Section 4 are based. The bibliometric assessment is done by considering the number of search hits, their distribution through the years, and the coverage of the specific discussed phenomena.
The examined literature includes theses, white papers and brochures from industry and standards. A total of about 150 items have been identified with various search keywords after removal of duplicates. Keywords used to perform the search were selected from the following set: “supraharmonic”, “propagation” or “aggregation” or “summation”, “photovoltaic” (also “PV”) or “wind” or “electric vehicle”, adding the terms “medium voltage” and “experimental” to narrow down the search and find some hits to beef up otherwise less considered aspects. In addition, other sources were found by using the list of references in the first set of positive hits. The search process ended when all successive searches did not retrieve any new entry. The so collected items were then subject to deeper examination to remove those not providing quantitative information related to the issues discussed in Section 2. The remaining items were 81 and their distribution in terms of year of publication, type of publication and characterizing keywords is shown in Figure 2. With a reduced database size, to avoid erratic fluctuations in the publication years, they have been paired in the most recent years, and grouped by 4 between 2006 and 2009 or cumulatively all comprehensively before 2005.
It may be seen that the number of publications on this subject has increased through the years, although recently the number is reducing, probably because the contribution to the standardization activities has been somewhat reduced and the focus has been moved to evaluation of spectra, equivalence between algorithms and detectors, and related uncertainty. The activity in the newly EU funded project ADMIT should bring new research impetus, applied to the measurement of SH phenomena with Instrument Transformers in particular in MV networks. The recorded number of contributions is in agreement with what reported in [45], where a reduction for the years 2021 and 2022 is pointed out, although the absolute numbers are more than double due to the larger scope of the publication.
For what regards the type of publication, there are some special conferences on power quality and distribution grids (such as CIRED and CIGRE congress) that have attracted several publications; the fraction of journal papers is in any case significant, well positioned at one third of the all references.
As for the keywords indicating the subtopics dealt with by the respective publications, there is a good horizontal coverage of “losses”, “transformer behavior”, “aggregation” and “propagation”, “aging” (that we have discussed in Section 2), all with about 5% of coverage.

4. Lessons learned and compatibility levels for the SH interval

4.1. Existing normative limits and compatibility levels

Standards may indicate limits of emission, levels of immunity or reference compatibility levels. First of all a distinction must be made saying that we are focusing on differential mode conducted phenomena, for which many EMC standards are irrelevant as they consider mainly common-mode disturbance; an example is given by the EN 55014-1, providing emission limits for household appliances and electrical tools, but sometimes cited for comparison e.g. with compatibility levels.
Compatibility levels are defined as a reference level for coordination of emission limits and immunity levels for a given environment. They are also an indication of the expected level of disturbance in that environment. There is a set of “environment” EMC standards covering public networks at LV (EN 61000-2-2 [46]) and MV (EN 61000-2-12 [47]), as well as industrial networks (EN 61000-2-4 [48]). In reality for the SH frequency interval the EN 61000-2-12 does not contain any indication; from the list of sources (arc furnaces, adjustable speed drives, ...), it is evident that twenty years ago the impact on the grid of electric vehicles and renewables was not foreseen. The EN 61000-2-4 reports three environments, `1’ (or `2a’), `2b’ and `3’, the former corresponding to the residential/commercial LV environment of the EN 610000-2-2.
Emissions in the SH frequency interval are well covered for what concerns intentional (or in-band) and non-intentional (or out-of-band) emissions of PLC devices (standard EN 50065-1 [49]).

4.2. Limits based on documented negative effects

As reviewed in Section 2, there are documented negative effects (or, in general, “interference”) for different types of phenomena, that have different intensity levels and time dynamics. For example, losses and self heating are slower and appear at higher intensity than EMI to equipment, and in particular PLC devices.
In general, the influencing mechanisms are such that a reference level (or limit) that reduces with frequency may be expected: losses are proportional to the square root of frequency, induction is proportional to frequency, capacitive current increases with frequency. For interference to PLC devices, as the transmission level is constant over the operating frequency, a constant reference level may be expected, although a slight reduction of the received signal may be considered for increasing frequency (as caused by line attenuation).
From the previous discussion we may consider the following points:
  • documented interference to PLC devices, considering both cases of presence and absence of interference; to this aim the results shown in Figure 1 are used; values for mains signaling at the MV level are not established, as pointed out in the EN 61000-2-12 [47], still in the 2003 version;
  • losses and consequential heating taking the harmonic limits as reference for the Residential and Industrial applications, namely considering the current distortion limits of the EN 61000-3-2 (2019) [50] and EN 61000-3-12 (2019) [51], respectively; with a general assumption regarding the expected grid impedance, such limits are transformed into voltage distortion levels and then compared to those of the EN 61000-2-2 (2019) [46] and EN 61000-2-4 (2020) [48];
  • effects at MV level, considering the critical values impacting on the reliability of cable joints (see Section 2.4).
The other phenomena discussed in Section 2 were evidently relevant only at higher SH distortion levels and are thus not further analyzed.

4.2.1. Interference to PLC devices

Section 2.6 has discussed the problem of interference to PLC devices showing positive cases of interference as mostly reported in the standard EN 50627 [35]. Such levels, as shown previously in Figure 1, are reported in Figure 3 having overlapped some annotations and a proposal for an overall reference level to consider as limit with respect to interference to PLCs only. The purpose is to provide a good coverage of the SH interval in terms of demonstrated interference cases, as well as lower levels in the same scenarios at which no interference occurred. The objective is attained when the no interference levels are sufficiently separated from the corresponding interference cases and also well leveled with respect to the corresponding “no interference” or “interference” cases at other frequency values nearby (so to postulate a homogeneous behavior at similar, but not same, frequency values).
Three groups of points are highlighted by a dashed black circle and labeled as “A”, “B” and “C”. Such points show some contradictory behavior with respect to the expected arrangement with the interference case (the square symbol) above the no interference case (the circle symbol):
  • Group A: the points have a spread of 8 dB only but with the interfering value reported as the lowest one; these values come different PV inverters connected at the same grid where interference was reported for one of the PLC devices in the same grid, so that it is possible that the attenuation from the source to the victim PLC is variable and accounts to some dB of variation, as well as that these values are not really interfering or not interfering with the PLC operation as they fall outside the 42kHz–89kHz Prime PLC operating band.
  • Group B: similarly, this is an isolated point reported as interfering, but part of a broader spectrum where the interfering components fell inside the Prime PLC band.
  • Group C: these two pairs at 35 kHz and 40 kHz are also very likely outside the operating band of the PLC in question, whereas confirmed interference for the square symbols is caused by the other points of the same case (blue squares) at 60 kHz and 70 kHz.
In Figure 3 a dashed gray thick line is proposed the reference level separating the circles from the squares, so the “no interference” cases from the “interference” cases. It is observed that such division is approximate, especially at low frequency where the points are at the margin or outside the typical PLC band (in principle extended from 3 to 95 kHz and identified as CENELEC “A band” in [42]). In addition, it is possible to observe that higher levels may be allowed at lower frequency, just moving the corner point slightly back to about 20 kHz and tilting the dashed limit curve (resulting in the other darker dash-dot profile). It can be noted that in the low frequency part of the SH interval, between approximately 2 and 15 kHz, the variability of the proposed profile is significant and reference values here should be justified with other considerations, based on different approaches, such as extension of the harmonic limits for generic interference to equipment and limitation of losses, as well as other mechanisms of aging and deterioration (for example for MV cable joints), both considered in the following.

4.2.2. Losses and self-heating

This section contains a working example of assignment of convenient SH current limits starting from two assumptions: first, the harmonic limits for residential ( < = 16 A [50]) and industrial ( < = 75 A [51]) loads aim at limiting power losses and self heating; second, the number of SH components is known and it is assigned for three sub-bands of the SH interval, namely 2kHz–9kHz (3 components), 9kHz–50kHz (3 components) and 50kHz–150kHz (6 components). This assumption is in line with what reported in [52] for a complex load such as the inductive charger of an electric bus.
A Total Supra-Harmonic Distortion (TSHD) index is considered similar to the classic Total Harmonic Distortion (THD), that is corresponding to the root of the sum of the square of normalized components amplitudes. The use of subscript “I” indicates that the index is referred to the current.
Each component is combined with the others of the same sub-band with a square-root-of-frequency criterion, trying to balance the partial contribution to heat of each sub-band and then the complete TSHD is calculated, making it the same of the estimated T H D I following the limit of the respective standards for Residential or Industrial applications. The industrial case is taken with short circuit ration R s c = 66 . The result is shown in Figure 4, having also estimated the allowed tolerable voltage distortion taking the reference current I r e f as 16 A and 75 A, respectively, and having estimated the grid impedance using the curve of Fig. 20 in the IEC 62578 standard [31].
It is observed that the resulting SH limits in % are almost the same for the residential and industrial cases: this is due to the T H D I limit value used as reference that is 15 % and 16 % in the two cases.
It is also remarked that for a larger number of components in each sub-band ( N S H − B 1 , N S H − B 2 and N S H − B 3 ) the corresponding limit must be reduced. The reduction would be proportional to the square root of this number compared to the studied case ( N S H − B 1 = 3 , N S H − B 2 = 3 and N S H − B 3 = 6 ). The assumption that the components are not synchronized and independent is not necessary as the investigated effect is the power loss and consequential heating that follows by its own nature a rms summation.

4.2.3. Stress of MV cable joints

Limits can be derived for the stress on MV cable joints as outlined in [17] and sketched in Figure 5, having used the four curve profiles corresponding to “no risk” ( m < = 0.25 ), “moderate risk” ( 0.25 < m < = 0.5 ), “significant risk” ( 0.5 < m < = 1.0 ) and “unacceptable” ( m > 1.0 ). Provided that the reference value of 20 is correct and adequate to all situations, the derived limits (in terms of voltage distortion), seem to be less restrictive than those derived above for PLC interference and power losses.

4.3. Assessment and specifications for Instrument Transformers

SH distortion components relevant to interference and other negative effects have been discussed in Section 2 and reference levels (both in terms of voltage and current at SH frequencies) have been proposed earlier in this section. It is now worth verifying the current status of the measuring infrastructure in terms of capability to quantify these phenomena, in particular at the MV level.
The aim of this section is to provide an overview of the current literature and standards concerning Instrument Transformers (ITs) in relation to supraharmonics. As a matter of fact, ITs are the elements of the grid supposed to measure such power quality disturbances. However, since the SH issue became more relevant in recent years, ITs and their standards are not yet ready.
ITs play a crucial role in power systems, and their feature are outlined in many standards like the well-known IEC 61869 series. In [53] general requirements are established, including provisions for Electromagnetic Compatibility (EMC) and specific tests like the Switching Impulse Voltage Test and EMC tests. For Current Transformers (CTs) detailed in [54] no additional requirements are specified; similarly, [55,56,57] do not introduce extra conditions in the SH range for Inductive Voltage Transformers, Combined Transformers, and Low-Power Passive Voltage Transformers, respectively. However, the IEC 61869-5 [58] highlights a relevant point regarding Capacitor Voltage Transformers, stating that they can be equipped with or without carrier-frequency accessories for power line carrier-frequency applications. The IEC 61869-6 [59] introduces additional general requirements for the new generation of Low-Power Instrument Transformers (LPITs). It specifies tests for harmonic and inter-harmonic disturbance, conducted immunity tests at various frequency ranges, and radiated field immunity tests. These ensure the immunity of LPITs against a range of disturbances in the power supply. However, no additional information on SH testing is reported. Same comments can be extended to the IEC 61869-9 [60], which focuses on the digital interface for instrument transformers, and IEC 61869-10 [61] that outlines frequency dependence and response characteristics, particularly relevant for Rogowski coils used in low-power passive current transformers. The IEC 61869-14 [25] and IEC 61869-15 [62] specify accuracy tests on composite signals for current transformers and voltage transformers intended for DC applications, respectively. Overall, this short analysis clearly highlights the lack of consideration of SH phenomena inside the IEC 61869 series, confirming the need for new specific standards or a significant update of the existing ones.
Based on the above considerations, it is imperative to conduct a thorough evaluation of the measurement capabilities and related requirements for an IT in the SH frequency interval. These requirements can be categorized into three main aspects:
  • Frequency Response. The frequency response of an IT poses a significant challenge when measuring supraharmonics. Most ITs and LPITs exhibit optimal performance only within a limited frequency interval. For example inductive ITs are subject to resonances outside the traditional 50Hz–2500Hz operating range; in addition, their response at higher frequencies may significantly deviate from the required flat profile, necessitating a comprehensive characterization process [63]. Although LPITs generally demonstrate better frequency performance, preliminary characterization remains indispensable.
  • Amplitude of the Measured Signal and Sensitivity. Assessing the smaller SH amplitude proves challenging for ITs, which are inherently designed to achieve maximum accuracy at the rated voltage/current. Dealing with amplitudes that are 3 to 6 orders of magnitude lower than the nominal values presents a formidable task. Two potential solutions are conceivable: a) installing an additional IT dedicated to measuring the SH frequency range with the discussed amplitudes, or b) replacing all inadequate ITs with units capable of covering the entire frequency range between 50 Hz and 150 kHz. While both solutions entail considerable challenges and expenses, their phased implementation over several years could align with the economic and physical constraints of the system operator.
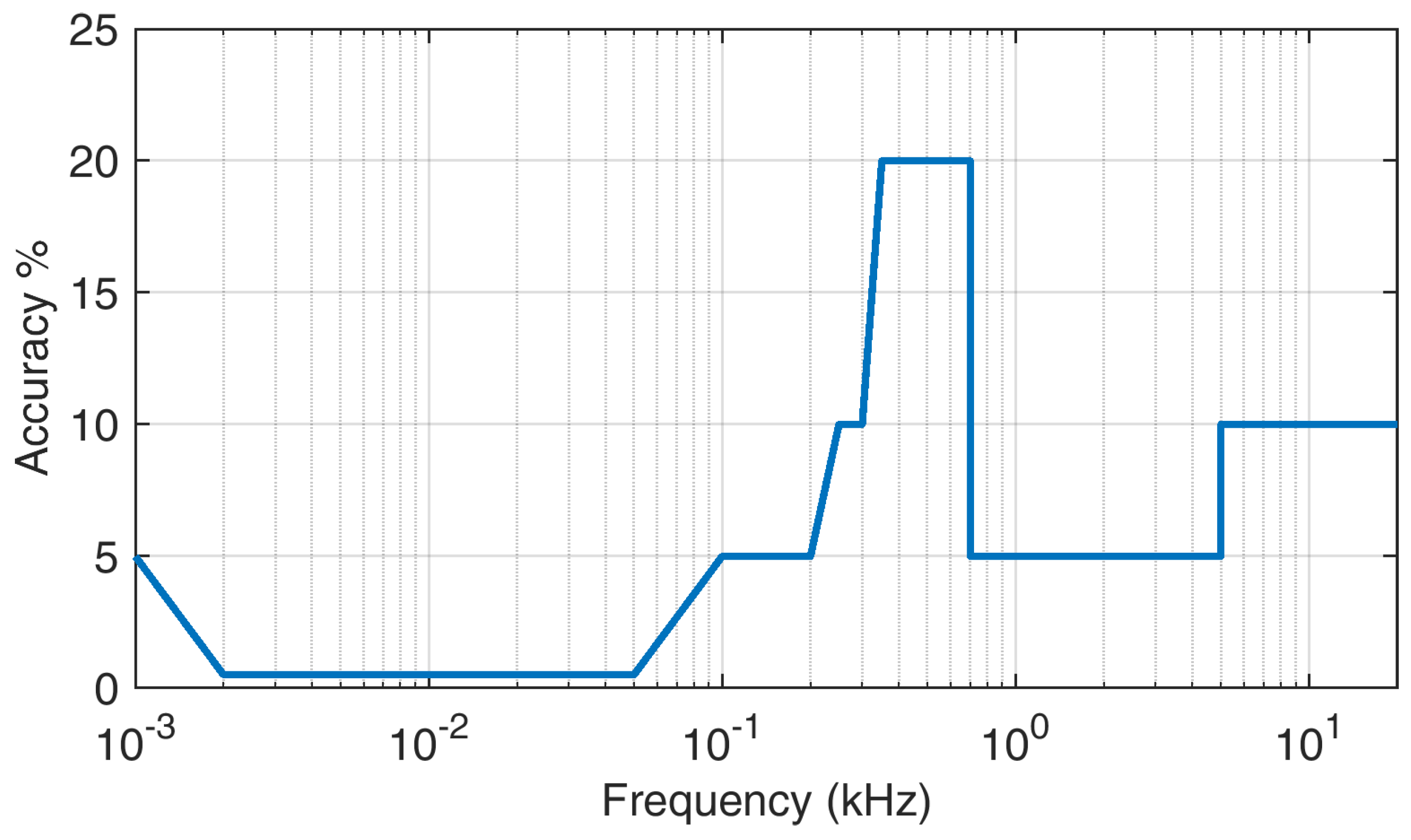
  • Accuracy. Measurement accuracy is not only another way of describing the sensitivity problem, but it is also crucial when small and large signals combine onto the same IT sensor at the same time [64]. Figure 6 provides a summary of the current situation, derived from the IEC 61869-6 [59] and related documents, for all frequency sub-intervals considered in the standard. The curve shows that accuracy limits presently extend up to 20 kHz, with an average accuracy ranging from 5 % to 10 %. Similar indications are strongly necessary also for frequencies above 20 kHz to cover entirely the SH interval, but need to be determined with a careful trade-off of all physical and practical limitations of these devices.

5. Conclusions

Supraharmonics are a new kind of distortion that is receiving more and ore attention for a variety of reasons, related to their intensity, time-frequency behavior and sometimes unexpected negative effects. This work has discussed the latter from different viewpoints: simple conduction losses (such as caused by skin effect and proximity effect, verifying the validity of the known formulas in the SH interval), dielectric losses and aging, including a particular form of stress at MV cable joints, influence on partial discharge phenomena (also causing aging of dielectrics) and interference to equipment and in particular to PLC devices. The objective was twofold: listing and describing all relevant negative effects in order to derive suitable limits for SH components and assessment methods, and as a consequence derive accuracy requirement and in general minimum performance for measuring instruments (in particular ITs, considering the occurrence of many negative effects also at the MV level).
The size of analyzed literature is significant and the overall set of works has been reduced to 81 relevant items on which the present work is based. A few research items that are not strictly related to SH, but support the discussion, have not been counted (such as the harmonic standards, works on power dissipation caused by harmonics, and so on).
Section 4 has provided indications for limits with respect to interference to PLC, to power losses and MV cable termination stress, judged as the most relevant among the reviewed ones. The most conservative turn out to be the limits providing protection against interference, set to values between 0.1 V and 1 V, whereas power losses and MV cable termination stress are satisfactorily addressed with limits in the order of some % (corresponding to some V in LV grids and several tens of V up to a hundred for MV grids).
At the moment ITs have standardized performance up to 20 kHz and accuracy specifications are such that in some cases provided limits cannot be verified, not to mention assessing the contribution of single sources (at a fraction of the respective limits). The effort for IT standardization should be thus directed to extend the frequency interval to cover comprehensively SH phenomena and to target the limits in the order of a fraction of V with less than 0.1 % accuracy figures. Technically speaking the latter may be achieved with new ITs by providing specific devices for the SH range (rejecting by construction Dc and mains fundamental) or improved devices with dramatically improved dynamic range, accompanied, hoewver, by digitizing systems with simlar performance.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yang, K.; Bollen, M.H.J.; Larsson, E.O.A. Aggregation and Amplification of Wind-Turbine Harmonic Emission in a Wind Park. IEEE Transactions on Power Delivery 2015, 30, 791–799. [Google Scholar] [CrossRef]
  2. Novitskiy, A.; Schlegel, S.; Westermann, D. Measurements and Analysis of Supraharmonic Influences in a MV/LV Network Containing Renewable Energy Sources. Electric Power Quality and Supply Reliability Conference (PQ) & Symposium on Electrical Engineering and Mechatronics (SEEM). IEEE, 2019. [CrossRef]
  3. Busatto, T.; Larsson, A.; Rönnberg, S.; Bollen, M. Supraharmonics Emission Assessment of Multi-level Converters Applied for Photovoltaic Grid-Connected Inverters. Renewable Energy and Power Quality Journal 2017, 1, 143–148. [Google Scholar] [CrossRef]
  4. Darmawardana, D.; Perera, S.; Meyer, J.; Robinson, D.; Jayatunga, U.; Elphick, S. Development of high frequency (Supraharmonic) models of small-scale (<5 kW), single-phase, grid-tied PV inverters based on laboratory experiments. Electric Power Systems Research 2019, 177, 105990. [Google Scholar] [CrossRef]
  5. Torquato, R.; Hax, G.R.T.; Freitas, W.; Nassif, A. Impact Assessment of High-Frequency Distortions Produced by PV Inverters. IEEE Transactions on Power Delivery 2021, 36, 2978–2987. [Google Scholar] [CrossRef]
  6. Sun, Y.; Jong, E.D.; Cuk, V.; Cobben, J. Ultra fast charging station harmonic resonance analysis in the Dutch MV grid: application of power converter harmonic model. CIRED - Open Access Proceedings Journal 2017, 2017, 879–882. [Google Scholar] [CrossRef]
  7. Cassano, S.; Silvestro, F.; Jaeger, E.D.; Leroi, C. Modeling of harmonic propagation of fast DC EV charging station in a Low Voltage network. 2019 IEEE Milan PowerTech. IEEE, 2019. [CrossRef]
  8. Chen, F.; Zhong, Q.; Zhang, H.; Zhu, M.; Müller, S.; Meyer, J.; Huang, W. Survey of harmonic and supraharmonic emission of fast charging stations for electric vehicles in China and Germany. CIRED 2021 - The 26th International Conference and Exhibition on Electricity Distribution. Institution of Engineering and Technology, 2021. [CrossRef]
  9. Alfieri, L.; Bracale, A.; Carpinelli, G.; Larsson, A. Accurate assessment of waveform distortions up to 150 kHz due to fluorescent lamps. 2017 6th International Conference on Clean Electrical Power (ICCEP). IEEE, 2017. [CrossRef]
  10. Li, T.; Rong, B.; Wu, Z.; Huang, J.; Huang, K. Research on supraharmonic emission characteristics and influence factors of two-stage single-phase frequency converter. Energy Reports 2023, 9, 1212–1224. [Google Scholar] [CrossRef]
  11. Gil-De-Castro, A.; Medina-Gracia, R.; Ronnberg, S.; Blanco, A.; Meyer, J. Differences in the performance between CFL and LED lamps under different voltage distortions. 2018 18th International Conference on Harmonics and Quality of Power (ICHQP). IEEE, 2018. [CrossRef]
  12. Sakar, S.; Ronnberg, S.; Bollen, M. Interferences in AC–DC LED Drivers Exposed to Voltage Disturbances in the Frequency Range 2–150 kHz. IEEE Transactions on Power Electronics 2019, 34, 11171–11181. [Google Scholar] [CrossRef]
  13. Knenicky, M.; Prochazka, R.; Hlavacek, J.; Sefl, O. Impact of High-Frequency Voltage Distortion Emitted by Large Photovoltaic Power Plant on Medium Voltage Cable Systems. IEEE Transactions on Power Delivery 2021, 36, 1882–1891. [Google Scholar] [CrossRef]
  14. Sefl, O. Influence of supraharmonics on aging rate of polymeric insulation materials. PhD thesis, Czech Technical University in Prague, 2021.
  15. Mariscotti, A. Power Quality Phenomena, Standards, and Proposed Metrics for DC Grids. Energies 2021, 14, 6453. [Google Scholar] [CrossRef]
  16. Palmer, J.A.; Degeneff, R.C.; McKernan, T.M.; Halleran, T.M. Pipe-type cable ampacities in the presence of harmonics. IEEE Transactions on Power Delivery 1993, 8, 1689–1695. [Google Scholar] [CrossRef]
  17. Espin-Delgado, A.; Letha, S.S.; Ronnberg, S.K.; Bollen, M.H.J. Failure of MV Cable Terminations Due to Supraharmonic Voltages: A Risk Indicator. IEEE Open Journal of Industry Applications 2020, 1, 42–51. [Google Scholar] [CrossRef]
  18. Klatt, M.; Kaiser, F.; Meyer, J.; Lakenbrink, C.; Gayner, C. Measurement and simulation of supraharmonic resonances in public Low Voltage networks. CIRED, 2019. [CrossRef]
  19. Letha, S.S.; Delgado, A.E.; Rönnberg, S.K.; Bollen, M.H.J. Evaluation of Medium Voltage Network for Propagation of Supraharmonics Resonance. Energies 2021, 14, 1093. [Google Scholar] [CrossRef]
  20. Bhagat, S.; Mariscotti, A.; Simonazzi, M.; Sandrolini, L. Variability of Conducted Emissions of EV Chargers due to Mutual Effects on a DC Grid. 2023 International Symposium on Electromagnetic Compatibility – EMC Europe. IEEE, 2023. [CrossRef]
  21. Ronnberg, S.; Wahlberg, M.; Bollen, M.; Lundmark, C. Equipment currents in the frequency range 9–95 kHz, measured in a realistic environment. 13th International Conference on Harmonics and Quality of Power. IEEE, 2008. [CrossRef]
  22. Espin-Delgado, A.; Rönnberg, S.; Busatto, T.; Ravindran, V.; Bollen, M. Summation law for supraharmonic currents (2–150 kHz) in low-voltage installations. Electric Power Systems Research 2020, 184, 106325. [Google Scholar] [CrossRef]
  23. Collin, A.J.; Femine, A.D.; Landi, C.; Langella, R.; Luiso, M.; Testa, A. The Role of Supply Conditions on the Measurement of High-Frequency Emissions. IEEE Transactions on Instrumentation and Measurement 2020, 69, 6667–6676. [Google Scholar] [CrossRef]
  24. Mariscotti, A.; Sandrolini, L.; Pasini, G. Variability Caused by Setup and Operating Conditions for Conducted EMI of Switched Mode Power Supplies Over the 2–1000 kHz Interval. IEEE Transactions on Instrumentation and Measurement 2022, 71, 1–9. [Google Scholar] [CrossRef]
  25. IEC 61869-14. Instrument Transformers — Additional requirements for current transformers for DC applications. IEC, Geneva, Switzwerland, 2019.
  26. Novitskiy, A.; Schlegel, S.; Westermann, D. Estimation of Power Losses Caused by Supraharmonics. E3S Web of Conferences 2020, 209, 07008. [Google Scholar] [CrossRef]
  27. IEC 60287-1-1. Electric cables — Calculation of the current rating. Part 1-1: Current rating equations (100 % load factor) and calculation of losses — General. IEC, Geneva, Switzwerland, 2023.
  28. Du, Y.; Burnett, J. Experimental investigation into harmonic impedance of low-voltage cables. IEE Proceedings - Generation, Transmission and Distribution 2000, 147, 322. [Google Scholar] [CrossRef]
  29. Topolski, L.; Warecki, J.; Hanzelka, Z. Methods for determining power losses in cable lines with non-linear load. Przegląd Elektrotechniczny 2018, 1, 87–92. [Google Scholar] [CrossRef]
  30. IEEE C57.110. IEEE Recommended Practice for Establishing Liquid Immersed and Dry-Type Power and Distribution Transformer Capability when Supplying Nonsinusoidal Load Currents. IEEE, New York, USA, 2018.
  31. IEC/TS 62578. Power electronics systems and equipment — Operation conditions and characteristics of active infeed converter (AIC) applications including design recommendations for their emission values below 150 kHz. IEC, Geneva, Switzwerland, 2015.
  32. Paulsson, L.; Ekehov, B.; Halen, S.; Larsson, T.; Palmqvist, L.; Edris, A.; Kidd, D.; Keri, A.; Mehraban, B. High-frequency impacts in a converter-based back-to-back tie; the eagle pass installation. IEEE Transactions on Power Delivery 2003, 18, 1410–1415. [Google Scholar] [CrossRef]
  33. de Castro, A.G.; Ronnberg, S.K.; Bollen, M.H.J. Harmonic interaction between an electric vehicle and different domestic equipment. 2014 International Symposium on Electromagnetic Compatibility. IEEE, 2014. [CrossRef]
  34. Mariscotti, A.; Sandrolini, L.; Simonazzi, M. Supraharmonic Emissions from DC Grid Connected Wireless Power Transfer Converters. Energies 2022, 15, 5229. [Google Scholar] [CrossRef]
  35. CLC/TR 50627. Study Report on Electromagnetic Interference between Electrical Equipment/Systems in the Frequency Range Below 150 kHz. CENELEC, Brussels, Belgium, 2015.
  36. CLC/TR 50669. Investigation Results on Electromagnetic Interference in the Frequency Range below 150 kHz. CENELEC, Brussels, Belgium, 2017.
  37. Slangen, T.M.H.; Lustenhouwer, B.R.F.; Cuk, V.; Cobben, J.F.G. The Effects of High-Frequency Residual Currents on the Operation of Residual Current Devices. Renewable Energy and Power Quality Journal 2021, 19, 67–72. [Google Scholar] [CrossRef]
  38. EN 61000-4-19. Electromagnetic compatibility (EMC). Part 4-19: Testing and measurement techniques — Test for immunity to conducted, differential mode disturbances and signalling in the frequency range 2 kHz to 150 kHz at a.c. power ports. CENELEC, Brussels, Belgium, 2014.
  39. Mariscotti, A. Harmonic and Supraharmonic Emissions of Plug-In Electric Vehicle Chargers. Smart Cities 2022, 5, 496–521. [Google Scholar] [CrossRef]
  40. EN 55014-1. Electromagnetic compatibility — Requirements for household appliances, electric tools and similar apparatus. Part 1: Emission. CENELEC, Brussels, Belgium, 2020.
  41. Ronnberg, S.K.; Bollen, M.H.J.; Wahlberg, M. Interaction Between Narrowband Power-Line Communication and End-User Equipment. IEEE Transactions on Power Delivery 2011, 26, 2034–2039. [Google Scholar] [CrossRef]
  42. Uribe-Pérez, N.; Angulo, I.; Hernández-Callejo, L.; Arzuaga, T.; de la Vega, D.; Arrinda, A. Study of Unwanted Emissions in the CENELEC-A Band Generated by Distributed Energy Resources and Their Influence over Narrow Band Power Line Communications. Energies 2016, 9, 1007. [Google Scholar] [CrossRef]
  43. Schottke, S.; Rademacher, S.; Meyer, J.; Schegner, P. Transfer characteristic of a MV/LV transformer in the frequency range between 2 kHz and 150 kHz. 2015 IEEE International Symposium on Electromagnetic Compatibility (EMC). IEEE, 2015. [CrossRef]
  44. Slangen, T.; de Jong, E.; Cuk, V.; Cobben, S. Transfer of supraharmonics through a MV/LV transformer. 27th International Conference on Electricity Distribution (CIRED 2023). Institution of Engineering and Technology, 2023. [CrossRef]
  45. Michalec, L.; Kostyła, P.; Leonowicz, Z. Supraharmonic Pollution Emitted by Nonlinear Loads in Power Networks — Ongoing Worldwide Research and Upcoming Challenges. Energies 2022, 16, 273. [Google Scholar] [CrossRef]
  46. EN 61000-2-2. Electromagnetic compatibility (EMC). Part 2-2: Environment — Compatibility levels for low-frequency conducted disturbances and signalling in public low-voltage power supply systems. CENELEC, Brussels, Belgium, 2019.
  47. EN 61000-2-12. Electromagnetic compatibility (EMC). Part 2-12: Environment — Compatibility levels for low-frequency conducted disturbances and signalling in public medium-voltage power supply systems. CENELEC, Brussels, Belgium, 2003.
  48. EN 61000-2-4. Electromagnetic compatibility (EMC). Part 2-4: Environment — Compatibility levels in industrial plants for low-frequency conducted disturbances. CENELEC, Brussels, Belgium, 2020.
  49. EN 50065-1. Signalling on low-voltage electrical installations in the frequency range 3 kHz to 148,5 kHz — Part 1: General requirements, frequency bands and electromagnetic disturbances. CENELEC, Brussels, Belgium, 2011.
  50. EN 61000-3-2. Electromagnetic compatibility (EMC). Part 3-2: Limits — Limits for harmonic current emissions (equipment input current ≤ 16 A per phase). CENELEC, Brussels, Belgium, 2019.
  51. EN 61000-3-12. Electromagnetic compatibility (EMC). Part 3-12: Part 3-12: Limits — Limits for harmonic currents produced by equipment connected to public low-voltage systems with input current > 16 A and ≤ 75 A perphase. CENELEC, Brussels, Belgium, 2019.
  52. Lodetti, S.; Bruna, J.; Sanz, J.F.; Melero, J.J. Characterization of the Emission of an Electric Bus Inductive Charging in the 2 kHz to 150 kHz Range. 2019 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE). IEEE, 2019. [CrossRef]
  53. IEC 61869-1. Instrument Transformers — General requirements for instrument transformers. IEC, Geneva, Switzwerland, 2023.
  54. IEC 61869-2. Instrument Transformers — Additional requirements for current transformers. IEC, Geneva, Switzwerland, 2012.
  55. IEC 61869-3. Instrument Transformers — Additional requirements for inductive voltage transformers. IEC, Geneva, Switzwerland, 2011.
  56. IEC 61869-4. Instrument Transformers — Additional requirements for combined transformers. IEC, Geneva, Switzwerland, 2014.
  57. IEC 61869-11. Instrument Transformers — Additional requirements for low-power passive voltage transformers. IEC, Geneva, Switzwerland, 2018.
  58. IEC 61869-5. Instrument Transformers — Additional requirements for capacitive voltage transformers. IEC, Geneva, Switzwerland, 2011.
  59. IEC 61869-6. Instrument Transformers — Additional requirements for low-power instrument transformers. IEC, Geneva, Switzwerland, 2016.
  60. IEC 61869-9. Instrument Transformers — Digital interface for instrument transformers. IEC, Geneva, Switzwerland, 2019.
  61. IEC 61869-10. Instrument Transformers — Additional requirements for low-power passive current transformers. IEC, Geneva, Switzwerland, 2018.
  62. IEC 61869-15. Instrument Transformers — Additional requirements for voltage transformers for DC applications. IEC, Geneva, Switzwerland, 2019.
  63. Crotti, G.; D’Avanzo, G.; Femine, A.D.; Gallo, D.; Giordano, D.; Iodice, C.; Landi, C.; Letizia, P.S.; Luiso, M.; Mazza, P. Characterization of Voltage Transformers for MV Applications Up to 150 kHz - A Preliminary Study. 2023 IEEE 13th International Workshop on Applied Measurements for Power Systems (AMPS). IEEE, 2023. [CrossRef]
  64. Crotti, G.; Giordano, D.; Letizia, P.; Signorino, D.; Iodice, C.; Luiso, M.; Mazza, P.; Palladini, D. How Undesired Non-Idealities of the Input Signal Affect the Accuracy Evaluation of Instrument Transformers at Power Frequency. 2023 IEEE 13th International Workshop on Applied Measurements for Power Systems (AMPS). IEEE, 2023. [CrossRef]
Preprints 94937 g001
Figure 1. Overview of emission levels:(blue and light blue lines) limits oif emissions from EN 50065-1 for PLCs of category 122 and 134; (purple lines) limits of emissions from the EN 50627 for various classes of converters; (green line) limits of emissions from the EN 55014-1; (pink lines) immunity test levels prescribed by the EN 61000-4-19 (level 3 and 4); (gray/black circles) AIC emissions data taken from the IEC 62578 for various categories ( > 75 A , < 75 A and “C1 and C2”); (green circles) emissions of various PV inverters taken from Uribe-Perez et al. [42]; (squares) confirmed PLC interference levels, reduced ones after mitigation (circle), with colors indicating various sources (detailed in the legend).
Figure 1. Overview of emission levels:(blue and light blue lines) limits oif emissions from EN 50065-1 for PLCs of category 122 and 134; (purple lines) limits of emissions from the EN 50627 for various classes of converters; (green line) limits of emissions from the EN 55014-1; (pink lines) immunity test levels prescribed by the EN 61000-4-19 (level 3 and 4); (gray/black circles) AIC emissions data taken from the IEC 62578 for various categories ( > 75 A , < 75 A and “C1 and C2”); (green circles) emissions of various PV inverters taken from Uribe-Perez et al. [42]; (squares) confirmed PLC interference levels, reduced ones after mitigation (circle), with colors indicating various sources (detailed in the legend).
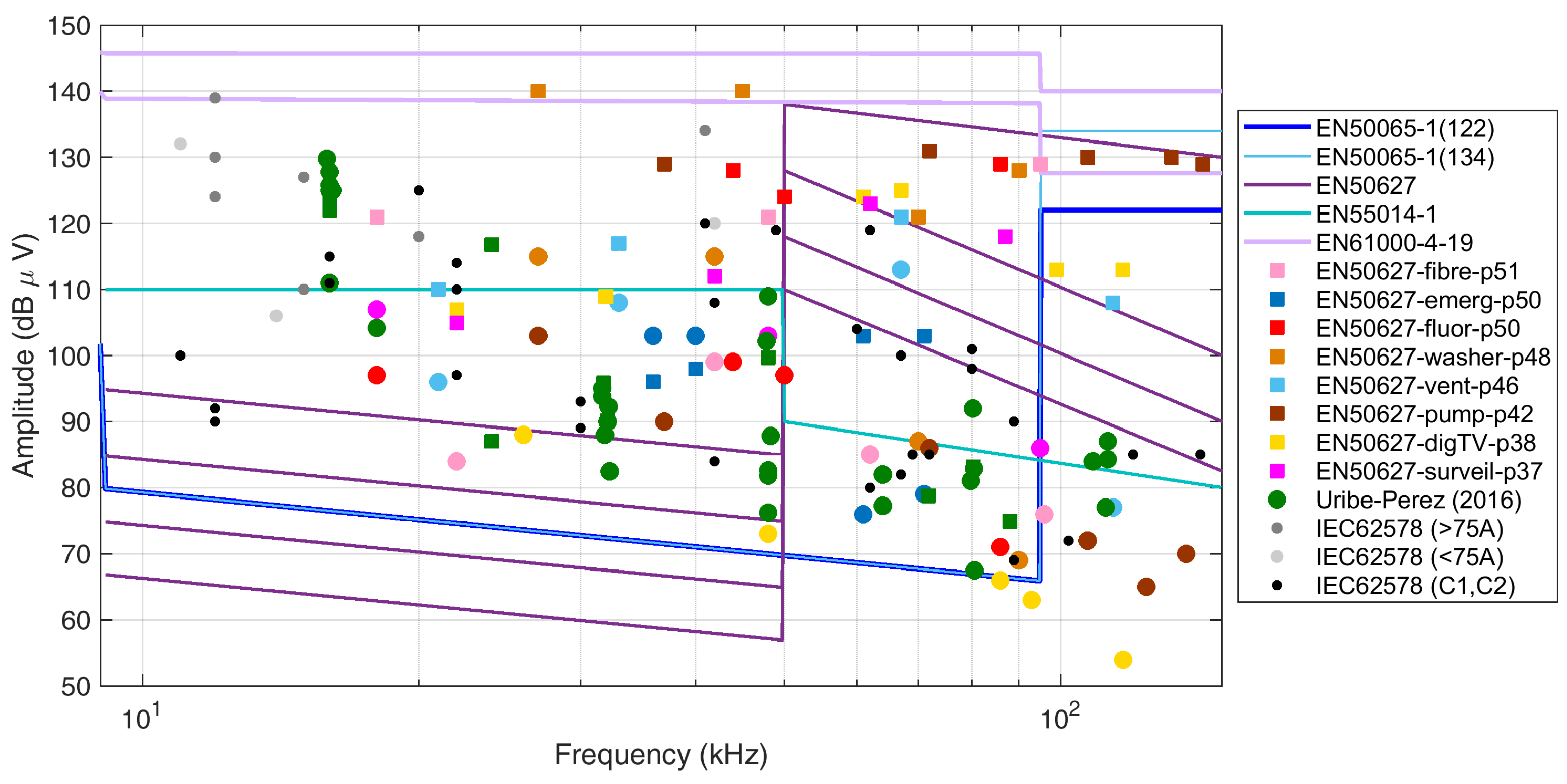
Preprints 94937 g001
Preprints 94937 g002
Figure 2. Bibliometric results: (a) number of sources through the years; (b) subdivision of sources per publication type; (c) share percentage of prevalent keywords.
Figure 2. Bibliometric results: (a) number of sources through the years; (b) subdivision of sources per publication type; (c) share percentage of prevalent keywords.
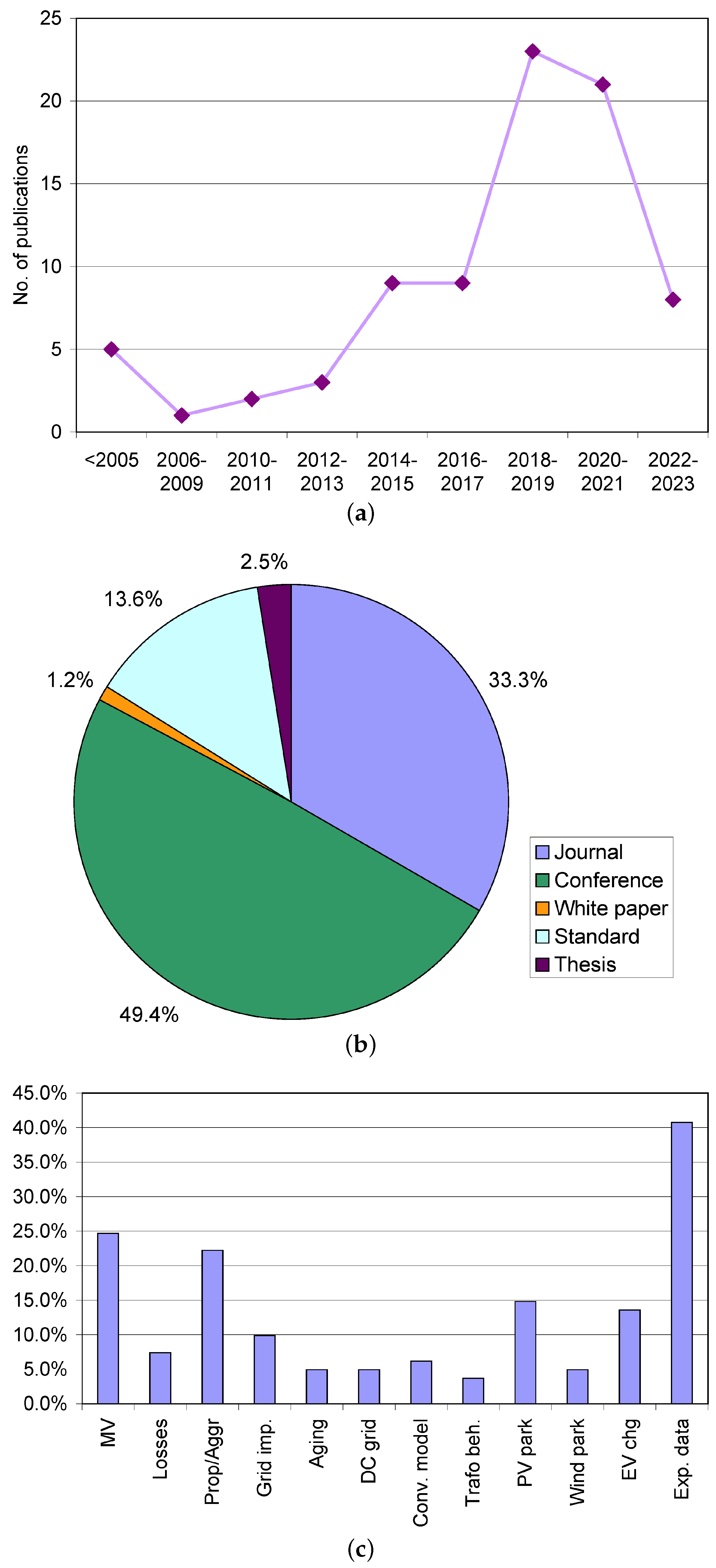
Preprints 94937 g002
Preprints 94937 g003
Figure 3. Details of the emission levels of Figure 1 with superposed proposed limit curves (in dashed and dot-dashed gray). Groups “A”, “B” and “C” are discussed in the text.
Figure 3. Details of the emission levels of Figure 1 with superposed proposed limit curves (in dashed and dot-dashed gray). Groups “A”, “B” and “C” are discussed in the text.
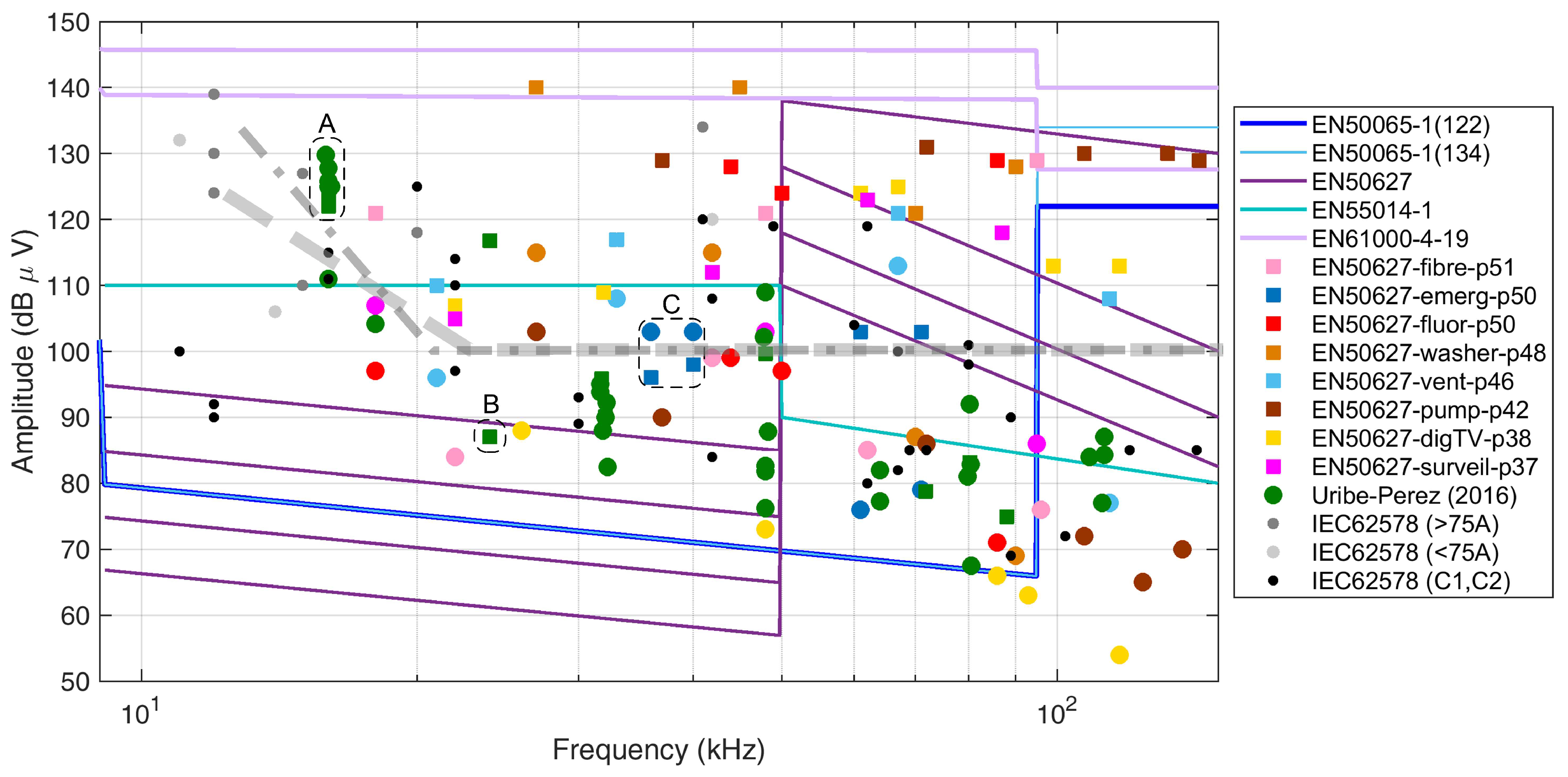
Preprints 94937 g003
Preprints 94937 g004
Figure 4. Example of SH limits for the three sub-bands (2kHz–9kHz, 9kHz–50kHz and 50kHz–150kHz): current (light blue) and derived voltage distortion value (light brown). On the left-hand side the corresponding current limits for the harmonic interval are visible. (a) Residential environment (reference standard IEC 61000-3-2 [50], Class D equipment); (b) Industrial environment (reference standard IEC 61000-3-12 [51]).
Figure 4. Example of SH limits for the three sub-bands (2kHz–9kHz, 9kHz–50kHz and 50kHz–150kHz): current (light blue) and derived voltage distortion value (light brown). On the left-hand side the corresponding current limits for the harmonic interval are visible. (a) Residential environment (reference standard IEC 61000-3-2 [50], Class D equipment); (b) Industrial environment (reference standard IEC 61000-3-12 [51]).
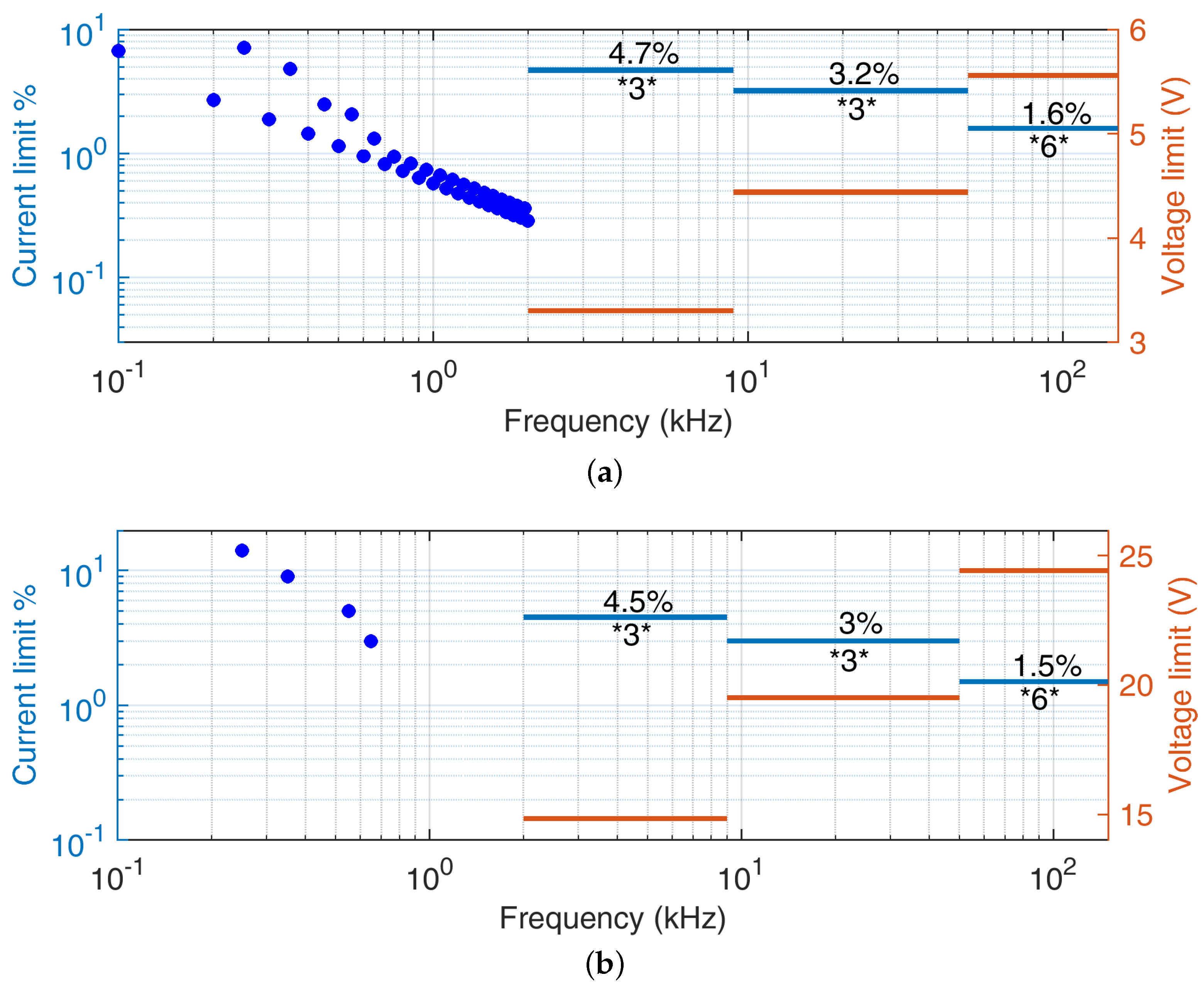
Preprints 94937 g004
Preprints 94937 g005
Figure 5. Limit curves for the percent SH voltage distortion based on the assumed Q l i m = 20 of [17] and for m values covering m < = 0.25 , 0.25 < m < = 0.5 , 0.5 < m < = 1.0 and m > 1.0 , with meaning of colors as in [17], namely “no risk”, “moderate risk”, “significant risk” and “unacceptable”.
Figure 5. Limit curves for the percent SH voltage distortion based on the assumed Q l i m = 20 of [17] and for m values covering m < = 0.25 , 0.25 < m < = 0.5 , 0.5 < m < = 1.0 and m > 1.0 , with meaning of colors as in [17], namely “no risk”, “moderate risk”, “significant risk” and “unacceptable”.
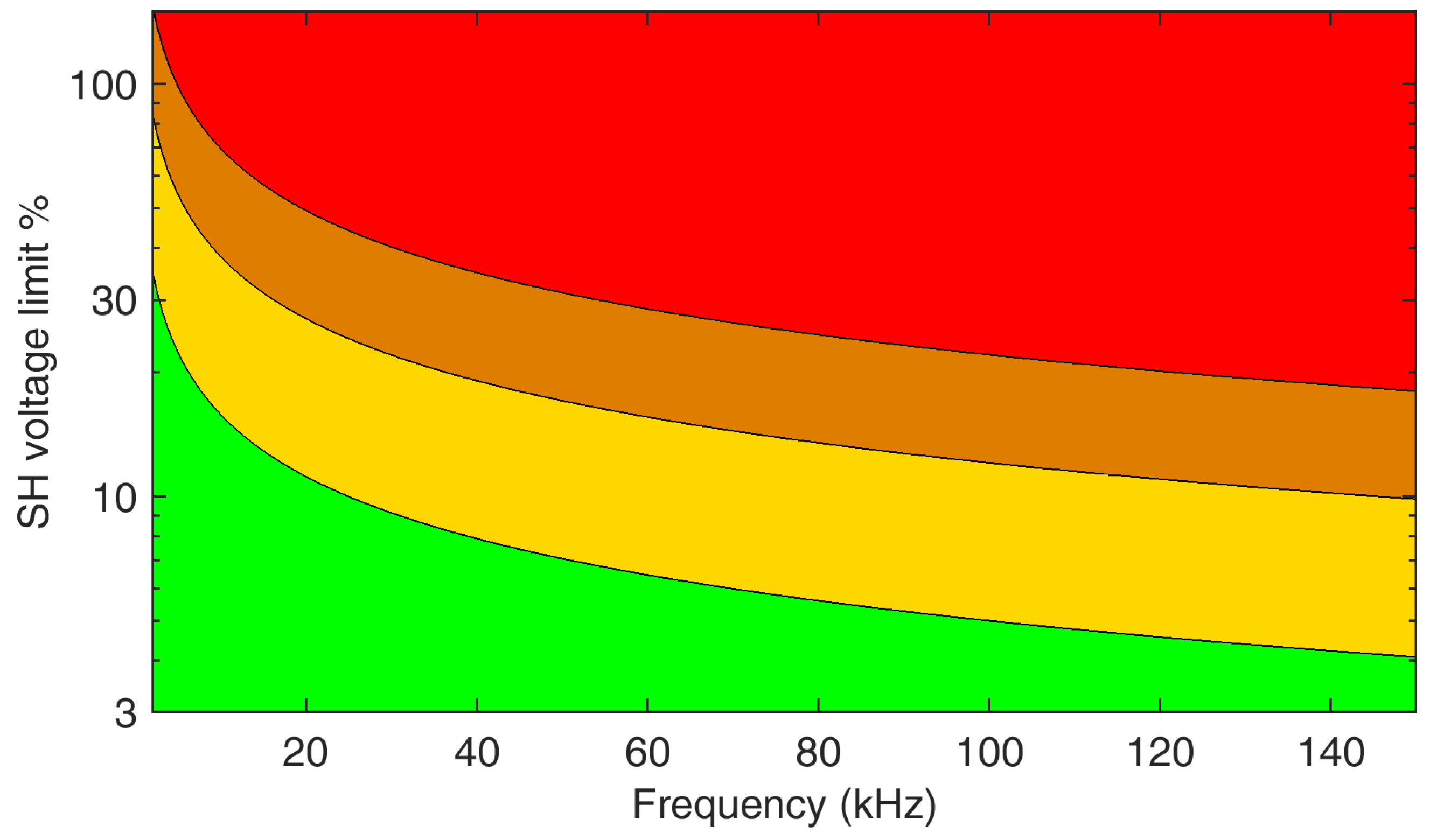
Preprints 94937 g005
Preprints 94937 g006
Figure 6. Accuracy limits vs. frequency as specified in the IEC 61869 standards (for the moment limited to 20 kHz.
Figure 6. Accuracy limits vs. frequency as specified in the IEC 61869 standards (for the moment limited to 20 kHz.
Preprints 94937 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated